HydroMuseum – Частота вращения

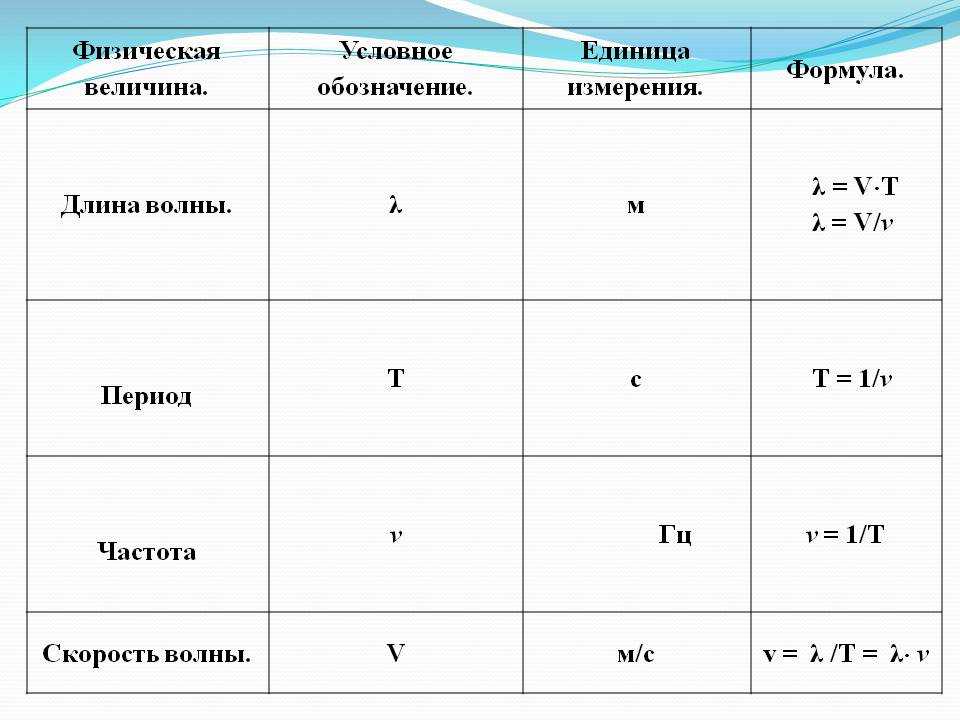
Частота вращения—физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — υ, f, ω или F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка «Сигналы, помехи, ошибки».

В теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается

ω). Циклическая частота связана с частотой колебаний соотношением ω=2πf. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с⁻¹, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т.  д.

Другие величины, связанные с частотой

• Ширина полосы частот — f_max − f_min
• Частотный интервал — log(f_max /f_min)
• Девиация частоты —Δf/2
• Период — 1/f
• Длина волны — υ/f
• Угловая скорость (скорость вращения) — dφ/ dt; 2πF_BP

Метрологические аспекты

Измерения

Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра.

Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др.

Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.

Эталоны

Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ

Вторичный эталон единицы времени и частоты ВЭТ 1-10-82 — находится в СНИИМ (Новосибирск)

5 важных фактов, которые вы должны знать

Периодическое движение — это повторяющееся и непрерывное движение объекта через равные промежутки времени. Простое гармоническое движение — это разновидность периодического движения.

Линейная частота — это количество колебаний, повторений или колебаний, совершаемых объектом или телом за единицу секунды. Величина, обратная периоду времени, дает частоту. Слово линейная частота используется, чтобы отличить ее от пространственной частоты и угловой частоты.  

Время, которое требуется объекту для покрытия полного цикла, — это период времени. Например: если камертон вибрирует 5 раз в секунду, то линейная частота будет 5 Гц. Частота играет жизненно важную роль в физике, чтобы рассказать о скорости колебаний и вибраций, таких как звуковые сигналы, радиоволны и свет.

Изображение Фото: Викинана38, ลูกตุ้ม ธรรมชาติ, CC BY-SA 4.0

Линейное частотное уравнение 

Под линейной частотой обычно понимают время, необходимое для завершения одного колебания или вибрации.^{Период времени определяет время, затрачиваемое объектом на выполнение одного цикла. Частота и период взаимосвязаны следующим образом:}

[латекс]f = \frac{1}{T}[/latex]

Для волнового уравнения линейная частота вычисляется из уравнения:

[латекс]f = \frac{c}{\lambda}[/latex]

Здесь,

c равна скорости волны

λ — длина волны. 

Линейная частота рассчитывается из соотношения:

ω = 2πf

Линейные единицы измерения частоты

Для колебаний, волн и простая гармоника движения, частота – это количество колебаний в одну секунду. {-1}[/латекс]

Линейный символ частоты 

Частота говорит о колебаниях или циклах, совершенных за единицу времени. Жизненно важно определить природу и характер многих важных физических понятий, таких как колебания, периодическое движение, волны, свет и изменение тока и напряжения. 

Стандартный символ, который используется для представления линейной частоты, — f. Обычно для колебания и SHM используется f. Но для света и волн есть другой символ, обозначающий частоту. Это греческий символ ν.  

Угловая частота против линейной частоты 

Угловая частота колебания и его линейная частота — это два разных понятия. Для колеблющегося объекта угловая частота говорит об изменении фазы, которое представляет собой угловое смещение. В то же время частота говорит о совершении колебания за единицу времени.

Он дает соотношение между частотой и угловая частота колебания. Для простого гармонического движения или просто колебаний формула угловой частоты получается путем умножения линейной частоты на угол, который покрывают колеблющиеся частицы. Для одного полного цикла угол равен 2π.

Например, мяч колеблется и совершает 5 оборотов за 1 секунду. Тогда частота будет 5 Гц, а угловая частота будет 10π рад / с. 

Угловая частота	Линейная частота
Изменение угла колеблющегося тела или просто угловое смещение известно как угловая частота.	Колебания или колебания, завершенные за одну секунду, — это частота объекта или частицы.
Угловая частота обозначается символом ω.	Линейная частота обозначается буквой ν.
Его стандартная единица измерения — радиан в секунду (рад / с).	Единица измерения частоты в системе СИ — герц (Гц).
Формула для угловой частоты: ω = 2πf или [латекс]\омега = \фрак{2 \пи}{Т}[/латекс]	Уравнение для линейной частоты: [латекс]f = \frac{1}{T}[/latex]

Разница между угловой частотой и линейной частотой

Как найти линейную частоту 

Чтобы найти линейную частоту любого вибрирующего объекта или колеблющегося тела, используются следующие формулы: 

[латекс]f = \frac{1}{T}[/latex]

f — частота, а T — период

Or

[латекс]f = \frac{c}{\lambda}[/latex]

c — скорость волны, а λ — длина волны.  

Изображение Фото: Штюндле (модификация Идеофаг), Маятник без текста, CC BY-SA 4.0

Например, маятник колеблется с периодом 0.5 секунды. Тогда частота маятника будет:

[латекс]f = \frac{1}{T}[/latex]

[латекс]f = \frac{1}{0.5}[/latex]

[латекс]f = \frac{10}{5}[/latex]

[латекс]f = 2 Гц[/латекс]

Во втором случае, если скорость волны задана как 320 м / с, а соответствующая длина волны задана как 8 м, то частота будет: 

[латекс]f = \frac{c}{\lambda}[/latex]

[латекс]f = \frac{320}{8}[/latex]

[латекс]f = 4 Гц[/латекс]

При расчете частоты важно сохранять все величины в их стандартных единицах измерения, например, секунды для времени, для длины это должен быть метр. 

Теперь предположим, что мяч делает 360 циклов за одну минуту, тогда частота будет:

[латекс]f = \frac{360}{1 мин}[/latex]

[латекс]f = \frac{360}{60 с}[/latex]

[латекс]f = 6 Гц[/латекс]

Часто задаваемые вопросы (FAQ)

Объясните частоту простыми словами.  

В физике линейная частота определяется как количество колебания или колебания завершаются за одну секунду. 

Частота в простейшем понимании — это количество появлений какого-либо явления. Предположим, мяч отскакивает 8 раз, тогда частота прыгающего мяча составляет 8 Гц. 

Угловая частота совпадает с линейной частотой? 

Нет, угловая частота и линейная частота — это два разных физических понятия. 

Угловая частота говорит об угловом смещении или изменении фазы объекта. В то же время линейная частота говорит о количестве колебаний или вибраций, которые объект покрывает за единицу времени.

Как связаны линейная частота и угловая частота?

Угловая частота и линейная частота связаны формулой:

ω = 2πf

ω — угловая частота 

f — линейная частота 

Символ частоты ν или f? 

Оба ν и f используются для представления частоты. Для волновой системы используется ν, тогда как для других колеблющихся тел, таких как маятник и пружина, используется символ f. 

Какое общее правило частоты? 

Частота дает представление о циклах, совершаемых колеблющимся телом за одну секунду. 

Общая формула или правило для определения значения частоты дается как:

[латекс]f = \frac{1}{T}[/latex]

Т представляет период. Он показывает время, необходимое для завершения одного полного колебания. Единица измерения частоты — герц (Гц).

Как рассчитать частоту?

Для расчета частоты используется формула f = 1 / T и f = c / λ.

Во-первых, чтобы вычислить частоту, все значения времени или длины волны и скорости должны быть в их стандартных единицах измерения после того, как преобразование заменяет значения в соответствующих уравнениях и выполняет упрощения. 

Например, тело совершает одно колебание за ½ минуты. Тогда первым шагом будет преобразование периода в секунды, то есть:

[латекс]T = \frac{1}{2} мин[/latex]

[latex]T = \frac{1}{2} \times 60 секунд[/latex]

[латекс]T = 30 секунд[/латекс]

Теперь подставляя значение T в формулу, получаем:

[латекс]f = \frac{1}{T}[/latex]

[латекс]f = \frac{1}{30}[/latex]

[латекс]f = 0.03 Гц[/латекс]

Гравитационная волна | Детекторы, обнаружение и скорость

Космическая антенна лазерного интерферометра (LISA)

Посмотреть все СМИ

Ключевые люди:

Альберт Эйнштейн Кип Торн Райнер Вайс Барри С. Бэриш Рассел Алан Халс

Похожие темы:

сила тяжести волна общая теория относительности гравитация

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

Знать об открытии гравитационных волн и их роли в раскрытии тайн Вселенной

Посмотреть все видео к этой статье поле в виде волн. Согласно общей теории относительности кривизна пространства-времени определяется распределением масс, а движение масс определяется кривизной. Вследствие этого вариации гравитационного поля передаются с места на место в виде волн, точно так же, как вариации электромагнитного поля распространяются в виде волн. Если массы, являющиеся источником поля, изменяются со временем, они излучают энергию в виде волн кривизны поля. Гравитационные волны были впервые обнаружены лазерным интерферометром гравитационно-волновой обсерватории (LIGO) в 2015 году9.0003

Теория и источники

На первый взгляд, между гравитацией и электромагнетизмом есть много общего. Например, закон Ньютона для гравитационной силы между двумя точечными массами и закон Кулона для электрической силы между двумя точечными зарядами показывают, что обе силы изменяются пропорционально обратному квадрату расстояния. Тем не менее, в теории электромагнетизма шотландского физика Джеймса Клерка Максвелла ускоренные заряды испускают сигналы (электромагнитное излучение), которые движутся со скоростью света, тогда как в теории гравитации Ньютона ускоренные массы передают информацию (действие на расстоянии), которая движется с бесконечной скоростью.

Эта дихотомия исправляется теорией гравитации Эйнштейна, согласно которой ускоренные массы также производят сигналы (гравитационные волны), которые распространяются только со скоростью света. И точно так же, как электромагнитные волны могут дать о себе знать, толкая туда-сюда электрически заряженные тела, так и гравитационные волны можно обнаружить, дергая туда-сюда массивные тела. Однако, поскольку связь гравитационных сил с массами по своей сути намного слабее, чем связь электромагнитных сил с зарядами, генерация и обнаружение гравитационного излучения намного сложнее, чем электромагнитного излучения. Действительно, прошло почти 100 лет после открытия Эйнштейном общей теории относительности в 1919 г.16, что имело место прямое обнаружение гравитационных волн.

Тест «Британника»

Физика и законы природы

Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.

Тем не менее были веские основания полагать, что такое излучение существовало. Наиболее убедительны радиохронометрические наблюдения пульсара PSR 1913+16, расположенного в двойной звездной системе с периодом обращения 7,75 часа. Этот объект, обнаруженный в 1974, имеет период импульса около 59 миллисекунд, который изменяется примерно на одну тысячную часть каждые 7,75 часа. Интерпретируемые как доплеровские сдвиги, эти вариации подразумевают орбитальные скорости порядка 1/1000 скорости света. Несинусоидальная форма кривой скорости во времени позволяет сделать вывод, что орбита совершенно некруговая (действительно, это эллипс с эксцентриситетом 0,62, длинная ось которого прецессирует в пространстве на 4,2° в год). Система состоит из двух нейтронных звезд, каждая из которых имеет массу около 1,4 массы Солнца, с расстоянием между большими полуосями всего 2,8 радиуса Солнца. Согласно общей теории относительности Эйнштейна, такая система должна терять орбитальную энергию из-за излучения гравитационных волн со скоростью, которая заставит их скручиваться по спирали в масштабе времени примерно 3 × 10

8 лет. Наблюдаемое уменьшение периода обращения за годы, прошедшие после открытия двойного пульсара, действительно указывает на то, что две звезды движутся по спирали навстречу друг другу точно с предсказанной скоростью. Гравитационное излучение — единственное известное средство, с помощью которого это могло произойти. (Американские физики Рассел Халс и Джозеф Х. Тейлор-младший получили Нобелевскую премию по физике в 1993 г. за открытие PSR 1913+16.)

Схлопывание ядра массивной звезды с образованием нейтронной звезды перед взрывом сверхновой, если оно происходит несферически-симметричным образом, должно обеспечить мощный всплеск гравитационного излучения. Простые оценки дают высвобождение доли дефицита массы-энергии, примерно 10

53 эрг, при этом излучение в основном выходит в периоды волн между периодом колебаний нейтронной звезды, примерно 0,3 мс, и временем затухания гравитационного излучения, примерно 300 мс.

Детекторы и наблюдения

Три типа детекторов были разработаны для поиска гравитационного излучения, которое очень слабое. Изменения кривизны пространства-времени соответствовали бы расширению в одном направлении и сжатию под прямым углом к ​​этому направлению. Одна схема, впервые опробованная около 1960, использовал массивный цилиндр, который мог быть приведен в механическое колебание гравитационным сигналом. Авторы этого аппарата утверждали, что сигналы были обнаружены, но их утверждение не было подтверждено.

Во второй схеме оптический интерферометр устанавливается со свободно подвешенными отражателями на концах длинных путей, расположенных под прямым углом друг к другу. Сдвиги интерференционных полос, соответствующие увеличению длины одного плеча и уменьшению длины другого, указывали бы на прохождение гравитационных волн. Одним из таких интерферометров является лазерная интерферометрическая гравитационно-волновая обсерватория (LIGO), которая состоит из двух интерферометров с длиной плеча 4 км (2 мили), один в Хэнфорде, штат Вашингтон, а другой в Ливингстоне, штат Луизиана. LIGO была первой обсерваторией, которая напрямую обнаружила гравитационные волны. 14 сентября 2015 года он наблюдал две черные дыры на расстоянии 1,3 миллиарда световых лет от нас, которые находились на расстоянии 36 и 29раз превышает массу Солнца, скручиваясь по спирали внутрь, образуя новую черную дыру в 62 массы Солнца. Остальные три массы Солнца были преобразованы в гравитационные волны.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Планируется третья схема, усовершенствованная космическая антенна с лазерным интерферометром (eLISA), в которой используются три отдельных, но не независимых интерферометра, установленных на трех космических кораблях, расположенных в углах треугольника со сторонами около 5 миллионов км (3 миллиона миль). . Миссия по тестированию технологии eLISA, LISA Pathfinder, была запущена в 2015 г.

Эта статья была недавно пересмотрена и обновлена ​​Робертом Льюисом.

Частота и таблицы частот

Частота конкретного значения данных является количество раз, когда значение данных встречается.

Например, если четыре студента набрали 80 баллов по математике, и тогда говорят, что счет 80 имеет частоту 4. Частота значения данных часто обозначается цифрой 9.0071 ф .

Таблица частот создается путем упорядочивания значений собранных данных в порядке возрастания с соответствующими им частотами.

Пример 5

Оценки, выставленные за задание для класса 8 класса из 20 студентов были следующими:
     6     7 5     7 7     8 7     6 97
     4     10 6     8 8     9 5     6 4     8

Представьте эту информацию в таблице частот.

Решение:

Для построения таблицы частот поступаем следующим образом:

Шаг 1:

Создайте таблицу с тремя столбцами. Первый столбец показывает, что упорядочивается в порядке возрастания (т.е. метки). самая низкая оценка – 4. Итак, начните с 4 в первом столбце, как показано ниже.

Шаг 2:

Просмотрите список меток. Первая отметка в list равно 6, поэтому поставьте отметку против 6 во втором столбце. вторая отметка в списке — 7, поэтому поставьте итоговую отметку против 7 во второй столбец. Третья отметка в списке — 5, поэтому поставьте итоговую отметку против 5. в третьем столбце, как показано ниже.

Продолжаем этот процесс до тех пор, пока все метки в списке не будут подсчитано.

Шаг 3:

Подсчитайте количество отметок для каждой отметки и запишите их в третьем столбце. Готовая таблица частот выглядит следующим образом:

Обычно:

Мы используем следующие шаги для построения таблицы частот:

Шаг 1:

Создайте таблицу с тремя столбцами. Затем в первый столбец, запишите все значения данных в порядке возрастания величины.

Шаг 2:

Чтобы заполнить второй столбец, просмотрите список данных значений и поставьте одну метку в соответствующем месте второго столбец для каждого значения данных. Когда пятый счет достигнут для отметку, проведите горизонтальную линию через первые четыре контрольные отметки, как показано для 7 в приведенной выше таблице частот. Продолжаем этот процесс, пока все значения данных в списке подсчитываются.

Шаг 3:

Подсчитайте количество контрольных меток для каждого значения данных и запишите его в третью колонку.

Интервалы классов (или группы)

Когда набор значений данных разбросан, трудно настроить частотную таблицу для каждого значения данных, так как их будет слишком много строки в таблице. Итак, мы группируем данные в интервалов классов (или группы), чтобы помочь нам организовать, интерпретировать и проанализировать данные.

В идеале у нас должно быть от пяти до десяти строк в таблица частот. Имейте это в виду при определении размера класса интервал (или группа).

Каждая группа начинается со значения данных, кратного группа. Например, если размер группы равен 5, то группы должно начинаться с 5, 10, 15, 20 и т.  д. Точно так же, если размер группы равно 10, то группы должны начинаться с номеров 10, 20, 30, 40 и т. д.

Частота группы (или интервала класса) — это количество значений данных, попадающих в диапазон определяется этой группой (или интервалом класса).

Пример 6

Количество звонков от автомобилистов в сутки на обочину услуга была зарегистрирована за декабрь 2003 года. Результаты следует:

Настройте таблицу частот для этого набора значений данных.

Решение:

Для построения таблицы частот поступаем следующим образом:

Шаг 1. Создайте таблицу с тремя столбцами и напишите группы данных или интервалы классов в первом столбце. Размер каждого группа 40. Таким образом, группы будут начинаться с 0, 40, 80, 120, 160 и 200 до включить все данные. Обратите внимание, что на самом деле нам нужно 6 групп (на 1 больше, чем мы первая мысль).

Шаг 2. Просмотрите список значений данных. Во-первых значение данных в списке, 28, поставить контрольную отметку против группы 0-39 в второй столбец. Для второго значения данных в списке, 122, поместите подсчет отметьте против группы 120-159 во второй колонке. Для третьих данных значение в списке, 217, поставить итоговую отметку против группы 200-239в второй столбец.

Мы продолжаем этот процесс до тех пор, пока все значения данных в наборе подсчитываются.