Частота колебаний – величина, формула, график
4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
Частота колебаний – это один из параметров, описывающих колебательные процессы в природе. Многие явления зависят от частоты, и происходят по-разному при ее изменении. Рассмотрим это понятие подробнее.
Колебания в природе
Колебания различных величин очень широко распространены в природе. Явление колебаний заключается в том, что измеряемый параметр меняет свое значение вокруг некоторого среднего.
Рис. 1. Колебания в природе.Колебания могут быть периодическими (маятник), а могут быть непериодическими (флаг на ветру). Поскольку любое непериодическое колебание может быть представлено в виде бесконечной суммы периодических, то в первую очередь изучаются периодические колебания. График таких колебаний представляет собой синусоиду, которая хорошо изучена в математике.
Маятник
Для рассмотрения базовых понятий колебательных процессов в качестве примера удобно взять маятник – подвешенную на тонкой легкой нити небольшую массу. Если ее качнуть, она начнет совершать равномерные движения.
Каждое движение маятника, начинающееся от крайней точки, и заканчивающееся в ней же, называется колебанием.
Частота колебаний
Если взять несколько маятников разной длины, можно убедиться, что они будут совершать колебания «с разной скоростью» (хотя линейная скорость груза при этом может быть одинаковой). То есть «скорость колебаний» и скорость движения груза маятника – это не одно и то же.
Для характеристики «скорости колебаний» используют специальное понятие – частоту колебаний.
Число колебаний, которое совершается за единицу времени, называется частотой колебаний. Для обозначения используется греческая буква $\nu$ («ню»).
Единица частоты колебаний в системе СИ – Герц (Гц). Один Герц – это число колебаний, происходящих в одну секунду.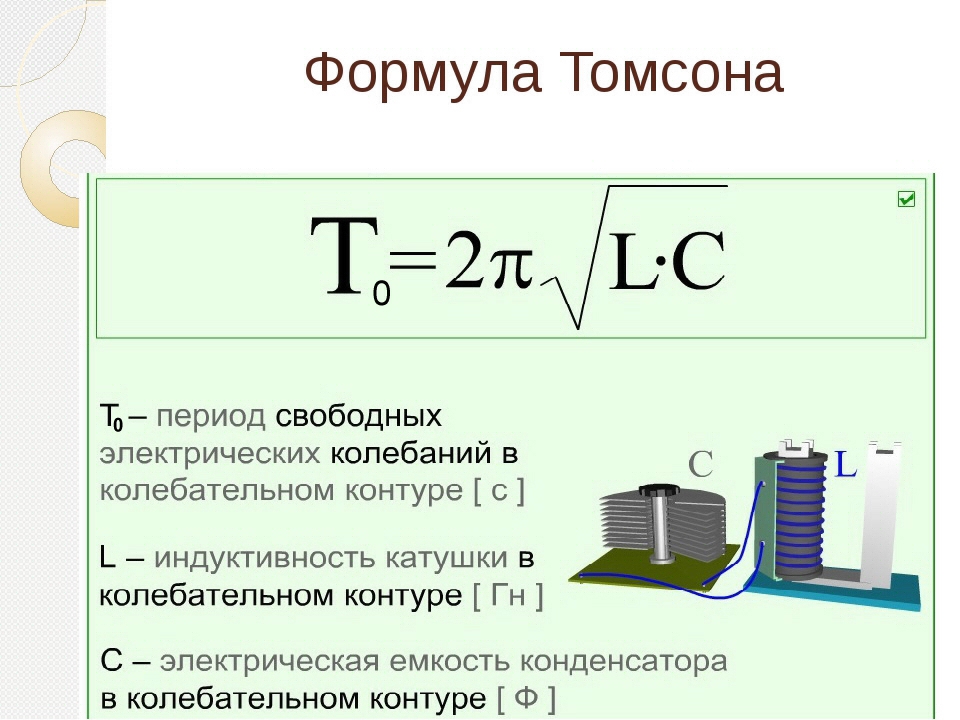 {25}$ Гц (жесткое гамма-излучение).
{25}$ Гц (жесткое гамма-излучение).
Что мы узнали?
Колебание – это изменение измеряемой величины от начальной точки до точки максимального отклонения и дальнейшее возвращение в исходную точку. Число колебаний, происходящих в единицу времени, называется частотой колебаний.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Егор Князев
4/5
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 113.
А какая ваша оценка?
Механические колебания. Механические волны. Звук
13 декабря 2021
В закладки
Обсудить
Жалоба
TG 4ЕГЭ
Пробные работы ОГЭ по физике
Вопросы для проведения теоретического зачёта в 9 классе по теме «Механические колебания. Механические волны. Звук».
Учащиеся знакомятся с вопросами заранее, начиная с момента изучения данной темы.
mehanicheskie-kolebanija.docx
1. Привести примеры механических колебаний.
2. Какова общая черта механических колебаний?
3. Что понимается под периодом механических колебаний?
4. Каков основной признак колебательного движения?
5. Назовите ещё одну общую черту механических колебаний.
6. Какие величины и каким образом изменяются при любом колебательном движении?
7. Какие колебания называются свободными?
8. Какая система называется колебательной?
9. Привести примеры колебательных систем.
11. Что такое маятник?
12. Что представляет собой нитяной маятник?
13. Что представляет собой пружинный маятник?
14. Амплитуда колебаний (определение, обозначение, единица измерения).
15. Чему равен путь, проходимый маятником за одно полное колебание?
16.
 Период колебаний (определение, обозначение, единица измерения, формула).
Период колебаний (определение, обозначение, единица измерения, формула).17. Частота колебаний (определение, обозначение, единица измерения).
18. Связь периода и частоты колебаний (формула).
19. Период и частота колебаний нитяного маятника (формулы и их пояснения).
21. Как период и частота колебаний нитяного маятника зависят от длины нити?
22. Как период и частота колебаний нитяного маятника зависят от массы груза?
23. Собственная частота колебательной системы (определение).
24. Период и частота колебаний пружинного маятника (формулы и их пояснения).
25. От чего зависит период и частота колебаний пружинного маятника?
26. Как период и частота колебаний пружинного маятника зависят от массы груза?
27. Как период и частота колебаний пружинного маятника зависят от жёсткости пружины?
28. В каком случае два маятника совершают колебания в противоположных фазах?
29. В каком случае два маятника совершат колебания в одинаковых фазах?
 В каком случае два маятника совершат колебания с определённой разностью фаз?
В каком случае два маятника совершат колебания с определённой разностью фаз?31. Чем характеризуется любое колебательное движение?
32. Гармонические колебания (определение).
33. Что представляет собой график гармонических колебаний?
34. Какие характеристики можно определить по графику гармонических колебаний?
35. Как называется кривая, соответствующая графику гармонических колебаний?
36. Гармоничные колебания (второе определение).
37. Математический маятник (определение).
38. Какие величины и каким образом изменяются при гармоничных колебаниях?
40. Второй закон Ньютона (формулировка, формула и её пояснение).
41. В каких положениях маятника смещение, скорость, ускорение, сила принимают наибольшие значения, а в каких положениях – наименьшие значения?
42. Чем обусловлены потери энергии при механических колебаниях?
43. Затухающие колебания (определение).
44. Что представляет собой график затухающих колебаний?
45.
 От чего и как зависит скорость затухания механических колебаний?
От чего и как зависит скорость затухания механических колебаний?47. Вынужденные колебания (определение).
48. Что происходит с амплитудой при возникновении вынужденных механических колебаний?
49. Когда амплитуда вынужденных механических колебаний перестаёт изменяться?
50. Когда говорят, что вынужденные механические колебания установились?
51. Чему равна частота (период) установившихся вынужденных механических колебаний?
52. Вынуждающая сила (определение).
53. Привести примеры вынужденных механических колебаний.
54. До каких пор будут происходить вынужденные механические колебания?
55. Резонанс механических колебаний (определение).
56. Что представляет собой график резонанса (резонансная кривая)?
58. Привести примеры полезного проявления механического резонанса.
59. Привести примеры вредного проявления механического резонанса.
60. Возмущения (определение).

61. Волны (определение).
62. Каково общее свойство бегущих волн?
63. Что происходит с энергией и массой вещества при распространении механической волны?
64. Упругие волны (определение).
65. Почему механические волны называются упругими?
66. Какие механические волны называются продольными?
67. Какие механические волны называются поперечными?
68. Какая деформация необходима для возникновения поперечной волны?
70. Что представляют собой продольные волны?
71. Что представляют собой поперечные волны?
72. Где могут распространяться поперечные волны?
73. Где могут распространяться продольные волны?
74. Длины волны (определение, обозначение, единица измерения, формула).
75. Связь длины волны, скорости и периода (формула и её пояснение).
76. Связь длины волны, скорости и частоты (формула и её пояснение).
77. От чего и как зависит длина волны?
78. Скорость распространения волны (2 формулы и их пояснение).

79. Источник звука (определение).
80. Каково общее свойство всех звуков?
81. Звуковые колебания (определение).
82. Ультразвуковые колебания (определение).
83. Инфразвуковые колебания (определение).
84. Применение инфра- и ультразвука.
85. Эхолокация (определение, формула и её пояснение).
86. От чего и как зависит высота звука?
87. Единицы измерения звонкости звука, уровня громкости и уровня звукового давления.
88. Шум (определение).
89. Каково влияние звука на организм человека?
90. Почему в вакууме звук не распространяется?
91. Какие тела плохо проводят звук? почему? Где и как это используется?
92. Какие тела хорошо проводят звук? почему? Где и как это используется?
94. Как возникает, распространяется и воспринимается звук?
95. Что представляет собой звук в воздухе?
96. Чему примерно равна скорость звука в воздухе?
97. Как скорость звука в газах зависит от температуры? Почему?
98.
 Как скорость звука в газах зависит от свойств среды? Почему?
Как скорость звука в газах зависит от свойств среды? Почему?99. Сравнить скорость звука в газах, жидкостях и твёрдых телах. Чем объясняются эти различия?
100. Как образуется эхо?
101. В каких случаях слышится эхо?
102. Почему это не слышно в небольшой квартире?
103. Что препятствует образованию эха?
104. Рупор (определение).
105. Почему рупор усиливает мощность звука?
106. Что представляет собой камертон? Для чего он применяется?
107. В чём заключается акустический резонанс?
108. Что такое резонатор?
109. Для чего используется резонатор? почему он усиливает звук?
110. От чего зависит тембр звука музыкальных инструментов?
111. Как происходит возникновение и усиление голоса человека?
112. Разность хода двух волн (определение).
113. Условие минимумов (формула и формулировка).
114. Условие максимумов (формула и формулировка).
115. Когерентные волны и источники (определение).
116. Интерференционная картина (определение).

117. Интерференция (определение).
118. Для каких волн наблюдается интерференция.
Автор: Добрый Александр Иванович.
Расчет длины волны и частоты и уравнение
Расчет соотношения длины волны к частоте и частоты к длине волны важен в физике и технике. Вот уравнение, связывающее длину волны и частоту, примеры расчетов и таблица общих значений.
Связь между длиной волны и частотой
Простое уравнение связывает длину волны с частотой:
v = λf
- v = скорость волны (насколько быстро волна распространяется в среде)
- повторяется)
- f = частота волны (количество волн в единицу времени)
Для света и другого электромагнитного излучения в вакууме скорость волны равна скорости света (c):
c = λf
Но скорость волны различна для других видов волн и для света, проходящего через среду.
- Свет в воздухе или вакууме: 299 792 458 метров в секунду
- Свет в воде: 224 901 000 м/с
- Звук в воздухе: 343,2 м/с
- Звук в воде (20 °C): 1 480 4 9001 м/с
Длина волны и частота обратно пропорциональны.
 С увеличением длины волны частота уменьшается. С увеличением частоты длина волны уменьшается.
С увеличением длины волны частота уменьшается. С увеличением частоты длина волны уменьшается.Как рассчитать длину волны по частоте
Измените уравнение и рассчитайте длину волны по частоте:
λ = v/f
Например, найдите длину волны музыкальной ноты A4, частота которой составляет 440 Гц.
Единственная трудность в расчетах — правильность единиц измерения. Обычно вы работаете с метрами и герцами, а затем конвертируете в другие единицы (например, нанометры, ТГц, ГГц). В этой задаче скорость волны равна скорости звука в воздухе (343,2 м/с). Частота 440 Гц. Один герц равен одному циклу (волне) в секунду, поэтому частота 440 Гц равна 440 с -1 .
λ = v/f
λ = (343,2 м/с)/(440 с -1 )
λ = 0,78 м или 78 смВ качестве другого примера найдите частоту зеленого света северного сияния , частота которого составляет 5,38 x 10 14 Гц.
Здесь уравнение: -7 m = 557,6 нм
Как рассчитать частоту по длине волны
Измените уравнение и рассчитайте частоту по длине волны:
f = v/λ
Например, найдите длину волны оранжевого света с частотой 4,8×10 14 Гц.

f = v/λ (но v равно c для света)
f = c/λ
f = (3,00 × 10 8 м/с)/(4,8 × 10 14 с -1 )
f = 6,2 x 10 -7 m = 620 нмДиаграмма длины волны и частоты
На этой диаграмме показано отношение длины волны к частоте для электромагнитного излучения:
Electromagnetic Radiation Wavelength Frequency Gamma radiation 1 pm 300 EHz X-ray 1 nm 300 PHz Ультрафиолет 100 нм 3 ФГц Видимый свет 400-700 нм 430-700 ТГц 100 μm 3 THz EHF (Extremely high frequency) 1 mm 300 GHz SHF (Super high frequency) 1 cm 30 GHz UHF ( Ultra high frequency) 1 dm 3 GHz VHF (Very high frequency) 10 m 30 MHz ELF (Extremely low frequency) 100,000 km 3 Гц Ссылки
- Ависон, Джон (1999).
 Мир физики . Нельсон Торнс. ISBN 978-0-17-438733-6.
Мир физики . Нельсон Торнс. ISBN 978-0-17-438733-6. - Кэссиди, Дэвид С.; Холтон, Джеральд Джеймс; Резерфорд, Флойд Джеймс (2002). Понимание физики . Биркхойзер. ISBN 0-387-98756-8.
- Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли. ISBN 0-201-11609-X.
Два уравнения света: Часть первая
Два уравнения света: Часть первая — λν = cДва уравнения, управляющие поведением света: часть первая
λν = cПроблемы длины волны и частоты № 1–10 Перейти ко второй части уравнения света Проблемы длины волны и частоты № 11–20 Вернуться в меню «Электроны в атомах» Есть два уравнения, касающиеся света, которые обычно преподаются в средней школе. Как правило, обоих учат без каких-либо выводов о том, почему они такие, какие они есть. Это то, что я буду делать в следующем.
Уравнение номер один: λν = c
Краткая историческая справка: я не уверен, кто написал это уравнение (или его эквивалент) первым.
 Волновая теория света берет свое начало в конце 1600-х годов и математически развивалась с начала 1800-х годов. Джеймс Клерк Максвелл в 1860-х годах первым предсказал, что свет представляет собой электромагнитную волну, и вычислил (а не измерил) ее скорость. Кстати, доказательство конечности скорости света было опубликовано в 1676 г., а первые достоверные измерения скорости света, очень близкие к современному значению, имели место в конце 1850-х гг.
Волновая теория света берет свое начало в конце 1600-х годов и математически развивалась с начала 1800-х годов. Джеймс Клерк Максвелл в 1860-х годах первым предсказал, что свет представляет собой электромагнитную волну, и вычислил (а не измерил) ее скорость. Кстати, доказательство конечности скорости света было опубликовано в 1676 г., а первые достоверные измерения скорости света, очень близкие к современному значению, имели место в конце 1850-х гг.Каждый символ в уравнении обсуждается ниже. Кроме того, прямо перед примерами упоминаются два основных типа задач, которые учителя будут задавать, используя уравнение. Рекомендую внимательно изучить этот раздел.
1) λ — греческая буква лямбда, обозначающая длину волны света. Длина волны определяется как расстояние между двумя последовательными гребнями волны. При изучении света наиболее распространенными единицами длины волны являются: метр, сантиметр, нанометр и ангстрем. Несмотря на то, что официальной единицей измерения, используемой в системе СИ, является метр, вы увидите объяснения и задачи, в которых используются остальные три.
 Реже вы увидите использование других юнитов; пикометр является наиболее распространенным среди менее часто используемых единиц длины волны. Ангстрем — это единица, не входящая в систему СИ, которую обычно включают в обсуждение единиц СИ из-за ее широкого использования.
Реже вы увидите использование других юнитов; пикометр является наиболее распространенным среди менее часто используемых единиц длины волны. Ангстрем — это единица, не входящая в систему СИ, которую обычно включают в обсуждение единиц СИ из-за ее широкого использования.Запомните следующие определения:
один сантиметр равен 10¯ 2 метр
один нанометр равен 10¯ 9 метр
один ангстрем равен 10¯ 8 сантиметрСимвол Ангстрема — Å.
Безусловно, вам нужно будет легко перемещаться из одного подразделения в другое. Например, обратите внимание, что 1 Å = 10¯ 10 метра. Это означает, что 10 Å = 1 нм. Итак, если вам дано значение Ангстрема для длины волны, а требуется нанометровое значение, разделите значение Ангстрема на 10. Если вы не можете легко переходить между различными метрическими единицами, вам лучше вернуться к изучению и практике в этой области. еще немного.
2) ν — греческая буква ню.
 Это НЕ буква v, это греческая буква nu. Это означает частоту световой волны. Частота определяется как количество волновых циклов, проходящих фиксированную контрольную точку за одну секунду. При изучении света единицей измерения частоты является герц (его символ — Гц). Один герц — это когда один полный цикл проходит фиксированную точку за одну секунду, поэтому миллион Гц — это когда миллион циклов проходит фиксированную точку за одну секунду.
Это НЕ буква v, это греческая буква nu. Это означает частоту световой волны. Частота определяется как количество волновых циклов, проходящих фиксированную контрольную точку за одну секунду. При изучении света единицей измерения частоты является герц (его символ — Гц). Один герц — это когда один полный цикл проходит фиксированную точку за одну секунду, поэтому миллион Гц — это когда миллион циклов проходит фиксированную точку за одну секунду.Следует отметить важный момент, касающийся единиц измерения в Гц. Это НЕ обычно записывается как циклы в секунду (или циклы в секунду), а только как сек¯ 1 (правильнее писать как s¯ 1 ; нужно знать оба варианта). Часть «циклы» удалена, хотя иногда вы можете столкнуться с проблемой, связанной с ее использованием.
Краткое упоминание о цикле: представьте волну, застывшую во времени и пространстве, где гребень волны точно совпадает с нашей фиксированной точкой отсчета. Теперь позвольте волне двигаться, пока следующий гребень точно не выровняется с контрольной точкой, затем зафиксируйте волну на месте.
 Это один цикл волны, и если все это произошло за одну секунду, то частота волны равна 1 Гц.
Это один цикл волны, и если все это произошло за одну секунду, то частота волны равна 1 Гц.В любом случае, единственной научно полезной частью единицы измерения является знаменатель, поэтому используется «в секунду» (помните, обычно как s¯ 1 ). Числитель «циклы» не нужен, поэтому его наличие просто понятно, и, если необходимо записать дробь, будет использоваться единица, например, 1/сек.
3) c (нижний регистр) — обозначение скорости света, скорости, с которой движется все электромагнитное излучение в идеальном вакууме. (Свет распространяется медленнее при прохождении через такие объекты, как вода, но никогда не распространяется быстрее, чем в идеальном вакууме.)
Для записи значения используются оба способа, показанные ниже. Вы должны знать оба:
3,00 x 10 8 м/с
3,00 x 10 10 см/сФактическое значение чуть меньше, но указанные выше значения обычно используются на вводных занятиях.
 (иногда вы увидите 2,9979, а не 3,00.) Будьте осторожны при использовании комбинации показателя степени и единицы измерения. Метры длиннее сантиметров, поэтому выше их используется меньше.
(иногда вы увидите 2,9979, а не 3,00.) Будьте осторожны при использовании комбинации показателя степени и единицы измерения. Метры длиннее сантиметров, поэтому выше их используется меньше.Поскольку есть две переменные (λ и ν), у нас может быть два типа вычислений:
а) зная длину волны, вычислить частоту; используйте это уравнение: ν = c / λ
(б) зная частоту, рассчитайте длину волны; используйте это уравнение: λ = c / ν
И последнее замечание: иногда вы видите, что буква f используется для частоты, заменяя греческую букву nu. Как это:
с = λf
Скорее всего, это не вызовет у вас проблем, но я все же хотел об этом упомянуть.
Интересная мелочь о свете: свет проходит примерно один фут за каждую наносекунду. Вы можете попробовать сделать правильный расчет, прежде чем проверять ответ.
Пример №1: Какова частота электромагнитного излучения с длиной волны 210,0 нм?
Решение:
1) Перевести нм в м:
210,0 нм x (1 м / 10 9 нм) = 210,0 x 10 -9 м
Мы можем оставить его здесь или преобразовать в экспоненциальное представление:
2.
 100 x 10 -7 м
100 x 10 -7 мЛюбой вариант работает нормально в следующем расчете. Узнайте у своего учителя, есть ли у него предпочтения. Затем следуйте их предпочтениям.
2) Используйте λν = c
(2,100 x 10 -7 м) (ν) = 3,00 x 10 8 м/с
ν = 3,00 x 10 8 м/с разделить на 2,100 x 10 -7 м
ν = 1,428 x 10 15 с -1
Пример №2: Какова частота фиолетового света с длиной волны 4000 Å?
Приведенное ниже решение зависит от преобразования Å в см. Это означает, что вы должны помнить, что преобразование равно 1 Å = 10¯9.0052 8 см. Решение:
λν = с
(4000 x 10¯ 8 см) (ν) = 3,00 x 10 10 см/с ν = 7,50 x 10 14 с¯ 1
Обратите внимание, что я не удосужился преобразовать 4000 x 10¯ 8 в экспоненциальное представление.
 Если бы я это сделал, значение было бы 4.000 x 10¯ 5 . Обратите также внимание, что я фактически считаю 4000 4 значащими цифрами.
Если бы я это сделал, значение было бы 4.000 x 10¯ 5 . Обратите также внимание, что я фактически считаю 4000 4 значащими цифрами.Комментарий: имейте в виду, что диапазон от 4000 до 7000 Å считается диапазоном видимого света. Обратите внимание, как частоты остаются более или менее в средней области 10 14 , в диапазоне от 4,29 до 7,50, но всегда 10 14 . Если вы столкнулись с этим расчетом и знаете, что длина волны является видимой (скажем, 5550 Å, что также равно 555 нм), то вы знаете, что показатель степени частоты ДОЛЖЕН быть 10 14 . Если это не так, то ВЫ (не учитель) допустили ошибку.
Пример №3: Какова частота ЭМИ с длиной волны 555 нм? (ЭМИ — это сокращение от электромагнитного излучения.)
1) Переведем нм в метры. Так как один метр содержит 10 9 нм, мы имеем следующее преобразование:
555 нм x (1 м / 10 9 нм)
555 x 10¯ 9 м = 5,55 x 10¯ 7 м
2) Подстановка в λν = c дает:
(5,55 x 10¯ 7 м) (x) = 3,00 x 10 8 м с¯ 1
x = 5,40 x 10 14 с¯ 1 3
- Ависон, Джон (1999).


 С увеличением длины волны частота уменьшается. С увеличением частоты длина волны уменьшается.
С увеличением длины волны частота уменьшается. С увеличением частоты длина волны уменьшается.
 Мир физики . Нельсон Торнс. ISBN 978-0-17-438733-6.
Мир физики . Нельсон Торнс. ISBN 978-0-17-438733-6. Волновая теория света берет свое начало в конце 1600-х годов и математически развивалась с начала 1800-х годов. Джеймс Клерк Максвелл в 1860-х годах первым предсказал, что свет представляет собой электромагнитную волну, и вычислил (а не измерил) ее скорость. Кстати, доказательство конечности скорости света было опубликовано в 1676 г., а первые достоверные измерения скорости света, очень близкие к современному значению, имели место в конце 1850-х гг.
Волновая теория света берет свое начало в конце 1600-х годов и математически развивалась с начала 1800-х годов. Джеймс Клерк Максвелл в 1860-х годах первым предсказал, что свет представляет собой электромагнитную волну, и вычислил (а не измерил) ее скорость. Кстати, доказательство конечности скорости света было опубликовано в 1676 г., а первые достоверные измерения скорости света, очень близкие к современному значению, имели место в конце 1850-х гг.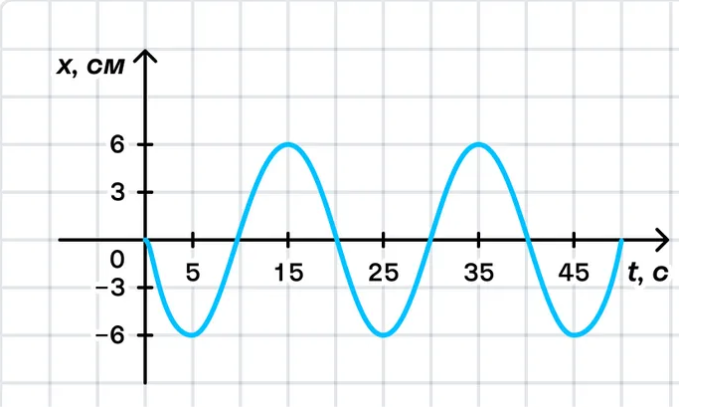 Реже вы увидите использование других юнитов; пикометр является наиболее распространенным среди менее часто используемых единиц длины волны. Ангстрем — это единица, не входящая в систему СИ, которую обычно включают в обсуждение единиц СИ из-за ее широкого использования.
Реже вы увидите использование других юнитов; пикометр является наиболее распространенным среди менее часто используемых единиц длины волны. Ангстрем — это единица, не входящая в систему СИ, которую обычно включают в обсуждение единиц СИ из-за ее широкого использования. Это НЕ буква v, это греческая буква nu. Это означает частоту световой волны. Частота определяется как количество волновых циклов, проходящих фиксированную контрольную точку за одну секунду. При изучении света единицей измерения частоты является герц (его символ — Гц). Один герц — это когда один полный цикл проходит фиксированную точку за одну секунду, поэтому миллион Гц — это когда миллион циклов проходит фиксированную точку за одну секунду.
Это НЕ буква v, это греческая буква nu. Это означает частоту световой волны. Частота определяется как количество волновых циклов, проходящих фиксированную контрольную точку за одну секунду. При изучении света единицей измерения частоты является герц (его символ — Гц). Один герц — это когда один полный цикл проходит фиксированную точку за одну секунду, поэтому миллион Гц — это когда миллион циклов проходит фиксированную точку за одну секунду. Это один цикл волны, и если все это произошло за одну секунду, то частота волны равна 1 Гц.
Это один цикл волны, и если все это произошло за одну секунду, то частота волны равна 1 Гц.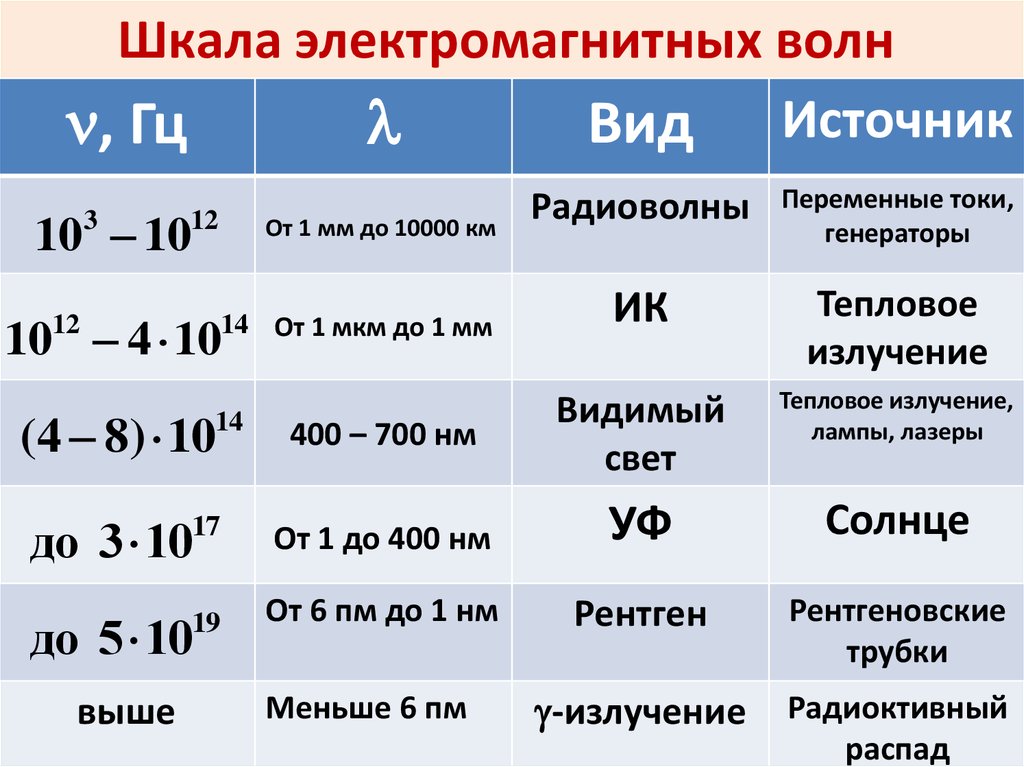 (иногда вы увидите 2,9979, а не 3,00.) Будьте осторожны при использовании комбинации показателя степени и единицы измерения. Метры длиннее сантиметров, поэтому выше их используется меньше.
(иногда вы увидите 2,9979, а не 3,00.) Будьте осторожны при использовании комбинации показателя степени и единицы измерения. Метры длиннее сантиметров, поэтому выше их используется меньше. 100 x 10 -7 м
100 x 10 -7 м Если бы я это сделал, значение было бы 4.000 x 10¯ 5 . Обратите также внимание, что я фактически считаю 4000 4 значащими цифрами.
Если бы я это сделал, значение было бы 4.000 x 10¯ 5 . Обратите также внимание, что я фактически считаю 4000 4 значащими цифрами.