Цепь переменного тока с емкостью
| Под
действием этого напряжения конденсатор
будет разряжаться и заряжаться.
Мгновенное значение заряда на обкладках
конденсатора: |
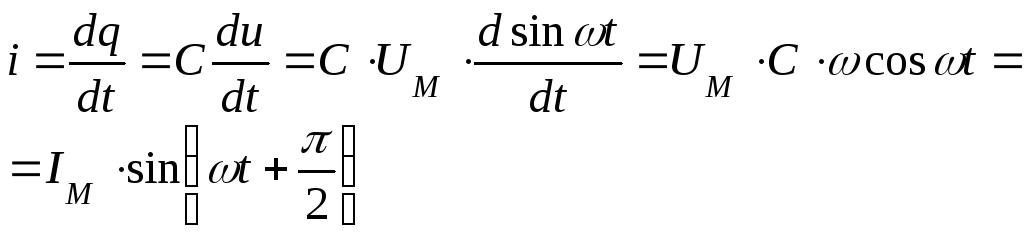
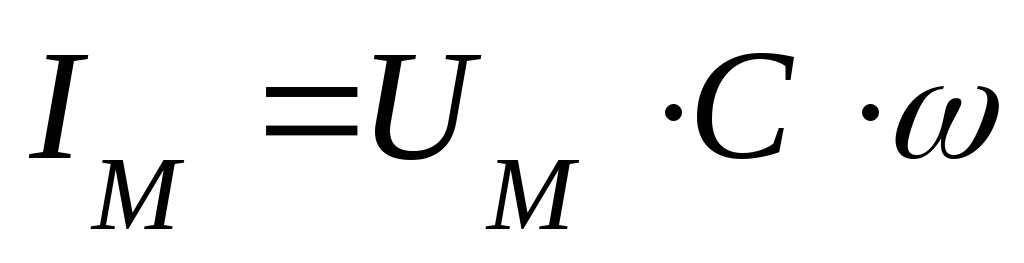
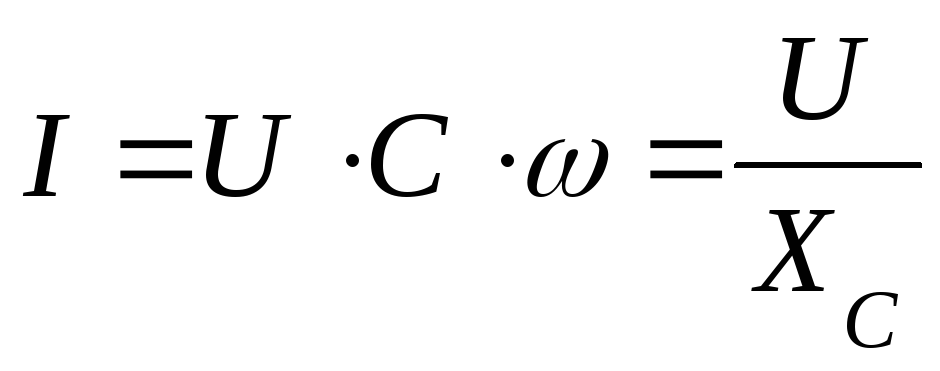
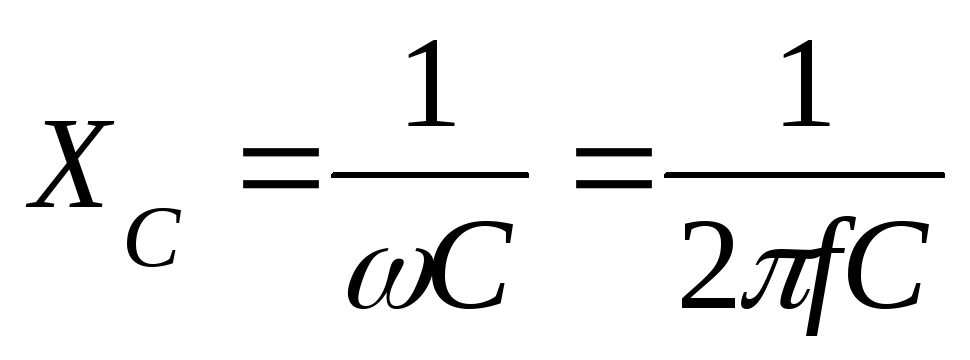 — реактивное
емкостное сопротивление
— реактивное
емкостное сопротивление
Т.о. ток в цепи с емкостью опережает напряжение на угол 900.
Физически емкостное сопротивление характеризует препятствие, оказываемое переменному току цепью с емкостью. В результате поляризации диэлектрика конденсатора в нем образуется свое внутренне электрическое поле, которое направлено противоположно внешнему полю, приложенному к диэлектрику.
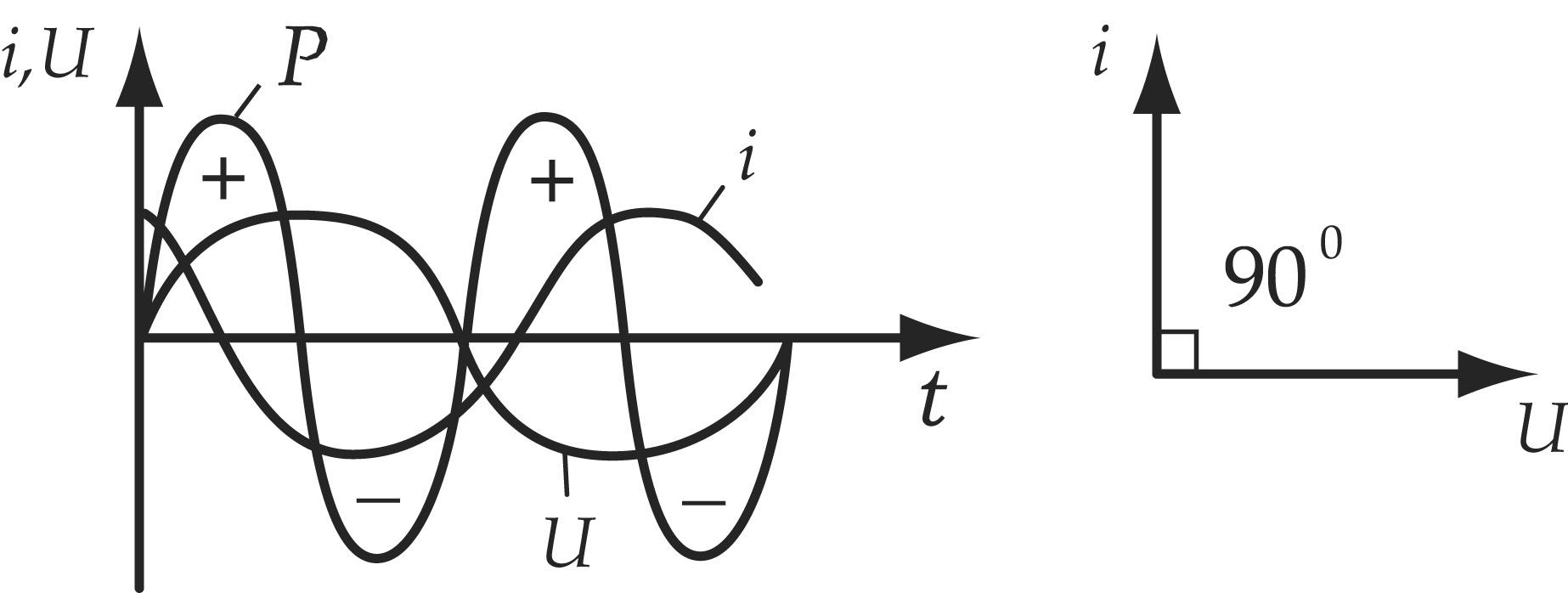
Мощность цепи:
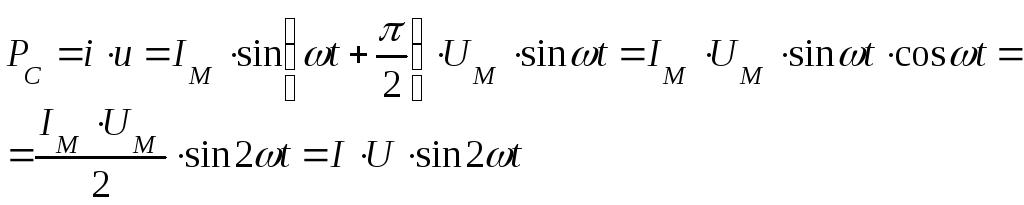
Мощность изменяется с двойной частотой относительно тока и напряжения. В течении первой четверти периода, когда напряжение, приложенное к конденсатору, возрастает, мгновенная мощность положительна. Это означает, что конденсатор получает и запасает энергию источника в виде электрического поля.
В течении второй четверти, когда напряжение, приложенное к конденсатору, уменьшается, запасенная энергия возвращается к источнику, т.е.
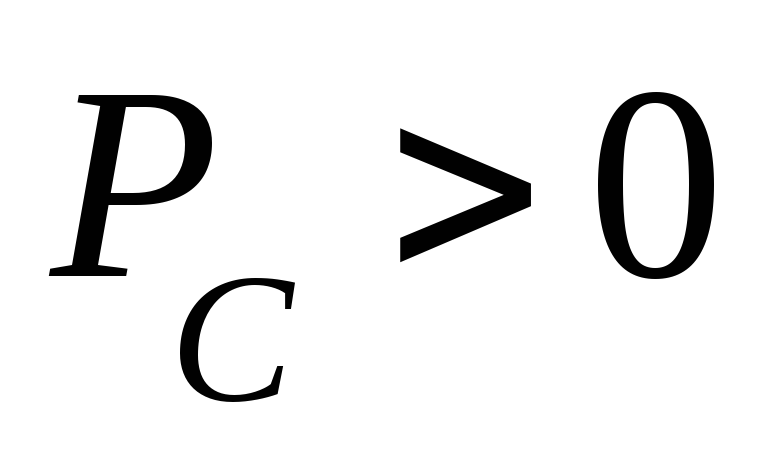 — цепь работает
потребителем;
— цепь работает
потребителем;
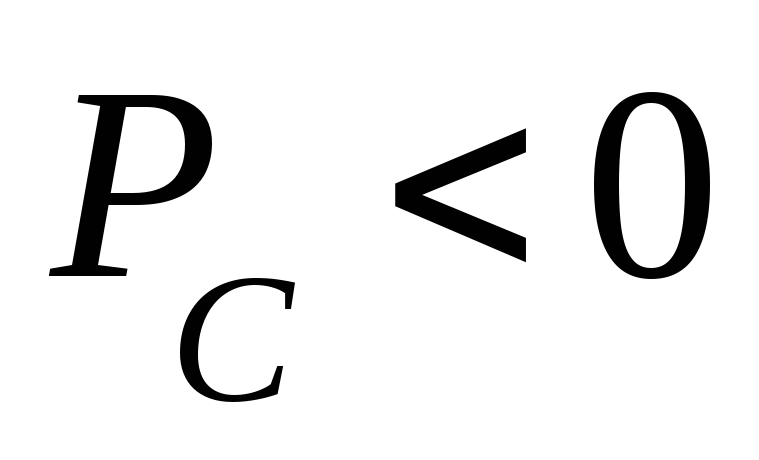 — цепь работает
источником.
— цепь работает
источником.
Максимальное значение мощности цепи с емкостью называют реактивной емкостной мощностью:
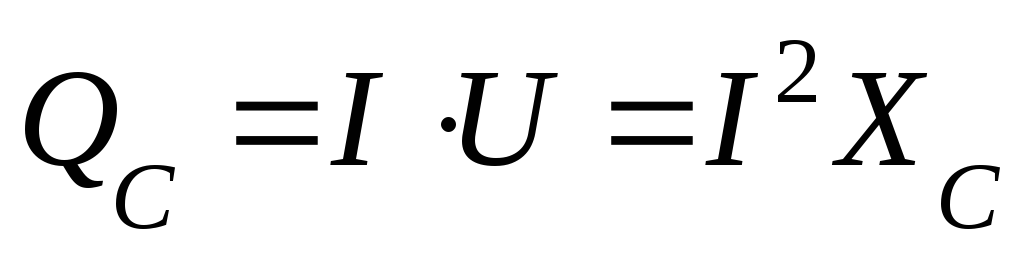
Она характеризует скорость обмена энергией между источником и цепью с емкостью.
Максимальное значение энергии, запасенной в цепи:
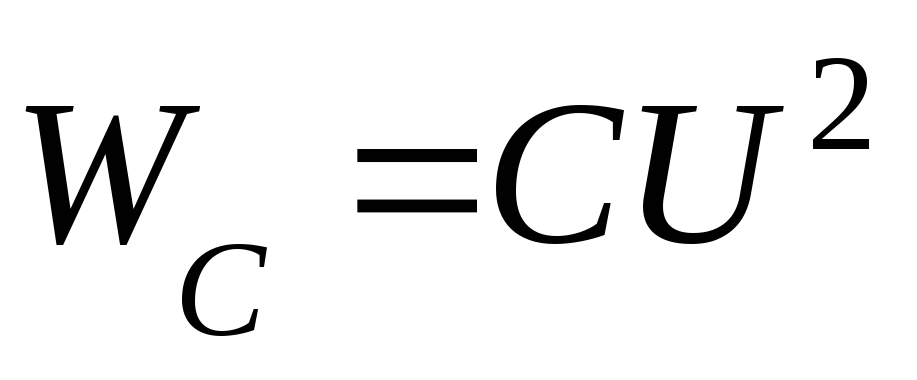
Неразветвленная цепь переменного тока с активным сопротивлением и индуктивностью
Таким сопротивлением (активным и индуктивным) обладают катушки индуктивности, обмотки трансформаторов и электрических машин.
Т.о. напряжение
опережает ток в этой цепи на угол  ,
причем
,
причем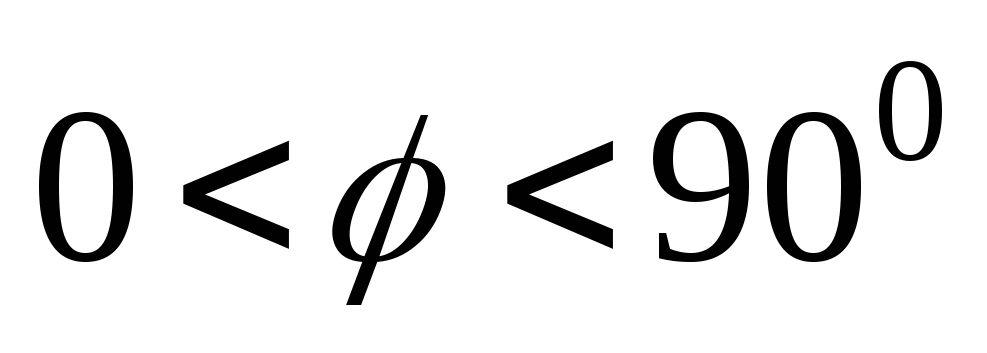 .
.
|
|
Мощность цепи:
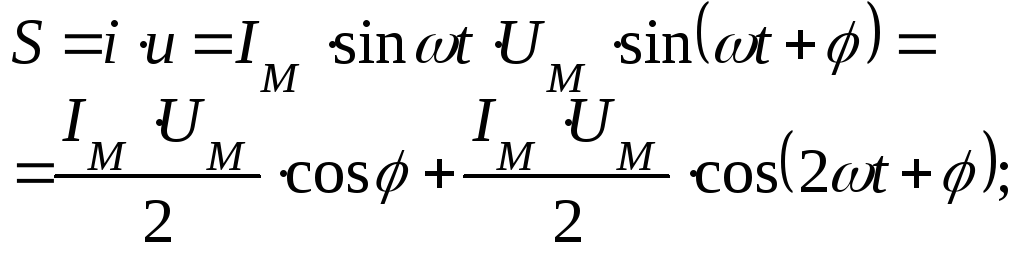
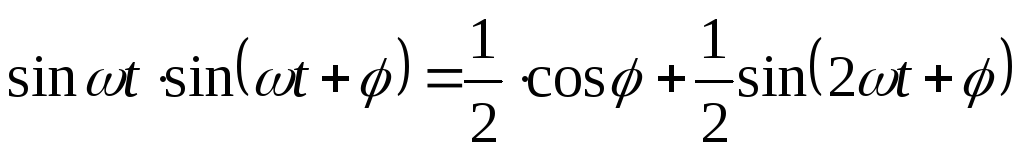
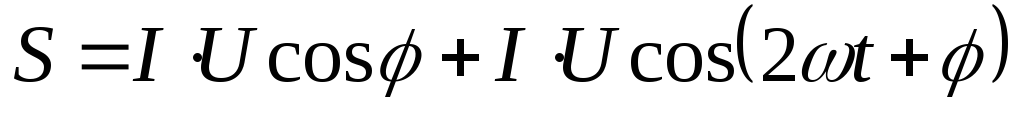
Т.о. мгновенная
мощность состоит из двух составляющих:
постоянной 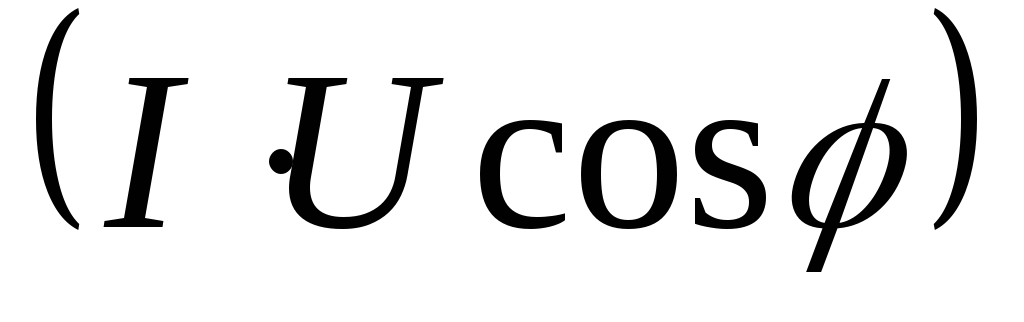
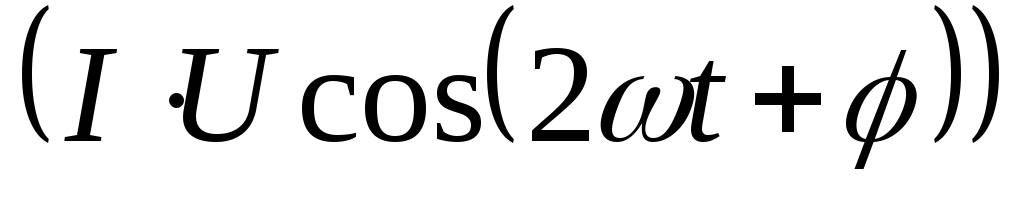 ,
среднее значение за период которой
равно нулю.
,
среднее значение за период которой
равно нулю. 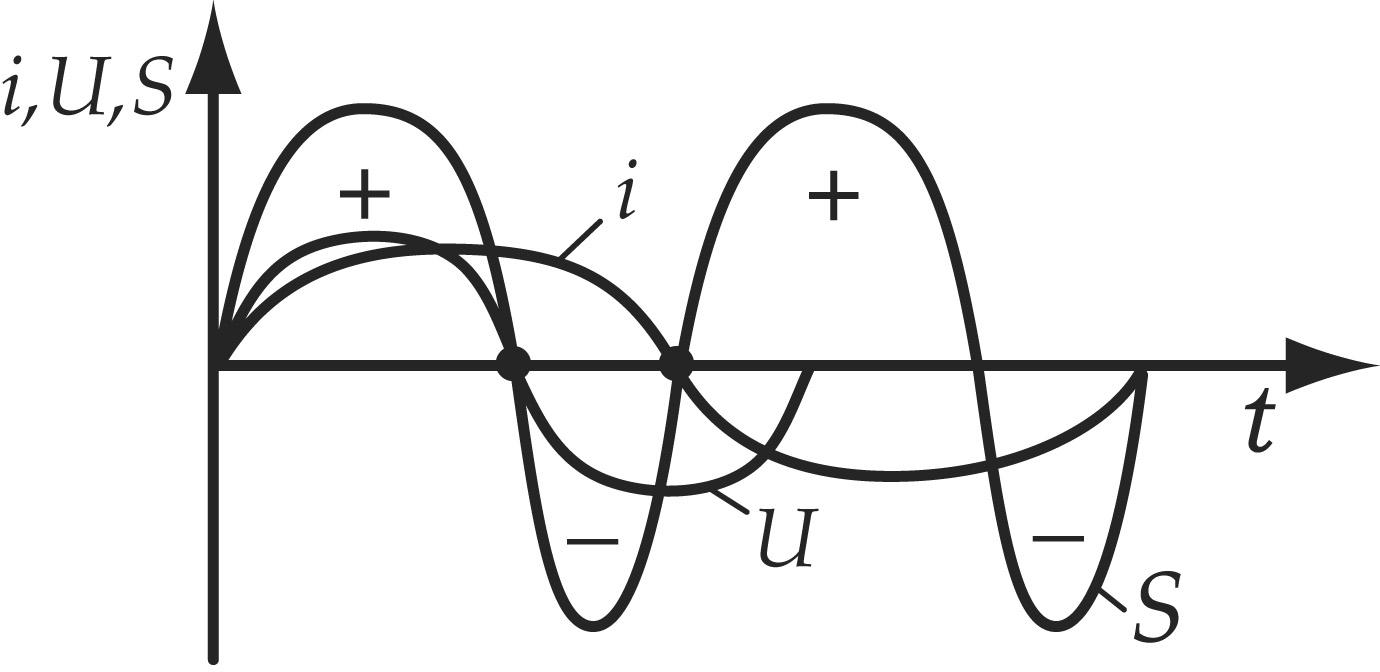
Мощность принимает как положительные так и отрицательный значения. Когда мощность положительна, то цепь потребляет энергию, а когда мощность отрицательна, то цепь возвращает запасенную энергию в цепь. Но т.к. потребляет энергию и активное сопротивление и индуктивное, а возвращает в цепь только индуктивность, то положительная будет значительно больше.
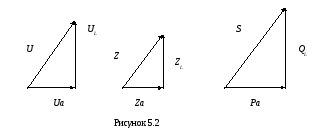
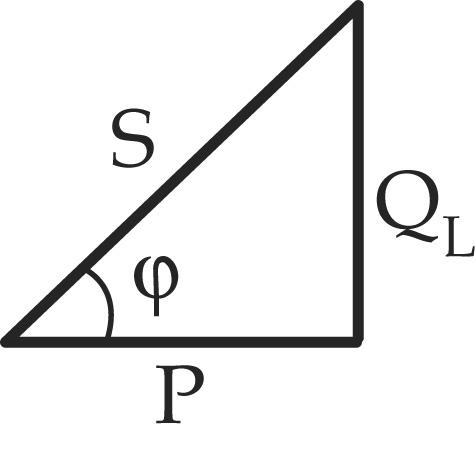
Треугольники напряжений, сопротивлений, мощностей
|
| Если стороны треугольника напряжений уменьшить или разделить на величину тока, то получим треугольник сопро-тивлений |
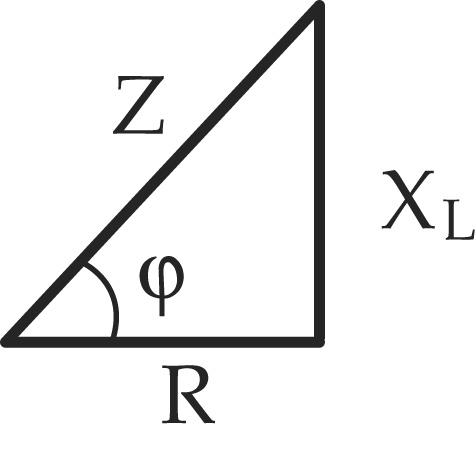 |
|
| — закон Ома для цепи с активным и индуктивным сопротивлением. |
Если стороны треугольника напряжений уменьшить на ток, то получим треугольник мощностей.
|
|
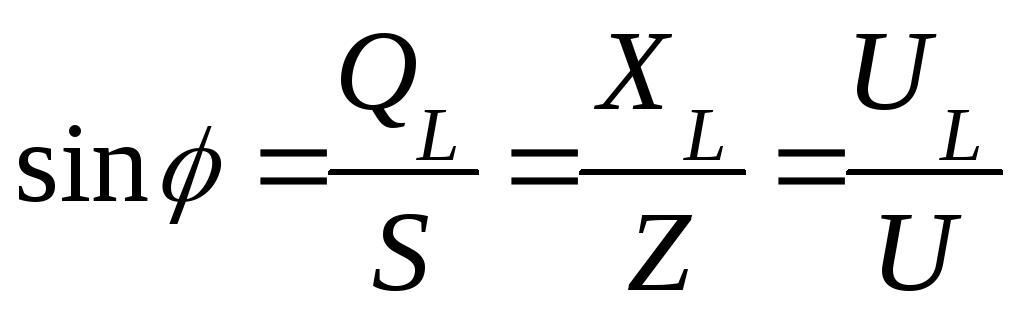
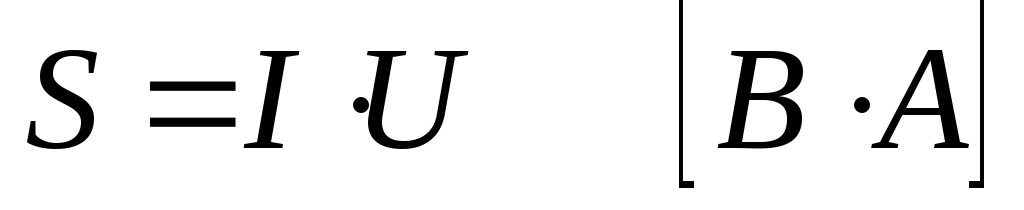
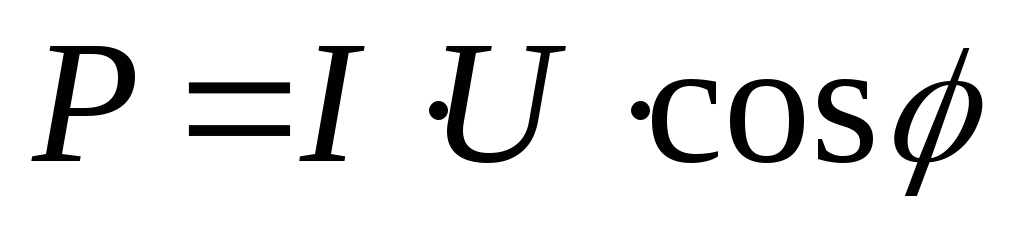 — реактивная
мощность
— реактивная
мощность
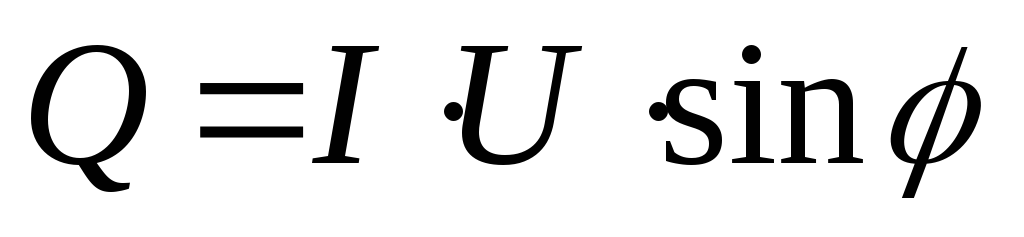 — активная мощность
— активная мощность
Коэффициент мощности показывает, какая часть полной мощности потребляется безвозвратно.
Цепь переменного тока с активным сопротивлением, емкостью и индуктивностью
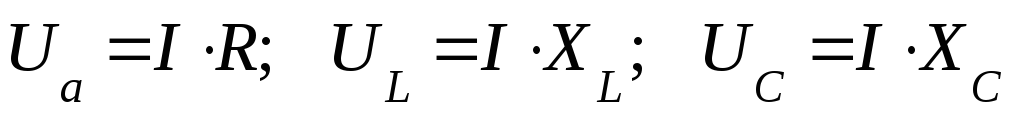
Допустим:
1. 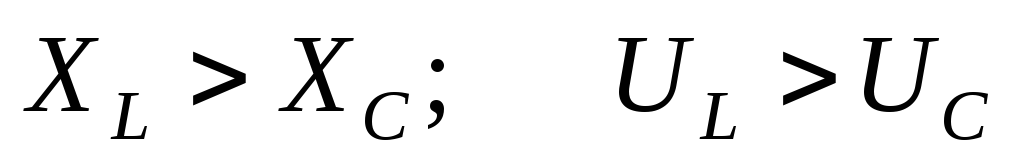
2. 
Общий случай неразветвленной цепи
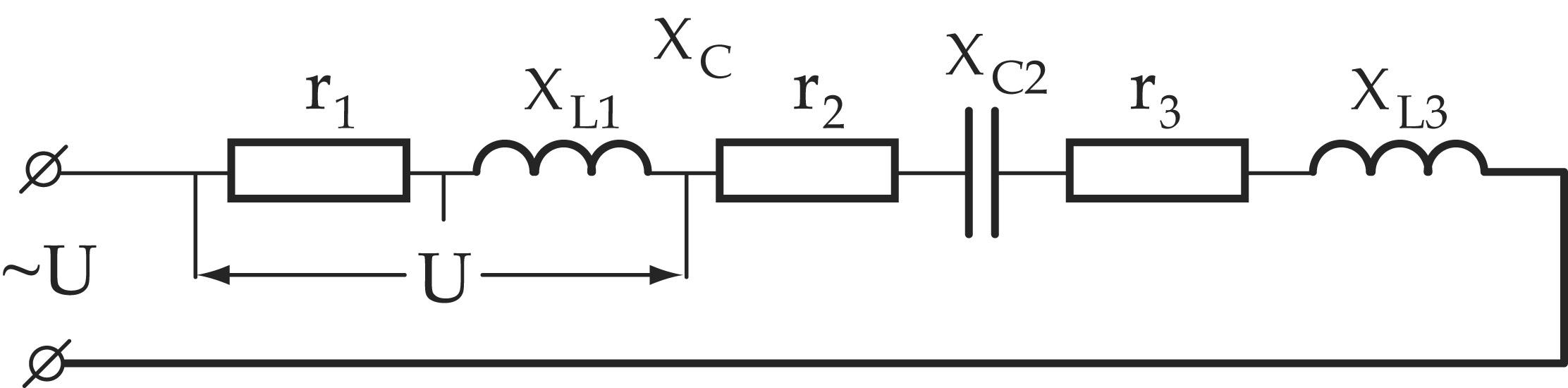
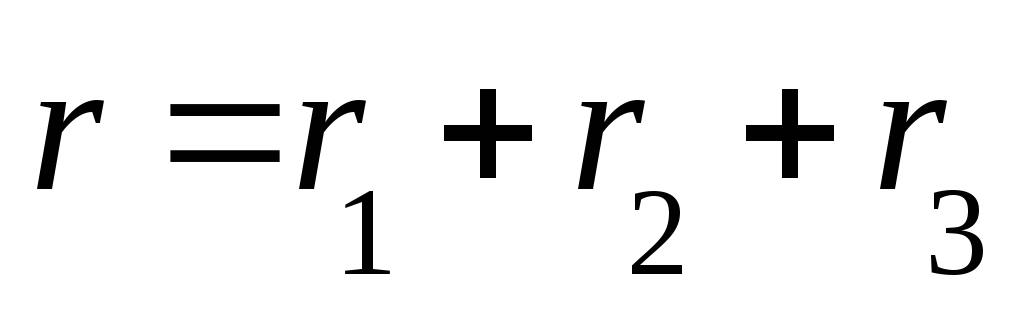
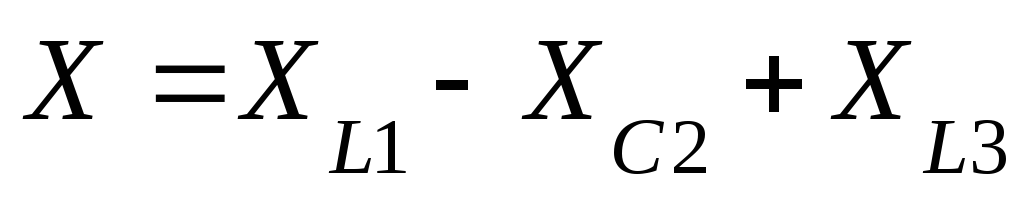
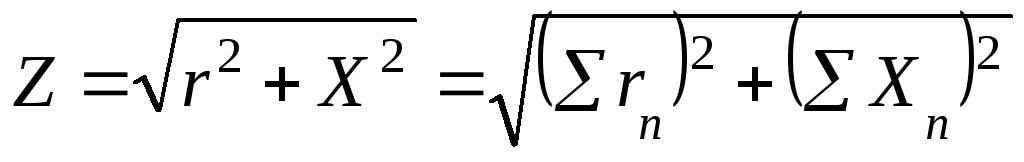
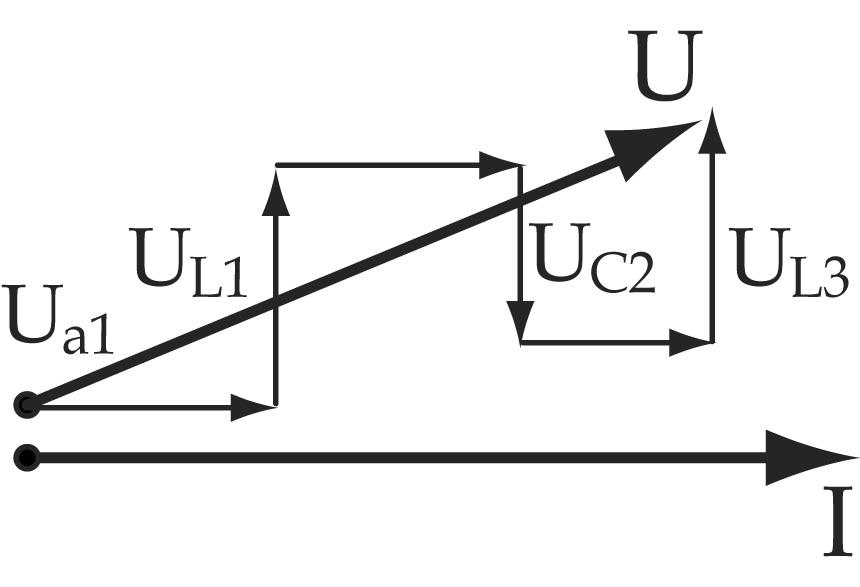
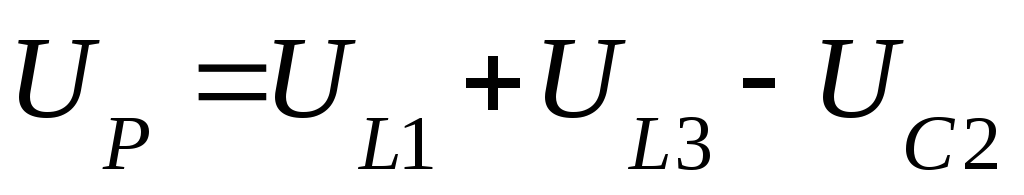
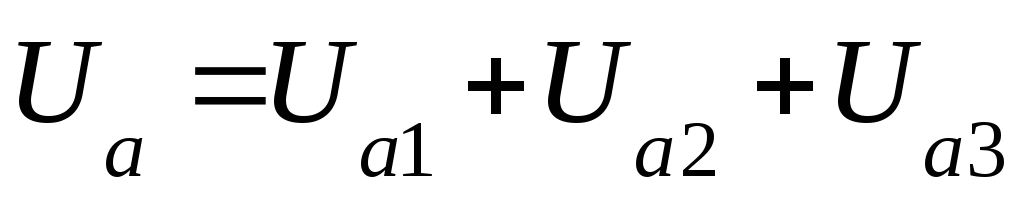
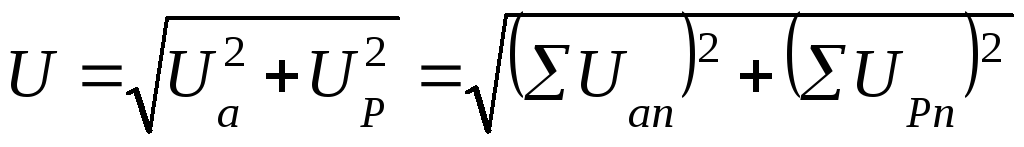
Резонанс напряжений
Результирующий
ток 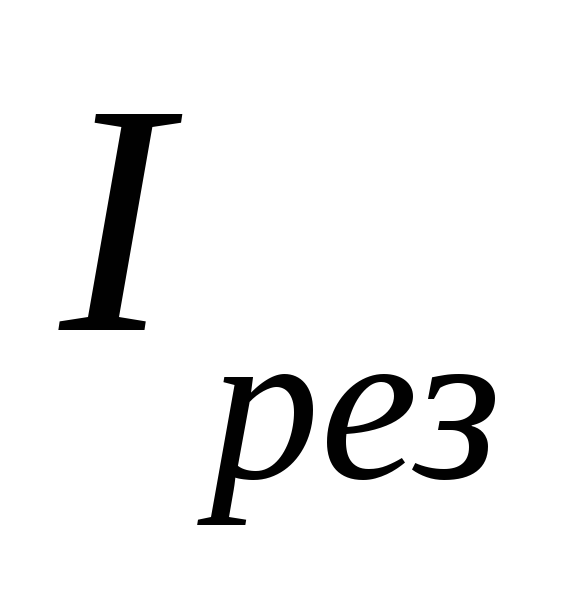 резко увеличивается, т.к. индуктивное
и емкостное сопротивления компенсируют
друг друга.
резко увеличивается, т.к. индуктивное
и емкостное сопротивления компенсируют
друг друга.
Если параметры
цепи подобрать так, что 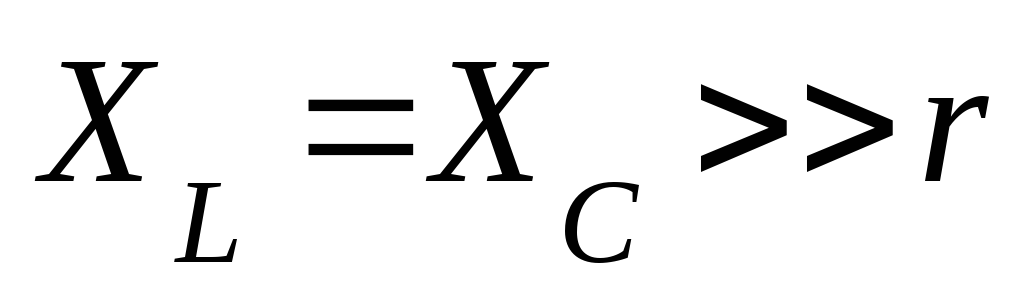
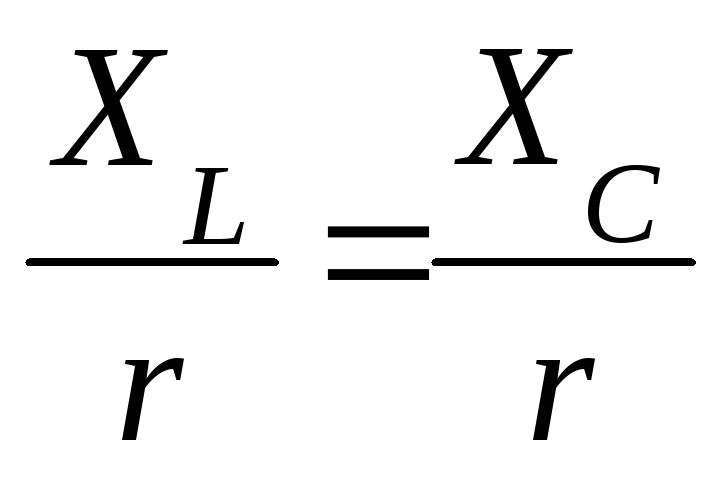 раз. Отношение
раз. Отношение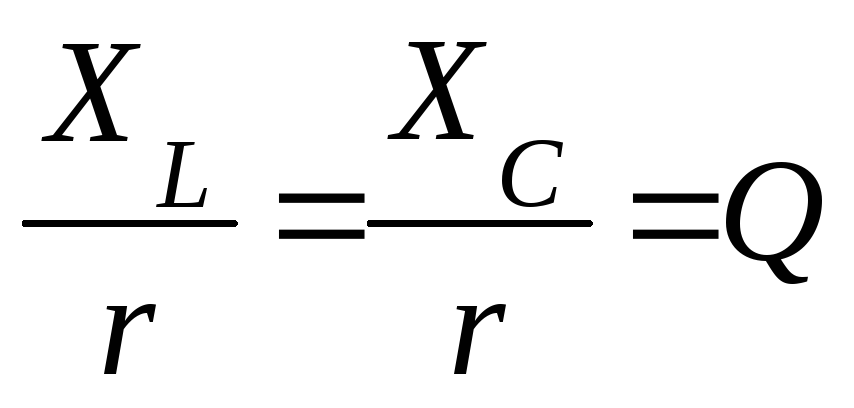 называетсядобротностью цепи
(контура).
называетсядобротностью цепи
(контура). 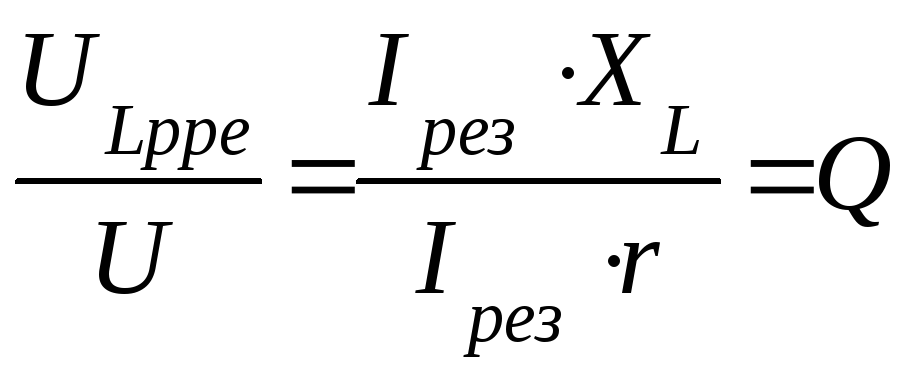

Т.о. напряжение на
емкости и индуктивности будут превышать
напряжение сети в  раз, что может привести к пробою
диэлектрика в конденсаторе или
сопротивлений изоляции индуктивности,
поэтому явление резонанса напряжений
в электрических цепях нежелательно, но
в то же время в радиотехнике его используют
(колебательные контуры приемника и
передатчика).
раз, что может привести к пробою
диэлектрика в конденсаторе или
сопротивлений изоляции индуктивности,
поэтому явление резонанса напряжений
в электрических цепях нежелательно, но
в то же время в радиотехнике его используют
(колебательные контуры приемника и
передатчика).
Возникновение напряжений на LиС, превышающих напряжение на зажимах цепи объясняется способностью емкости и индуктивности накапливать электрическую энергию.
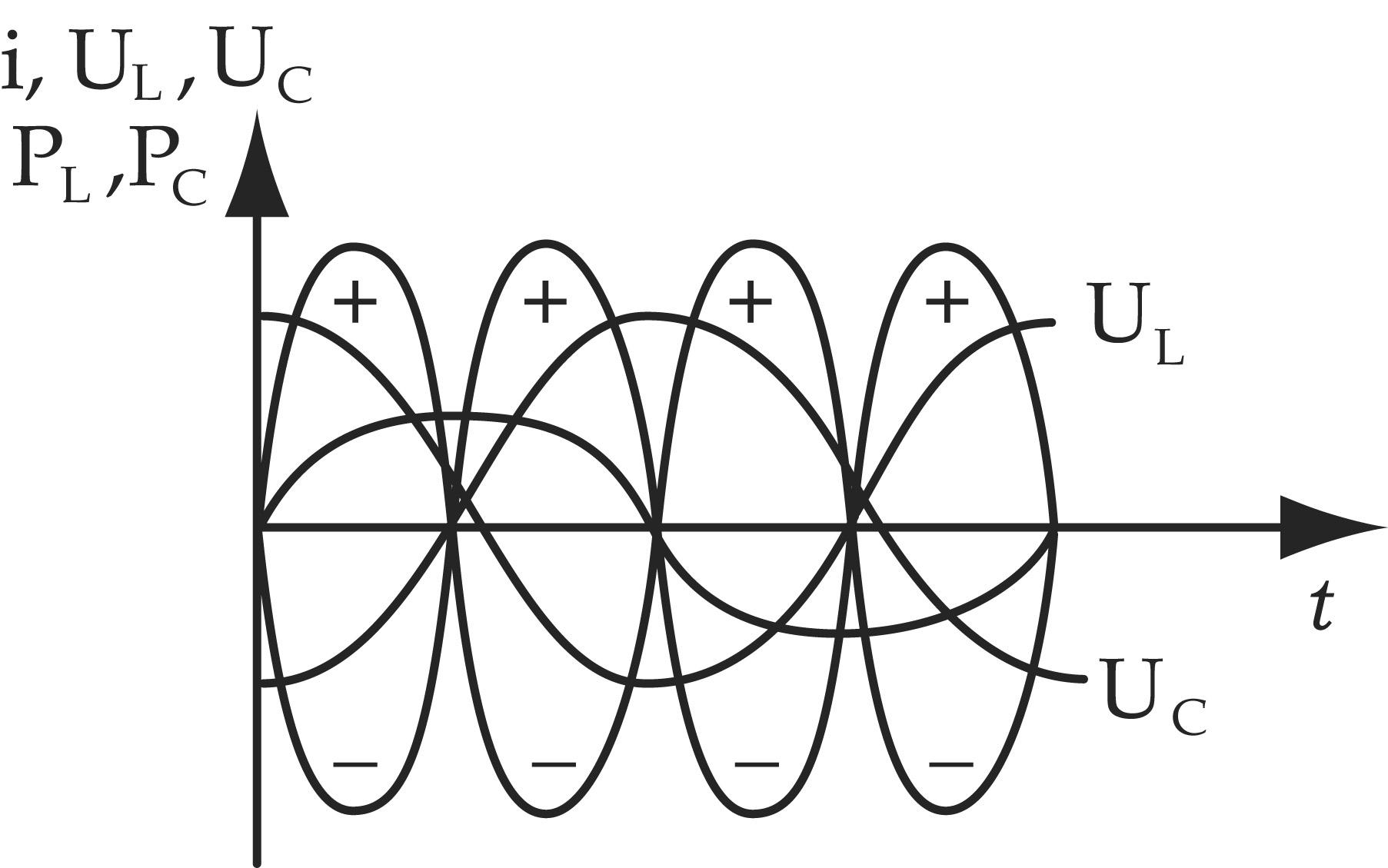
Между емкостью и индуктивностью происходит непрерывный обмен энергией, который называется собственными колебаниями.
Частоту собственных
колебаний можно определить при условии,
что 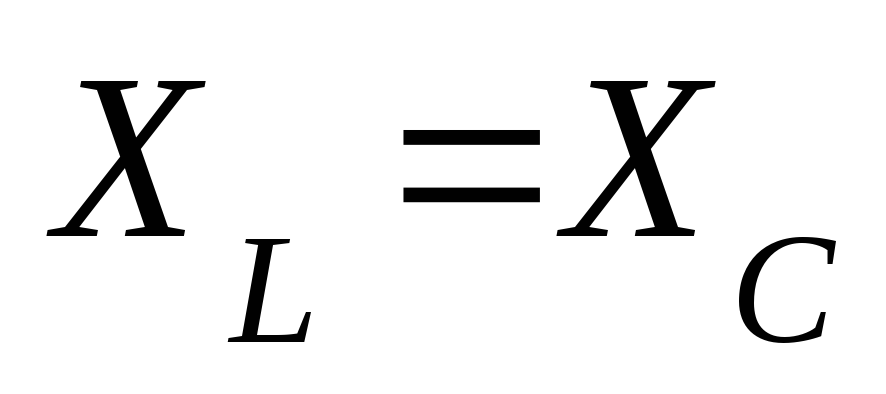 .
.
| Т.о. резонанс можно получить, изменяя частоту тока питающей сети, или изменяя емкость или индуктивность.
|
Цепь с активным сопротивлением — Знаешь как
Содержание статьи
Напряжение и ток
 Цепь, изображенная на рис. 5-17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.
Цепь, изображенная на рис. 5-17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.
При прохождении переменного тока i в цепи будет индуктироваться э. д. с. самоиндукции eL.
Согласно второму правилу Кирхгофа u + eL = ir
откуда напряжение на зажимах цепи
и = it — eL = ir + L (di/dt)= ua + u
Первая слагающая uа = ir называется активным напряжением, мгновенное значение которого пропорционально току, а вторая uL = — eL = L(di/dt) реактивным напряжение м, мгновенное значение которого пропорционально скорости изменения тока.
Если ток изменяется по закону синуса
i — Iм sin ωt
то активное напряжение
uа = ir = Iмr sin ωt = Uа м sin ωt
Рис. 5-17, Цепь с активным сопротивлением и индуктивностью.
Оно изменяется также синусоидально, совпадая по фазе с током.

Амплитудное значение активного напряжения
Uа м = Iмr,
а действующее значение
Uа = Ir,
Реактивное напряжение
uL = L di/dt = ωLIM cos ωt = ULм sin(ωt + π/2)
Оно изменяется синусоидально, опережая по фазе ток на 90°.
Амплитудное значение реактивного напряжения
ULм = ωLIM
 а действующее значение
а действующее значение
UL = ωLI = xLI
Напряжение на зажимах цепи
и= иa + uL = Uа м sin ωt + ULM sin (ωt + π/2) = UMsin (ωt + φ).
Напряжение на зажимах изменяется синусоидально, опережая ток по фазе на угол φ.
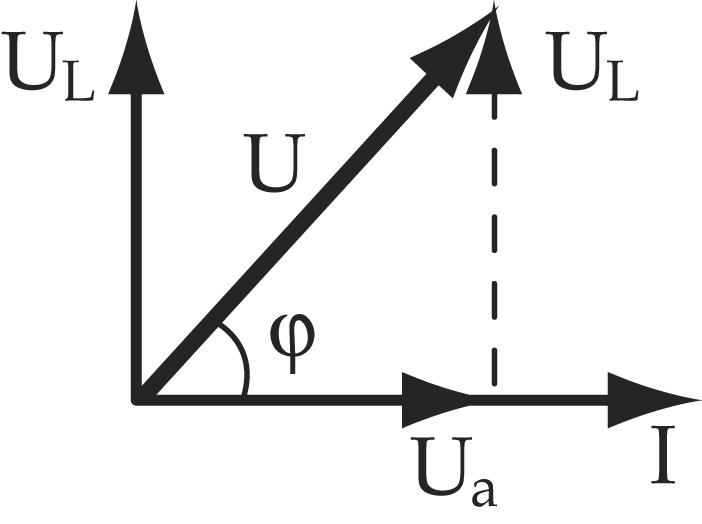
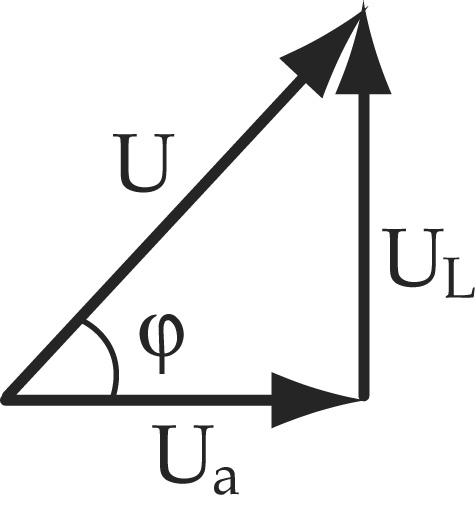
На рис. 5-18 показаны графики; i, иa, uL и и, а на рис. 5-19 — векторная диаграмма цепи. На диаграмме векторы напряжений U, Ua и UL образуют прямоугольный треугольник напряжений, из которого непосредственно следует соотношение, связывающее эти величины:
U=√(U2a + U2L ) .
Аналогичная зависимость имеет место и для амплитудных значений
Угол сдвига фаз между напряжением на зажимах
Рис 5-18. Графики тока и напряжения в цепи с активным сопротивлением и индуктивностью.
Рис 5-19. Векторная диаграмма цепи с активным сопротивлением и индуктивностью.
цепи и током в ней находится из треугольника напряжений по одной из формул
cos φ = Ua/U и tg φ = UL/Ua
 Чем больше реактивное напряжение по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения на зажимах цепи.
Чем больше реактивное напряжение по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения на зажимах цепи.
Сопротивления цепи
Уравнение (5-30) можно переписать в следующем виде
U = √(Ir)2 + (IxL)2 = I√r2 + x2L = Iᴢ
откуда ток в цепи
I = U/z = U / √(r2 + x2L)
Величина
z = √(r2 + x2L) = √(r2 + ωL)2
называется полным сопротивлением цепи.
Сопротивления r, xL и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20), который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.
Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через
cos φ = Ua /U
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью
Мощности
Мгновенное значение мощности р = ui = Uм sin (ωt + φ) Iм sin ωt = UмIм sin (ωt + φ) sin ωt Учитывая, что
sin (со/ + φ) sin ωt = 1/2 cos φ — 1/2 cos (2ωt + φ)
а также (5-28), можно написать другое выражение ной мощности
Р = UI cos φ — UI cos (2ωt + φ)
Написанное выражение состоит из двух членов: постоянного, независимого от времени UI cos φ и переменного си-
нусоидального UI cos (2ωt + φ). Среднее значение мощности за период, которым обычно пользуются при расчете цепей переменного тока, будет равно постоянному члену UI cos φ, так как среднее значение за период синусоидальной функции равно нулю.
Таким образом, среднее значение мощности цепи равно произведению действующих значений напряжения и тока, умноженному на cos φ, т.е.
P = UI cos φ.
Так как U cos φ = U r/z = Ir = Ua,
то
P = UаI = I2r
Следовательно, средняя мощность цепи равна среднему значению мощности в активном сопротивлении. Поэтому среднюю мощность любой цепи называют; еще и активной мощностью.

Реактивная мощность цепи:
Q = ULI= I2xL = I2z sin φ = UI sin φ
т.е. реактивная мощность цепи равна произведению действующих значений напряжения и тока, умножен ному на sin φ.
Рис.5-21. Треугольник мощностей
Полной мощностью цепи называется произведение действующих значений напряжения и тока, т. е.
S = UI
Учитывая, что sin2 φ + cos2 φ = 1 можно написать: (UI cos φ)2 + (UI sin φ)2 = (UI)2
или, что то же,
P2 + Q2 = S2,
следовательно,
S = √(P2 + Q2)
Мощности Р, Q и S графически можно изобразить сторонами прямоугольного треугольника — треугольника мощностей (рис 5-21), который можно получить из треугольника напряжений, умножая на I все его стороны.
т.е отношение активной мощности к полной называется коэффициентом мощности.
Единица полной мощности с называется вольт-ампер (в •а).
Необходимость применения понятия полной мощности обусловлена тем, что конструкция, габариты, вес и стоимость машины или аппарата определяются их номинальной полной мощностью Sн = UнIн а полная мощность S при том или ином режиме работы их определяет степень их использования.
Статья на тему Цепь с активным сопротивлением
1.2. Цепь с активным сопротивлением и емкостью
Методика
изучения цепи с R и С (рис. 4,а) аналогична методике изучения
цепи с R и L. Задаемся
током 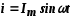 .
Тогда напряжение на активном сопротивлении
.
Тогда напряжение на активном сопротивлении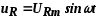 .
Напряжение на емкости отстает по фазе
от тока на уголπ/2:
.
Напряжение на емкости отстает по фазе
от тока на уголπ/2: 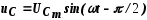 .
На основании приведенных выражений
построим векторную диаграмму для
этой цепи (рис. 4,б).
.
На основании приведенных выражений
построим векторную диаграмму для
этой цепи (рис. 4,б).
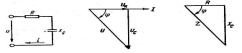
а) б) в)
Рис. 4. К анализу цепи с последовательным соединением R и С
Закон Ома для цепи с R и С.
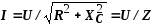
где 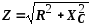 – полное
сопротивление цепи.
– полное
сопротивление цепи.
Треугольник сопротивлений для рассматриваемой цепи показан на рис. 4, в. Расположение его сторон соответствует расположению сторон треугольника напряжений на векторной диаграмме рис. 3,б. Сдвиг фаз φ в этом случае отрицателен, так как напряжение отстает по фазе от тока:
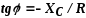 ;
; 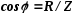
Мощности:
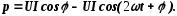
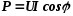 .
.
Реактивная
мощность характеризует
интенсивность обмена энергией между
емкостью и источником 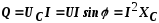 .
.
Так как φ<0, то реактивная мощность Q<0. Физически это означает, что когда емкость отдает энергию, то индуктивность ее потребляет, если они находятся в одной цепи.
Треугольник мощностей для данной цепи приведен на рис. 6.
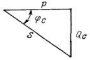
Рис. 6. Треугольник мощностей для цепи с R и С
1.3. Цепь с активным сопротивлением, индуктивностью и емкостью
Цепь с R, L и С представляет собой общий случай
последовательного соединения активных
и реактивных сопротивлений и является
последовательным колебательным контуром
(рис. 5,а). Принимаем фазу тока нулевой: 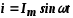 .
.
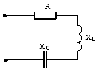
 а) б) в)
а) б) в)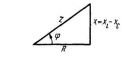
Рис. 5. Схема цепи переменного тока с R и L,
ее векторная диаграмма, треугольник сопротивлений
Тогда
напряжение на активном сопротивлении 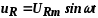 , напряжение
на индуктивности
, напряжение
на индуктивности 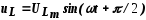 ,
напряжение на емкости
,
напряжение на емкости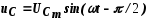 .
Построим векторную диаграмму при условииXL>
Хс, т.е. UL = IXL> UC = IXC.
.
Построим векторную диаграмму при условииXL>
Хс, т.е. UL = IXL> UC = IXC.
Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL и UС (рис. 5,б). Вектор UL + Uc определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью.
Закон Ома для цепи с R, L и С.
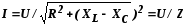
где 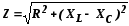 – полное
сопротивление цепи;
– полное
сопротивление цепи;
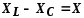 –реактивное
сопротивление цепи, Ом.
–реактивное
сопротивление цепи, Ом.
При XL> Xc реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер, при XL< Xc реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостной характер.
Таким образом, при XL≠XC преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С.
Мощности:
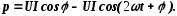
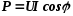
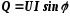
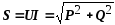
Знак сдвига фаз φ определяется по формуле
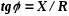
Ответьте на следующий вопрос:
Полное
сопротивление Z
приведенной цепи при 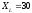 Ом
и
Ом
и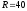 Ом
составляет…
Ом
составляет…

50 Ом
100 Ом
400 В
50 Гц
Вывод по первому вопросу: процессы, протекающие в однофазных цепях переменного тока со смешанным последовательным соединением приемников, характеризуются появлением понятий полного сопротивления, полной мощности, треугольников сопротивлений и мощностей, повторяющих треугольник напряжений. В них также необходимо учитывать взаимные фазовые сдвиги напряжений и токов. Умение анализировать однофазные цепи со смешанным соединением резисторов является важным при изучении трехфазных цепей, принципа действия и устройства электрических машин.
§5.4. Цепь с активным сопротивлением и индуктивностью
Как и для цепи с R, мгновенное значение мощности определяется произведением мгновенных значений напряжения и тока: р=ui=UmImsin(ωt+π/2)sinωt=UmImcosωtsinωt.
Так как sinωtcosωt=sin2ωt/2 и UmIm/2 =UI, то окончательно имеем
p=UIsin2ωt. | (5.9) |
Из графика рис. 5.9 видно, | что при одинаковых знаках напряжения и тока мгновенная |
мощность положительна, а при разных знаках — отрицательна. Физически это означает, что в
первую четверть периода переменного тока энергия источника преобразуется в энергию магнитного поля катушки. Во вторую четверть периода, когда ток убывает, катушка возвращает накопленную энергию источнику. В следующую четверть периода процесс передачи энергии источником повторяется и т. д.
Таким образом, в среднем катушка не потребляет энергии и, следовательно, активная мощность P=0.
Реактивная мощность.
Для количественной характеристики интенсивности обмена энергией между источником и
катушкой служит реактивная мощность: |
|
|
|
|
| |||
|
| Q=UI. |
|
| (5.10) |
|
|
|
Единицей реактивной мощности является вольт-ампер реактивный (ВАр). |
|
| ||||||
|
|
| Карточка № 5.2 (189). |
|
|
|
| |
|
|
| Цепь с индуктивностью |
|
|
|
| |
ЭДС индукции в катушке достигает максимума, когда ток | максимум |
|
| 50 | ||||
проходит через |
|
|
|
|
|
| ||
|
|
| нулевое значение |
| 6 | |||
Ток в цепи с L изменяется по закону i=Imsin(ωt-π/2). | u=Umsinωt; |
|
| 2 | ||||
Как изменится напряжение и ЭДС самоиндукции в цепи? | eL=Emsin(ωt-π). |
|
| |||||
|
|
|
|
| u=Umsin(ωt-π/2). |
| 16 | |
|
|
|
|
| eL=Emsin(ωt+π/2). |
|
| |
|
|
|
|
| u=Umsin(ωt+π/2).; |
| 7 | |
|
|
|
|
| eL=Emsin(ωt-π/2). |
|
| |
Укажите параметр | переменного | тока, от | которого зависит | Действующее значение | 3 | |||
индуктивное сопротивление катушки |
| напряжения U |
|
| ||||
|
|
|
|
|
|
|
| |
|
|
|
|
| Фаза напряжения ψ |
| 137 | |
|
|
|
|
| Период | переменного | 98 | |
|
|
|
|
| тока T |
|
|
|
Оказывает | ли | индуктивная | катушка | сопротивление | Оказывает |
|
| 123 |
постоянному току, если Rк=0? |
|
|
|
|
| |||
|
| Не оказывает |
| 42 | ||||
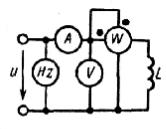
К источнику переменного тока подключена катушка с R=0. В | Амперметра |
| и | 125 | ||||
схему кроме амперметра и вольтметра включены частотомер Hz | вольтметра |
|
|
| ||||
и ваттметр W, измеряющий среднее значение мощности. |
|
| ||||||
Амперметра, вольтметра | 82 | |||||||
Показания | каких | приборов дают возможность рассчитать | и ваттметра |
|
|
| ||
индуктивность L катушки? |
|
|
|
|
|
| ||
|
| Амперметра, вольтметра | 41 | |||||
|
|
|
|
| ||||
|
|
|
|
| и частотомера |
|
| |
|
|
|
|
|
|
|
|
|
Цепь (рис. 5.10) состоит из участков, свойства которых известны. Проанализируем работу данной цепи. Пусть ток в цепи изменяется по закону i=Imsinωt. Тогда напряжение на активном сопротивлении uR=URmsinωt, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке uL=ULmsin(ωt+π/2), поскольку на индуктивности напряжение опережает
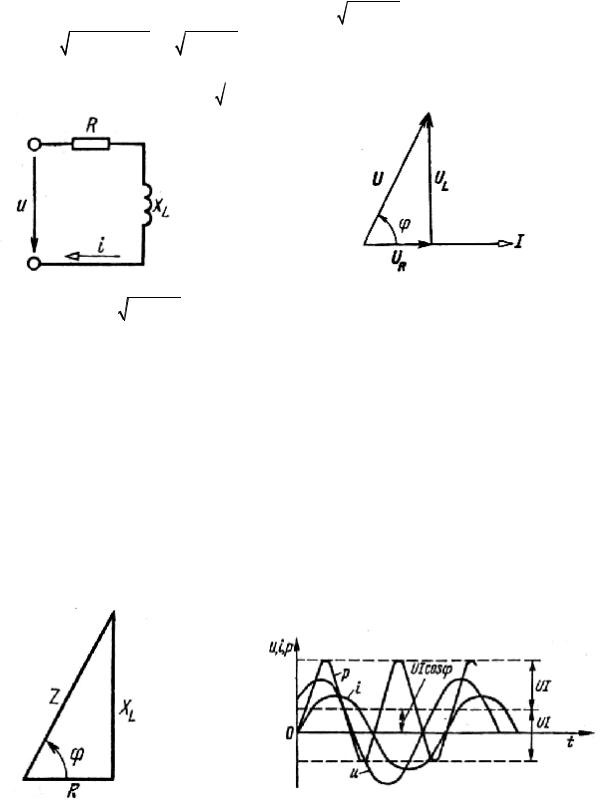
по фазе ток на угол π/2. Построим векторную диаграмму для рассматриваемой цепи (рис. 5.11). Сначала откладываем вектор тока I, затем вектор напряжения UR, совпадающий по фазе с вектором тока. Начало вектора UL, опережающего вектор тока на угол π/2, соединим с концом вектора UR для удобства их сложения. Суммарное напряжение и=Umsin(ωt+ϕ) изображается вектором U, сдвинутым по фазе относительно вектора тока на угол ϕ. Векторы UR, UL и U образуют треугольник напряжений. Выведем закон Ома для этой цепи. На основании теоремы
|
|
|
|
|
|
|
|
|
|
|
|
|
Пифагора для | треугольника | напряжений |
| имеем U = UR2 +UL2 . Но UR=I/R, a UL=IXL; | ||||||||
следовательно, | U = | I 2 R2 + I 2 X L2 | = I | R2 + X L2 |
| откуда |
|
|
| |||
|
|
|
| I = |
|
| U | (5.11) |
| |||
|
|
|
|
|
|
|
|
|
| |||
|
|
|
| R2 | + X L2 |
| ||||||
|
|
|
|
|
|
|
|
| ||||
Рис. 5.10. Схема цепи переменного тока с R и L | Рис. 5.11. Векторная диаграмма для цепи с R и L | ||
Введем обозначение |
| = Z , где Z — полное сопротивление цепи. Тогда выражение | |
R2 + XL2 | |||
закона Ома примет вид |
| ||
| I=U/Z. | (5.12) | |
Так как полное сопротивление цепи Z определяется по теореме Пифагора, ему соответствует треугольник сопротивлений (рис. 5.12). Поскольку при последовательном соединении напряжения на участках прямо пропорциональны сопротивлениям, треугольник сопротивлений подобен треугольнику напряжений. Сдвиг фаз ϕ между током и напряжением
определяется из треугольника сопротивлений: |
|
tgϕ=XL/R; | (5.13) |
cosϕ=R/Z. | (5.14) |
Для последовательной цепи условимся отсчитывать угол ϕ от вектора тока I. Поскольку вектор U сдвинут по фазе относительно вектора I на угол ϕ против часовой стрелки, этот угол имеет положительное значение. В дальнейшем покажем, что знак угла ϕ определяется по формальному признаку.
Выведем энергетические соотношения для цепи с активным сопротивлением и индуктивностью.
Рис. 5.12. Треугольник сопротивлений для цепи с R и L | Рис. 5.13. Временные диаграммы напряжения, тока и | |
мгновенной мощности для цепи с R и L | ||
|
Мгновенная мощность.
Мгновенная мощность выражается соотношениями

(5.15)
p= ui = Um Im sin (ωt +ϕ )sinωt =
=Um Im (sinωt cosϕ + cosωt sinϕ )sinωt =
=Um Im (sin2 ωt cosϕ + sinωt cosωt sinϕ ) =
=Um Im æç1- cos 2ωt cosϕ + sin 2ωt sinϕ ö÷ =
è2 2 ø
= Um2Im (cosϕ -(cos 2ωt cosϕ -sin 2ωt sinϕ ))
или
p = UI cosϕ -UI cos(2ωt +ϕ )
Анализ выражения (5.15) и рис. 5.13, построенного на его основе, показывает, что мгновенное значение мощности колеблется около постоянного уровня UIcosj, который характеризует среднюю мощность. Отрицательная часть графика определяет энергию, которая переходит от источника к индуктивной катушке и обратно.
Средняя мощность.
Средняя, или активная, мощность для данной цепи характеризует расход энергии на активном сопротивлении и, следовательно, P=URI. Из векторной диаграммы (см. рис. 5.11) видно, что UR=Ucosj. Тогда
P=UIcosj. (5.16)
Реактивная мощность.
Реактивная мощность характеризует интенсивность обмена энергией между индуктивной катушкой и источником:
Q=ULI=UIsinϕ. (5.17)
Полная мощность.
Понятие полной мощности применяют для оценки предельной мощности электрических машин:
S=UI. | (5.18) | |
Так как sin2ϕ+cos2ϕ=l, то |
| (5.19) |
S = P2 + Q2 | ||
Единицей полной мощности является вольт-ампер (В×А).
§ 5.3. Цепь с индуктивностью
Анализ формулы (5.3) и рис. 5.4, соответствующего этой формуле, показывает, что мгновенная мощность, оставаясь все время положительной, колеблется около уровня UI.
Средняя мощность.
Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности. Для вывода выражения средней мощности найдем сначала расход энергии в цепи с активным сопротивлением R за время Т/2:
| T /2 | T / 2 |
|
| Т /2 | Т / 2 |
|
|
|
| W = ò pdp = | ò (UI −UI cos 2ωt)dt = ò UIdt − ò UI cos2ωtdt |
|
| |||||
| 0 | 0 |
| 0 | 0 |
|
|
| |
Так как W = Tò/2 | pdp = Tò/ 2UI cos2ωtdt = 0, | то | W =UI | T |
|
|
| ||
0 | 0 |
|
|
|
| 2 |
|
|
|
Разделив полученное выражение для W на Т/2, получим среднюю скорость расхода энергии | |||||||||
или среднюю (активную) мощность: |
|
|
|
|
|
|
|
| |
| P=UI. |
|
|
|
| (5.4) |
|
|
|
Единицами активной мощности являются ватт (Вт), киловатт (кВт) и мегаватт (МВт): | |||||||||
1кВт=103Вт; 1МВт=106Вт. | Карточка № 5.1 (188). |
|
|
|
| ||||
|
|
|
|
|
| ||||
| Цепь с активным сопротивлением |
|
|
| |||||
В цепи с активным сопротивлением энергия источника | магнитного поля |
| 88 |
| |||||
преобразуется в энергию |
|
|
|
|
|
| |||
|
|
| электрического поля | 135 |
| ||||
|
|
|
|
| тепловую |
| 9 |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
| магнитного, | электрического | 47 |
| |
|
|
|
|
| полей и тепловую |
|
|
| |
Возможно ли практически реализовать чисто активное | Возможно |
| 57 |
| |||||
сопротивление? |
|
|
|
|
|
|
|
| |
|
|
|
| Невозможно |
| 61 |
| ||
Напряжение на зажимах данной цепи и=100sin314t. | I=1А; U=100В |
| 15 |
| |||||
Определить показание амперметра и вольтметра, если |
|
|
|
| |||||
I=0,7А; U=70В |
| 52 |
| ||||||
R=100Ом |
|
|
|
|
|
|
|
|
|
|
|
|
| I=0,7А; U=100В |
| 1 |
| ||
|
|
|
|
|
|
| |||
|
|
|
|
|
| ||||
Напряжение на зажимах цепи с | активным | i=4,4sin314t |
| 32 |
| ||||
сопротивлением | изменяется | по | закону |
|
|
|
| ||
i=4,4sin(314t+π/4) |
| 12 |
| ||||||
u=220sin(314t+π/4). Определить закон изменения тока в |
|
|
|
| |||||
i=3,lsin(314t+π/4) |
| 115 |
| ||||||
цепи, если R = 50Ом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
При каком соотношении между t и Т | (период | t >>T |
| 21 |
| ||||
переменного тока) нельзя воспользоваться | формулой |
|
|
|
|
| |||
i=kT | (k—целое | положительное | 73 |
| |||||
W=R/t для определения расхода энергии за время? |
| число) |
|
|
| ||||
|
|
|
|
| t <T |
|
| 54 |
|
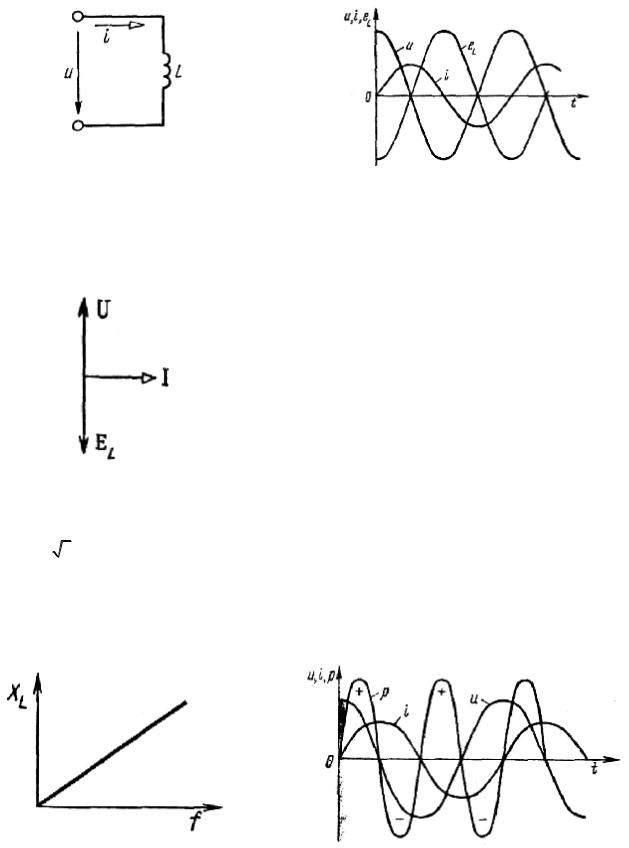
Под действием синусоидального напряжения в цепи с индуктивной катушкой без ферромагнитного сердечника (рис. 5.5) проходит синусоидальный ток i=Imsinωt. В результате
этого вокруг катушки возникает переменное магнитное поле и в катушке и наводится ЭДС самоиндукции. При R=0 напряжение источника целиком идет на уравновешивание этой ЭДС;
следовательно, и=—еL. Так как e = −L di , то |
|
| ||||
|
| L | dt |
|
| |
u = L | di | = L | d (Im sinωt) | = Im sinωL cosωt | (5.5) | |
dt | dt | |||||
|
|
|
| |||
или
u = Um sin (ωt +π / 2)
Рис. 5.5. Схема цепи переменного тока с индуктивностью | Рис. 5.6. Временные диаграммы напряжения, тока и ЭДС | |
для цепи с индуктивностью | ||
|
Сопоставляя выражения для мгновенных значения тока и напряжения, приходим к выводу, что ток в цепи с индуктивностью отстает по фазе от напряжения на угол π/2. Физически это объясняется тем, что индуктивная катушка реализует инерцию электромагнитных процессов. Индуктивность катушки L является количественной мерой этой инерции. Фазовые соотношения между током, напряжением и ЭДС для цепи с индуктивностью показаны на рис. 5.6 и 5.7.
Рис. 5.7. Векторная диаграмма напряжения, тока и ЭДС
для цепи с индуктивностью
Выведем закон Ома для этой цепи. Из выражения (5.6) следует, что Im=Um/(ωL). Пусть ωL=2πfL=XL, где XL — индуктивное сопротивление цепи. Тогда получим выражение
которое является законом Ома для амплитудных значений. Разделив левую и правую части этого
выражения на 2 , получим закон Ома для действующих значений: |
|
I=U/XL. | (5.8) |
Проанализируем выражение для XL=2πfL. С увеличением частоты тока f индуктивное сопротивление XL увеличивается (рис. 5.8). Физически это объясняется тем, что возрастает скорость изменения тока, а следовательно, и ЭДС самоиндукции.
Рассмотрим энергетические характеристики цепи с индуктивностью.
Рис. 5.8. Зависимость индуктивного сопротивления XL от | Рис. 5.9. Временные диаграммы напряжения, тока и |
частоты f | мгновенной мощности для цепи с индуктивностью |
Мгновенная мощность.
5.3 Неразветвленная цепь с активным сопротивлением, емкостью и индуктивностью
5.3.1 Рекомендации для студента
В неразветвленной цепи протекает ток 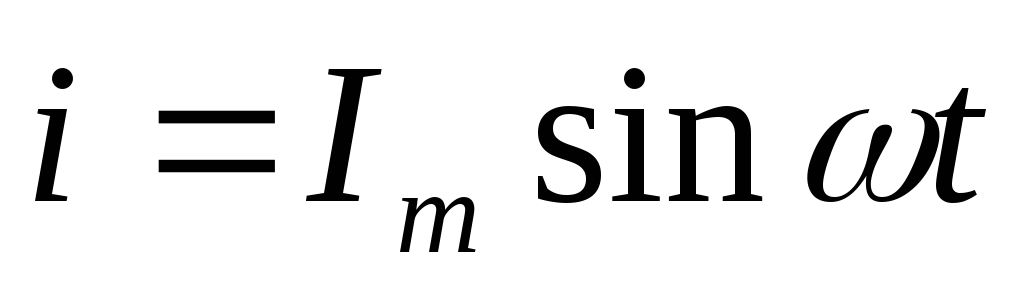 ;
;
Для неразветвленной цепи переменного тока с активным, емкостным и индуктивным сопротивлениями справедливы следующие соотношения:
 — напряжение на активном сопротивлении;
— напряжение на активном сопротивлении; — напряжение на индуктивности;
— напряжение на индуктивности; — напряжение на емкости;
— напряжение на емкости; — общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;
— общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL; —
действующее напряжение в цепи;
—
действующее напряжение в цепи; —
закон Ома;
—
закон Ома; — полное (кажущееся) сопротивление;
— полное (кажущееся) сопротивление; ;
; ;
; ;
; — полная мощность цепи;
— полная мощность цепи; — активная мощность цепи;
— активная мощность цепи; — реактивная мощность в цепи.
— реактивная мощность в цепи.
5.3.2 Примеры решения задач
Задача№5.4
Последовательная цепь (рисунок 5.7) подключена к источнику переменного напряжения U=36В. Параметры выбраны следующие:R=10Ом,L=10мГн,C=1мкФ. Определить характеристики полного сопротивления и тока цепи при частоте 7961,8Гц.
Дано: U=36В
R=10Ом
L=10мГн
C=1мкФ
F=7961,8Гц
————————
Определить: I, Z
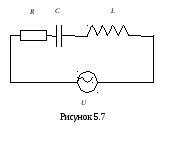
Решение задачи
Находим полное сопротивление: ;
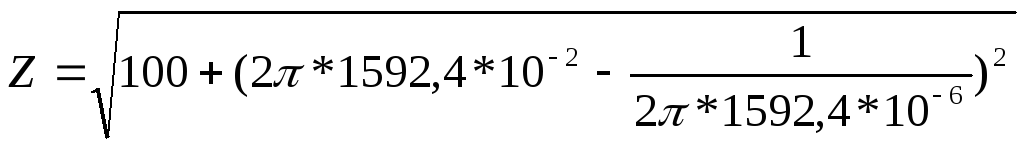 =10
Ом;
=10
Ом;
Находим ток: I=U/Z;
I=36/10=3,6А.
5.4 Резонанс напряжений
5.4.1 Рекомендации для студента
В цепях переменного тока с последовательно соединенными катушкой, резистором и конденсатором, в которых реактивные сопротивления равны между собой (XL=XС), наступает резонанс напряжений. В этом случае сопротивление становится минимальным и равным активному сопротивлению. Так как реактивные сопротивления зависят от частоты, то резонанс наступит при определенной частоте, которая называется резонансной.
 — циклическая резонансная частота;
— циклическая резонансная частота; —
резонансная частота тока;
—
резонансная частота тока; — волновое сопротивление;
— волновое сопротивление; — добротность цепи;
— добротность цепи; —
мощность при резонансе напряжений.
—
мощность при резонансе напряжений.
Напряжения на индуктивности и емкости при резонансе равны между собой и могут оказаться больше по значению напряжения цепи. Понятие добротности имеет важное практическое значение (например, для антенн).
5.4.2 Примеры решения задач
Задача№5.5
В сеть синусоидального тока с частотой f= 50 Гц включены последовательно реостат с сопротивлениемR=5 Ом, индуктивностьLи емкостьC. Вычислить индуктивностьLи емкостьC, если напряжения наR, LиCодинаковы.
Дано: f= 50 Гц
R=5 Ом
UL=UC=UR
————————
Определить: L, C;
Решение задачи
Так как в неразветвленной цепи ток на всех участках (сопротивлениях) имеет одинаковое значение, то и падение напряжения на всех участках цепи имеет одинаковое значение при одинаковых сопротивлениях участков.
R=5 Ом,XL=5 Ом,XC=5 Ом.
Схема цепи изображена на рисунке 5.8
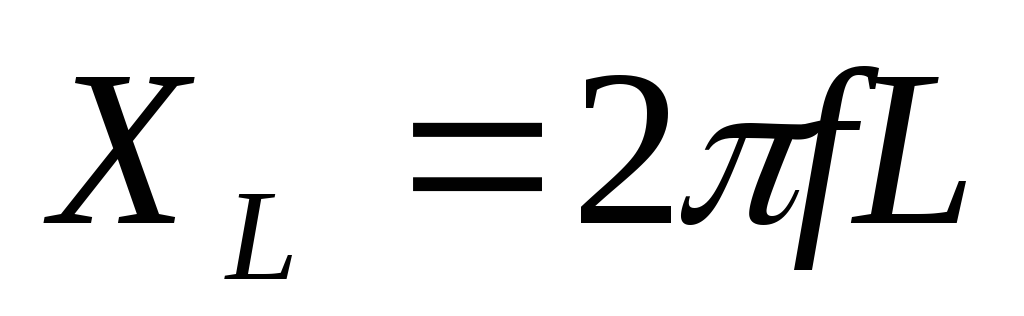 -индуктивное сопротивление;
-индуктивное сопротивление;
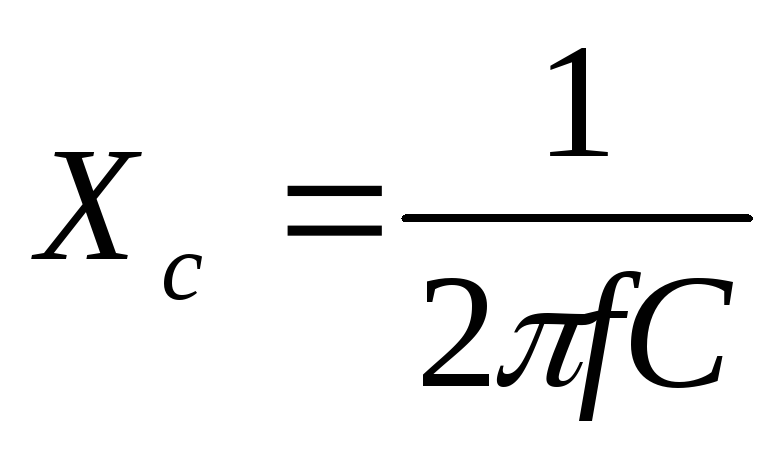 — емкостное сопротивление;
— емкостное сопротивление;
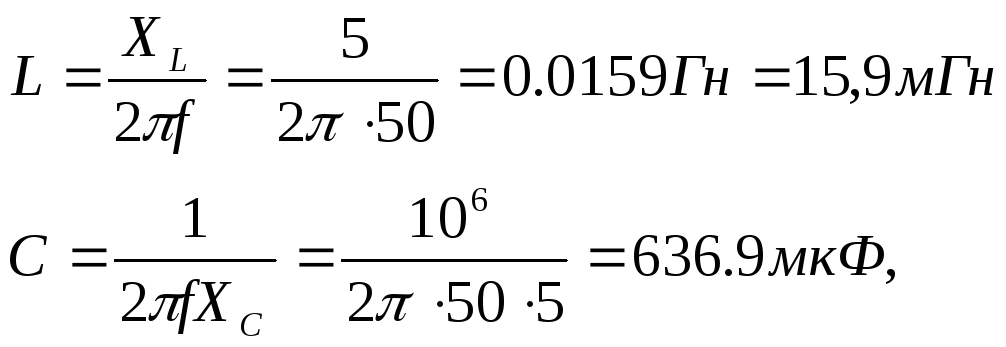
В цепи имеет место резонанс напряжений, так как равенство напряжений на реактивных элементах возможно только при наличии резонанса.
5.5 Общий случай неразветвленной цепи
5.5.1 Рекомендации для студента
В неразветвленной цепи в общем случае может быть включено несколько активных, несколько реактивных сопротивлений. Такие цепи рассчитываются аналогично цепям, содержащим активное, емкостное и индуктивное сопротивления. Находим эквивалентные сопротивления: активное, емкостное, индуктивное, как суммы соответствующих сопротивлений.
Тема 3.1
Начальные сведения о переменном токе
Однофазные электрические цепи переменного тока
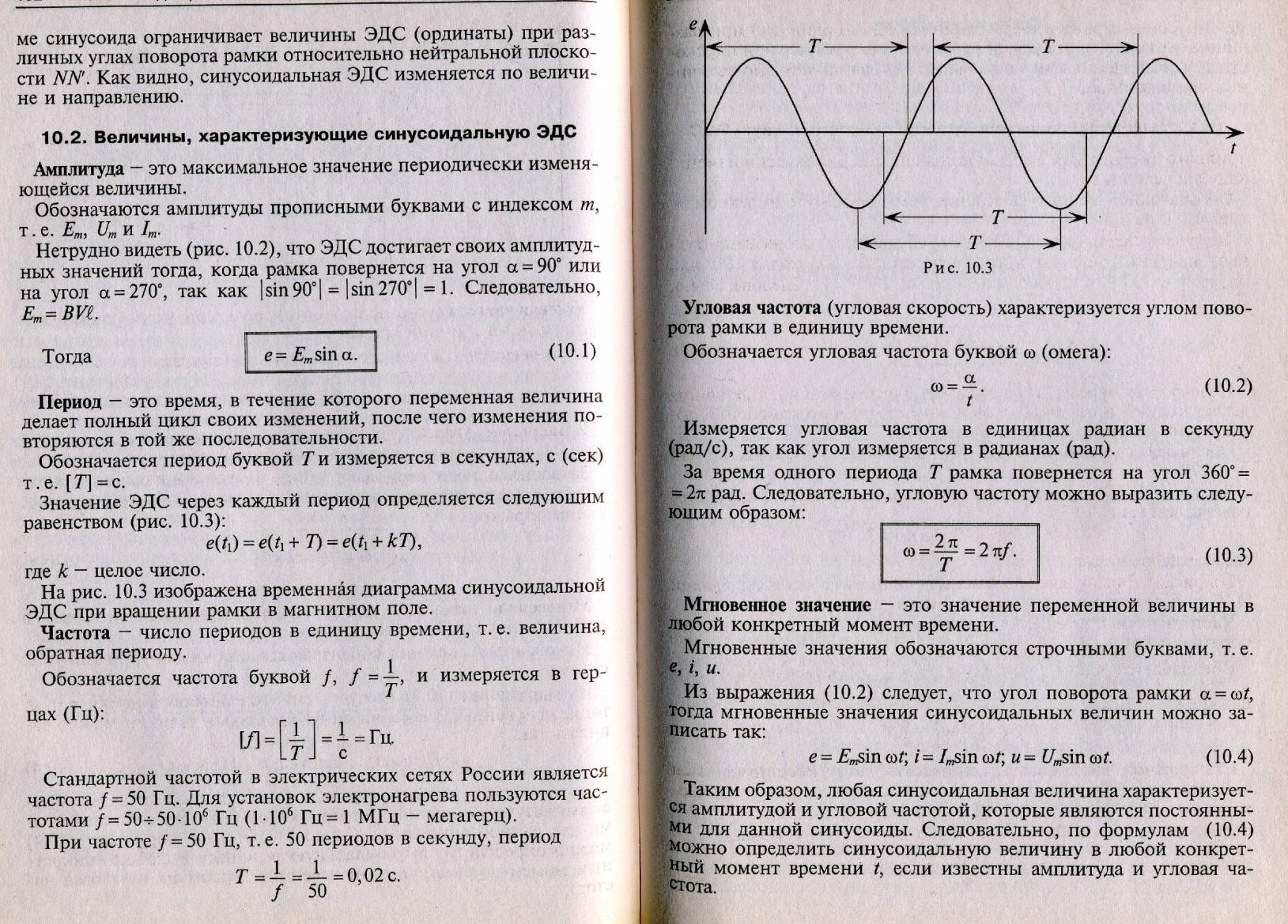
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение.
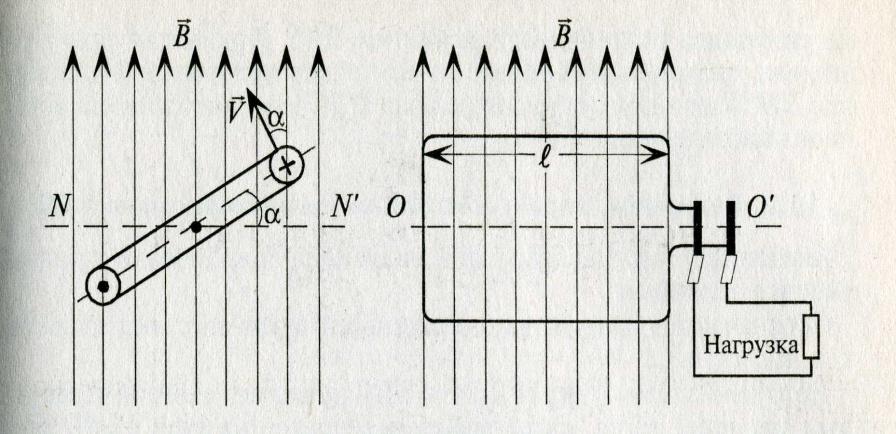
Рисунок 1
e= BVlsinα
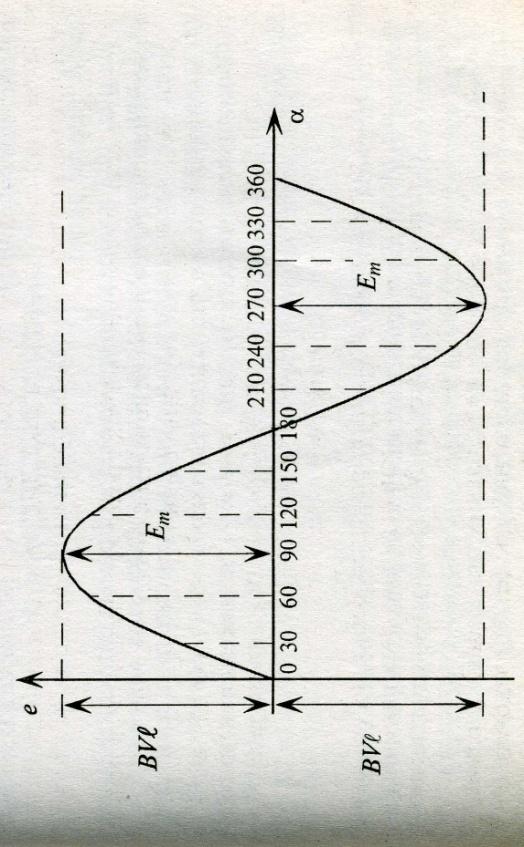
Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка длиной l индуктируется ЭДС электромагнитной индукции, которая будет равна: e= BVlsinα; (смотрите рисунок 1)
ТЕМА 3.2
Электрические цепи переменного тока
Расчет электрических цепей переменного синусоидального тока может быть проведен несколькими методами:
1.С помощью векторных диаграмм;
2.Символический метод;
3.Метод круговых диаграмм.
Расчет электрических цепей синусоидального тока проводится преимущественно с помощью векторных диаграмм. Сущность этого метода состоит в том, что активную и реактивную составляющие токов, напряжений, сопротивлений можно представить в виде векторов, имеющих разное направление.
Расчет цепи с активным сопротивлением и индуктивностью
Реальные электрические цепи не могут состоять из идеальных реактивных сопротивлений, в них присутствует активное сопротивление. В цепи, с последовательно соединенными активным сопротивлением и индуктивностью (рисунок 5.1), активное напряжение совпадает по фазе с током, индуктивное напряжение опережает ток по фазе на угол 900.
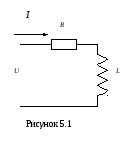
При протекании тока 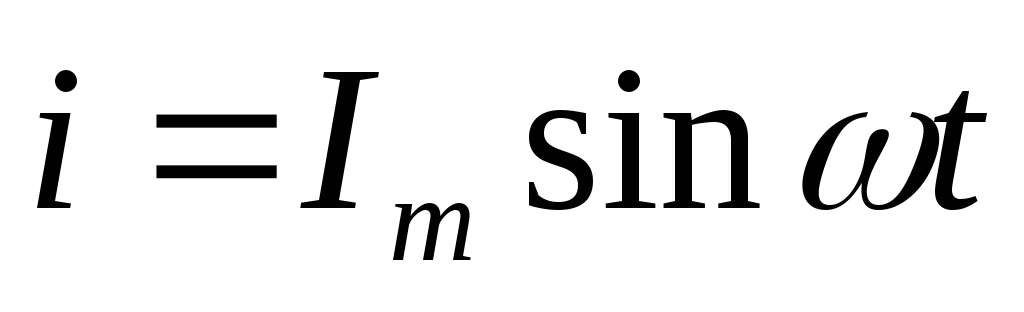 в электрической цепи с активным
сопротивлением и индуктивностью
справедливы следующие соотношения:
в электрической цепи с активным
сопротивлением и индуктивностью
справедливы следующие соотношения:
Треугольники напряжений, сопротивлений, мощностей.
Цепь с активным сопротивлением и емкостью
В цепи (рисунок 5.4) с активным сопротивлением и емкостью напряжение на реактивном сопротивлении отстает от тока по фазе на 900.
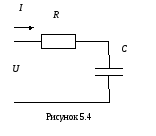
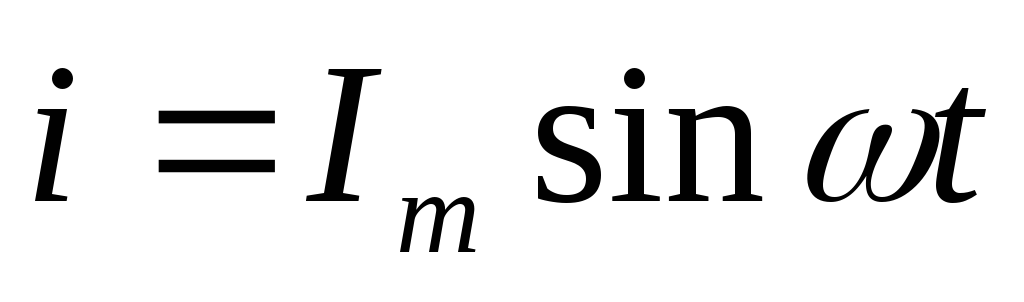 —
ток в цепи;
—
ток в цепи;
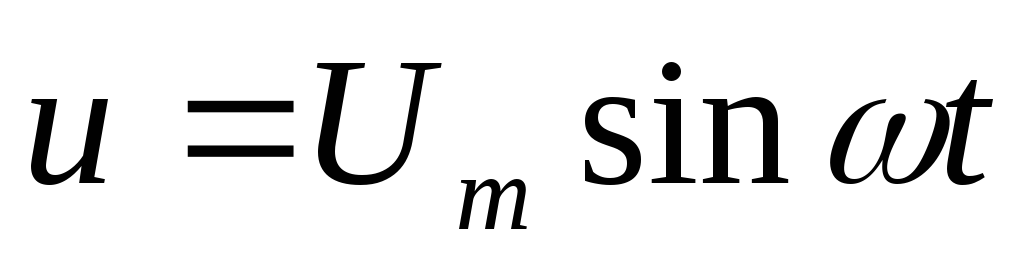 -напряжение на активном сопротивлении;
-напряжение на активном сопротивлении;
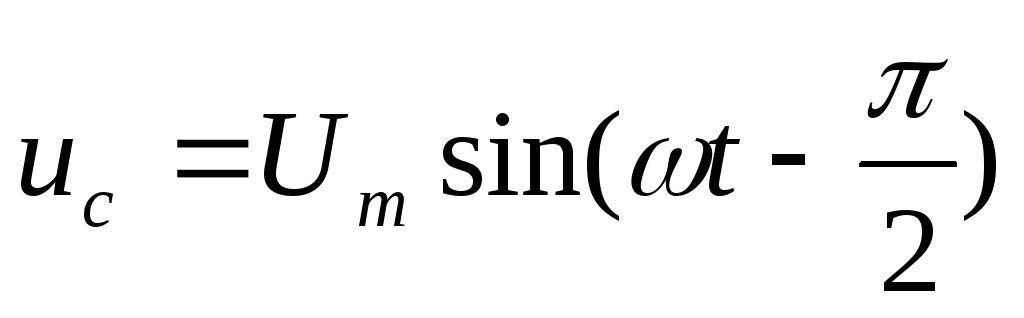 — напряжение на емкостном сопротивлении;
— напряжение на емкостном сопротивлении;
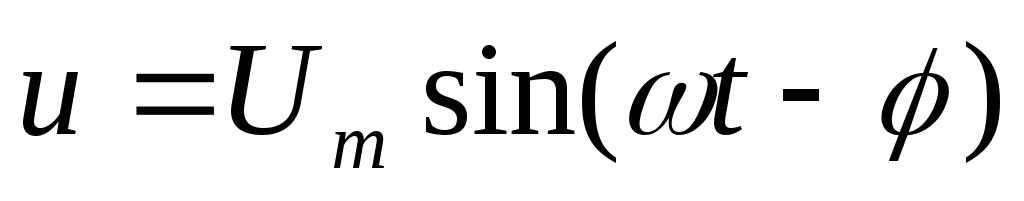 —
напряжение цепи;
—
напряжение цепи;
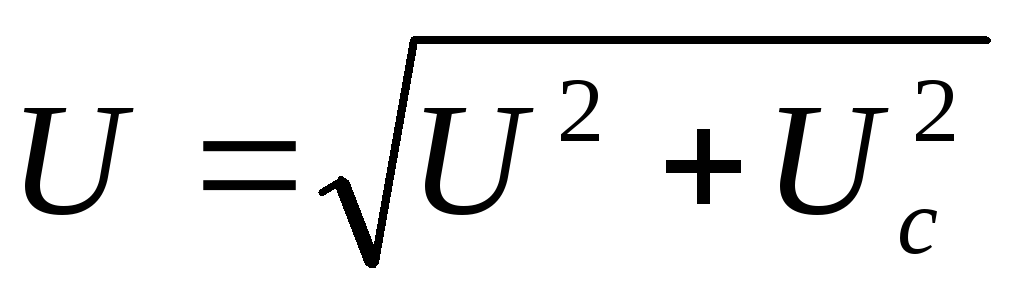 =
=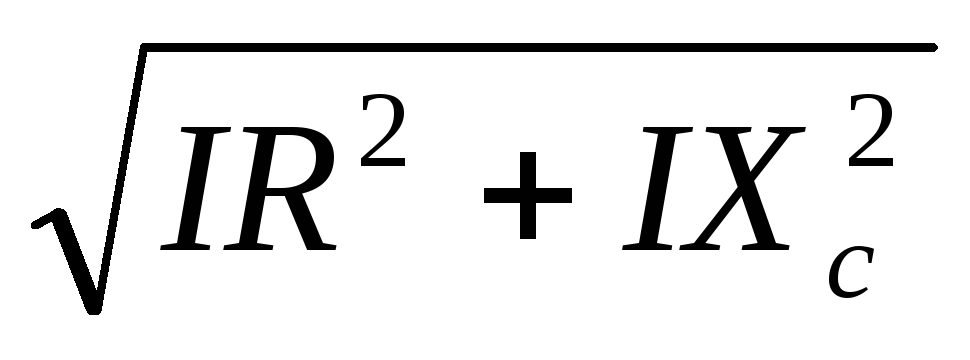 =
=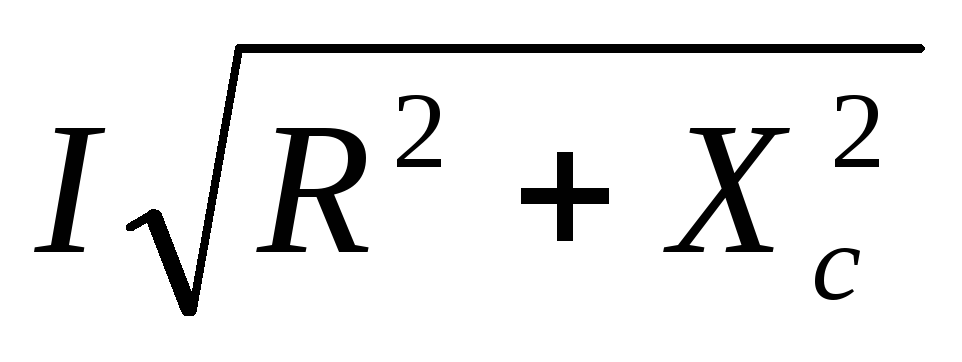 — действующее напряжение в цепи;
— действующее напряжение в цепи;
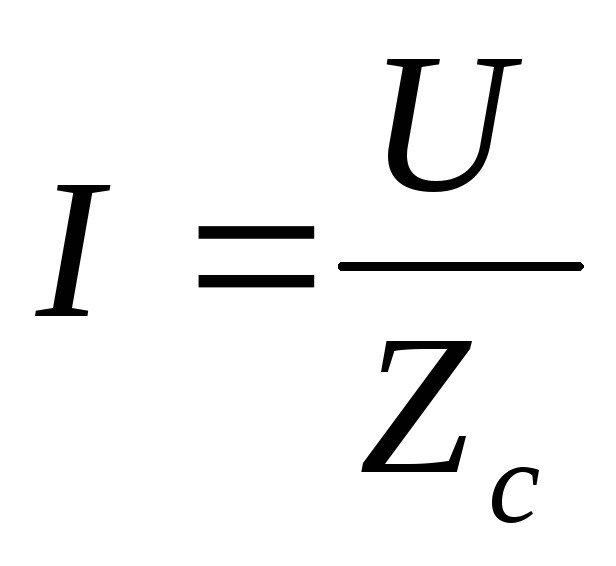 — ток в этой цепи определяется по закону
Ома;
— ток в этой цепи определяется по закону
Ома;
Неразветвленная цепь с активным сопротивлением, емкостью и индуктивностью
В неразветвленной цепи протекает ток 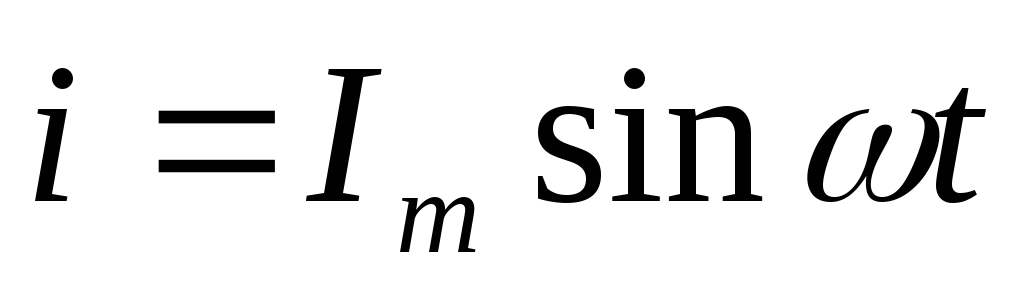 ;
;
Для неразветвленной цепи переменного тока с активным, емкостным и индуктивным сопротивлениями справедливы следующие соотношения:
 — напряжение на активном сопротивлении;
— напряжение на активном сопротивлении; — напряжение на индуктивности;
— напряжение на индуктивности; — напряжение на емкости;
— напряжение на емкости; — общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;
— общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL; —
действующее напряжение в цепи;
—
действующее напряжение в цепи; —
закон Ома;
—
закон Ома; — полное (кажущееся) сопротивление;
— полное (кажущееся) сопротивление; ;
; ;
; ;
; — полная мощность цепи;
— полная мощность цепи; — активная мощность цепи;
— активная мощность цепи; — реактивная мощность в цепи.
— реактивная мощность в цепи.


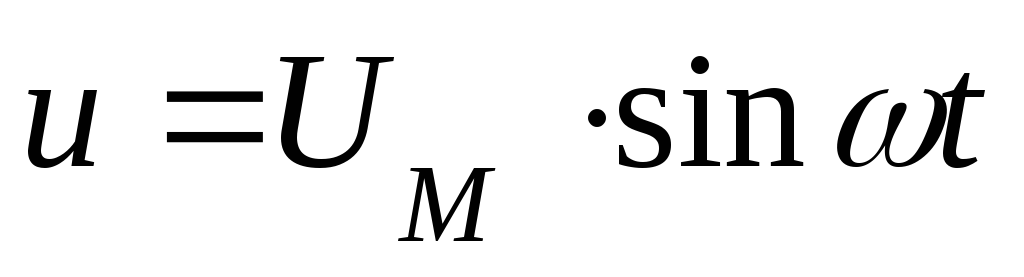
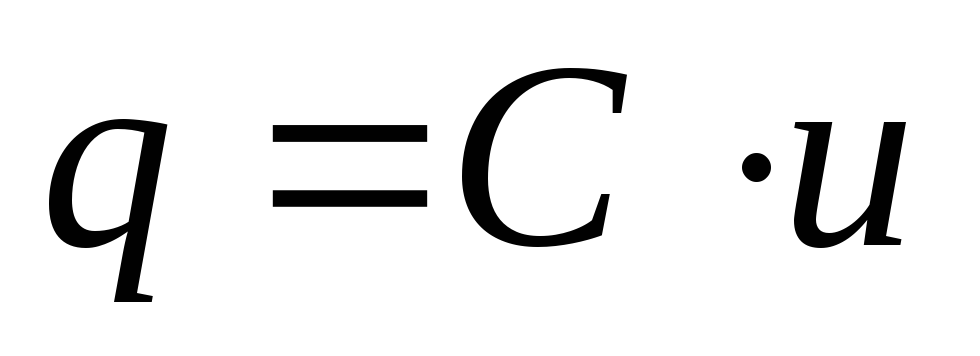
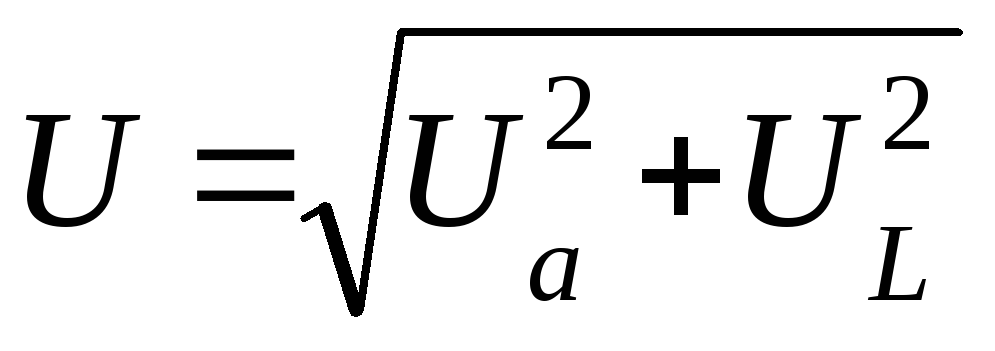
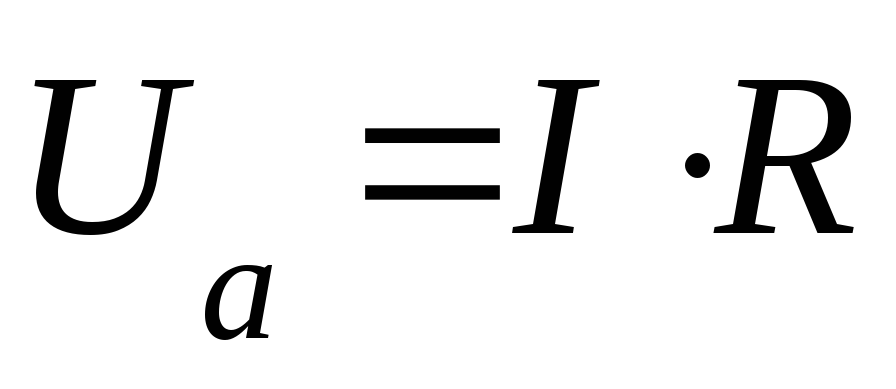
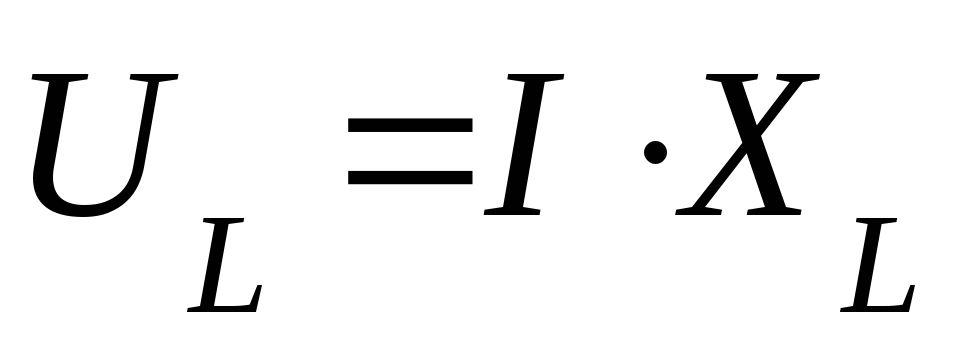
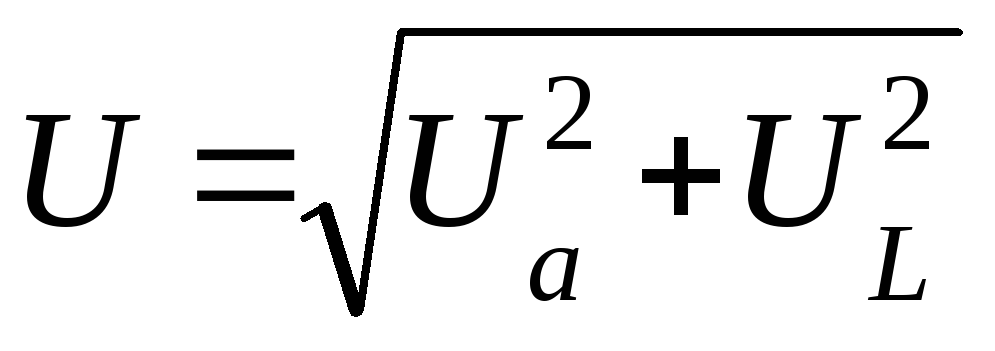
 — полное
сопротивление цепи
— полное
сопротивление цепи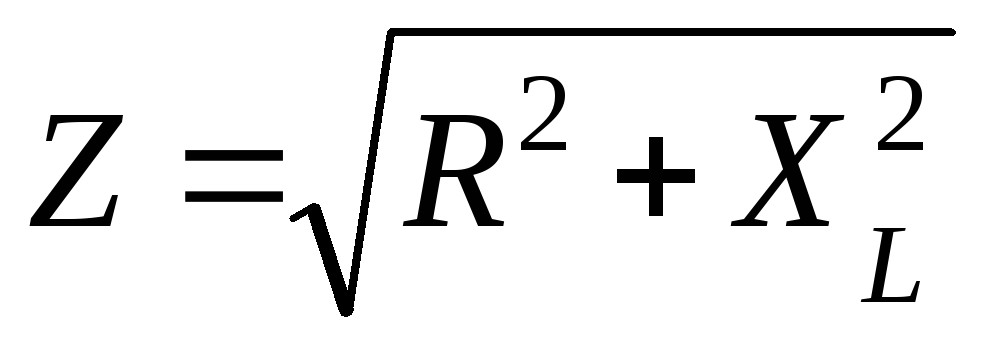
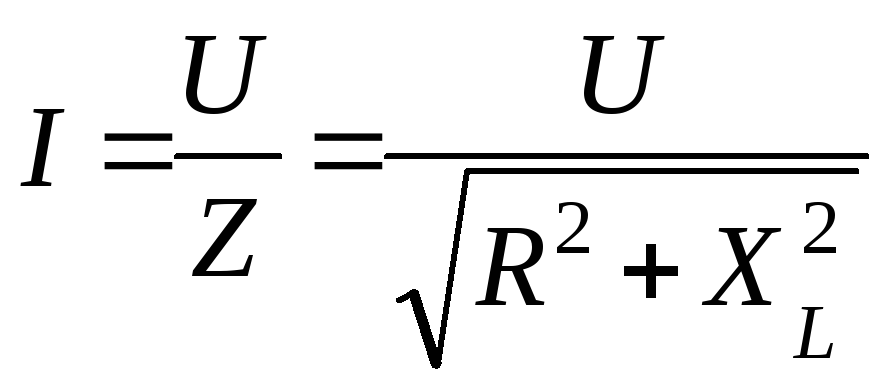
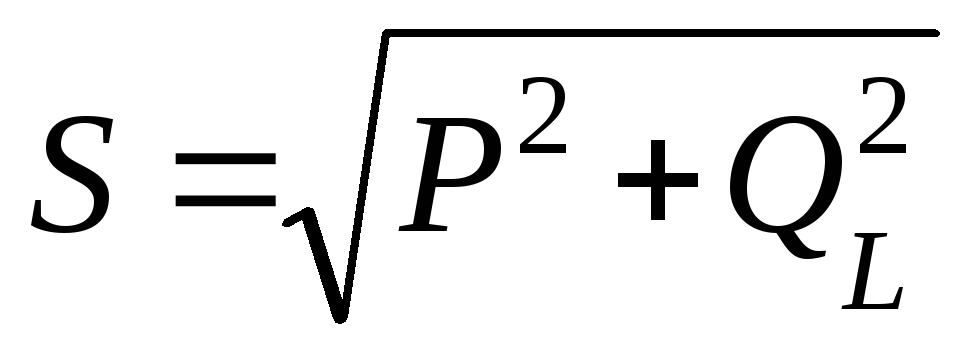
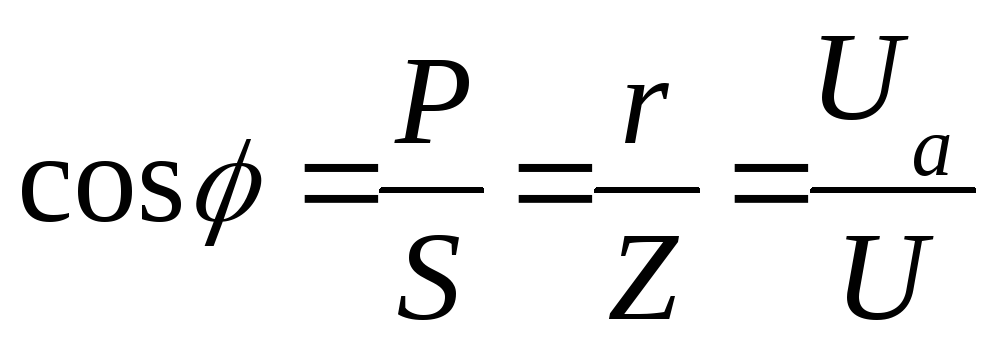 —
коэффициент мощности
—
коэффициент мощности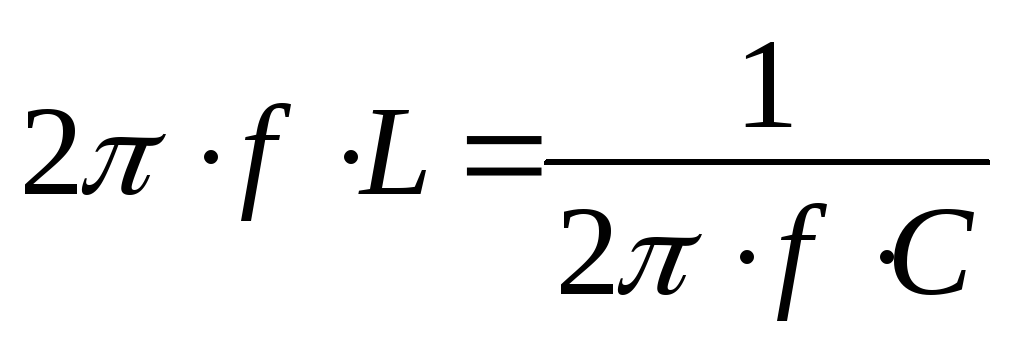
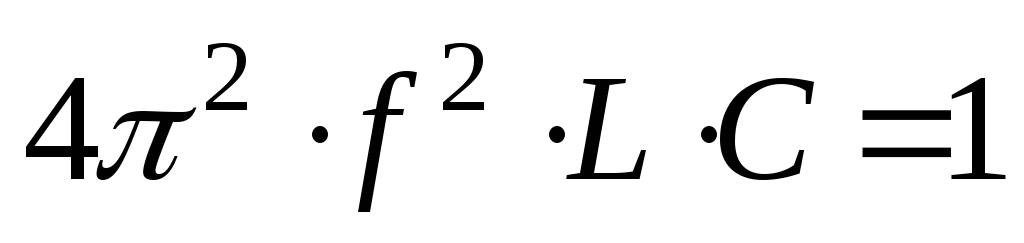
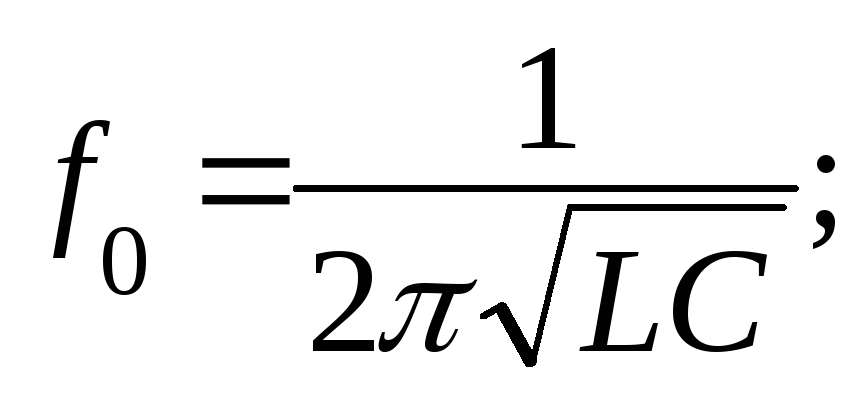
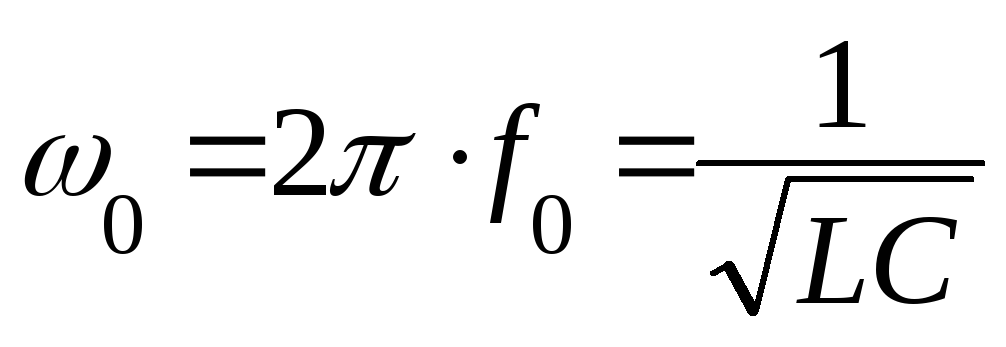
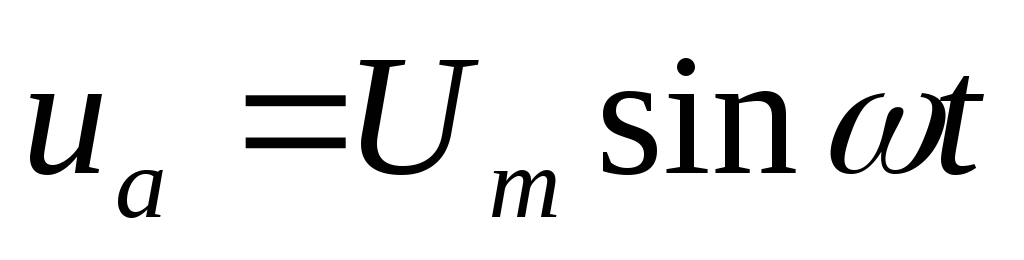 — напряжение на активном сопротивлении;
— напряжение на активном сопротивлении;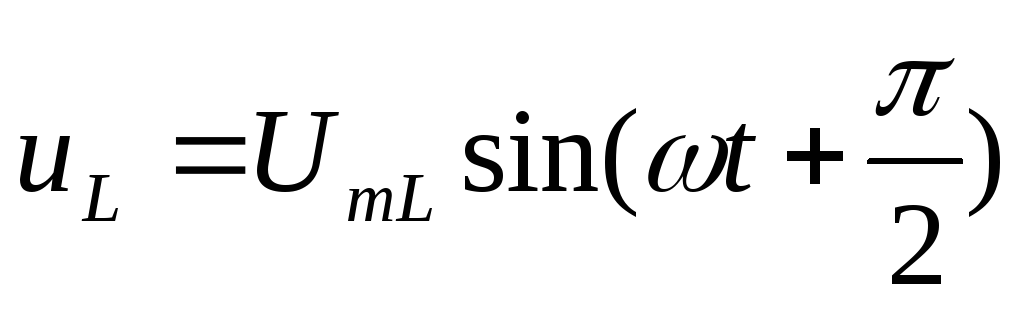 — напряжение на индуктивности;
— напряжение на индуктивности;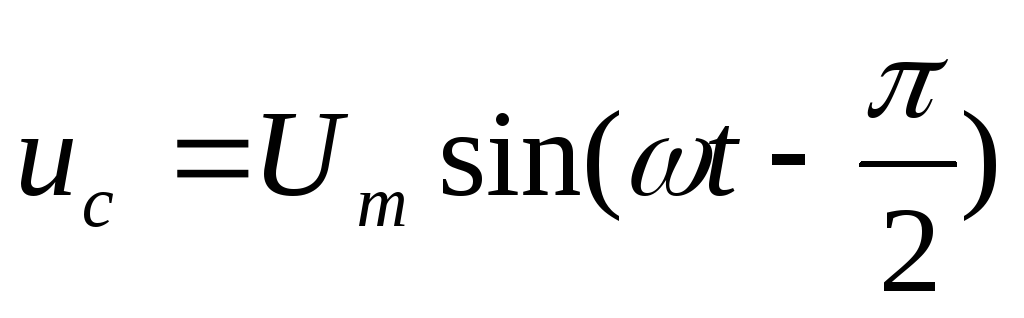 — напряжение на емкости;
— напряжение на емкости;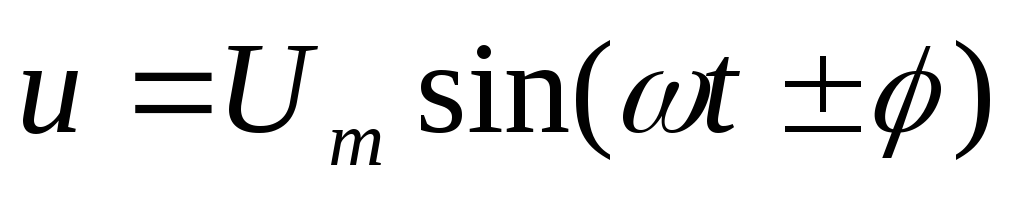 — общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;
— общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;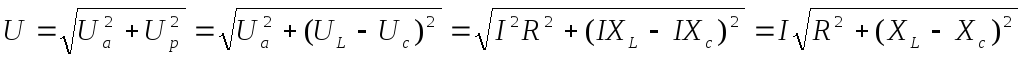 —
действующее напряжение в цепи;
—
действующее напряжение в цепи;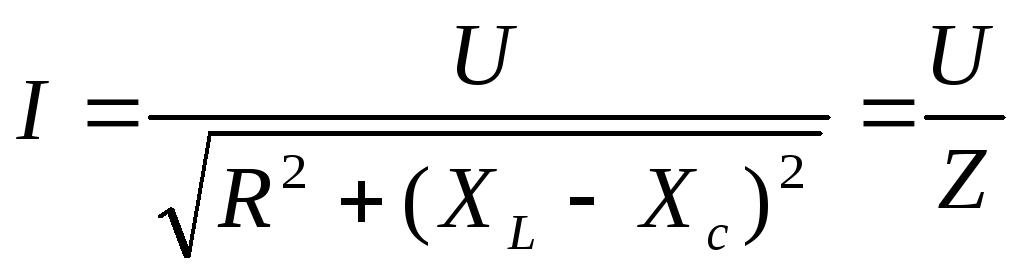 —
закон Ома;
—
закон Ома;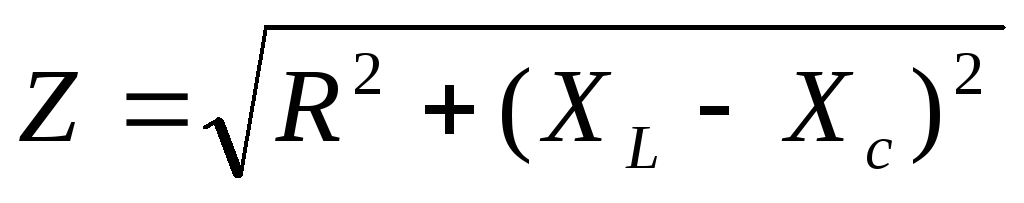 — полное (кажущееся) сопротивление;
— полное (кажущееся) сопротивление;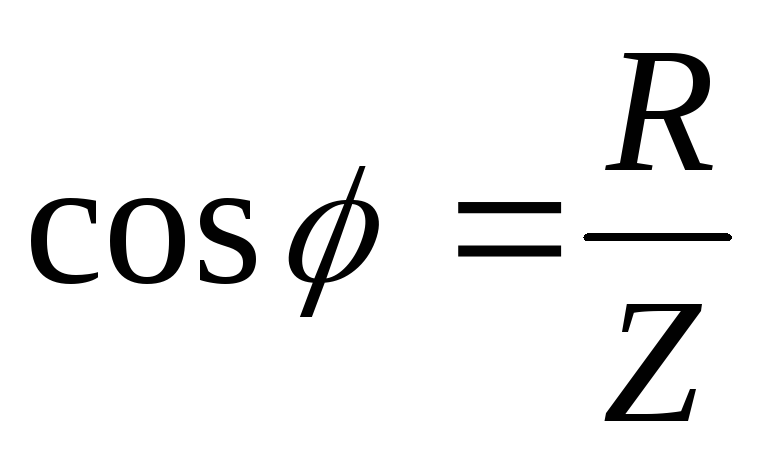 ;
;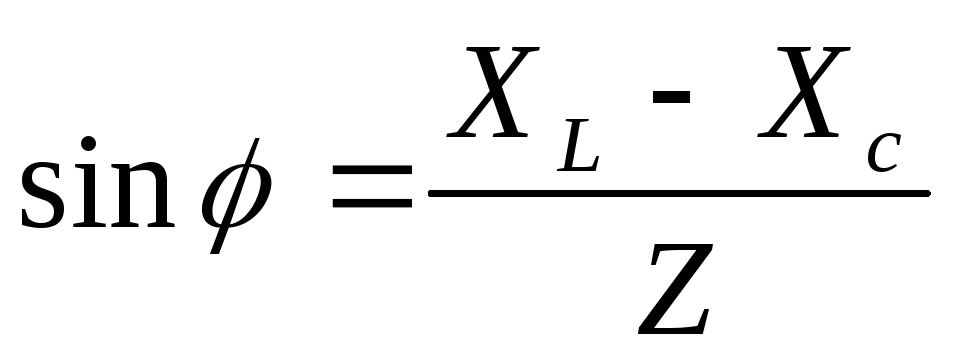 ;
;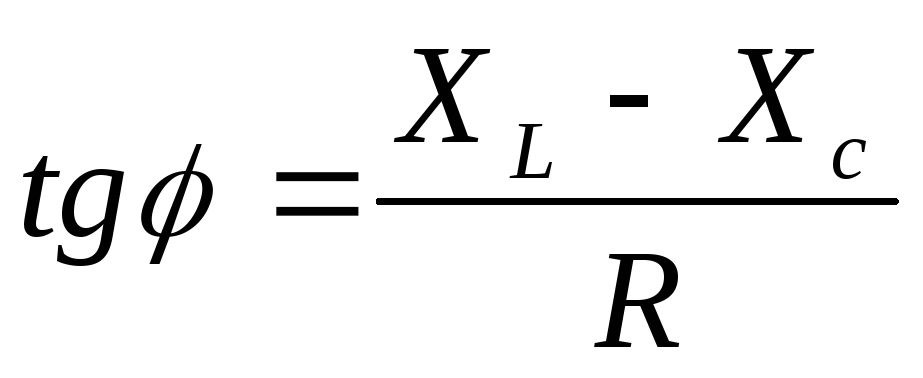 ;
;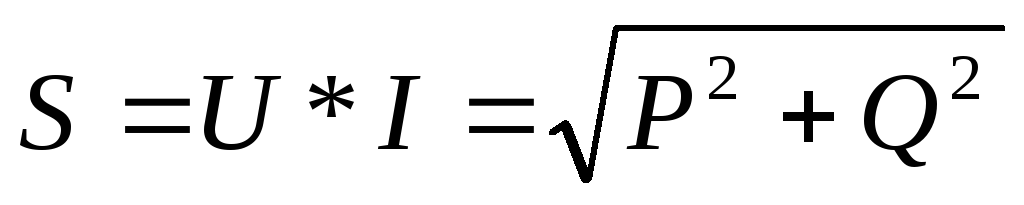 — полная мощность цепи;
— полная мощность цепи;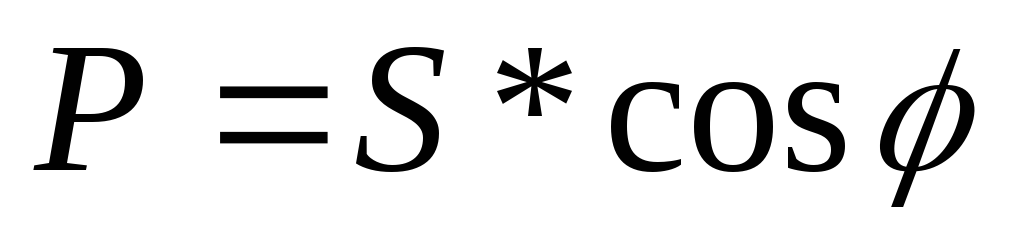 — активная мощность цепи;
— активная мощность цепи;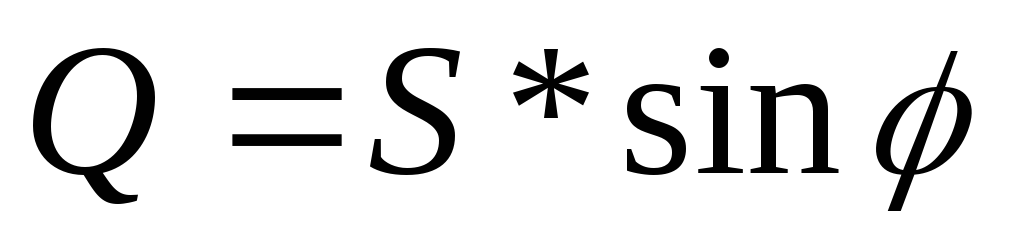 — реактивная мощность в цепи.
— реактивная мощность в цепи.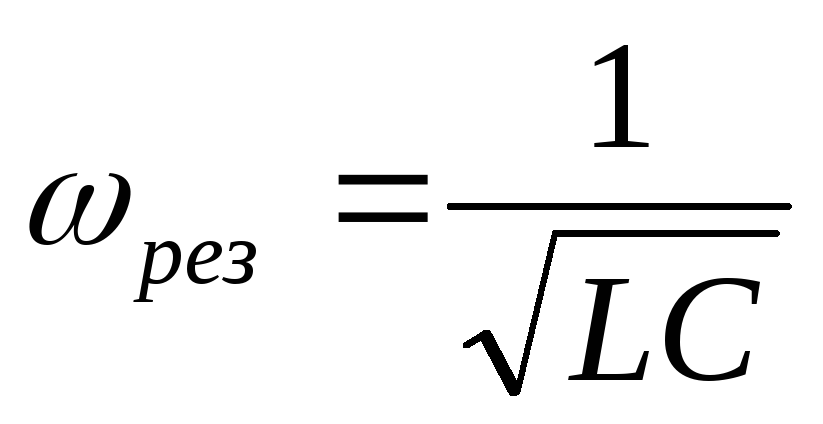 — циклическая резонансная частота;
— циклическая резонансная частота;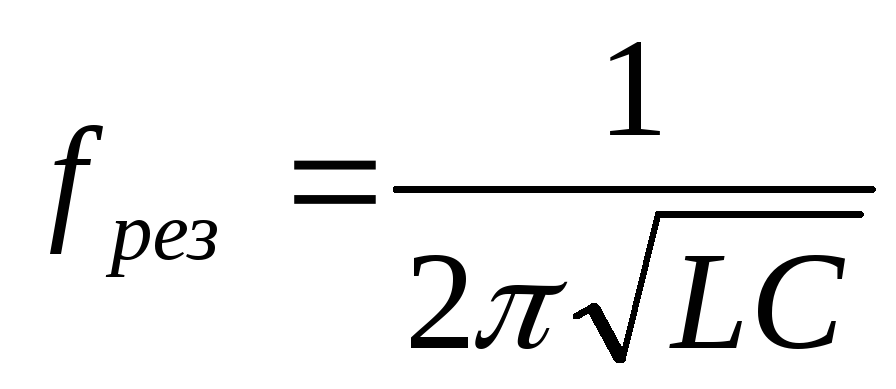 —
резонансная частота тока;
—
резонансная частота тока;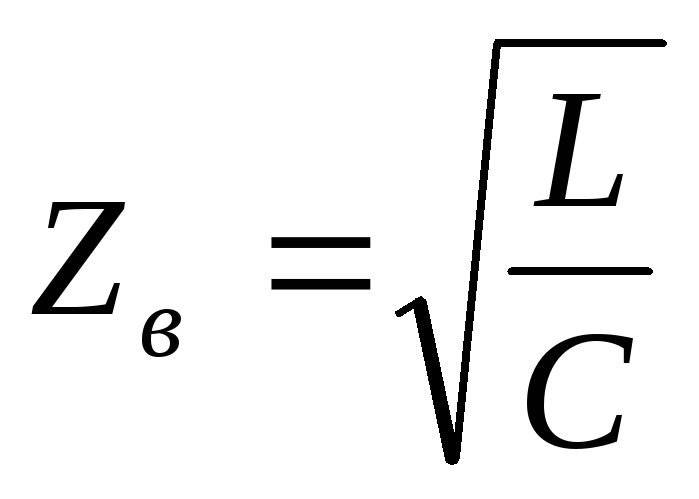 — волновое сопротивление;
— волновое сопротивление;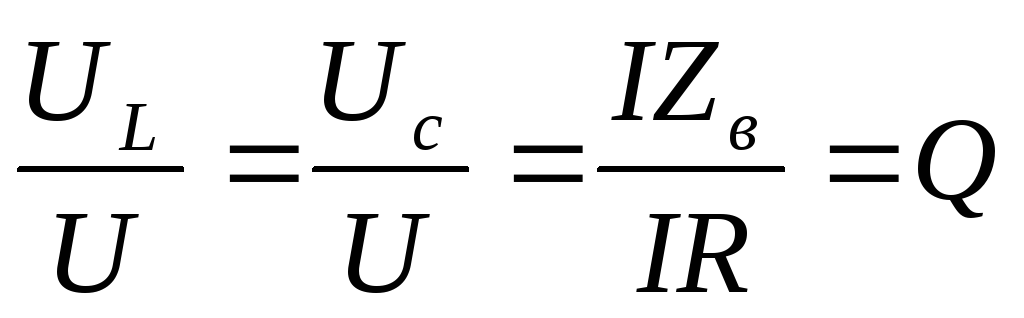 — добротность цепи;
— добротность цепи;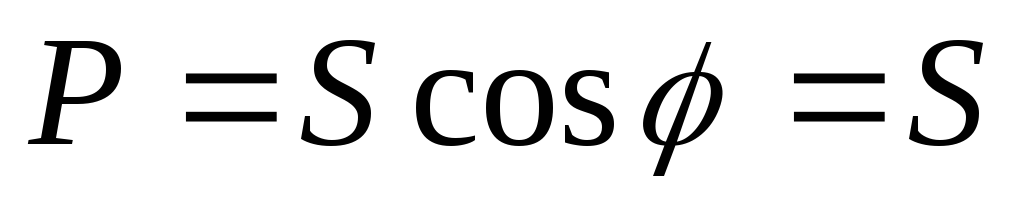 —
мощность при резонансе напряжений.
—
мощность при резонансе напряжений.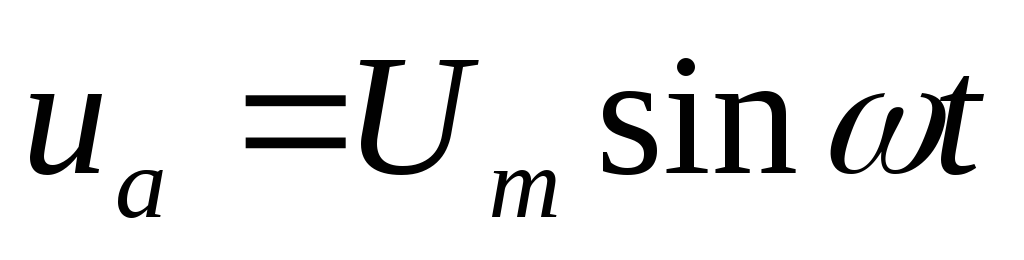 — напряжение на активном сопротивлении;
— напряжение на активном сопротивлении;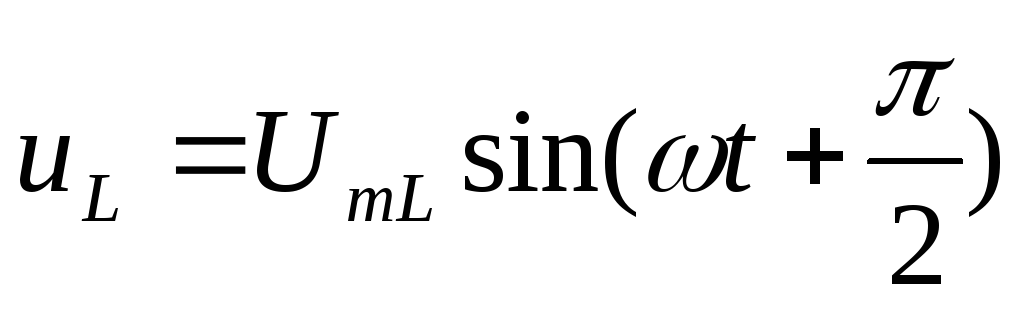 — напряжение на индуктивности;
— напряжение на индуктивности;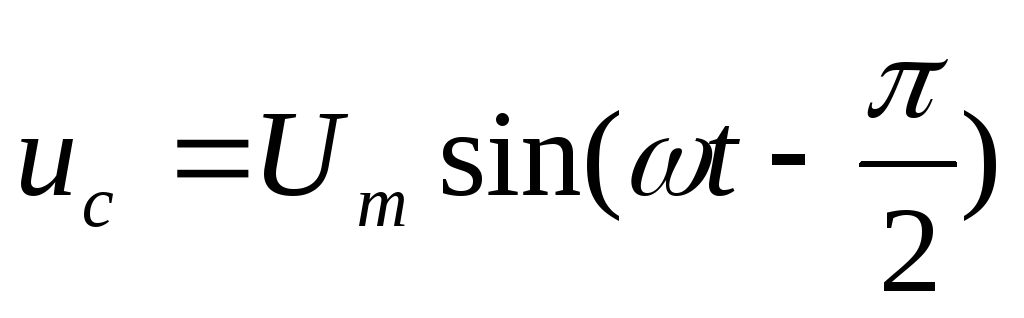 — напряжение на емкости;
— напряжение на емкости;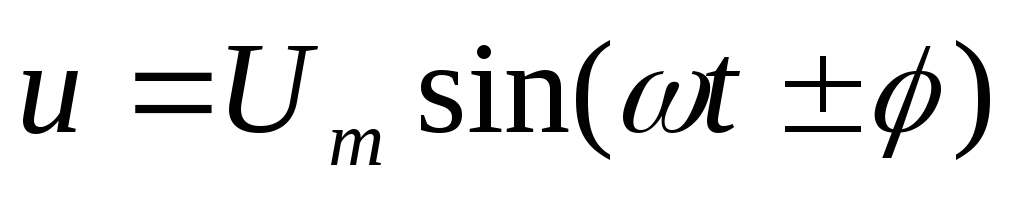 — общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;
— общее напряжение в цепи, знак «+» для
цепи, в которойXcменьшеXL,
знак «-« для цепи, в которойXcбольшеXL;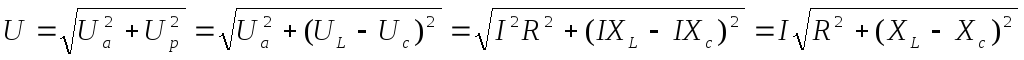 —
действующее напряжение в цепи;
—
действующее напряжение в цепи;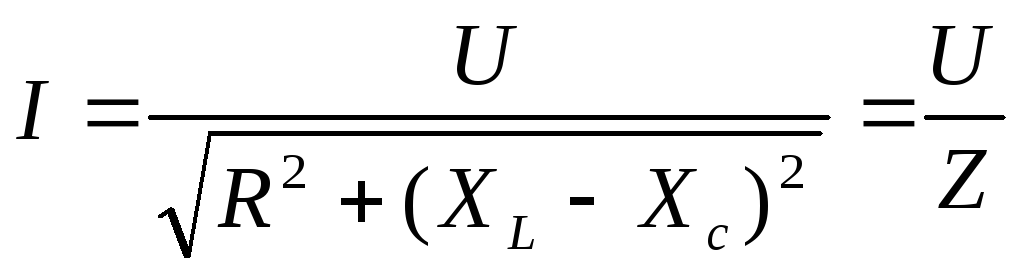 —
закон Ома;
—
закон Ома;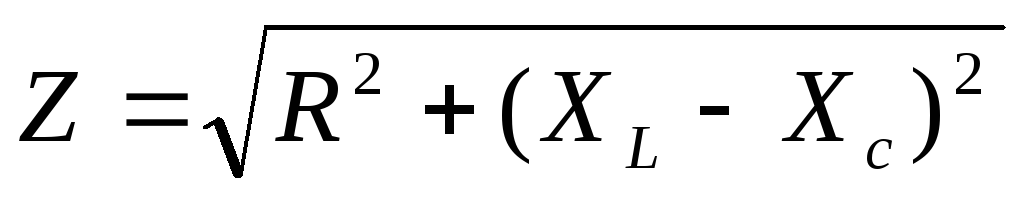 — полное (кажущееся) сопротивление;
— полное (кажущееся) сопротивление;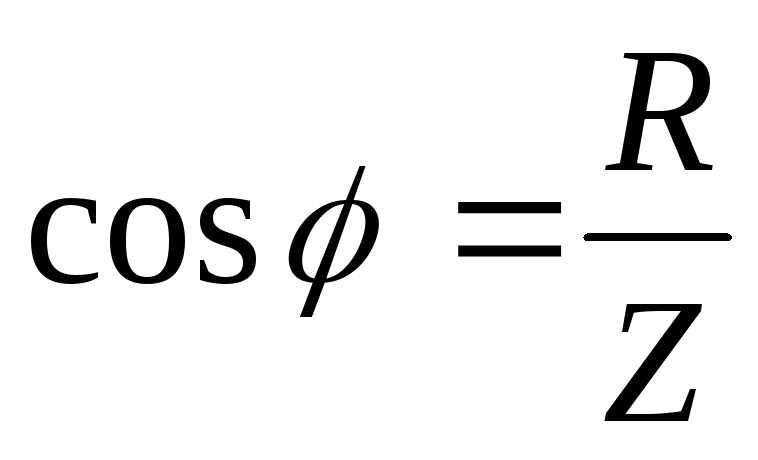 ;
;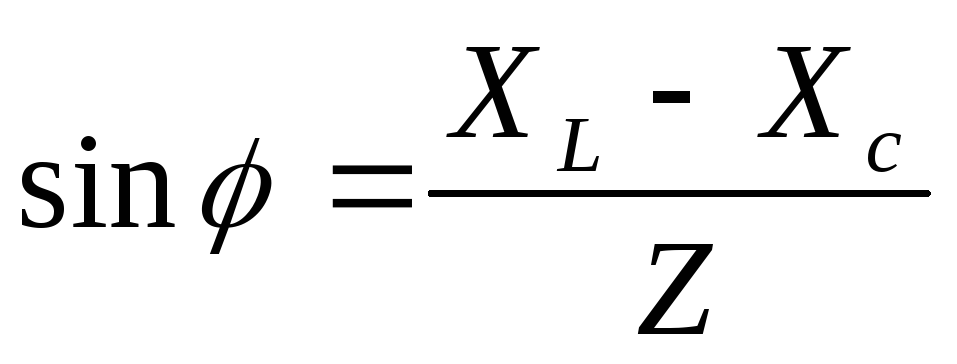 ;
;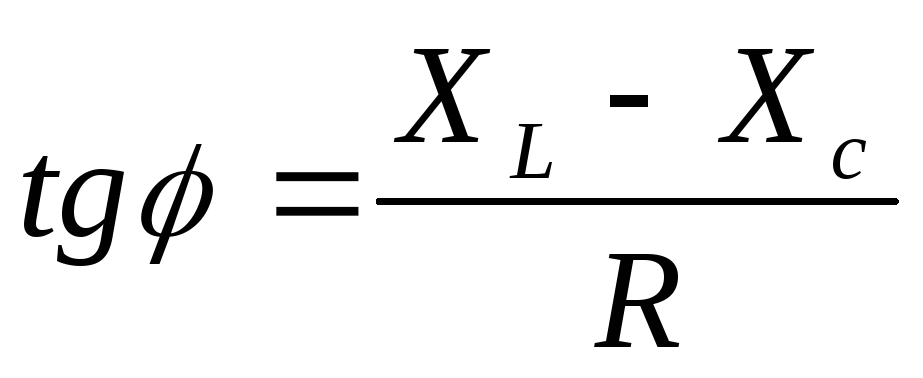 ;
;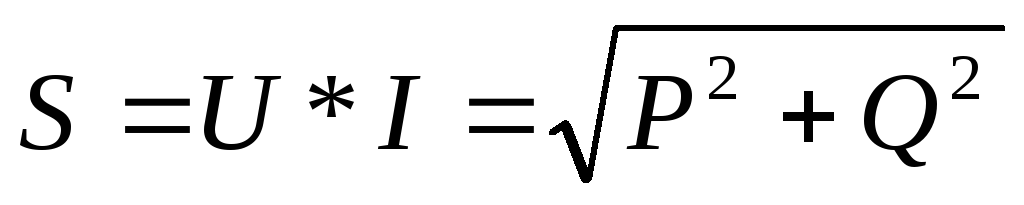 — полная мощность цепи;
— полная мощность цепи;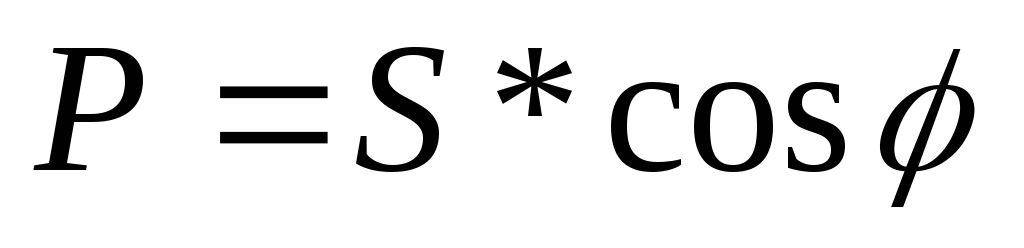 — активная мощность цепи;
— активная мощность цепи;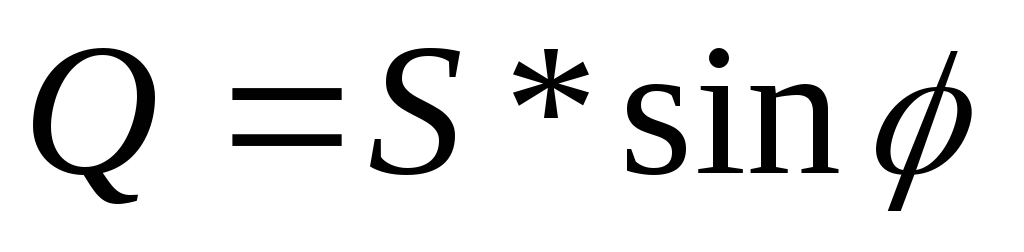 — реактивная мощность в цепи.
— реактивная мощность в цепи.