Цепь переменного тока с индуктивностью

Дата публикации: 30 марта 2015.
Категория: Электротехника.

В статье «ЭДС самоиндукции и индуктивность цепи» говорится, что при включении и при всяком изменении тока в электрической цепи вследствие пересечения проводника своим же собственным магнитным полем в нем возникает индуктированная электродвижущая сила (ЭДС). Эту ЭДС мы назвали ЭДС самоиндукции. ЭДС самоиндукции имеет реактивный характер. Так, например, при увеличении тока в цепи ЭДС самоиндукции будет направлена против ЭДС источника напряжения, и поэтому ток в электрической цепи не может установиться сразу. И, наоборот, при уменьшении тока в цепи индуктируется ЭДС самоиндукции такого направления, что, мешая току исчезать, она поддерживает этот убывающий ток.

Рисунок 1. Цепь переменного тока, содержащая индуктивность

Как нам уже известно, ЭДС самоиндукции зависит от скорости изменения тока в цепи и от индуктивности этой цепи (числа витков, наличия стальных сердечников).

В цепи переменного тока ЭДС самоиндукции возникает непрерывно, так как ток в цепи непрерывно изменяется.

На рисунке 1 представлена схема цепи переменного тока, содержащей катушку с индуктивностью L без стального сердечника. Для простоты будем считать сначала, что активное сопротивление катушки очень мало и им можно пренебречь.

Рассмотрим внимательнее изменение переменного тока за время одного периода. На рисунке 2 показана кривая изменения переменного тока. Первая половина периода разбита на мелкие одинаковые части.

Рисунок 2. Определение скорости изменения переменного тока

За промежуток времени 0 – 1 величина тока изменилась от нуля до 1 – 1’. Прирост величины тока за это время равен а.

За время, обозначенное отрезком 1 – 2, мгновенная величина выросла до 2 – 2’, причем прирост величины тока равен б.

В течение времени, обозначенного отрезком 2 – 3, ток увеличивается до 3 – 3’, прирост тока показывает отрезок в и так далее.

Так, с течением времени переменный ток возрастет до максимума (при 90°). Но, как видно из чертежа, прирост тока делается все меньше и меньше, пока, наконец, при максимальном значении тока этот прирост не станет равным нулю.

При дальнейшем изменении тока от максимума до нуля убыль величины тока становится все больше и больше, пока, наконец, около нулевого значения ток, изменяясь с наибольшей скоростью, не исчезнет, но тут же появляется вновь, протекая в обратном направлении.

Рассматривая изменение тока в течение периода, мы видим, что с наибольшей скоростью изменяется ток около своих нулевых значений. Около максимальных значений скорость изменения тока падает, а при максимальном значении тока прирост его равен нулю. Таким образом, переменный ток меняется не только по величине и направлению, но также и по скорости своего изменения. Переменный ток, проходя по виткам катушки, создает переменное магнитное поле. Магнитные линии этого поля, пересекая витки своей же катушки, индуктируют в них ЭДС самоиндукции.

На рисунке 3 кривая i показывает изменение переменного тока в катушке. Как было уже указано, величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности катушки. Но так как индуктивность катушки в нашем случае остается без изменения, ЭДС самоиндукции будет зависеть только от скорости изменения тока. Выше было показано, что наибольшая скорость изменения тока имеет место около нулевых значений тока. Следовательно, наибольшее изменение ЭДС самоиндукции имеет те же моменты.

Рисунок 3. ЭДС самоиндукции в катушке, включенной в цепь переменного тока

В момент а ток резко и быстро увеличивается от нуля, а поэтому, как следует из вышеприведенной формулы, ЭДС самоиндукции (кривая e_L) имеет отрицательное максимальное значение. Так как ток увеличивается, то ЭДС самоиндукции по правилу Ленца должна препятствовать изменению (здесь увеличению) тока. Поэтому ЭДС самоиндукции при возрастании тока будет иметь направление, обратное току (положение б), что следует также из указанной формулы. Скорость изменения тока по мере приближения его к максимуму уменьшается. Поэтому ЭДС самоиндукции также уменьшается, пока, наконец, при максимуме тока, когда изменения его будут равны нулю, она не станет равной нулю (положение в).

Переменный ток, достигнув максимума, начинает убывать. По правилу Ленца ЭДС самоиндукции будет мешать току убывать и, направленная уже в сторону протекания тока, будет его поддерживать (положение г).

При дальнейшем изменении переменный ток быстро убывает до нуля. Резкое уменьшение тока в катушке повлечет за собой также быстрое уменьшение магнитного поля и в результате пересечения магнитными линиями витков катушки в них будет индуктироваться наибольшая ЭДС самоиндукции (положение д).

Рисунок 4. Ток в катушке опережает ЭДС самоиндукции по фазе на 90°

Во вторую половину периода изменения тока картина повторяется и снова при возрастании тока ЭДС самоиндукции будет мешать ему, имея направление, обратное току (положение е).

При убывании тока ЭДС самоиндукции, имея направление в сторону тока, будет поддерживать его, не давая ему исчезнуть сразу (положение з).

На рисунке видно, что ЭДС самоиндукции отстает по фазе от тока на 90° или на ¼ периода. Так как магнитный поток совпадает по фазе с током, то можно сказать, что ЭДС, наводимая магнитным потоком, отстает от него по фазе на 90° или на ¼ периода.

Нам уже известно, что две синусоиды, сдвинутые одна относительно другой на 90°, можно изобразить векторами, расположенными под углом 90° (рисунок 4).

Так как ЭДС самоиндукции в цепях переменного тока непрерывно противодействует изменениям тока, то, чтобы дать возможность току протекать по виткам катушки, напряжение сети должно уравновешивать ЭДС самоиндукции. Иными словами, напряжение сети в каждый момент времени должно быть равно и противоположно ЭДС самоиндукции.

Рисунок 5. Приложенное к катушке напряжение сети опережает ток на 90° и противоположно ЭДС самоиндукции

Вектор напряжения сети, равный и противоположный ЭДС самоиндукции e_L, мы обозначим через U (рисунок 5). Только при условии, что к зажимам катушки будет приложено напряжение сети, равное и противоположное ЭДС самоиндукции, и, стало быть, это напряжение сети U уравновесит ЭДС самоиндукции e_L, по катушке сможет проходить переменный ток I.

Но в этом случае напряжение сети U будет опережать по фазе ток I на 90°.

Таким образом, в цепях переменного тока ЭДС самоиндукции, возникая непрерывно, вызывает сдвиг фаз между током и напряжением. Возвращаясь к рисунку 3, мы видим, что ток i по катушке будет проходить и тогда, когда напряжение сети (кривая u_L) равно нулю (положение в), и даже тогда, когда напряжение сети направлено в сторону, обратную току (положение г и з).

Итак отметим, что в цепи переменного тока, когда ЭДС самоиндукции отсутствует, напряжение сети и ток совпадают по фазе. Индуктивная же нагрузка в цепях переменного тока (обмотки электродвигателей и генераторов, обмотки трансформаторов, индуктивные катушки) всегда вызывает сдвиг фаз между током и напряжением.

Можно показать, что скорость изменения тока пропорциональна угловой частоте ω. Следовательно, действующее значение ЭДС самоиндукции e_L может быть найдено по формуле:

e_L = ω × L × I = 2 × π × f × L × I .

Как было отмечено выше, напряжение, приложенное к зажимам цепи, содержащей индуктивность, в каждый момент времени должно быть по величине равно ЭДС самоиндукции:

u_L = e_L.

Поэтому

u_L = 2 × π × f × L × I .

Обозначая 2 × π × f × L = x_L , получим

u_L = x_L × I .

Формула закона Ома для цепи переменного тока, содержащего индуктивность, будет такова:

Величина x_L называется индуктивным сопротивлением цепи, или реактивным сопротивлением индуктивности, и измеряется в омах. Таким образом, реактивное индуктивное сопротивление представляет собой своеобразное препятствие, которое оказывает цепь изменениям тока в ней. Оно равно произведению индуктивности на угловую частоту. Формула индуктивного сопротивления имеет вид:

x_L = ω × L .

Индуктивное сопротивление проводника зависит от частоты переменного тока и индуктивности проводника. Поэтому индуктивное сопротивление катушки, включаемой в цепь токов различной частоты, будет различным. Например, если имеется катушка индуктивностью 0,05 Гн, то путем расчета индуктивного сопротивления выяснится, что в цепи частотой 50 Гц ее индуктивное сопротивление будет:

x_L1 = 2 × π × f₁ × L = 2 × 3,14 × 50 × 0,05 = 15,7 Ом ,

а в цепи тока частотой 400 Гц

x_L2 = 2 × π × f₂ × L = 2 × 3,14 × 400 × 0,05 = 125,6 Ом .

Та часть напряжения сети, которая идет на преодоление (уравновешивание) ЭДС самоиндукции, называется индуктивным падением напряжения или реактивной слагающей напряжения.

u_L = x_L × I .

Рассмотрим теперь, какая мощность потребляется от источника переменного напряжения, если к его зажимам подключена индуктивность.

Рисунок 6. Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность

На рисунке 6 даны кривые мгновенных значений напряжения, тока и мощности для этого случая. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:

p = u × i .

Из чертежа видно, что если u и i имеют одинаковые знаки, то кривая p положительная и располагается выше оси ωt. Если же u и i имеют разные знаки, то кривая p отрицательна и располагается ниже оси ωt.

В первую четверть периода ток, а в месте с ним и магнитный поток катушки увеличиваются. Катушка забирает из сети мощность. Площадь, заключенная между кривой p и осью ωt, есть работа (энергия) электрического тока. За первую четверть периода энергия, забираемая из сети, идет на создание магнитного поля вокруг витков катушки (мощность положительная). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить по формуле:

За вторую четверть периода ток убывает. ЭДС самоиндукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает уменьшаться, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает в сеть энергию, запасенную в ее магнитном поле. Мощность отрицательна, и на рисунке 6 кривая p располагается ниже оси ωt.

За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой мощность возвращается источнику.

В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I.

Тот же результат мы получим, если вычислим среднюю или активную мощность по формуле, приведенной выше:

P = U × I × cos φ .

В нашем случае между напряжением и током существует сдвиг фаз, равный 90°, и cos φ = 90° = 0.

Поэтому активная мощность также равна нулю, то есть расхода мощности нет.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

напряжение, ток, мощность, векторная диаграмма. Индуктивное сопротивление.

Рассмотрим цепь, в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение. Протекающий через катушку переменный ток создаёт в ней ЭДС самоиндукции eL, которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока.      Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению.

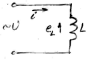
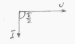
Это соотношение представляет собой закон Ома для цепи с идеальной индуктивностью, а величина X_L = ω∙L называется индуктивным сопротивлением. Индуктивное сопротивление измеряется в Омах. Из формулы (4.12) мы видим, что в рассмотренной цепи ток отстаёт по фазе от напряжения на угол π/2. Векторная диаграмма этой цепи:

Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна: p(t) = I_m∙U_m∙sinωt∙sin(ωt — π/2) =  ∙sin2ωt

Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные – возврату запасённой энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью энергии не потребляет – это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно.

36. Цепь переменного тока с емкостью: напряжение, ток, мощность, векторная диаграмма. Ёмкостное сопротивление.

Рассмотрим электрическую цепь, в которой переменное напряжение U(t) = U

m∙sinωt приложено к ёмкости.

Мгновенное значение тока в цепи с ёмкостью равно скорости изменения заряда на обкладках конденсатора    i =, но q = CU, то

I = C∙ = ω∙C∙U_m∙cosωt = I_m∙sin(ωt + π/2)    (4.24), где

ω∙C∙U_m = I_m     (4.25).

Мы видим, что в этой цепи ток опережает напряжение на угол π/2. Перейдя в формуле (4.25) к действующим значениям переменного тока I = Im / √2, U = Um / √2, получим:         I = U / Xc    (4.26).

Это закон Ома для цепи переменного тока с ёмкостью, а величина Xc = 1 / ω∙C называется емкостным сопротивлением. Векторная диаграмма для этой цепи:

Здесь ток опережает напряжение на π/2.Посмотрим, что будет представлять собой мгновенная мощность в цепи, содержащей ёмкость.

p(t) = I_m∙U_m∙sinωt∙sin(ωt + π/2) =  I_m∙U_m∙sin2ωt   (4.27).Временная диаграмма показана ниже.

Мы видим, что мгновенная мощность изменяется с удвоенной частотой. При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные – возврату запасённой энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергии между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность является реактивным сопротивлением.

37. Неразветвленная цепь переменного тока ri: напряжение, ток, мощность, векторная диаграмма напряжений. Треугольник сопротивлений и мощностей. Нет(

39. Общий случай последовательного соединения RLC: напряжение, ток, мощность, полное сопротивление. Векторные диаграммы напряжений а)

Xl=Xc б)Xl>Xc в)Xl<Xc.

Расчетная величина х = х­_L — х_C называется  реактивным сопротивлением цепи. Для рассматриваемой цепи Если   х_L   больше х_C,   то цепь в целом носит индуктив­ный   характер,   т. е.   вектор тока I отстает по фазе от вектора напряжения цепи U. Если же х_Cбольше x_L то цепь в целом носит емкостный характер, т. е. вектор тока I опережает по фазе вектор об­щего напряжения U.

Векторная диаграмма напряжений: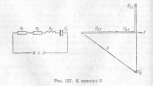

42. Расчет разветвленных цепей методом проводимостей.

В цепи переменного тока существует 3 вида проводимостей. Проводимость – это величина обратной сопротивлению. G=R/Z^2 ;G- активная(R) , В=X/Z^2- реактивная (Xl,Xc)

43. Расчет разветвленных цепей символическим методом.

Переменный ток можно изображать графическим путем, формулой векторной диаграммой и с помощью комплексных чисел . С помощью комплексных уравнений очень удобно находить углы между током и напряжением или просто для напряжения, тока. Существует 3 формы записи числа: А=а+-jв – алгеьраическая форма, А=АCos+jASin – тригонометрическая, А=Ае в степени +-i(альфа)- показательная.

44. Колебательный контур. Собственная частота.

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона: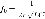

45. Резонанс напряжений. Свойство последовательного контура на резонансной частоте.

Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.

на соединенные последовательно L и С контура (рис.1 а), т.е. включен внутри контура. В такой цепи имеется активное сопротивление г и общее реактивное сопротивление х, равное

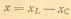
Разность хL, и xC берется потому, что индуктивное и емкостное сопротивления оказывают противоположные влияния на ток. Первое вызывает отставание по фазе тока от напряжения, а второе, наоборот, создает отставание напряжения от тока

Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:

Пример.  Активное  сопротивление  катушки  составляет  5 ом,  а  ее  полное сопротивление Z=30 ом. Определить угол сдвига фаз.

Решение.

При соs =0,25 угол =75°.

§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ

На рис. 57, а изображена цепь переменного тока, в которую  включены  последовательно  активное  сопротивление r,  индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.

Под действием переменного напряжения в этой цепи протекает переменный ток.

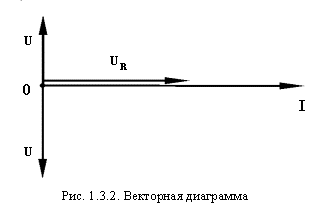
Выясним, чему равно общее напряжение на за­жимах цепи. Построим векторную диаграмму то­ка и напряжений для рас­сматриваемой цепи (рис. 57, б). Так как сопротив­ления соединены последовательно, то в них проте­кает одинаковый ток. Отложим по горизонтали, в  выбранном  масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпа­дают  по  фазе,  поэтому вектор напряжения Uа от­кладываем по вектору тока.

Напряжение на индуктивности опережает ток на угол  = 90°. Поэтому век­тор UL откладываем вверх

под углом 90° к вектору тока.

В цепи с емкостью, наоборот, напряжение отстает от тока на угол  = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.

Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий вектор­ную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на за­жимах цепи.

На основании теоремы Пифагора из треугольника напряжений АО Б следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис. 57, в). Его сторонами являются сопро­тивления r, (ХL — Хс) и полное сопротивление цепи Z.

Пользуясь теоремой Пифагора, можно написать, что

Отсюда полное сопротивление цепи

Силу тока в цепи с активным, индуктивным и емкостным сопро­тивлениями определяют по закону Ома:

На векторной диаграмме (рис. 57, б) видно, что в рассматри­ваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

Из треугольника сопротивлений

§ 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ

На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.

Полное сопротивление первой катушки

Полное сопротивление второй катушки

Напряжение на  зажимах  катушек  равно  напряжению генератора.

Сила  тока в каждой  катушке  определяется  согласно  закону Ома:

Из этих равенств можно сделать вывод, что в такой цепи токи раз­ветвляются обратно пропорционально полным сопротивлениям ветвей.

Для определения угла сдвига фаз между напряжением и током

в каждой катушке вычисляют  и    и по таблице тригонометрических функций находят значения углов 1 и 2.

Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощ­ности (cos ).

Так как первый закон Кирхгофа справедлив для цепей перемен­ного тока, то в рассматриваемой цепи общий ток определяется гео­метрическим сложением векторов (рис. 58,6).

По горизонтали в выбранном масштабе отложим вектор напря­жения U. Так как ток в цепи с индуктивностью отстает от напря­жения, то вектор тока  I1 выбранном масштабе отложим с по­мощью транспортира под углом 1 к вектору напряжения U, а век­тор тока I2 и отложим под углом 2. Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбран­ного масштаба.

Чтобы найти общий ток, нужно воспользоваться тем, что актив­ная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:

а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережаю­щие):

После чего определяют общий ток:

Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.

Пример. Три катушки соединены параллельно и к ним подключено перемен­ное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;

Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.

Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.

Решение. Индуктивное сопротивление катушек:

Полное сопротивление катушек:

Сила тока в катушках:

Цепь переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений

Oпределение: Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.

Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е.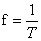

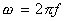и измеряется в герцах (Гц). Величина называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду

Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, I

m). Существует также понятие, действующего значения переменного тока

Переменный ток можно математически записать в виде:

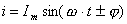
Рассмотрим цепь с активным, индуктивным и емкостным сопротивлениями, включенными последовательно (рис. 1.3.1).

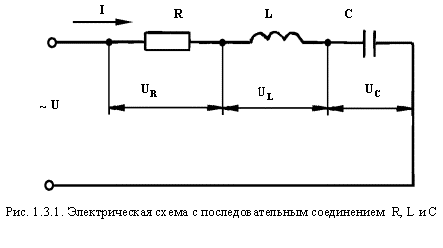
Для анализа схемы разложим напряжение сети U на три составляющие:
U_R — падение напряжения на активном сопротивлении,
U_L — падение напряжения на индуктивном сопротивлении,

U_C — падение напряжения на емкостном сопротивлении.

Ток в цепи I будет общим для всех элементов:

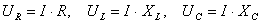
Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I.
Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном — отстает от него на 90°.
Графически это можно показать на векторной диаграмме (рис. 1.3.2).

Изображенные выше три вектора падения напряжений можно геометрически сложить в один (рис. 1.3.3).

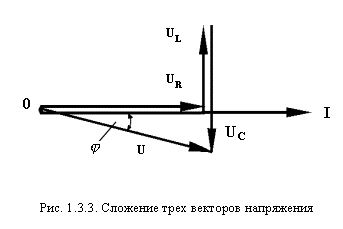
В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак.
Интересным является режим, когда = 0.
В этом случае

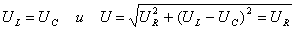
Такой режим работы схемы называется резонансом напряжений.
Полное сопротивление при резонансе напряжений имеет минимальное значение:

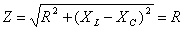, и при заданном напряжении U ток I может достигнуть максимального значения.
Из условия 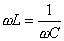определим резонансную частоту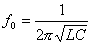

Явления резонанса напряжений широко используется в радиотехнике и в отдельных промышленных установках.

Цепь переменного тока с параллельным соединением активного, индуктивного и емкостного сопротивлений

Электрические цепи, в которых электрические величины (токи, напряжения и ЭДС) изменяются с течением времени по периодическому закону, принято называть цепями переменного тока.

Oпределение: Переменными называют токи и напряжения, изменяющиеся во времени, по величине и направлению. Их величина в любой момент времени называется мгновенным значением. Обозначаются мгновенные значения малыми буквами: i, u, e, p.

Токи, значения которых повторяются через равные промежутки времени, называются периодическими. Наименьший промежуток времени, через который наблюдаются их повторения, называется периодом и обозначается буквой Т. Величина, обратная периоду, называется частотой, т.е. 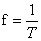и измеряется в герцах (Гц). Величина 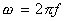называется угловой частотой переменного тока, она показывает изменение фазы тока в единицу времени и измеряется в радианах, деленных на секунду Максимальное значение переменного тока или напряжения называется амплитудой. Оно обозначается большими буквам с индексом »m» (например, I_m). Существует также понятие, действующего значения переменного тока (I).

 

Переменный ток можно математически записать в виде:

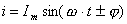
Здесь индекс выражает начальную фазу. Если синусоида начинается в точке пересечения осей координат, то = 0, тогда

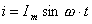
Начальное значение тока может быть слева или справа от оси ординат. Тогда начальная фаза будет опережающей или отстающей.

 

 

Цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью (рис. 1.4.1).

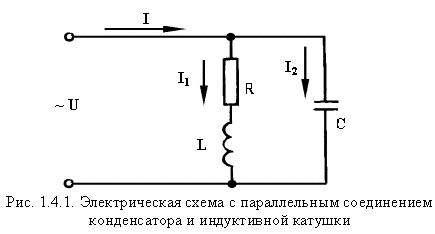В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z₁ и ток I₁определяются по формуле:

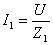, где

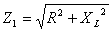
Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол .

Покажем это на векторной диаграмме (рис. 1.4.2).

Спроецируем вектор тока I₁ на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I_1R, а вертикальная — I_1L. Количественные значения этих составляющих будут равны:

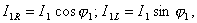где

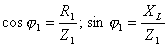
Во вторую ветвь включен конденсатор. Его сопротивление

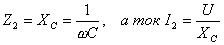
Этот ток опережает по фазе напряжение на 90°.
Для определения тока I в неразветвленной части цепи воспользуемся формулой:

<>

Его значение можно получить и графическим путем, сложив векторы I₁ и I₂(рис.1.4.3)
Угол сдвига между током и напряжением обозначим буквой j.
Здесь возможны различные режимы в работе цепи. При = +90° преобладающим будет емкостный ток, при = -90° — индуктивный. Возможен режим, когда = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I_1L = I₂, т.е. при равенстве реактивных составляющих тока в ветвях.

Н 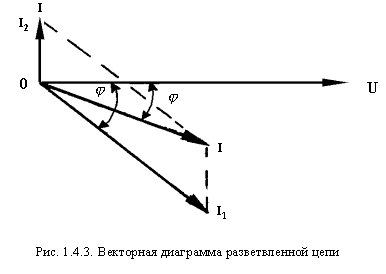а векторной диаграмме это будет выглядеть так (рис. 1.4.4):

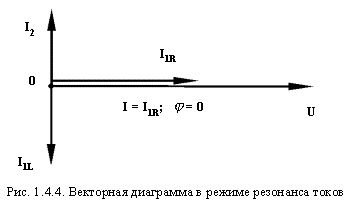
Такой режим называется резонансом токов. Также как в случае с резонансом напряжений, он широко применяется в радиотехнике.
Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosj для электроустановок. Известно, что cosjявляется технико-экономическим параметром в работе электроустановок. Определяется он по формуле:

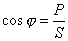, где

Р — активная мощность электроустановок, кВт,
S — полная мощность электроустановок, кВт.
На практике cosj определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgj . Далее по таблицам находят и cosj. Чем больше cosj, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosj приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosj, в сравнении с низким. К мероприятиям по повышению cos относятся:
— недопущение холостых ходов электрооборудования,
— полная загрузка электродвигателей, трансформаторов и т.д.
Кроме этого, на cosj, положительно сказывается подключение к сети статических конденсаторов.

17. Трехфазный переменный ток и его получение

Oпределение: Трехфазные электрические цепи представляют собой совокупность трех однофазных цепей переменного тока, сдвинутых по фазе относительно друг друга на 1/3 периода.
Источником трехфазного переменного тока является генератор, на статоре которого расположены три одинаковые обмотки А_x, B_y, C_z, размещенные под углом 120°.

При вращении ротора, представляющего собой двухполюсный магнит, в каждой фазной обмотке статора индуктируется ЭДС:

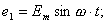
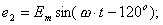
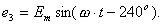
Графически ЭДС можно изобразить тремя синусоидами, сдвинутыми на 1/3 периода, или тремя векторами, находящимися под углом 120° друг к другу.