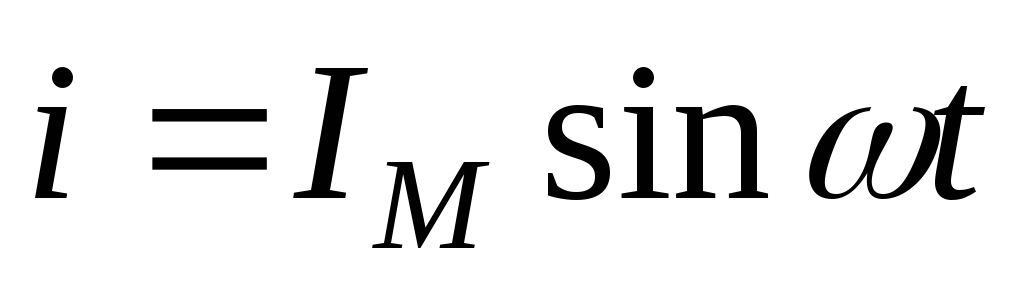Лекция по электротехнике по теме «Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью»
Лекция № 9
Тема1.3.Основные положения теории переменного тока. Цепи переменно тока
План
Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью.
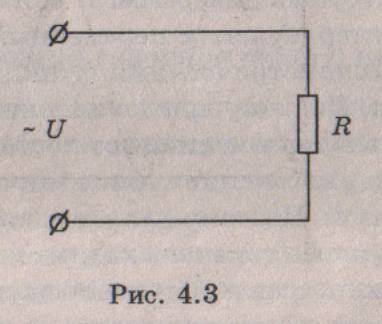
1.Цепь переменного тока с активным сопротивлением. Рассмотрим цепь (рис, 4,3), в которой к активному сопротивлению (резистору) приложено синусоидальное напряжение: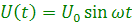 
Тогда по закону Ома ток в цепи будет равен: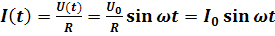
Мы видим, что ток и напряжение совпадают по фазе. Векторная диаграмма для этой цепи приведена на рис. 4.4, а зависимости тока и напряжения от времени (временная диаграмма) — на рис. 4.5:
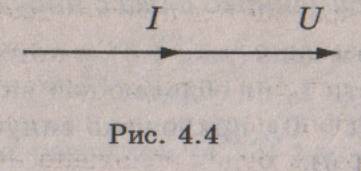
Мгновенное значение мощности равно произведению мгновенных значений тока и напряжения:
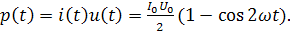
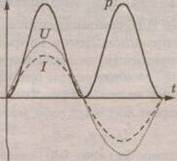
Из этой формулы мы видим, что мгновенная мощность всегда положительна и пульсирует с удвоенной частотой (рис4.5).
Это означает, что электрическая энергия необратимо превращается в теплоту независимо от направления тока в цепи.
Те элементы цепи, на которых происходит необратимое преобразование электрической энергии в другие виды энергии (не только в теплоту), называются активными сопротивлениями. Поэтому резистор представляет собой активное сопротивление.
Цепь переменного тока с индуктивностью. Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6).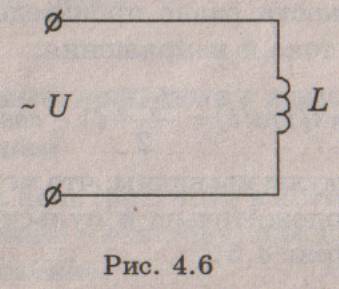 
Протекающий через катушку переменный ток создает в ней ЭДС самоиндукции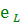 
, которая в соответствии с правилом Ленца направлена таким образом, что препятствует изменению тока. Другими словами, ЭДС самоиндукции направлена навстречу приложенному напряжению. Тогда в соответствии со вторым правилом Кирхгофа можно записать:
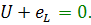(4.9) Согласно закону Фарадея ЭДС самоиндукции
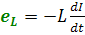(4.10) Подставив (4.10) в (4.9), получим:
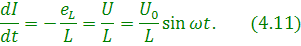
Решение этого дифференциального уравнения имеет вид: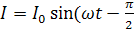 
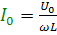(4.13)Деля обе части равенства (4.13) на
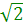, получим для действующих значений 
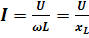(4.14)
Соотношение (4.14) представляет собой закон Ома для цепи с идеальной индуктивностью, а величина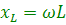 
Мгновенная мощность в цепи с чисто индуктивным сопротивлением равна:
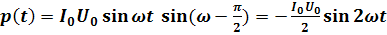(4.15)Положительные значения мощности соответствуют потреблению энергии катушкой, а отрицательные — возврату запасенной энергии обратно источнику. Средняя за период мощность равна нулю. Следовательно, цепь с индуктивностью мощности не потребляет — это чисто реактивная нагрузка. В этой цепи происходит лишь перекачивание электрической энергии от источника в катушку и обратно. Индуктивное сопротивление
Цепь переменного тока с индуктивностью и активным сопротивлением. Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Поэтому рассмотрим электрическую цепь (рис. 4.9), в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток
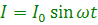(4.16)
Через катушку и резистор протекает один и же ток, поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.
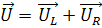(4.17)Напряжение на резисторе, как было показано выше, будет совпадать по фазе с током:
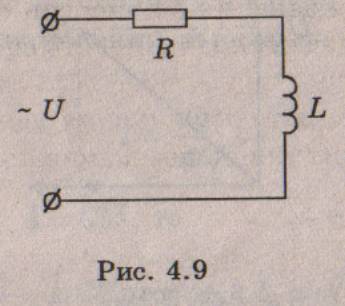
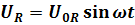
а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму правилу Кирхгофа):
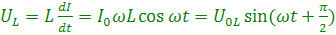. (4.19)Мы видим, что напряжение на индуктивности опережает ток на угол ?/2. Построив векторы
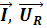и 
,
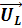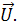Векторная диаграмма показана на рис. 4.10. Мы видим, что в рассматриваемой цепи ток I отстает по фазе от приложенного напряжения U, но не на / 2, как в случае чистой индуктивности, а на некоторый угол 
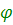. Этот угол может принимать значения от 0 до ? / 2 и при заданной индуктивности зависит от значения активного сопротивления: с увеличением R угол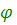 
Как видно из векторной диаграммы, модуль вектора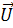 
равен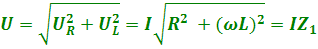 
, где величина 
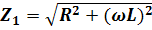называется полным сопротивлением цепи.
Сдвиг по фазе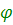
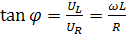(4.22) Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (4.6) приложено к емкости С.
Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора:
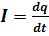; но поскольку q = СU
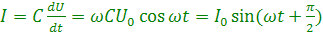, где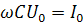 
(4.25) Мы видим, что в этой цепи ток опережает напряжение на 2. Переходя в формуле (4.25) к действующим значениям переменного тока
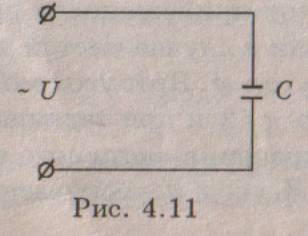
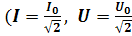) , получим:
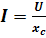(4.26)
Это закон Ома для цепи переменного тока с емкостью, а величина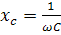 
— называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
Мгновенная мощность в цепи, содержащей емкость:
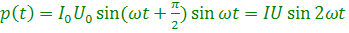(4.27)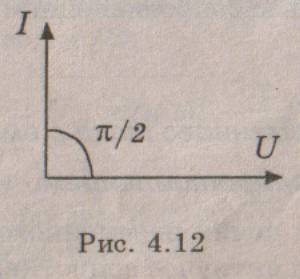
Мы видим, что мгновенная мощность изменяется с удвоенной частотой (рис. 4.13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные — его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность, является реактивным сопротивлением.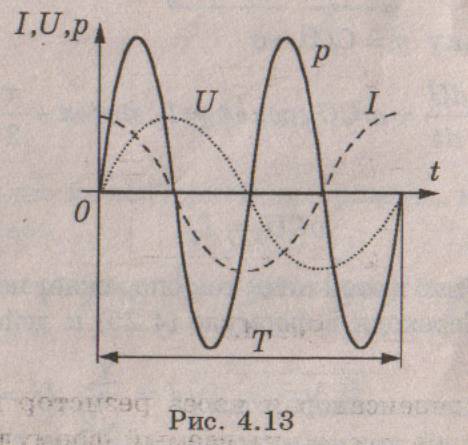
Вопросы для самопроверки:
Дать определение понятию « Активное сопротивление».
Выразить закон Ома для цепи переменного тока с активным сопротивлением.
Дать определение понятию « Индуктивность».
Выразить закон Ома для цепи переменного тока с индуктивностью.
Дать определение понятию « Емкость».
Описать основные параметры цепей переменного тока с активным сопротивлением, индуктивностью и емкостью.
Дать определение понятию « Активное сопротивление».
Дать определение понятию « Индуктивность».
Выразить закон Ома для цепи переменного тока.
Цепи переменного тока с активным сопротивлением
|
|
На величину тока и его характер в цепях переменного тока оказывает влияние не только сопротивление, определяемое материалом и геометрическими размерами, но и наличием в цепи емкости и индуктивности. Любая электрическая цепь обладает сопротивлением, индуктивностью и емкостью. Однако, часто тот или иной элемент преобладает над другим, поэтому их влиянием можно пренебречь.
Один и тот же проводник имеет различное сопротивление в цепях постоянного и переменного тока, причем, в цепях переменного тока это сопротивление больше.
| — постоянный ток |
| — переменный ток |
Это объясняется тем, что переменный ток в отличие от постоянного, который протекает по сечению проводника с равномерной плотностью, частично вытесняется из внутренних слоев проводника к наружным. В результате чего плотность тока в различных слоях неодинакова. Это явление называется поверхностным эффектом.Это объясняется тем, что внутренние слои проводника сцеплены с большим числом магнитных силовых линий, чем наружные, и поэтому в них наводится большая ЭДС самоиндукции, которая препятствует протеканию тока и вытесняет его к наружным слоям, где ЭДС самоиндукции меньше.
Разделив обе части
равенства на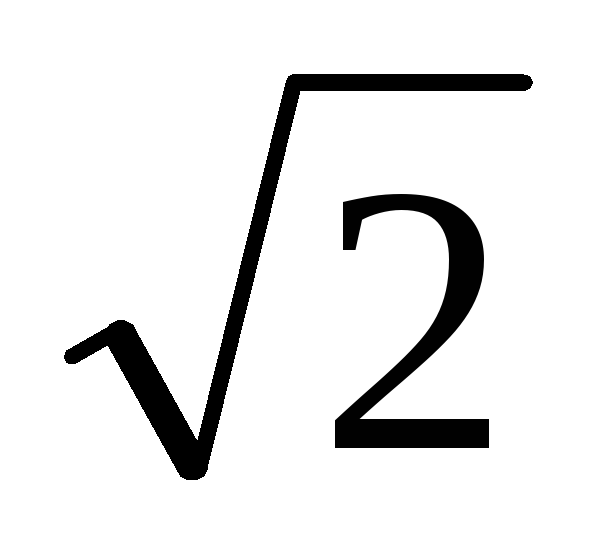 
,
получим действующие значения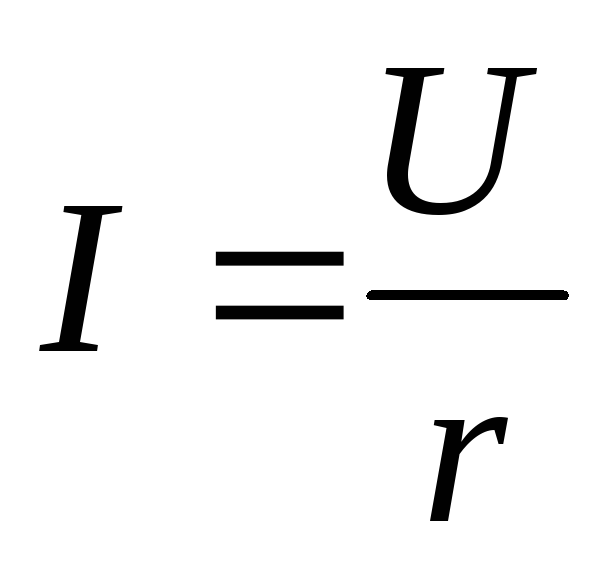
.
Ток и напряжение в цепи с активным сопротивлением совпадают по фазе.
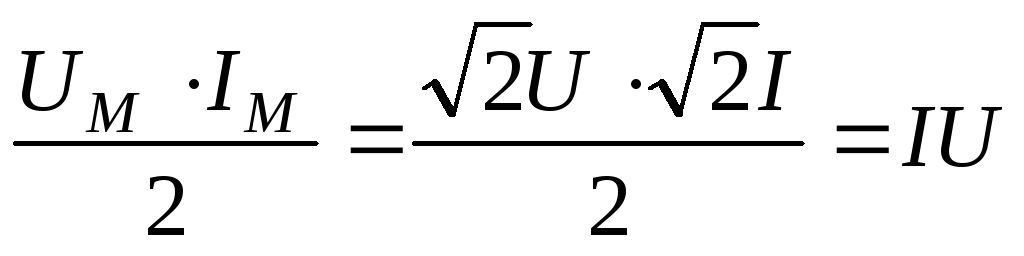
Таким
образом, мощность состоит из постоянной
составляющей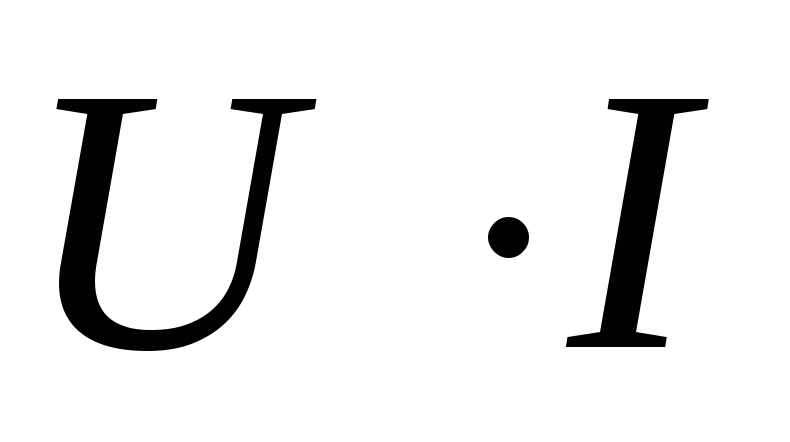 
и переменной составляющей
,
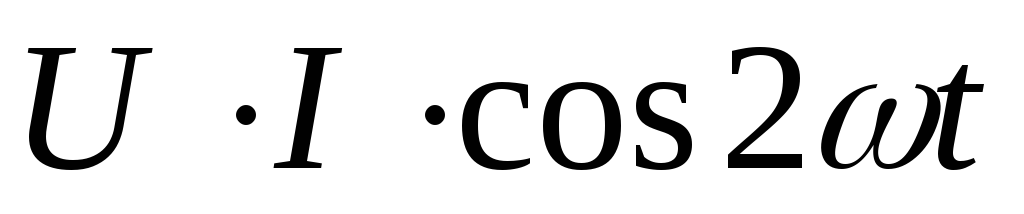среднеезначение которых за период
равно нулю. Таким образом, постоянная
составляющая мощности
выражает среднее за период значение
мощности и называетсяактивной
мощностью:
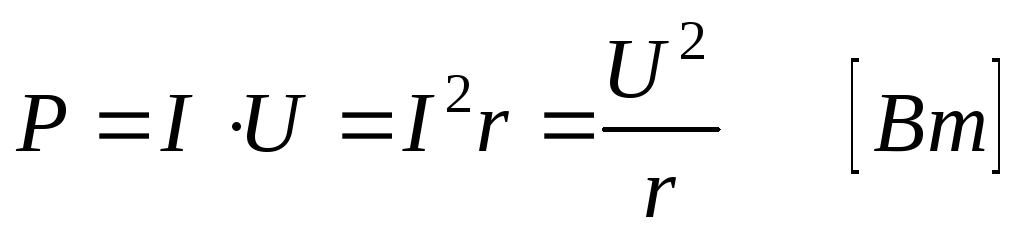
Мощность в оба полупериода положительна. Это означает, что цепь с сопротивлением rтолько потребляет энергию из сети и назад ее не возвращает, т.к. она преобразуется в другие виды энергии.
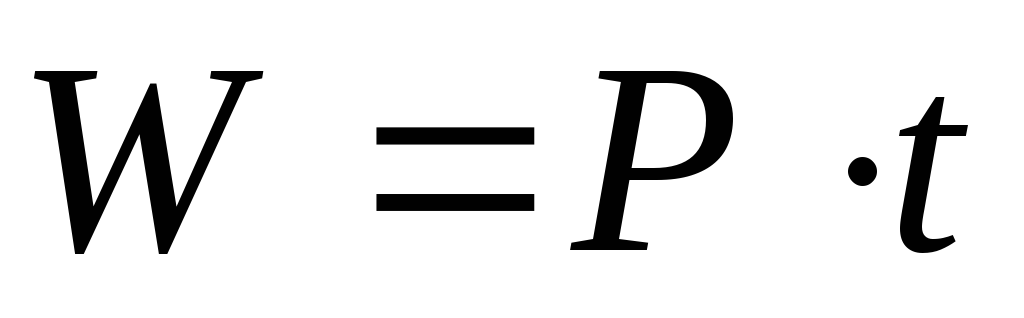
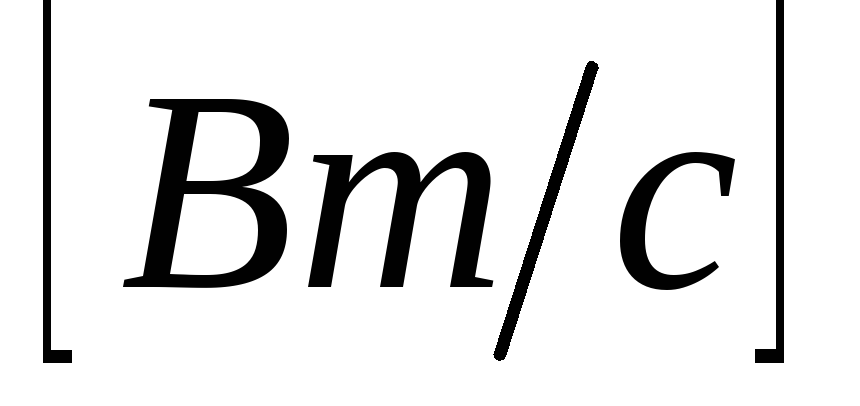
Цепи переменного тока с индуктивностью
| Допустим, что под действием напряжения в этой цепи протекает ток. Под действием переменного тока в катушке возникает переменный магнитный поток, который наводи в ней ЭДС самоиндукции.
|
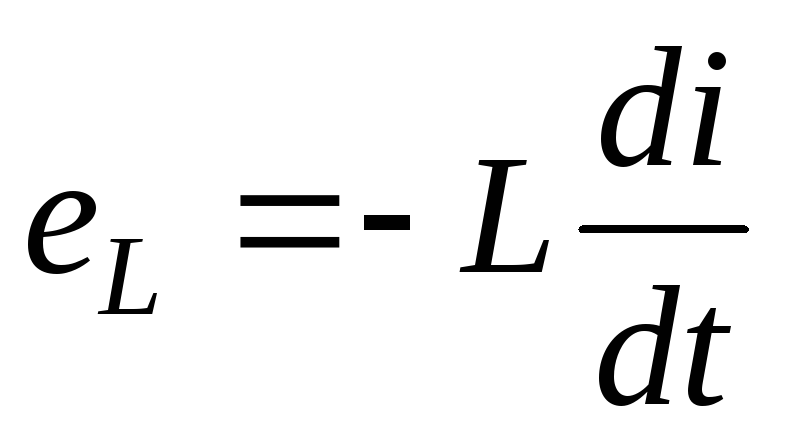
ЭДС самоиндукции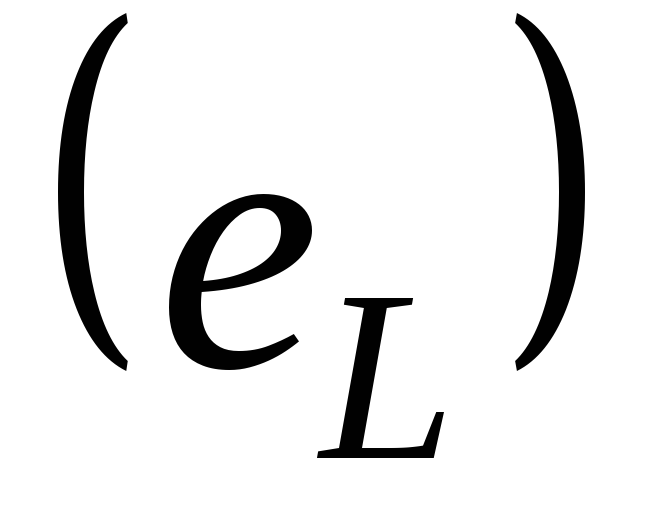 
в любой момент времени уравновешивается
напряжением:
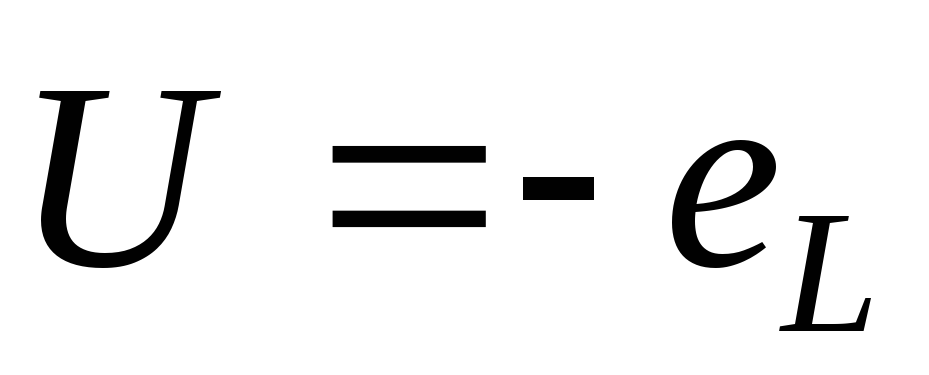
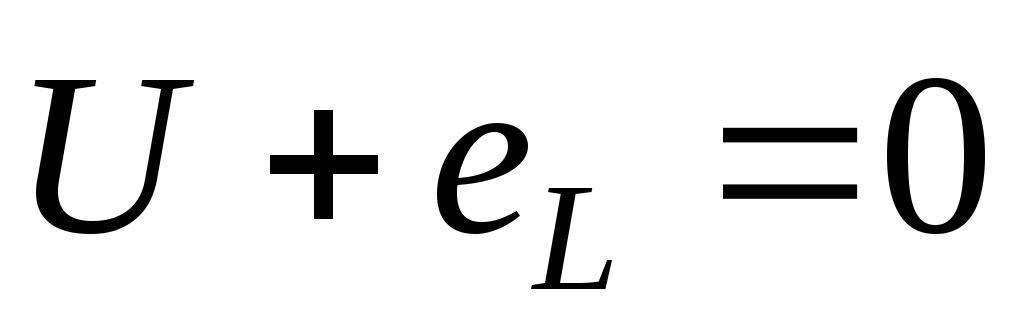
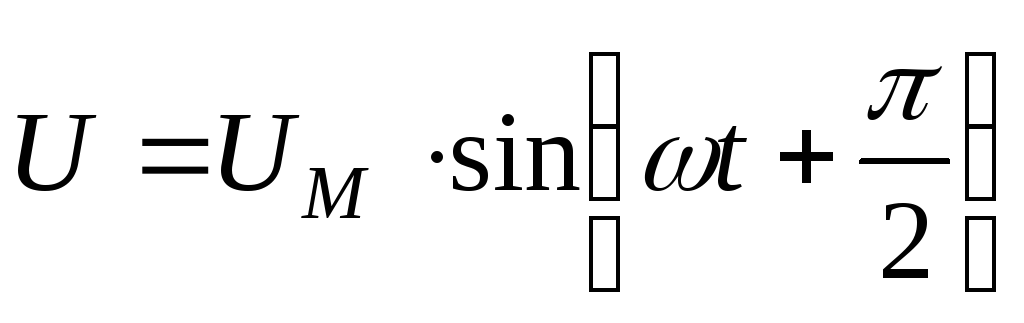
Т.о. в цепи с индуктивностью напряжение опережает ток на угол 900.
—
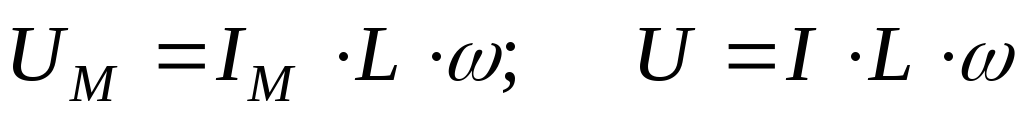
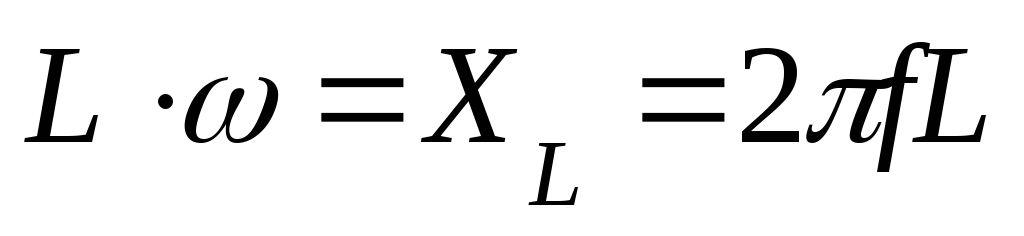
индуктивное (реактивное) сопротивление.
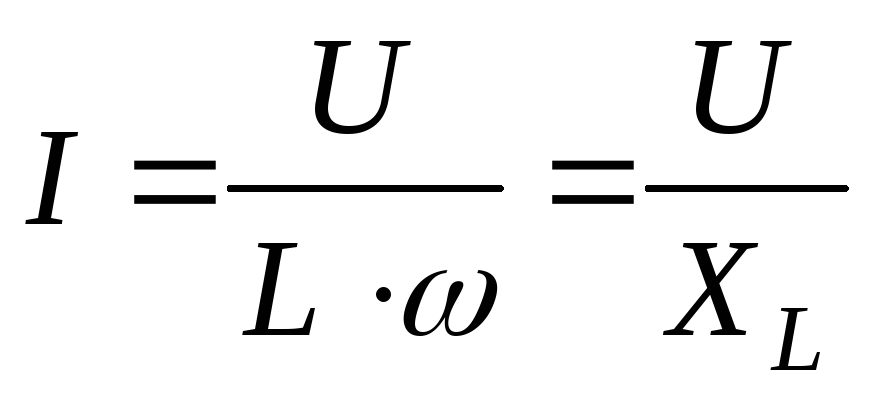— закон Ома для
цепи с индуктивностью.
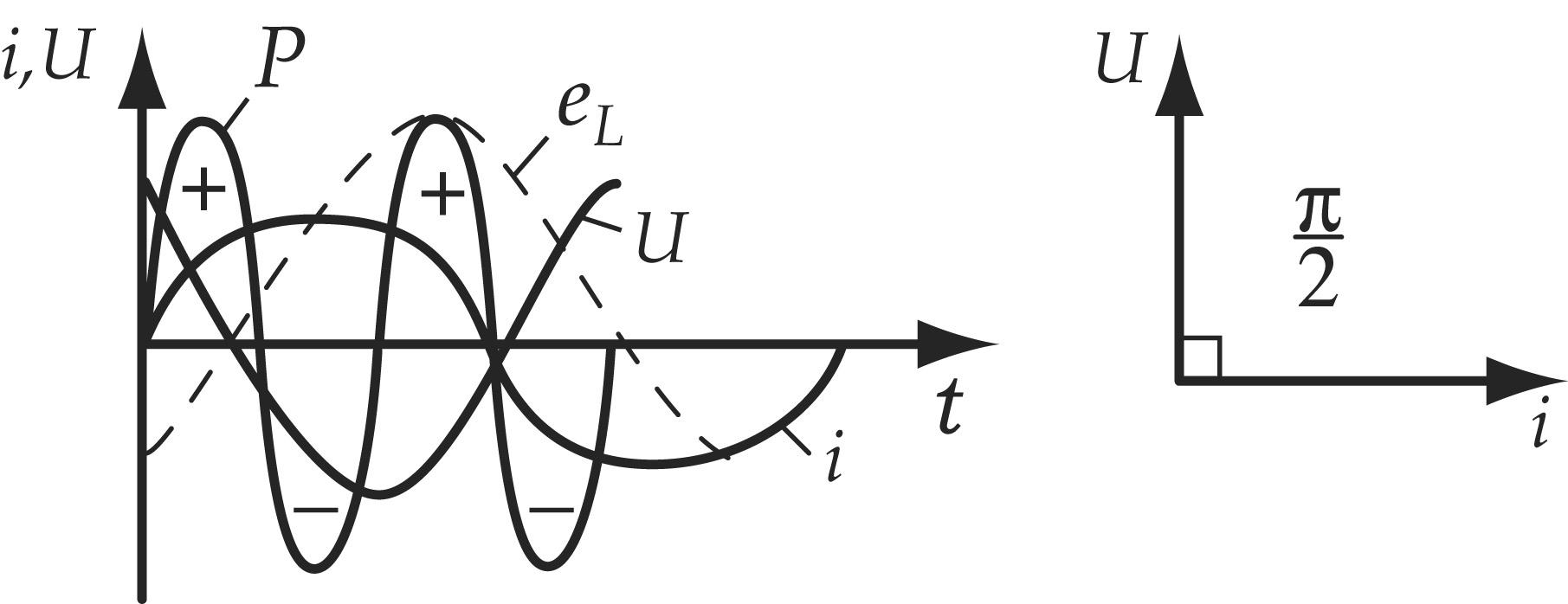
Физически индуктивное сопротивление характеризует препятствие, оказываемое переменному току в результате наличия ЭДС самоиндукции.
Мощность цепи:
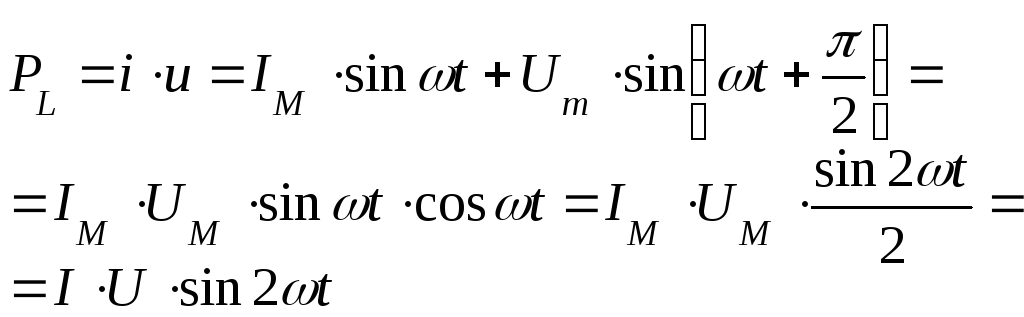
Т.о. мощность изменяется с двойной частотой и может быть положительной и отрицательной. Когда она «+» индуктивность потребляет электрическую энергию от источника и запасает ее от магнитного поля. Когда мощность «-» индуктивность возвращает запасенную энергию обратно к источнику.
Т.о. между источником и индуктивностью происходит непрерывный обмен энергией, при котором:
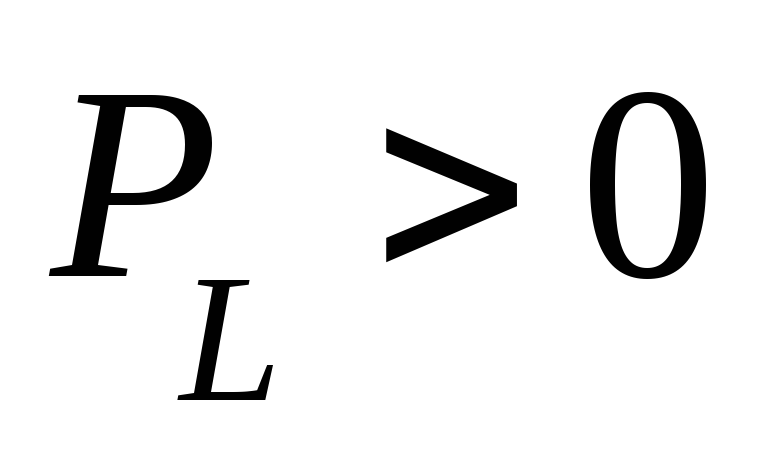— цепь работает
потребителем
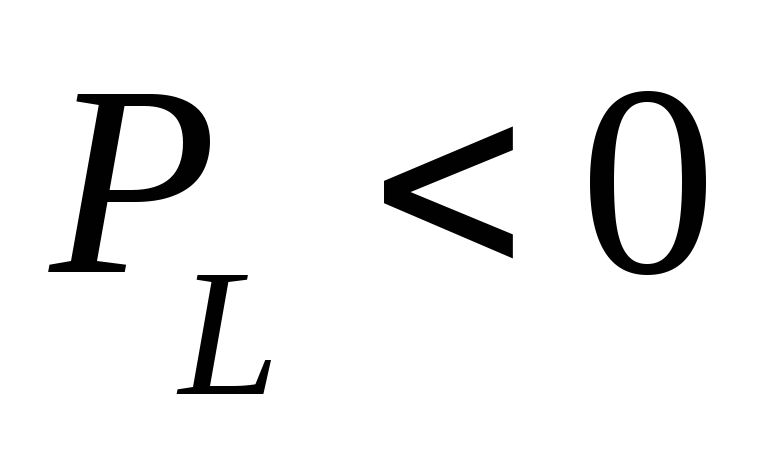— цепь работает
генератором.
Максимальное значение мощности цепи индуктивности называется реактивной мощностью:
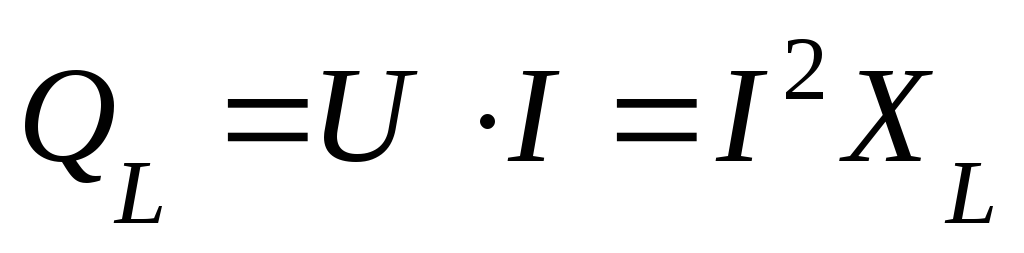
Энергия, запасенная в магнитном поле катушки, равна
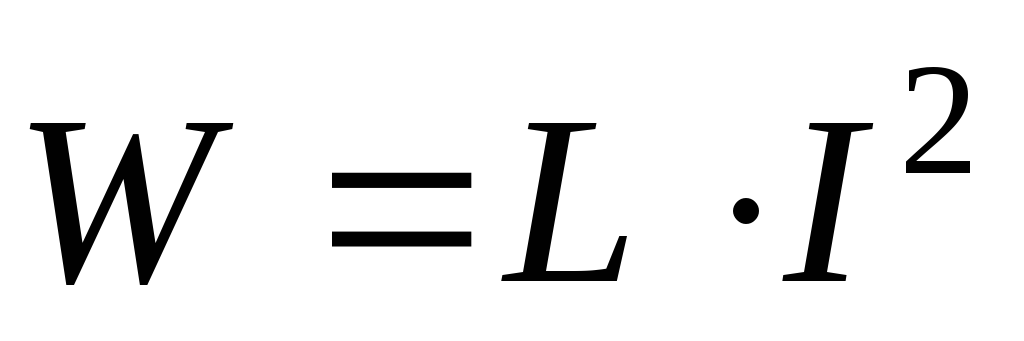
Цепь переменного тока с активным и индуктивным сопротивлениями
Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.
Таким образом. емкостное сопротивление:
где Хс — емкостное сопротивление, ом;
ώ — угловая частота переменного тока, рад/сек;
С —емкость, ф.
Известно, что угловая частота . Поэтому емкостное сопротивление можно определить так:
где f— частота переменного тока, гц.
Если включенная емкость измеряется в микрофарадах, то емкостное сопротивление
Если емкость измеряется в пикофарадах, то
Следует подчеркнуть, что имеется существенное различие между емкостным и активным сопротивлениями. Как известно, активная нагрузка безвозвратно потребляет энергию генератора переменного тока.
Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде конденсатора.
Следовательно, емкостная нагрузка не потребляет энергию генератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.
Пример. Конденсатор емкостью С=2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:
1) его емкостное сопротивление при частоте f=50 гц;
2) емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.
Решение. Емкостное сопротивление конденсатора переменному току при частоте f=50 гц
При частоте f=500 гц
Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изменяется, конденсатор практически обладает бесконечно большим сопротивлением и поэтому он постоянного тока не пропускает.
§ 55. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ И ИНДУКТИВНЫМ СОПРОТИВЛЕНИЯМИ
Любая проволочная катушка, включенная в цепь переменного тока, обладает активным сопротивлением, зависящим от материала, Длины и сечения проволоки , и индуктивным сопротивлением, которое зависит от индуктивности катушки и частоты переменного тока, протекающего по ней (ХL=ωL=2πfL). Такую катушку можно рассматривать как приемник энергии, в котором активное и индуктивное сопротивления соединены последовательно.
Рассмотрим цепь переменного тока, в которую включена катушка индуктивности (рис. 56, а) с активным r и индуктивным ХL сопротивлением. Падение напряжения на активном сопротивлении
Падение напряжения на индуктивном сопротивлении
Построим векторную диаграмму тока и напряжения (рис. 56, б) для рассматриваемой цепи.
Пример. Падение напряжения на активном сопротивлении Ua=15в. Напряжение на индуктивном сопротивлении UL=26 в. Вычислить общее напряжение, приложенное к цепи.
Решение. Общее напряжение на зажимах цепи переменного тока с последовательно соединенными активным и индуктивным сопротивлениями.
Чтобы определить полное сопротивление цепи переменного тока с активным и индуктивным сопротивлениями, следует разделить векторы Ua=Ir и UL =IXL на число I, выражающее силу тока в цепи, и построить треугольник А’О’В’ (рис. 56, в), стороны которого меньше сторон треугольника напряжений в I раз. Образованный треугольник называется треугольником сопротивлений. Его сторонами являются сопротивления r и ХL и полное сопротивление цепи Z.
Пользуясь теоремой Пифагора, можно написать что,
отсюда полное сопротивление цепи
Пример. Активное сопротивление катушки r=7 ом, а ее индуктивное сопротивление ХL=24 ом. Вычислить полное сопротивление катушки.
Решение. Полное сопротивление катушки переменному току
Сила тока в цепи с активным и индуктивным сопротивлениями определяется по закону Ома:
На векторной диаграмме видно, что в цепи переменного тока с активным и индуктивным сопротивлениями ток и напряжение не совпадают по фазе. Ток отстает от напряжения — на угол .
Угол сдвига между током и напряжением можно определить, если известен косинус этого угла.
Из треугольника напряжений косинус угла сдвига фаз
Теперь можно, пользуясь таблицей тригонометрических функций, определить угол .
Пример. Падение напряжения на активном сопротивлении катушки Ua =30 в. Общее напряжение на ее зажимах U=60в. Определить угол сдвига фаз между током и напряжением в цепи.
Решение. На основании данных найдем
По таблице тригонометрических функций угол сдвига фаз при со =0,5 составляет 60°.
2.2. Цепь переменного тока с активным сопротивлением
Известно, что сопротивление одного и того же проводника переменному току больше, чем постоянному току. Это объясняется явлением поверхностного эффекта, сущность которого заключается в следующем. Электрические заряды, обуславливающие постоянный ток, распределяются по сечению проводника равномерно, примерно так, как показано на рис. 2.3, а. При прохождении по проводнику переменного тока, создаваемый им переменный магнитный поток вытесняет электрические заряды из центральной части проводника к его периферийным слоям (рис. 2.3, б).
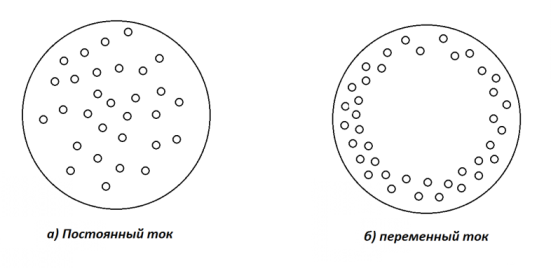
а) постоянный ток б) переменный ток
Рис. 2.3 Распределение электрических зарядов по сечению проводника
Чем выше частота тока в цепи, тем ближе к поверхности проводника располагаются электрические заряды. При этом плотность зарядов на поверхности проводника увеличивается и его сопротивление возрастает. Сопротивление проводника постоянному току называют омическим сопротивлением, а его сопротивление переменному току – активным сопротивлением. К активным сопротивлениям относят электрические лампы накаливания, электрические печи, различные нагревательные приборы и провода, где электрическая энергия почти целиком превращается в тепловую энергию.
Рассмотрим цепь, состоящую из активной нагрузки с сопротивлением R (рис. 2.4), к зажимам которой приложено переменное напряжение.
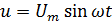(2.5)
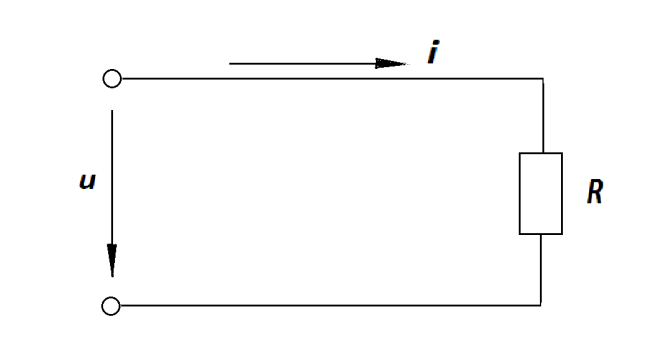
Рис. 2.4 Цепь переменного тока с активной нагрузкой.
Мгновенное значение тока в цепи определяется по закону Ома
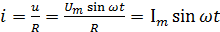(2.6)
где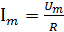 
Сравнивая между собой выражения (2.5) и (2.6), отметим, что в цепи переменного тока с активным сопротивлением напряжение и ток совпадают по фазе друг с другом.
Мгновенная мощность такой цепи равна произведению мгновенных значений тока и напряжения.
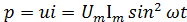(2.7)
Построим волновую и векторную диаграммы цепи переменного тока с активным сопротивлением (рис. 2.5).
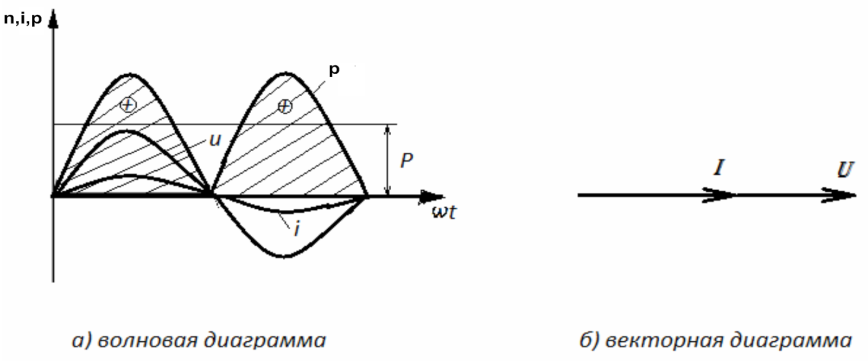
Рис. 2.5 Волновая и векторная диаграммы цепи переменного тока с активным сопротивлением.
Как видно из волновой диаграммы, потребление мощности в сети с активной нагрузкой периодически изменяется от нуля до максимального значения и опять до нуля. При этом знак мощности всё время остаётся положительным. Это означает, что в активной нагрузке происходит процесс необратимого преобразования электрической энергии в тепловую энергию.
Мощность цепи переменного тока принято оценивать по среднему значению мгновенной мощности за период:
=
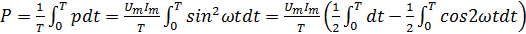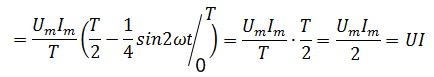
Следовательно, в
цепи переменного тока с активным
сопротивлением активная мощность
определяется как произведение действующих
значений тока и напряжения: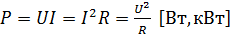 
2.3 Цепь переменного тока с индуктивным сопротивлением.
Многие элементы
электрических установок состоят из
индуктивных катушек, обладающих
индуктивностью L.
При включении такой катушки в цепь
переменного тока, в ней мгновенно
проявляется действие ЭДС самоиндукции
— 
,
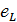препятствующее изменению тока. Величина
этой ЭДС настолько значительна, что на
ее уравновешивание затрачивается
основная часть напряжения, приложенного
к катушке, и лишь его небольшая часть
приходится на падение напряжения в
активном сопротивлении катушки. Поэтому
часто активное сопротивление катушки
приравнивается к нулю, и такую катушку
называют идеальной катушкой индуктивности.
Цепь переменного тока с такой катушкой
называется цепью с индуктивной нагрузкой
(рис. 2.6).
Рис. 2.6 Цепь переменного тока с индуктивной нагрузкой.
К зажимам цепи
подведено синусоидальное напряжение u. Под действием
этого напряжения в цепи возникает ток,
мгновенное значение которого равно 
(2.8.)
Ток возбуждает в катушке ЭДС самоиндукции, пропорциональную скорости изменения тока в цепи
(2.9)
В любой момент
времени ЭДС самоиндукции —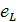
уравновешивается напряжением на зажимах
цепи u
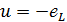(2.10)
Подставляя (2.8) и (2.10) в (2.9), имеем:
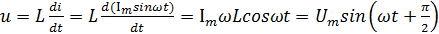(2.11)
где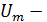 
амплитудное значение напряжения:
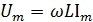(2.12)
Разделив обе части
уравнения (2.12) на 
,
получим выражение закона Ома для цепи
с идеальной катушкой индуктивности.
(2.13)
Рассмотрим размерность знаменателя выражения (2.13)
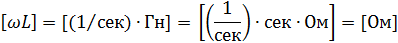
Обозначим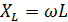 
и назовем индуктивным сопротивлением
идеальной катушки. Его величина зависит
от индуктивности катушки и частоты
питающего тока.
Сравнивая между собой уравнения (2.8) и (2.11) делаем вывод: в цепи переменного тока с индуктивной нагрузкой напряжение опережает ток на угол в 90°.
Мгновенная мощность цепи определяется как произведение мгновенных значений тока и напряжения, т.е.
Таким образом, мгновенная мощность в цепи переменного тока с индуктивностью изменяется во времени с удвоенной частотой по отношению к частоте тока.
Построим векторную и волновую диаграммы цепи с индуктивным сопротивлением (рис. 2.7).
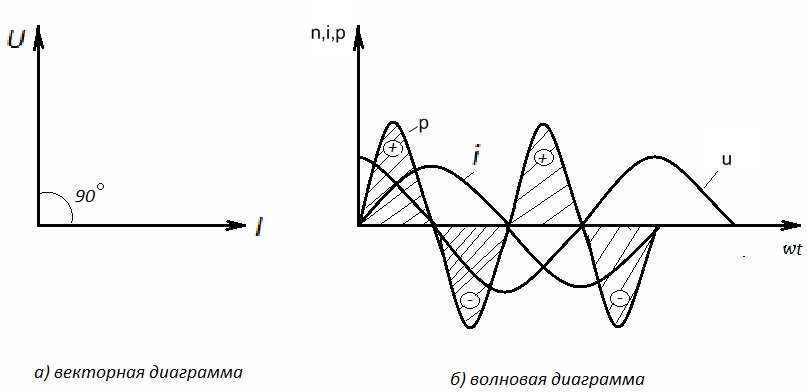
Рис. 2.7 Векторная и волновая диаграммы цепи переменного тока с индуктивным сопротивлением.
Анализ волновой диаграммы позволяет сделать следующие выводы:
В течение первой и третьей четвертей периода переменного тока при его изменении от нуля до амплитудного значения, мощность положительна. Это означает, что энергия, посылаемая источником во внешнюю цепь, запасается в катушке индуктивности в форме энергии магнитного поля
.
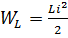В течении второй и четвёртой четвертей периода, при изменении тока от амплитудного значения до нуля, мощность отрицательна. Это означает, что катушка индуктивности возвращает запасенную энергию источнику.
Таким образом, в цепи переменного тока с идеальной катушкой индуктивности происходит периодический обмен энергией между внешним источником и магнитным полем катушки. Средняя активная мощность за период оказывается равной нулю, т.е. источник в такой цепи не расходует энергии и, следовательно, в индуктивности не происходит необратимого преобразования электрической энергии в другие виды энергии.
Мощность цепи с идеальной катушкой оценивают по величине индуктивной мощности QL, измеряемой в ВАр (вольт-ампер реактивный) и характеризующей интенсивность обмена энергией между генератором и магнитным полем катушки
.
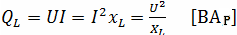
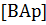Индуктивная мощность в отличие от активной мощности не может быть использована в практических целях.
3.4.7. Цепь с активным сопротивлением, индуктивностью и емкостью
Цепь с активным сопротивлением, индуктивностью и емкость, представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 51).
Рис. 51 Рис. 52 Рис. 53
Снова принимаем фазу тока нулевой:
.
Тогда напряжение на активном
сопротивлении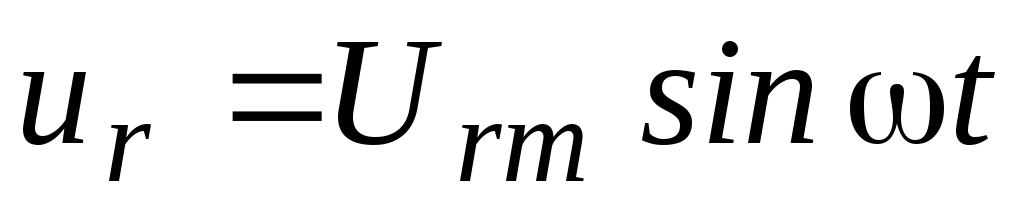
напряжение на индуктивности
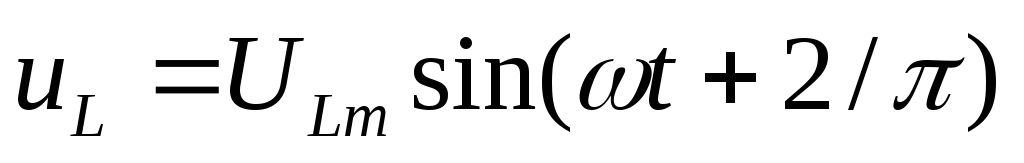напряжение
на емкости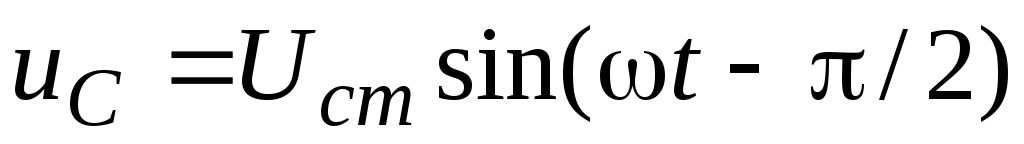
.
Построим векторную диаграмму при условии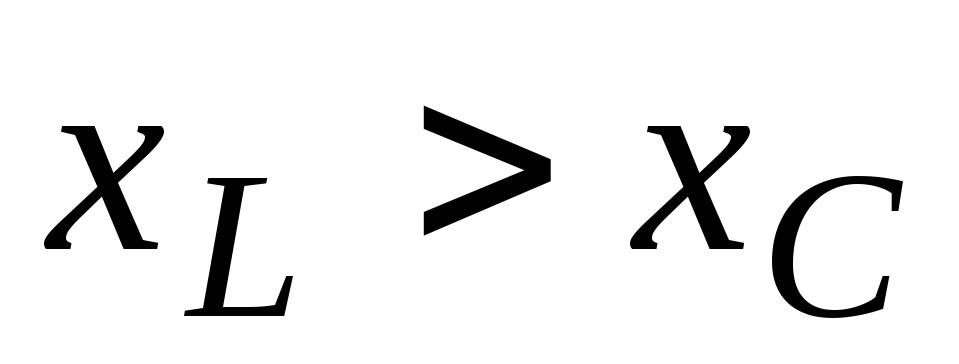
т. е.
. Вектор
результирующего напряжения 
замыкает многоугольник векторов
,
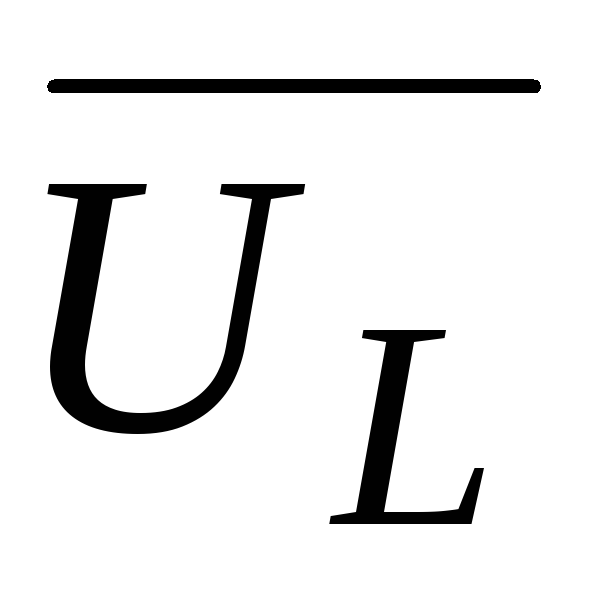и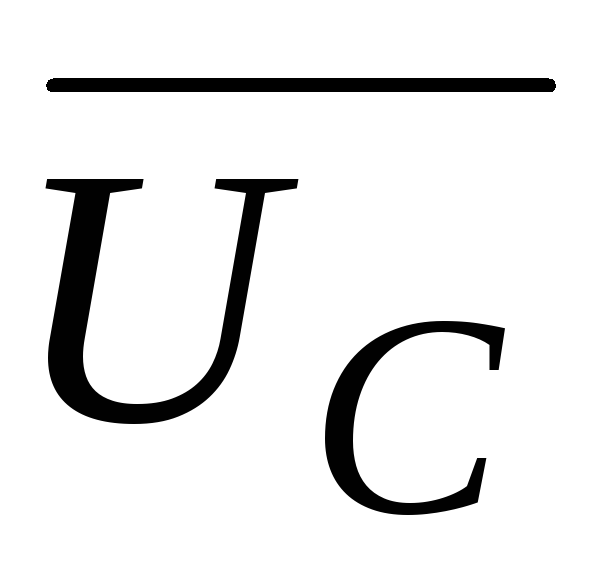
(рис. 52). Вектор
+
определяет напряжение на индуктивности
и емкости. Как видно из диаграммы это
напряжение может быть меньше напряжения
на каждом из участков в отдельности.
Это объясняется процессом обмена
энергией между индуктивностью и емкостью.
Выведем закон Ома для рассматриваемой
цепи. Так как модуль вектора 
+
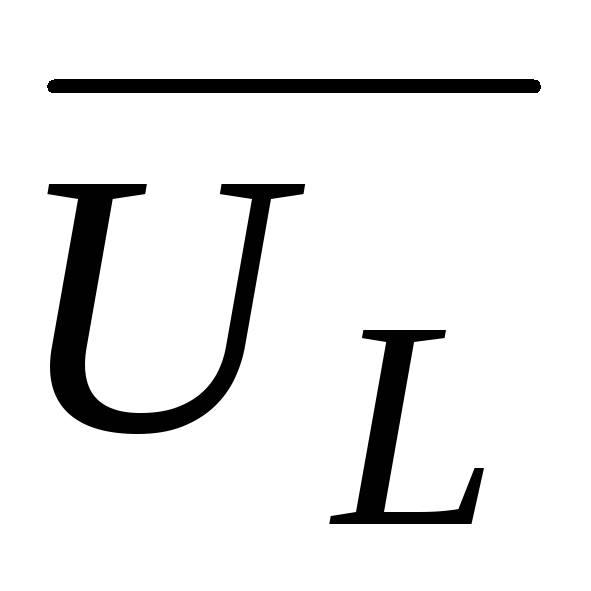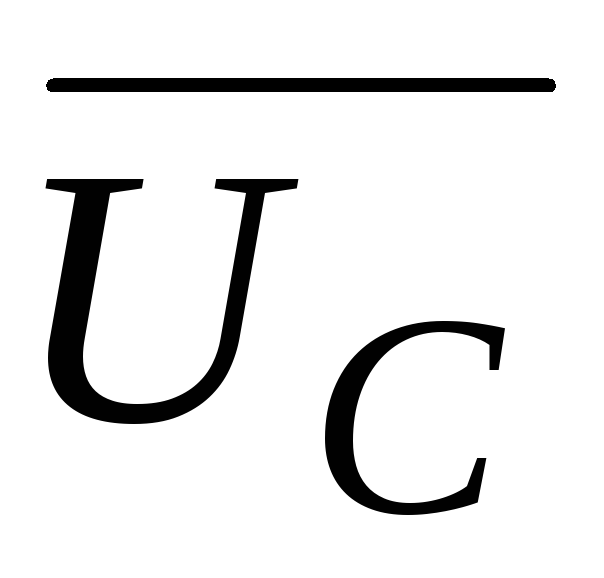определяют как разность действующих
значений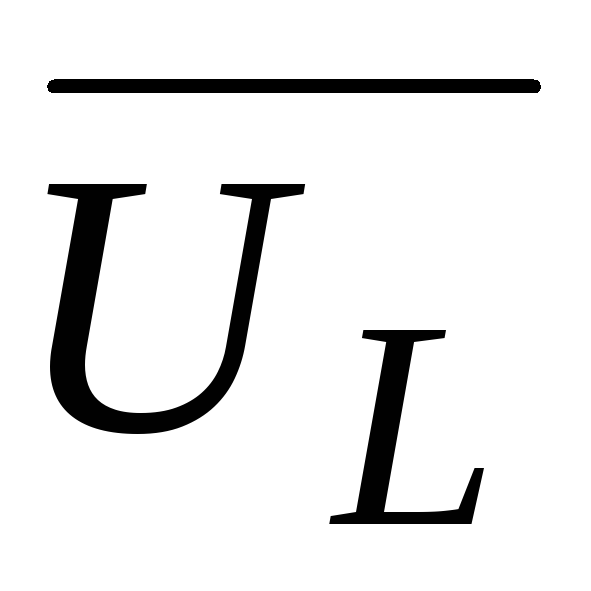
,
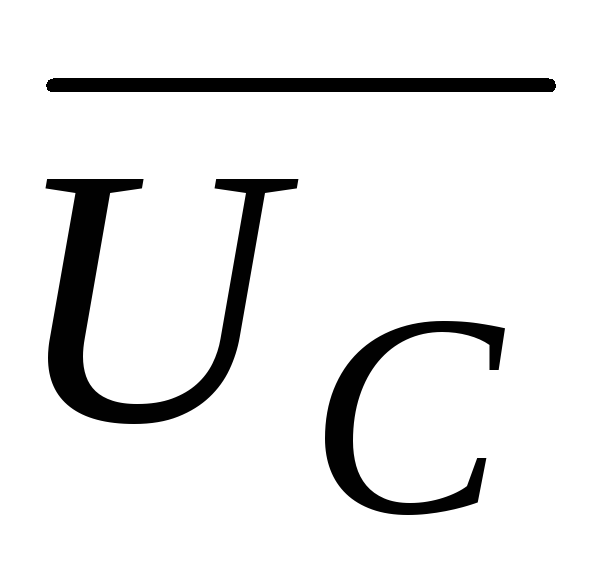из диаграммы рис. 52 ,что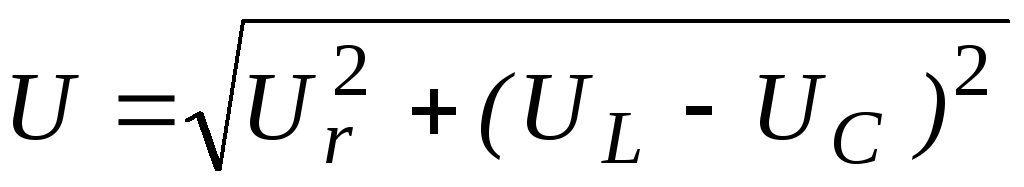
.
Но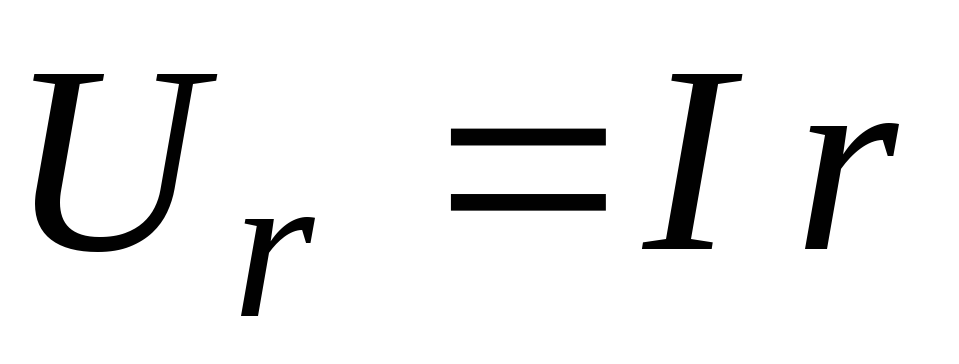 
;
; 
,
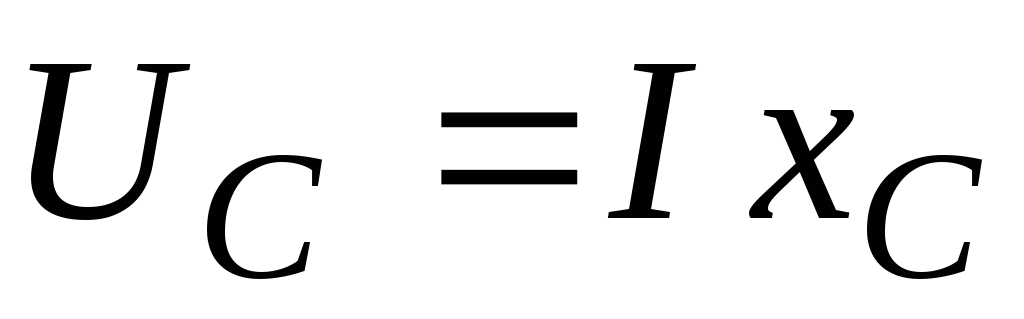следовательно,
,
откуда
.
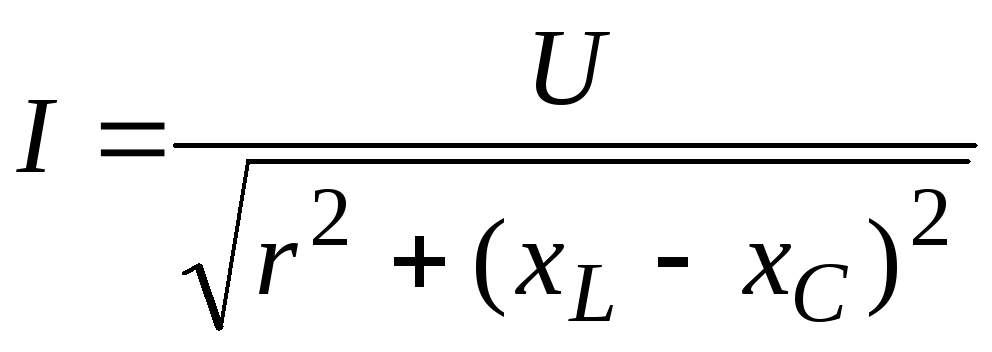(3.37)
Вводя
обозначения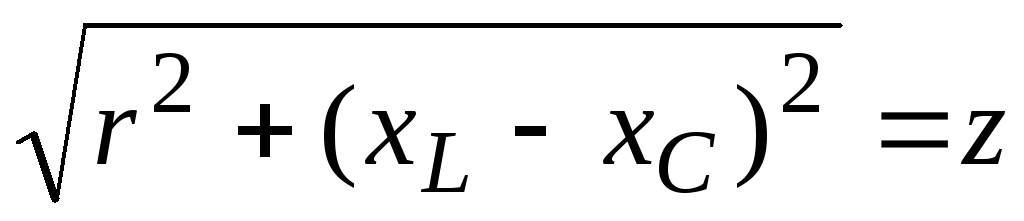 
,
гдеz — полное сопротивление цепи, получим
.
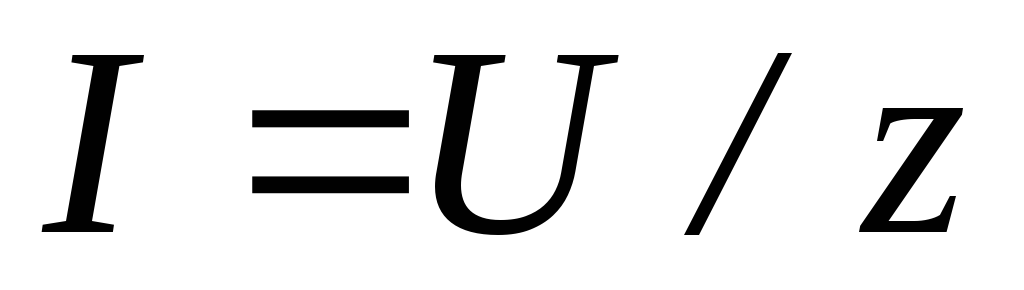(3.38)
Разность
между индуктивным и емкостным
сопротивлениями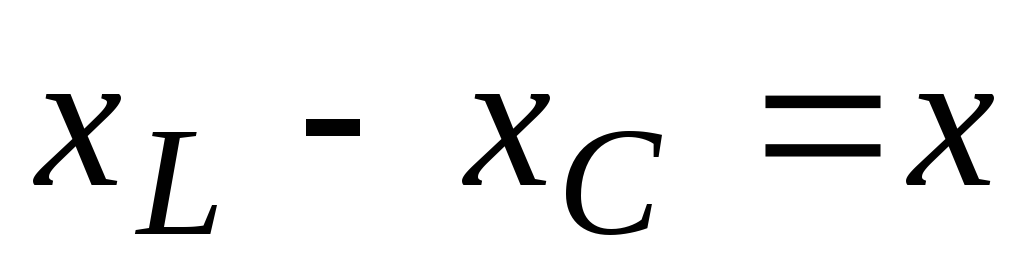 
называют реактивным сопротивлением
цепи. Учитывая это, получим треугольник
сопротивлений для цепи сr, L и С (рис.53). При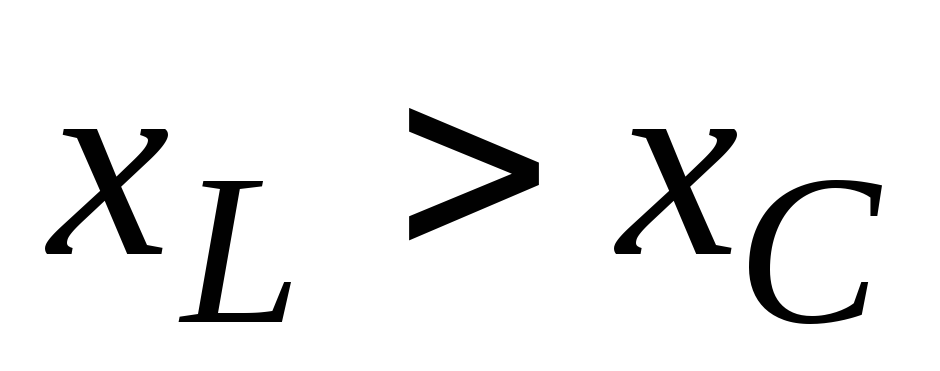 
реактивное сопротивление положительно
и сопротивление цепи носит
активно-индуктивный характер.
При 
реактивное сопротивление отрицательно
и сопротивление цепи носит активно-емкостный
характер. Знак угла сдвига фаз между
током и напряжением получаем автоматически,
так как реактивное сопротивление —
величина алгебраическая:
.
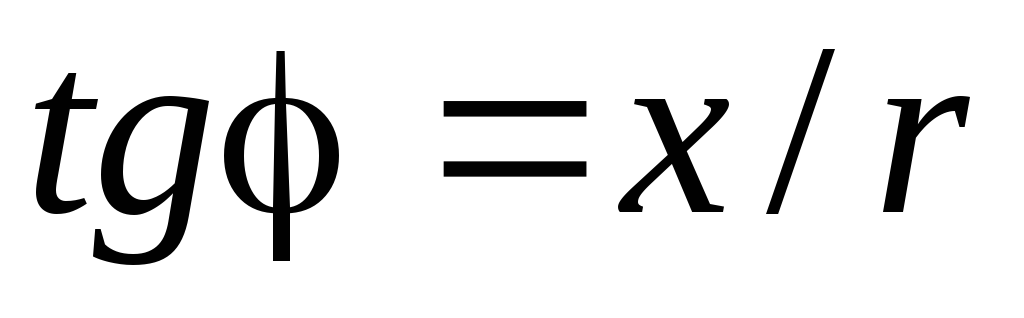(3.39)
Таким
образом, при 
преобладает или индуктивное, или
емкостное сопротивление, т, е. с
энергетической точки зрения цепь сr, L и С сводится к цепи с r, L или с с r,
С. Тогда
мгновенное значение мощности
,
причем знак φ определяется по формуле (3.39). Соответственно активная, реактивная и полная мощности определяются выражениями.
; 
.
.
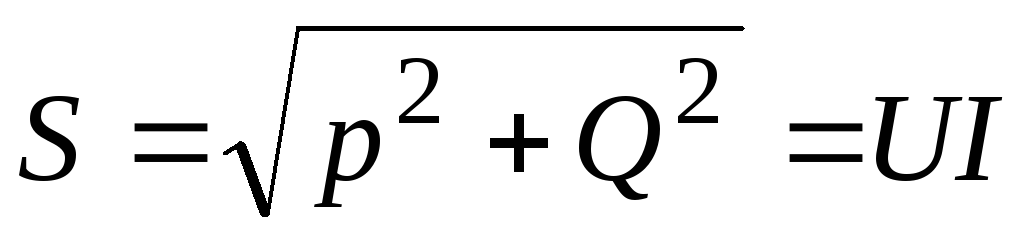3.4.8. Резонанс напряжений
Резонансом напряжения называется явление в цепи с последовательным колебательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
На рис.54 показана схема последовательного колебательного контура.
Рис. 54
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление к цепи должно равняться нулю, так как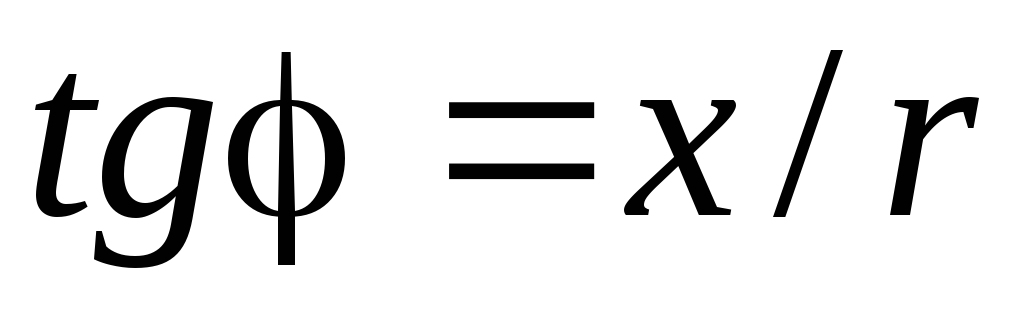
. Таким
образом, условием резонанса напряжений
является х
= 0 или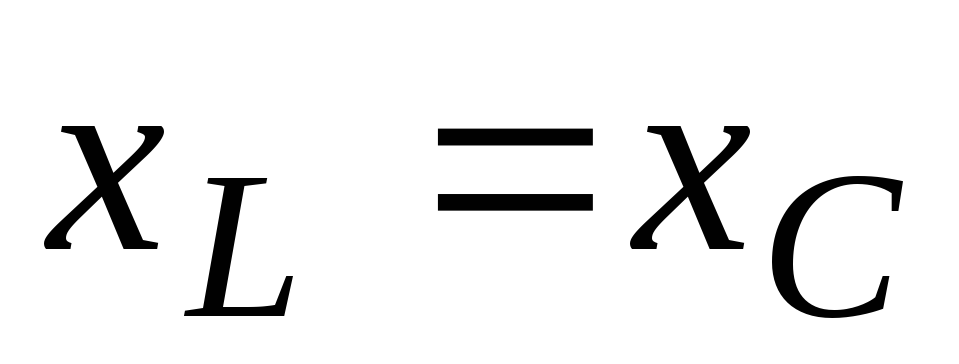 
.
Но 
,
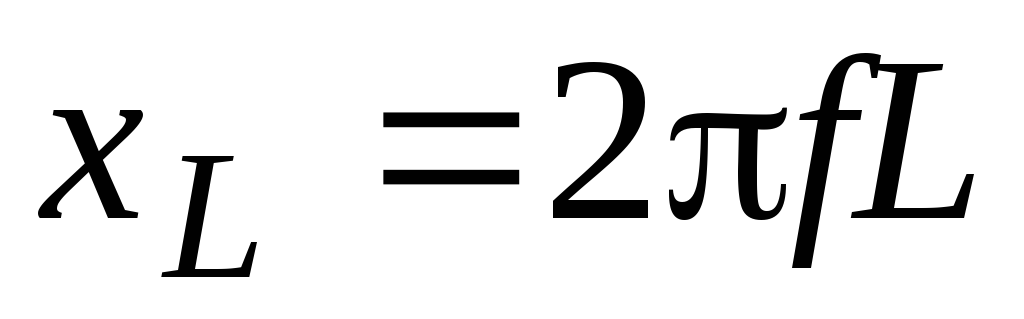а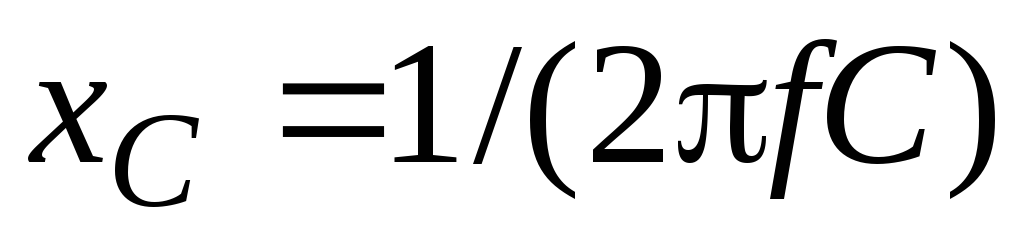
,
гдеf — частота источника питания.
В результате можно записать
.
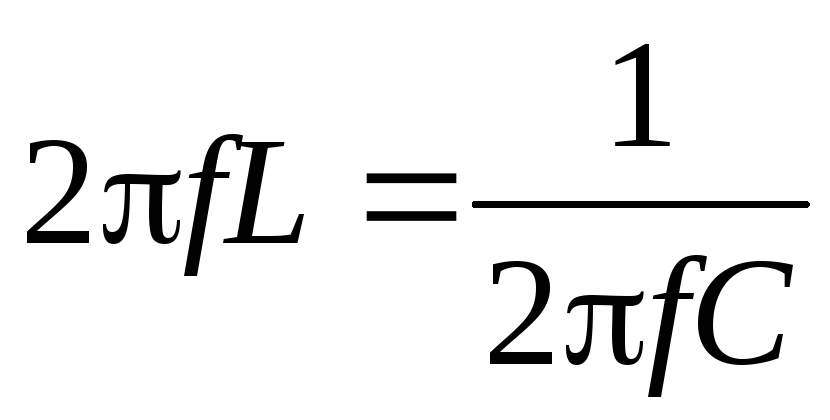Решая это уравнение относительно f , находим
(3.40)
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение
(3.40) является формулой Томсона, определяющей
зависимость собственной частоты
колебаний контура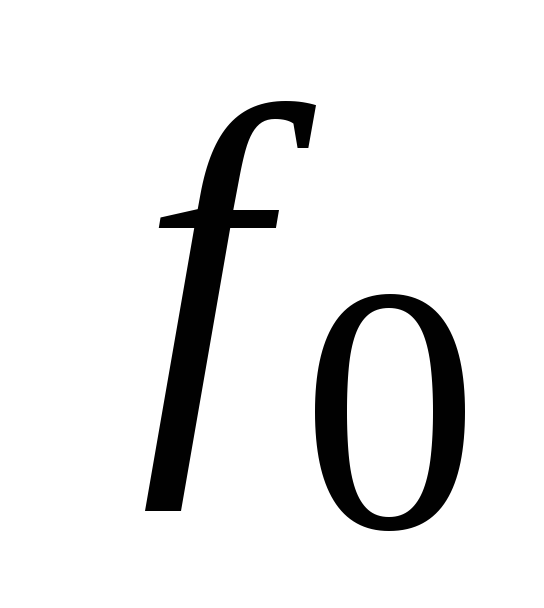 
,
от параметровL и С.
Следует вспомнить, что если конденсатор
контура зарядить от источника
постоянного тока, а затем замкнуть его
на индуктивную катушку, то в контуре
возникнет переменный ток частоты 
.
Вследствие потерь колебания в контуре
будут затухать, причем время затухания
зависит от величины потерь.
Рис. 55
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис.55. На основании этой диаграммы и закона Ома для цепи с r, L и С сформулируем признаки резонанса напряжений: а)
сопротивление всей цепи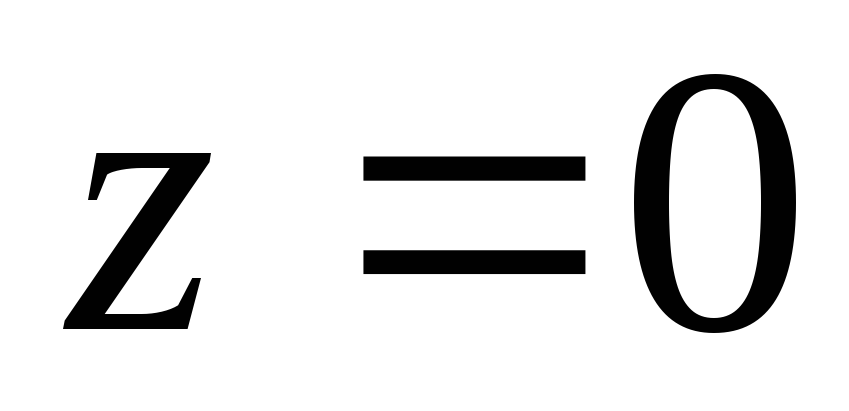 
минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
Рис. 56 Рис. 57
в) напряжение на индуктивной катушке равно напряжению на емкости и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на индуктивности и емкости обусловлено накопленной в них энергией, величина которой тем больше, чем меньше потери в цепи. Количественно указанное явление характеризуется добротностью контура Q, которая представляет собой отношение напряжения на катушке или емкости к напряжению на зажимах цепи при резонансе;
.
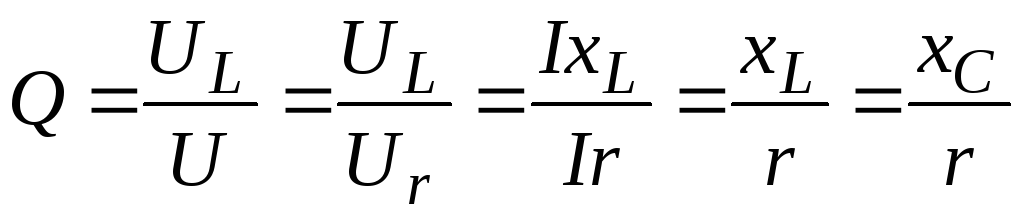(3.41)
При
резонансе 
Величина 
называется волновым сопротивлением
контура. Таким образом,
(3.42)
Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 56).
Резонансная кривая показывает зависимость действующего значения тока в контуре от частоты источника при неизменной собственной частоте контура.
Эта зависимость определяется законом Ома для цепи с r, L и С. Действительно, I = U/z, где
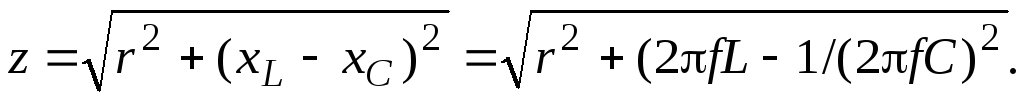(3.43)
На
рис. 57 показана зависимость реактивного
сопротивления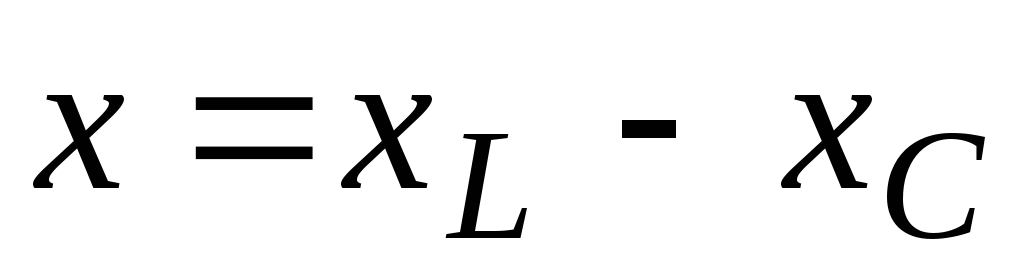 
от частоты источника. Анализ этого
графика и выражения (3.43) показывает, что
при низких и высоких частотах реактивное
сопротивление велико и ток в контуре
мал. При частотах, близких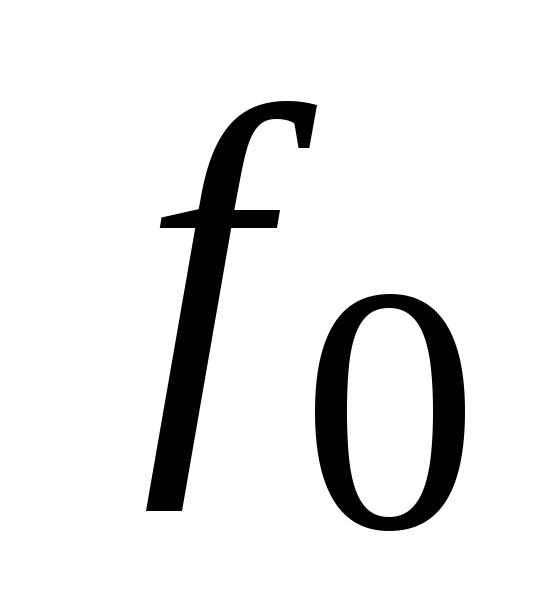
реактивное сопротивление мало и ток
контура велик. При этом, чем больше
добротность контураQ , тем острее
резонансная кривая контура.
Цепь переменного тока с активным сопротивлением. Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R приложено синусоидальное напряжение u= Umsinώt, то и ток в этой цепи изменяется по синусоидальному закону (рис. 11.1 в):
где
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (ψi = ψU = O).
М
атематическое
выражение закона Ома для цепи переменного
тока
с активным сопротивлением имеет вид:
Т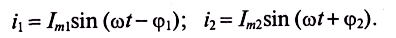
аким
образом,
действующее значение синусоидального
тока I
пропорционально
действующему значению синусоидального
напряжения U и обратно
пропорционально сопротивлению R
участка,
к которому приложено напряжение U.
Цепь переменного тока с индуктивным сопротивлением.
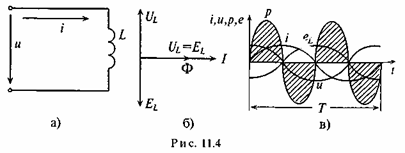
ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90°.
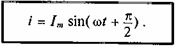
Напряжение,
приложенное к цепи с идеальной
индуктивностью,
как и ток в этой цепи, изменяется по
синусоидальному закону,
но опережает ток по фазе на угол 90°.
В
ывод: для
существования тока в цепи с идеальной
индуктивностью необходимо приложить
к цепи напряжение, которое в любой момент
времени
равно по величине, но находится в противофазе с ЭДС, вызванной этим током (рис. 11.46, в).
Это уравнение и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Т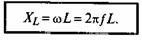
аким
образом,
Закон Ома для этой цепи можно записать иначе:
Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Цепь переменного тока с емкостным сопротивлением.
Цепь с емкостью
Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе Uc отстает по фазе от напряжения источника при зарядке, и при разрядке конденсатора.
Очевидно,
ток в цепи конденсатора достигает
амплитудного
значения
тогда, когда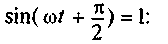
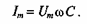
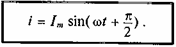Тогда
Ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°
Это равенство и является математическим выражением закона Ома для цепи переменного тока с емкостью. Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:
Тогда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему.
Неразветвленная RL-цепь.
Неразветвленная RC-цепь.
Неразветвленная RLC-цепь.
§5.7. Цепь с активным сопротивлением, индуктивностью и емкостью
Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий
случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 5.22).
Рис. 5.22. Схема цепи переменного тока с R, L и С Рис. 5.23. Векторная диаграмма для цепи с R, L и С
Принимаем фазу тока нулевой: i=Imsinωt.
Тогда напряжение на активном сопротивлении uR=—URmsinωt, напряжение на индуктивности uL=ULmsin(ωt+p/2), напряжение на емкости uC=UCmsin(ωt—π/2). Построим векторную диаграмму при условии XL>ХC, т. е. UL=IXL>UC=IXC.
Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL и UC (рис. 5.23). Вектор UL+UC определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью. Выведем закон Ома для рассматриваемой цепи. Так как модуль вектора UL+UC рассчитывают как
разность действующих | значений | UL—UC, то из диаграммы рис. 5.23 следует, что | |||||||||
U = | UR2 + (UL −UC )2 | . Но UR=IR; UL=IXL, UC=IXC; следовательно, U = I | R2 + (X L − XC )2 | откуда | |||||||
|
|
|
|
| I = |
|
| U | |||
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| R2 + (X L − XC )2 | ||||||
|
|
|
|
|
|
|
| ||||
|
|
|
| = Z , где Z — полное сопротивление цепи, найдем | |||||||
| Введя обозначение |
| R2 + (X L − XC )2 | ||||||||
|
|
|
| I=U/Z. |
|
|
| (5.28) |
| ||
Рис. 5.24. Треугольник сопротивлении для цепи с R, L и С
Разность между индуктивным и емкостным сопротивлениями XL—XC=X называют реактивным сопротивлением цепи. Учитывая это, получим треугольник сопротивлений для цепи с R, L и С (рис. 5.24). При XL>XС реактивное сопротивление положительно и сопротивление цепи носит активноиндуктивный характер. При XL<XC реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостный характер. Знак сдвига фаз между током и напряжением получим автоматически, так как реактивное сопротивление — величина алгебраическая:
tgϕ=X/R. (5.29)
Таким образом, при XL¹XC преобладает или индуктивное, или емкостное сопротивление, т.е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С. Тогда
мгновенная мощность
p=UIcosϕ—UIcos(2wt+ϕ),
причем знак ϕ определяется по формуле (5.29). Соответственно активная, реактивная и полная мощности характеризуются выражениями P=UIcosϕ; Q=UIsinϕ; S = 
P2 + Q2 = UI .
Карточка № 5.6 (356).
Цепь с активным сопротивлением, индуктивностью и емкостью
Назовите цепь, которой не соответствует эта диаграмма |
| Цепь с R, L и C(XL>ХС) | 133 | |
|
| Цепь с R, L и C(XL<ХС) | 26 | |
|
| Цепь R и L |
| 112 |
|
|
|
| |
При каком соотношении между XL и ХС показание ваттметра | XL>ХС |
| 58 | |
будет максимальным? |
|
|
|
|
| XL<ХС |
| 71 | |
|
| XL=ХС |
| 75 |
|
|
|
| |
В схемах а) и б) U=100В; R1=R2=3Ом; ХL1=10Ом; ХС1=6Ом; | I1>I2 |
| 13 | |
XL2=100Oм; ХС2=96Ом. Что можно сказать о соотношении |
|
|
| |
I1<I2 |
| 100 | ||
между точками в этих схемах? |
|
|
|
|
| I1=I2 |
| 87 | |
|
|
| ||
|
|
|
| |
Каково соотношение между показаниями вольтметра, | UAБa>UAБб |
| 117 | |
включенного между точками А и Б в приведенных выше |
|
|
| |
UAБa=UAБб |
| 76 | ||
схемах? |
|
|
|
|
| UAБa<UAБб |
| 65 | |
|
|
| ||
|
|
|
| |
В приведенной схеме U=100В; R=4Ом; XL=3Ом; ХC=6Ом. | Активная | мощность | 144 | |
Как изменится активная и реактивная мощности | при | увеличится, | реактивная |
|
замыкании ключа K? |
| уменьшится |
|
|
|
|
|
|
|
|
| Активная | мощность | 84 |
|
| уменьшится, | реактивная |
|
|
| увеличится |
|
|
|
|
|
|
|
|
| Активная и | реактивная | 92 |
|
| мощности не изменятся |
| |
|
|
|
|
|
§ 5.8. Резонансный режим работы цепи
Пусть электрическая цепь содержит одну или несколько индуктивностей и емкостей (рис. 5.25). Под резонансным режимом работы цепи понимают режим, при котором сопротивление является чисто активным. По отношению к источнику питания элементы цепи ведут себя в
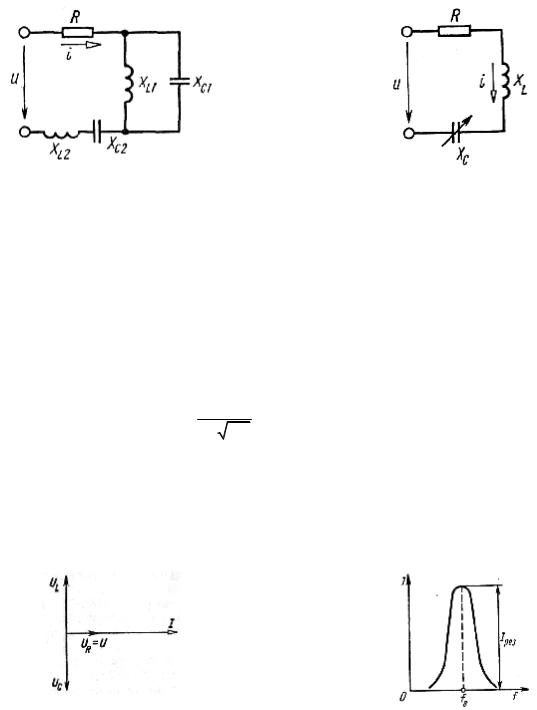
(5.30)
резонансном режиме как активное сопротивление, поэтому ток и напряжение в неразветвленной части совпадают по фазе. Реактивная мощность цепи при этом равна нулю.
Различают два основных режима: резонанс напряжений и резонанс токов.
Рис. 5.25. Резонансный режим работы цепи | Рис. 5.26. Схема последовательного колебательного | |
контура | ||
|
§ 5.9. Резонанс напряжений
Резонансом напряжений называют явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
На рис. 5.26 показана схема последовательного колебательного контура.
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как tgϕ=X/R.
Таким образом, условием резонанса напряжений является Х=0 или XL=XC. Но XL=2πfL, а XC=l/(2πfC), где f — частота источника питания. В результате можно записать
2πfL=l/(2πfC).
Решив это уравнение относительно f, получим f = 2π 1LC = f0
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение (5.30) является формулой Томсона, определяющей зависимость собственной частоты колебаний контура f0 от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f0. Вследствие потерь колебания в контуре будут затухать, причем время затухания зависит от значения возникших потерь.
Рис. 5.27. Векторная диаграмма при резонансе | Рис. 5.28. Резонансная кривая последовательного контура | |
напряжений | ||
|
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 5.27.
На основании этой диаграммы и закона Ома для цепи с R, L и С сформулируем признаки резонанса напряжений:
а) сопротивление цепи Z = R минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которой тем больше, чем меньше потери в цепи. Количественно указанное
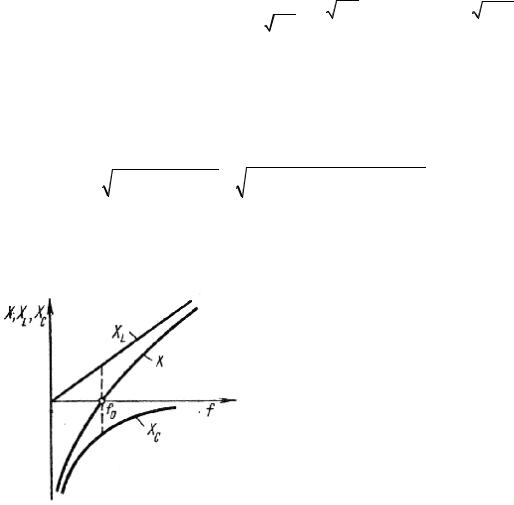
явление характеризуется добротностью контура Q, которая представляет собой отношение напряжения на катушке или конденсаторе к напряжению на зажимах цепи при резонансе:
Q=UL/U=UL/UR=IXL/(IR)=XL/R=XC/R. (5.31)
|
| = 2π fL = 2π |
| 1 |
|
|
|
|
|
|
|
|
При резонансе | X L |
|
| L | = LC . Величину | L / C = ZB | называют | |||||
2π |
|
| ||||||||||
|
|
|
| LC |
|
|
|
|
|
| ||
волновым сопротивлением контура. Таким образом, |
|
|
|
|
|
| ||||||
|
| Q=Zв/R. |
|
|
| (5.32) |
|
|
| |||
Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 5.28).
Резонансная кривая показывает зависимость действующего значения тока в контуре от частоты источника при неизменной собственной частоте контура.
Эта зависимость определяется законом Ома для цепи с R, L и С. Действительно, I=U/Z, где
|
|
|
|
|
|
|
|
| ë( | ) | ( |
| )û |
| ( |
| ) |
|
| ( |
| L |
| C ) | 2 = |
| 2 |
| |||||||
Z = | R2 + |
| X |
| — X |
| R2 + é | 2π fL -1 / |
| 2π fC | ù |
| 5.33 |
| |||
На рис. 5.29 показана зависимость реактивного сопротивления X=XL—XC от частоты источника f. Анализ этого графика и выражения (5.33) показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При частотах, близких к f0, реактивное сопротивление мало и ток контура велик. При этом чем больше добротность контура Q, тем острее резонансная кривая контура.
Рис. 5.29. Зависимость реактивного сопротивления X от
частоты источника
Резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты.
