системы счисления — Почему некоторые разработчкики записывают числа в 16-ричном представлении? (C#)
Вопрос задан
Изменён 5 лет 7 месяцев назад
Просмотрен 171 раз
Здравствуйте! Достаточно часто в open-source проектах замечаю, что разработчики записывают числа не так:
int i = 2147483647;
А так:
int i = 0x7FFFFFFF;
Даёт это один и тот же результат: у нас имеется переменная, содержащая значение = int.MaxValue, но в чем глубокая логика такой записи? Просто, мол: «Я умею записывать числа в 16-ричном представлении, посмотрите на меня!» Или же тут есть некоторые плюсы? Может, присвоение идет на наносекунды быстрее и/или машине их проще так воспринимать? Разрешите, пожалуйста, мои сомнения по сему поводу!
- c#
- системы-счисления
Очевидно, что данное значение инициализатора
int i = 2147483647;
запомнить сложно.
Нужно постоянно сверяться со справочником, чтобы правильно выписать все цифры.
Такая запись
int i = 0x7FFFFFFF;
не требует наличия феноменальной памяти.
Но в любом случае было бы проще, лучше и яснее записать
int i = int.MaxValue;
так как такая запись самодокументируемая.
Запись
int i = 0x7FFFFFFF;
предпочтительнее предыдущей записи лишь в одном случае: когда переменная i используется как некоторая маска для битовых операций.
2
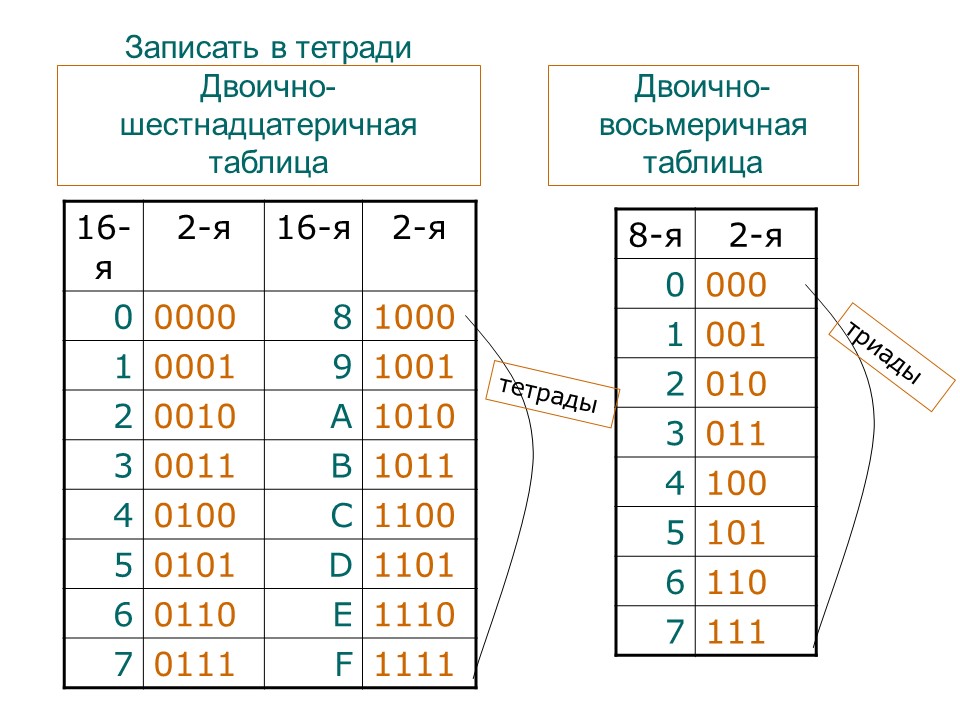
Часто необходимо записать двоичное беззнаковое целое. Каждая шестнадцатиричная цифра может заменить собой 4 бита в бинарном представлении, т.е. байт — две «сконкатенированных» шеснадцатиричных цифры. Это удобнее читать и записывать, чем ряды двоичных разрядов.
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Повторение
Умножение и деление на разрядную единицу    
Как и в десятичной системе счисления, так и в любой другой, умножение и деление чисел на разрядные единицы (элементы базиса) сводится к передвижению запятой на соответствующее количество знаков влево или вправо. Соответствие чисел, записанных в системах счисления с основанием 2k    
Составляя таблицы сложения и умножения в двоичной системе счисления, вы убедились, что запомнить эти таблицы достаточно легко, выполнять действия над числами в двоичной системе счисления также просто. 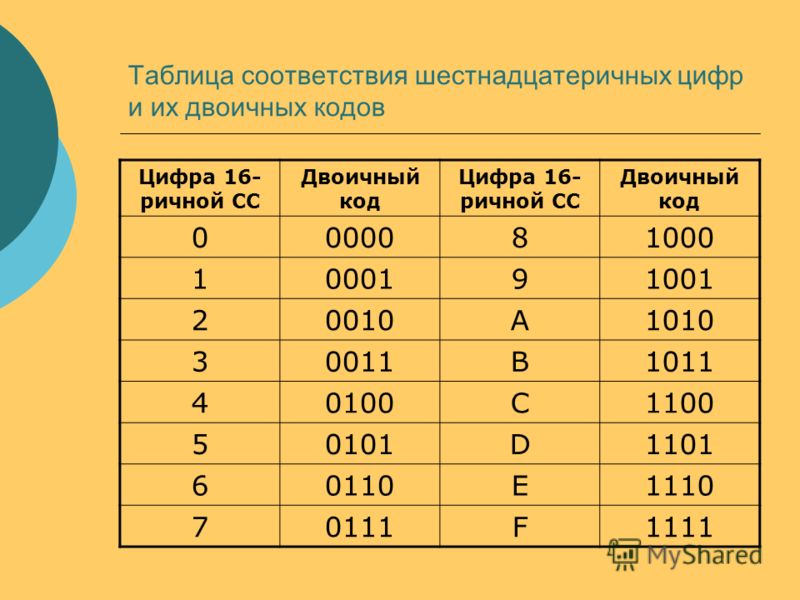     Поэтому для внешнего представления данных в компьютере, а также для адресации байтов оперативной памяти, на большинстве современных компьютеров имеется еще одна система счисления – 16-ричная.     Существуют простые алгоритмы перевода двоичных чисел в шестнадцатеричные и обратно. Эти алгоритмы базируются на том, что 16 – четвертая степень двойки, значит, двоичную запись числа из 4-х цифр можно представить в виде 16-ричной цифры.    А теперь каждую цифру 16-ричного числа заменим на соответствующую ей четверку двоичных знаков: С16=1210=11002; В16=1110=10112; А16=1010=1010      Таким образом, для перевода 16-ричных чисел в двоичные каждая 16-ричная цифра представляется в виде 4-х разрядного двоичного числа – двоичной тетрады. Совокупность этих двоичных цифр и дает двоичную запись 16-ричного числа.     Пример 1. А1F416→X2. Переведем каждую цифру числа в двоичную тетраду:    A=1010    1=0001    F=1111    Выпишем ответ: А1F416=10100001111101002.    Пример 2. 4E316→X2. Выполним те же действия:    4=0100    E=1110    3=0011    Выпишем ответ. Нули старшей цифры, стоящие слева, в двоичной записи числа можно не указывать: 4E316=100111000112.    Так же переводятся и дроби, только при этом можно не указывать нули младшей цифры дробной части, стоящие справа.     Пример 3. 5D,B816→X2.    5=0101    D=1101    B=1011    8=1000    Получим: 5D,B816=1011101,101112.    Сформулируем правило: Для перевода 16-ричных чисел в двоичные нужно каждую цифру 16-ричного числа представить в виде двоичной тетрады и записать полученную последовательность двоичных цифр, не указывая нули старшей цифры целой части, стоящие слева, и нули младшей цифры дробной части, стоящие справа.    При обратном переводе нужно группировать цифры двоичного числа в тетрады, и каждую тетраду заменять 16-ричной цифрой. При этом иногда нужно дописывать недостающие нули в целой и дробной частях.  Заменив каждую полученную тетраду 16-ричной цифрой, получим: 0001 0100 1011,11002=14B,C16.    Итак, для перевода двоичных чисел в 16-ричные нужно двоичное число разбить на тетрады – для целой части – справа налево, для дробной части – слева направо, дописывая недостающие нули. Для каждой тетрады записать ее 16-ричное значение.    Подобные алгоритмы перевода справедливы для всех систем счисления, основания которых равны некоторой степени двойки. А также в общем случае — для всех пар систем счисления, в которых основание одной системы счисления есть некая степень основания другой системы счисления.    Например, для перевода восьмеричных чисел в двоичные, нужно каждую цифру восьмеричного числа представить в виде тройки двоичных чисел (двоичной триады), поскольку 8=2 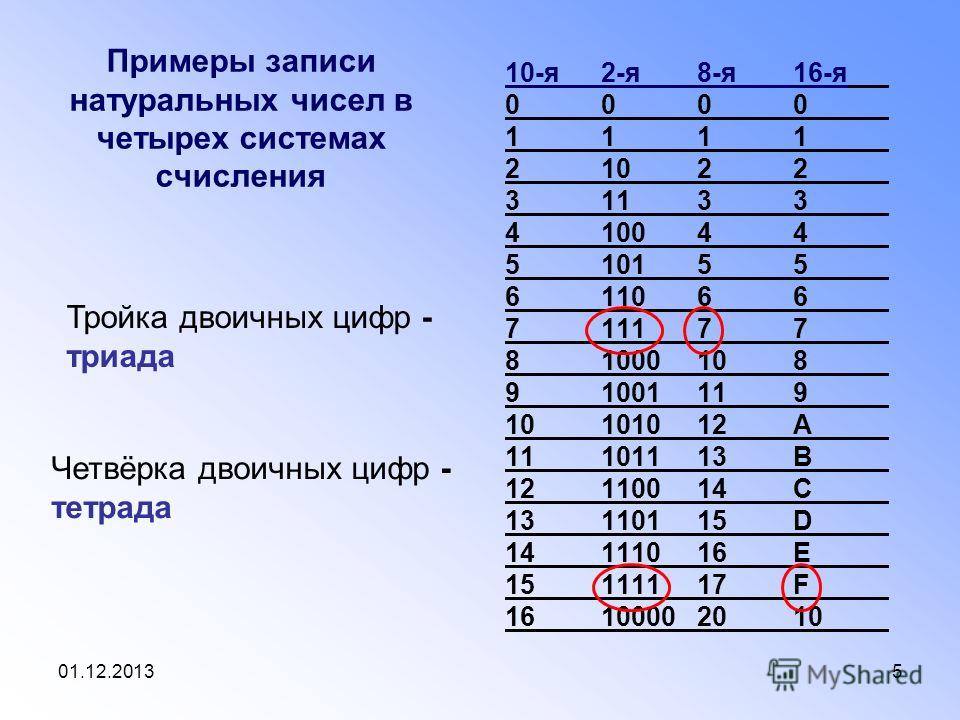    Пример 5. 135,78→X2.    1=001    3=001    5=101    7=111    Получим: 135,78=1011101,1112.    Пример 6. 10 111,000 0112→X8. Заменив каждую триаду восьмеричной цифрой, получим: 010 111,000 0112=27,038. Задачи |
Удивительные закономерности в квадратных числах (1, 4, 9, 16…) – BetterExplained
Быстрая загадка для вас — посмотрите на первые несколько квадратных чисел:
1, 4, 9, 16, 25, 36, 49 …
А теперь найдите разницу между последовательными квадратами:
1 к 4 = 3 от 4 до 9 = 5 от 9 до 16 = 7 от 16 до 25 = 9 от 25 до 36 = 11 …
А? Нечетные числа зажаты между квадратами?
Странно, но факт.
Потратьте некоторое время, чтобы выяснить, почему — еще лучше, найдите причину, которая подействовала бы на девятилетнего ребенка. Иди, я буду здесь.
Изучение закономерностей
Мы можем объяснить эту закономерность несколькими способами. Но цель состоит в том, чтобы найти убедительное объяснение, где мы ударяем по форхендам «а, вот почему!». Давайте перейдем к трем объяснениям, начиная с наиболее интуитивных, и посмотрим, как они помогут объяснить остальные.
Восторг геометра
Легко забыть, что квадратные числа, ну… квадратные! Попробуйте нарисовать их камешками
Ничего не заметили? Как перейти от одного квадратного числа к другому? Ну и вытаскиваем каждую сторону (правую и нижнюю) и заправляем уголок:
В то время как на 4 (2×2) мы можем перейти к 9 (3×3) с расширением: мы добавляем 2 (справа) + 2 (снизу) + 1 (угол) = 5. И да, 2 ×2 + 5 = 3×3. И когда мы на 3, мы переходим к следующему квадрату, вытягивая стороны и заполняя угол: Действительно, 3 × 3 + 3 + 3 + 1 = 16.
Каждый раз изменение на 2 больше, чем раньше, так как у нас есть еще одна сторона в каждом направлении (правая и нижняя).
Еще одно интересное свойство: переход к следующей клетке всегда нечетный, так как мы меняем на «2n + 1» (2n должно быть четным, поэтому 2n + 1 нечетное). Поскольку изменение нечетное, это означает, что квадраты должны циклически повторяться: четное, нечетное, четное, нечетное…
И подождите! Это имеет смысл, потому что сами целые числа циклически повторяют четное, нечетное, четно-нечетное… в конце концов, квадрат сохраняет «четность» корня числа (четное * четное = четное, нечетное * нечетное = нечетное).
Забавно, сколько понимания скрывается в простом шаблоне. (Я называю эту технику «геометрией», но, наверное, это неправильно — это просто визуализация чисел).
Прозрение алгебраиста
Рисовать квадраты камешками? Что это, древняя Греция? Нет, современный студент мог бы возразить:
- У нас есть два последовательных числа, n и (n+1)
- Их квадраты равны n 2 и (n+1) 2
- Разница равна (n+1) 2 – n 2 = (n 2 + 2n + 1) – n 2 = 2n + 1
Например, если n=2, то n 2 =4.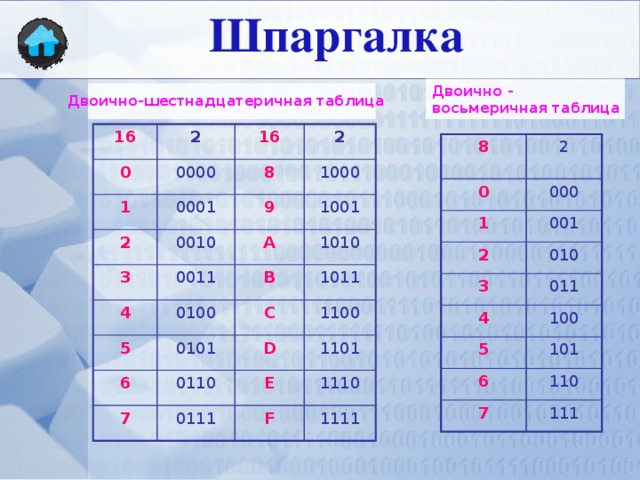
Таким образом, разница до следующего квадрата равна (2n + 1) = 5.
Действительно, мы нашли ту же самую геометрическую формулу. Но удовлетворяет ли алгебраическая манипуляция? Для меня это немного стерильно и не имеет того самого «ага!» хлопнуть по лбу. Но это другой инструмент, и когда мы комбинируем его с геометрией, понимание становится глубже. 92 получаем:
Близко, но не совсем! Где недостающий +1?
Давайте отступим. Исчисление исследует плавные, непрерывные изменения, а не «прыгающую» последовательность, которую мы взяли от 2 2 до 3 2 (как бы мы пропустили от 2 до 3, не посетив сначала 2,5 или 2,00001?).
Но не теряйте надежды. Исчисление имеет алгебраические корни, а +1 скрыто. Давайте стряхнем пыль с определения производной:
Забудьте пока о границах — сосредоточьтесь на том, что это значит (чувство, любовь, связь!). Производная говорит нам: «Сравни до и после и раздели на внесенное изменение». Если мы сравним «до и после» для f(x) = x^2 и назовем наше изменение «dx», мы получим:
Теперь мы к чему-то пришли.
Производная глубокая, но сосредоточьтесь на общей картине — она сообщает нам «отдачу от доллара», когда мы меняем нашу позицию с «x» на «x + dx». На каждую единицу «dx», которую мы идем, наш результат изменится на 2x + dx.
Например, если мы выбираем «dx» равным 1 (например, переходим от 3 к 4), производная говорит: «Хорошо, на каждую единицу, которую вы переходите, выход изменяется на 2x + dx (2x + 1, в данном случае ), где x — ваша первоначальная начальная позиция, а dx — общее количество перемещений». Давайте попробуем:
Переход от 3 2 к 4 2 будет означать:
- x = 3, dx = 1
- изменение на единицу ввода: 2x + dx = 6 + 1 = 7
- сумма сдачи: dx = 1
- ожидаемое изменение: 7 * 1 = 7
- фактическое изменение: 4 2 – 3 2 = 16 – 9 = 7
Мы предсказали сдачу 7, а получили сдачу 7 — сработало! И мы можем менять «dx» сколько угодно. Давайте перепрыгнем с 3 2 на 5 2 :
- х = 3, дх = 2
- изменение на единицу ввода: 2x + dx = 6 + 2 = 8
- количество изменений: dx = 2
- общее ожидаемое изменение: 8 * 2 = 16
- фактическое изменение: 5 2 – 3 2 = 25 – 9 = 16
Ого! Уравнение сработало (я тоже был удивлен).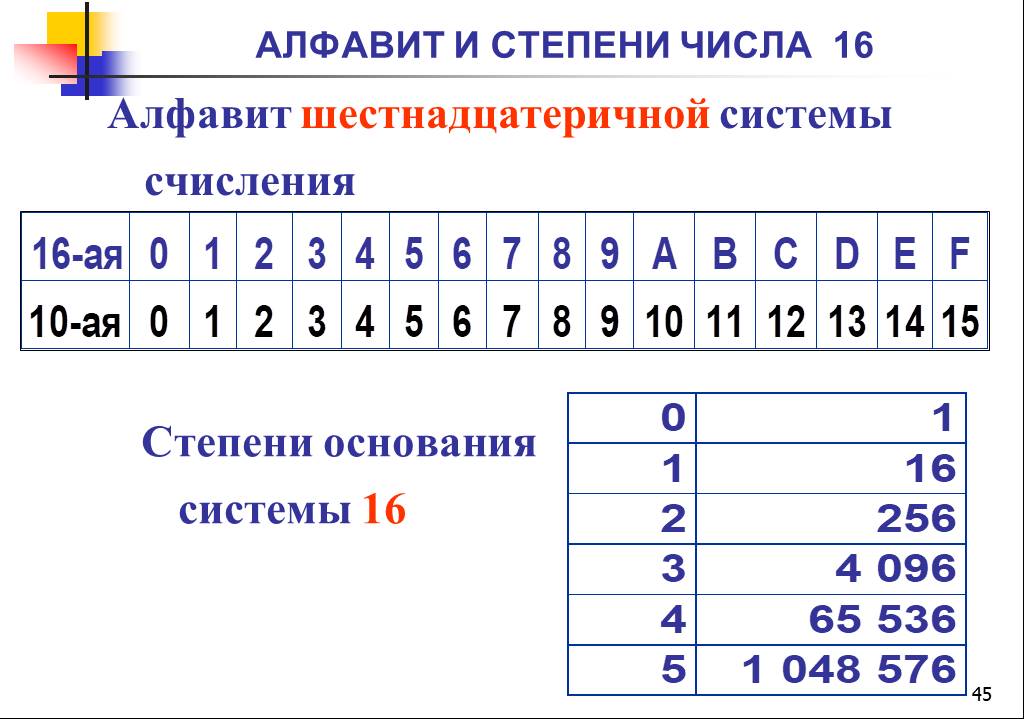
Мы можем не только перепрыгнуть через скучный «+1» с 3 2 на 4 2 , мы могли бы даже перейти с 3 2 на 10 2 , если бы захотели!
Конечно, мы мог бы вычислить это с помощью алгебры — но с нашей шапкой исчисления мы начали думать о произвольных количествах изменений, а не только +1. Мы взяли нашу скорость и масштабировали ее, точно так же, как расстояние = скорость * время (скорость 50 миль в час не означает, что вы можете путешествовать только в течение 1 часа, верно? Почему 2x + dx должны применяться только для одного интервала?).
Мой педантометр гудит, так что помните гигантское предостережение: исчисление касается микромасштаба. Производная «хочет», чтобы мы исследовали изменения, которые происходят через крошечные интервалы (мы перешли от 3 к 4, не посещая сначала 3,000000001!). Но не обижайтесь — нам пришла в голову идея исследовать произвольный интервал «dx», и, черт возьми, мы с ней справились.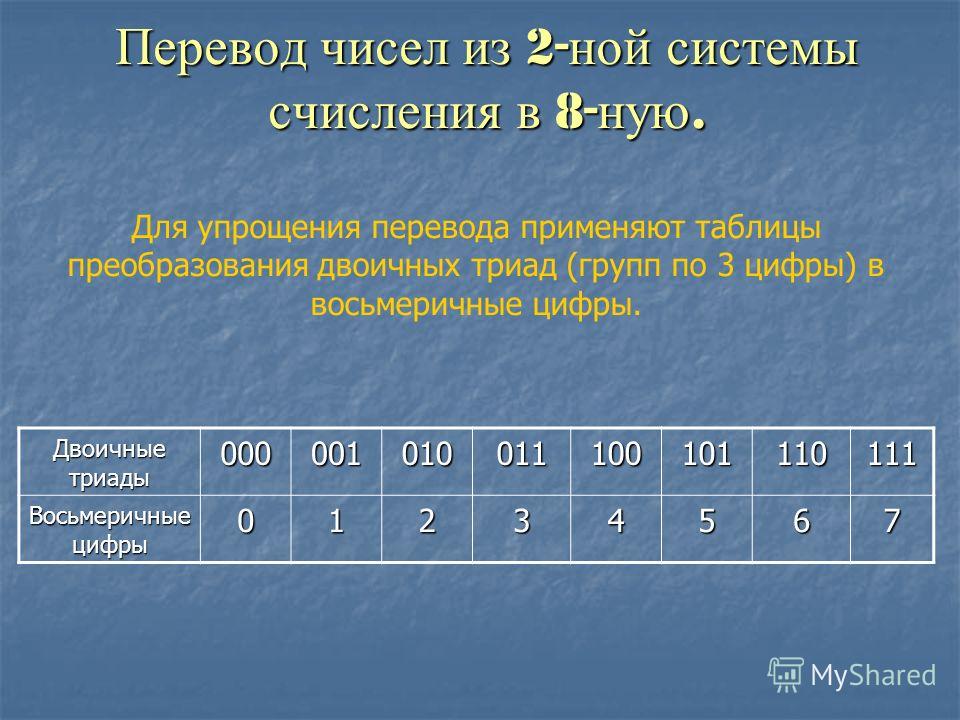
Мы сохраним крошечные приращения на другой день.
Извлеченные уроки
Изучение квадратов дало мне несколько идей:
- Казалось бы, простые шаблоны (1, 4, 9, 16…) можно исследовать с помощью нескольких инструментов, чтобы получить новое понимание для каждого. Я совершенно забыл, что идеи исчисления (от x к x + dx) могут помочь исследовать дискретные последовательности.
- Слишком легко помещать в песочницу математический инструмент, такой как геометрия, и думать, что он не может пролить свет на более высокие уровни (геометрические изображения действительно помогают алгебре, особенно +1, поп). Даже с исчислением мы привыкли сводить его к крошечным изменениям — почему бы не оставить dx большим?
- Аналогии работают на нескольких уровнях. Понятно, что квадраты и коэффициенты переплетены — начиная с одного сета, можно разобраться и в другом. Исчисление расширяет эту связь, позволяя нам переключаться между интегралом и производной.
Изучая новые техники, не забывайте применять их к урокам старых.
Счастливая математика.
Приложение: Кубики!
Ничего не могу с собой поделать: квадраты мы изучали, а теперь кубики?
1, 8, 27, 64…
Как они меняются? Представьте, что куб (состоящий из гальки!) растет до все больших и больших размеров — как меняется объем?
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Краткий обзор: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с ограждением)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Как найти общее различие в последовательностях
Все ресурсы по алгебре 1
10 Диагностические тесты 557 практических тестов Вопрос дня Карточки Учитесь по концепции
Алгебра 1 Помощь » Функции и линии » Последовательности » Как найти общую разность последовательностей
Какое из следующих чисел не может быть тремя последовательными членами арифметической прогрессии?
Возможные ответы:
Правильный ответ:
Пояснение:
В каждой группе чисел сравните разность второго и первого слагаемых с разностью третьего и второго слагаемых.
Группа, в которой они неравны, является правильным выбором.
Последняя группа чисел является правильным выбором.
Сообщить об ошибке
Рассмотрим арифметическую последовательность
.
Если , найдите общую разницу между последовательными терминами.
Возможные ответы:
Правильный ответ:
Объяснение:
В арифметических последовательностях общая разность — это просто значение, которое добавляется к каждому члену для получения следующего члена последовательности. Один из подходов к решению этого уравнения заключается в подстановке 5 вместо , чтобы найти числа, составляющие эту последовательность. Например,
, поэтому 14 — это первый член последовательности. Однако гораздо проще использовать только два последних условия и .
Разница между этими выражениями равна 8, поэтому это должна быть общая разница между последовательными терминами в последовательности.
Сообщить об ошибке
Найдите общую разницу в следующей арифметической последовательности.
Возможные ответы:
Правильный ответ:
Объяснение:
Арифметическая последовательность прибавляет или вычитает фиксированную сумму (общую разность), чтобы получить следующий член последовательности. Если вы знаете, что у вас есть арифметическая прогрессия, вычтите первый член из второго члена, чтобы найти общую разницу.
Сообщить об ошибке
Найдите общую разность в следующей арифметической последовательности.
Возможные ответы:
Правильный ответ:
Объяснение:
Арифметическая последовательность прибавляет или вычитает фиксированную сумму (общую разность), чтобы получить следующий член последовательности.
Если вы знаете, что у вас есть арифметическая прогрессия, вычтите первый член из второго члена, чтобы найти общую разницу.
(т. е. последовательность увеличивается за счет вычитания 27)
Сообщить об ошибке
В чем общее отличие этой последовательности?
Возможные ответы:
Правильный ответ:
Объяснение:
Общая разница — это расстояние между каждым числом в последовательности. Обратите внимание, что каждое число на 3 больше предыдущего числа.
Сообщить об ошибке
Какая общая разница в следующей последовательности?
Возможные ответы:
Правильный ответ:
Пояснение:
Какая общая разница в следующей последовательности?
Общие различия связаны с арифметическими последовательностями.
Обычное различие — это различие между последовательными числами в арифметической последовательности. Чтобы найти его, просто вычтите первый член из второго, или второй из третьего, или так далее…
Видите, как каждый раз мы прибавляем 8, чтобы получить следующий член? Это означает, что наша общая разница равна 8,9.0003
Сообщить об ошибке
Какая общая разница в следующей последовательности:
Возможные ответы:
Правильный ответ:
Объяснение:
Общее различие в этом наборе — линейная величина интервала между каждым числом в наборе.
Вычесть первое число из второго числа.
Проверьте это число, вычитая второе число из третьего числа.
Каждый интервал или общее различие:
Сообщить об ошибке
В чем общее различие?
Возможные ответы:
Правильный ответ:
Объяснение:
Общая разность может быть определена путем вычитания первого члена со вторым членом, второго члена с третьим членом и так далее.
