Действующее значение тока и напряжения
Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как говорят, по действующей, эффективной его величине.
Действующее или эффективное значение переменного тока равно силе такого постоянного тока, который, протекая по данному проводнику, выделяет в нем ежесекундно то же количество энергии в виде тепла, что и переменный ток.
Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых достигает переменный ток, но и от формы тока.
Вообще говоря, в электротехнике, и особенно в радиотехнике, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы нескольких синусоидальных токов с различными частотами, амплитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.
Если известна амплитуда переменного синусоидального тока, то действующее или эффективное его значение определяется по формуле:
то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.
Аналогичная формула применяется и для вычисления эффективного значения синусоидального напряжения:
Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эффективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Среднее и действующие значения синусоидальных токов и напряжений
Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
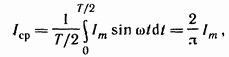
т.
е. среднее значение синусоидального
тока составляет 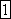
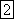
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
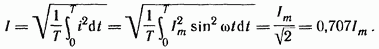
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,
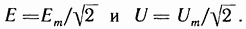
Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,
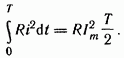
Выделенная
за то же время постоянным током теплота
равна 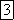 Приравняем
их:
Приравняем
их:
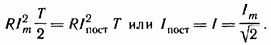
Таким
образом, действующее значение
синусоидального тока 
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
| T |
| T |
|
w = | ∫ | i2r dt = | ∫ | Im2sin2 ωt r dt.. |
| 0 |
| 0 |
|
При неизменном во времени токе энергия
W = I2rT
Приравняв правые части
| T |
|
I2rT = | ∫ | Im2sin2 ωt r dt,. |
| 0 |
|
получим действующее значение тока
I = | √ | 1 |
| = | Im | = 0,707 | ||||||
T | √2 |
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = Em /√2, U = Um /√2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
Im = √2I = 1,41 • 10 = 14,1 A,
и мгновенное значение тока
i = Im sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
| T2 |
|
|
|
|
| ||||
Еср = | ∫ | ∫ | sin ωt dωt = | |cos ωt|π0 = | = 0,637Ет . | |||||
| 0 |
| 0 |
|
|
|
Аналогично можно найти средние значения тока и напряжения:
Iср = 2Iт /π; Uср = 2Uт /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
Кф = | Е | = | I | = | U | = | π | = 1,11. |
Ес | Iср | Uср | 2√2 | |||||
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления. Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
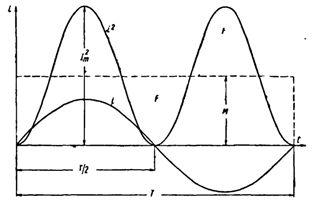
Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r. Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время. Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M, Величина I называется действующим значением переменного тока. Среднее значение i2 при переменном токе определим следующим образом. Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.
Действующее значение переменного тока Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2 Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид: U = Um / √2,E= Em / √2 Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е). На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии. Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения. При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется. |
Действующее значение синусоидального переменного напряжения – тока.
Действующее значение синусоидального
переменного напряжения – тока.
data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.
Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т.
Количество периодов переменного тока за 1 секунду, есть частота f.
Частота переменного тока f измеряется в герцах .
f = 1 / T.
Например.
Частота в нашей электрической сети 50 Гц. Период этих колебаний будет равен:
T = 1 / f = 1 / 50 = 0,02 сек.
Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.
Umax = Ua и Imax = Ia
За один период напряжение принимает эти значения два раза: + Ua и — Ua .
♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.
Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:
Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока
Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения
На все эти теоретические размышления можно посмотреть иначе!
♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.
Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.
♦На рисунке приняты обозначения:
Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.
Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.
P = Ua х Ia = Uд х Iд = U х I
♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.
Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.
data-ad-client=»ca-pub-5076466341839286″
data-ad-slot=»1404500382″>
Активное сопротивление. Действующие значения силы тока и напряжения
Активное сопротивление. Действующие значения силы тока и напряжения
«Физика — 11 класс»
Активное сопротивление
Сила тока в цепи с резистором
Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.
Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.
Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Напряжение на зажимах цепи меняется по гармоническому закону:
u = Um cos ωt
Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.
По закону Ома мгновенное значение силы тока:
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством
Мощность в цепи с резистором
В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.
При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
Р = I2R
Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
Р = i2R
Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):
График зависимости мгновенной мощности от времени (рис.а):
Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.Тогда средняя мощность равна:
Действующие значения силы тока и напряжения.
Среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.
Действующее значение силы переменного тока обозначается через I:
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично:
Закон Ома для участка цепи переменного тока с резистором в действующих значениях:
В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.
Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:
р = I2R = UI.
Итак:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы
Действующие значения тока — Знаешь как
 Расчет цепей переменного тока упрощается, если пользоваться понятием действующего (эффективного) значения переменного тока.
Расчет цепей переменного тока упрощается, если пользоваться понятием действующего (эффективного) значения переменного тока.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период переменного тока то же количество тепла.
Согласно ГОСТ действующие значения обозначаются прописными буквами, т. е ток I, напряжение U.
На шкалах измерительных приборов всегда наносятся действующие значения тока или напряжения.
Если ток изменяется по синусоидальному закону, то действующее значение его составляет 0,707 амплитудного значения тока, т. е.
I = (Iм : √2) = Iм: 1,41 = 0,707Iм
То же соотношение имеет место и для синусоидального напряжения, т. е.
U = (Uм : √2) = 0,707Uм
Докажем правильность приведенных соотношений. Количество тепла, выделенного постоянным током I в сопротивлении r за период переменного тока Т:
Q’ = I2rT
Количество тепла, выделенного переменным током в том же сопротивлении за период Т, может быть выражено через среднее значение мощности Р переменного тока
Q» = PT
Если Q’= Q», то
I2rT=РТ.
В последнем выражении согласно данному выше определению значение эквивалентного постоянного тока I равно действующему значению переменного тока. Таким образом, действующее значение тока
I = √ (P : r)
Мгновенная мощность при синусоидальном токе p = i2r = I2мr sin2ωt
или, приняв во внимание, что sin2 α = (11 : 2) — (1 : 2) cos 2α, получим:
p = (I2мr : 2) — (I2мr : 2) cos 2ωt
Мгновенная мощность при синусоидальном токе может быть представлена суммой двух слагаемых постоянной ½ I2мr и переменной, изменяющейся по периодическому синусоидальному закону.
Среднее значение мощности синусоидального тока будет равно постоянной слагаемой
P = ½I2мr
так как среднее значение за пер и синусоидальной слагаемой ½I2мr cos 2ωt равно нулю.
Действующее значение переменного синусоидального тока
I = √(P : r) = √ (½I2мr : r) = Iм : √2 = 0,707Iм
Так как действующие значения синусоидальных токов и
напряжений в √2 раз меньше амплитудных значений, то вектор, выражающий в одном масштабе амплитудное значение, в другом масштабе представляет действующее значение той же величины. В дальнейшем выбор масштабов векторов будет производиться, исходя из действующих значений.
Пример 5-4. Вольтметр,, включенный в сеть, показал напряжение 380 в.
Определить амплитуду напряжения сети:
UM = √2 U = 1,41 • 380=536 в.
ОБЩИЕ ЗАМЕЧАНИЯ О ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Любая электрическая цепь обладает параметрами: .сопротивлением r, индуктивностью L и емкостью С,
В цепи постоянного тока при неизменном напряжении будут неизмененными: ток, мощность и запас энергии в электрическом и магнитном полях.
При переменном напряжении на зажимах цепи в ней будет проходить переменный ток, будет изменяться и энергия электрического и магнитного полей. В технике встречаются цели, физические явления в которых определяются наличием одного из параметров r, L или С, тогда как другие параметры выявлены слабо и влиянием их можно пренебречь.
Например, лампу накаливания, нагревательный прибор, реостат можно рассматривать как цепь с сопротивлением r, влиянием емкости и индуктивности которой можно пренебречь.
Цепь ненагруженного трансформатора можно рассматривать как индуктивность, пренебрегая влиянием сопротивления и емкости этой цепи.
Наконец, кабель, работающий вхолостую, можно рассматривать как емкость, так как влияние индуктивности и сопротивления этой цепи незначительны.
Статья на тему Действующие значения тока
Среднее и действующее значения синусоидально изменяющейся величины


Среднее значение
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.
Среднее значение тока:

т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.
Действующее значение
Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).
Действующее значение тока:

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично 

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна RI2пост Т. Приравняем их:

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывает действующее значение измеряемой величины.
Эффективные значения тока и напряжения
Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:
\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2.2\right).\]Следовательно, можно записать, что:
\[\left\langle P\right\rangle =P_{tR}=\frac{1}{2}{I^2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:
\[P=I_{ef}U\ \left(2.4\right),\]если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:
\[I_{ef}=\frac{I_m}{\sqrt{2}},\ U_{ef}=\frac{U_m}{\sqrt{2}}\left(2.5\right).\]Следовательно, мощность тока можно записать как:
\[P_{tR}=U_{ef}I_{ef}cos \varphi \left(2.6\right),\]где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$