|
Алгоритм — это точно установленное предписание (инструкция) о выполнении в определённом порядке некоторой последовательности операций, однозначно ведущих к решению той или иной конкретной задачи. Предписание алгоритма представляет собой конечный набор правил, который задаёт потенциально осуществимый вычислительный процесс (процесс исполнения алгоритма), ведущий от варьирующих в определённых пределах исходных данных к получению результата, однозначно определяемого допустимыми исходными данными. Последнее подразумевает, что результат выполнения алгоритма напрямую зависит от исходных данных: то есть один и тот же алгоритм при разных исходных данных даст разные результаты; с другой стороны, если одному и тому же алгоритму передать несколько раз одни и те же данные, он должен столько же раз выдать один и тот же результат. Простейшими примерами алгоритмов являются арифметические правила сложения, вычитания, умножения, деления и тому подобные. Формальные свойства алгоритмов [в явной или неявной форме] включают следующий ряд общих требований:
Предписание алгоритма, как правило, фиксируется (записывается) в виде текста некотором формализованном языке (см. Слово «алгоритм» происходит от имени арабского учёного IX века Мухамеда бен Мусы аль-Хорезми, который впервые описал правила выполнения арифметических действий в десятичной системе счисления, придуманной в Индии. Впоследствии термином «алгоритм» стали обозначать эти правила вычислений. Однако с течением времени понятие алгоритма постепенно расширялось, наряду с его экспансией из чистой математики в другие сферы, и в XX веке под ним стали понимать точную последовательность действий, приводящую к решению поставленной задачи, при условии, что эта задача является заведомо решаемой. Алгоритм — одно из основных понятий математической логики (см. Логика математическая) и математики. Хотя неформально математики всё время занимались поиском алгоритмов, данное понятие было уточнено лишь в 30-х годах XX века. Первыми такими уточнениями были абстрактные определения частично-рекурсивных и представимых функций в формальной теории чисел, появившиеся в связи с задачами теории доказательств. В машине Тьюринга памятью является потенциально бесконечная лента, в каждой клетке которой записан символ из заранее заданного конечного алфавита. Более того, достаточно рассматривать ленту, каждая клетка которой содержит один бит информации, то есть либо пуста, либо содержит символ |. Процессор машины Тьюринга состоит из головки (каретки), которая в любой момент обозревает одну клетку, и программы, состоящей из конечного числа команд, обычно нумеруемых натуральными числами. Каждая команда представляет собой условное действие, зависящее от символа, записанного в клетке. Это действие имеет вид совокупности элементарных инструкций формы Машина Поста представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы. В машине имеются регистры, содержащие натуральные числа, элементарные операции увеличения и уменьшения числа на 1 и условный переход, если число в регистре равно 0. Машина Поста состоит из: а) бесконечной ленты, поделённой на одинаковые ячейки-секции (ячейка может быть пустой [ Одновременно А. Чёрч и X. Б. Карри создали одно из самых абстрактных уточнений алгоритма: λ-определимость, выразимость с помощью терма комбинаторной логики (см. Логика комбинаторная). Выяснилось, что и ранее созданные теоретические понятия, и самые элементарные, и самые абстрактные, из вновь появившихся уточнений алгоритма оказались эквивалентны. Этот факт, подтверждённый в дальнейшем для всех вновь появлявшихся точных определений алгоритма, послужил основой утверждения, скромно называемого в математике тезисом Чёрча, хотя степень его подтверждённости ныне выше, чем у любого физического «закона». Впоследствии появились и другие уточнения понятия алгоритма. Хотя по объёму определяемых функций существующие уточнения в целом эквивалентны, они различаются по своей направленности. Эти различия можно подчеркнуть, рассматривая относительные алгоритмы, строящиеся на основе некоторых абстрактных структур данных и операций над ними. Относительные алгоритмы, получающиеся на основе различных определений алгоритма, могут определять разные классы функций при одних и тех же исходных структурах и элементарных операциях. Так, например, машины Тьюринга приводят к одним из наиболее узких определений относительных алгоритмов, а комбинаторная логика и рекурсивные схемы — наоборот, к весьма широким. При модификации машин Тьюринга разделением входной и выходной ленты (со входной можно лишь читать, на выходную — лишь писать, причём после шага записи и чтения лента необратимо сдвигается на одну ячейку) получается важное понятие конечного автомата, моделирующее вычислительные машины без внешней памяти. С понятием алгоритма тесно связано понятие порождающего процесса, или исчисления. Порождающий процесс отличается от алгоритма тем, что он принципиально недетерминирован, его правила суть не предписания, а разрешения выполнить некоторое действие. Примером исчисления может служить логический вывод либо разбор в формальной грамматике. Одним из первых результатов теории алгоритмов стала теорема о том, что не любую вычислимую функцию можно продолжить до всюду определённой вычислимой функции. Практическим примером таких функций является любой интерпретатор программ, например, BASIC. Если не ограничивать возможности программиста, то нельзя создать интерпретатор, который невозможно было бы привести в нерабочее состояние исполнением синтаксически корректной программы. Множество, характеристическое свойство которого является всюду определённым вычислимым предикатом, называется разрешимым. Следует отметить, что схема вычислительного процесса в современном его понимании — написание программы на языке высокого уровня, трансляция её в машинный язык и исполнение компьютером — имеет теоретической основой теорему об универсальном алгоритме. Например, определение алгоритма может быть записано как слово в некотором алфавите, а если взять определение алгоритма, в котором рассматриваются лишь натуральные числа, такое слово может быть естественно представлено как число в системе счисления, основанием которой является количество букв в алфавите. Тогда имеется универсальный алгоритм U, перерабатывающий любую пару (ϕ, P), где ϕ — конструктивный объект, называемый записью или программой (относительно U) алгоритма ϕ, в результат применения ϕ к P. Универсальный алгоритм не может быть всюду определён. Если рассматривать лишь конструктивные объекты, то алгоритм естественно отождествить с его программой относительно некоторого U. Обобщение теории алгоритмов на абстрактные вычисления и объекты высших порядков является одним из основных направлений исследований современной теории алгоритмов. Другим наиболее важным её направлением развития служит теория сложности вычислений, рассматривающая проблемы оценки ресурсов, необходимых для работы алгоритмов, основы которой закладывали А. Н. Колмогоров и А. А. Марков и С. Кальмар. На основе теории сложности А. Н. Колмогоров, Л. А. Левин, П. Мартин-Лёф и другие развили алгоритмическую теорию вероятностей. Следует отметить, что тезис Чёрча содержит одно важное онтологическое предположение: о невозможности обозреть вечность. Поэтому в общей теории относительности (в частности, во вселенной Гёделя, в которой время может ходить по кругу) имеются миры, в которых, пролетая сквозь вращающуюся чёрную дыру, можно вычислить алгоритмически невычислимую функцию. Класс функций, которые могут быть вычислены в таких Вселенных, называется гиперарифметическим. Он неопределим в арифметике и определим лишь в анализе. |
о сложном – простыми словами
О том, что такое алгоритмы и как они влияют на нашу жизнь.

Наверняка вы слышали слово «алгоритм». Этот термин широко используется в современной жизни. И если вставить слово в повседневный разговор не составит труда, намного сложнее объяснить, что именно это такое. Сегодня поговорим о значении слова и об истинной природе алгоритмов, которые существовали в человеческой жизни еще до момента появления компьютерных технологий.
1. Алгоритм – это набор конкретных инструкций
istockphoto.com
Простыми словами, «алгоритм – это последовательность инструкций», говорит Педро Домингос, профессор компьютерных наук в Вашингтонском университете и автор книги «Верховный алгоритм. Как машинное обучение изменит наш мир».
Как испечь пирог, найти значение суммы 2+2 или управлять страной в соответствии с Конституцией – все это алгоритмы. Но чаще всего это слово связывают со сферой IT. В этом случае под «алгоритмом» понимается «последовательность инструкций, которые говорят компьютеру, что делать».
Любая компьютерная программа – это алгоритм, написанный на языке компьютерного программирования, который компьютер может понять и выполнить.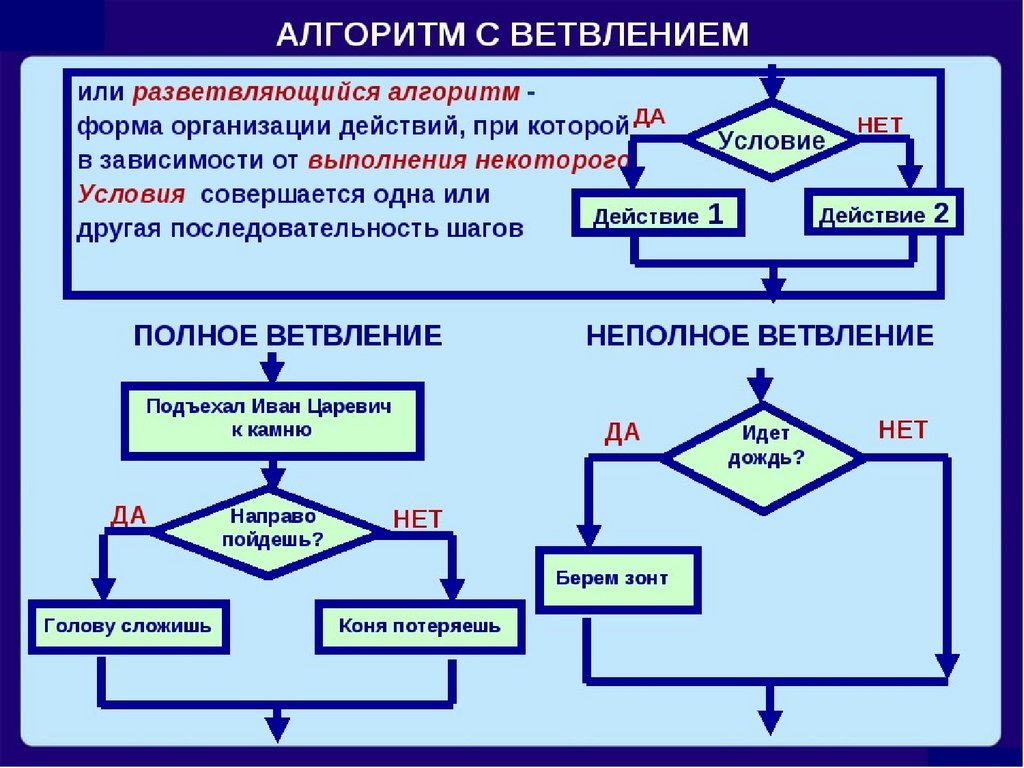 И это устроено намного сложнее, чем в обычной жизни.
И это устроено намного сложнее, чем в обычной жизни.
«Компьютерные алгоритмы должны быть предельно точны. Для их определения могут потребоваться миллионы строк», – подчеркивает профессор.
2. Люди писали и использовали алгоритмы задолго до появления компьютеров
Pixel
Несмотря на то что сегодня алгоритмы используются в контексте компьютерных технологий, их история намного старше ПК. Люди создавали алгоритмы еще в Вавилонскую эпоху – они помогали им решать математические уравнения и управлять земледельческим обществом.
«Все потому, что для выполнения алгоритма не всегда нужен компьютер – им могут управлять сами люди», – утверждает Домингос.
С появлением и распространением компьютеров во второй половине XX-го века алгоритмы начали активно использоваться в военной сфере (для определения того, куда навести ракету), а позже в области бизнес-администрирования (в приложениях для расчета заработной платы) и науки (прогноз погоды).
Поворотный момент для развития современных алгоритмов наступил, когда Ларри Пейдж и Сергей Брин создали Google PageRank.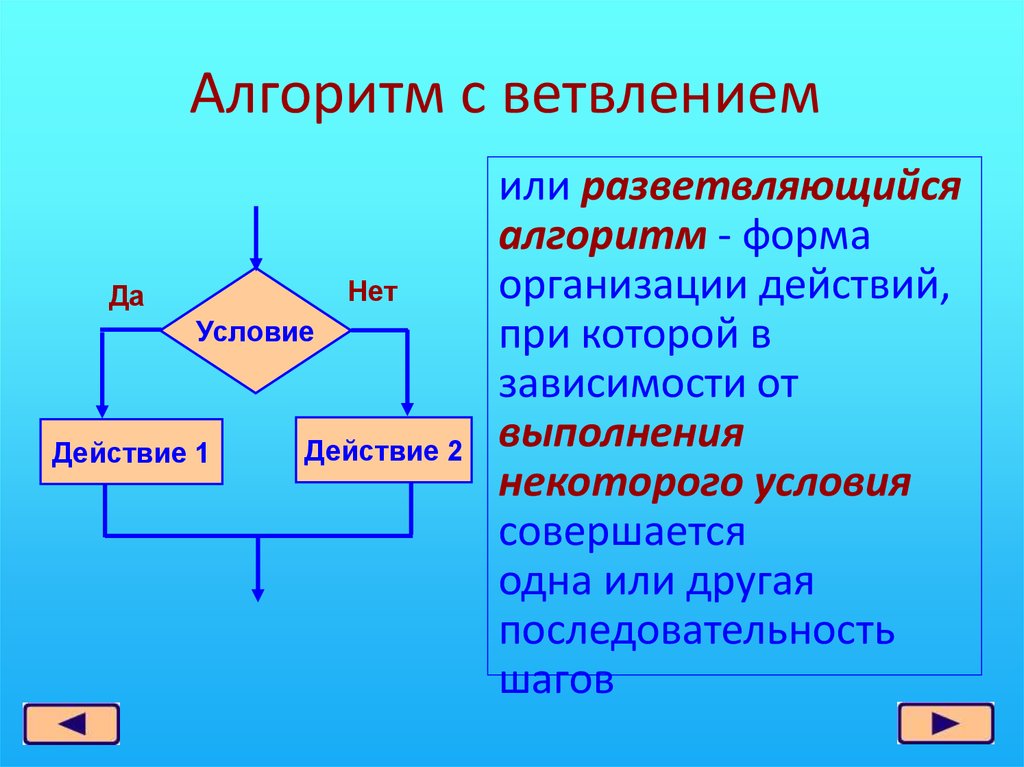 Вместо того чтобы просто полагаться на информацию на странице для определения ее релевантности поисковому запросу, алгоритм поисковой системы учитывал множество других сигналов, которые помогали ему выявлять наилучшие результаты.
Вместо того чтобы просто полагаться на информацию на странице для определения ее релевантности поисковому запросу, алгоритм поисковой системы учитывал множество других сигналов, которые помогали ему выявлять наилучшие результаты.
Например, сколько других ссылок указывало на статью и насколько авторитетными были эти статьи, в зависимости от количества ссылок, указывающих на эти страницы, и так далее.
3. Сегодня алгоритмы повсюду
pixabay.com
С распространением компьютеров и Интернета алгоритмы стали неотъемлемой частью нашей повседневной жизни. На них основаны новостные ленты социальных сетей, которые определяют, какой контент показывать вам при скроллинге, а также механизмы интернет-магазинов, предлагающих вам товары, которые могли бы вам понравиться.
«******** может разместить в вашей новостной ленте кучу постов и публикаций, но благодаря алгоритму он довольно избирателен, – сказал Домингос. – Обычно он учитывает целую комбинацию факторов.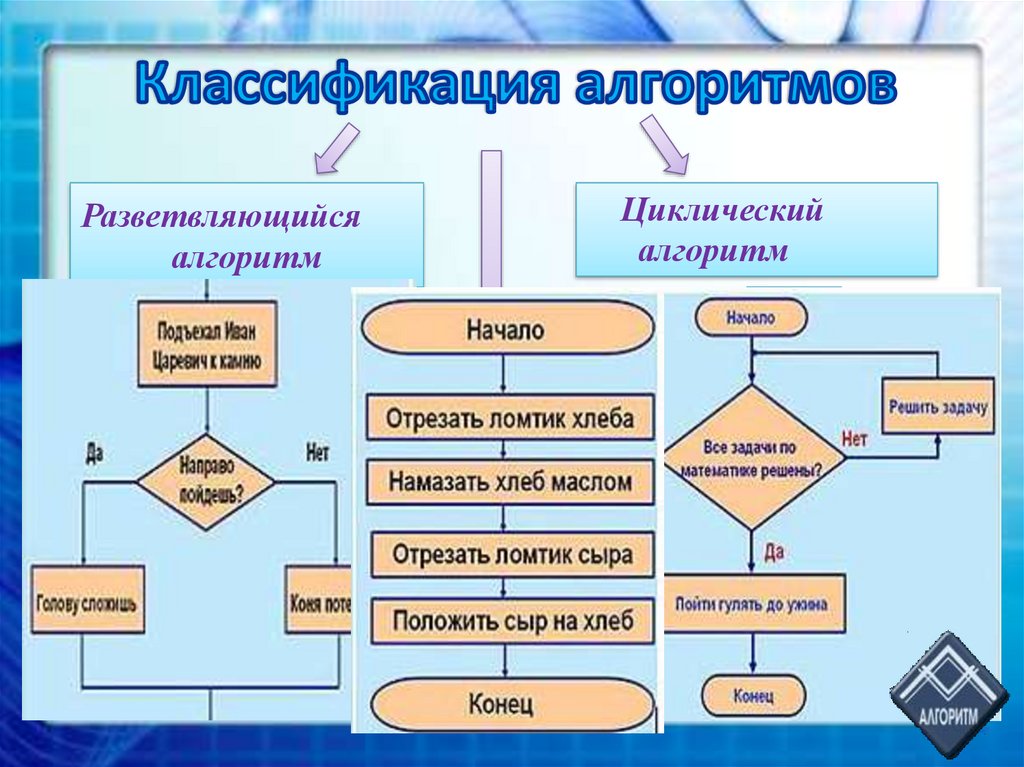 Например, как часто вы взаимодействуете с людьми, которые прямо или косвенно создали этот пост; насколько публикации близки вам в вашей социальной сети; насколько они актуальны с точки зрения тематики, насколько свежи и т. д.».
Например, как часто вы взаимодействуете с людьми, которые прямо или косвенно создали этот пост; насколько публикации близки вам в вашей социальной сети; насколько они актуальны с точки зрения тематики, насколько свежи и т. д.».
По словам профессора Домингоса, мы сталкиваемся с алгоритмами на протяжении всей нашей жизни и даже можем об этом не подозревать. Например, благодаря алгоритму посудомоечная машина узнает, когда пора переходить от стирки к сушке. Это алгоритм определяет, как ваш автомобиль регулирует потребление топлива и понимает, когда его бак на заправке становится полным.
«Совершенно очевидно, что каждый раз, когда вы пользуетесь компьютером или Интернетом, вы имеете дело с алгоритмами, – подчеркнул Домингос. – В наши дни они задействованы практически во всем».
4. В самых сложных алгоритмах используется машинное обучение
pixabay.com
Благодаря технологическому прогрессу современные алгоритмы претерпевают дальнейшие изменения.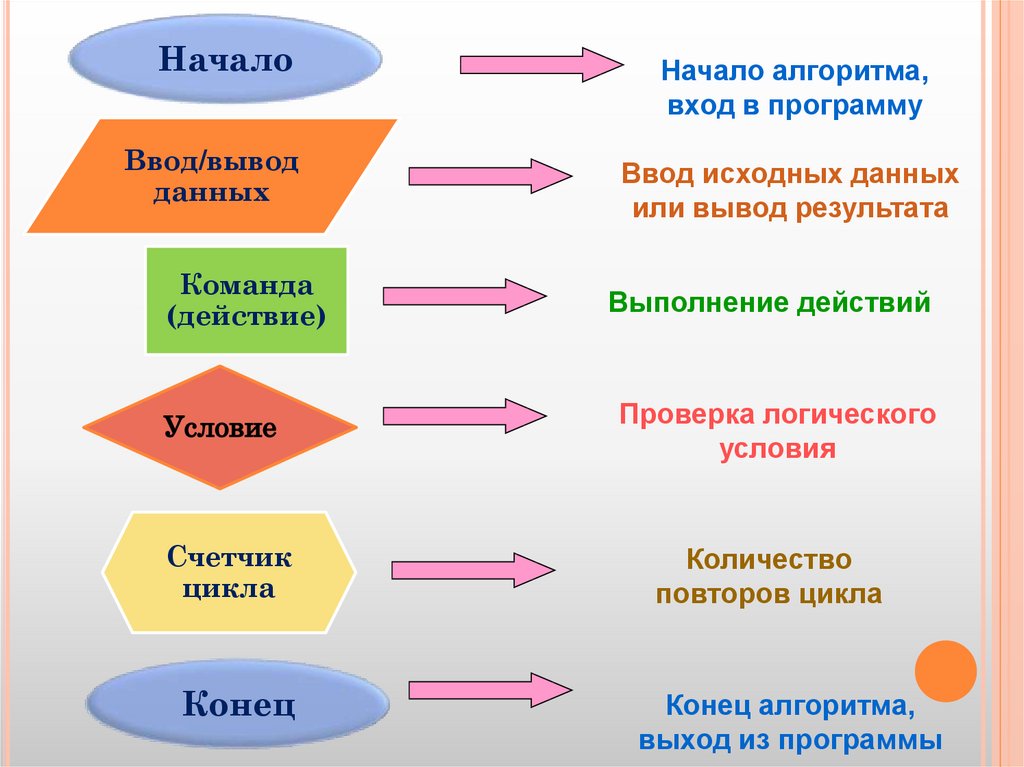 Особенно с появлением машинного обучения – разновидности искусственного интеллекта (ИИ).
Особенно с появлением машинного обучения – разновидности искусственного интеллекта (ИИ).
«В традиционном программировании человек должен записывать каждую мелочь, для того чтобы это сделал другой, что очень затратно по времени и средствам, – объяснил Домингос. – Машинное обучение – это компьютер, использующий свои собственные алгоритмы вместо того, чтобы ему говорили, что делать».
Другими словами, машинное обучение – это когда программист вводит в программу необработанные данные в качестве отправной точки, а затем задает конечную точку того, как выглядит организованная, классифицированная версия этих данных.
Остальное делает программа: она самостоятельно выясняет, как добраться из пункта А в пункт Б. Рассмотрим пример из кулинарии. Человек, который умеет готовить, может превратить обычный лук из сырого в карамелизированные обжаренные кусочки.
В традиционном варианте программист должен был бы прописать каждый шаг инструкции по приготовлению лука. Но в алгоритме, разработанном ИИ, с учетом конечной точки-цели, программа сама должна выяснить, как перейти от сырого состояния к карамелизированному. Это значит, что машина учится этому самостоятельно.
Но в алгоритме, разработанном ИИ, с учетом конечной точки-цели, программа сама должна выяснить, как перейти от сырого состояния к карамелизированному. Это значит, что машина учится этому самостоятельно.
Такие типы алгоритмов становятся еще более мощными, когда человек не знает, как добраться из точки А в точку Б. Например, человеческий процесс, такой как способность понимать, что кошка это кошка, требует сложных умственных способностей, которые невозможно расписать пошагово.
Но если дать программе набор фотографий кошки и предметов, которые кошкой не являются, и показав желаемую конечную точку в качестве категоризации изображения кошки в виде животного, компьютер научится выполнять этот процесс самостоятельно.
«Это возможность создавать мощные сложные алгоритмы с минимальным вмешательством человека», – подчеркивает Домингос.
5. Алгоритмы – это не волшебство
Pixel
Из-за большого количества обрабатываемых алгоритмов данных может показаться, что они ключ ко всем загадкам человечества. Но важно помнить, что алгоритм – всего лишь набор инструкций. Более того, его создают люди, а это значит, что он может быть ошибочным. Люди, которые не очень разбираются в компьютерах, часто полагают, что «алгоритмы идеальны». Что в корне неверно.
Но важно помнить, что алгоритм – всего лишь набор инструкций. Более того, его создают люди, а это значит, что он может быть ошибочным. Люди, которые не очень разбираются в компьютерах, часто полагают, что «алгоритмы идеальны». Что в корне неверно.
Pixel
Домингос объяснил, что программисты тратят огромное количество времени на исправление ошибок в алгоритмах. Все для того, чтобы они давали соответствующие результаты.
«Кроме того, в традиционном программировании вы должны беспокоиться о предвзятости программиста, – говорит Домингос. – В машинном обучении вы в основном должны беспокоиться о предвзятости, исходящей от данных».
Например, алгоритм найма, основанный на машинном обучении, может использовать в качестве отправной точки множество резюме кандидатов, а в качестве результата – резюме людей, которые были наняты в прошлом. Однако большинство технологических компаний не отличаются расовым разнообразием.
Таким образом, автоматизированный алгоритм, который дает рекомендации по найму, может отражать это реальное неравенство: исследования показали, что искусственный интеллект может отражать гендерные и расовые стереотипы людей, которые их обучают.
6. Алгоритмы по-прежнему способны изменить мир
unsplash.com
Алгоритмы могут быть несовершенными, но они все равно меняют наш мир. «Все эти вещи, которые мы принимаем как должное – Интернет, социальные сети и так далее, – они бы не существовали без алгоритмов», – сказал Домингос.
«Современные алгоритмы делают для умственного труда то же, что когда-то сделала промышленная революция с ручным трудом. Алгоритмы – это автоматизация интеллекта. И очень мощное средство: то, что раньше требовало больших умственных и физических усилий, теперь можно сделать с помощью алгоритма… Алгоритмы никуда не денутся. Но только от нас зависит то, какими мы их создадим – предвзятыми или справедливыми, полезными или вредными», – подытожил профессор.
Обложка: 1Gai.Ru / istockphoto.com
Источник статьи: What is an algorithm, anyway?
Алгоритм Определение и значение — Merriam-Webster
ал · го · ритм ˈal-gə-ˌri-t͟həm
: процедура решения математической задачи (например, нахождения наибольшего общего делителя) за конечное число шагов, которая часто включает повторение операции
широко : пошаговая процедура решения проблемы или достижения какой-либо цели
Существует несколько поисковых систем, крупнейшими из которых являются Google, Yahoo и Bing. Каждая поисковая система имеет собственный алгоритм вычислений (называемый «алгоритмом»), который ранжирует веб-сайты по каждому ключевому слову или комбинации ключевых слов. — Джули Бринтон
Каждая поисковая система имеет собственный алгоритм вычислений (называемый «алгоритмом»), который ранжирует веб-сайты по каждому ключевому слову или комбинации ключевых слов. — Джули Бринтон
… иногда вы решаете проблему, придумывая какой-то алгоритм. Но иногда вы решаете проблему очень нестандартным способом. — Уильям Х. Хаггинс
алгоритмический
ˌal-gə-ˈrit͟-mik
прилагательное
алгоритмически
ˌal-gə-ˈrit͟-mi-k(ə-)lē
наречие
Знаете ли вы?
Текущий термин выбора для процедуры решения проблем, алгоритм , обычно используется в настоящее время для набора правил, которым машина (и особенно компьютер) следует для достижения определенной цели.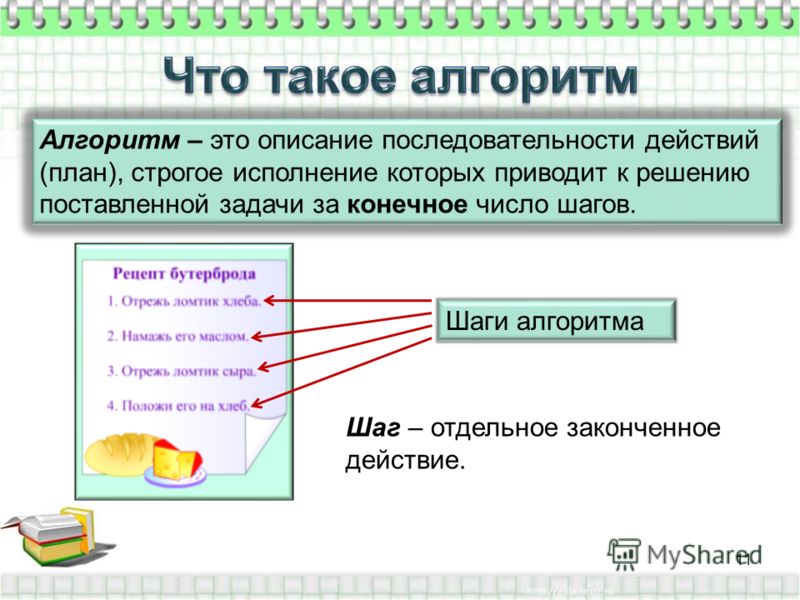 Однако это не всегда применимо к деятельности, опосредованной компьютером. Этот термин можно точно так же использовать для обозначения этапов приготовления пиццы или сборки кубика Рубика, как и для компьютерного анализа данных.
Однако это не всегда применимо к деятельности, опосредованной компьютером. Этот термин можно точно так же использовать для обозначения этапов приготовления пиццы или сборки кубика Рубика, как и для компьютерного анализа данных.
Алгоритм часто сочетается со словами, определяющими действие, для которого был разработан набор правил. Алгоритм поиска , например, представляет собой процедуру, которая определяет, какая информация извлекается из большого массива данных. Алгоритм шифрования представляет собой набор правил, по которым информация или сообщения кодируются таким образом, чтобы посторонние лица не могли их прочитать.
Хотя впервые засвидетельствовано в начале 20-го века (и до недавнего времени использовалось строго как термин математики и вычислительной техники), 9Алгоритм 0031 имеет удивительно глубокую историю. Он был образован из алгоритма «системы арабских цифр», слова, которое восходит к среднеанглийскому языку и в конечном итоге происходит от имени персидского математика 9-го века Абу-Джафар Мухаммеда ибн-Муса аль-Хуваризми, который важные работы в области алгебры и числовых систем.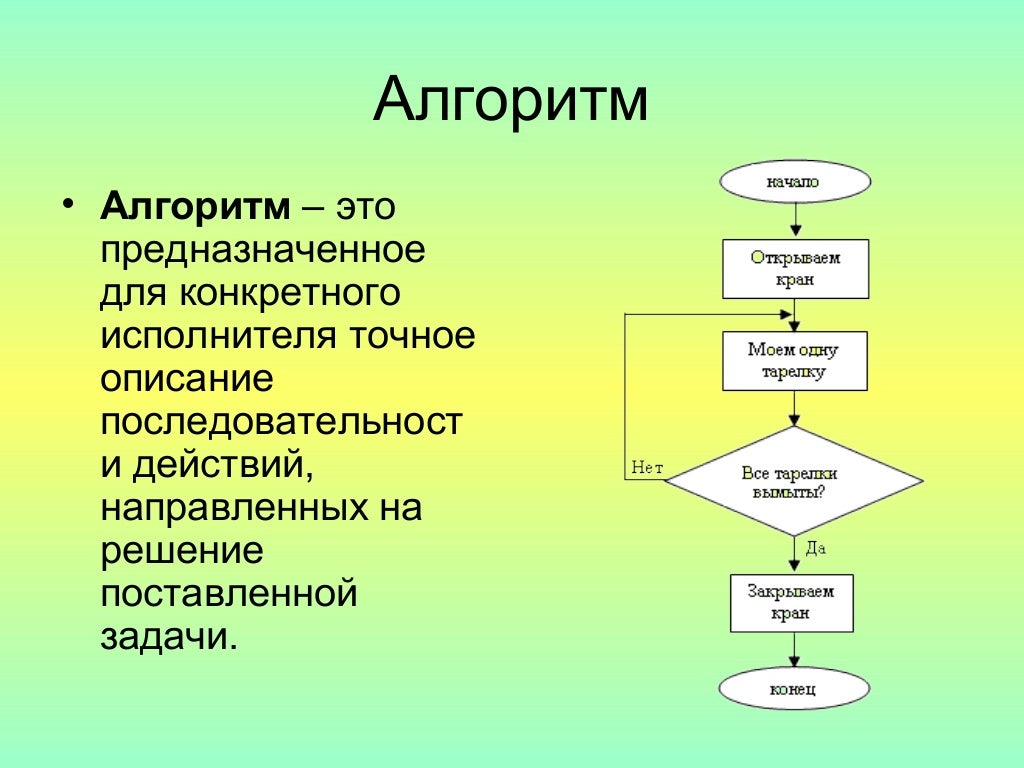
Примеры предложений
Недавние примеры в Интернете
Стремительно растущие цены на билеты для известных знаменитостей некоторое время были тенденцией из-за 9Алгоритм 0031 , называемый динамическим ценообразованием, анализирует спрос и предложение на рынке в режиме реального времени, аналогично тому, как оцениваются авиабилеты и доли в поездках.
— Рэй Джонсон, The Courier-Journal , 16 марта 2023 г.
Чтобы проверить, как частота кадров влияет на время обучения, команда сравнила Sample Factory с алгоритмом Google Brain, открытым исходным кодом в марте, который предназначен для значительного повышения эффективности глубокого RL.
— IEEE Spectrum , 15 марта 2023 г. То же самое верно и для нового алгоритма стадирования сна Oura , который в настоящее время находится в стадии бета-тестирования.
— Виктория Сонг, The Verge , 15 марта 2023 г.
Компания делится этим с другими действиями, и реальная выгода заключается в том, что всемогущий алгоритм стримера учитывает это.
— Хью Макинтайр, 9 лет.0031 Forbes , 8 марта 2023 г.
Вот почему агентство использует алгоритм для выявления потенциальных красных флажков в декларациях, которые необходимо исправить, чтобы уменьшить количество недоплат в IRS и увеличить налоговые поступления.
— Элизабет Бухвальд, USA TODAY , 2 марта 2023 г.
Эта обратная связь в реальном времени поступает прямо в набор данных, который затем подключается к алгоритму 9.
То же самое верно и для нового алгоритма стадирования сна Oura , который в настоящее время находится в стадии бета-тестирования.
— Виктория Сонг, The Verge , 15 марта 2023 г.
Компания делится этим с другими действиями, и реальная выгода заключается в том, что всемогущий алгоритм стримера учитывает это.
— Хью Макинтайр, 9 лет.0031 Forbes , 8 марта 2023 г.
Вот почему агентство использует алгоритм для выявления потенциальных красных флажков в декларациях, которые необходимо исправить, чтобы уменьшить количество недоплат в IRS и увеличить налоговые поступления.
— Элизабет Бухвальд, USA TODAY , 2 марта 2023 г.
Эта обратная связь в реальном времени поступает прямо в набор данных, который затем подключается к алгоритму 9. 0032, который может соответствующим образом изменить рецепт.
— Чери Лукас Роулендс, Longreads , 1 марта 2023 г.
Разработка и реализация алгоритма может быть полна ловушек и неожиданностей.
— Друв Кхуллар, The New Yorker , 27 февраля 2023 г.
Кроме того, в коде или алгоритме есть очень тонкие детали, которые потребители никогда не заметят.
— Лоран Бельси, 9 лет.0031 The Christian Science Monitor , 27 февраля 2023 г.
Узнать больше
0032, который может соответствующим образом изменить рецепт.
— Чери Лукас Роулендс, Longreads , 1 марта 2023 г.
Разработка и реализация алгоритма может быть полна ловушек и неожиданностей.
— Друв Кхуллар, The New Yorker , 27 февраля 2023 г.
Кроме того, в коде или алгоритме есть очень тонкие детали, которые потребители никогда не заметят.
— Лоран Бельси, 9 лет.0031 The Christian Science Monitor , 27 февраля 2023 г.
Узнать больше
Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «алгоритм». Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
История слов
Этимология
изменение среднеанглийского algorisme из старофранцузского и средневековой латыни; Старофранцузский, от средневековой латыни algorismus , от арабского al-khuwārizmi , от al-Khwārizmī процветал в году н.э. 825 Исламский математик
Первое известное использование
1926, в значении, определенном выше
Путешественник во времени
Первое известное использование алгоритм был в 1926 году
Другие слова того же года алгоритмист
алгоритм
алгоритмика
Посмотреть другие записи рядом
Процитировать эту запись
Стиль
MLChicagoAPAMМерриам-Вебстер
«Алгоритм. » Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/algorithm. По состоянию на 31 марта 2023 г.
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/algorithm. По состоянию на 31 марта 2023 г.
Копировать цитирование
Детское определение
алгоритм
существительное
ал · го · ритм ˈal-gə-ˌrit͟h-əm
: пошаговый метод решения задачи (например, нахождения наибольшего общего делителя) или достижения цели
Еще от Merriam-Webster об алгоритме
ДинамикиBritannica English: Перевод алгоритма для носителей арабского языка
Britannica. com: Энциклопедическая статья об алгоритме
com: Энциклопедическая статья об алгоритме
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
взять самоотвод
См. Определения и примеры »
Получайте ежедневное электронное письмо «Слово дня»!
Старая добрая викторина
- виноградная дробилка стиральная машина
- маслобойка мышеловка
Прослушайте слово и напечатайте его. Сколько вы можете получить правильно?
Сколько вы можете получить правильно?
ПРОЙДИТЕ ТЕСТ
Сможете ли вы составить 12 слов из 7 букв?
ИГРАТЬ
Что такое алгоритм?
В этом уроке мы узнаем, что такое алгоритмы, на примерах.
В терминах компьютерного программирования алгоритм представляет собой набор четко определенных инструкций для решения конкретной задачи. Он принимает набор входных данных и производит желаемый результат. Например,
Алгоритм сложения двух чисел:
Ввести два числа
Добавление номеров с помощью оператора +
Показать результат
Качества хорошего алгоритма
- Вход и выход должны быть точно определены.
- Каждый шаг алгоритма должен быть четким и однозначным.
- Алгоритмы должны быть наиболее эффективными среди многих различных способов решения проблемы.
- Алгоритм не должен включать компьютерный код.
 Вместо этого алгоритм должен быть написан таким образом, чтобы его можно было использовать на разных языках программирования.
Вместо этого алгоритм должен быть написан таким образом, чтобы его можно было использовать на разных языках программирования.
Примеры алгоритмов
Алгоритм сложения двух чисел
Алгоритм нахождения наибольшего среди трех чисел
Алгоритм нахождения всех корней квадратного уравнения Алгоритм ряда Фибоначчи
Алгоритм 1: Сложение двух введенных пользователем чисел
Шаг 1: Начните
Шаг 2: Объявите переменные num1, num2 и sum.
Шаг 3: Считайте значения num1 и num2.
Шаг 4: Добавьте num1 и num2 и присвойте результат сумме.
сумма ← число1+число2
Шаг 5: Показать сумму
Шаг 6: Остановитесь
Алгоритм 2: Найдите наибольшее число среди трех чисел
Шаг 1: Начните
Шаг 2: Объявите переменные a, b и c.
Шаг 3: Считайте переменные a, b и c.
Шаг 4: Если а > б
Если а > с
Отображение а — это наибольшее число.
Еще
Отображение c — это наибольшее число.
Еще
Если б > с
Отображение b — это наибольшее число. Еще
Отображение c — наибольшее число.
Шаг 5: Остановитесь
Еще
Отображение c — наибольшее число.
Шаг 5: Остановитесь
Алгоритм 3: поиск корней квадратного уравнения ax
2 + bx + c = 0
Шаг 1: Начните
Шаг 2: Объявить переменные a, b, c, D, x1, x2, rp и ip;
Шаг 3: вычислить дискриминант
D ← b2-4ac
Шаг 4: Если D ≥ 0
r1 ← (-b+√D)/2a
r2 ← (-b-√D)/2a
Отобразите r1 и r2 как корни.
Еще
Вычислить действительную часть и мнимую часть
рп ← -б/2а
ip ← √(-D)/2a
Отображать rp+j(ip) и rp-j(ip) как корни
Шаг 5: Остановитесь
Алгоритм 4: найти факториал числа
Шаг 1: Начните
Шаг 2: Объявите переменные n, factorial и i.
Шаг 3: Инициализируйте переменные
факториал ← 1
я ← 1
Шаг 4: Чтение значения n
Шаг 5: Повторяйте шаги, пока i = n
5.1: факториал ← факториал*i
5.2: я ← я+1
Шаг 6: Показать факториал
Шаг 7: Остановитесь
Алгоритм 5: Проверка, является ли число простым
Шаг 1: Начните Шаг 2: Объявите переменные n, i, flag.



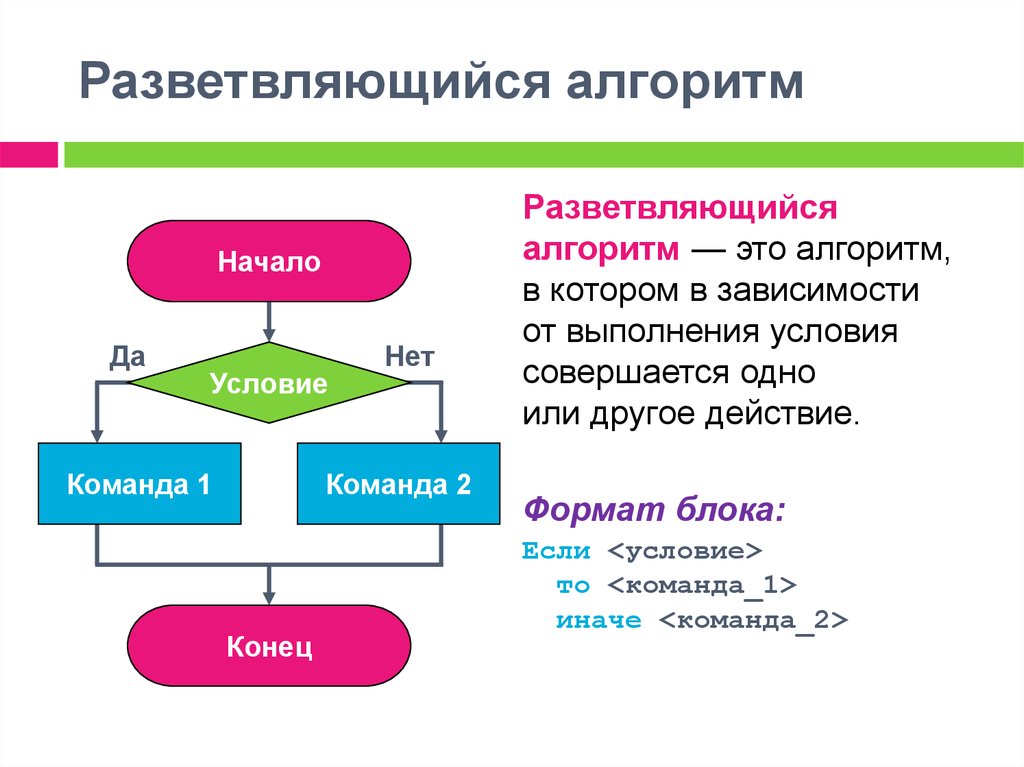
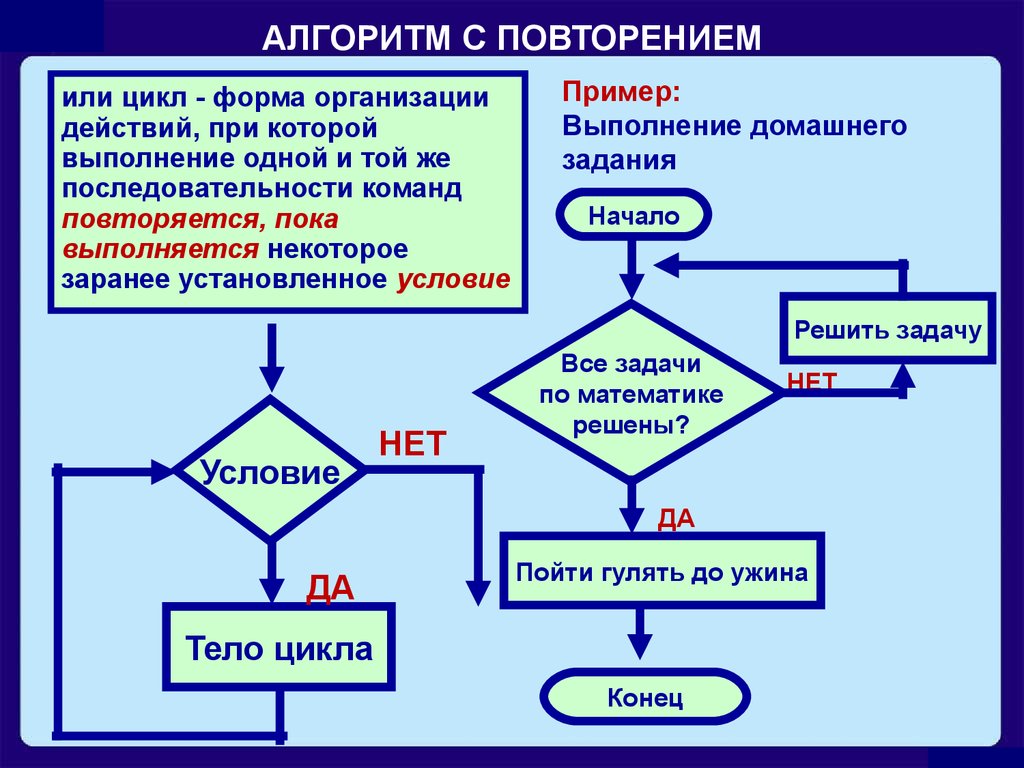 Язык формализованный), называемого программой. Понятие программы формулируется в чисто структурных терминах синтаксиса этого языка, без какого-либо обращения к смысловым категориям. Точно такой же характер носит и описание процедуры выполнения программы. Поэтому в роли исполнителя алгоритмов, записанных на формализованных [алгоритмических] языках, может выступать не только человек, но и наделённое соответствующими [вычислительными] возможностями автоматическое устройство,
Язык формализованный), называемого программой. Понятие программы формулируется в чисто структурных терминах синтаксиса этого языка, без какого-либо обращения к смысловым категориям. Точно такой же характер носит и описание процедуры выполнения программы. Поэтому в роли исполнителя алгоритмов, записанных на формализованных [алгоритмических] языках, может выступать не только человек, но и наделённое соответствующими [вычислительными] возможностями автоматическое устройство, 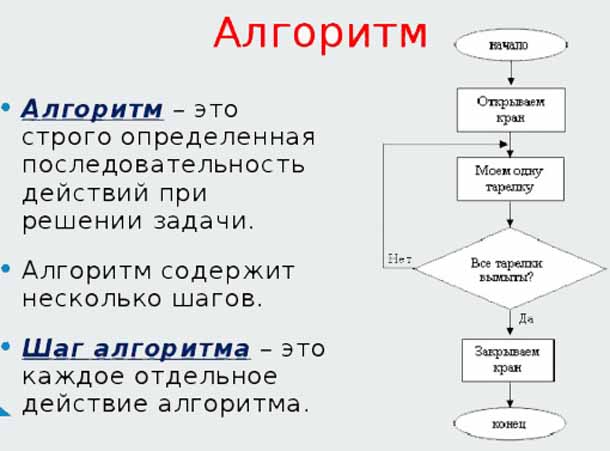

 Буква L означает приказ сдвинуться на следующем такте на одну клетку влево, R — вправо, S — остаться на месте. Элементарная инструкция означает следующее: если машина видит
Буква L означает приказ сдвинуться на следующем такте на одну клетку влево, R — вправо, S — остаться на месте. Элементарная инструкция означает следующее: если машина видит 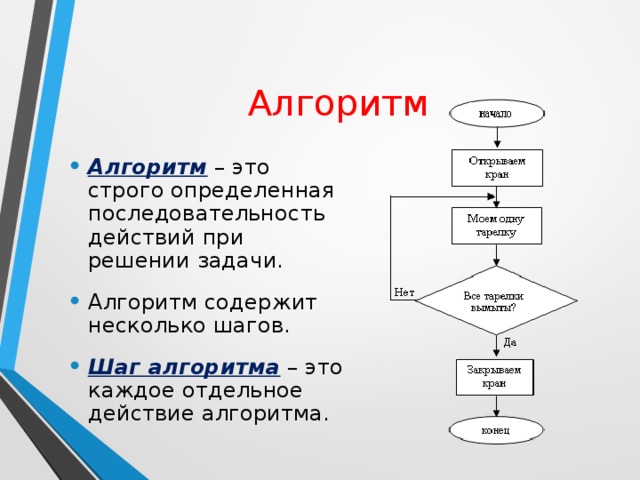 Состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты — это информация о том, какие секции пусты, а какие отмечены. Шаг — это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Элементарные действия (команды) машина Поста проще команд машины Тьюринга, поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Команды машины Поста предвосхитили систему команд современных вычислительных машин.
Состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты — это информация о том, какие секции пусты, а какие отмечены. Шаг — это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Элементарные действия (команды) машина Поста проще команд машины Тьюринга, поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Команды машины Поста предвосхитили систему команд современных вычислительных машин.
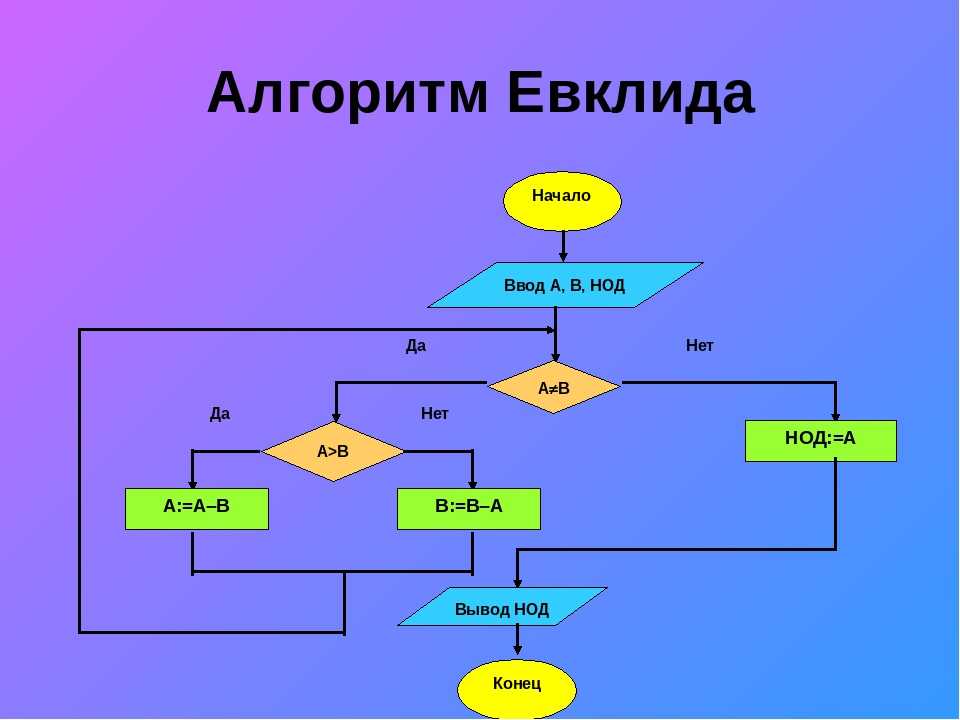
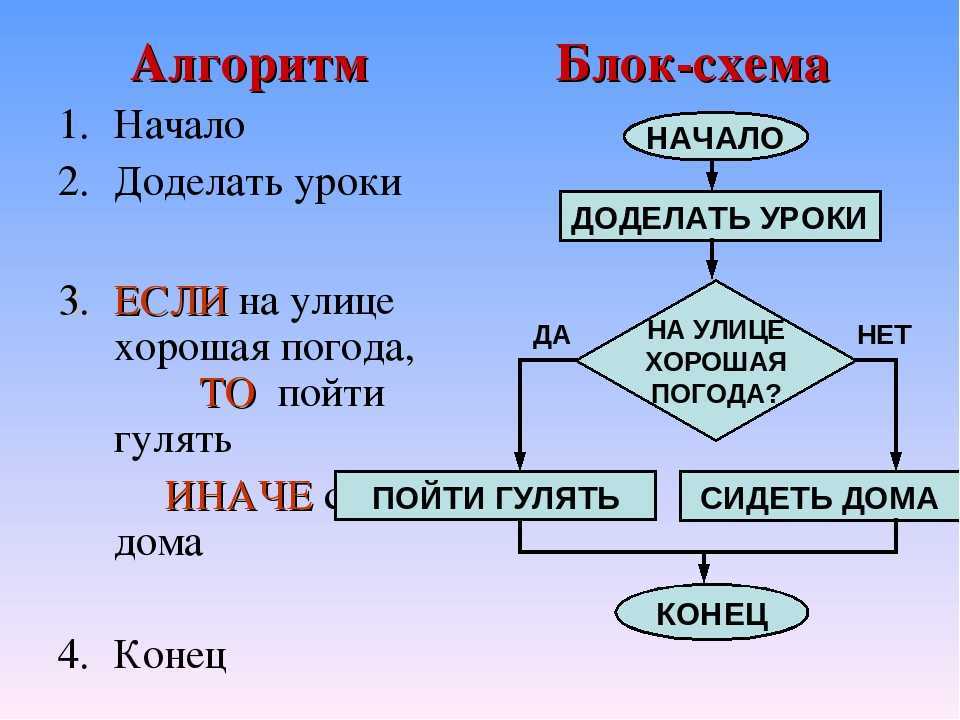 Множество, принадлежность элемента которому можно установить за конечное число шагов применением некоторого алгоритма, называется перечислимым. Например, множество тавтологий классической логики высказываний (см. Логика высказываний) разрешимо, а множество тавтологий классической логики предикатов (см. Логика предикатов) перечислимо. Следует отметить, что в случае перечислимого множества алгоритмически установить можно лишь истинность, а не ложность. В классической математике имеет место следующий критерий разрешимости: множество разрешимо, если и оно, и его дополнение перечислимы. В конструктивной математике этот критерий эквивалентен принципу Маркова. Другая характеризация перечислимого множества — множество объектов, выводимых в некотором исчислении.
Множество, принадлежность элемента которому можно установить за конечное число шагов применением некоторого алгоритма, называется перечислимым. Например, множество тавтологий классической логики высказываний (см. Логика высказываний) разрешимо, а множество тавтологий классической логики предикатов (см. Логика предикатов) перечислимо. Следует отметить, что в случае перечислимого множества алгоритмически установить можно лишь истинность, а не ложность. В классической математике имеет место следующий критерий разрешимости: множество разрешимо, если и оно, и его дополнение перечислимы. В конструктивной математике этот критерий эквивалентен принципу Маркова. Другая характеризация перечислимого множества — множество объектов, выводимых в некотором исчислении. При любом точном определении алгоритмов каждый алгоритм может быть задан своим определением, которое является конструктивным объектом. Этот конструктивный объект может быть алгоритмически в содержательном смысле (и при этом достаточно просто и естественно) закодирован тем видом конструктивных объектов, которые обрабатываются данными алгоритмами.
При любом точном определении алгоритмов каждый алгоритм может быть задан своим определением, которое является конструктивным объектом. Этот конструктивный объект может быть алгоритмически в содержательном смысле (и при этом достаточно просто и естественно) закодирован тем видом конструктивных объектов, которые обрабатываются данными алгоритмами. То, что такое отождествление является ограниченным, показывают проблемы современной теории и практики программирования. Одной из самых трудных возникающих в этом случае проблем является восстановление алгоритма по реализующей его конкретной программе. Если понятие алгоритма, перерабатывающего реальные конструктивные объекты, можно считать однозначно определённым, то его обобщение на объекты высших типов допускает многочисленные варианты, неэквивалентные друг другу.
То, что такое отождествление является ограниченным, показывают проблемы современной теории и практики программирования. Одной из самых трудных возникающих в этом случае проблем является восстановление алгоритма по реализующей его конкретной программе. Если понятие алгоритма, перерабатывающего реальные конструктивные объекты, можно считать однозначно определённым, то его обобщение на объекты высших типов допускает многочисленные варианты, неэквивалентные друг другу. Основой данной теории явилось содержательное определение случайной последовательности по Р. Мизесу. Двоичная последовательность случайна, если из неё нельзя выбрать никакую последовательность с другой частотой нулей и единиц. Например, последовательность 0, 1, 0, 1… неслучайна, поскольку последовательность её чётных членов состоит из одних единиц. В классической математике такое определение пусто. А. Н. Колмогоров уточнил его, предложив рассматривать лишь алгоритмические перестановки подмножеств членов данной последовательности. Оказалось, что случайность связана со сложностью определения. Сложность фрагментов случайной последовательности пропорциональна длине их записи. Итак, содержательно случайные объекты являются приближениями к случайным последовательностям. Для любой совокупности программ, имеющих ограниченную сложность, можно построить ограниченный универсальный алгоритм, исполняющий все их без ошибок, но его сложность будет неизмеримо выше, чем сложность исполняемых программ.
Основой данной теории явилось содержательное определение случайной последовательности по Р. Мизесу. Двоичная последовательность случайна, если из неё нельзя выбрать никакую последовательность с другой частотой нулей и единиц. Например, последовательность 0, 1, 0, 1… неслучайна, поскольку последовательность её чётных членов состоит из одних единиц. В классической математике такое определение пусто. А. Н. Колмогоров уточнил его, предложив рассматривать лишь алгоритмические перестановки подмножеств членов данной последовательности. Оказалось, что случайность связана со сложностью определения. Сложность фрагментов случайной последовательности пропорциональна длине их записи. Итак, содержательно случайные объекты являются приближениями к случайным последовательностям. Для любой совокупности программ, имеющих ограниченную сложность, можно построить ограниченный универсальный алгоритм, исполняющий все их без ошибок, но его сложность будет неизмеримо выше, чем сложность исполняемых программ. Далее, возможно построить алгоритмический процесс, расширяющий ограниченный универсальный алгоритм с тем, чтобы включить любую предъявленную программу, не входящую в данный класс, но при этом сложность универсального метода станет ещё выше. Уже один шаг данного процесса диагонализации далеко выводит за рамки класса функций, считающихся реально вычислимыми.
Далее, возможно построить алгоритмический процесс, расширяющий ограниченный универсальный алгоритм с тем, чтобы включить любую предъявленную программу, не входящую в данный класс, но при этом сложность универсального метода станет ещё выше. Уже один шаг данного процесса диагонализации далеко выводит за рамки класса функций, считающихся реально вычислимыми. Вместо этого алгоритм должен быть написан таким образом, чтобы его можно было использовать на разных языках программирования.
Вместо этого алгоритм должен быть написан таким образом, чтобы его можно было использовать на разных языках программирования. Еще
Отображение c — наибольшее число.
Шаг 5: Остановитесь
Еще
Отображение c — наибольшее число.
Шаг 5: Остановитесь
