|
Алгоритм — это точно установленное предписание (инструкция) о выполнении в определённом порядке некоторой последовательности операций, однозначно ведущих к решению той или иной конкретной задачи. Предписание алгоритма представляет собой конечный набор правил, который задаёт потенциально осуществимый вычислительный процесс (процесс исполнения алгоритма), ведущий от варьирующих в определённых пределах исходных данных к получению результата, однозначно определяемого допустимыми исходными данными. Последнее подразумевает, что результат выполнения алгоритма напрямую зависит от исходных данных: то есть один и тот же алгоритм при разных исходных данных даст разные результаты; с другой стороны, если одному и тому же алгоритму передать несколько раз одни и те же данные, он должен столько же раз выдать один и тот же результат. Простейшими примерами алгоритмов являются арифметические правила сложения, вычитания, умножения, деления и тому подобные. Формальные свойства алгоритмов [в явной или неявной форме] включают следующий ряд общих требований:
Предписание алгоритма, как правило, фиксируется (записывается) в виде текста некотором формализованном языке (см. Слово «алгоритм» происходит от имени арабского учёного IX века Мухамеда бен Мусы аль-Хорезми, который впервые описал правила выполнения арифметических действий в десятичной системе счисления, придуманной в Индии. Впоследствии термином «алгоритм» стали обозначать эти правила вычислений. Однако с течением времени понятие алгоритма постепенно расширялось, наряду с его экспансией из чистой математики в другие сферы, и в XX веке под ним стали понимать точную последовательность действий, приводящую к решению поставленной задачи, при условии, что эта задача является заведомо решаемой. Алгоритм — одно из основных понятий математической логики (см. Логика математическая) и математики. Хотя неформально математики всё время занимались поиском алгоритмов, данное понятие было уточнено лишь в 30-х годах XX века. Первыми такими уточнениями были абстрактные определения частично-рекурсивных и представимых функций в формальной теории чисел, появившиеся в связи с задачами теории доказательств. В машине Тьюринга памятью является потенциально бесконечная лента, в каждой клетке которой записан символ из заранее заданного конечного алфавита. Более того, достаточно рассматривать ленту, каждая клетка которой содержит один бит информации, то есть либо пуста, либо содержит символ |. Процессор машины Тьюринга состоит из головки (каретки), которая в любой момент обозревает одну клетку, и программы, состоящей из конечного числа команд, обычно нумеруемых натуральными числами. Каждая команда представляет собой условное действие, зависящее от символа, записанного в клетке. Это действие имеет вид совокупности элементарных инструкций формы Машина Поста представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы. В машине имеются регистры, содержащие натуральные числа, элементарные операции увеличения и уменьшения числа на 1 и условный переход, если число в регистре равно 0. Машина Поста состоит из: а) бесконечной ленты, поделённой на одинаковые ячейки-секции (ячейка может быть пустой [0 или пустота] или содержать метку [ Одновременно А. Чёрч и X. Б. Карри создали одно из самых абстрактных уточнений алгоритма: λ-определимость, выразимость с помощью терма комбинаторной логики (см. Логика комбинаторная). Выяснилось, что и ранее созданные теоретические понятия, и самые элементарные, и самые абстрактные, из вновь появившихся уточнений алгоритма оказались эквивалентны. Этот факт, подтверждённый в дальнейшем для всех вновь появлявшихся точных определений алгоритма, послужил основой утверждения, скромно называемого в математике тезисом Чёрча, хотя степень его подтверждённости ныне выше, чем у любого физического «закона». Впоследствии появились и другие уточнения понятия алгоритма. Хотя по объёму определяемых функций существующие уточнения в целом эквивалентны, они различаются по своей направленности. Эти различия можно подчеркнуть, рассматривая относительные алгоритмы, строящиеся на основе некоторых абстрактных структур данных и операций над ними. Относительные алгоритмы, получающиеся на основе различных определений алгоритма, могут определять разные классы функций при одних и тех же исходных структурах и элементарных операциях. Так, например, машины Тьюринга приводят к одним из наиболее узких определений относительных алгоритмов, а комбинаторная логика и рекурсивные схемы — наоборот, к весьма широким. При модификации машин Тьюринга разделением входной и выходной ленты (со входной можно лишь читать, на выходную — лишь писать, причём после шага записи и чтения лента необратимо сдвигается на одну ячейку) получается важное понятие конечного автомата, моделирующее вычислительные машины без внешней памяти. С понятием алгоритма тесно связано понятие порождающего процесса, или исчисления. Порождающий процесс отличается от алгоритма тем, что он принципиально недетерминирован, его правила суть не предписания, а разрешения выполнить некоторое действие. Примером исчисления может служить логический вывод либо разбор в формальной грамматике. Одним из первых результатов теории алгоритмов стала теорема о том, что не любую вычислимую функцию можно продолжить до всюду определённой вычислимой функции. Практическим примером таких функций является любой интерпретатор программ, например, BASIC. Если не ограничивать возможности программиста, то нельзя создать интерпретатор, который невозможно было бы привести в нерабочее состояние исполнением синтаксически корректной программы. Множество, характеристическое свойство которого является всюду определённым вычислимым предикатом, называется разрешимым. Следует отметить, что схема вычислительного процесса в современном его понимании — написание программы на языке высокого уровня, трансляция её в машинный язык и исполнение компьютером — имеет теоретической основой теорему об универсальном алгоритме. Например, определение алгоритма может быть записано как слово в некотором алфавите, а если взять определение алгоритма, в котором рассматриваются лишь натуральные числа, такое слово может быть естественно представлено как число в системе счисления, основанием которой является количество букв в алфавите. Тогда имеется универсальный алгоритм U, перерабатывающий любую пару (ϕ, P), где ϕ — конструктивный объект, называемый записью или программой (относительно U) алгоритма ϕ, в результат применения ϕ к P. Универсальный алгоритм не может быть всюду определён. Если рассматривать лишь конструктивные объекты, то алгоритм естественно отождествить с его программой относительно некоторого U. Обобщение теории алгоритмов на абстрактные вычисления и объекты высших порядков является одним из основных направлений исследований современной теории алгоритмов. Другим наиболее важным её направлением развития служит теория сложности вычислений, рассматривающая проблемы оценки ресурсов, необходимых для работы алгоритмов, основы которой закладывали А. Н. Колмогоров и А. А. Марков и С. Кальмар. На основе теории сложности А. Н. Колмогоров, Л. А. Левин, П. Мартин-Лёф и другие развили алгоритмическую теорию вероятностей. Следует отметить, что тезис Чёрча содержит одно важное онтологическое предположение: о невозможности обозреть вечность. Поэтому в общей теории относительности (в частности, во вселенной Гёделя, в которой время может ходить по кругу) имеются миры, в которых, пролетая сквозь вращающуюся чёрную дыру, можно вычислить алгоритмически невычислимую функцию. Класс функций, которые могут быть вычислены в таких Вселенных, называется гиперарифметическим. Он неопределим в арифметике и определим лишь в анализе. |
АЛГОРИТМ | Энциклопедия Кругосвет
Содержание статьи- Проблема определения понятия «алгоритм».

- Понятие «алгоритма».
- Наличие исходных данных и некоторого результата.
- Детерминированность.
- Результативность.
- Определенность.
- Формы представления алгоритмов.
- Формализация понятия алгоритмов. Теория алгоритмов.
- История конечных автоматов: машина Поста и машина Тьюринга.
- Современный взгляд на алгоритмизацию.
АЛГОРИТМ – система правил, сформулированная на понятном исполнителю языке, которая определяет процесс перехода от допустимых исходных данных к некоторому результату и обладает свойствами массовости, конечности, определенности, детерминированности.
Слово «алгоритм» происходит от имени великого среднеазиатского ученого 8–9 вв. Аль-Хорезми (Хорезм – историческая область на территории современного Узбекистана). Из математических работ Аль-Хорезми до нас дошли только две – алгебраическая (от названия этой книги родилось слово алгебра) и арифметическая. Вторая книга долгое время считалась потерянной, но в 1857 в библиотеке Кембриджского университета был найден ее перевод на латинский язык. В ней описаны четыре правила арифметических действий, практически те же, что используются и сейчас. Первые строки этой книги были переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм. Термин алгоритм употреблялся для обозначения четырех арифметических операций, именно в таком значении он и вошел в некоторые европейские языки. Например, в авторитетном словаре английского языка Webster’s New World Dictionary, изданном в 1957, слово алгоритм снабжено пометкой «устаревшее» и объясняется как выполнение арифметических действий с помощью арабских цифр.
В ней описаны четыре правила арифметических действий, практически те же, что используются и сейчас. Первые строки этой книги были переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм. Термин алгоритм употреблялся для обозначения четырех арифметических операций, именно в таком значении он и вошел в некоторые европейские языки. Например, в авторитетном словаре английского языка Webster’s New World Dictionary, изданном в 1957, слово алгоритм снабжено пометкой «устаревшее» и объясняется как выполнение арифметических действий с помощью арабских цифр.
Слово «алгоритм» вновь стало употребительным с появлением электронных вычислительных машин для обозначения совокупности действий, составляющих некоторый процесс. Здесь подразумевается не только процесс решения некоторой математической задачи, но и кулинарный рецепт и инструкция по использованию стиральной машины, и многие другие последовательные правила, не имеющие отношения к математике, – все эти правила являются алгоритмами. Слово «алгоритм» в наши дни известно каждому, оно настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм успеха» и т.д.
Слово «алгоритм» в наши дни известно каждому, оно настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм успеха» и т.д.
Проблема определения понятия «алгоритм».
На протяжении многих веков понятие алгоритма связывалось с числами и относительно простыми действиями над ними, да и сама математика была, по большей части, наукой о вычислениях, наукой прикладной. Чаще всего алгоритмы представлялись в виде математических формул. Порядок элементарных шагов алгоритма задавался расстановкой скобок, а сами шаги заключались в выполнении арифметических операций и операций отношения (проверки равенства, неравенства и т.д.). Часто вычисления были громоздкими, а вычисления вручную – трудоемкими, но суть самого вычислительного процесса оставалась очевидной. У математиков не возникала потребность в осознании и строгом определении понятия алгоритма, в его обобщении. Но с развитием математики появлялись новые объекты, которыми приходилось оперировать: векторы, графы, матрицы, множества и др. Как определить для них однозначность или как установить конечность алгоритма, какие шаги считать элементарными? В 1920-х задача точного определения понятия алгоритма стала одной из центральных проблем математики. В то время существовало две точки зрения на математические проблемы:
Как определить для них однозначность или как установить конечность алгоритма, какие шаги считать элементарными? В 1920-х задача точного определения понятия алгоритма стала одной из центральных проблем математики. В то время существовало две точки зрения на математические проблемы:
Все проблемы алгоритмически разрешимы, но для некоторых алгоритм еще не найден, поскольку еще не развиты соответствующие разделы математики.
Есть проблемы, для которых алгоритм вообще не может существовать.
Идея о существовании алгоритмически неразрешимых проблем оказалась верной, но для того, чтобы ее обосновать, необходимо было дать точное определение алгоритма. Попытки выработать такое определение привели к возникновению теории алгоритмов, в которую вошли труды многих известных математиков – К.Гедель, К.Черч, С.Клини, А.Тьюринг, Э.Пост, А.Марков, А.Колмогоров и многие другие.
Точное определение понятия алгоритма дало возможность доказать алгоритмическую неразрешимость многих математических проблем.
Появление первых проектов вычислительных машин стимулировало исследование возможностей практического применения алгоритмов, использование которых, ввиду их трудоемкости, было ранее недоступно. Дальнейший процесс развития вычислительной техники определил развитие теоретических и прикладных аспектов изучения алгоритмов.
Понятие «алгоритма».
В повседневной жизни каждый человек сталкивается с необходимостью решения задач самой разной сложности. Некоторые из них трудны и требуют длительных размышлений для поиска решений (а иногда его так и не удается найти), другие же, напротив, столь просты и привычны, что решаются автоматически. При этом выполнение даже самой простой задачи осуществляется в несколько последовательных этапов (шагов). В виде последовательности шагов можно описать процесс решения многих задач, известных из школьного курса математики: приведение дробей к общему знаменателю, решение системы линейных уравнений путем последовательного исключения неизвестных, построение треугольника по трем сторонам с помощью циркуля и линейки и т. д. Такая последовательность шагов в решении задачи называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть упорядоченными. Правда, существуют параллельные алгоритмы, для которых это требование не соблюдается.
д. Такая последовательность шагов в решении задачи называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть упорядоченными. Правда, существуют параллельные алгоритмы, для которых это требование не соблюдается.
Понятие алгоритма близко к другим понятиям, таким, как метод (метод Гаусса решения систем линейных уравнений), способ (способ построения треугольника по трем сторонам с помощью циркуля и линейки). Можно сформулировать основные особенности именно алгоритмов.
Наличие исходных данных и некоторого результата.
Алгоритм – это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Массовость, т.е. возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.
Детерминированность.
При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.
Результативность.
Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике. Например, алгоритм работы системы сбора метеорологических данных состоит в непрерывном повторении последовательности действий («измерить температуру воздуха», «определить атмосферное давление»), выполняемых с определенной частотой (через минуту, час) во все время существования данной системы.
Определенность.
На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.
Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.
Формы представления алгоритмов.
Для записи алгоритмов необходим некоторый язык, при этом очень важно, какой именно язык выбран. Записывать алгоритмы на русском языке (или любом другом естественном языке) громоздко и неудобно.
Например, описание алгоритма Евклида нахождения НОД (наибольшего общего делителя) двух целых положительных чисел может быть представлено в виде трех шагов. Шаг 1: Разделить m на n. Пусть p – остаток от деления.
Шаг 2: Если p равно нулю, то n и есть исходный НОД.
Шаг 3: Если p не равно нулю, то сделаем m равным n, а n равным p. Вернуться к шагу 1.
Приведенная здесь запись алгоритма нахождения НОД очень упрощенная. Запись, данная Евклидом, представляет собой страницу текста, причем последовательность действий существенно сложней.
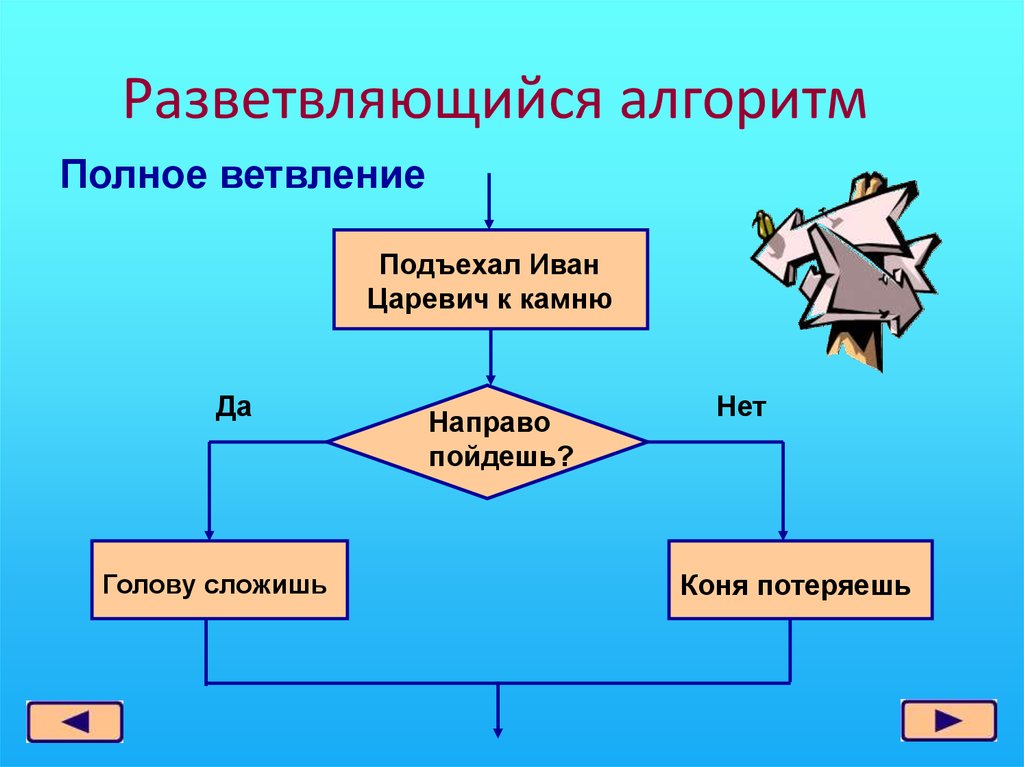
Одним из распространенных способов записи алгоритмов является запись на языке блок-схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. Каждый элемент – это «шаг» алгоритма. Элементы блок-схемы делятся на два вида. Элементы, содержащие инструкцию выполнения какого-либо действия, обозначают прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из прямоугольников всегда выходит только одна стрелка (входить может несколько), а из ромбов – две (одна из них помечается словом «да», другая – словом «нет», они показывают, соответственно, выполнено или нет проверяемое условие).
На рисунке представлена блок-схема алгоритма нахождения НОД:
Построение блок-схем из элементов всего лишь нескольких типов дает возможность преобразовать их в компьютерные программы и позволяет формализовать этот процесс.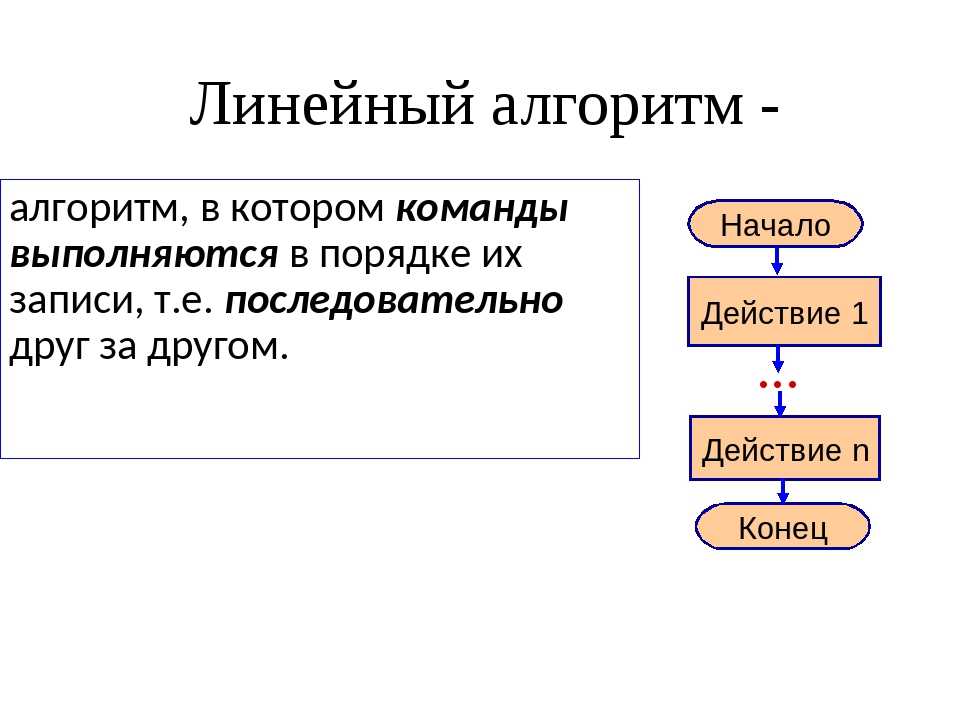
Формализация понятия алгоритмов. Теория алгоритмов.
Приведенное определение алгоритма нельзя считать представленным в привычном математическом смысле. Математические определения фигур, чисел, уравнений, неравенств и многих других объектов очень четки. Каждый математически определенный объект можно сравнить с другим объектом, соответствующим тому же определению. Например, прямоугольник можно сравнить с другим прямоугольником по площади или по длине периметра. Возможность сравнения математически определенных объектов – важный момент математического изучения этих объектов. Данное определение алгоритма не позволяет сравнивать какие-либо две таким образом определенные инструкции. Можно, например, сравнить два алгоритма решения системы уравнений и выбрать более подходящий в данном случае, но невозможно сравнить алгоритм перехода через улицу с алгоритмом извлечения квадратного корня. С этой целью нужно формализовать понятие алгоритма, т.е. отвлечься от существа решаемой данным алгоритмом задачи, и выделить свойства различных алгоритмов, привлекая к рассмотрению только его форму записи. Задача нахождения единообразной формы записи алгоритмов, решающих различные задачи, является одной из основных задач теории алгоритмов. В теории алгоритмов предполагается, что каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина), Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было выполнять любой алгоритм. Механизм работы машины должен быть максимально простым по логической структуре, но настолько точным, чтобы эта структура могла служить предметом математического исследования. Впервые это было сделано американским математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных вычислительных машин и (практически одновременно) английским математиком Аланом Тьюрингом (машина Тьюринга).
Задача нахождения единообразной формы записи алгоритмов, решающих различные задачи, является одной из основных задач теории алгоритмов. В теории алгоритмов предполагается, что каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина), Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было выполнять любой алгоритм. Механизм работы машины должен быть максимально простым по логической структуре, но настолько точным, чтобы эта структура могла служить предметом математического исследования. Впервые это было сделано американским математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных вычислительных машин и (практически одновременно) английским математиком Аланом Тьюрингом (машина Тьюринга).
История конечных автоматов: машина Поста и машина Тьюринга.
Машина Поста – абстрактная вычислительная машина, предложенная Постом (Emil L.Post), которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».
В 1935 американский математик Пост опубликовал в «Журнале символической логики» статью Финитные комбинаторные процессы, формулировка 1. В этой статье и появившейся одновременно в Трудах Лондонского математического общества статье английского математика Тьюринга О вычислимых числах с приложением к проблеме решения были даны первые уточнения понятия «алгоритм». Важность идей Поста состоит в том, что был предложен простейший способ преобразования информации, именно он построил алгоритмическую систему (алгоритмическая система Поста). Пост доказал, что его система обладает алгоритмической полнотой. В 1967 профессор В.Успенский пересказал эти статьи с новых позиций. Он ввел термин «машина Поста». Машина Поста – абстрактная машина, которая работает по алгоритмам, разработанным человеком, она решает следующую проблему: если для решения задачи можно построить машину Поста, то она алгоритмически разрешима. В 1970 машина Поста была разработана в металле в Симферопольском университете. Машина Тьюринга была построена в металле в 1973 в Малой Крымской Академии Наук.
Машина Тьюринга была построена в металле в 1973 в Малой Крымской Академии Наук.
Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V». У машины есть головка, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, либо проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста. Работа машины Поста заключается в том, что головка передвигается вдоль ленты (на одну клетку за один шаг) влево или вправо, наносит или стирает метки, а также распознает, есть ли метка в клетке в соответствии с заданной программой, состоящей из отдельных команд.
Машина Тьюринга состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, …, qs , принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний), при этом q0 называется начальным состоянием. Читающая и пишущая головка может читать буквы рабочего алфавита A = {a0, a1, …, at }, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква а0 – «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты – текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты, при этом возможна ситуация выхода за левый край ленты, которая является аварийной (недопустимой), или машинного останова, когда машина выполняет предписание об остановке.
Современный взгляд на алгоритмизацию.
Теория алгоритмов строит и изучает конкретные модели алгоритмов. С развитием вычислительной техники и теории программирования возрастает необходимость построения новых экономичных алгоритмов, изменяются способы их построения, способы записи алгоритмов на языке, понятном исполнителю. Особый тип исполнителя алгоритмов – компьютер, поэтому необходимо создавать специальные средства, позволяющие, с одной стороны, разработчику в удобном виде записывать алгоритмы, а с другой – дающие компьютеру возможность понимать написанное. Такими средствами являются языки программирования или алгоритмические языки.
Анна Чугайнова
о сложном – простыми словами
О том, что такое алгоритмы и как они влияют на нашу жизнь.
Наверняка вы слышали слово «алгоритм». Этот термин широко используется в современной жизни. И если вставить слово в повседневный разговор не составит труда, намного сложнее объяснить, что именно это такое. Сегодня поговорим о значении слова и об истинной природе алгоритмов, которые существовали в человеческой жизни еще до момента появления компьютерных технологий.
1. Алгоритм – это набор конкретных инструкций
istockphoto.com
Простыми словами, «алгоритм – это последовательность инструкций», говорит Педро Домингос, профессор компьютерных наук в Вашингтонском университете и автор книги «Верховный алгоритм. Как машинное обучение изменит наш мир».
Как испечь пирог, найти значение суммы 2+2 или управлять страной в соответствии с Конституцией – все это алгоритмы. Но чаще всего это слово связывают со сферой IT. В этом случае под «алгоритмом» понимается «последовательность инструкций, которые говорят компьютеру, что делать».
Любая компьютерная программа – это алгоритм, написанный на языке компьютерного программирования, который компьютер может понять и выполнить. И это устроено намного сложнее, чем в обычной жизни.
«Компьютерные алгоритмы должны быть предельно точны. Для их определения могут потребоваться миллионы строк», – подчеркивает профессор.
2. Люди писали и использовали алгоритмы задолго до появления компьютеров
Pixel
Несмотря на то что сегодня алгоритмы используются в контексте компьютерных технологий, их история намного старше ПК. Люди создавали алгоритмы еще в Вавилонскую эпоху – они помогали им решать математические уравнения и управлять земледельческим обществом.
Люди создавали алгоритмы еще в Вавилонскую эпоху – они помогали им решать математические уравнения и управлять земледельческим обществом.
«Все потому, что для выполнения алгоритма не всегда нужен компьютер – им могут управлять сами люди», – утверждает Домингос.
С появлением и распространением компьютеров во второй половине XX-го века алгоритмы начали активно использоваться в военной сфере (для определения того, куда навести ракету), а позже в области бизнес-администрирования (в приложениях для расчета заработной платы) и науки (прогноз погоды).
Поворотный момент для развития современных алгоритмов наступил, когда Ларри Пейдж и Сергей Брин создали Google PageRank. Вместо того чтобы просто полагаться на информацию на странице для определения ее релевантности поисковому запросу, алгоритм поисковой системы учитывал множество других сигналов, которые помогали ему выявлять наилучшие результаты.
Например, сколько других ссылок указывало на статью и насколько авторитетными были эти статьи, в зависимости от количества ссылок, указывающих на эти страницы, и так далее.
3. Сегодня алгоритмы повсюду
pixabay.com
С распространением компьютеров и Интернета алгоритмы стали неотъемлемой частью нашей повседневной жизни. На них основаны новостные ленты социальных сетей, которые определяют, какой контент показывать вам при скроллинге, а также механизмы интернет-магазинов, предлагающих вам товары, которые могли бы вам понравиться.
«Facebook может разместить в вашей новостной ленте кучу постов и публикаций, но благодаря алгоритму он довольно избирателен, – сказал Домингос. – Обычно он учитывает целую комбинацию факторов. Например, как часто вы взаимодействуете с людьми, которые прямо или косвенно создали этот пост; насколько публикации близки вам в вашей социальной сети; насколько они актуальны с точки зрения тематики, насколько свежи и т. д.».
По словам профессора Домингоса, мы сталкиваемся с алгоритмами на протяжении всей нашей жизни и даже можем об этом не подозревать. Например, благодаря алгоритму посудомоечная машина узнает, когда пора переходить от стирки к сушке. Это алгоритм определяет, как ваш автомобиль регулирует потребление топлива и понимает, когда его бак на заправке становится полным.
Это алгоритм определяет, как ваш автомобиль регулирует потребление топлива и понимает, когда его бак на заправке становится полным.
«Совершенно очевидно, что каждый раз, когда вы пользуетесь компьютером или Интернетом, вы имеете дело с алгоритмами, – подчеркнул Домингос. – В наши дни они задействованы практически во всем».
4. В самых сложных алгоритмах используется машинное обучение
pixabay.com
Благодаря технологическому прогрессу современные алгоритмы претерпевают дальнейшие изменения. Особенно с появлением машинного обучения – разновидности искусственного интеллекта (ИИ).
«В традиционном программировании человек должен записывать каждую мелочь, для того чтобы это сделал другой, что очень затратно по времени и средствам, – объяснил Домингос. – Машинное обучение – это компьютер, использующий свои собственные алгоритмы вместо того, чтобы ему говорили, что делать».
Другими словами, машинное обучение – это когда программист вводит в программу необработанные данные в качестве отправной точки, а затем задает конечную точку того, как выглядит организованная, классифицированная версия этих данных.
Остальное делает программа: она самостоятельно выясняет, как добраться из пункта А в пункт Б. Рассмотрим пример из кулинарии. Человек, который умеет готовить, может превратить обычный лук из сырого в карамелизированные обжаренные кусочки.
В традиционном варианте программист должен был бы прописать каждый шаг инструкции по приготовлению лука. Но в алгоритме, разработанном ИИ, с учетом конечной точки-цели, программа сама должна выяснить, как перейти от сырого состояния к карамелизированному. Это значит, что машина учится этому самостоятельно.
Такие типы алгоритмов становятся еще более мощными, когда человек не знает, как добраться из точки А в точку Б. Например, человеческий процесс, такой как способность понимать, что кошка это кошка, требует сложных умственных способностей, которые невозможно расписать пошагово.
Но если дать программе набор фотографий кошки и предметов, которые кошкой не являются, и показав желаемую конечную точку в качестве категоризации изображения кошки в виде животного, компьютер научится выполнять этот процесс самостоятельно.
«Это возможность создавать мощные сложные алгоритмы с минимальным вмешательством человека», – подчеркивает Домингос.
5. Алгоритмы – это не волшебство
Pixel
Из-за большого количества обрабатываемых алгоритмов данных может показаться, что они ключ ко всем загадкам человечества. Но важно помнить, что алгоритм – всего лишь набор инструкций. Более того, его создают люди, а это значит, что он может быть ошибочным. Люди, которые не очень разбираются в компьютерах, часто полагают, что «алгоритмы идеальны». Что в корне неверно.
Pixel
Домингос объяснил, что программисты тратят огромное количество времени на исправление ошибок в алгоритмах. Все для того, чтобы они давали соответствующие результаты.
«Кроме того, в традиционном программировании вы должны беспокоиться о предвзятости программиста, – говорит Домингос. – В машинном обучении вы в основном должны беспокоиться о предвзятости, исходящей от данных».
Например, алгоритм найма, основанный на машинном обучении, может использовать в качестве отправной точки множество резюме кандидатов, а в качестве результата – резюме людей, которые были наняты в прошлом. Однако большинство технологических компаний не отличаются расовым разнообразием.
Таким образом, автоматизированный алгоритм, который дает рекомендации по найму, может отражать это реальное неравенство: исследования показали, что искусственный интеллект может отражать гендерные и расовые стереотипы людей, которые их обучают.
6. Алгоритмы по-прежнему способны изменить мир
unsplash.com
Алгоритмы могут быть несовершенными, но они все равно меняют наш мир. «Все эти вещи, которые мы принимаем как должное – Интернет, социальные сети и так далее, – они бы не существовали без алгоритмов», – сказал Домингос.
«Современные алгоритмы делают для умственного труда то же, что когда-то сделала промышленная революция с ручным трудом. Алгоритмы – это автоматизация интеллекта. И очень мощное средство: то, что раньше требовало больших умственных и физических усилий, теперь можно сделать с помощью алгоритма… Алгоритмы никуда не денутся. Но только от нас зависит то, какими мы их создадим – предвзятыми или справедливыми, полезными или вредными», – подытожил профессор.
Алгоритмы – это автоматизация интеллекта. И очень мощное средство: то, что раньше требовало больших умственных и физических усилий, теперь можно сделать с помощью алгоритма… Алгоритмы никуда не денутся. Но только от нас зависит то, какими мы их создадим – предвзятыми или справедливыми, полезными или вредными», – подытожил профессор.
Обложка: 1Gai.Ru / istockphoto.com
Источник статьи: What is an algorithm, anyway?
Что такое алгоритм? Характеристики, типы и способ записи
Алгоритм — это пошаговая процедура, определяющая набор инструкций, которые необходимо выполнять в определенном порядке для получения желаемого результата. Алгоритмы обычно разрабатываются независимо от базовых языков, что означает, что алгоритм может быть реализован более чем на одном языке программирования. Однозначность, точность, эффективность и независимость от языка — вот некоторые из характеристик алгоритма. Масштабируемость и производительность алгоритма являются основными факторами, влияющими на его важность.
Что такое алгоритм?
- Алгоритм — это набор команд, которые должны выполняться компьютером для выполнения вычислений или других операций по решению задач.
- Согласно формальному определению, алгоритм — это конечный набор инструкций, выполняемых в определенном порядке для выполнения конкретной задачи.
- Это не вся программа или код; это простая логика проблемы, представленная в виде неформального описания в виде блок-схемы или псевдокода.
- Проблема: Проблема может быть определена как реальная проблема или реальная проблема, для которой вам необходимо разработать программу или набор инструкций. Алгоритм — это набор инструкций.
- Алгоритм: Алгоритм определяется как пошаговый процесс, который будет разработан для решения проблемы.
- Входные данные: после разработки алгоритма алгоритм получает необходимые и желаемые входные данные.
- Блок обработки: входные данные будут переданы блоку обработки, производя желаемый результат.

- Выход: Результат или результат программы называется выходом.
После определения того, что такое алгоритм, вы теперь посмотрите на характеристики алгоритма.
Характеристики алгоритма
Алгоритм имеет следующие характеристики:
- Входные данные: Алгоритму требуются некоторые входные значения. В качестве входных данных алгоритму может быть задано значение, отличное от 0.
- Вывод: В конце алгоритма у вас будет один или несколько результатов.
- Однозначность: Совершенный алгоритм определяется как недвусмысленный, что означает, что его инструкции должны быть ясными и прямыми.
- Конечность: Алгоритм должен быть конечным. Конечность в данном контексте означает, что алгоритм должен иметь ограниченное число инструкций, т. е. инструкции должны быть счетными.
- Эффективность: Поскольку каждая инструкция в алгоритме влияет на весь процесс, она должна быть адекватной.
- Независимость от языка: Алгоритм должен быть независимым от языка, что означает, что его инструкции могут быть реализованы на любом языке и давать одинаковые результаты.

Продолжая изучение этого учебника «Что такое алгоритм», вы узнаете, зачем вам нужен алгоритм.
Зачем нужен алгоритм?
Вам нужны алгоритмы по следующим причинам:
Масштабируемость
Помогает понять масштабируемость. Когда у вас есть крупная реальная проблема, вы должны разбить ее на небольшие шаги, чтобы быстро проанализировать.
Производительность
Реальный мир сложно разбить на более мелкие шаги. Если проблему можно легко разделить на более мелкие шаги, это означает, что проблема разрешима.
Поняв, что такое алгоритм и зачем он нужен, вы увидите, как его написать на примере.
Как написать алгоритм?
- Не существует четко определенных стандартов для написания алгоритмов. Однако это проблема, зависящая от ресурсов. Алгоритмы никогда не пишутся с расчетом на конкретный язык программирования.
- Как вы все знаете, базовые конструкции кода, такие как циклы do, for, while, во всех языках программирования совместно используют управление потоком, такое как if-else и так далее.
 Алгоритм может быть написан с использованием этих общих конструкций.
Алгоритм может быть написан с использованием этих общих конструкций. - Алгоритмы обычно пишутся поэтапно, но это не всегда так. Написание алгоритма — это процесс, который происходит после четкого определения проблемной области. То есть вы должны знать проблемную область, для которой разрабатываете решение.
Пример
Теперь используйте пример, чтобы научиться писать алгоритмы.
Задача: Создайте алгоритм, который умножает два числа и отображает результат.
Шаг 1 — Запуск Шаг 2 — объявить три целых числа x, y и z Шаг 3 — определение значений x и y Шаг 4 — умножить значения x и y Шаг 5 — сохранить результат шага 4 до z Шаг 6 — напечатайте z Шаг 7 — Стоп |
Алгоритмы учат программистов писать код. Кроме того, алгоритм можно записать так:
Шаг 1 — Запуск мульти Шаг 2 — получить значения x и y Шаг 3 — z ← x * y Шаг 4 — отображение z Шаг 5 — Стоп |
При разработке и анализе алгоритмов для описания алгоритма обычно используется второй метод. Это позволяет аналитику анализировать алгоритм, легко игнорируя все нежелательные определения. Они могут видеть, какие операции используются и как продвигается процесс. Необязательно писать номера шагов. Чтобы решить данную проблему, вы создаете алгоритм. Проблема может быть решена различными способами.
Это позволяет аналитику анализировать алгоритм, легко игнорируя все нежелательные определения. Они могут видеть, какие операции используются и как продвигается процесс. Необязательно писать номера шагов. Чтобы решить данную проблему, вы создаете алгоритм. Проблема может быть решена различными способами.
В результате может быть получено множество алгоритмов решения данной задачи. Следующим шагом является оценка предложенных алгоритмов решения и реализация наиболее подходящего решения.
По мере прохождения этого руководства «что такое алгоритм» вы узнаете о некоторых компонентах алгоритма.
Факторы алгоритма
При разработке алгоритма следует учитывать следующие факторы:
- Модульность: эта функция была идеально разработана для алгоритма, если вам дают задачу и разбивают ее на маленькие-маленькие модули или маленькие-маленькие шаги, что является основным определением алгоритма.
- Корректность: Корректность алгоритма определяется, когда заданные входные данные дают желаемый результат, что указывает на то, что алгоритм был разработан правильно.
 Алгоритм анализа выполнен правильно.
Алгоритм анализа выполнен правильно. - Ремонтопригодность: это означает, что алгоритм должен быть разработан простым и структурированным образом, чтобы при переопределении алгоритма в него не вносились существенные изменения.
- Функциональность: Он учитывает различные логические шаги для решения реальной проблемы.
- Надежность: Надежность относится к способности алгоритма четко определить вашу проблему.
- Удобный для пользователя: если алгоритм сложен для понимания, разработчик не будет объяснять его программисту.
- Простота: если алгоритм прост, его легко понять.
- Расширяемость: Ваш алгоритм должен быть расширяемым, если другой разработчик алгоритма или программист захочет его использовать.
Теперь вы поймете, почему алгоритм так важен, после понимания некоторых его компонентов.
Важность алгоритма
Есть два фактора, в которых алгоритм является фундаментальным:
Теоретическая значимость
Когда вам дают реальную проблему, вы должны разбить ее на более мелкие модули. Чтобы разобрать проблему, вы должны сначала понять все ее теоретические аспекты.
Чтобы разобрать проблему, вы должны сначала понять все ее теоретические аспекты.
Практическая значимость
Как вы все знаете, теория не может быть завершена без практического применения. В результате значимость алгоритмов можно рассматривать как теоретически, так и практически.
По мере изучения этого учебника «что такое алгоритм» вы увидите алгоритмические подходы.
Подходы алгоритма
После рассмотрения как теоретической, так и практической важности разработки алгоритма были использованы следующие подходы:
Этот алгоритм использует общую логическую структуру для разработки алгоритма. Его также называют алгоритмом исчерпывающего поиска, потому что он исчерпывает все возможности для предоставления требуемого решения. Существует два вида таких алгоритмов:
- Оптимизация: поиск всех возможных решений проблемы и последующий выбор наилучшего прекращается, если известно наилучшее решение.
- Жертвоприношение: Оно прекратится, как только будет найдено лучшее решение.

Разделяй и властвуй
Это простая реализация алгоритма. Это позволяет вам создавать алгоритм поэтапно. Он деконструирует алгоритм для решения проблемы различными способами. Это позволяет вам разделить проблему на разные методы, генерируя действительный вывод для действительного ввода. Этот точный вывод передается другой функции.
Жадный алгоритм
Это парадигма алгоритма, которая делает наилучший возможный выбор на каждой итерации в надежде найти наилучшее решение. Он прост в настройке и имеет более короткое время выполнения. Однако очень мало случаев, когда это лучшее решение.
Динамическое программирование
Повышает эффективность алгоритма за счет сохранения промежуточных результатов. Он проходит пять шагов, чтобы найти наилучшее решение проблемы:
- Делит проблему на подзадачи, чтобы найти наилучшее решение.

- После разбивки задачи на подзадачи, она находит лучшее решение из этих подзадач.
- Запоминание — это процесс запоминания результатов подзадач.
- Повторно используйте результат, чтобы предотвратить его повторное вычисление для тех же подзадач.
- Наконец, он вычисляет выходные данные сложной программы.
С помощью алгоритма ветвей и границ можно решить только задачи целочисленного программирования. Этот метод делит все допустимые наборы решений на меньшие подмножества. Эти подмножества затем оцениваются далее, чтобы найти наилучшее решение.
Как и в случае со стандартным алгоритмом, у вас есть предопределенные входные и выходные данные. Детерминированные алгоритмы имеют определенный набор информации и требуемых результатов и выполняют некоторые описанные шаги. Они более эффективны, чем недетерминированные алгоритмы.
Возврат
Это алгоритмическая процедура, которая рекурсивно отбрасывает решение, если оно не удовлетворяет ограничениям задачи.
После того, как вы поняли, что такое алгоритм и его подходы, вы теперь посмотрите на анализ алгоритма.
Анализ алгоритма
Алгоритм можно исследовать на двух уровнях: до и после его создания. Два алгоритма анализа следующие:
Априорный анализ
В этом контексте априорный анализ относится к теоретическому анализу алгоритма, выполненному до реализации алгоритма. Перед реализацией алгоритма можно учитывать различные факторы, такие как скорость процессора, которая не влияет на реализацию.
Апостериорный анализ
В этом контексте апостериорный анализ относится к практическому анализу алгоритма. Алгоритм реализуется на любом языке программирования для проведения экспериментальных исследований. Этот анализ определяет, сколько времени и места требуется для работы.
Переходя к этому учебнику «что такое алгоритм», вы теперь рассмотрите сложность алгоритма.
Сложность алгоритма
Производительность алгоритма можно измерить двумя способами:
Сложность времени
Количество времени, необходимое для завершения выполнения алгоритма, называется временной сложностью. Обозначение «большой O» используется для обозначения временной сложности алгоритма. Асимптотическая нотация для описания временной сложности в этом случае — это нотация большого O. Временная сложность рассчитывается в первую очередь путем подсчета количества шагов, необходимых для завершения выполнения. Давайте рассмотрим пример временной сложности.
Обозначение «большой O» используется для обозначения временной сложности алгоритма. Асимптотическая нотация для описания временной сложности в этом случае — это нотация большого O. Временная сложность рассчитывается в первую очередь путем подсчета количества шагов, необходимых для завершения выполнения. Давайте рассмотрим пример временной сложности.
мул = 1; // Предположим, вам нужно вычислить умножение n чисел. для i=1 до n мул = мул *1; // когда цикл заканчивается, тогда mul содержит умножение n чисел возврат мул; |
Временная сложность оператора цикла в предыдущем коде не меньше n, и чем больше значение n, тем больше временная сложность. При этом сложность кода, т.е. возвращает mul, будет постоянной, поскольку его значение не зависит от важности n и даст результат за один шаг. Обычно рассматривается сложность наихудшего времени, потому что это максимальное время, необходимое для любого заданного размера входных данных.
Космическая сложность
Объем памяти, который требуется алгоритму для решения задачи и получения результата, называется его пространственной сложностью. Пространственная сложность, как и временная сложность, выражается в большой нотации O.
Пространство требуется для алгоритма по следующим причинам:
- Для хранения программных инструкций.
- Для хранения трека постоянных значений.
- Для хранения отслеживания значений переменных.
- Для хранения отслеживания вызовов функций, операторов перехода и т. д.
Сложность пространства = вспомогательное пространство + размер ввода
Наконец, поняв, что такое алгоритм, его анализ и подходы, вы рассмотрите различные типы алгоритмов.
Типы алгоритмов
Существует два типа алгоритмов:
- Поиск Алгори
- Алгоритм сортировки
Алгоритм поиска
Каждый день вы ищете что-то в своей повседневной жизни. Точно так же в случае компьютера в компьютере хранится большой объем данных, и всякий раз, когда пользователь запрашивает данные, компьютер ищет эти данные в памяти и возвращает их пользователю. В основном существует два метода поиска данных в массиве:
Точно так же в случае компьютера в компьютере хранится большой объем данных, и всякий раз, когда пользователь запрашивает данные, компьютер ищет эти данные в памяти и возвращает их пользователю. В основном существует два метода поиска данных в массиве:
Алгоритм поиска бывает двух типов:
Линейный поиск
Линейный поиск — это простой алгоритм, который начинает поиск элемента или значения в начале массива и продолжает до тех пор, пока нужный элемент не будет найден. Он сравнивает искомый элемент со всеми элементами массива; если совпадение найдено, возвращается индекс элемента; в противном случае возвращается -1. Этот алгоритм можно применить к несортированному списку.
Бинарный поиск
Двоичный алгоритм — это самый простой алгоритм, и он очень быстро ищет элементы. Он используется для поиска элемента в отсортированном списке. Для реализации бинарного алгоритма элементы должны храниться в последовательном порядке или отсортированы. Если элементы хранятся случайным образом, бинарный поиск не может быть реализован.
Если элементы хранятся случайным образом, бинарный поиск не может быть реализован.
Алгоритм сортировки
Алгоритмы сортировки переставляют элементы в массиве или заданной структуре данных в порядке возрастания или убывания. Оператор сравнения определяет новый порядок элементов.
Теперь, когда вы завершили руководство по теме «что такое алгоритм», вы подведете итог тому, что уже узнали.
Получите прочную основу для Java, наиболее часто используемого языка программирования в разработке программного обеспечения, с помощью учебного курса сертификации Java.
Следующие шаги
В этом руководстве вы узнали, что такое алгоритм и каковы его характеристики. После этого вы рассмотрели, зачем вам нужны алгоритмы, как их писать и насколько они важны. После того, как вы узнали о подходах и факторах алгоритма, вы узнали о сложности и типах алгоритмов.
Предположим, вы ищете более обширное исследование, которое выходит за рамки разработки программного обеспечения и охватывает наиболее востребованные сегодня языки программирования и возможности. В этом случае вам подойдет магистерская программа Full Stack Java Developer от Simplilearn. Изучите эту всемирно известную программу учебных курсов и будьте уверены, что ее завершение станет самым разумным шагом, который вы можете сделать, чтобы войти в профессию разработчика программного обеспечения и расти в ней.
В этом случае вам подойдет магистерская программа Full Stack Java Developer от Simplilearn. Изучите эту всемирно известную программу учебных курсов и будьте уверены, что ее завершение станет самым разумным шагом, который вы можете сделать, чтобы войти в профессию разработчика программного обеспечения и расти в ней.
У вас есть какие-либо вопросы об этом руководстве о том, что такое алгоритм? Если вы это сделаете, пожалуйста, оставьте их в разделе комментариев внизу этой страницы. Наши специалисты ответят на Ваши вопросы максимально быстро!
Что такое алгоритм в математике? Определение, свойства, примеры
Что такое алгоритм?
Алгоритм — это пошаговый процесс решения конкретной проблемы.
Думайте об этом как о математическом «рецепте», позволяющем добраться до сути проблемы. Если вы будете следовать инструкциям, вы сможете получить ответ в кратчайшие сроки!
Пример алгоритма: Простым примером алгоритма, который вы используете каждый день, является ваша утренняя рутина. Скажем, вы встаете в 6:30 утра, чтобы идти в школу. Если вы всегда встаете, чистите зубы, пьете воду, идете в ванную, а затем принимаете ванну, это может быть алгоритмом, которому следует ваше тело! Алгоритмы вокруг нас. Важно обнаружить их, чтобы узнать, как они функционируют, а затем создать свои собственные.
Скажем, вы встаете в 6:30 утра, чтобы идти в школу. Если вы всегда встаете, чистите зубы, пьете воду, идете в ванную, а затем принимаете ванну, это может быть алгоритмом, которому следует ваше тело! Алгоритмы вокруг нас. Важно обнаружить их, чтобы узнать, как они функционируют, а затем создать свои собственные.
В повседневной жизни мы применяем множество процедур, которые, как мы не понимаем, являются алгоритмами.
Сюда входят:
Завязывание шнурков
Расписание дня, которому вы следуете в школе
Правила алгебраических формул, такие как сложение и вычитание
Техника, которой вы пользуетесь во время занятий спортом
Правила игр с друзьями
Алгоритмы в математике
Определение математического алгоритма
Алгоритм в математике — это процедура, описание набора шагов, которые можно использовать для решения математических вычислений.
Например, пошаговая процедура, используемая в длинных делениях, является распространенным примером математического алгоритма.
Пример математического алгоритма: Процесс решения математической задачи, такой как «Сколько 82 разделить на 3?» можно получить, выполнив следующий алгоритм:
Сколько раз 3 входит в 8?
Ответ 2.
Сколько еще осталось? 2
Поставьте 2 (десятки) перед 3.
Сколько раз 3 входит в число 22?
Ответ равен 7 с остатком 1.
И, конечно же, ответ равен 27 с остатком 1.
Стандартный алгоритм сложения
Стандартный алгоритм сложения состоит из четырех простых шагов:
Шаг 1. Выровняйте числа по вертикали, сопоставляя места ценности.
Шаг 2. Сложите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите сумму под каждым столбцом.
Шаг 4: Если сумма в столбце больше 9, перенесите цифру десятков в следующий столбец.
Стандартный алгоритм вычитания
Стандартный алгоритм сложения состоит из четырех простых шагов:
Шаг 1. Выровняйте числа по вертикали, сопоставив разряды.
Шаг 2. Вычтите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите разницу под каждым столбцом.
Шаг 4: Если число в верхней части столбца меньше числа в нижней части, перегруппируйте перед вычитанием.
Стандартный алгоритм умножения
Перейдите по ссылке, чтобы проверить стандартный алгоритм умножения.
Преимущества алгоритмов
Алгоритмы необходимы из-за большого разнообразия приложений, в которых они используются. Понимание того, как работают алгоритмы, также имеет решающее значение для развития навыков решения проблем и построения логических рассуждений. Ниже перечислены некоторые преимущества алгоритма:
- Процесс создания алгоритма позволяет вам смотреть на что-то рационально и расчетливо, что очень помогает, когда дело доходит до решения разного рода задач.
- Алгоритмы помогают преодолеть разрыв в общении, когда следование процедуре поможет вам найти необходимое решение, не повторяя процесс повторно.
 Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение. - Алгоритмы используют определенную процедуру, и, используя и оптимизируя их, люди могут решать проблемы намного быстрее.
- Алгоритмы легко отлаживать, поскольку каждый шаг имеет свою логическую последовательность.
- Когда мы используем алгоритмы, мы можем разбить проблемы на более мелкие шаги или части, и поэтому программист может легко преобразовать их в настоящую программу.
Как только вы поймете основы алгоритмов, вы сможете создавать свои собственные, сэкономив себе много времени. С веселыми заданиями и играми SplashLearn вы можете проверить свои математические способности и найти алгоритмы в решаемых вами вопросах.
Свойства алгоритмов
Алгоритмы должны использоваться для решения трех задач:
- Правильное выполнение задачи: Работа, которую вы хотите выполнить, должна быть выполнена с ожидаемыми результатами.
- Эффективно обработайте предоставленную информацию: Время и ресурсы вашей системы должны использоваться надлежащим образом для понимания и последующего решения проблемы.

- Быть понятным: Алгоритмы предназначены для облегчения работы и в идеале должны поддерживаться на базовом уровне понимания.
Примеры алгоритмов в реальном мире
Многие компании в реальном мире используют алгоритмы, чтобы помочь своим клиентам или развивать свой бизнес, и часто пытаются улучшить их каждый день.
- YouTube : Посмотрев несколько видео определенного канала, вы заметите, что вам рекомендуют все больше и больше видео этого канала. Это связано с алгоритмом рекомендаций YouTube, который собирает информацию из вашей предыдущей истории для представления видео того же типа в вашей ленте, чтобы вы продолжали смотреть видео на платформе.
- Социальные сети : Если вы перейдете на страницу «Обзор» в Instagram, вы заметите, что многие из отображаемых сообщений связаны с теми, которые вы обычно ищете или ставите лайки/комментарии. Алгоритм здесь идентифицирует сообщения, с которыми вы взаимодействуете, и показывает вам больше таких сообщений, потому что считает, что вам нравятся такие сообщения.

- Google : Google использует очень известный алгоритм под названием PageRank для сортировки результатов поиска в порядке, который показывает наиболее посещаемые и аутентичные сайты вверху. Этот алгоритм учитывает десятки параметров и быстро предоставляет сайты, которые вы хотите найти.
- Lyft/Uber : компании по совместному использованию такси, такие как Lyft или Uber, используют алгоритмы позиционирования, чтобы помочь клиентам находить автомобили рядом с ними для оптимального опыта. Эти глобальные алгоритмы позиционирования также помогают водителям находить самые быстрые маршруты для достижения определенного пункта назначения. Алгоритмы также помогают таким приложениям решить, какого клиента они должны выбрать первым или отказаться от него.
- Распознавание лиц : Всякий раз, когда компании требуют проверки пользователей, они могут перейти от таких методов, как идентификаторы пользователей и пароли, к более безопасной аутентификации, такой как распознавание лиц.
 Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Советы по освоению алгоритмов
Вы можете освоить алгоритмы, научившись замечать их в повседневной жизни. После этого вы можете разбить алгоритм на шаги размером с укус. Возможно, вам придется проверить это несколько раз, чтобы заметить закономерность в том, как что-то происходит, но как только вы ее найдете, вы сможете обнаруживать ее снова и снова.
Попытайтесь понять, почему происходит каждый шаг в процессе. Как только вы поймете, почему что-то происходит, вам будет легче соединить точки и выяснить логическую последовательность событий. Кроме того, это очень удобно для того, чтобы понять, как создавать алгоритмы для себя. С помощью веселых занятий и игр на SplashLearn вы сможете быстро освоить основы алгоритмов!
Решенные примеры
Пример 1 : Запишите этапы приготовления бутерброда с арахисовым маслом и желе.
Ответ: Этапы приготовления бутерброда с арахисовым маслом и желе:
Шаг 1: Возьмите 2 ломтика хлеба.
Шаг 2: Нанесите арахисовое масло на одну сторону ломтика.
Шаг 3: Нанесите желе на одну сторону другого ломтика.
Шаг 4: Сожмите оба ломтика хлеба вместе.
Пример 2: Запишите шаги стандартного алгоритма вычитания.
Ответ: Стандартный алгоритм вычитания состоит из следующих 4 шагов:
Шаг 1: Выстройте числа по вертикали, сопоставив разряды.
Шаг 2. Вычтите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите разницу под каждым столбцом.
Шаг 4: Если число в верхней части столбца меньше числа в нижней части, перегруппируйте перед вычитанием.
Пример 3: Напишите алгоритм, определяющий, является ли число четным или нечетным.
Ответ: Алгоритм определения четности или нечетности числа:
Шаг 1: Разделите число на 2.
Шаг 2: Если число полностью делится на 2, оно четное, иначе — нечетное.
Пример 4: Напишите алгоритм для нахождения площади прямоугольника.
Ответ: Алгоритм нахождения площади прямоугольника:
Шаг 1: Запишите длину меньшей стороны как «b».
Шаг 2: Запишите длину большей стороны как «l».
Шаг 3: Площадь прямоугольника будет произведением «l» и «b».
Практические задачи
2,4,1,3
2,1,4,3
2,1,3,4
2,4,1,3
Правильный ответ: 2,1, 4,3
Данная последовательность расставляет сову в правильной последовательности.
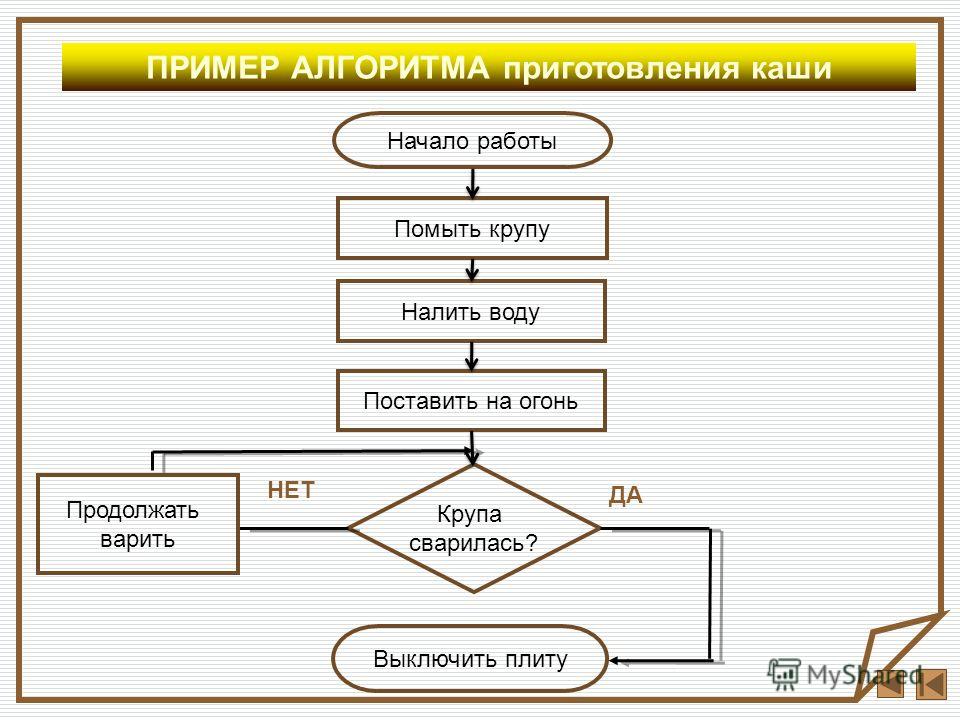
1. Нагрейте кастрюлю, пока вода не закипит
2. Включите плиту
3. Возьмите пустую кастрюлю
4. Поставьте наполненную водой кастрюлю на огонь
5. Налейте воду в пустую кастрюлю
2,3, 5,4,1
3,5,4,2,1
3,5,2,4,1
2,3,4,5,1
Правильный ответ: 3,5,2,4,1
Дано последовательность дает правильный алгоритм кипячения воды.
Добавление цифр любого столбца
Добавление цифр столбца единиц
Размещение цифр в столбцах вертикально
Перенос цифр столбца
Правильный ответ: Расстановка цифр в столбцах вертикально
расположите их вертикально в столбцах.
A
B
C
D
Правильный ответ: D
Эта опция правильно умножает заданные числа.
Часто задаваемые вопросы
Как алгоритмы связаны с математикой?
Алгоритм в математике — это процедура, набор шагов, описывающих, как можно решить математическую задачу. Например, пошаговые процедуры длинного деления или десятичного умножения.
Где мы используем алгоритмы в реальной жизни?
Алгоритмы в основном используются в вычислениях. В нашей повседневной жизни повсюду можно увидеть алгоритмы, решающие наши повседневные проблемы. Рекомендации YouTube и Netflix, поиск в Google, приложения GPS и многое другое основаны на алгоритмах.
Рекомендации YouTube и Netflix, поиск в Google, приложения GPS и многое другое основаны на алгоритмах.
Каковы недостатки использования алгоритмов?
Алгоритмы трудно применять к более крупным и сложным задачам. Они отнимают много времени. Не всегда легко показать ветвление и циклы в алгоритмах. Понять сложную логику, применяемую в алгоритмах, может быть очень сложно.
Каковы важные характеристики алгоритмов?
Шаги алгоритмов должны быть точно указаны. Алгоритм получает ввод и производит вывод после выполнения конечного числа инструкций. Определение
в кембриджском словаре английского языка
Примеры из литературы- «Я спросил ее, как найти счетчик программ вызывающей процедуры в стеке, и она придумала алгоритм в режиме реального времени.
 »
» - «Этот алгоритм фальшивый.»
- Кроме того, более интеллектуальный алгоритм может подразумевать более долгосрочные затраты на сложность и поиск ошибок, чем это оправдано повышением скорости.
- Выбор за людьми тогда делает какой-то алгоритм или вычислительная машина.
- Те, кто убежден, что такие шаблоны и алгоритмы улавливают всю суть личности, смотрят на эту перспективу с приятным ожиданием.
Примеры алгоритма
алгоритм
Дайте нам обзор того, что они из себя представляют, что они ищут, например, какие маршруты пытаются создать алгоритмы.
Из NPR
Компьютерная анимация использует всевозможные формулы и алгоритмы в зависимости от программного обеспечения и места, где вы его используете.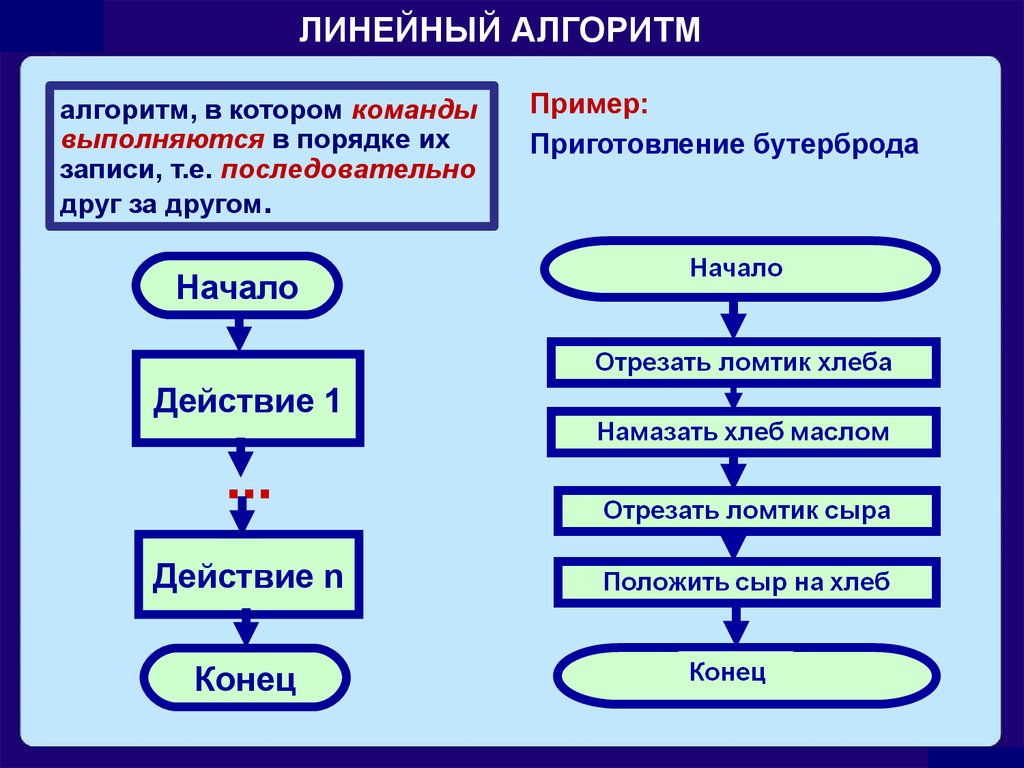
От Гизмодо
Я начал проверять алгоритмы музыкального генома оракула и потоковые сайты на наличие связанных действий.
Из проводного
Это не книга, загруженная диаграммами, электронными таблицами и алгоритмами, а скорее простая анекдотическая статья, в которой каждый найдет что-то для себя.
От Huffington Post
Что еще хуже, все это зависит от алгоритмов машинного обучения, которые являются грубыми и невероятно сложными для улучшения.
Из Атлантики
Алгоритм определенно не был идеальным, и он мог работать только с ограниченным набором слов, которые читали пациенты.
От Гизмодо
И алгоритмы продолжают двигаться, учиться и развиваться, чтобы реагировать на каждое молекулярное движение с субмолекулярной скоростью.
От Huffington Post
Понятно, что алгоритм сопоставления и e-harmony дал мне много ложных срабатываний, но для этого требуется только одно истинное срабатывание, так что неважно.
Из Fast Company
О да, конечно, мы всегда совершенствуем наши коды, оптимизируем наши алгоритмы.
Из Fast Company
Эти моменты появились в доказательствах-дополнениях, а может алгоритмах.
Из журнала Slate
Тем не менее, компания разрабатывает алгоритмы, которые отделяют вредоносные флаги от соответствующих данных.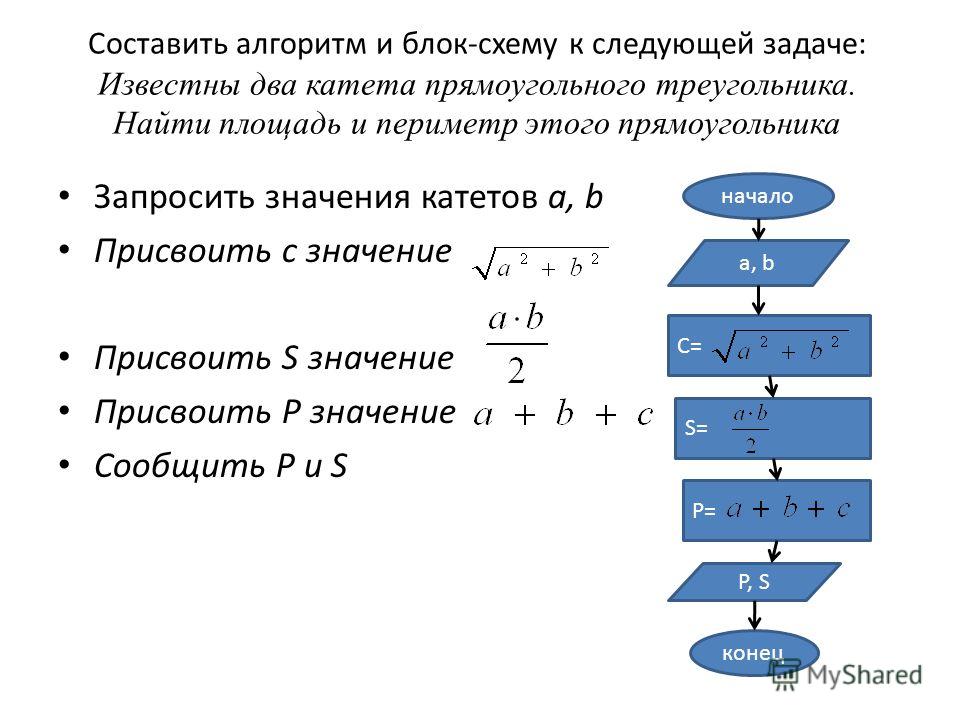



 Язык формализованный), называемого программой. Понятие программы формулируется в чисто структурных терминах синтаксиса этого языка, без какого-либо обращения к смысловым категориям. Точно такой же характер носит и описание процедуры выполнения программы. Поэтому в роли исполнителя алгоритмов, записанных на формализованных [алгоритмических] языках, может выступать не только человек, но и наделённое соответствующими [вычислительными] возможностями автоматическое устройство,
Язык формализованный), называемого программой. Понятие программы формулируется в чисто структурных терминах синтаксиса этого языка, без какого-либо обращения к смысловым категориям. Точно такой же характер носит и описание процедуры выполнения программы. Поэтому в роли исполнителя алгоритмов, записанных на формализованных [алгоритмических] языках, может выступать не только человек, но и наделённое соответствующими [вычислительными] возможностями автоматическое устройство, 
 Буква L означает приказ сдвинуться на следующем такте на одну клетку влево, R — вправо, S — остаться на месте. Элементарная инструкция означает следующее: если машина видит a, записать в клетку b, передвинуться в соответствии с командой и перейти к исполнению команды
Буква L означает приказ сдвинуться на следующем такте на одну клетку влево, R — вправо, S — остаться на месте. Элементарная инструкция означает следующее: если машина видит a, записать в клетку b, передвинуться в соответствии с командой и перейти к исполнению команды 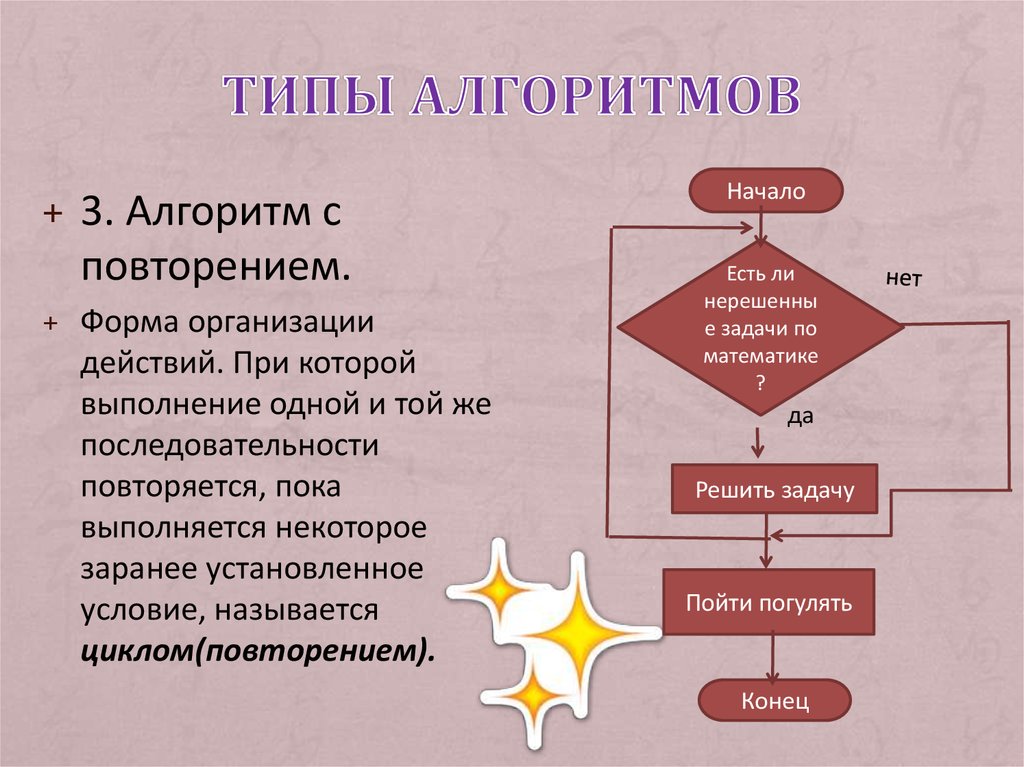 Состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты — это информация о том, какие секции пусты, а какие отмечены. Шаг — это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Элементарные действия (команды) машина Поста проще команд машины Тьюринга, поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Команды машины Поста предвосхитили систему команд современных вычислительных машин.
Состояние машины Поста описывается состоянием ленты и положением каретки. Состояние ленты — это информация о том, какие секции пусты, а какие отмечены. Шаг — это движение каретки на одну ячейку влево или вправо. Состояние ленты может изменяться в процессе выполнения программы. Элементарные действия (команды) машина Поста проще команд машины Тьюринга, поэтому программы для машины Поста имеют большее число команд, чем аналогичные программы для машины Тьюринга. Команды машины Поста предвосхитили систему команд современных вычислительных машин.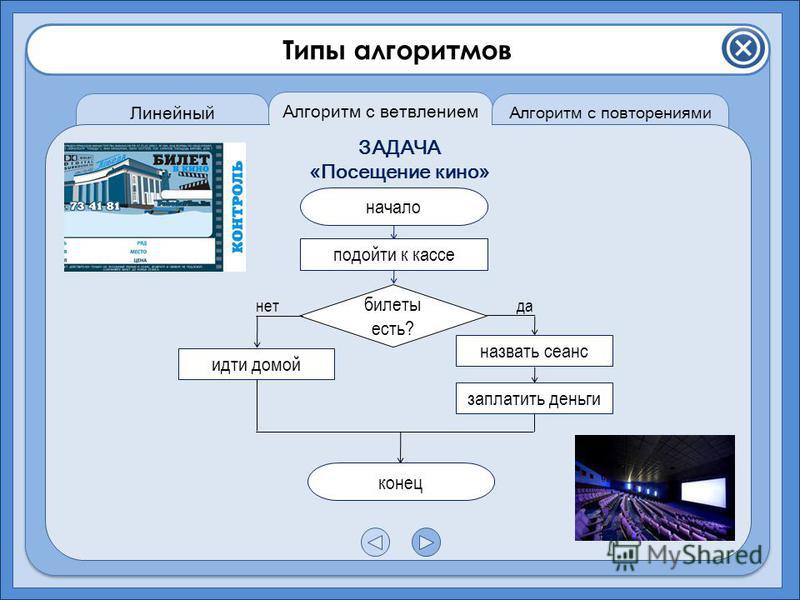

 Множество, принадлежность элемента которому можно установить за конечное число шагов применением некоторого алгоритма, называется перечислимым. Например, множество тавтологий классической логики высказываний (см. Логика высказываний) разрешимо, а множество тавтологий классической логики предикатов (см. Логика предикатов) перечислимо. Следует отметить, что в случае перечислимого множества алгоритмически установить можно лишь истинность, а не ложность. В классической математике имеет место следующий критерий разрешимости: множество разрешимо, если и оно, и его дополнение перечислимы. В конструктивной математике этот критерий эквивалентен принципу Маркова. Другая характеризация перечислимого множества — множество объектов, выводимых в некотором исчислении.
Множество, принадлежность элемента которому можно установить за конечное число шагов применением некоторого алгоритма, называется перечислимым. Например, множество тавтологий классической логики высказываний (см. Логика высказываний) разрешимо, а множество тавтологий классической логики предикатов (см. Логика предикатов) перечислимо. Следует отметить, что в случае перечислимого множества алгоритмически установить можно лишь истинность, а не ложность. В классической математике имеет место следующий критерий разрешимости: множество разрешимо, если и оно, и его дополнение перечислимы. В конструктивной математике этот критерий эквивалентен принципу Маркова. Другая характеризация перечислимого множества — множество объектов, выводимых в некотором исчислении. При любом точном определении алгоритмов каждый алгоритм может быть задан своим определением, которое является конструктивным объектом. Этот конструктивный объект может быть алгоритмически в содержательном смысле (и при этом достаточно просто и естественно) закодирован тем видом конструктивных объектов, которые обрабатываются данными алгоритмами.
При любом точном определении алгоритмов каждый алгоритм может быть задан своим определением, которое является конструктивным объектом. Этот конструктивный объект может быть алгоритмически в содержательном смысле (и при этом достаточно просто и естественно) закодирован тем видом конструктивных объектов, которые обрабатываются данными алгоритмами.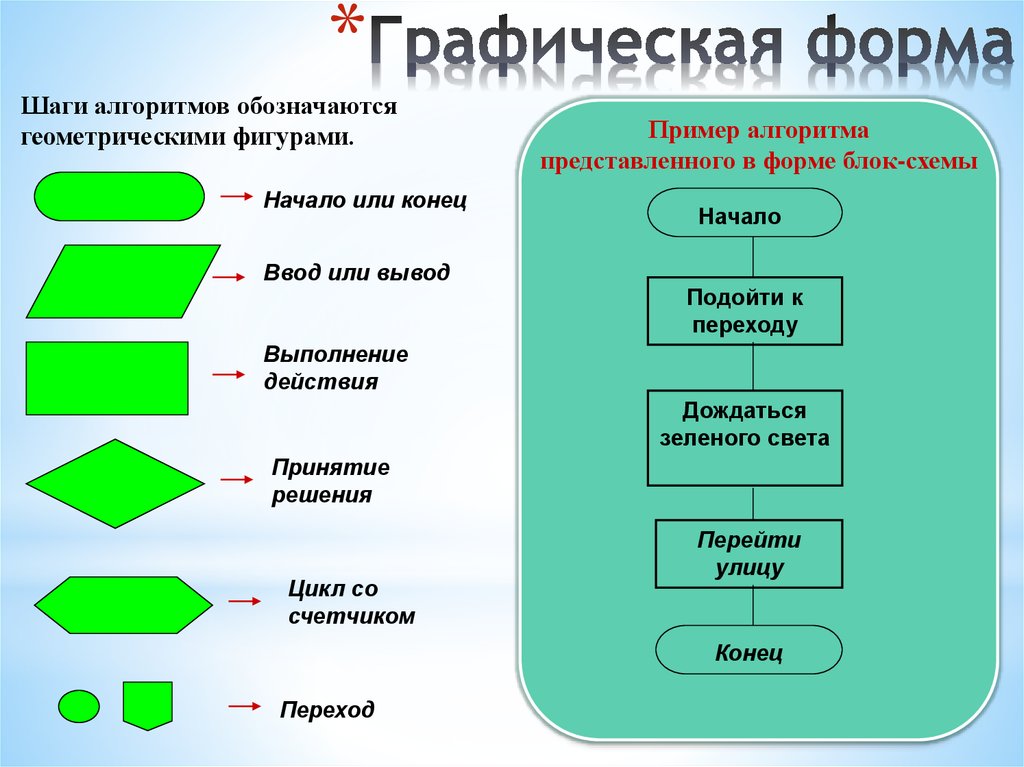 То, что такое отождествление является ограниченным, показывают проблемы современной теории и практики программирования. Одной из самых трудных возникающих в этом случае проблем является восстановление алгоритма по реализующей его конкретной программе. Если понятие алгоритма, перерабатывающего реальные конструктивные объекты, можно считать однозначно определённым, то его обобщение на объекты высших типов допускает многочисленные варианты, неэквивалентные друг другу.
То, что такое отождествление является ограниченным, показывают проблемы современной теории и практики программирования. Одной из самых трудных возникающих в этом случае проблем является восстановление алгоритма по реализующей его конкретной программе. Если понятие алгоритма, перерабатывающего реальные конструктивные объекты, можно считать однозначно определённым, то его обобщение на объекты высших типов допускает многочисленные варианты, неэквивалентные друг другу.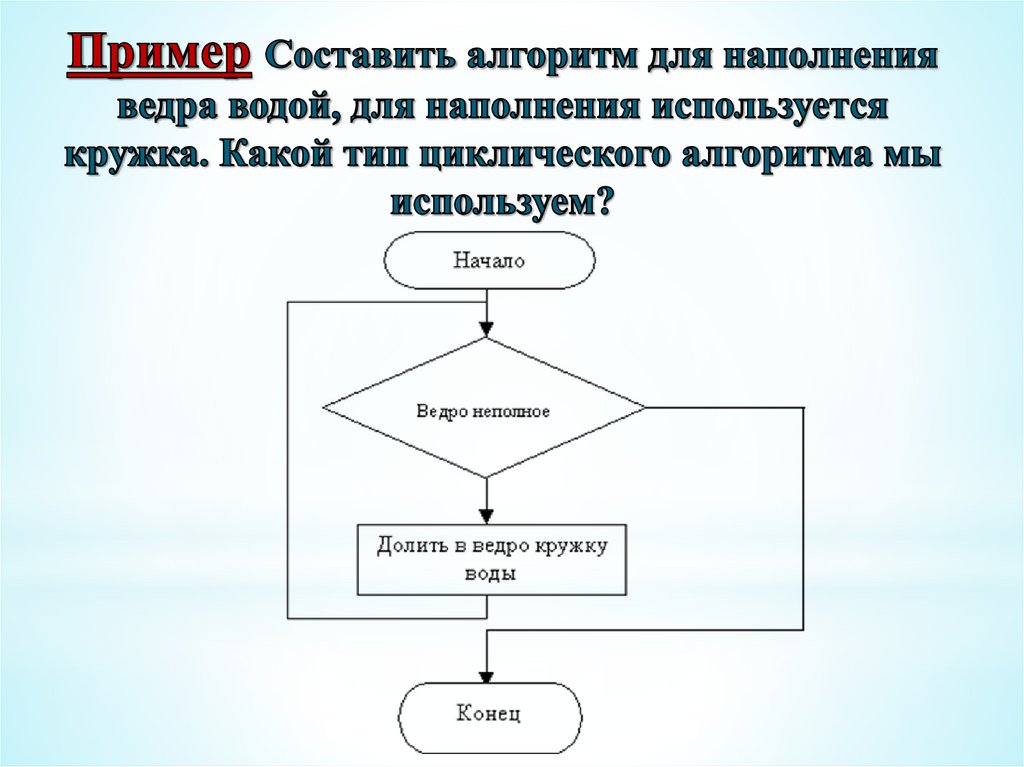 Основой данной теории явилось содержательное определение случайной последовательности по Р. Мизесу. Двоичная последовательность случайна, если из неё нельзя выбрать никакую последовательность с другой частотой нулей и единиц. Например, последовательность 0, 1, 0, 1… неслучайна, поскольку последовательность её чётных членов состоит из одних единиц. В классической математике такое определение пусто. А. Н. Колмогоров уточнил его, предложив рассматривать лишь алгоритмические перестановки подмножеств членов данной последовательности. Оказалось, что случайность связана со сложностью определения. Сложность фрагментов случайной последовательности пропорциональна длине их записи. Итак, содержательно случайные объекты являются приближениями к случайным последовательностям. Для любой совокупности программ, имеющих ограниченную сложность, можно построить ограниченный универсальный алгоритм, исполняющий все их без ошибок, но его сложность будет неизмеримо выше, чем сложность исполняемых программ.
Основой данной теории явилось содержательное определение случайной последовательности по Р. Мизесу. Двоичная последовательность случайна, если из неё нельзя выбрать никакую последовательность с другой частотой нулей и единиц. Например, последовательность 0, 1, 0, 1… неслучайна, поскольку последовательность её чётных членов состоит из одних единиц. В классической математике такое определение пусто. А. Н. Колмогоров уточнил его, предложив рассматривать лишь алгоритмические перестановки подмножеств членов данной последовательности. Оказалось, что случайность связана со сложностью определения. Сложность фрагментов случайной последовательности пропорциональна длине их записи. Итак, содержательно случайные объекты являются приближениями к случайным последовательностям. Для любой совокупности программ, имеющих ограниченную сложность, можно построить ограниченный универсальный алгоритм, исполняющий все их без ошибок, но его сложность будет неизмеримо выше, чем сложность исполняемых программ.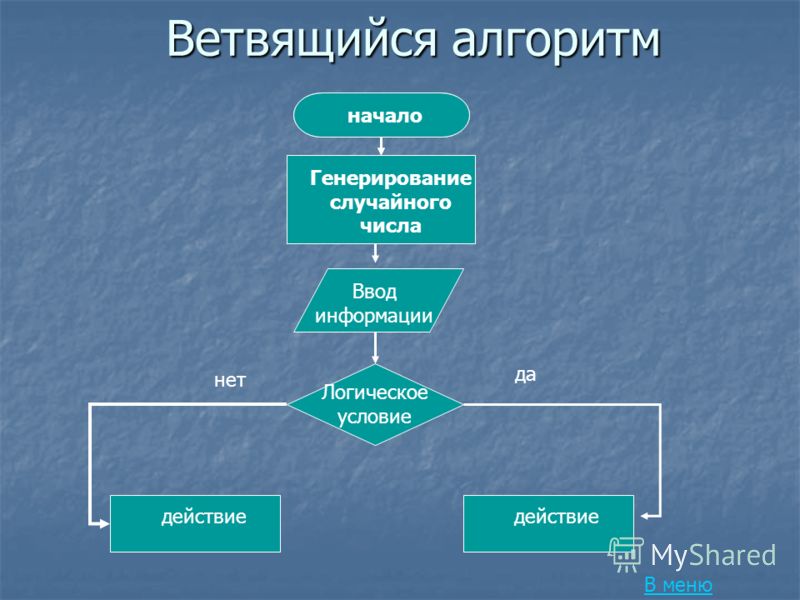 Далее, возможно построить алгоритмический процесс, расширяющий ограниченный универсальный алгоритм с тем, чтобы включить любую предъявленную программу, не входящую в данный класс, но при этом сложность универсального метода станет ещё выше. Уже один шаг данного процесса диагонализации далеко выводит за рамки класса функций, считающихся реально вычислимыми.
Далее, возможно построить алгоритмический процесс, расширяющий ограниченный универсальный алгоритм с тем, чтобы включить любую предъявленную программу, не входящую в данный класс, но при этом сложность универсального метода станет ещё выше. Уже один шаг данного процесса диагонализации далеко выводит за рамки класса функций, считающихся реально вычислимыми.



 Алгоритм может быть написан с использованием этих общих конструкций.
Алгоритм может быть написан с использованием этих общих конструкций. Алгоритм анализа выполнен правильно.
Алгоритм анализа выполнен правильно.
 Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.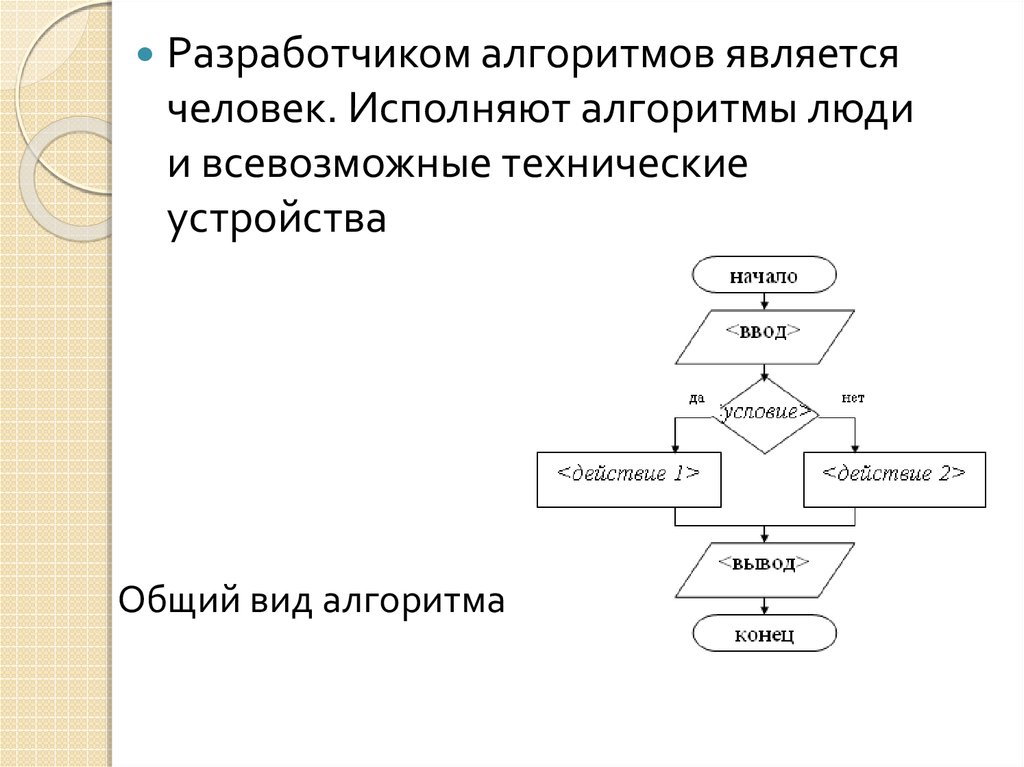

 Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.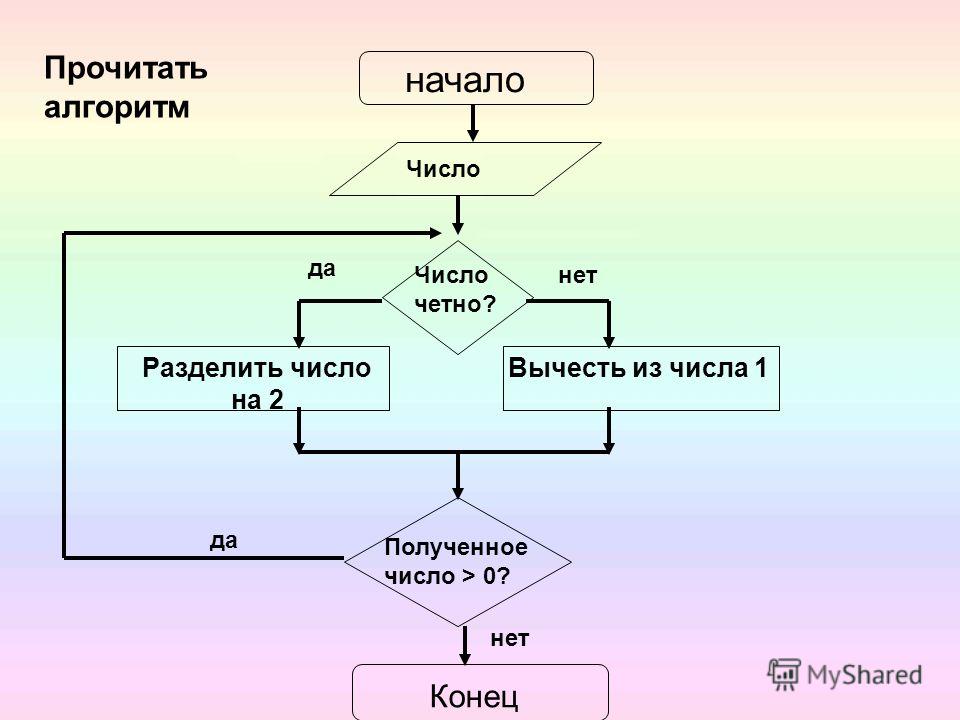 »
»