1.1. Логические выражения и логические операции
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель). Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Примеры высказываний:
Высказывания 1 и 3 являются истинными. Следующие предложения высказываниями не являются:
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают. С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примеры высказываний:
Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в пермом предложении — погоды, во втором — окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь». В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно — 0. Простые высказывания назвали логическими переменными, а сложные — логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С. Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита. Существуют разные варианты обозначения истинности и ложности логических переменных:
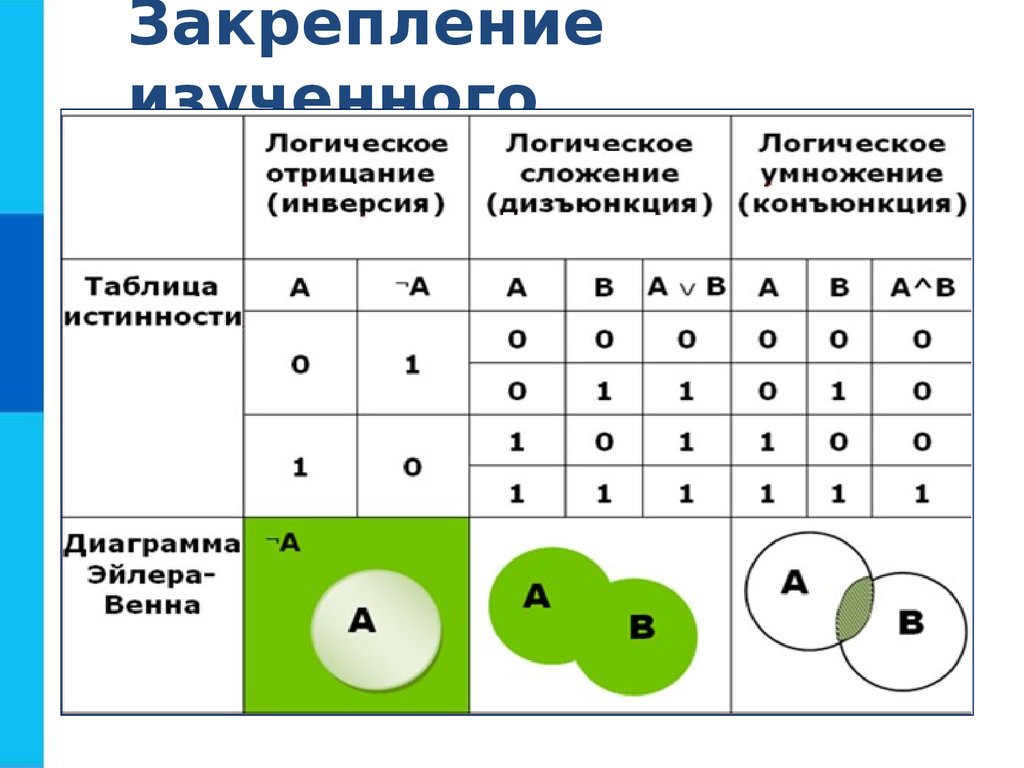
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением). Логическое выражение — это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение. Введем перечисленные логические операции. Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь):
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И»сложное высказывание также считается ложным. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Итак, если два высказывания соединены союзом «И», то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение, различие):
Дизъюнкция — это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Итак, если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний. Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание. Инверсия — отрицание (от латинского disjunctio — разобщение, различие):
Отрицание — логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.
Итак, если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация): Высказывание, составленное из двух высказываний при помощи связки «если .
A => B «Из А следует В» Итак, новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) — истинно, а следствие (заключение В) — ложно и истинно во всех остальных случаях. Пример. Дано сложное высказывание: «Если выглянет солнце, то станет тепло». Требуется записать его в виде логической формулы. Обозначим через А простое высказывание «выглянет солнце», а через В — «станет тепло». Тогда логической формулой этого сложного высказывания будет импликация: A -> B.
Эквивалентность (логическое тождество): Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называется эквивалентностью (эквивалентность — логическое тождество, равнозначность, взаимная обусловленность. )
A <=> B «А равносильно В» Итак, новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Примеры записи сложных высказываний с помощью обозначения логических связок:
|
16.Алгебра логики. Понятие высказывания. Логические константы, переменные, функции. Логические выражения.
Алгебра логики (высказываний) — раздел математической логики, изучающий высказывания и логические операции над ними.
Высказывание(суждение) – любое повествовательное предложение в отношении которого можно однозначно сказать, истинно оно или ложно.
Примеры высказываний:
1) Земля — планета Солнечной системы.
2) 2+8<5
3) 5×5=25
4) Всякий квадрат есть параллелограмм
5) Каждый параллелограмм есть квадрат
6) 2×2=5
Высказываниями не являются:
«он сероглаз»
«x2-4x+3=0»
Алгебра логики (высказываний) работает
с высказываниями.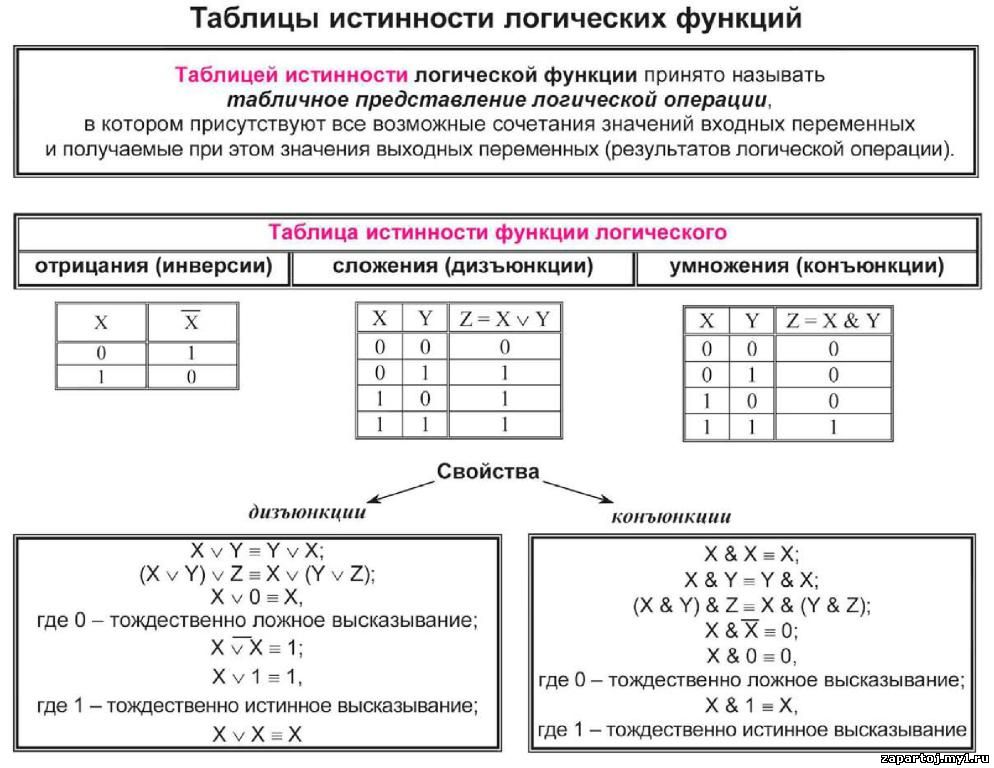
Различают:
Истина: Аристотель — основоположник логики.
Ложь: На яблонях растут бананы.
Логические переменные (предикаты)– логические высказывания, значения которых меняются в зависимости от входящих в них переменных, обозначаются заглавными латинскими буквами А, В, С,D,F,…
А = {Аристотель — основоположник логики} – истина.
В = {На яблонях растут бананы} – ложь.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.
Логические функции (логические формулы) – сложные логические выражения, образованные из простых и связанные логическими операциями
Высказывание «Все мышки и кошки с хвостами» является сложным и состоит из двух простых высказываний.
А=«Все мышки с хвостами» и В=«Все кошки с хвостами»
Его можно записать в виде логической
функции, значение которой истинно:
F(A,B)=AиB.
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно.
Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только ложь (0)илиистина (1).
В алгебре логики высказывания принято обозначать прописными латинскими буквами: A, B, X, Y.
Логические высказывания:
Логические выражения бывают простымиилисоставными (сложными).
Простое логическое выражение состоит из одного высказывания и не содержит логических операций. В нём возможно только два результата – либо «истина», либо «ложь».
17.Операции алгебры логики. Таблицы истинности логических операций. Вычисление логических выражений.
Сложное логическое высказывание строится из простых с помощью логических связок (таких как «И», «ИЛИ
Основные логические операции:
НЕ(логическое отрицание,инверсия)
ИЛИ(логическое сложение,дизъюнкция)
И(логическое умножение,конъюнкция)
Операция НЕ (отрицание, инверсия)
Отрицание (инверсия) – операция логического отрицания.
Добавляется частица НЕили словаНЕВЕРНО, ЧТО…
Обозначение: не, not, ¬ , ¯.
Если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то оно будет истинным.
А – Земля вращается вокруг Солнца – истинно
¬А – Земля не вращается вокруг Солнца – ложно
Операция И (логическое умножение, конъюнкция)
Конъюнкция (логическое умножение) – соединение двух логических выражений
(высказываний) с помощью союзаИ.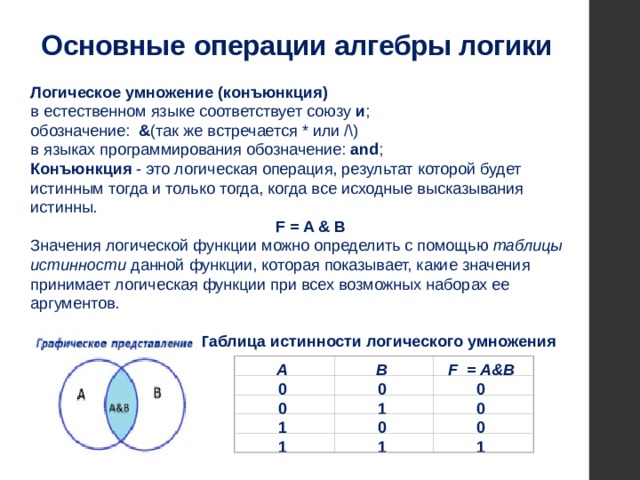
Обозначение: и, and, ×, & ,Ù
Логическая операция конъюнкция истинна только в том случае, если оба простых высказывания истинны, в противном случае она ложна.
А – У меня есть знания для сдачи зачета.
В – У меня есть желание для сдачи зачета.
У меня есть знания И желание для сдачи зачета.
AÙB
Операция ИЛИ (логическое сложение, дизъюнкция)
Дизъюнкция (логическое сложение) – соединение двух логических высказываний с помощью союза ИЛИ.
Обозначение: или, or, +,V
Логическая операция дизъюнкция ложна, если оба простых высказывания ложны. В остальных случаях она истинна.
A – Летом я поеду в лагерь
B
Летом я поеду в лагерь или поеду к бабушке
AVB
Другие логические операции:
Импликация («если …, то …»)
Импликация (логическое следование)– связывает два логических выражения,
из которых первое является условием,
а второе – следствием из этого условия.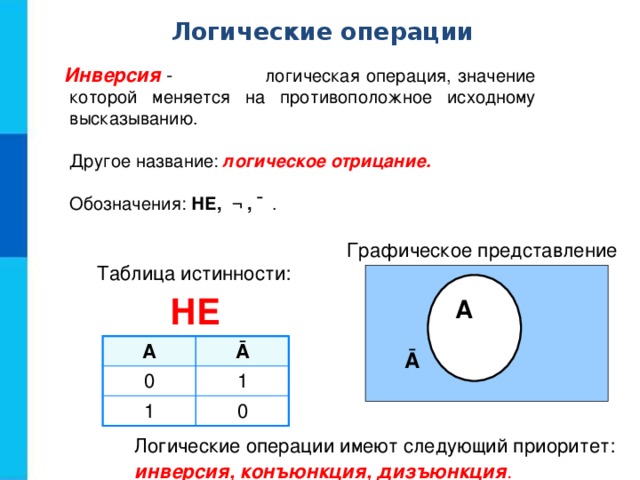 Операция обозначается словами: «Если…,
то…» (Если А, то В).
Операция обозначается словами: «Если…,
то…» (Если А, то В).
Результат операции импликацииложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
А – идёт дождь
В – на улице сыро
Если идёт дождь, то на улице сыро.
А → В
Эквивалентность («тогда и только тогда, …»)
Эквивалентность (логическое тождество, равнозначность) – определяет результат сравнения двух логических выражений. Операция обозначается словами: «…тогда и только тогда, когда…» (А т. и т. т. когда В)
Обозначение: «,Û,º, ~
Результат операции эквивалентностьистинен только тогда, когда А и В одновременно истинны или одновременно ложны.
А – день сменяет ночь
В – солнце скрывается за горизонтом
День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом.
А ~ В
Таблицы истинности:
Таблица истинности отрицания (Операция НЕ (отрицание, инверсия):
Таблица истинности конъюнкции (Операция И (логическое умножение, конъюнкция):
Таблица истинности дизъюнкции (Операция ИЛИ (логическое сложение, дизъюнкция):
Таблица истинности импликации(Импликация («если …, то …»):
Таблица истинности эквивалентности (Эквивалентность («тогда и только тогда, …»):
Логические операции над высказываниями / Алгебра логики [Г.
 И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] / 3dstroyproekt.ru
И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] / 3dstroyproekt.ruСуществует 5 логических операций:
Отрицание высказывания $X$
Обозначается $\bar { X } $, читается как «не $X$» или «неверно, что $X$». Логические значения высказывания $\bar { X } $ можно описать с помощью таблицы
| $x$ | $\bar { x } $ |
| 1 | 0 |
| 0 | 1 |
Таблицы такого вида принято называть таблицами истинности.
Конъюнкция высказываний $X$ и $Y$
Конъюнкцией двух высказываний $X$, $Y$ называется высказывание, которое считается истинным, если оба высказывания $X$, $Y$ истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний $X$, $Y$ обозначается символом $X$&$Y$ или $X$$\wedge$$Y$ , читается «$X$ и $Y$». Высказывания $X$ и $Y$ называются членами конъюнкции или конъюнктивными элементами.
Логические значения конъюнкции описываются следующей таблицей истинности:
| $x$ | $y$ | $x$&$y$ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Дизъюнкция высказываний $X$ и $Y$
Дизъюнкцией двух высказываний $X$ и $Y$ называется высказывание, которое считается истинным, если хотя бы одно из высказываний $X$ и $Y$ истинно, и ложным, если они оба ложны.
Дизъюнкция высказываний $X$ и $Y$ обозначается символом $X$$\vee$$Y$, читается «$X$ или $Y$», где «или» используется в неразделительной форме. Высказывания $X$ и $Y$ называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:
| $x$ | $y$ | $x\vee y$ |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Например, высказывание «В треугольнике $DFE$ угол $D$ или угол $E$ острый» истинно, так как обязательно истинно хотя бы одно из высказываний: «В треугольнике $DFE$ угол $D$ острый», «В треугольнике $DFE$ угол $E$ острый».
Импликация высказываний $X$ и $Y$
Импликацией двух высказываний $X$ и $Y$ называется высказывание, которое считается ложным, если $X$ истинно, а $Y$ — ложно, и истинным во всех остальных случаях.
Импликация высказываний $X$ и $Y$ обозначается символом $X \rightarrow Y$, читается «если $X$, то $Y$» или «из $X$ следует $Y$». Высказывание $X$ называют посылкой, высказывание $Y$ – заключением.
Высказывание $X$ называют посылкой, высказывание $Y$ – заключением.
Логические значения операции импликации описываются следующей таблицей истинности:
| $x$ | $y$ | $x\rightarrow y$ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Например, высказывание «Если число 12 делится на 6, то оно делится на З», очевидно, истинно, так как здесь истинна посылка «Число 12 делится на 6» и истинно заключение «Число 12 делится на 3».
Употребление слов «если …, то …» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание $X$ ложно, то высказывание «Если $X$, то $Y$» вообще не имеет смысла. Кроме того, строя предложение вида «если $X$, то $Y$» в обыденной речи, мы всегда подразумеваем, что предложение $Y$ вытекает из предложения $X$.
Употребление слов «если .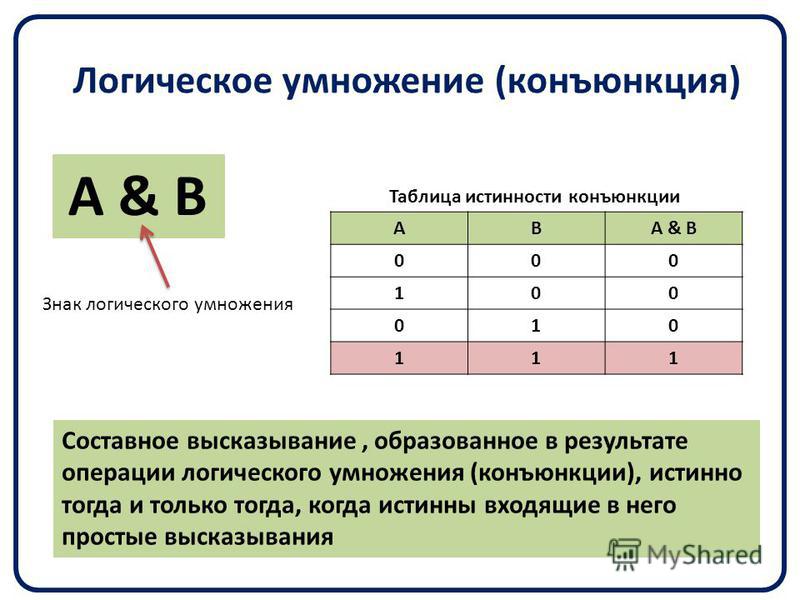 .., то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
.., то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
Эквиваленция высказываний $X$ и $Y$
Эквиваленцией { или эквивалентностью } двух высказываний $X$ и $Y$ называется высказывание, которое считается истинным, когда оба высказывания $X$, $Y$ либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквиваленция высказываний $X$, $Y$ обозначается символом $X$$\leftrightarrow $$Y$, читается «для того, чтобы $X$, необходимо и достаточно, чтобы $Y$» или «$X$ тогда и только тогда, когда $Y$». Высказывания $X$, $Y$ называются членами эквиваленции.
Логические значения операции эквиваленции описываются следующей таблицей истинности:
| $x$ | $y$ | $x\leftrightarrow y$ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Например, эквиваленция «Треугольник $SPQ$ с вершиной $S$ и основанием $PQ$ равнобедренный тогда и только тогда, когда $\angle P = \angle Q$» является истинной, так как высказывания «Треугольник $SPQ$ с вершиной $S$ и основанием $PQ$ равнобедренный» и «В треугольнике $SPQ$ с вершиной $S$ и основанием $PQ$ $\angle P = \angle Q$» либо одновременно истинны, либо одновременно ложны.
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Операция «Штрих Шеффера»
Однако существуют операции, с помощью которых может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция «Штрих Шеффера». Эта операция обозначается символом $X|Y$ и определяется следующей таблицей истинности:
| $x$ | $y$ | $x|y$ |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Штрих Шеффера — функция, принимающая значение ложь, если $X$ – истинно и $Y$ – истинно. Очевидно, имеют место равносильности:
Очевидно, имеют место равносильности:
1) $\overline { X } \equiv X|X$
2) $X\wedge Y \equiv (X|Y)|(X|Y)$
Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию «Штрих Шеффера».
Отметим, что $X|Y\equiv\overline { X\wedge Y } $.
Стрелка Пирса { функция Вебба }
Стрелка Пирса { функция Вебба } $X \downarrow Y$ – функция, принимающая значение истина, когда $X$ – ложно и $Y$ – ложно.
| $x$ | $y$ | $x\downarrow y$ |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Отметим, что $X\downarrow Y = \overline { X } \wedge \overline { Y } = \overline { X \vee Y } $
Cумма Жегалкина
Функция сложение по модулю 2 { функция разноименности, или сумма Жегалкина } $X\oplus Y$ — функция, принимающая значение истинно, когда $X$ и $Y$ принимают противоположные значения.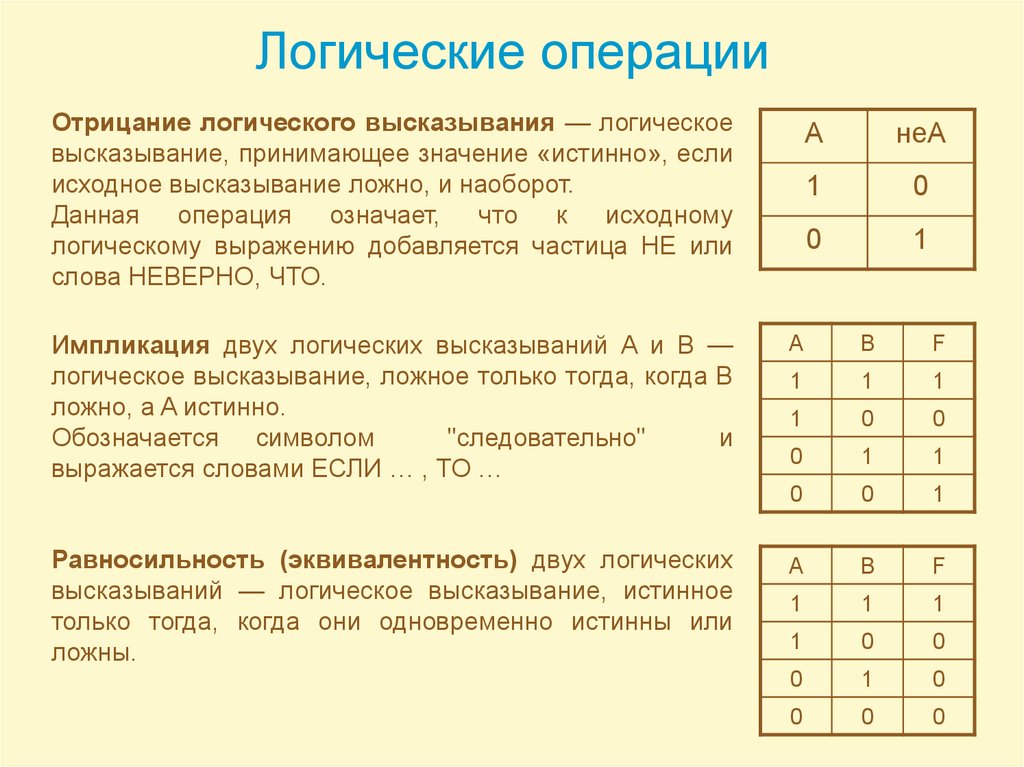
| $x$ | $y$ | $x\oplus y$ |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Отметим, что $X\oplus Y = (\overline { X } \wedge Y)\vee (X\wedge\overline { Y } )$
Итак, в математической логике для записи сложных высказываний используются следующие логические операции над простыми высказываниями:
$ \neg$− не;
$\And $, $\wedge $− и;
$\vee $− или;
$\rightarrow $− влечет;
$\sim $, $\leftrightarrow $− эквивалентно;
$\oplus $− либо, либо.
С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками. Например, из трех высказываний $X, Y, Z$ можно построить высказывания
$(X\wedge Y)\vee Z$ и $X\rightarrow (\overline { Y\vee (X\wedge Z) } )$
Первое из них есть дизъюнкция конъюнкции $X, Y$ и отрицания выказывания $Z$, а второе высказывание есть импликация, посылкой которой является высказывание $X$, а заключением — отрицание дизъюнкции высказывания $Y$ и конъюнкции высказываний $X, Z$.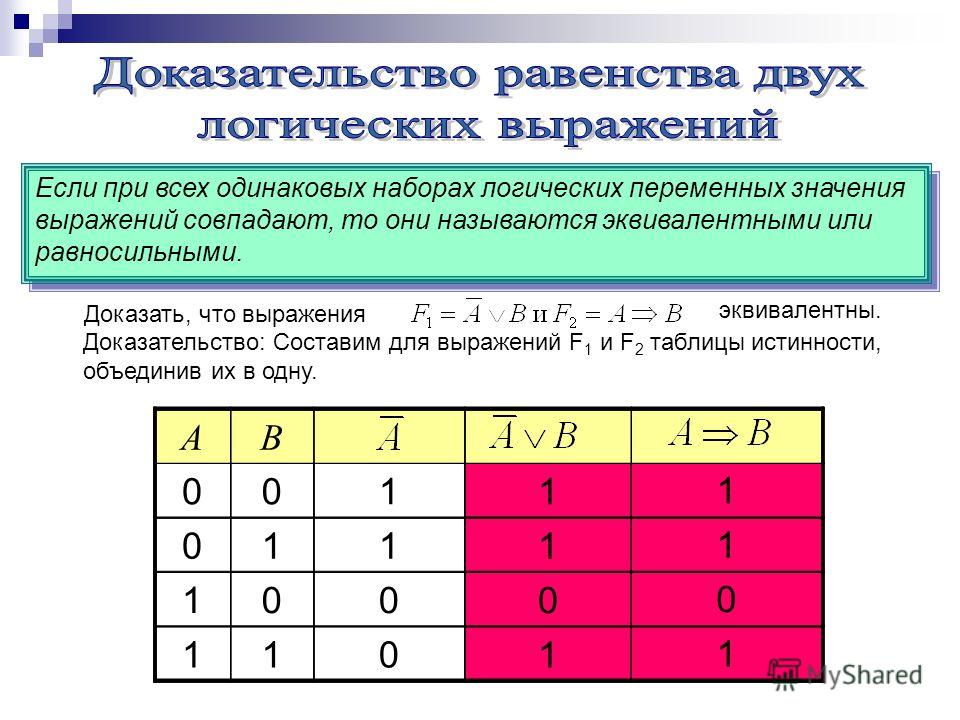
Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, называется формулой алгебры логики.
Высказывания обозначаются большими буквами латинского алфавита $A, B, C, …$
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются:
Для отрицания скобки опускаются;
$\And $ имеет приоритет перед $\vee , \rightarrow, \equiv $;
$\vee $ имеет приоритет перед $\rightarrow, \equiv $;
В связи с этим формулы
$(X\wedge Y)\vee Z$ и $X\rightarrow (\overline { Y\vee (X\wedge Z) } )$
могут быть записаны так:
$X\wedge Y\vee Z$ и $X\rightarrow \overline { Y\vee X\wedge Z } $
Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в нее элементарных высказываний.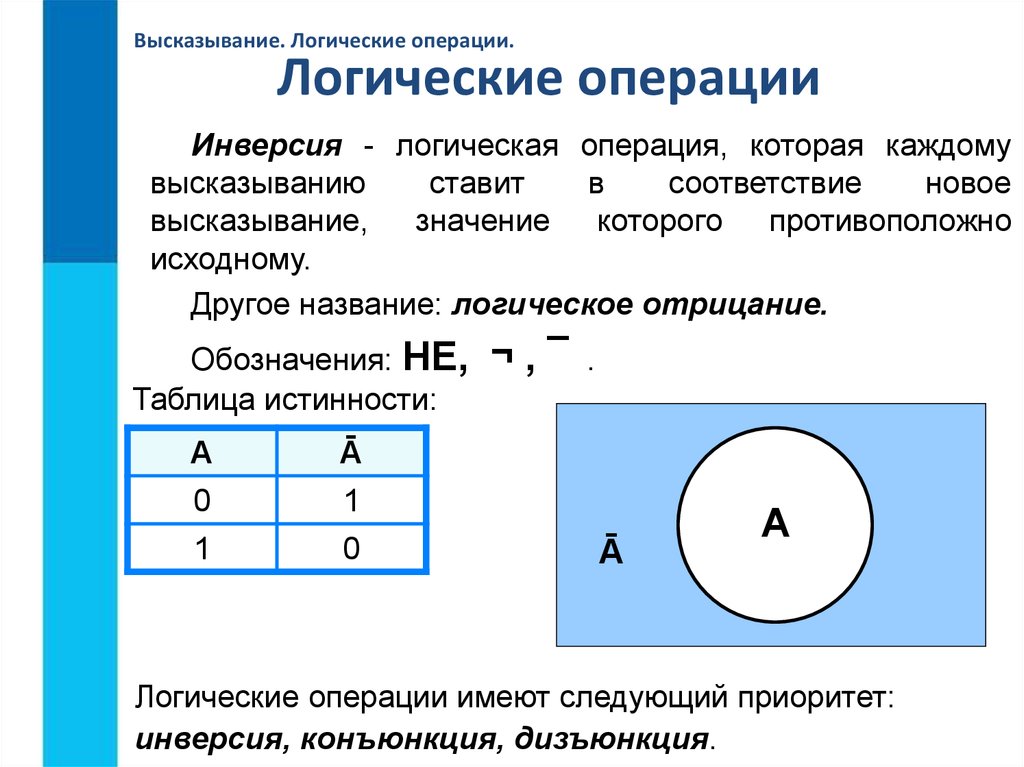 { n } $ строк.
{ n } $ строк.
Далее:
Примеры применения цилиндрических и сферических координат
Упрощение логических функций
Соленоидальное векторное поле
Поверхностный интеграл первого рода и его свойства
Теорема об аналоге СДНФ в Pk
Поток векторного поля через поверхность
Замена переменных в тройном интеграле
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Определение тройного интеграла. Теорема существования тройного интеграла
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
Нормальные формы
Теорема Остроградского
Огравление $\Rightarrow $
04 сентября 2016, 12:58 проектирование км, кмд, кж Алгебра логики [Г. И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 17926 0
И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 17926 0
«Алгебра высказываний, логические выражения и таблицы истинности»
Цели урока:
- закрепление знаний учащихся по теме “Основы логики”,
- познакомить учащихся с основными понятиями алгебры высказываний.
Задачи урока:
- обучающие – дать учащимся представление о подходах к пониманию алгебры высказываний; познакомить с основными логическими операциями; научить строить по логическим выражениям таблицы истинности;
- развивающие – развитие познавательного
интереса учащихся; памяти; внимания; обучение
рациональным способам построения таблиц
истинности; развитие логического мышления;
выработка рефлексивных навыков оценки
собственной мыслительной деятельности через
экспериментальное получение результатов;
формирование навыков эвристического мышления.

- воспитательные – воспитание чувства ответственности, аккуратности, трудолюбия; сочетание индивидуальной и коллективной работы; ответственность за выполнение домашнего задания.
Тип урока: урок формирования знаний, умений с элементами практики, систематизация изученного материала.
Вид урока: сдвоенный, продолжительность 80 минут.
Возраст учащихся: 11 класс.
Оборудование:
- программы Microsoft Excel и NumLock Calculator 3.2
- раздаточный материал (теория по теме, практическая работа, карточки с самостоятельной работой)
- слайды с ответами к самостоятельной работе
Оформление доски: доска разделена на две части – в правой части кроссворд, слева – домашнее задание и приоритет логических операций (на плакате).
План урока:
- Организационный момент – 5 минут.

- Повторение и актуализация знаний по теме “Логика”.
- Лекция-беседа (тема ”Логика высказываний).
- Повторение и актуализация знаний по теме “Microsoft Excel”.
- Практическая работа по теме урока.
- Решение задачи с использованием программы NumLock Calculator 3.2.
- Лекция – беседа (тема “Логические выражения и таблицы истинности”).
- Решение задачи на построение таблиц истинности.
- Самостоятельная работа по теме урока.
- Домашнее задание.
- Подведение итогов урока.
- Список используемой литературы
Ход урока
1. Подготовка учащихся к уроку, сообщение темы и целей проведения урока.
2. Повторение пройденного материала по предыдущей теме проводится в виде кроссворда:
Кроссворд по теме “Логика”
По горизонтали:
- Форма мышления, посредством которой из одного
или нескольких суждений, называемых посылками,
по определённым правилам логического вывода
получается новое знание о предметах реального
мира.

- Высказывание, состоящее из простых высказываний.
- Наука об общих операциях, которые могут выполняться над различными математическими объектами.
- Форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов.
- Форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и соотношениях между ними.
- Мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других, ранее обоснованных выводов.
По вертикали :
Наука о способах и формах мышления.
3. Алгебра в широком смысле этого слова –
наука об общих операциях, аналогичных сложению и
умножению, которые могут выполняться над
различными математическими объектами (алгебра
переменных и функций, алгебра векторов, алгебра
множеств и так далее). Объектами алгебры логики
являются высказывания.
Объектами алгебры логики
являются высказывания.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт – истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель – основоположник логики};
B = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному – 0. Таким образом, А = 1, В = 0.
Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания
Логическая операция КОНЪЮНКЦИЯ (логическое умножение):
- в естественном языке соответствует союзу и;
- в алгебре высказываний обозначение &;
- в языках программирования обозначение And.

Конъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
| Таблица истинности | Диаграмма Эйлера-Венна | ||
| А | В | А&B | |
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 | |
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):
- в естественном языке соответствует союзу или;
- обозначение ;
- в языках программирования обозначение Or.

Дизъюнкция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
| Таблица истинности | Диаграмма Эйлера-Венна | ||
| А | В | АB | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | |
Логическая операция ИНВЕРСИЯ (отрицание):
- в естественном языке соответствует словам неверно, что… и частице не;
- обозначение ;
- в языках программирования обозначение Not.

Инверсия – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество , дополняющее его до универсального множества.
| Таблица истинности | Диаграмма Эйлера-Венна | ||
| А | не А | ||
| 0 | 1 | ||
| 1 | 0 | ||
4. Для закрепления теоретического материала
данной части урока проводится практическая
работа с использованием программы Microsoft Excel,
которая изучалась ранее. Именно поэтому
необходимо повторить знания по теме Microsoft Excel в
виде опроса по основным понятиям:
Для закрепления теоретического материала
данной части урока проводится практическая
работа с использованием программы Microsoft Excel,
которая изучалась ранее. Именно поэтому
необходимо повторить знания по теме Microsoft Excel в
виде опроса по основным понятиям:
а) для чего предназначены электронные таблицы;
б) из каких элементов состоит электронная таблица;
в) как можно определить адрес ячейки;
г) как ввести нужную информацию в любую ячейку;
д) как исправить или отредактировать данные в ячейке;
е) что значит выделить ячейку ли сделать её активной;
ж) как можно скопировать формулу в другие ячейки;
з) как осуществить ввод функции с помощью мастера функций.
5. Практическое задание по теме “Логические функции в Excel”
1. Откройте программу Microsoft Excel.
2. Выделите ячейки A1, B1, C1 (для этого нажав на
кнопку мыши внутри ячейки А1, протяните мышь до
ячейки С1).
3. Нажмите на панели инструментов кнопку “Объединить и поместить в центре”: (если этой кнопки не видно, нажмите )
4. Напишите в объединенной ячейке слово “Конъюнкция”.
5. В столбцах А и В введите значения логических аргументов (см. рис. ниже).
6. Аналогично объедините ячейки E1, F1, G1 и напишите слово “Дизъюнкция”. Введите также значения логических аргументов.
7. Аналогично сделайте для Инверсии (см. рис.).
8. Сделайте активной ячейку С2 и выполните команду Вставка – Функция. В разделе “Категория” выберите “Логические”, а в разделе “Функция” – “И”, нажмите ОК. Сдвиньте вниз серую панель (взявшись за нее в любом месте и потянув вниз), так, чтобы были видны заполненные ячейки.
9. Щелкните по ячейке А2 – в окне “Логическое1”
появится адрес А2, затем поставьте курсор в
окошко “Логическое2” и щелкните по ячейке В2 – в
окошке появится адрес В2, нажмите ОК.
10. В ячейке С2 появилось значение ЛОЖЬ, а в строке формул (наверху) мы видим формулу =И(А2;В2). Теперь эту формулу надо скопировать в нижние три ячейки. Для этого ухватите за маркер в правом нижнем углу ячейки (при этом курсор приобретет форму маленького черного крестика) и потяните вниз на три ячейки (там тоже появятся значения логической функции).Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J).
11. Теперь займемся оформлением таблиц. Выделите диапазон ячеек А1:С5 и нажмите кнопку “Границы”: . Аналогично сделайте границы для остальных таблиц.
12. Выделите строки со 2-й по 5-ю (протянув мышкой по номерам строк — с левой стороны) и нажмите кнопку “По центру”: .
13. Раскрасим таблицы. Выделите диапазон А2:С5 и
нажмите кнопку “Цвет заливки”: , выберите бледно-зеленый
цвет. Заголовок таблицы раскрасьте в изумрудный
цвет, а цвет текста в заголовке сделайте белым (с
помощью кнопки “Цвет шрифта”: ).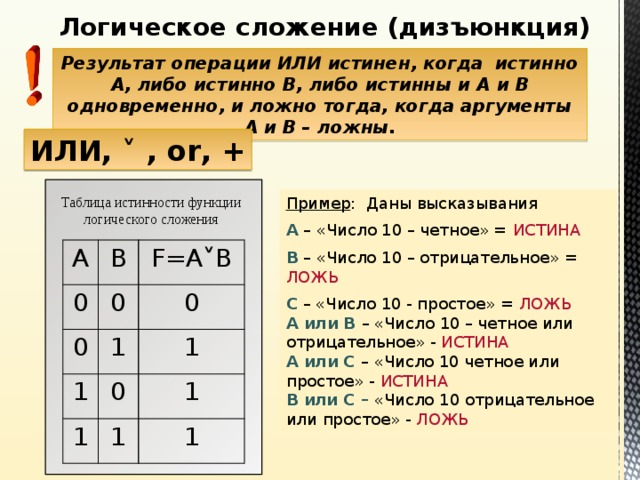 Увеличьте размер
шрифта в заголовке до 12 и сделайте его
полужирным.
Увеличьте размер
шрифта в заголовке до 12 и сделайте его
полужирным.
14. Аналогичные операции проделайте с остальными таблицами.
15. Выделите первую таблицу и, взявшись за рамку этой таблицы, перетащите ее вниз-вправо так, чтобы ее верхний левый угол был в ячейке В4. Вторую таблицу перетяните в ячейку F4, а третью – в J4.
16. Уменьшите ширину столбца А (для этого возьмитесь за границу между названиями столбцов А и В и потяните ее влево). Аналогично уменьшите ширину столбцов Е и I.
17. Объедините ячейки В2:К2 и напишите (заглавными буквами) общий заголовок “ЛОГИЧЕСКИЕ ОПЕРАЦИИ”. Сделайте его красного цвета, размером 12, полужирным.
18. У вас должно получиться следующее:
6. Решение задачи с использованием программы NumLock Calculator 3.2.
Примеры представлены в приложении (Приложение)
9. Самостоятельная работа по всей теме урока
проводится на компьютере и состоит из двух
заданий. Всего – три варианта карточек. (Приложение 1).
Всего – три варианта карточек. (Приложение 1).
10. Домашнее задание.
11. Подведение итогов урока.
Оценка знаний учащихся по новой теме с учётом знаний по предыдущим темам (повторение), а также краткое сообщение о теме следующего урока.
12. Список используемой литературы:
- Информатика и информационные технологии.10-11:Учебник для 10-11 классов. Угринович Н.Д. – М.: БИНОМ. Лаборатория знаний, 2007;
- Практикум по информатике и информационным технологиям: Учебное пособие. Угринович Н.Д. и др. – М.: БИНОМ. Лаборатория знаний, 2007;
Теоретический материал на тему: « Алгебра логики»
Теоретический материал на тему:
« Алгебра логики»
Алгебра логики (булева алгебра). В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики.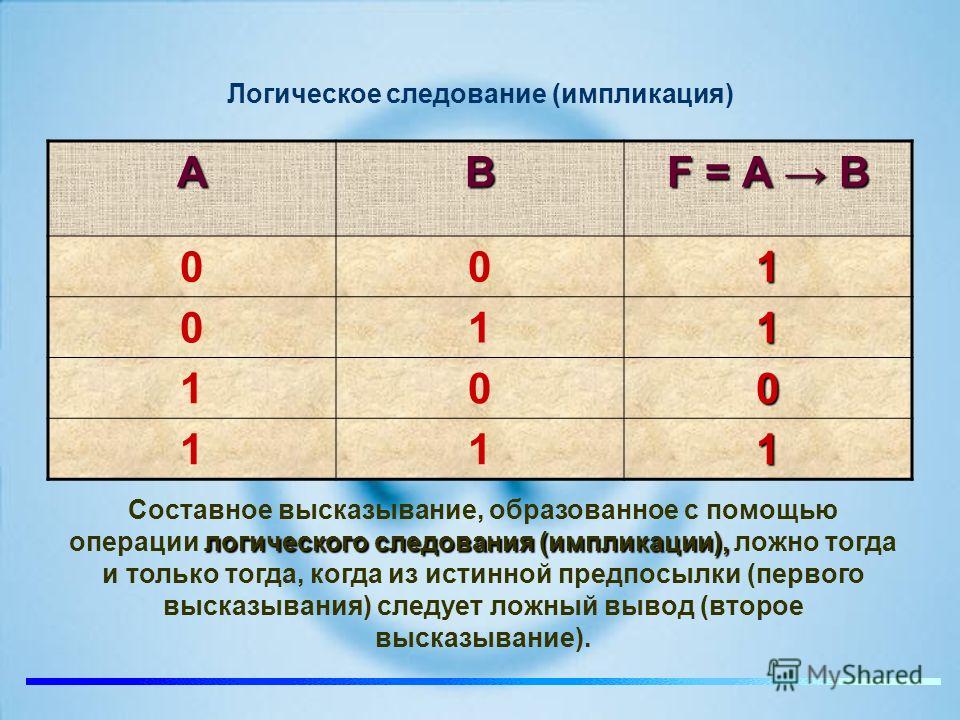 Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.
Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.
Что же собой представляет алгебра логики? Алгебра логики – раздел математики, изучающий высказывания с точки зрения их логических значений сложных логических высказываний с помощью алгебраических методов и логических операций над ними. Булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.
Формы мышления
Первые учения о формах и способах рассуждений возникли в странах древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями.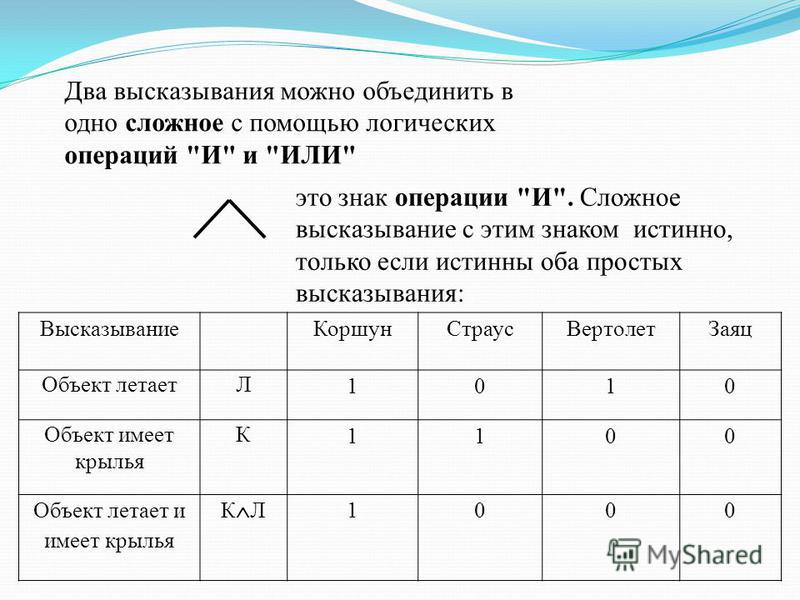 Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания.
Что же собой представляет алгебра логики? Алгебра логики – раздел математики, изучающий высказывания с точки зрения их логических значений сложных логических высказываний с помощью алгебраических методов и логических операций над ними. Булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.
Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются:
Понятие — это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта.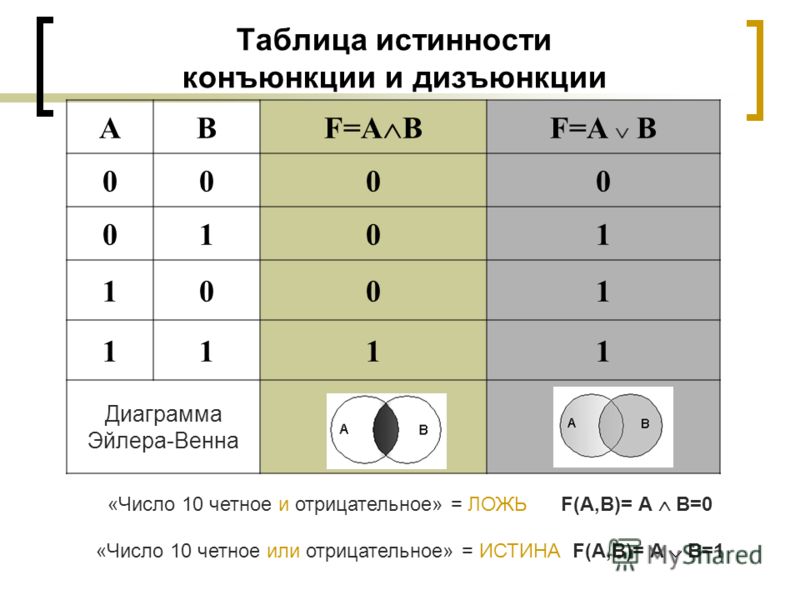 Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов.
Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов.
Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это устройство для автоматической обработки информации, предназначенное для одного пользователя».
Объем понятия определяется совокупностью предметов, на которые оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Что такое простое логическое высказывание (суждение)? Это форма мышления, которое может быть истинно (верно) или ложно (два плюс два равно четырем – это истина, два плюс два равно пяти — это ложь). Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.
Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.
Умозаключение — это форма мышления с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (вывод).
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае, можно придти к ложному умозаключению.
Логические выражения. Логические операции
Логические выражения могут быть простыми и сложными. В основе логики работы компьютера, как правило, лежит преобразование сложных логических выражений. Рассмотрим основные логические операции.
Конъюнкция (умножение) & ()
A | B | A&B |
| Конъюнкцией называется логическая операция, ставящая в соответствие двум простым логическим выражениям новое – сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения. |
0 | 0 | 0 |
| |
0 | 1 | 0 |
| |
1 | 0 | 0 |
| |
1 | 1 | 1 |
|
Дизъюнкция (сложение) V
A | B | AVB |
| Дизъюнкцией называется логическая операция, ставящая в соответствие двум простым логическим выражениям новое – сложное логическое выражение, которое будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений. |
0 | 0 | 0 |
| |
0 | 1 | 1 |
| |
1 | 0 | 1 |
| |
1 | 1 | 1 |
|
Отрицание (инверсия) ¬ (Ā)
A | ¬A |
| Логическая операция отрицание определяется над одним логическим выражением следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным. |
0 | 1 |
| |
1 | 0 |
| |
|
| ||
|
|
Импликация (следование) ®
A | B | A®B |
| В разговорном языке операция импликация выражается словами если…, то… Результатом импликации является ложь если из истинного логического выражения следует ложное логическое выражение. |
0 | 0 | 1 |
| |
0 | 1 | 1 |
| |
1 | 0 | 0 |
| |
1 | 1 | 1 |
|
Эквивалентность (равнозначность) «
A | B | A«B |
| Результатом данной операции является истина, если значения логических переменных равны между собой. |
0 | 0 | 1 |
| |
0 | 1 | 0 |
| |
1 | 0 | 0 |
| |
1 | 1 | 1 |
|
Исключающая дизъюнкция (исключающее ИЛИ) (XOR)
A | B | A XOR B |
| Исключающей дизъюнкцией называется логическая операция, ставящая в соответствие двум простым логическим выражениям новое – сложное логическое выражение, которое будет ложным, если значения логических переменных A и B равны между собой, и истинным, если не равны. |
0 | 0 | 0 |
| |
0 | 1 | 1 |
| |
1 | 0 | 1 |
| |
1 | 1 | 0 |
| |
|
|
|
Сложным логическим выражением называется логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью рассмотренных логических операций.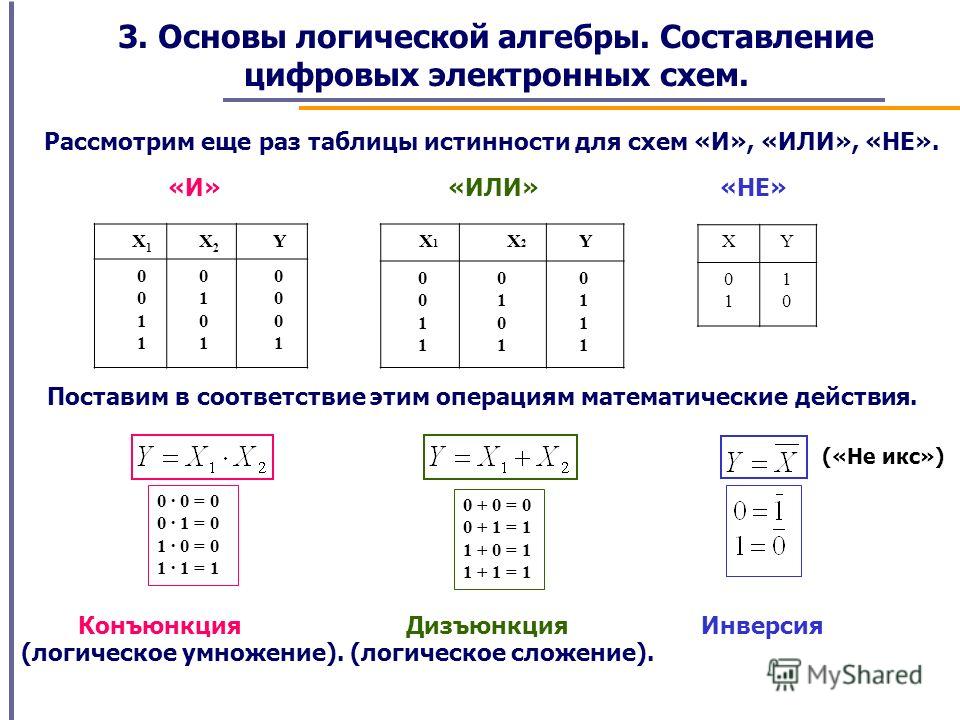
Порядок следования логических операций
отрицание (¬), конъюнкция (& () ), дизъюнкция (V), импликация (®), эквивалентность («)
Таблицы истинности
Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то:
Количество строк =
Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.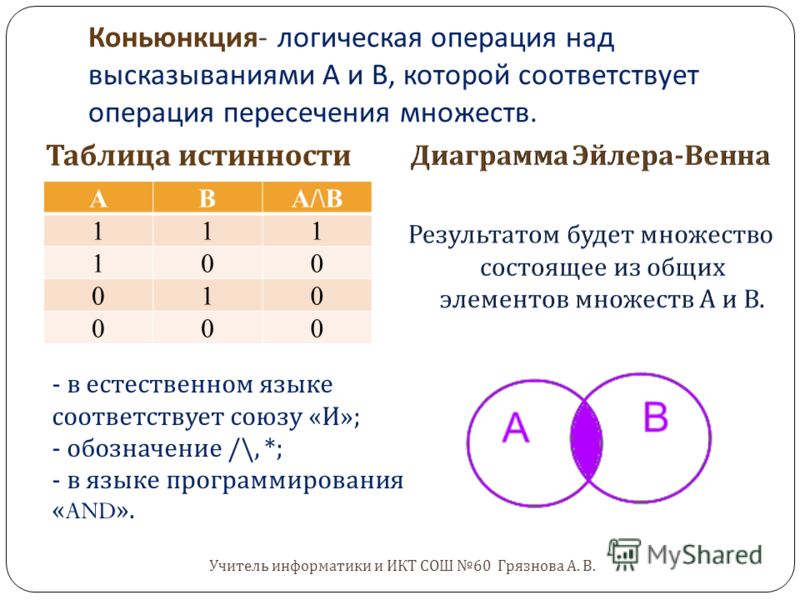
В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных. Наборы входных переменных, во избежание ошибок, рекомендуют вводить следующим образом:
1.разделить столбец значений первой переменной на 2 и заполнить верхнюю половину колонки нулями, а нижнюю – единицами;
2.разделить столбец значений второй переменной на 4 и заполнить четверти чередующимися группами нулей и единиц, начиная с группы нулей;
3.продолжить деление столбцов значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей и единиц до тех пор, пока группа нулей (единиц) не будет состоять из одного символа.
В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
Пример:
Логические выражения, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Итак, чтобы составить таблицу истинности для логической формулы, надо выполнить следующие шаги:
подсчитать количество переменных n в логическом выражении;
определить число строк в таблице, которое равно Q = 2n
подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учётом скобок и приоритетов;
заполнить столбцы входных переменных наборами значений;
провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Логические основы компьютера
В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.
Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.
Переключательные схемы
В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.
Вентили, триггеры и сумматоры
Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.
Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.
Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.
Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.
Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.
Законы алгебры логики
Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
Законы рефлексивности
a ∨ a = a
a ∧ a = aЗаконы коммутативности
a ∨ b = b ∨ a
a ∧ b = b ∧ aЗаконы ассоциативности
(a ∧ b) ∧ c = a ∧ (b ∧ c)
(a ∨ b) ∨ c = a ∨ (b ∨ c)Законы дистрибутивности
a ∧ (b ∨ c) = a ∧ b ∨ a ∧ c
a ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c)Закон отрицания отрицания
¬ (¬ a) = aЗаконы де Моргана
¬ (a ∧ b) = ¬ a ∨ ¬ b
¬ (a ∨ b) = ¬ a ∧ ¬ bЗаконы поглощения
a ∨ a ∧ b = a
a ∧ (a ∨ b) = a
Логические элементы.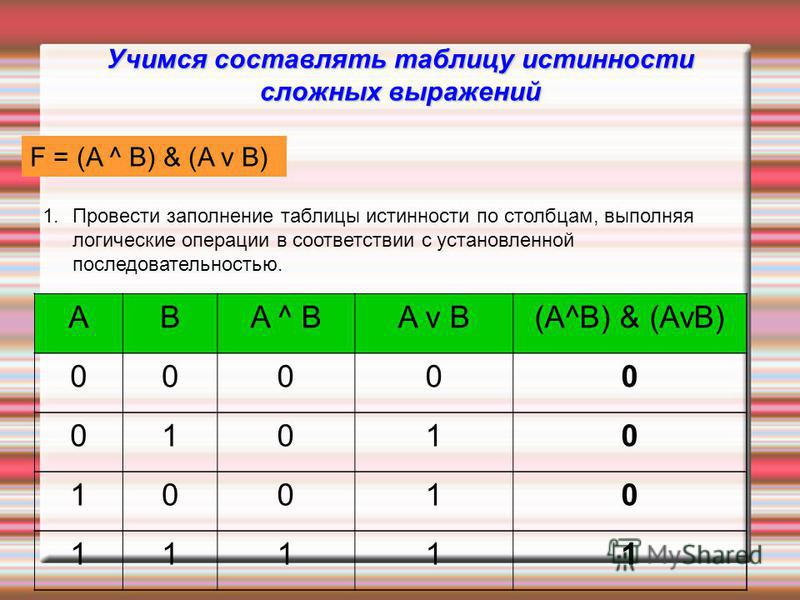 Вентили
Вентили
В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ.
Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ.
Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит (выдает высокое или низкое напряжение) от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.
В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.
Выходной сигнал вентиля можно выражать как функцию от входных.
Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.
Алгебра логики — основные законы, свойства и формулы раздела информатики » Kupuk.net
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.
Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.
Переместительный закон — предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.
Сочетательный закон — применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.
Распределительный закон — имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.
Закон двойственности и инверсии (закон Моргана) — основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.
Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Примеры:
Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Пример:
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов.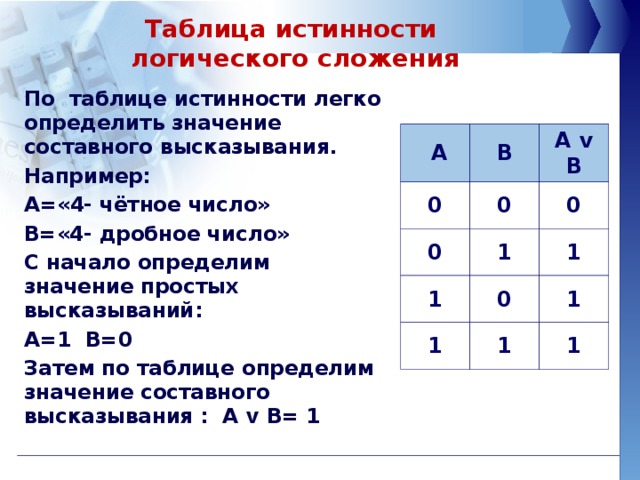 Рассмотрим их последовательно.
Рассмотрим их последовательно.
Логическое отрицание (инверсия) —НЕ
Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если…, то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if…then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
Операция эквивалентности (равнозначности) — А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
2.1: Операторы и логические операторы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7039
- Тед Сандстром
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
ПРОСМОТР \(\PageIndex{1}\): составные операторы
Математики часто разрабатывают способы создания новых математических объектов из существующих математических объектов.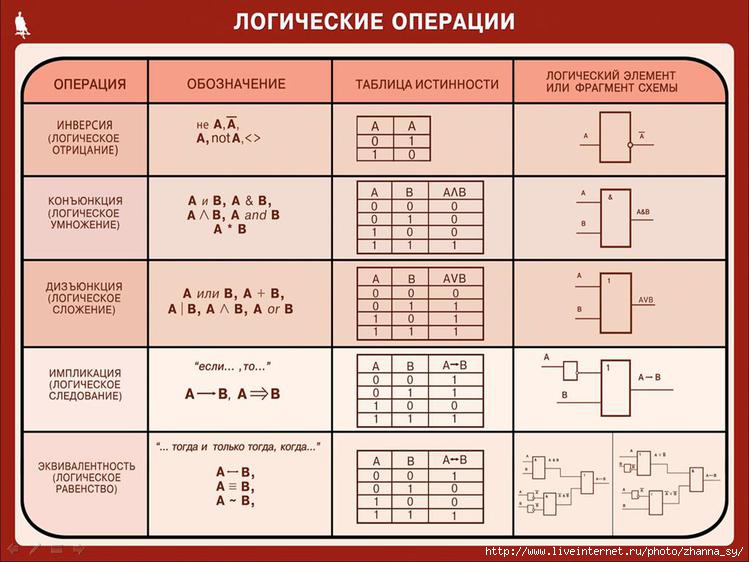 Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или отрицая утверждение. Логический оператор
Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или отрицая утверждение. Логический оператор
- Конъюнкцией утверждений \(P\) и \(Q\) является высказывание «\(P\) и \(Q\)» и обозначается через \(P \клин Q\). Утверждение \(P \клин Q\) истинно только тогда, когда оба \(P\)
- Дизъюнкция операторов \(P\) и \(Q\) является оператором «\(P\) или \(Q\)» и обозначается через \(P \vee Q\).
 Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно.
Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно. - Отрицание ( утверждения ) утверждения \(P\) является утверждением « не \(P\)» и обозначается \(\urcorner P\). Отрицание \(P\) истинно только тогда, когда \(P\) ложно, а \(\urcorner P\) ложно только тогда, когда \(P\) истинно.
Некоторые комментарии о дизъюнкции.
Важно понимать использование оператора «или». В математике мы используем « включительно или », если не указано иное. Это означает, что \(P \vee Q\) истинно, когда оба \(P\) и \(Q\) истинны, а также когда только одно из них истинно.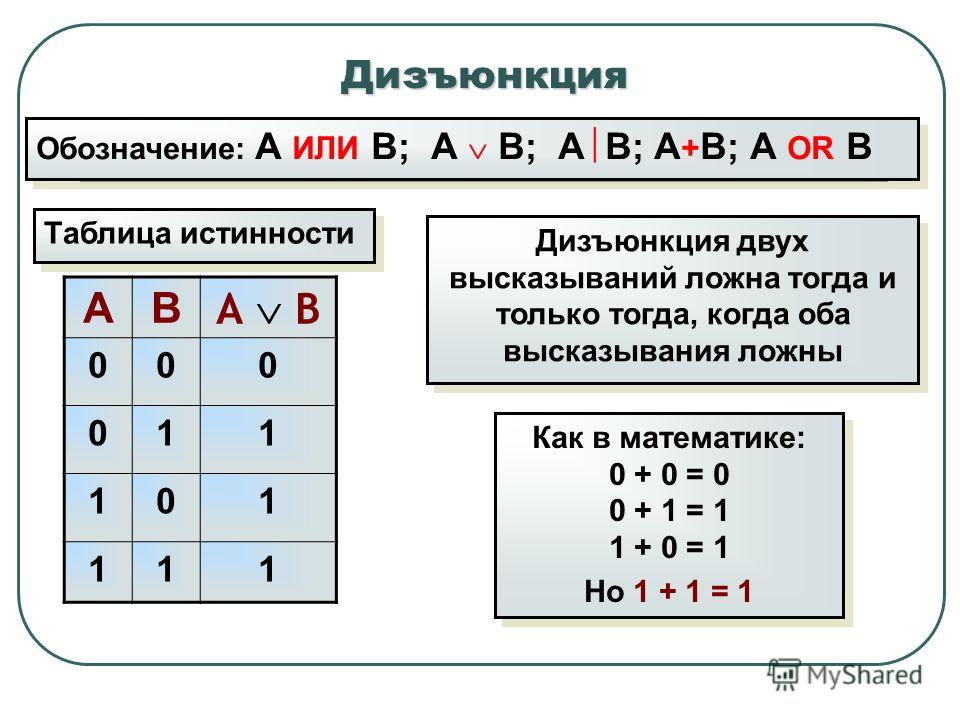 То есть \(P \vee Q\) истинно, когда хотя бы одно из \(P\) или \(Q\) истинно, или \(P \vee Q\) ложно только тогда, когда оба \(P\ ) и \(Q\) ложны.
То есть \(P \vee Q\) истинно, когда хотя бы одно из \(P\) или \(Q\) истинно, или \(P \vee Q\) ложно только тогда, когда оба \(P\ ) и \(Q\) ложны.
Другое использование слова «или» — « эксклюзивное или ». Для исключающего или результирующее утверждение ложно, когда оба утверждения истинны. То есть «\(P\) исключающее или \(Q\)» истинно только тогда, когда истинно одно из \(P\) или \(Q\). В повседневной жизни мы часто используем исключающее или. Когда кто-то говорит: «На перекрестке поверните налево или идите прямо», этот человек использует исключающее или.
Некоторые комментарии к отрицанию . Хотя утверждение \(\urcorner P\) можно прочитать как «Это не так, что \(P\)», часто есть лучшие способы сказать или написать это на английском языке. Например, мы обычно говорим (или пишем):
- Отрицание утверждения «391 — простое число» равносильно «391 — не простое число».
- Отрицание утверждения «\(12 < 9\)» равно «\(12 \ge 9\)».

- Для заявлений
\(P\): 15 нечетно \(Q\): 15 просто
запишите каждое из следующих утверждений в виде предложений на английском языке и определите, истинны они или ложны.
(а) \(P \клин Q\). (б) \(P \vee Q\). (c) \(P \клин \urcorner Q\). (d) \(\urcorner P \vee \urcorner Q\). - Для заявлений
P : 15 нечетно R: 15 < 17
запишите каждое из следующих утверждений в символической форме, используя операторы \(\wedge\), \(\vee\) и \(\urcorner\)
(a) 15 \(\ge\) 17. (b) 15 нечетно или 15 \(\ge\) 17.
(c) 15 четно или 15 <17. (г) 15 нечетно и 15 \(\ge\) 17.
ПРЕДВАРИТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ\(\PageIndex{2}\): истинностные значения утверждений
Мы будем использовать следующие два утверждения во всех этих предварительных действиях:
- \(P\) — это утверждение «Идет дождь».
- \(Q\) — это утверждение «Дейзи играет в гольф».
В каждой из следующих четырех частей истинностное значение будет присвоено утверждениям \(P\) и \(Q\).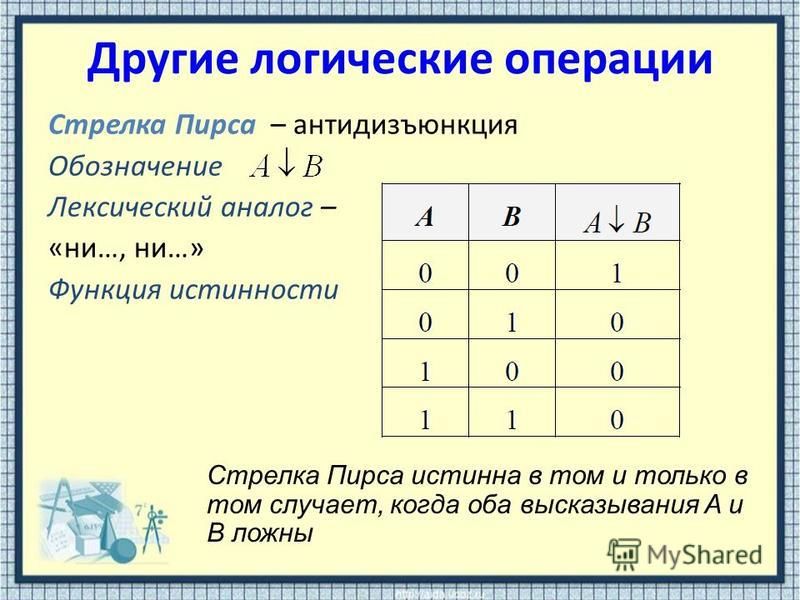 Например, в вопросе (1) мы будем предполагать, что каждое утверждение верно. В вопросе (2) мы будем предполагать, что \(P\) истинно, а \(Q\) ложно. В каждой части определите истинность каждого из следующих утверждений:
Например, в вопросе (1) мы будем предполагать, что каждое утверждение верно. В вопросе (2) мы будем предполагать, что \(P\) истинно, а \(Q\) ложно. В каждой части определите истинность каждого из следующих утверждений:
(a) (\(P \wedge Q\)) Идет дождь, а Дейзи играет в гольф.
(b) (\(P \vee Q\)) Идет дождь или Дейзи играет в гольф.
(c) (\(P \to Q\)) Если идет дождь, то Дейзи играет в гольф.
(d) (\(\urcorner P\)) Дождя нет.
Какие из четырех утверждений [(a)–(d)] верны, а какие нет в каждой из следующих четырех ситуаций?
1. Когда верно \(P\) (идет дождь) и верно \(Q\) (Дейзи играет в гольф).
2. Когда \(P\) истинно (идет дождь), а \(Q\) ложно (Дейзи не играет в гольф).
3. Когда \(P\) ложно (дождя нет) и \(Q\) истинно (Дейзи играет в гольф).
4. Когда \(P\) ложно (дождя нет) и \(Q\) ложно (Дейзи не играет в гольф).
В предварительных заданиях для этого раздела мы узнали о составных утверждениях и их значениях истинности.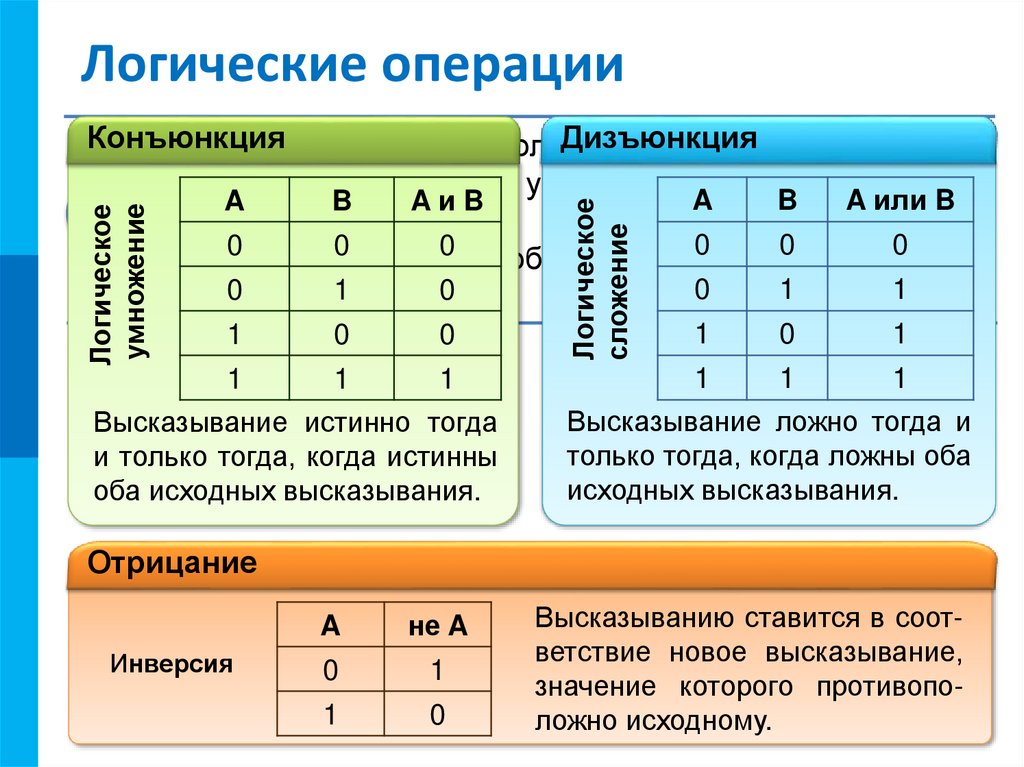 Эту информацию можно обобщить с помощью таблиц истинности, как показано ниже.
Эту информацию можно обобщить с помощью таблиц истинности, как показано ниже.
| \(П\) | \(\угол П\) |
|---|---|
| Т | Ф |
| Ф | Т |
| \(П\) | \(Q\) | \(P \клин Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| \(П\) | \(Q\) | \(P \vee Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
| \(П\) | \(Q\) | \(П\к Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Вместо того, чтобы запоминать таблицы истинности, многим людям проще запомнить правила, обобщенные в Таблице 2. 1.
1.
| Оператор | Символическая форма | Сводка значений истинности |
|---|---|---|
| Соединение | \(П \клин Q\) | Истина, только если оба \(P\) и \(Q\) верны |
| Разделение | \(P \vee Q\) | Ложь, только если и \(P\), и \(Q\) ложны |
| Отрицание | \(\угол П\) | Значение истинности, противоположное \(P\) |
| Условный | \(П\к Q\) | Ложь, только если \(P\) истинно, а \(Q\) ложно |
Другие формы условных операторов
Условные операторы чрезвычайно важны в математике, потому что почти все математические теоремы сформулированы (или могут быть сформулированы) в форме условного оператора в следующей форме:
Если «соблюдаются определенные условия», то «что-то происходит».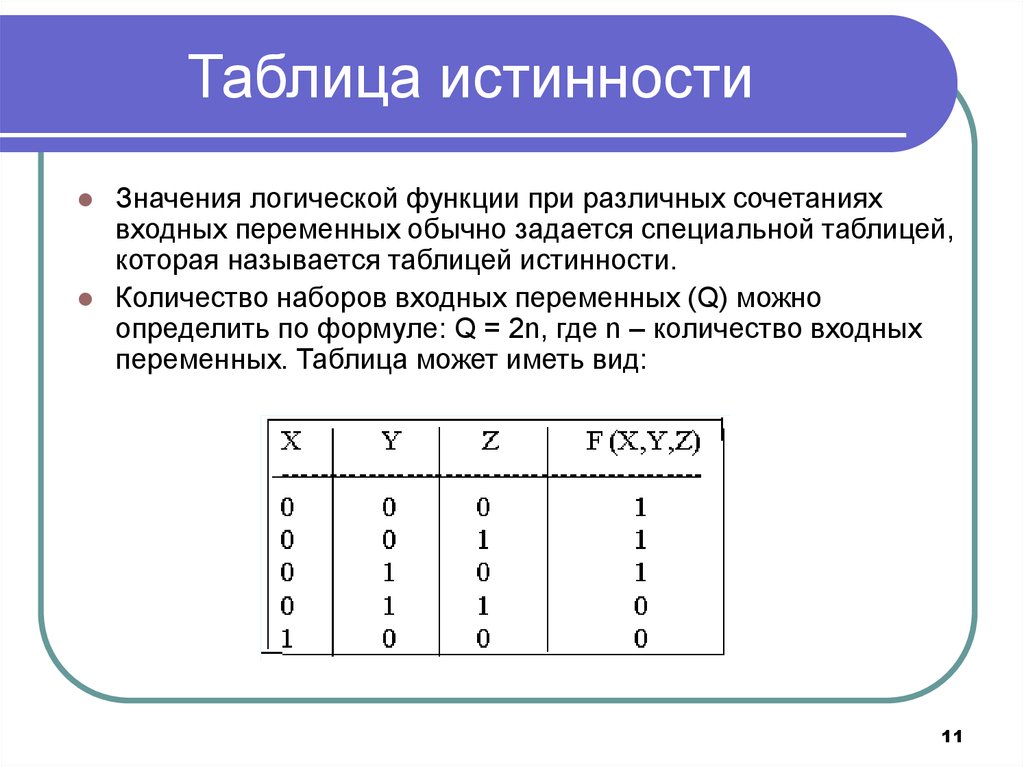
Крайне важно, чтобы все учащиеся, изучающие математику, полностью понимали значение условного утверждения и таблицу истинности условного утверждения.
Мы также должны знать, что в английском языке есть другие способы выражения условного оператора \(P \to Q\), кроме «If \(P\), then \(Q\)». Ниже приведены некоторые распространенные способы выражения условного оператора \(P \to Q\) в английском языке:
Проверка выполнения 2.1: утверждение «Только если»
Напомним, что четырехугольник — это четырехугольник. Пусть \(S\) представляет собой следующее истинное условное утверждение:
Если четырехугольник является квадратом, то он является прямоугольником.
Напишите это условное выражение на английском языке, используя
- слово «когда бы ни»
- фраза «только если»
- фраза «необходимо для»
- фраза «достаточно для»
- Ответить
Добавьте текст сюда.
 Не удаляйте этот текст первым.
Не удаляйте этот текст первым.
Построение таблиц истинности
Таблицы истинности для составных утверждений можно построить, используя таблицы истинности для основных связок. Чтобы проиллюстрировать это, мы построим таблицу истинности для. \((P \клин \urcorner Q) \к R\). Первым шагом является определение необходимого количества рядов.
- Для таблицы истинности с двумя разными простыми утверждениями необходимы четыре строки, поскольку существует четыре различных комбинации значений истинности для двух утверждений. Мы должны быть последовательны в том, как мы настраиваем ряды. В этом тексте мы будем делать это следующим образом: пометим строки для первого утверждения (T, T, F, F), а строки для второго утверждения — (T, F, T, F). Все таблицы истинности в тексте имеют эту схему.
- Для таблицы истинности с тремя различными простыми утверждениями требуется восемь строк, поскольку существует восемь различных комбинаций значений истинности для трех утверждений.
 Наша стандартная схема для этого типа таблицы истинности показана в таблице 2.2 .
Наша стандартная схема для этого типа таблицы истинности показана в таблице 2.2 .
Следующим шагом является определение используемых столбцов. Один из способов сделать это — работать в обратном направлении от формы данного утверждения. Для \((P \wedge \urcorner Q) \to R\) последним шагом является работа с условным оператором \((\to)\). Для этого нам нужно знать истинностные значения \((P \клин \urcorner Q)\) и \(R\). Чтобы определить истинностные значения для \((P \клин \urcorner Q)\), нам нужно применить правила для оператора конъюнкции \((\клин)\) и нам нужно знать истинностные значения для \(P\ ) и \(\urcorner Q\).
Таблица 2.2 представляет собой заполненную таблицу истинности для \((P \клин \urcorner Q) \to R\) с номерами шагов, указанными внизу каждого столбца. Номера шагов соответствуют порядку заполнения столбцов.
| \(П\) | \(Q\) | \(R\) | \(\угол Q\) | \((P \клин\угол Q)\) | \((П\клин \уругол Q)\к R\) |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Ф | Т |
| Т | Т | Ф | Ф | Ф | Т |
| Т | Ф | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Ф |
| Ф | Т | Т | Ф | Ф | Т |
| Ф | Т | Ф | Ф | Ф | Т |
| Ф | Ф | Т | Т | Ф | Т |
| Ф | Ф | Ф | Т | Ф | Т |
| 1 | 1 | 1 | 2 | 3 | 4 |
- Заполняя столбец для \(P \клин \urcorner Q\), помните, что конъюнкция истинна только тогда, когда оба \(P\) и \(\urcorner Q\) истинны.

- Заполняя столбец для \((P \клин \urcorner Q) \to R\), помните, что единственное время, когда условное утверждение ложно, это когда гипотеза \((P \клин \urcorner Q)\) верна и заключение \(R\) ложно.
Последний введенный столбец представляет собой таблицу истинности для утверждения \((P \wedge \urcorner Q) \to R\) с использованием настройки в первых трех столбцах.
Проверка выполнения 2.2: построение таблиц истинности
Построить таблицу истинности для каждого из следующих утверждений:
- \(P \клин \urcorner Q\)
- \(\угол(P\клин Q)\)
- \(\угол P \клин \urугол Q\)
- \(\угол P \vee \urугол Q\)
Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?
- Ответить
Добавьте текст сюда. Не удаляйте этот текст первым.
Биусловное утверждение
Некоторые математические результаты формулируются в форме «\(P\) тогда и только тогда, когда \(Q\)» или «\(P\) необходимо и достаточно для \(Q\)».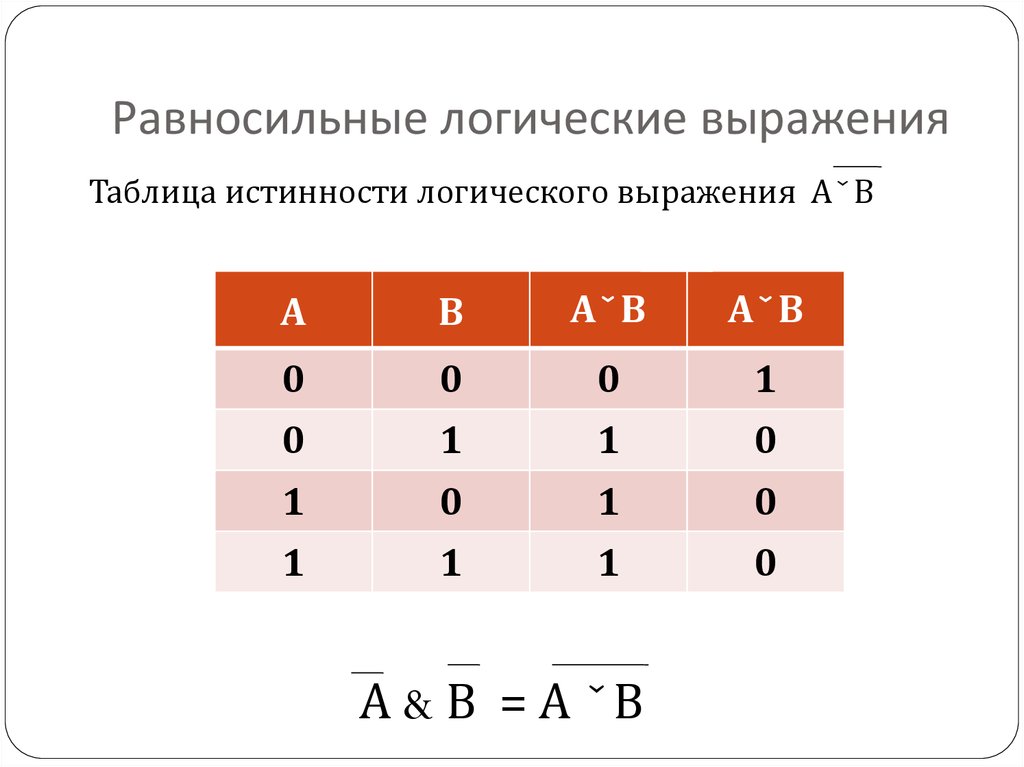 Примером может быть: «Треугольник равносторонний тогда и только тогда, когда три его внутренних угла конгруэнтны». Символическая форма биусловного утверждения «\(P\) тогда и только тогда, когда \(Q\)» — это \(P \leftrightarrow Q\). Чтобы определить таблицу истинности для биусловного утверждения, полезно внимательно посмотреть на форму фразы «\(P\) тогда и только тогда, когда \(Q\)». Слово «и» предполагает, что это высказывание является союзом. На самом деле это конъюнкция утверждений «\(P\), если \(Q\)» и «\(P\), только если \(Q\)». Символическая форма этого соединения: \([(Q \to P) \wedge (P \to Q]\).
Примером может быть: «Треугольник равносторонний тогда и только тогда, когда три его внутренних угла конгруэнтны». Символическая форма биусловного утверждения «\(P\) тогда и только тогда, когда \(Q\)» — это \(P \leftrightarrow Q\). Чтобы определить таблицу истинности для биусловного утверждения, полезно внимательно посмотреть на форму фразы «\(P\) тогда и только тогда, когда \(Q\)». Слово «и» предполагает, что это высказывание является союзом. На самом деле это конъюнкция утверждений «\(P\), если \(Q\)» и «\(P\), только если \(Q\)». Символическая форма этого соединения: \([(Q \to P) \wedge (P \to Q]\).
Проверка выполнения 2.3: Таблица истинности для биусловного оператора
Заполните таблицу истинности для \([(Q \to P) \wedge (P \to Q]\). Используйте следующие столбцы: \(P\) , \(Q\), \(Q \к P\), \(P \к Q\) и \([(Q \к P) \клин (P \к Q]\). Последний столбец эта таблица будет истинной для \(P \leftrightarrow Q\).
- Ответ
Добавьте текст сюда.
 Не удаляйте этот текст первым.
Не удаляйте этот текст первым.
Другие формы биусловного оператора
Как и в случае с условным оператором, существует несколько распространенных способов выражения биусловного оператора \(P \leftrightarrow Q\) в английском языке.
Пример
- \(P\) есть и только если \(Q\).
- \(P\) необходимо и достаточно для \(Q\).
- \(P\) подразумевает \(Q\), а \(Q\) подразумевает \(P\).
Тавтологии и противоречия
Определение: тавтология
Тавтология — это составное утверждение S, истинное для всех возможных комбинаций значений истинности составных утверждений, являющихся частью \(S\). А противоречие является составным утверждением, которое ложно для всех возможных комбинаций значений истинности составных утверждений, входящих в \(S\).
То есть тавтология обязательно истинна при любых обстоятельствах, а противоречие обязательно ложно при всех обстоятельствах.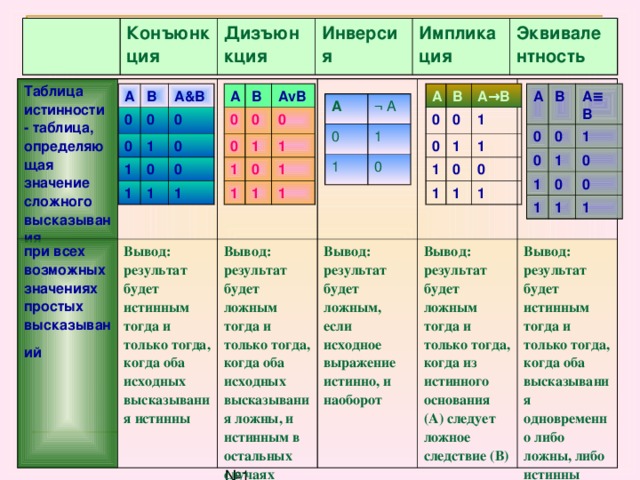
Проверка прогресса 2.4 (тавтологии и противоречия)
Для утверждений \(P\) и \(Q\):
- Используйте таблицу истинности, чтобы показать, что \((P \vee \urcorner P)\) является тавтология.
- Используйте таблицу истинности, чтобы показать, что \((P \клин \urcorner P)\) является противоречием.
- Используйте таблицу истинности, чтобы определить, является ли \(P \to (P \vee P)\) тавтологией, противоречием или ни тем, ни другим.
- Ответить
Добавьте текст сюда. Не удаляйте этот текст первым.
Упражнения к разделу 2.1
- Предположим, что Дейзи говорит: «Если не будет дождя, я буду играть в гольф». Позже в тот же день вы узнаете, что шел дождь, но Дейзи все еще играла в гольф. Было ли утверждение Дейзи правдой или ложью? Поддержите свой вывод.
- Предположим, что \(P\) и \(Q\) являются высказываниями, для которых истинно \(P \to Q\) и для которых \(\urcorner Q\) истинно.
 Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?(a) \(P\)
(b) \(P \клин Q\)
(c) \(P \vee Q\) - Предположим, что \(P\) и \(Q\) являются утверждениями, для которых \(P \to Q\) ложно. Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
(a) \(\угол P \to Q\)
(b) \(Q \to P\)
(c) \(P \ vee Q\) - Предположим, что \(P\) и \(Q\) являются высказываниями, для которых \(Q\) ложно, а \(\угол P\to Q\) истинен (и неизвестно, если \(R\) истинно или ложно). Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
(a) \(\угол Q \к P\)
(b) \(P\)
(c) \(P \клин R\)
(d) \(R \к \urcorner P\) - Постройте таблицу истинности для каждого из следующих утверждений:
(a) \(P \to Q\)
(b) \(Q \to P\)
(c) \(\urcorner P \to \urcorner Q\)
(d) \(\urcorner Q \ to \urcorner P\)Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?
- Постройте таблицу истинности для каждого из следующих утверждений:
(a) \(P \vee \urcorner Q\)
(b) \(\urcorner (P \vee Q)\)
(c) \(\urcorner P \vee \urcorner Q\)
(d) \(\urcorner P \wedge \urcorner Q\)Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?
- Построить таблицу истинности для \(P \клин (Q \клин R)\) и \((P \клин Q) \ви (P \клин R)\).
 Что вы наблюдаете.
Что вы наблюдаете. - Предположим, что каждое из следующих утверждений верно.
- Лаура учится в седьмом классе.
- ��Лора получила пятерку за тест по математике или Сара получила пятерку за тест по математике.
- ��Если Сара получила пятёрку за контрольную по математике, значит Лора не учится в седьмом классе.
Если возможно, определите истинность каждого из следующих утверждений. Внимательно объясните свои рассуждения. 92\) четно». Выразите условное утверждение \(P \to Q\) на английском языке, используя
(a) Форма условного оператора «if then»
(b) Слово «подразумевает»
(c) Форма «только если» условного оператора условное утверждение
(d) Фраза «необходимо для»
(e) Фраза «достаточно для» - Повторите упражнение (9) для условного оператора \(Q \to P\).
- Для утверждений \(P\) и \(Q\) используйте таблицы истинности, чтобы определить, является ли каждое из следующих утверждений тавтологией, противоречием или ни тем, ни другим.

(a) \(\urcorner Q \vee (P \to Q)\).
(b) \(Q \клин (P \клин \urcorner Q)\).
(c) \((Q \клин P) \клин (P \к \углу Q)\).
(г) \(\угол Q \к (Р \клин \угол Р)\). - Для утверждений \(P\), \(Q\) и \(R\):
(a) Покажите, что \([(P \to Q) \клин P] \to Q\) является тавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая modus ponens .
(b) Покажите, что \([(P \to Q) \wedge (Q \to R)] \to (P \to R)\) является атавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая силлогизмом .Исследования и деятельность
- Работа с условными операторами. Заполните следующую таблицу:
Английская форма Гипотеза Заключение Символическая форма Если \(P\), то \(Q\) \(П\) \(К\) \(П\к Q\) \(Q\) только если \(P\) \(К\) \(П\) \(К\к П\) \(P\) необходимо для \(Q\) \(P\) достаточно для \(Q\) \(Q\) необходимо для \(P\) \(P\) подразумевает \(Q\) \(P\) только если \(Q\) \(P\) если \(Q\) если \(Q\), то \(P\) если \(\urcorner Q\), то \(\urcorner P\) если \(Q\), то \(Q \клин R\) если \(P \vee Q\), то \(R\) - Работа с истинностными значениями утверждений.
 Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.
Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.Какие из следующих утверждений верны, какие ложны, и для каких утверждений невозможно определить, истинно оно или ложно? Обоснуйте свои выводы.
(a) \((P \vee Q) \vee (U \клин W)\) (f) \((\urcorner P \vee \urcorner U) \клин (Q \vee \urcorner V)\)
(b) \(P \клин (Q \to W)\) (g) \((P \клин \urcorner Q) \клин (U \vee W)\)
(c) \(P \клин ( W \к Q)\) (h) \((P \vee \urcorner Q) \to (U \клин W)\)
(d) \(W \to (P \клин U)\) (i) \((P \vee W) \to (U \клин W)\)
(e) \(W \to (P \клин \urcorner U)\) (j) \((U \клин \urcorner V) \to (P \клин W)\)
- Ответить
Добавьте текст сюда. Не удаляйте этот текст первым.
Эта страница под названием 2.1: Операторы и логические операторы распространяется в соответствии с лицензией CC BY-NC-SA 3.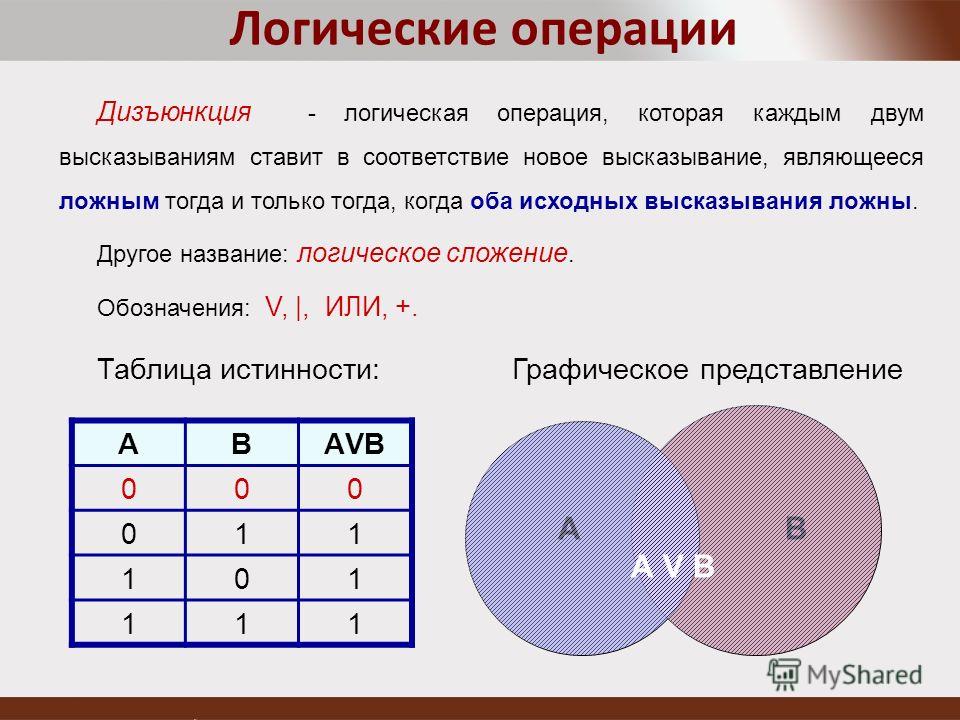 0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстрем
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- Биусловный оператор
- составные операторы
- источник@https://scholarworks.
 gvsu.edu/books/7
gvsu.edu/books/7 - Таблица правды
Логика и выражения
Использование и изучение логики включает поиск нового факта путем анализа того, могут ли некоторые другие факты вместе оказаться истинными. Некоторые факты или условия, рассматриваемые вместе, могут доказать, что другой факт является истинным, а может быть, и ложным.
Если на улице минусовая температура и у вас нет пальто, вам будет холодно. Если вы не больны, то будете чувствовать себя хорошо. Если вы умеете плавать или кататься на лодке по воде, вы останетесь на плаву. Это утверждения о фактах, которые являются результатом истинности некоторых условий.
Взяв некоторые факты и придав им логическую форму, мы можем произвести арифметические действия, которые помогут нам проанализировать их и сделать вывод. Используя только что упомянутые примеры, давайте превратим их в некоторые логические словесные уравнения:
-
Температура снаружи замерзаетИУ меня нет пальто=Мне холодно - НЕ
болен=чувствую себя хорошо -
Я умею плаватьИЛИЯ в лодке=Я плаваю
Вы видите И, НЕ и ИЛИ в примерах словесных уравнений? Это наши логические операторы . Каждый день мы принимаем решения, когда вместе обдумываем один или несколько фактов, используя эти операторы. Иногда необходимо, чтобы все факты были верными, чтобы вывод был верным. Это тот случай, когда используется оператор AND. При анализе фактов с помощью оператора ИЛИ только факт должен быть верным, чтобы вывод также был верным.
Каждый день мы принимаем решения, когда вместе обдумываем один или несколько фактов, используя эти операторы. Иногда необходимо, чтобы все факты были верными, чтобы вывод был верным. Это тот случай, когда используется оператор AND. При анализе фактов с помощью оператора ИЛИ только факт должен быть верным, чтобы вывод также был верным.
Для принятия решения может потребоваться больше, чем один или два факта. Когда это происходит, требуется другой оператор, чтобы объединить факты вместе, чтобы сделать вывод. В последнем словесном уравнении вы на самом деле не можете быть плавающим, если только эти два условия верны. Чтобы правильно доказать, что вы на самом деле плаваете, вам нужно указать, что вы тоже находитесь в воде.
- (
Я умею плаватьИЛИЯ в лодке) ИЯ в воде=Я плаваю
Чтобы доказать, что вы плаваете, два факта, что вы умеете плавать или что вы находитесь в лодке, должны быть объединены в один факт, объединенный с другим фактом, что вы также находитесь в воде. В противном случае, если вы умеете плавать, но все еще на суше, или в лодке, стоящей на берегу, вы не плаваете.
В противном случае, если вы умеете плавать, но все еще на суше, или в лодке, стоящей на берегу, вы не плаваете.
Булева алгебра
Чтобы привести условия или факты, как мы их назвали, к более компактной форме, была изобретена алгебра. Джордж Буль разработал тип арифметики (булева алгебра), в которой используются символы для условий, операторов и результата. Условия рассматриваются как переменные, которые имеют значение либо истина или ложь . такие операторы, как И, ИЛИ и НЕ, являются односимвольными символами. Если мы хотим преобразовать утверждение «Я счастлив, когда солнечно или когда я ем пончик» в логическое уравнение, мы могли бы начать с превращения условий в переменные.
- Переменная
A="Солнечно" - Переменная
B="Я съел пончик"
Результатом является переменная с именем Q это верно, когда вы счастливы, и это значение операции A с B .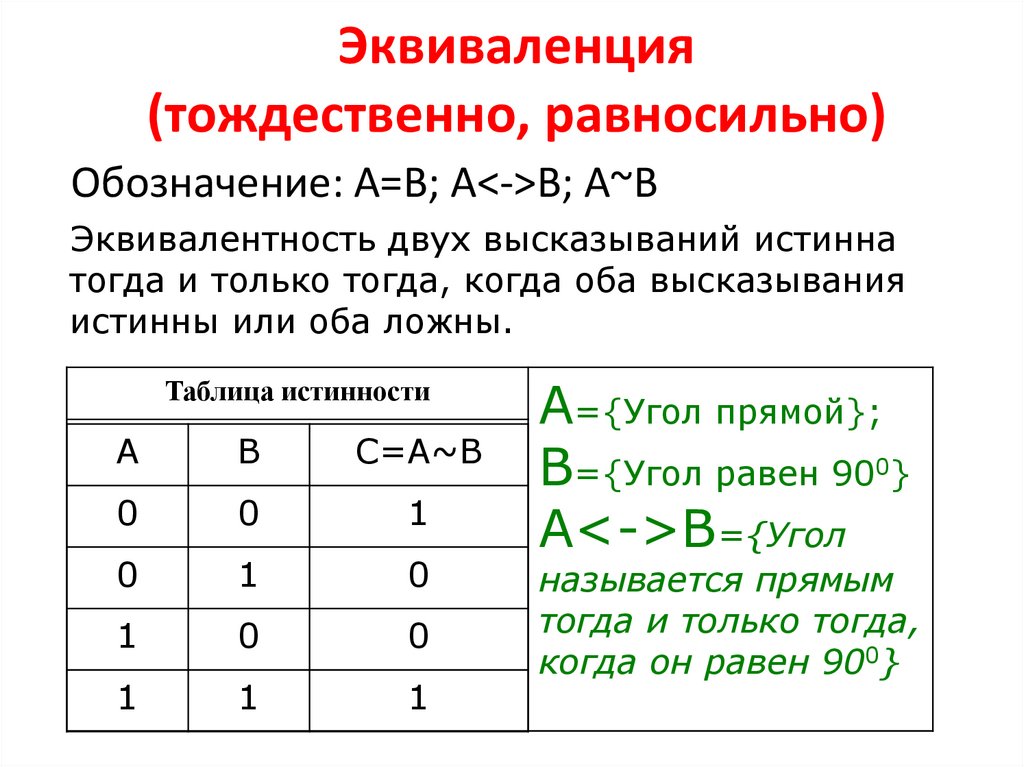 Это операция ИЛИ, которая представлена символом
Это операция ИЛИ, которая представлена символом + .
Q = A + B
Результатом Q является true , когда либо солнечно, либо вы съели пончик. Если другие вещи делают вас счастливыми, например, отпуск, вы можете добавить это к уравнению.
- Переменная
C="Я в отпуске"
Q = A + B + C
Возможно, вам легко угодить, и вам просто нужно чувствовать себя хорошо, чтобы быть счастливым. Итак, вы счастливы, когда НЕ больны. Мы будем использовать ~ для обозначения НЕ в нашем уравнении.
- Переменная
A="Я болен"
Q = ~A
В ситуации, когда все условия должны быть истинными, чтобы результат был истинным, в условиях используется операция И. Чтобы солнце светило на вас, небо должно быть ясным и должно быть дневное время.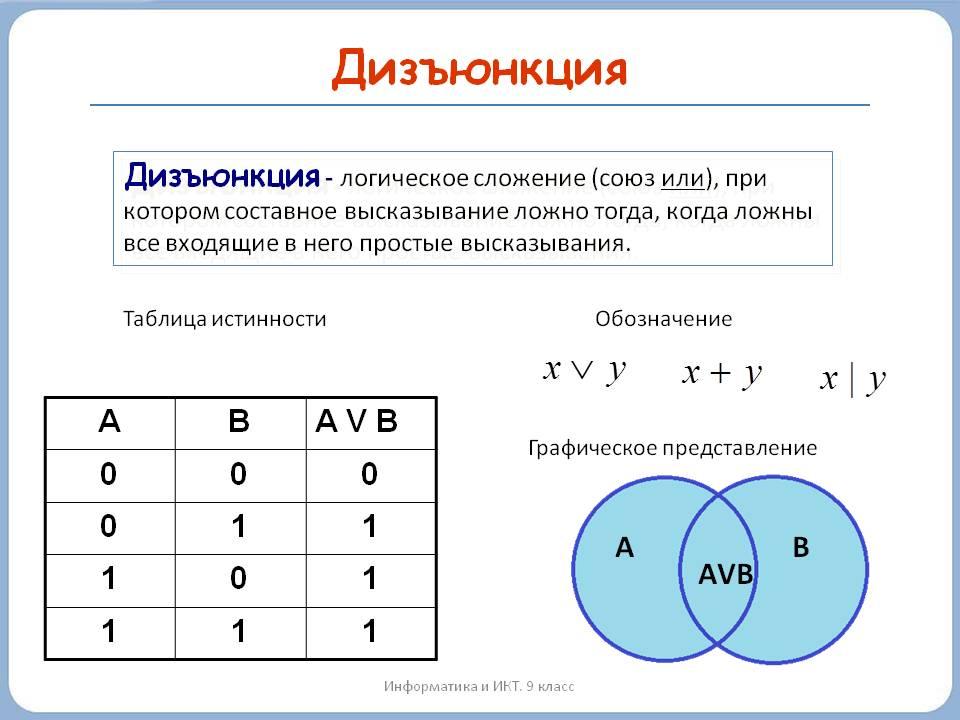 Мы соединяем эти два факта с помощью символа AND 9.1038 · .
Мы соединяем эти два факта с помощью символа AND 9.1038 · .
- Переменная
A="Небо чистое" - Переменная
B="Сейчас день" - Результат
Q="Солнце светит"
Q = A · B
Выражения
Иногда разные операции при одних и тех же условиях могут дать одинаковые результаты. Если мы возьмем случай, противоположный последнему примеру, когда солнце не светит, переменные для этого будут следующими:
- Переменная
A="Небо чистое" - Переменная
B="Сейчас день" - Результат
Q="Солнце светит" - Результат
~Q="Солнце НЕ светит"
Чтобы сделать противоположным "солнце светит" , мы отрицаем, используем символ НЕ в обеих частях уравнения.
~Q = ~(А · В)
Теперь давайте подумаем о том, что солнце НЕ светит из-за неблагоприятных условий. Если небо не чистое ИЛИ сейчас не день, значит, солнце не светит. Итак, перед переменными для каждого условия ставится символ НЕ, так что "солнце НЕ светит" имеет другое уравнение, подобное этому:
~Q = ~A + ~B
Мы видим, стороны с переменными A и B в обоих уравнениях эквивалентны друг другу, поскольку они оба равны ~Q :
~(A · B) = ~A + ~B
Логическое уравнение теперь не включает результирующую переменную Q , но вместо этого есть два выражения , которые логически эквивалентно с каждой стороны.
Таблицы истинности
Таблица истинности позволяет увидеть все возможные условия для переменных в логическом выражении и представить результаты в виде диаграммы. Используя утверждение о том, когда на улице мороз, а у вас нет пальто, вот таблица истинности, показывающая возможные условия и их результаты:
| Морозы | У меня нет пальто | Мне холодно |
|---|---|---|
| ложный | ложь | ложь |
| ложный | правда | ложь |
| правда | ложь | ложь |
| правда | правда | правда |
Поскольку вам холодно только тогда, когда оба условия истинны, оператор становится выражением И в булевой алгебре.
- Переменная
A="замерзает" - Переменная
B=«У меня нет пальто»
A · B = Q
Таблица истинности для переменных в выражении имеет те же значения, что и таблица истинности утверждения ( верно и неверно сокращены до T и Ф ).
| А | Б | Вопрос |
|---|---|---|
| Ф | Ф | Ф |
| Ф | Т | Ф |
| Т | Ф | Ф |
| Т | Ф | Т |
Что произойдет, если мы изменим условие «У меня нет пальто» на «У меня есть пальто» ? Как это влияет на таблицу истинности того, насколько вам холодно?
| Холодно | У меня есть пальто | Мне холодно |
|---|---|---|
| ложный | ложь | ложь |
| ложный | правда | ложь |
| правда | ложь | правда |
| правда | правда | ложь |
| А | Б | Q |
|---|---|---|
| Ф | Ф | Ф |
| Ф | Т | Ф |
| Т | Ф | Т |
| Т | Ф | Ф |
Чтобы написать логическое уравнение для случая, когда вам холодно, мы находим условия в таблице, где Q равно true . Здесь мы видим, что вам будет холодно только в одном ряду, когда условие
Здесь мы видим, что вам будет холодно только в одном ряду, когда условие A равно true и условие B это ложное . Логическое уравнение для этих условий выглядит следующим образом:
A · ~B = Q
Изменить эту страницу на GitHub
Изменить шаблон этой страницы на GitHub
Таблицы истинности | Математика для гуманитарных наук
Результаты обучения
- Объединение наборов с использованием булевой логики и соответствующих обозначений
- Использование операторов и условий для написания и интерпретации выражений
- Используйте таблицу истинности для интерпретации сложных утверждений или условий
- Напишите таблицы истинности с учетом логического следствия и связанных с ним утверждений — обратных, обратных и контрапозитивных
- Определить, являются ли два оператора логически эквивалентными
- Использовать законы ДеМоргана для определения логических эквивалентностей утверждения
Поскольку сложно представить сложные логические утверждения, мы можем создать таблицу истинности , чтобы разбить сложное утверждение на простые утверждения и определить, истинны они или нет. Таблица поможет отслеживать все значения истинности простых утверждений, составляющих сложное утверждение, что приведет к анализу всего утверждения.
Таблица поможет отслеживать все значения истинности простых утверждений, составляющих сложное утверждение, что приведет к анализу всего утверждения.
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности простых утверждений.
Пример
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с шезлонгом». Постройте таблицу истинности, описывающую элементы условий этого утверждения и соблюдение условий.
Показать решение
Некоторые символы, которые обычно используются для и , или и , а не облегчают использование таблицы истинности.
Символы
Символ [латекс]\клин[/латекс] используется для и : А и В обозначается как [латекс]А\клин{В}[/латекс].
Символ [латекс]\vee[/латекс] используется для или : A или B обозначается как [латекс]A\vee{B}[/латекс]
Символ [латекс]\ sim[/latex] используется для , а не : не A обозначается как [latex]\sim{A}[/latex]
Вы можете запомнить первые два символа, связав их с фигурами объединения и пересечения. [latex]A\wedge{B}[/latex] – это элементы, существующие в обоих наборах, в [latex]A\cap{B}[/latex]. Точно так же [latex]A\vee{B}[/latex] будет элементами, которые существуют в любом наборе, в [latex]A\cup{B}[/latex].
[latex]A\wedge{B}[/latex] – это элементы, существующие в обоих наборах, в [latex]A\cap{B}[/latex]. Точно так же [latex]A\vee{B}[/latex] будет элементами, которые существуют в любом наборе, в [latex]A\cup{B}[/latex].
В предыдущем примере таблица истинности просто обобщала то, что мы уже знаем о том, как работают операторы или . Таблицы истинности для основных 9Ниже показаны операторы 1029 и , или и , а не .
Основные таблицы истинности
| А | Б | [латекс]A\клин {B}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| А | Б | [латекс]A\vee{B}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
| А | [латекс]\sim{A}[/латекс] |
|---|---|
| Т | Ф |
| Ф | Т |
Попробуйте
Таблицы истинности очень полезны при анализе более сложных логических выражений.
Пример
Создайте таблицу истинности для оператора [latex]A\wedge\sim\left(B\vee{C}\right)[/latex]
Показать решение
Попробуйте
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой 9.0034 следствие .
Импликации
Импликации - это логические условные предложения, утверждающие, что утверждение p , называемое антецедентом, подразумевает следствие q .
Импликации обычно записываются как [latex]p\rightarrow{q}[/latex]
Импликации аналогичны условным операторам, которые мы рассматривали ранее; [latex]p\rightarrow{q}[/latex] обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие.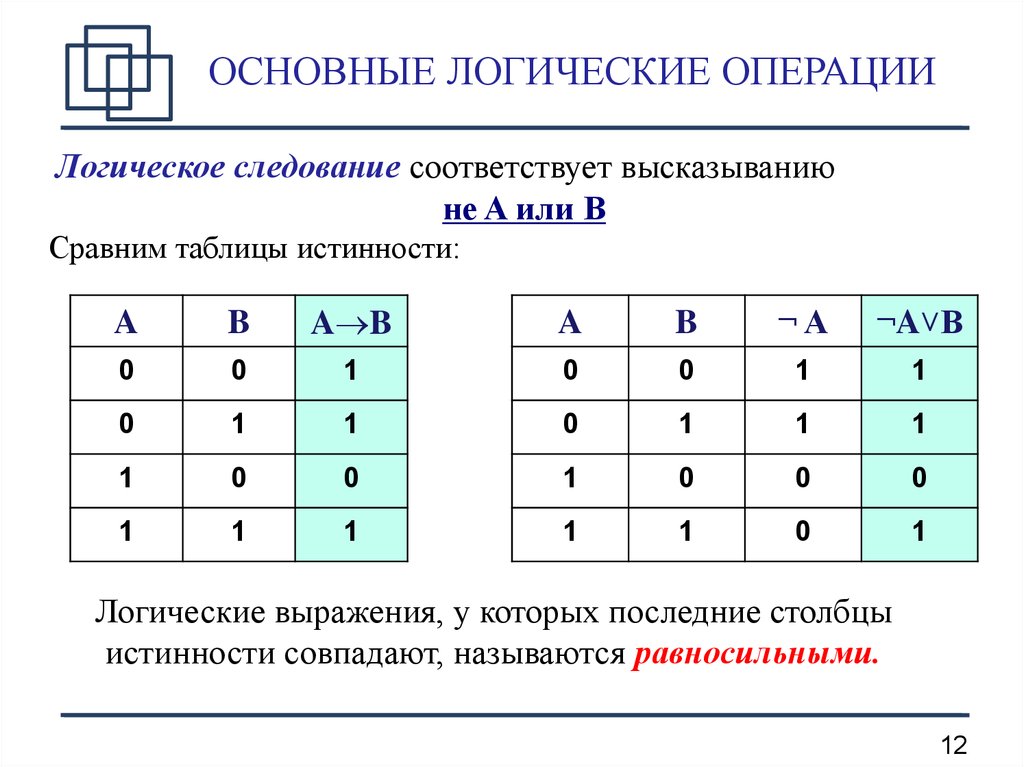 Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Пример
Английское высказывание «Если идет дождь, то облака — это небо» является логическим следствием. Является ли это веским аргументом, почему или почему нет?
Показать решение
Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.
Пример
Друг говорит вам, что «если вы загрузите это изображение на Facebook, вы потеряете работу». Опишите возможные результаты, связанные с этим утверждением, и определите, является ли утверждение вашего друга недействительным.
Показать решение
В традиционной логике импликация считается достоверной (истинной), если нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.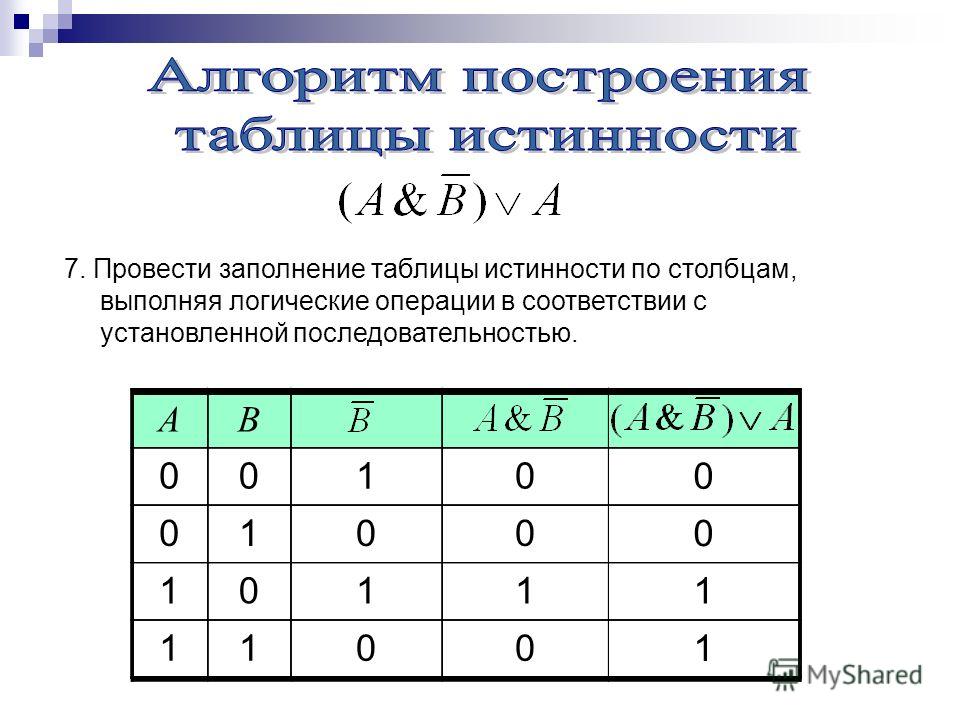
Значения истинности для импликаций
| р | q | р → q |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Пример
Построить таблицу истинности для утверждения [латекс]\левый(м\клин\сим{р}\правый)\стрелка вправо{г}[/латекс]
Показать решение
Попробуйте
Для любого следствия есть три взаимосвязанных утверждения: обратное, обратное и противоположное.
Связанные операторы
Первоначальный вывод: «если p , то q »: [latex]p\rightarrow{q}[/latex]
Обратное: «если q , то p » [latex]q\rightarrow{p}[/latex]
Обратное: «если не p , то не q »: [latex]\sim{p}\rightarrow\sim{q}[/latex]
Противоположный вариант: «если не q , то не p »: [latex]\sim{q}\rightarrow{p}[/latex]
Пример
Рассмотрим еще раз верный вывод: «Если идет дождь, то на небе облака».
Напишите соответствующие обратные, обратные и противоположные утверждения.
Показать решение
Попробуйте
Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.
| Значение | Конверс | Инверсия | Противоположный | ||
|---|---|---|---|---|---|
| р | q | [латекс]p\стрелка вправо{q}[/латекс] | [латекс] q {\ rightarrow} р [/латекс] | [латекс]\sim{p}\стрелка вправо\sim{q}[/латекс] | [латекс]\sim{q}\стрелка вправо\sim{p}[/латекс] |
| Т | Т | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Ф |
| Ф | Т | Т | Ф | Ф | Т |
| Ф | Ф | Т | Т | Т | Т |
Эквивалентность
Условное утверждение и его противоположность логически эквивалентны.
Обратное и обратное утверждения логически эквивалентны.
Булева логика | Математика для гуманитарных наук
Результаты обучения
- Объединение наборов с использованием логической логики с использованием соответствующих обозначений
- Использование операторов и условий для написания и интерпретации выражений
- Используйте таблицу истинности для интерпретации сложных утверждений или условий
- Напишите таблицы истинности с учетом логического следствия и связанных с ним утверждений — обратных, обратных и контрапозитивных
- Определить, являются ли два оператора логически эквивалентными
- Использовать законы ДеМоргана для определения логических эквивалентностей утверждения
Логика — это, по сути, изучение правильных рассуждений. При поиске в Интернете мы используем логическую логику — такие термины, как «и» и «или», — чтобы помочь нам найти определенные веб-страницы, которые соответствуют интересующим нас множествам. После изучения этой формы логики мы рассмотрим логические аргументы. и как мы можем определить обоснованность претензии.
После изучения этой формы логики мы рассмотрим логические аргументы. и как мы можем определить обоснованность претензии.
Булева логика
Мы часто можем классифицировать элементы как принадлежащие наборам. Если бы вы пришли в библиотеку, чтобы найти книгу, и вас попросили бы выразить ваш поиск, используя союзы, пересечения и дополнения множеств, это было бы немного странно. Вместо этого мы обычно используем такие слова, как «и», «или» и «не», чтобы связать наши ключевые слова вместе и сформировать поиск. Эти слова, составляющие основу Булева логика , напрямую связаны с операциями над множествами с той же терминологией.
Булева логика
Булева логика объединяет несколько утверждений, которые либо истинны, либо ложны, в выражение, которое либо истинно, либо ложно.
- В отношении наборов логический поиск верен, если рассматриваемый элемент является частью искомого набора.
Предположим, что M — это набор всех детективных книг, а C — это набор всех комедийных книг.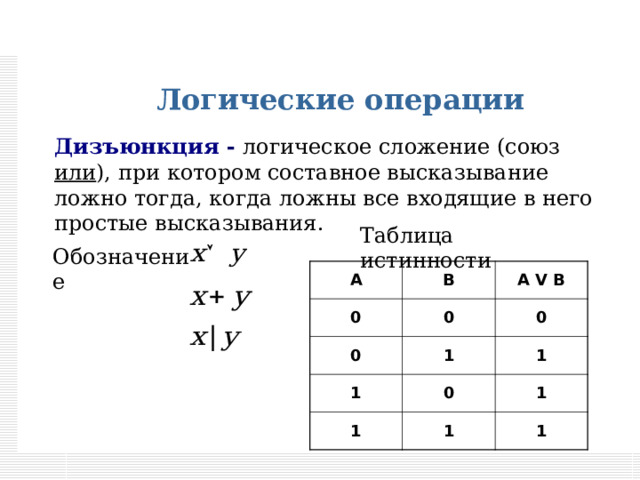 Если мы ищем «тайна», мы ищем все книги, которые являются элементом набора 9.1029 М ; поиск верен для книг, которые есть в наборе.
Если мы ищем «тайна», мы ищем все книги, которые являются элементом набора 9.1029 М ; поиск верен для книг, которые есть в наборе.
Когда мы ищем «тайна и комедия», мы ищем книгу, которая является элементом обоих наборов, на пересечении. Если бы мы искали «тайна или комедия », мы ищем книгу, которая является детективом, комедией или и тем, и другим, то есть объединением наборов. Если мы искали «, а не комедия», мы ищем любую книгу в библиотеке, которая не является комедией, дополнением к набору 9.1029 С .
Соединение с установленными операциями
A и B Элементы на пересечении A ⋂ B
A или B .
A .2929.
3. НЕТ БЕЗ. . . .. 9109 9109... 9103. НЕТ НЕТ БЕЗ 9109. НЕТ НЕТ НЕТ НЕТ НЕМЕР. A элементы в дополнении Ac Обратите внимание, что или не являются исключительными. В этом разница между использованием слова в булевой логике и обычным повседневным использованием. Когда ваша вторая половинка спрашивает: «Хочешь пойти в парк или в кино?» они обычно предлагают эксклюзивный выбор — один вариант или другой, но не оба. В булевой логике или не являются эксклюзивными — это больше похоже на вопрос в ресторане: «Вы хотите картошку фри или напиток к этому?» Ответ «оба, пожалуйста» является приемлемым ответом.
В этом разница между использованием слова в булевой логике и обычным повседневным использованием. Когда ваша вторая половинка спрашивает: «Хочешь пойти в парк или в кино?» они обычно предлагают эксклюзивный выбор — один вариант или другой, но не оба. В булевой логике или не являются эксклюзивными — это больше похоже на вопрос в ресторане: «Вы хотите картошку фри или напиток к этому?» Ответ «оба, пожалуйста» является приемлемым ответом.
В следующем видео Вы увидите примеры использования логических операторов для обозначения множеств.
Пример
Предположим, мы ищем в библиотечной базе данных мексиканские университеты. Выразите разумный поиск, используя булеву логику.
Показать решение
В большинстве поисковых систем нет необходимости включать слово и ; поисковая система предполагает, что если вы укажете два ключевых слова, вы ищете оба. В поиске Google ключевое слово или пишется с большой буквы как ИЛИ, а знак минус перед словом используется для обозначения , а не . Кавычки вокруг фразы означают, что следует искать всю фразу. Поиск из предыдущего примера в Google мог бы быть записан:
В поиске Google ключевое слово или пишется с большой буквы как ИЛИ, а знак минус перед словом используется для обозначения , а не . Кавычки вокруг фразы означают, что следует искать всю фразу. Поиск из предыдущего примера в Google мог бы быть записан:
Университет Мексики - «Нью-Мексико»
Пример
Опишите числа, которые удовлетворяют условию:
четное и меньше 10 и больше 0
Показать решение
Попробуйте
Что на первом месте?
Иногда высказывания на английском языке могут быть двусмысленными. По этой причине в булевой логике для обозначения прецедента используются круглые скобки, как и в алгебраическом порядке операций.
Английская фраза «Иди в магазин и купи мне яйца и рогалики или хлопья» неоднозначна; неясно, всегда ли запрашивающие просят яйца вместе с рогаликами или хлопьями, или они просят либо сочетание яиц и рогаликов, либо только хлопья.
По этой причине использование круглых скобок поясняет намерение:
| Яйца и (бублики или хлопья) средства | Вариант 1: яйца и рогалики, вариант 2: яйца и хлопья |
| (Яйца и рогалики) или зерновые средства | Вариант 1: яйца и рогалики, вариант 2: хлопья |
Пример
Опишите числа, которые удовлетворяют условию:
нечетное число и меньше 20 и больше 0 и (кратно 3 или кратно 5)
Показать решение
Имейте в виду, что когда строка условий записывается без группирующих символов, она часто интерпретируется слева направо, что приводит к последней интерпретации.
Условные выражения
Помимо поиска, логическая логика обычно используется в приложениях для работы с электронными таблицами, таких как Excel, для выполнения условных вычислений. Утверждение — это то, что либо истинно, либо ложно.
Пример
Утверждение типа 3 < 5 верно; утверждение вроде «крыса — это рыба» ложно. Утверждение типа «x < 5» верно для некоторых значений 9.1029 x
и false для других.Когда действие выполняется или нет, в зависимости от значения оператора, оно формирует условное .
Утверждения и условия
Утверждение может быть либо истинным, либо ложным.
Условный — это составной оператор формы
«если p , то q» или «если p , то q , иначе s ».
На обычном языке примером условного оператора может быть: «Если идет дождь, мы пойдем в торговый центр. В противном случае мы пойдем в поход».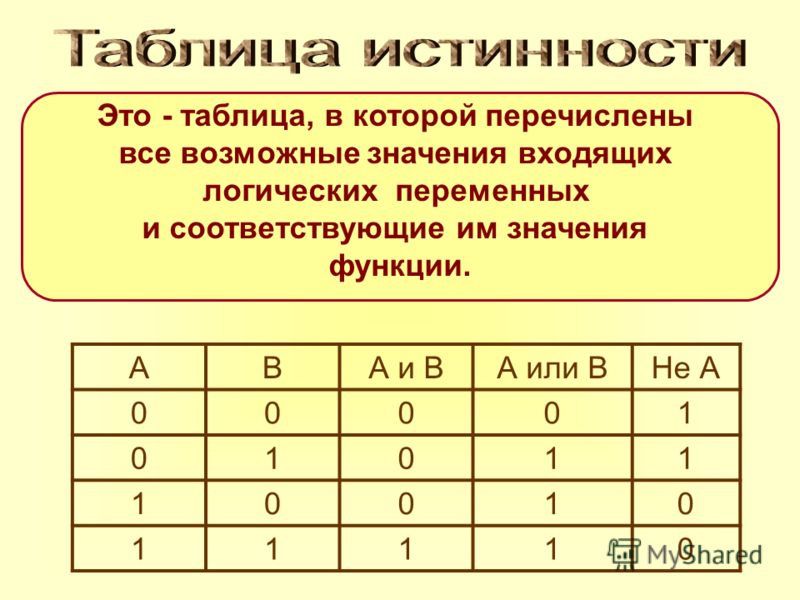
Утверждение «Если идет дождь» является условием — оно может быть истинным или ложным для любого данного дня. Если условие истинно, то мы последуем первому курсу действий и пойдем в торговый центр. Если условие ложно, то воспользуемся альтернативой и отправимся в поход.
Попробуйте
Excel
Условные операторы обычно используются в приложениях для работы с электронными таблицами, таких как Excel. В Excel вы можете ввести такое выражение, как
=ЕСЛИ(A1<2000, A1+1, A1*2)
Обратите внимание, что после ЕСЛИ есть три части. Первая часть — это условие, а вторые две — расчеты.
Excel просмотрит значение в ячейке A1 и сравнит его с 2000. Если это условие верно, то используется первое вычисление, и 1 добавляется к значению A1, и результат сохраняется. Если условие ложно, то используется второе вычисление, а A1 умножается на 2 и результат сохраняется.
Другими словами, это утверждение эквивалентно высказыванию «Если значение A1 меньше 2000, то добавьте 1 к значению в A1.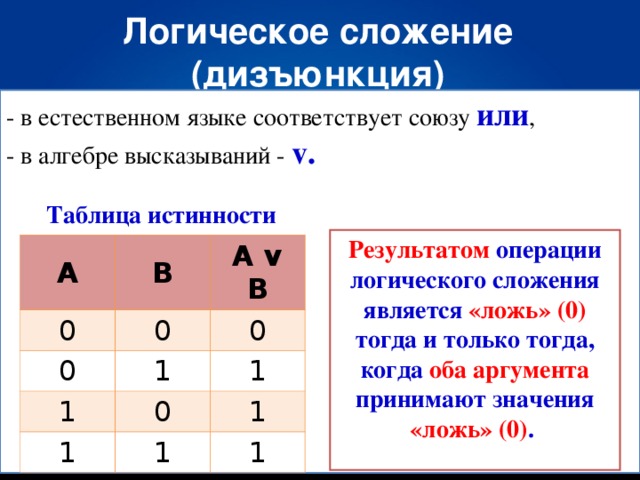 В противном случае умножьте A1 на 2 дюйма
В противном случае умножьте A1 на 2 дюйма
Пример
Напишите команду Excel, которая создаст условие «A1 < 3000 и A1 > 100».
Показать решение
Пример
Учитывая выражение Excel:
ЕСЛИ(A1 > 5, 2*A1, 3*A1)
Найдите следующее:
- результат, если A1 равен 3, и
- результат, если A1 равен 8
Показать раствор
Попробуйте
Пример
Бухгалтеру необходимо удержать 15% дохода для уплаты налогов, если доход составляет менее 30 000 долларов США, и 20 % дохода, если доход составляет 30 000 долларов США или более. Напишите выражение Excel, которое будет вычислять сумму удержания.
Показать решение
Попробуйте
Как и раньше, мы можем создавать более сложные условия, используя операторы и , или и вместо , чтобы объединить более простые условия.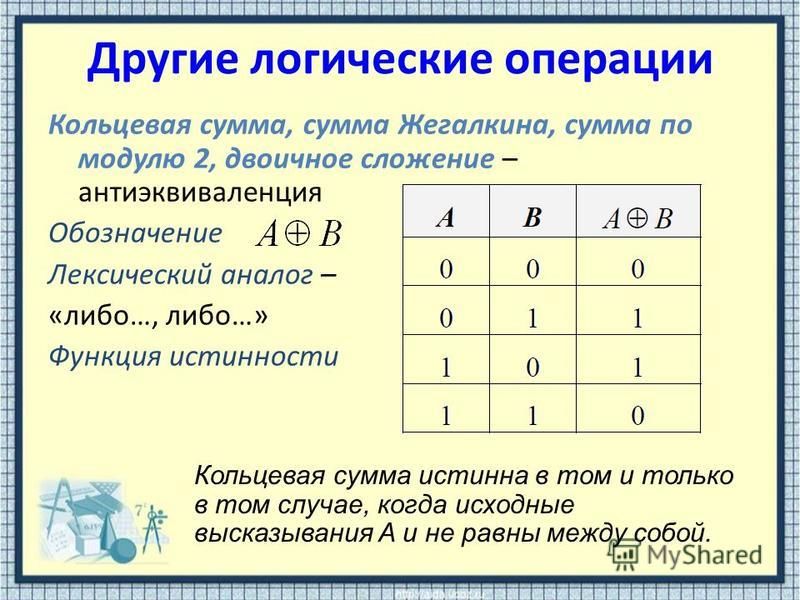
Пример
Родитель может сказать своему ребенку: «Если ты уберешь свою комнату и вынесешь мусор, то сможешь съесть мороженое». При каких обстоятельствах это условие будет истинным?
Показать решение
Обратите внимание, что если родитель сказал: «Если ты уберешь свою комнату или вынеси мусор, тогда можно есть мороженое», то ребенку нужно будет выполнить только одно задание, чтобы выполнить условие.
Пример
В электронной таблице ячейка A1 содержит годовой доход, а ячейка A2 содержит количество иждивенцев.
Определенный налоговый кредит применяется, если кто-то без иждивенцев зарабатывает менее 10 000 долларов США и не имеет иждивенцев, или если кто-то с иждивенцами зарабатывает менее 20 000 долларов США. Напишите правило, описывающее это.
Показать решение
Логика, простые и составные утверждения, логические операции и таблицы истинности, условные утверждения и доказательства Экзаменационные уроки
СОДЕРЖАНИЕ
- Значение простых и составных утверждений.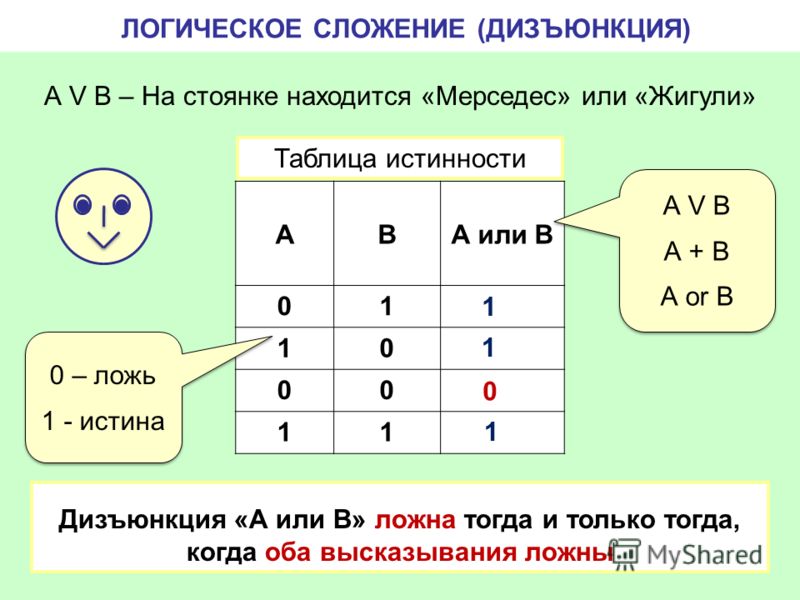
– Логические операции и таблицы истинности.
- Условные утверждения и косвенные доказательства.
ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЛОЖЕНИЯ
Предлог — это утверждение или предложение, которое либо истинно, либо ложно, но не то и другое одновременно. Мы будем использовать заглавные буквы английского алфавита, такие как A, B, C, D, P, Q, R, S, …, для обозначения простых утверждений или предлогов. Простое высказывание или предложение — это высказывание, не содержащее связок. Другими словами, предложение считается простым, если оно не может быть разбито на подпредложения. С другой стороны, сложное предложение состоит из двух или более предложений, соединенных связками. Этими связками являются и, или, если… то, тогда и только тогда, когда. Их также называют логическими операторами. В таблице ниже показаны логические операторы и их символы. 9
- The statement ∼P is known as отрицание P.
 Q означает P и Q.
Q означает P и Q. - Утверждение PV Q называется дизъюнкцией P и Q. Таким образом, PV Q означает либо P, либо Q, либо оба P и Q. Обратите внимание, что используется включающее или.
- Утверждение P ⇒ Q называется условным оператором P и Q. Условный оператор также известен как импликация P ⇒ Q означает, что если P, то Q или P подразумевает Q. Q, где символ ⇔ означает тогда и только тогда, когда (или если и только если для краткости). Таким образом, P ⇔ Q означает P ⇔ Q и Q ⇔ P.
Таблицы истинности
Истинность или ложность предложения есть его истинностное значение, т.е. Истинное предложение имеет значение истинности T, а ложное предложение имеет значение истинности F. Таблицы истинности для логических операторов приведены ниже.
Figure 2
| P | ~P |
| T | F |
| F | T |
If P is true (T), then ~P is false и если P ложно, то ~P истинно.
Обратное, обратное и контрапозитивное — условные и биусловные операторы, логика, геометрия
Обратное условного утверждения «если P, то Q» — это условное утверждение «если Q, то P», т. е. обращение P⇒ Q есть Q ⇒ P.
Обратное утверждение
Обратное условному утверждению «если P, то Q» является условным утверждением «если не P, то не Q».
, т. е. обратным P ⇒ Q является ∼P ⇒ ∼Q.
Противоположное высказывание
Обратным условному высказыванию «если P, то Q» является условное высказывание «если не Q, то не P».
, то есть контрапозитив P ⇒ Q - ∼P, щула P
Логические операции и таблицы истины com="" category="" mathematics-olevel=""> ТАТОЛОГИЯ И ВОЗМОЖНОСТИ3 ТАТОЛОГИЯ И ВОЗМОЖНОСТИ
3 ТАТОЛОГИЯ И ВОЗМОЖНОСТИ
3 ТАТОЛОГИЯ И ВОЗМОЖНОСТИ
3 3 ТАТОЛОГИЯ И ВОЗМОЖНОСТИ
3 3 . составляющие его утверждения, это называется тавтологией . С другой стороны, когда предложение всегда ложно, оно называется противоречием.
ЦЕПОЧНОЕ ПРАВИЛО Цепное правило гласит, что если X, Y и Z являются утверждениями такими, что X ⇒ Y и Y ⇒ Z, то X ⇒ Z. цепочка утверждений может иметь любое количество звеньев. ' по мере необходимости.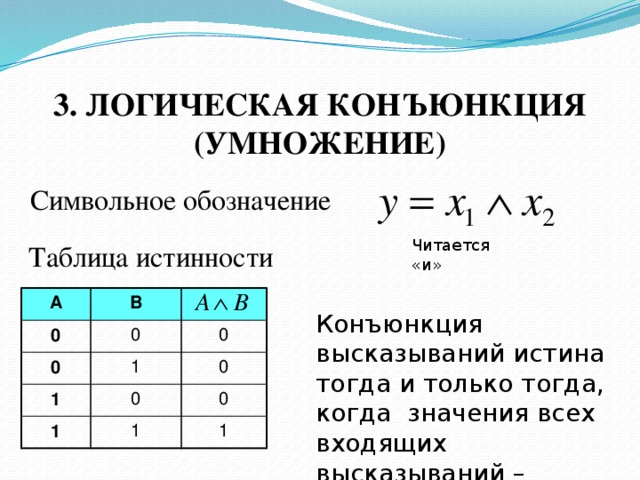 Пример 5 является примером цепного правила.
Пример 5 является примером цепного правила.
При использовании правила цепочки. Важно, чтобы стрелки импликации указывали в одном направлении. Например, не имеет большой ценности иметь что-то вроде X ⇒ Q ⇐ R, потому что из этого нельзя сделать никаких полезных выводов.
Пример
В следующем рассуждении определите, обязательно ли следует вывод из данных посылок.
Все водители осторожны. (1 ST предпосылка)
Осторожные люди - терпеливые (2 и Предметка)
Следовательно, все водители являются терпеливыми (заключение)
, если D: люди, которые являются водителями
C: люди, которые осторожен
3. : терпеливые люди
, затем D ⇒ C (1 -я предпосылка)
и C,P (2 nd )
Если D ⇒ C и C ⇒ P
Затем D ⇒ P (цепное правило)
помещение.
youtube.com/embed/0T0QrHO56qg?feature=oembed" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen="">УСЛОВНЫЕ ЗАЯВЛЕНИЯ И КОСВЕННЫЕ ДОКАЗАТЕЛЬСТВА.
Другой метод, который мы можем использовать для определения достоверности аргументов, особенно более сложных, заключается в построении таблиц истинности, как будет показано в следующих примерах.
Присоединяйтесь к дискуссионному форуму и выполняйте задание : Найдите вопросы в конце каждого урока. Нажмите здесь, чтобы обсудить свои ответы на форуме
Объявление: Получите БЕСПЛАТНУЮ Библию : Обрести истинный покой. Нажмите здесь, чтобы узнать, как получить БЕСПЛАТНУЮ Библию.
По вопросам размещения рекламы/партнерства пишите [email protected]
Загрузите наше бесплатное мобильное приложение для Android :
Сохраняйте свои данные при использовании нашего бесплатного приложения. Нажмите на картинку, чтобы скачать. Нет подписки.
Нажмите на картинку, чтобы скачать. Нет подписки.
Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.com. Нажмите кнопку «Поделиться» ниже!
Таблицы истинности и значения истинности
Таблица истинности указывает, является ли утверждение истинным или ложным.
Если это правда, то он получает T.
Если он неверен, то он получает F.
Логические утверждения могут быть только истинными или ложными. Между ними нет.
Мы можем использовать переменные для представления логических операторов: 9q относится к утверждению «Художественное шоу было приятным, И в комнате было жарко».
v означает «или» ( дизъюнкция )). Например, p v q относится к утверждению «Выставка была приятной ИЛИ в комнате было жарко».
-> означает «если тогда» или « подразумевает ». Например, q -> ~p относится к «если в комнате было жарко, то художественная выставка не была приятной».
<-> означает «если и только если» или « эквивалентно ». Например, пусть:
p : Число четное.
q : Число делится на 2
Тогда мы имеем: p <-> q
Давайте посмотрим на базовую таблицу истинности. Эта таблица выглядит так:
| p | ~ | стр.
| Т | Ф |
| Ф | Т |
Эта таблица говорит вам о том, что:
9с)
Оператор AND требует, чтобы p и q оба были TRUE, чтобы оператор AND был истинным. В противном случае оператор AND ложен.
9Таблица истинности утверждения 0034 ИЛИ выглядит следующим образом в отношении p и q.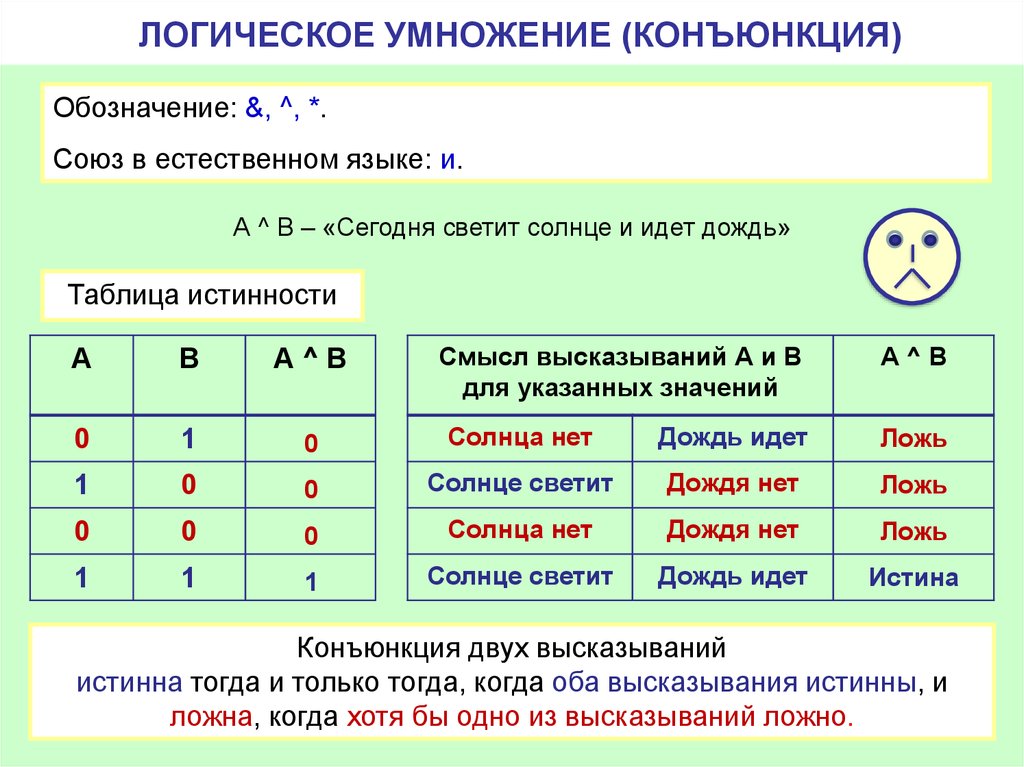
| р | q | (п в кв) |
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
Оператор ИЛИ требует, чтобы p и q были равны ЛОЖЬ, чтобы оператор ИЛИ был ложным. В противном случае оператор ИЛИ верен.
Таблица истинности утверждения ПРЕДПОЛАГАЕТ в отношении p и q выглядит следующим образом.
| р | q | (р -> к) |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Если p истинно и q истинно, то подразумеваемое утверждение p -> q также истинно.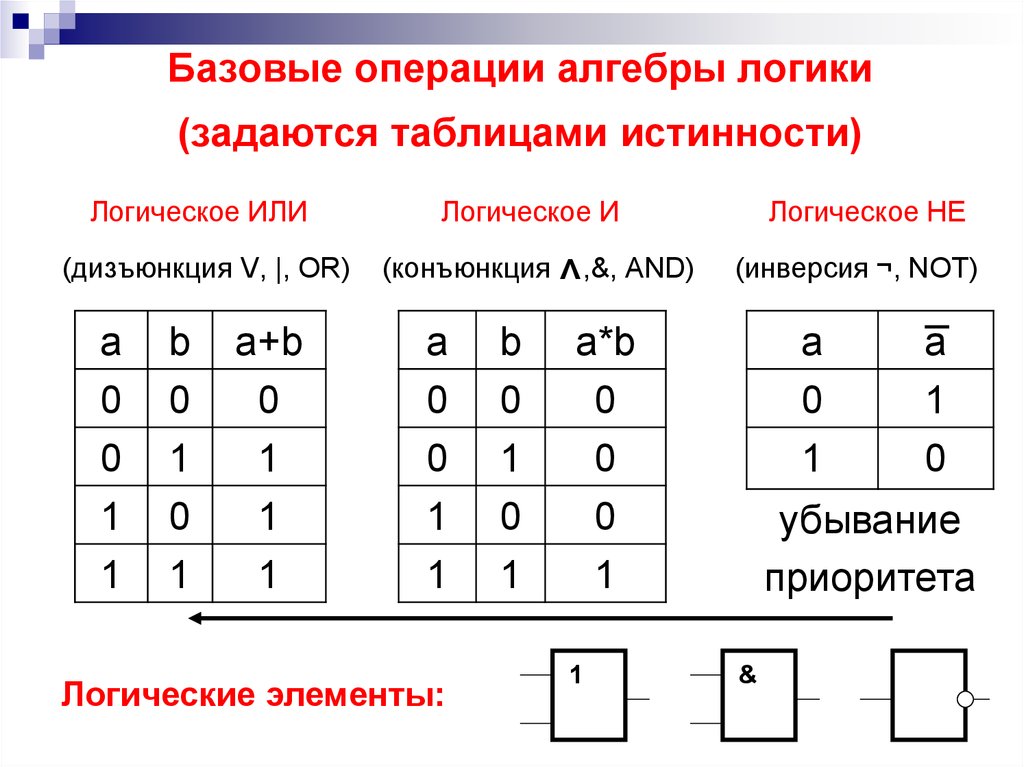
Если p истинно, а q ложно, то подразумеваемое утверждение p -> q ложно.
Если p ложно, то подразумеваемое утверждение p -> q всегда истинно, независимо от того, истинно ли q или ложно.
На самом деле p -> q не применяется, когда p ложно. Однако само подразумеваемое утверждение по правилам логики должно быть истинным или ложным. Между ними нет. Поскольку нельзя показать, что утверждение p -> q ложно, когда p ложно, то утверждение должно быть истинным, когда p ложно.
Правила для оператора IMPLIES:
Если p истинно, то p -> q истинно, когда q истинно, и ложно, когда q ложно.
Если p ложно, то p -> q неприменимо, но по правилу логики считается истинным независимо от того, истинно ли q или ложно.
Оператор IMPLIES также называется " условным оператором ".
Таблица истинности утверждения ЭКВИВАЛЕНТНОСТЬ выглядит следующим образом в отношении p и q.
| р | q | (р<->к) |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Т |
p <-> q — это еще один способ сказать: «p истинно тогда и только тогда, когда q истинно».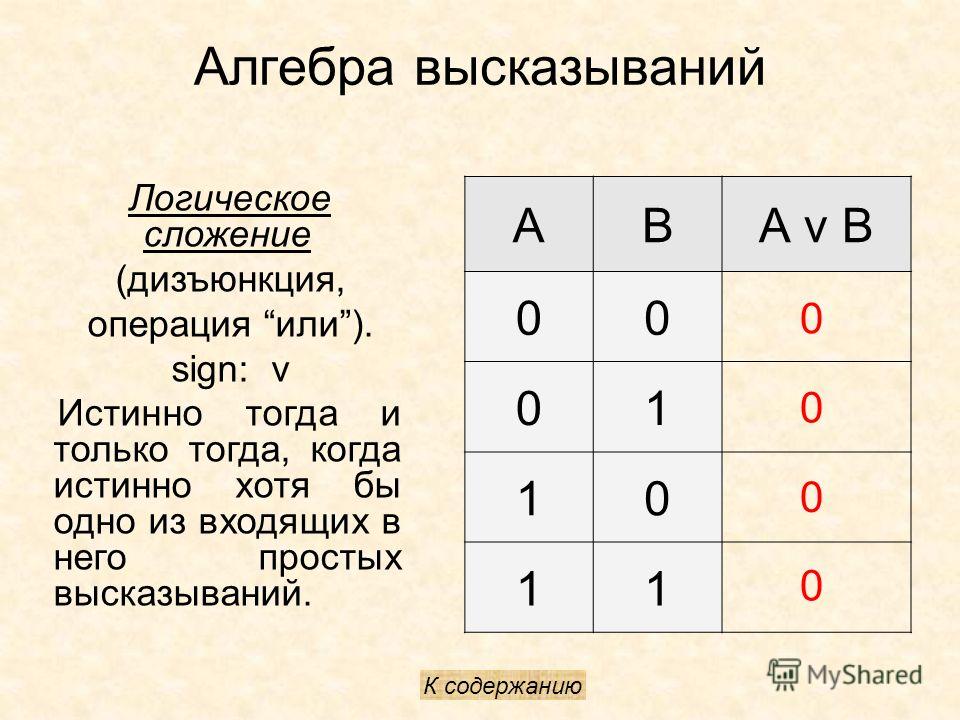


 Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.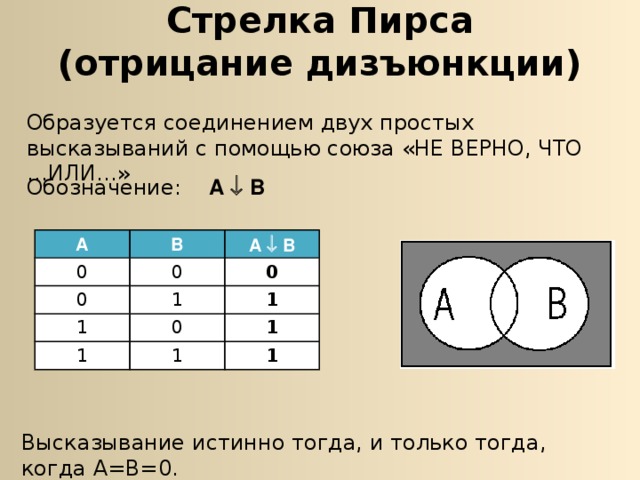
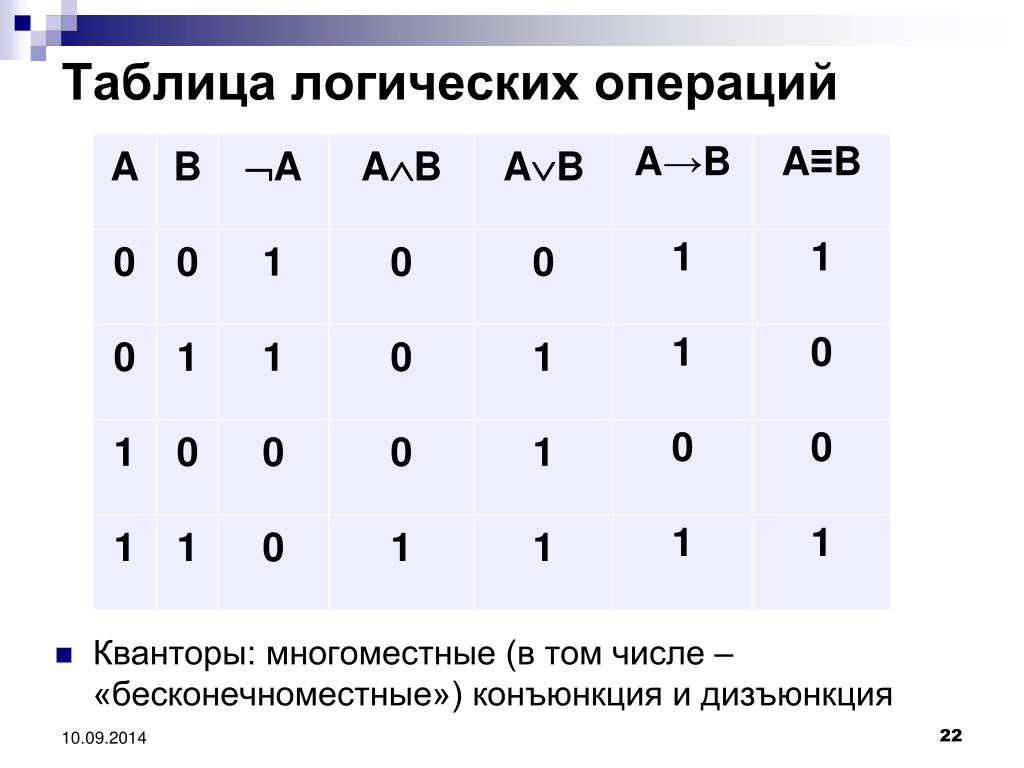 В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.


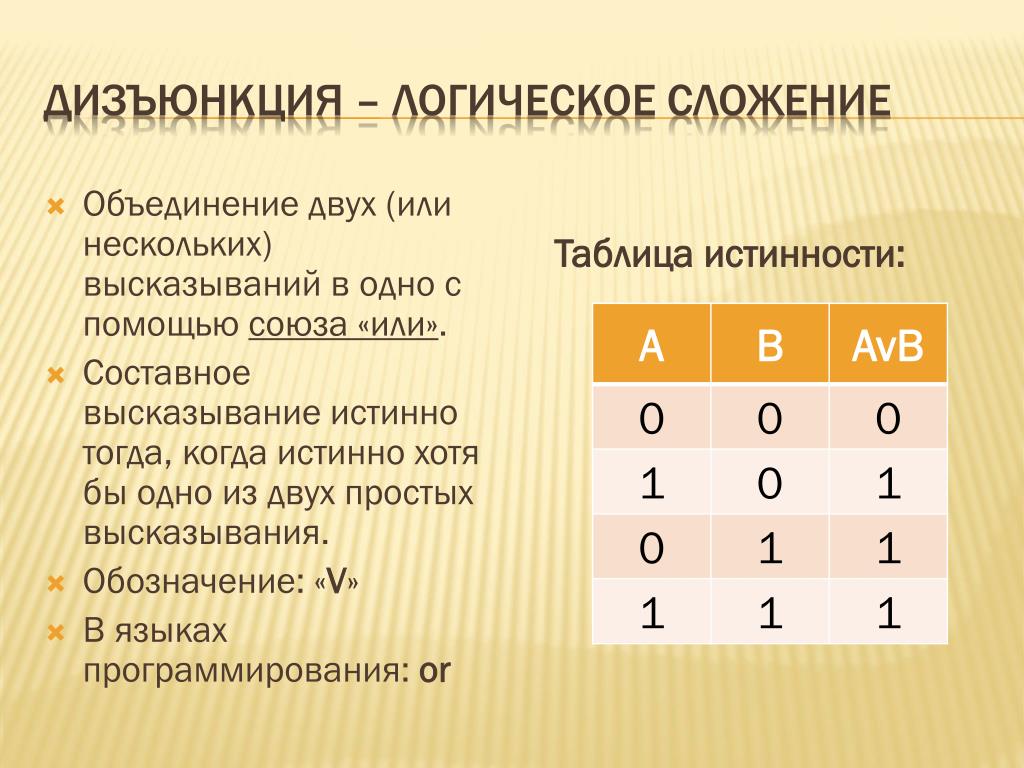

 е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества. 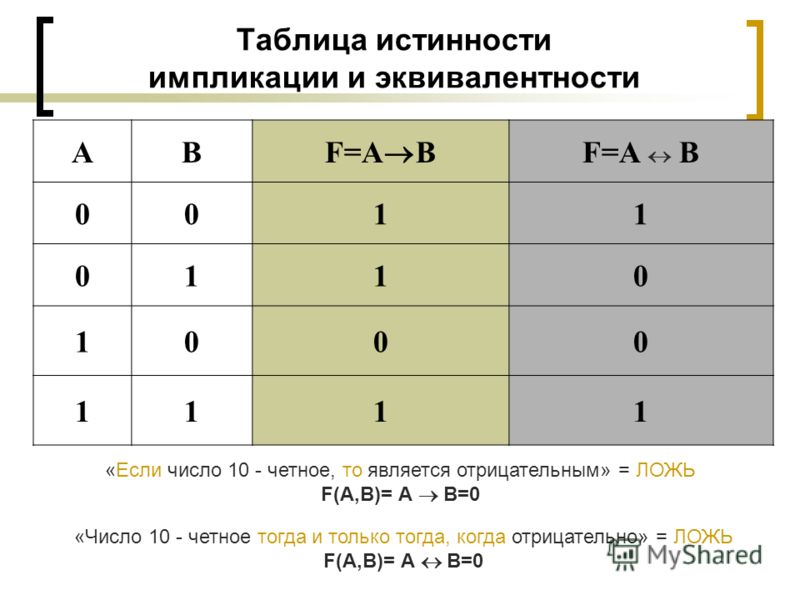 .., то …», называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю).
.., то …», называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю). 

 » (В. Шекспир) А V ¬ A <=> В
» (В. Шекспир) А V ¬ A <=> В
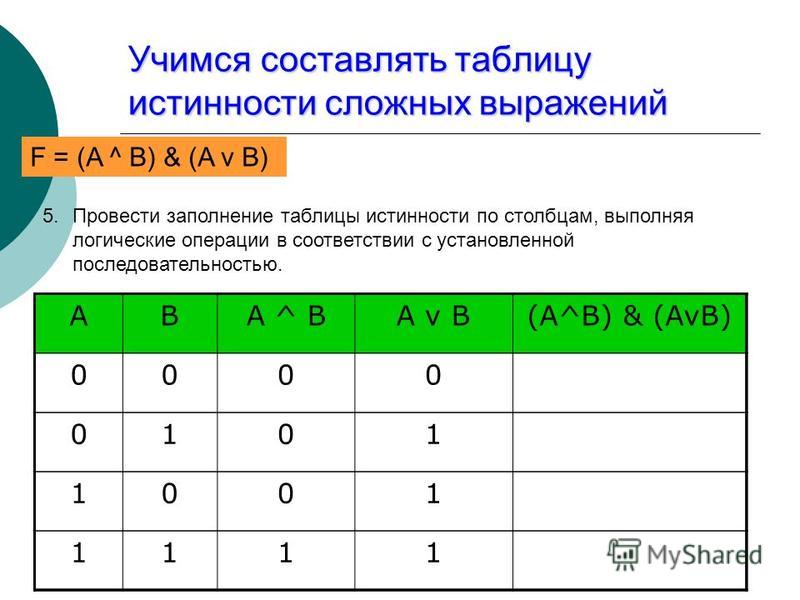




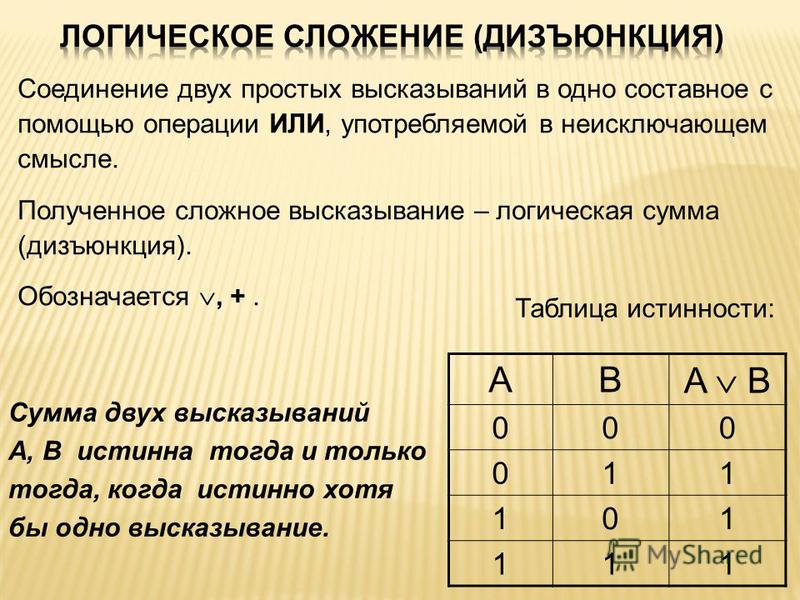
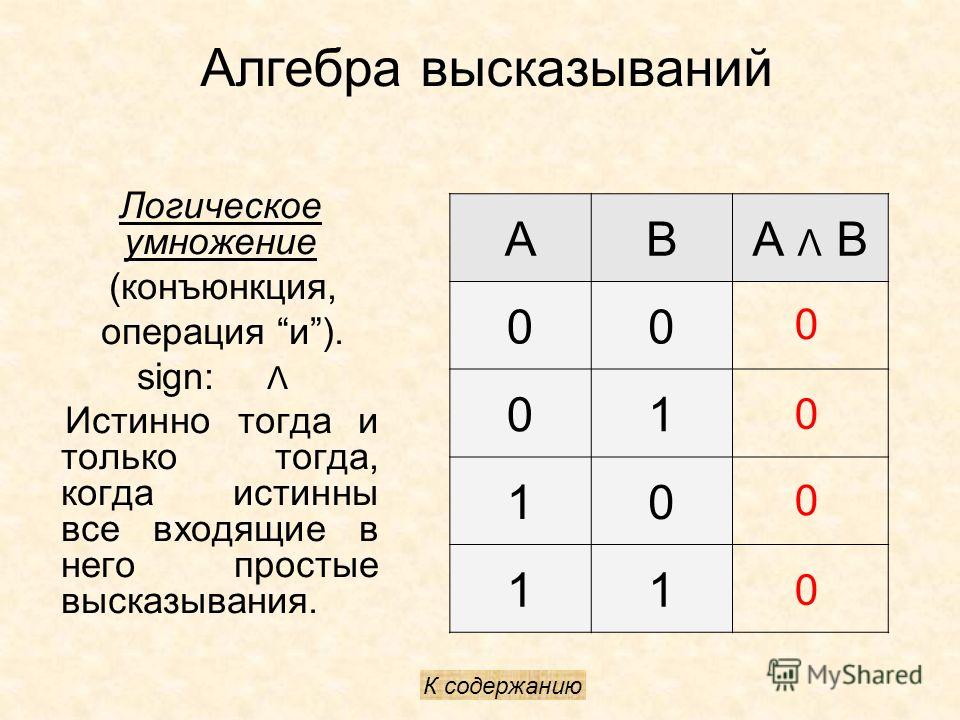
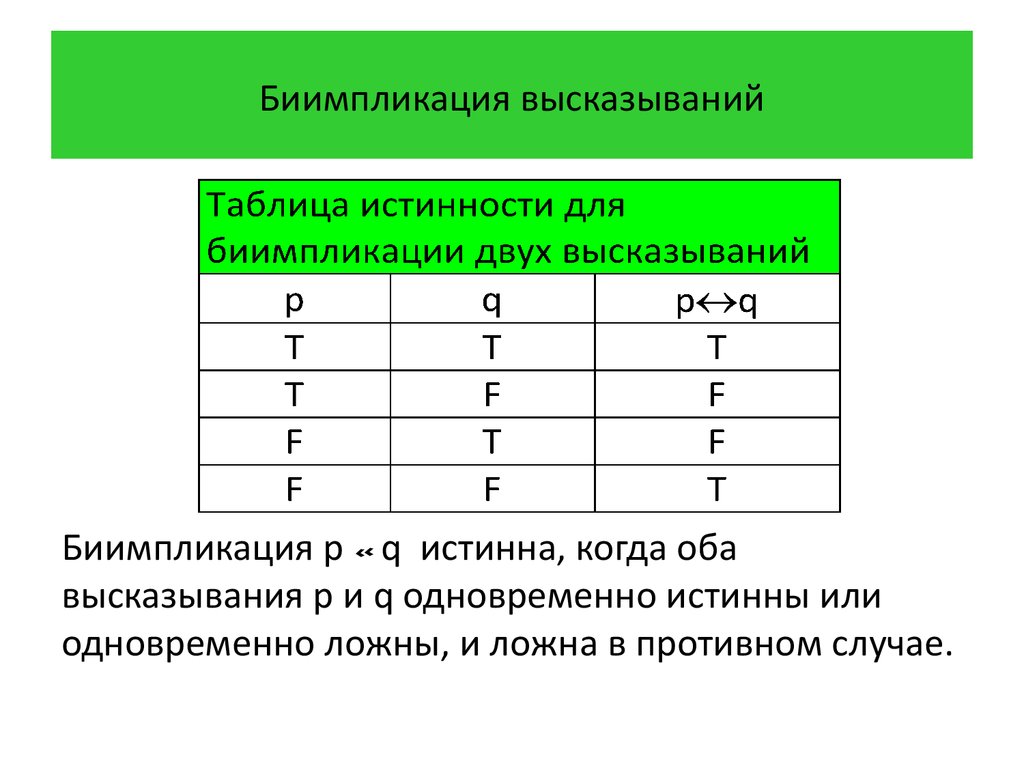 И наоборот, если исходное выражение ложно, то его отрицание будет истинным.
И наоборот, если исходное выражение ложно, то его отрицание будет истинным.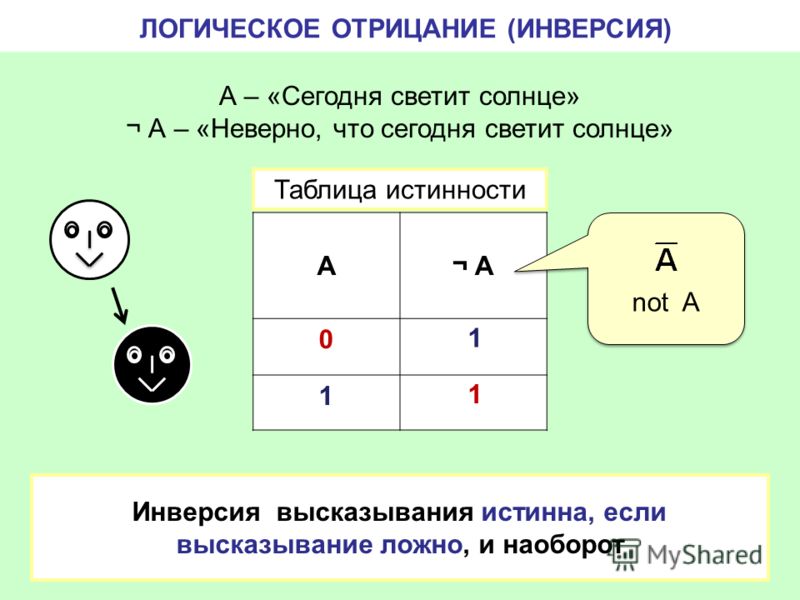 В противном случае результатом является истина.
В противном случае результатом является истина. В противном случае результатом является ложь.
В противном случае результатом является ложь.
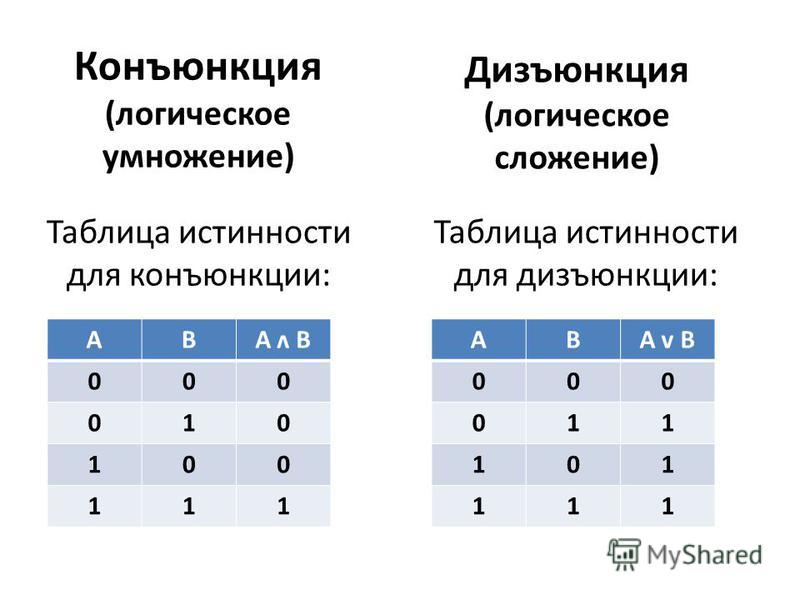
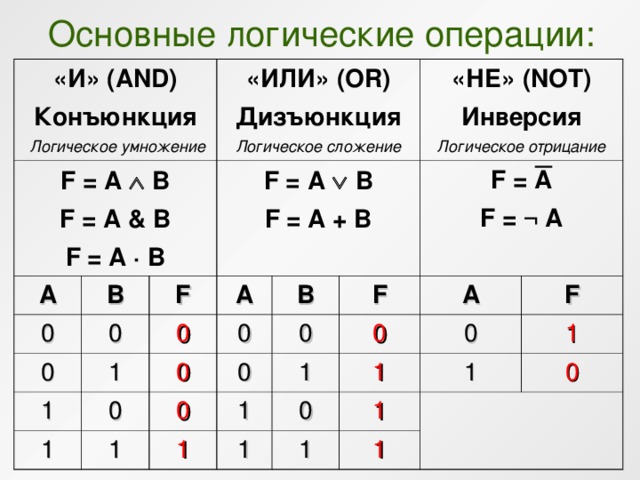 Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно.
Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно.
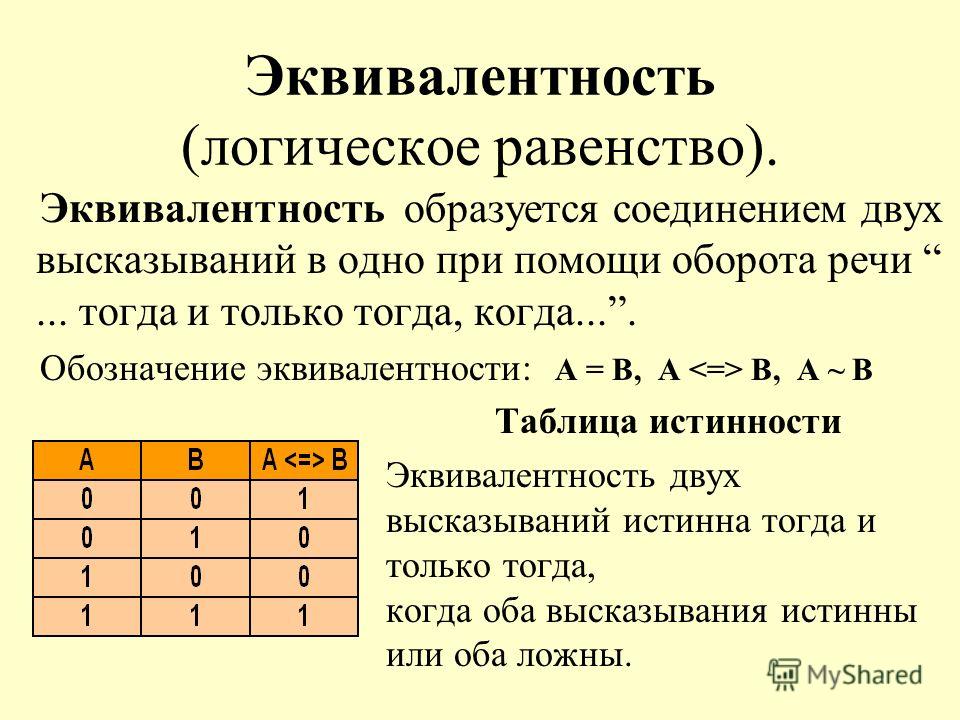 Не удаляйте этот текст первым.
Не удаляйте этот текст первым. Наша стандартная схема для этого типа таблицы истинности показана в таблице 2.2 .
Наша стандартная схема для этого типа таблицы истинности показана в таблице 2.2 .
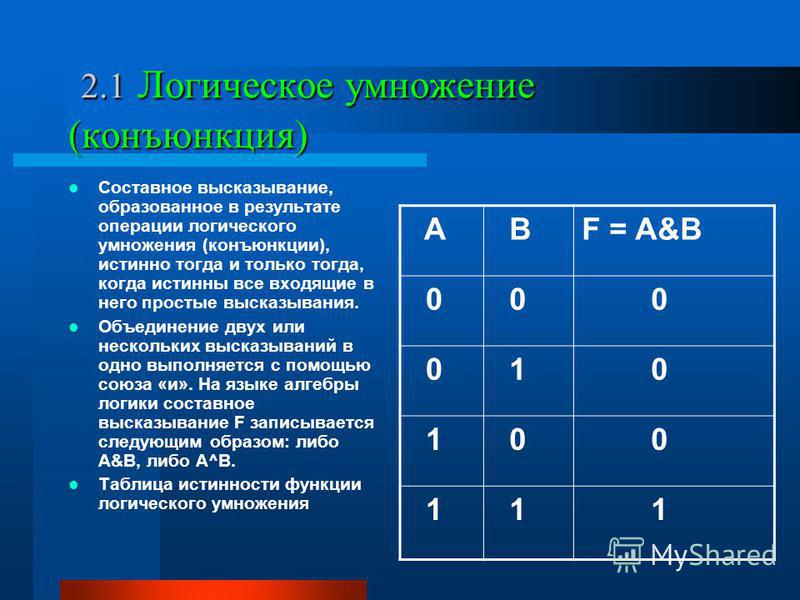 Не удаляйте этот текст первым.
Не удаляйте этот текст первым. Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?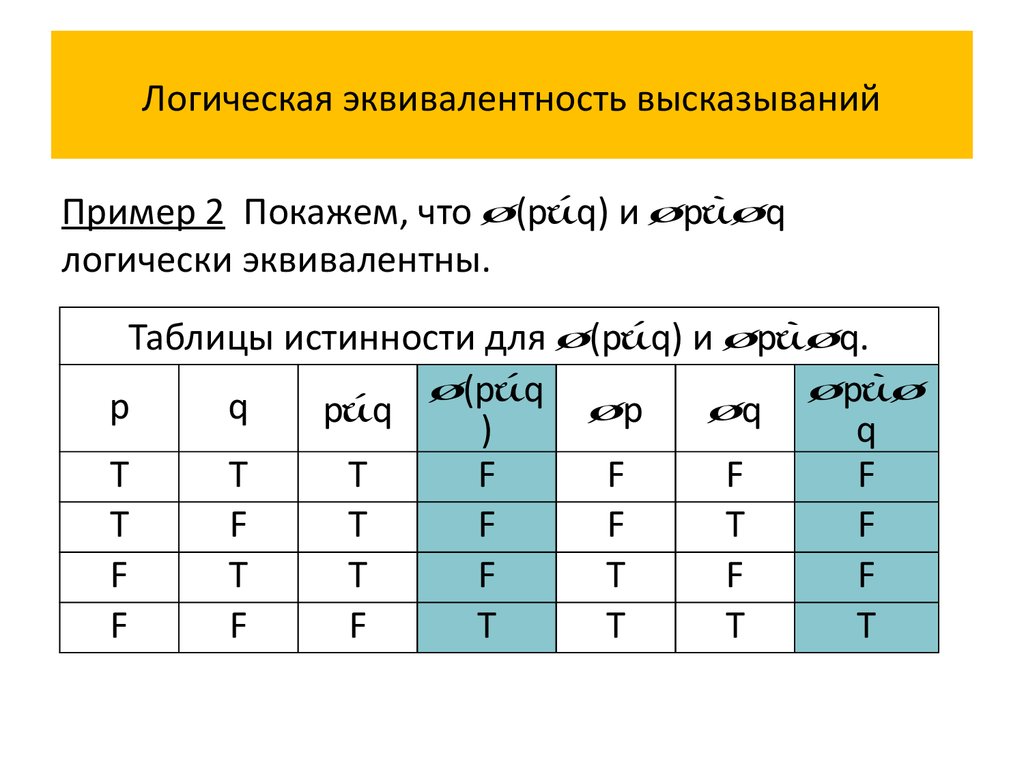 Что вы наблюдаете.
Что вы наблюдаете.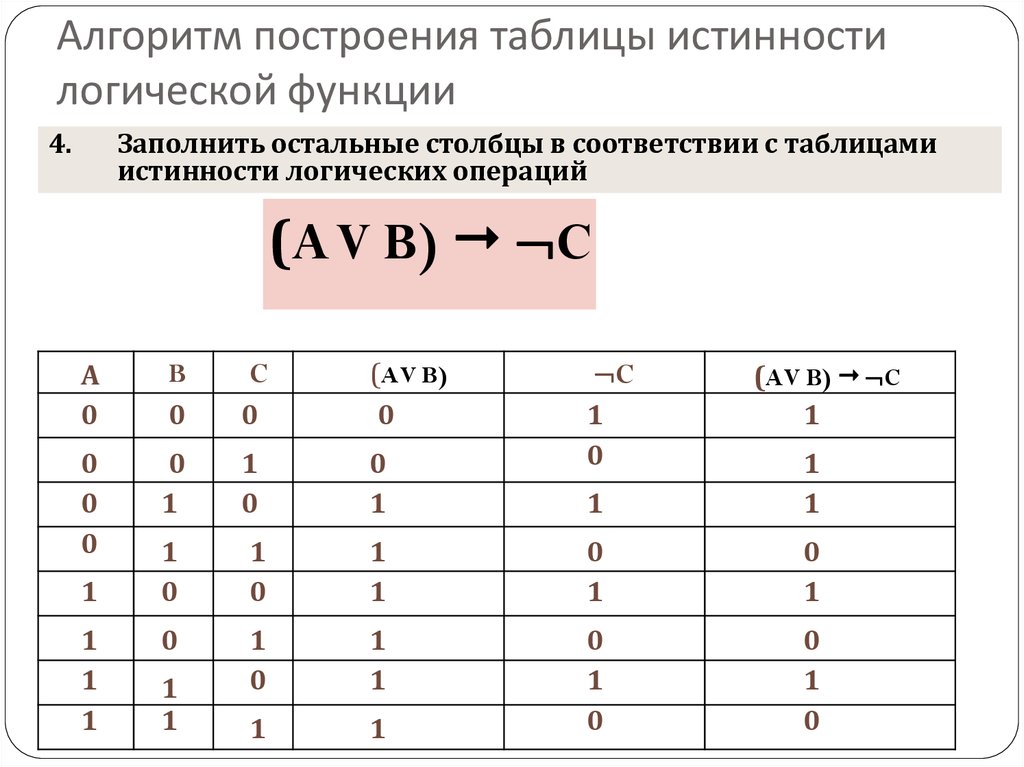
 Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.
Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.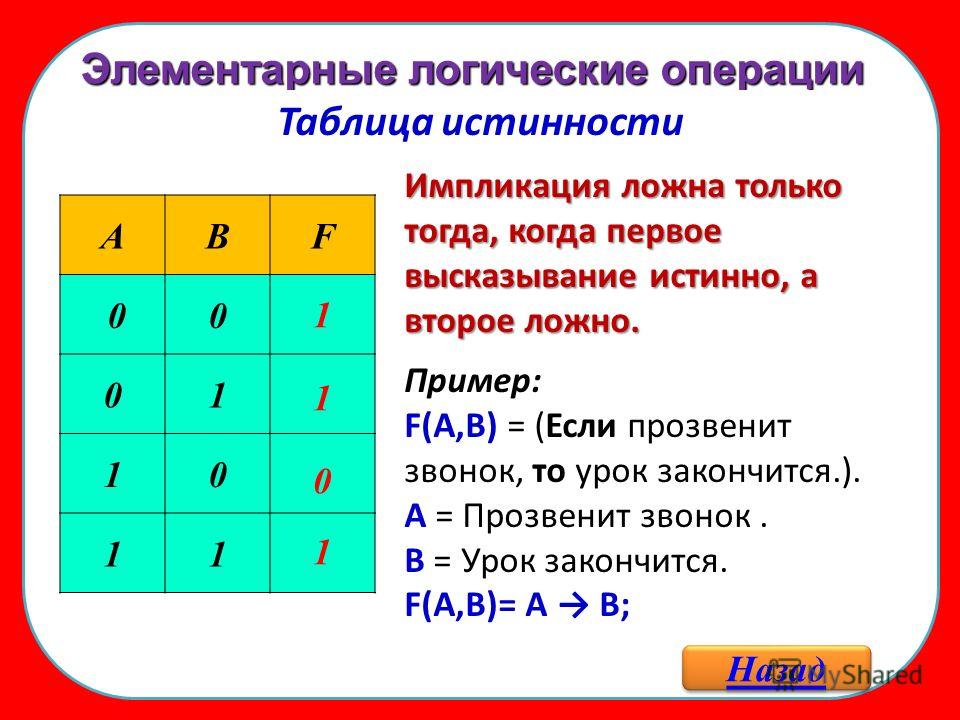 gvsu.edu/books/7
gvsu.edu/books/7 Q означает P и Q.
Q означает P и Q.