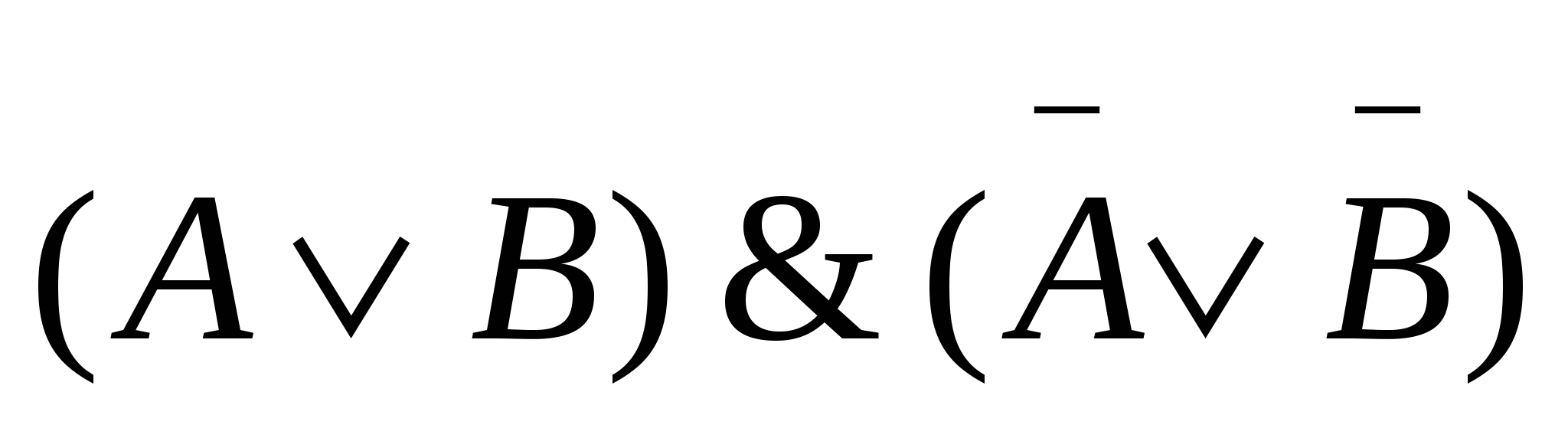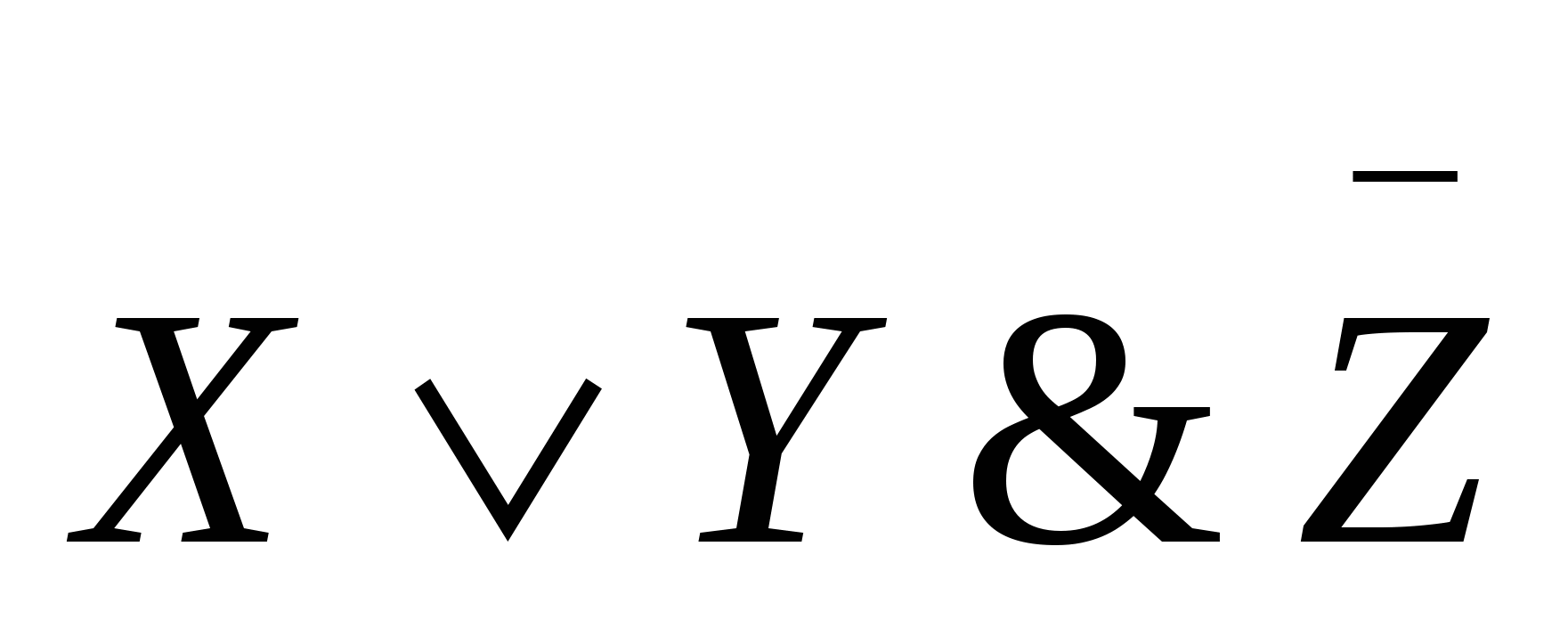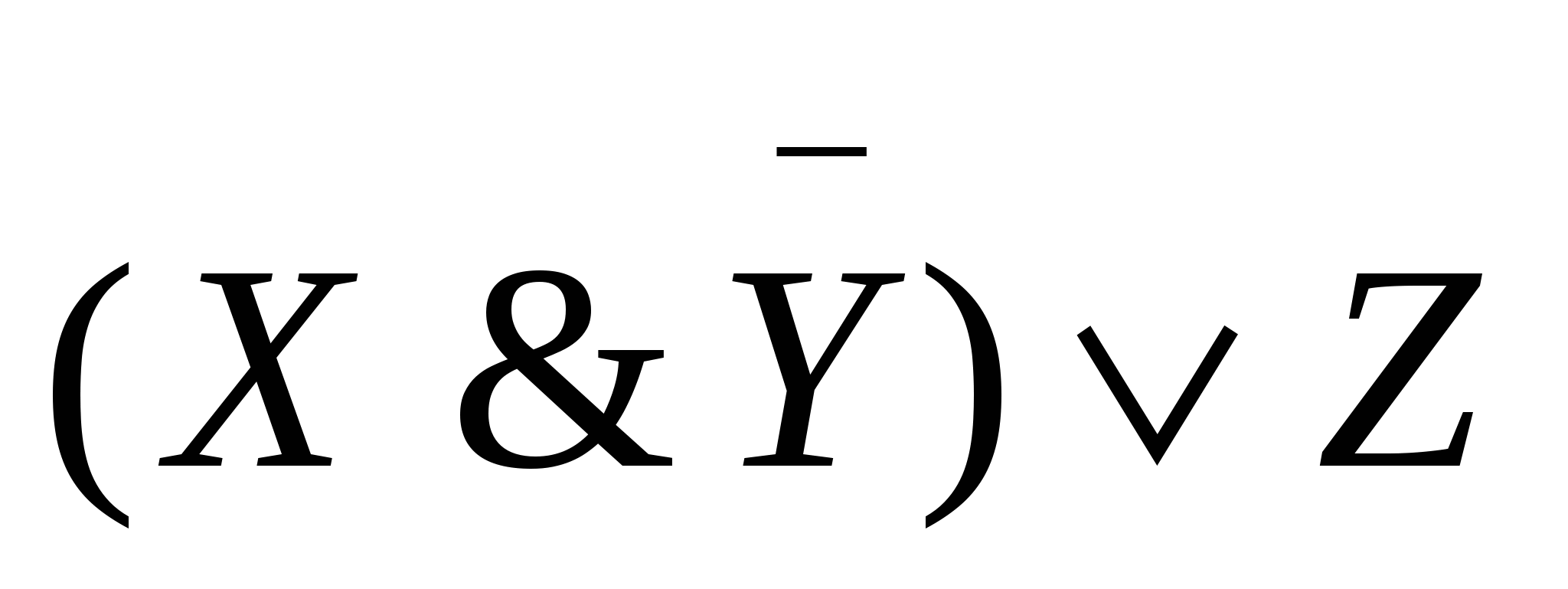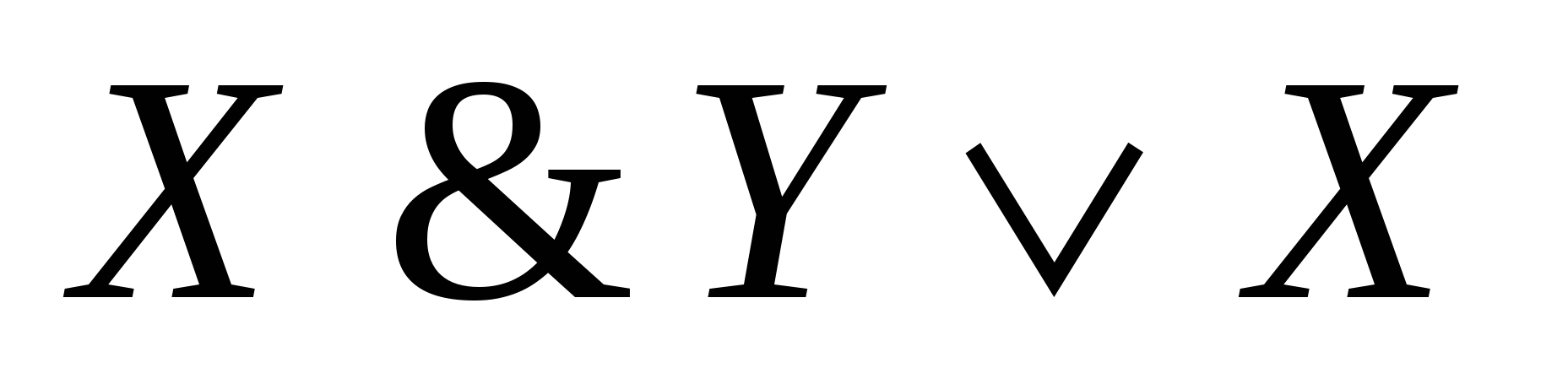Универсальная алгебра, алгебраическая логика и базы данных | Плоткин Б.И.
Плоткин Б.И.
Аннотация: Излагается одна из возможных точно математически обоснованных математических моделей’баз данных?? важнейшего понятия программирования. Развиваются алгебраические, в частности, категорные основы теории, различные подходы, направленные на алгебраизацию узкого исчисления предикатов, алгебраические модели базы данных. Дается обзор проблем теории баз данных и сопоставлены различные подходы исследований в этой области. Для специалистов в области алгебры и математической логики, а также в теоретическом и практическом программировании. От себя: IMHO, одна из лучших книг в этой области, которая дает наконец понимание того, зачем же вообще в жизни нужна абстрактная алгебра, кроме как для умозрительных заключений 🙂 Другие книги по математической логике на сайте: Никольская И.Л. Математическая логика Мендельсон Э. Введение в математическую логику Мальцев А.Н. Алгоритмы и рекурсивные функции Мальцев А.И. Избранные труды, в 2-х томах Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов Крайзель Г. Исследования по теории доказательств Колмогоров А.Н., Драгалин А.Г. Введение в математическую логику Клини С.К. Математическая логика Гохман А.В. Сборник задач по математической логике и алгебре множеств Гилберт Д., Аккерман В. Основы теоретической логики Гилберт Д., Бернайс П. Основания математики Р. Грэхем, Д. Кнут, О. Паташник Конкретная математика. Основание информатики Другие книги по общей алгебре на сайте: Мальцев А.И. Избранные труды, в 2-х томах Ленг С. Алгебра Курош А.Г. Теория групп Курош А.Г. Общая алгебра Кострикин А.И. Сборник задач по алгебре Кострикин А.И. Введение в алгебру. Основы алгебры Кон П. Универсальная алгебра Биркгоф Г., Барти Т. Современная прикладная алгебра Биркгоф Г. Теория решеток Биркгоф Г. Теория структур Гретцер Г. Общая теория решеток Гохман А.В. Сборник задач по математической логике и алгебре множеств Бурбаки Н. Основные структуры анализа Бурбаки Н. Алгебра. Том 1. Алгебраические структуры. Линейная и полилинейная алгебра Бурбаки Н. Алгебра. Том 2. Многочлены и поля Бурбаки Н. Алгебра. Том 3. Модули, кольца, формы Бурбаки Н. Алгебра. Том 4. Гомологическая алгебра
Методическое пособие по информатике на тему «Основы алгебры логики»
Методическое пособие
по дисциплине «Информатика и ИКТ»
«Основы алгебры логики»
для студентов 1 курса
Омск — 2015
Разработчик: Лиличенко И.Г., преподаватель БОУ СПО «ОмТТ»
Данное методическое пособие предназначено для студентов 1 курса, при освоении темы «Основы алгебры логики», «Построение таблиц истинности». В данном пособии представлен теоретический материал по данным темам, рассмотрены примеры. Представлены задания для самостоятельной работы студентов.
Основные понятия
Логика – это наука о законах и формах мышления.
Высказывание (суждение) — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Например: «Москва – столица России»
Утверждение – это суждение, которое требуется доказать или опровергнуть.
Например: «Сумма внутренних углов треугольника равна 1800»
Рассуждение – это цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Например: «Если хотите начать работать на компьютере, то необходимо сначала включить электропитание»
Умозаключение – это логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.
Например: «Все металлы электропроводны». «Ртуть является металлом». Путем умозаключения можно сделать вывод, что «Ртуть электропроводна».
Логическое выражение – это запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)
Сложное логическое выражение – это логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
Например: (А ۸ (В ۷ С))
Логические операции – это мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логические операции и таблицы истинности
A
B
1
1
1
1
0
0
0
1
0
0
0
0
F = A & B.Логическое умножение — КОНЪЮНКЦИЯ — это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И. Обозначения , &, , AND, И
A
F
1
1
1
1
0
1
0
1
1
0
0
0
F = A + BЛогическое сложение – ДИЗЪЮНКЦИЯ — это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ. Обозначения , +, OR, ИЛИ
A

1
0
0
1
Логическое отрицание — ИНВЕРСИЯ — если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО. Обозначения , , NOT, НЕ,
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1
F= A B Логическое следование — ИМПЛИКАЦИЯ — связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом «следовательно» и выражается словами
A
B
F
1
1
1
1
0
0
0
1
0
0
0
1
F=A BЛогическая равнозначность — ЭКВИВАЛЕНТНОСТЬ
Порядок выполнения логических операций в сложном логическом выражении:
1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Для изменения указанного порядка выполнения операций используются скобки.
Таблица истинности логической формулы (функции) выражает соответствие между всеми возможными наборами значений логических переменных и значением функции.
Для функции от двух переменных существует 22 = 4 комбинации наборов значений переменных, для функции трех переменных – 23 = 8, для функции четырех переменных – 24 = 16 комбинаций значений наборов переменных.
В общем случае для функции от N переменных число строк M в таблице истинности вычисляется по формуле:
M = 2N
Последовательность построения таблицы истинности:
Определить количество N используемых переменных в логическом выражении.
Вычислить количество всевозможных наборов значений переменных M = 2N , равное количеству строк в таблице.
Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
Заполнить окончательный столбец значений для функции F.
ПРИМЕРЫ:
Составить таблицу истинности сложного логического выражения
D =  & ( B+C )
& ( B+C )
А, В, С — три простых высказывания, поэтому:
количество строк = 23 = 8 (n=3, т.к. на входе три элемента А, В, С)
количество столбцов:
1) А
2) В
3) С
4)  это инверсия А
это инверсия А
5) B + C это операция дизъюнкции
6) D =  & ( B+C ) это операция конъюнкции
& ( B+C ) это операция конъюнкции
1
2
3
4
5
6
А
В
С

В+С
 & ( B+C )
& ( B+C )
1
1
1
0
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
1
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
0
0
1
0
0
Составить таблицу истинности сложного логического выражения
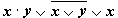
Х, Y – два простых высказывания, поэтому:
количество строк = 22 = 4 (n=2, т.к. на входе два элемента Х, Y)
количество столбцов:
1) Х
2) Y
3) 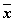
4) 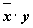
5) 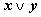
6) 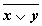
7) 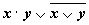
8) 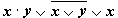
Переменные
Промежуточные логические формулы
Формула
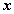
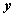
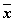
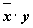
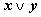
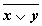
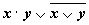
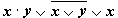
0
0
1
0
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
0
1
0
0
1
1
1
0
0
1
0
0
1
Составить таблицу истинности сложного логического выражения
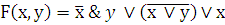
Переменные
Промежуточные логические формулы
Функция F
x
y
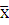
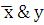
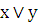
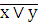
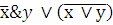
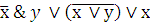
0
0
1
0
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
0
1
0
0
1
1
1
0
0
1
0
0
1
Составить таблицу истинности сложного логического выражения
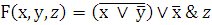
Переменные
Промежуточные логические формулы
Функция F
x
y
z
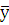
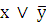
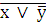
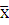
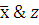
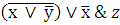
0
0
0
1
1
0
1
0
0
0
0
1
1
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
1
0
0
1
1
0
0
0
0
1
0
1
1
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
1
0
1
0
0
0
0
Проверь себя:
Соедините правильно определения или обозначения:
Логика
Высказывание
Алгебра логики
Логическая константа
Дизъюнкция
Инверсия
Конъюнкция
Логическое сложение
Наука о формах и способах мышления
Логическое отрицание
ИСТИНА и ЛОЖЬ
&
Наука об операциях над высказываниями
Повествовательное предложение, в котором что-либо утверждается или отрицается.
Задания для самостоятельной работы:
Составьте ТИ выражений:
Книги и учебники по логике и логическому мышлению
На данной странице мы подобрали полезные книги и учебники, которые помогут вам углубить свои знания в логике и логическом мышлении:
Оглавление:
«Прикладная логика». Николай Николаевич Непейвода
 Учебник «Прикладная логика» Николая Николаевича Непейводы является простейшим пособием по современной математической логике. Книга рекомендована Государственным комитетом Российской Федерации по высшему образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальностям «Прикладная математика», «Математика», «Лингвистика», «Психология» и «Философия». Учебник дает подробное и комплексное описание прикладной логики, а также логического аппарата, систематически используемого для решения конкретных практических задач.
Учебник «Прикладная логика» Николая Николаевича Непейводы является простейшим пособием по современной математической логике. Книга рекомендована Государственным комитетом Российской Федерации по высшему образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальностям «Прикладная математика», «Математика», «Лингвистика», «Психология» и «Философия». Учебник дает подробное и комплексное описание прикладной логики, а также логического аппарата, систематически используемого для решения конкретных практических задач.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Учебник логики». Георгий Иванович Челпанов
 «Учебник логики» Георгия Ивановича Челпанова – является одним из самых известных в России. Он был написан выдающимся русским философом и логиком, отмечен премией Петра Великого и еще в дореволюционный период пережил девять изданий. Когда в СССР после войны было решено включить логику в перечень предметов средней школы, первым учебником стало издание труда Г. И. Челпанова в сокращенном варианте. Сам автор говорил о книге, что она предназначена не только для гимназий, но и для самообразования.
«Учебник логики» Георгия Ивановича Челпанова – является одним из самых известных в России. Он был написан выдающимся русским философом и логиком, отмечен премией Петра Великого и еще в дореволюционный период пережил девять изданий. Когда в СССР после войны было решено включить логику в перечень предметов средней школы, первым учебником стало издание труда Г. И. Челпанова в сокращенном варианте. Сам автор говорил о книге, что она предназначена не только для гимназий, но и для самообразования.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Краткий курс логики: искусство правильного мышления». Дмитрий Алексеевич Гусев
 Этот труд Дмитрия Алексеевича Гусева посвящен детальному анализу аристотелевской (или формальной) логики – научной области о получении знания на основе применения законов и правил мышления. Прекрасно подойдет учащимся старших классов, всем интересующимся логикой. Книга написана простым и понятным языком. Несомненным плюсом книги является размещение в конце тестовых заданий и сборника занимательных логических задач и головоломок, благодаря которым мы и любим логику.
Этот труд Дмитрия Алексеевича Гусева посвящен детальному анализу аристотелевской (или формальной) логики – научной области о получении знания на основе применения законов и правил мышления. Прекрасно подойдет учащимся старших классов, всем интересующимся логикой. Книга написана простым и понятным языком. Несомненным плюсом книги является размещение в конце тестовых заданий и сборника занимательных логических задач и головоломок, благодаря которым мы и любим логику.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика». Евгений Акимович Иванов
 В основу учебника положены лекции, прочитанные автором – Евгением Акимовичем Ивановым, доктором философских наук, профессором. Книга специально адаптирована для будущих юристов. Материал (иллюстрации, описанные примеры) также подобран соответственно потребностям целевой аудитории.
В основу учебника положены лекции, прочитанные автором – Евгением Акимовичем Ивановым, доктором философских наук, профессором. Книга специально адаптирована для будущих юристов. Материал (иллюстрации, описанные примеры) также подобран соответственно потребностям целевой аудитории.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика. Учебник для юридических вузов». В. И. Кириллов, А. А. Старченко
 Учебник переиздавался больше пяти раз и сегодня остается одним из лучших материалов для самоподготовки и подготовки к экзаменам в рамках изучения логики студентами юридических специальностей. Последний нюанс нашел в книге достаточное обоснование – ключевые моменты проиллюстрированы на примерах из юридической практики. Темы раскрыты кратко и по существу, как и должно быть в учебнике логики. В то же время материал излагается просто и доступно.
Учебник переиздавался больше пяти раз и сегодня остается одним из лучших материалов для самоподготовки и подготовки к экзаменам в рамках изучения логики студентами юридических специальностей. Последний нюанс нашел в книге достаточное обоснование – ключевые моменты проиллюстрированы на примерах из юридической практики. Темы раскрыты кратко и по существу, как и должно быть в учебнике логики. В то же время материал излагается просто и доступно.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика для юристов» (со сборником задач). А. Д. Гетманова
 Учебник посвящен тем аспектам логики, которые широко применяются юристами и правоведами. Он предназначен для изучения логики на юридических факультетах и отделениях по маркетингу, в юридических вузах, юридических колледжах, а также для изучения права в общеобразовательных школах. Подойдет для студентов, юристов, учителей, слушателей в системе повышения квалификации и всех интересующихся проблемами логики и юриспруденции.
Учебник посвящен тем аспектам логики, которые широко применяются юристами и правоведами. Он предназначен для изучения логики на юридических факультетах и отделениях по маркетингу, в юридических вузах, юридических колледжах, а также для изучения права в общеобразовательных школах. Подойдет для студентов, юристов, учителей, слушателей в системе повышения квалификации и всех интересующихся проблемами логики и юриспруденции.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика. Учебник для гуманитарных факультетов». А. А. Ивин
 Рекомендованный Министерством образования учебник логики для вузов, студенты которых изучают науки гуманитарного цикла. Этому заданию подчинена структура и поднимаемые в тексте проблемы логики. Особое внимание уделяется логическому анализу естественного языка, проблеме понимания и искусству полемики и дискуссии. Структура и подбор тем позволяют моделировать курс логики соответственно объему учебного времени и профилю учебного заведения.
Рекомендованный Министерством образования учебник логики для вузов, студенты которых изучают науки гуманитарного цикла. Этому заданию подчинена структура и поднимаемые в тексте проблемы логики. Особое внимание уделяется логическому анализу естественного языка, проблеме понимания и искусству полемики и дискуссии. Структура и подбор тем позволяют моделировать курс логики соответственно объему учебного времени и профилю учебного заведения.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика. Учебник для средней школы». С. Н. Виноградов, А. Ф. Кузьмин
 Советский учебник 1954 г. одобренный Министерством просвещения РСФСР. «В труде и в быту, в учебной и общественной работе, в научном трактате и в школьном сочинении – везде и всегда необходимо правильное, т. е. определённое, непротиворечивое, последовательное, обоснованное, мышление. Без правильного мышления, которое осуществляется с помощью языка, человек не мог бы ни трудиться, ни общаться с другими людьми». В простой и доступной форме этот школьный учебник и должен был дать основы знаний о логике.
Советский учебник 1954 г. одобренный Министерством просвещения РСФСР. «В труде и в быту, в учебной и общественной работе, в научном трактате и в школьном сочинении – везде и всегда необходимо правильное, т. е. определённое, непротиворечивое, последовательное, обоснованное, мышление. Без правильного мышления, которое осуществляется с помощью языка, человек не мог бы ни трудиться, ни общаться с другими людьми». В простой и доступной форме этот школьный учебник и должен был дать основы знаний о логике.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
«Логика. Конспект лекций». Д. А. Шадрин
 Книга-шпаргалка с лекциями, которые по утверждению авторов имеют ответы на самые распространенные вопросы зачетов и экзаменов. Конспект лекций составлен в соответствии с общегосударственным стандартом по указанной дисциплине; призван помочь систематизировать полученные ранее знания и успешно сдать экзамен или зачет по логике.
Книга-шпаргалка с лекциями, которые по утверждению авторов имеют ответы на самые распространенные вопросы зачетов и экзаменов. Конспект лекций составлен в соответствии с общегосударственным стандартом по указанной дисциплине; призван помочь систематизировать полученные ранее знания и успешно сдать экзамен или зачет по логике.
Узнать больше, а также скачать и прочитать книгу вы cможете на данной странице.
Отзывы и комментарии
Если вы знаете и другие полезные учебники по логическому мышлению или хотите поделиться своим мнением об описанных выше книгах, можете оставить комментарий в форме ниже.
 Кирилл Ногалес
Кирилл Ногалес
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
| 2011 — 2018 | |||||||||||||||||||||||||||||||||||||||||||||||