Задание 4. — Удивительный мир логики
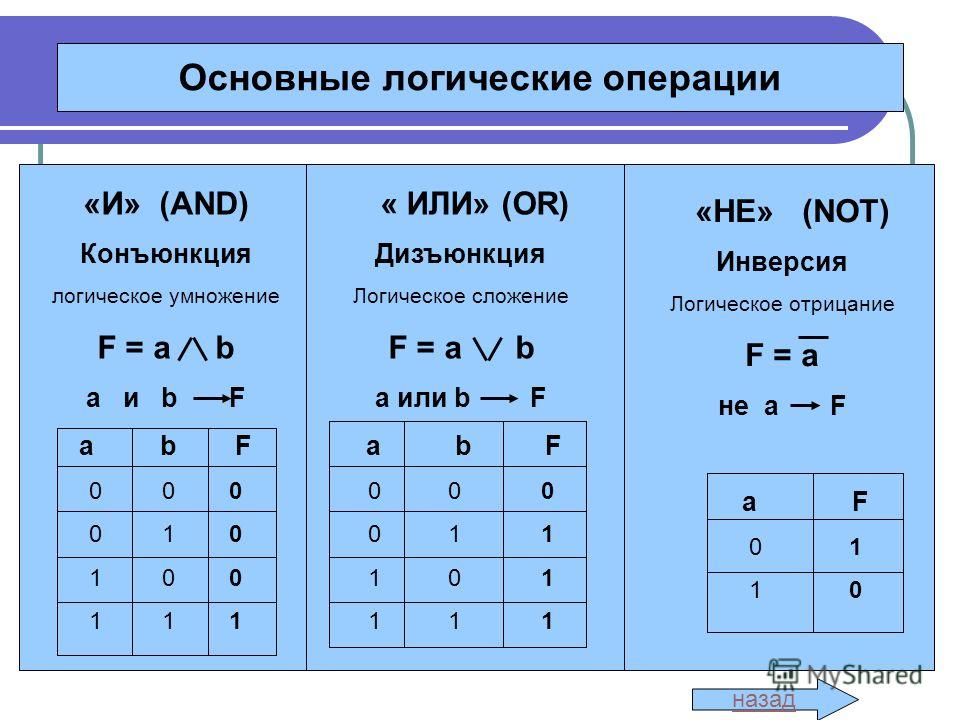
Конъюнкцией называют «логическое умножение» или «логическое И» , а часто просто «И» . В естественном языке конъюнкцию заменяют союзом И. Для обозначения конъюнкции применяют различные символы. Это может быть знак &, AND. Но чаще всего для обозначения конъюнкции используют символ /\ . Рассмотрим пример. Пусть есть два высказывания: A = «Москва — столица России» и B = «Сегодня солнечно». Тогда конъюнкция этих высказываний будет выглядеть так «Москва — столица России И сегодня солнечно», а обозначаться так: A /\ B Так как на клавиатуре нет символа конъюнкции, его можно набрать из слэша ( / ) и бэкслэша ( \ ) — получится /\ — похоже на обозначение конъюнкции. Таблица истинности для конъюнкции выглядит так: Запомнить довольно просто — конъюнкция истинна только в одном случае — когда оба исходных высказывания истинны. Следующая логическая операция, которую мы рассмотрим после конъюнкции — дизъюнкция. Дизъюнкция — логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражений ложны. Обозначение: A\/ B Таблица истинности для дизъюнкции выглядит так: Часто можно встретить другие названия этой операции — логическое сложение, логическое ИЛИ или просто ИЛИ. В естественном языке дизъюнкция заменяется союзом ИЛИ. Логическое отрицание или Инверсия — это сложное логическое выражение, в котором если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоброт, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими словами, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО… Таблица истинности для инверсии выглядит так: Рекомендуется к просмотру: В качестве примера решения задач с логическими выражениями рассмотрим следующую задачу: Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящих гонок. — Вот увидишь, Шумахер не придет первым, — сказал Джон. — Первым будет Хилл. — Да нет, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым. Питер, к которому обратился Ник, возмутился: — Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину. По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки? Решение:
Теперь вам предстоит заполнить Google-форму и решить задания. Критерии оценивания записаны ниже: Задачи и задания на логикуКРИТЕРИИ ОЦЕНКИ:
Успехов вам! |
Основы алгебры логики в одной странице — Сайт учителя информатики Лосева А.В.
Изображение:
Краткая подсказка по логическим операциям и таблицам истинности.
Скачать шпаргалку «Основы алгебры логики в одной странице»
Логические операции
Инверсия (отрицание)
Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или .
Читается «НЕ» (например, «не А»).
Конъюнкция (логическое умножение)
Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
Дизъюнкция (логическое сложение)
Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б»)
Импликация (следование)
Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б»)
Эквивалентность (равнозначность)
Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
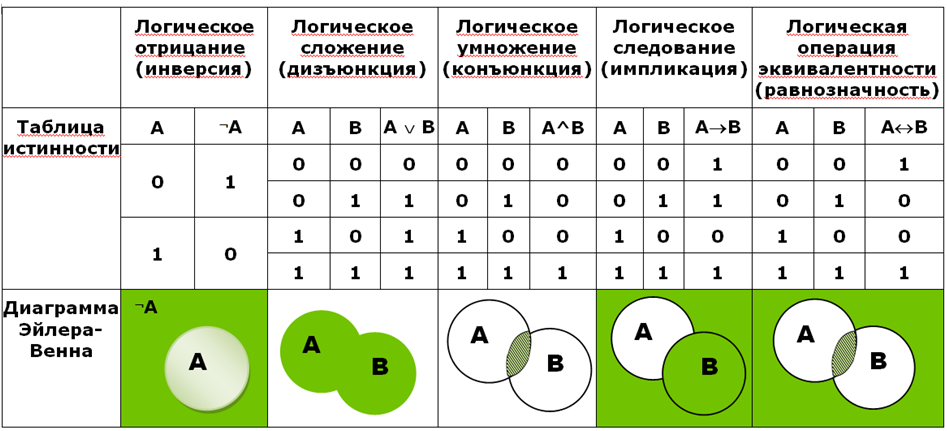
Таблицы истинности
|
|
|
|
|
Статью подготовил учитель информатики Лосев Антон Владимирович
10 класс, ученику, логика, алгебра логики, операции, конъюнкция, дизъюнкция, объяснение, таблица истинности, в помощь
соединений и дизъюнкций в математике (определение и примеры)
Написано
Малкольм МакКинси
, проверенные по фактам, с помощью
Пол Маццола
в математическом логике, слов имеют сознания.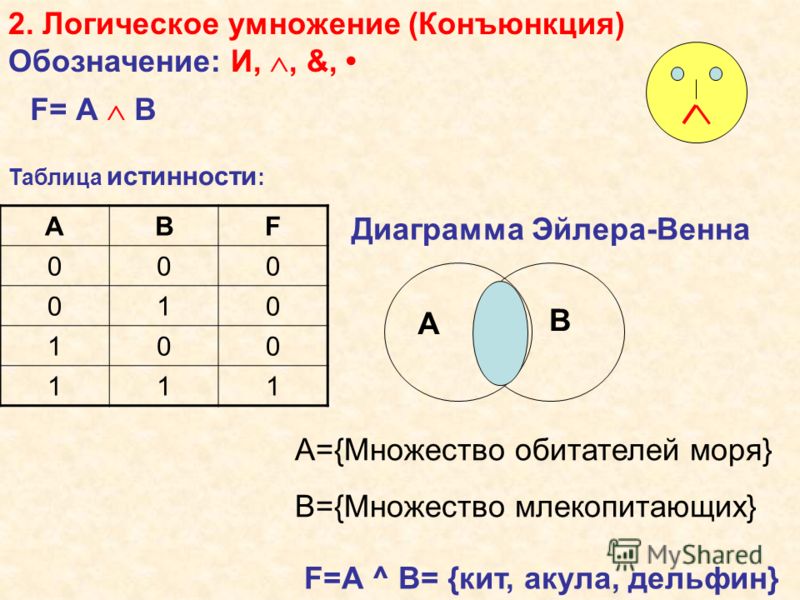
Логика пытается показать правдивые выводы, вытекающие из правдивых предпосылок, или надежно выявляет ложь.
Математические и логические операторы соединяются соединителями; конъюнкции и дизъюнкции — это два типа логических соединителей.
с логикой, операторов могут быть помечены как истинные или ложные, такие как:
Все цифры являются целыми числами
Некоторые отрицательные номера
квадраты. параллелограммы
Четырехугольники имеют 11 сторон
Прямоугольники имеют четыре стороны
Ясно, что некоторые из этих шести утверждений ложны, но дело в том, что их можно проверить. Они не высказывают мнения. Сравните их, скажем, «Мне нравятся чизбургеры», что показывает мнение.
Логические разъемы
Операторы часто обозначаются буквами p и q. Они связаны вместе с помощью соединителей, поэтому вы можете комбинировать идеи, используя «и» или «или» между утверждениями.
Два оператора, соединенные соединителями, создают составной оператор . Соединение логических утверждений — это не то же самое, что связывание идей в обычном английском разговоре. Сравните:
Первые связанные высказывания, одно составное высказывание, являются мнениями. Второе составное утверждение является логическим утверждением (но составное утверждение ложно).
Два типа соединителей называются союзами («и») и дизъюнкциями («или»). В соединениях используется математический символ ∧ , а в дизъюнкциях используется математический символ ∨ .
Союзы в математике
Соединение двух утверждений с помощью «и» является соединением , что означает, что оба утверждения должны быть истинными, чтобы все составное утверждение было истинным. Соединения обозначаются символом ∧ , поэтому эти два отдельных утверждения можно объединить в составное утверждение:
Утверждение p : Квадраты являются прямоугольниками
Утверждение q : У прямоугольников четыре стороны
Составное утверждение (в математических символах): p∧q
Только если обе части составного утверждения верны, все утверждение истинно.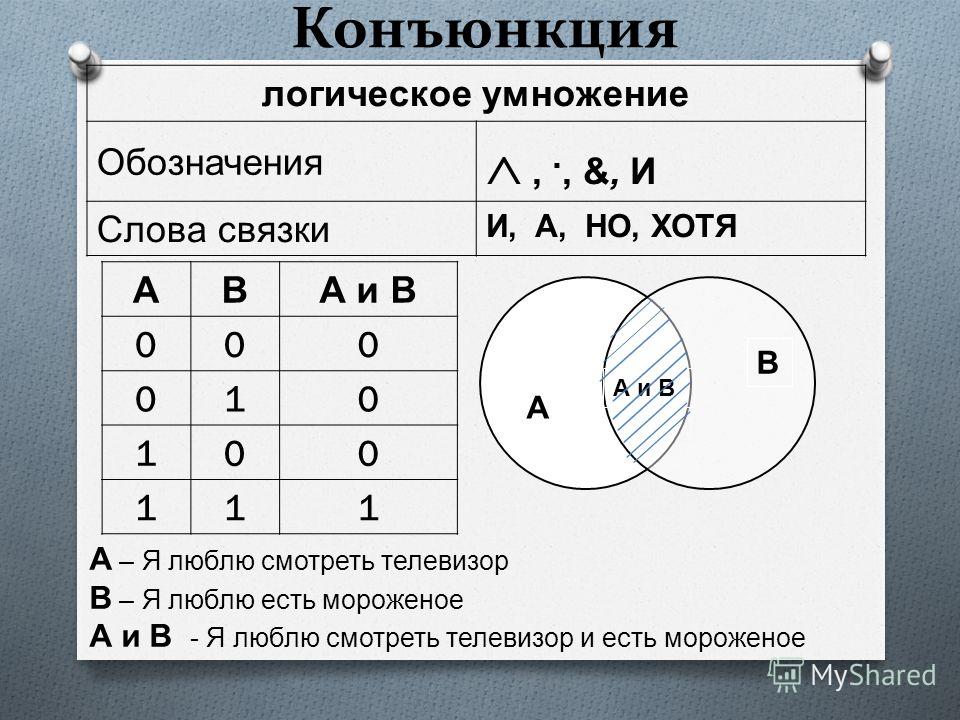
Дизъюнкции в математике
Когда связующим звеном между двумя операторами является «или», у вас есть дизъюнкция . В этом случае только одно утверждение в составном утверждении должно быть истинным, чтобы все составное утверждение было истинным.
Давайте еще раз посмотрим на исходные утверждения:
Все числа целые
Некоторые отрицательные числа целые
Квадраты являются прямоугольниками
0003
Четырехугольники имеют 11 сторон
Прямоугольники имеют четыре стороны
Истинное составление заявления:
P : квадраты — прямоугольники
Q : Квадрилатары имеют 11 сторон
P∨Q : All Produes — это прямоугольные или квалификации, 11019 P∨Q : All Cquares Ha Hafterlals 11 Sines 11 Sines 11 Sines 11 Sines 11 Sines P∨Q.0003
Примеры соединения и дизъюнкции
Вот еще четыре составных утверждения, взятые из наших исходных утверждений.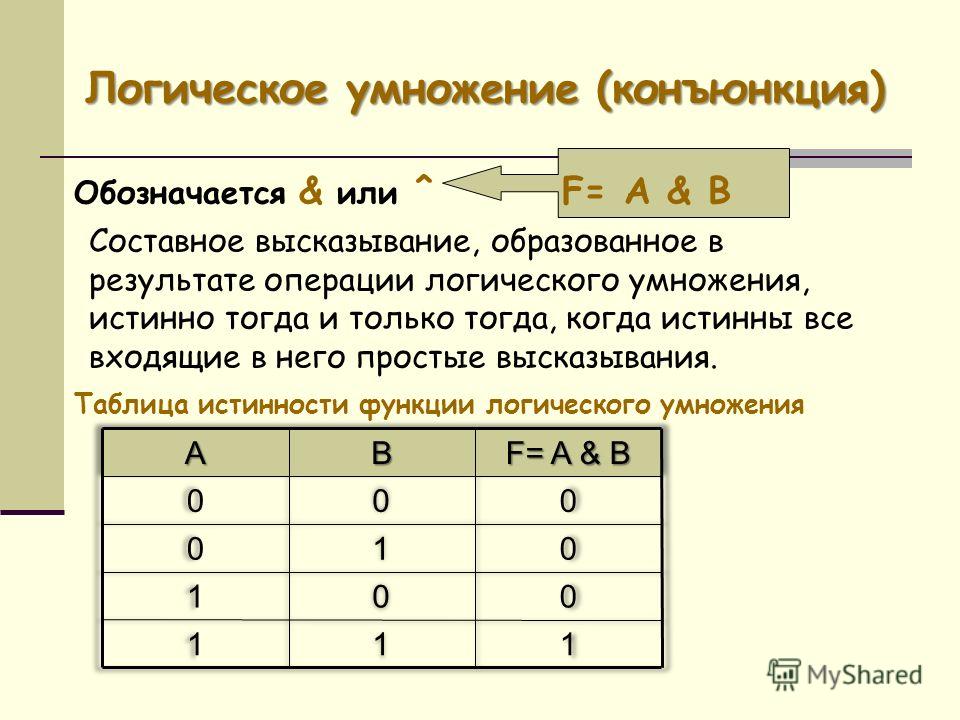
Определите символы и истинны или ложны составные утверждения:
p : Некоторые отрицательные числа являются целыми числами
q : Квадраты являются прямоугольниками
квадратыцелые числа .
Вы сказали p∧q , и вы оценили это как правду? Оба утверждения верны, поэтому составное утверждение, соединенное союзом «и», истинно.
p : Некоторые четырехугольники являются параллелограммами
q : Четырехугольники имеют 11 сторон
Вы сказали p∨q и оценили это составное утверждение как истинное? Хотя у четырехугольников нет 11 сторон, союз «или» делает составное утверждение верным, поскольку некоторые четырехугольники являются параллелограммами.
p : Четырехугольники имеют 11 сторон
q : Четырехугольники имеют четыре стороны
Вы сказали p∧q ? Что еще более важно, вы сказали, что это составное утверждение было ложным? Поскольку у четырехугольников нет 11 сторон, конъюнкция неверна.
p : Все числа целые
q : Квадраты являются прямоугольниками
Все числа являются целыми числами или квадраты являются прямоугольниками.
Вы написали p∨q ? Вы сказали, что это ложно, поскольку обе части составного утверждения ложны?
Соединения и дизъюнкции — это способы соединения логических утверждений, при этом каждое составное высказывание может быть либо истинным, либо ложным. Для союзов оба утверждения должны быть истинными, чтобы составное утверждение было истинным.
Для дизъюнкций только одно утверждение должно быть истинным, чтобы составное утверждение было истинным.
Nemeth Tutorial — Lesson 10.2
Логические операторы — составные операторы
В логических функциях используются два типа составных операторов. Они называются конъюнкция и дизъюнкция. Конъюнкция означает, что оба утверждения верны, а дизъюнкция означает, что хотя бы одно утверждение истинно.
С союзом утверждения соединяются словом «и», а с дизъюнкцией утверждения соединяются словом «или».
Символ соединения ∧. Это двухклеточный символ точки четыре, за которой следуют точки один четыре шесть.
Символ дизъюнкции ∨. Это также двухклеточный символ точки четыре, за которой следуют точки три четыре шесть.
Правила для этих символов аналогичны другим знакам сравнения.
Если перед оператором появляется тильда, это означает, что нужно найти дополнение к оператору.
Символы конъюнкции и дизъюнкции считаются операциями. Таким образом, перед символом или после него нет пробела. Он расположен аналогично знаку плюс или минус.
Если знаки соединения или разъединения имеют другие символы, такие как полосы или точки, надписанные или подписанные, такой символ считается знаком сравнения.
Бикондиционал (знаки формы: стрелки)
Стрелки используются для различных целей в математике. Их примеры включают использование в качестве знаков сравнения, следовательно, приближений или уступок, в качестве наложенных символов для обозначения лучей или векторов или в качестве внутренних символов в других формах.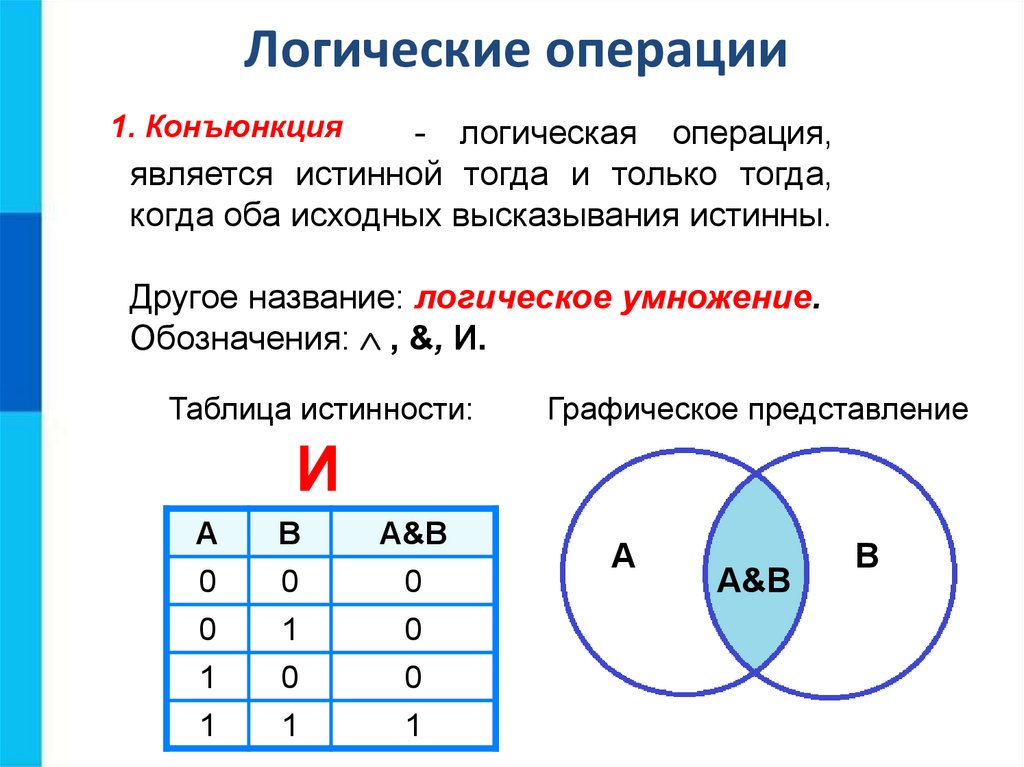
При построении стрелок индикатор формы вычерчивается первым. Затем стрелки расшифровываются в том порядке, в котором появляются их символы, то есть в вертикальном направлении, если это уместно, древке или наконечнике стрелы. У стрелки, указывающей влево, наконечник стрелки будет напечатан шрифтом Брайля после индикатора формы, за которым следует стержень. Стрелка, указывающая вправо, сначала напечатала бы вал. Стрелки, указывающие в направлениях, отличных от левого или правого, требуют соответствующего указателя направления стрелки, следующего за индикатором формы, как указано ниже.
1. указатель непосредственно над индикатором, точки одна две шесть, для стрелок, направленных вверх
2. указатель непосредственно под индикатором, точки один четыре шесть, для стрелок, направленных вниз влево или вверх вправо
4. Нижний индекс для стрелок, указывающих вниз влево или вниз вправо.
Древко стрелы, когда оно отображается, состоит из двух ячеек точек два пять для стрелы с одним древком и двух ячеек точек два три пять шесть для стрелы с двойным древком.
Ниже перечислены некоторые распространенные стрелки.
стрелы с полным зазубрином:
направленные вправо, суженной формы →
⠫⠕
направленные вправо, несуженной формы, с одним стержнем →
⠫⠒⠒⠕
с направлением влево, с одним стержнем ←⒠
двойной шип на обоих концах ↔
⠫⠪⠒⠒⠕
правый, двойной стержень ⇒
⠫⠶⠶⠕
левый, двойной стержень ⇐ 4-09,690, направленный вниз вал ↓
⠫⠩⠒⠒⠕
направлен вверх, одинарный вал ↑
⠫⠣⠒⠒⠕
В отличие от логических операторов, стрелки считаются знаками сравнения и располагаются соответствующим образом.
