41)Алгебра логики. Упрощение логических выражений.
Алгебра логики— раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.
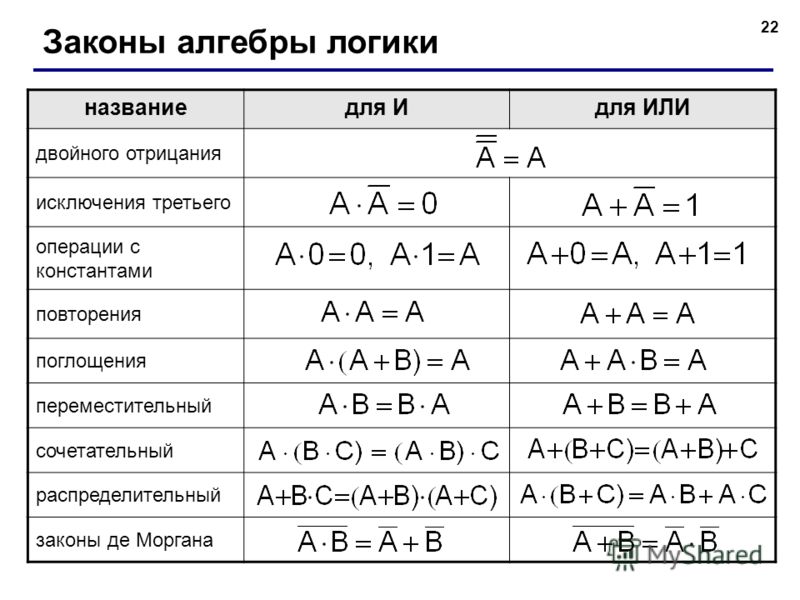
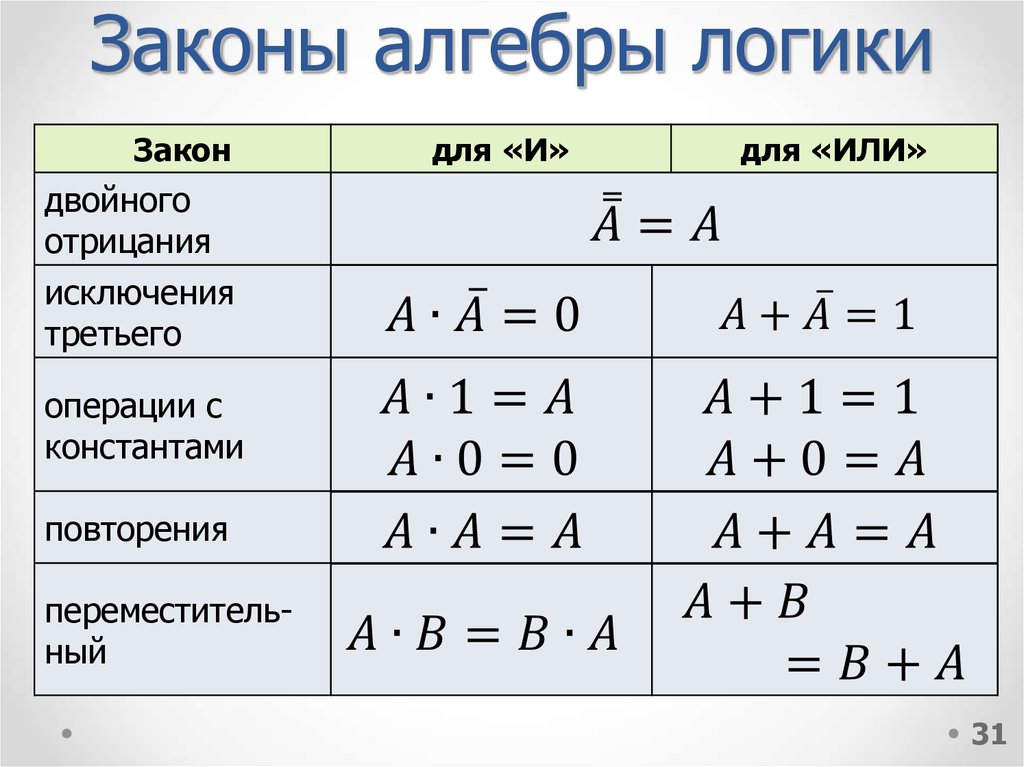
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Под упрощением формулы понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Некоторые
преобразования логических формул похожи
на преобразования формул в обычной
алгебре (вынесение общего множителя за
скобки, использование переместительного
и сочетательного законов и т.п.), тогда
как другие преобразования основаны на
свойствах, которыми не обладают операции
обычной алгебры (использование
распределительного закона для конъюнкции,
законов поглощения, склеивания, де
Моргана и др.
1):сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания.
2) : к отрицаниям формул применяется правило де Моргана; используются законы двойного отрицания и склеивания.
Алгебра логики— раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях. Функциональная схема – это логическая диаграмма, графический (геометрический, точнее — топологический) аппарат математической логики, показывающий её работу.
Доказать законы алгебры логики можно с помощью диаграммы Эйлера-Венна, которая является функциональной схемой.
Леонард
Эйлер при решении задач изображал
множества с помощью кругов, и в его честь
этот метод был назван «методом кругов
Эйлера». Однако такой прием очень
полезен и при решении логических задач,
когда с помощью кругов изображаются
высказывания. После Эйлера метод получил
развитие в работах других ученых,
однако наибольшего расцвета графические
методы достигли в работах логика Венна,
поэтому такие схемы называют «диаграммами
Эйлера-Венна».
Однако такой прием очень
полезен и при решении логических задач,
когда с помощью кругов изображаются
высказывания. После Эйлера метод получил
развитие в работах других ученых,
однако наибольшего расцвета графические
методы достигли в работах логика Венна,
поэтому такие схемы называют «диаграммами
Эйлера-Венна».
Закон де Моргана (Если существует операция логического умножения двух и более элементов, операция «и»—(A&B), то для того, чтобы найти обратное от всего суждения~(A&B), необходимо найти обратное от каждого элемента и объединить их операцией логического сложения,операцией «или»— (~A+~B). Закон работает аналогично в обратном направлении:~(A+B)= (~A&~B)) . Докажем его с помощью диаграммы эйлера-венна.
Для наглядного представления левой части равенства
Для
визуального представления правой части
равенства выполним
последовательно: заштрихуем область
для отображения инверсии (¬А) серым
цветом и аналогично область ¬В также
серым цветом; затем для отображения
конъюнкции нужно взять пересечение
этих серых областей (результат наложения
представлен черным цветом):Видим,
что области для отображения левой и
правой части равны.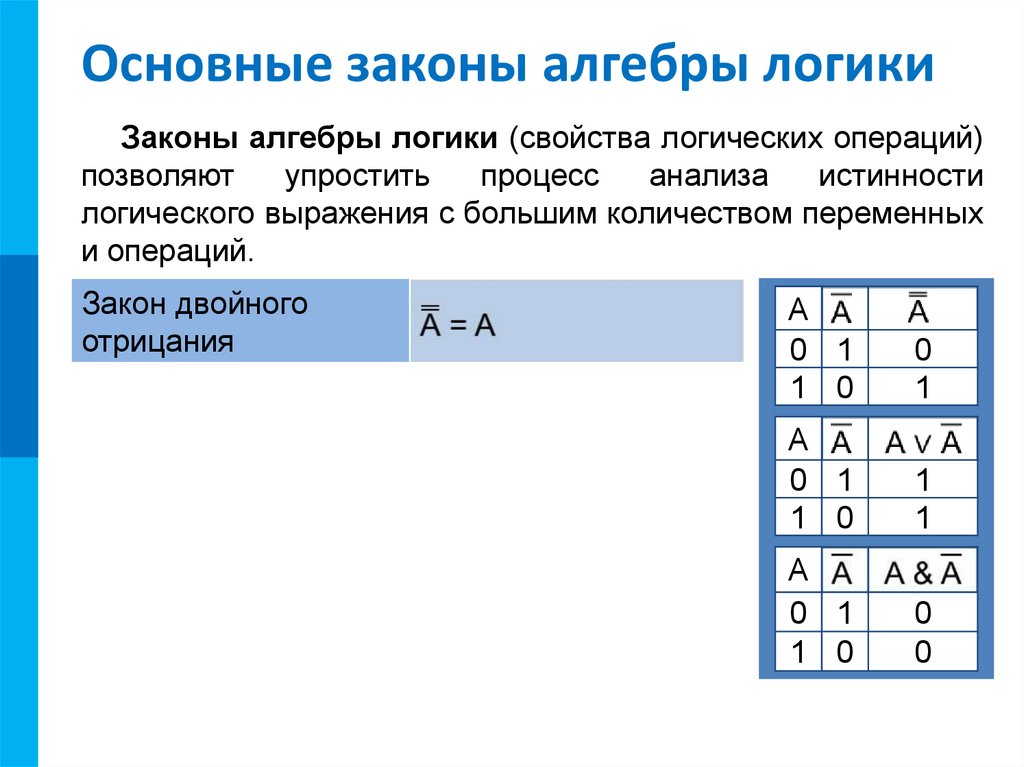 Что и требовалось
доказать.
Что и требовалось
доказать.
Логика: Алгебра логики
Основные связки
В двоичной логике каждому утверждению приписывается одно из двух значений: истина (\(\T\)) или ложь (\(\F\)). Константное утверждение (\(A\) : «сейчас идет дождь») называется высказыванием. Утверждение может зависеть от переменных \(P(x):~ x>0\). Такие переменные утверждения (\(=\) предикаты) истинны при одних \(x\) и ложны при других.
Это очень ограниченная модель «человеческой логики». Высказывание «сейчас идёт дождь» истинно или ложно, и третьего не дано. Хотя для многих «одна дождинка — ещё не дождь». Тем не менее, в формальных теориях, таких как математика, двоичной логики вполне достаточно.
Простые утверждения (высказывания, предикаты) объединяют
в более сложные при помощи логических связок (=операций) \(\neg\), \(\&\),\(\vee\), \(\equiv\).
Эти связки являются функциями, аргументы и значения которых принадлежат
множеству \(\{\T,\F\}.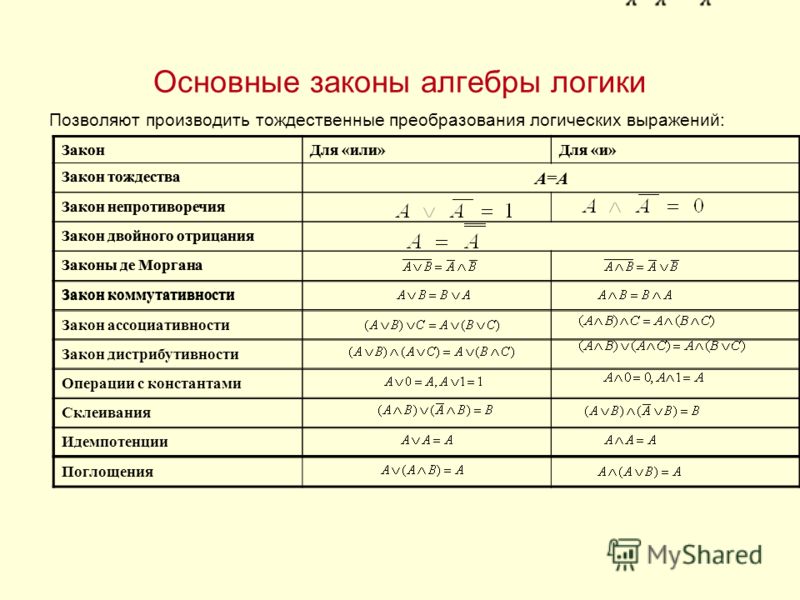 \)
\)
Логическое «ИЛИ» \(A\vee B\) истинно, если истинно или \(A\) или \(B\) или оба (хотя бы одно). Представим это утверждение при помощи таблицы истинности, где в колонках \(A\) и \(B\) перечисленны все варианты значений истинности высказываний \(A\) и \(B\), а под символом \(\vee\) находится результат логической операции \(A\vee B\) (она называется также
Так \(\F\vee \F\) — это \(\F\), а \(\F \vee \T\) — это \(\T\). Справа кругами изображены области истинности предикатов \(A(x)\) и \(B(x)\) на плоскости всех значений \(x\in\mathbb X\). Заштрихованная область — это результирующий предикат \(A(x)\vee B(x)\).
Логическое «И» или конъюнкция истинно, только если истинны оба высказывания:
Предикат конъюнкции \(A(x)\,\&\,B(x)\) истинен в области пересечения множеств истинности \(A(x)\) и \(B(x)\).
Исключающее ИЛИ
В качестве примера рассмотрим разделительное «ИЛИ» \(A\oplus B\): «она любит или Колю или Васю» (но не обоих). Оно отлично от объединяющего «ИЛИ» \(A\,\vee\,B\), которое истинно и когда истинны оба высказывания. Разделительное «ИЛИ» описывается следующей таблицей истинности и двумя эквивалентными логическими выражениями:
Так, подстановка последней строки в таблице истинности во вторую формулу даёт:
\[(\T\vee \T)\,\&\,(\bar{\T}\vee\bar{\T})\equiv
\T\,\&\,(\F\vee\F)\equiv\T\,\&\,\F \equiv \F.\]
Отметим, что:
\[
A\vee B \equiv A\oplus B\oplus (A\,\&\, B),~~~~~
\neg A \equiv A\oplus \T,
\]
т.е. все связки выражаются через \(\oplus\), \(\&\) и \(\T\) (т. н. полиномы Жегалкина).
н. полиномы Жегалкина).
Дерево формулы
Любую логическую формулу (=выражение) можно представить в виде дерева, задающего последовательность вычислений:
В вершине дерева стоит последняя вычисляющаяся функция, а внизу, на «листьях» — высказывания. Вычисление выражения идёт снизу-вверх. Если на «листьях» стоят одни и те-же высказывания их можно объединить, получив
Введём соглашение о приоритетах логических функций:
самый высокий приоритет у отрицания «\(\neg\)», чуть ниже у «\(\&\)» и ещё ниже у «\(\vee\)»;
самый низкий приоритет у эквивалентности «\(\equiv\)».
Если на приоритеты не полагаются, то используют скобки. Например, формула
\(A\,\&\, B \vee \neg C \, \& \, D\)
— это тоже, что и \((A\,\&\, B ) \vee ((\neg C) \, \& \, D),\)
а формула \(A\vee B\equiv C\,\&\,D\)
— это \((A\vee B)\equiv(C\,\&\,D)\).
Тавтологии
Логическое выражение, истинное при любых значениях входящих в него высказываний, называется общезначимым или тавтологией. Докажем, например, общезначимость следующей формулы: \[ A \,\&\, (A\vee B) ~ \equiv~ A . \] Для этого запишем её таблицу истинности. Высказывания принимают значение \(\F\) и \(\T\). Если \(A\equiv \F\), то \(B\) может быть равно \(\F\) или \(\T\). Аналогично для \(A\equiv \T\). Это даёт четыре варианта, которые подпишем под высказываниями, входящими в формулу. Затем под каждой логической связкой (сначала \(\vee\), затем \(\&\) ) будем подписывать её результат:
Осталось сравнить подчёркнутые значения. Так как они совпадают, в колонке \(\equiv\) везде необходимо поставить \(\T\), т.е. это тавтология.
В качестве простого упражнения предлагается доказать, что формула \(A\vee \neg A\)
также является тавтологией. Она имеет смысл закона исключения третьего
(«или \(A\) или не \(A\)»). На месте \(A\)
может стоять как константное высказывание «сейчас идет дождь»,
так и предикат. Например: \((x=y)\,\vee\,\neg (x=y)\), т.е. \(x\)
или равно или не равно \(y\).
Она имеет смысл закона исключения третьего
(«или \(A\) или не \(A\)»). На месте \(A\)
может стоять как константное высказывание «сейчас идет дождь»,
так и предикат. Например: \((x=y)\,\vee\,\neg (x=y)\), т.е. \(x\)
или равно или не равно \(y\).
Булева алгебра
Существует множество формул, имеющих одинаковые таблицы истинности. Соединение их символом эквивалентности «\(\equiv\)» приводит к тавтологиям. Часть из них составляет булеву алгебру.
Так, логические «И», «ИЛИ» — симметричны и ассоциативны:
\[
\begin{array}{llcllcll}
~
&A\, \&\,B
& ~\equiv~
& B \,\&\, A
, & ~~~~& A \,\&\,(B \,\&\, C)
& ~\equiv~
& (A \,\&\, B) \,\&\, C
, \\[2mm]
&A \vee B
& ~\equiv~
& B \vee A
, &~~~~~& A \vee (B \vee C)
& ~\equiv~
& (A \vee B) \vee C.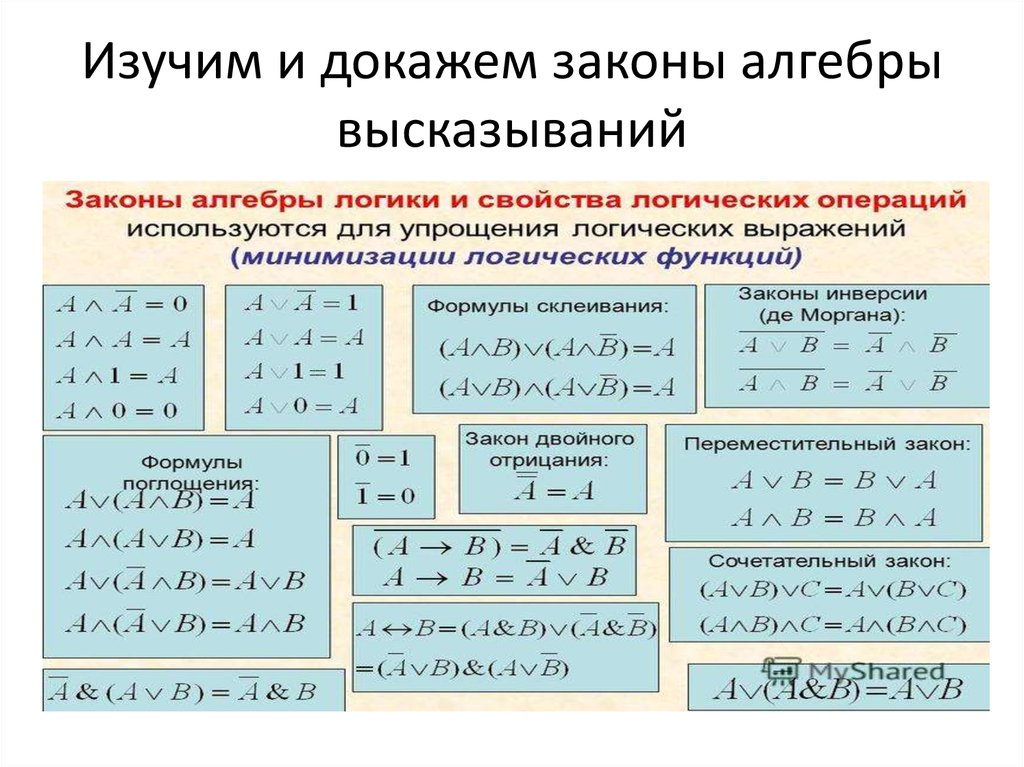 \end{array}
\]
Для них выполняются законы дистрибутивности:
\[
\begin{array}{llcl}
~~~~~~~~~~~~~~
&A \, \& \, (B \vee C)
& ~\equiv~
& (A \,\&\, B)\, \vee \, (A \,\&\, C),
\\[2mm]
&A \vee (B \,\&\, C)
& ~\equiv~
& (A \vee B) ~\&~ (A \vee C)
\end{array}
\]
и более специфические свойства поглощения:
\[
\begin{array}{llcllcll}
~~~~~~~~~~
&A \,\&\, A
& ~\equiv~
& A
, & ~~~~~~~~~~~~& A\,\&\,(A\vee B)
& ~\equiv~
& A
, \\[2mm]
&A \vee A
& ~\equiv~
& A
, & ~~~~~~~~~~~~& A\vee(A\,\&\,B)
& ~\equiv~
& A.
\end{array}
\]
Справедлив закон двойного отрицания и правила де-Моргана:
\[
\begin{array}{llcllcll}
&\neg(\neg A)
& ~\equiv~
& A
,&~~~~~~~~& \neg(A \,\&\, B)
&~\equiv~
& \neg A \vee \neg B
,\\[2mm]
& & & &~~~~~~~~& \neg(A \vee B)
& ~\equiv~
& \neg A \,\&\, \neg B.
\end{array}
\]
Для них выполняются законы дистрибутивности:
\[
\begin{array}{llcl}
~~~~~~~~~~~~~~
&A \, \& \, (B \vee C)
& ~\equiv~
& (A \,\&\, B)\, \vee \, (A \,\&\, C),
\\[2mm]
&A \vee (B \,\&\, C)
& ~\equiv~
& (A \vee B) ~\&~ (A \vee C)
\end{array}
\]
и более специфические свойства поглощения:
\[
\begin{array}{llcllcll}
~~~~~~~~~~
&A \,\&\, A
& ~\equiv~
& A
, & ~~~~~~~~~~~~& A\,\&\,(A\vee B)
& ~\equiv~
& A
, \\[2mm]
&A \vee A
& ~\equiv~
& A
, & ~~~~~~~~~~~~& A\vee(A\,\&\,B)
& ~\equiv~
& A.
\end{array}
\]
Справедлив закон двойного отрицания и правила де-Моргана:
\[
\begin{array}{llcllcll}
&\neg(\neg A)
& ~\equiv~
& A
,&~~~~~~~~& \neg(A \,\&\, B)
&~\equiv~
& \neg A \vee \neg B
,\\[2mm]
& & & &~~~~~~~~& \neg(A \vee B)
& ~\equiv~
& \neg A \,\&\, \neg B.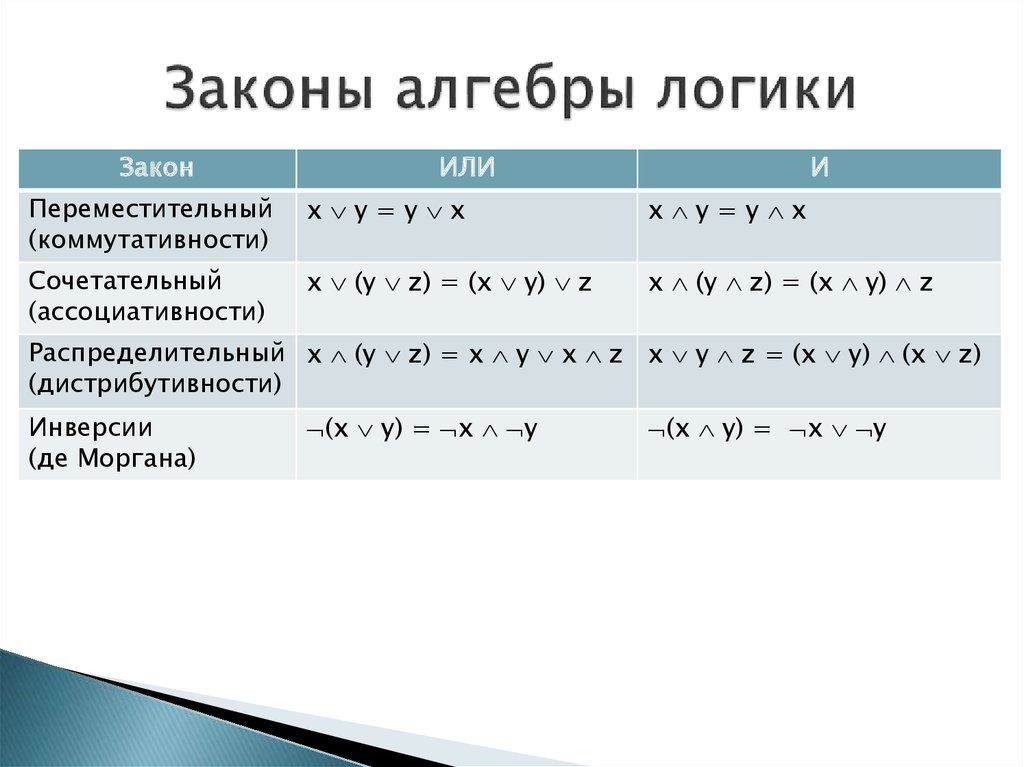 \end{array}
\]
В алгебру можно ввести константы: «\(\T\)» (истина), «\(\F\)» (ложь)
и записать закон исключения третьего в двух формах:
\[
~~~~~~~~~~~~~~~A\,\&\, \neg A ~\equiv~ \F,~~~~~~~~~~~~~~~~~~~~~~
A \vee \neg A ~\equiv~ \T,
\]
а также следующие очевидные соотношения:
\[
~~~A\,\&\, \F ~\equiv~ \F,~~~~~~~
A\,\&\,\T ~\equiv~ A,~~~~~~~~
A \vee \T ~\equiv~ \T,~~~~~~~
A \vee \F ~\equiv~ A.
\]
Стоит обратить внимание на симметричность всех формул
относительно перестановки \(\&\) и \(\vee\), с одновременной заменой \(\F\) на \(\T\) и наоборот.
\end{array}
\]
В алгебру можно ввести константы: «\(\T\)» (истина), «\(\F\)» (ложь)
и записать закон исключения третьего в двух формах:
\[
~~~~~~~~~~~~~~~A\,\&\, \neg A ~\equiv~ \F,~~~~~~~~~~~~~~~~~~~~~~
A \vee \neg A ~\equiv~ \T,
\]
а также следующие очевидные соотношения:
\[
~~~A\,\&\, \F ~\equiv~ \F,~~~~~~~
A\,\&\,\T ~\equiv~ A,~~~~~~~~
A \vee \T ~\equiv~ \T,~~~~~~~
A \vee \F ~\equiv~ A.
\]
Стоит обратить внимание на симметричность всех формул
относительно перестановки \(\&\) и \(\vee\), с одновременной заменой \(\F\) на \(\T\) и наоборот.
\(\diamond\)
Проведём при помощи этих тождеств упрощение следующего логического выражения:
\[
A ~ \& ~ (\bar{A}\,\vee\,B) ~\equiv~
(A\,\&\, \bar{A})\,\vee\,(A\,\&\, B)
~\equiv~
\F\,\vee\,(A\,\&\, B)
~\equiv~
A ~\&~ B,
\]
где сначала использовано свойство дистрибутивности конъюнкции (\(\&\)), затем закон исключения третьего и
тождество \(\F\vee A\equiv A\).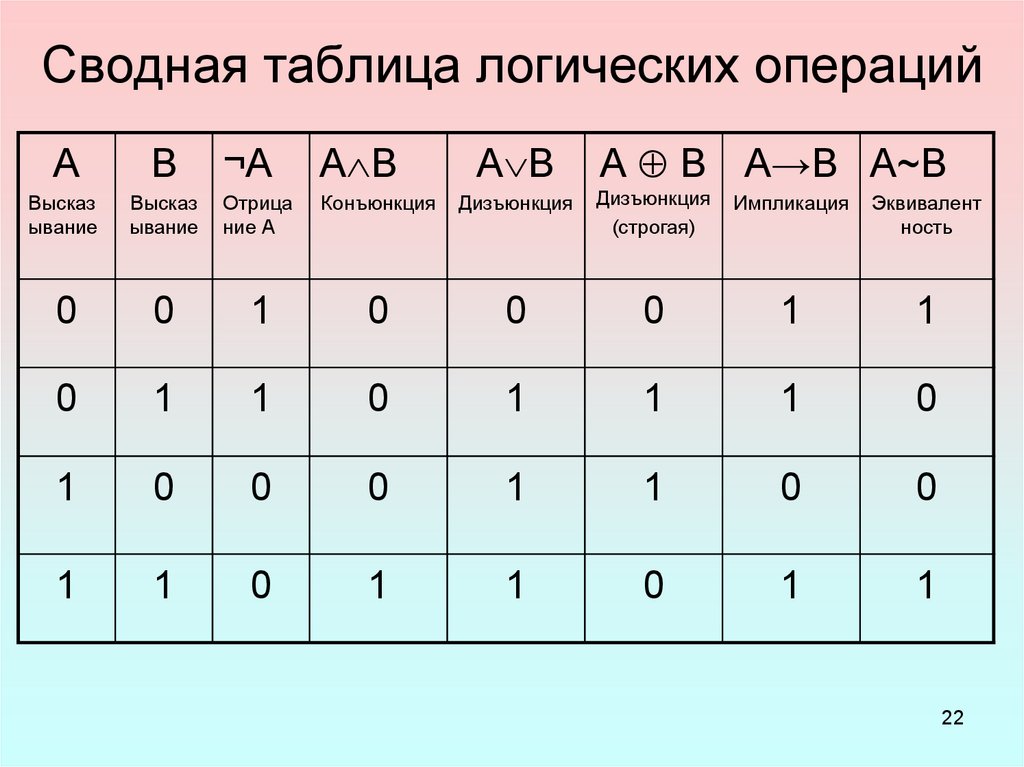 Непрерывная цепочка
эквивалентностей основана на свойстве транзитивности: если \(A\equiv B\)
и \(B\equiv C\),
то \(A\equiv C\), что записывается как \(A\equiv B \equiv C\).
Аналогично стоит доказать, что \(A \, \vee \, (\bar{A}~\&~B) ~~\equiv~ A \,\vee\, B\). \(\square\)
Непрерывная цепочка
эквивалентностей основана на свойстве транзитивности: если \(A\equiv B\)
и \(B\equiv C\),
то \(A\equiv C\), что записывается как \(A\equiv B \equiv C\).
Аналогично стоит доказать, что \(A \, \vee \, (\bar{A}~\&~B) ~~\equiv~ A \,\vee\, B\). \(\square\)
Булева алгебра
Булева алгебраБулева алгебра
Два логических значения: true и false
Используется для управления потоком управления в программах
- что будет дальше
- если условие истинно, делаем одно, если ложно делаем другое
C не имеет логического типа данных — мы заменяем целочисленные переменные с логическим значением.
- мы используем 0 для обозначения ложного
- C интерпретирует любое ненулевое значение как истинное, но обычно мы используем 1 для обозначения истинного
- мы можем использовать #define, чтобы сделать это более понятным для читателей:
#define TRUE 1
#define FALSE 0
Два вида операторов в C возвращают логические значения:
1. Арифметика:
Арифметика:
| Реляционные операторы | |
| < | меньше |
| <= | меньше или равно |
| == | равно |
| >= | больше или равно |
| > | больше |
| != | не равно |
Пример
интервал х, у;
… /* инициализируем x и
y каким-то образом */
Выражение x < y является логическим выражением; он возвращает true, если значение, хранящееся в x
меньше, чем значение, хранящееся в y.
Операнды для реляционных операндов обычно являются числовыми (int или float), но мы также используйте их для сравнения символов.
Два вида операторов в C возвращают логические значения:
2. Логический:
Логический:
| Логические операторы | |
| && | И |
| || | ИЛИ |
| ! | НЕ |
Логические операторы принимают логические операнды и возвращают логический результат.
&& и || взять два операнда
! принимает один операнд
Операнды для логических операторов могут быть:
- выражения с использованием операторов отношения
- выражений с использованием других логических операторов
- логические переменные
Примеры:
x > y && y > z /* x и y являются числовыми типами */
x && y /* x и y — логические переменные */
(х && у) || !z /* x, y и z — логические переменные */
Таблицы истинности для логических операторов:
|
|
|
Упрощение логических выражений
Упрощение требует использования эквивалентностей:
- !(х = у) х != у
- !(х < у) х >= у
- !(х <= у) х > у
- !(х > у) х <= у
- !(х >= у) х < у
- !(х && у) ! х || ! г
- !(х || у) ! Икс && ! г
- !(! х) х
Пример:
!((!х && у) && (х || !у)
!(!х && у) || ! (x || !y) (по г)
!(!х) || !у || !(x || !y) (по f)
!(!х) || !у || !x && !(!y) (по г)
х || !у || !x && y (через h, применяется дважды)
1.
 2: Алгебра Булена — Инженерные тексты LibreTexts
2: Алгебра Булена — Инженерные тексты LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6709
- Кэрол Кричлоу и Дэвид Дж. Эк
- Колледжи Хобарта и Уильяма Смита
До сих пор мы обсуждали, как писать и интерпретировать предложения. В этом разделе рассматривается манипулирование ими. Для этого нам понадобится алгебра. Обычная алгебра, которую преподают в старшей школе, касается манипулирования числами, переменных, представляющих числа, и таких операторов, как \(+\) и \(×\), которые применяются к числам. Теперь нам нужна алгебра, применимая к логическим значениям, пропозициональным переменным и логическим операторам. Первым человеком, подумавшим о логике с точки зрения алгебры, был математик Джордж Буль, который представил эту идею в книге, опубликованной им в 1854 году. Алгебра логики теперь называется 9.0031 Булева алгебра в его честь.
Первым человеком, подумавшим о логике с точки зрения алгебры, был математик Джордж Буль, который представил эту идею в книге, опубликованной им в 1854 году. Алгебра логики теперь называется 9.0031 Булева алгебра в его честь.
Алгебра чисел включает в себя большое количество правил для работы с выражениями. Закон распределения, например, говорит, что \(x(y + z) = xy + xz\), где \(x, y,\) и \(z\) — переменные, обозначающие любые числа или числовые выражения. Этот закон означает, что всякий раз, когда вы видите что-то в форме \(xy + xz\) в числовом выражении, вы можете заменить \(x(y + z)\) без изменения значения выражения, и наоборот. Обратите внимание, что знак равенства в \(x(y + z) = xy + xz\) означает «имеет то же значение, что и независимо от числовых значений \(x, y,\) и \(z\)».
В булевой алгебре мы работаем с логическими значениями, а не с числовыми значениями. Есть только два логических значения, истинное и ложное. Мы запишем эти значения как \(\mathbb{T}\) и \(\mathbb{F}\). Символы \(\mathbb{T}\) и \(\mathbb{F}\) играют в булевой алгебре ту же роль, что и постоянные числа, такие как 1 и 3,14159, в обычной алгебре. Вместо знака равенства в булевой алгебре используется логическая эквивалентность ≡, имеющая по существу тот же смысл4. Например, для предложений p, q и r оператор ≡ в \(p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r\) означает «имеет то же значение, что и независимо от того, какие логические значения имеют \(p, q,\) и \(r\)». 95\) Это также пример более общего факта, известного как двойственность, который утверждает, что из любой тавтологии, использующей только операторы ∧, ∨ и ¬, можно получить другую тавтологию, заменив ∧ на ∨ и \( \mathbb{T}\) с \(\mathbb{F}\). Мы не будем пытаться доказать это здесь.
Символы \(\mathbb{T}\) и \(\mathbb{F}\) играют в булевой алгебре ту же роль, что и постоянные числа, такие как 1 и 3,14159, в обычной алгебре. Вместо знака равенства в булевой алгебре используется логическая эквивалентность ≡, имеющая по существу тот же смысл4. Например, для предложений p, q и r оператор ≡ в \(p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r\) означает «имеет то же значение, что и независимо от того, какие логические значения имеют \(p, q,\) и \(r\)». 95\) Это также пример более общего факта, известного как двойственность, который утверждает, что из любой тавтологии, использующей только операторы ∧, ∨ и ¬, можно получить другую тавтологию, заменив ∧ на ∨ и \( \mathbb{T}\) с \(\mathbb{F}\). Мы не будем пытаться доказать это здесь.
Просто в качестве примера, давайте проверим первое правило в таблице, закон двойного отрицания. Этот закон — просто старое основное грамматическое правило, согласно которому два отрицания дают положительное. Хотя это правило сомнительно, поскольку оно применимо к английскому языку в том виде, в каком оно используется на самом деле, — что бы ни говорил грамматик, «я не могу получить удовлетворение» на самом деле не означает «я могу получить удовлетворение», — действительность правила в логику можно проверить, просто вычислив два возможных случая: когда \(p\) истинно и когда \(p\) ложно. Когда p истинно, то по определению оператора ¬ \(¬p\) ложно. Но тогда, опять же по определению ¬, значение \(¬(¬p)\) истинно, что совпадает со значением \(p\). Точно так же в случае, когда \(p\) ложно, \(¬(¬p)\) также ложно. Организованный в виде таблицы истинности, этот аргумент принимает довольно простую форму 9.0005
Когда p истинно, то по определению оператора ¬ \(¬p\) ложно. Но тогда, опять же по определению ¬, значение \(¬(¬p)\) истинно, что совпадает со значением \(p\). Точно так же в случае, когда \(p\) ложно, \(¬(¬p)\) также ложно. Организованный в виде таблицы истинности, этот аргумент принимает довольно простую форму 9.0005
Тот факт, что первый и последний столбцы идентичны, показывает логическую эквивалентность \(p\) и \(¬(¬p)\). Дело здесь не только в том, что \(¬(¬p) ≡ p\), но и в том, что эта логическая эквивалентность действительна, поскольку ее можно проверить вычислительным путем, основываясь только на соответствующих определениях. Его достоверность не следует из того факта, что «это очевидно» или «это общеизвестное правило грамматики». Студенты часто спрашивают: «Зачем мне что-то доказывать, если это очевидно». Дело в том, что логика — и математика в целом — это отдельный маленький мир со своим набором правил. Хотя этот мир как-то связан с реальным миром, когда вы говорите, что что-то очевидно (в реальном мире), вы не играете по правилам мира логики. Настоящая магия математики заключается в том, что, играя по ее правилам, вы можете придумывать вещи, которые явно не очевидны, но которые все же говорят что-то о реальном мире — часто что-то интересное и важное.
Настоящая магия математики заключается в том, что, играя по ее правилам, вы можете придумывать вещи, которые явно не очевидны, но которые все же говорят что-то о реальном мире — часто что-то интересное и важное.
Каждое из правил на рис. 1.2 можно проверить таким же образом, составив таблицу истинности для проверки всех возможных случаев.
Важно понимать, что пропозициональные переменные в законах булевой алгебры могут обозначать любые пропозиции, в том числе составные пропозиции. Это не просто верно, как утверждает Закон двойного отрицания, что \(¬(¬p) ≡ p\). Также верно, что \(¬(¬q) ≡ q\), что \(¬(¬(p∧q)) ≡ (p∧q)\), что \(¬(¬(p → (q ∧ ¬p))) ≡ (p → (q ∧ ¬p))\) и бесконечное количество других утверждений того же вида. Здесь «утверждение той же формы» — это высказывание, которое можно получить, подставив что-то вместо p в обоих местах, где оно встречается в \(¬(¬p) ≡ p\). Как я могу быть уверен, что все эти бесконечно много утверждений верны, если все, что я проверил, — это одна маленькая двухстрочная таблица истинности? Ответ заключается в том, что любое данное высказывание Q, каким бы сложным оно ни было, имеет конкретное истинностное значение, либо истинное, либо ложное. Таким образом, вопрос о справедливости \(¬(¬Q) ≡ Q\) всегда сводится к одному из двух случаев, которые я уже проверил в таблице истинности. (Обратите внимание, что для того, чтобы этот аргумент был действительным, один и тот же Q должен быть заменен на p в каждой позиции, где он встречается.) Хотя этот аргумент может быть «очевидным», это не совсем доказательство, но пока мы просто примем его. справедливость следующей теоремы: 96\)
Таким образом, вопрос о справедливости \(¬(¬Q) ≡ Q\) всегда сводится к одному из двух случаев, которые я уже проверил в таблице истинности. (Обратите внимание, что для того, чтобы этот аргумент был действительным, один и тот же Q должен быть заменен на p в каждой позиции, где он встречается.) Хотя этот аргумент может быть «очевидным», это не совсем доказательство, но пока мы просто примем его. справедливость следующей теоремы: 96\)
Первый закон подстановки позволяет вам заниматься алгеброй! Например, вы можете заменить \(p → q\) на \(p\) в законе двойного отрицания, \(¬(¬p) ≡ p\). Это позволяет вам «упростить» выражение \(¬(¬(p → q)) до p → q\) с уверенностью, что результирующее выражение будет иметь то же логическое значение, что и выражение, с которого вы начали. (Вот что означает логическая эквивалентность \(¬(¬(p → q))\) и \(p → q\).) Подобные трюки можно проделывать со всеми законами, изображенными на рис. 1.2. Еще более важным является второй закон подстановки, который гласит, что вы можете заменить выражение на логически эквивалентное выражение, где бы оно ни встречалось.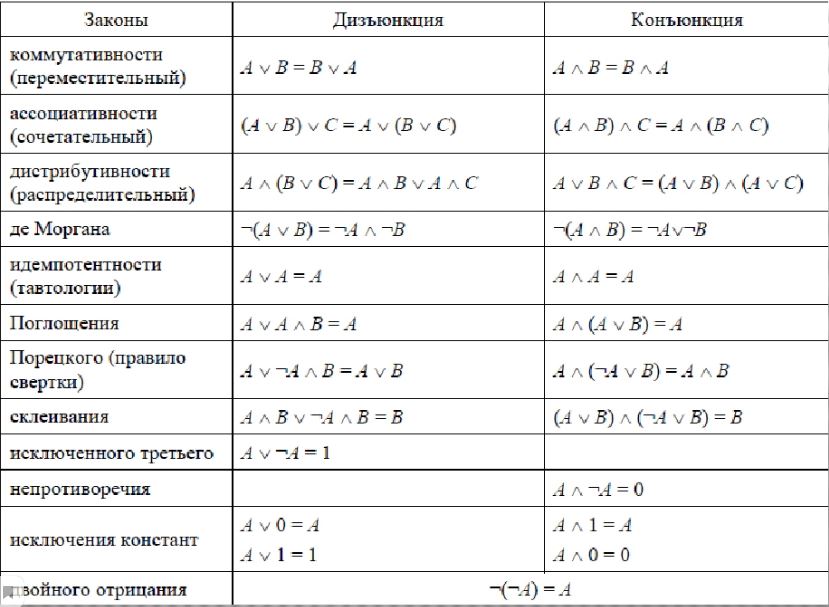 Опять же, мы примем это как теорему, не пытаясь доказать ее здесь. Удивительно трудно выразить этот закон словами:
Опять же, мы примем это как теорему, не пытаясь доказать ее здесь. Удивительно трудно выразить этот закон словами:
Теорема 1.2 Второй закон подстановки
Предположим, что \(P\) и \(Q\) — любые предложения такие, что \(P ≡ Q\). Предположим, что \(R\) — любое составное предложение, в котором \((P)\) встречается как подпредложение. Пусть \(R′\) будет предложением, полученным заменой \((Q)\) на вхождение \((P)\) в \(R\). Тогда \(R ≡ R′\).
Обратите внимание, что в этом случае теорема не требует замены \((Q)\) на каждое вхождение \((P)\) в \(R\). Вы можете заменить одно, два или столько вхождений \((P)\) сколько хотите, и результат по-прежнему будет логически эквивалентен \(R\).
Второй закон подстановки позволяет нам использовать логическую эквивалентность \(¬(¬p) ≡ p\) для «упрощения» выражения \(q → (¬(¬p))\) заменой \((p)\ ) для \((¬(¬p))\). Полученное выражение \(q → (p)\) или просто \(q → p\) без круглых скобок логически эквивалентно исходному \(q → (¬(¬p))\). И снова мы должны быть осторожны со скобками: тот факт, что \(p ∨ p ≡ p\), не позволяет нам переписать \(q∧p∨p∧r\) как \(q∧p∧r\) . Проблема в том, что \(q∧p∨p∧r\) означает \((q∧p)∨(p∧r)\), так что \((p∨p)\) не является подвыражением. Таким образом, хотя на практике мы не всегда будем писать все скобки, вы всегда должны знать, где они должны быть. 96\) Я добавил здесь скобки вокруг \(Q\) по техническим причинам. Иногда круглые скобки необходимы, чтобы убедиться, что \(Q\) оценивается как единое целое, так что его окончательное значение используется вместо \(p\). В качестве примера того, что может пойти не так, рассмотрим \(q ∧ r\). Если это буквально заменить \(p\) в \(¬(¬p)\), без круглых скобок, результатом будет \(¬(¬q ∧ r)\). Но это выражение означает \(¬((¬q) ∧ r)\), что не эквивалентно \(q ∧ r\).
И снова мы должны быть осторожны со скобками: тот факт, что \(p ∨ p ≡ p\), не позволяет нам переписать \(q∧p∨p∧r\) как \(q∧p∧r\) . Проблема в том, что \(q∧p∨p∧r\) означает \((q∧p)∨(p∧r)\), так что \((p∨p)\) не является подвыражением. Таким образом, хотя на практике мы не всегда будем писать все скобки, вы всегда должны знать, где они должны быть. 96\) Я добавил здесь скобки вокруг \(Q\) по техническим причинам. Иногда круглые скобки необходимы, чтобы убедиться, что \(Q\) оценивается как единое целое, так что его окончательное значение используется вместо \(p\). В качестве примера того, что может пойти не так, рассмотрим \(q ∧ r\). Если это буквально заменить \(p\) в \(¬(¬p)\), без круглых скобок, результатом будет \(¬(¬q ∧ r)\). Но это выражение означает \(¬((¬q) ∧ r)\), что не эквивалентно \(q ∧ r\).
Закон подстановки: Эквивалентность \(Q ≡ R\) позволяет нам заменить \(R\) на \(Q\) в утверждении \(P ≡ Q\), что дает \(P ≡ R\). (Помните, что согласно определению 1.4 логическая эквивалентность определяется в терминах предложения. ) Это означает, что мы можем показать, что два составных предложения логически эквивалентны, найдя цепочку логических эквивалентностей, ведущих от одного предложения к другому. Например:
) Это означает, что мы можем показать, что два составных предложения логически эквивалентны, найдя цепочку логических эквивалентностей, ведущих от одного предложения к другому. Например:
\(p ∧ (p → q) ≡ p ∧ (¬p ∨ q)\) определение \(p → q\), Теорема 1.2
\(≡ (p ∧ ¬p) ∨ (p ∧ q )\) Распределительный закон
\(≡ \mathbb{T} ∨ (p ∧ q)\) Закон противоречия, теорема 1.2
\(≡ (p ∧ q)\) Закон тождества
Каждый шаг в цепочке имеет свое обоснование. В некоторых случаях закон замещения используется без указания этого. В первой строке, например, определение \(p → q\) состоит в том, что \(p → q ≡ ¬p ∨ q\). Второй закон подстановки позволяет нам заменить \((¬p ∨ q)\) на \((p → q)\). В последней строке мы неявно применили первый закон подстановки к закону тождества \(\mathbb{T} ∨ p ≡ p\), чтобы получить \(\mathbb{F} ∨ (p ∧ q) ≡ (p ∧ к)\).
Цепочка эквивалентностей в приведенном выше примере позволяет нам заключить, что \(p ∧ (p → q)\) логически эквивалентно \(p ∧ q\). Это означает, что если бы вы составили таблицу истинности для этих двух выражений, значения истинности в столбце для \(p ∧ (p → q)\) были бы идентичны значениям в столбце для \(p ∧ q\) . Мы знаем это, не составляя таблицы. В этом случае таблица будет состоять всего из четырех строк, и ее будет достаточно легко составить. Но булеву алгебру можно применять в тех случаях, когда количество пропозициональных переменных слишком велико, чтобы таблица истинности была практичной.
Это означает, что если бы вы составили таблицу истинности для этих двух выражений, значения истинности в столбце для \(p ∧ (p → q)\) были бы идентичны значениям в столбце для \(p ∧ q\) . Мы знаем это, не составляя таблицы. В этом случае таблица будет состоять всего из четырех строк, и ее будет достаточно легко составить. Но булеву алгебру можно применять в тех случаях, когда количество пропозициональных переменных слишком велико, чтобы таблица истинности была практичной.
Давайте сделаем еще один пример. Напомним, что составное предложение является тавтологией, если оно истинно для всех возможных комбинаций значений истинности содержащихся в нем пропозициональных переменных. Но другой способ сказать то же самое состоит в том, что \(P\) является тавтологией, если \(P ≡ T\). Таким образом, мы можем доказать, что составное предложение \(P\) является тавтологией, найдя цепочку логических эквивалентностей, ведущих от \(P к T\). Например:
\(((p ∨ q) ∧ ¬p) → q\)
\(≡ (¬((p ∨ q) ∧ ¬p)) ∨ q\) определение →
\(≡ (¬(p ∨ q) ∨ ¬(¬p)) ∨ q\) Закон Де Моргана, теорема 1. 2
2
\(≡ (¬(p ∨ q) ∨ p) ∨ q \) Двойное отрицание, теорема 1.2
\(≡ (¬(p ∨ q)) ∨ (p ∨ q)\) Ассоциативный закон для ∨
\(≡T\) Закон исключенного третьего
Из этой цепочки эквивалентностей мы можем заключить, что \(((p ∨ q) ∧ ¬p) → q\) является тавтологией.
Нужна некоторая практика, чтобы посмотреть на выражение и понять, какие правила к нему можно применить; например, чтобы увидеть \((¬(p ∨ q)) ∨ (p ∨ q)\) как приложение закона исключенного третьего, вам нужно мысленно заменить \((p ∨ q)\) на p в закон, как это указано на рисунке 1.2. Часто применяется несколько правил, и нет четких указаний относительно того, какое из них вам следует попробовать. Это то, что делает алгебру чем-то вроде искусства.
Безусловно, неверно, что все возможные правила булевой алгебры приведены на рис. 1.2. Во-первых, существует множество правил, которые легко вытекают из перечисленных здесь правил. Например, хотя таблица утверждает только, что \(\mathbb{F} ∨ p ≡ p\), также верно, что \(p ∨ \mathbb{F} ≡ p\).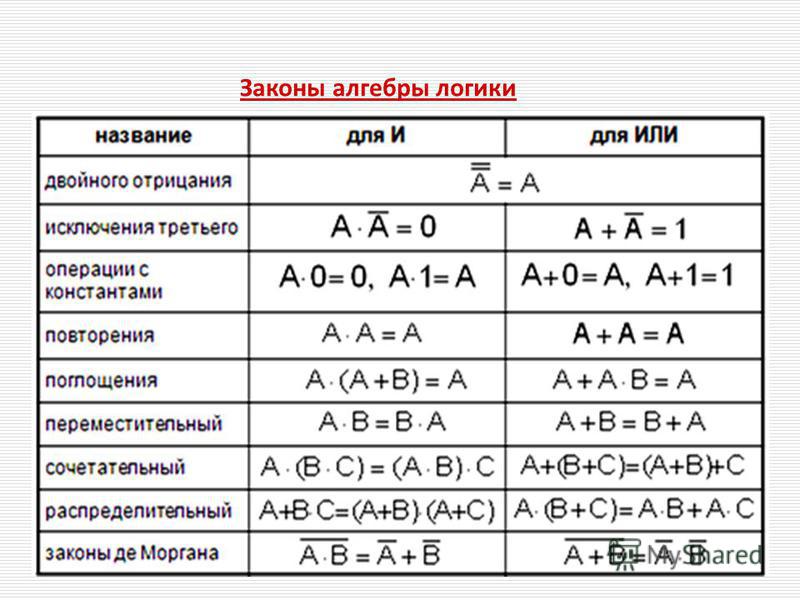 Это можно проверить непосредственно или простым вычислением:
Это можно проверить непосредственно или простым вычислением:
\(p ∨ \mathbb{F} ≡ \mathbb{F} ∨ p\) Коммутативный закон
\(≡ p\) Закон тождества, как указано в таблице
Дополнительные правила можно получить, применив коммутативный закон к другим правилам в таблице, и мы будем свободно использовать такие правила в будущем.
Другой вид простого расширения можно применить к ассоциативному закону: \((p∨q)∨r ≡ p∨(q∨r)\). Закон сформулирован для оператора ∨, примененного к трем терминам, но он обобщается на четыре или более терминов. Например
\(((p∨q)∨r)∨s\)
\(≡ (p ∨ q) ∨ (r ∨ s)\) по ассоциативному закону для трех членов
\(≡ p ∨ (q ∨ (r ∨ s))\) по Ассоциативному закону на три срока
Мы, конечно, часто будем писать это выражение как \(p ∨ q ∨ r ∨ s\) вообще без круглых скобок, зная, что везде, где мы ставим круглые скобки, значение остается тем же.
Еще одна вещь, которую вы должны иметь в виду, это то, что правила могут применяться в любом направлении.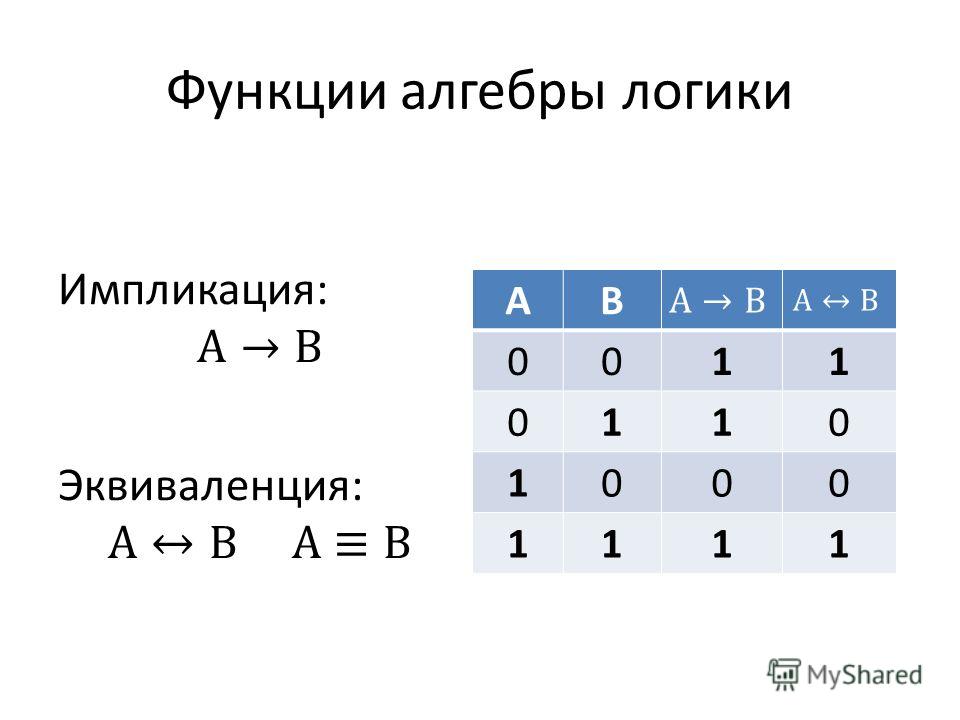 Закон распределения, например, позволяет вам распределить \(p\) в \(p∨(q∧¬p) \), чтобы получить \((p∨q)∧(p∨¬p)\). Но его также можно использовать в обратном порядке, чтобы «вынести за скобки» термин, например, когда вы начинаете с \((q∨(p → q))∧(q∨(q → p))\) и выносите за скобки \( q\), чтобы получить \(q∨((p → q)∧(q → p))\).
Закон распределения, например, позволяет вам распределить \(p\) в \(p∨(q∧¬p) \), чтобы получить \((p∨q)∧(p∨¬p)\). Но его также можно использовать в обратном порядке, чтобы «вынести за скобки» термин, например, когда вы начинаете с \((q∨(p → q))∧(q∨(q → p))\) и выносите за скобки \( q\), чтобы получить \(q∨((p → q)∧(q → p))\).
До сих пор в этом разделе я работал с законами булевой алгебры, не говоря много о том, что они означают или почему они разумны. Конечно, вы можете применять законы в расчетах, не понимая их. Но если вы хотите понять, какие расчеты делать, вам нужно некоторое понимание. Большинство законов достаточно ясны, если немного подумать. Например, если мы уже знаем, что q ложно, то \(p ∨ q\) будет истинным, когда \(p\) истинным, и ложным, когда p ложным. То есть \(p ∨ \mathbb{F}\) имеет то же логическое значение, что и \(p\). Но это именно то, что говорит Закон Тождества для \(∨\). Некоторые из законов нуждаются в более подробном обсуждении. 97) Закон противоречия, \(p ∧ ¬p ≡ \mathbb{F}\), говорит, что одновременно \(p\) и \(¬p\) не могут быть истинными. Оба эти правила очевидны.
Оба эти правила очевидны.
Законы Распределения нельзя назвать очевидными, но на нескольких примерах можно показать, что они разумны. Рассмотрим утверждение: «Эта карта — туз пик или треф». Ясно, что это эквивалентно «Эта карта — туз пробелов или эта карта — туз треф». Но это всего лишь пример первого распределительного закона! Например, пусть a представляет предложение «Эта карта — туз», пусть s представляет «Эта карта — пика», а пусть c представляет «Эта карта — трефовая». Тогда «Эта карта — туз пик или треф» можно перевести в логическую форму как \(a ∧ (s ∨ c)\), а «Эта карта — туз пик или эта карта — туз треф» становится \ ((а ∧ s) ∨ (а ∧ с)\). А дистрибутивный закон уверяет нас, что \(a∧(s∨c)≡(a∧s)∨(a∧c)\). Второй закон распределения говорит нам, например, что «Эта карта либо джокер, либо бубновая десятка» логически эквивалентна «Эта карта либо джокер, либо десятка, и это либо джокер, либо бубновая кость». ” То есть \(j ∨(t∧d) ≡ (j ∨t)∧(j ∨d)\). Законы дистрибутивности являются мощными инструментами, и вы должны помнить о них всякий раз, когда сталкиваетесь со смесью операторов \(∧\) и \(∨\). 97) В логике высказываний это легко проверить с помощью небольшой таблицы истинности. Но существует удивительное количество споров о том, действителен ли этот закон во всех ситуациях. В реальном мире часто кажется, что между правдой и ложью есть серая зона. Даже в математике есть люди, которые считают, что должно быть третье истинностное значение, означающее что-то вроде «неизвестно» или «не доказано». Но математиков, которые думают таким образом, большинство других математиков считают немного странными.
97) В логике высказываний это легко проверить с помощью небольшой таблицы истинности. Но существует удивительное количество споров о том, действителен ли этот закон во всех ситуациях. В реальном мире часто кажется, что между правдой и ложью есть серая зона. Даже в математике есть люди, которые считают, что должно быть третье истинностное значение, означающее что-то вроде «неизвестно» или «не доказано». Но математиков, которые думают таким образом, большинство других математиков считают немного странными.
Законы ДеМоргана также не должны быть очевидными, поскольку люди часто понимают их неправильно. Но они имеют смысл. Рассматривая \(¬(p ∧ q)\), вы должны спросить себя, как может \(«p и q»\) не быть правдой. Оно не будет истинным, если либо \(p\) ложно, либо \(q\) ложно (или и то, и другое). То есть \(¬(p ∧ q)\) эквивалентно \((¬p)∨(¬q)\). Рассмотрим предложение «Ворон большой и черный». Если птица не большая и не черная, то это не ворон. Но что именно означает быть «не (большим и черным)»? Как узнать, верно ли утверждение «не (большой и черный)» в отношении чего-либо? Это будет верно, если он либо не большой, либо не черный.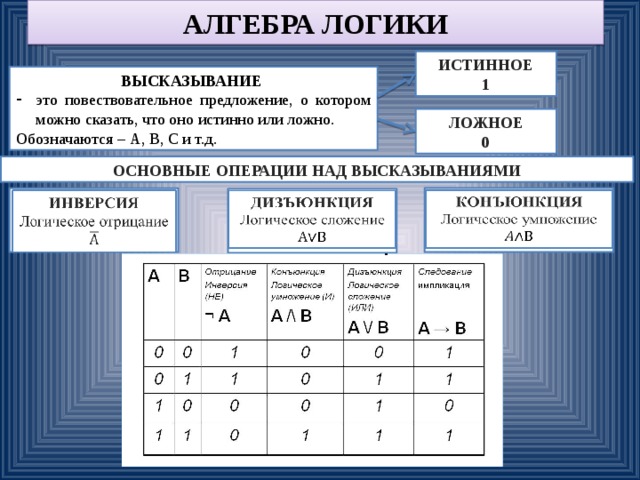 (Это не обязательно должно быть и то, и другое — оно может быть большим и белым, оно может быть маленьким и черным.) Точно так же, чтобы \(«p или q»\) не было истинным, оба \(p\) и \(q\) должно быть ложным. То есть \(¬(p ∨ q)\) эквивалентно \((¬p) ∧ (¬q)\). Это второй закон Де Моргана.
(Это не обязательно должно быть и то, и другое — оно может быть большим и белым, оно может быть маленьким и черным.) Точно так же, чтобы \(«p или q»\) не было истинным, оба \(p\) и \(q\) должно быть ложным. То есть \(¬(p ∨ q)\) эквивалентно \((¬p) ∧ (¬q)\). Это второй закон Де Моргана.
Вспоминая, что \(p → q\) эквивалентно \((¬p)∨q\), мы можем применить закон Де Моргана, чтобы получить формулу для отрицания импликации:
\(¬(p → q) ≡ ¬((¬p) ∨ q)\)
\(≡ (¬(¬p)) ∧ (¬q)\)
\(≡ p ∧ ¬q\)
То есть \(p → q\) ложно ровно тогда, когда и \(p\) истинно, и \(q\) ложно. Например, отрицание фразы «Если у вас есть туз, вы выигрываете» означает «У вас есть туз, и вы не выигрываете». Подумайте об этом так: если у вас был туз, но вы не выиграли, то утверждение «Если у вас туз, вы выиграли» неверно.
- Постройте таблицы истинности, чтобы продемонстрировать справедливость каждого из распределительных законов.
- Постройте следующие таблицы истинности:
a) Постройте таблицы истинности, чтобы продемонстрировать, что \(¬(p ∧ q)\) равно , а не , что логически эквивалентно
\((¬p) ∧ (¬q)\).
b) Постройте таблицы истинности, чтобы продемонстрировать, что \(¬(p ∨ q)\) не логически эквивалентно \((¬p) ∨ (¬q)\).
c) Построить таблицы истинности, чтобы продемонстрировать справедливость обоих законов ДеМоргана. - Постройте таблицы истинности, чтобы продемонстрировать, что ¬(p → q) логически не эквивалентно ни одному из следующих утверждений.
a) \((¬p) → (¬q)\)
b) \((¬p) → q\)
c) \(p → (¬q)\)
См. вернуться к этому разделу для формулы, которая логически эквивалентна ¬(p → q). - Является ли \(¬(p ↔ q)\) логически эквивалентным \((¬p) ↔ (¬q)\)?
- В алгебре чисел существует распределительный закон умножения над сложением: \(x(y + z) = xy + xz\). Как будет выглядеть распределительный закон сложения над умножением? Является ли это действительным законом в алгебре чисел?
- Законы распределения, приведенные на рис.
 1.2, иногда называют левыми законами распределения. Законы правой дистрибутивности говорят, что \((p∨q)∧r ≡ (p∧r)∨(q∧r) \) и что \((p∧q)∨r ≡ (p∨r)∧(q∨ р)\). Покажите, что правые дистрибутивные законы также являются действительными законами булевой алгебры. (Примечание: на практике и левый, и правый законы распределения называются просто законами распределения, и оба они могут свободно использоваться в доказательствах.)
1.2, иногда называют левыми законами распределения. Законы правой дистрибутивности говорят, что \((p∨q)∧r ≡ (p∧r)∨(q∧r) \) и что \((p∧q)∨r ≡ (p∨r)∧(q∨ р)\). Покажите, что правые дистрибутивные законы также являются действительными законами булевой алгебры. (Примечание: на практике и левый, и правый законы распределения называются просто законами распределения, и оба они могут свободно использоваться в доказательствах.) - Покажите, что \(p∧(q∨r∨s) ≡ (p∧q)∨(p∧r)∨(p∧s)\) для любых предложений \(p, q, r,\) и \( с\). На словах можно сказать, что конъюнкция распределяется по дизъюнкции трех терминов. (Напомним, что оператор \(∧\) называется конъюнкцией, а оператор \(∨\) называется дизъюнкцией.) Переведите в логику и проверьте тот факт, что конъюнкция распределяется по дизъюнкции четырех членов. Утверждают, что на самом деле конъюнкция распределяется по дизъюнкции любого числа терминов.
- Есть еще два основных закона логики, включающие два выражения \(p∧\mathbb{F} и \(p ∨ \mathbb{T}\).
 Каких законов не хватает? Покажите, что ваши ответы на самом деле таковы. , законы.
Каких законов не хватает? Покажите, что ваши ответы на самом деле таковы. , законы. - Для каждой из следующих пар предложений покажите, что два предложения логически эквивалентны, найдя цепочку эквивалентностей от одного к другому. Укажите, какое определение или закон логики оправдывает каждую эквивалентность в цепочке.
а) \(p∧(q∧p), p∧q\)
б) \((¬p)→q, p∨q\)
в) \((p∨q)∧¬q, p∧¬q\)
г) \(p→ (q→r), (p∧q)→r\)
e) \((p→r)∧(q→r), (p∨q)→r\)
f) \( р→(р∧q), р→q\) - Для каждого из следующих составных предложений найдите более простое предложение, которое логически эквивалентно. Постарайтесь найти максимально простое предложение.
а) \((p∧q)∨¬q\)
б) \(¬(p∨q)∧p\)
в) \(p → ¬p\)
d) \(¬p∧(p∨q)\)
e) \((q∧p)→q\)
f) \((p→q)∧(¬p→ к)\) - Выразите отрицание каждого из следующих предложений на естественном английском языке:
a) Это солнечно и холодно.

б) Торт или пирог.
c) Если сегодня вторник, то это Бельгия.
d) Если вы сдадите выпускной экзамен, вы сдадите курс. - Примените один из законов логики к каждому из следующих предложений и перепишите его как эквивалентное предложение. Укажите, какой закон вы применяете.
а) Я возьму кофе и пирожное или пирог.
б) У него нет ни таланта, ни амбиций.
c) У вас может быть спам, или у вас может быть спам.
Эта страница под названием 1.2: Boolen Algebra распространяется в соответствии с лицензией CC BY-NC-SA, авторами, ремиксами и/или кураторами являются Кэрол Кричлоу и Дэвид Дж. Эк.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кэрол Кричлоу и Дэвид Дж.




 1.2, иногда называют левыми законами распределения. Законы правой дистрибутивности говорят, что \((p∨q)∧r ≡ (p∧r)∨(q∧r) \) и что \((p∧q)∨r ≡ (p∨r)∧(q∨ р)\). Покажите, что правые дистрибутивные законы также являются действительными законами булевой алгебры. (Примечание: на практике и левый, и правый законы распределения называются просто законами распределения, и оба они могут свободно использоваться в доказательствах.)
1.2, иногда называют левыми законами распределения. Законы правой дистрибутивности говорят, что \((p∨q)∧r ≡ (p∧r)∨(q∧r) \) и что \((p∧q)∨r ≡ (p∨r)∧(q∨ р)\). Покажите, что правые дистрибутивные законы также являются действительными законами булевой алгебры. (Примечание: на практике и левый, и правый законы распределения называются просто законами распределения, и оба они могут свободно использоваться в доказательствах.)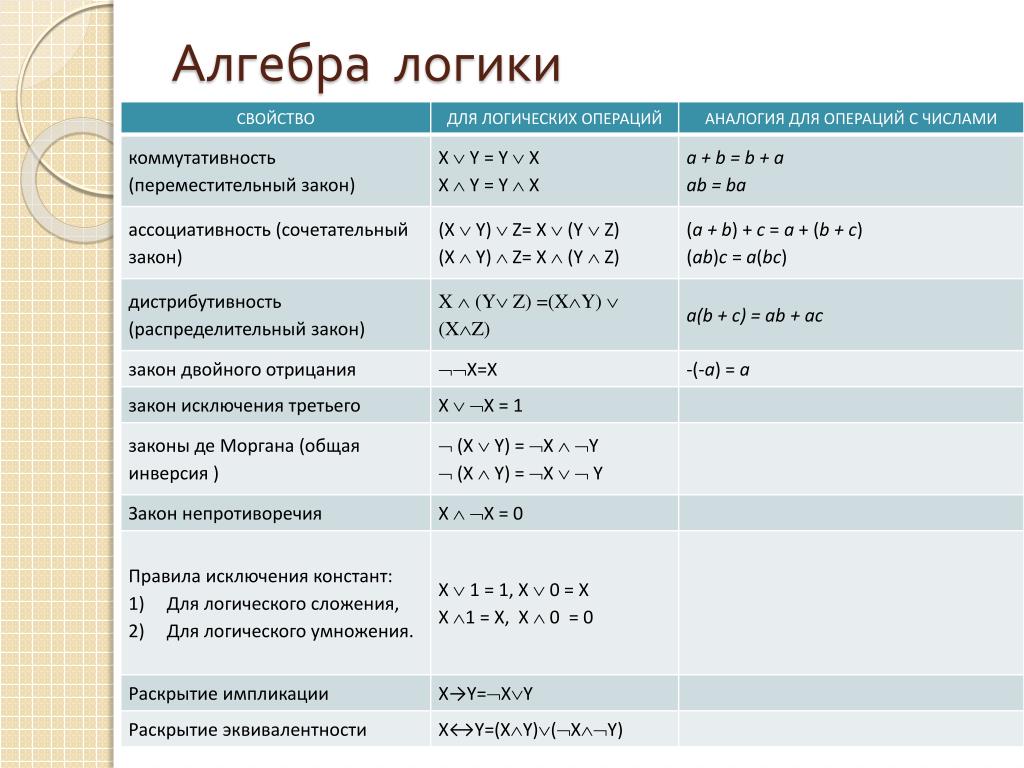 Каких законов не хватает? Покажите, что ваши ответы на самом деле таковы. , законы.
Каких законов не хватает? Покажите, что ваши ответы на самом деле таковы. , законы.
