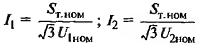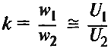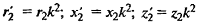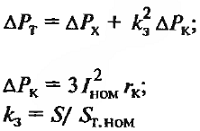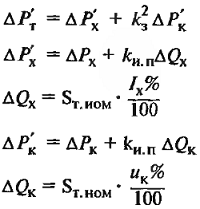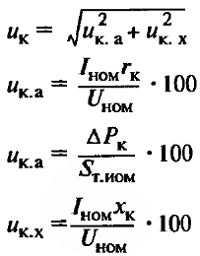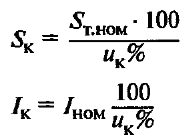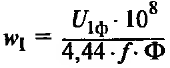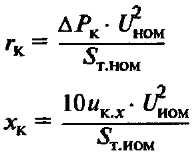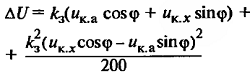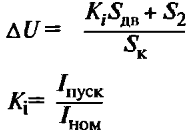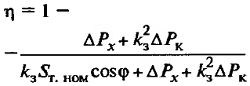Реактивное сопротивление трансформатора: формулы расчета

Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.

Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков

В катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.

Потери реактивных мощностей

Вспомним, как работает идеальный двухобмоточный трансформатор (см. рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.

Рис. 2. Устройство трансформатора

В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U₁ и U₂ – напряжения в первой и второй обмотке соответственно, а w₁ и w₂ – количество витков обмоток, то справедлива формула: U₁ / U₂ = w₁ / w₂.

Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.

Величину w₁ / w₂ = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.

В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает  магнитопровод и выходит за пределы обмоток.

Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.

Обозначим активное сопротивление обмоток символами R₁ и R₂ соответственно, а реактивное – буквами X₁ и X₂. Тогда импеданс первичной обмотки можно записать в виде: Z₁= R₁+jX₁. Для рабочей катушки соответственно будем иметь: Z₂= R₂+jX₂, где j – коэффициент, зависящий от типа сердечника.

Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = R_L – R_C. Учитывая, что R_L =  ωL, а R_C = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления:

X = ωL – 1/ωC.

Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:

Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.

Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.

Режимы работы

Двухобмоточный трансформатор способен работать в одном из трёх режимов:

• вхолостую;
• в режиме нагрузки;
• в состоянии короткого замыкания.

Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:

• уровень потерь активной мощности при работе на холостом ходу;
• величины потерь активной мощности в короткозамкнутом приборе;
• напряжение короткого замыкания;
• силу тока холостого хода;
• активное и реактивное сопротивление в короткозамкнутом трансформаторе.

Параметры режима холостого хода

Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.

Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.

Рис. 3. Схема режима холостого хода

Формула, применяемая для  расчётов параметров реактивной проводимости, выглядит так: В_т = I_х%*S_ном  / 100* U_{в ном}²  Умножитель 100 в знаменателе применён потому, что величина тока холостого хода I_х обычно выражается в процентах.

Режим короткого замыкания

Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.

Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔP_k = 3* I_1ном * R_т. Выразив ток I_{1 ном} через напряжение U_ка и сопротивление R_т, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение R_т в предыдущую формулу, получим:

Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.

Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

Отсюда находим:

Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления U_{к р} ≈ U_к, поэтому для практических расчётов можно пользоваться формулой: X_T = U_k*U_{в ном}² / 100*S_ном

Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.

Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.

Расчетные формулы основных параметров трансформаторов

Представляю вашему вниманию таблицу с расчетными формулами для определения основных параметров силовых трансформаторов, а также таблицу коэффициента изменения потерь kн.п. в трансформаторах.

Таблица 1 – Расчетные формулы для определения основных параметров трансформаторов

Наименование величин	Формулы	Обозначение
Токи обмоток		I1, I2 — токи первичной и вторичной обмоток, А; U1, U2 — то же линейное напряжение, В;
Коэффициент трансформации		w1, w2 – числа витков одной фазы обмоток
Приведение величин вторичной обмотки к первичной		Приведенные величины обозначают штрихом
Сопротивление короткого замыкания		rк, хк, zк – активные, реактивные и полное сопротивления КЗ фазы трансформатора
Активные потери мощности в трансформаторе при нагрузке		∆Рх – активные потери холостого хода, кВт; ∆Рк – активные нагрузочные потери в обмотках при номинальном токе, кВт; kз – коэффициент загрузки; Sт.ном. – номинальная мощность трансформатора.
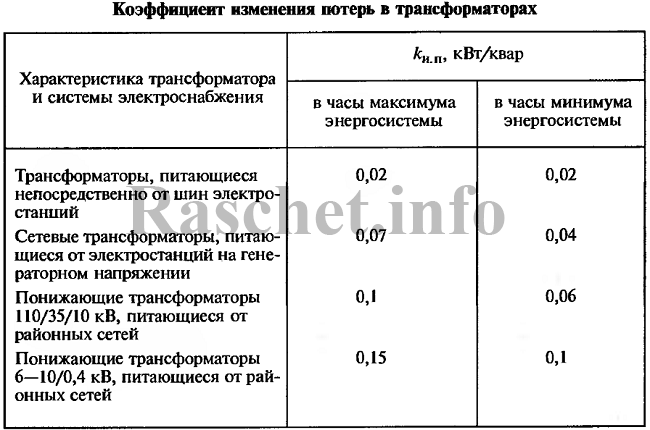
Приведенные активные потери мощности в трансформаторе при нагрузке		S – фактическая нагрузка трансформатора; kи.п. – коэффициент изменения потерь, кВт/квар; ∆Qх – реактивные потери мощности холостого хода; ∆Qк – реактивные потери мощности КЗ; Значения kи.п. даны ниже.
Напряжение КЗ		Uк – напряжение КЗ, В или %; Uк.а, Uк.х – активная и реактивная составляющие напряжения КЗ, В или %.
Мощность и ток КЗ трансформатора		Sк –мощность КЗ, кВА
Число витков первичной обмотки		U1ф – фазное напряжение первичной обмотки, В Ф – фазный поток; Ф = Вст*Qст мкс; Вст –индукция в стержне; Вст = 13 – 14,5 103 Гс; Qст – активное сечение стержня, см2
Активное и реактивное сопротивление двухобмоточного трансформатора, Ом
Падение напряжения в обмотках трансформатора при нагрузке		Если нагрузка смешанная (активная и индуктивная), то вторым членом можно пренебречь
Потери напряжения при пуске асинхронного короткозамкнутого двигателя (приближенно)		∆U – потеря напряжения, %; Sдв. – номинальная мощность двигателя, кВА; S2 – мощность других потребителей, присоединенных к шинам трансформаторов, кВА; Ki – кратность пускового тока относительно номинального.
КПД трансформатора

Исходные данные, которые приводятся в паспорте (шильдике) на трансформатор:

• Потери холостого хода ∆Рх, кВт;
• Потери короткого замыкания ∆Pк, кВт;
• Напряжения короткого замыкания Uк, %;
• Ток холостого хода Iхх,%.

Таблица 2 – Коэффициент изменения потерь в трансформаторах

Литература:

1. Справочная книга электрика. В.И. Григорьева, 2004 г.

коэффициент трансформации, мощность и ток кз трансформатора, напряжение кз, сопротивление короткого замыкания

Поделиться в социальных сетях

Благодарность:

Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding».

Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.

Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.

1.4. Определение сопротивления трансформатора.

Сопротивления трансформатора находятся по данным опыта короткого замыкания. Схема опыта показана на рисунке.

Из схемы опыта короткого замыкания видно, что напряжение короткого замыкания равно 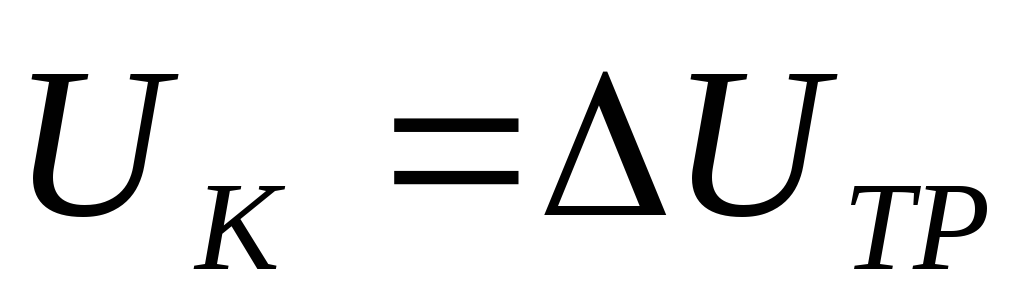при номинальной нагрузке трансформатора.

Умножив на 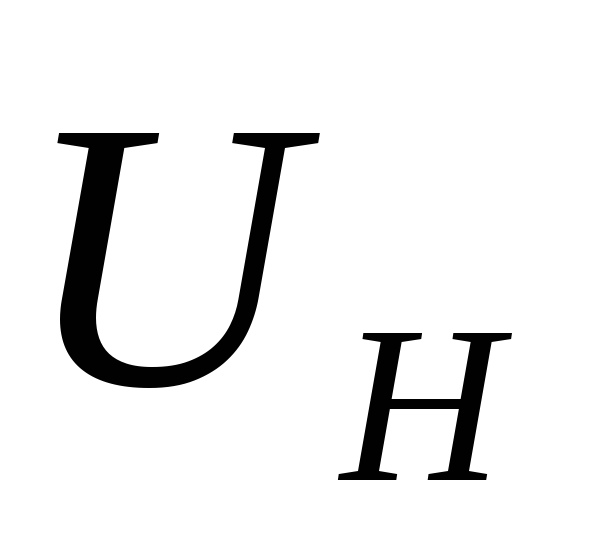числитель и знаменатель, получим

У силовых трансформаторов , поэтому для них с достаточной точностью принимают, что

В опыте короткого замыкания ваттметр показывает сумму потерь активной мощности в стали и в меди. Поскольку U_к в % составляет 5 – 17 %, то пропорциональный напряжению магнитный поток в стальном сердечнике невелик.

Потери активной мощности в стали приблизительно пропорциональны квадрату магнитного потока, поэтому в опыте короткого замыкания они очень малы и, или можно пренебречь.

В результате:

, откуда

или

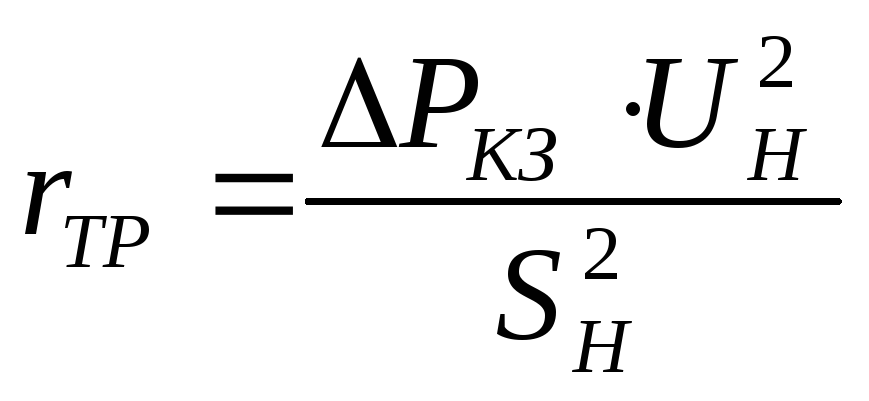
1.5. Определение проводимостей трансформатора.

Проводимости g_т и b_т находятся по данным опыта холостого хода. Схема опыта показана на рисунке.

Ток холостого хода мал и составляет 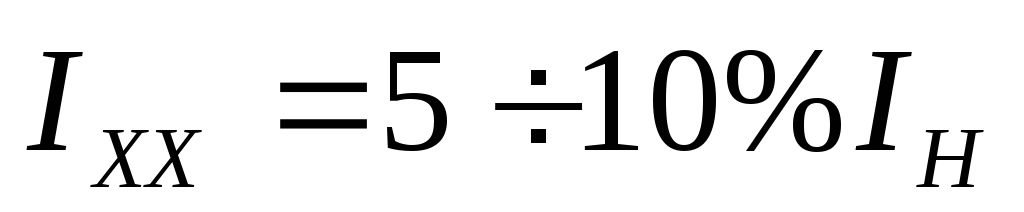. Потери мощности, в первичной обмотке, зависящей от квадрата этого тока, незначительны, в результате чего принимают, что .

Потери в стали определяются выражением 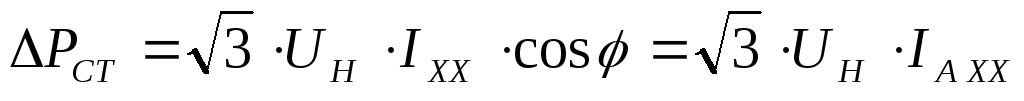, где

– активная составляющая тока холостого хода, которая равна

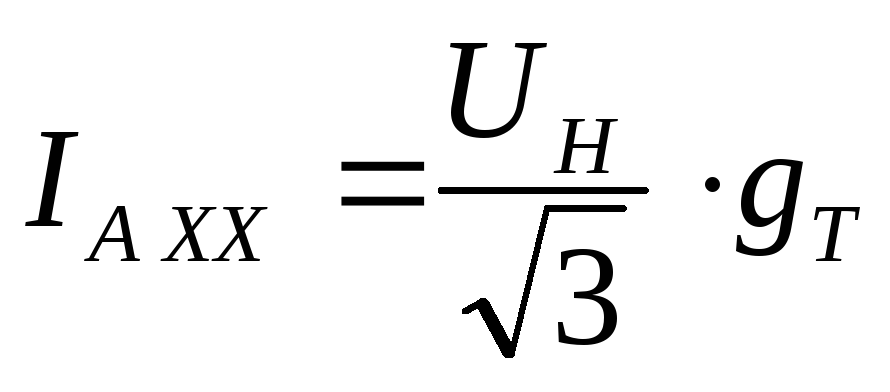
Выраженные через потери мощности в стали равны

Токи холостого хода активная составляющая которых покрывает потери активной мощности в стальном сердечнике на гистерезис и вихревые токи, в 5 – 10 раз меньше реактивной составляющей. Приближённо принимают

Отсюда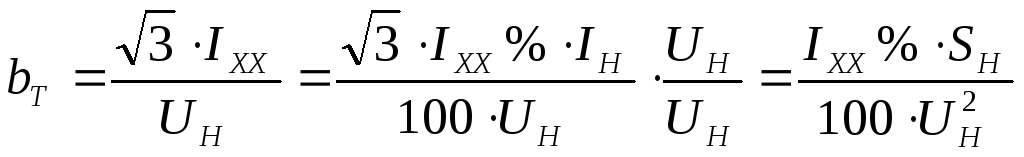

окончательно имеем .

Таким образом

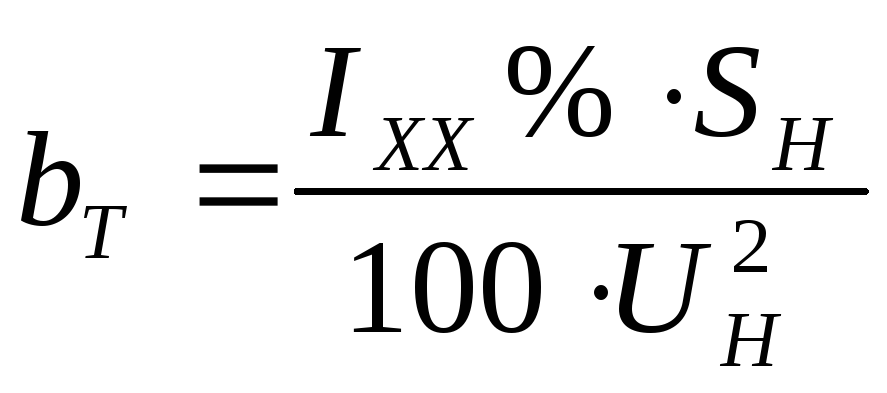
2. Трёхобмоточные трансформаторы.

Понижающие подстанции иногда питают распределительные сети двух напряжений, например 10(6) и 35 кВ. Если нагрузки этих сетей соизмеримы, то целесообразно применять трёхобмоточные трансформаторы с двумя вторичными обмотками вместо установки двух двухобмоточных трансформатора.

2.1. Соединение обмоток трёхобмоточных трансформаторов.

У силовых трансформаторов обмотки ВН и СН соединяются в звезду, обмотка НН в треугольник. Соответственно группа соединения у/у/Д-0-11.

На тяговых подстанциях для совместного питания тяги и района устанавливают трёхобмоточные трансформаторы.

Их первичная обмотка соединяется в звезду, а тяговая в треугольник. Соединение районной обмотки зависит от её напряжений. Если она имеет напряжение 11(6,6 кВ), то соединяют в треугольник, при напряжении 38,5 кВ – в звезду.

Сопротивление элементов схемы замещения в сети 0,4 кВ

Содержание

Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).

Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.

Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].

Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:

Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].

Пример

Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.

Решение

Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.

Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:

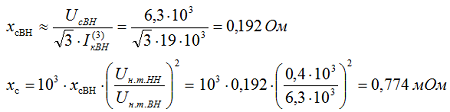
Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:

Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

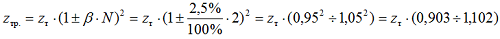
Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

Как видно, формулы из ГОСТ 28249-93 совпадают с формулами приведенными в [Л3. с. 28].

Для упрощения расчета активного и индуктивного сопротивления тр-ра, можно использовать таблицу 2-4 [Л3. с. 29] для схем соединения обмоток трансформатора Y/Yo и ∆/Yo. Причем для схем соединения обмоток трансформатора ∆/Yo, значения активного (r0) и индуктивного (х0) сопротивления нулевой последовательности равны значениям активного и индуктивного сопротивления прямой последовательности: r0 = rт и х0 = хт.

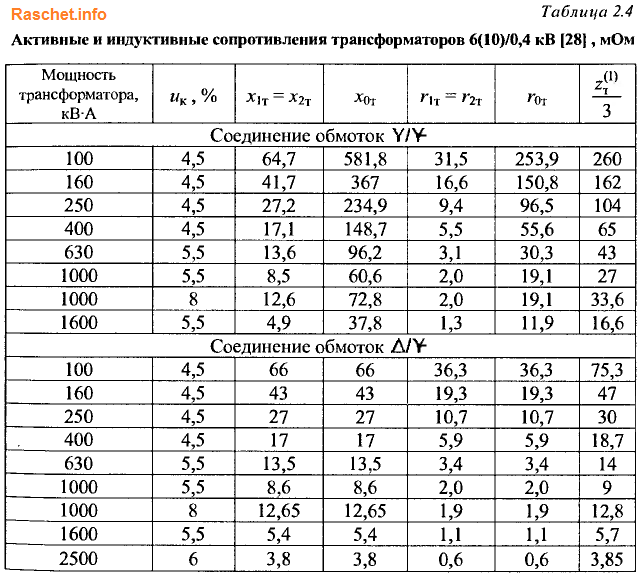
Пример

Определить сопротивление трансформатора ТМ 50/6 со схемой соединения обмоток ∆/Yо.

Решение

По справочным данным определяем технические данные трансформатора: Sном. = 50 кВА, Uном.ВН = 6,3 кВ, Uном.НН = 0,4 кВ, Uкз = 4%, ∆Ркз=1,1 кВт.

Определяем полное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-8:

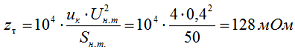
Определяем активное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-9:

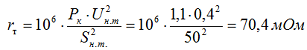
Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-10:

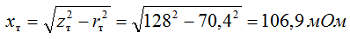
Значения активного и индуктивного сопротивления кабелей определяются по формуле 2-11 [Л3. с. 29].

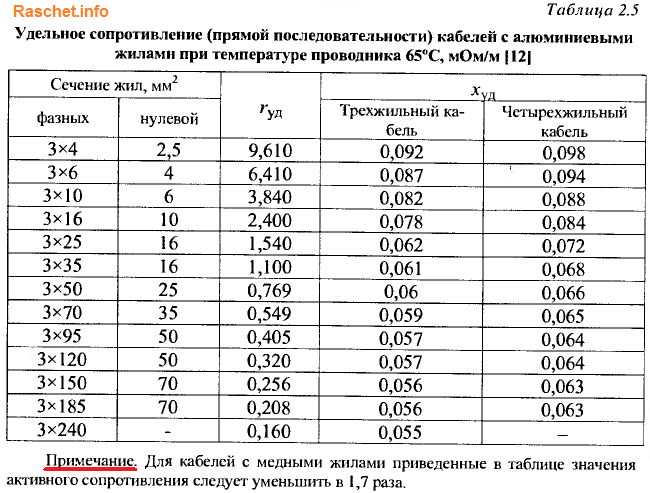
Сопротивление шин и шинопроводов длиной 5м и меньше, можно не рассчитывать, так как они не влияют на значение токов КЗ.

Значения активного и индуктивного сопротивления шин и шинопроводов определяется аналогично кабелям.

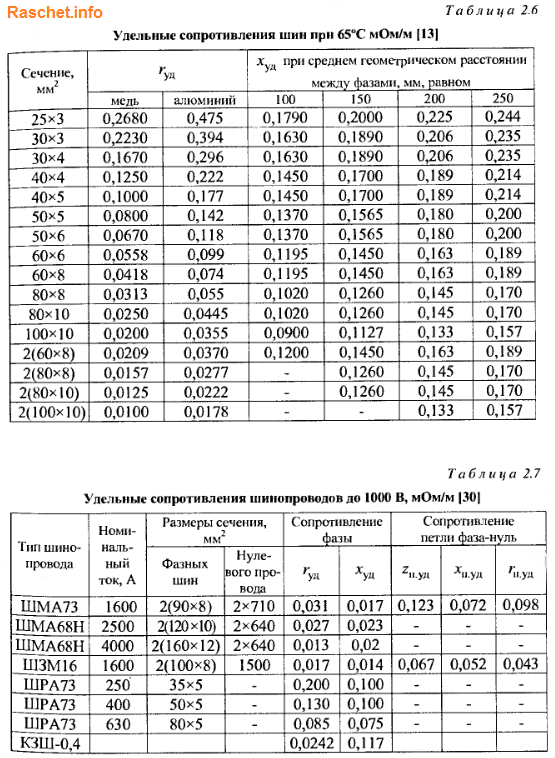
Зная расстояние между прямоугольными шинами, можно приближенно определить индуктивное сопротивление (мОм/м) по формуле 2-12 [Л3. с. 29].

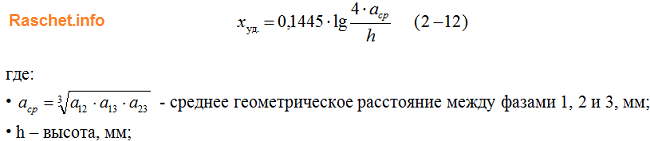
Пример

Определить активное и индуктивное сопротивление алюминиевых шин сечением 60х8 мм2 от трансформатора ТМ-630/6 до распределительного щита 0,4 кВ, общая длина проложенных от трансформатора до РП-0,4 кВ составляет 10 м. В данном примере определим сопротивление шин, когда шины находятся как в горизонтальном положении, так и в вертикальном.

Решение

4.1 Определим активное и индуктивное сопротивление шин при горизонтальном расположении.

По таблице 2.6 определяем погонное активное сопротивление r_уд. = 0,074 мОм/м, индуктивное сопротивление определяем по формуле 2-12 [Л3. с. 29].

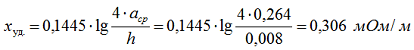
где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 60 + 200 = 460 мм, а среднегеометрическое расстояние:

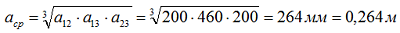
Сопротивление шин от тр-ра до РП-0,4 кВ:

4.2 Определим активное и индуктивное сопротивление шин при вертикальном расположении

При вертикальном расположении шин, активное сопротивление не изменяется, а индуктивное сопротивление составляет:

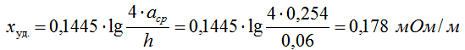
где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 8 + 200 = 408 мм, а среднегеометрическое расстояние:

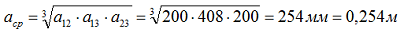
Сопротивление шин от тр-ра до РП-0,4 кВ:

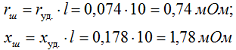
Активное и индуктивное сопротивления линий определяется по той же формуле 2-11 [Л3. с. 29], что и кабели.

Значение индуктивного сопротивления для проводов из цветных металлов можно приближенно принимать равным 0,3 мОм/м, активного по табл. 2.8.

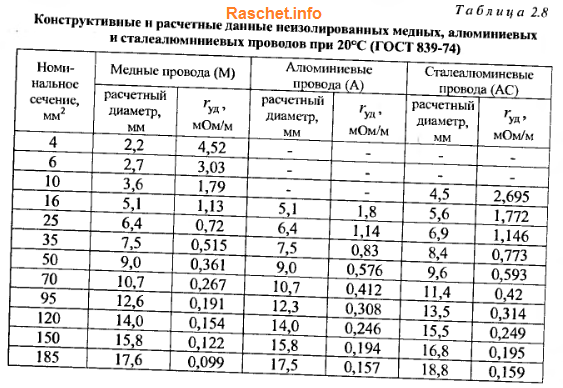
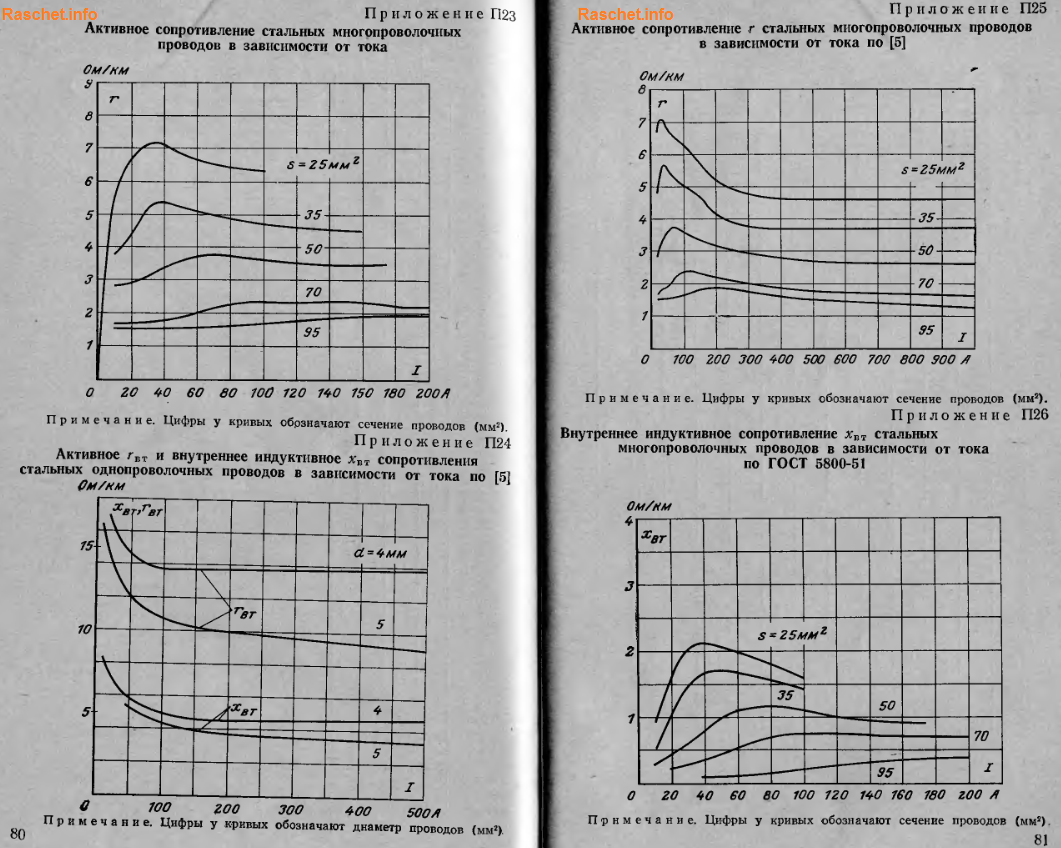
Для стальных проводов активное и индуктивное сопротивление определяется исходя из конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается, из-за большого количества переменных (сечение провода, температура окружающего воздуха, которая постоянно меняется в течении года, времени суток; нагревом провода током КЗ), которые влияют на значение сопротивление стальных проводов.

Поэтому учесть все эти зависимости практически не возможно и на практике активное сопротивление условно принимают при температуре 20°С и определяют по кривым зависимости стальных проводов от проходящего по ним токам, представленных в приложениях П23-П27 [Л4. с. 80-82].

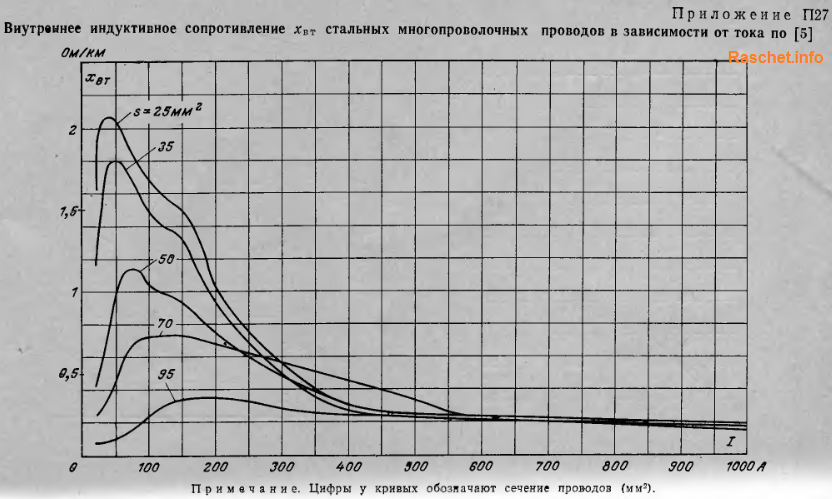
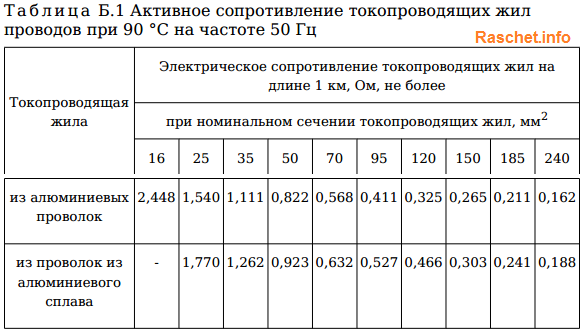
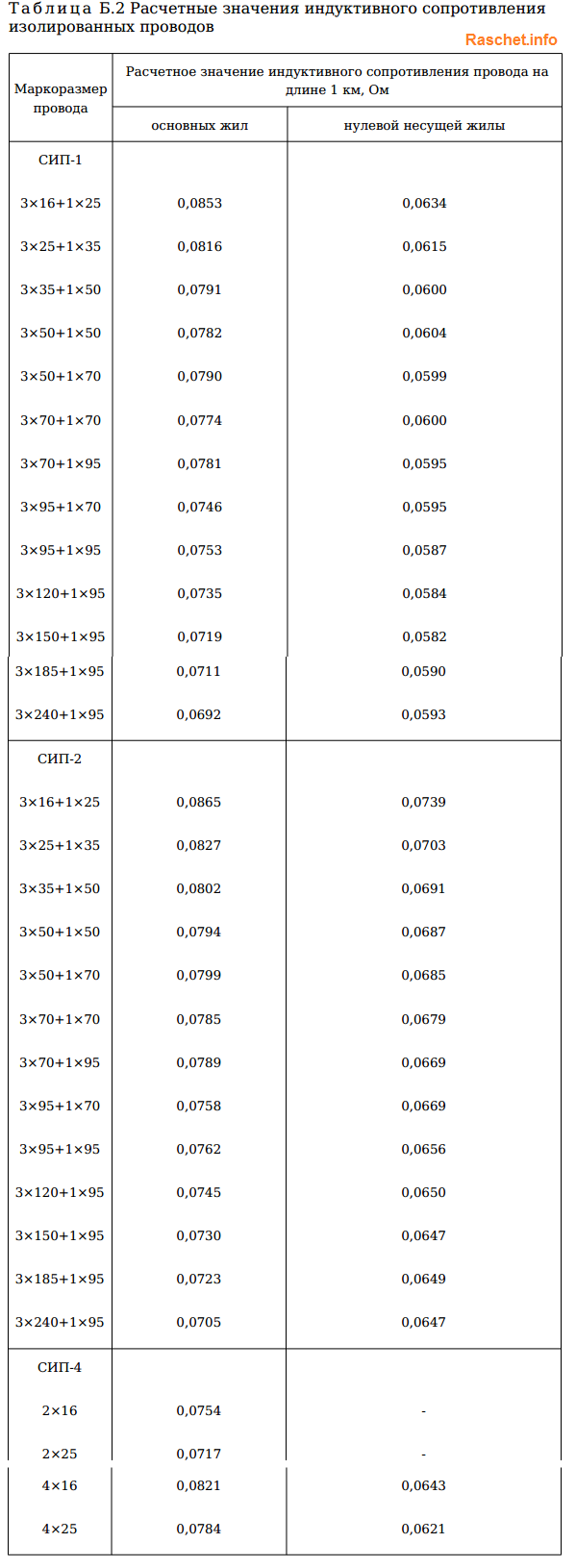
Активное и индуктивное сопротивление для проводов самонесущих изолированных (СИП) определяют по таблицам Б.1, Б.2 [Л5. с. 23-26].

Номинальные параметры реактора уже заданы в обозначении самого реактора типа РТТ и РТСТ. Например у реактора типа РТТ-0,38-100-0,15:

• 0,38 – номинальное напряжение 380 В;
• 100 – номинальный ток 100 А;
• 0,15 – индуктивное сопротивление при частоте 50 Гц равно 150 мОм.

Активное сопротивление для исполнения У3 (алюминиевая обмотка) — 17 мОм, для исполнения Т3 (медная обмотка) – 16 мОм.

Значения активных и индуктивных сопротивлений трансформаторов тока принимаются по приложению 5 таблица 20 ГОСТ 28249-93. Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.

Согласно [Л3. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.

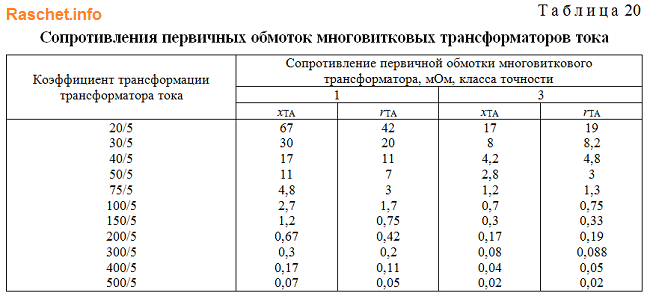
Приближенные значения сопротивлений разъемных контактов коммутационных аппаратов напряжением до 1 кВ определяются по приложению 4 таблица 19 ГОСТ 28249-93. При приближенном учете сопротивление коммутационных аппаратов принимают — 1 мОм.

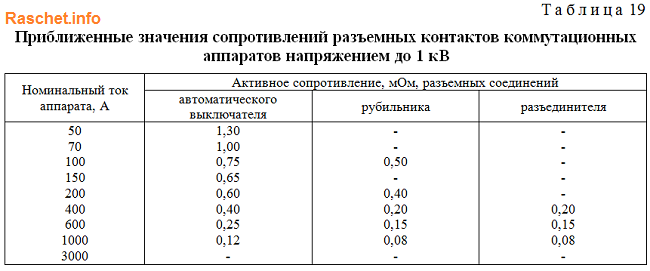
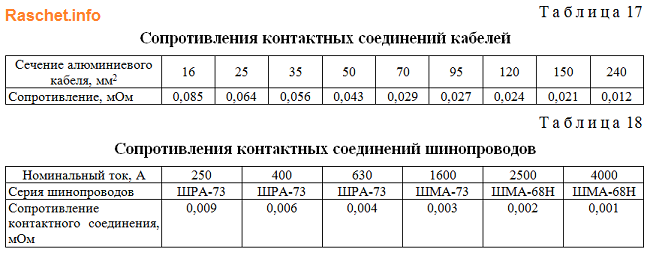
Значения сопротивления контактных соединений кабелей и шинопроводов определяют по приложению 4 таблицы 17,18 ГОСТ 28249-93. Для упрощения расчетов, данными сопротивлениями можно пренебречь. При приближенном учете сопротивлений контактов принимают: • rк = 0,1 мОм — для контактных соединений кабелей;
• rк = 0,01 мОм — для шинопроводов.

1. Рекомендации по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.
4. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
5. ТУ 16-705.500-2006. Провода самонесущие изолированные и защищенные для воздушных линий электропередач.

Активные сопротивления обмоток трансформатора

Активные сопротивления обмоток определяем при расчетной температуре 115ºС.

Коэффициенты добавочных потерь.

Определение коэффициента Роговского.

Величина для трансформатора с частичным разделением вторичной обмотки:

(20.1)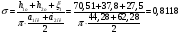

(20.2)

Коэффициент добавочных потерь первичной обмотки.

Для круглого провода:

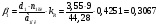
(20.3)

где мкОм*м [1].

Принимаем завышенное значение коэффициента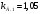

Коэффициент добавочных потерь вторичной обмотки:

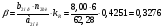. (20.4)

Для основной вторичной обмотки:

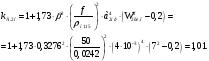(20.5)

Поскольку для дополнительной вторичной обмотки коэффициент добавочных потерь будет еще меньше (), то для всей вторичной обмотки принимаем завышенное значение коэффициента .

Активные сопротивления обмоток при параллельном включении катушек:

Ом;

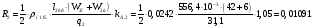Ом. (20.6)

Сопротивление короткого замыкания трансформатора, приведенное к вторичной обмотке:

Ом. (20.7)

21. Определение токов и напряжений дуги при максимальном и минимальном токах и проверка на устойчивость

Ток, напряжение и мощность дуги при номинальном напряжении и максимальном сварочном токе:

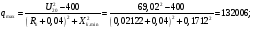
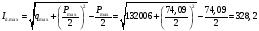А;

В;

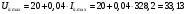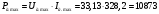Вт. (21.1)

Ток, напряжение и мощность дуги при номинальном напряжении и минимальном сварочном токе:

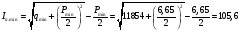А;

В;

Вт. (21.2)

Ток, напряжение и мощность дуги при пониженном на 10% напряжении и максимальном сварочном токе:

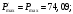
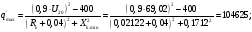
А;

В;

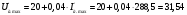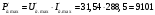Вт. (21.3)

Ток, напряжение и мощность дуги при пониженном на 10% напряжении и минимальном сварочном токе:

А;

В;

Вт. (21.4)

Максимальная полезная мощность трансформатора и граничные значения тока и напряжения для режимов максимального и минимального токов при номинальном напряжении:

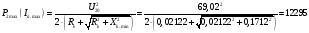Вт>10873 Вт;

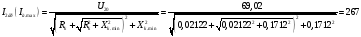А;

267 А<328,2 А;

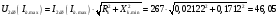В>33,13 В;

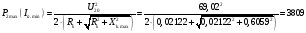Вт>2558 Вт;

А;

79,4 А<105,6 А;

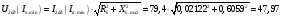В>24,22 В. (21.5)

Условия проверки при номинальном питающем напряжении выполняются.

Максимальная полезная мощность трансформатора и граничные значения тока и напряжения для режимов максимального и минимального токов при пониженном на 10% напряжении:

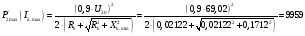Вт>9101 Вт;

А;

240,3 А<288,5 А;

В>31,54 В;

Вт>2224 Вт;

А;

71,46 А<93,64 А;

В>23,75 В. (21.6)

Условия проверки при пониженном на 10% напряжении выполняются.

Проверка условия повторного зажигания дуги для минимального сварочного тока при пониженном на 10% напряжении:

Находим напряжение зажигания при токе 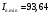А [1]:

В, определяем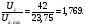

Находим минимально допустимое отношение [1], откуда:

В < 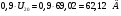(21.7)

Условие проверки выполнено в самом неблагоприятном случае.

22. Вольтамперные характеристики дуги и трансформатора при номинальном и пониженном на 10% напряжении

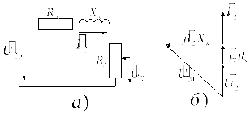
Рисунок 4 – Упрощенная схема замещения (а) и векторная диаграмма сварочного трансформатора (б)

_{При номинальном напряжении:}

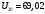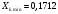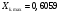В; Ом; 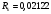Ом; Ом.

Токи короткого замыкания при минимальном и максимальном индуктивных сопротивлениях:

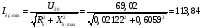А;

А. (22.1)

Вольтамперная характеристика дуги и трансформатора находятся исходя из схемы замещения и векторной диаграммы трансформатора (рисунок 4):

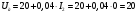В;

В;

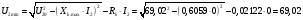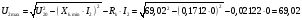В. (22.2)

Дальнейший расчет сведем в таблицу 1:

Таблица 1 – Расчет вольтамперных характеристик дуги и трансформатора при номинальном напряжении

	0	16	32	48	64	80	96	112	128	144	160	176	192
	20	20,64	21,28	21,92	22,56	23,2	23,84	24,48	25,12	25,76	26,4	27,04	27,68
	69,02	68	65,56	61,57	55,74	47,44	35,12	10,22	—	—	—	—	—
	69,02	68,63	68,12	67,51	66,79	65,95	65	63,93	62,73	61,41	59,96	58,36	56,62

Продолжение таблицы 1

	208	224	240	256	272	288	304	320	336	352	368	384	400
	28,32	28,96	29,6	30,24	30,88	31,52	32,16	32,8	33,44	34,08	34,72	35,36	36
	—	—	—	—	—	—	—	—	—	—	—	—	—
	54,71	52,63	50,36	47,89	45,17	42,19	38,88	35,19	31,01	26,18	20,38	12,87	0,13

При напряжении, пониженном на 10%:

В;

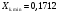Ом; 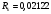Ом; Ом.

Токи короткого замыкания при минимальном и максимальном индуктивных сопротивлениях:

А;

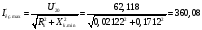А. (22.3)

Вольтамперная характеристика дуги и трансформатора:

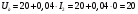В;

В;

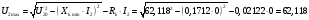В. (22.4)

Дальнейший расчет сведем в таблицу 2:

Таблица 2 – Расчет вольтамперных характеристик дуги и трансформатора при пониженном на 10% напряжении

	0	16	32	48	64	80	96	112	128	144	160	176	192
	20	20,64	21,28	21,92	22,56	23,2	23,84	24,48	25,12	25,76	26,4	27,04	27,68
	62,118	61,02	58,34	53,87	47,17	37,15	19,76	—	—	—	—	—	—
	62,118	61,72	61,2	60,55	59,79	58,89	57,87	56,71	55,41	53,96	52,36	50,59	48,63

Продолжение таблицы 2

	208	224	240	256	272	288	304	320	336	352	368	384	400
	28,32	28,96	29,6	30,24	30,88	31,52	32,16	32,8	33,44	34,08	34,72	35,36	36
	—	—	—	—	—	—	—	—	—	—	—	—	—
	46,48	44,11	41,49	38,59	35,34	31,67	27,46	22,49	16,32	7,6	—	—	—

По приведенным расчетам построим вольтамперные характеристики дуги и трансформатора при номинальном и пониженном на 10% напряжении.

3.2. Сопротивления и проводимости трансформаторов и автотрансформаторов

При расчете передачи с трансформаторами сопротивления, напряжения и токи ли­ний и трансформаторов приводятся к какому-то одному напряжению. Чаще всего приведение делается к входной стороне, т. е. при понижающем трансформаторе к стороне высшего напряжения.

Здесь и в дальнейшем напряжение, к которому производится приведение (в данном случае ) будет обозначаться через .

3. 3.2.1. Активные и индуктивные сопротивления трансформатора

Для двухобмоточных трансформаторов активное сопротивление:

(3.7)

Потери короткого замыкания даются в паспортных данных. Для трехобмоточных трансформаторов заводами да­ются потери короткого замыканиядля худшего случая, которым является протекание тока по двум обмот­кам при третьей разомкнутой. Сопротивление трансформатора определяется как:

. (3.8)

Для автотрансформаторов заводами даются потери короткого замыкания для каждой пары обмоток 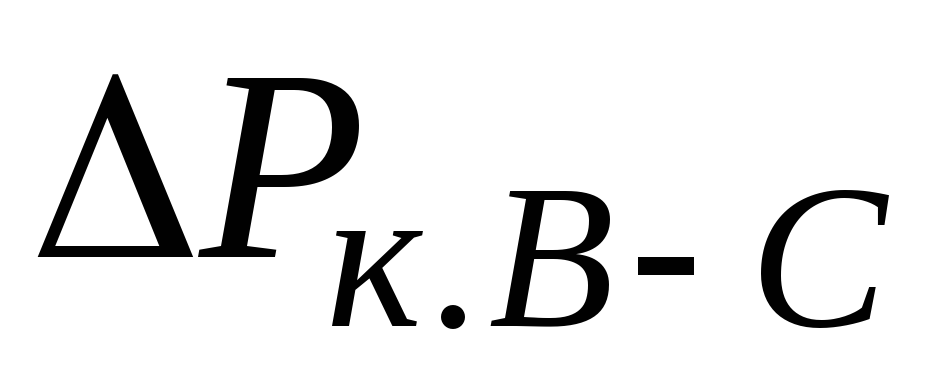,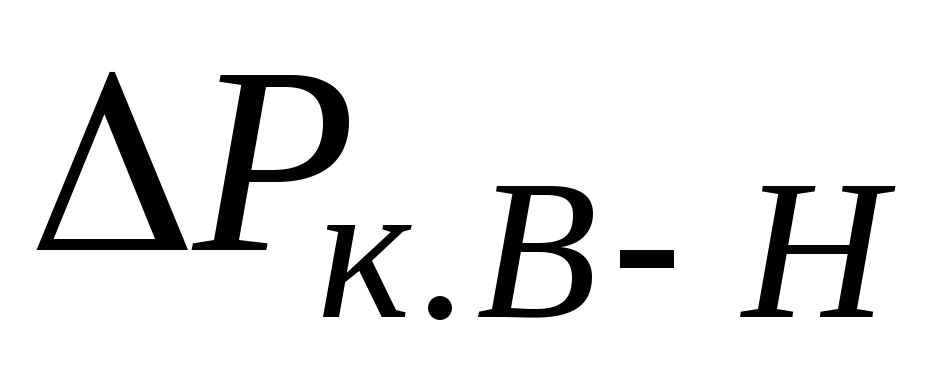и. Чтобы определить сопротивление каждого луча, можно ориенти­ровочно принять:

, (3.9)

. (3.10)

Аналогично находятся и потери . Тогда:

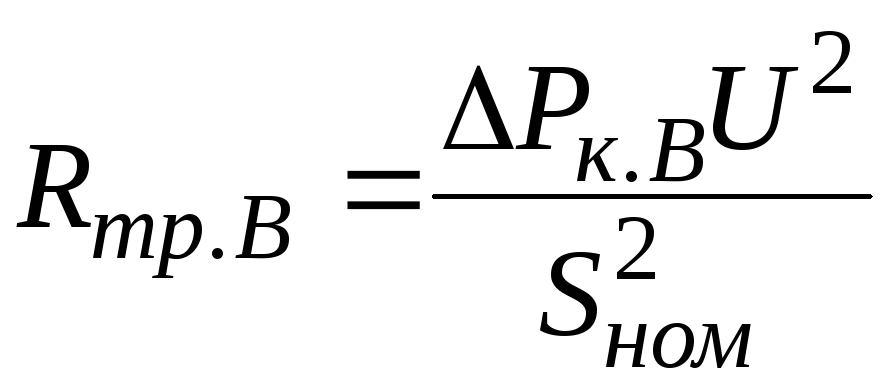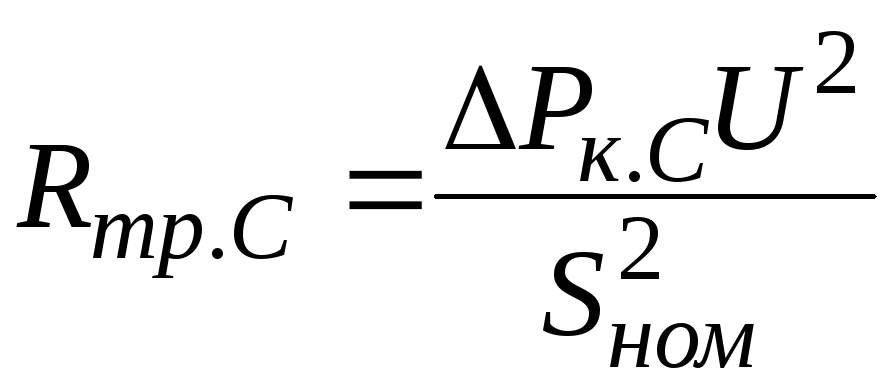, ,. (3.11)

Индуктивное сопротивление для двухобмоточного трансформатора:

, (3.12)

где — напряжение короткого замыкания в процентах от номи­нального.

Для трехобмоточных трансформаторов и автотрансформаторов напряжения ко­роткого замыкания даются заводами для каждой пары обмоток в процентах от номинального, поэтому индуктивное сопротивление каждого луча, %, аналогично (3.14) и (3.15):

. (3.13)

Откуда:

. (3.14)

Аналогично рассчитываются и.

Индуктивные сопротивления мощных трансформаторов и авто­трансформаторов в противоположность кабельным линиям во много раз больше активных.

3.2.2. Активные и реактивные проводимости трансформаторов

Активные проводимости обусловлены перемагничиванием и вихревыми токами и могут быть определены как:

, (3.15)

где 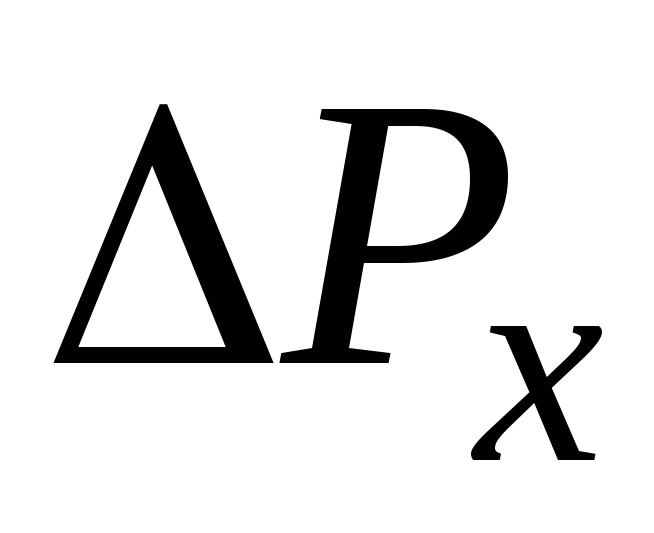— потери холостого хода, Вт.

Реактивные проводимости обусловлены намагничивающей мощностью, имеют индуктивный характер, противоположный реактивной проводимости линий и определя­ются как:

, (3.16)

где — ток холостого хода в процентах от номинального.

Полная проводимость трансформатора:

. (3.17)

3.3. Эквивалентное сопротивление элементов системы

Чтобы определить обобщенные постоянные всей линии передачи, четырехполюсники соединяются после­довательно, параллельно или последовательно и параллельно в зависимости от характера передачи (рис. 3). Для получения эквивалентного сопротивления двухполюсников при последовательном их соединении складывают­ся сопротивления, а при парал­лельном — проводимости. При одинаковых параллельно соеди­ненных четырехполюсни­ках сопротивления делятся по­полам, а проводимости умножа­ются на два.

Схема четырехполюсников в общем виде может быть представлена, как показано на рис. 4, а. Тогда обобщенные по­стоянные 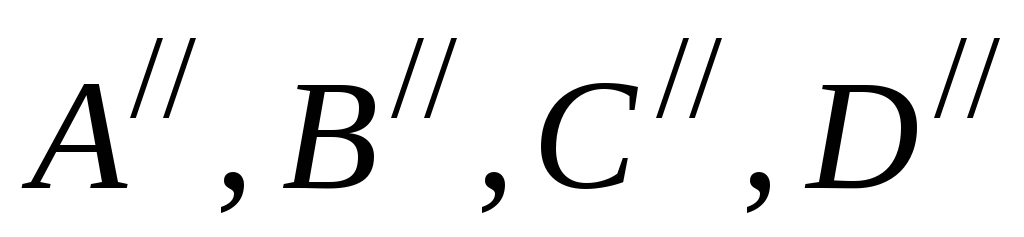параллельно включенных одинаковых 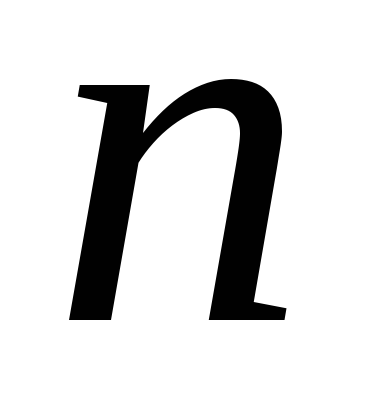элементов (линий или трансформаторов) запишутся как:

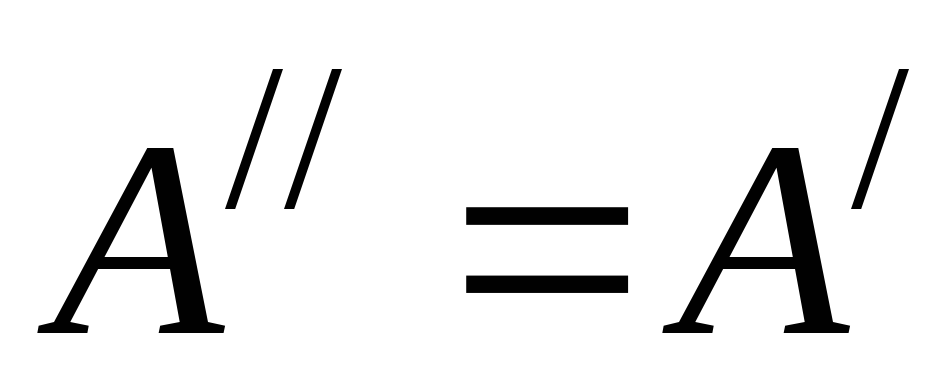; ; ; , (3.18)

где — постоянные одного элемента.

Схема принимает вид, показанный на рис. 4, б. Два четы­рехполюсника этой схемы можно соединить последовательно. Окончательные значения обобщенных постоянных (рис. 4, в) можно представить в виде:

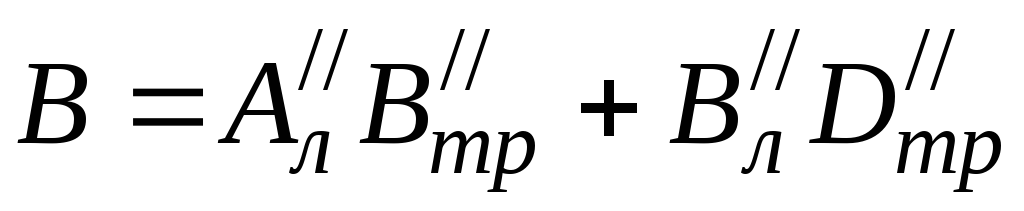; ; (3.19)

; .

Активное сопротивление — трансформатор — Большая Энциклопедия Нефти и Газа, статья, страница 1

Активное сопротивление — трансформатор

Cтраница 1

Активное сопротивление трансформатора обычно точнее всего определяется после его изготовления.  [1]

Активное сопротивление трансформаторов принимаем равным 4 % от их индуктивного сопротивления. В конечном счете при полной поперечной компенсации схема приводится к виду, представленному на фиг.  [2]

Активные сопротивления трансформаторов и автотрансформаторов высокого напряжения большой мощности очень малы по сравнению с индуктивными.  [3]

Активные сопротивления трансформаторов и автотрансформаторов высокого напряжения большой мощности очень малы по сравнению с индуктивными. Поэтому в практических расчетах сетей с крупными трансформаторами и автотрансформаторами можно активными сопротивлениями и потерями мощности в них пренебречь, не внеся в результаты существенной погрешности.  [4]

Активные сопротивления трансформаторов или реакторов приняты равными нулю.  [5]

Активное сопротивление трансформатора весьма мало. Если при этом принять, что индуктивное сопротивление рассеяния трансформатора приближенно изменяется пропорционально квадрату числа витков его обмоток ( что довольно близко к действительности), то заданное значение ик %, следует считать от напряжения холостого хода того ответвления регулируемой обмотки, которое установлено у трансформатора.  [6]

Активное сопротивление трансформатора, отнесенное к базисной мощности.  [8]

Активное сопротивление трансформатора обычно точнее всего определяется после его изготовления.  [9]

Междуобмоточные активные сопротивления трансформатора определяются по соответствующим потерям к.  [10]

Активное сопротивление трансформатора напряжения, изменяющееся в зависимости от его параметров в пределах 3 — 15 кОм, уменьшает постоянную времени разряда и позволяет, как показали результаты измерений, практически полностью снять напряжение с участка линии 500 кВ длиной 250 — 300 км в течение 0 05 с. На линии длиной до 500 км необходима установка двух комплектов трансформаторов напряжения, которые должны размещаться по концам участка. В этом случае коммутационные перенапряжения при ТАПВ будут ограничены по величине до уровня, регистрируемого при включении линии.  [11]

Активным сопротивлением трансформатора пренебречь, вентили идеальные.  [12]

Определить активное сопротивление трансформатора при холостом ходе, коротком замыкании и нагрузке, если известно, что ток холостого хода / х2 5 А, ток короткого замыкания / 26 А, ток нагруженного трансформатора / j24 А.  [13]

Определение активных сопротивлений трансформаторов с расщепленными обмотками производится аналогично определению сопротивлений для трехоб-моточных трансформаторов.  [14]

Но поскольку активное сопротивление трансформаторов сравнительно невелико, обычно принимают гт.  [15]

Страницы:      1    2    3    4