Активное сопротивление — проводник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Активное сопротивление — проводник
Cтраница 1
Активное сопротивление проводника зависит от его размеров и формы. [1]
Активное сопротивление проводника для токов высокой частоты определяется удельным сопротивлением его поверхностного слоя. Для уменьшения этого сопротивления поверхность проводников, работающих в цепях высокой частоты, часто покрывают слоем серебра. [2]
Активное сопротивление проводника зависит от его размеров и формы. [3]
Активное сопротивление проводника различно при постоянном и переменном токе из-за поверхностного эффекта и эффекта близости. [4]
Активное сопротивление проводника увеличивается с увеличением частоты протекающего по нему переменного тока. Для частоты 50 гц, применяющейся в промышленной электротехнике, это увеличение незначительно, а для частот более высоких активное сопротивление проводника может весьма заметно превышать омическое. Кроме того, неравномерное распределение тока обусловливает уменьшение магнитного потока внутри самого провода, вследствие чего уменьшается его индуктивность тем резче, чем выше частота переменного тока, передаваемого по проводу. [6]
Активное сопротивление проводника увеличивается по мере возрастания частоты переменного тока. Например, стальной провод диаметром 5 мм и длиной 1 км имеет при постоянном токе сопротивление, равное 20 омам, а при переменном токе с частотой 20 000 герц — 75 омам. Для частоты переменного тока в 50 герц, применяемого обычно в электрических установках, увеличение сопротивления незначительно. [7]
Активное сопротивление проводников тока определяют измерительными мостами или методом амперметра-вольтметра. Когда нужно знать действительное значение сопротивления проводников, пользуются мостами постоянного тока или методом амперметра-вольтметра. Чтобы установить, находится ли измеряемое сопротивление в допустимых пределах, используют одинарные или двойные автоматические мосты. Для определения процента отклонения измеряемого сопротивления от номинального его значения применяют одинарные или двойные процентные измерительные мосты. [8]
Активное сопротивление проводников токопроводящих частей измеряют методом сопротивления. [9]
Зная активное сопротивление проводника, нетрудно определить и мощность, которая в нем выделяется. [10]
Поскольку активное сопротивление проводника зависит от величины поперечного сечения того поверхностного слоя проводника, в котором течет ток, то для токов СВЧ активное сопротивление тонкостенной трубки не отличается от активного сопротивления проводника в виде сплошного стержня, сделанного из того же металла и имеющего тот же диаметр, что и сплошная трубка. Для уменьшения сопротивления поверхность проводников, применяемых в цепях высокой частоты, часто покрывают слоем металла, обладающего малым удельным сопротивлением, например серебра. [11]
Поскольку активное сопротивление проводника зависит от величины поперечного сечения того поверхностного слоя проводника, в котором течет ток, то для токов сверхвысокой частоты активное сопротивление тонкостенной трубки не отличается от активного сопротивления проводника в виде сплошного стержня, сделанного из того же металла и имеющего тот же диаметр, что и сплошная трубка. [12]
Увеличение активного сопротивления проводников тока якоря и катушек полюсов происходит из-за надрыва и трещин в проводниках или повреждения контактных соединений — распайки концов обмотки в петушках коллектора якоря, ослабления крепления или распайки наконечников. [13]
Под активным сопротивлением проводника понимают такое сопротивление, в котором энергия выделяется в виде теплоты. Электрическая цепь обладает активным сопротивлением К, индуктивностью L и емкостью С, которые являются ее параметрами. [14]
Яэ —
Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта
В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в диапазоне частот от 50 до 2000 Гц. Выведена расчетная формула для активного сопротивления цилиндрического провода на произвольной частоте. Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и площади поперечного сечения.
Ключевые слова: поверхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого провода
This article has shown the problem of high-harmonics influence on cylindrical wire resistance according to the frequency range from 50 to 2000 Hz. Cylindrical wire resistance estimation for any frequency has been deduced.We have also analyzed cylindrical wire resistance dependence of copper and aluminum wires due to the frequency and cross section area.
Keywords: skin effect, high-harmonics, copper wire resistance, aluminum wire resistance
В Российской Федерации системы электроснабжения общего назначения работают на фиксированной частоте 50 Гц. Кроме основной гармоники, в сетях присутствуют также высшие гармоники токов и напряжений [1]. Исследования указывают на то, что при наличии в сети нелинейных нагрузок, наибольшим искажениям подвергается форма кривой тока, в то время как кривая напряжения практически не изменяется [5, 6]. Это объясняется тем, что реальные генераторы по своим свойствам близки к идеальным источникам ЭДС. Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери мощности, с другой происходит ускоренный износ изоляции, изоляторов, растяжение проводов и другие негативные последствия [2]. По мере увеличения частоты, начинает проявляться поверхностный эффект, приводящий к перераспределению плотности тока в сечении проводника, от центра к поверхности, в результате изменяется его сопротивление, что в свою очередь влияет на потери мощности и энергии в линиях электропередачи электрической распределительной сети.
Задача данного исследования: определить степень изменения плотности тока в сечении провода и его сопротивления в зависимости от частоты гармоники тока протекающего по проводнику. Это позволит более точно рассчитать дополнительные потери мощности на нагрев проводов, обусловленные несинусоидальностью питающего напряжения электрической распределительной сети.
Провод можно приближенно представить в виде цилиндрического проводника, длина которого многократно превышает радиус. Для нахождения плотности тока используют уравнения Максвелла, решение которых производится в цилиндрической системе координат [3]. В результате выражения для плотности тока и напряженности магнитного поля в любой точке сечения цилиндрического проводника:
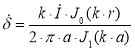 (1)
(1)
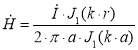 (2)
(2)
где 
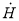 — напряженность магнитного поля, А/м;
— напряженность магнитного поля, А/м; 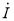 — комплексный ток, А; J0 — функция Бесселя 1-го рода 0-го порядка; J1 — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м;
— комплексный ток, А; J0 — функция Бесселя 1-го рода 0-го порядка; J1 — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м; 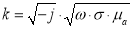 — комплексное волновое число, м-1;
— комплексное волновое число, м-1; 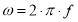
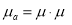 — абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.
— абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ 0= 4·π·10–7 Гн/м — магнитная постоянная.Формулы (1), (2) не учитывают «эффект близости», т. к. для этого необходимо точно знать пространственное расположение проводников. При расстоянии между проводами многократно превышающем радиус и невысоких значениях тока «эффектом близости» можно пренебречь.
Мощность рассеиваемую цилиндрическим проводом определяют по закону Джоуля-Ленца в комплексной форме:
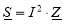 (3)
(3)
С другой стороны рассеиваемую мощность находим, используя теорему Умова-Пойнтинга [3]:
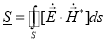 (4)
(4)
Приравнивая выражения (3) и (4) получаем:
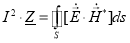 (5)
(5)
В результате комплексное сопротивление выражаем формулой:
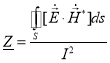 (6)
(6)
Вектор напряженности электрического поля 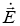 вычисляем по формуле:
вычисляем по формуле:
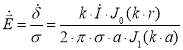 (7)
(7)
где σ — удельная проводимость, См/м.
Учитывая, что площадь боковой поверхности цилиндрического проводника равна S=2·π·a·lи радиус поверхности равен радиусу провода r=a получаем:
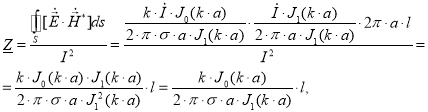
где l — длина проводника, м.
Таким образом, окончательное выражение для комплексного сопротивления цилиндрического провода приняло вид:

Активное сопротивление при этом определяем, как действительную часть полного комплексного сопротивления:
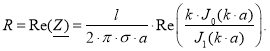 (8)
(8)
Рассчитаем сопротивления медных проводов и алюминиевых проводов марок А, АКП, АН, АНКП, АЖ, АЖКП. Сечения выберем самые распространенные: 16, 25, 35, 50, 70, 95, 120, 150, 185 мм2 [4], хотя каких-либо ограничений по сечению проводов нет. Единственное условие данного метода: длина должна быть много больше радиуса l>>a. Удельная проводимость меди σCu=56·106 См/м, а удельная проводимость алюминия σAl=37·106 См/м. Относительная магнитная проницаемость обоих материалов приблизительно равна µ=1 (медь является диамагнетиком, а алюминий парамагнетиком). Радиус провода выражаем из формулы площади круга:
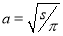 ,
,
где s — площадь сечения провода, мм2.
Расчета активного сопротивления медных проводов различных сечений, выполнен в диапазоне частот 0–2 кГц (рисунок 1.). Аналогичный расчет проведен для алюминиевых проводов (рисунок 2.). Выбор диапазона обосновывается тем, что согласно ГОСТ Р54149–2010, гармоники нормируются до 40-й включительно, что соответствует наибольшему значению частоты 2кГц [1].
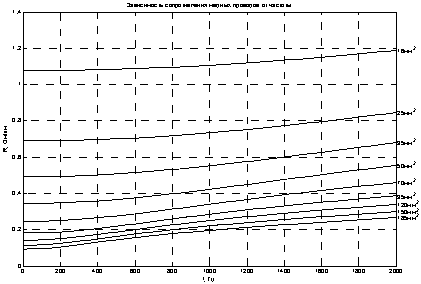
Рис. 1. Зависимость активного сопротивления медных проводов различных сечений от частоты
Семейства графиков (рисунки 1, 2) показывает зависимость погонного сопротивления проводов как от их сечения, так и от частоты. В полосе частот от 0 до 2000 Гц (рисунок 1.) величина возрастания сопротивления от 10,4 % до 183,9 %, в зависимости от сечения провода. Причем наибольший, в процентном отношении, прирост сопротивления наблюдается на больших сечениях. Например, при сечении 16 мм2 погонное сопротивление увеличивается с 1,08 до 1,19 Ом/км, что составляет 10,4 %, а при наибольшем сечении 185 мм2 погонное сопротивление увеличивается с 0,09 до 0,27 Ом/км, что в пересчете на проценты составляет 183,9 %. Это объясняется большей неравномерностью плотности тока при большем радиусе сечений проводов.
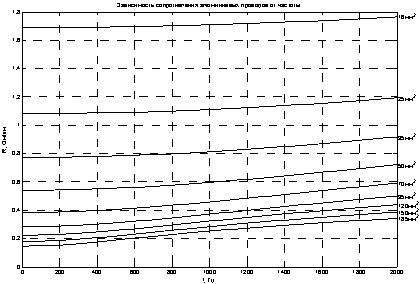
Рис. 2. Зависимость активного сопротивления алюминиевых проводов различных сечений от частоты
Результаты, полученные для алюминиевых проводов (рисунок 2.), аналогичны результатам для медных проводов. Сопротивление возрастает на величину от 4,4 % до 133,8 %, в зависимости от сечения провода, наименьший прирост погонного сопротивления наблюдается при сечении 16 мм2, в этом случае погонное сопротивление увеличивается с 1,69 до 1,76 Ом/км, что составляет 4,4 %, а при наибольшем приведенном на графике сечении 185 мм2 погонное сопротивление увеличивается с 0,15 до 0, 34 Ом/км, что в пересчете на проценты составляет 133,8 %.
Таким образом для проводников большего сечения поверхностный эффект оказывает более выраженное влияние на сопротивление (для меди сопротивление возросло на 183,9 %, а для алюминия на 133,8 %, в полосе частот от 0 до 2000 Гц), уменьшение же сечения приводит к существенному возрастанию активного сопротивления (рисунки 1,2.). Проводники с большей удельной проводимостью более подвержены влиянию поверхностного эффекта. При равном сечении, по мере увеличения частоты, активное сопротивление медного провода возрастает быстрее, чем активное сопротивление алюминиевого провода.
Литература:
- ГОСТ 32144–2013 Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. [Текст] — М.: Стандартинформ — 2014г. — 38 с.
- Григорьев О. Высшие гармоники в сетях электроснабжения 0,4 кВ/ О. Григорьев, В. Петухов, В. Соколов, И. Красилов [Текст] //«Новости электротехники», № 6(18) 2002–1(19) 2003.
- Бессонов Л. А. Теоретические основы электротехники [Текст] — М.: Высшая школа — 1964г. — 750 с.
- Будзко И. А. Элетроснабжение сельского хозяйства/ И. А. Будзко, Т. Б. Лещинская, В. И. Сукманов [Текст] — М: Колос — 2000 г. — 536 с.
- Бессонов Л. А. Линейные электрические цепи / Л. А. Бессонов. — М: Высшая школа, 1983. — 336 с.
- Лосев А. К. Теория Линейных электрических цепей / А. К. Лосев. — М: Высшая школа, 1987. — 512 с.
Основные термины (генерируются автоматически): активное сопротивление, погонное сопротивление, цилиндрический провод, поверхностный эффект, провод, сечение, сечение провода, радиус провода, цилиндрический проводник, алюминиевый провод.
Электрическое сопротивление ~ Электро мастер
Электрическое сопротивление
Любое тело, по которому протекает электрический ток, оказывает току сопротивление – это явление называется электрическим сопротивлением.
Сопротивление обозначается латинскими буквами R, X, Z. Используются также прописные буквы r, x, z.
R – активное сопротивление (омическое)
X – реактивное сопротивление (индуктивное, емкостное)
Z – полное сопротивление (активное)
Размерность сопротивления Ом, размерность записывается так – Ом.
Сопротивление рассчитывается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать по формуле:
R=U/I
гдеR – сопротивление
U – разность электрических потенциалов на концах проводника (напряжение)
I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения).
Сопротивление различных проводников зависит от материала и называется удельным сопротивление, единица измерения удельного сопротивления Ом*м, а величина удельного сопротивления обозначается символом ρ (ро).
Удельное сопротивление
Удельное сопротивление проводника может быть рассчитано по формуле:
R= (ρ *l)/S
гдеρ – удельное сопротивление проводника
l – длинна проводника
S – площадь сечения проводника
Удельное сопротивление некоторых веществ (при t 20° C)
Вещество | Удельное сопротивление, ρ |
Алюминий | 0,028 |
Вольфрам | 0,055 |
Железо | 0,098 |
Золото | 0,023 |
Константан | 0,44-0,52 |
Латунь | 0,025-0,06 |
Манганин | 0,42-0,48 |
Медь | 0,0175 |
Молибден | 0,057 |
Никелин | 0,39-0,45 |
Никель | 0,100 |
Олово | 0,115 |
Ртуть | 0,958 |
Свинец | 0,221 |
Серебро | 0,016 |
Тантал | 0,155 |
Фехраль | 1,1-1,3 |
Хром | 0,027 |
Цинк | 0,059 |
Чем больше сопротивление проводника, тем хуже он проводит электрический ток.
Удельное сопротивление обратно пропорционально электрической проводимости.
Электрическая проводимость – это способность материала пропускать через себя электрический ток.
Из выше изложенного следует – чем меньше сопротивление проводника, тем больше его электрическая проводимость, тем легче электрическому току пройти через этот проводник.
Виды электрического сопротивления:
Существует четыре вида электрического сопротивления:
1. Омическое сопротивление (активное сопротивление постоянному току)
2. Активное сопротивление (сопротивление переменному току)
3. Индуктивное сопротивление (реактивное сопротивление)
4. Емкостное сопротивление (реактивное сопротивление)
Рассмотрим каждое подробно:
Омическое сопротивление – сопротивление цепи постоянному току вызывающие безвозвратные потери энергии постоянного тока.
Величина омического сопротивления не зависит от величины тока, это сопротивление материала (удельное сопротивление) и рассчитывается по формуле:
R=U/I
гдеR – сопротивление
U – разность электрических потенциалов на концах проводника (напряжение)
I – сила тока, протекающая между концами проводника под действием разности потенциалов (напряжения).
Причиной потерь постоянного тока при омическом сопротивление является преодоление противодействия материала (его удельного сопротивления), энергия затраченная на преодоления противодействия материала превращается в тепловую.
Активное сопротивление – это сопротивление цепи переменному току вызывающие безвозвратные потери энергии переменного тока. Активное сопротивление обозначается латинской буквой Z и рассчитывается по формуле:
Z=R+jX
гдеZ – импеданс
R — величина активного сопротивления
X — величина реактивного сопротивления
j — мнимая единица
Основной причиной вызывающей потери при активном сопротивление остается тоже, что и при омическом сопротивление – преодоление противодействия материала. Есть и другие причины, такие как
— поверхностный эффект
— вихревые токи
— потери за счет излучения электромагнитной энергии и др.
Абстрактно омическое и активное сопротивление можно представить как передвижение человека по узкому захламленному (препятствиями) коридору, который основную часть своей энергии будет безвозвратно тратить на преодоление этих препятствий, и чем больше удельное сопротивление проводника, тем захламленнее будет коридор.
Индуктивное сопротивление — обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Не вызывает безвозвратных потерь энергии.
Индуктивное сопротивление рассчитывается по формуле:
XL=ωL=2πfL
гдеXL — индуктивное сопротивление проводника переменному току
ω — циклическая частота переменного тока
L — индуктивность проводника (катушки)
f- частота
На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки тоже будет убывать, пересекая витки катушки и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом, вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, что значит не вызывающим безвозвратных потерь энергии.
Абстрактно индуктивное сопротивление можно представить как воду, текущую по трубе в которой установлена крыльчатка (водомер (счетчик воды) который установлен почти в каждой квартире), крыльчатка создает индуктивное сопротивление, чем больше ток (в нашем случае напор воды), тем больше сопротивление, при убывании напора воды крыльчатка пропустить всю оставшуюся воду, так как она крутиться в том же направлении, в которой течет вода. Из этого примера видно что такое индуктивное сопротивление и почему оно не вызывает безвозвратных потерь.
Индуктивную нагрузку (сопротивление) вызывают – индукционные печи и плиты, асинхронные двигатели (пылесосы, миксеры, фены) и т.д.
При индуктивной нагрузке в сеть генеруется реактивная мощность (ток по фазе отстает от напряжения), которая является паразитной и приводит к перегрузке электрический сетей и требует компенсации. Подробнее об этом будет написано в следующих статьях.
Емкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью цепи (или ее участка).
Емкостное сопротивление рассчитывается по формуле:
Xc=1/ωC=1/2πfC
Xc — емкостное сопротивление проводника переменному току
C — емкости элемента
Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом, емкостное сопротивление является реактивным.
Абстрактно емкостное сопротивление можно представить как кастрюлю объемом 5 литров, в нашем случае объем кастрюли это не что иное, как ее емкость. При ее наполнении водой до краев, она будет переворачиваться, и вода из неё выливаться, после чего кастрюля будет снова наполняться (так же как и конденсатор при полном заряде будет разряжаться в сеть, после чего вновь заряжаться).
При емкостной нагрузке (конденсаторы) в сеть генерируется активная мощность (ток по фазе опережает напряжение). Активная мощность (конденсаторные батареи) используется для компенсации реактивной мощности.
Переменный электрический ток. Активные и реактивные сопротивления в цепях переменного тока.
— Переменным называется ток, изменение которого по величине и направлению повторяется периодически через равные промежутки времени Т.
— В электрической цепи переменного тока существует два вида сопротивлений: активноеи реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
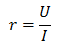
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивноесопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
— Задача на определение периода и частоты свободных колебаний в колебательном контуре.

— Задача на применение формулы сопротивления параллельно соединенных резисторов.
Смотреть в тетради
— Задача на движение или равновесие частицы в электрическом поле.

— Задача на применение закона Джоуля – Ленца.

— Задача на применение закона Кулона.


— Задача на расчет удельного сопротивления материала проводника.

— Задача на применение закона Ома для полной цепи.
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

— Задача на расчет общего сопротивления последовательно соединенных резисторов.
Задача: проводники сопротивлением 5 и 6 Ом соединены последовательно и включены в сеть напряжением 33 В. Определите силу тока в каждом проводнике.
| Дано: R1=5 Ом R2=6 Ом U=33 В I — ? | Решение: R=R1+R2 R=5 Ом+6 Ом=11 Ом I=U/R I=33В/11 Ом=3А |
Ответ. I=3А.
Задача: проводники сопротивлением 4, 8 и 8 Ом соединены последовательно и включены в сеть напряжением 20 В. Определите силу тока в каждом проводнике.
| Дано: R1=4 Ом R2=8 Ом R3=8 Ом U=20 В I — ? | Решение: R=4 Ом+8 Ом+8 Ом=20 Ом. I=U/R I=20В/20 Ом=1А. |
Ответ. I=1А.
Задача: два проводника сопротивлением 15 и 10 Ом соединены параллельно. Вычислите их общее сопротивление и силу тока в первом проводнике, если во втором она равна 1,5 А.
| Дано: R1=15 Ом R2=10 Ом I2=1,5А R — ? I1 — ? | Решение: 1/R=1/R1+1/R2 1/R=1/15+1/10=1/6. R=6 Ом. U=I*R U2=1,5А*10 Ом=15В Так как соединение параллельное, то U2=U1=Uобщ.I1=U1/R1. I1=15В/15 Ом=1 А. |
Ответ. R=6 Ом; I1=1 А.
— Задача на применение формулы мощности постоянного тока.
Задача: сопротивление электрического паяльника 440 Ом. Он работает при напряжении 220 В. определите мощность, потребляемую паяльником.
| Дано: R=440 Ом U=220В P — ? | Решение: P=I*U I=U/R I=220В/440 Ом=0,5А. P=0,5А*220В=110В*А=110Вт |
Ответ. P=110Вт
Задача: электрическая лампа включена в сеть напряжением 220В. Сила тока, проходящего через лампу, равна 0,45А. Чему равна мощность электрического тока в лампе за 2 с?
| Дано: U=220В I=0,45А t=2с P — ? | Решение: P=I*U P=0.45А*220В=99Вт Примечание: время t — лишние данные задачи, т.к. мощность не зависит от времени. |
Ответ. P=99Вт.
Задача: определите сопротивление электрической лампочки, на баллоне которой написано: «100Вт; 220 В».
| Дано: P=100Вт U=220В R — ? | Решение: P=U*I => I=P/U R=U/I I=100Вт/220В=0,4545 R=220В/0,4545А=484Ом. |
Ответ. 484 Ом.
Магнитное поле и ЭМИ
3. Электродвижущая сила
| Если цепь замкнута, то разделение зарядов протекает непрерывно. |
Сопротивление и проводимость
Электрическое сопротивление
Проводник оказывает противодействие электрическому току, которое характеризует электрическое сопротивление проводника.
За единицу эл.
сопротивления принят Ом. Более
крупными единицами электрического
сопротивления являютсякОм иМом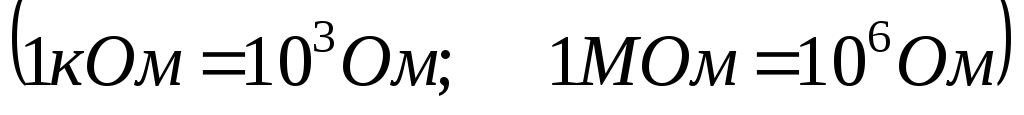 .
.
Устройства, имеющие сопротивления и включаемые в электрическую цель для ограничения или регулирования тока, называются резисторами иреостатами.
Сопротивление,
которым обладает изготовленный из
данного материала провод длиной 1мс поперечным сечением1мм2 при температуре 200С,
называют удельным
электрическим сопротивлением.Удельное сопротивление обозначаюти выражают в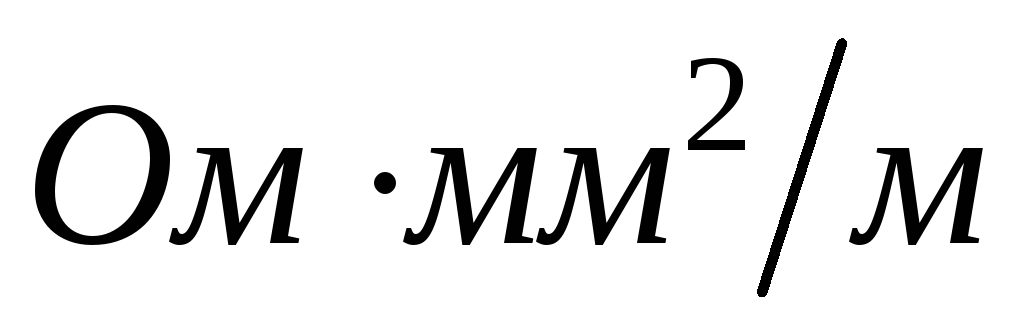 .
.
Выясним влияние длины металлического проводника lи его сеченияSна электрическое сопротивление.
Известно, что сопротивление проводника вызвано столкновением движущихся электронов с атомами и молекулами проводника. Количество таких столкновений, а значит, и электрическое сопротивление возрастает при удлинении проводника и уменьшается с увеличением его поперечного сечения. Поэтому сопротивление проводника при температуре 200Сопределяют по формуле:

l – длина проводника,м;
S – площадь поперечного сечения,мм2.
Зависимость эл. сопротивления от температуры
Для определения сопротивления проводника при температуре, отличной от 200С, необходимо знать его температурный коэффициент сопротивления.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления при изменении температуры проводника на 10С.
Реостаты и резисторы
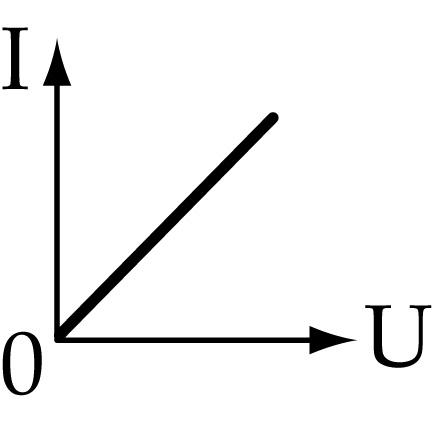
Резистор – прибор, имеющий сопротивление и предназначенный для ограничения или регулирования тока в электрической цепи. Резисторы бывают регулируемые, нерегулируемые, проволочные и непроволочные. Зависимость тока резистора Iот подводимого напряженияUназывают еговольт-амперной характеристикой.
Различают линейные инелинейные сопротивления резисторов. Если сопротивление резистора не зависит от тока, его вольт-амперная характеристика представляет собой прямую, проходящую через начало координат.
| Такое сопротивление называется линейным. |
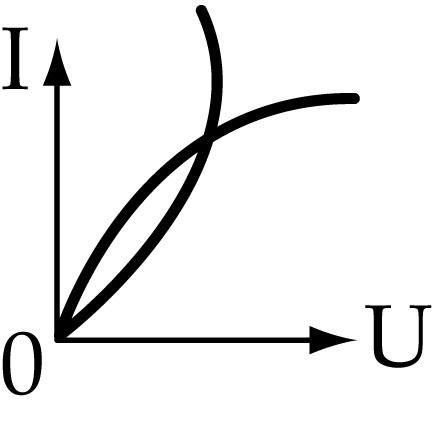
Нелинейные сопротивления являются функцией тока или напряжения. Вольт-амперная характеристика нелинейных резисторов отклоняется от прямой линии.
| К нелинейным сопротивлениям относятся осветительные лампы с вольфрамовой и угольной нитью накаливания, вентильные элементы (селеновые, германиевые, кремниевые). |
Электрические цепи, содержащие только линейные элементы, называют линейными. Если в цепи имеется хотя бы один нелинейный элемент, то вся цепь называетсянелинейной.
Проводимость
Величина, обратная
сопротивлению называется проводимостьюи обозначаетсяg: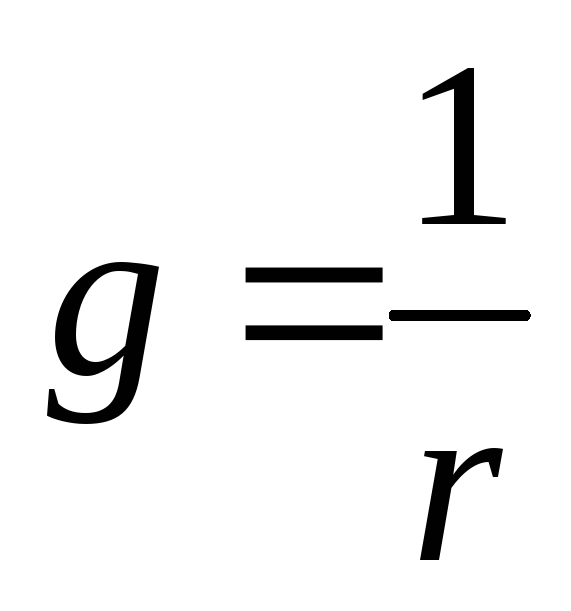 .
.
Единица проводимости
называется сименсом: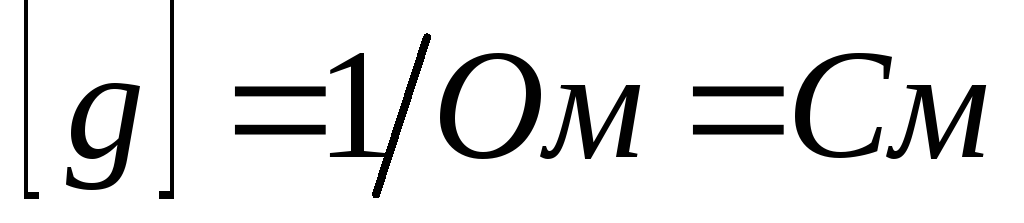 ,
а величина, обратная удельному
сопротивлению –удельной проводимостью:
,
а величина, обратная удельному
сопротивлению –удельной проводимостью: 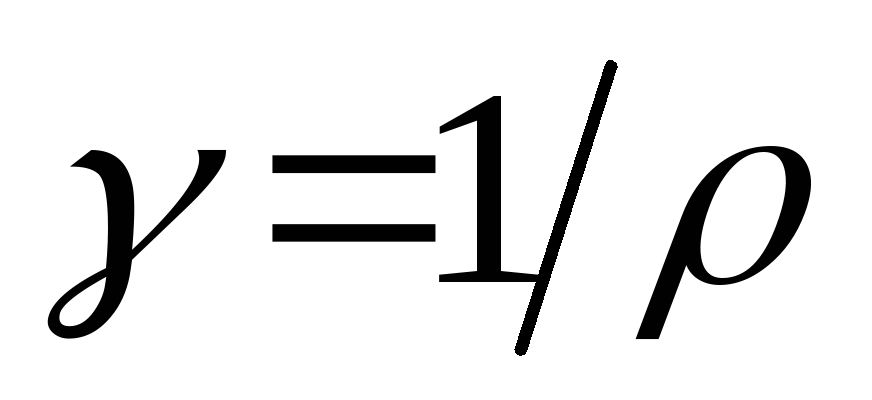 .
.
Если удельное
сопротивление выражается в 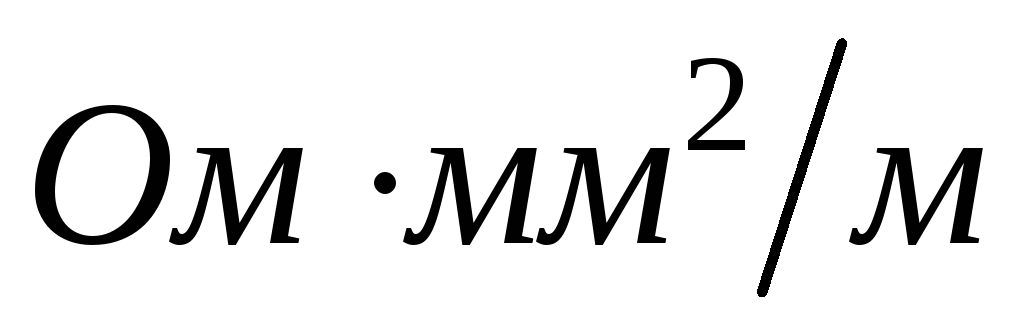 ,
то удельная проводимость – в
,
то удельная проводимость – в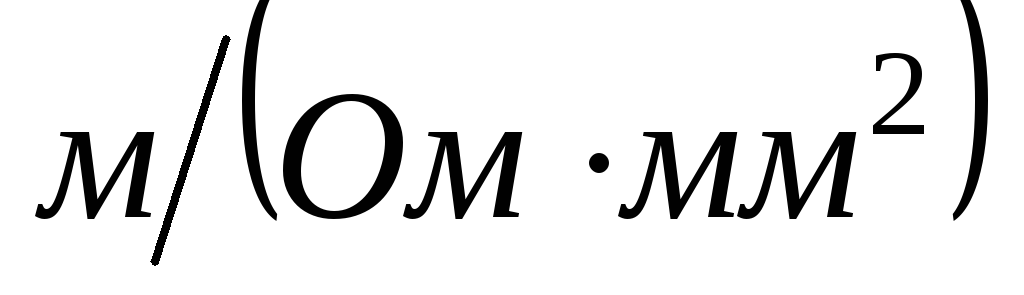 .
.
Чем меньше сопротивление проводника, тем больше его проводимость, и, следовательно, он лучше проводит ток.
3.5. Погонные (удельные) параметры линий
Погонное (удельное) (на единицу длины) активное сопротивление rо при частоте 50 Гц и обычно применяемых сечениях алюминиевых или медных проводов и жил кабелей можно принять равным погонному омическому сопротивлению. Явление поверхностного эффекта начинает заметно сказываться только при сечениях порядка 500 мм2.
Активное сопротивление – это сопротивление при протекании по проводнику переменного тока, омическое — это сопротивление при протекании по тому же проводнику постоянного тока. Для сталеалюминиевых проводов явление поверхностного эффекта также незначительно и может не учитываться.
Значительное влияние на активное сопротивление оказывает температура материала проводников, которая зависит от температуры окружающей среды и тока нагрузки.
Погонные (удельные) реактивные (индуктивные) сопротивления фаз линий в общем случае получаются разными. Они определяются взаимным расположением фаз и геометрическими параметрами. При расчетах симметрических рабочих режимов пользуются средними значениями (независимо от транспозиции фаз линии).
Задания для самостоятельной работы:
1. Выбор трансформаторов.
2. Методы определения параметров сети при различных конструктивных исполнениях, номинальных напряжениях и назначениях в составе ЭЭС.
3. Изучение удельных параметров проводов ЛЭП, кабельных линий, а именно воздействия на них температуры окружающей среды.
4. Составление принципиальной электрической схемы сети: генератор-двухобмоточный трансформатор-линия- двухобмоточный трансформатор-нагрузка.
Лекция 4. Схемы замещения ЛЭП. Определение параметров схемы замещения ЛЭП.
Схемы замещений лэп для напряжений 35-220 кВ
Линия электрической сети теоретически рассматривается состоящей из бесконечно большого количества равномерно распределенных вдоль нее активных и реактивных сопротивлений и проводимостей.
Точный учет влияния распределенных сопротивлений и проводимостей сложен и необходим при расчетах очень длинных линий, которые в этом курсе не рассматривается.
На практике ограничиваются упрощенными методами расчета, рассматривая линию с сосредоточенными активными и реактивными сопротивлениями и проводимостями.
Для проведения расчетов принимают упрощенные схемы замещения линии, а именно: П-образную схему замещения, состоящую из последовательно соединенных активного (rл) и реактивного (xл) сопротивлений. Активная (gл) и реактивная (емкостная) (bл) проводимости включены в начале и конце линии по 1/2.
Р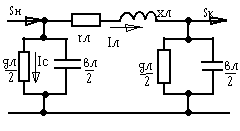 ис.
4.1. П-образная схема замещения характерна
для воздушных
ЛЭП напряжением 110-220
кВ длиной до 300-400 км.
ис.
4.1. П-образная схема замещения характерна
для воздушных
ЛЭП напряжением 110-220
кВ длиной до 300-400 км.
Активное и реактивное сопротивления линий. Расщепление проводов
Активное сопротивление определяется по формуле
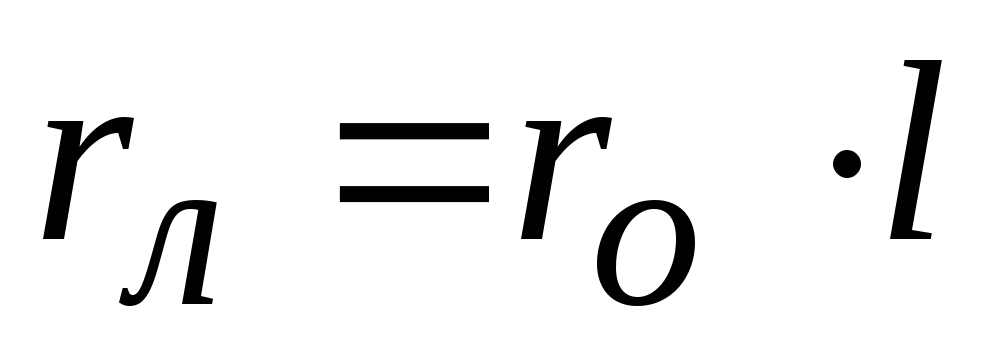 ,
,
где rо – удельное сопротивление Ом/км при tо провода + 20о ,
l – длина линии, км
Активное сопротивление проводов и кабелей при частоте 50 Гц обычно примерно равно омическому сопротивлению. Не учитывается явление поверхностного эффекта.
Удельное активное сопротивление rо для сталеалюминиевых и других проводов из цветных металлов определяется по таблицам в зависимости от поперечного сечения.
Для стальных проводов нельзя пренебрегать поверхностным эффектом. Для них rо зависит от сечения и протекающего тока и находится по таблицам.
При температуре провода, отличной от 20о С сопротивление линии уточняется по соответствующим формулам.
Реактивное сопротивление определяется:
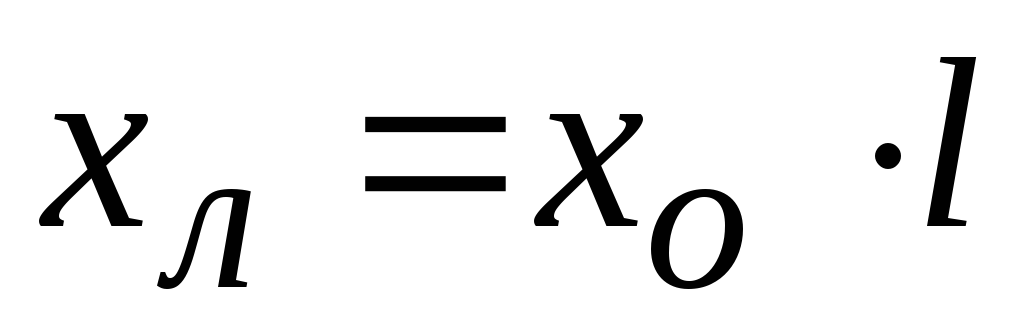 ,
,
где
xо — удельное реактивное сопротивление Ом/км. Удельные индуктивные сопротивления фаз ВЛ в общем случае различны (об этом уже говорилось).
При расчетах симметричных режимов используют средние значения xо :
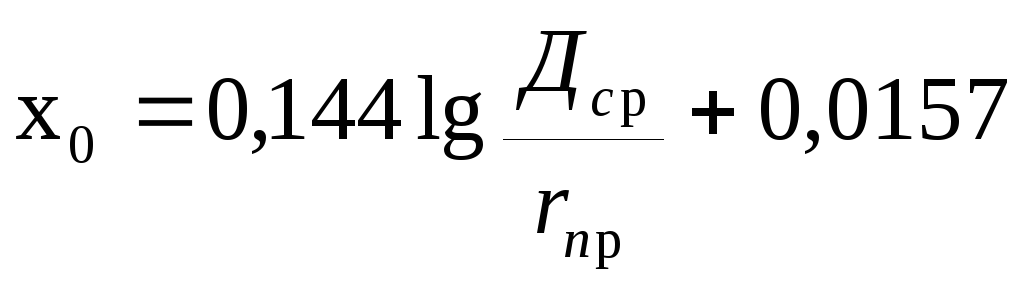
 (1),
(1),
где rпр — радиус провода, см;
Дср — среднегеометрическое расстояние между фазами, см, определяется следующим выражением:
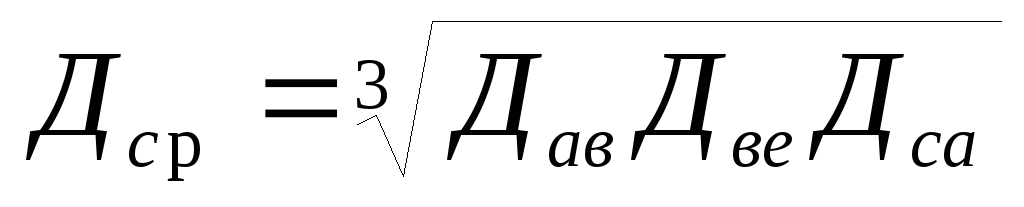 ,
,
Где Дав, Двс, Дса — расстояния между проводами соответствующих фаз А, В, С.
Н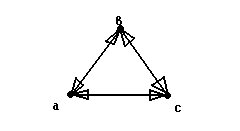 апример,
при расположении фаз по углам
равностороннего треугольника со сторонойД,
среднегеометрическое расстояние равно Д.
апример,
при расположении фаз по углам
равностороннего треугольника со сторонойД,
среднегеометрическое расстояние равно Д.
Дав=Двс=Дас=Д
При расположении проводов ЛЭП в горизонтальном положении:
Д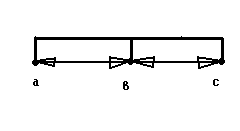 ав=Двс=Д
ав=Двс=Д
Дас=2Д
При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение Х0 из-за влияния второй цепи зависит от расстояния между цепями. Отличие Х0 одной цепи при учете и без учета влияния второй цепи не превышает 5-6% и не учитывается в практических расчетах.
В
линиях электропередач при 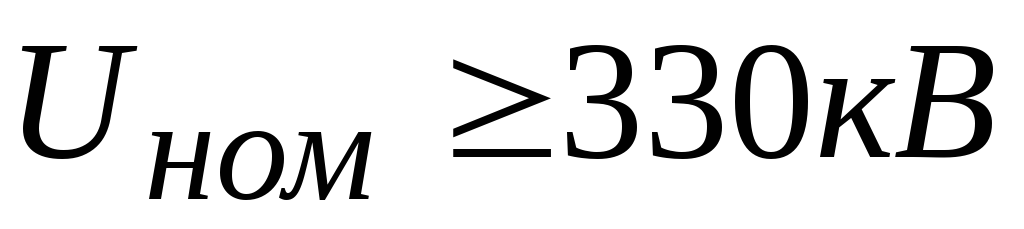 (иногда и при напряжении 110 и 220 кВ) провод
каждой фазы расщепляется на несколько
проводов.
(иногда и при напряжении 110 и 220 кВ) провод
каждой фазы расщепляется на несколько
проводов.



Рис. 4.2. Пример участка ВЛ с расщеплением провода одной фазы на три провода: подвешивают одновременно несколько проводов на фазу.
Это соответствует увеличению эквивалентного радиуса. В выражении для Х0:
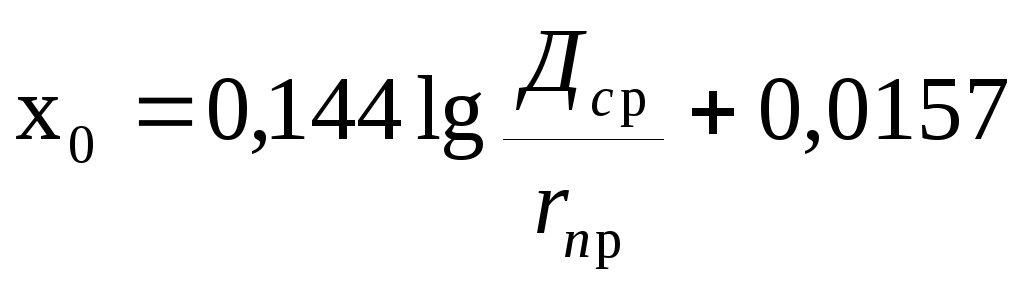 (1)
(1)
вместо rпр используется
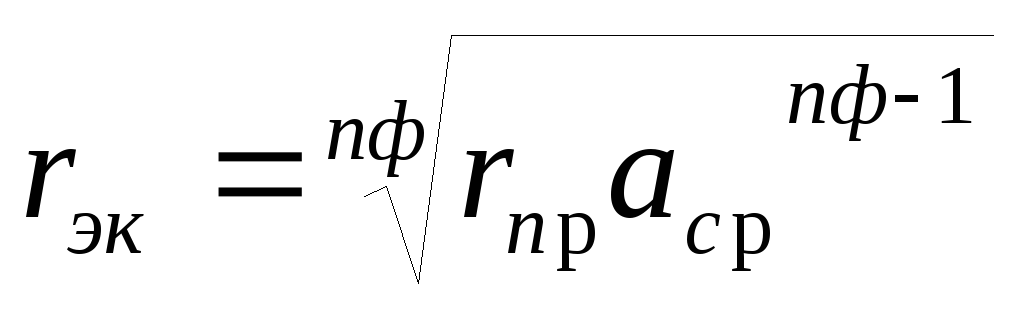 ,
,
где rэк — эквивалентный радиус провода, см;
аср — среднегеометрическое расстояние между проводами одной фазы, см;
nф— число проводов в одной фазе.
Для
линии с расщепленными проводами последнее
слагаемое в формуле 1 уменьшается в nф раз, т.е. имеет вид 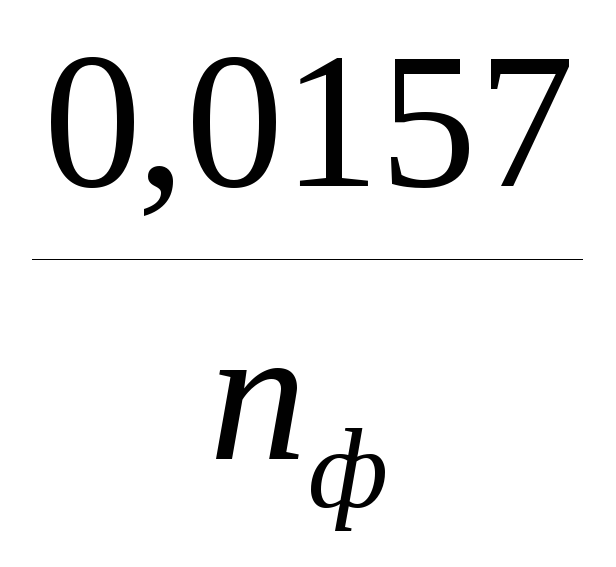 .
.
Удельное активное сопротивление фазы линии с расщепленными проводами определяются так : r0= r0пр / nф ,
Где r0пр — удельное сопротивление провода данного сечения, определенное по справочным таблицам. Для сталеалюминиевых проводов Х0 определяется по справочным таблицам, в зависимости от сечения, для стальных в зависимости от сечения и тока.