| Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями

По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:

Пример.  Активное  сопротивление  катушки  составляет  5 ом,  а  ее  полное сопротивление Z=30 ом. Определить угол сдвига фаз.

Решение.

При соs =0,25 угол =75°.

§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ

На рис. 57, а изображена цепь переменного тока, в которую  включены  последовательно  активное  сопротивление r,  индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.

Под действием переменного напряжения в этой цепи протекает переменный ток.

Выясним, чему равно общее напряжение на за­жимах цепи. Построим векторную диаграмму то­ка и напряжений для рас­сматриваемой цепи (рис. 57, б). Так как сопротив­ления соединены последовательно, то в них проте­кает одинаковый ток. Отложим по горизонтали, в  выбранном  масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпа­дают  по  фазе,  поэтому вектор напряжения Uа от­кладываем по вектору тока.

Напряжение на индуктивности опережает ток на угол  = 90°. Поэтому век­тор UL откладываем вверх

под углом 90° к вектору тока.

В цепи с емкостью, наоборот, напряжение отстает от тока на угол  = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.

Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий вектор­ную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор

U, изображающий общее напряжение на за­жимах цепи.

На основании теоремы Пифагора из треугольника напряжений АО Б следует, что

отсюда общее напряжение

Определим полное сопротивление цепи переменного тока, со­держащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис. 57, в). Его сторонами являются сопро­тивления r, (ХL — Хс) и полное сопротивление цепи Z.

Пользуясь теоремой Пифагора, можно написать, что

Отсюда полное сопротивление цепи

Силу тока в цепи с активным, индуктивным и емкостным сопро­тивлениями определяют по закону Ома:

На векторной диаграмме (рис. 57, б) видно, что в рассматри­ваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что

Из треугольника сопротивлений

§ 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ

На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.

Полное сопротивление первой катушки

Полное сопротивление второй катушки

Напряжение на  зажимах  катушек  равно  напряжению генератора.

Сила  тока в каждой  катушке  определяется  согласно  закону Ома:

Из этих равенств можно сделать вывод, что в такой цепи токи раз­ветвляются обратно пропорционально полным сопротивлениям ветвей.

Для определения угла сдвига фаз между напряжением и током

в каждой катушке вычисляют  и    и по таблице тригонометрических функций находят значения углов 1 и 2.

Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощ­ности (cos ).

Так как первый закон Кирхгофа справедлив для цепей перемен­ного тока, то в рассматриваемой цепи общий ток определяется гео­метрическим сложением векторов (рис. 58,6).

По горизонтали в выбранном масштабе отложим вектор напря­жения U. Так как ток в цепи с индуктивностью отстает от напря­жения, то вектор тока  I1 выбранном масштабе отложим с по­мощью транспортира под углом 1 к вектору напряжения U, а век­тор тока I2 и отложим под углом 2.

Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбран­ного масштаба.

Чтобы найти общий ток, нужно воспользоваться тем, что актив­ная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:

а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережаю­щие):

После чего определяют общий ток:

Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.

Пример. Три катушки соединены параллельно и к ним подключено перемен­ное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;

Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.

Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.

Решение. Индуктивное сопротивление катушек:

Полное сопротивление катушек:

Сила тока в катушках:

UNEC – Azərbaycan Dövlət İqtisad Universiteti — Page not found

Why UNEC?

Regionda iqtisad elmini dərindən öyrədən fundamental tədris mərkəzidir;
Tədris prosesi və kadr hazırlığı Amerika və Avropa təhsil sisteminə uyğundur;
İxtisaslar bakalavr, magistr və doktorantura təhsil pillələri üzrə
azərbaycan, ingilis, rus və türk dillərində tədris edilir;

Auditoriyada mərkəz nöqtəsi tələbədir;
Tələbə universiteti iki və daha çox ixtisasla (dual major) bitirə bilər;
Tələbələrin müxtəlif mübadilə proqramlarında iştirak etmək imkanı vardır;
Universitetdə 10 fakültə və 17 kafedra fəaliyyət gös­tərir;
403 professor və dosent çalışır.

Son xəbərlər Elanlar Bütün xəbərlər ALL ANNOUNCEMENTS

The Journal of Economic Sciences: Theory and Practice

№ 2

ECONOMIC HERITAGE OF HEYDAR ALIYEV

Connect with
rector

• Graduates

  Mikayıl Cabbarov

  İqtisadiyyat naziri

• Graduates

  Ceyhun Bayramov

  Xarici işlər naziri

• Graduates

  Şahin Mustafayev

  Azərbaycan Respublikası Baş Nazirinin müavini

• Graduates

  Muxtar Babayev

  Ekologiya və təbii sərvətlər naziri

• Graduates

  Fərid Qayıbov

  Gənclər və idman naziri

• Graduates

  Səttar Möhbalıyev

  Azərbaycan Həmkarlar İttifaqları Konfederasiyasının sədri

• Graduates

  Vüqar Gülməmmədov

  Hesablama Palatasının sədri

• Graduates

  Vüsal Hüseynov

  Dövlət Miqrasiya Xidmətinin rəisi

• Graduates

  Ramin Quluzadə

  Azərbaycan Respublikası Prezidentinin İşlər müdiri

• Graduates

  Natiq Əmirov

  Azərbaycan Respublikası Prezidentinin İqtisadi islahatlar üzrə köməkçisi

• Graduates

  Kərəm Həsənov

  Prezident Administrasiyasının Dövlət nəzarəti məsələləri şöbəsinin müdiri

• Graduates

  Azər Əmiraslanov

  Nazirlər Kabineti Aparatının İqtisadiyyat şöbəsinin müdiri

• Graduates

  Rövşən Nəcəf

  AR Dövlət Neft Şirkətinin prezidenti

• Graduates

  Firudin Qurbanov

  Elm və təhsil nazirinin müavini

• Graduates

  İdris İsayev

  Elm və təhsil nazirinin müavini

• Graduates

  Sevinc Həsənova

  İqtisadiyyat nazirinin müavini

• Graduates

  Şirzad Abdullayev

  İqtisadiyyat nazirinin müşaviri

• Graduates

  Azər Bayramov

  Maliyyə nazirinin müavini

• Graduates

  Sahib Məmmədov

  İqtisadiyyat nazirinin müavini

• Graduates

  Məmməd Musayev

  Azərbaycan Respublikası Sahibkarlar (İşəgötürənlər) Təşkilatları Milli Konfederasiyasının prezidenti

• Graduates

  Vüsal Qasımlı

  İqtisadi İslahatların Təhlili və Kommunikasiya Mərkəzinin direktoru

• Graduates

  İlqar Rəhimov

  Milli Paralimpiya Komitəsinin prezidenti

• Graduates

  Rüfət Rüstəmzadə

  Qida Təhlükəsizliyi Agentliyinin sədr müavini

• Graduates

  Rəşad Mafusov

  Qida Təhlükəsizliyi Agentliyinin sədr müavini

• Graduates

  Rauf Səlimov

  Dövlət Statistika Komitəsi sədrinin müavini

• Graduates

  Cabbar Musayev

  Dövlət Statistika Komitəsinin Aparat rəhbəri

• Graduates

  Fərhad Hacıyev

  Gənclər və idman nazirinin müavini

• Graduates

  Süleyman Qasımov

  AR Dövlət Neft Şirkətinin iqtisadi məsələlər üzrə vitse-prezidenti

• Graduates

  Fərhad Tağı-zadə

  General-leytenant

• Graduates

  Ziyad Səmədzadə

  Millət vəkili

• Graduates

  Xanhüseyn Kazımlı

  Azərbaycan Sosial Rifah Partiyasının sədri

• Graduates

  Mikayıl İsmayılov

  AR Dövlət Neft Şirkətinin vitse-prezidenti

• Graduates

  Vahab Məmmədov

  Dövlət Statistika Komitəsi sədrinin birinci müavini

• Graduates

  Yusif Yusifov

  Dövlət Statistika Komitəsi sədrinin müavini

• Graduates

  Fəxrəddin İsmayılov

  Auditorlar Palatası sədrinin müavini

• Graduates

  Xalid Əhədov

  Birinci vitse-prezidentin köməkçisi

• Graduates

  Emin Hüseynov

  Birinci vitse-prezidentin köməkçisi

• Graduates

  Qəşəm Bayramov

  Auditorlar Palatası aparatının rəhbəri

• Graduates

  Rafiq Aslanov

  Meliorasiya və Su Təsərrüfatı Açıq Səhmdar Cəmiyyətinin sədr müavini

• Graduates

  Tahir Mirkişili

  Millət vəkili, Milli Məclisin İqtisadi siyasət, sənaye və sahibkarlıq komitəsinin sədri

• Graduates

  Əli Məsimli

  Millət vəkili

• Graduates

  Vüqar Bayramov

  Millət vəkili

• Graduates

  Eldar Quliyev

  Millət vəkili

• Graduates

  Əli Nuriyev

  AMEA-nın müxbir üzvü

• Graduates

  İqbal Məmmədov

  Millət vəkili

• Graduates

  Şahin Əliyev

  Nəqliyyat, Rabitə və Yüksək Texnologiyalar Nazirliyi yanında Elektron Təhlükəsizlik Xidmətinin rəisi

• Graduates

  Şahin Bayramov

  Mingəçevir Dövlət Universitetinin rektoru

• Graduates

  Balakişi Qasımov

  İctimai Televiziya və Radio Yayımları Şirkətinin baş direktoru

• Graduates

  Elnur Rzayev

  Xaçmaz Rayon İcra Hakimiyyətinin başçısı

• Graduates

  Kamran İbrahimov

  “Azərpoçt” MMC-nin baş direktor müavini

• Graduates

  Alim Quliyev

  Mərkəzi Bankın sədrinin birinci müavini

• Graduates

  Vadim Xubanov

  Mərkəzi Bankın sədrinin müavini

• Graduates

  Aftandil Babayev

  Mərkəzi Bankın sədrinin müavini

• Graduates

  Mehman Məmmədov

  “Expressbank” ASC-nin İdarə Heyətinin sədri

• Graduates

  Anar Həsənov

  AccessBankın İdarə Heyətinin Sədri

• Graduates

  Fərid Hüseynov

  «Kapital Bank»ın İdarə Heyəti sədrinin I müavini

• Graduates

  Rövşən Allahverdiyev

  Kapital Bankın İdarə Heyətinin sədri

• Graduates

  Rza Sadiq

  “Bank BTB” Müşahidə Şurasının Sədri

• Graduates

  Elnur Qurbanov

  “AFB Bank” ASC-nin Müşahidə Şurasının Sədri

• Graduates

  Zaur Qaraisayev

  “AFB Bank” ASC-nin İdarə Heyətinin Sədri

• Graduates

  Kamal İbrahimov

  “Baku Steel Company” şirkətinin direktoru

• Graduates

  Vaqif Həsənov

  «Qarant Sığorta» ASC-nin İdarə Heyətinin sədri

Elektron Kitabxana

ABCÇDEƏFGĞHXIİJKQLMNOÖPRSŞTUÜVYZ0-9

Налоги и налогообложение в Азербайджане

460 PAGES | DOWNLOAD

Dördüncü sənaye inqilabı

204 PAGES | DOWNLOAD

Mühasibat hesabatı

258 PAGES | DOWNLOAD

İaşə məhsullarının texnologiyası kursundan laboratoriya praktikumu

219 PAGES | DOWNLOAD

Susuz həyat yoxdur

215 PAGES | DOWNLOAD

Elektron kommersiya

212 PAGES | DOWNLOAD

www.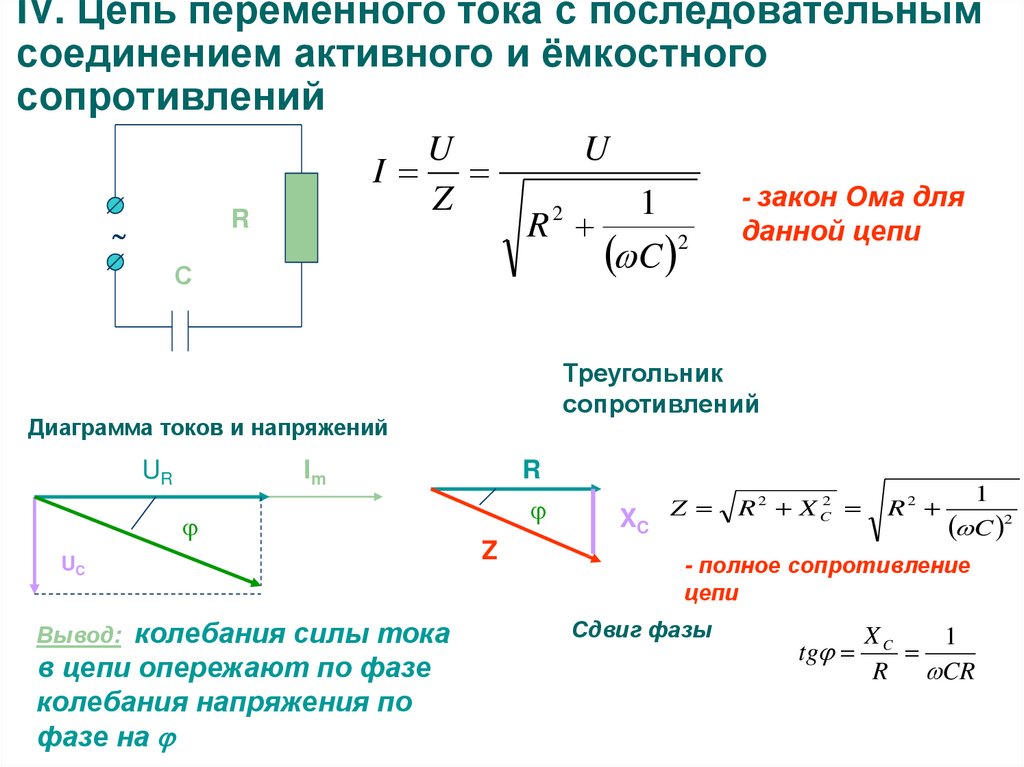 president.az www.mehriban-aliyeva.org www.heydar-aliyev-foundation.org www.azerbaijan.az www.edu.gov.az www.tqdk.gov.az www.economy.gov.az www.science.gov.az www.azstat.org www.atgti.az www.virtualkarabakh.az www.ecosciences.edu.az www.polpred.com

Реактивное, индуктивное и емкостное сопротивление | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Расчет индуктивных и емкостных реактивных сопротивлений.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное сопротивление

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рисунке 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:

Напряжение переменного тока в катушке индуктивности

Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L дается вариантом закона Ома:

I=VXLI=\frac{V}{{X}_{L}}\\I=XL​V​

, где В — среднеквадратичное напряжение на катушке индуктивности, а X _L определяется как

XL=2πfL{X}_{L}=2\pi{fL}\\XL​=2πfL

, где f частота источника переменного напряжения в герцах (Анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). Х _Д называется индуктивным сопротивлением , потому что индуктор препятствует протеканию тока. X _L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в единицах (циклов/с) (Ом ⋅ с) = Ом)), что согласуется с его ролью в качестве эффективное сопротивление. Имеет смысл, что X _L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X _L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I / Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения X _L = 2πf L . Когда для каждой частоты найдено X _L , можно использовать закон Ома, как указано в уравнении I = V / X X _L для определения тока на каждой частоте.

Раствор для (а)

Ввод частоты и индуктивности в уравнение x _L = 2πf L Приведен

x _L = 2πf L = 6.28 (60,0/с) (3,00 м) = 1,13 ° HS.

Аналогично, на частоте 10 кГц

X _L   = 2πf L = 6,28 (1,00 × 10 ⁴ /с) (3,00 мГн) при 180 кОм.

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении 9.0025 I = В / X _L , учитывая приложенное среднеквадратичное значение напряжения 120 В. Для первой частоты это дает

I=VXL=120 В1,13 Ом=106 А при =\frac{V}{{X}_{L}}=\frac{120\text{ V}}{1.13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\ \I=XL​V​=1,13 Ом, 120 В​=106 A при 60 Гц

. Точно так же на частоте 10 кГц

I=VXL=120 V188 Ω=0,637 A на частоте 10 кГц I=\frac{V}{{X}_{L}}=\frac{120\text{V}}{188\ text{ }\Omega}=0,637\text { A при } 10 кГц}\\I=XL​V​=188 Ω120 В​=0,637 A при 10 кГц

.

Обсуждение

Индуктор реагирует очень по-разному на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию.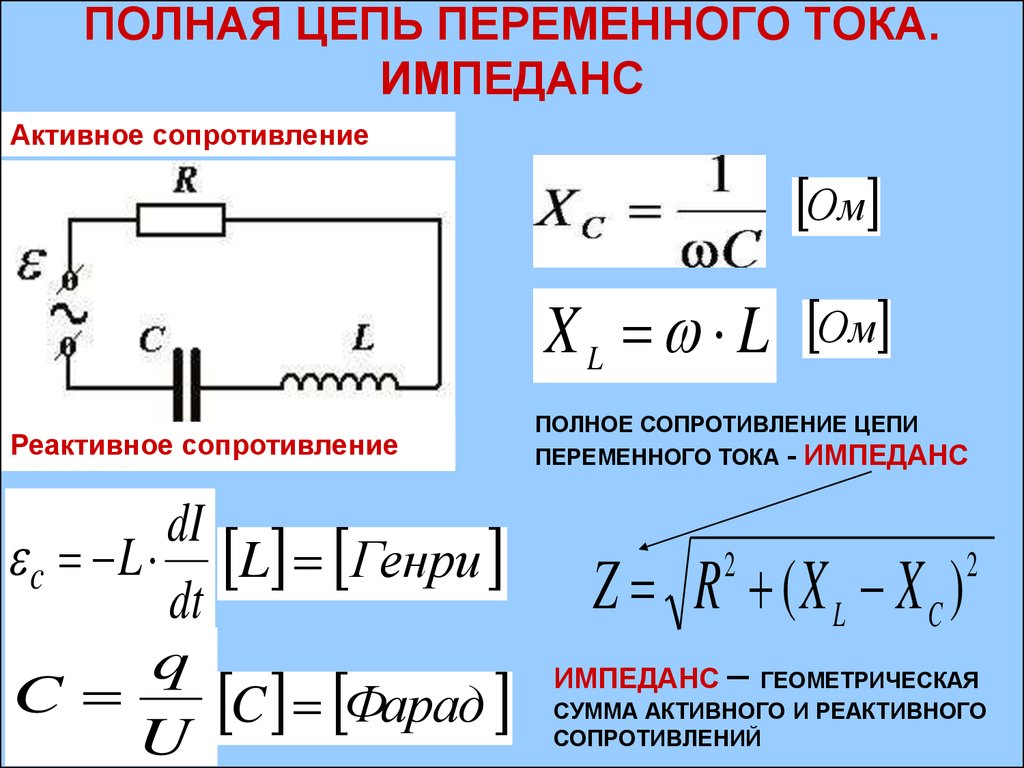 При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Конденсаторы и емкостные реактивные сопротивления

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, имеющим пренебрежимо малое сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q = 0 на нем) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:

Напряжение переменного тока в конденсаторе

Когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на угол сдвига фаз 90º.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C по другой версии закона Ома определяется как

I=VXCI=\frac{V}{{X}_{C}}\\I=XC​V​

, where V is the rms voltage and X _C is defined (As with X _L , this expression for X _C results from an analysis of the circuit using правила Кирхгофа и вычисления) равным

XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC​=2πfC1​

, где X _C называется емкостным реактивным сопротивлением , потому что конденсатор реагирует на сопротивление току. X _C измеряется в омах (проверка оставлена ​​читателю в качестве упражнения).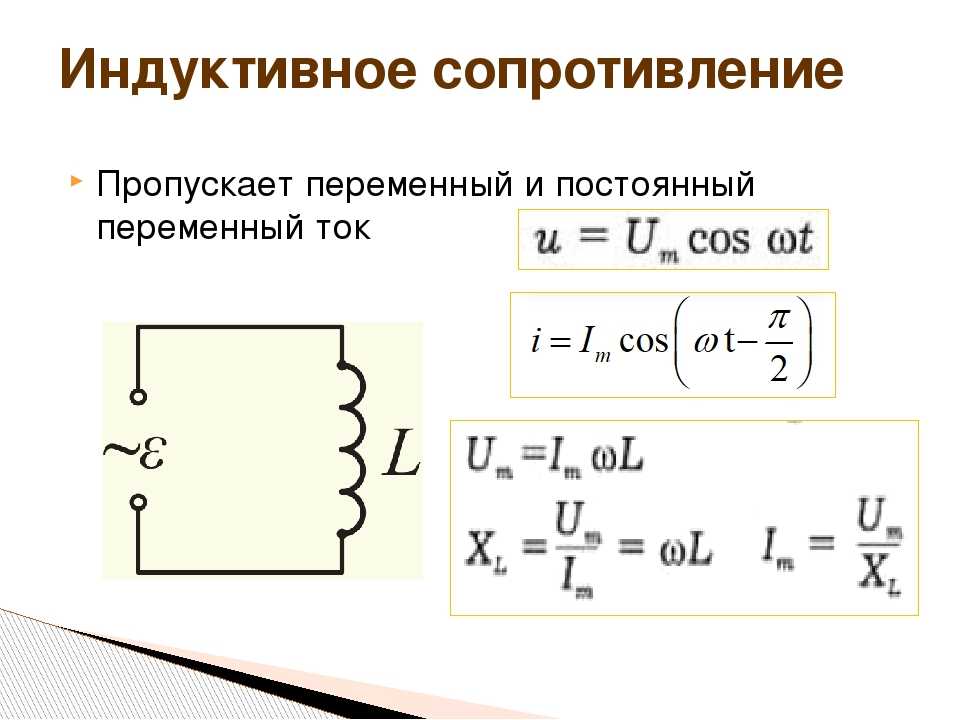 X _C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное сопротивление находится непосредственно из выражения в

XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC​=2πfC1​

. После того, как X _C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = В / X _C тока на каждой частоте.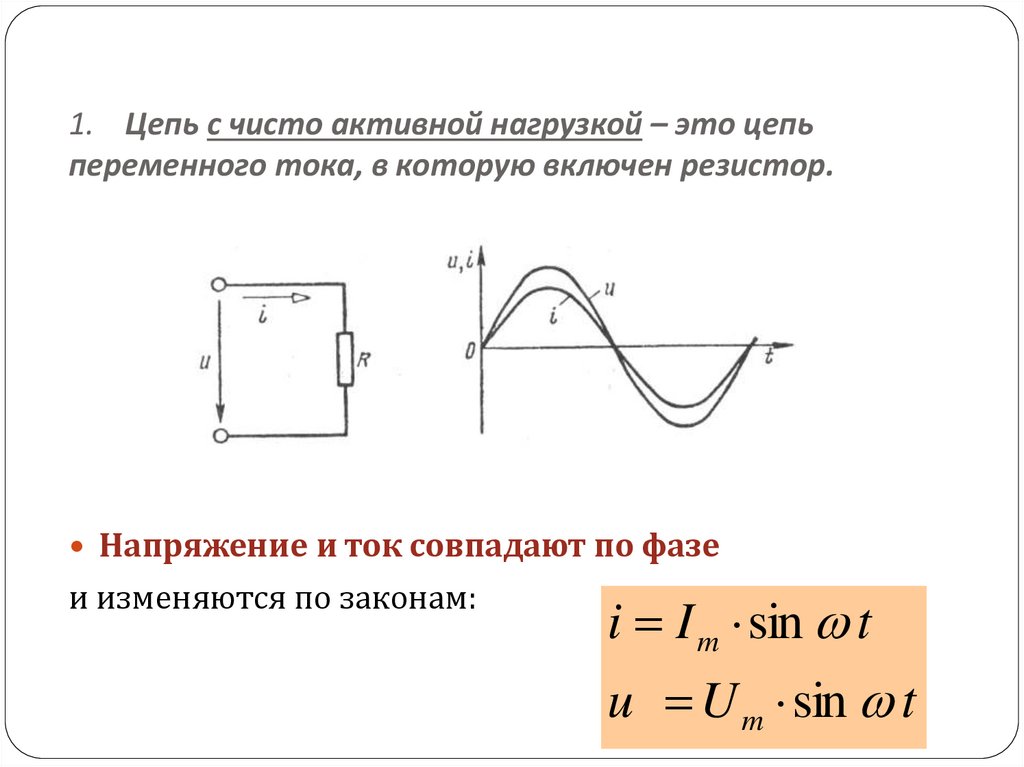

Раствор для (а)

Ввод частоты и емкости в

XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC​=2πfC1​

дает

XC=12πfC=16,28(60,0 /с)(5,00 мкФ)=531 Ом при 60 Гц\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{ 1}{6.28\left(60.0/\text{s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ в }60 \text{ Гц}\end{массив}\\XC​==​2πfC1​6,28(60,0/с)(5,00 мкФ)1​=531 Ом при 60 Гц​ 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\XC​==​2πfC1​=6,28(1,00×104/с)(5,00 мкФ)1​3,18 Ом при 10 кГц​

.

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = В / X _C , учитывая приложенное среднеквадратичное напряжение 120 В.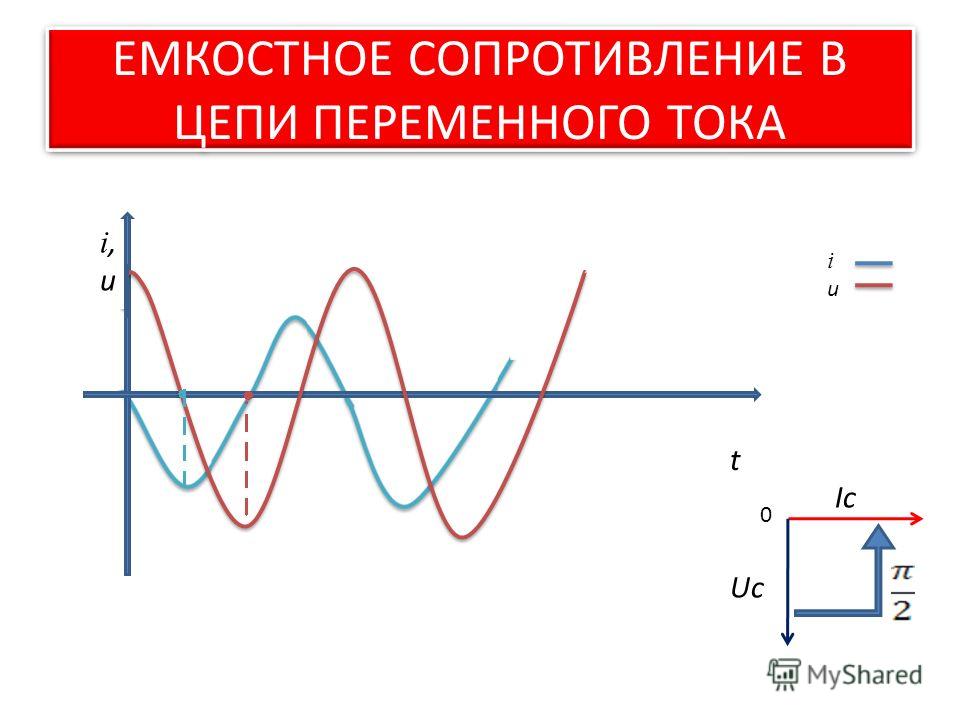 Для первой частоты это дает

I= VXC=120 V531 Ом=0,226 A при 60 ГцI=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{531\text{ }\Omega}=0,226 \text { A при }60\text{ Гц}\\I=XC​V​=531 Ω120 В​=0,226 A при 60 Гц

. Точно так же на частоте 10 кГц

I=VXC=120 V3,18 Ω=3,37 A при 10 Гц I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{ 3,18\text{ }\Omega}=3,37 \text{ A при }10 \text{ Гц}\\I=XC​V​=3,18 Ω120 В​=3,37 A при 10 Гц

.

Обсуждение

Конденсатор реагирует совершенно по-разному на двух разных частотах, и совершенно противоположным образом реагирует катушка индуктивности. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают на цепи переменного тока противоположное действие катушек индуктивности .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Переменное напряжение на резисторе

Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.

Резюме раздела

• Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
• Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
• Закон Ома для катушки индуктивности:

  I=VXLI=\frac{V}{{X}_{L}}\\I=XL​V​

  ,

  где В — среднеквадратичное напряжение на катушке индуктивности.
• X _L определяется как индуктивное сопротивление, определяемое как

  XL=2πfL{X}_{L}=2\pi fL\\XL​=2πfL

  ,

  с f частота источника переменного напряжения в герцах.
• Индуктивное сопротивление  X _L выражается в омах и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора:

  I=VXCI=\frac{V}{{X}_{C}}\\I=XC​V​

  ,

  где В — среднеквадратичное напряжение на конденсаторе.
• Х _С определяется как емкостное реактивное сопротивление, определяемое как

  XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC​=2πfC1​

  .

• X _C измеряется в омах и максимальна на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как фон 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?

5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.

Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.

6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?

Задачи и упражнения

1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?

3. Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?

4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?

7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, создает ток силой 2,00 А. Индуктивность какая?

8. Источник 20,0 Гц, 16,0 В производит ток силой 2,00 мА при подключении к конденсатору. Какова емкость?

9. (а) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, включена последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. а) Какая емкость необходима, чтобы получить реактивное сопротивление

10,0 мОм 10,0 м\Омега 10,0 мОм

для сигнала 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12. Необоснованные результаты  При записи напряжений, вызванных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

13. Создайте свою собственную задачу Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное реактивное сопротивление:

противодействие катушки индуктивности изменению тока; рассчитывается как X _L  = 2π fL

емкостное реактивное сопротивление:

сопротивление конденсатора изменению тока; рассчитано по формуле

XC=12πfC{X}_{C}=\frac{1}{2\pi fC}\\XC​=2πfC1​

Избранные решения задач и упражнений

1. 531 Гц

3. 1,33 нФ

5. (а) 2,55 А (б) 1,53 мА

7. 63,7 мкГн 9. (а) 21,2 мГн (б) 8,00 Ом

Лицензии и ссылки

Контент по лицензии CC, совместно используемый ранее

• College Physics. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии

Простые цепи переменного тока, реактивное сопротивление и импеданс: значение, индуктивная цепь

• Автор Балсара Джей
• Последнее изменение 19-07-2022

Простые цепи переменного тока, реактивное сопротивление и импеданс: Переменный ток, как мы все знаем, стал неотъемлемой частью нашей жизни. Как правило, для электричества в нашем доме мы предпочитаем подачу переменного тока вместо источника постоянного тока по нескольким причинам. Ниже перечислены некоторые из причин:
1. Переменный ток может передаваться на большие расстояния
2. Переменный ток дешевле генерировать, чем постоянный
3. В переменном токе происходит непрерывная генерация, а в постоянном токе необходимо заменить батареи
4. Переменный ток безопасен по сравнению с постоянным током
5. Переменный ток можно легко преобразовать в постоянный, тогда как обратное преобразование затруднено
6. Переменный ток имеет незначительные потери в меди привлекательный шок, в то время как DC дает отталкивающий шок и некоторые проблемы с хранением. Еще переменный ток используется для максимальных электрических устройств дома. В настоящее время такие устройства разрабатываются с работами на гибриде переменного и постоянного тока. Это означает, что он использует преимущества как переменного, так и постоянного тока.

Итак, в этой статье мы рассмотрим несколько простых цепей переменного тока и поймем некоторые связанные с ними термины.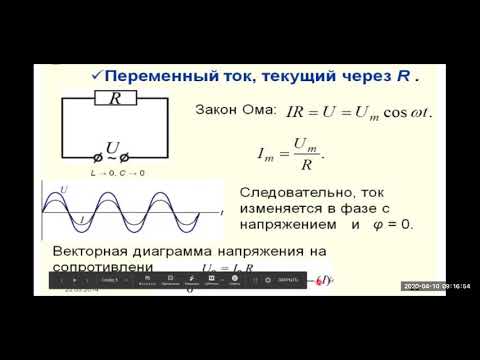

Узнайте о питании в цепях переменного тока

Чисто резистивная цепь

В этой цепи резистор подключен к источнику переменного тока, как показано на схеме. Здесь напряжение, подаваемое на цепь, определяется выражением:
\(V = {V_m}\sin \left( {\omega t} \right)\)
подается напряжение
По закону Ома мы знаем, что ток, протекающий через резистор, будет:
\(i = \frac{V}{R}\)
\(i = \frac{{{V_m}}}{R}\ sin \left( {\omega t} \right)\)
\(\следовательно i = {i_m}\sin \left({\omega t} \right)\)
Здесь \({i_m} = \frac {{{V_m}}}{R}\) — максимальное значение тока, проходящего через резистор. Теперь, если вы посмотрите на уравнения напряжения и тока, между ними нет разности фаз. Следовательно, говорят, что ток и напряжение в этой цепи находятся в фазе друг с другом. Диаграммы, показанные ниже, представляют собой векторные диаграммы и графики зависимости параметров от времени для чисто резистивных цепей переменного тока.

Чисто индуктивная цепь

В этой цепи катушка индуктивности подключена к источнику переменного тока, как показано на схеме. Здесь напряжение, подаваемое схемой, остается таким же, как и предыдущее.
\(V = {V_m}\sin \left( {\omega t} \right)\)
Разность потенциалов на катушке индуктивности определяется уравнением:
\({V_L} = L\frac{{di} }{{dt}}\)
Следовательно, ток, протекающий через этот индуктор, будет:
\(i = \int {\frac {{{V_L}}}{L}dt} \)
\(i = \ frac{1}{L}\int {{V_m}\sin\left( {\omega t} \right)dt} \)
\(i = \, – \frac{{{V_m}}}{{\omega L}}\cos \left( {\omega t} \right)\)
\(i = \frac{{{V_m }}}{{{X_L}}}\sin \left( {\omega t – \frac{\pi }{2}} \right)\)
Здесь \({X_L} = \omega L\) равно известное как индуктивное реактивное сопротивление, которое представляет собой сопротивление, предлагаемое катушкой индуктивности источнику переменного тока.
\(\следовательно i = {i_m}\sin \left( {\omega t — \frac{\pi }{2}} \right)\)
Здесь \({i_m} = \frac{{{V_m }}}{{{X_L}}}\) — максимальный ток, протекающий по цепи. Теперь, если вы посмотрите на уравнения тока и напряжения на катушке индуктивности, вы увидите, что между ними есть разность фаз \(\frac{\pi }{2}\). Напряжение опережает ток на угол \(\frac{\pi }{2}.\) Векторная диаграмма и кривая переменного тока чисто индуктивной цепи показаны ниже.

Чисто емкостная цепь

Здесь конденсатор подключен к сети переменного тока, как показано на схеме. Напряжение, подаваемое на конденсатор, равно:
\(V = {V_m}\sin \left( {\omega t} \right)\)
Разность потенциалов на пластинах конденсатора определяется уравнением:
\( {V_c} = \frac{q}{c}\)
\({V_c} = \frac{1}{C}\int {idt} \)
Следовательно, ток, протекающий через этот конденсатор, будет:
\ (i = C\frac{{dV}}{{dt}}\)
\(i = C\frac{d}{{dt}}\left( {{V_m}\sin \left( {\omega t } \справа)} \справа)\)
\(i = \omega C{V_m}\cos \left({\omega t} \right)\)
\(i = \frac{{{V_m}}}{{\frac{1}{{\ омега C}}}}\sin \left( {\omega t + \frac{\pi }{2}} \right)\)
\(i = \frac{{{V_m}}}{{{X_c} }}\sin \left( {\omega t + \frac{\pi }{2}} \right)\)
Здесь \({X_c} = \frac{1}{{\omega c}}\) известно как емкостное реактивное сопротивление, которое представляет собой сопротивление, предлагаемое конденсатором источнику переменного тока.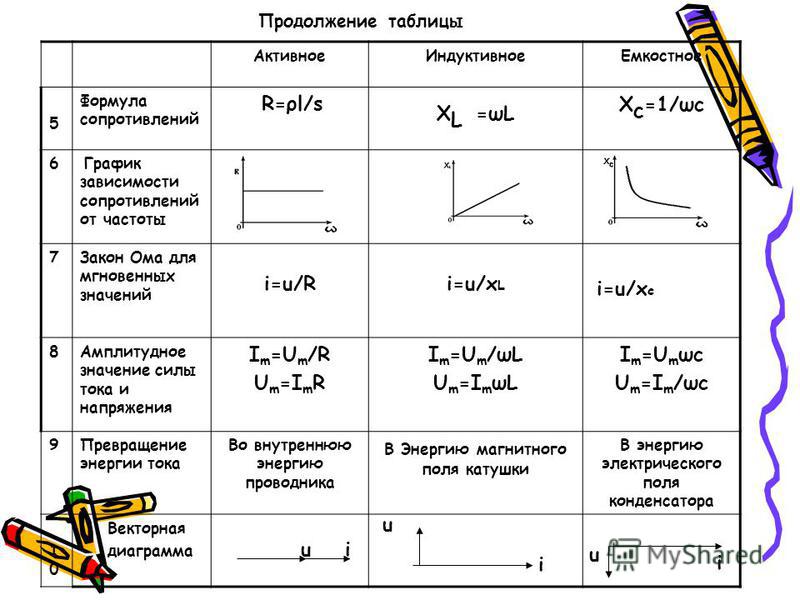
\(\следовательно i = {i_m}\sin \left( {\omega t + \frac{\pi} {2}} \right)\)
Здесь \({i_m} = \frac{{{V_m }}}{{{X_c}}}\) — максимальный ток, протекающий по цепи. Теперь, если вы посмотрите на уравнения тока и напряжения через конденсатор, вы увидите, что между ними есть разность фаз \(\frac{\pi }{2}\). Напряжение отстает от конденсатора на угол \(\frac{\pi }{2}.\) Векторная диаграмма и кривая переменного тока для чисто емкостной цепи переменного тока показаны ниже:

Цепь серии RLC

Эта цепь включает резистор, катушку индуктивности и конденсатор, соединенные последовательно друг с другом, как показано на схеме.
Если бы это был случай цепи постоянного тока, мы бы просто распределили общее напряжение между резистором, катушкой индуктивности и конденсатором. Но поскольку речь идет о питании переменным током, все может пойти немного по-другому. Катушка индуктивности и конденсатор известны как пассивные элементы цепи, тогда как резистор известен как активный элемент цепи.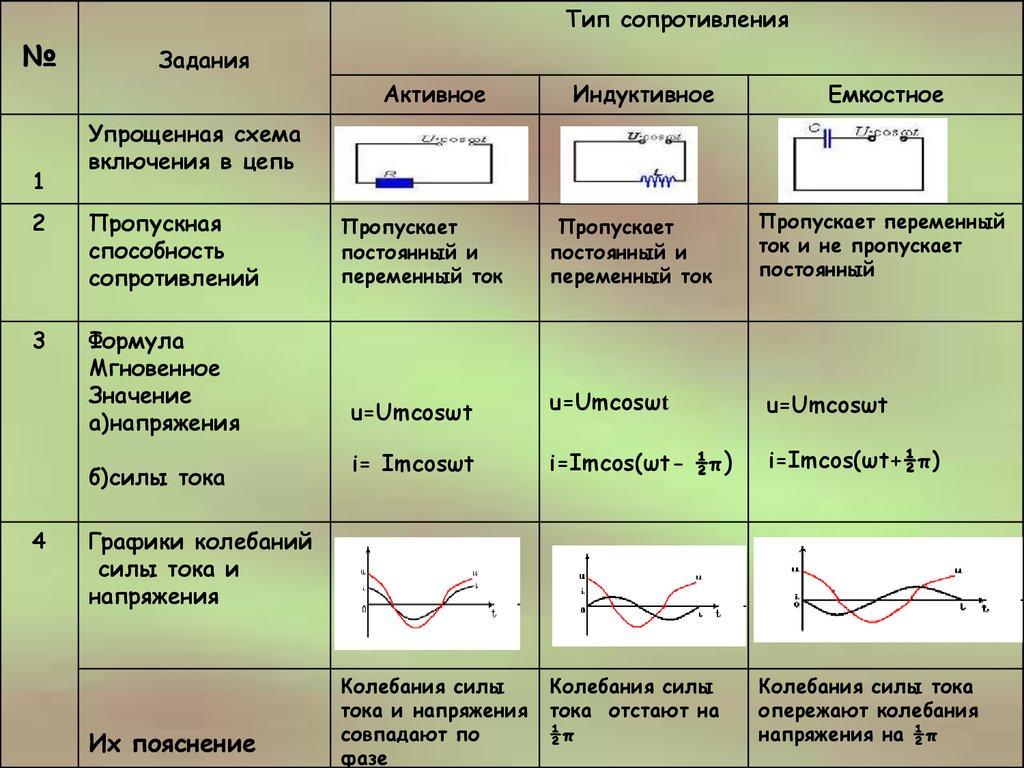
Активные элементы означают те элементы, которые способны генерировать/потреблять энергию от источника, тогда как пассивные элементы — это те элементы, которые используются для накопления энергии от источника.

Поскольку все три соединены последовательно друг с другом, ток, проходящий через них, будет считаться одинаковым. Теперь, как мы обсуждали ранее в этой статье, напряжение и ток для резистора находятся в одной фазе; напряжение опережает ток на разность фаз \(\frac{\pi }{2}\) для катушки индуктивности, а ток опережает напряжение на разность фаз \(\frac{\pi }{2}\) для конденсатора, мы можем нарисовать векторную диаграмму для полной цепи серии RLC, как показано ниже. 92}} \) известен как импеданс цепи, который представляет собой общее сопротивление току всех элементов, присутствующих в цепи вместе взятых.

Поскольку мы предположили, что напряжение на катушке индуктивности больше, чем напряжение на конденсаторе, напряжение в цепи опережает ток на некоторый угол. Эту разность фаз в цепи можно найти с помощью векторной диаграммы.
\(\tan \theta = \frac{{{V_L} — {V_C}}}{{{V_R}}}\)
\(\tan \theta = \frac{{i{X_L}} — i{X_C }}}{{iR}}\)
\(\tan \theta = \frac{{{X_L} – {X_C}}}{R}\)
Следовательно, разность векторов может быть определена как:
\(\theta = \left( {\frac{ {{V_L} – {V_C}}}{{{V_R}}}} \right) = \left( {\frac {{{X_L} – {X_C}}}{R}} \right)\)

Если напряжение питания в цепи равно \(V = {V_m}\sin \left( {\omega t} \right),\), то ток, подаваемый в цепь, будет \(i = {i_m}\sin \ влево ( {\ omega t — \ theta } \ right). \) Если \ ({X_L} > {X_C}, \) общее напряжение в цепи является опережающим током. Если \({X_C} > {X_L}.\), общий ток является ведущим в цепи. 92}} \)
Из этого уравнения можно сказать, что импедансом цепи можно управлять, управляя частотой в цепи. А контролируя импеданс, мы можем даже контролировать ток, подаваемый в цепь.

Резюме

Из этой статьи мы узнали о преимуществах и недостатках переменного тока по сравнению с постоянным.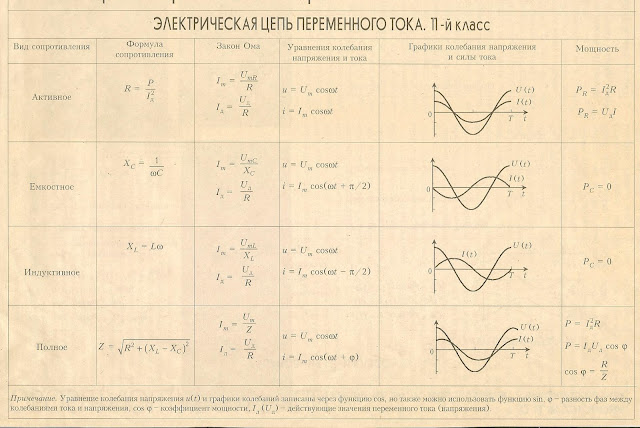 Затем мы получили некоторые базовые знания о работе цепи переменного тока, подключив резистор, конденсатор и катушку индуктивности по отдельности к источнику питания. В случае резистора напряжение и ток находятся в одной фазе друг с другом. Этот элемент считается активным элементом схемы. В то время как в случае конденсатора и катушки индуктивности разность фаз между током и напряжением составляет \(\ frac{\pi }{2}\), где опережает либо ток, либо напряжение. Здесь мы узнали об индуктивном реактивном сопротивлении и емкостном реактивном сопротивлении, которые противостоят току индуктора и конденсатора соответственно в цепи переменного тока. Катушка индуктивности и конденсатор считаются пассивными элементами цепи переменного тока. 92}} \)
Разность фаз между током и напряжением для последовательной цепи RLC:
\(\theta = \left( {\frac {{{V_L} – {V_C}}}{{{V_R}}}} \right ) = \left( {\frac{{{X_L} – {X_C}}}{R}} \right)\)

Часто задаваемые вопросы

Q. 1. Что такое реактивное сопротивление?
Ответ: Реактивное сопротивление — это сопротивление току элемента в цепи переменного тока. Если это источник постоянного тока, нам нужно учитывать только сопротивление, но для источника переменного тока нам нужно учитывать как активные, так и пассивные элементы. 92}} .\)

Q.4. Что вы имеете в виду под импедансом?
Ответ: Импеданс – это сопротивление электрическому потоку в цепи переменного тока всеми объединенными элементами.

Q.5. Что такое цепь серии RLC?
Ответ: Когда резистор, катушка индуктивности и конденсатор соединены последовательно с источником переменного тока, то результирующая цепь называется последовательной цепью RLC.

Узнайте об электродвигателе здесь

Мы надеемся, что эта статья о простых цепях переменного тока, реактивном сопротивлении и импедансе помогла вам. Если у вас есть какие-либо вопросы, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.