7.4 Фильтры нижних частот
Простейшим фильтром нижних частот является RC – фильтр, схема которого и его частотные характеристики представлены на рис. 68. Комплексная амплитуда Y(ω) выходного напряжения y(t) связана с комплексной амплитудой Z(ω) входного напряжения z(t) соотношением, обычным для схемы делителя напряжения:
.
АФЧХ фильтра составляет:
.
Произведение активного сопротивления фильтра на емкость конденсатора имеет размерность времени и называется постоянной времени T=RC, обратная величина образует круговую частоту среза. Соответствующая линейная частота равна. АЧХ и ФЧХ фильтра составляют соответственно:
,
.
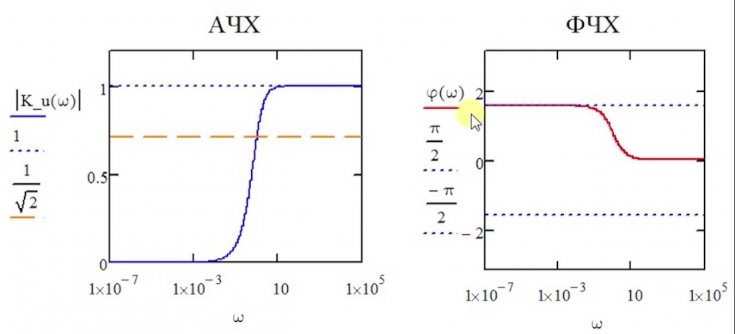
Графики АЧХ и ФЧХ фильтра представлены на рис. 7.4 при частоте среза . При условииАЧХ фильтра принимает значение.
Диапазон
частот от 0 до
называется полосой пропускания или
диапазоном прозрачности фильтра,
диапазон частот отдо бесконечности образует полосу
задержания.
Простейший RC – фильтр еще очень далек от идеального фильтра. Однако и такой фильтр способен в значительной степени повысить отношение «сигнал – шум».
Пусть, например, на вход фильтра подается сигнал в смеси с высокочастотным шумом , то есть
.
Мощность гармонического колебания равна половине квадрата амплитуды, поэтому отношение «сигнал – шум» равно 100. На выходе фильтра образуется сигнал:
На
рис. 7.5 изображен графиксигналав аддитивной смеси с шумом.
Видно, что гармоника сильно искажена.
Рядом нарисован выходной сигнал фильтра
низких частот с граничной частотой- результат фильтрации. Получается почти
чистая гармоника, но она запаздывает
по времени относительно исходного
сигнала.
Это запаздывание равно постоянной
времени фильтра, то есть 0.001 с.
Для более четкой фильтрации используются фильтры более высоких порядков. Наибольшее распространение получили следующие типы фильтров низких частот.
1.Фильтры Баттерворда – фильтры с максимально плоской амплитудно – частотной характеристикой в полосе пропускания. АЧХ фильтра Баттерворда порядка определяется выражением
,
где n – порядок фильтра. При усиление фильтра равноне зависимо от порядка фильтра. Поэтому АЧХ фильтров Баттерворда любого порядка проходят через одну и ту же точку, отделяющую полосу пропускания фильтра от полосы задержания (рис. 70).
На
рис. 7.6 представлены графики АЧХ фильтров
Баттерворда порядков
при одной и той же частоте среза.
Приn=1
имеем уже рассмотренный простейший RC
– фильтр с довольно пологой характеристикой.
По мере увеличения порядка фильтра
крутизна спада его амплитудно – частотной
характеристики возрастает, полосы
пропускания и задержания вырисовываются
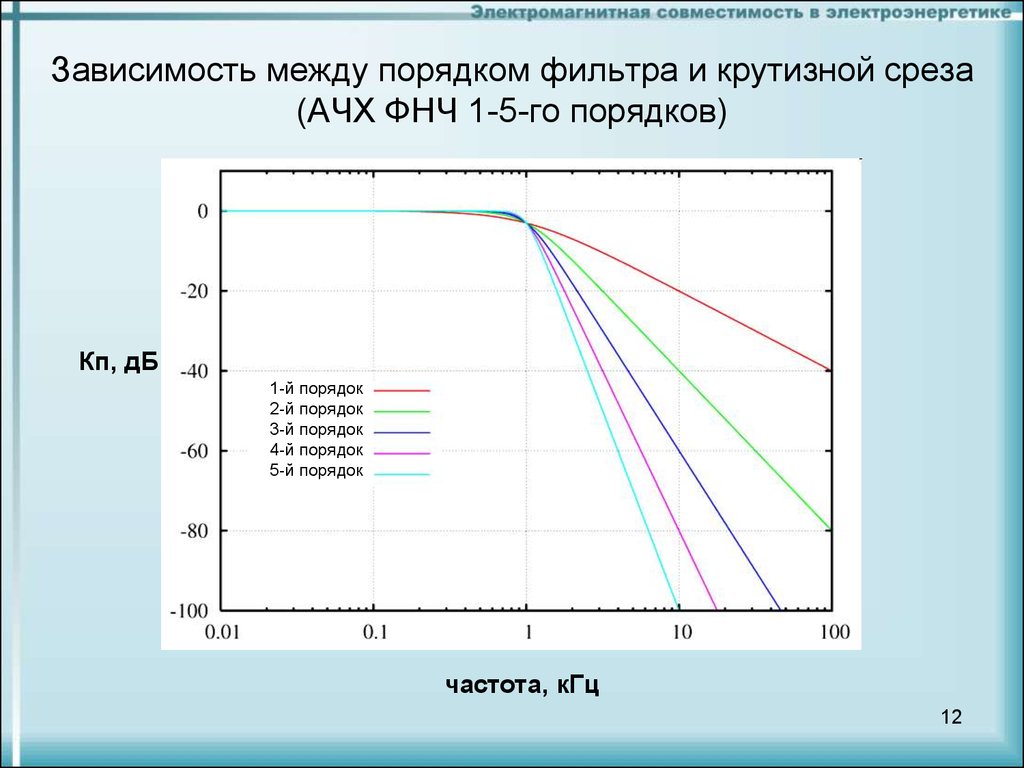
все более четко.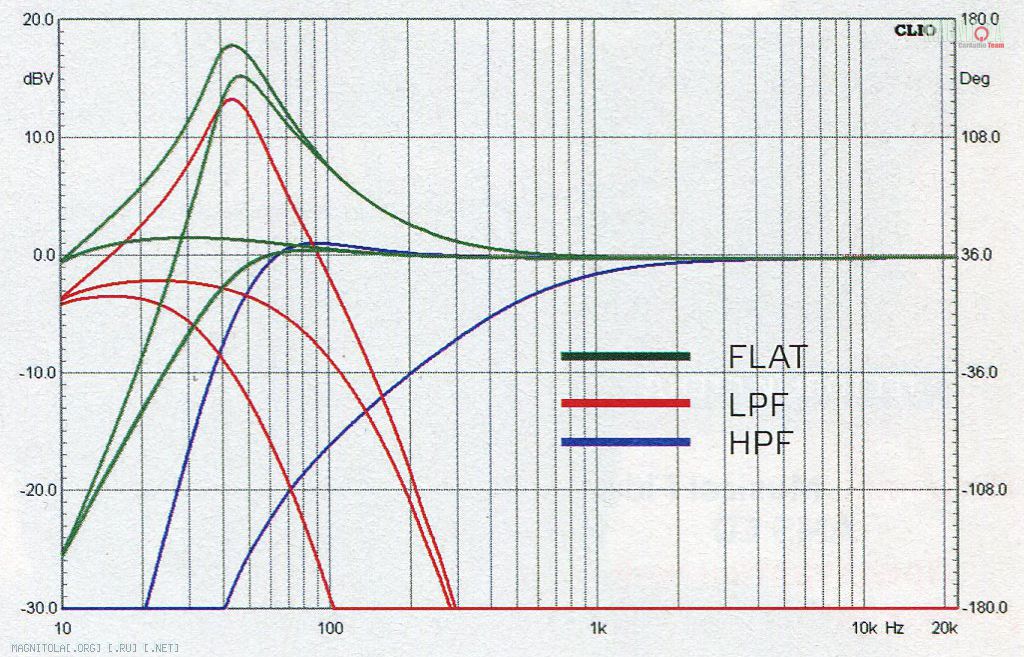
Анализ графиков на рис. 7.6 позволяет также сделать вывод о том, что не имеет большого смысла повышать порядок фильтра выше четвертого, поскольку при больших порядках фильтра крутизна спада его АЧХ возрастает все более и более медленно.
Проектирование фильтра Баттерворда заключается в следующем:
выбирается порядок фильтра в зависимости от требуемой крутизны спада его амплитудно – частотной характеристики,
подбирается электронная схема построения фильтра,
подбираются параметры схемы, при которых АЧХ фильтра совпадает с АЧХ фильтра Баттерворда соответствующего порядка.
Так
на рис. 7.7 представлен активный фильтр
низких частот 2-го порядка по схеме
Саллена – Ку. Фильтр состоит из
операционного усилителя AR3,
охваченного соответствующим образом
сформированными цепями положительной
и отрицательной обратных связей. Емкости
и сопротивления резисторов принимаются
одинаковыми и равными С4=С5=C
и R8=R9=R,
сопротивления плеч делителя напряжения
на выходе схемы принимаются равными R6
и R7=(α-1)·R6.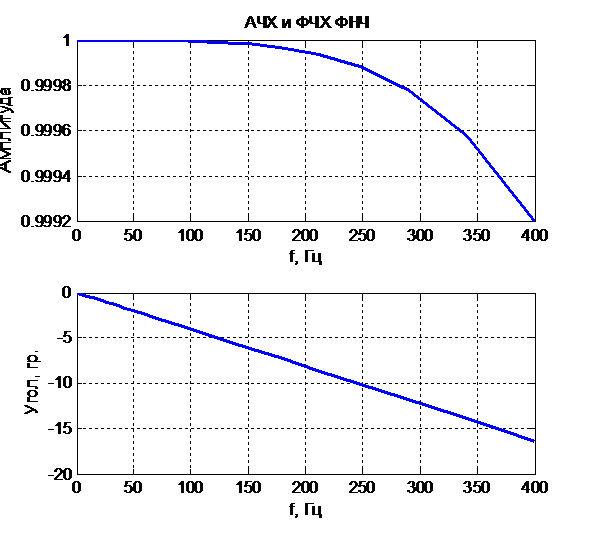
.
Вычислим амплитудно – частотную характеристику фильтра:
Для того, чтобы рассматриваемый фильтр стал фильтром Баттерворда 2-го порядка, необходимо, чтобы коэффициент при в знаменателе этого выражения обратился в нуль:
В этом случае амплитудно – частотная характеристика фильтра повторяет АЧХ фильтра Баттерворда 2-го порядка с частотой среза :
.
Уже из этого примера видно, что построение хорошего фильтра требует его точной регулировки (выбора соотношения плеч делителя напряжения R6, R7) и точной подгонки значений емкостей и сопротивлений. Еще более сложной задачей является построение и регулировка фильтров более высокого порядка. Поэтому редко используются фильтры Баттерворда порядка выше пятого.
2. Фильтры Чебышева 1-го рода.
Основой
построения фильтров Чебышева являются
полиномы Чебышевапорядкаn.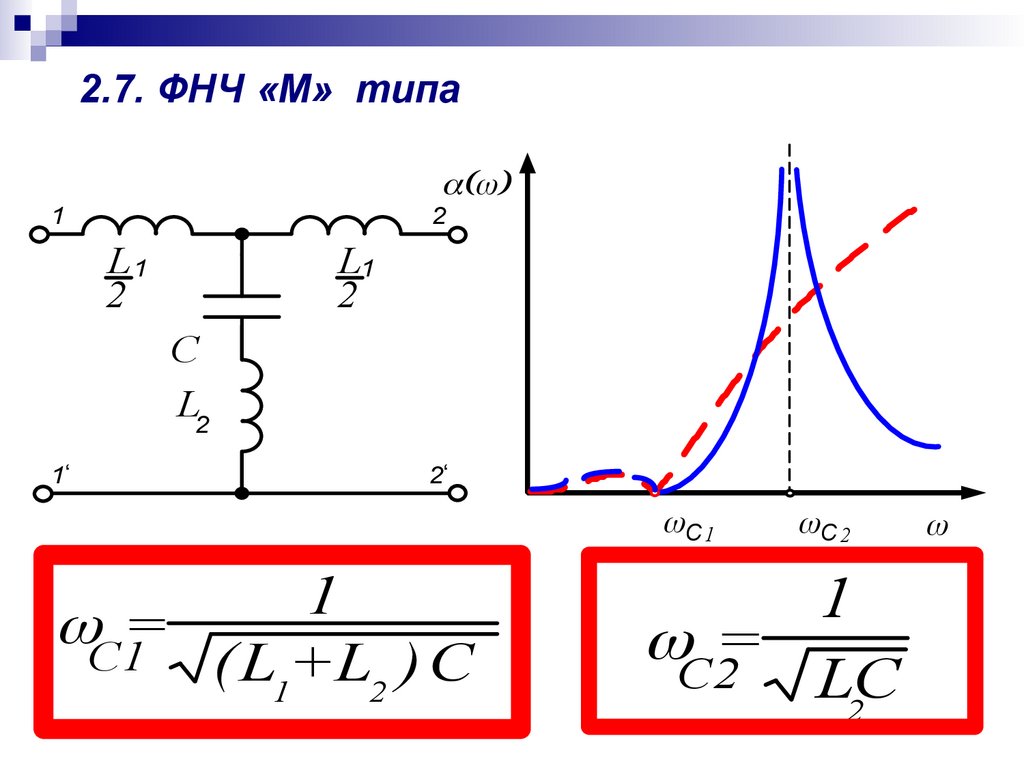
Первые шесть полиномов Чебышева имеют следующий вид:
Они изображены графически на рис. 7.8. Порядок полинома совпадает с его наивысшей степенью. С увеличением порядка полинома он приобретает все более колебательный характер, изменяясь от –1 до +1 и все более круто возрастая по мере приближения аргумента к единице.
Фильтром Чебышева 1-го рода порядка n называется фильтр, амплитудно – частотная характеристика которого описывается выражением
где
ε – коэффициент, определяющий
неравномерность амплитудно – частотной
характеристики фильтра в полосе
пропускания. В полосе пропускания АЧХ
колеблется в диапазоне от 1 до
,
а за пределами полосы пропускания
монотонно убывает до нуля.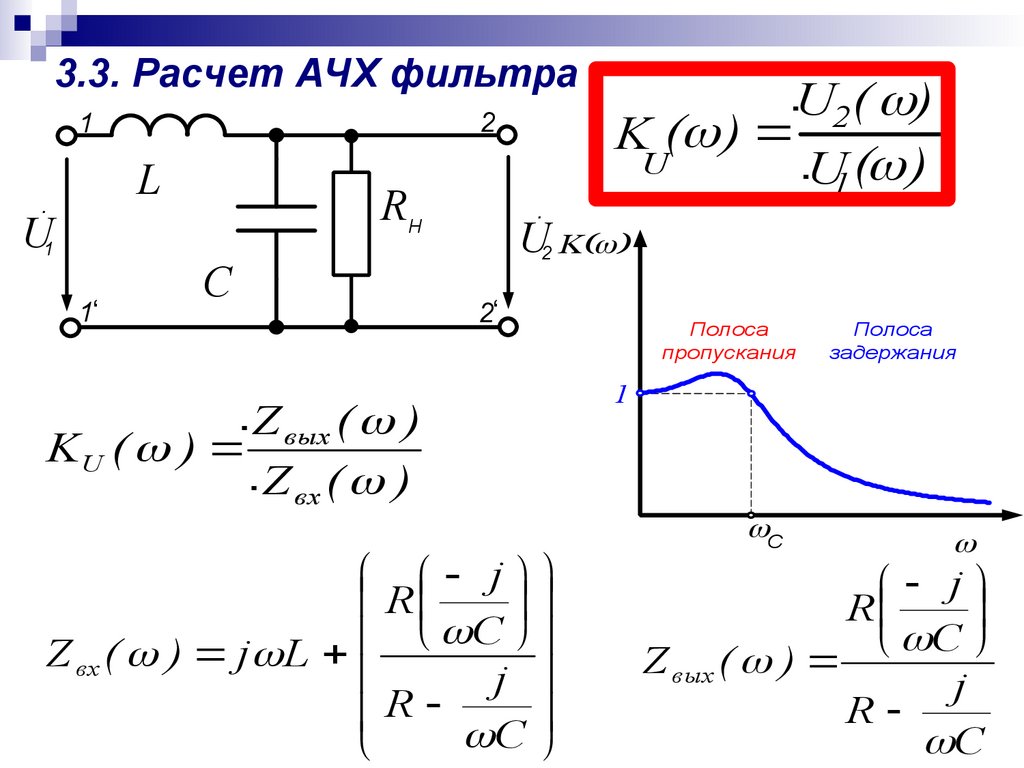
На рис. 7.9
представлены амплитудно – частотные
характеристики фильтров Чебышева первых
шести порядков при ε=0.4 для частоты среза.
Видно, насколько велика крутизна спада
АЧХ при частотах, больших частоты среза.
Повышение порядка фильтра делает спад
все более и более крутым, однако не имеет
большого смысла увеличивать порядок
фильтра свыше пятого.
Проектирование фильтра Чебышева заключается в следующем:
выбирается частота среза и порядок фильтра в зависимости от требуемой крутизны спада его амплитудно – частотной характеристики,
подбирается электронная схема построения фильтра,
подбираются параметры схемы, при которых АЧХ фильтра совпадает с АЧХ фильтра Чебышева соответствующего порядка.
Так АЧХ фильтра Чебышева 2-го порядка должна иметь вид:
Если
для построения фильтра использовать
схему Саллена — Ку, представленную на
рис.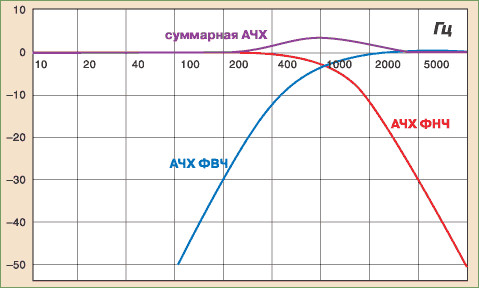
71, с амплитудно – частотной
характеристикой
,
то, приравнивая коэффициенты при соответствующих степенях частоты, получим:
,
Этих соотношений достаточно для определения всех параметров фильтра.
3. Фильтры Чебышева 2-го рода или инверсные фильтры Чебышева. Выражение для амплитудно – частотной характеристики фильтра имеет несколько иной вид:
.
Благодаря
такой структуре амплитудно – частотная
характеристика фильтра плавно спадает
в полосе пропускания до значения
и затухает до нуля, колеблясь в соответствии
с характером изменения полинома Чебышева.
На рис. 7.9 представлены амплитудно –
частотные характеристики инверсных
фильтров Чебышева первого, третьего и
пятого порядков, построенные при ε=10
для частоты среза.
В отличии от предыдущего случая полоса
пропускания здесь гораздо меньше частоты
среза и существенно зависит от порядка
фильтра, но в области затухания АЧХ
отличается от нуля не более, чем на.
СВЧ цепи. Анализ и автоматизированное проектирование
СВЧ цепи. Анализ и автоматизированное проектирование
ОглавлениеПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮГлава 1. ОСНОВНЫЕ СВОЙСТВА ЛИНИЙ ПЕРЕДАЧИ 1.1. ВОЛНОВОЕ СОПРОТИВЛЕНИЕ ЛИНИИ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ 1.2. ОСНОВНЫЕ ПАРМЕТРЫ ЛИНИЙ ПЕРЕДАЧИ 1.3. ЧЕТЫРЕХПОЛЮСНИК, ЭКВИВАЛЕНТНЫЙ ОТРЕЗКУ ЛИНИИ ПЕРЕДАЧИ 1.4. ТРАНСФОРМАЦИЯ СОПРОТИВЛЕНИЙ 1.5. КОРОТКОЗАМКНУТЫЕ И РАЗОМКНУТЫЕ НА КОНЦЕ ОТРЕЗКИ ЛИНИИ 1.6. РЕЖИМ ПОЛНОГО ОТРАЖЕНИЯ 1.7. ЛИНИЯ ПРИ ЧИСТО АКТИВНОМ ЛИБО РЕАКТИВНОМ СОПРОТИВЛЕНИИ НАГРУЗКИ Глава 2. ЛИНИИ ПЕРЕДАЧИ 2.2. ДВУХПРОВОДНАЯ ЛИНИЯ 2.3. ПРЯМОУГОЛЬНЫЙ ВОЛНОВОД 2.4. КРУГЛЫЙ ВОЛНОВОД 2.5. СИММЕТРИЧНАЯ ПОЛОСКОВАЯ ЛИНИЯ 2.6. МИКРОПОЛОСКОВАЯ ЛИНИЯ 2.7. ЧЕТНАЯ И НЕЧЕТНАЯ МОДЫ В СВЯЗАННЫХ ПОЛОСКОВЫХ ЛИНИЯХ 2.7.2. СВЯЗАННЫЕ МИКРОПОЛОСКОВЫЕ ЛИНИИ Глава 3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА 3.2. КОНЕЧНО-РАЗНОСТНАЯ АППРОКСИМАЦИЯ УРАВНЕНИЯ ЛАПЛАСА 3.2.2. ОДНОРОДНЫЙ ДИЭЛЕКТРИК. НЕРАВНОМЕРНЫЕ СЕТКИ 3. 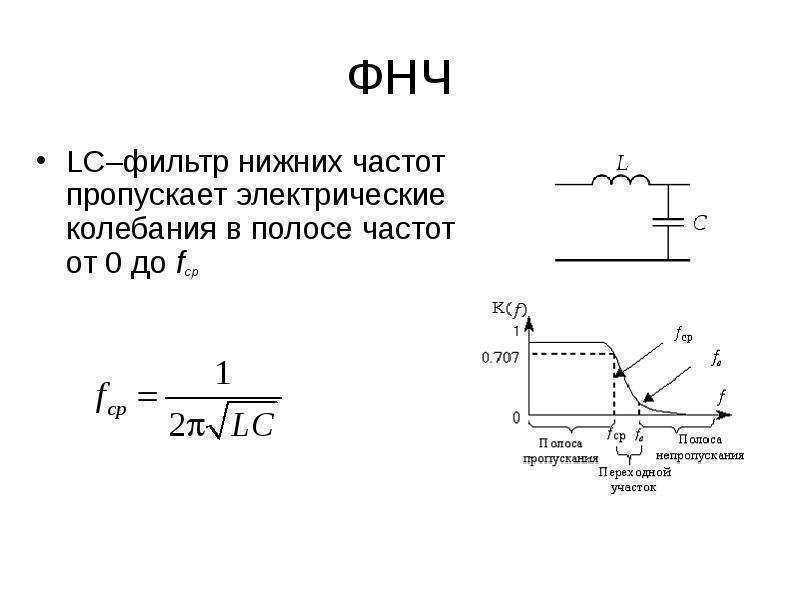 2.3. ОДНОРОДНЫЙ ДИЭЛЕКТРИК. КРИВОЛИНЕЙНЫЕ ГРАНИЦЫ3.2.4. ОДНОРОДНЫЙ ДИЭЛЕКТРИК. ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ 3.2.5 СЛОИСТЫЙ ДИЭЛЕКТРИК 3.2.6. МЕТОДЫ, УСКОРЯЮЩИЕ РЕШБНИЕ СИСТЕМ ИЗ КОНЕЧНО-РАЗНОСТНЫХ УРАВНЕНИЙ 3.3. ОПРЕДЕЛЕНИЕ ПОГОННОЙ ЕМКОСТИ 3.4. РАСЧЕТ МИКРОПОЛОСКОВОЙ ЛИНИИ 3.4.2. СВЯЗАННАЯ ЛИНИЯ 3.5. МЕТОД МОНТЕ-КАРЛО 3.6. ЗАКОН ГАУССА 3.7. МЕТОД МОМЕНТОВ Глава 4. СОГЛАСУЮЩИЕ УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ И РАСПРЕДЕЛЕННЫХ ЭЛЕМЕНТАХ. МЕТОДЫ СОГЛАСОВАНИЯ 4.1.1. ДИАГРАММА ПРОВОДИМОСТЕЙ 4.2. ДИАГРАММА СМИТА ПРИ ОТРИЦАТЕЛЬНЫХ ЗНАЧЕНИЯХ АКТИВНОГО СОПРОТИВЛЕНИЯ 4.3. СОГЛАСУЮЩИЕ ЦЕПИ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ 4.3.2. СОГЛАСУЮЩИЕ ЦЕПИ НА РЕАКТИВНЫХ ЭЛЕМЕНТАХ 4.3.3. АТТЕНЮАТОРЫ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ 4.4. ПОЛУВОЛНОВЫЕ И ЧЕТВЕРТЬВОЛНОВЫЕ ОТРЕЗКИ ЛИНИЙ ПЕРЕДАЧИ 4.5. СОГЛАСУЮЩИЕ ШЛЕЙФЫ 4.6. АНАЛИЗ КАСКАДНЫХ ЦЕПЕЙ 4.6.1. ABCD-МАТРИЦЫ 4.6.2. ABCD-МАТРИЦЫ ПРОСТЕЙШИХ ЧЕТЫРЕХПОЛЮСНИКОВ 4.6.3. МАТРИЦА РАССЕЯНИЯ Глава 5.  СВЧ ЦЕПИ НА ОТРЕЗКАХ ЛИНИЙ ПЕРЕДАЧИ5.1. ПРОЕКТИРОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ 5.1.1. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ 5.1.2. ПЕРБХОД ОТ ФИЛЬТРА-ПРОТОТИПА НИЖНИХ ЧАСТОТ К ПОЛОСОВОМУ ФИЛЬТРУ 5.2. ФИЛЬТРЫ НИЖНИХ ЧАСТОТ НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 5.2.1. ВЛИЯНИЕ НЕОДНОРОДНОСТЕЙ 5.3. ПРОЕКТИРОВАНИЕ ФИЛЬТРОВ ВЕРХНИХ ЧАСТОТ НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 5.4. ПРОЕКТИРОВАНИЕ ПОЛОСОВЫХ ФИЛЬТРОВ НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ 5.5. СТУПЕНЧАТЫЕ ТРАНСФОРМАТОРЫ 5.6. ПЛАВНЫЕ ПЕРЕХОДЫ 5.7. ШЛЕЙФНЫЕ ОТВЕТВИТЕЛИ 5.8. КОЛЬЦЕВОЙ МОСТ (180°-НОЕ ГИБРИДНОЕ СОЧЛЕНЕНИЕ) 5.9. ДЕЛИТЕЛЬ (СУММАТОР) МОЩНОСТИ 5.10. ОТВЕТВИТЕЛЬ ЛАНГЕ СПИСОК ЛИТЕРАТУРЫ |
Как описать частотную характеристику цепей фильтров
Схемы фильтров (такие как фильтры нижних частот, фильтры верхних частот, полосовые фильтры и режекторные фильтры) формируют частотный состав сигналов, пропуская только определенные частоты пройти через.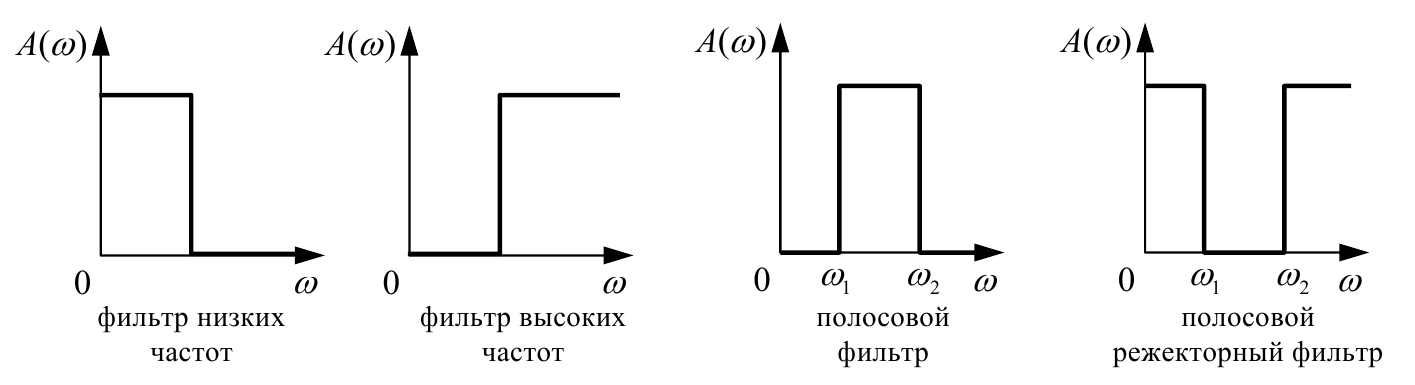
Вы можете описать эти фильтры на основе простых схем.
Вы находите синусоидальный установившийся выходной сигнал фильтра, оценивая передаточную функцию T(s) при s = j ω . Передаточная функция связывает входные/выходные сигналы в s -домен и предполагает нулевые начальные условия. Частота в радианах ω — это переменная, обозначающая частоту синусоидального входа. После замены s = j ω на T(s) передаточная функция становится отношением комплексных чисел T(j ω ) .
Поскольку функция T(j ω ) является комплексным числом для всех частот, можно определить усиление | T(j ω ) | и фаза θ (j ω ) . Вот отношения усиления и фазы:
Вы можете представить усиление и фазу как функцию частоты ω графически, как показано в этом приближении типичного фильтра. В области полосы пропускания функция усиления имеет почти постоянное усиление для диапазона частот.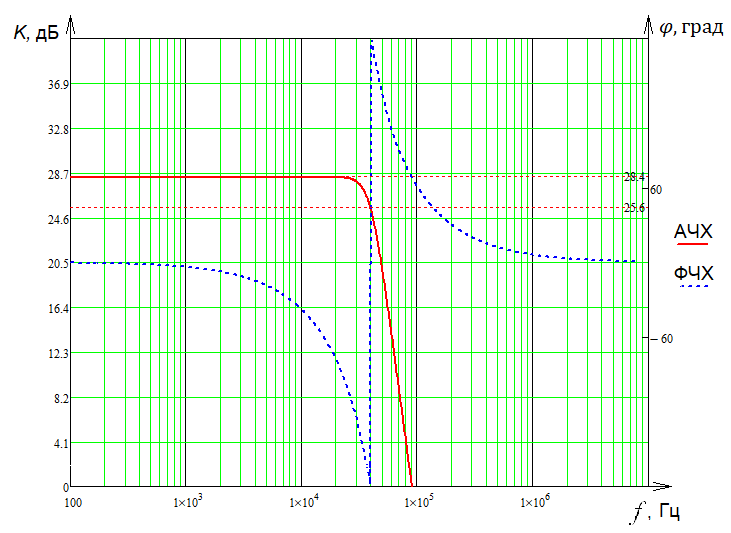
В области полосы задерживания усиление значительно снижается для диапазона частот.
Для неидеальных фильтров возникает переходная область между соседними областями полосы пропускания и полосы задерживания. Частота среза ω C находится в переходной области согласно заданному определению. В одном широко используемом определении говорится, что частота среза возникает, когда коэффициент усиления полосы пропускания уменьшается в 0,707 раза по сравнению с максимальным значением T MAX . Таким образом, математическое условие для ω C равно
На частоте среза выходная мощность упала до половины максимального значения в полосе пропускания. Здесь в полосу пропускания входят те частоты, где относительная мощность больше точки половинной мощности (0,707 от максимального значения передаточной функции). Частоты ниже точки половинной мощности попадают в полосу задерживания.
Фильтр нижних частот
ФНЧ имеет коэффициент усиления с диапазоном частот от нулевой частоты (DC) до ω С .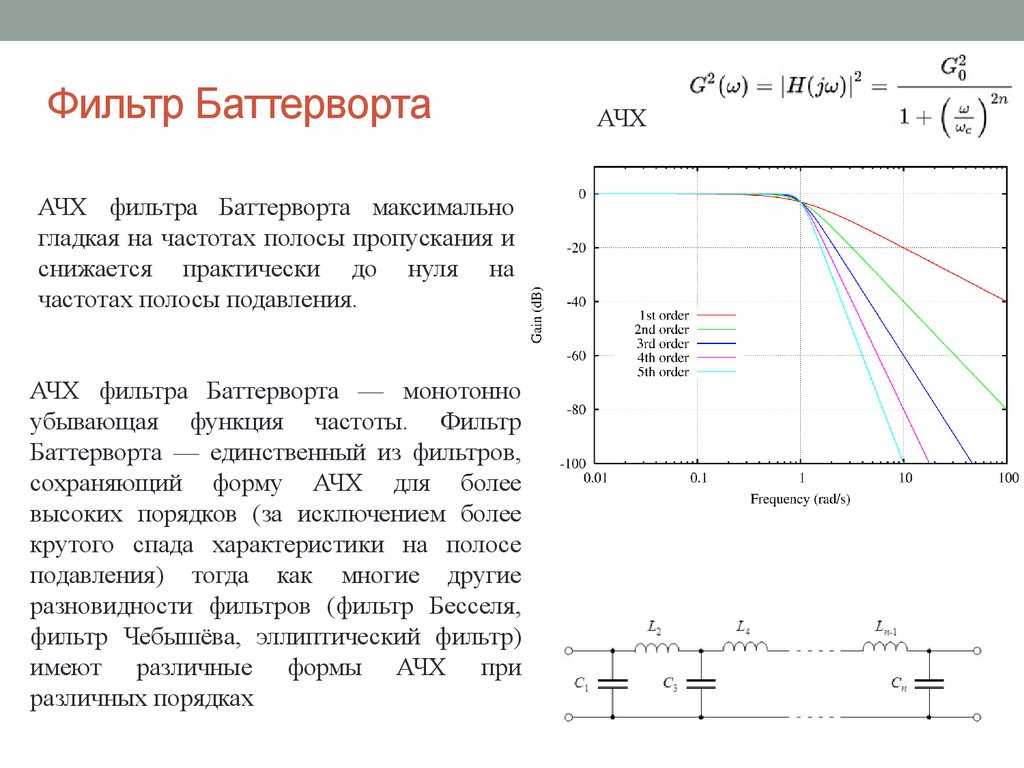
Любой вход, частота которого ниже частоты среза ω C , получает пропуск, а все, что выше, ослабляется или отбрасывается. Коэффициент усиления приближается к нулю при увеличении частоты до бесконечности.
Показанный здесь входной сигнал фильтра имеет равные амплитуды на частотах ω 1 и ω 2 . После прохождения фильтра нижних частот выходная амплитуда на уровне ω 1 не изменяется, так как ниже частоты среза ω C . Однако при ω 2 амплитуда сигнала значительно уменьшается, поскольку она выше ω C .
Фильтр верхних частот
Фильтр верхних частот имеет характеристику усиления с частотным диапазоном от ω C до бесконечности. Любой вход с частотой ниже частоты среза ω C ослабляется или отклоняется. Все, что выше ω C , проходит без изменений.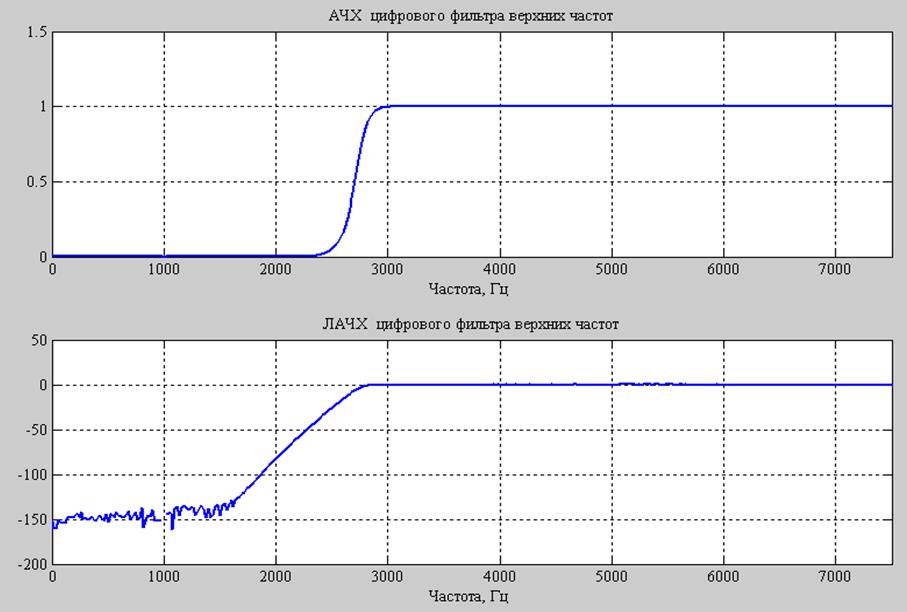
Показанный здесь входной сигнал фильтра имеет одинаковую амплитуду на частотах ω 1 и ω 2 . После прохождения через фильтр верхних частот выходная амплитуда на ω 1 значительно уменьшается, поскольку она ниже ω C и при ω 2 амплитуда сигнала не изменяется, поскольку она выше ω C .
Полосовые фильтры
Фильтр с полосовым проходом имеет отклик усиления с диапазоном частоты от ω C 1 до ω C 2 . Любой вход с частотами в диапазоне ω C 1 и ω C 2 получает пропуск, и все, что находится за пределами этого диапазона, считается пропущенным или отклоненным.
Входной сигнал фильтра, показанного здесь, имеет равную амплитуду на частотах ω 1 , ω 2 и Ом 3 .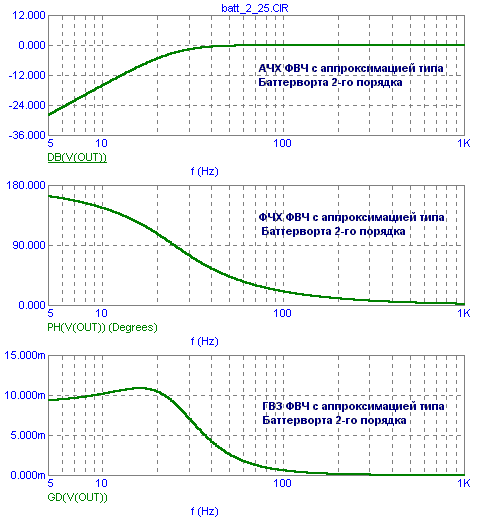
После прохождения через полосовой фильтр амплитуда выходного сигнала составляет ω 1 и ω 3 значительно уменьшаются, потому что они выходят за пределы желаемого диапазона частот, в то время как частота на ω 2 находится в пределах желаемого диапазона, поэтому его сигнал находится в пределах желаемого диапазона амплитуда проходит без изменений.
Полосовой фильтр можно рассматривать как последовательное или каскадное соединение фильтра нижних частот с частотой ω C 2 и ФВЧ с частотой ω C 1 . Каскадное соединение ФНЧ и ФВЧ образует полосовой фильтр; порядок фильтров не имеет значения.
Если вы собираетесь на скорую руку разработать полосовой фильтр на основе фильтра нижних частот и фильтра верхних частот, убедитесь, что вы выбрали правильные частоты среза. Например, если вы зададите фильтру нижних частот более низкую частоту среза ω C 1 и фильтр с высоким частотом.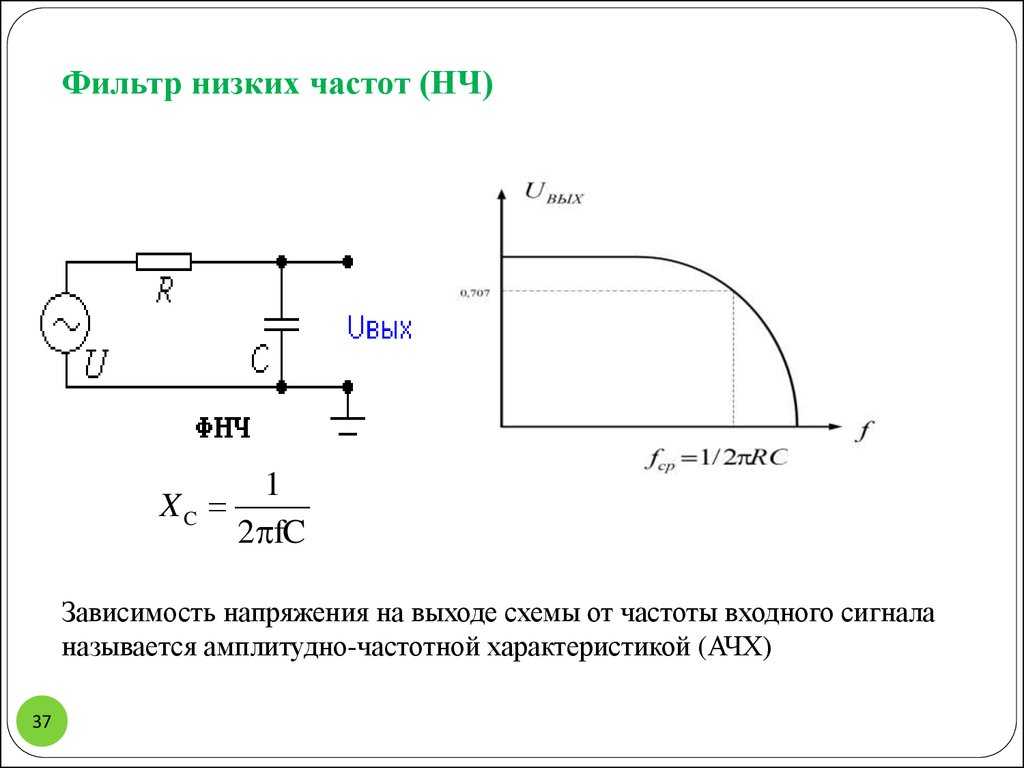
Частота верхнего отсечения ω C 2 , вы получите очень маленький сигнал на выходе, выходе, выходе или непроходной фильтр — все отбрасывается.
Заграждающие (заграждающие) фильтры
Полосовой режекторный фильтр, или режекторный фильтр, имеет характеристику усиления в диапазоне частот от нуля до ω C 1 и от ω C 2 до бесконечности. Любой вход, который имеет частоты между ω C 1 и ω C 2 . Страшено, и все за пределами этого дальности получает проход.
Показанный здесь входной сигнал фильтра имеет одинаковую амплитуду на частотах ω 1 , ω 2 , и ω 3 . После прохождения через фильтр с полосой, выходная амплитуда при ω 1 и ω 3 не затронуты, потому что эти частоты выпадают за пределы диапазона C 9005 669 C 9 66669 C 9 6669 C 9 6.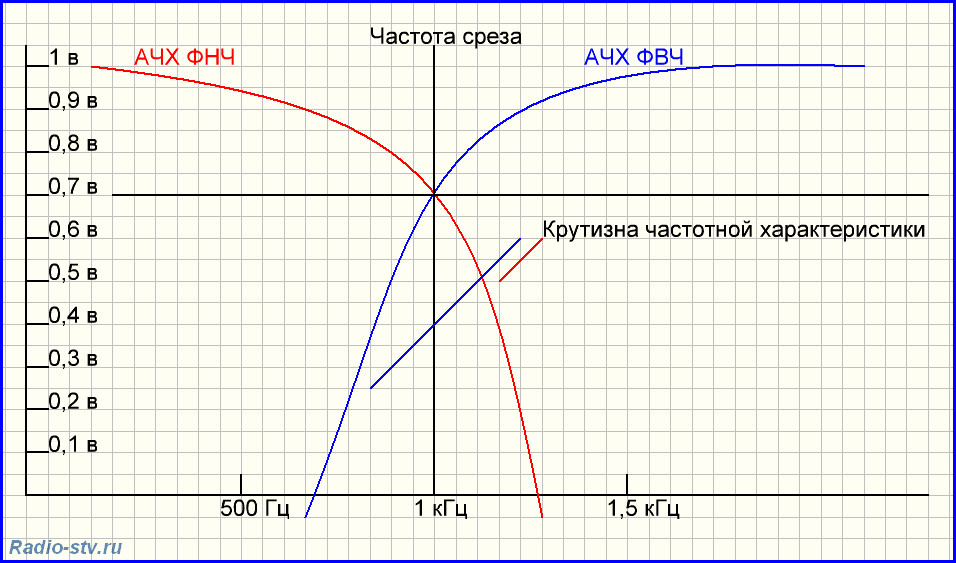
1 — ω C 2 . Но в ω 2 амплитуда сигнала затухает, поскольку попадает в этот диапазон.
Полосовой фильтр можно рассматривать как параллельное соединение фильтра нижних частот с частотой среза ω C 1 и фильтра верхних частот с частотой среза ω C 2 .с суммированием их выходов. На нижней диаграмме показано параллельное соединение фильтра нижних частот и фильтра верхних частот для формирования режекторного фильтра.
Удостоверьтесь, что вы выбрали правильные частоты среза, когда вы делаете быструю и грязную конструкцию полосового режекторного фильтра на основе фильтра нижних частот и фильтра верхних частот, соединенных параллельно. Как показано здесь, если задать фильтру нижних частот нижнюю частоту среза ω C 2 , а фильтру верхних частот — верхнюю частоту среза ω 5 6 C 1 , вы будете иметь сигналы всех частот, проходящих через фильтр, что не очень хорошо для режекторного фильтра.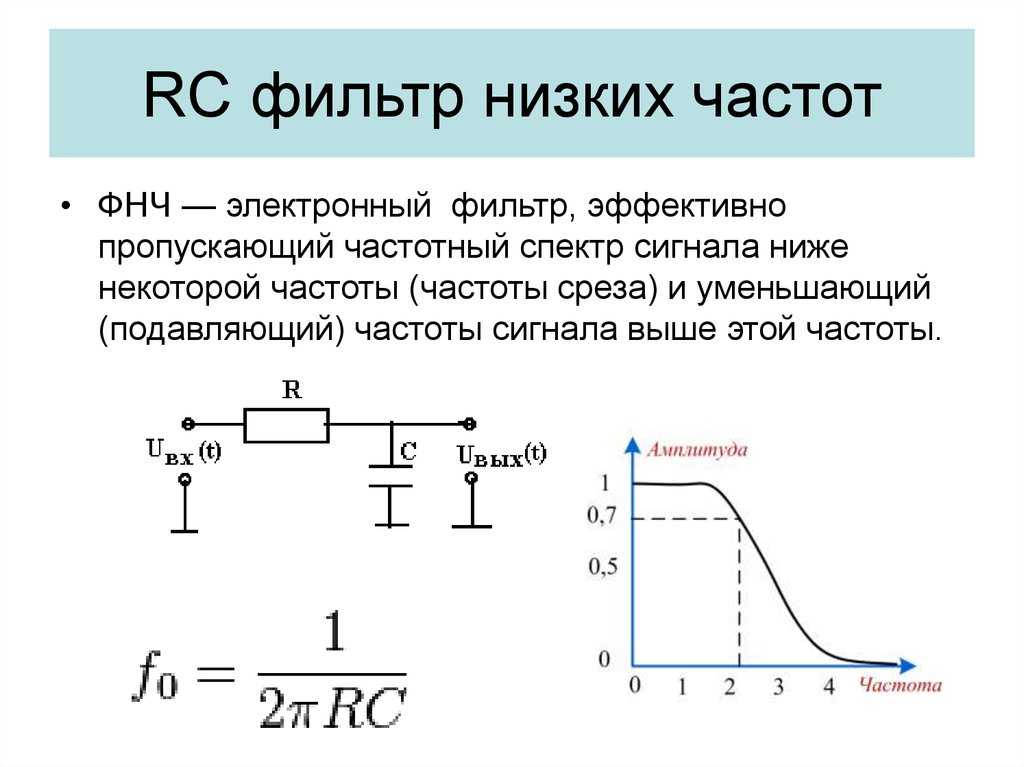
Вместо этого вы спроектируете всепропускающий фильтр. Это как использовать кофейный фильтр с большим толстым отверстием — все проходит, включая кофейную гущу.
Найти выходной сигнал в фильтре нижних частот для заданного диапазона частот среза
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 193 раза
$\begingroup$
У меня есть сценарий, в котором 𝑥(𝑡)=2⋅sin150𝜋t +sin250𝜋t и g(t)=𝑥(𝑡)sin250𝜋 . Сигнал g(t) подается на вход через идеальный фильтр нижних частот с частотой среза (fc) = 300 и коэффициентом усиления в полосе пропускания = 3.
Каким будет выходной сигнал фильтра нижних частот? Пожалуйста, предложите, есть ли какая-либо формула или представление для расчета этого?
Я знаю, что идеальная функция фильтра низких частот предназначена для блокировки всех высоких частот и разрешения низких частот.
Может ли кто-нибудь предложить какую-либо формулу для оценки этого?
Я новичок в этой концепции фильтрации.
С уважением
Sameer
- фильтры
- конструкция фильтра
- фильтр нижних частот
- цифровые фильтры
- полосовой
91
61 $\endgroup$
$\begingroup$
Идеальный (и нереализуемый) фильтр нижних частот — это фильтр с кирпичной стеной, который пропускает все частоты ниже своего среза с коэффициентом усиления 3 и подавляет все, что выше среза. Формула представляет собой просто прямоугольную функцию, и упражнение здесь для вас состоит в том, чтобы увидеть, можете ли вы распознать отдельные частоты и амплитуды в вашей формуле для формы волны.
Используйте правило произведения синуса, чтобы определить g(t), а затем посмотрите, какие из этих частотных составляющих выше или ниже отсечки. Для любых частотных составляющих ниже отсечки умножьте амплитуду на коэффициент усиления полосы пропускания.
