A b c таблица истинности: Онлайн-калькулятор по информатике — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Перевод в восьмеричную систему счисления

Пример №1. Перевести число 132,267₁₀ в восьмеричное представление.
Решение находим с помощью калькулятора. Переводим целую часть числа, т.е. 132.

Целая часть от деления	Остаток от деления
132 div 8 = [16].5 = `16`	132 mod 8 = 4 (132 — `16`*8)
16 div 8 = 2	16 mod 8 = 0	2 div 8 = 0	2 mod 8 = 2	0 div 8 = 0	0 mod 8 = 0

Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 0204
132 = 0204₈

Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.267*8 = 2.136 (целая часть 2)
0.136*8 = 1.088 (целая часть 1)
0.088*8 = 0.704 (целая часть 0)
0.704*8 = 5. 632 (целая часть

5)
Получаем число в 8-ой системе счисления: 2105
0.267 = 2105₈

Таким образом, число 132,267 записывается в восьмеричной системе счисления как 204,2105₈

Пример №2. Перевести число 1000000010,1001₂ в восьмеричное представление.
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
1000000010₂ = 001 000 000 010 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 001 000 000 010 ₂ = 1002₈

Переводим дробную часть числа.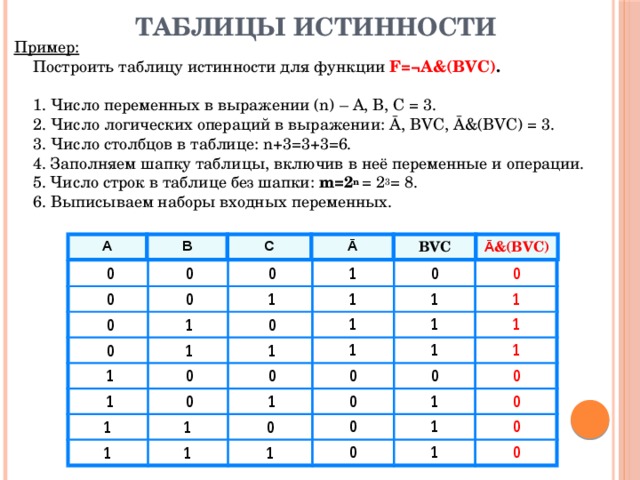 Для этого разделим исходный код на группы по 3 разряда.
1001₂ = 100 100₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 100 100₂ = 44₈
Таким образом, число 1000000010,1001₂ в восьмеричной системе счисления записывается как 1002,44.

Пример №3. Перевести число 132,267₁₀ в восьмеричное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная СС	Шестнадцатеричная СС
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Получаем число: A5F₁₆ = 101001011111₂

Переводим дробную часть числа.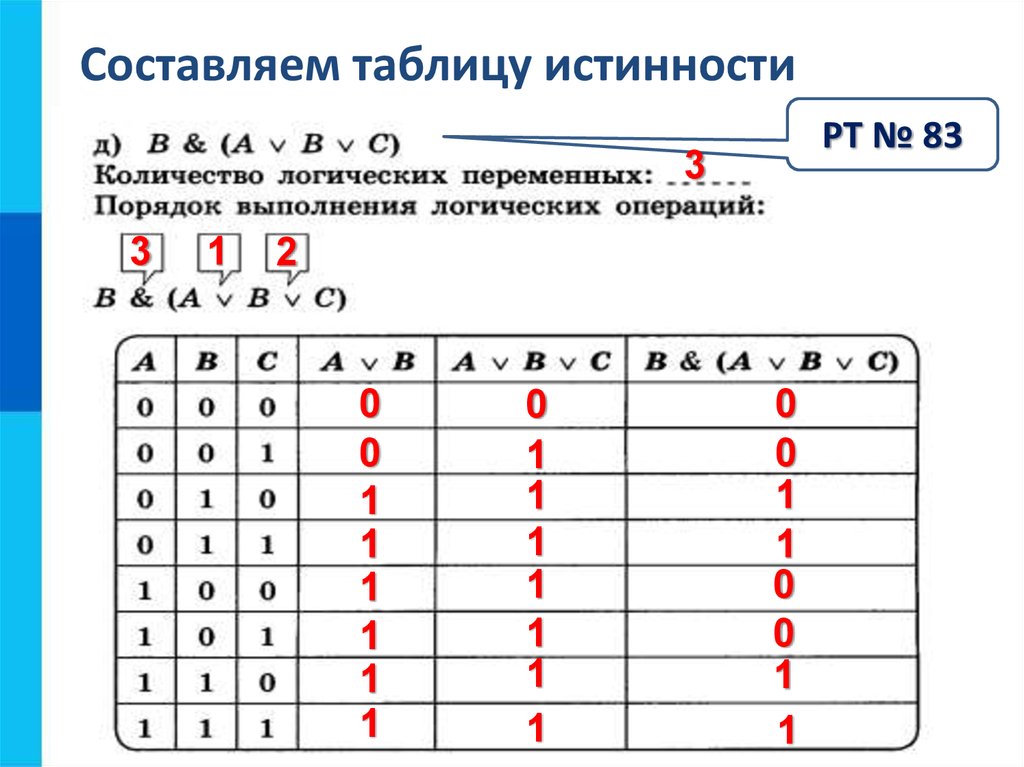
Получаем число: 3B₁₆ = 00111011₂
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
101001011111

2 = 101 001 011 111 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 101 001 011 111 ₂ = 5137₈

Переводим дробную часть числа. Для этого разделим исходный код на группы по 3 разряда.
00111011₂ = 001 110 110₂

Затем заменяем каждую группу на код из таблицы.
Получаем число: 001 110 110₂ = 166₈
Таким образом, число A5F,3B₁₆ в восьмеричной системе счисления записывается как 5137,166.

Перейти к онлайн решению своей задачи

Построение таблицы истинности для вектора значений !(!AB+!ABC)@!(!AB+!BC)+C

… у нас не курят! …

Список литературы

Генератор кроссвордов

Генератор титульных листов

Таблица истинности ONLINE

Прочие ONLINE сервисы

Общая таблица истинности:

Логическая схема:

Совершенная дизъюнктивная нормальная форма (СДНФ):

По таблице истинности:

F_сднф = ¬AB∧¬ABC∧¬BC∧¬C ∨ ¬AB∧¬ABC∧¬BC∧C ∨ ¬AB∧¬ABC∧BC∧¬C ∨ ¬AB∧¬ABC∧BC∧C ∨ ¬AB∧ABC∧¬BC∧¬C ∨ ¬AB∧ABC∧¬BC∧C ∨ ¬AB∧ABC∧BC∧¬C ∨ ¬AB∧ABC∧BC∧C ∨ AB∧¬ABC∧¬BC∧¬C ∨ AB∧¬ABC∧¬BC∧C ∨ AB∧¬ABC∧BC∧¬C ∨ AB∧¬ABC∧BC∧C ∨ AB∧ABC∧¬BC∧C ∨ AB∧ABC∧BC∧¬C ∨ AB∧ABC∧BC∧C
Логическая cхема:

Совершенная конъюнктивная нормальная форма (СКНФ):

По таблице истинности:

F_скнф = (¬AB∨¬ABC∨BC∨C)
Логическая cхема:

Построение полинома Жегалкина:

По таблице истинности функции

Построим полином Жегалкина:
F_ж = C₀₀₀₀ ⊕ C₁₀₀₀∧AB ⊕ C₀₁₀₀∧ABC ⊕ C₀₀₁₀∧BC ⊕ C₀₀₀₁∧C ⊕ C₁₁₀₀∧AB∧ABC ⊕ C₁₀₁₀∧AB∧BC ⊕ C₁₀₀₁∧AB∧C ⊕ C₀₁₁₀∧ABC∧BC ⊕ C₀₁₀₁∧ABC∧C ⊕ C₀₀₁₁∧BC∧C ⊕ C₁₁₁₀∧AB∧ABC∧BC ⊕ C₁₁₀₁∧AB∧ABC∧C ⊕ C₁₀₁₁∧AB∧BC∧C ⊕ C₀₁₁₁∧ABC∧BC∧C ⊕ C₁₁₁₁∧AB∧ABC∧BC∧C

Так как F_ж(0000) = 1, то С₀₀₀₀ = 1.

Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
F_ж(1000) = С₀₀₀₀ ⊕ С₁₀₀₀ = 1 => С₁₀₀₀ = 1 ⊕ 1 = 0
F_ж(0100) = С₀₀₀₀ ⊕ С₀₁₀₀ = 1 => С₀₁₀₀ = 1 ⊕ 1 = 0
F_ж(0010) = С₀₀₀₀ ⊕ С₀₀₁₀ = 1 => С₀₀₁₀ = 1 ⊕ 1 = 0
F_ж(0001) = С₀₀₀₀ ⊕ С₀₀₀₁ = 1 => С₀₀₀₁ = 1 ⊕ 1 = 0
F_ж(1100) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С

0100 ⊕ С₁₁₀₀ = 0 => С₁₁₀₀ = 1 ⊕ 0 ⊕ 0 ⊕ 0 = 1
F_ж(1010) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₀₁₀ ⊕ С₁₀₁₀ = 1 => С₁₀₁₀ = 1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(1001) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₀₀₁ ⊕ С₁₀₀₁ = 1 => С₁₀₀₁ = 1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(0110) = С₀₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₁₀ ⊕ С₀₁₁₀ = 1 => С₀₁₁₀ = 1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(0101) = С₀₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₀₁ ⊕ С₀₁₀₁ = 1 => С₀₁₀₁ = 1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(0011) = С₀₀₀₀ ⊕ С₀₀₁₀ ⊕ С₀₀₀₁ ⊕ С₀₀₁₁ = 1 => С₀₀₁₁ = 1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(1110) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₁₀ ⊕ С₁₁₀₀ ⊕ С₁₀₁₀ ⊕ С₀₁₁₀ ⊕ С₁₁₁₀ = 1 => С₁₁₁₀ = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1 = 1
F_ж(1101) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₀₁ ⊕ С₁₁₀₀ ⊕ С₁₀₀₁ ⊕ С₀₁₀₁ ⊕ С₁₁₀₁ = 1 => С₁₁₀₁ = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1 = 1
F_ж(1011) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₀₁₀ ⊕ С₀₀₀₁ ⊕ С₁₀₁₀ ⊕ С₁₀₀₁ ⊕ С₀₀₁₁ ⊕ С₁₀₁₁ = 1 => С₁₀₁₁ = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(0111) = С₀₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₁₀ ⊕ С₀₀₀₁ ⊕ С₀₁₁₀ ⊕ С₀₁₀₁ ⊕ С₀₀₁₁ ⊕ С₀₁₁₁ = 1 => С₀₁₁₁ = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 = 0
F_ж(1111) = С₀₀₀₀ ⊕ С₁₀₀₀ ⊕ С₀₁₀₀ ⊕ С₀₀₁₀ ⊕ С₀₀₀₁ ⊕ С₁₁₀₀ ⊕ С₁₀₁₀ ⊕ С₁₀₀₁ ⊕ С₀₁₁₀ ⊕ С₀₁₀₁ ⊕ С₀₀₁₁ ⊕ С₁₁₁₀ ⊕ С₁₁₀₁ ⊕ С₁₀₁₁ ⊕ С₀₁₁₁ ⊕ С₁₁₁₁ = 1 => С₁₁₁₁ = 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1 = 1

Таким образом, полином Жегалкина будет равен:
F_ж = 1 ⊕ AB∧ABC ⊕ AB∧ABC∧BC ⊕ AB∧ABC∧C ⊕ AB∧ABC∧BC∧C
Логическая схема, соответствующая полиному Жегалкина:

Вход на сайт

Информация

В нашем каталоге

Околостуденческое

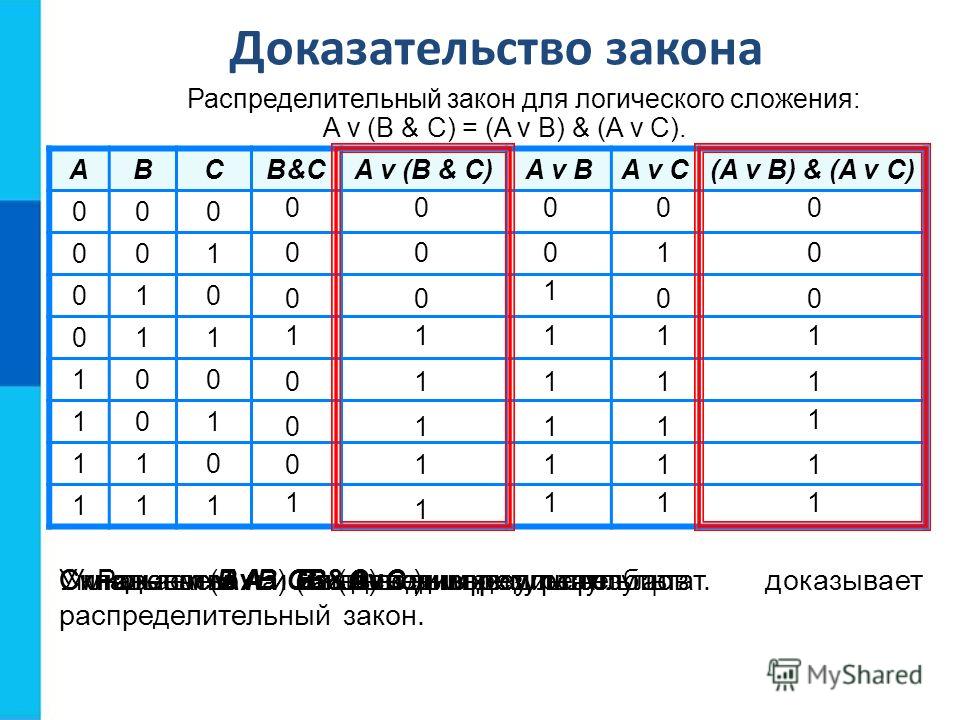
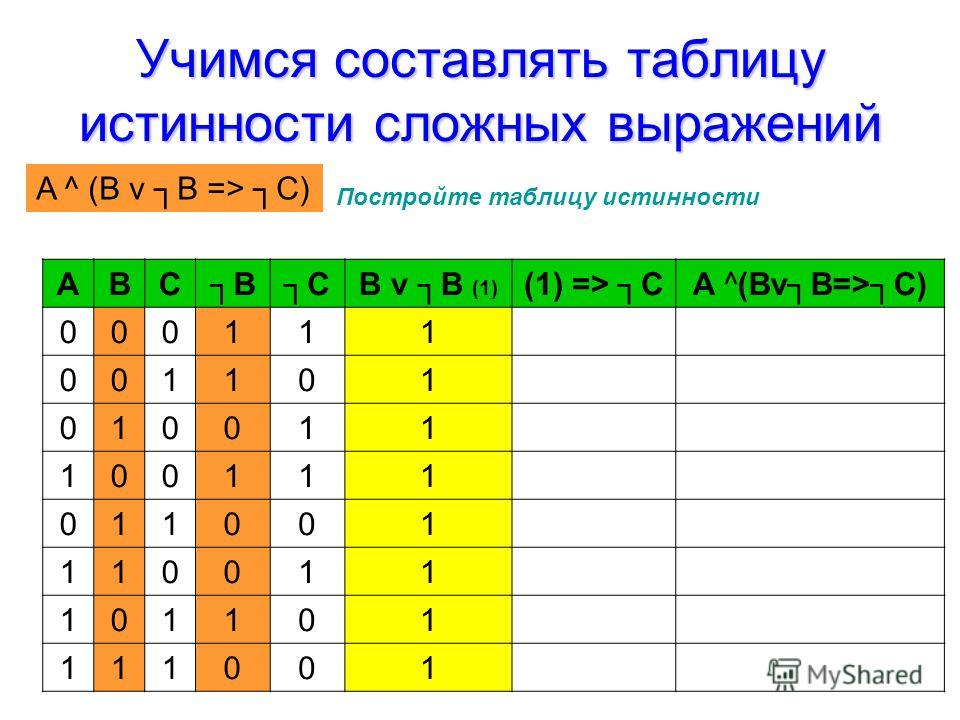
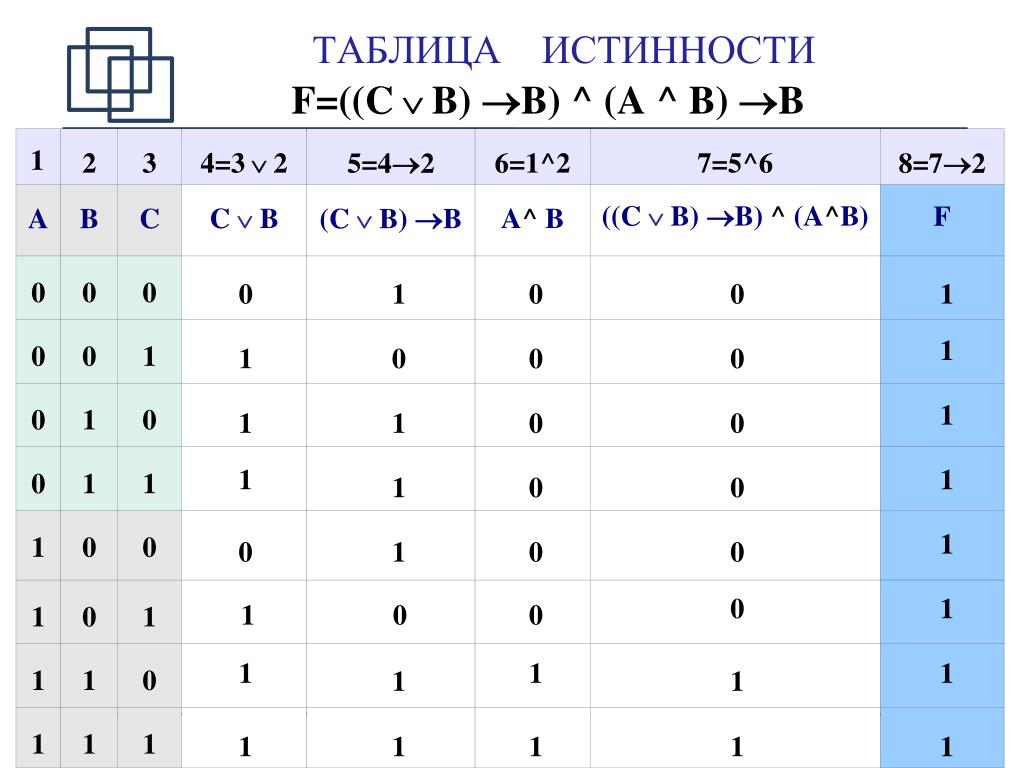
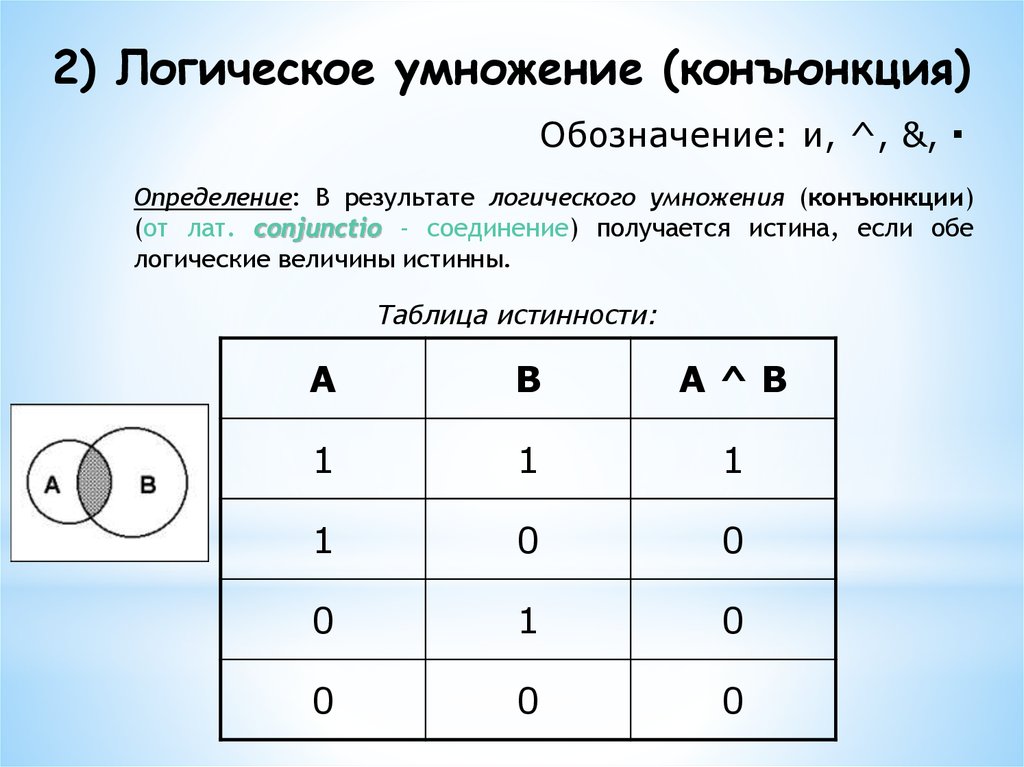
как составить таблицу истинности из логического выражения

A, B, C и D являются булевыми переменными, что означает, что каждая из них принимает значение «правда или ложь».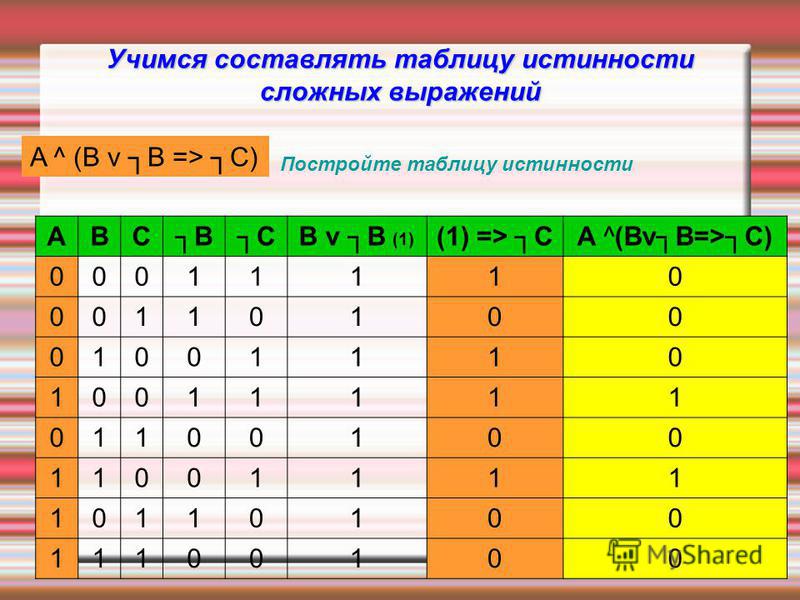

Более сложные выражения имеют значение «истина» или «ложь». в зависимости от значений этих переменных, так, например, A’BD’ истинно, если А ложно, В истинно, D ложно, С либо истинно, либо ложно.

Сказать, что F = G, где F и G комплексные выражения, означает, что нет независимо от того, какие значения имеют логические переменные, значение F одинаково как значение G (то есть F и G либо оба истинны, либо оба ложны). Так, например, у нас есть

 АВ + АС = А(В+С)

, потому что если А истинно и либо В, либо С истинно, то обе стороны верны, а в любом другом случае обе стороны ложны—нет возможности присвоить значения для A, B, C так, чтобы две стороны вышли по-разному.

Как упоминалось в предыдущих постах, вы всегда можете доказать (или опровергнуть!) равенство, перебирая все возможные присваивания «true» и «false» переменные. Цель, кажется, состоит в том, чтобы доказать «теоремами», то есть используя операции, ранее подтвержденные. Как вы говорите, мы можем либо манипулировать одну сторону уравнения, пока она не примет вид другой стороны, или мы мог манипулировать обеими сторонами и привести их в общую форму.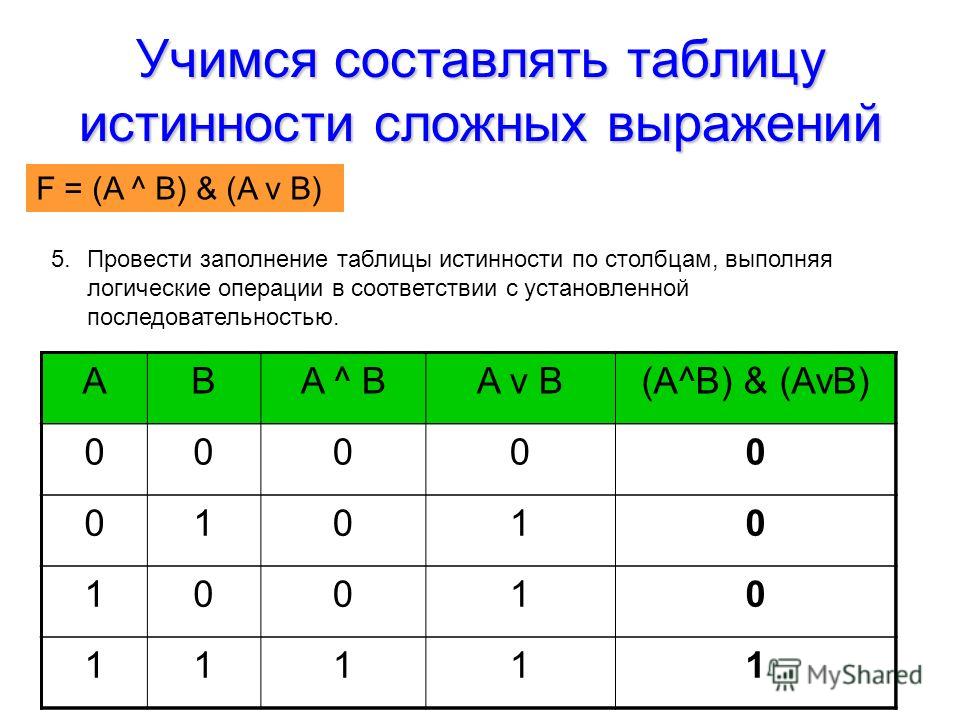

В этом случае первое, на что следует обратить внимание, это то, что правая сторона (RHS) является копией LHS с некоторыми дополнительными элементами, прикрепленными к концу. Для этого причина, по которой проще всего манипулировать только RHS, чтобы избавиться от избыток! Мы можем начать с этой основной теоремы:

, если Q истинно всякий раз, когда истинно P, то Q = Q + P

Мы можем доказать эту теорему, систематически рассматривая все возможности для P и Q. Или посмотрите на это так: если Q истинно, то обе части уравнение верно. А если Q ложно, то и P должно быть ложно (поскольку по предположение, если бы P было истинным, Q было бы истинным), следовательно, обе стороны ложны.

Учитывая эту теорему, мы доказываем:

 XY + X'Z = XY + X'Z + YZ

Доказательство: пусть P будет YZ, а Q будет XY+X’Z. Предположим, что P истинно, то есть Y и Z оба верны. Но если Y и Z оба истинны, то XY+X’Z должны быть истинны. (Причина: если X истинно, то, поскольку Y истинно, XY истинно.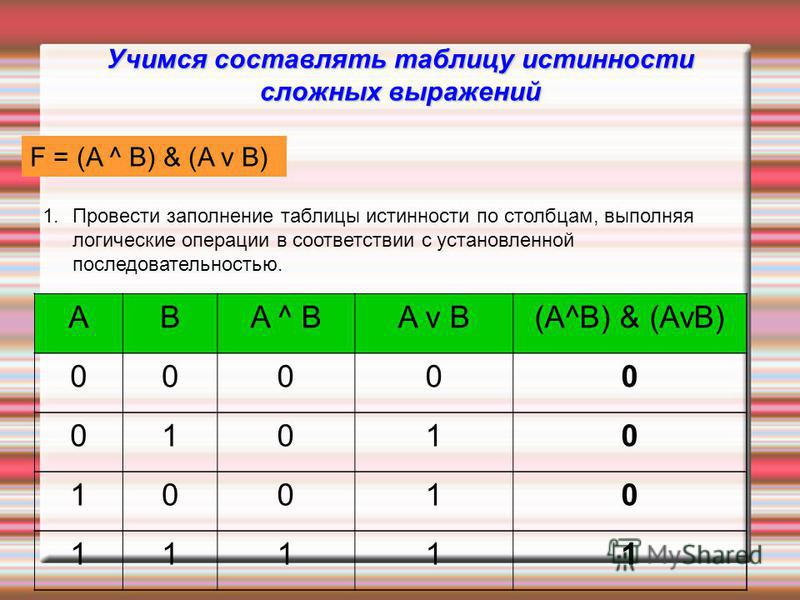 И если X истинно ложно, тогда, поскольку Z истинно, X’Z истинно. Таким образом, в любом случае XY+X’Z равно верно.) Итак, мы показали, что Q истинно всякий раз, когда истинно P, следовательно, предыдущую теорему Q = Q + P, которую в данном случае мы и хотели доказать.

Теперь мы можем доказать

 A'D' + AC' = A'D' + AC' + C'D'

Это то же самое, что и предыдущая теорема, полагая A вместо X, D’ вместо Y, и C’ вместо Z.

Из последней теоремы следует, что

 B(A'D' + AC') = B(A'D' + AC' + C'D')

то же, что и

 A'BD' + ABC' = A'BD' + ABC' + BC'D'

Учитывая это, мы можем взять правую часть оригинала и заменить A’BD’ + ABC’ для A’BD’ + ABC’ + BC’D’, то есть мы можем опустить термин BC’D’.

Шагами, аналогичными описанным выше, мы можем доказать эти две теоремы:

 A'BD' + BCD = A'BD' + BCD + A'BC
 BCD + ABC' = BCD + ABC' + ABD

, которые позволяют нам опустить последние два члена RHS оригинала, завершение доказательства.

Примеры таблиц истинности

Примеры булевой алгебры Двоичный/булев основной индекс

[Примеры таблиц истинности] [Упрощение логических выражений] [Примеры логических вентилей]

Таблицы истинности для основных операций:

А
А	Б	АВ
0	0	0
0	1	0
1	0	0
1	1	1

или
А	В	А+В
0	0	0
0	1	1
1	0	1
1	1	1

Не
А	А
0	1
1	0

Для более сложных выражений таблицы строятся из таблицы истинности их основных частей.

Вот несколько:

• Нарисуйте таблица истинности для A+BC .
А	В	С	ВС	А+ВС
0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	1	1
1	0	0	0	1
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

6 10

• Нарисуйте таблица истинности для A(B+D) .
А	В	D	Б+Г	А(Б+Г)
0	10 900	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	1	0
1	0	0	0	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

• Нарисуйте таблица истинности для (A+B)(A+C) .
A	B	C	A+B	A+C	(A+B)(A+C)
0	0	0	0	0	0
0	0	1	0	1	0
0	1	0	1	0	0
0	1	1	1	1	1
1	0	0	1	1	1
1	0	1	1	1	1
1	1	0	1	1	1
1	1	1	1	1	1

W (x+y).

• Нарисуйте таблица истинности для W(X+Y)Z .
W	x	Y	Z	W	x+Y	W (x+Y)	W (x+Y) z	0	1	0	0	0
0	0	0	1	1	0	0	0
0	0	1	0	1	1	1	0
0	0	1	1	1	1	1	1
0	1	0	0	1	1	1	0
0	1	0	1	1	1	1	1
0	1	1	0	1	1	1	0
0	1	1	1	1	1	1	1
1	0	0	0	0	0	0	0
1	0	0	1	0	0	0	0
1	0	1	0	0	1	0	0
1	0	1	1	0	1	0	0
1	1	0	0	0	1	0	0
1	1	0	1	0	1	0	0
1	1	1	0	0	1	0	0
1	1	1	1	0	1	0	0

• Нарисуйте таблица истинности для PT(P+Z) .