Формула второго закона Кирхгофа

Какой бы сложной не была электрическая цепь, она имеет элементы двух видов: узлы и замкнутые контуры. Узлом цепи называют точку разветвления цепи, в которой сходятся три или более проводника с током. Расчеты в любой самой сложной цепи можно провести, используя закон Ома и закон сохранения заряда. Для упрощения расчетов цепей постоянного тока используют правила (законы) Кирхгофа, которые позволяю составить линейные уравнения вычисления сил токов, текущих в элементах цепи.

Падение напряжения это произведение силы тока на сопротивление (). Если в цепи источников ЭДС будет несколько, то следует ЭДС суммировать, учитывая знаки. ЭДС принято считать положительной, если при обходе контура первым встречается отрицательный полюс источника. Направление обхода контура выбирают произвольно, (по часовой стрелке или против нее). Один раз выбрав направление обхода контура при решении задачи не следует его изменять.

Теперь к самой формуле, отображающей второй закон Кирхгофа:

   

Формула второго закона Кирхгофа говорит о том, что сумма произведений силы токов (I) (с учетом знака) на внешние и внутренние сопротивления всех участков замкнутого контура равны сумме величин ЭДС () источников, которые включены в данный контур (суммирование ЭДС происходит с учетом знаков). При составлении и уравнений с использованием формулы второго закона Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго правил Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второе правило Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач по теме «Второй закон Кирхгофа»

Второй закон Кирхгофа — Основы электроники

Второй закон Кирхгофа или закон напряжений Кирхгофа формулируется так: полная ЭДС, действующая в замкнутом контуре, равна сумме падений напряжения на всех резисторах в этом контуре.

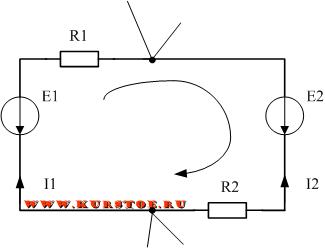
Рассмотрим схему на рисунке. 1, состоящую из одного контура.

Здесь полная ЭДС Е₁ + Е₂, действующая внутри контура, равна сумме падений напряжения на резисторах R1 и R2:

E₁ + E₂ = U_R1 + U_R2

Если изменить полярность Е₂ на противоположную (рис. 2), то она будет иметь то же направление (против часовой стрелки), что и U_R1 и U_R2

E₁— Е₂ = U_R1 + U_R2 или E₁ = Е₂ + U_R1 + U_R2

Рассмотрим схему, имеющую несколько контуров (рис. 3).

Для кон­тура ABEF можно записать

E₁= U_R1 + U_R2,

а для контура ACDF

E₁ -Е₂ = U_R1 + U_R3

Обходя контур BCDE, видим, что ЭДС Е2 имеет то же направление (про­тив часовой стрелки), что и U_R3:

Е₂ + U_R3 = U_R2

В цепи с одним контуром второй закон Кирхгофа является частным случаем закона Ома.

ДРУГИЕ СТАТЬИ ПО ТЕМЕ:

Первый и второй законы Кирхгофа — статья в интернет-журнале ЭЛЕКТРОН, где подробно с примерами расчетов и моделирования на компьютере изложены эти основопологающие законы элеектротехники.

Видеоурок по расчету цепей с помощью первого и второго закона Кирхгофа.

 

Хотите подробностей? Посмотрите это видео, поясняющее второй закон Кирхгофа:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

 

Добавить комментарий

Второй закон Кирхгофа. Второе правило Киргофа для расчета цепей постоянного тока

Второй закон Кирхгофа

• Алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре.
• Алгебраическая сумма падений напряжений в замкнутом контуре равна сумме действующих ЭДС в этом контуре. Если в контуре нет источников электродвижущей силы, то суммарное падение напряжений равно нулю.
• Алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю.
• Алгебраическая сумма падений напряжений на пассивных элементах равна алгебраической сумме ЭДС и напряжений источников тока, действующих в этом контуре.

Т.е. падение напряжения на R1 со своим знаком плюс падение напряжения на R2 со своим знаком равно напряжение источника эдс 1 со своим знаком  плюс напряжение на источнике электродвижущей силы 2 со своим знаком. Алгоритм расстановки знаков в уравнениях по закону Кирхгофа описан на отдельной странице.

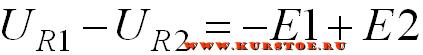
Уравнение для второго закона Кирхгофа

Составлять уравнения по второму закону Кирхгофа можно разными способами. Самым удобным считается первая формула.

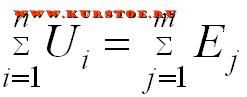
Так же можно уравнения писать в таком виде.

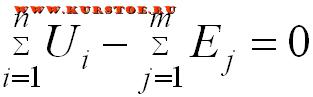
Физический смысл второго закона Кирхгофа

Второй закон устанавливает связь между падением напряжения на замкнутом участке электрической цепи и действием источников ЭДС на этом же замкнутом участке. Он связан с понятием работы по переносу электрического заряда. Если перемещение заряда выполняется по замкнутому контуру, возвращаясь в ту же точку, то совершенная работа равна нулю. Иначе бы не выполнялся закон сохранения энергии. Это важное свойство потенциального электрического поля описывает 2 закон Кирхгофа для электрической цепи.

Второй закон Кирхгофа

Господа, всем привет!

Сегодня мы рассмотрим второй закон Кирхгофа. Он чуть сложнее, чем первый закон Кирхгофа, который мы уже рассматривали ранее, поэтому я сперва дам общую формулировку, а потом мы постараемся аккуратно разобраться во всем этом деле. 

Итак, второй закон Кирхгофа гласит, что алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Может быть сложновато для восприятия, если вы читаете это в первый раз, не спорю. Но сейчас попробуем разобраться более детально во всем этом. Для начала давайте определим, что же такое контур электрической цепи, где эти самые ЭДС действуют. Пожалуй, это тот случай, когда проще нарисовать картинку, чем объяснять словами. Взглянем на рисунок 1.

Рисунок 1 – Контура в схеме

На нем мы можем видеть три контура: я обозначил их красным, оранжевым и синим цветами. То есть контур –  это некоторая замкнутая часть электрической цепи, состоящая из нескольких ветвей.

То есть что говорит второй закон Кирхгофа? У нас есть большая и сложная электрическая схема. В ней много различных контуров. Будем рассматривать подробно один из этих контуров, любой на выбор. И вот если мы в этом контуре сложим ЭДС всех источников, какие там есть, то их сумма будет равна сумме падений напряжения на всех сопротивлениях этого контура. И это верно для любого контура в нашей схеме. Довольно интересный факт. И если про первый закон Кирхгофа можно говорить, что он интуитивно очевиден, то здесь, вообще говоря, это не совсем так. А поскольку он не очевиден на первый взгляд, тем больше поводов показать его верность математически.

Господа, прошу обратить внимание на рисунок 2. На нем изображен один из контуров какой-то сложной электрической схемы.

Рисунок 2 – Контур схемы

Почему он именно такой, можете вы спросить? Да просто так! Я рисовал его так, как подскажет фантазия в тот момент. Вы можете смело заявить, что ваша фантазия лучше и нарисовать какой-либо другой контур с другими компонентами. Потом повторите все действия, которые я буду производить над этим контуром, и в конечном счете у вас должен получиться точно такой же результат, как и у меня.

Первым делом давайте зададимся направлением обхода контура. Это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода контура у нас по часовой стрелке, и я показал его синей стрелочкой на рисунке 2.

Следующим шагом нам надо расставить предполагаемое направление токов в каждой ветви. Тут опять же все целиком отдается вашей фантазии. На данном этапе можно рисовать любое направление токов. Если мы угадали – отлично, если нет – в конце всех расчетов получим ток с другим знаком. Я расставил на рисунке 2 все токи черными стрелками и рядом с ними подписал их величины (I

1…I₄).

А теперь внимание, господа. Пришло время вспомнить то выражение, ради получения которого я написал предыдущую статью. На всякий случай, если вдруг кто забыл, напоминаю его

Оно означает, что если потенциалы на концах ветви равны φ₁ и φ₂, то их разность равна ЭДС источника в ветви минус произведение тока в ветви на сопротивление в ветви.

Применим это выражение для каждой ветви нашего контура, изображенного на рисунке 2. Поскольку у нас в контуре четыре ветви, то всего мы получим четыре уравнения. Резонный вопрос – а как быть со знаками при записи этих уравнений? Правила тут два.

• Если направление работы источника напряжения совпадает с направлением обхода контура, то берем его со знаком плюс. Если не совпадает – со знаком минус. Совсем просто: если стрелка в источнике напряжения совпадает со стрелкой обхода, то Е в уравнении пишется без изменения знака, если стрелки в разные стороны – то надо поставить минус перед E.
• Если направление тока, которое мы сами выбрали чуть раньше, совпадает с направлением обхода, то в нашем уравнении перед произведением тока на сопротивление так и остается знак минус. Если они направлены в разные стороны, то знак минус меняем на плюс.

Пользуясь этими простыми правилами, запишем уравнения для каждой ветви.

Очевидно, что если в цепи нет источника ЭДС, то у нас не будет первого слагаемого в правой части. А если нет сопротивления, то не будет второго слагаемого в правой части. Собственно, это и видно из составленных уравнений.

Господа, надеюсь вы помните, что с уравнениями в одной системе можно творить всякие интересные штуки? Например, можно все их сложить между собой (правые и левые части). Легко заметить, что при сложении всех этих четырех уравнений в левой части будет нолик, то есть все потенциалы волшебным образом самоликвидируются. Сделаем это! Получим

А теперь давайте перенесем все слагаемые с ЭДС в одну сторону, а с током и сопротивлением – в другую. Имеем

А имеем мы, собственно, второй закон Кирхгофа. Все честно, как я и писал в начале – алгебраическая сумма ЭДС, действующих в контуре равна алгебраической сумме падений напряжения в ветвях контура. Надеюсь, господа, после статьи про закон Ома у вас не возникает вопросов, почему произведение тока на сопротивление – это падение напряжения на сопротивлении?  Если возникает – срочно, очень срочно, прямо сейчас пройдитесь по этой ссылке и разрешите эти вопросы!

А что же все-таки тут понимается под словом алгебраическая сумма? Это словосочетание нам уже встречалось. Это значит, что складывать надо с учетом знака. А как выбирать правильно этот самый знак? Господа, взгляните еще разок на рисунок 2. Там у нас задано направление обхода контура и направление токов. Все это мы выбирали (я бы даже сказал придумывали) сами. Ну и направление работы источника еще видно по его графическому изображению.

Так вот, если направление работы источника ЭДС совпадает с направлением обхода контура, то мы ему приписываем знак плюс, а если не совпадает – минус. Аналогично и для правой части. Если направление тока совпадет с направлением обхода, то мы пишем произведение тока на сопротивление со знаком плюс. Иначе – со знаком минус.

Специально для труЪ-математиков привожу запись второго закона Кирхгофа с использованием хитрых значков суммирования. Вне всякого сомнения, если вы будете использовать эту запись, то произведете впечатление человека, который шарит в теме!

Здесь у нас N источников c ЭДС E_i и M ветвей с сопротивлениями R_j и токами I_j. Разумеется, суммирование идет все так же с учетом знаков.

Может возникнуть резонный вопрос: «Как же так? Получается, я сам все придумываю: и направление обхода, и направление токов и это значит, что знак может получиться любой. Поверну стрелку тока в другую сторону и сразу знак у слагаемого поменяется! Но ведь в реальной схеме токи всегда текут в своем направлении вне зависимости от того, что я там нарисую на листочке! Какое-то противоречие!» Господа, вопрос весьма справедливый. Но предлагаю разобраться в нем в следующей статье. Сохраним некоторую интригу на текущий момент, как принято во всяких этих сериальчиках . А сейчас – спасибо, что прочитали статью, огромной вам всем удачи, и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Формулы законов Кирхгофа

Законы Кирхгофа применяют для составления систем уравнений из которых находят силы тока, которые текут в элементах рассматриваемой цепи.

Любую точку цепи, в которой сошлись три или более проводников с токами называют узлом.

Формула первого закона Кирхгофа (правило узлов)

   

Выражение (1) означает, что алгебраическая сумма токов в любом узле цепи (при учете знаков токов) равна нулю. Знаки токов выбирают произвольно, но при этом следует считать, например, все токи, входящие в узлы положительными, тогда все токи, исходящие из узлов отрицательными. При решении одной задачи важно не путать знаки. Для того, чтобы не допускать ошибок со знаками при составлении суммы токов, часто на схемах силы токов изображают стрелками с направлениями от узла или к узлу.

Первый закон Кирхгофа — следствие закона сохранения заряда. Так как при постоянном токе никакая точка проводника (или участок цепи) не могут накапливать заряд. В противном случае токи не были бы постоянными.

Формула второго закона Кирхгофа (правило контуров)

   

Формула (2) означает, что произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура.

Направление положительного обхода выбирают для всех контуров одинаковым в одной задаче. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).

Втрое правило Кирхгофа является следствием обобщенного закона Ома.

Примеры решения задач по теме «Законы Кирхгофа»

Понравился сайт? Расскажи друзьям!

Второе правило Кирхгофа, теория и примеры

Второе правило Кирхгофа – это один из приемов, который применяют для упрощения расчетов параметров сложных разветвленных цепей постоянного тока. Электрические цепи постоянного тока могут иметь в своем составе большое число сопротивлений, источников тока, множество замкнутых контуров и узлов. Параметры цепи постоянного тока любой сложности можно вычислить, если применять законы Ома и законы сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов, с их помощью можно значительно упростить процедуру написания уравнений, связывающих силы тока, сопротивления и электродвижущие силы (ЭДС) для рассматриваемой цепи.

Первое правило Кирхгофа называют правилом узлов. Оно предназначено для написания уравнения для токов, которые сходятся в узле цепи.

Второе правило Кирхгофа относится к замкнутым контурам, которые выделяют в разветвленной цепи. Это правило еще называют правилом контуров.

Формулировка второго правила Кирхгофа

Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В виде формулы второй закон Кирхгофа записывают как:

   

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа — это следствие закона Ома.

Количество независимых уравнений, получаемых при использовании правил Кирхгофа

Применяя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже рассмотренных контуров. Число независимых контуров () равно:

   

где – число ветвей в цепи; – количество узлов.

Количество независимых уравнений, которые дадут первое и второе правила Кирхгофа равно ():

   

Вывод: количество независимых уравнений, полученных с использованием обоих правил Кирхгофа равно числу разных токов в рассматриваемой цепи.

Примеры решения задач

1.2. Законы Кирхгофа

Ранее были рассмотрены законы Ома для участка цепи и замкнутой цепи с одним источников э.д.с.

Сложная электрическая цепь, содержащая несколько источников э.д.с. и замкнутых контуров, не может быть рассчитана только с использованием законов Ома. Рассчитать и проанализировать сложную цепь можно с помощью двух законов Кирхгофа (сам Кирхгоф и некоторые современные специалисты называют эти законы «правилами», поскольку они являются следствием закона сохранения энергии применительно к электрическим цепям).

Для понимания формулировок и использования этих законов необходимо напомнить основные термины, относящиеся к электрическим цепям.

Электрическая цепь – это совокупность элементов, создающих пути для протекания электрических токов. Основными элементами электрической цепи являютсяисточники электроэнергии, преобразующие механическую, химическую и другие виды энергии в электрическую, иприемники, преобразующие электрическую энергию в другие виды: тепловую (резисторы), механическую (электродвигатели), химическую (зарядка аккумуляторов) и др. Кроме источников и приемников, элементами электрической цепи являются соединительные провода, электроизмерительные приборы, коммутирующие (переключающие) устройства, аппаратура защиты, автоматики и др.

Электрический узел – это часть электрической цепи, в которой сходится не менее трех ветвей (токов).

Ветвь–участок цепи между двумя узлами, на всем протяжении которого ток один и тот же.

Контур–замкнутая часть схемы, которая представляет собой неразветвленную цепь, если отключить все не входящие в нее ветви.

Первый закон Кирхгофа

На рисунке 5 показан электрический узел, в котором сходятся n= 5 ветвей с токами, часть из которых направлены к узлу, а часть – от него.

Первый закон Кирхгофав первой редакции читается следующим образом:алгебраическая сумма токов в узле равна нулю, то есть

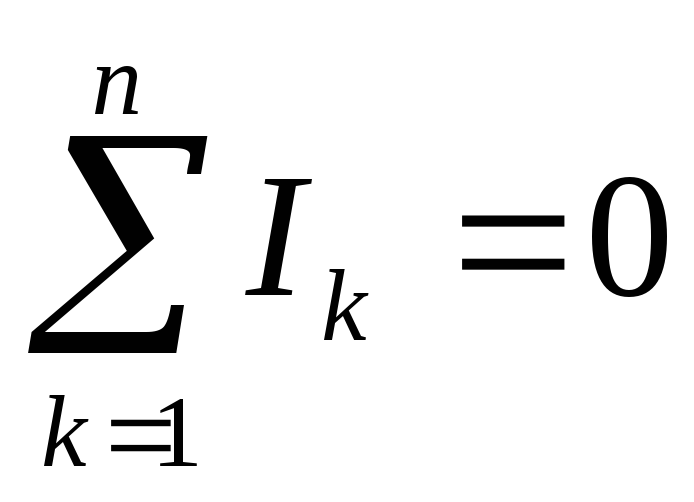
(8)

.

Вуравнении (8) токи, направленные к узлу, подставляют обычно со знаком «+», а от узла – со знаком «» (можно и наоборот).

Применительно к узлу, показанному на рисунке 5, равенство (8) записывается в свернутом виде:

или в развернутом:

.

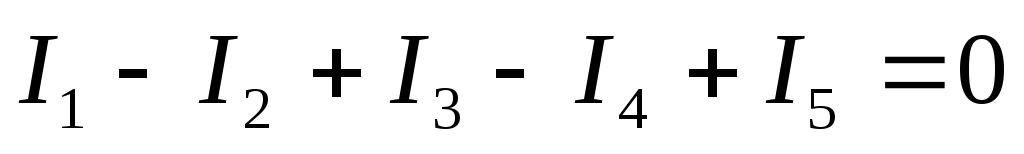Е

(9)

сли перенести в последнем равенстве отрицательные токи в правую часть, то получим: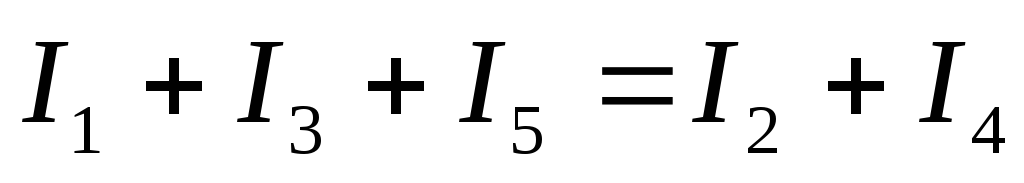

.

Из равенства (9) вытекает вторая редакция первого закона Кирхгофа:

Сумма токов, входящих в узел, равна сумме токов, выходящих из узла.

Справедливость первого закона Кирхгофа можно подтвердить рассуждением «от противного». Если предположить, что в узел в каждый момент времени притекает больше зарядов, чем вытекает (или наоборот), то электрические потенциалы узлов все время будут изменяться, а, следовательно, будет изменяться и распределение токов в элементах схемы, что практически не наблюдается и противоречит здравому смыслу.

Второй закон Кирхгофа

На рисунке 6 показана часть сложной электрической цепи в виде замкнутого контура, состоящего из m= 5 ветвей и содержащегоn= 3 источников э.д.с.

Второй закон Кирхгофачитается следующим образом:в замкнутом электрическом контуре алгебраическая сумма напряжений равна нулю (первая редакция).

В этой формулировке следует различать напряжение как падение напряжения, создаваемое током I_k k-той ветви в сопротивлении R_k этой ветви, и напряжение источника ЭДС, которое равно величине этой ЭДС, но направлено (как разность электрических потенциалов внутри источника) от положительного зажима к отрицательному, то есть встречно с направлением ЭДС.

В показанном на рисунке 6 контуре токи ветвей создают падения напряженияI_kR_k, которые при заданном направлении обхода берутся со знаком «+», если направление токаI_kсовпадает с направлением обхода, и со знаком «», если направление тока встречно с направлением обхода. Что касается напряжений (разностей потенциалов) на зажимах источников ЭДС Е_k, то необходимо учитывать, что потенциал на положительном зажиме источника выше, чем на входном, а величина этихнапряжений(а непадений напряжений!) равна по абсолютному значению соответствующей э.д.с. Е_k. С учетом этогонапряжение источникаберется со знаком «», если направление э.д.с. совпадает с направлением обхода, и со знаком «+», если направление обхода направлено встречно с направлением э.д.с.

Рис. 6

П

(10)

рименительно к контуру (рис. 6), согласно приведенной выше формулировке второго закона Кирхгофа, можно записать: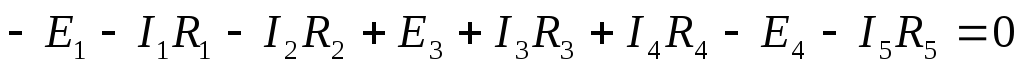

П

(10а)

еренесем напряжения источников э.д.с. в правую часть равенства (10):

В правой части равенства (10а) оказалась алгебраическая сумма э.д.с., а не напряжений источников. В результате получается вторая редакция второго закона Кирхгофа: в замкнутом контуре алгебраическая сумма э.д.с. равна алгебраической сумме падений напряжения в ветвях, образующих этот замкнутый контур, то есть:

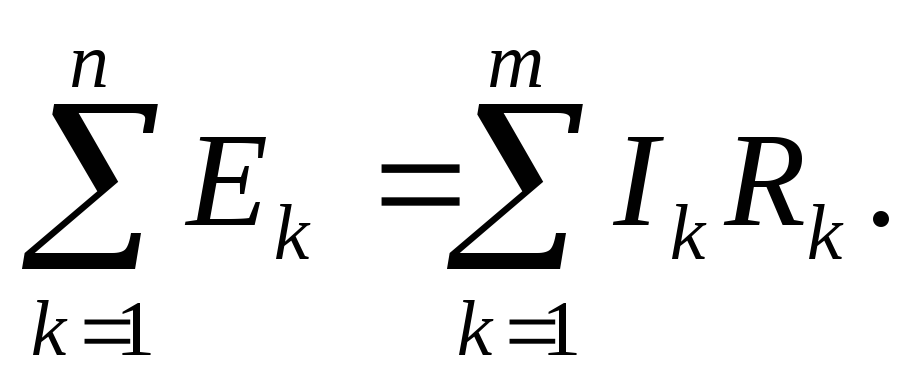
(11)

Применительно к контуру (рс. 6) равенство (11) примет вид

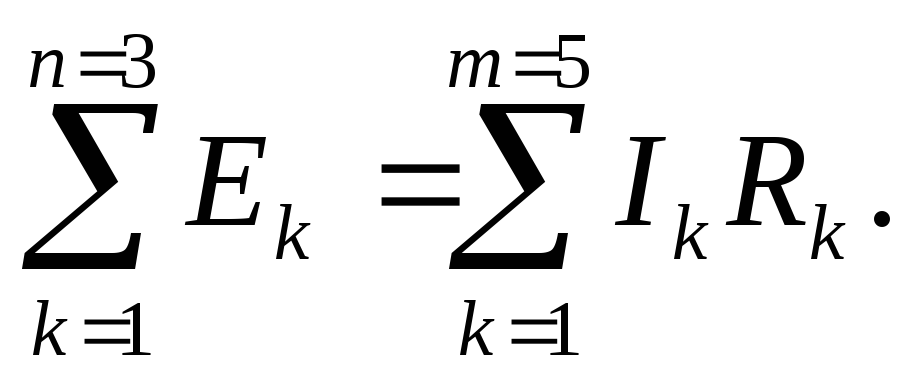
(11а)

В такой формулировке, где напряжения источников заменены на э.д.с. источников, при обходе контура э.д.с. берется со знаком «+», если она совпадает с направлением обхода, и со знаком «-», если она действует встречно (как это следует из равенства (10а)).

Вторая формулировка закона Кирхгофа (10а) и (11) получила наибольшее применение на практике по сравнению с первой (10).