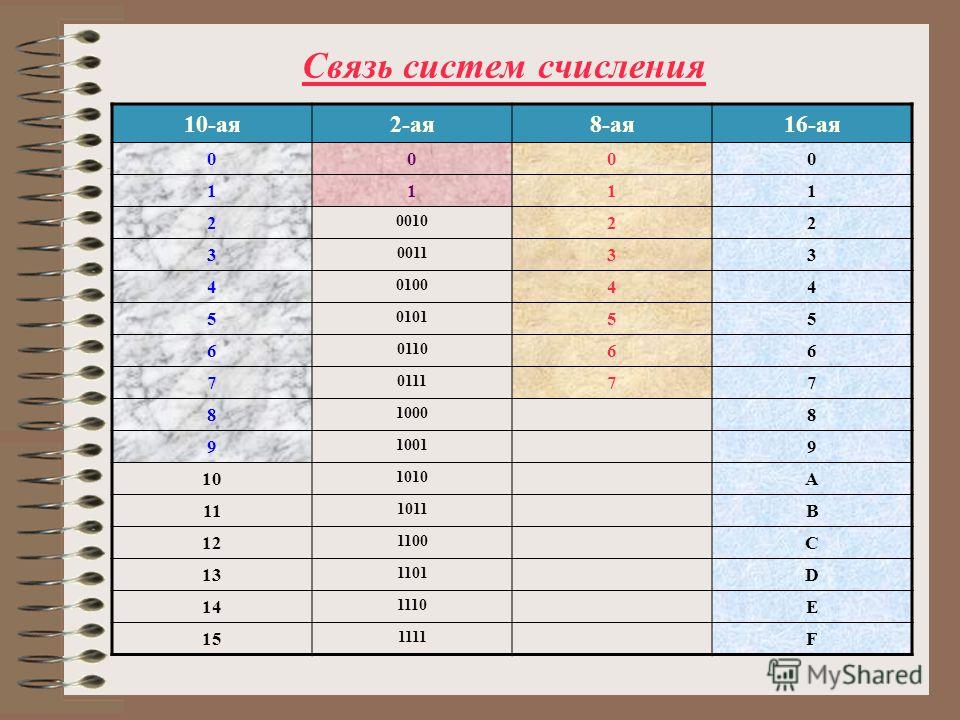
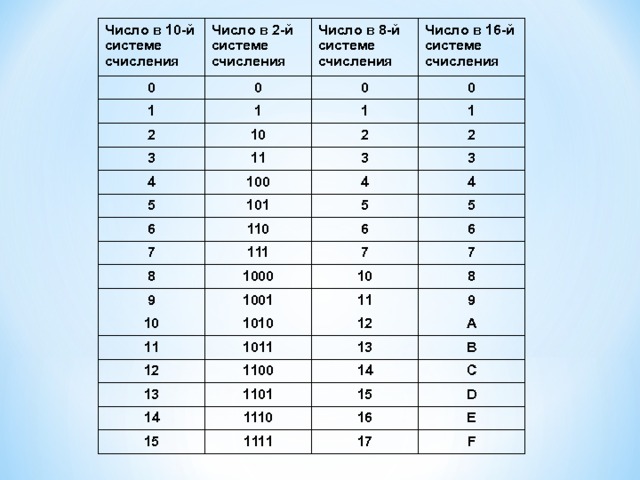
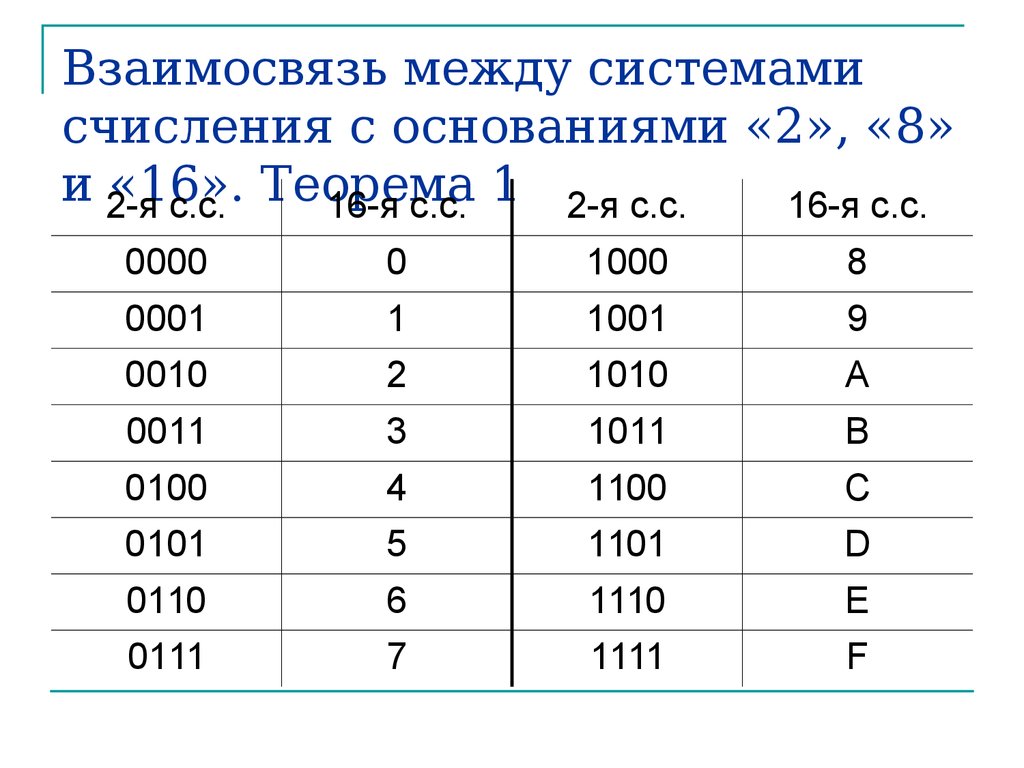
2 система счисления: Двоичная система счисления — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Как объяснить двоичную систему счисления детям

Как компьютер считает

Когда в древности люди только изобретали счёт, они, как сейчас маленькие дети, считали на пальцах. Пальцев на руках – десять, поэтому и система счисления у нас – десятичная. Однако наша система счёта компьютеру не слишком-то понятна: ему ближе двоичная. У компьютера нет десяти пальцев, но, с другой стороны, и двух тоже нет. Откуда тогда взялась двоичная система, что это за ноль и единица, которыми думает компьютер? И как из них получаются обычные, понятные цифры?

Для того чтобы в общих чертах понять, как думает компьютер, начнём с самого начала. Компьютер, по сути, – это много всякой электроники, собранной вместе в правильном порядке. А электроника (до того, как к ней добавили программу) понимает только одно: включена она или выключена, есть сигнал или нет сигнала.

Обычно «есть сигнал» обозначают единицей, а «нет сигнала» – нулём: отсюда и выражение, что «компьютер говорит на языке нулей и единиц».

Этот язык нулей и единиц называют ещё двоичной системой счисления – потому что в ней всего две цифры. Наша привычная система счисления – десятичная, в ней десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Но есть и множество других – восьмеричная, пятеричная, одиннадцатиричная и какая угодно ещё.

У нас с вами нет цифры «десять», правда? Число 10 состоит из двух цифр – 1 и 0.

Точно так же в пятеричной системе счисления не будет цифры «5», только 0, 1, 2, 3 и 4.

Посчитаем в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100 (!!!), 101, 102 и так далее. Можно сказать, что как система счисления называется, такой цифры в ней и нет. В нашей десятичной нет цифры «10», в пятеричной нет цифры «5» (и всех, которые после неё), в восьмеричной – «8» и так далее.

А в шестнадцатиричной «16», например, есть! Поэтому нам шестнадцатиричную систему понять ещё сложнее. Давайте посчитаем в шестнадцатиричной:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…97, 98, 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2… F7, F8, F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 10A, 10B, 10C и так далее.

Двоичная система счисления, впрочем, тоже выглядит странновато для непривычного взгляда:

0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…

Вот примерно такими числами и думает компьютер где-то внутри себя. Но человеку такими числами думать совершенно неудобно, поэтому мы преобразуем числа из двоичной в более удобную систему счисления.

В компьютерных программах часто используют восьмеричную и шестнадцатиричную системы: компьютеру легко их понять (потому что 8=2*2*2, 16=2*2*2*2, а с двоичной системой компьютер знаком изначально), а для людей это удобно, потому что поближе к привычной десятичной.

Как переводить числа из одной системы счисления в другую

Чтобы понять принцип, будем, как мы с вами любим, разбираться на конфетах.

И на конфетах мы с вами будем переводить число 33 в восьмеричную систему счисления. Мы решим, что единицы – это сами конфеты, а десятки – это коробки, в каждой из которых лежит по десять конфет. Вот и получится, что 33 – это 3 коробки по 10 конфет и ещё 3 конфеты где-то сбоку.

Но мы переводим наше конфетное богатство в восьмеричную систему счисления, а это значит, что нам надо вытряхнуть все конфеты из коробочек по 10, сложить в коробочки по 8 и посмотреть, что из этого выйдет.

Из 33 получится 4 полных восьмеричных коробочки и 1 конфета останется сама по себе, так как 33/8=4 (ост. 1). То есть 33=8*4+1 – так в восьмеричной системе счисления получается число 41.

33 в десятичной – это 41 в восьмеричной. Это одно и то же число, просто разложенное по разным коробочкам, переведённое в разное основание.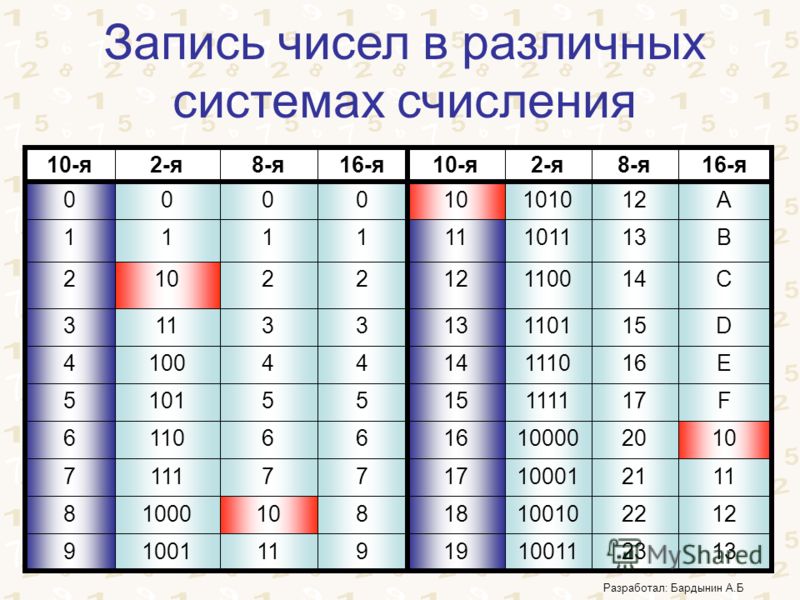

Количество конфет не поменялось, мы просто считали их по-разному!

Двоичная система, как мы уже выяснили, более странная и непривычная для человеческого взгляда. Давайте попробуем перевести 33 в двоичную – получится аж 16 коробочек по 2! И что же делать? Писать 16 как-то странно, помня о том, что в двоичной системе есть только ноль и единица, а шестёрки, которая нам нужна для шестнадцати, совершенно точно нет!

Посмотрим на нашу десятичную систему. В ней мы считаем десятки – 10, 20, 30, 40, 50, 60, 70, 80, 90 – а когда у нас набирается десять десятков, мы достаём большую коробку – 100.

У нас 100 – это 10*10, 1000 – 10*10*10, 10 000 – 10*10*10*10 и так далее. Для других систем счисления это работает точно так же! В восьмеричной системе 100=8*8, 1000=8*8*8; в двоичной 100=2*2, а 1000=2*2*2; а в шестнадцатиричной (есть и такая, помните?) 100=16*16, 1000=16*16*16.

Здесь нам пригодятся степени. Если вы их ещё не проходили в школе, не пугайтесь, степени – это очень просто. Число в степени – это число, сколько-то раз умноженное на само себя. То есть 5³=5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 8⁵=8*8*8*8*8 (восемь в

пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).

Если мы вспомним про наши 10 000=10*10*10*10 в десятичной и 1000=8*8*8 в восьмеричной, то можно легко заметить, что сколько нулей, столько раз и умножаем на само себя. Другими словами, количество символов в числе минус один – это степень, в которую надо возвести основание. В числе 1000 у нас четыре символа, значит умножать надо 4–1, то есть 3 раза. Если основание 10, то тысяча – это 10, три раза умноженная сама на себя: 10*10*10. Если основание 8, то тысяча – это 8, три раза умноженная сама на себя: 8*8*8.

Обо всём этом мы заговорили, пытаясь перевести 33 в двоичную систему.

Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.

Для перевода из десятичной системы в двоичную удобно помнить степени двойки. Даже можно сказать, что без этой хитрости со степенями мы устанем, умаемся и немножко сойдем с ума. А степени двойки выглядят как-то так:

Теперь, глядя на табличку, мы видим, что 33=2⁵+1, то есть 33=2*2*2*2*2+1. Вспоминаем – сколько раз умножаем, столько будет нулей – то есть наше 2*2*2*2*2 в двоичной системе будет 100000. Не забудем оставшуюся в стороне единичку, и получится, что 33 в десятичной – это 100001 в двоичной. Правильно и красиво это записывают так:

33₁₀=100001₂

Давайте (чтобы совсем хорошо понять) переведём в двоичную систему число 15.

В первую очередь – смотрим в табличку.

а) Какое самое близкое к 15 число в ней? Нет, 16 не подходит, оно больше, а нам нужно самое близкое, которое меньше. Получается, что это 8, то есть 2³, то есть 2*2*2.

б) Восемь конфет из 15 разобрали, осталось – 15-8 – семь. Какое ближайшее число из таблички? Нет, восемь снова не подойдет, см. выше. Подойдет четыре, то есть

2², то есть 2*2.

в) Четыре из семи конфет разобрали, осталось – 7-4 – три. Из таблички понимаем, что самое близкое число – 2, то есть 2¹, то есть просто 2.

г) Три минус два – осталась 1 конфета, тут уже табличка не понадобится. В таблички такого рода можно не смотреть, когда ваш остаток меньше основания, а наша единица точно меньше двойки.

Собираем всё найденное в табличке вместе: 15=2³ + 2² + 2¹ + 1, оно же: 15=2*2*2 + 2*2 + 2 + 1.
В двоичной системе 2*2*2=1000, 2*2=100, 2=10, помните? И у нас получается 1000+100+10+1, то есть 1111.

Итак,

15₁₀=1111₂

Когда просто смотришь на все эти шаги, кажется, что это просто свалка из Кучи Разных Странно Написанных Цифр. И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.

И наоборот это тоже работает! Например, число 11010101₂ – как из него сделать понятное десятичное? Точно так же, при помощи таблички. Пойдем с конца:

1*2

0+0*2¹+1*2²+0*2³+1*2⁴+0*2⁵+1*2⁶+1*2⁷=

1*1+0*2+1*4+0*8+1*16+0*32+1*64+1*128=

1+0+4+0+16+0+64+128=213

То есть,

11010101₂= 213₁₀

Вот примерно так компьютер понимает привычные нам числа.

Когда смотришь на это в первый раз, кажется, что это, во-первых, совершенно непостижимо, а, во-вторых, вообще не сработает. Поэтому сейчас мы с вами сделаем немножко математической магии, чтобы убедиться, что системы счисления – это такая же реальная вещь, как, например, задача «раздать пятерым детям пятнадцать печенек поровну».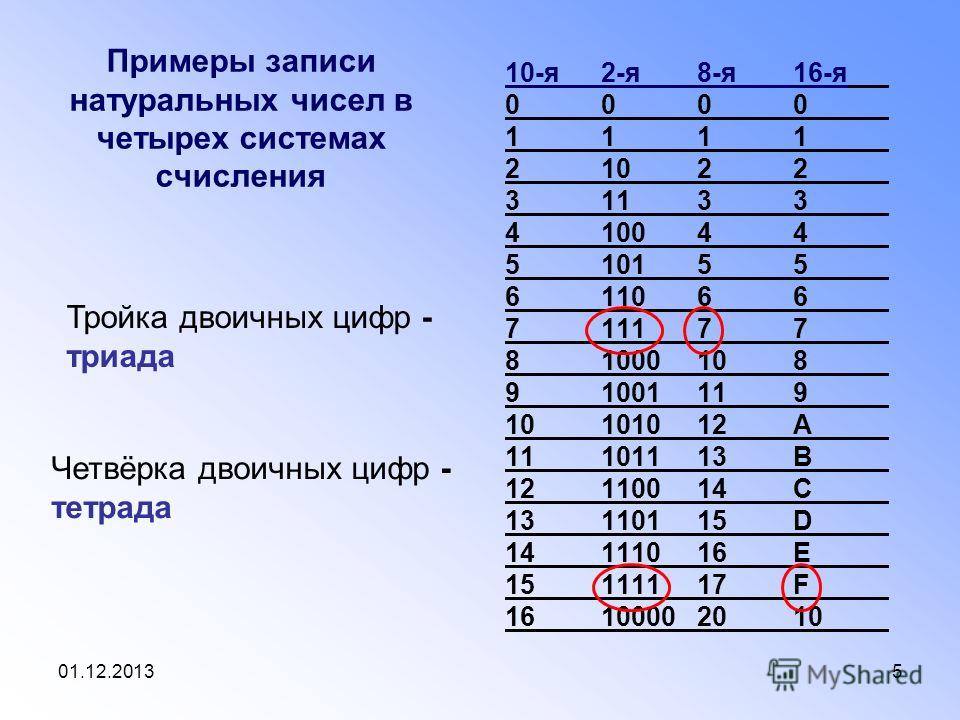

Итак, возьмем пример 15+6 и решим его в разных системах счисления. Понятно, что в нашей, десятичной, получится 21. А что выйдет, например, в восьмеричной?

Переводим 15 в восьмеричную систему счисления. Первый шаг у нас при переводе в другую систему – посмотреть в табличку степеней. 8² – это уже 64, и в 15 оно точно уже никак не влезет, поэтому берем 8¹ – то есть просто 8. 15–8=7, оно меньше нашего основания 8, поэтому с ним мы ничего не делаем.

Итак, получилось, что 15=8¹+7.

В восьмеричной системе логика точно такая же, как, например, в двоичной: 8

3 – это 1000, 8² – это 100, 8¹ – это 10. Получилось, что:

15₁₀=17₈

Напомню, наш пример был 15+6. 15 мы перевели в восьмеричную систему, как же перевести 6? Она меньше 8, нашего основания, поэтому ответ – оставить как есть. Наш пример сейчас выглядит так:

15₁₀+6₁₀=17₈+6₈

Теперь мы будем складывать в восьмеричной системе счисления.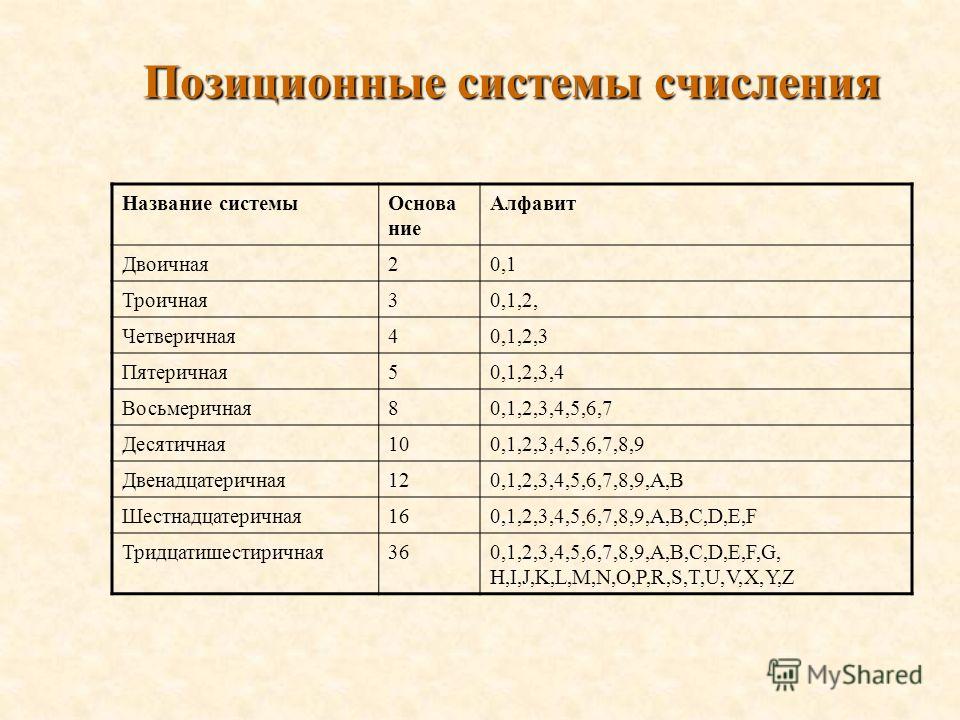 Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.

Когда мы считаем в десятичной системе, по сути, мы делаем так:

15+6=15+5+1=20+1=21

Попробуем проделать тот же фокус в восьмеричной системе:

17₈+6₈=17₈+1₈+5₈=20₈+5₈=25₈

Почему 17+1? Потому что 7+1=8, а 8 – это наш десяток! В восьмеричной системе 7+1=10, а значит, 17+1=20. Если на этом месте ваш мозг начинает бить тревогу и рассказывать, что здесь что-то не так, вернитесь в начало статьи, где мы с вами считали в разных системах счисления.

Теперь наш пример выглядит как

15₁₀+6₁₀=17₈+6₈=25₈

Переведем 25

8 обратно в нашу систему счисления. В десятичной мы бы, увидев число 25, могли сказать, что в нём две десятки и пять единиц.

В восьмеричной, как вы, наверное, уже догадались, число 25₈ – это две восьмерки и пять единиц. То есть 25₈=2*8+5=21₁₀.

Итак, наш пример целиком:

15₁₀+6₁₀=17₈+6₈=25₈=21₁₀

Получилось точно такое же 21, какое вышло у нас в самом начале, когда мы посчитали 15+6 привычным нам способом в десятичной системе.

Арифметические правила не меняются от того, что мы выбрали другую систему счисления.

Поэтому и компьютер, переводя всё в нули и единицы, которые для нас выглядят непонятно и бессмысленно, не теряет при этом информацию, которую мы ему дали, и может, посчитав в удобной ему форме, выдать результат, переведя его обратно в привычный нам вид.

Кодирование информации в информатике

Мы обсуждили, как компьютер понимает числа. Они получаются из других чисел – двоичных, которые компьютер понимает. А как быть с буквами? Картинками? Играми?

Какие вообще бывают виды кодирования информации в науке обращения с компьютером – информатике?

Тут надо на секунду задуматься, как общаются сами люди.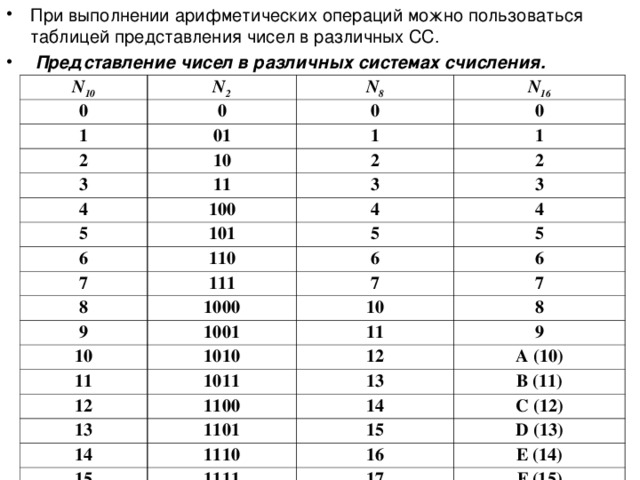 Мы используем слова, из слов делаем предложения, из предложений – текст, рассказ, диалог. Но чтобы сделать слово, мы используем буквы, которых всего-навсего 33 штуки!

Просто представьте: все книги, которые вы когда-либо читали – это лишь разные сочетания одних и тех же 33 букв.

Но мы делаем из букв слова по определённым правилам, а словами обозначаем предметы, свойства, действия, эмоции, фантазии. Буквы – это кубики, из которых мы строим слова. А слова – это код, которым мы обозначаем всё, что встречается в нашей жизни, чтобы потом об этом кому-нибудь рассказать.

Точно так же происходит и с компьютером. При помощи цифр мы объясняем компьютеру, что у него есть монитор, мышка, клавиатура и другие детали, рассказываем, как с ними обращаться и как реагировать, когда что-то делаем мы.

Но сейчас мы с вами поговорим о более конкретных и практических кодах. И начнём с того, как компьютер понимает буквы.

Раз компьютер знает только цифры, значит и буквы он видит через цифры.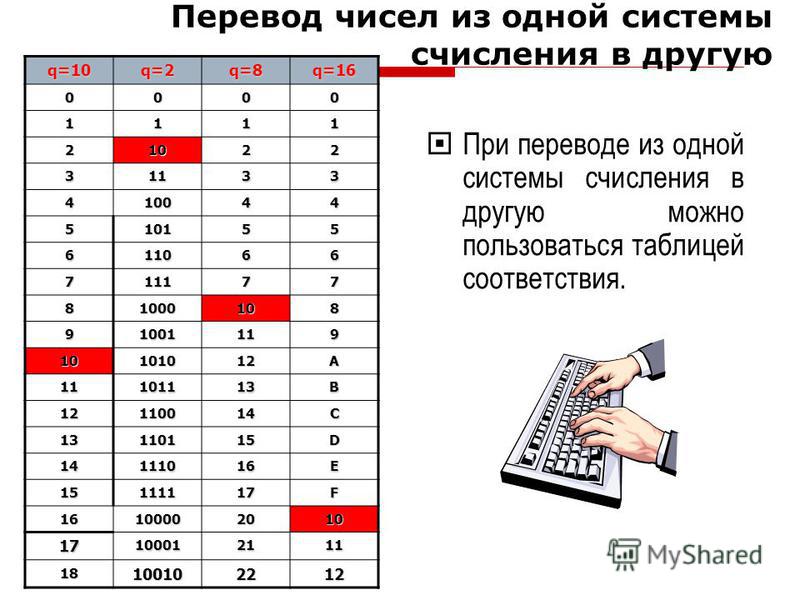 Это, примерно, как если бы мы букву А записали как 1, Б как 2, В как 3, и так далее.

Примерно такие таблицы (только больше и сложнее) компьютер и использует, чтобы понимать буквы.

Представьте себе: кто-то записал анекдот на компьютер и прислал вам. Вы открываете документ, а там ничего непонятно. Примерно вот так:

Р§РµР”РѕРІРµРє СЃРµР№С‡Р°СЃ СѓРІРёРґРёС‚ Р”РёС€СЊ С‚Рѕ, С‡С‚Рѕ РѕР¶РёРґР°РµС‚ СѓРІРёРґРµС‚СЊ.

Это компьютер ошибся с кодировкой. Что такое кодирование в информатике? Так обычно называют присвоение каждому символу (букве, знакам препинания и так далее) определённого кода согласно специальной табличке. Кодировка – это способ, которым зашифровывает и расшифровывает буквы компьютер, можно сказать, табличка, которую он выбирает. Табличек у него на такой случай много, и надо знать, по какой расшифровывать, иначе получится белиберда.

Давайте немножко побудем компьютером. У нас с вами будет две таблички: в одной сначала будет идти алфавит, а потом знаки препинания, в другой – наоборот.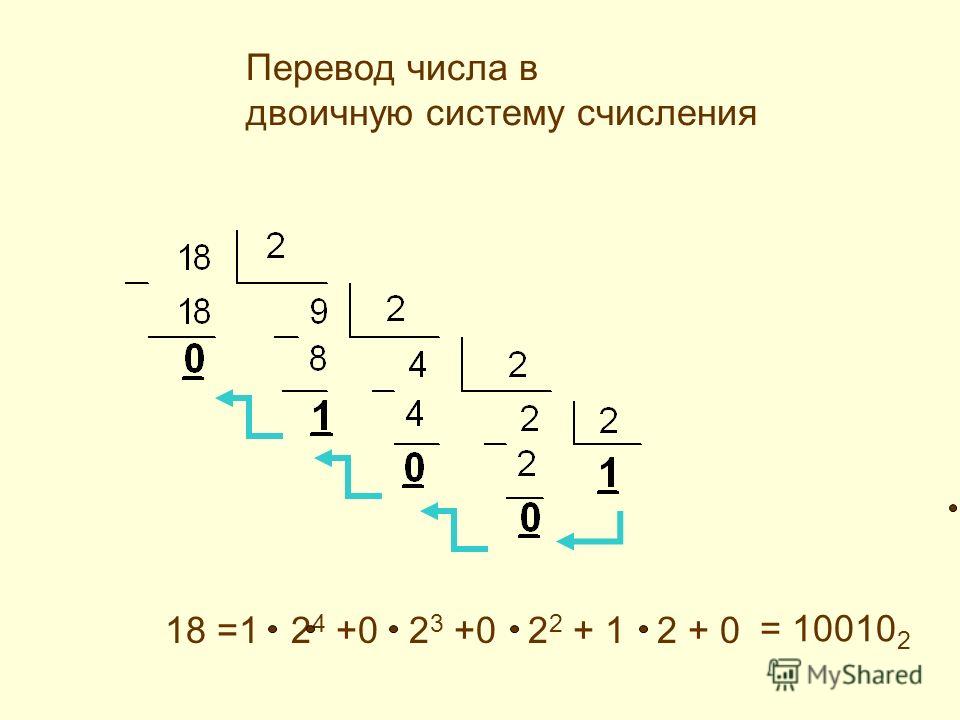

Кодировочная Таблица 1:

Кодировочная Таблица 2:

Зашифруем с вами фразу «Пароль – три зелёных свистка». Зашифровывать мы будем по первой таблице, а расшифровывать – по второй.

Первая буква – П. В первой таблице у неё номер 17. Дальше буква А. У неё номер 1. Продолжите сами и проверьте себя, правильно ли у вас получится!

А получилась в итоге вот такая строчка:

17-1-18-16-13-30 38 20-18-10 9-6-13-6-15-29-23 19-3-10-19-20-12-1

Теперь попробуем расшифровать её при помощи второй таблицы.

Во второй таблице цифра 17 у буквы И, цифра 1 у точки и так далее (расшифруйте сами).

У нас получилось:

И.йзех э лйв(жфо к?вклд

Итак, результат, во-первых, непонятный, а, во-вторых, совершенно не похож на ту фразу, которую мы хотели передать.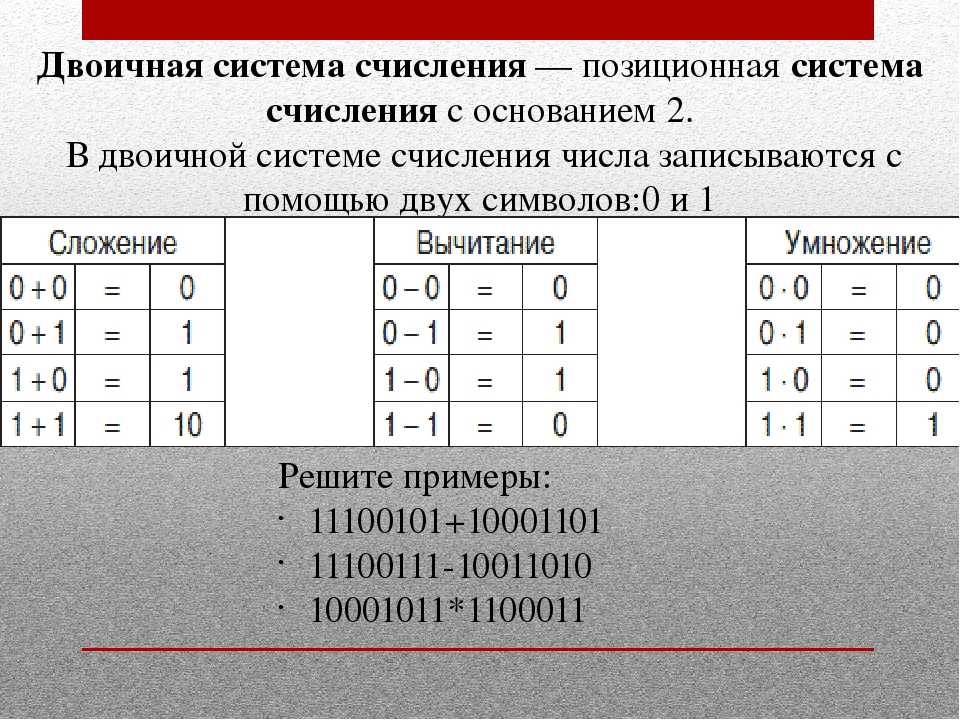 И получилось это из-за того, что таблица для шифровки и таблица для дешифровки не совпали.

Точно так же с фразой и с текстом вроде «Р§РµР”РѕРІРµРє СЃРµР№С‡Р°СЃ» – так получается, когда компьютер пытается расшифровать текст не по той таблице, по которой он был зашифрован. Ещё в таких случаях говорят, что «в тексте неправильная кодировка». Сам текст от этого не испортился, просто программе где-нибудь в настройках надо указать, какой кодировкой воспользоваться (обычно это utf8, или UNICODE, или как в этом случае Windows-1251).

Давным-давно, когда компьютеры были большими, а жёсткие диски в них –маленькими, придумали кодировку ASCII (читается как «аскИ»).

Это табличка, где зашифрованы буквы латинского алфавита (мы обычно привыкли о них думать, как об английских буквах), знаки препинания и некоторые служебные символы (например, символ, который обозначает, что надо продолжить с нового абзаца).

Когда в компьютерах придумывают что-то новое, однажды бывает очень важно, чтобы кто-то сказал: «А теперь ВОТ ЭТО мы все делаем одинаково». Например, весь вай-фай в мире работает примерно одинаково, поэтому почти любой телефон может подключиться почти к любой точке вай-фай.

Точно так же произошло и с кодировочной таблицей. Мы с вами раньше уже убедились, что она обязательно должна быть одинаковая у отправителя и получателя, и этой одинаковой таблицей стала ASCII аж в 1963 году.

Сначала всё было замечательно, но потом компьютеры стали становиться меньше и удобнее, ими стали пользоваться разные люди, в том числе не знающие английского. А русский, например, алфавит (который также называют «кириллица») в ASCII не входит. Как быть? Куда бежать? И в 1991 году был придуман UNICODE (читается как «Юникод» или «Уникод» – почти как «Универмаг», но не магазин).

Юникод может закодировать очень большое число символов из разных письменностей: китайские иероглифы, математические символы, буквы греческого алфавита, латиницы и кириллицы.

ASCII стала первой частью Юникода, и специальные договоренности в программах позволяют читать при помощи Юникода текст, который был закодирован в ASCII.

Когда вы сохраняете файл в том же «Блокноте», вы можете выбрать кодировку и при выборе заметить, что их гораздо больше, чем мы разобрали в статье.

В заключение давайте поговорим, где какая кодировка нужна.

Обычно выбором кодировки занимаются люди, работающие с компьютерами профессионально – при написании программ, настройки баз данных и т. п. Мы с вами не будем вникать во все тонкости, и рассмотрим этот вопрос в общих чертах:

– Windows-1251

Как видно из названия, это основная кодировка операционных систем семьи Windows. Когда вы точно знаете, что все компьютеры, которые будут работать с файлами, используют Windows – она отличный выбор. Если же нет, могут возникнуть проблемы с невидимыми символами. Потому что Windows-1251 их считает служебными, а многие другие кодировки решают, что это такие буквы непонятные, и в результате случается неразбериха.

– ASCII

Старая, но надёжная. Подойдёт, если ваш текст на английском, а компьютер, где надо открыть файл – очень, очень старый.

– UNICODE

Это рекомендуемая кодировка для всех систем! Если друг прислал вам файл, а у вас в нём кракозябры, попросите его пересохранить файл с кодировкой unicode, и, скорее всего, проблема будет решена.

– UTF-8

Вариант записи того же Юникода. Он специфический, и обычно используется программами при общении внутри себя самих (например, общение программы со своей базой данных).

Итак, кодированием текста в информатике обычно называют способ компьютера перевести текст в понятный ему вид по одной из общепринятых табличек. Если файл был сохранён в одной кодировке, а открыт в другой – обычно получается белиберда вместо текста.

Все компьютеры знают одни и те же кодировки, чтобы понимать файлы, сделанные другими компьютерами, но кодировки существуют разные – под разные цели. Лучше всего сохранять файлы в кодировке UNICODE – так больше всего шансов, что у другого человека этот файл откроется.

Как можно увидеть, криптография – это не только наука про тайны и не только детская игра. У этой науки есть множество простых практических точек приложения, и если ребёнок знаком с её концепциями, то многое, что может испугать, сбить с толку и привести в отчаяние, для него будет просто задачей, к которой надо найти правильное решение.

Двоичная система счисления — презентация онлайн

Похожие презентации:

Двоичная система счисления

Представление информации в двоичной системе счисления

Системы счисления. Двоичное кодирование в компьютере

Двоичная система счисления

Системы счисления. (9 класс)

Системы счисления. Двоичная система счисления

Системы счисления

Двоичная и шестнадцатеричная системы счисления

Системы счисления

1. Двоичная система счисления

LOGO
Компьютер
работает
с числами в
двоичной системе
счисления!!!
Company Logo
Системой счисления
называют определенные
правила записи чисел и
связанные с ними способы
выполнения вычислений.

Company Logo
Десятичная и двоичная
системы счисления
Система счисления, к которой мы все
привыкли, называется десятичной.
Объясняется это название тем, что в ней
используются десять цифр: 0, 1, 2, 3, 4, 5,
6, 7, 8, 9.
Число
цифр
определяет
основание
системы счисления.
Если число цифр — десять, то основание
системы
счисления
равно
десяти.
В
двоичной же системе существует всего две
цифры: 0 и 1. Основание равно двум.
Company Logo

5. Развёрнутая форма записи числа

33310 = 3 • 102 + 3 • 101 + 3 • 10° =
300 + 30 + 3
825710 = 8 • 103 + 2 • 102 + 5 • 101 +
+7 • 10° =
= 8000 + 200 + 50 + 7
Company Logo

6. Перевод двоичных чисел в десятичную систему

1101012
Двойка
внизу
справа
указывает
на
основание системы счисления. Это нужно для
того, чтобы не перепутать двоичное число с
десятичным. Ведь существует же десятичное
число 110101!
Вес каждой следующей цифры в двоичном
числе при продвижении справа налево
возрастает в 2 раза.

Развернутая форма
записи данного двоичного числа выглядит
так:
1101012 = 1 • 25 + 1 • 24 + 0 • 23 +
1 • 22 + + 0 • 21 + 1 • 20 = 5310
Company Logo

7. Перевести числа в десятичную систему счисления

102 =
1002 =
10002 =
100002 =
1000002 =
Company Logo

8. Перевести числа в десятичную систему счисления

1
2
102 = = 2;
1002 =
10002 =
100002 =
1000002 =
Company Logo

9. Перевести числа в десятичную систему счисления

1
2
102 = = 2;
2
1002 = 2 = 4;
10002 =
100002 =
1000002 =
Company Logo

10. Перевести числа в десятичную систему счисления

1
2
102 = = 2;
2
1002 = 2 = 4;
3
10002 = 2 = 8;
100002 =
1000002 =
Company Logo

11. Перевести числа в десятичную систему счисления

1
2
102 = = 2;
2
1002 = 2 = 4;
3
10002 = 2 = 8;
4
100002 = 2 = 16;
1000002 =
Company Logo

12.

Перевести числа в десятичную систему счисления1
2
102 = = 2;
2
1002 = 2 = 4;
3
10002 = 2 = 8;
4
100002 = 2 = 16;
5
1000002 = 2 = 32.
Company Logo

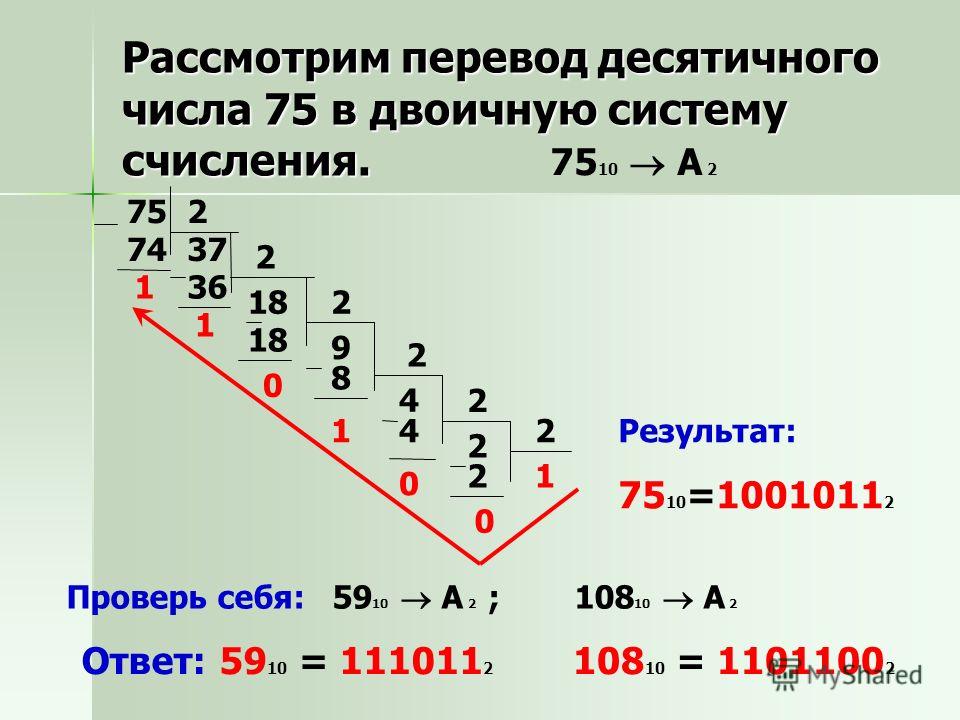
13. Перевод десятичных чисел в двоичную систему

3710=100101
2
Company Logo

14. Арифметика двоичных чисел

0+0=0
0+1=1
1+0=1
1+1=10
0x0=0
0x1=0
1×0=0
1×1=1
Company Logo

15. Арифметика двоичных чисел

011011101
111010110
10010110011
+
Company Logo

16. Арифметика двоичных чисел

1101101
101
1101101
1101101
1000100001
Company Logo

17. Вопросы

1. Дайте определение системы счисления.
2. Что такое развёрнутая форма числа?
3. Как перевести двоичное число в
десятичную систему счисления?
4. Как перевести десятичное число в
двоичную систему счисления?
5. Каковы правила сложения и
умножения двоичных чисел?
Company Logo
Выполните письменно задания:
1.

Переведите десятичные числа 367;
2065; 212 в двоичную систему
счисления.
2. Переведите числа 10110112,
10010101012, 10011111112 в
десятичную систему счисления.
Company Logo

English Русский Правила

СИСТЕМЫ СЧИСЛЕНИЯ — STUDYTRONICS

Десятичная система счисления:-
Системой счисления, которую мы используем в нашей повседневной жизни, является десятичная система счисления. Десятичная система счисления имеет основание 10, так как использует 10 цифр от 0 до 9. В десятичной системе счисления последовательные позиции слева от десятичной точки представляют единицы, десятки, сотни, тысячи и так далее.
Каждая позиция представляет определенную степень основания (10). Например, десятичное число 1234 состоит из цифры 4 в позиции единиц, 3 в позиции десятков, 2 в позиции сотен и 1 в позиции тысяч, и его значение можно записать как 9.0005

Двоичные номера Система

Характеристики бинарных номеров следующие:

Бинарные номеры Система использует две цифры 0 и 1.
Также называется базой 2 численной системы.
Каждая позиция в двоичном числе представляет нулевую степень основания (2).

Последняя позиция в двоичном числе представляет x степень основания (2).

Пример 2x, где x представляет последнюю позицию — 1.

Пример:-
Двоичное число: 101012

Вычисление десятичного эквивалента:-

ПРИМЕЧАНИЕ: 101012 обычно записывается как 10101.

Восьмеричная система счисления

Характеристики восьмеричной системы счисления:

Использует восемь цифр 0,1,2,3,4,5,6,7.
Также называется системой счисления с основанием 8.
Каждая позиция в восьмеричном числе представляет собой нулевую степень основания (8). Пример 80
Последняя позиция в восьмеричном числе представляет степень x основания (8). Пример 8x, где x представляет последнюю позицию — 1.

Пример: —
Восьмеричное число: 125708

Вычисление десятичного эквивалента:-

Примечание: 125708 обычно написан как 12570.

Система шестнадцатеричных чисел

Характеристики шестнадцатеричных чисел следующие:

Используются 10 цифр и 6 букв, 0,1,2,3 ,4,5,6,7,8,9,А,В,С,D,Е,F.
Буквы обозначают числа, начинающиеся с 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15.
Также называется системой счисления с основанием 16. нулевая степень основания (16). Пример 160
Последняя позиция в шестнадцатеричном числе представляет степень x основания (16). Пример 16x, где x представляет последнюю позицию — 1.

Пример:-
Шестнадцатеричное число: 19FDE16

Вычисление десятичного эквивалента :-

Представление двоичного числа

Выше мы видели, что в десятичной системе счисления вес каждой цифры слева увеличивается в 10 раз. (3) ) и т. д. Например, преобразование Двоичный код в десятичный число будет: —

Если сложить ВСЕ значения десятичных чисел справа налево в позициях, которые представлены «1», мы получим: (256) + (64) + (32) + (4) + (1) = 35710 или триста пятьдесят семь в виде десятичного числа. Затем мы можем преобразовать двоичное число в десятичное, найдя десятичный эквивалент двоичного массива цифр 1011001012 и разложив двоичные цифры в ряд с основанием 2, что даст эквивалент 35710 в десятичной системе счисления. .

Повторяемый метод подразделения-2

Другое название этого метода- Double Dabble Метод. Выше мы видели, как преобразовать двоичные числа в десятичные, но как преобразовать десятичное число в двоичное. Простой метод преобразования эквивалентов десятичных чисел в двоичные состоит в том, чтобы записать десятичное число и постоянно делить на 2 (два), чтобы получить результат, а остаток либо «1», либо «0» до окончательного результата. равен нулю.

Так, например:- Преобразуйте десятичное число 29410 в эквивалентное ему двоичное число.

Итак, двоичный эквивалент 29410 :- 1001001102

Другой пример :- Преобразуйте десятичное число 67510 в его двоичный эквивалент.

Итак, двоичный эквивалент 67510 :- 10101000112

Другой способ представления десятичного числа в двоичной форме Каждая десятичная цифра преобразуется в четырехбитную двоичную.
( 325 )10 =(

0011

0010

0101

)
3 2 5

( 739 )10 =(

0111

0011

1001

)
7 3 5

BCD ДОПОЛНЕНИЕ

1. добавьте BCD.
2. Если сумма недействительна в двоично-десятичном коде или если в добавлении создается перенос, добавьте (0110), эквивалентный (6), к сумме.
1 1
3 2 9 — 0 0 1 1 0 0 1 0 1 0 0 1
+

1 8 2

—

0 0 0 1 0 0 0 0 0 1 0

5 1 1 0 1 0 1 1 0 1 1- НЕДВИЖИМОСТЬ BCD 1 0 1 1- НЕДВИЖИМИ BCD
+

0 1 1 0

0 1 0 1

0 0 0 1

5 1 1

ДЕЙСТВИТЕЛЬНЫЙ И НЕДЕЙСТВИТЕЛЬНЫЙ BCD

Двоичная система дополняет

, поскольку бинарная система имеет базовую r = 2. Таким образом, два типа дополнений для бинарной системы являются дополнение 2 и дополнение 1.

Дополнение до 1
Дополнение числа до 1 находится путем замены всех 1 на 0 и всех 0 на 1. Это называется дополнением или дополнением до 1. Пример дополнения 1 выглядит следующим образом.

Дополнение до 2

Дополнение до 2 двоичного числа получается путем добавления 1 к младшему значащему биту (LSB) дополнения до 1 числа.

Дополнение до 2 = Дополнение до 1 + 1
Пример Дополнения до 2 выглядит следующим образом.

Система счисления с основанием 2

Когда мы считаем, мы обычно делаем это с основанием 10. Это означает, что каждый разряд в числе может занимать одно из десяти значений, от 0 до 9. В двоичном коде мы считаем по основанию два, где каждое место может содержать одно из двух значений: 0 или 1. Шаблон счета такой же, как и в основании 10, за исключением того, что когда вы переносите в новый столбец, вы должны переносить каждый раз, когда место идет выше, чем один (в отличие от выше, чем 9 в основе 10).

Например, числа один и ноль одинаковы в системе счисления 10 и базе 2. Но в системе счисления 2, как только вы дойдете до числа 2, вы должны перенести единицу, что приведет к представлению «10». Добавление единицы снова дает «11» (3), а добавление единицы снова дает «100» (4).

В отличие от счета по основанию 10, где каждый десятичный разряд представляет степень числа 10, каждый разряд в двоичном числе представляет степень числа два (или бит). Крайний правый бит — это бит 1 (два в нулевой степени), следующий бит — это бит 2 (два в первой степени), затем 4, 8, 16, 32 и так далее.

Двоичное число 1010 равно 10 по основанию 2, потому что бит 8 и бит 2 включены. В Python вы можете записывать числа в двоичном формате, начиная число с 0b. При этом с числами можно работать как с любым другим числом.

То есть:

—	—	—	—	система
1	2	4	8	основание 10
0/1	0/1	0/1	0/1	основание 2
Примеры	—	—	—	—
0	1	0	0	по основанию 10 равно 2
0	1	0	1	по основанию 10 равно 10
0	0	1	0	по основанию 10 равно 4
1	0	1	0	в базе 10 в 5

В Python вам нужно только инвертировать значения:

—	—	—	—	система
8	4	2	1	основание 10
Примеры	—	—	—	—
0	0	1	0	по основанию 10 равно 2
1	0	1	0	по основанию 10 равно 10

Здесь вы можете найти пример использования Python:

 >>> напечатать 0b1,
1
>>> напечатать 0b10,
2
>>> напечатать 0b11,
3
>>> напечатать 0b100,
4
>>> напечатать 0b101,
5
>>> напечатать 0b110,
6
>>> напечатать 0b111
7
>>> напечатать "******"
******
>>> напечатать 0b1 + 0b11
4
>>> напечатать 0b11 * 0b11
9>>>

Практика 1

Попробуйте полностью заполнить значения:

 один = 0b1
два = 0b10
три = 0b11
четыре
пять
шесть
Семь
восемь
девять
десять
одиннадцать
двенадцать

Ответ:

 один = 0b0001
два = 0b0010
три = 0b0011
четыре = 0b0100
пять = 0b0101
шесть = 0b0110
семь = 0b0111
восемь = 0b1000
девять = 0b1001
десять = 0b1010
одиннадцать = 0b1011
двенадцать = 0b1100

бин()

Существуют функции Python, которые могут помочь вам с побитовыми операциями. Чтобы напечатать число в его двоичном представлении, вы можете использовать bin() функция. bin() принимает целое число в качестве входных данных и возвращает двоичное представление этого целого числа в строке. (Имейте в виду, что после использования функции bin вы больше не сможете работать со значением как с числом.)

Вы также можете представлять числа с основанием 8 и 16, используя функции oct() и hex() .

Например:

 >>> корзина печати(1)
0b1 #Это строка! Будьте осторожны!
>>>

целое()

В Python есть функция int(), которую вы уже видели. Он может преобразовать нецелочисленный ввод в целое число. Возможно, вы не знаете, что функция int` имеет необязательный второй параметр.

 >>> целое число("110", 2)
6

Если задана строка, содержащая число и основание, в котором находится это число, функция вернет значение этого числа, преобразованное в десятичное основание.