Про системы счисления / Хабр
Что же это, чёрт возьми, такое, как работают нули-единицы, и кто и зачем это вообще придумал.
Начинаю серию статей с простым объяснением всяких фундаментальных вещей с иллюстрациями. Школьнику, которого учитель информатики заставляет переводить числа туда-сюда, а он вообще не врубается, что происходит. Дизайнеру, который не знает, что значит цвет #FFDD00. Тем, кто всё знает, но не против ещё раз укрепить модель.
В статье всё замаскировано под исторические события. Это фикция, я не знаю историю, поэтому придумал свою, чтобы было проще рассказывать.
Жил-был древний человек.
И были у него овцы.
И решил он однажды посчитать, сколько у него овец. Но считать ещё не умел.
Древний человек придумал оставлять засечки на камне. Одна засечка — одна овца. Когда рождается овца, человек рисовал засечку, когда умирала — стирал.
И жил так прекрасно древний человек, пока не поумнел и не решил узнать что-нибудь об окружающем его мире. И захотел он посчитать количество звёзд на небе — тем же способом.
И захотел он посчитать количество звёзд на небе — тем же способом.
И умер.
Это, конечно, такой естественный отбор был. Человек должен с копьём на кабана охотиться, а не звёзды считать.
Потом были древние римляне. Их было много, поэтому, очевидно, были те, кто поумнее, и все остальные. Последние охотились на кабана с копьём, а умные считали добычу и столкнулись с той же проблемой, что и древний человек.
И они подумали: «а давайте нарисуем ещё больше разных закорючек, и они будут кратко обозначать большие числа».
И придумали, что эти закорючки будут такими:
V = IIIII,
X = VV,
L = XXXXX,
C = LL,
D = CCCCC,
M = DD.
Ещё они придумали хитрые правила, чтобы, например, вместо VIIII писать IX, но для простоты повествования мы про эти правила забудем.
И смогли римляне посчитать, что средняя продолжительность жизни — лет L, а звёзд на небе видно примерно MMD. Им этого хватало.
Но время шло, и человечеству понадобилось записывать всё большие числа. Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.
Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.
И нашёлся один умный человек, который придумал такую сложную и непонятную систему, что я не удивлюсь, если его за это потом сожгли.
Заметьте, что во всех предыдущих способах записи закорючки (цифры), стоящие рядом, просто складываются. Если древний человек написал II, это значит «I засечка и ещё I засечка». Если римлянин написал VII, это значит буквально IIIII + I + I, то есть IIIIIII.
Умный человек (горе ему) придумал вот что:
Пусть у нас будет сколько-то закорючек, например, X (здесь и дальше X — римская цифра, а не «неизвестное»). Позвал знакомого араба, сказал ему: «придумай мне X закорючек». Араб почесал репу и нарисовал: 0123456789.
Пусть 0 означает «ничего», а каждая следующая цифра сама по себе означает число, больше предыдущего на 1.
А дальше вообще отвал башки.
Пусть чем раньше в числе стоит цифра, тем большую «значимость» она имеет.
 3 и так далее.
3 и так далее.Немного терминологии, чтобы привязать знания к реальности.
Система счисления — это способ записывать количество какими-то чёрточками. Способ подсчёта овец древним человеком — система счисления. Запись чисел с помощью V, X и M римлянами — система счисления. Новый и прогрессивный способ, придуманный умным человеком, — тоже.
Непозиционная система счисления — та, где от положения цифры её значение не меняется. Древний человек придумал именно такую систему — I всегда значит I.
Позиционная система счисления — та, где, наоборот, положение цифры влияет на её значение. Такую систему изобрёл умный человек. Например, в числе 456 цифра 4 означает 400, а в числе 546 — всего 40.
Основание системы счисления — общее количество закорючек (цифр) в ней. Умный человек придумал систему счисления с основанием X (в этой системе, в свою очередь, X записывается как 10).
Разряд — положение цифры в числе.
Что будет, если изменить основание системы счисления, например, на 2?
В целом, то же самое, только: — цифры остались всего две — можем придумать любые, но для удобства обычно берут символы из нашей системы счисления.
 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10.Выходит, 1010 в двоичной системе счисления обозначает такое же количество, какое 10 — в нашей, десятичной.
Двоичная система удобна, потому что в ней достаточно иметь всего две возможные позиции в каждом из разрядов — «ток течёт» или «ток не течёт», «палец загнут» или «палец выпрямлен».
Например, загибая пальцы рук, можно посчитать от 00000 00000 до 11111 11111, если принять левый мизинец за старший разряд, а правый мизинец — за младший, нулевой. Получается, в переводе на десятичную систему счисления на пальцах можно посчитать от нуля до 1023.
Первое, на что я хочу обратить внимание, — основание системы счисления в этой же системе всегда записывается как «10». В двоичной системе счисления число 2 записывается как «10», потому что 1 * 2 + 0 = 2. В шестнадцатеричной системе счисления число 16 записывается как «10», потому что 1 * 16 + 0 = 16. Ну вы поняли.
В связи с этим есть мем:
Инопланетянин говорит, что камней «10», потому что использует систему счисления с основанием 4 по-нашему.
 В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.Кстати, про шестнадцатеричную систему счисления. Десять привычных нам цифр уже есть, а где ещё шесть взять? Да давайте просто возьмём ещё шесть букв. После 9 идёт A, потом B, потом C, D, E, F, и только потом — 10. Получается, что последние цифробуквы шестнадцатеричной системы счисления переводятся в десятичную так:
A = 10,
B = 11,
C = 12,
D = 13,
E = 14,
F = 15.И последнее на сегодня — для дизайнеров. Что означает запись #FFDD00 для цвета? Наверняка вы знаете, что каждый пиксель на экране состоит из трёх лампочек — красного, зелёного и синего цвета, а все остальные цвета получаются смешиванием этих трёх в разной пропорции.
Каждая из лампочек может светить с условной яркостью от 0 до 255. #FFDD00 — это три числа: FF, DD и 00, где каждое число обозначает яркость каждой лампочки.
FF = 15 * 16 + 15 = 255.

DD = 13 * 16 + 13 = 221.
00 = 0.Получается, красная лампочка включена на все 255, зелёная на 221, а синяя полностью выключена.
#FFFFFF — все лампочки горят на максимум и дают белый цвет. #000000 — все выключены, чёрный цвет.
Вот так, короче.
Следующая статья будет (наверное) про то, что такое, чёрт возьми, электричество, сила тока, чем она отличается от напряжения, что такое заряд, сопротивление и потенциал.
Подписывайтесь на меня в Твиттере: https://twitter.com/adam_arutyunov
А ещё есть канал — «Адам Арутюнов поднимается до мидла». В нём — вы не поверите. t.me/cdarr
Системы счисления — презентация онлайн
1. Системы счисления
2. Литература
Острейковский В.А. Информатика: Учеб.
для вузов .-М. : Высш. шк.,20003. Система счисления
Система счисления — это метод записи
чисел с помощью набора специальных
знаков, которые называются цифрами.
Множество цифр, используемых в системе
счисления, называется алфавитом.
Системы счисления бывают позиционными
и непозиционными.
Непозиционные системы счисления
Вес цифры (т.е. тот вклад, который она
вносит в значение числа) не зависит от ее
позиции в записи числа.
Пример. Римская система счисления:
в числе ХХХII (тридцать два) вес цифры Х
в любой позиции равен десяти, вес цифры
I в любой позиции равен единице и т.д.5. Позиционные системы счисления
В позиционных системах счисления
значимость (вес) каждой цифры числа
зависит от позиции, которую она занимает
в числе.
Пример: в числе 757,7 первая семерка
означает 7 сотен, вторая – 7 единиц, а
третья – 7 десятых долей единицы.6. Позиционные системы счисления
Сама запись числа 757,7 означает
сокращенную запись выражения
700+50+7+0,7 = 7•102+5•101+7•100+7•10-1= 757,7
Любая позиционная система счисления
характеризуется своим основанием.7. Позиционные системы счисления
За основание системы счисления можно
принять любое натуральное число — 2, 3, 4
и т. д.
д.
Следовательно, возможно бесчисленное
множество позиционных систем: двоичная,
троичная, четверичная и т.д.8. Алфавит позиционной системы счисления
Для записи чисел в позиционной системе с
основанием q нужен алфавит из q цифр.
Таким образом, основание позиционной
системы счисления — это количество цифр в
её алфавите.
Обычно при q < 10 используют q первых
арабских цифр, а при n > 10 к десяти арабским
цифрам добавляют латинские буквы.9. Алфавит позиционной системы счисления
Примеры алфавитов нескольких систем:
Если требуется указать основание системы, к
которой относится число, то основание
приписывается нижним индексом к этому
числу. Пример:
1011012, 36718, 3B8F16.10. Позиционные системы счисления
Запись чисел в каждой из систем счисления с
основанием q означает сокращенную запись
многочлена:
an-1qn-1 + an-2qn-2 +…+ a1q1 + a0q0 + a-1q-1 +…+ a-mq-m,
Здесь:
ai – цифры системы счисления;
n и m – число целых и дробных разрядов,
соответственно.
11. Позиционные системы счисления
Примеры:
Это и есть способ перевода числа из
системы счисления с основанием q в 10-ю
систему счисления.12. Перевод числа из системы счисления с основанием q в 10-ю систему счисления
Пример.
Дано действительное число 101,012.
Записать его в десятичной системе
счисления.
Решение.
101,012 = 1•22 + 0•21 + 1•20 + 0•2-1 + 1•2-2 = 4 +
0 + 1 + 0 + 0,25 = 5,251013. Перевод числа из системы счисления с основанием q в 10-ю систему счисления
Пример: перевести число из 16-ой системы
счисления в 10-ю.
Решение:14. Задачи
Перевести данные числа в 10-ю систему счисления:
А) 10000012
Б) 1000011111,01012
В) 1216,048
Г) 29А,51615. Задачи
Пример. Определить наименьшие основания
позиционных систем счисления, при которых
56X = 63Y.
Решение. Запишем числа в виде многочленов:
56x = 5∙x1 + 6 ∙x0 и 63Y = 6∙y1 + 3 ∙y0
Получаем равенство: 5x + 6 = 6y + 3
Преобразуем равенство: x = (6y — 3)/5
При этом имеем еще 2 ограничения:
Х > 6 и Y > 6.
Теперь нужно найти значения X и Y,
удовлетворяющие всем трем условиям.16. Пример
Перебирая значения Y>6 по возрастанию,
подбираем такое при котором X должно
быть целое:
Y=7: x = (6 ∙ 7 — 3)/5 = 39 / 5 – не целое
Y=8: x = (6 ∙ 8 — 3)/5 = 45 / 5 = 9
Ответ: Y = 8, X = 9.17. Порождение чисел в позиционных системах счисления
В системе счисления цифры упорядочены в соответствии с
их значениями: 1 > 0, 2 > 1 и т.д.
Порождаются числа в позиционных системах счисления с
помощью правила продвижения цифры.
Продвижение цифры – это замена её на следующую по
величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть
цифру 2 значит заменить её на 3 и т.д.
Продвинуть старшую цифру (например, 9 в 10-ой системе)
значит заменить её на 0.
В двоичной системе, использующей только две цифры – 0 и
1, продвижение 0 означает замену его на 1, а
продвижение 1 – замену её на 0.18. Порождение чисел в позиционных системах счисления
Целые числа в любой системе счисления
порождаются с помощью Правила счета:
Для образования целого числа, следующего за
любым данным целым числом, нужно
продвинуть самую правую цифру числа;
если какая-либо цифра после продвижения
стала нулем, то нужно продвинуть цифру,
стоящую слева от неё.
19. Порождение чисел в позиционных системах счисления
Пример. Применяя правило счета, записать
первые десять целых чисел в 2-ой, 3-ой, 5ой, 8-ой системах счисления.
Решение.
2-я: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
3-я: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
5-я: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
8-я: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.20. Перевод целых десятичных чисел в систему счисления с основанием q
При переводе целого десятичного числа Х в
систему с основанием q данное число
нужно последовательно делить на q до тех
пор, пока не будет получен остаток < q.
Число в системе с основанием q
записывается как последовательность
остатков от деления, записанных в
обратном порядке, начиная с последнего.21. Перевод целых десятичных чисел в систему счисления с основанием q
Пример. Перевести число 7510 из 10-й в 2-ю с.с.
Решение.
1 001 011222. Задача
Перевести число 3710 в 2-ю.
Решение.
Ответ: 3710 = 1001012 .23. Перевод целых десятичных чисел в систему счисления с основанием q
Пример. Перевести число 31510 в 8-ю и 16-ю с.с.
Решение.
8-я с.с.
16-я с.с.
Ответ:
31510 = 4738 = 13B16
Примечание. 1110 – это B16.24. Задача
Перевести число 7510 в восьмеричную и
шестнадцатеричную:
72
3 8
1
1
1138
Ответ: 7510 = 1138 = 4B16.
64
11
4
4(11)8 = 4В1625. Перевод правильной десятичной дроби в систему счисления с основанием q
1. Дробь умножается на q.
2. Результат умножения разделяется на 2 части целая часть произведения записывается в
результат, а дробная снова умножается.
3. Умножение производится, пока дробная часть
произведения не станет равной нулю (дробь
переводится точно), или не выявится период или
не будет достигнута заданная точность (например,
до 5 знаков после запятой).26. Перевод правильной десятичной дроби в систему счисления с основанием q
Пример. Перевести десятичную дробь 0,1875 в 2-ю, 8-ю и 16-ю c.с.
Перевести десятичную дробь 0,1875 в 2-ю, 8-ю и 16-ю c.с.
Решение.
2-я
8-я
16-я
0,1875
×
2
0,3750
×
2
0,750
× 2
1,50
× 2
1,00
0,1875
×
8
0,5000
× 2
4,0
0,1875
×
16
11350
1 875
3,0000
Результат: 0,316
Результат: 0,148
Результат: 0,00112
Здесь в левом столбце находится целая часть чисел, а в
правом — дробная. Умножается только дробная.
Ответ: 0,187510 = 0,00112 = 0,148 = 0,31627. Задача
Пример: Перевести число 0,3510 в 2-ю с.с.
Решение.
0, 35
×
2
0, 70
× 2
1, 4
× 2
0, 8
× 2
1, 6
× 2
1, 2
× 4
0, 8
× 2
1, 6 и т.д
Результат: 0,3510 = 0,0101101…2 = 0,01(011)228. Задача
Пример: Перевести число 0,3510 в 8-ю с.с.
Решение.
0, 35
×
8
2, 80
× 8
6, 4
× 8
3, 2
× 8
1, 6
× 2
1, 2
× 4
0, 8
× 8
6, 4 и т.д.
Результат: 0,3510 = 0,2631106…8 = = 0,2(63110)829.
 ЗадачаПример: Перевести число 0,3510 в 2-ю, 8-ю и 16-ю.
ЗадачаПример: Перевести число 0,3510 в 2-ю, 8-ю и 16-ю.
Решение.
0, 35
× 16
5, 60
×16
9, 6
× 16
9, 6 и т.д.
Результат: 0,3510 = 0,5(9)1630. Перевод смешанных десятичной чисел в систему счисления с основанием q
Перевод смешанных чисел, содержащих целую
и дробную части:
1. Переводится целая часть по алгоритму
перевода целых чисел.
2. Переводится дробная часть по алгоритму
перевода правильной десятичной дроби .
3. В итоговой записи числа в новой системе
счисления целая часть отделяется от
дробной запятой (точкой).31. Задачи
1. Перевести число 20,37510 в 2-ю, 8-ю и 16-ю.
Ответ: 20,37510 =10100,0112 = 24,38 = 14,316
2. Перевести число 44,289062510 в 2-ю, 8-ю и
16-ю.
Ответ: 44,289062510 = 101100,01001012 = 54,2218 =
2С,4А1632. Схема быстрого перевода между системами счисления, основания которых – это степени одного числа
Пример таких оснований — 2, 4, 8, 16.
Перевод осуществляется через систему счисления,
основание которой равно возводимому степень
числу. Для примера – это двоичная с.с.
Для примера – это двоичная с.с.
Перевод 8-х чисел в 2-ю с.с.: каждую 8-ю цифру
заменяем эквивалентной ей двоичной триадой тройкой цифр (23 = 8).
Перевод 16-х чисел в 2-ю с.с.: каждую 16-ю цифру
заменяем эквивалентной ей двоичной тетрадой
— четверкой цифр (24 = 16).33. Схема быстрого перевода между системами счисления, основания которых – это степени одного числа
Таблицы перевода:
10 — я
0
1
2
3
2–я
00
01
10
11
4–я
0
1
2
3
10 — я
0
1
2
3
4
5
6
7
2–я
000
001
010
011
100
101
110
111
8–я
0
1
2
3
4
5
6
7
10 — я
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2–я
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
16 – я
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F34.
 Схема быстрого перевода между системами счисления, основания которых – это степени одного числаПример: Число 1111010101,112 перевести в 16-ю с.с.
Схема быстрого перевода между системами счисления, основания которых – это степени одного числаПример: Число 1111010101,112 перевести в 16-ю с.с.
Решение:35. Задачи
Перевести число 10101001,101112 :
А) в 8-ю
Б) в 16-ю36. Арифметические операции в системе счисления с основанием q
Правила выполнения сложения, вычитания,
умножения и деления те же, что и в
десятичной системе счисления —сложение,
вычитание и умножение выполняются
столбиком, а деление углом.
Эти правила применимы и ко всем другим
позиционным системам счисления37. Двоичная система счисления: сложение
Таблица сложения:
Пример: Сложить число 11112 и 1102
перенос38. Задача
Сложить два числа:
Решение.39. Восьмеричная система счисления: сложение
Пример. 75368 + 4728
Решение. 7 5 3 68
+
4 7 28
7 9(10)8
-8
7 9(11)0
-8
7(10)3 0
-8
8 2 30
-8
1 0 2 3 08 Ответ: 75368 + 4728 = 10230840.
 16-я система счисления: сложениеПример. 7B3E16 + 7AD16
16-я система счисления: сложениеПример. 7B3E16 + 7AD16
Решение. Сначала заменим буквы числами
7B3E16 + 7AD16 = 7(11)3(14)16+ 7(10)(13)16
7 (11) 3 (14)16
+ 7 (10) (13)16
7 (18) (13) (27)
— 16
7 (18) (14) (11)
— 16
8 2 (14) (11)
Заменим числа на буквы :
8 2 E
B 16
Ответ: 7B3E16 + 7AD16 = 82EB1641. Задачи
1.
Решение:
Ответ: 311,28
2. A8D,816 + 93B,C16
Ответ: 13C9,41642. Двоичная система счисления: вычитание
Выполнить действие:
Решение:
Ответ:
= 10001101,1243. Задача
1100000011,0112 — 101010111,1(2)
Решение:
—
Ответ: 110101011,111244. 8-я система счисления: вычитание
Выполнить действие:
Решение:
Ответ:
= 215,4845. Задача
1510,28 – 1230,548
Решение:
—
Ответ: 257,44846. 16-я система счисления: вычитание
Выполнить действие:
Решение:
(12) 9 , 4
3 (11),(12)
8 (13), 8
Ответ:
= 8D,81647.
 ЗадачаВычислить: 27D,D816 – 191,216
ЗадачаВычислить: 27D,D816 – 191,216
Решение:
1 — заём
—
2 7 (13),(13) 8
1 9 1 , 2
(14)(12),(11) 8
Ответ: 27D,D816 – 191,216 = EC,B81648. 2-я система счисления: умножение
При умножении в двоичной системе счисления
выполняется по правилам умножения в столбик.
Пример: 1001112 10001112
Решение:
Ответ: 1001112 10001112 = 101011010001249. Задача
Выполнить умножение:
Ответ: 11100112 ● 1100112 = 1011011101001250. 8-я система счисления: умножение
Пример. Вычислить 1638 × 638
Умножаем на разряды 2-го
Решение. × 2 6 38
сомножителя, пока не учитывая
5 38
перенос.
Теперь, начиная с младших,
6 (18) 9
+
последовательно корректируем
10 (30) (15)
разряды, значение которых > 7:
10 (36) (34) 1
9 : 8 = частное 1 и остаток 1
10 (40) 2 1 Частное – это перенос, остаток –
это цифра разряда.
(15) 0 2 1
34 : 8 = частное 4 и остаток 2
40 : 8 = частное 5 и остаток 0
Заменяем двухразрядные числа на буквы:
Ответ: 1638 × 638 = F021851.
 ЗадачаВыполнить умножение:
ЗадачаВыполнить умножение:
Ответ: = 13351852. 16-я система счисления: умножение
Пример. Вычислить 61A16 40D16
Решение. Заменяем буквы числами и перемножаем:
6 1 (10)16 Умножаем на разряды 2-го
× 4 0 (13) сомножителя, пока не учитывая
16
перенос.
(78)(13)(130)
Начиная с младших,
+
(24) 4 (40)
корректируем разряды,
значение которых > 15:
(24) 4(118)(13)(130)
130 : 16 = частное 8 и остаток 2
(24) 4(118)(21) 2
21 : 16 = частое 1 и остаток 5
(24) 4(119) 5 2
119 : 16 = частое 7 и остаток 7
24 : 16 = частое 1 и остаток 8
(24)(11) 7 5 2
Заменяем числа > 9 на буквы.
1 8 (11) 7 5 2
Ответ: 61A16 40D16 = 18B7521653. Задача
Выполнить умножение: 173C16 4FA16
Ответ: = 73A09816Шестнадцатеричная система счисления (определение, преобразование и примеры)
Двоичная система счисления является естественным выбором для систем с двумя состояниями. Но в этой системе числа имеют тенденцию становиться короткими, а довольно длинными.
 Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0003 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.
Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0003 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.Из таблицы 44.3 видно, что существует 16 комбинаций 4-битных двоичных чисел и наборов 4-битные двоичные числа можно вводить в компьютер в виде шестнадцатеричных (шестнадцатеричных) цифр. Эти числа должны быть преобразованы в двоичные представления с использованием схем преобразования шестнадцатеричных чисел в двоичные, прежде чем они смогут быть обработаны цифровыми схемами.
Счет в шестнадцатеричной системе счисления: Эта система широко используется в микропроцессорной работе.
Эта система широко используется в микропроцессорной работе.Как мы будем считать в шестнадцатеричной системе счисления, когда дойдем до F ? Просто начните с другого столбца и продолжайте следующим образом:
С двумя шестнадцатеричными цифрами мы можем сосчитать до FF 16 , что равно 255 10 . Для подсчета сверх этого требуются три шестнадцатеричных цифры. Например, 100 16 равно 256 10 , 101 16 равно 257 10 и так далее. Максимальное трехзначное шестнадцатеричное число — FFF 16 , что равно 4095 10 .
Преобразование шестнадцатеричных чисел в десятичные:Шестнадцатеричное число можно преобразовать в его десятичный эквивалент, умножив каждую шестнадцатеричную цифру на ее вес, а затем взяв сумму этих произведений. Веса шестнадцатеричных чисел являются возрастающими степенями 16 (справа налево).
 Для четырехзначного шестнадцатеричного числа веса следующие:
Для четырехзначного шестнадцатеричного числа веса следующие:Для иллюстрации рассмотрим несколько примеров.
Пример 44.41: Найдите десятичный эквивалент шестнадцатеричного числа 1A53.
Решение:
Пример 44.42: Преобразовать (FF3B) 16 в эквивалентное десятичное число.
Решение:
Преобразование десятичного числа в шестнадцатеричное:Повторное деление десятичного числа на 16 даст эквивалентное шестнадцатеричное число, образованное остатком от каждого деления. . Это похоже на повторное деление на 2 для десятичного преобразования в двоичное и повторное деление на 8 для десятичного преобразования в восьмеричное. Следующие примеры иллюстрируют процедуру.
Пример 44.44: Преобразуйте следующее число: (374,37) 10 = ( ) 16
Решение:
900 02
Преобразование шестнадцатеричной системы в двоичную:Шестнадцатеричная числа могут быть преобразованы в эквивалентные двоичные числа путем замены каждой шестнадцатеричной цифры ее эквивалентным 4-битным двоичным числом.
 Эта процедура проиллюстрирована ниже.
Эта процедура проиллюстрирована ниже.Пример 44.46: Выполните следующее преобразование: (1684) 16 до ( ) 2
Решение:
Пример 44.47: Преобразование следующего числа (A6B.F5) 1 6 → (?) 2 .
Решение: Преобразование каждой шестнадцатеричной цифры в двоичное число бит, которое мы имеем процесс выше. Двоичное число группируется в группы по 4 бита, начиная с LSB и продвигаясь к MSB для целой части, а затем каждая группа из четырех бит заменяется ее шестнадцатеричным представлением. Нули добавляются по мере необходимости для завершения 4-битной группы.
Для дробной части описанная выше процедура повторяется, начиная с бита, следующего за двоичной точкой, и продвигаясь вправо.
Пример 44.49: Преобразовать длинное двоичное число 1001001101010001 в восьмеричное и шестнадцатеричное.
Решение: (1001001101010001) 2
Преобразование из шестнадцатеричного в восьмеричное и наоборот.
Шестнадцатеричные числа могут быть преобразованы в эквивалентные восьмеричные числа, а восьмеричные числа могут быть преобразованы в эквивалентные шестнадцатеричные числа путем преобразования шестнадцатеричного/восьмеричного числа в эквивалентное двоичное, а затем в восьмеричное/шестнадцатеричное соответственно. Процедура иллюстрируется следующим примером.
Пример 44.50: Преобразовать (F2A4) 16 в ( ) 8 .
Решение: (F2A4) 16
Пример 44.51: Преобразовать шестнадцатеричное число A5F1 в эквивалентное восьмеричное число.
Решение:
Шестнадцатеричная арифметика:Правила арифметических операций с шестнадцатеричными числами аналогичны правилам для десятичных, восьмеричных и двоичных чисел. Информация может обрабатываться только в двоичной форме в цифровой схеме, и ее удобно и проще вводить с помощью шестнадцатеричных чисел.
 Поскольку арифметические операции выполняются цифровыми схемами над двоичными числами, шестнадцатеричные числа должны быть сначала преобразованы в двоичные числа. Следующие несколько примеров иллюстрируют процедуру.
Поскольку арифметические операции выполняются цифровыми схемами над двоичными числами, шестнадцатеричные числа должны быть сначала преобразованы в двоичные числа. Следующие несколько примеров иллюстрируют процедуру.Пример 44.56: Найдите шестнадцатеричную сумму (93) 16 + (DE) 16
Решение:
900 05
Пример 44.58: Выполнение указанной операции FC2 16 x DE 16 «=»
Решение:
Пример 44.59: Разделить 1EC87
Решение:
Эпоха 16-битной и шестнадцатеричной
Перейти к плейлисту эпизодовДавайте поговорим о 16-битной эпохе и новой системе нумерации. Нам нужно вычислить большие числа.
 Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.
Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.Основные выводы из этого эпизода:
- Шестнадцатеричное (шестнадцатеричное) более сжатое обозначение
- Позволяет ввести до 16 цифр: 0-9 + A-F
- Одна шестнадцатеричная запись аналогична 4-битным группам в двоичной
- Полезно для больших чисел
- Цветовые коды используют шестнадцатеричный код
Учебные заметки
Помните : Большие числа = больше мощности
Процесс преобразования двоичного числа в десятичное занимает несколько шагов. Сложнее посмотреть на образец 1 и 0 и вытащить точный десятичный эквивалент.
Преобразование больших чисел
Как упростить представление?
Новая 16-битная система счисления:
Из каких блоков состоит наша новая 16-битная система счисления? Начнем с восьмеричной.

В восьмеричном формате у нас есть семь битов, которые также являются цифрами от 0 до 7. Он использует группировку 3-битных двоичных чисел для представления цифр.
Обратите внимание, что мы использовали все образцы единиц и нулей.
16-разрядное преобразование:
Давайте рассмотрим преобразование этого двоичного числа в нашу новую 16-разрядную систему счисления. Мы группируем его по 4 битам, что означает, что для 2-байтового двоичного шаблона имеется 4 цифры. Всегда начинайте с младшего значащего бита (крайнего справа).
Обозначение этого нового числа — 0x1445, где x обозначает шестнадцатеричный или шестнадцатеричный формат. Сокращенное обозначение: 1455 16 .
Теперь сравните эту новую запись чисел с восьмеричной. Вы видите, что использование шестнадцатеричной формы лучше для больших чисел?
Хотите знать, где вы когда-нибудь будете использовать шестнадцатеричный?
Цветовые коды указаны в шестнадцатеричном формате.

Преобразуем шестнадцатеричное представление цвета «белый» в двоичный, восьмеричный и десятичный форматы.
Практическое использование Hex
- Цветовые коды
- Сообщения об ошибках
- Штриховой код
- Взаимодействие с API
Эй… эй ты… да ты!… Хорошо проводишь время? Учиться новому? Хороший!
Эпизоды
Общее время работы лаборатории: 02:59:07
- 1 Введение в лабораториюбесплатно 03:56
- 2 Электроника «включена» и «выключена» 12:11
- 3 Символ для представления количества бесплатно 14:26
- 4 Система счисления для Statefree 12:44
- 5 Двоичный — объединение 1 и 0 бесплатно 19:25
- 6 Улучшение бинарного представленияfree 13:45
- 7 Эпоха 16-битных и шестнадцатеричных чисел 15:15
- 8
- 9 Отрицательное целочисленное представление данных — часть 1бесплатно 10:06
- 10 Отрицательное целочисленное представление данных.



 3 и так далее.
3 и так далее. 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10.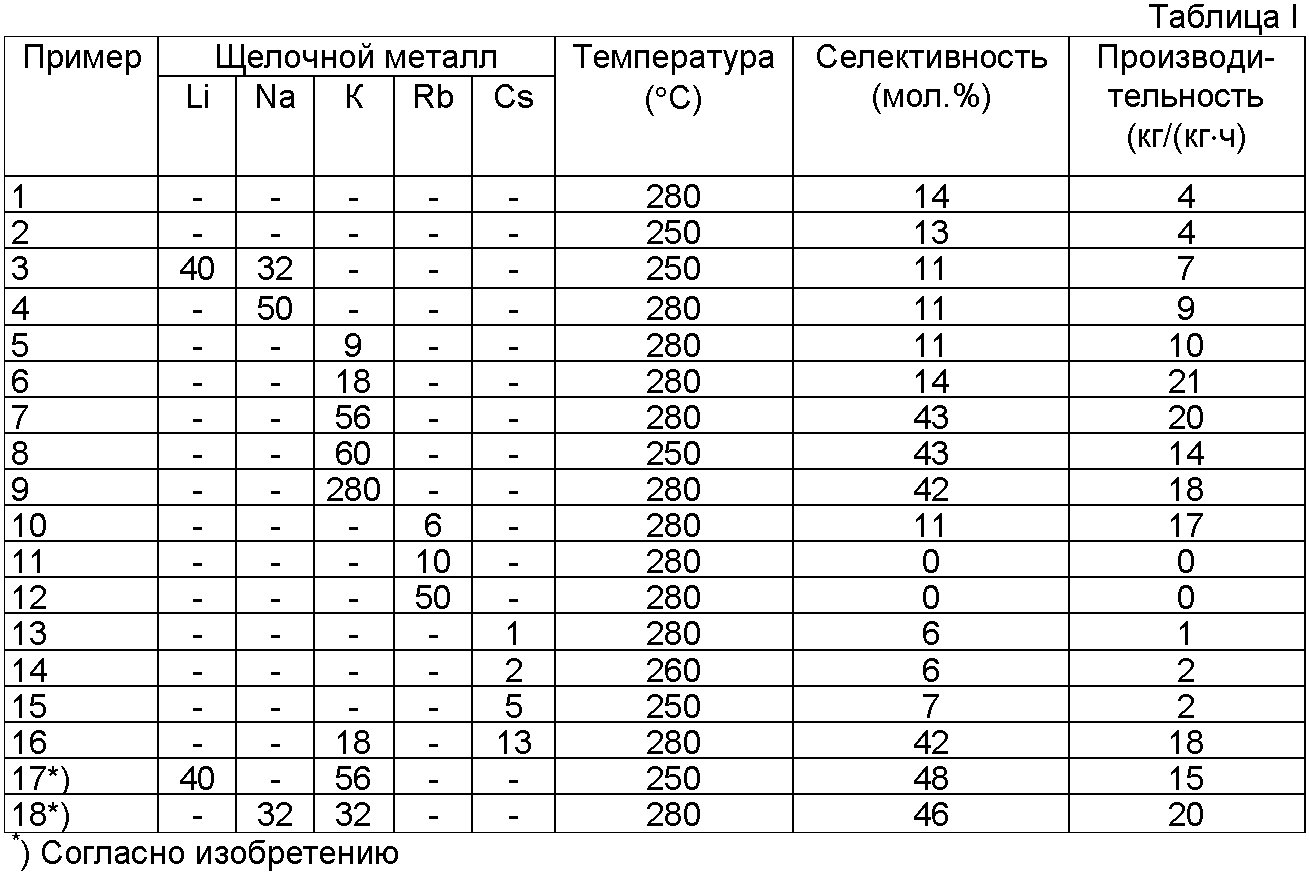 В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.

 д.
д.



 Перевести десятичную дробь 0,1875 в 2-ю, 8-ю и 16-ю c.с.
Перевести десятичную дробь 0,1875 в 2-ю, 8-ю и 16-ю c.с. ЗадачаПример: Перевести число 0,3510 в 2-ю, 8-ю и 16-ю.
ЗадачаПример: Перевести число 0,3510 в 2-ю, 8-ю и 16-ю. Для примера – это двоичная с.с.
Для примера – это двоичная с.с. Схема быстрого перевода между системами счисления, основания которых – это степени одного числаПример: Число 1111010101,112 перевести в 16-ю с.с.
Схема быстрого перевода между системами счисления, основания которых – это степени одного числаПример: Число 1111010101,112 перевести в 16-ю с.с. 16-я система счисления: сложениеПример. 7B3E16 + 7AD16
16-я система счисления: сложениеПример. 7B3E16 + 7AD16 ЗадачаВычислить: 27D,D816 – 191,216
ЗадачаВычислить: 27D,D816 – 191,216 ЗадачаВыполнить умножение:
ЗадачаВыполнить умножение: Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0003 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15.
Следовательно, чтобы уменьшить длину данного числа, довольно часто используется шестнадцатеричная система счисления. Шестнадцатеричная система счисления имеет основание 16, то есть состоит из 16 цифр и символов. В нем используются цифры от 0 до 9, а также буквы A, B, C, D, E и F. Поскольку для представления цифр в шестнадцатеричной системе счисления используются как числовые цифры, так и алфавиты, это число 9.0003 буквенно-цифровая система счисления . В таблице 44.3 показано соотношение между шестнадцатеричным, десятичным и двоичным форматами. Важно отметить, что шестнадцатеричные (сокращение от шестнадцатеричных) цифры от A до F эквивалентны десятичным значениям от 10 до 15. Эта система широко используется в микропроцессорной работе.
Эта система широко используется в микропроцессорной работе. Для четырехзначного шестнадцатеричного числа веса следующие:
Для четырехзначного шестнадцатеричного числа веса следующие: Эта процедура проиллюстрирована ниже.
Эта процедура проиллюстрирована ниже.
 Поскольку арифметические операции выполняются цифровыми схемами над двоичными числами, шестнадцатеричные числа должны быть сначала преобразованы в двоичные числа. Следующие несколько примеров иллюстрируют процедуру.
Поскольку арифметические операции выполняются цифровыми схемами над двоичными числами, шестнадцатеричные числа должны быть сначала преобразованы в двоичные числа. Следующие несколько примеров иллюстрируют процедуру. Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.
Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.

