Шестнадцатеричная система | это… Что такое Шестнадцатеричная система?
ТолкованиеПеревод
- Шестнадцатеричная система
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2 = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Нужно решить контрольную?
- Шестнадцатеричный редактор
- Шестиконечная звезда
Полезное
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.
При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.
Перевод чисел из шестнадцатеричной системы в десятичную
Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле
Примеры.
АЕ0716=10∙163+14∙162+0∙161+7∙160=4455110.
10016=1∙162+0∙161+0∙160=25610.
5816=5∙161+8∙160=.88
2А16=2∙161+10∙160=4210.
D16 = 1310.
Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.
Перевод чисел из шестнадцатеричной системы в двоичную и обратно
Перевести любое
шестнадцатеричное число в двоичное
можно следующим образом. Каждая цифра
шестнадцатеричной записи числа
записывается четырехзначным двоичным
числом — тетрадой.
После этого нули, стоящие слева, можно
отбросить.
016 = 00002
416 = 01002
816 = 10002
C16 = 11002
116 = 00012
516 = 01012
916 = 10012
D16 = 11012
216 = 00102
616 = 01102
A16 = 10102
E16 = 11102
316 = 00112
716 = 01112
B16 = 10112
F16 = 11112
1) D= 11012. | 2) 2A= 0010 10102= 1010102. | 3) 5816= 0101 10002= 10110002. |
И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.
Примеры.
1. 11012=D.
2. 1010102= 10 10102= 2A.
3. 10110002= 101 10002= 5816.
Восьмеричная система счисления
Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:
0, 1, 2, 3, 4, 5, 6, 7.
Перевод числа из
десятичной системы в восьмеричную и
обратно осуществляется по аналогии с
переводом в двоичную / из двоичной.
Перевод чисел из восьмеричной системы в двоичную и обратно
Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой.
08 = 0002
48 = 1002
18 = 0012
58 = 1012
28 = 0102
68 = 1102
38 = 0112
78 = 1112
Примеры.
25638= 010 101 110 0112=101011100112.
10011012= 001 001 1012= 1158.
Методические материалы для лабораторного занятия №1
Тема лабораторного занятия: Системы счисления. Измерение информации.
Количество часов: 2.
Примеры с решениями
Перевод из p-ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде
.
111001102 = 1∙27 + 1∙26 + 1∙25 + 0∙24 + 0∙23 + 1∙22 + 1∙21 + 0∙20 = 128 + 64 + 32 + 4 + 2 = 23010.
24015 = 2∙53 + 4∙52 + 0∙51 + 1∙50 = 250 + 100 + 0 + 1 = 351.
Перевод из 10-ичной системы в p-ичную.
2.1 9810 → Х2.
Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.
98 : 2 = 49. Остаток — 0.
49 : 2 = 24. Остаток — 1.
24 : 2 = 12. Остаток — 0.
12 : 2 = 6. Остаток — 0.
6 : 2 = 3. Остаток — 0.
3 : 2 = 1. Остаток — 1.
Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 9810 = 11000102.
2.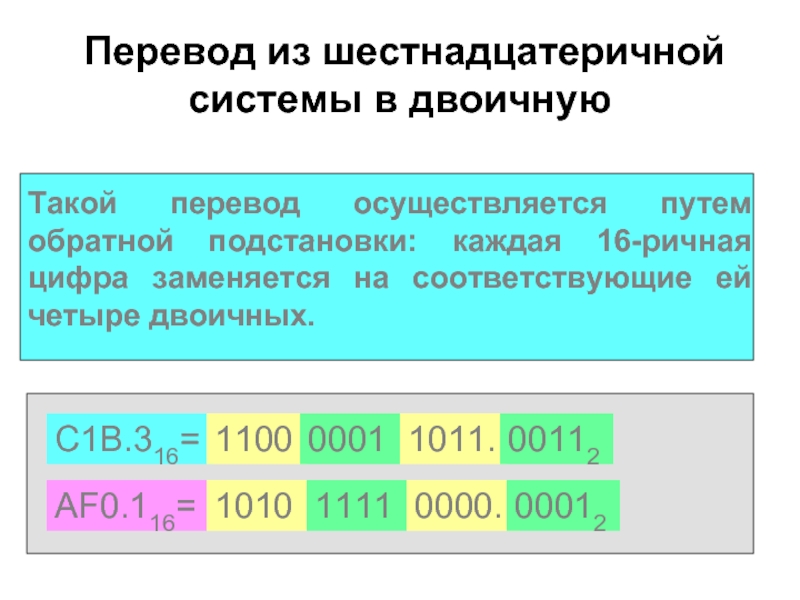 2 239110 → Х16.
2 239110 → Х16.
Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.
2391 : 16 = 149. Остаток — 7.
149 : 16 = 9. Остаток — 5.
Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 239110 = 95716.
2.3 1216510 → Х2.
Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.
1216510 = 276058 = 010 111 110 000 101 = 10111110000101.
Определение основания системы счисления p.

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?
Решение. Надо определить основание системы счисления p. Так как мы знаем, что пальцев на ногах всего 1010, то 12p=1∙p+2 = 1010. Отсюда получаем уравнение p + 2 = 10 p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 248 = 2∙8+4 = 2010, а на ногах — 128 = 1∙8+2 = 1010.
Преобразование десятичного числа 16 в шестнадцатеричное
Как записать 16 в шестнадцатеричное (по основанию 16)?
16 равно 10 в шестнадцатеричной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 16 в шестнадцатеричное или Преобразование десятичного числа в шестнадцатеричное.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответы на такие вопросы, как: Преобразование десятичного числа 16 в шестнадцатеричное или Преобразование десятичного числа в шестнадцатеричное.
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 90 008 5101 | |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 90 009 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | 900 08 А12 | 1010 | |
| 11 | Б | 13 | 1011 |
| 12 | С | 14 | 1100 |
| 13 | D | 15 | 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Декабрь | Шестнадцатеричный | Октябрь | Корзина |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 1 7 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 25 | 19 | 31 | 11001 | 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1С | 34 | 11100 |
| 29 | 1D | 35 9 0009 | 11101 |
| 30 | 1Е | 36 | 11110 |
| 31 | 1F | 37 | 11111 |
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 32 | 20 | 40 | 100000 |
| 33 | 21 | 41 | 100001 |
| 34 | 22 | 900 08 42100010 | |
| 35 | 23 | 43 | 100011 |
| 36 | 24 | 44 | 100100 |
| 37 | 25 | 45 | 100101 |
| 38 | 26 | 46 90 009 | 100110 |
| 39 | 27 | 47 | 100111 |
| 40 | 28 | 50 | 101000 |
| 41 | 29 | 51 | 101001 |
| 42 | 2А | 52 | 101010 |
| 43 | 2B | 53 | 101011 |
| 44 | 2C | 54 | 10110 0 |
| 45 | 2D | 55 | 101101 |
| 46 | 2E | 56 | 101 110 |
| 47 | 2F | 57 | 101111 |
| Декабрь | Шестнадцатеричный | Октябрь | Корзина |
|---|---|---|---|
| 48 | 30 | 60 | 110000 |
| 49 | 31 | 61 | 110001 9000 9 |
| 50 | 32 | 62 | 110010 |
| 51 | 33 | 63 | 110011 |
| 52 | 34 | 64 | 110100 |
| 53 | 35 | 65 | 110101 |
| 54 | 36 | 66 | 110110 |
| 55 | 37 | 67 | 110111 900 09 |
| 56 | 38 | 70 | 111000 |
| 57 | 39 | 71 | 111001 90 009 |
| 58 | 3А | 72 | 111010 |
| 59 | 3B | 73 | 111011 |
| 60 | 3C 9000 9 | 74 | 111100 |
| 61 | 3D | 75 | 111101 |
| 62 | 3Е | 76 | 111110 |
| 63 | 3F | 77 | 111111 |
| Декабрь | Шестнадцатеричный | 9 Октябрь0070 | Корзина |
|---|---|---|---|
| 64 | 40 | 100 | 1000000 |
| 65 9000 9 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 100001 0 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 105 | 1000101 |
| 70 | 46 | 106 | 1000110 |
| 71 90 009 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001 000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4A | 112 | 100101 0 |
| 75 | 4Б | 113 | 1001011 |
| 76 | 4C | 114 | 1001100 |
| 77 90 009 | 4D | 115 | 1001101 |
| 78 | 4E | 116 | 1001 110 |
| 79 | 4F | 117 | 1001111 |
| Декабрь | Hex | Октябрь | Корзина |
|---|---|---|---|
| 80 | 50 | 120 | 1010000 |
| 81 | 51 | 121 | 1010001 | 90 010
| 82 | 52 | 122 | 1010010 |
| 83 | 53 | 123 | 1010011 |
| 84 | 54 | 124 | 1010100 |
| 85 | 55 | 1 25 | 1010101 |
| 86 | 56 | 126 | 1010110 |
| 87 | 57 | 127 | 1010111 | 90 010
| 88 | 58 | 130 | 1011000 |
| 89 | 59 | 131 | 1011001 |
| 90 | 5A | 132 | 1011010 |
| 91 | 5B | 1 33 | 1011011 |
| 92 | 5С | 134 | 1011100 |
| 93 | 5D | 135 | 1011101 | 90 010
| 94 | 5E | 136 | 1011110 |
| 95 | 5F | 137 | 1011111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 96 | 60 90 009 | 140 | 1100000 |
| 97 | 61 | 141 | 1100001 |
| 98 | 62 | 142 9000 9 | 1100010 |
| 99 | 63 | 143 | 1100011 |
| 100 9 0009 | 64 | 144 | 1100100 |
| 101 | 65 | 145 | 1100101 |
| 66 | 146 | 1100110 | |
| 103 | 67 | 147 | 1100111 |
| 104 | 68 | 150 90 009 | 1101000 |
| 105 | 69 | 151 | 1101001 |
| 10 6 | 6А | 152 | 1101010 |
| 107 | 6B | 153 | 1101011 |
| 6С | 154 | 1101100 | |
| 109 | 6D | 155 | 1101101 |
| 110 | 6E | 156 | 1101110 |
| 111 | 6F | 157 | 1101111 |
| Декабрь | Hex | Oct | Bin |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 | 90 010
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | 163 | 1110011 |
| 116 | 74 | 164 | 1 110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 11101 10 |
| 119 | 77 | 167 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79 | 171 | 1111001 |
| 122 | 7А | 172 | 90 008 1111010|
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7D | 175 | 1111101 |
| 126 | 7E | 176 | 1111110 |
| 127 | 7F | 177 | 1111111 |
| Декабрь | Шестнадцатеричный 9007 0 | Октябрь | Ячейка |
|---|---|---|---|
| 128 | 80 | 200 | 10000000 |
| 129 | 81 9000 9 | 201 | 10000001 |
| 130 | 82 | 202 | 10000010 |
| 131 | 83 | 203 | 10000011 |
| 132 | 84 | 204 | 10000100 |
| 133 | 85 | 205 | 10000101 |
| 134 | 86 | 206 | 10000110 |
| 135 9000 9 | 87 | 207 | 10000111 |
| 136 | 88 | 210 | 10001000 |
| 137 | 89 | 211 9 0009 | 10001001 |
| 138 | 8А | 212 | 10001010 |
| 139 | 8Б | 213 | 10001011 |
| 140 | 8C | 214 | 10001100 |
| 8D | 215 | 10001101 | |
| 142 | 8E | 216 | 10001110 |
| 143 | 8F | 217 | 10001111 |
| Декабрь | Шестнадцатеричный | Октябрь | Bin 90 070 |
|---|---|---|---|
| 144 | 90 | 220 | 10010000 |
| 145 | 91 | 221 | 9000 8 10010001|
| 146 | 92 | 222 | 10010010 |
| 147 | 93 | 223 | 10010011 |
| 148 | 94 | 224 | 10010100 |
| 149 | 95 | 225 | 10010101 |
| 150 | 96 | 226 | 10010110 |
| 151 | 97 | 227 | 10010111 |
| 152 | 98 | 230 | 10011000 |
| 153 | 99 | 231 | 10011001 90 009 |
| 154 | 9A | 232 | 10011010 |
| 155 | 9B 90 009 | 233 | 10011011 |
| 156 | 9C | 234 | 10011100 |
| 157 | 9D 9000 9 | 235 | 10011101 |
| 158 | 9E | 236 | 10011110 |
| 159 | 9F | 237 | 10011111 |
| Декабрь | Шест. 160 160 | А0 | 240 | 10100000 |
|---|---|---|---|---|
| 161 | A1 | 241 | 10100001 | |
| 162 | А2 | 242 | 10100010 | |
| 163 | A3 | 243 | 10100011 | |
| 164 | A4 9 0009 | 244 | 10100100 | |
| 165 | A5 | 245 | 10100101 | 90 010|
| 166 | А6 | 246 | 10100110 | |
| 167 | A7 | 247 | 10100111 | |
| 168 | А8 | 250 | 10101000 | |
| 169 | A9 | 251 | 10101001 | |
| 170 | АА | 252 | 10101010 | |
| 171 | АВ | 253 | 10 101011 | |
| 172 | AC | 254 | 10101100 | |
| 173 | AD | 255 | 10101101 | |
| 174 | АЕ | 256 | 10101110 | |
| 175 | AF | 257 | 10101111 |
| Hex | Oct | Bin | |
|---|---|---|---|
| 192 | C0 | 300 | 1100000 0 |
| 193 | C1 | 301 | 11000001 |
| 194 | C2 | 302 | 90 008 11000010|
| 195 | С3 | 303 | 11000011 |
| 196 | C4 | 304 | 11000100 |
| 197 | C5 | 305 | 11000101 |
| 198 | C6 | 90 008 30611000110 | |
| 199 | C7 | 307 | 11000111 |
| 200 | C8 | 310 | 11001000 |
| 201 | C9 | 311 | 11001001 |
| 202 | СА | 312 | 1100101 0 |
| 203 | СВ | 313 | 11001011 |
| 204 | СС 9 0009 | 314 | 11001100 |
| 205 | CD | 315 | 11001101 |
| 206 | CE 9 0009 | 316 | 11001110 |
| 207 | CF | 317 | 11001111 |
| Дек | He x | Окт | Корзина |
|---|---|---|---|
| 208 | D0 | 320 | 11010000 | 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 900 09 |
| 211 | D3 | 323 | 11010011 |
| 212 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 |
| 214 | D6 | 326 | 1 1010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 110110 00 |
| 217 | D9 | 331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | БД | 333 | 11011011 |
| 220 | ДК | 334 | 11011100 |
| 221 | ДД | 335 | 11011101 |
| 222 | DE | 336 90 009 | 11011110 |
| 223 | ДФ | 337 | 11011111 |
| Декабрь | Шестнадцатеричный | Октябрь | 900 69 Корзина|
|---|---|---|---|
| 224 | E0 | 340 | 11100000 |
| 225 | E 1 | 341 | 11100001 |
| 226 | E2 | 342 | 11100010 |
| 227 | Е3 | 343 | 11100011 |
| 228 | E4 | 344 | 11100100 |
| 229 | E5 | 3 45 | 11100101 |
| 230 | E6 | 346 | 11100110 |
| Е7 | 347 | 11100111 | |
| 232 | E8 | 350 | 11101000 |
| 233 | Е9 | 351 | 11101001 |
| 234 | EA | 352 | 11101010 |
| 235 | EB 9 0009 | 353 | 11101011 |
| 236 | ЕС | 354 | 11101100 | 90 010
| 237 | ЭД | 355 | 11101101 |
| 238 | EE | 356 | 11101110 |
| 239 | ЭФ | 357 | 11101111 |
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 240 | F0 | 360 | 11110000 |
| 241 | F1 | 361 9000 9 | 11110001 |
| 242 | F2 | 362 | 11110010 |
| 243 | F3 | 363 | 11110011 |
| 244 | F4 | 364 | 11110100 |
| 245 | F5 | 365 | 111101 01 |
| 246 | F6 | 366 | 11110110 |
| 247 | F7 | 367 | 11110111 |
| 248 | F8 | 370 | 11111000 |
| 249 | F9 | 371 | 11111001 |
| 250 | FA | 372 | 11111010 |
| 251 | FB | 373 900 09 | 11111011 |
| 252 | FC | 374 | 11111100 |
| 25 3 | ФД | 375 | 11111101 |
| 254 | FE | 376 | 11111110 |
| FF | 377 | 11111111 |
Преобразователь базы чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 2540 восьмеричное в десятичное
- 11111001011 двоичное в восьмеричное
- 33554432 десятичное в восьмеричное
- 28672 десятичное в двоичное 92 858
- 160 десятичный в восьмеричный
- A9 шестнадцатеричный в восьмеричный
- 47 восьмеричный в двоичный
- двоичный до восьмеричной
- 11010001 двоичное число в десятичное
Случайный преобразователь | Преобразование шестнадцатеричной системы счисления в шестнадцатеричную Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (на массу)Конвертер удельной энергии, теплоты сгорания (на объем) температура Конвертер интервалов Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиKine Конвертер вязкости maticПоверхностное натяжение КонвертерПроницаемость, проницаемость, паропроницаемость Конвертер скорости пропускания паров влаги Конвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер силы светаКонвертер освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеОптическая мощность (диоптрий) Конвертер ) в увеличение (X)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаПреобразователь электрического токаКонвертер линейной плотности токаПреобразователь поверхностной плотности токаКонвертер напряженности электрического поляПреобразователь потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь проводимостиПреобразователь емкостиВ Преобразователь электрической проводимостиПреобразователь реактивной мощности переменного токаПреобразователь американского калибра проводовПреобразование Уровни в дБм, дБВ, Ваттах и других единицах измерения. двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 — 8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36Частота и длина волныЗнаете ли вы, что некоторые животные намного лучше различают цвета, чем люди, и они даже могут видеть ультрафиолетовый и инфракрасный свет? Нажмите или коснитесь, чтобы узнать больше о длине волны и цвете! Обзор Различные способы представления чисел Индо-арабские цифры Римская Системы в других культурах Унарная Позиционная система Двоичная Классификация чисел Отрицательные числа Рациональные числа Натуральные числа Целые числа Комплексные числа Простые числа Интересные факты о числах Цифры против мошенничества Современный счет в торговле Группировка цифр Несчастливые числа Изучайте технический английский с помощью этого видео! ОбзорПриложение-калькулятор для iPhone Число — это абстрактное математическое понятие, представляющее количество. Различные способы представления чиселНекоторые исследователи считают, что понятие числа создавалось независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания. Индийско-арабские цифры Индуистско-арабская система счисления сегодня является одной из наиболее широко используемых в мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках. Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). РимскиеРимские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Римские цифры основаны на семи цифрах, записанных буквами латинского алфавита:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что два должны быть добавлены, но меньшее число перед большим означает, что меньшее число вычитается из большего. Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, которая имеет только два клинописных символа, для одного (чем-то напоминающего букву «Т») и для десяти (немного похожего на букву «С»). Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Унарная система счисления. Метки подсчета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная системаПозиционная система работает с основанием. Например, в базе 10 у нас есть следующее:
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисленияДвоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу: Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» единицы. 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нуль, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательного числа. Простые числаПростые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничества Для предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется 10-кратная система счисления, по-прежнему свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чисел И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это взято из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четных чисел считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже неудачный, потому что он представляет духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Японии другое несчастливое число — 9.2896 9 , что имеет то же произношение, что и «страдание». В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». Это подразумевает, что жизнь окончена, и относится к смерти. 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией. Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Ссылки Эта статья была написана Катериной Юрием Преобразование десятичного числа в основание 32 Преобразование двоичного числа в шестнадцатеричное Преобразовать восьмеричное в десятичное Преобразование десятичной системы счисления в 36-ю Преобразование десятичной системы в 24-ю Преобразование 3-й системы счисления в десятичную Преобразование двоичной системы в восьмеричную Преобразование десятичной системы в шестнадцатеричную Вам могут быть интересны другие преобразователи из группы Общие преобразователи единиц:Конвертер длины и расстояния Конвертер массы Объем сухого вещества и общие измерения для приготовления пищи Преобразователь площади Преобразователь объема и общего измерения для приготовления пищи Преобразователь температуры Давление, стресс, мод Юнга Преобразователь улуса Преобразователь энергии и работы Преобразователь мощности Преобразователь силы Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Конвертер топливной эффективности, расхода топлива и экономии топлива Конвертер единиц хранения информации и данных Конвертер метрических префиксов Конвертер передачи данных Курсы обмена валют Размеры мужской одежды и обуви 9 0003 Женская одежда и обувь Размеры Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут получите ответ от опытных технических переводчиков. |


 также
также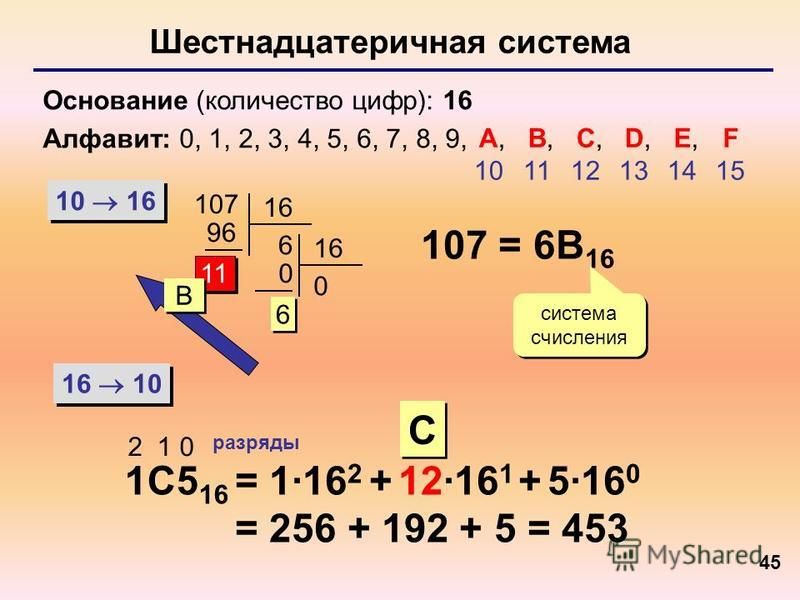 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
 также
также

 Конвертер магнитодвижущей силы. Конвертер напряженности магнитного поля. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Конвертер магнитодвижущей силы. Конвертер напряженности магнитного поля. Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.
Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.

 Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.

 Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
 Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
 Один из таких, по слухам, случаев насмешек привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Один из таких, по слухам, случаев насмешек привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
 Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1.
Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1.