Системы счисления | Hexlet Guides
В этом гайде разберемся, что такое системы счисления, для чего программисты используют непривычные способы для записи чисел и как их понимать.
- Что такое системы счисления
- От десятичных чисел к двоичным
- Зачем нужна двоичная система
- Как переводить двоичные числа в десятичные
- Как переводить десятичные числа в двоичные
- Шестнадцатеричная система счисления
- Восьмеричная система счисления
- Конвертация чисел в программах
- Сервисы для перевода из системы в систему
- Заключение
Что такое системы счисления
С давних пор людям нужно было записывать числа. В торговле числа нужны, чтобы знать, сколько товаров есть на складе и сколько денег принесла сделка. Записи о положении небесных тел помогли шумерам составить первый календарь, а календарь, в свою очередь, пригодился, чтобы заранее готовиться к посевным и сбору урожая. Строительные сметы, переписи населения, распределение наследства — числа оказались очень востребованными даже в самых древних государствах.
Так что люди научились записывать числа в незапамятные времена. Небольшие числа легко записывались зарубками или насечками, но если в числе несколько знаков, требуется иная система записи. Эту проблему в разных странах решали по-разному.
Сейчас разные способы записи чисел называются системами счисления.
Систем счисления было придумано довольно много, и даже в наши дни мы используем две системы, возникшие в далёкой древности. Из Древнего Рима к нам пришла римская система счисления, где цифры обозначаются буквами латинского алфавита. За основу римляне взяли количество пальцев на одной руке — 5, и на двух руках — 10. Числа 1, 5 и 10 в римской системе обозначаются буквами I, V и X, и с помощью них можно записать любое число от 1 до 49. Например, VII это 7, а XIX — 19.
От Древних Шумеров мы научились делить дроби на шестьдесят частей. Именно из-за них в нашем часе 60 минут, а в минуте 60 секунд. Шумерская система счисления так и называется — шестидесятеричная.
Но, конечно, наиболее привычной выглядит численная запись в системе, которую придумали в Древней Индии. Сейчас ее называют арабской или десятичной системой счисления.
От десятичных чисел к двоичным
Разберемся, как устроена десятичная система, на примере произвольного большого числа.
Это четырехзначное число, потому что оно состоит из четырёх цифр. И, поскольку речь идёт о десятичной системе, мы можем использовать десять различных цифр.
Величина, которая скрывается за каждой цифрой, зависит от её позиции, поэтому такую систему счисления называют также и позиционной. Справа мы записываем самые младшие значения — единицы, слева от них десятки, затем сотни, и так далее. Запись 1702 означает буквально следующее.
Цифры, записанные в соседних позициях, различаются в десять раз — это и есть десятичная система. Однако, как мы говорили ранее, привычная нам десятичная система — далеко не единственная. Однако, опираясь на неё, нам будет проще понять принципы работы других систем счисления.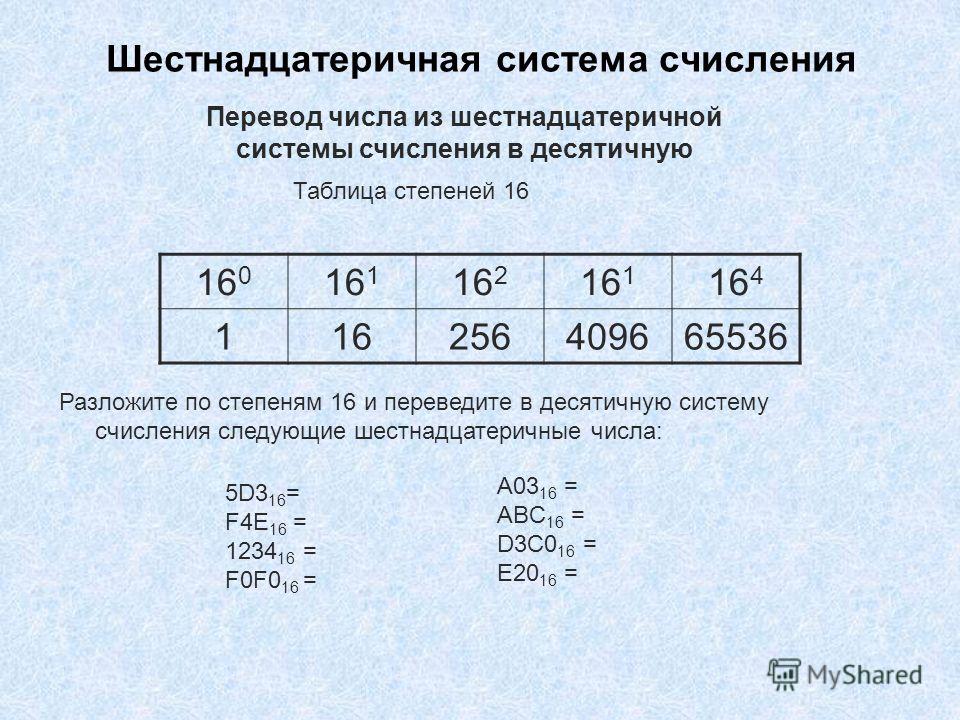
Например, для записи того же самого числа 1702 в двоичной системе надо придерживаться тех же правил, но вместо десяти цифр нам потребуется всего две — 0 и 1.
Цифры, записанные в соседних позициях, будут различаться не в десять раз, а в два. То есть там, где в десятичной системе мы видим 1, 10, 100, 1 000, 10 000, в двоичной будут числа 1, 2, 4, 8, 16 и так далее.
Это очень большое двоичное число. Давайте запишем его в привычной форме:
Это число могло бы быть очень большим десятичным числом, потому что состоит из тех же цифр. Чтобы отличать двоичные числа от десятичных, в качестве индекса у них указывают основание системы счисления, то есть 2.
Это особенно важно, когда в тексте одновременно встречаются десятичные и двоичные числа.
Зачем нужна двоичная система
Двоичная система выглядит очень непривычно и числа, записанные в ней, получаются огромными. Зачем она вообще нужна? Разве компьютеры не могут работать с привычной нам десятичной системой?
Оказывается, когда-то они именно так и работали.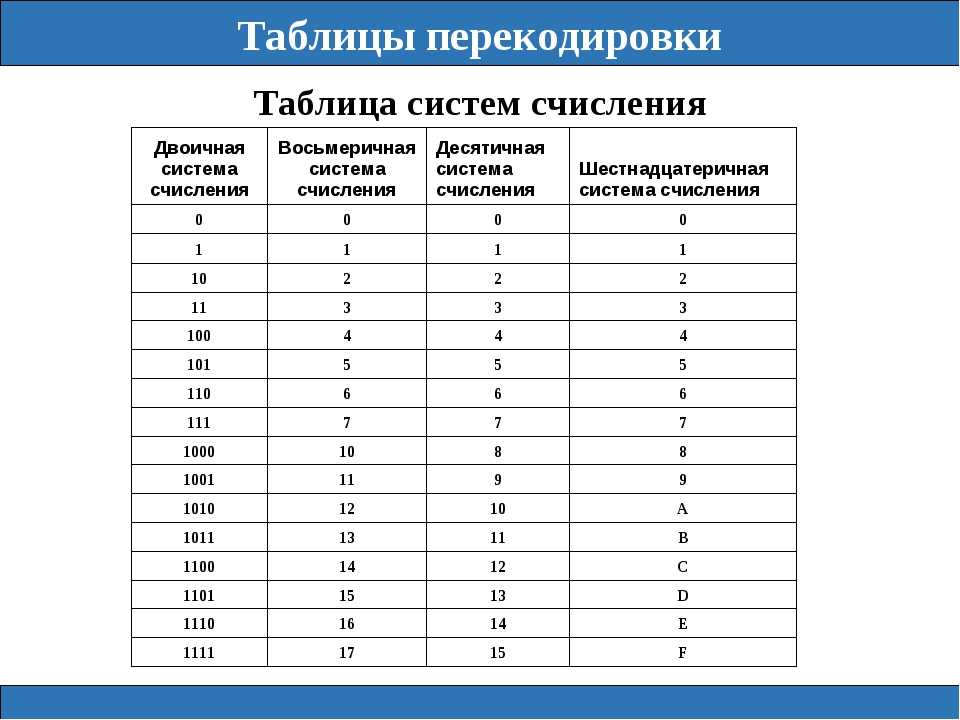
Самый первый компьютер ENIAC, разработанный в 1945 году, хранил числа в десятичной системе счисления. Для хранения одной цифры применялась схема, которая называется кольцевым регистром, она состояла из десяти радиоламп.
Чтобы записать все числа до миллиона — от 0 до 999 999 — надо шесть цифр, значит, для хранения таких чисел нужно целых 60 ламп.
Инженеры заметили, что если бы они кодировали числа в двоичной системе, то для хранения таких же больших чисел им бы потребовалось всего двадцать радиоламп — в три раза меньше!
Первое преимущество двоичных чисел — простота схем. Второе, и не менее важное — быстродействие. Сложение чисел, хранящихся в кольцевом регистре, требует до десяти тактов процессора на каждую операцию. Сложение двоичных чисел можно выполнить за один такт — то есть в десять раз быстрее.
Группа инженеров, создавших первый компьютер, в 1946 году опубликовала статью, где обосновала преимущество двоичной системы для представления чисел в компьютерах.
Первой среди авторов была указана фамилия американского математика Джона фон Неймана. Поэтому сейчас принципы проектирования компьютеров называются архитектурой фон Неймана, хотя это не совсем справедливо по отношению к другим изобретателям компьютера.
При разработке программы с двоичной записью столкнуться довольно сложно: компьютер в подавляющем большинстве случаев сам переводит двоичные числа в десятичные и обратно. Можно долго писать код, даже не подозревая, что внутри компьютера данные хранятся каким-то особым образом.
Зачем изучать двоичную систему, если компьютер делает всю работу за нас? Иногда программистам приходится писать программы, которые работают напрямую с оборудованием. Например, разработчики игр должны знать, как работают видеокарты, чтобы сделать компьютерную графику быстрее. А разработчики операционных систем понимают, как устроены диски, чтобы надежно хранить данные.
Программы, которые работают с железом напрямую, называются системными или низкоуровневыми.
Для их создания разработчик должен понимать, как устроен компьютер. Поэтому изучение систем счисления позволяет программисту расширить свой профессиональный диапазон и стать специалистом широкого профиля.
Поэтому для того, чтобы писать сложные системные программы, нужно понимать, как устроена двоичная система счисления.
Как переводить двоичные числа в десятичные
Разберемся, как быстро переводить двоичные числа в десятичные. Для примера потребуется достаточно большое двоичное число, чтобы мы не могли вычислить его на пальцах.
Запишем его в математической записи, помня, что вместо основания 10, мы используем основание 2.
Из этого примера видно, что у всех слагаемых только два множителя — 0 и 1. Слагаемые с множителем 0 равны нулю, поэтому их можно отбросить, оставив только слагаемые с множителем 1.
У слагаемых с множителем 1 этот множитель можно не записывать.
Теперь нетрудно посчитать сумму.
Вывод: число 11010 в двоичной записи — то же самое, что 26 в десятичной.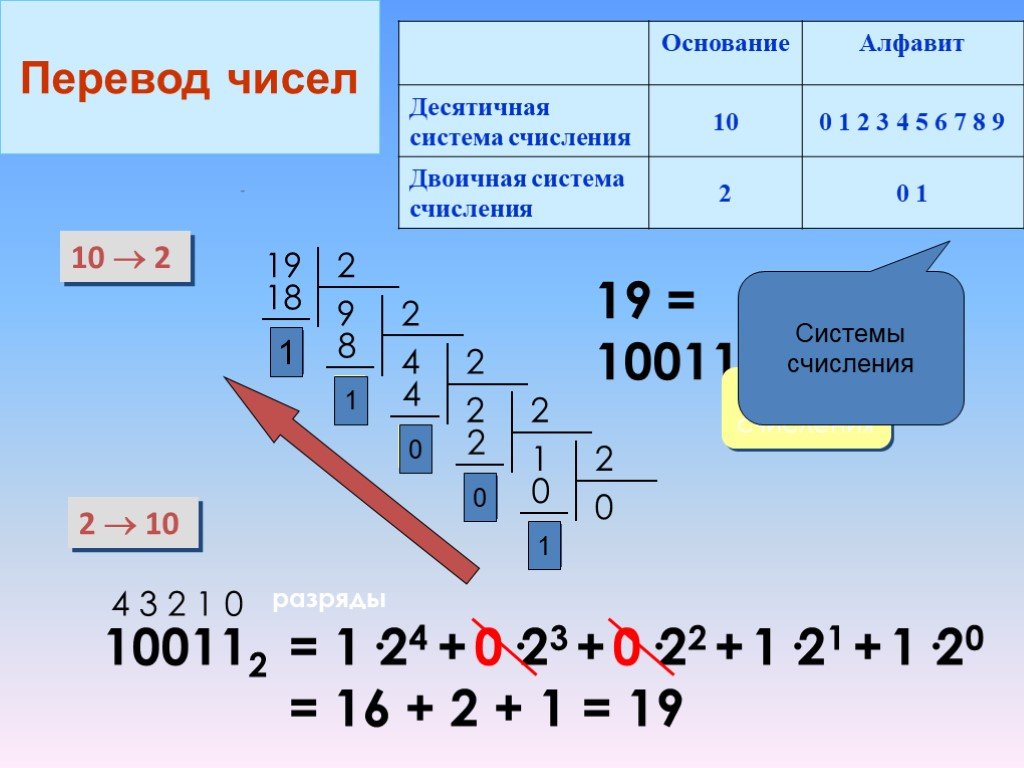
Ещё раз повторим, как перевести двоичное число в десятичное.
- Записать число в математическом виде
- Отбросить слагаемые с множителем 0
- Сложить результат
Программисты иногда запоминают некоторые степени числа два, чтобы уметь оценивать порядок двоичных чисел. Вы можете подглядывать в эту таблицу:
| Двоичное число | Степень 2 | Десятичное число |
|---|---|---|
| 12 | 20 | 1 |
| 102 | 21 | 2 |
| 1002 | 22 | 4 |
| 10002 | 23 | 8 |
| 1 00002 | 24 | 16 |
| 10 00002 | 25 | 32 |
| 100 00002 | 26 | 64 |
| 1000 00002 | 27 | 128 |
| 1 0000 00002 | 28 | 256 |
| 10 0000 00002 | 29 | 512 |
| 100 0000 00002 | 210 | 1 024 |
| 1 0000 0000 0000 0000 | 216 | 65 536 |
| 1 0000 0000 0000 0000 0000 00002 | 224 | 16 777 216 |
| 1 0000 0000 0000 0000 0000 0000 0000 00002 | 232 | 4 294 967 296 |
С помощью этой таблицы можно переводить числа из двоичной системы в десятичную практически «в уме».
Как переводить десятичные числа в двоичные
Эта задача похожа на математическую загадку, и её можно встретить на олимпиаде для школьников.
Чтобы научиться её решать, давайте ещё раз посмотрим на первые натуральные числа в двоичной и десятичной записи.
| Десятичное число | Двоичное число |
|---|---|
| 1 | 12 |
| 2 | 102 |
| 3 | 112 |
| 4 | 1002 |
| 5 | 1012 |
| 6 | 1102 |
| 7 | |
| 8 | 10002 |
| 9 | 10012 |
Обратим внимание на следующую закономерность: все чётные числа — 2, 4, 6 и 8 — в двоичной записи заканчиваются на 0.
Все нечётные числа 1, 3, 5, 7 и 9 — на 1. Этому есть простое объяснение — в двоичной записи число 2 это как 10 в десятичной. Если двоичное число делится на два, оно круглое. Математики говорят, что чётные числа делятся на 2 без остатка (или с остатком 0), а нечётные — с остатком 1:
- при делении 4 на 2 остаток 0;
- при делении 5 на 2 остаток 1;
- при делении 6 на 2 остаток 0;
- при делении 9 на 2 остаток 1.
Попробуем перевести десятичное число 26 в двоичную систему. Для этого используем деление уголком на 2.
Если 26 разделить на 2, то в результате получится 13, остаток от деления 0. Продолжаем дальше:
- 13 разделить на 2, в результате получится 6, остаток от деления 1;
- 6 разделить на 2, в результате получится 3, остаток от деления 0;
- 3 разделить на 2, в результате получится 1, остаток от деления 1;
- 1 разделить на 2, в результате получится 0, остаток от деления 1;
Из остатков 1, 1, 0, 1 и 0 складывается нужная нам двоичная запись.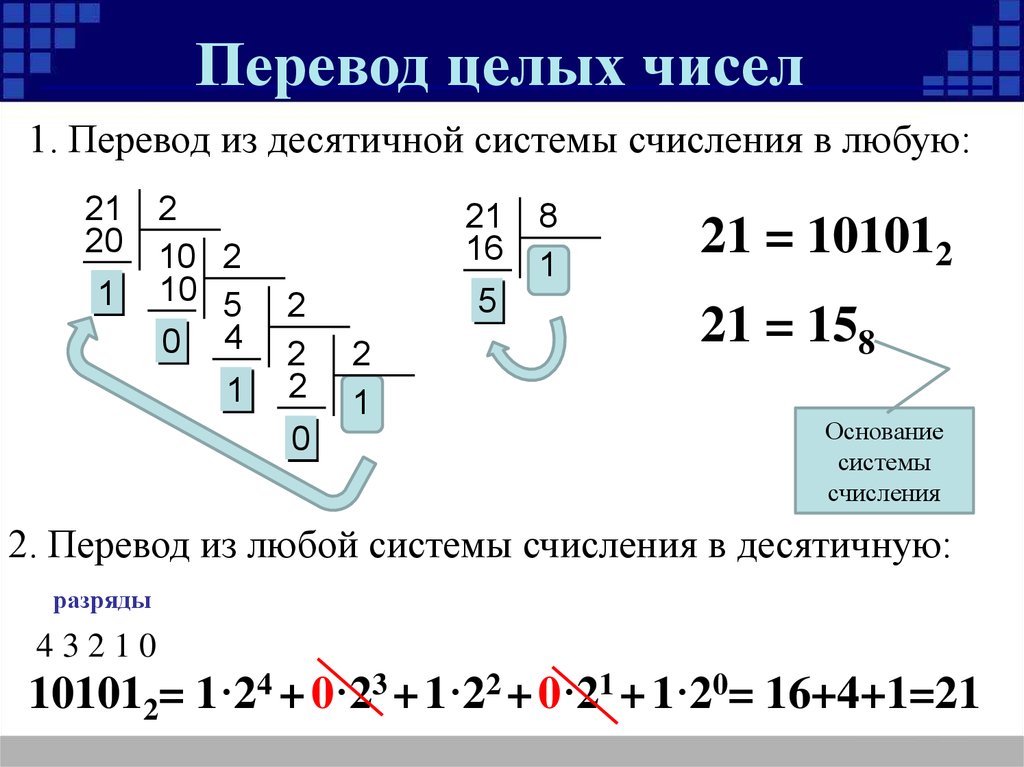
Шестнадцатеричная система счисления
Мы знаем, что компьютер использует числа для представления любой информации. Например, цвета хранятся в виде трёх чисел — яркости красной, зелёной и синей компонентов цвета. На каждый компонент отводится восемь двоичных позиций, поэтому максимальная яркость компонента равна 11111111₂ или 255. Цвет целиком описывается большим 24-х разрядным двоичным числом, например, 11111010 10000000 01110010. Это цвет Salmon из таблицы цветов HTML, он же лососевый цвет.
Старшие восемь позиций отводятся для хранения красного компонента, средние восемь — зелёного, и младшие восемь — синего. Мы видим, что такая запись очень громоздка и неудобна.
Кажется, что цвет удобнее записать как десятичное число 16416882. Хотя оно занимает меньше места, по нему трудно понять, какова яркость каждого компонента.
Чтобы записывать большие двоичные числа, программисты придумали использовать шестнадцатеричную систему счисления:
- В десятичной системе десять цифр, а в шестнадцатеричной — шестнадцать
- В десятичной системе соседние позиции отличаются в десять раз, а в шестнадцатеричной — в шестнадцать раз
Как и в случае с двоичной системой, цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 заимствуются из десятичной системы.
| Основание 16 | Основание 10 | Основание 2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Шестнадцатеричная система счисления хороша тем, что группа из четырёх двоичных цифр кодируется одной шестнадцатеричной цифрой.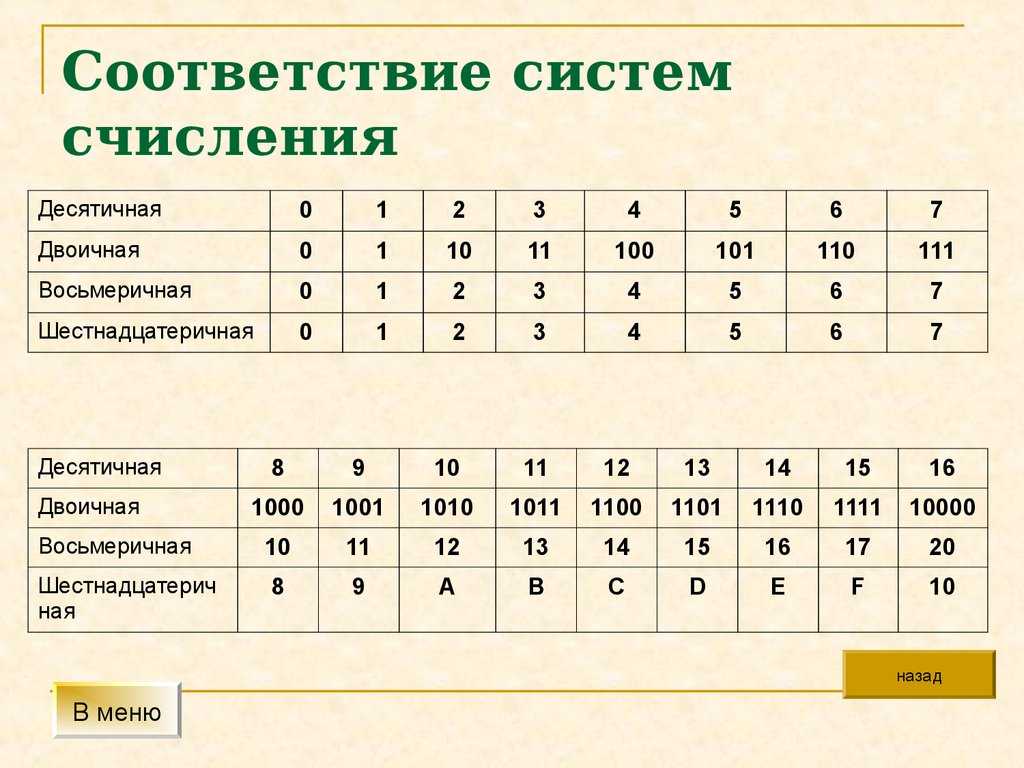
Таким образом, лососевый цвет выглядит как:
В шестнадцатеричной системе счисления он записывается так:
Вначале трудно понять, каков порядок у шестнадцатеричного числа FA. Как и в случае с двоичными числами, программисты обычно помнят порядки круглых шестнадцатеричных чисел. Но можно не запоминать, а подглядывать в эту таблицу:
| Шестнадцатеричное число | Десятичное число |
|---|---|
| 1016 | 16 |
| 2016 | 32 |
| 3016 | 48 |
| 4016 | 64 |
| 5016 | 80 |
| 6016 | 96 |
| 7016 | 112 |
| 8016 | 128 |
| 9016 | 144 |
| A016 | 160 |
| B016 | 176 |
| C016 | 192 |
| D016 | 208 |
| E016 | 224 |
| F016 | 240 |
| 10016 | 256 |
| 100016 | 4 096 |
| 1 000016 | 65 536 |
| 10 000016 | 1 048 576 |
| 100 000016 | 16 777 216 |
| 1000 000016 | 268 435 456 |
| 1 0000 000016 | 4 294 967 296 |
Чтобы переводить числа из десятичной системы в шестнадцатеричную и обратно, двоичное представление можно использовать как промежуточное.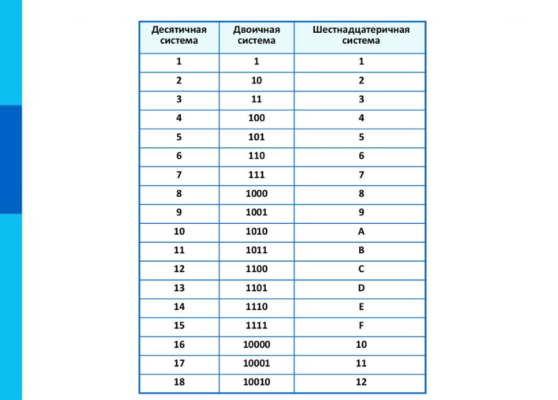
Часто это самый простой способ: двоичное и шестнадцатеричное представления без труда переводятся друг в друга.
Восьмеричная система счисления
Восьмеричная система когда-то использовалась наравне с шестнадцатеричной. Из названия понятно, что она использует всего восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричная система подходит для представления шести-, девяти- и двенадцатиразрядных двоичных чисел.
Такие числа встречаются нечасто. Один из самых известных примеров использования восьмеричных чисел — права доступа в операционной системе UNIX. Они записываются девятизначным двоичным числом, например 110100100 или 111101100. Запоминать и передавать такие числа неудобно, поэтому программисты предпочитают восьмеричную систему счисления, и записывают права доступа в виде 644 или 754.
Популярные операционные системы Linux и MacOS берут своё начало в UNIX, поэтому там права доступа также задаются восьмеричным числом.
Пользователи UNIX используют команду stat, чтобы узнать права доступа, и команду chmod, чтобы изменить их.
На рисунке вы видите, что команды stat и chmod используют восьмеричные числа. Подробный рассказ об этих командах выходит за рамки нашей статьи. Узнаете больше о правах доступа, и о том, что означают эти числа, можно изучив командную строку Linux.
Подводя итог, можно сказать, что восьмеричные числа сейчас используются редко. В подавляющем большинстве случаев программисты используют шестнадцатеричную запись.
Конвертация чисел в программах
Языки программирования умеют работать с числами, записанными в разных системах счисления, и переводить их из одной системы в другую. Для примера рассмотрим работу с разными системами счисления на Python и JavaScript.
Python
Чтобы записать в Python двоичное число, добавьте перед ним префикс 0b. Десятичное число 26 можно записать в виде 0b11010. У шестнадцатеричных чисел префикс 0x, а у восьмеричных — 0o.
print(0b11010) # => 26 print(0x1a) # => 26 print(0o32) # => 26
Во всех случаях, чтобы записать число, мы пишем сначала цифру ноль «0», а затем букву, которая определяет систему счисления.
Буква «b» — первая в слове binary (двоичный), а буква «o» — в слове octal (восьмеричный). Буква «x» выбивается из общего правила — это третья буква в слове hexadecimal (шестнадцатеричный).
Функции bin(), hex() и oct() преобразуют число в двоичную, шестнадцатеричную и восьмеричную системы.
print(bin(26)) # => '0b11010' print(hex(26)) # => '0x1a' print(oct(26)) # => '0o32'
Благодаря префиксной записи и функциям bin(), hex() и oct(), мы можем преобразовывать числа из любой системы в любую.
print(hex(0o32)) // >= '0x1a'
JavaScript
В JavaScript для представления чисел используются те же самые префиксы, что и в Python. 0b11010, 0x1a и 0o32 — записи числа 26 в двоичной, шестнадцатеричной и восьмеричной системах счисления.
console.log(0b11010) // => 26 console.log(0x1a) // => 26 console.log(0o32) // => 26
Для преобразования чисел в другую систему счисления нужно вызывать метод toString(), передав в качестве параметра основание системы.
Обычно в JavaScript мы можем вызвать метод у объекта с помощью точки. Например, если мы сохранили число в переменной i, мы можем узнать его шестнадцатеричное представление, вызвав метод i.toString(16). Но мы не можем вызывать метод у числа 2 — 2.toString(16) — потому что в JavaScript точка в записи чисел разделяет целую и дробную части. Если дробная часть равна нулю, её можно не записывать, поэтому «2.» означает то же самое, что и «2.0».
В примере вы видите три корректных способа обойти эту проблему, и вызвать метод toString() у числа 26.
console.log((26).toString(2)) // => '11010' console.log(26..toString(16)) // => '1a' console.log(26 .toString(8)) // => '32'
Сервисы для перевода из системы в систему
Существует множество сервисов для перевода чисел из системы в систему. Это умеет даже Google.
Чтобы перевести двоичное число, например, 11010 в десятичную систему, надо ввести запрос 0b11010 decimal.
Чтобы перевести десятичное число, например, 26 в двоичную систему, надо ввести запрос 26 binary.
Обратите внимание, что Google использует префикс 0b, чтобы отличать двоичные числа от десятичных.
Чтобы перевести десятичное число 137 в шестнадцатеричную систему, введите запрос 137 hex.
Чтобы перевести шестнадцатеричное число 2BAD в десятичную систему, введите запрос 0x2BAD decimal.
Google использует префикс 0x для того, чтобы отличать шестнадцатеричные числа от всех прочих. Чтобы перевести число 121 в восьмеричную систему, введите запрос 121 octal.
Чтобы перевести число обратно, введите в строке поиска запрос 0o171 decimal.
Мы видим, что Google для представления чисел в двоичной, шестнадцатеричной и восьмеричной системах счисления использует такие же префиксы, которые мы видели в примерах на Python и JavaScript.
Заключение
Люди изобрели разные способы записывать числа.
Мы называем их системами счисления. Привычный для нас способ записи называется десятичной системой счисления.
Компьютеры, которые работали в десятичной системе, оказались сложными и медленными. Хранение чисел в двоичной системе позволило упростить схемы и ускорить работу компьютеров.
Обычно нам не нужно знать, как именно компьютер хранит числа, потому что он умеет переводить их в привычную нам форму. Но если мы хотим разрабатывать программы, которые работают с оборудованием напрямую — системные утилиты или компьютерные игры, — нужно разобраться, как устроены двоичная и шестнадцатеричная системы.
Существует ряд алгоритмов, которые помогают перевести число из одной системы в другую, но они достаточно запутанные. Проще использовать Google.
Двоичная запись чисел очень громоздкая, поэтому программисты предпочитают записывать числа в шестнадцатеричной системе счисления. Восьмеричная запись чисел сейчас используется очень редко.
Вы можете конвертировать числа из системы в систему на своём любимом языке программирования.
Перевод 8-миричных и 16-тиричных чисел в двоичную систему счисления.
Для перевода 8-ного числа в 2-ую с.с. надо каждую 8-ую цифру заменить двоичным кодом.
Для перевода 16-ного числа в 2-ую с.с. надо каждую 16-ую цифру заменить двоичным кодом.
Например:
8-ая и 16-ая с.с. используются для удобства чтения двоичных чисел.
Перевод в 10-ую систему счисления
Чтобы перевести число из системы
счисления с основанием q
в систему счисления с основанием 10 надо
представить число в виде суммы произведений
значений разрядов на их веса, т.е. перевод
в десятичную систему числа x, записанного
в q-ичной cистеме счисления (q = 2, 8 или 16)
в виде xq = (anan-1 … a0 , a-1 a-2 … a-m)q сводится к вычислению значения
многочлена
x10 = an qn +
an-1 qn-1 + .
.. + a0 q0 + a-1 q-1 + a-2 q-2 + … + a-m q-m
средствами десятичной арифметики.
Примеpы:
Перевод из 10-ой системы счисления
Для перевода десятичного числа в систему счисления с основанием q надо разделить в десятичной системе счисления это десятичное число на q и найти остаток. Если частное больше q, то разделить его на q и найти остаток. Эту операцию выполнять до тех пор пока не получим частное меньшеq. Чтобы получить искомое число надо записать последнее частное старшим разрядом искомого числа, последний остаток следующим разрядом искомого числа и т.д. Младшим разрядом будет первое частное.
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 7510 = 1 001 0112
= 1138 = 4B16.
Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2.
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Для чисел, имеющих как целую, так и
дробную части, перевод из десятичной
системы счисления в другую осуществляется
отдельно для целой и дробной частей по
правилам, указанным выше.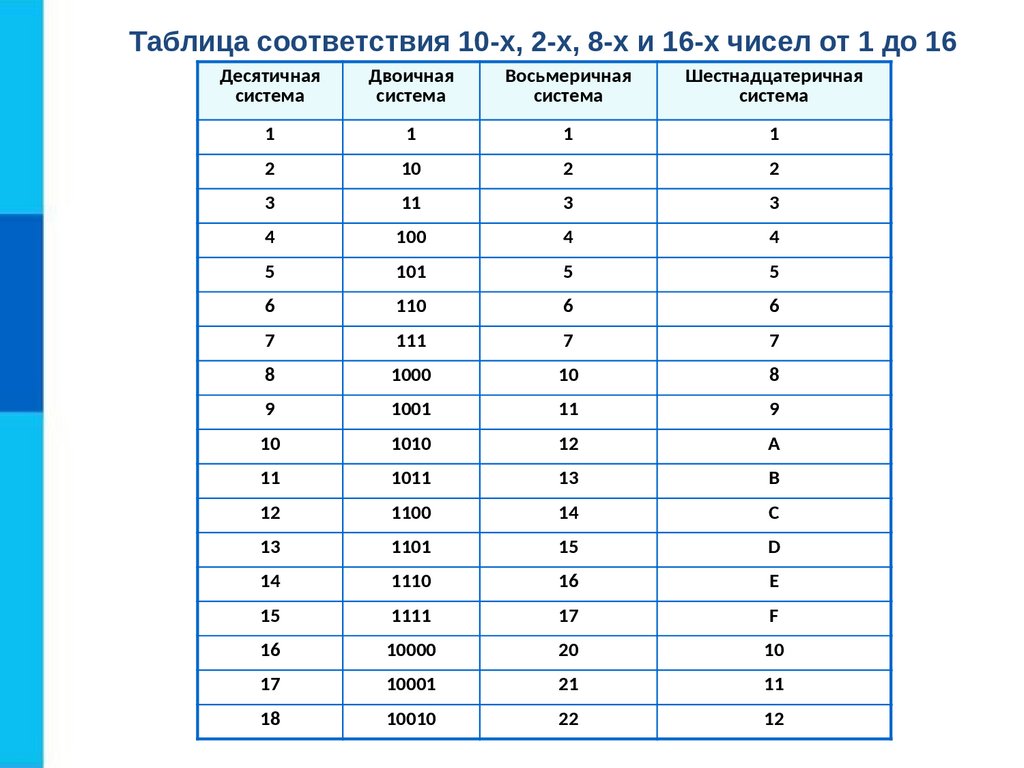
Сводная таблица переводов целых чисел из одной системы счисления в другую
Рассмотрим только те системы счисления, которые применяются в компьютерах – десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:
На этом рисунке использованы следующие обозначения:
в кружках записаны основания систем счисления;
стрелки указывают направление перевода;
номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице.
Например: означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
Сводная таблица переводов целых чисел
Заметим, что восьмеричная и шестнадцатеричная
ПСС непосредственно не используются в
ЭВМ для реализации операций, а служат
лишь для облегчения чтения и записи
человеком-оператором «машинных» кодов
и широко используются в технике
программирования.
Преобразование дробей в десятичные числа
Преобразование дробей в десятичные числа| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
Таблицы преобразования дробей в десятичные числаВажное примечание: любой диапазон чисел, равный , подчеркнутый означает, что эти числа повторяются.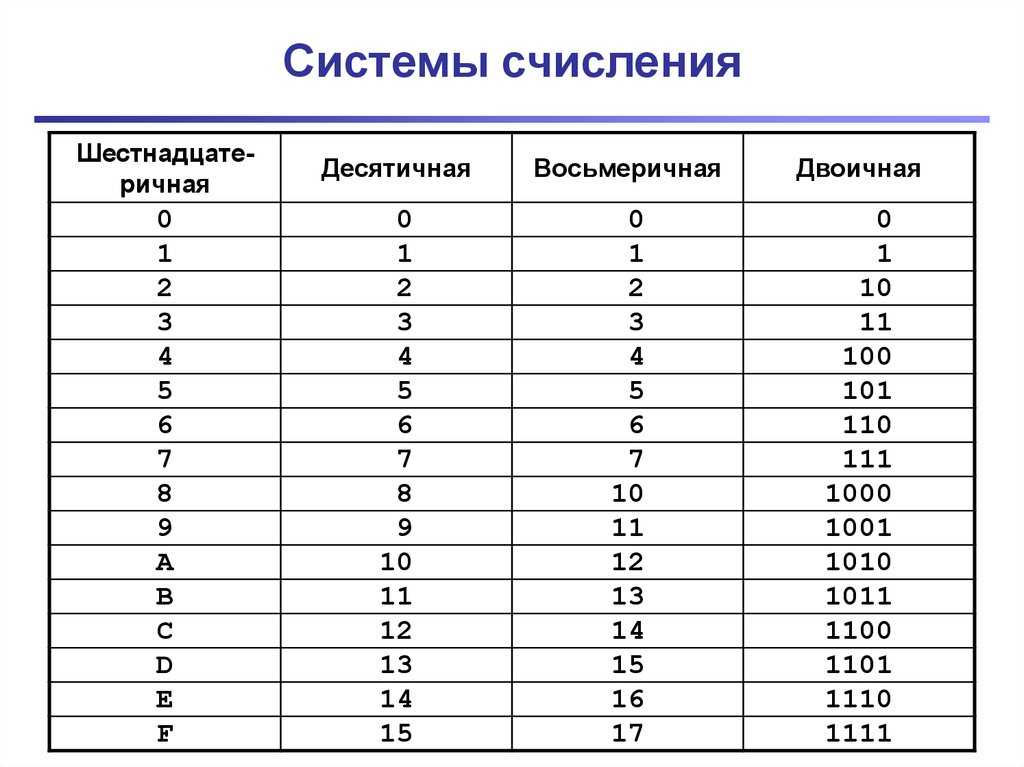 Например, 0, 09 означает 0,09.0909…. Перечислены только дроби в наименьшем выражении. Например, чтобы найти 2/8, сначала упростите его до 1/4, а затем выполните поиск.
в таблице ниже.
Нужно преобразовать повторяющуюся десятичную дробь в дробь? Следуйте этим примерам: ПРИМЕЧАНИЕ Образец, если нули, предшествующие повторному десятичному делу: Чтобы преобразовать десятичную дробь, которая начинается с неповторяющейся части , например
как 0,21 456 456456456456…, до дроби, запишите в виде суммы
неповторяющаяся часть и повторяющаяся часть.  |
142857 
09 
2 2222222… = 2/9 