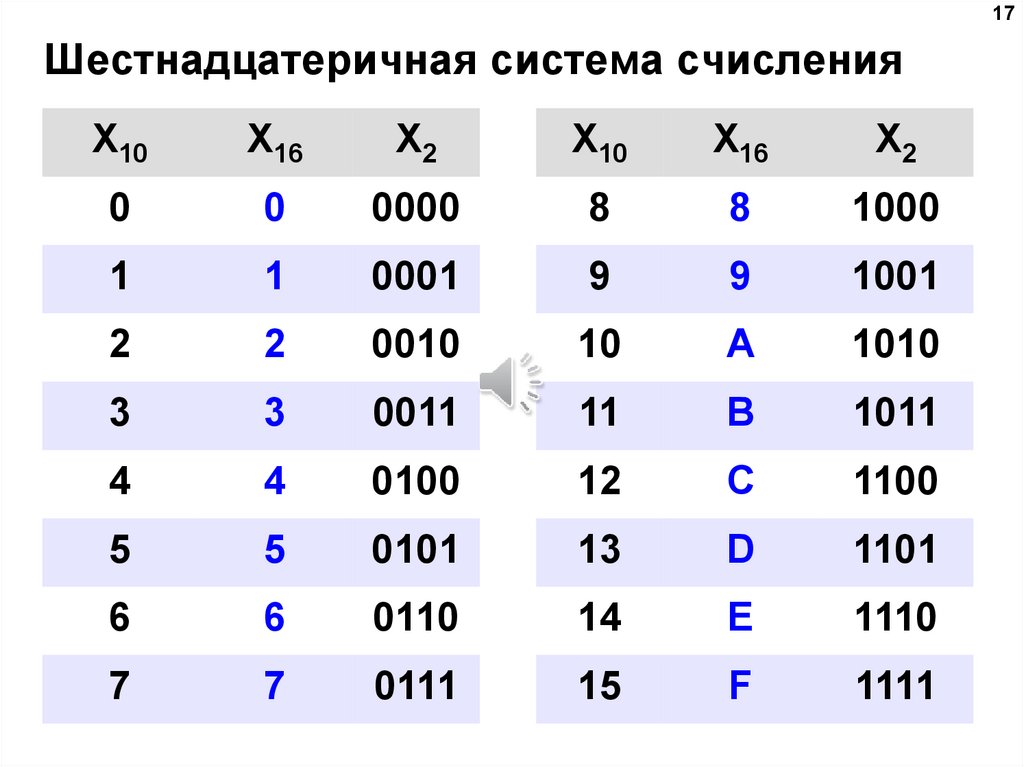
Системы счисления

Кодирование информации — представление информации в той или иной стандартной форме.

Например, письменность и арифметика — кодирование речи и числовой информации, музыку кодируют с помощью нот.

Чтобы использовать числа их нужно как-то записывать и называть.

Самые первые системы нумерации возникли в древнем Египте и Месопотамии — применяли иероглифы.

Системы счисления — способы кодирования числовой информации, то есть способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.

В древнем Вавилоне делили час на 60 минут, угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток. 

В Риме семь чисел обозначают буквами. 1-I, 5-V, 10-X, 50- L,100-C, 500-D, 1000-M.

IV (4=5-1)

VI (6=5+1)

Значение числа определяется как сумма или разность цифр числа. Это непозиционная система счисления.

Славяне числа кодировали буквами А=1, В=2, Г=3; чтобы избежать путаницы ставился специальный знак ~  титло. Алфавитная система счисления. Славянская нумерация сохранялась до конца XVII века.

При Петре I возобладала так называемая арабская нумерация. Славянская нумерация сохранилась в богослужебных книгах.

Самой популярной системой кодирования чисел оказалась позиционная, десятичная. Используются десять цифр. Значение каждой определяется той позицией, которую цифра занимает в записи числа.

Эта система пришла из Индии, где она появилась не позднее VI века, европейцы заимствовали ее у арабов, назвав ее арабской. Из арабского языка заимствовано слово «цифра». Причина ее возникновения анатомическая — 10 пальцев. Анатомическая система счисления (существовали пятеричные, двадцатеричные системы счисления).

Например, 23 — три единицы, два десятка 32 — две единицы, три десятка 400 — 4 сотни, два 0 вклад в число не дают, нужны для того, чтобы указывать позицию 4.  

В десятичной позиционной системе особую роль играет число 10 и его степени, например, 1996 — 6 единиц, 9 десятков, 9 сотен 1 тысяча или 1996=6+9*10+9*100+1*1000, т.к.1000=10³, 100=10², 10=10¹, таким образом, 1996=1*10³ + 9*10² + 9*10

1 +6*10^0.

Любое число в нулевой степени равно единице 0,1⁰ = 1

То есть любое 4-х значное число можно записать в следующем виде:

N=a₃*10³+a₂*10²+a₁*10¹+a₀*10⁰

a₃, a_2, a₁, a₀-десятичные цифры, от 1 до 9 или коэффициенты 3 2 1 0 — разряды, степени числа 10 со степенями называют основанием системы счисления.

Но основанием системы может быть не обязательно число 10, мы можем записать число в р-ичной системе, где основанием будут степени числа р. Любое число N в р-ичной системе мы можем представить в виде формулы:

N=a_n*Pⁿ+a_n-1*P^n-1+. ..+a₁*P¹+a₀*P⁰

Если взять за основание 60, то придется использовать 60 разных цифр. Такая система была в Древнем Вавилоне. Если основанием возьмем 2, получим систему всего с двумя цифрами 0 и 1. К сожалению, в этой системе даже небольшие числа записываются слишком длинно, так 1995 в двоичной системе записывается 1995₁₀=11111001011₂

Система счисления, где 2 является основанием системы называется двоичной системой счисления, относится к машинной системе счисления, к машинным системам счисления относятся и восьмеричная и шестнадцатеричная. Таким образом существуют следующие системы счисления: вавилонская, римская, алфавитные, анатомические, машинные.

Системы счисления делятся также на позиционные и непозиционные. 

Перевод из двоичной системы счисления в десятичную.

Как узнать чему равно девятизначное двоичное число N=111110100₂

Подпишем сверху каждый разряд

87654321010 — 1 разряды (степени двойки)

111110100₂

В двоичной системе особую роль играет двойка и ее степени.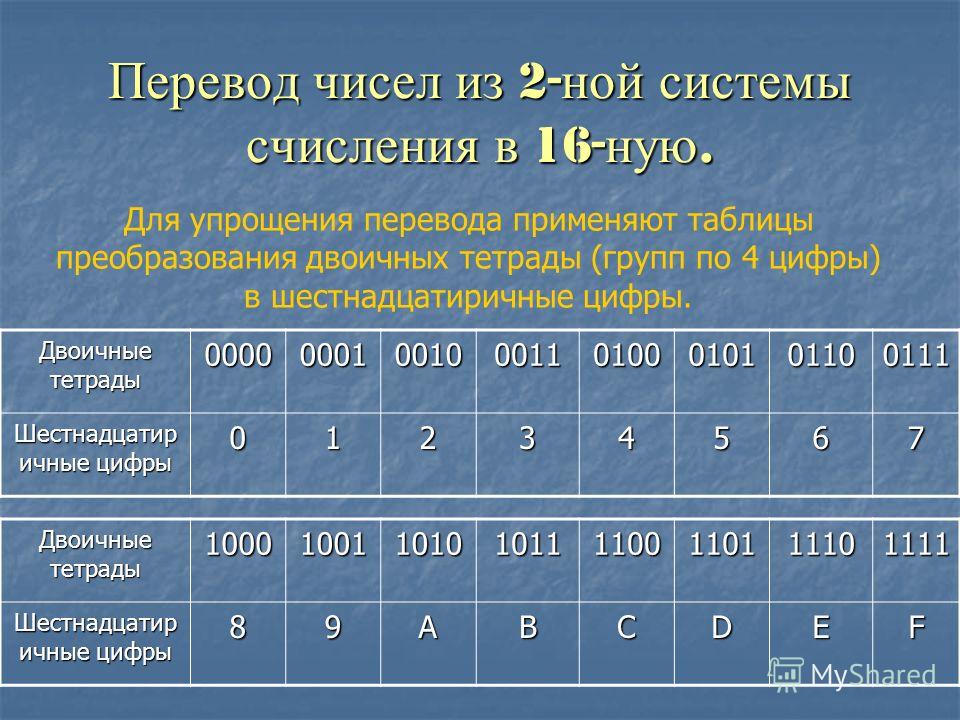

Таким образом:

111110100=1*2₈ +1*2₇ +1*2₆ +1*2₅ +1*2₄ +0*2₃ +1*2₂ +0*2₁ +0*2₀ =1*256+1*128+1*64 +1*32 +1*16 +0*8 +1*4 +0*2 +0*1=256 + 128 + 64 + 32 + 16 + 0 + 4 + 0 +0 =500

Перевод из десятичной системы счисления в двоичную.

Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.

Выписав все остатки, начиная с последнего 3 в обратном порядке, получим двоичное разложение числа.

234₁₀ = 11101010₂

Восьмеричная и шестнадцатеричная системы счисления.

Запись числа в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной восьмеричная система счисления использует 8 цифр: 0,1,2,3,4,5,6,7.

Единица, записанная в самом младшем разряде означает просто единицу (1*8 в нулевой степени), та же единица в следующем разряде обозначает 8 (1*8 в первой степени), в следующем 64 (1*8 во второй степени) и так далее.

2 1 0 1 — разряды (степени восьмерки)

100₈ = 1*8² + 0*8¹ + 0*8⁰ = 1*64 + 0 + 0 = 64₁₀

8 — это 2 в третьей степени. При переводе в восьмеричную систему двоичное число из трех цифр записывается одной цифрой.

Восьмеричная запись	Двоичное представление	впереди стоящий 0 ничего не значит
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Для перевода  из двоичной в восьмеричную число, записанное в двоичной системе делим на триады справа налево

Например, 11011100011=11 011 100 011 и заменить каждую группу одной восьмеричной цифрой 2 2 4 2 и получим 2242₈

Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады (1 в двоичной системе 1 добавляем до триады впереди 00)

6	1	1
110	001	001

Еще компактней выглядит запись двоичного числа в шестнадцатеричной системе счисления.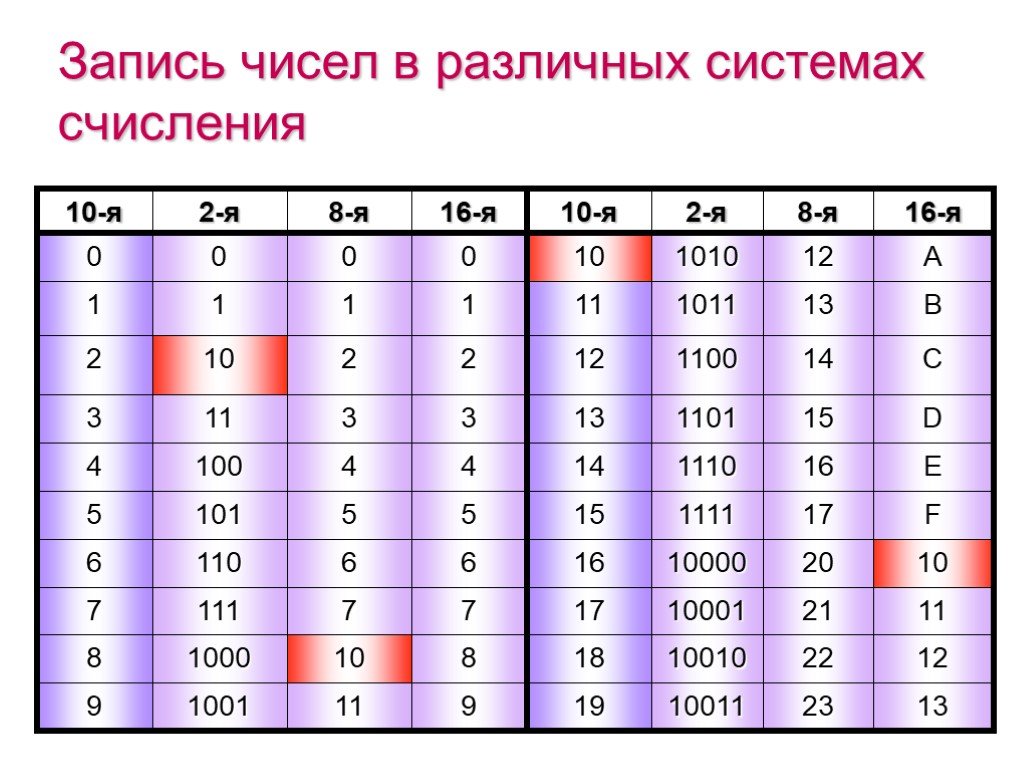

Для первых 10 из 16 шестнадцатеричных цифр используются привычные цифры 0 1 2 3 4 5 6 7 8 9, а для остальных используют первые буквы латинского алфавита

A-10 D-13

B-11 E-14

C-12 F-15

Цифра 1 в самом младшем разряде означает 1, в следующем разряде означает 16 (в первой степени), в следующем разряде 16*16 (16

2)=256, в следующем разряде 1*16³ и так далее.

100¹⁶ =256¹⁰

Цифра F, записанная в самом младшем разряде означает 15 в десятичной системе, F в следующем разряде означает 15*16 в первой степени в десятичной системе и т.д.

2 1 0 — 1 разряды (степени числа 16)

Число 210₁₆=10*16²+15*16¹+0*16⁰

210₁₆=10*256+240+0*1=2560+240+0=2800₁₀

2 1 0

BAD₁₆=11*16₂+1 0*16₁+13*1 6₀ = 11 * 256+10 *16+13*1=2816+160+13=2989₁₀

16 — это 2 в четвертой степени.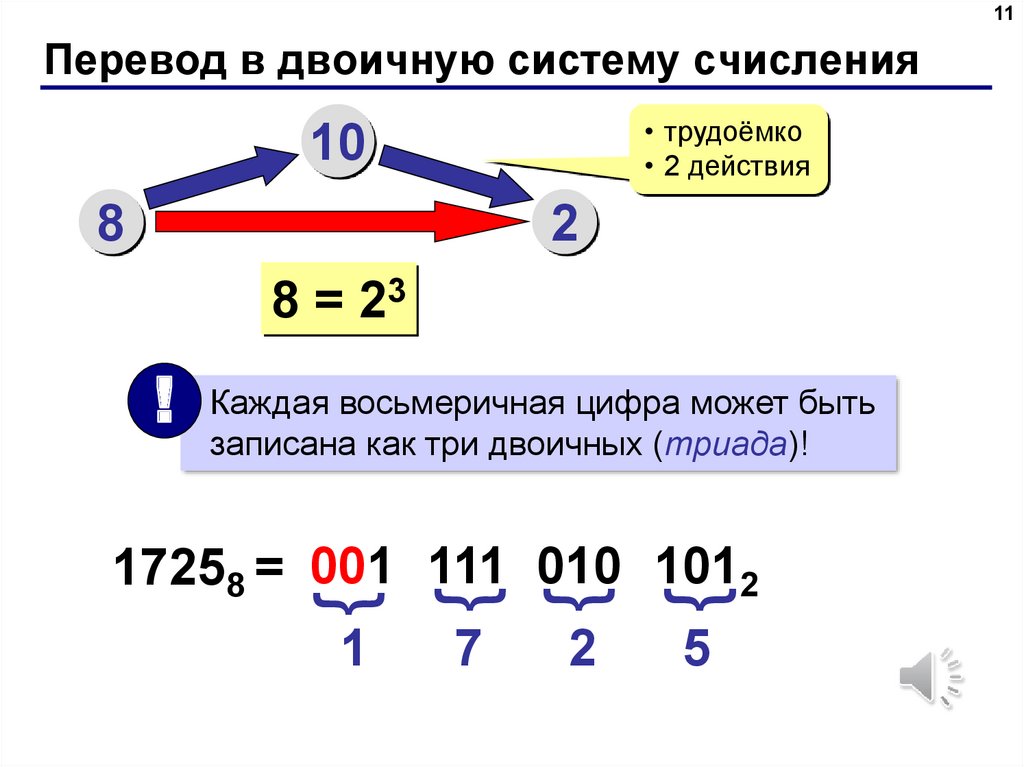

При переводе из двоичной системы в шестнадцатеричную число двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатеричной системе.

Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную, представив каждую цифру в виде сочетания четырех 1 и 0

A	O	F	AOF16
1010	0000	1111

Как осуществить перевод чисел из двоичной системы в шестнадцатеричную? Необходимо разбить число, записанное в двоичной системе на группы по 4 разряда справа налево, заменив каждую группу одной шестнадцатеричной цифрой.

1101	1010	1101	в двоичной
11	10	13	в десятичной
B	A	D	в шестнадцатеричной

 

10	2	8	16
0	000	0	0
1	001	1	1
2	010	2	2
3	011	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Системы счисления — Умскул Учебник

На этой странице вы узнаете

• В каких случаях 10 не равно 10?
• Как купить шоколадку у инопланетянина?

Привычная нам система счисления называется десятичной, потому что нам с детства удобно считать 10 пальцев на руках. Но так было не всегда: раньше людям было удобнее считать до 12, по количеству фаланг на пальцах одной руки. Для них и для нас число 10 имеет совершенно разное значение.

Виды систем счисления

Система счисления — это модель, которая позволяет записывать числа по определенным правилам.

Основных типов систем счисления две:

• позиционные,
• непозиционные.

Непозиционные системы счисления основываются на том, что значение цифр никак не зависит от того, на какой позиции в числе они находятся.

Возьмем фермера и его овец. Какой способ записать количество овец — самый удобный? Самый простой пример — подсчет с помощью одной насечки. Тогда мы подсчитываем овец в своем стаде поштучно, обозначая при записи каждую отдельной засечкой.

Очевидно, что это неудобно. В наших интересах размножать овец. Но чем их больше, тем менее читаема такая запись.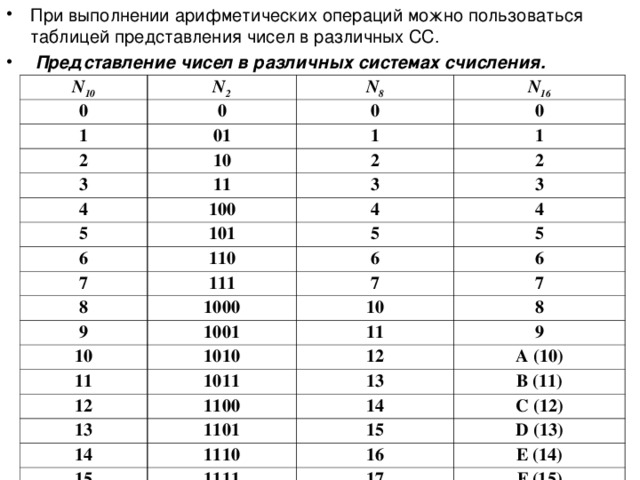 Когда мы добьемся невиданных высот в скотоводстве, и у нас станет 2796 голов, их подсчет с помощью одной засечки будет невозможен.

Римская система счисления — еще один известный пример непозиционной системы счисления. В ней уже появляются символы для обозначения отдельных чисел. Но в какой бы позиции символ ни стоял, он все еще значит только самого себя:

• I — 1;
• V — 5;
• X — 10 и так далее.

Римская система счисления упрощает запись чисел, но не решает проблему неудобства чтения полностью. Например, число 2796 в римской записи будет выглядеть как MMDCCXCVI. Уже неприятно.

В позиционных системах счисления значение цифры зависит от того, на какой позиции она стоит. 

На примере нашей родной десятичной системы счисления, мы с вами понимаем, что в числе 1234:

• 1 — количество тысяч, и обозначает не 1, а 1000;
• 2 обозначает количество сотен и понимается как 200;
• 3 отвечает за количество десятков и означает 30;
• 4 стоит на самой последней позиции и означает количество единиц, поэтому в данном случае 4 — это 4.

Это сильно упрощает чтение чисел любого размера, так как меняется сам принцип их чтения:

• В непозиционной системе счисления (на примере римской): СХХIII = 100 + 10 + 10 + 1 + 1 + 1 = 123.
• В позиционной: 123 = 100 + 20 + 3.

Именно позиционную систему счисления выберет грамотный фермер, чтобы подсчитать количество овечек.

Основание позиционной системы счисления

Позиционная система счисления характеризуется ее основанием — количеством цифр, которые она использует для записи чисел.

• Десятичная система счисления (10сс) использует 10 цифр — от 0 до 9, с ней мы знакомы с детства.

• Компьютеру роднее двоичная система счисления (2сс), которая использует 2 цифры — 1 и 0.
•  В двенадцатеричной системе счисления (12сс) помимо цифр 0–9 необходимы еще два символа. Для удобства заменим их буквами: A = 10, B = 11. Теперь имеем 12 символов от 0 до B.
• Также небезызвестная система счисления — шестнадцатеричная. Для нее кроме цифр 0–9 нужно еще больше символов, чтобы обозначить все цифры. Происходит это по аналогии — каждая новая буква отвечает за большее значение: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

В каких случаях 10 не равно 10? Мы используем числа тогда, когда кончаются цифры. Привычная нам система счисления называется десятичной, потому что использует 10 цифр — от 0 до 9. Для записи значений больше 9, мы начинаем строить числа из цифр. Первое такое число — 10. Если бы мы использовали другое количество цифр, всё выглядело бы иначе. При использовании цифр от 0 до 6, нам пришлось бы строить числа уже для записи значений, больше 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления.

Построение числа в непривычных нам системах счисления происходит точно так же, как и в 10сс:

1. Увеличиваем значения единиц, используя доступные цифры.
2. Как только цифры закончились, значение единиц обнуляется. Появляется новый разряд десятков, который также увеличивается от 1 до предела системы счисления.
3. Когда любой разряд числа принимает значение максимальной цифры — разряд выше увеличивается на 1, а текущий разряд обнуляется.

Например:

• В 10сс число 88 будет увеличиваться так:
  88 → 89 → 90 → 91 → 92 → … 99 → 100;

• В 2сс разряды будут появляться быстрее из-за маленького количества цифр: 
  1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000;

• В 12сс чуть медленнее, так как цифр больше: 
  8 → 9 → A → B → 10 → 11 → … 18 → 19 → 1A → 1B → 20 → … 99 → 9A → 9B → A0 → A1 → … AA → AB → B0 → B1 → … BA → BB → 100.

Арифметика, как и построение числа, во всех системах счисления одинакова:

• Изменение разрядов происходит с единиц.
• При сложении избыток суммы увеличивает разряд выше (то самое “6 пишем, 1 в уме”).
• В вычитании при необходимости занимаем значение из старшего разряда, уменьшая его на 1.

Расширенная запись числа и перевод из Nсс в 10сс

Как купить шоколадку у инопланетянина? Уметь переводить числа из 10сс в другие и обратно важно для того, чтобы торговать с инопланетянами. Однажды мы, вероятно, достучимся до внеземных цивилизаций. Но у них может оказаться не 10 пальцев на руках, а 7, 12 или любое другое количество. Если их представления о математике шли путем, подобному нашему, какую систему счисления придумали они? Когда мы захотим купить инопланетный сникерс за 2256 межгалактических юнитов, вполне может оказаться, что наши представления о числах сильно отличаются.

Подсчитав количество пальцев на руках продавца шоколадок, важно научиться переводить числа из одной системы счисления в другую.

Полная запись числа a₁a₂a₃…a_i, где a_i — цифра числа под номером i, состоящей из k символов и с основанием системы счисления n, будет выглядеть как:

a₁a₂a₃…a_i…a_k = a₁ * n^{k — 1} + a₂ * n^{k — 2} + … + a_i * n^{k — i} + … + a_k * n⁰.

На примерах:

• 123 в 10сс расписывается как: 1 * 10² + 2 * 10¹ + 3 * 10⁰;
• 1010 в 2сс: 1 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰;
• A9B в 12сс:  10 * 12² + 9 * 12¹ + 11 * 12⁰.

Такой записи числа достаточно, чтобы перевести значение числа из любой системы счисления в 10сс — нужно посчитать значение составленной записи:

• 1010₂ = 1 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰ = 8 + 0 +2 + 0 = 10₁₀;
• 525₉ = 5 * 9² + 2 * 9¹ + 5 * 9⁰ = 5 * 8¹ + 2 * 9 + 5 * 1 = 428₁₀;
• A9B₁₂ = 10 * 12² + 9 * 12¹ + 11 * 12⁰ = 10 * 144 + 9 * 12 + 11 * 1 = 1559₁₀.

Перевод из 10сс в Ncc

Принцип деления с остатком поможет переводить числа в другую сторону — из 10сс в любую другую систему счисления.

Алгоритм перевода следующий:

1. Делим исходное число на основание новой системы счисления.

2. Остаток от деления — новая найденная цифра числа.

3. Целую часть от деления снова делим на основание. Записываем остаток как новую цифру искомой записи, а целую часть от деления — как цель следующего деления. Снова делим целую часть на основание.

4. Деление происходит до тех пор, пока целая часть от деления не станет равна 0.

5. Полученные в качестве остатков от деления цифры нового числа читаются в обратном порядке.

Для примера давайте переведем число 2589 в 7сс:

1. На первом шаге делим исходное число на 7, записывая остаток от деления как новую цифру и целую часть как оставшееся значение.

2. На втором шаге делаем то же самое, но с целой частью предыдущего деления — теперь делим ее на 7.

3. И так до тех пор, пока целая часть от деления не будет равна 0.

Интересующее нас значение находится в самом правом столбце и читается снизу вверх.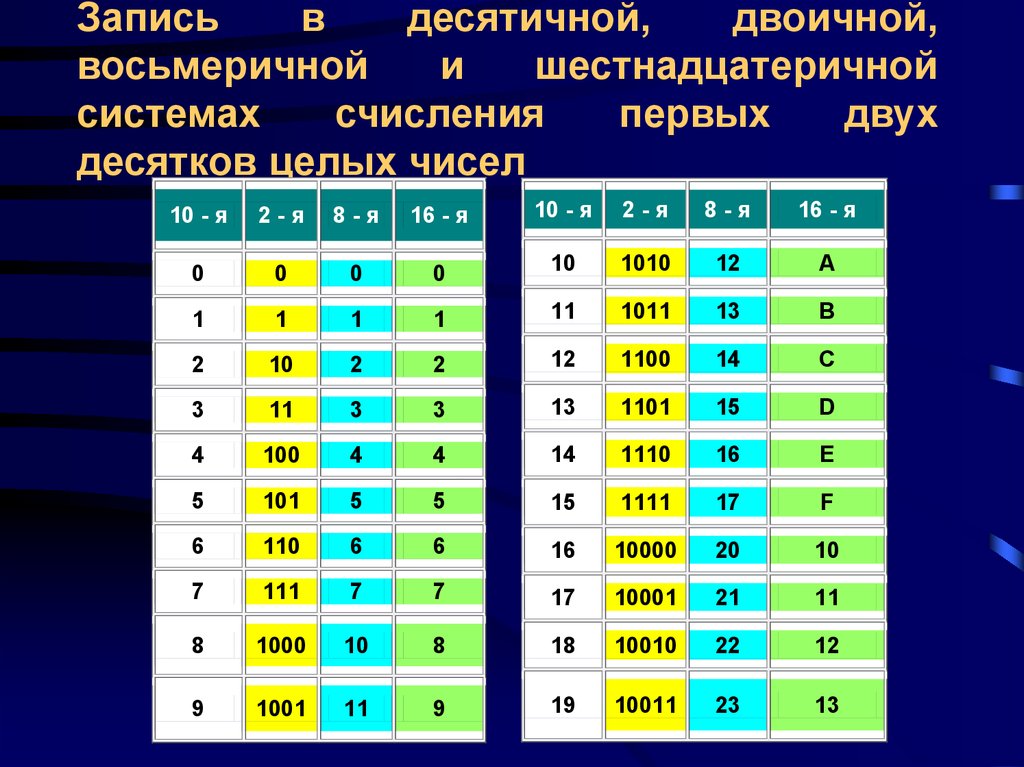

2589₁₀ = 10356₇

Перевод в системы счисления с основанием, больше 10, происходит так же. Просто надо не забывать, что цифры больше 9, будут обозначаться соответствующими буквами.

Например, таблица перевода десятичного числа 48406 в 16сс будет выглядеть следующим образом:

И искомое значение будет BD16.

Лайфхак или как быстрее закодировать геном

Представим, что нам нужно написать программу для биологов, которую они будут применять в исследованиях ДНК и нам надо реализовать хранение ДНК в памяти компьютера. 

В ДНК встречается четыре вида азотистых оснований: аденин (A), гуанин (G), тимин (T) и цитозин (C). Всю ДНК можно записать как последовательность этих 4 символов. Но можно же записать тогда эту последовательность букв как число в 4сс, сопоставив цифры символам, например, код A – 0, C – 1, G – 2, T – 3. Тогда кусок ДНК GGT будет записан в 4сс как 223.

Но чтобы закодировать геном в компьютере, его надо перевести из 4сс в 2сс. Делать это делением может оказаться очень долго, ведь геном может быть очень длинным и делить его просто неэффективно. К счастью, есть выход!

Между 2сс и системами счисления, в основании которых стоит степень двойки (4сс, 8сс, 16сс), есть связь, которую можно использовать для быстрого перевода из 2сс в них и обратно. Для этого используется следующая таблица:

Алгоритм перевода состоит в следующем:

1. Вычисляется степень, в которую нужно возвести 2, чтобы получить основание необходимой системы счисления.

2. Используется количество столбцов таблицы, равное этой степени. Отсчет ведем с правого столбца.

3. При переводе из 2сс весь код разбивается на кодовые слова длиной, равной степени — при необходимости в начало записи добавляются нули. Отдельные кодовые слова подставляются в нижнюю строку таблицы. Цифра записи числа в новой системе счисления будет равна сумме цифр верхней строки, под которыми стоит 1 кодового слова.

4. При переводе в 2сс каждая цифра представляется как сумма цифр верхней строки таблицы. Цифрам, которые используются в сумме, соответствуют 1 кодового слова 2сс, а не использующимся — 0.

На примере:

• Для перевода между 2сс и 4сс используется часть таблицы:

• Перевод из 2сс в 4сс:
  110001 = 11.00.01 = (2 + 1).(0 + 0).(0 + 1) = 3.0.1 = 301

• Перевод из 4сс в 2сс:
  103 = 1.0.3 = (0 + 1).(0 + 0).(2 + 1) = 01.00.11 = 10011

• Для перевода между 2сс и 8сс используется часть таблицы:

• Перевод из 2сс в 8сс:
  10101011100 = 010.101.011.100 = (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1).(4 + 0 + 0) = 2.5.3.4 = 2534

• Перевод из 8сс в 2сс:
  1753 = 1.7.5.3 = (0 + 0 + 1).(4 + 2 + 1).(4 + 0 + 1).(0 + 2 + 1) = 001.111.101.011 = 1111101011

• Для перевода между 2сс и 16сс используется вся таблица:

• Перевод из 2сс в 16сс:
  101101111000001 = 0101. 1011.1100.0001 = (0 + 4 + 0 + 1).(8 + 0 + 2 + 1).(8 + 4 + 0 + 0).(0 + 0 + 0 + 1) = 5.11.12.1 = 5BC1

• Перевод из 16сс в 2сс:
  F87A = 15.8.7.10 = (8 + 4 + 2 + 1).(8 + 0 + 0 + 0).(0 + 4 + 2 + 1).(8 + 0 + 2 + 0) = 1111.1000.0111.1010 = 1111100001111010

Перевод между системами счисления на Python

Перевод больших чисел между системами счисления вручную неудобен и может занимать много времени. Иногда выгоднее было бы написать программу.

Перевод из 10сс в другие будем выполнять по описанному выше алгоритму. Пока исходное число больше 0, делим его на основание системы счисления. Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.

1. Основным циклом программы будет while, который работает, пока исходное число больше 0.
2. Новую цифру числа берем как остаток от деления исходного числа на основание новой системы счисления с помощью оператора %. Новые цифры будем записывать в новую строку, в которой и будет храниться искомая запись. Чтобы не переворачивать число в конце, можем сразу заносить каждую новую цифру не в конец, а в начало строки.
3. Уменьшаем само число, деля его нацело на основание с помощью оператора //.

Например, перевод числа 258936 в 5сс.

---

number = 258936
n = 5
new_number = ""
while number > 0:
	d = number % n
	new_number = str(d) + new_number
	number //= n
print(new_number)
_____________________________________________________________________
Вывод: 31241221

Перевод в 10сс из других систем счисления будем производить по описанной выше формуле:

a₁a₂a₃…a_i…a_k = a₁ * n^{k — 1} + a₂ * n^{k — 2} + … + a_i * n^{k — i} + … + a_k * n⁰.

1. Главный цикл программы — for. Он будет перебирать цифры исходного числа, а точнее, их индексы, с помощью диапазона range по длине исходного числа.
2. На каждом шаге цикла цифру ai числа будем умножать на основание системы счисления этого числа n в степени, равной разности длины числа k и порядкового номера текущей цифры i — ai*nk — i . Не забываем, что индексация строки начинается с 0, а не с 1, поэтому порядковый номер цифры — на 1 больше ее индекса.

Например, переведем число 31241221 из 5сс обратно в 10сс.

---

number = "31241221"
n = 5
new_number = 0
k = len(number)
for i in range(k):
	new_number += int(number[i]) * n ** (k - i - 1)
print(new_number)
_____________________________________________________________________
Вывод: 258936

---

Лайфхаки по переводу между системами счисления программой:

• для перевода числа из 10сс в 2сс, 8сс и 16сс есть встроенные команды: bin, oct и hex соответственно
  • bin(123) — “0b1111011”
  • oct(123) — “0o173”
  • hex(123) — “0x7b”

Важно заметить, что первые два символа в записи числа окажутся лишними в нашем случае — они будут обозначать идентификатор системы счисления, в которую мы перевели число.

Чтобы сразу от него избавиться, при переводе можно использовать срез, который будет учитывать все число без этого идентификатора:

• bin(123)[2:] — “1111011”
• oct(123)[2:] — “173”
• hex(123)[2:] — “7b”

• перевести число из любой системы счисления в 10сс можно с помощью команды int. Ей необходимо передать два параметра: исходное число в виде строки и основание его системы счисления:
  • int(«31241221», 5) — 258936
  • int(«7b», 16) — 123

Хорошо. А зачем всё это, если мы не генетики и не торгуем с инопланетянами?

Системы счисления — одно из базовых понятий информатики и оттого используются в большом количестве заданий на ЕГЭ. С применением различных систем счисления придется столкнуться при решении задачи 14, при построении большинства алгоритмов задачи 5, в заданиях на расчет объема информации в номере 7. Также, хотя это не упоминается в условиях заданий явно, в задаче 22 немалая часть алгоритмов связана с переводом числа из одной системы в другую.

Фактчек

• В позиционных системах счисления, в отличие от непозиционных, значение цифры зависит от ее положения в числе.
• Основание позиционной системы счисления определяет количество используемых в ней цифр для записи чисел.
• Для перевода из 10сс в любую другую: берем остаток от деления на основание новой системы счисления в качестве цифр нового числа и записываем их в обратном порядке.
• Для перевода из любой системы счисления в 10сс: умножаем каждую цифру числа на основание его системы счисления, возведенную в степень разности длины числа и порядкового номера данной цифры.

Проверь себя

Задание 1.
Какая цифра не может использоваться в 8сс?

1. 0
2. 3
3. 7
4. 8

Задание 2.
Для записи цифр 10-15 в 16сс используются …

1. буквы A-F
2. буквы А-Д
3. буквы U-Z
4. любые символы по договоренности

Задание 3.
Десятичное число 101 в 2сс будет выглядеть как…

1. 101
2. 101101
3. 1100101
4. 1010011

Задание 4.
Шестнадцатеричное число FBA000 в 10сс будет выглядеть как …

1. 16490496
2. 69409461
3. 61400900
4. Это некорректная запись числа в 16сс

Задание 5.
Что сделает запись на языке Python — int(“777”, 8)?

1. Переведет число 777 из 10сс в 8сс
2. Переведет число 8 из 10сс в 777сс
3. Переведет число 777 из 8сс в 10сс

Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.

F То, что вы (вероятно) не знали о шестнадцатеричной системе счисления

Шестнадцатеричная система счисления, или основание 16, ^{Сноска 1} десятилетиями использовалась в качестве компьютерного языка. Но многое из того, что было написано о развитии термина шестнадцатеричной и связанной с ней самой системы счисления, неверно.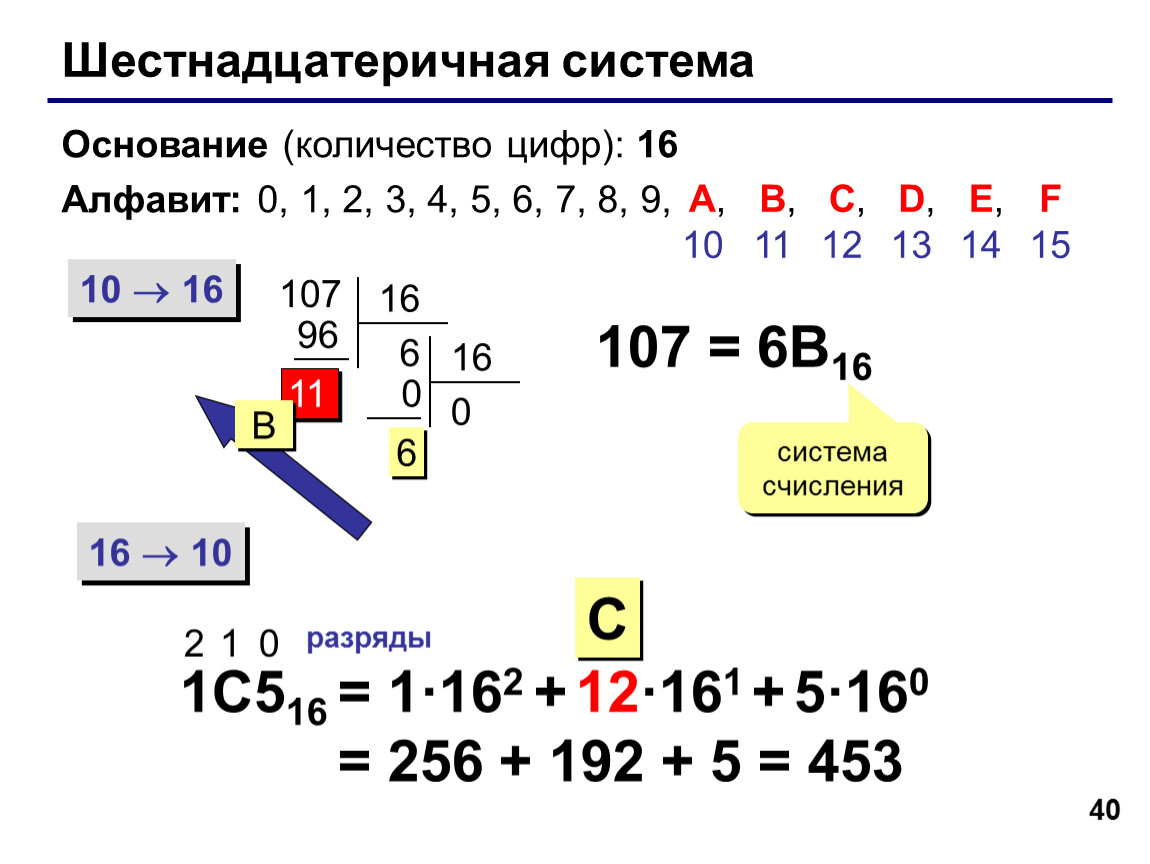 В этой короткой статье мы углубимся в историю термина, системы счисления и ее обозначения, чтобы предложить более полную (и точную!) историю шестнадцатеричной системы счисления и развеять некоторые мифы, возникшие на этом пути. Итак, вот F или пятнадцать вещей, которые вы (вероятно) не знали о шестнадцатеричном формате:

1

Первая аттестация Oxford English Dictionary из шестнадцатеричных дат от новостного бюллетеня в январе 1954 года, в котором использовалось слово для описания миниацкого, ^{Стонетка 2} . что его можно «управлять шестнадцатеричным числом» [2, с. 6]. На самом деле это слово может быть датировано 1950 годом, когда оно использовалось для обозначения обозначения, используемого для ввода чисел и инструкций в восточный автоматический компьютер стандартов (SEAC), разработанный и построенный Национальным бюро стандартов, правительственным учреждением США. базируется в Мэриленде [1, с. 123]. ^{Сноска 3} . Однако часто высказываемое утверждение, что IBM придумала в шестнадцатеричном формате (см., например, [6, стр. 118]), неверно.

                        2

Шестнадцатеричные цифры, выбранные Национальным бюро стандартов, представляли собой западно-арабские цифры 0–9 и латинские буквы A–F, и с тех пор они остаются стандартными. Это не всем понравилось. В 1968 году Брюс Алан Мартин [13, с. 658] жаловался, что «[с] нелепым выбором букв A, B, C, D, E, F в качестве символов шестнадцатеричных чисел, усугубляющих и без того неприятные проблемы различения восьмеричных (или шестнадцатеричных) чисел от десятичных чисел (или имен переменных) , настало время пересмотреть наши числовые символы». С этой целью он набросал пятнадцать новых символов для ненулевых цифр шестнадцатеричной системы счисления:

Однако предложение Мартина о замене цифр 0–9 и A–F ни к чему не привело, или .

                        3

Вдохновение для выбора Национальным бюро стандартов A–F в качестве шести дополнительных цифр могло быть получено из книги Джозефа Боудена Special Topics in Theoretical Arithmetic (1936), в которой он предположил, что [ , п. 50] ^{Сноска 4}

[i]Если мы хотим использовать основание больше десяти, мы можем вместо использования новых символов использовать буквы для дополнительных цифр. Таким образом, с 2 ⁵ для основания мы можем считать следующим образом:

1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, K, L, M, N, P, Q, R, S, T, U, V, W, X, Y, 10.

Боуден также рассмотрел достоинства основания 16, которое он назвал сексуальным числом , а этот термин он, по-видимому, позаимствовал у Роберта Морриса Пирса, который использовал его в 1898 году. 9] выбрал строчные латинские буквы a, b, c, d, e, f. С целью предоставления информации, которая могла бы поддержать попытку отойти от десятичной системы общественного пользования, он показал, как работают стандартные арифметические операции в системах счисления 8, 10, 12 и 16.

                        4

In Искусство компьютерного программирования , Дональд Кнут [8, с. 202] отмечает, что преобладающий сегодня термин для основания 16, шестнадцатеричное , представляет собой «смесь греческих и латинских основ», ^{Сноска 6} , а именно греческое ἕξ ( hex , «шесть») и латинское decem ( «десять»). Это все равно, что смешать английские и немецкие корни, чтобы получить sixzehn или sechsteen . Конечно, результат все еще можно понять, и некоторые гибриды (такие как телевидение) стали повсеместными, но греческие и латинские корни, как правило, лучше хранить отдельно, так как объединение их словарей увеличивает распространенность омографов (т. правописание), из-за чего гораздо сложнее понять, что означает чеканка; например, только допустив их разделение, можно быть уверенным, что педология есть изучение (λόγος · логос ) почвы ( π έδον · pédon ), не ноги ( pedes ).

                        5

Кнут [8, с. 202] также утверждает, что «более подходящими терминами были бы «сениденарный», «седцатеричный» или даже «шестнадцатеричный». . Это ложное число на , вероятно, происходит из-за неправильного деления числа 9.0005 шестидесятеричный (термин, используемый для обозначения основания 60; буквально «относящийся к шестидесяти») как шестидесятеричный . ^{Footnote 7} Искаженный термин шестнадцатеричный впервые появился в 1895 году в словаре Уильяма Дуайта Уитни The Century Dictionary [24, p. 5535]. ^{Сноска 8} К сожалению, искажение уже укоренилось: в книге по этимологии математических терминов Шварцман [18, стр. 5, 105] ошибочно принимает шестнадцатеричное за этимологически правильную альтернативу 9.0005 шестнадцатеричный .

                        6

Согласно Кнуту [8, с. 201], первым, кто использовал основание 16, был шведско-американский инженер Джон Уильям Нистром (1825–1885). Это неверно, как мы увидим. Но Нистром был, по крайней мере, очень ярым сторонником основания 16, которое он очень подробно изложил в книге, опубликованной в 1862 году, и в серии статей, опубликованных годом позже. ^{Сноска 9} Он предложил заменить знакомую десятичную систему системой с основанием 16, которую он назвал 9.0005 тон . Название не имеет ничего общего с музыкой; скорее, в системе Нистрома число 10 (то есть 16 в десятичной системе) произвольно названо тонн . Фактически Нистром [14, с. 16–17] придумал новые названия для всех чисел, выраженных в его тональной системе; например, 0 — нолл, 9 — ко, 100 — сан, 1000 — милль, 1000000 — санбонг и т. д. Для тональной записи он предложил [14, с. 15] следующие символы: ^{Footnote 10}

Нистром был настолько очарован своей тональной системой, что не только предложил новые единицы измерения веса и меры, но и изобрел циферблат часов, который делил день на шестнадцать часов. Он даже предложил разделить год на 16 месяцев примерно по 23 дня в каждом, причем каждый месяц имел собственное новое название (первыми тремя были Ануарий, Дебрян и Тимандр). ^{Footnote 11} Помимо числа 16, допускающего более удобное двоичное деление (т. е. деление на 2), чем число 10, Нистром [14, с. 23] также предпочитал 16-ю системе счисления по основанию 10, потому что первая требует «меньшего количества цифр для выражения большого числа».

                         7

Однако в 1867 г. У. Б. Тейлор из Патентного бюро США рассмотрел предложение Нистрома и пришел к выводу, что 16-кратное основание не намного экономичнее, чем 10-е, как утверждал Нистром. Тейлор [22, с. 120] продемонстрировал, что, когда дело дошло до выражения очень больших чисел, таких как «количество песчинок, необходимое для образования земного шара размером с нашу Землю», около 659 г.квинтиллион, ^{Сноска 12} порядковая система (предпочтительный термин Тейлора для основания 16) была едва ли более удобной, чем десятичная, поскольку в то время как десятичная система потребовала бы 33 цифры для выражения такого большого числа, десятеричная все равно потребовала бы 28: незначительно», по мнению Тейлора. Не завоевав поддержки своей тональной системы, Нистром позже отказался от своих усилий по ее продвижению, вместо этого рекомендовав публичное принятие дуоденальной (т. е. двенадцатеричной или двенадцатеричной) системы [16, с.

                        8

Нистром не заявлял, что основание 16 является его собственным изобретением. Он писал, что король Швеции Карл XII (1682–1718) рассматривал возможность введения в Швеции системы с основанием 16, но его возражение против вытекающего из этого требования новых символов для дополнительных цифр заставило его предпочесть восьмеричную (с основанием 8) систему. вместо этого [15, с. 263–264]. Однако Нистром не представил никаких доказательств своего утверждения, и оно опровергается свидетельством очевидца Эмануэля Сведенборга (1668–1772), в котором описывается интерес Карла XII к восьмеричной системе и даже к основанию 64, но не к основанию 16 [21].

                        9

Нистром был, по крайней мере, прав в том, что он не был изобретателем базы 16, даже если он не был прав в том, кто до него дошел. Почти двумя десятилетиями ранее, в 1845 году, английский школьный учитель и математик Томас Райт Хилл (1763–1851) предложил систему счисления с основанием 16 в докладе, зачитанном на собрании Британской ассоциации содействия развитию науки в Кембридже, Англия. Статья была опубликована посмертно как «Система числовой номенклатуры и обозначений, основанная на принципах абстрактной полезности» [7, ​​с. 63–85]. Хилл называл свою систему с основанием 16 числом 9.0005 полудесятичный . Латинское слово для шестнадцати — sedecim (что дает английское sedecim ), но оно также может быть записано как sexdecim , так что выбор термина Хиллом этимологически верен.

                        A

Хилл [7, с. 69] черпал свое вдохновение из различного использования термина камень в графстве Йоркшир, Англия, для обозначения веса в 16 фунтов, а не в 14 фунтов, как в других местах Британии. Хилл отметил, что практика Йоркшира допускает более удобное деление пополам, что предполагает, что преимущества можно получить, приняв основание 16 в более широком смысле. Вместо того, чтобы определить шестнадцать различных цифр для своей десятичной системы счисления, Хилл [7, с. 78] придумал девять элементов, которые можно комбинировать, чтобы сформировать любое положительное или отрицательное значение в секс-десятичной системе счисления:

На основе этих элементов Хилл сгенерировал отличительные имена для всех положительных и отрицательных шестнадцатеричных значений; например, dĭn  = +1, dĭkōn  = +16 (поскольку х или 1 стоит на месте 16, а k стоит перед ō 900), разделитель 6 0 ō 900 dĭdōkōn = +256 (поскольку х , или 1, стоит на месте 256, а d и k перед каждым ō ), действует как разделитель мест kĭn  = −1, kĭkōn  = −16 и т. д., где ō  может предшествовать либо d , либо k , в зависимости от предпочтений в произношении, поскольку на + или − это не влияет.

Б

Холм [7, с. 74] считал, что шестнадцатеричная система до сих пор не нашла сторонников, заявив: «Насколько мне известно, его число [т. е. 16] до сих пор публично не рекомендовалось». Хилл был прав в том, что секс-десятеричная система раньше публично не рекомендовалась, но это не значит, что он был первым, кто ее придумал. Фактически, основание 16 было изобретено в семнадцатом веке эрудитом Готфридом Вильгельмом Лейбницем (1646–1716), который хорошо известен рядом других математических нововведений, таких как исчисление и двоичная система. Первоначально термин Лейбница для основания 16 был равен 9.0005 десятеричный . В своем первом сочинении по основанию 16 Лейбниц [9] разработал, как преобразовать десятичное число 1679, представляющее год его изобретения, в десятеричное счисление.

C

Лейбниц экспериментировал с различными формами записи десятеричных чисел. В своей первой работе на эту тему [9] он использовал латинские буквы m, n, p, q, r и s для шести дополнительных цифр, прежде чем отказаться от них в пользу шести аретинских слогов ut, re, mi, фа, соль и ла, ^{Сноска 13} сокращено Лейбницем до u, r, m, f, s и ℓ. Объединив эти слоги с немецкими словами, обозначающими числа, он создал совершенно новый набор терминов для значений, выраженных в десятеричной системе счисления. Например, utzehn , комбинация слога ut , обозначающего десять, и немецкого слова zehn , которое традиционно означало десять, но было перепрофилировано Лейбницем для обозначения шестнадцати, было термином Лейбница для обозначения десятичного числа. 26 выражено в десятеричной системе счисления (1u в системе обозначений Лейбница).

D

Лейбниц [10] также экспериментировал с различными формами записи основания 16. В другом раннем сочинении, в котором он назвал систему счисления сидячей , ^{. Сноска 14} , он сложил точки и тире, используя точка для каждого 0-бита и тире для каждого 1-бита, со старшим битом вверху и наименее значащим битом внизу:

Лейбниц. -20, или виценарная) система счисления, в которой помимо специального символа «оболочки» для нуля используются только два символа, точка (для 1) и черта (для 5), с набором точек и полос, используемых для формирования чисел. до 19и вертикальная позиционная система для представления еще больших чисел [3, с. 764]. Однако нет никаких доказательств того, что Лейбниц знал майя, поэтому сходство, безусловно, является случайным.

E

В 1682 году или около того Лейбниц [11] набросал еще одну форму обозначения малоподвижности на обратной стороне конверта. На этот раз он начинает с вогнутого полукруга для обозначения 0 и вогнутого вниз полукруга для обозначения 1, а затем изменяет эти символы, чтобы получить оставшиеся цифры:

Делая выводы из своих описаний (или инструкций), Лейбниц основывал каждую цифру на латинских буквах, одиночных или соединенных, причем некоторые из них были «двухвостыми», то есть удлинялись хвостом ( cauda на латыни) на с обеих сторон, а другие «антехвостые», то есть удлиненные хвостом только с левой стороны.

F

Вероятно, в своей последней работе по 16-кратному счислению Лейбниц [12] нарисовал таблицу, показывающую десятичные числа от 0 до 40, представленные в каждом основании от 2 до 16. В этой таблице Лейбниц использовал строчные латинские буквы a, b, c, d, e и f для шести дополнительных цифр его сидячего набора символов, первый и единственный раз, когда он это сделал. Это предвосхитило, а не повлияло на современное соглашение об использовании A, B, C, D, E и F для шести дополнительных цифр, поскольку работы Лейбница о малоподвижном образе жизни только сейчас начинают публиковаться [20].

Примечания

1. Под «основанием 16» мы подразумеваем позиционную систему счисления, использующую 16 в качестве основания. Таким образом, мы исключаем практику деления целых величин на шестнадцать дробных частей без позиции. Такие практики зафиксированы, например, в тамильской литературе и Древнем Риме. О них см. [19] и [23, с. 336].

2. Словарь Merriam-Webster также дает 1954 год как год , шестнадцатеричный , который был впервые использован, предположительно по той же причине.

3. В 1988 году название агентства было изменено на Национальный институт стандартов и технологий.

4. В 1903 г. Боуден [4, с. 26] цитируется страница 9 из книги Пирса, на которой сексиденальных занимает видное место. К сожалению, при этом Боуден увековечил ошибку Пирса: i в сексиденальном — это интерфикс, т. е. короткий звук (обычно гласный), не имеющий значения, вставленный между частями слова в сложном слове для облегчения произношения. Греко-латинские заимствования изобилуют интерфиксами, но есть и слова, секс («шесть») — один из них, правильно составляющий без интерфикса. В английском языке на самом деле нет интерфиксов, но в нем есть несколько схожих явлений, например, и , которые становятся и перед гласной, и то, как некоторые люди произносят , рисуя , как если бы оно писалось как , рисование .

5. Собственно, корни.

6. В исходной латинице sexagesimus («шестидесятый»), ‑agesimus — «‑десятая» часть; соответственно латиница сексадецим похож на английский sixtiteen .

7. Этимология записи отмечает, что это слово «Prop. *sexdecimal », звездочка, указывающая на то, что форма не засвидетельствована (из-за неполных знаний этого лексикографа).

8. Нистром [14, с. 3] впервые предложил свою систему с основанием 16 на собрании Международной ассоциации по получению единой десятичной системы весов, мер и монет, состоявшемся в Брэдфорде, Англия, 11 октября 1859 г..

9. Обратите внимание, что «старые цифры в Тональной Системе несут [ sic ] старое значение (кроме 9) один за другим» [14, с. 17], так что приведенный выше порядок не ошибочен.

10. «>

    Другими были Гостус, Сувенарий, Билиан, Ратамбер, Месудий, Никтоарий, Колумбиан, Хусамбер, Викториус, Ламбориус, Полиан, Филандер и Тонбориус.

11. Здесь Тейлор дает квинтиллион его значения по длинной шкале (1 000 000 ⁵ = 10 ³⁰ ). Эквивалентное число в короткой шкале будет 659 нониллионов.

12. Они превратились в сольфа, который Джули Эндрюс декламирует в песне «Do-Re-Mi» в The Sound of Music .

13. Читая эту короткую статью, вы не могли не заметить необычное изобилие имен для основания 16. Мы привели восемь, и вполне вероятно, что другие формы также использовались. Мы уже приводили причины, по которым шестнадцатеричное число , шестидесятеричный и шестидесятеричный вызывают возражения, в то время как тональный совершенно идиосинкразичен. Но как насчет остальных четырех —  порядкового числа , шестнадцатеричного числа , порядкового числа и порядкового числа ? Каждый из них так же хорош, как и другие? Или есть какое-то обоснованное основание, по которому можно отдать предпочтение? Sedecimal и sexdecimal каждое происходит от одного из двух вариантов написания латинского слова для кардинального числительного шестнадцать с английским суффиксом — al добавлено для образования прилагательного; они одинаково действительны, но формы без x встречаются чаще, как на английском, так и на латинице. Sedenary и senidenary в конечном счете происходят, соответственно, от sedeni и senideni — латинских дистрибутивных числительных, значение которых наиболее естественно выражается в английском языке такими фразами, как «шестнадцать за один раз» или «в шестнадцать». ” Из этих двух классов прилагательных те, которые образованы от дистрибутивных числительных, предпочтительнее, чем производные от количественных числительных, потому что смысл дистрибутивов лучше соответствует системе, в которой количество, выражаемое каждой последующей позицией, увеличивается на кратное основанию (в этом случае, на 16 за раз), а также потому, что эти прилагательные являются промежуточным производным от предварительно сформированных латинских прилагательных, которые заканчиваются на — arius (в данном случае sedenarius и senidenarius ). Наконец, между столь же безупречными сидячими и сидячими выбирать особо не из чего; стоит только отметить, что senideni предшествовали sedeni .

Ссылки

1. Аноним. SEAC — Национальное бюро стандартов Восточного автоматического компьютера. Национальное бюро стандартов Бюллетень технических новостей 34:9 (1950), 121–125. Доступно по адресу https://jovial.com/documents/SEAC.pdf.

2. Аноним. Миниак. Информационный бюллетень цифровых компьютеров 6: 1 (1954), 6. Доступно по адресу https://nsarchive.gwu.edu/sites/default/files/documents/5008299/Office-of-Naval-Research-Mathematical-Science.pdf.

3. Джеймс К. Бидуэлл. Арифметика майя. Учитель математики 60:7 (1967), 762–768. Доступно по адресу https://www.jstor.org/stable/27957685.

4. Джозеф Боуден. Элементы теории целых чисел . Макмиллан, 1903 г. Доступно по адресу https://archive.org/details/elementsoftheory00bowd.

5. Джозеф Боуден. Специальные разделы теоретической арифметики . Джозеф Боуден, 1936 г. Доступно по адресу https://hdl.handle.net/2027/uc1.$b543512.

6. Ян Гилленбок. Энциклопедия исторической метрологии, весов и мер , том. 1. Биркхойзер, 2018.

7. Томас Райт Хилл. Выдержки из бумаг покойного Томаса Райта Хилла, эсквайра. Ф.Р.А.С. Джон В. Паркер и сын, 1860 г. Доступно на https://archive.org/details/selectionsfromhi00hilluoft.

8. Дональд Э. Кнут. Искусство компьютерного программирования. Том 2 : Получисловые алгоритмы , третье издание. Addison-Wesley, 1988.

9. Готфрид Вильгельм Лейбниц. Секретарная прогрессия. Неопубликованная рукопись с маркой LH 35, 13, 3 Bl. 23, принадлежит Библиотеке Готфрида Вильгельма Лейбница — Niedersächsische Landesbibliothek, Ганновер, 1679 г..

10. Готфрид Вильгельм Лейбниц. Progressio binaria est pro theoria, sedenaria pro praxi. Неопубликованная рукопись с маркой LH 35, 3 B 17 Bl. 4 ^r , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1679.

11. Готфрид Вильгельм Лейбниц. Рукопись без названия. Неопубликованная рукопись с маркой LH 35, 3 B 5 Bl. 77, принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1682 г.

12. Готфрид Вильгельм Лейбниц. Рукопись без названия. Неопубликованная рукопись с маркой LH 35, 3 B 11 Bl. 11 ^v , принадлежит Библиотеке Готфрида Вильгельма Лейбница – Niedersächsische Landesbibliothek, Ганновер, 1703.

13. Брюс А. Мартин. О двоичной записи. Сообщения ACM 11:10 (1968), 658. Доступно на https://dl.acm.org/doi/pdf/10.1145/364096.364107.

14. Джон В. Нистром. Проект новой системы арифметики, веса, меры и монет, которую предлагается назвать тональной системой, с шестнадцатью по основанию . JB Lippincott & Co., 1862. Доступно на https://books.google.com/books?id=aNYGAAAAYAAJ.

15. Джон В. Нистром. О новой системе арифметики и метрологии, называемой тональной системой. Журнал Института Франклина 76 (1863), 263–275, 337–348, 402–407. Доступно на https://archive.org/details/journalfranklini76fran.

16. Джон В. Нистром. Новый трактат об элементах механики, устанавливающий строгую точность в значении динамических терминов, с приложением по дуоденальной арифметике и метрологии . Портер и Коутс, 1875 г. Доступно по адресу https://books.google.com/books?id=eUYOAAAAAYAAJ.

17. Роберт М. Пирс. Задачи числа и меры . Роберт М. Пирс, 1898 г. Доступно по адресу https://gdz.sub.uni-goettingen.de/id/PPN603882684.

18. Стивен Шварцман. Слова математики: этимологический словарь математических терминов, используемых в английском языке . Издательство Кембриджского университета, 1996.

19. С. Шринивасан, Дж. В. М. Джозеф и П. Харикумар. Расшифровка индусского письма: метод подобия в действии. Текущая наука 103: 3 (2012), 268–281. Доступно по адресу https://www.jstor.org/stable/24085030.

20. Ллойд Стрикленд и Гарри Льюис. Лейбниц о двоичном коде: изобретение компьютерной арифметики . MIT Press, 2022.

21. Эмануэль Сведенборг. Любопытные мемуары г-на Эмануэля Сведенборга о Карле XII. Швеции. Журнал джентльмена и историческая хроника 24 (1754), 423–424. Д. Генри и Р. Кейв у ворот Святого Иоанна. Доступно по адресу https://www.google.com/books?id=WKwUAAAAQAAJ.

22. У. Б. Тейлор. Доклад об улучшенной системе счисления. В Годовом отчете попечительского совета Смитсоновского института , показывающем операции, расходы и состояние учреждения за 1867 год , стр. 119–120. Государственная типография, 1867 г. Доступно по адресу https://archive.org/details/annualreportofbo1867smith.

23. Роберт Б. Ульрих. Роман Деревообработка . Издательство Йельского университета, 2007.

    . Google Scholar

24. Уильям Дуайт Уитни. Словарь века: энциклопедический словарь английского языка, Том VII. The Century Co., 1895 г. Доступно по ссылке https://archive.org/details/centiciona07whit.

Ссылки на скачивание

Благодарности

Мы хотели бы поблагодарить анонимного рецензента за полезные комментарии к предыдущей версии этой статьи. Ллойд Стриклэнд также благодарен Gerda Henkel Stiftung, Дюссельдорф, за предоставление исследовательской стипендии (AZ 46/V/21), которая сделала возможной эту статью.

Информация о авторе

Авторы и принадлежность

1. Департамент истории, политики и философии, Манчестерский столичный университет, Geoffrey Manton Build

   Owain Daniel Jones

Авторы

1. Lloyd Strickland

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Академия

2. Owain Daniel Jones

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

Автор, ответственный за переписку

Ллойд Стрикленд.

Дополнительная информация

Примечание издателя

Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Права и разрешения

Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете автора(ов) оригинала. и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.

Перепечатка и разрешения

Об этой статье

Шестнадцатеричные числа — Electronics-Lab.com

Шестнадцатеричные числа

Шестнадцатеричный (16) номер представляет собой основание-16 систему счисления 16 (16) 16 (16) 16 для представления значения его цифры. В шестнадцатеричном числе используется группа или набор из четырех (4) двоичных цифр для формирования шестнадцатеричной цифры . Другими словами, шестнадцатеричная цифра эквивалентна полубайту, а из предыдущей статьи мы знаем, что полубайт — это четырехбитное двоичное число. Крайний правый полубайт образует наименее значимую шестнадцатеричную цифру, а слева от него можно добавлять полубайты для представления большего шестнадцатеричного числа.

Архитектура цифровых систем рассчитана на 8-, 16-, 32- и 64-битные и т. д. двоичные числа и представление этих чисел нулями (0) и единицами (1) становятся довольно запутанными и сложными. Чтение и запись больших двоичных чисел может привести к ошибкам, и информация действительно может стать сомнительной. Представлением больших двоичных чисел можно управлять с помощью системы нумерации с более высоким базовым значением, которая будет вмещать больше значений в однозначных цифрах по сравнению с двоичными цифрами (битами). Восьмеричная цифра (с основанием 8) может использовать восемь (8) чисел (от 0 до 7) и может вмещать 3-битное двоичное число. 3-битное двоичное число довольно мало и не подходит для 8-, 16-, 32- и 64-битных архитектур и т. д. Точно так же десятичное число подходит для представления 3-битного двоичного числа, но тратит впустую два (8 и 9).) числовые значения. Другими словами, восьмеричная система счисления более подходит по сравнению с десятичными (десятичными) числами, когда речь идет о представлении двоичных чисел.

Подходящей и подходящей системой нумерации является та, которая может вмещать 4-битное двоичное число. Как мы знаем, 4-битное число может содержать шестнадцать (16) значений (два, возведенные в степень четыре). Для этого требуется система счисления, имеющая набор из шестнадцати значений, то есть от 0 до 15. Десятичная цифра имеет диапазон чисел от 0 до 9, и такие числа, как 10, 11, 12, 14 и 15, не могут быть представлены, поскольку они предполагает использование ранее использовавшихся номеров. В шестнадцатеричном формате значения выше девяти (9) представлены английскими алфавитами, такими как A, B, C и т. д. Использование этих алфавитов решает проблему повторения чисел для десяти (10) и более значений.

Это означает, что A, B, C, D, E и F в шестнадцатеричном формате представляют собой десятичные числа: десять (10), одиннадцать (11), двенадцать (12), тринадцать (13), четырнадцать (14) и пятнадцать ( 15). То же самое верно для представления эквивалентных двоичных чисел «1010», «1011», «1100», «1101», «1110». и «1111» соответственно. Сложность представления большего двоичного числа можно облегчить, разбив двоичное число на группы по 4 бита. Например, рассмотрим (1101100111001010 ₂ ) — 16-битное двоичное число, которое можно записать как (1101 1001 1100 1010 ₂ ) . Последнее достигается путем разбиения на группу или набор из 4 битов, и полученное двоичное число намного легче читать.

Длину и сложность двоичных чисел можно дополнительно уменьшить, преобразовав их в эквивалентные шестнадцатеричные числа. Однако шестнадцатеричные числа являются сложными по сравнению с десятичными числами и используются только в цифровых системах. Четырехбитные двоичные числа «0000», «0001», «0010», … и «1111» представлены одной шестнадцатеричной цифрой. Четырехбитное двоичное число называется «полубайтом», что эквивалентно шестнадцатеричной цифре. Байт состоит из 8 бит или двух полубайтов, и две шестнадцатеричные цифры представляют его эквивалент. Например, двоичное число (10100111 ₂ ) разделен на две половинки/кусочки (1010 0111 ₂ ) . При этом (1010 ₂ ) эквивалентно (10 ₁₀ ) в десятичном виде и ( A ₁₆ ) в шестнадцатеричном. Точно так же второй полубайт (0111 ₂ ) эквивалентен (7) в десятичном и шестнадцатеричном формате. Таким образом, двоичное число (10100111 ₂ ) эквивалентно (A7 ₁₆ ) в шестнадцатеричном формате.

Шестнадцатеричные числа

В следующей таблице перечислены десятичные числа от 0 до 15 и их эквиваленты в двоичных и шестнадцатеричных числах.

В приведенной выше таблице показаны эквивалентные десятичные числа от 0 до 15 для шестнадцатеричных цифр. Для подсчета чисел после пятнадцати (F) в шестнадцатеричном формате используется процедура, аналогичная другим системам счисления, т.е. включая значащую цифру слева. Например, число «16», преобразованное в двоичное число, равно 9.0616 (0001 0000) ₂ и его эквивалент в шестнадцатеричном формате (10 ₁₆ ). Точно так же эквивалентом 17 в шестнадцатеричном формате является (11 ₁₆ ) , и, следуя той же процедуре, шестнадцатеричное число может быть расширено до желаемого значения.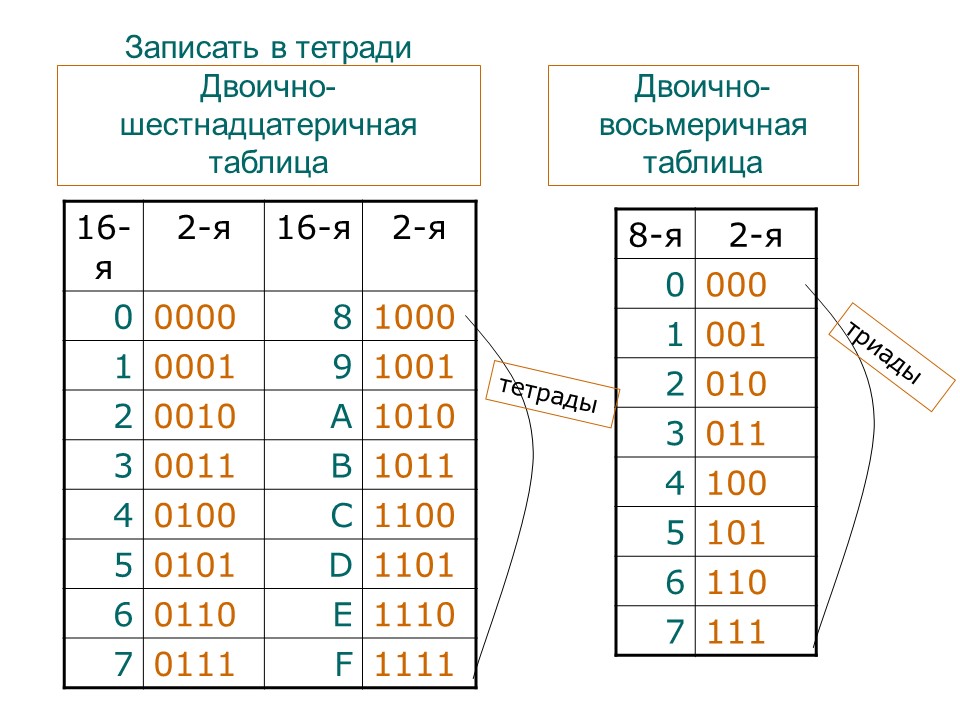 Используя приведенную выше таблицу, любое двоичное число можно легко преобразовать в эквивалентное ему шестнадцатеричное число. Например, 16-битное число (1010 1100 0111 1011 ₂ ) , преобразованное в шестнадцатеричное, равно (AC7B ₁₆ ) . Гораздо проще написать и запомнить это шестнадцатеричное число, чем 16-битный ряд из 0 и 1. Следовательно, рекомендуется записывать двоичные числа в шестнадцатеричной системе счисления, чтобы избежать ошибок и т. д.

В цифровых системах, особенно при написании программ, знак «#» (решётка) значащая цифра для обозначения шестнадцатеричного значения. Например, указанное выше шестнадцатеричное число (AC7B ₁₆ ) также можно записать как 9.0616 (#AC7B) .

Счет в шестнадцатеричном формате

Как описано выше, значение шестнадцатеричного числа можно расширить, используя дополнительные значащие цифры. Одна шестнадцатеричная цифра, начинающаяся с «0», может составлять до #F (15 X 16 ⁰ = 15 ₁₀ ) , расширенная до двух цифр, может составлять до #FF (15 X 16 ^1). +15 х 16 ⁰ = 255 ₁₀ ) . Точно так же #FFFF и #FFFF могут считать до 9.0616 4095 ₁₀ и 65535 ₁₀ , соответственно. В следующей таблице указан вес каждой цифры в шестнадцатеричном числе.

Добавление нулей к двоичному числу

Поскольку двоичное число разбивается на группы, состоящие из 4 битов, для определения его эквивалентного шестнадцатеричного числа. Для этого требуется двоичное число, состоящее из битов, кратных четырем (4), например. 4, 18, 12, 16 и 20 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 4 бита, начиная с младшего значащего бита (LSB), и, в конце концов, у нас останется менее 4 бит в конце. Ведущие нули добавляются к оставшимся битам, увеличивая их длину до 4 бит. Эта группа из 4 битов составляет старшую значащую цифру (MSD) шестнадцатеричных чисел. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 1010 ₁₀ ) преобразуется в 16-разрядное (делящееся на 4) двоичное число путем добавления ведущих нулей, а затем определяется его эквивалентное шестнадцатеричное число.

В приведенном выше примере 13-битное число требует добавления 3 битов с нулевыми значениями к крайней левой стороне, чтобы сделать его 16-битным двоичным числом. Точно так же 10-битное двоичное число потребует добавления шести (6) нулевых битов. Использование шестнадцатеричных чисел сокращает длину двоичных чисел в четыре (4) раза, а преобразование из двоичного в шестнадцатеричное или из шестнадцатеричного в двоичное выполняется легко и быстро.

Преобразование шестнадцатеричных чисел в десятичные

Преобразование шестнадцатеричных значений в десятичные достигается с помощью метода взвешенной суммы цифр, описанного в предыдущей статье. В следующем примере шестнадцатеричное число (#7DE5) преобразуется в десятичное число.

Преобразование десятичного числа в шестнадцатеричное

Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16, который использовался для преобразования десятичного числа в эквивалентное ему двоичное значение в предыдущей статье. То же десятичное число (238 ₁₀ ) используется для получения эквивалентного ему шестнадцатеричного числа в следующем примере.

Пример преобразования двоичного числа в шестнадцатеричное

Ниже показано преобразование 8-битного двоичного числа (11011001 ₂ ) в шестнадцатеричное число.

Шестнадцатеричный код в двоичный и десятичный Пример

Преобразование #8C4A в его эквивалентное двоичное и десятичное число показано ниже в качестве примера.

Вывод

• В шестнадцатеричном числе используется система счисления с основанием 16, и его цифры могут состоять из шестнадцати (16) цифр от 0 до 15. В шестнадцатеричном формате буквы с заглавными буквами: A, B, C, D, E и F используются как эквивалентно 10, 11, 12, 13, 14 и 15 соответственно.
• В шестнадцатеричных числах каждая цифра представляет собой группу или набор из 4 битов. Эквивалент двоичного числа в шестнадцатеричном формате получается путем разбиения двоичного числа на группы по 4 бита, а затем, в зависимости от значения каждой 4-битной группы, каждой группе присваивается эквивалентное шестнадцатеричное значение от «0» до «F».
• Двоичные числа могут потребовать добавления начальных нулей в крайнюю левую (наиболее значащую) сторону для формирования 4-битных групп.
• Шестнадцатеричное число представляется с помощью «16» в качестве нижнего индекса или решетки (#) с крайней левой стороны, например. 2A7E ₁₆ или #2A7E.
• Шестнадцатеричное число можно преобразовать в десятичное число с помощью метода взвешенной суммы цифр. Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16.