Site Loader
Posted on 11.05.2023

Содержание

Число 11, 0x00000B, одиннадцать — BiKubik.com

Энциклопедия чисел

Свойства натурального числа 11, 0x00000B, 0xB:

Системы счисления Основные свойства Степени, корни

Тригонометрия Хэши, криптография Языки программирования

Дата и время Цвет по числу Интернет

Другие свойства

Рейтинг 6.6 из 10, оценок: 20.

Системы счисления, перевод в систему счисления

Десятичное число 11

  • 11 в шестнадцатеричной системе счисления
    B
  • 11 в двоичной системе счисления
    1011
  • 11 в восьмеричной системе счисления
    13

Шестнадцатеричное число B

  • B в десятичной системе
    11
  • B в двоичной системе
    1011
  • B в восьмеричной системе
    13

Двоичное число 1011

  • 1011 в десятичной системе
    11
  • 1011 в шестнадцатеричной системе
    B
  • 1011 в восьмеричной системе
    13

Восьмеричное число 13

  • 13 в десятичной системе
    11
  • 13 в шестнадцатеричной системе
    B
  • 13 в двоичной системе
    1011

Основные арифметические и алгебраические свойства

  • Число 11 на русском языке, number in Russian, число 11 прописью:
    одиннадцать
  • Четность
    Нечетное число 11
  • Разложение на множители, делители числа 11
    11, 1
  • Простое или составное число
    Простое число 11
  • Числа делящиеся на целое число 11
    22, 33, 44, 55, 66, 77, 88, 99
  • Число 11 умноженное на число два
    22
  • 11 деленное на число 2
    5. 5
  • Список 8-ми простых чисел перед числом
    7, 5, 3, 2
  • Сумма десятичных цифр
    2
  • Количество цифр
    2
  • Десятичный логарифм 11
    1.0413926851582
  • Натуральный логарифм 11
    2.3978952727984
  • Это число Фибоначчи?
    Нет
  • Число на 1 больше числа 11,
    следующее число
    число 12
  • Число на 1 меньше числа 11,
    предыдущее число
    10

Степени числа, корни

  • 11 во второй степени (в квадрате)
    (функция x в степени 2 — x²)
    121
  • В третьей степени (в кубе, 11 в степени 3, x³) равно
    1331
  • Корень квадратный из 11
    3.3166247903554
  • Корень кубический из числа 11 =
    2.2239800905693

Тригонометрические функции, тригонометрия

  • Синус, sin 11 градусов, sin 11°
    0. 1908089954
  • Косинус, cos 11 градусов, cos 11°
    0.9816271834
  • Тангенс, tg 11 градусов, tg 11°
    0.1943803091
  • Синус, sin 11 радиан
    -0.9999902065507
  • Косинус, cos 11 радиан
    0.0044256979880508
  • Тангенс, tg 11 радиан равно
    -225.9508464542
  • 11 градусов, 11° =
    0.19198621771938 радиан
  • 11 радиан =
    630.25357464391 градуса, 630.25357464391°

Контрольные суммы, хэши, криптография

  • MD-5 хэш(11)
    6512bd43d9caa6e02c990b0a82652dca
  • CRC-32, CRC32(11)
    3596227959
  • SHA-256 hash, SHA256(11)
    4fc82b26aecb47d2868c4efbe3581732a3e7cbcc6c2efb32062c08170a05eeb8
  • SHA1, SHA-1(11)
    17ba0791499db908433b80f37c5fbc89b870084b
  • ГОСТ Р 34. 11, GOST R 34.11-94, GOST(11)
    6a015a0f86de26f49624ca463ced5dd911c7dfe148e1c40cee995d1c5bfa1228
  • Base64
    MTE=

Языки программирования

  • C++, CPP, C значение 11
    0x00000B, 0xB
  • Delphi, Pascal значение числа 11
    $00000B

Дата и время

  • 11-й день простого и високосного года
    11 января
  • Конвертация UNIX timestamp 11 в дату и время
    UTC
    в Москве, Россия
    в Лондоне, Великобритания
    в Нью-Йорке, США

Интернет

  • Конвертация в IPv4 адрес Интернет
    0.0.0.11
  • 11 в Википедии:
    11

Другие свойства числа

  • Короткая ссылка на эту страницу, DEC
    https://bikubik.com/ru/11
  • Короткая ссылка на эту страницу, HEX
    https://bikubik.com/ru/xB
  • Номер телефона
    11
  • Телефонный код страны
    +11

Цвет по числу 11, цветовая гамма

  • html RGB цвет 11, 16-ричное значение
    #00000B — (0, 0, 11)
  • HTML CSS код цвета #00000B
    .color-mn { color: #00000B; }
    .color-bg { background-color: #00000B; }

Цвет для данного числа 11

 

Здесь вы можете изменить составляющую цвета для данного числа 11 или цвета 00000B:

5 в шестнадцатеричной системе.

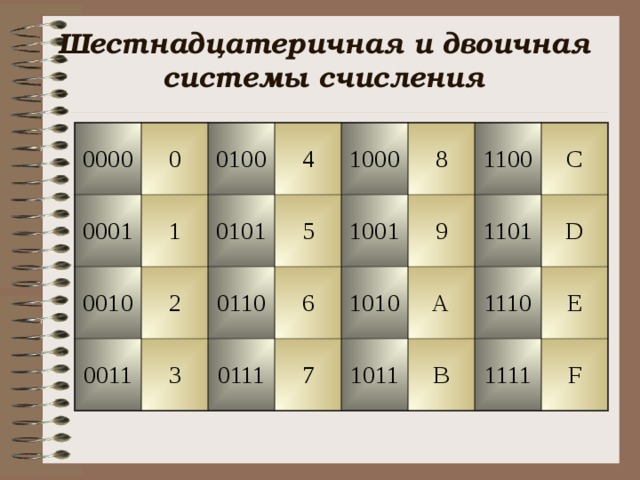Шестнадцатеричная и двоичная системы счисления

Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.

При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.

Перевод чисел из шестнадцатеричной системы в десятичную

Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле

Примеры.

    АЕ07 16 =10∙16 3 +14∙16 2 +0∙16 1 +7∙16 0 =44551 10 .

    100 16 =1∙16 2 +0∙16 1 +0∙16 0 =256 10 .

    58 16 =5∙16 1 +8∙16 0 =.88 10 .

    2А 16 =2∙16 1 +10∙16 0 =42 10 .

Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.

Перевод чисел из шестнадцатеричной системы в двоичную и обратно

Перевести любое шестнадцатеричное число в двоичное можно следующим образом. Каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом —

тетрадой . После этого нули, стоящие слева, можно отбросить.

2) 2A= 0010 1010 2 = 101010 2 .

3) 58 16 = 0101 1000 2 = 1011000 2 .

И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.

Примеры.

2. 101010 2 = 10 1010 2 = 2A.

3. 1011000 2 = 101 1000 2 = 58 16 .

Восьмеричная система счисления

Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:

0, 1, 2, 3, 4, 5, 6, 7.

Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.

Перевод чисел из восьмеричной системы в двоичную и обратно

Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой .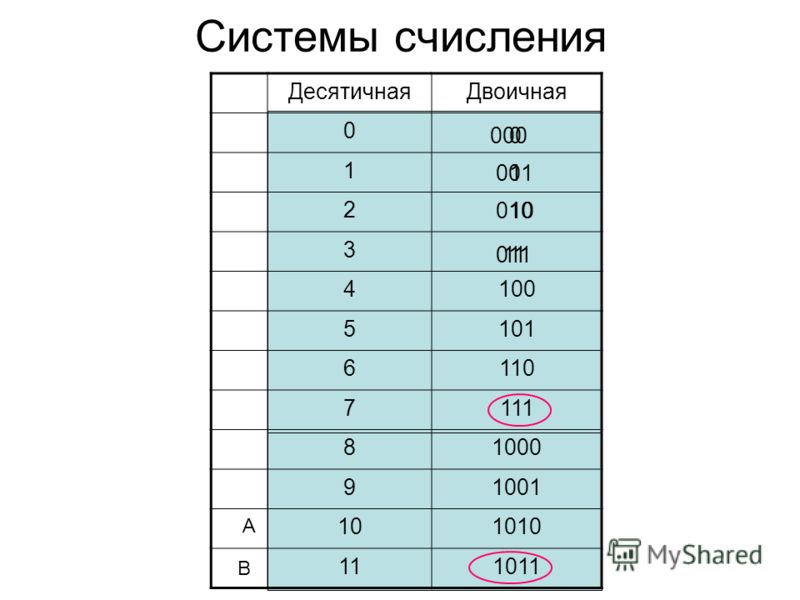

Примеры.

2563 8 = 010 101 110 011 2 =10101110011 2 .

1001101 2 = 001 001 101 2 = 115 8 .

Методические материалы для лабораторного занятия №1

Тема лабораторного занятия: Системы счисления. Измерение информации.

Количество часов: 2.

Примеры с решениями

    Перевод из p -ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде

11100110 2 = 1∙2 7 + 1∙2 6 + 1∙2 5 + 0∙2 4 + 0∙2 3 + 1∙2 2 + 1∙2 1 + 0∙2 0 = 128 + 64 + 32 + 4 + 2 = 230 10 .

2401 5 = 2∙5 3 + 4∙5 2 + 0∙5 1 + 1∙5 0 = 250 + 100 + 0 + 1 = 351.

    Перевод из 10-ичной системы в p -ичную.

2.1 98 10 → Х 2 .

Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.

    98: 2 = 49. Остаток — 0 .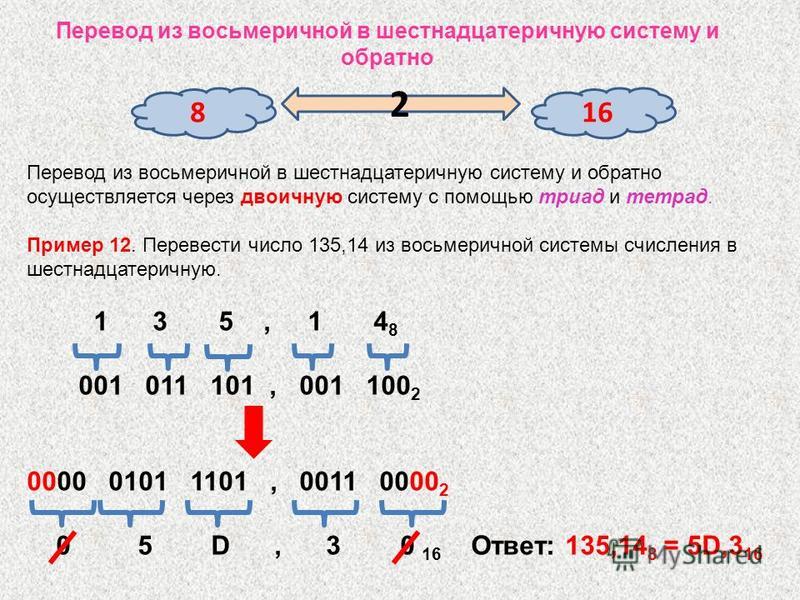

    49: 2 = 24. Остаток — 1 .

    24: 2 = 12. Остаток — 0 .

    12: 2 = 6. Остаток — 0 .

    6: 2 = 3. Остаток — 0 .

    3: 2 = 1 . Остаток — 1 .

Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 98 10 = 1100010 2 .

2.2 2391 10 → Х 16 .

Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.

    2391: 16 = 149. Остаток — 7 .

    149: 16 = 9 . Остаток — 5 .

Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 2391 10 = 957 16 .

2.3 12165 10 → Х 2 .

Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.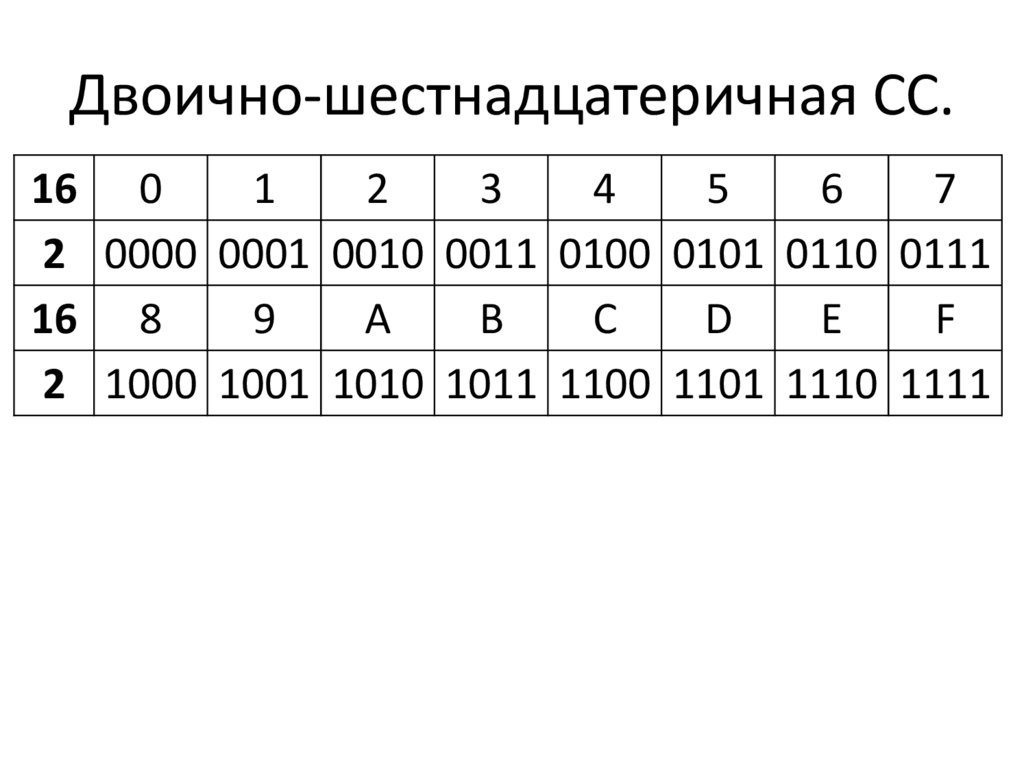

12165 10 = 27605 8 = 010 111 110 000 101 = 10111110000101.

    Определение основания системы счисления p .

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?

Решение. Надо определить основание системы счисления p . Так как мы знаем, что пальцев на ногах всего 10 10 , то 12 p =1∙p +2 = 10 10 . Отсюда получаем уравнение p + 2 = 10  p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 24 8 = 2∙8+4 = 20 10 , а на ногах — 12 8 = 1∙8+2 = 10 10 .

0123456789ABCDEF. Приняв за основание число 16, получаем шестнадцатеричную систему счисления. Здесь мы можем воспользоваться 10 знаками десятичной системы, добавив еще 6 знаков – буквы латинского алфавита (A, B, C, D, E, F): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 10 11 12 13 14 15 Всего 16 разных знаков составляют алфавит шестнадцатеричной системы счисления.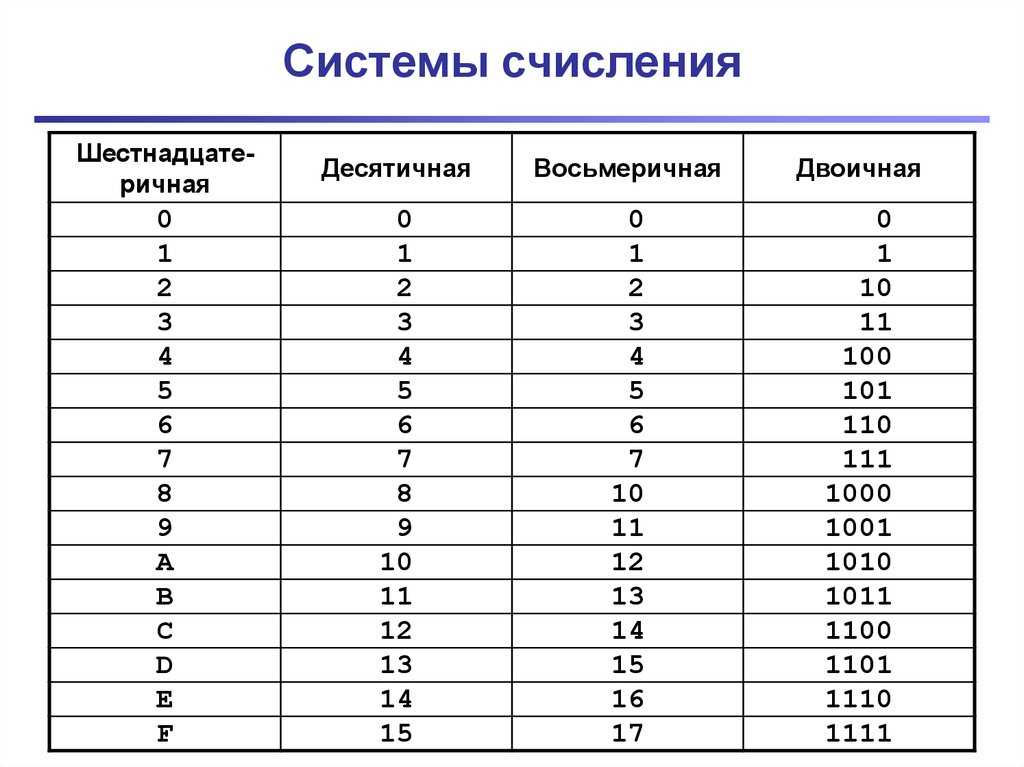

Можно записать любое число включая все эти знаки: А37, 1В45, F302, 1A3C5… — обратите внимание: используем знаки от 0 до F. Для шестнадцатеричной системы счисления q=16. Содержание.

Слайд 32 из презентации «История счёта и систем счисления»

. Размер архива с презентацией 2292 КБ.

Информатика 9 класс

краткое содержание других презентаций

««Моделирование» 9 класс» — Моделирование как метод познания. Файловая система ПК. Тест завершён. Птолемей построил модель мира. Модель человека в виде детской куклы. Удобнее всего при описании траектории движения объекта использовать информационную модель. Существующие признаки объекта. Описание дерева. Удобнее всего использовать информационную модель. Список депутатов государственной Думы. Список учащихся школы; план классных комнат.

«История счёта и систем счисления» — Основание системы счисления. Десятки. Десятичное число. Славянская кириллическая нумерация.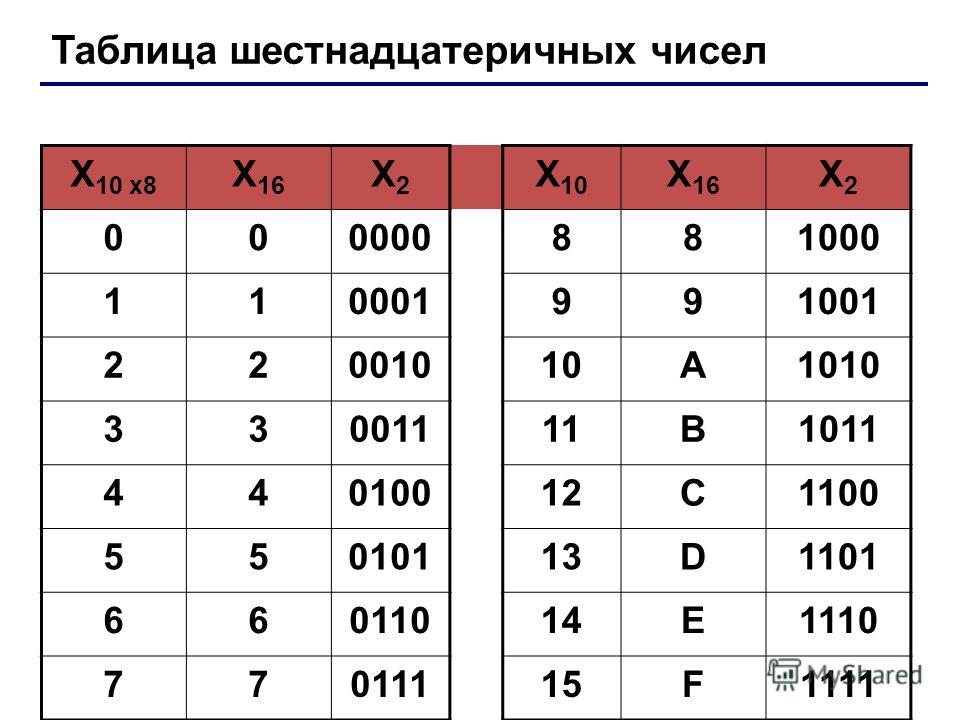

Нумерация. Цветок лотоса. Позиция цифры в числе называется разрядом. Положение цифры. В древние времена люди ходили босиком. Позиционная система счисления характеризуется своим основанием. Деление на основание. Запись чисел нового типа. Умножение двоичных чисел. Перевод десятичного числа. Арифметические действия.

«Сортировка в электронных таблицах» — Сортировка и поиск данных в электронных таблицах. Поиск данных в ЭТ. Порядок проведения вложенной сортировки. Отдел. Условия поиска записей. Запишите фамилии. Практическая работа. Сортировка по возрастанию. Порядок следования строк. Сортировка и поиск данных. Оклад и возраст. Рефлексивный экран. Сортировка данных. Выберите примеры баз данных. Сортировка записей. Разница между записью и полем. Порядок использования автофильтра.

«Циклические программы» — Составить программу. Найти сумму. Введите целое число. Найти количество трехзначных натуральных чисел. Найти сумму натуральных чисел. Вычислить. Цикл с постусловием. Напечатать на экране таблицу. Первоначальный взнос. Цикл с предусловием. Делители. Циклические программы. Информатика. Табулирование функции. Понятие цикла. Цикл с параметром. Ввод исходных данных. Таблица перевода долларов. Найти количество чисел.

«Моделирование как метод научного познания» — Таблица типа «объекты-объекты-один». Описания объекта. Метод познания окружающего мира. Решение задач. Образовательные ресурсы. Пятеро ребят. Формализация. Этапы моделирования. Мальчик. Иерархическая модель. Описание объекта моделирования. Юра. Сирень. Обозначения серверов. Технические модели. Ярусные диаграммы. Диаграмма. Тип. Моделирование как метод познания. Модели на графах. Задачи, решаемые с помощью графов.

«Что такое электронная почта» — Адрес электронной почты. Маршутизация почты. Письмо. Как работает электронная почта. X-mailer. Вопрос появления электронной почты. Дата. Копия. Электронное письмо. Структура письма. История электронной почты. Отправитель. Электронная почта.

Шестнадцатеричная система счисления. аша первая программа.

Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.

Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).

В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл.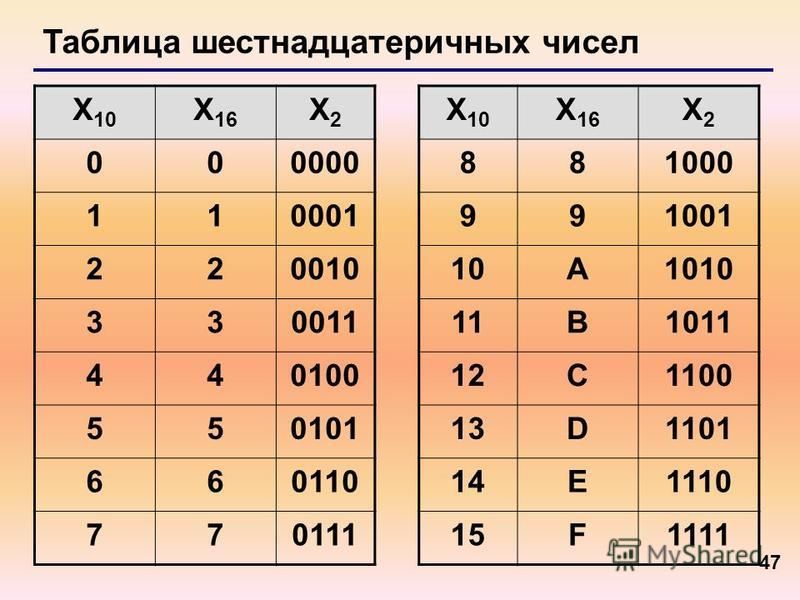 1).

Десятичное число

Шестнадцатеричное число

Таблица 1. Десятичная и шестнадцатеричная системы.

Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.

Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.

Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.

Т.о. Пример 1 (см. выше) правильнее будет записать так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h. Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h = 1000h.

Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.

Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.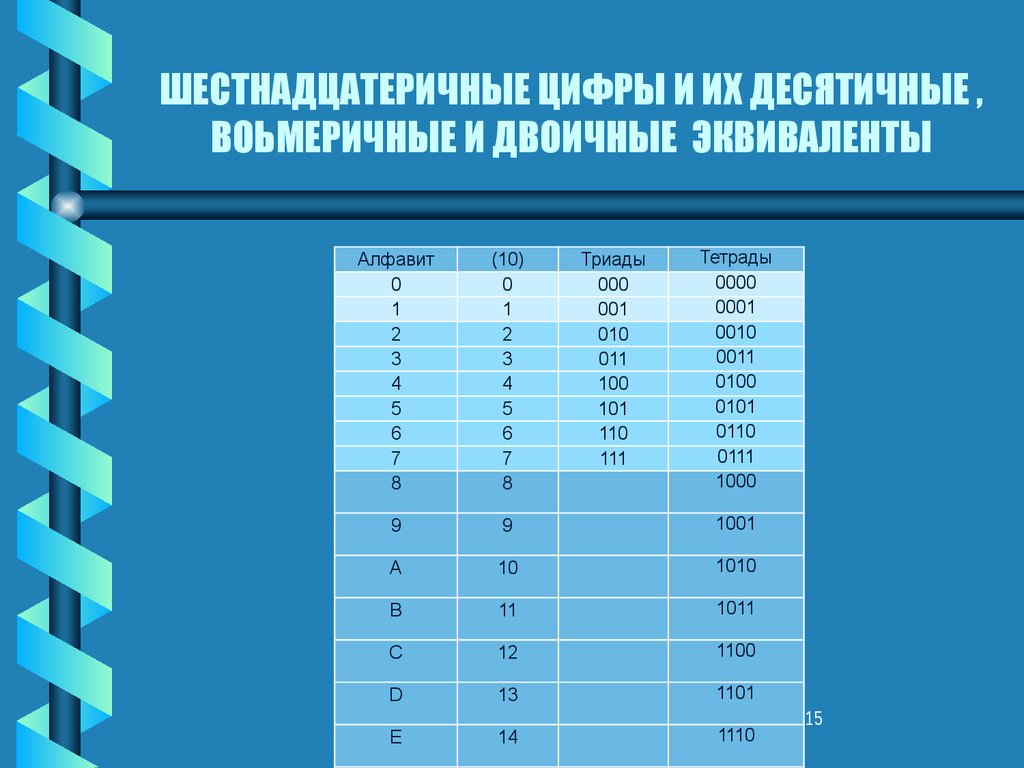

Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.

Примерно так:

строкКод программы
(1)mov ah,9

Объяснения:

В строке (1) мы делаем то-то, а в строке (15) то-то.

Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.

И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:

Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.

Итак, переходим к нашей первой программе:

(1) CSEG segment

(2) org 100h

(4) Begin:

(6) mov ah,9

(7) mov dx,offset Message

(8) int 21h

(10) int 20h

(11)

(12) Message db «Hello, world!$»

(13) CSEG ends

(14) end Begin

Для того, чтобы объяснить все операторы данного примера, нам потребуется несколько выпусков. Поэтому описание некоторых команд мы просто опустим на данном этапе. Просто считайте, что так должно быть. В самое ближайшее время мы рассмотрим эти операторы подробно. Итак, строки с номерами (1), (2) и (13) вы просто игнорируете.

Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.

Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin ( Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).

Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).

Регистр процессора это специально отведенная память для хранения какого-нибудь числа.

Например:

Если мы хотим сложить два числа, то в математике запишем так:

A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .

Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.

В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).

Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.

Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.

Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):

Программа сложения двух чисел

НачалоПрограммы

A=5 в переменную A заносим значение 5

B=8 в переменную B значение 8

ВызовПодпрограммы Сложение

теперь С равно 13

A=10 тоже самое, только другие числа

B=25

ВызовПодпрограммы Сложение

теперь С равно 35

КонецПрограммы

Подпрограмма Сложение

C=A+B

ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали

КонецПодпрограммы

В данном примере мы дважды вызвали подпрограмму Сложение , которая сложила два числа, переданные ей в переменных A и B.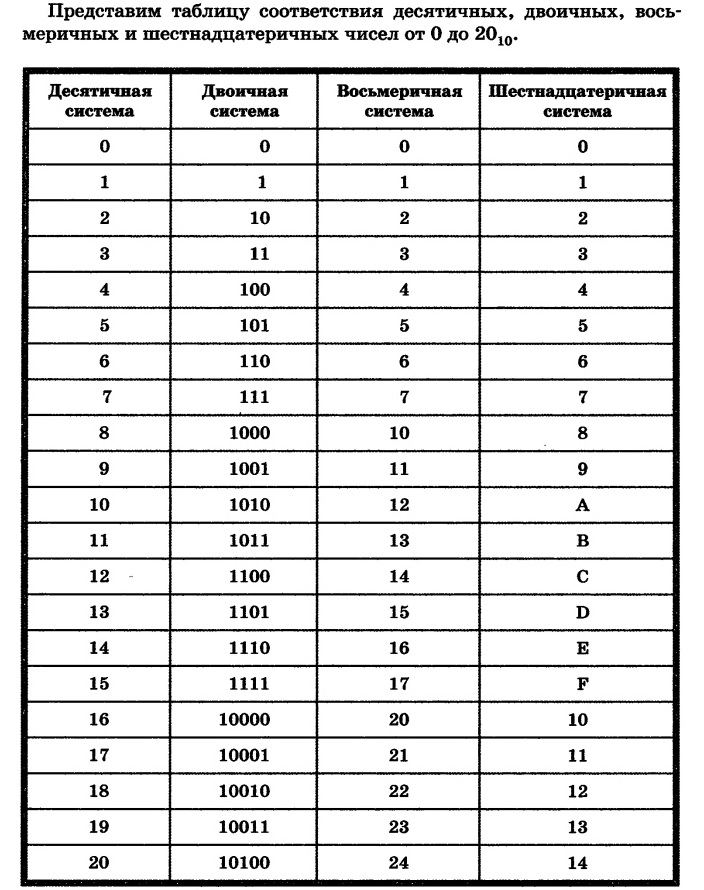 Результат помещается в переменную С. Когда вызывается подпрограмма, компьютер запоминает с какого места она была вызвана, а затем, когда закончила работу подпрограмма, компьютер возвращается в то место, откуда она вызывалась. Т.о. можно вызывать подпрограммы неопределенное количество раз с любого места.

При выполнении строки (8) программы на Ассемблере мы вызываем подпрограмму (в данном случае это называется прерывание), которая выводит на экран строку. Для этого мы, собственно, и помещаем необходимые значения в регистры. Всю необходимую работу (вывод строки, перемещение курсора) берет на себя подпрограмма. Эту строку можно прочитать так: вызываем двадцать первое прерывание ( int от англ. interrupt прерывание). Обратите внимание, что после числа 21 стоит буква h. Это, как мы уже знаем, шестнадцатеричное число (33 в десятичной системе). Конечно, нам ничего не мешает заменить строку int 21h на int 33. Программа будет работать корректно. Просто в Ассемблере принято указывать номер прерывания в шестнадцатеричной системе.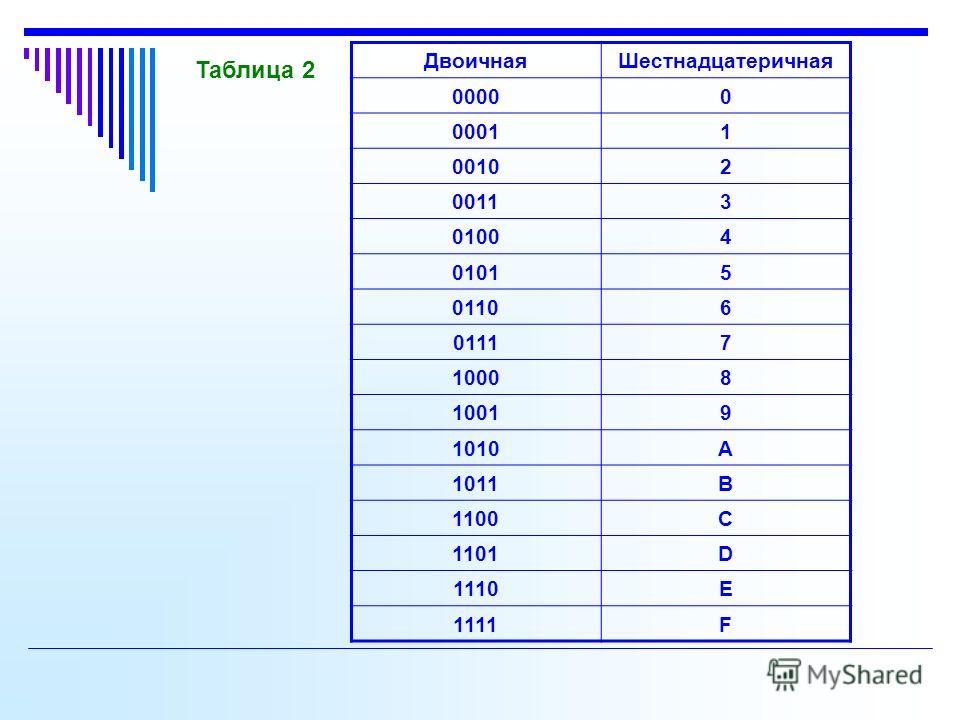

В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.

Строка (12) содержит сообщение для вывода. Первое слово ( message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.

Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:

(10) mov dx,offset Mess2

(13) Message db «Hello, world!$»

(14) Mess2 db «Это Я! $»

и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет

Обратите внимание на последний символ в строках Message и Mess2 — $. Он указывает на конец строки. Если мы его уберем, то 21 h прерывание продолжит вывод до тех пор, пока не встретится где-нибудь в памяти символ $. На экране мы увидим мусор .

Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.

Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.

Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная

Системы счисления

Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.

Понятие шестнадцатеричной системы

Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.

Где применяется

Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники.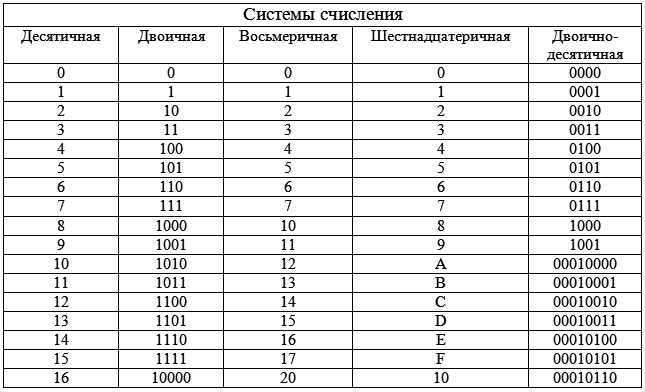 С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.

Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.

Для представления чисел в микропроцессоре используется двоичная система счисления .
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=a n a n-1 ..a 1 a 0 ,a -1 a -2 …a -m запишется в двоичной системе счисления как

x = a n ·2 n +a n-1 ·2 n-1 +…+a 1 ·2 1 +a 0 ·2 0 +a -1 ·2 -1 +a -2 ·2 -2 +…+a -m ·2 -m

где a i — двоичные цифры (0 или 1).

Восьмеричная система счисления

В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.

Шестнадцатеричная система счисления

В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:

10 10 = A 16 12 10 = C 16 14 10 = E 16
11 10 = B 16 13 10 = D 16 15 10 = F 16 .

Например, число 175 10 в шестнадцатеричной системе счисления запишется как AF 16 . Действительно,

10·16 1 +15·16 0 =160+15=175

В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.

ДесятичнаяДвоичнаяВосьмеричнаяШестнадцатеричная
00 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10

Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.

Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.

Пример: Преобразовать число 1101110,01 2 в восьмеричную систему счисления.

Объединяем двоичные цифры в триады справа налево. Получаем

001 101 110,010 2 = 156,2 8 .

Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:

156,2 8 = 001 101 110,010 2 .

Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.

Пример: Преобразовать число 1101110,11 2 в шестнадцатеричную систему счисления.

Объединяем двоичные цифры в тетрады справа налево. Получаем

0110 1110,1100 2 = 6E,C 16 .

Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом.

преобразовать двоичное число 11 в шестнадцатеричное

Как записать 11 в шестнадцатеричном формате (с основанием 16)?

11 равно 3 в шестнадцатеричной форме

Преобразование в другие базы

Бинарный:
Четвертичный:
Восьмеричный:
Десятичная дробь:
Шестнадцатеричный:
База 32:

Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования двоичной базы. Здесь вы можете найти ответ на такие вопросы, как: преобразовать двоичное число 11 в шестнадцатеричное или преобразовать двоичное число в шестнадцатеричное.

99109999 900099999999999998
Dec Hex Oct Bin
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6 6 11000 6 6
6
6 6.0007 7 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14
13 D
13 D 15 1101
14 E 16 1110
15 F 17 1111

0009
Dec Hex Oct Bin
16 10 20 10000
17 11 21 10001
18 12 10001
18 120009 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 9009
24 18 30
11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1d 35 11101
30 1E 36 1E 360009
31 1F 37 11111

359 290009
Dec Hex Oct Bin
32 20 40 100000
33 21 41 100001
34 22 42 100010
35 23 43
23 43 100011
36 24 44 100100
37 25 45 100101
38 26 46 100110
39 27 47 100111
40 28 50 101000
41 51 101001 29 51 101001 51 101001
42 2A 52 101010
43 2B 53 101011
44 2C 54 101100
45 2D 55 101101
46 2E 56 101110
47 2F 57 101111 2F 57 101111
0060

0009
Dec Hex Oct Bin
48 30 60 110000
49 31 61 110001
50 32 62 110010
51 33 63 110011
52 34 64 110100 34 64 110100 34 64 110100
53 35 65 110101
54 36 66 110110
55 37 67 110111
56 38 70 111000
57 39 71 111001
58 3A 72 11101099
72 11101099
72 11101099
72 11101099
0007 59 3B 73 111011
60 3C 74 111100
61 3D 75 111101
62 3E 76 111110
63 3F 77 111111

00090009
DEC HEX Oct9. октябрь99 октябрь9999 октябрь99.0070
64 40 100 1000000
65 41 101 1000001
66 42 102 1000010
67 43 103 1000011
68 44 104 1000100
69 45 100009 1000101 45 1000101
70 46 106 1000110
71 47 107 1000111
72 48 110 1001000
73 49 111 1001001
74 4A 112 1001010
75 4B 113 1001011 4B 1001011
76 4C 114 1001100
77 4D 115 1001101
78 4E 116 1001110
79 4F 117 1001111

00090009
Dec Hex Oct Bin
80 50 120 1010000
81 51 121 1010001
82 52 122 1010010
83 53 123 1010011
84 54 124 1010100
85 55 125 1010101
56 126
86 56 126
86 56 126
1010110
87 57 127 1010111
88 58 130 1011000
89 59 131 1011001
90 5A 132 1011010
91 5B 133 1011011
92 5C 134
92 5C 134
1011100
93 5D 135 1011101
94 5E 136 1011110
95 5F 137 1011111

0

0009
Dec HEX OCT BIN
96 60 140 1100000
97
97 61 141 1100001
98 62 142 1100010
99 63 143 1100011
100 64 144 1100100
101 65 145 1100101
102 66 146 1100110
103 9000 67 147 1100111
104 68 150 1101000
105 69 151 1101001
106 6A 152 1101010
107 6B 153 1101011
108 6C 154 1101100
1098 6D 155 1101101
110 6E 156 1101110
111 6F 157 1101111

000900090009
Dec Hex октября Bin
112 70 160 1110000
113 71 161 110001 161999 110001
114 72 162 1110010
115 73 163 1110011
116 74 164 1110100
117 75 165 1110101
118 76 166 1110110
119 167 111011119 77 167 111011111119
120 78 170 1111000
121 79 171 1111001
122 7A 172 1111010
123 7B 173 1111011
124 7C 174 1111100
125 7D 175999 11111111119 7D 175999 1111101
126 7E 176 1111110
127 7F 177 1111111

0009
Dec Hex Oct Bin
128 80 200 10000000
129 81 201 10000001
130 82 202 10000010
131 83 203 10000011
132 84 204 10000100
133 85 205 10000101
134 86 206 10000110
135 87 207 10000111
136
0008 88 210 10001000
137 89 211 10001001
138 8A 212 10001010
139 8B 213 10001011
140 8C 214 10001100
141 215 10001101
142 10001101
142 8E 216 10001110
143 8F 217 10001111

9000 920009 90000009
Dec Hex Oct Bin
144 90 220 10010000
145 91 221 10010001
146 222 10010010 222 10010010
147 93 223 10010011
148 94 224 10010100
149 95 225 10010101
150 96 226 10010110
151 97 227 10010111
152 98 230 152 230 10011000
153 99 231 10011001
154 9A 232 10011010
155 9B 233 10011011
156 9C 234 10011100
157 9D 235 10011101
158 236
158 236
10011110
159 9F 237 10011111

9000
Dec Hex Oct Bin
160 A0 240 10100000
161 A1 241 10100001
162 A2 242 10100010
163 10100010
163

009

A3 243 10100011
164 A4 244 10100100
165 A5 245 10100101
166 A6 246 10100110
167 A7 247 10100111
168 A8 10101000
10101000
169 A9 251 10101001
170 AA 252 10101010
171 AB 253 10101011
172 AC 254 10101100
173 г. н.э. 255 10101101
174 AE 256 101011100010
175 AF 257 10101111

008 263000009
Dec Hex Oct Bin
176 B0 260 10110000
177 B1 261 10110001
178 B2 262 10110010
179 B3
10110011
180 B4 264 10110100
181 B5 265 10110101
182 B6 266 10110110
183 B7 267 101101119
184 B8 270 10111000
185 B

00

185 B
185 B
185 B9 271 10111001
186 BA 272 10111010
187 BB 273 10111011
188 BC 274 10111100
189 BD 275 10111101
190 BE 276 101110
191 10111110
191 BF 277 10111111

0008 11001001
Dec Hex Oct Bin
192 C0 300 11000000
193 C1 301 11000001
194 C2 302 11000010
195 C3 303 11000011 303 11000011 11000011 11000011
196 C4 304 11000100
197 C5 305 11000101
198 C6 306 11000110
199 C7 307 11000111
200 C8 310 11001000
201 C9 311 C9 311
202 CA 312 11001010
203 CB 313 11001011
204 CC 314 11001100
205 CD 315 11001101
206 CE 316 11001110
207 CF 317009 11001111

Dec Hex Oct Bin
208 D0 320 11010000
209 D1 321 11010001
210 D2 322 11010010
211 D3 323 11010011
212 11010011
2120009 D4 324 11010100
213 D5 325 11010101
214 D6 326 11010110
215 D7 327 110101119
216 D8 330 11011000
217 D9 331 11011001
331 11011001
0008 218 DA 332 11011010
219 DB 333 11011011
220 DC 334 11011100
221 DD 335 11011101
222 DE 336 11011110
223 DF 337 1101111190010

900001
Dec Hex Oct Bin
224 E0 340 11100000
225 E1 341 11100001
226 E2 342 11100010
227 E3 343 11100011
228 E4
228 344 11100100
229 E5 345 11100101
230 E6 346 11100110
231 E7 347 11100111
232 E8 350 11101000
233 E9 351 11101001
234 EA
2340009 352 11101010
235 EB 353 11101011
236 EC 354 11101100
237 ED 355 11101101
238 EE 356 11101110
239 EF 357 111011

 110009

9000

Dec Hex Oct Bin
240 F0 360 11110000
241 F1 361 11110001
242 F2 362 11110010
243 F3 363 11110011
244 F4 364 111010090009
245 F5 365 11110101
246 F6 366 11110110
247 F7 367 11110111
248 F8 370 11111000
249 F9 371 11111001
250 FA 3720008 11111010
251 FB 373 11111011
252 FC 374 11111100
253 FD 375 11111101
254 FE 376 11111110
255 FF 377 111111111999910

Номерная базовая конвертер

Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.

  • 3000 octal to decimal
  • 11110100000000 binary to hexadecimal
  • BF hexadecimal to octal
  • 11011101 binary to octal
  • 33000 octal to decimal
  • 198 decimal to octal
  • 1991 decimal to binary
  • 1700 восьмеричное в десятичное
  • 10000000000000000000000000000000 двоичное в десятичное

Десятичный 11 в шестнадцатеричном формате | работа, решение

Как написать 11 в шестнадцатеричном формате?

11 записывается как b в шестнадцатеричном формате

Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 11 в шестнадцатеричном формате | работа, решение или преобразование десятичного в шестнадцатеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.

Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.

С помощью этого конвертера вы можете получить ответы на такие вопросы, как:

  • Что такое 11 в двоичном формате?
  • Что такое 11 в шестнадцатеричном формате?
  • Что такое восьмеричное число 11?
  • Как преобразовать число 11 в двоичное?
  • Как преобразовать число 11 в двоичное? И так далее.

Преобразование десятичной в двоичную диаграмму, включая шестнадцатеричную и восьмеричную

0
Декабрь Шестнадцатеричный Октябрь Бин
0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6 6 110999
6 110999
6 110999
6 110999
60009 110999
6 110009 60009 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 11009
13 D 15
13 D 15
0009 1101
14 E 16 1110
15 F 17 1111

0008 22
Dec Hex Oct Bin
16 10 20 10000
17 11 21 10001
18 12 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30
0008 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 111110
31 1F 37 11111

9000 290009
Dec Hex Oct Bin
32 20 40 100000
33 21 41 100001
34 22 42 100010
35 23 43
100011
36 24 44 100100
37 25 45 100101
38 26 46 100110
39 27 47 100111
40 28 50 101000
41 51 101001 29 51 101001 51 101001
42 2A 52 101010
43 2B 53 101011
44 2C 54 101100
45 2D 55 101101
46 2E 56 101110
47 2F 57 101111 2F 57 101111
0060

0009
Dec Hex Oct Bin
48 30 60 110000
49 31 61 110001
50 32 62 110010
51 33 63 110011
52 34 64 110100 34 64 110100 34 64 110100
53 35 65 110101
54 36 66 110110
55 37 67 110111
56 38 70 111000
57 39 71 111001
58 3A 72 11101099
72 11101099
72 11101099
72 11101099
0007 59 3B 73 111011
60 3C 74 111100
61 3D 75 111101
62 3E 76 111110
63 3F 77 111111

Образцы конверсии базы