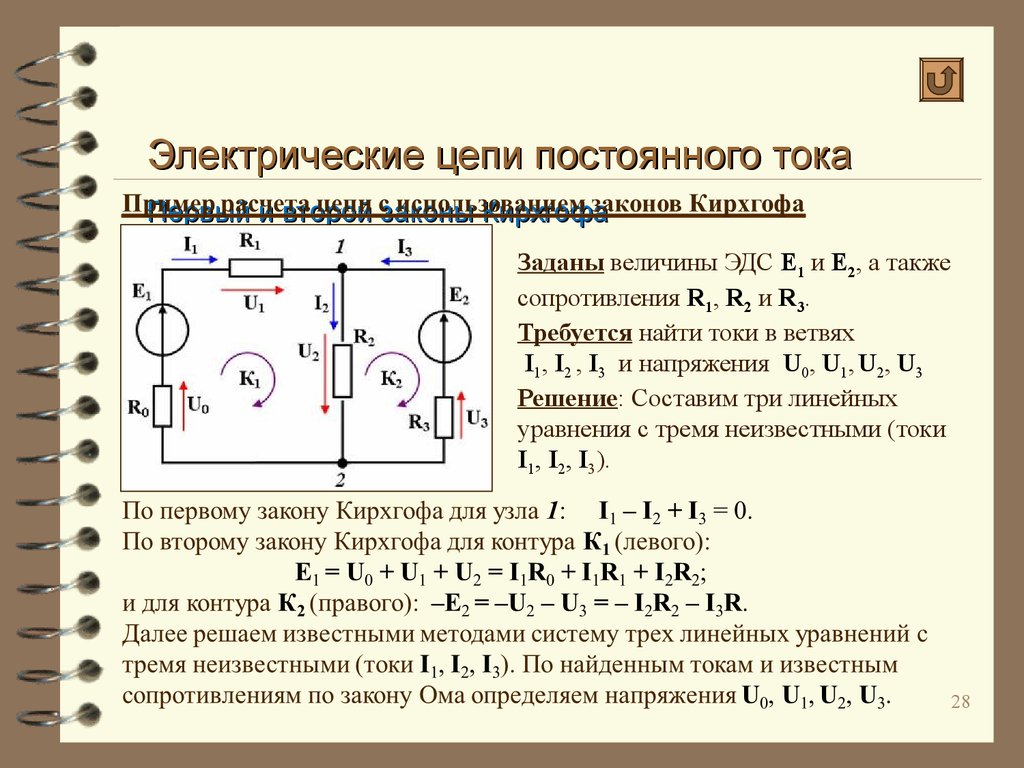
Законы Кирхгофа — презентация онлайн

Похожие презентации:

Закон Кирхгофа

Законы Кирхгофа

Законы постоянного тока. Законы Кирхгофа

Электротехника. Основные понятия и законы. (лекция 2)

Законы Кирхгофа. (Лекция 2)

Анализ сложной линейной электрической цепи постоянного тока

Электротехника и электроника. Электрические цепи постоянного тока. (Лекция 1)

Электротехника и электроника

Основные законы электротехники

Теория электрических цепей

ПРЕЗЕНТАЦИЯ
Тема: законы Кирхгофа

2. Узел – место соединения трех и более ветвей или проводов Ветвь – участок электрической цепи между двумя узлами, по которому протекает оди

Узел – место соединения трех и
более ветвей или проводов
Ветвь – участок электрической цепи
между двумя узлами, по которому
протекает один и тот же ток
Замкнутый контур – любой
замкнутый путь электрической
цепи, проходящий по нескольким
ветвям

3.

Первый закон Кирхгофа

4. I1, I2 > 0; I3, I4 < 0

I1, I2 > 0; I3, I4 < 0
Токи, втекающие в узел,
принято считать
положительными; токи,
вытекающие из узла –
отрицательными.
В узлах цепи
постоянного тока не
может происходить
накопление зарядов.
Суммарный заряд в
узле равен нулю.

6. Формулировка I закон Кирхгофа Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю I1 + I2 + I3 + … + In = 0 ∑ I = 0

Формулировка I закон
Кирхгофа
Алгебраическая сумма сил
токов для каждого узла в
разветвленной цепи равна
нулю
I1 + I2 + I3 + … + In = 0
∑I=0

7. Второй закон Кирхгофа В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднор

Второй закон Кирхгофа
В разветвленной цепи всегда
можно выделить некоторое
количество замкнутых путей,
состоящих из однородных и
неоднородных участков,
которые называются
контурами.

8. Цепь содержит два узла a и d, в которых сходятся одинаковые токи

9. В цепи можно выделить три контура abcd, adef и abcdef

Задаем положительное направление тока
и положительное направление обхода
контура.
Для участков контура abcd обобщенный
закон Ома записывается в виде:
I1R1 + I2R2 = = –Е1 – Е2
Аналогично, для контура adef можно
записать
– I2R2 + I3R3 = Е2 + Е3

10. Формулировка II закон Кирхгофа

В любого замкнутом контуре
алгебраической сумма ЭДС
равна алгебраической сумме
падений напряжения на
активных элементах данного
контура.
∑E=∑IR
Первое и второе правила
Кирхгофа, записанные для всех
независимых узлов и контуров
разветвленной цепи, дают в
совокупности необходимое и
достаточное число
алгебраических уравнений для
расчета электрической цепи.

12. ЛИТЕРАТУРА

1. Морозова Н.Ю. «Электротехника и
электроника» — М., 2007
2. Данилов И.А., Иванов М.П. «Общая
электротехника с основами
электроники» — М., Высшая школа,
1998
3. Лоторейчук Е.А. «Теоретические
основы электротехники» — М., 2003

English     Русский Правила

1.3. Законы Кирхгофа для магнитных цепей.

Законы Кирхгофа для магнитных цепей. При расчетах магнитных цепей, как и электрических, используют первый и вто­рой законы (правила) Кирхгофа.

Первый закон Кирхгофа: алгебраическая сумма маг­нитных потоков в любом узле магнитной цепи равна нулю:

Первый закон Кирхгофа для магнитных цепей следует из прин­ципа непрерывности магнитного потока, известного из курса физи­ки (см. также § 21.8 [1]).

Второй закон Кирхгофа: алгебраическая сумма паде­ний магнитного напряжения, вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль того же контура:

Второй закон Кирхгофа для магнитных цепей, по сути дела, есть иная форма записи закона полного тока.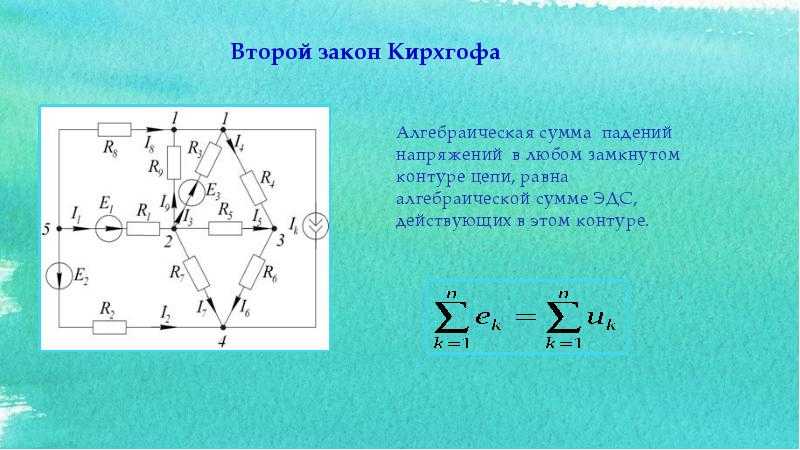

Перед тем как записать уравнения по законам Кирхгофа, сле­дует произвольно выбрать положительные направления потоков в ветвях и положительные направления обхода контуров.

Если направление магнитного потока на некотором участке сов­падает с направлением обхода, то падение магнитного напряжения

этого участка входит в сумму ∑U_m со знаком плюс, если встречно ему, то со знаком минус.

Аналогично, если МДС совпадает с направлением обхода, она входит в ∑Iw со знаком плюс, в противном случае — со знаком минус.

В качестве примера составим уравнения по законам Кирхгофа для разветвленной магнитной цепи, изображенной на рис. 14.12.

Левую ветвь назовем первой, и все относящиеся к ней величины запишем с индексом I (поток Ф₁, напряженность поля H₁, длина пути в стали l₁, длина воздушного зазора δ₁, МДС I₁w₁).

Среднюю ветвь назовем второй, и все относящиеся к ней величи­ны будут соответственно с индексом

2 (поток Ф₂, напряженность поля H₂, длина пути в стали l₂, длина воздушного зазора δ₂, МДС I₂w₂).

Все величины, относящиеся к правой ветви, имеют индекс 3 (поток Ф₃, длина пути на вертикальном участке l΄₃, суммарная дли­на пути на двух горизонтальных участках l΄΄₃).

Произвольно выберем направление потоков в ветвях. Положим, что все потоки (Ф₁, Ф₂, Ф₃) направлены вверх (к узлу а). Число урав­нений, которые следует составить по законам Кирхгофа, должно быть равно числу ветвей цепи (в рассматриваемом случае нужно составить три уравнения).

По первому закону Кирхгофа необходимо составить столько уравнений, сколько в цепи узлов без единицы (см.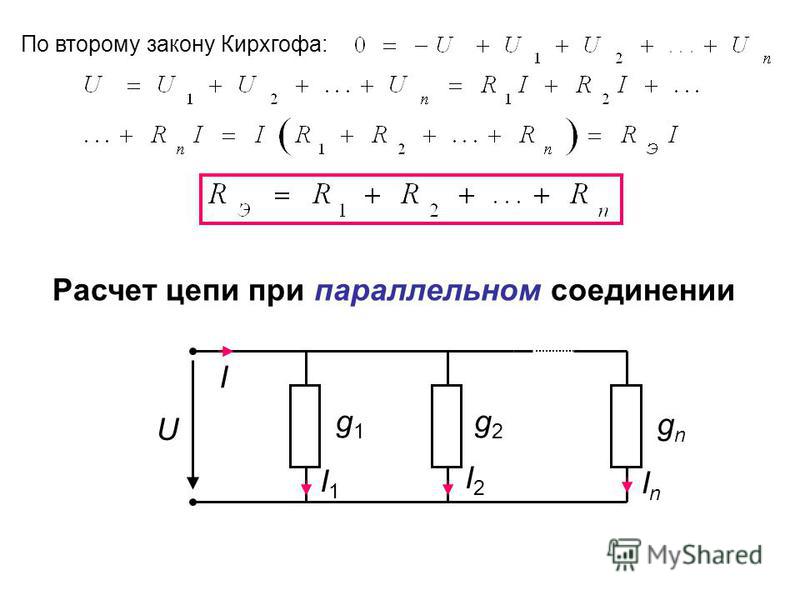 § 2.8 [1]).

В цепи (рис. 14.12) два узла; следовательно, по первому закону Кирхгофа составим одно уравнение:

По второму закону Кирхгофа следует составить число уравне­ний, равное числу ветвей, за вычетом числа уравнений, составленных по первому закону Кирхгофа. В рассматриваемом примере по второму закону Кирхгофа составим 3 — 1 = 2 уравнения.

Первое из этих уравнений составим для контура, образованного первой и второй ветвями, второе — для контура, образованного первой и третьей ветвями (для периферийного контура).

Перед составлением уравнений по второму закону Кирхгофа необходимо выбрать положительное направление обхода контуров. Будем обходить контуры по часовой стрелке.

Уравнение для контура, образованного первой и второй ветвя­ми, имеет вид

где H_δ1 и H_δ2 — напряженности поля соответственно в воздушных зазорах δ1 и δ2.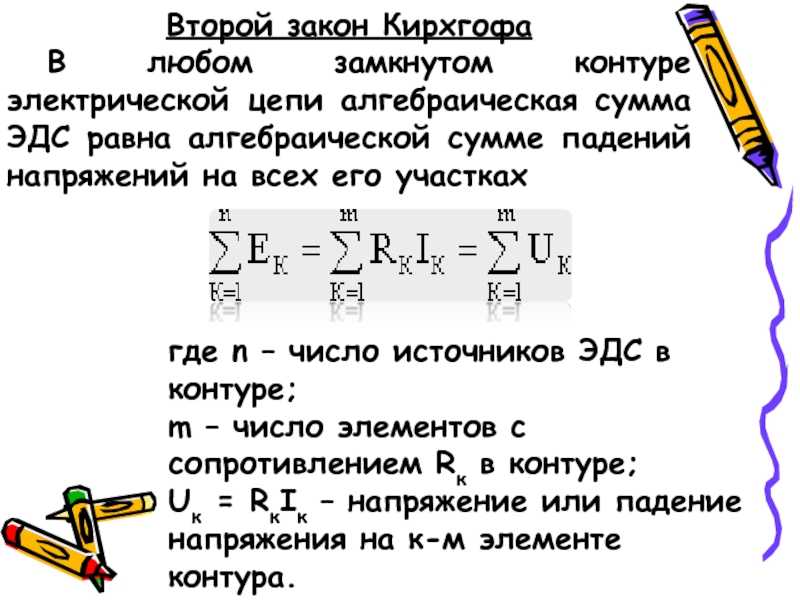

В левую часть уравнения вошли слагаемые H₁l₁ и H_δ1δ₁ со знаком плюс, так как на первом участке поток Ф₁ направлен согласно с обходом контура, слагаемые H₁l₁ и H_δ2δ₂ — со знаком минус, так как поток Ф₂ направлен встречно обходу контура.

В правую часть уравнения МДС I₁w₁ вошла со знаком плюс, так как она направлена согласно с обходом контура, а МДС I₂w₂ — со знаком минус, так как она направлена встречно обходу контура.

Составим уравнение для периферийного контура, образованно­го первой и третьей ветвями:

Совместно решать уравнения (а) — (в) с тремя неизвестными (Ф₁, Ф₂, Ф₃) не будем, так как в § 14.8 [1] дается решение рассматрива­емой задачи более совершенным методом, чем метод на основе законов Кирхгофа — методом двух узлов.

Применение к магнитным цепям всех методов, исполь­зуемых для расчета электрических цепей с нелинейными резистора­ми. В гл. 13 [1] подробно рассматривались различные методы расчета электрических цепей с НР. Эти методы полностью применимы и к расчету магнитных цепей, так как и магнитные и электрические цепи подчиняются одним и тем же законам — законам Кирхгофа.

Аналогом тока в электрической цепи является поток в магнит­ной цепи, аналогом ЭДС — МДС, аналогом вольт-амперной харак­теристики нелинейного резистора — вебер-амперная характери­стика участка магнитной цепи.

Обзор применения Законов рядов и параллельных потоков Кирхгофа в фармакологии: определение клиренса органов

Обзор

. 2022 ноябрь;239:108278.

doi: 10.1016/j.pharmthera.2022.108278. Epub 2022 6 сентября.

Джонатан Ашер Пахтер ¹ , Кен Дилл ¹ , Джаслин К Содхи ² , Лесли З Бенет ³

Принадлежности

• ¹ Университет штата Нью-Йорк, Стоуни-Брук, Центр физической и количественной биологии Лауфера и факультет физики и астрономии, Стоуни-Брук, Нью-Йорк, США.
• ² Калифорнийский университет в Сан-Франциско, Школы фармации и медицины, Департамент биоинженерии и терапевтических наук, Сан-Франциско, Калифорния, США.
• ³ Калифорнийский университет в Сан-Франциско, факультеты фармации и медицины, отделение биоинженерии и терапевтических наук, Сан-Франциско, Калифорния, США. Электронный адрес: [email protected].

• PMID: 36075300
• DOI: 10.1016/j.pharmthera.2022.108278

Обзор

Jonathan Asher Pachter et al. Фармакол Тер. 2022 ноябрь

. 2022 ноябрь;239:108278.

doi: 10.1016/j.pharmthera.2022.108278. Epub 2022 6 сентября.

Авторы

Джонатан Ашер Пахтер ¹ , Кен Дилл ¹

, Джаслин К Содхи ² , Лесли З Бенет ³

Принадлежности

• ¹ Университет штата Нью-Йорк, Стоуни-Брук, Центр физической и количественной биологии Лауфера и факультет физики и астрономии, Стоуни-Брук, Нью-Йорк, США.
• ² Калифорнийский университет в Сан-Франциско, Школы фармации и медицины, Департамент биоинженерии и терапевтических наук, Сан-Франциско, Калифорния, США.
• ³ Калифорнийский университет в Сан-Франциско, факультеты фармации и медицины, отделение биоинженерии и терапевтических наук, Сан-Франциско, Калифорния, США. Электронный адрес: [email protected].

• PMID: 36075300
• DOI: 10.1016/j.pharmthera.2022.108278

Абстрактный

Решения о дозировке лекарств и изменения дозирования у пациента в связи с болезненными состояниями, взаимодействием лекарств и фармакогеномикой основаны на клиренсе, показателе способности организма выводить лекарство. Первичными органами выделения являются печень и почки. Клиренс для каждого из этих органов представляет собой суммативную композицию биологических процессов. В 1857 году Густав Кирхгоф впервые разработал свои законы для описания «движения электричества в проводниках … [и] … в проводах», признав, что суммирующие процессы происходят либо параллельно, либо последовательно. С тех пор законы Кирхгофа также применялись к теплообмену, диффузии и силе сопротивления падающих предметов, но не к фармакологии. Хотя это и не было известно ранее, почечный клиренс всегда подчиняется законам Кирхгофа, как и печеночный клиренс для препаратов, в которых базолатеральные транспортеры не являются клинически значимыми. Однако, когда базолатеральные транспортеры клинически значимы, мы демонстрируем, что принятый в настоящее время подход несовместим с признанными процессами распределения лекарств. Однако это соотношение зазоров можно легко исправить с помощью законов Кирхгофа. Цель этого обзора — продемонстрировать, что законы Кирхгофа, которые определяют подход к скорости процессов, происходящих параллельно, по сравнению с процессами, происходящими последовательно, могут быть применимы к фармакологии в дополнение к более чем 160-летнему признанию их использования в физических науках. . Мы ожидаем, что применение к разрешению будет только первым из многих таких фармакологических анализов.

Ключевые слова: Клиренс; внутренний зазор; Почка; законы Кирхгофа; Печень.

Copyright © 2022 Elsevier Inc. Все права защищены.

Заявление о конфликте интересов

Декларация о конкурирующих интересах Авторы заявляют об отсутствии конфликта интересов.

Похожие статьи

• Тезисы презентаций на собрании Ассоциации ученых-клиницистов 143 ^rd Луисвилл, Кентукки, 11–14 мая 2022 г.

  [Нет авторов в списке] [Нет авторов в списке] Энн Клин Lab Sci. 2022 май; 52(3):511-525. Энн Клин Lab Sci. 2022. PMID: 35777803 Аннотация недоступна.

• Пределы законов Кирхгофа в плазмонике.

  Разинскас Г., Бьяджони П., Хехт Б. Разинскас Г. и соавт. Научный представитель 2018 г., 30 января; 8 (1): 1921. doi: 10.1038/s41598-018-20239-x. Научный представитель 2018. PMID: 29382908 Бесплатная статья ЧВК.

• Нарушение законов Кирхгофа для когерентной RC-цепи.

  Габелли Дж., Фев Г., Берруар Дж.М., Пласе Б., Каванна А., Этьен Б., Джин И., Глаттли Д.К. Габелли Дж. и др. Наука. 2006 28 июля; 313 (5786): 499-502. doi: 10.1126/science.1126940. Epub 2006 13 июля. Наука. 2006. PMID: 16840660

• Бальфур Стюарт и Густав Роберт Кирхгоф: два независимых подхода к «закону излучения Кирхгофа».

  Зигель DM. Сигель Дм. Исида. 1976 декабрь; 67 (239): 565-600. дои: 10.1086/351669. Исида. 1976 год. PMID: 794025 Аннотация недоступна.

• Джеймс Клерк Максвелл, законы Кирхгофа и их значение для моделирования физиологии.

  Валентинуцци М.Э., Коэн А.Дж. Валентинуцци М.Е. и др. IEEE Импульс. 2013 март-апрель;4(2):40-6. doi: 10.1109/МПЮЛ.2013.2240078. IEEE Импульс. 2013. PMID: 23558503 Обзор. Аннотация недоступна.

Посмотреть все похожие статьи

Типы публикаций

Назовите два правила Кирхгофа, используемые в электрических сетях. Как обосновываются правила? — Физика

Реклама Удалить все объявления

Реклама Удалить все объявления

Реклама Удалить все объявления

Укажите два правила Кирхгофа, используемые в электрических сетях. Как обосновываются правила?

Государственные правила Кирхгофа. Кратко объясните, чем обоснованы эти правила.

Раствор 1

Первое правило Кирхгофа:

В любой электрической сети алгебраическая сумма токов, встречающихся в узле, всегда равна нулю.

∑I=0

В приведенном ниже соединении пусть I ₁ , I ₂ , I ₃ , I ₄ и I ₅ являются направлением тока в проводнике, как показано на рисунке. рисунок ниже. I ₅ и I ₃ — токи, которые входят и токи I ₁ , I ₂ и I ₄ уйти.

По закону Кирхгофа имеем

(–I ₁ ) + (−I ₂ ) + I ₃ + (−I _{4 0 6} ) 6 I I ₁ + I ₂ + I ₄ = I ₃ + I ₅

Таким образом, в любом соединении нескольких элементов цепи сумма токов, входящих в соединение, должна равняться сумме токов, выходящих из соединения.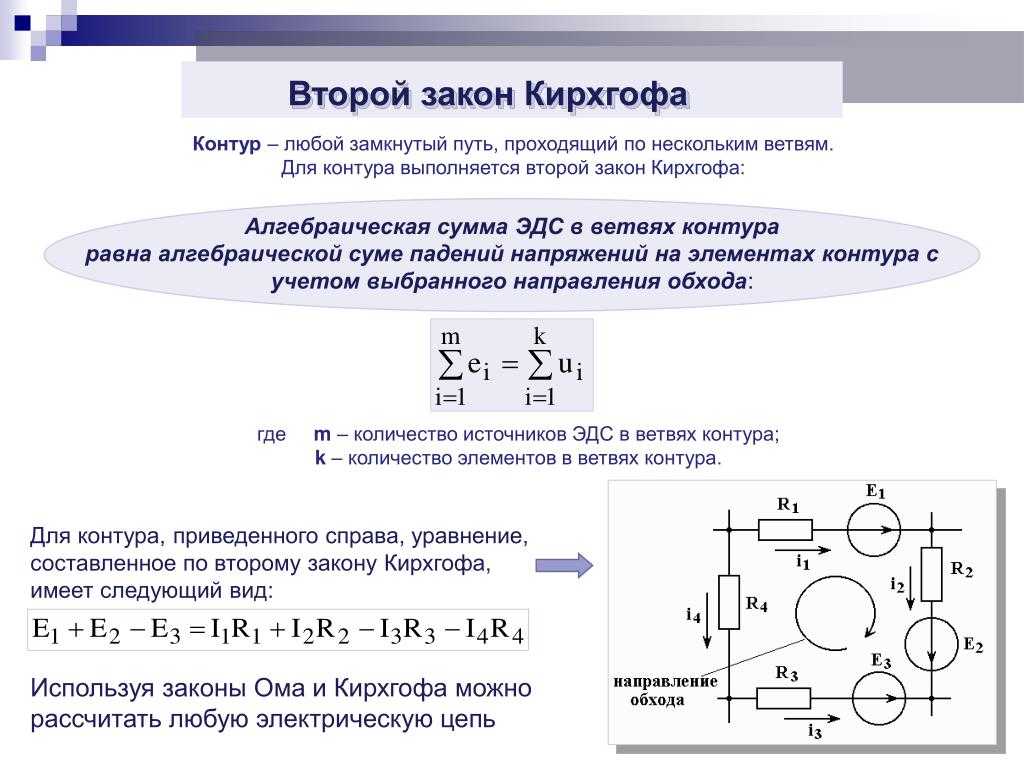 это. Это следствие сохранения заряда и предположения, что токи постоянны, т. е. в переходе заряд не накапливается.

Второе правило Кирхгофа: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура, включающего резисторы и ячейки в контуре, равна нулю. или

Алгебраическая сумма э.д.с. в любой петле цепи равна алгебраической сумме произведений токов и сопротивлений в ней.

Математически правило цикла может быть выражено как ∑E = ΣIR.

Решение 2

Первый закон Кирхгофа — правило соединения

В электрической цепи алгебраическая сумма токов, встречающихся в соединении, всегда равна нулю.

I ₁ , I ₂ I ₃ и I ₃ , и I 4 , и I 4 , и I 4 , и I 4 , 6 проводов соответственно.

Условное обозначение:

Ток, текущий к переходу, считается положительным.

Ток, протекающий от перехода, считается отрицательным.

I ₃ + (− I ₁ ) + (− I ₂ ) + (− I ₄ ) = 0

Этот закон основан на законе сохранения заряда.

Второй закон Кирхгофа – правило контура

В замкнутом контуре алгебраическая сумма ЭДС с равна алгебраической сумме произведений сопротивлений и токов, протекающих через них.

Для замкнутого контура BACB:

E ₁ − E ₂ = I ₁ R ₁ + I ₂ R ₂ − I ₃ R ₃

For the closed loop CADC:

E ₂ = I ₃ R ₃ + I ₄ R ₄ + I ₅ R ₅

This law is based on the law of conservation of энергия

Концепция: правила Кирхгофа

  Есть ли ошибка в этом вопросе или решении?

2014-2015 (март) Набор Панчкула 3

Q 9 Q 8Q 10.