1 гаусс: Гаусс (единица измерения) — Википедия – Гаусс (единица измерения) — Карта знаний — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Гаусс (единица магнитной индукции) — это… Что такое Гаусс (единица магнитной индукции)?

Гаусс (единица магнитной индукции): Гаусс, единица магнитной индукции в СГС системе единиц (гауссовой и СГСМ). Названа в честь К. Гаусса. Сокращённое обозначение: русское гс, международное Gs. 1 гс равен индукции однородного магнитного поля, в котором прямой проводник длиной 1 см, расположенный перпендикулярно вектору индукции поля, испытывает силу в 1 дин, если по этому проводнику протекает ток в 1 единицу тока СГСМ. Г. также можно определить как магнитную индукцию, при которой через сечение площадью в 1 см, нормальное к направлению линий индукции, проходит магнитный поток в 1 максвелл. Соотношение между единицами магнитной индукции СГС и СИ: 1 тл = 104 гс. На практике применяют ещё единицу килогаусс = 1000 гс. До 1930 Г. называли также единицу напряжённости магнитного поля, равную 79,577 а/м. В 1930 решением Международной электротехнической комиссии для напряжённости магнитного поля была принята особая единица эрстед.

Гаусманит
Гаусс Карл Фридрих

Смотреть что такое «Гаусс (единица магнитной индукции)» в других словарях:

ГАУСС (единица магнитной индукции) — ГАУСС, единица магнитной индукции (см. МАГНИТНАЯ ИНДУКЦИЯ) в СГС системе единиц (см. СГС СИСТЕМА ЕДИНИЦ). Названа в честь К. Гаусса, обозначается Гс. 1 Гс=10 4 тесла (см. ТЕСЛА (единица магнитной индукции)) … Энциклопедический словарь
Гаусс (единица магнитной индукции) — … Википедия
ТЕСЛА (единица магнитной индукции) — ТЕСЛА, единица магнитной индукции (см. МАГНИТНАЯ ИНДУКЦИЯ) (В) в системе СИ, названа в честь физика Н. Теслы. Обозначается Тл. 1 Тл = 1 Н/(А.м) 1 Тл (тесла) магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н… … Энциклопедический словарь
Тесла (единица магнитной индукции) — Тесла, единица магнитной индукции Международной системы единиц, равная магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью 1 м2 равен 1 веберу. Названа по имени Н. Тесла. Обозначения: русское тл, международное Т. 1… … Большая советская энциклопедия
Гаусс (единица измерения)
— У этого термина существуют и другие значения, см. Гаусс. Гаусс (русское обозначение Гс, международное G) единица измерения магнитной индукции в системе СГС. Названа в честь немецкого физика и математика Карла Фридриха Гаусса. 1 Гс =… … Википедия
Гаусс — Гаусс: Гаусс, Карл Фридрих немецкий математик, физик и астроном Гаусс единица магнитной индукции в системе СГС Гаусс кратер на Луне Вулкан Гаусс вулкан в Антарктике гаусс жаргонное название пушки Гаусса GAUSS … … Википедия
ГАУСС — единица магнитной индукции в СГС системе единиц. Названа в честь К. Гаусса, обозначается Гс. 1 Гс=10 4 тесла … Большой Энциклопедический словарь
Гаусс (Gauss) — единица магнитной индукции, равная 1 максвеллу на квадратный сантиметр. 1 Гс = 10 4 тесла. Источник: Медицинский словарь … Медицинские термины
ГАУСС — единица магнитной индукции в СГС системе единиц. Названа по имени К. Гаусса, обозначается Гс: 1 Гс= 10 4 тесла … Естествознание. Энциклопедический словарь
Гаусс — I Гаусс (Gauss) Карл Фридрих (30.4.1777, Брауншвейг, 23.2.1855, Гёттинген), немецкий математик, внёсший фундаментальный вклад также в астрономию и геодезию. Родился в семье водопроводчика. С 1795 по 1798 учился в Гёттингенском… … Большая советская энциклопедия

Гаусс (единица измерения) — это… Что такое Гаусс (единица измерения)?

1967 год в музыке
Кара-Балта

Смотреть что такое «Гаусс (единица измерения)» в других словарях:

Максвелл (единица измерения) — У этого термина существуют и другие значения, см. Максвелл. Максвелл единица измерения магнитного потока в системе СГС. Русское сокращение Мкс (не путать с микросекундой, её сокращённое обозначение мкс записывается со строчной буквы).… … Википедия
Тесла (единица измерения) — У этого термина существуют и другие значения, см. Тесла. Тесла (русское обозначение: Тл; международное обозначение: T) единица измерения индукции магнитного поля в Международной системе единиц (СИ), численно равная индукции такого… … Википедия
Эрстед (единица измерения) — У этого термина существуют и другие значения, см. Эрстед. Эрстед (русское обозначение Э, международное обозначение Oe) единица измерения напряжённости магнитного поля в системе СГС. Введена в 1930 году Международной электротехнической… … Википедия
Гаусс, Карл Фридрих — У этого термина существуют и другие значения, см. Гаусс. Карл Фридрих Гаусс Carl Friedrich Gauß … Википедия
ГАУСС — (Gauss) Карл Фридрих (1777 1855), немецкий математик. В детстве был необыкновенно одаренным ребенком, из бедной семьи. Его образование оплачивал богатый аристократ герцог Брауншвейгский, который узнал о нем от его учителя. Еще в подростковом… … Научно-технический энциклопедический словарь
гаусс — Гс … Справочник технического переводчика
Гаусс — а; мн. род. гауссов и гаусс; м. Единица измерения магнитной индукции. ● По фамилии немецкого математика К. Гаусса (1777 1855). * * * Гаусс единица магнитной индукции в СГС системе единиц. Названа по имени К. Гаусса, обозначается Гс. 1 Гс = 10… … Энциклопедический словарь
гаусс — а; мн. род. га/уссов и га/усс; м. Единица измерения магнитной индукции. По фамилии немецкого математика К. Гаусса (1777 1855) … Словарь многих выражений
К. Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
Карл Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия

Гаусс — Большая советская энциклопедия

Га́усс (Gauss)

Карл Фридрих (30.4.1777, Брауншвейг, — 23.2.1855, Гёттинген), немецкий математик, внёсший фундаментальный вклад также в астрономию и геодезию. Родился в семье водопроводчика. С 1795 по 1798 учился в Гёттингенском университете. В 1799 получил доцентуру в Брауншвейге, в 1807 — кафедру математики и астрономии в Гёттингенском университете, с которой была также связана должность директора Гёттингенской астрономической обсерватории. На этом посту Г. оставался до конца жизни. Отличительными чертами творчества Г. являются глубокая органическая связь в его исследованиях между теоретической и прикладной математикой, необычайная широта проблематики. Работы Г. оказали большое влияние на развитие высшей алгебры, теории чисел, дифференциальной геометрии, теории притяжения, классической теории электричества и магнетизма, геодезии, целых отраслей теоретической астрономии. Во многих областях математики труды Г. содействовали повышению требований к логической отчётливости доказательств, однако сам Г. оставался в стороне от работ по строгому обоснованию математического анализа, которые проводил в его время О. Коши.

Первое крупное сочинение Г. по теории чисел и высшей алгебре — «Арифметические исследования» (1801) — во многом предопределило дальнейшее развитие этих дисциплин. Г. даёт здесь обстоятельную теорию квадратичных вычетов (См. Квадратичный вычет), первое доказательство квадратичного закона взаимности — одной из центральных теорем теории чисел. Г. даёт также новое подробное изложение арифметической теории квадратичных форм, до того построенной Ж. Лагранжем, в частности тщательную разработку теории композиции классов таких форм. В конце книги излагается теория уравнений деления круга (т. е. уравнений

xⁿ — 1 = 0), которая во многом была прообразом Галуа теории (См. Галуа теория). Помимо общих методов решения этих уравнений, Г. установил связь между ними и построением правильных многоугольников. Он, впервые после древнегреческих учёных, сделал значительный шаг вперёд в этом вопросе, а именно: Г. нашёл все те значения n, для которых правильный n-угольник можно построить циркулем и линейкой; в частности, решив уравнение х¹⁷—1 = 0, он дал построение правильного 17-угольника при помощи циркуля и линейки. Г. придавал этому открытию очень большое значение и завещал выгравировать правильный 17-угольник, вписанный в круг, на своём надгробном памятнике, что и было исполнено.

Астрономические работы Г. (1800—20) в основном связаны с решением проблемы определения орбит малых планет и исследованием их возмущений. Г. как астроном получил широкую известность после разработки метода вычисления эллиптических орбит планет по трём наблюдениям, успешно примененного им к первым открытым малым планетам Церера (1801) и Паллада (1802). Результаты исследований по вычислению орбит Г. опубликовал в сочинении «Теория движения небесных тел» (1809). В 1794—95 открыл и в 1821—23 разработал основной математический метод обработки неравноценных наблюдательных данных (Наименьших квадратов метод). В связи с астрономическими вычислениями, основанными на разложении интегралов соответствующих дифференциальных уравнений в бесконечные ряды, Г. занялся исследованием вопроса о сходимости бесконечных рядов [в работе, посвященной изучению гипергеометрического ряда (См. Гипергеометрический ряд) (1812)].

Работы Г. по геодезии (1820—30) связаны с поручением провести геодезическую съёмку и составить детальную карту Ганноверского королевства; Г. организовал измерение дуги меридиана Гёттинген — Альтона, в результате теоретической разработки проблемы создал основы высшей геодезии («Исследования о предметах высшей геодезии», 1842—47). Для оптической сигнализации Г. изобрёл специальный прибор — Гелиотроп. Изучение формы земной поверхности потребовало углублённого общего геометрического метода для исследования поверхностей. Выдвинутые Г. в этой области идеи получили выражение в сочинении «Общие изыскания о кривых поверхностях» (1827). Руководящая мысль этого сочинения заключается в том, что при изучении поверхности как бесконечно тонкой гибкой плёнки основное значение имеет не уравнение поверхности в декартовых координатах, а дифференциальная квадратичная форма, через которую выражается квадрат элемента длины и инвариантами которой являются все собственные свойства поверхности — прежде всего её кривизна в каждой точке. Др. словами, Г. предложил рассматривать те свойства поверхности (т. н. внутренние), которые не зависят от изгибаний поверхности, не изменяющих длин линий на ней. Созданная таким образом внутренняя геометрия поверхностей послужила образцом для создания n-mepной римановой геометрии (См. Риманова геометрия).

Исследования Г. по теоретической физике (1830—40) являются в значительной мере результатом тесного общения и совместной научной работы с В. Вебером. Вместе с Вебером Г. создал абсолютную систему электромагнитных единиц и сконструировал в 1833 первый в Германии электромагнитный телеграф. В 1835 Г. основал магнитную обсерваторию при Гёттингенской астрономической обсерватории. В 1838 он издал труд «Общая теория земного магнетизма». Небольшое сочинение «О силах, действующих обратно пропорционально квадрату расстояния» (1834—40) содержит основы теории потенциала. К теоретической физике примыкают также разработка (1829) Г. принципа наименьшего принуждения (см. Гаусса принцип) и работы по теории капиллярности (1830). К числу физических исследований Г. относятся и его «Диоптрические исследования» (1840), в которых он заложил основы теории построения изображения в системах линз.

Очень многие исследования Г. остались неопубликованными и в виде очерков, незаконченных работ, переписки с друзьями входят в его научное наследие. Вплоть до 2-й мировой войны оно тщательно разрабатывалось Гёттингенским учёным обществом, которое издало 12 тт. сочинений Г. Наиболее интересными в этом наследии являются дневник Г. и материалы по неевклидовой геометрии и теории эллиптических функций. Дневник содержит 146 записей, относящихся к периоду от 30 марта 1796, когда 19-летний Г. отметил открытие построения правильного 17-угольника, по 9 июля 1814. Эти записи дают отчётливую картину творчества Г. в первой половине его научной деятельности; они очень кратки, написаны на латинском языке и излагают обычно сущность открытых теорем. Материалы, относящиеся к неевклидовой геометрии, обнаруживают, что Г. пришёл к мысли о возможности построения наряду с евклидовой геометрией и геометрии неевклидовой в 1818, но опасение, что эти идеи не будут поняты, и, по-видимому, недостаточное сознание их научной важности были причиной того, что Г. их не разрабатывал далее и не опубликовывал. Более того, он категорически запрещал опубликовывать их тем, кого посвящал в свои взгляды. Когда вне всякого отношения к этим попыткам Г. неевклидова геометрия была построена и опубликована Н. И. Лобачевским (См. Лобачевский), Г. отнёсся к публикациям Лобачевского с большим вниманием, был инициатором избрания его член-корреспондентом Гёттингенского учёного общества, но своей оценки великого открытия Лобачевского по существу не дал. Архивы Г. содержат также обильные материалы по теории эллиптических функций и своеобразную их теорию; однако заслуга самостоятельной разработки и публикации теории эллиптических функций принадлежит К. Якоби и Н. Абелю (См. Абель).

Соч.: Werke, Bd 1 —, Gött., 1908 —; в рус. пер. — Общие исследования о кривых поверхностях, в сборнике: Об основаниях геометрии, 2 изд., Каз., 1895; Теоретическая астрономия. (Лекции, читанные в Гёттингене в 1820—26 гг., записанные Купфером), в кн.: Крылов А. Н., Собр. трудов, т. 6, М. — Л., 1936; Письма П. С. Лапласа, К. Ф. Гаусса, Ф. В. Бесселя и др. к академику Ф. И. Шуберту, в сборнике: Научное наследство, т 1, М. — Л., 1948, с. 801—22.

Лит.: Клейн Ф., Лекции о развитии математики в 19 столетии, пер. с нем., ч. 1, М. — Л., 1937: Карл Фридрих Гаусс. Сб. ст., М., 1956.

К. Ф. Гаусс.

Га́усс

единица магнитной индукции в СГС системе единиц (См. СГС система единиц) (гауссовой и СГСМ). Названа в честь К. Гаусса. Сокращённое обозначение: русское гс, международное Gs. 1 гс равен индукции однородного магнитного поля, в котором прямой проводник длиной 1 см, расположенный перпендикулярно вектору индукции поля, испытывает силу в 1 дин, если по этому проводнику протекает ток в 1 единицу тока СГСМ. Г. также можно определить как магнитную индукцию, при которой через сечение площадью в 1 см, нормальное к направлению линий индукции, проходит магнитный поток в 1 максвелл. Соотношение между единицами магнитной индукции СГС и СИ: 1 тл = 10⁴ гс. На практике применяют ещё единицу килогаусс = 1000 гс. До 1930 Г. называли также единицу напряжённости магнитного поля, равную 79,577 а/м. В 1930 решением Международной электротехнической комиссии для напряжённости магнитного поля была принята особая единица эрстед.

Источник: Большая советская энциклопедия на Gufo.me

Значения в других словарях

Гаусс — орф. Гаусс, -а: постоянная Гаусса, принцип Гаусса, распределение Орфографический словарь Лопатина
гаусс — Га́усс/. Морфемно-орфографический словарь
ГАУСС — ГАУСС (Gauss) Карл Фридрих (1777-1855), немецкий математик. В детстве был необыкновенно одаренным ребенком, из бедной семьи. Его образование оплачивал богатый аристократ герцог Брауншвейгский, который узнал о нем от его учителя. Научно-технический словарь
гаусс — ГАУСС -а; мн. род. гауссов и гаусс; м. Единица измерения магнитной индукции. ● По фамилии немецкого математика К. Гаусса (1777 — 1855). Толковый словарь Кузнецова
ГАУСС — (Гс, Gs), единица магн. индукции в СГС системе единиц (симметричной, или Гауссовой) и СГСМ. Названа в честь нем. учёного К. Ф. Гаусса (К. F. Gau8). 1 Гс=10-4 тесла. Физический энциклопедический словарь
гаусс — орф. гаусс, -а, р. мн. -ов, счетн. ф. гаусс (ед. измер.) Орфографический словарь Лопатина
ГАУСС — ГАУСС — единица магнитной индукции в СГС системе единиц. Названа в честь К. Гаусса, обозначается Гс. 1 Гс=10-4 тесла. ГАУСС (Gau?) Карл Фридрих (1777-1855) — немецкий математик… Большой энциклопедический словарь
Гаусс — (Carl-Friedrich Gauss) — знаменитый немецкий математик. Род. 28 апреля 1777 года в Брауншвейге и с раннего возраста обнаружил выдающиеся математические способности. Рассказывают, что, будучи трех лет… Энциклопедический словарь Брокгауза и Ефрона
гаусс — гаусс м. Единица измерения магнитной индукции. Толковый словарь Ефремовой
гаусс — Гаусс, гауссы, гаусса, гауссов, гаусс, гауссу, гауссам, гаусс, гауссы, гауссом, гауссами, гауссе, гауссах Грамматический словарь Зализняка
гаусс — сущ., кол-во синонимов: 1 единица 830 Словарь синонимов русского языка

Гаусс — Tanki Online Wiki

Пушка большой дальности. Комплектуется разрывными снарядами, которые могут поразить несколько танков одновременно. При удержании кнопки стрельбы использует электромагнитный ускоритель для эффективной стрельбы по удалённым целям.

Обозначения в таблице:

● — параметр применяется в стандартном режиме стрельбы (одиночными выстрелами)
▢ — параметр применяется в прицельном режиме стрельбы (с захватом цели)

Характеристики пушки

Мин. урон в прицельном режиме (hp) — минимально возможное повреждение, наносимое цели за один выстрел из пушки в прицельном режиме.
Макс. урон в прицельном режиме (hp) — максимально возможное повреждение, наносимое цели за один выстрел из пушки в прицельном режиме.
Мин. урон в стандартном режиме (hp) — минимально возможное повреждение, наносимое цели за один выстрел из пушки в стандартном режиме.
Макс. урон в стандартном режиме (hp) — максимально возможное повреждение, наносимое цели за один выстрел из пушки в стандартном режиме.
Сила удара снаряда в стандартном режиме, в гараже — Сила удара (усл. ед) — физическое воздействие снаряда пушки на цель при стрельбе в стандартном режиме, которое приводит к смещению танка с места.
Сила удара взрыва в стандартном режиме (усл. ед) — физическое воздействие на танки в радиусе поражения от точки попадания снаряда пушки при стрельбе в стандартном режиме, которое приводит к смещению танков с места.
Отдача в стандартном режиме (усл. ед) — физическое воздействие пушки на собственный корпус при стрельбе в стандартном режиме.
Сила удара снаряда в прицельном режиме (усл. ед) — физическое воздействие снаряда пушки на цель при стрельбе в прицельном режиме, которое приводит к смещению танка с места.
Сила удара взрыва в прицельном режиме (усл. ед) — физическое воздействие на танки в радиусе поражения от точки попадания снаряда пушки при стрельбе в прицельном режиме, которое приводит к смещению танков с места.
Отдача в прицельном режиме (усл. ед) — физическое воздействие пушки на собственный корпус при стрельбе в прицельном режиме.
Перезарядка в стандартном режиме (с) — пауза между выстрелами при стрельбе в стандартном режиме.
Перезарядка в прицельном режиме (с) — период времени, в течение которого пушка перезаряжается после прицельного выстрела.
Наведение (с) — время, в течение которого нужно удерживать целеуказатель на цели для полного захвата.
Скорость поворота (град/с) — максимальная скорость, с которой пушка может поворачиваться.
Ускорение поворота (град/с²) — ускорение, с которым пушка разгоняется до максимальной скорости поворота.
Дальность слабого поражения в стандартном режиме, в гараже — Дальность (м) — дальность, на которой ослабление урона от дистанции при стрельбе в стандартном режиме достигает предела.
Дальность полного поражения в стандартном режиме (м) — дальность, в пределах которой пушка наносит полный урон при стрельбе в стандартном режиме. Если дальность до цели выше, то урон линейно снижается вплоть до дальности слабого поражения в стандартном режиме.
Процент слабого поражения в стандартном режиме (%) — указывает, какой процент от урона при стрельбе в стандартном режиме наносится на дистанции, большей или равной дальности слабого поражения в стандартном режиме.
Время восстановления наведения (с) — время, в течение которого можно восстановить наведение на цель без потери прогресса наводки.
Скорость снаряда (м/c) — скорость снаряда при стрельбе в стандартном режиме.
Радиус снаряда (м) — радиус от центра снаряда до его границы. Урон наносится, если снаряд проходит от цели не дальше, чем на это расстояние.
Радиус полного поражения взрывом в стандартном режиме (м) — расстояние от точки попадания снаряда при стрельбе в стандартном режиме, в пределах которого цели наносится полный урон. Если расстояние от точки попадания снаряда до цели больше, то урон снижается вплоть до предельного радиуса поражения взрывом в стандартном режиме.
Радиус промежуточного поражения взрывом в стандартном режиме (м) — дополнительная точка излома графика, по которому при стрельбе в стандартном режиме проходит снижение урона от взрыва с увеличением расстояния от точки попадания снаряда до цели. Превращает зависимость урона от радиуса из линейной в подобие экспоненциальной.
Предельный радиус поражения взрывом в стандартном режиме (м) — расстояние от точки попадания снаряда при стрельбе в стандартном режиме, на котором цели ещё наносится урон. Если расстояние от точки взрыва снаряда до цели больше, то урон не будет наноситься.
Процент промежуточного поражения взрывом в стандартном режиме (%) — указывает процент от урона, который при стрельбе в стандартном режиме наносится на дальности от точки попадания снаряда, равной радиусу промежуточног

Гауссова функция — Википедия

Эта статья — о гауссовой функции в общей форме. О её частном случае — функции плотности нормального распределения, также называемой гауссовой — см. Нормальное распределение.

Гауссова функция (гауссиан, гауссиана, функция Гаусса) — вещественная функция, описываемая следующей формулой:

g(x)=ae−(x−b)22c2{\displaystyle g\left(x\right)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}},

где параметры a,b,c{\displaystyle a,b,c} — произвольные вещественные числа. Введена Гауссом в 1809 году как функция плотности нормального распределения, и наибольшее значение имеет в этом качестве, в этом случае параметры выражаются через среднеквадратичное отклонение σ{\displaystyle \sigma } и математическое ожидание μ{\displaystyle \mu }:

a=1σ2π{\displaystyle a={\frac {1}{\sigma {\sqrt {2\pi }}}}}, b=μ{\displaystyle b=\mu }, c=σ{\displaystyle c=\sigma },

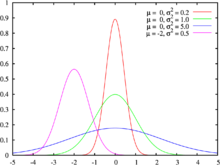$c=\sigma$ Форма графика плотности нормального распределения в зависимости от математического ожидания μ{\displaystyle \mu } и среднеквадратичного отклонения σ{\displaystyle \sigma }

График гауссовой функции при a>0{\displaystyle a>0} и c≠0{\displaystyle c\neq 0} — колоколообразная кривая, параметр a{\displaystyle a} определяет максимальную высоту графика — пик колокола, b{\displaystyle b} отвечает за сдвиг пика от нуля (при b=0{\displaystyle b=0} — пик в нуле), а c{\displaystyle c} влияет на ширину (размах) колокола.

Существуют многомерные обобщения функции^[⇨]. Кроме применений в теории вероятностей, статистике и других многочисленных приложениях как функции плотности нормального распределения, гауссиана имеет самостоятельное значение^[⇨] в математическом анализе, математической физике, теории обработки сигналов.

Свойства гауссовой функции связаны с её конструкцией из экспоненциальной функции и вогнутой квадратичной функции, логарифм гауссианы — вогнутая квадратичная функция.

Параметр c{\displaystyle c} связан с полушириной колокола графика следующим образом:

w=22ln⁡2 c≈2,35482⋅c{\displaystyle w=2{\sqrt {2\ln 2}}\ c\approx 2{,}35482\cdot c}.

Гауссова функция может быть выражена через полуширину w{\displaystyle w} колокола графика следующим образом:

g(x)=ae−4ln⁡(2)(x−b)2w2{\displaystyle g(x)=ae^{-{\frac {4\ln(2)(x-b)^{2}}{w^{2}}}}}.

Перегибы g(x){\displaystyle g(x)} — две точки, в которых x=b±c{\displaystyle x=b\pm c}.

Гауссова функция аналитична, в пределе к обеим бесконечностям стремится к нулю:

limx→±∞g(x)=0{\displaystyle \lim _{x\to \pm \infty }g(x)=0}.

Будучи составленной из экспоненциальной функции и арифметических операций, гауссиана является элементарной, однако её первообразная неэлементарна; интеграл гауссовой функции:

∫0xe−t2dt{\displaystyle \int \limits _{0}^{x}e^{-t^{2}}\,\mathrm {d} t}

— это (с точностью до постоянного множителя) — функция ошибок, являющаяся спецфункцией. При этом интеграл по всей числовой прямой (в связи со свойствами экспоненциальной функции) — константа^[1]:

∫−∞∞ae−(x−b)22c2dx=ac⋅2π{\displaystyle \int _{-\infty }^{\infty }ae^{-{(x-b)^{2} \over 2c^{2}}}\,dx=ac\cdot {\sqrt {2\pi }}}.

Этот интеграл обращается в единицу только при условии:

a=1c2π{\displaystyle a={\frac {1}{c{\sqrt {2\pi }}}}},

и это даёт в точности тот случай, когда гауссиана является функцией плотности нормального распределения случайной переменной с математическим ожиданием μ=b{\displaystyle \mu =b} и дисперсией σ2=c2{\displaystyle \sigma ^{2}=c^{2}}.

Произведение гауссиан — гауссова функция; свёртка двух гауссовых функций даёт гауссову функцию, притом параметр c{\displaystyle c} свёртки выражается из соответствующих параметров входящих в неё гауссиан: c2=c12+c22{\displaystyle c^{2}=c_{1}^{2}+c_{2}^{2}}. Произведение двух функций плотности нормального распределения, являясь гауссовой функцией, в общем случае не дает функцию плотности нормального распределения.

Пример двумерного варианта гауссовой функции:

g(x,y)=A⋅e(−((x−x0)22σx2+(y−y0)22σy2)){\displaystyle g(x,y)=A\cdot e^{\left(-\left({\frac {(x-x_{0})^{2}}{2\sigma _{x}^{2}}}+{\frac {(y-y_{0})^{2}}{2\sigma _{y}^{2}}}\right)\right)}},

здесь A{\displaystyle A} задаёт высоту колокола, (x0,y0){\displaystyle (x_{0},y_{0})} определяют сдвиг пика колокола от нулевой абсциссы, а (σx,σy){\displaystyle (\sigma _{x},\sigma _{y})} отвечают за размах колокола. Объём под такой поверхностью:

V=∫−∞∞∫−∞∞g(x,y)dxdy=2πAσxσy{\displaystyle V=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }g(x,y)\,dx\,dy=2\pi A\sigma _{x}\sigma _{y}}

В наиболее общей форме, двумерная гауссиана определяется следующим образом:

g(x,y)=Aexp⁡(−(a(x−x0)2+2b(x−x0)(y−y0)+c(y−y0)2)){\displaystyle g(x,y)=A\exp \left(-\left(a(x-x_{0})^{2}+2b(x-x_{0})(y-y_{0})+c(y-y_{0})^{2}\right)\right)},

где матрица:

[abbc]{\displaystyle \left[{\begin{matrix}a&b\\b&c\end{matrix}}\right]}

положительно определена.

Вариант гауссовой функции в n{\displaystyle n}-мерном евклидовом пространстве:

g(x)=exp⁡(−xTAx){\displaystyle g(x)=\exp(-x^{T}Ax)},

где x=(x1,…,xn){\displaystyle x=(x_{1},\dots ,x_{n})} — вектор-столбец из n{\displaystyle n} компонентов, A{\displaystyle A} — положительно определённая матрица размера n×n{\displaystyle n\times n}, и xT{\displaystyle x^{T}} — операция транспонирования над x{\displaystyle x}.

Интеграл такой гауссовой функции над всем пространством Rn{\displaystyle \mathbb {R} ^{n}}:

∫Rnexp⁡(−xTAx)dx=πndetA{\displaystyle \int _{\mathbb {R} ^{n}}\exp(-x^{T}Ax)\,dx={\sqrt {\frac {\pi ^{n}}{\det A}}}}.

Возможно определить n{\displaystyle n}-мерный вариант и со сдвигом:

g(x)=exp⁡(−xTAx+sTx){\displaystyle g(x)=\exp(-x^{T}Ax+s^{T}x)},

где s=(s1,…,sn){\displaystyle s=(s_{1},\dots ,s_{n})} — вектор сдвига, а матрица A{\displaystyle A} — симметричная (AT=A{\displaystyle A^{T}=A}) и положительно определённая.

Супергауссова функция — обобщение гауссовой функции, в которой аргумент экспоненты возводится в степень P{\displaystyle P}:

sg(x)=Aexp⁡(−((x−xo)22σx2)P){\displaystyle sg(x)=A\exp \left(-\left({\frac {(x-x_{o})^{2}}{2\sigma _{x}^{2}}}\right)^{P}\right)},

получившая применение для описания свойств гауссовых пучков^[2]. В двумерном случае супергауссова функция может быть рассмотрена с различными степенями по аргументам Px{\displaystyle P_{x}} и Py{\displaystyle P_{y}}^[3]:

sg(x,y)=Aexp⁡(−((x−xo)22σx2)Px−((y−yo)22σy2)Py){\displaystyle sg(x,y)=A\exp \left(-\left({\frac {(x-x_{o})^{2}}{2\sigma _{x}^{2}}}\right)^{P_{x}}-\left({\frac {(y-y_{o})^{2}}{2\sigma _{y}^{2}}}\right)^{P_{y}}\right)}.

Основное применение гауссовых функций и многомерных обобщений — в роли функции плотности вероятности нормального распределения и многомерного нормального распределения. Самостоятельное значение функция имеет для ряда уравнений математической физики, в частности, гауссианы являются функциями Грина для уравнения гомогенной и изотропной диффузии (соответственно, и для уравнения теплопроводности), и преобразование Вейерштрасса^[en] — операция свёртки обобщённой функции, выражающей начальные условия уравнения, с гауссовой функцией. Также гауссиана является волновой функцией основного состояния^[en]^* квантового гармонического осциллятора.

В вычислительной химии для определения молекулярных орбиталей используются так называемые гауссовы орбитали^[en] — линейные комбинации гауссовых функций.

Гауссовы функции и их дискретные аналоги (такие, как дискретное гауссово ядро^[en]) используются в цифровой обработке сигналов, обработке изображений, синтезе звука^[4]; в частности, через гауссианы определяются гауссов фильтр и гауссово размытие^[en]. В определении отдельных видов искусственных нейронных сетей также участвуют гауссовы функции.

L. M. B. C. Campos. 1.1. Evaluation of Integrals of Gaussian Functions // Generalized Calculus with Applications to Matter and Forces. — Boca Raton: CRC Press, 2014. — 823 с. — ISBN 978-1-4200-7115-3.

Гаусс (единица измерения) Википедия

У этого термина существуют и другие значения, см. Гаусс.

Га́усс (русское обозначение Гс, международное — G) — единица измерения магнитной индукции в системе СГС.

Названа в честь немецкого физика и математика Карла Фридриха Гаусса.

1 Гс = 100 мкТл = 10^-4Тл

Может быть выражена через основные единицы измерения системы СГС следующим образом:

1 Гс = 1 г^1/2·см^−1/2·с⁻¹.

10^-1 Гс² = 1 Дж·м⁻³ .

См. также[ | ]

Тесла (единица измерения)

Ссылки[ | ]

Словари и энциклопедии	Большая норвежская · Большая российская · Britannica (онлайн)
Нормативный контроль	Microsoft: 161794534

Это заготовка статьи о единицах измерения. Вы можете помочь проекту, дополнив её.

Пушка Гаусса — Википедия

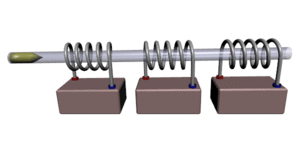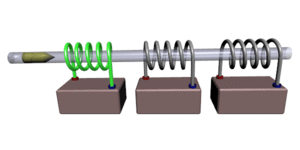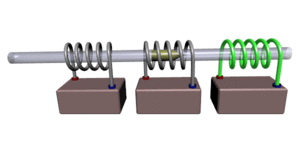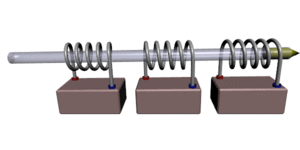Иллюстрация принципа стрельбы

Пушка Гаусса (англ. Gauss gun, Coil gun, Gauss cannon) — одна из разновидностей электромагнитного ускорителя масс. Названа по имени немецкого учёного Карла Гаусса, заложившего основы математической теории электромагнетизма. Следует иметь в виду, что этот метод ускорения масс используется в основном в любительских установках, так как не является достаточно эффективным для практической реализации. По своему принципу работы (создание бегущего магнитного поля) сходна с устройством, известным как линейный двигатель.

Пушка Гаусса состоит из соленоида, внутри которого находится ствол (как правило, из диэлектрика). В один из концов ствола вставляется снаряд, сделанный из ферромагнетика. При протекании электрического тока в соленоиде возникает электромагнитное поле, которое разгоняет снаряд, «втягивая» его внутрь соленоида. На концах снаряда при этом образуются полюса, ориентированные согласно полюсам катушки, из-за чего после прохода центра соленоида снаряд притягивается в обратном направлении, то есть тормозится. В любительских схемах иногда в качестве снаряда используют постоянный магнит, так как с возникающей при этом ЭДС индукции легче бороться. Такой же эффект возникает при использовании ферромагнетиков, но выражен он не так ярко благодаря тому, что снаряд легко перемагничивается (коэрцитивная сила).

Для наибольшего эффекта импульс тока в соленоиде должен быть кратковременным и мощным. Как правило, для получения такого импульса используются электролитические конденсаторы большой ёмкости и с высоким рабочим напряжением.

Параметры ускоряющих катушек, снаряда и конденсаторов должны быть согласованы таким образом, чтобы при выстреле к моменту подлета снаряда к соленоиду индукция магнитного поля в соленоиде была максимальна, но при дальнейшем приближении снаряда резко падала. Стоит заметить, что возможны разные алгоритмы работы ускоряющих катушек.

Кинетическая энергия снаряда

E=mv22{\displaystyle E={mv^{2} \over 2}}

m{\displaystyle m} — масса снаряда

v{\displaystyle v} — его скорость

Энергия, запасаемая в конденсаторе

E=CU22{\displaystyle E={CU^{2} \over 2}}

U{\displaystyle U} — напряжение конденсатора

C{\displaystyle C} — ёмкость конденсатора

Время разряда конденсаторов

Это время за которое конденсатор полностью разряжается:

T=πLC2{\displaystyle T={\pi {\sqrt {LC}} \over 2}}

L{\displaystyle L} — индуктивность

C{\displaystyle C} — ёмкость

Время работы катушки индуктивности

Это время, за которое ЭДС катушки индуктивности возрастает до максимального значения (полный разряд конденсатора) и полностью падает до 0. Оно равно верхнему полупериоду синусоиды.

T=2πLC{\displaystyle T=2\pi {\sqrt {LC}}}

L{\displaystyle L} — индуктивность

C{\displaystyle C} — ёмкость

Стоит заметить, что в представленном виде две последние формулы не могут применяться для расчетов пушки Гаусса, хотя бы по той причине, что по мере движения снаряда внутри катушки, её индуктивность все время изменяется.

Теоретически возможно применение пушек Гаусса для запуска лёгких спутников на орбиту, так как при стационарном использовании есть возможность иметь большой источник энергии. Основное применение — любительские установки, демонстрация свойств ферромагнетиков. Также достаточно активно используется в качестве детской игрушки или развивающей техническое творчество самодельной установки (простота и относительная безопасность)

Простейшие конструкции могут быть собраны из подручных материалов даже при школьных знаниях физики^[1]

Существует множество сайтов, в которых подробно описано, как собрать пушку Гаусса. Но стоит помнить, что создание оружия в некоторых странах может преследоваться по закону. Поэтому, перед тем, как создавать пушку Гаусса, стоит задуматься, как вы будете применять её.

Пушка Гаусса в качестве оружия обладает преимуществами, которыми не обладают другие виды стрелкового оружия. Это отсутствие гильз и неограниченность в выборе начальной скорости и энергии боеприпаса, возможность бесшумного выстрела (если скорость достаточно обтекаемого снаряда не превышает скорости звука) в том числе без смены ствола и боеприпаса, относительно малая отдача (равная импульсу вылетевшего снаряда, нет дополнительного импульса от пороховых газов или движущихся частей), теоретически, больша́я надёжность и, в теории, износостойкость, а также возможность работы в любых условиях, в том числе в космическом пространстве.

Однако, несмотря на кажущуюся простоту пушки Гаусса, использование её в качестве оружия сопряжено с серьёзными трудностями, главное из которых: большие затраты энергии.

Первая и основная трудность — низкий КПД установки. Лишь 1-7 % заряда конденсаторов переходят в кинетическую энергию снаряда. Отчасти этот недостаток можно компенсировать использованием многоступенчатой системы разгона снаряда, но в любом случае КПД редко достигает 27 %. В основном в любительских установках энергия, запасённая в виде магнитного поля, никак не используется, а является причиной использования мощных ключей (часто применяют IGBT модули) для размыкания катушки (правило Ленца).

Вторая трудность — большой расход энергии (из-за низкого КПД).

Третья трудность (следует из первых двух) — большой вес и габариты установки при её низкой эффективности.

Четвёртая трудность — достаточно длительное время накопительной перезарядки конденсаторов, что заставляет вместе с пушкой Гаусса носить и источник питания (как правило, мощную аккумуляторную батарею), а также высокая их стоимость. Можно, теоретически, увеличить эффективность, если использовать сверхпроводящие соленоиды, однако это потребует мощной системы охлаждения, что приносит дополнительные проблемы, и серьёзно влияет на область применения установки. Или же использовать заменяемые батареи-конденсаторы.

Пятая трудность — с увеличением скорости снаряда время действия магнитного поля, за время пролёта снарядом соленоида, существенно сокращается, что приводит к необходимости не только заблаговременно включать каждую следующую катушку многоступенчатой системы, но и увеличивать мощность её поля пропорционально сокращению этого времени. Обычно этот недостаток сразу обходится вниманием, так как большинство самодельных систем имеет или малое число катушек, или недостаточную скорость пули.

В условиях водной среды применение пушки без защитного кожуха также серьёзно ограничено — дистанционной индукции тока достаточно, чтобы раствор солей диссоциировал на кожухе с образованием агрессивных (растворяющих) сред, что требует дополнительного магнитного экранирования.

Таким образом, на сегодняшний день у пушки Гаусса нет перспектив в качестве оружия, так как она значительно уступает другим видам стрелкового оружия, работающего на других принципах. Теоретически, перспективы, конечно, возможны, если будут созданы компактные и мощные источники электрического тока и высокотемпературные сверхпроводники (200—300К). Однако, установка, подобная пушке Гаусса, может использоваться в космическом пространстве, так как в условиях вакуума и невесомости многие недостатки подобных установок нивелируются. В частности, в военных программах СССР и США рассматривалась возможность использования установок, подобных пушке Гаусса, на орбитальных спутниках для поражения других космических аппаратов (снарядами с большим количеством мелких поражающих деталей), или объектов на земной поверхности.

Довольно часто в литературе научно-фантастического жанра упоминается пушка Гаусса. Она выступает там в роли высокоточного смертоносного оружия.

Примером такого литературного произведения являются книги из серии «S.T.A.L.K.E.R.», написанные по серии игр S.T.A.L.K.E.R., где Гаусс-пушка была одним из мощнейших видов оружия, не считая РПГ-7. В свою очередь, идея такого оружия во вселенной серии было позаимствовано из серии игр Fallout.

Но первым в научной фантастике пушку Гаусса воплотил в реальность Гарри Гаррисон в своей книге «Месть Стальной Крысы». Цитата из книги: «Каждый имел при себе гауссовку — многоцелевое и особо смертоносное оружие. Его мощные батареи накапливали впечатляющий заряд. Когда нажимали на спуск, в стволе генерировалось сильное магнитное поле, разгоняющее снаряд до скорости, не уступающей скорости снаряда любого другого оружия с реактивными патронами. Но гауссовка имела то превосходство, что обладала более высокой скорострельностью, была абсолютно бесшумной и стреляла любыми снарядами, от отравленных иголок до разрывных пуль».

↑ Брага Н. Создание роботов в домашних условиях. — М.: НТ Пресс, 2007. — С. 141 — ISBN 5-477-00749-4.