Основы электроники и электротехники — Лабораторная работа №6
Исследование законов Кирхгофа
Цель работы: опытным путем проверить справедливость законов Кирхгофа.
1.Пояснение к работе
Краткие теоретические сведения
Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников иконтуры — замкнутые пути из проводников.
В этом случае законы формулируются следующим образом.
Первый закон
Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю(значения вытекающих токов берутся с обратным знаком).
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.
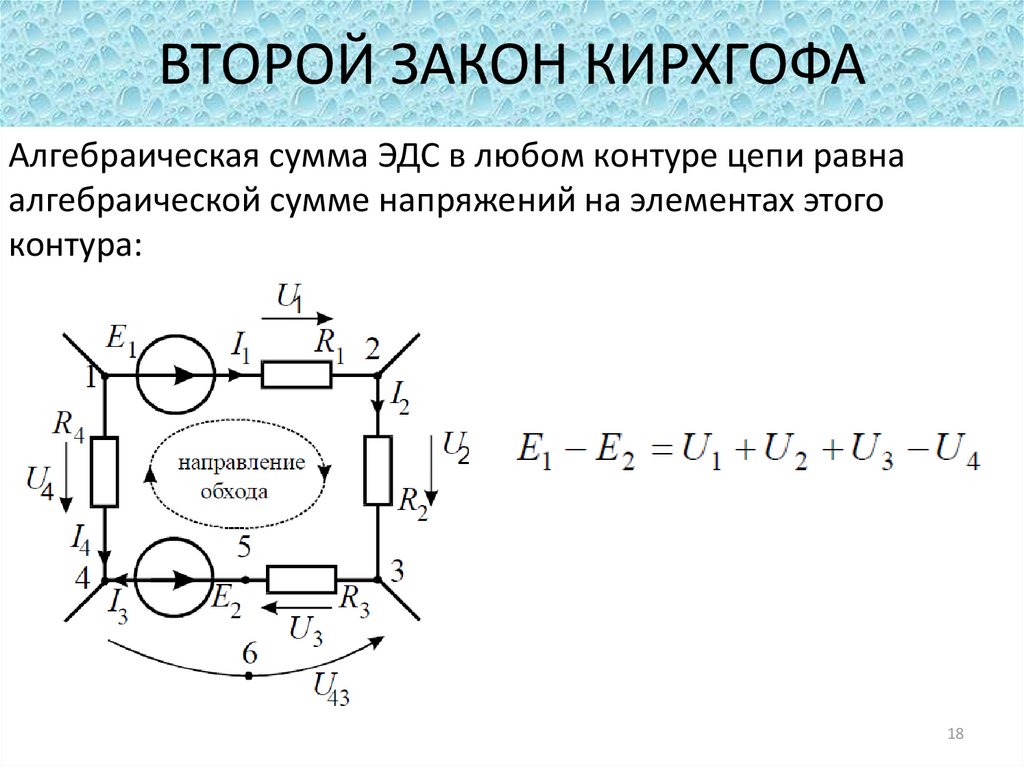
Второй закон
Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю.
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению.
2.Техническое задание
2.1. Собрать схему исследования (Рисунок 1).
2.2. Снять показания и занести их в отчёт.
2.3. Произвести расчёты.
2.4. Сделать вывод о проделанной работе.
3.Работа в лаборатории
3.1. Собрать схему (Рисунок 2).
Рисунок 2 — Схема исследования.
3.2. Установить ЭДС батареек по 5В.
3.3. Установить сопротивления резисторов R1 = 30 Ом + N, R2 = 50 Ом + N, R3 = 100 Ом + N, где N — номер студента по журналу.
3.4. При выключенном ключе S2 замкнуть ключ S1 и замерить токи I1 и I3.Записать их в таблицу.
3.5. При выключенном ключе S1 и замкнутом S2 замерить токи I2 и I3. Записать их в таблицу.
3.6. Замкнуть оба ключа S1 и S2. Записать показания всех амперметров I1, I2, I3 в таблицу.
3.7. Для контура ABEFA составить уравнение по второму закону Кирхгофа и определить Rо1.
3.8. Для контура BCDEB составить уравнение по второму закону Кирхгофа и определить R02.
3.9. Составить уравнение для контура ABCDEFA и проверить справедливость первого закона.
3.10.Сделать вывод по результатам работы.
Таблица 1 — Измеренные параметры
|
№ п/п |
E1 |
Е2 |
I1 |
I2 |
I3 |
Ro1 |
Ro2 |
R1 |
R2 |
|
|
В |
В |
А |
А |
А |
Ом |
Ом |
Ом |
Ом |
Ом |
|
|
1 |
5 |
6 |
— |
|||||||
|
2 |
6 |
7 |
— |
|||||||
|
3 |
7 |
8 |
4. Содержание отчета.
Содержание отчета.
4.1. Название и цель работы
4.2. Схемы
4.3. Таблицы
4.4. Ответы на контрольные вопросы
4.5. Вывод
5.Контрольные вопросы.
5.1. Что называется ветвью узлом и контуром?
5.2. Как читается первый закон Кирхгофа?
5.3. К какому участку электрической цепи он применим?
5.4. Как читается второй закон Кирхгофа?
5.5. К какому участку электрической цепи он применим?
Второй закон Кирхгофа: формула, определение
Все электрические сети подключаются к источнику питания, иначе это не цепь, а набор деталей. Это может быть батарейка, аккумулятор или понижающая трансформаторная подстанция.
Эти элементы сети вместе с электропроводкой и электроприборами составляют контур, распределение потенциалов в котором описывается второй закон Кирхгофа.
Определение второго правила Кирхгофа
Этот закон определяет напряжение и ЭДС (E) на различных элементах цепи и применяется к замкнутой сети или контуру. Поэтому он также известен как закон петли Кирхгофа.
Поэтому он также известен как закон петли Кирхгофа.
Второе правило так же носит название закон напряжения Кирхгофа. Оно выводится из закона сохранения энергии, что можно понять из следующего явления.
В замкнутом контуре количество полученного заряда равно количеству потерянной энергии, которая происходит из-за падения напряжения на резисторах, включенных в эту цепь. Следовательно, сумма подъёмов и падений потенциалов в замкнутой цепи должна быть равна нулю. Математически это можно представить как ΣU=0.
Формулировка №1: алгебраическая сумма падений напряжений в любом замкнутом контуре, равна алгебраической сумме ЭДС вдоль того же контура.
Формулировка №2: алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю.
Иначе говоря, внутри любого замкнутой сети сумма напряжений на всех элементах, поставляющих в сеть электрическую энергию, таких как батареи, генераторы или трансформаторы, должна равняться сумме напряжений на всех деталях, потребляющих электроэнергию.
Это является следствием двух законов — сохранения заряда и сохранения энергии. При этом второе правило Кирхгофа гласит, что электродвижущая сила или ЭДС, действующая на элементы замкнутого контура, должна быть равна сумме разностей потенциалов, имеющихся на всех составляющих этого контура.
При этом нужно принимать во внимание не только падение напряжения на пассивных элементах, но и внутреннее сопротивление источника питания.
| Важно! При наличии в цепи ёмкостного или индуктивного сопротивления следует учитывать не только активное, но и реактивное или полное падение напряжения. |
Физический смысл второго закона Кирхгофа
2 закон Кирхгофа позволяет выразить в числовой форме связь между ЭДС и падением напряжения на элементах замкнутой сети. Эти величины должны быть одинаковыми, иначе нарушается один из фундаментальных законов о сохранении энергии, сформулированный ещё Михаилом Ломоносовым и другими учёными:
- если бы ΣE > ΣU, то какая-то часть энергии источника питания исчезала бы бесследно;
- если бы ΣE < ΣU, то стало бы возможным создание «вечного» двигателя и получать энергию из «ниоткуда».

Оба этих явления ни разу не наблюдались экспериментально и, следовательно, являются невозможными.
Расчёты, использующие законы Кирхгофа, применяются при определении параметров электрических цепей. Есть два закона Кирхгофа: первый или закон тока и второй или закон напряжения. С их помощью составляются уравнения для отдельных компонентов (резисторов, конденсаторов и катушек индуктивности).
Применяя правила Кирхгофа, можно получить уравнения, позволяющие находить неизвестные данные. Это токи, ЭДС, напряжение и сопротивления для определения создается система уравнений, которых должно быть столько же, сколько имеется неизвестных. При этом уравнения могут иметь два решения, определяющие знаки различных величин.
Применяя первое правило Кирхгофа необходимо пометить ток в каждой ветви и решить, в каком направлении он течет. При этом отсутствует опасность выбора неправильного направления потому что, если оно было выбрано неверно, ток будет правильной величины, но c отрицательным значением, что не повлияет на конечный результат.
Применяя второе правило Кирхгофа, правило петли, нужно найти замкнутую цепь (контур) и решить, в каком направлении производить её обход, по часовой стрелке или против. При этом обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что соответствует умножению обеих частей уравнения на -1.
Применение законов Кирхгофа имеют ограничения. В некоторых ситуациях составит правильные уравнения сложно, а иногда невозможно. Правила Кирхгофа предназначены для сетей постоянного тока, поэтому при увеличении частоты растут неучтённые потери из-за ёмкостного и индуктивного сопротивления проводов.
Уравнение для второго закона Кирхгофа
Формула второго закона Кирхгофа может выражаться двумя способами — ΣE=ΣIR и ΣU=0. Более удобной для использования считается первое выражение. При расчёте используется алгебраическое сложение с использованием не только величины, но знака потенциала.
При этом на принципиальной схеме произвольным образом выбирается направление прохождения замкнутой цепи и так же случайно определяется направление электрического тока. Возле всех элементов отмечаются знаки для ЭДС и падений напряжения по следующим правилам:
Возле всех элементов отмечаются знаки для ЭДС и падений напряжения по следующим правилам:
- при совпадении направлений обхода контура и источника питания, ЭДС присваивают знак «+», в противном случае элемент имеет знак «-«;
- при одинаковом направлении тока и обхода контура, произведение (IR) имеет знак «+», иначе ему присваивается знак «-«.
В результате обхода сумма потенциалов, меняя знак и величину, должна вернуться к нулевому значению. Если это не произошло, значит, была допущена ошибка при подсчёте или не был учён какой-либо либо фактор, например, ёмкость проводов или внутреннее сопротивление элементов питания.
Несмотря та то, что направление электрического тока может выбираться любым, рекомендуется его принимать от «+» к «-» в цепи постоянного тока и от «L» к «N» в сети переменного тока.
Важно! Контур может быть не самостоятельным элементом, а частью схемы бОльших размеров. В этом случае источником напряжения является не батарея, а узлы подающие питание. |
У закона напряжения Кирхгофа есть несколько практических выводов, каждый из которых может использоваться в соответствующей ситуации:
- В сложной схеме можно выделить несколько контуров, каждый из которых рассчитывается по-отдельности. Алгебраические суммы ЭДС и напряжений в таком контуре равны ΣE=ΣU.
- Если в контуре нет источников питания, то ток в цепи отсутствует. В такой системе из-за отсутствия падения напряжения на резисторах ΣU=0.
Расчеты электрической цепи
Для примера рассмотрим схему с двумя источниками питания, включёнными параллельно. При этом одна ЭДС напряжением Е1=10 В, вторая Е2=20 В. Сопротивление нагрузки R1=10 Ом, R2=20 Ом, R3=40 Ом.
Прежде всего, необходимо выделить отдельные контуры и выбрать направление обхода контура и протекания тока. При этом, используя первый закон Кирхгофа, в нагрузке: I1+I2=I3.
Применяя второй закон Кирхгофа и приведенное выше правило о знаках, в первого контура получается следующее выражение: I1•R1+I3•R3 = E1, 10I1+40I3 = 10, или I1+4I3 = 1.
Для второго контура расчёт получится: I2•R2+I3•R3 = E2, 20I2+40I3 = 20, или 2I3+I2 = 1.
Для третьего контура: I1•R1-I2•R2 = E1-E2, 10I1-20I2 = 10-20, или -I1+2I2= 1.
Используя формулу I1+I2=I3 из первого закона Кирхгофа, подставляем выражение (0*) в выражение (1*): I1 +4(I1+I2) = 1, или 5I1+4I2 = 1.
Затем подставляем в выражение (2*) в выражение (0*). Уравнение для второго контура преобразовывается в выражение: 2(I1+I2)+I2 = 1, или 2I1+3I2 = 1
Теперь ток I1 можно найти из (выражения 5* подставляем в 4*): 2I1+3I2 = 5I1+4I2, или I1 = -(1/3)I2
Используя последнее уравнение и уравнение для третьего контура получаем ток I2:
Находим ток I1: I1 = -(1/3)•0,429 = -0,143 А.
Ток I3: I3 = I1+I2 = 0,429-0,143 = 0,286 А.
- I2=0,429 А;
- I1=–0,143 А;
- I3=0,286 А;
Друзья еще один пример решения уравнений по 1-му и 2-му законам Кирхгофа:
Вывод
Второй закон Кирхгофа гласит, что алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС, действующих вдоль этого контура.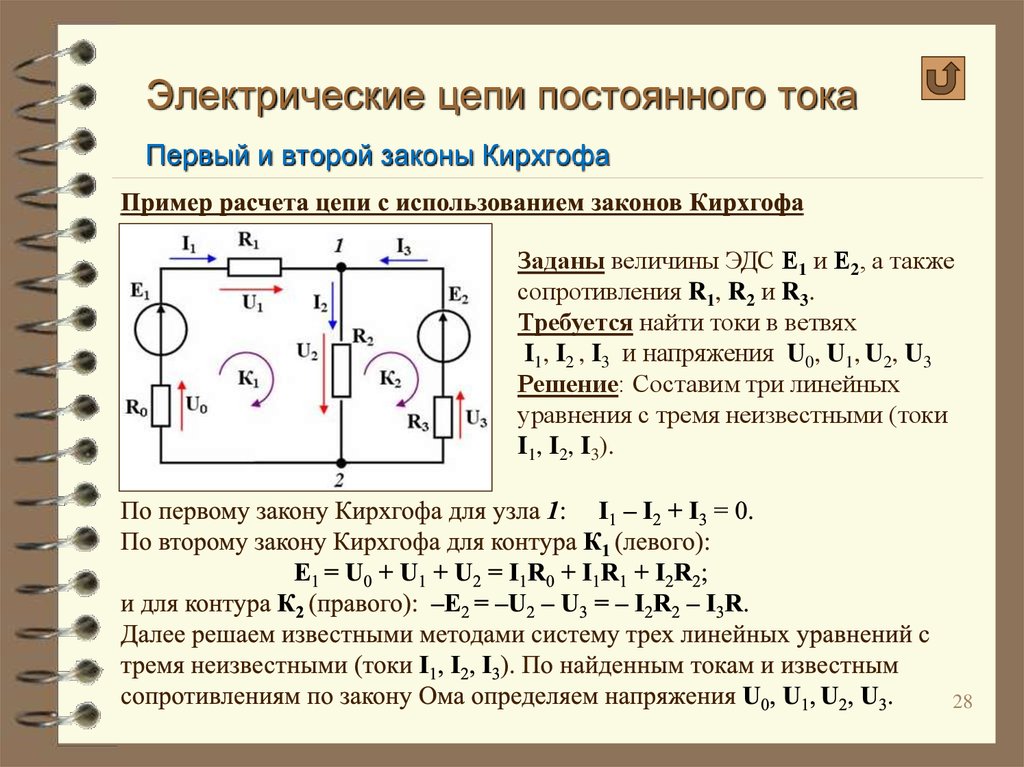
Это означает, что энергия, подаваемая батареей, расходуется всеми остальными компонентами цепи, поскольку энергия не может войти или выйти из замкнутого контура. Правило представляет собой применение закона сохранения энергии с точки зрения разности электрических потенциалов.
Другими словами — энергия сохраняется. Общее количество вложенной энергии (сумма ЭДС) равно общему количеству отведенной энергии (сумма падений напряжений). Этот закон используется для анализа сложных электросхем, которые нельзя рассчитать более простыми методами.
Похожие материалы на сайте:
- Пайка проводов паяльником
- Способы определить полярность диода
- Проверка исправности конденсатора
Урок 8 — Решение схем по законам Кирхгофа — Часть 2 | Репетитор по математике DVD
- домашний
- 2q — Анализ цепей, Том 1
- Урок 8 — Решение схем с Киром. . .
В этом уроке мы продолжим использовать закон Кирхгофа о напряжении и закон Кирхгофа о токе для решения проблем со схемой.
Просмотрите полный курс и учитесь, решая задачи шаг за шагом!
Стенограмма:
Здравствуйте, и добро пожаловать в этот раздел учебника по анализу цепей. Здесь мы собираемся решить эту проблему здесь, и мы собираемся использовать методы закона напряжения Кирхгофа, закона тока Кирхгофа, которые мы изучали, чтобы осуществить это. Вы заметили, что это немного похоже на последнюю задачу, которую мы решили. Во всяком случае, насколько поверхностно. Имеем источник напряжения, имеем резистор, резистор, резистор, форма схемы похожа. Эта задача на самом деле сложнее, потому что то, что нам дано… Смотрите, все, что я здесь нарисовал, это то, что дано вам. Верно? Много раз в вашей книге у вас будет схема, и вам скажут.
|
Мы пытаемся найти значение этого тока, значение этого тока и значение этого напряжения. Это все, о чем мы заботимся. Мы не заботимся ни о чем другом в цепи. Это то, что мы пытаемся найти. Все в порядке. Прежде чем мы сможем что-то сделать, вам действительно нужно пометить ваши токи. Потому что, когда я впервые смотрю на этот рисунок, я не знаю, как на самом деле перейти к ответу. Как и любая другая проблема. Я не знаю заранее, что я собираюсь сделать, чтобы добраться до ответа. Сначала я смотрю и вижу, есть ли что-нибудь, что легко вычислить. Я не вижу ничего легкого. Я не знаю, что это за напряжение.
|
Я не могу легко рассчитать ток. В последней задаче, которую мы решили, вам дали кое-что. Некоторые напряжения даны вам и некоторые простые вещи для расчета. Здесь у нас нет такой роскоши. Мне действительно нужно написать несколько уравнений для сверстников. Моя первая мысль: у меня здесь два узла в цепи. У меня есть этот узел и этот узел. Как мы говорили ранее, если у вас есть два узла в цепи, вы можете написать один узел для закона тока Кирхгофа. Вы можете написать один минус количество узлов, которые у вас есть. Я могу написать одно правильное уравнение узла, поэтому я могу написать уравнение узла, я должен сказать, уравнение закона тока Кирхгофа. Я собираюсь написать один для верхнего узла.
|
Мне нужно, чтобы там что-то было помечено, и я собираюсь выбрать направление, которое считаю верным, потому что я думаю, что оно исходит из источника в этом направлении. Я собираюсь написать все свои уравнения в соответствии с направлением, которое все токи обозначены на моей диаграмме. Это очень важно. Когда вы маркируете диаграмму в цепи как направление напряжения или если вы маркируете ток, тогда все ваши уравнения тока должны быть записаны в терминах, как если бы это направление тока было истинным. Тогда таким образом все самосогласованно. Когда я пишу свое уравнение узла, я действительно и искренне думаю, что этот парень выходит, этот парень выходит, этот парень входит и так далее. Позвольте мне написать это прямо сейчас.
|
Ну, я не знаю, что это такое. Я не знаю, что это такое, и я не знаю, что это такое. Я ничего не могу там сделать. Как и во всех проблемах, вы просто держите это в заднем кармане и продолжаете работать. Мы сделали уравнение узла здесь. Мы не можем больше писать уравнения узлов, потому что у нас есть только два узла в схеме, и мы знаем, что можем написать только одно уравнение узла из-за того, что мы обсуждали ранее. Мы должны обратиться к закону напряжения Кирхгофа. Запишем закон Кирхгофа для напряжений ……..
|
Законы Кирхгофа
Законы КирхгофаВСЕ ТАБЛИЦЫ НА ОДНОЙ СТРАНИЦЕ ДЛЯ ЛЕГКОЙ ПЕЧАТИ
КОНКРЕТНЫЕ ЦЕЛИ
- Чтобы узнать, как ведет себя ток в последовательных и параллельных цепях.

- Чтобы понять два закона Кирхгофа.
ОБОРУДОВАНИЕ
Печатная плата, батарейки типа D (2), провода, резисторы, мультиметр, и провода зонда.СИМВОЛЫ ДЛЯ ЭЛЕМЕНТОВ ЦЕПИ
В этой лаборатории вы будете использовать множество электрических компонентов, все это будет отображено на схематических диаграммах. Вам нужно будет распознавать эти компоненты, чтобы эффективно выполнять лабораторную работу.СХЕМА ПЕЧАТНОЙ ПЛАТЫ
ПРОЦЕДУРА
Подчеркнутые отрывки ниже требуют ответа или наброска в вашем блокнот.Часть 1. Ток в последовательных и параллельных цепях
- Если вы не принимаете данные, отключите аккумулятор; этот увеличит срок его службы.
- Выберите три резистора с одинаковым закодированным сопротивлением. Группы должно быть одинаковым; цвет и форма корпуса резистора могут отличаться.
- Запишите закодированное сопротивление и допуск в таблице ниже.
Запишите последовательное эквивалентное сопротивление в 4-ю строку таблицы.
 стол. Либо используйте теорию цепей для расчета последовательного эквивалента
сопротивление или просто используйте омметр для измерения сопротивления через
все три резистора (, убедитесь, что батарея НЕ
подключен при измерении сопротивления! ).
стол. Либо используйте теорию цепей для расчета последовательного эквивалента
сопротивление или просто используйте омметр для измерения сопротивления через
все три резистора (, убедитесь, что батарея НЕ
подключен при измерении сопротивления! ). - Соедините три резистора последовательно, как показано ниже.
используя пружины в нижней части доски, чтобы удерживать
резисторы.
- Ознакомьтесь с мерами предосторожности при использовании мультиметр как вольтметр.
- Измерьте напряжение на каждом из резисторов по очереди и запишите
ваши измерения (с единицами и ошибками) в таблице ниже.
Запишите напряжение на аккумуляторе в 4-ю строку таблицы.
Чтобы определить правильную настройку глюкометра, выключите глюкометр при самую большую настройку, затем перейдите к меньшим настройкам и остановитесь на настройка, которая может обрабатывать как размер данных для измерения и имеет наибольшее количество значащих цифр в чтении.

- Ознакомьтесь с мерами предосторожности при использовании мультиметр как амперметр.
- Просмотрите их еще раз. Быть АБСОЛЮТНО уверен, что ты умеешь правильно измерять ток. И вы, и ваш партнер по лаборатории потеряете два очка, если любой из вас перегорает предохранитель в мультиметре.
- Разомкните цепь в точке, указанной на рисунке ниже.
Измерьте ток I 1 , протекающий по проводу между
положительная клемма аккумулятора и резистор 1. Запишите
измерений (с единицами измерения и погрешностями) в таблице ниже.
- Снимите амперметр, снова подключите цепь и разорвите цепь разрыв между резистором 1 и резистором 2. Измерить ток I 2 течет через этот кусок провода. Запишите свои измерения (с единицами измерения и погрешностями) в таблицу ниже.
- Повторить для тока I 3 , протекающего между резистором 2 и резистором 3,
и ток I 4 , протекающий между резистором 3 и батареей.

Resistance Voltage Current 1 2 3 4 - Какое очевидное правило для тока в последовательной цепи?
- Повторите это упражнение с тремя неодинаковыми резисторами.
Сопротивление Напряжение Ток 1 2 3 4 - Действует ли очевидное правило? Объяснять.

- Верен ли закон Ома V=IR для каждого отдельного резистора? Объяснять.
- Справедлив ли закон Ома для последовательного эквивалентного сопротивления
(четвертая строка таблицы)? Объяснять.
- Соберите цепь с тремя одинаковыми резисторами, включенными параллельно.
- Запишите закодированные сопротивления и допуски в таблице ниже. В четвертой строке запишите теоретический параллельный эквивалент сопротивление. Или вы можете измерить эквивалентное сопротивление с функция омметра мультиметра, но обязательно отключить аккумулятор!
- Запишите напряжения на каждом резисторе (1,2,3) и батарея (4).
- Измерьте токи через каждый резистор (1,2,3) и ток
вытекающий из аккумулятора (4). Не забудьте
разомкнуть цепь и включить амперметр последовательно.
Resistance Voltage Current 1 2 3 4 5 4 9003 - Какое очевидное правило для тока в параллельной цепи?
- Повторите это упражнение с тремя неодинаковыми резисторами.

Сопротивление Напряжение Ток 1 2 3 4 - Действует ли очевидное правило? Объяснять.
- Верен ли закон Ома V=IR для каждого отдельного резистора? Объяснять.
- Справедлив ли закон Ома для параллельного эквивалентного сопротивления (четвертая строка таблицы)? Объяснять.
Часть 2 — Законы Кирхгофа
- Если вы не принимаете данные, отключите аккумулятор; этот увеличит срок его службы.
- Подключите цепь, показанную ниже, с помощью
- R 1 = 1000 Ом (вверху слева)
- R 2 = 2200 Ом (вверху справа)
- R 3 = 560 Ом (внизу слева)
- R 4 = 330 Ом (внизу справа)
- R 5 = 1000 Ом (средний резистор)
- Запишите эти значения сопротивления с допусками в таблицу
ниже.

- Какие резисторы включены последовательно или параллельно? Может какие резисторы объединять в последовательные или параллельные эквивалентные сопротивления?
- При отсутствии тока (аккумулятор отключен) измерить сопротивление между точками A и B, и запишите это значение в последнюю строку (B для батарея ) таблицы .
- При подключенной батарее измерьте напряжение на каждом резисторе. Запишите значения в таблицу. Также измерьте напряжение из пункта А в пункт Б и записывают в последнюю строку таблицы. На схеме, подобной приведенной выше, отметьте полярность напряжения. То есть отметьте «+» или «-» на сторонах резисторов, чтобы указать, какой сторона находится на более высоком напряжении и на более низком напряжении. мультиметр покажет положительное значение, если красный щуп находится на более высоком уровне. потенциал, чем черный зонд.
- Измерьте ток, протекающий через каждый резистор и запишите эти значения в таблицу .
 Также измерьте ток, вытекающий из батареи, и запишите его в последнюю строку таблицы . Не забудьте разомкнуть цепь и последовательно включить амперметр.
Также измерьте ток, вытекающий из батареи, и запишите его в последнюю строку таблицы . Не забудьте разомкнуть цепь и последовательно включить амперметр. Сопротивление Напряжение Ток 1 2 3 4 5 B - Определите суммарный ток в каждом соединении. Если ток течет из перекрестка, то это отрицательный.
- Определите полное падение напряжения вокруг двух из семи замкнутых контуров.
в цепи.




 Ток здесь называется I1. Ток здесь называется I2. Напряжение на нем составляет V sub 3. Или что-то еще. Тогда вам придется использовать это, и вы будете пытаться решить то, что вы пытаетесь решить. Здесь у нас есть предварительно помеченный IA. ИБ идет сюда. Падение напряжения на этом резисторе называется Vo, и мы пытаемся найти его.
Ток здесь называется I1. Ток здесь называется I2. Напряжение на нем составляет V sub 3. Или что-то еще. Тогда вам придется использовать это, и вы будете пытаться решить то, что вы пытаетесь решить. Здесь у нас есть предварительно помеченный IA. ИБ идет сюда. Падение напряжения на этом резисторе называется Vo, и мы пытаемся найти его. Я не знаю, что это за ток. Я не могу использовать закон Ома здесь. Я не знаю, какое на самом деле напряжение на этом парне, во всяком случае, напрямую. Это не 200 вольт, потому что здесь стоит резистор. Я не знаю, что это за падение напряжения на самом деле.
Я не знаю, что это за ток. Я не могу использовать закон Ома здесь. Я не знаю, какое на самом деле напряжение на этом парне, во всяком случае, напрямую. Это не 200 вольт, потому что здесь стоит резистор. Я не знаю, что это за падение напряжения на самом деле. Я просто запишу это. Текущий закон Кирхгофа в верхнем узле. Когда я это делаю, я сразу понимаю, что у меня нет тока, отмеченного здесь. Фиолетовым я возьму на себя смелость обозначить этот ток I sub S.
Я просто запишу это. Текущий закон Кирхгофа в верхнем узле. Когда я это делаю, я сразу понимаю, что у меня нет тока, отмеченного здесь. Фиолетовым я возьму на себя смелость обозначить этот ток I sub S. В этом узле у меня есть вход I sub S, поэтому он отрицательный I sub S. У меня выходит I sub A, так что это положительно, и у меня выходит I sub B, так что это положительно и равно 0. I остановись на секунду, я смотрю на это и говорю: «Хорошо, я могу здесь что-нибудь сделать?»
В этом узле у меня есть вход I sub S, поэтому он отрицательный I sub S. У меня выходит I sub A, так что это положительно, и у меня выходит I sub B, так что это положительно и равно 0. I остановись на секунду, я смотрю на это и говорю: «Хорошо, я могу здесь что-нибудь сделать?»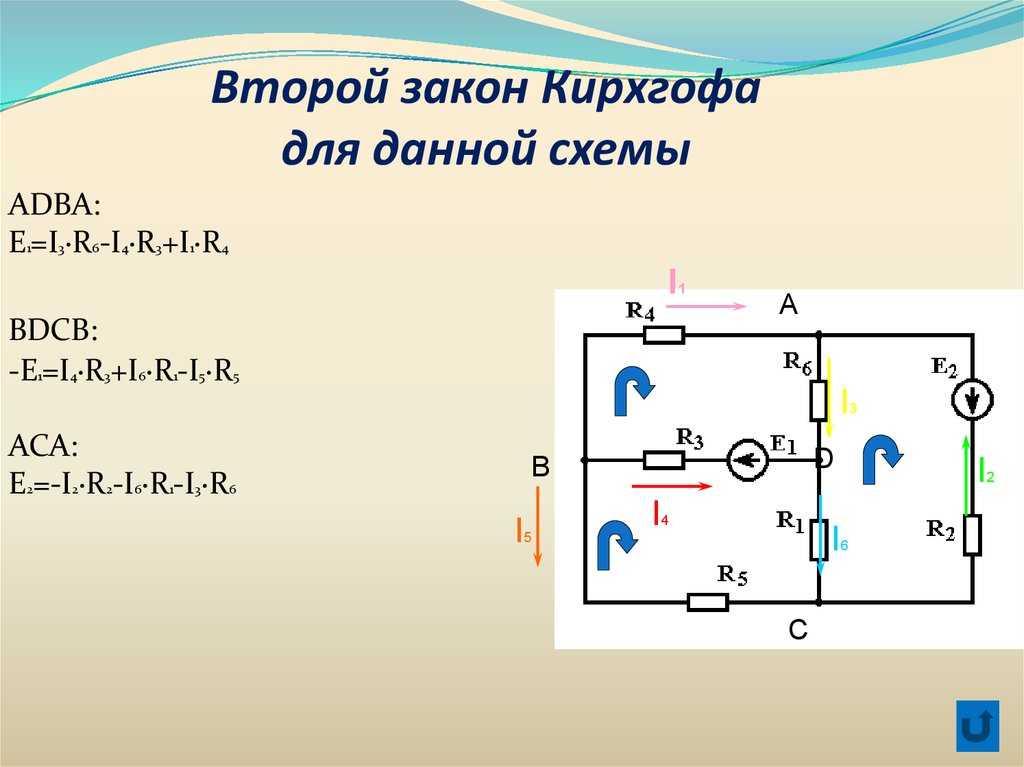
 стол. Либо используйте теорию цепей для расчета последовательного эквивалента
сопротивление или просто используйте омметр для измерения сопротивления через
все три резистора (, убедитесь, что батарея НЕ
подключен при измерении сопротивления! ).
стол. Либо используйте теорию цепей для расчета последовательного эквивалента
сопротивление или просто используйте омметр для измерения сопротивления через
все три резистора (, убедитесь, что батарея НЕ
подключен при измерении сопротивления! ). 




 Также измерьте ток, вытекающий из батареи, и запишите его в последнюю строку таблицы . Не забудьте разомкнуть цепь и последовательно включить амперметр.
Также измерьте ток, вытекающий из батареи, и запишите его в последнюю строку таблицы . Не забудьте разомкнуть цепь и последовательно включить амперметр. 