Что такое «Зона Френеля»? Препятствия на пути радиоволн.
Что такое «Зона Френеля»? Препятствия на пути радиоволн.
Радиоволна в процессе распространения в пространстве формирует эллипсоид вращения, в фокусах которого находятся передатчик и приемник. Этот эллипсоид вокруг прямой линии (LoS/Line of Sight), и называется Зоной Френеля. Не менее 60% зоны Френеля должно оставаться чистой от каких-либо препятствий, т.к. иначе начинаются существенные потери сигнала в канале.
На приведенном выше рисунке показано, что наличие прямой видимости не является достаточным условием для качественной работы высокочастотного радиолинка. Дело в том, что длина световых волн значительно короче волн радиодиапазона, поэтому, даже если мы можем видеть противоположную сторону линка, это не значит, что данное свободное пространство также «прозрачно» для волн радиодиапазона. В результате, если антенны установлены только исходя из наличия прямой видимости, радиолинк будет вести себя следующим образом: детектор качества сигнала будет показывать почти сто процентов, но скорость линка будет минимальной, потери и повтор пакетов, а также пропадания связи сделают работу линка невозможной.
Решить проблему можно только путем поднятия антенн на высоту, равную половине зоны Френеля в месте наличия препятствия. Разумеется, что если препятствие находится сбоку, например в случае построения линка, луч которого проходит, между двух зданий, должно соблюдаться то же самое условие. После подъема антенн на необходимую высоту на обеих сторонах, линк будет работать на максимальной скорости и с максимальной для данного расстояния отдачей.
Иными словами, должно выполняться условие: Н>=h+R*(1-40%)
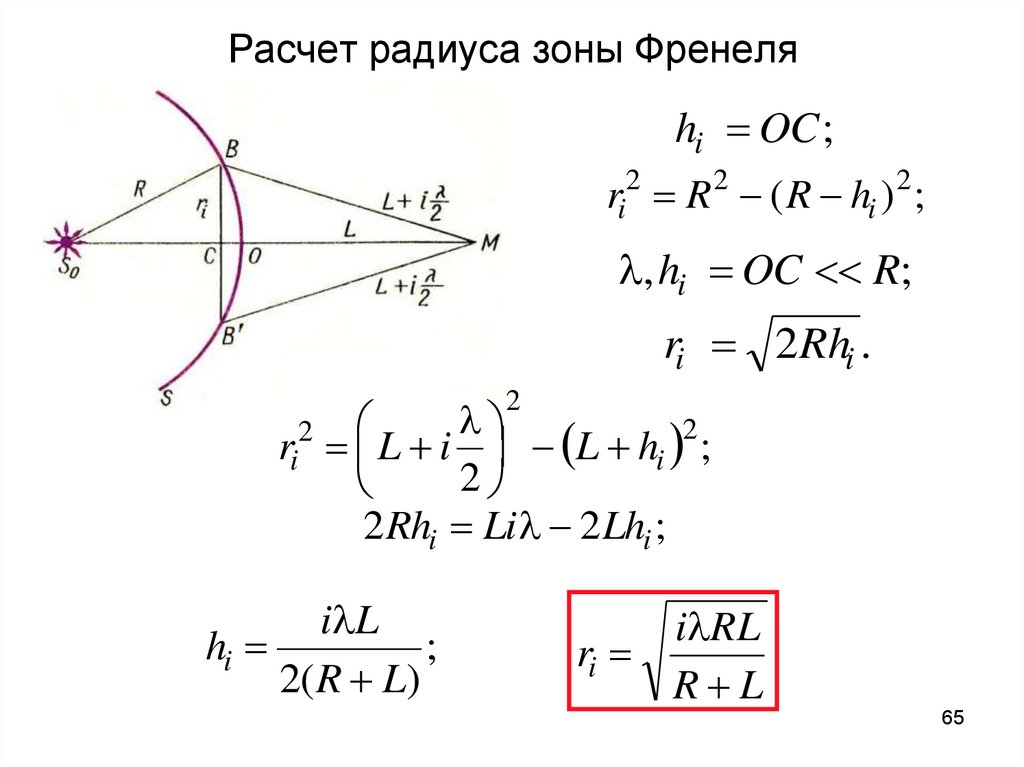
Радиус зоны Френеля в нужной точке пространства можно расчитать по формуле:
Где Freq— частота сигнала в ГЦ, а D1 и D2— расстояние в метрах
Подробнее можно прочитать здесь: https://en.wikipedia.org/wiki/Fresnel_zone
При выборе места монтажа учитывайте пожалуйста, что наша планета — круглая. Поэтому, для обеспечения прямой видимости между антеннами, их надо поднять на достаточную высоту.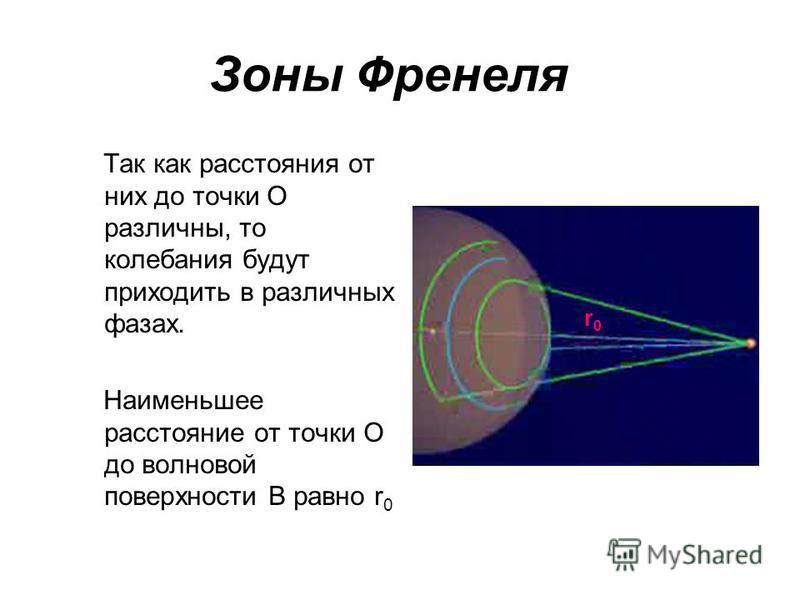
Дополнительную информацию можно получить здесь: Зависимость дальности прямой видимости от высоты антенн.
Для расчета высоты установки антенн также рекомендуем вам пользоваться Ubiquiti Outdoor Wireless Link Calculator
Историческая справка:
Френель (Fresnel) Огюстен Жан (10.5.1788, Брольи, — 14.7.1827, Виль-д’Авре, близ Парижа), французский физик, один из основателей волновой оптики, член Парижской АН (с 1823). Родился в семье архитектора. Окончил Политехническую школу (1806) и Школу дорог и мостов (1809) в Париже. Работал инженером по ремонту дорог. В период 100 дней за участие в военных действиях против Наполеона был отстранен от работы. К этому периоду относятся первые серьезные работы Ф. по оптике. В конце 1815 он был восстановлен в должности и в 1818 переведён в Париж, где занимался реорганизацией маяков, предложил принципиально новый способ маячного освещения. В 1815—23 Ф. выполнил классические исследования дифракции и поляризации света.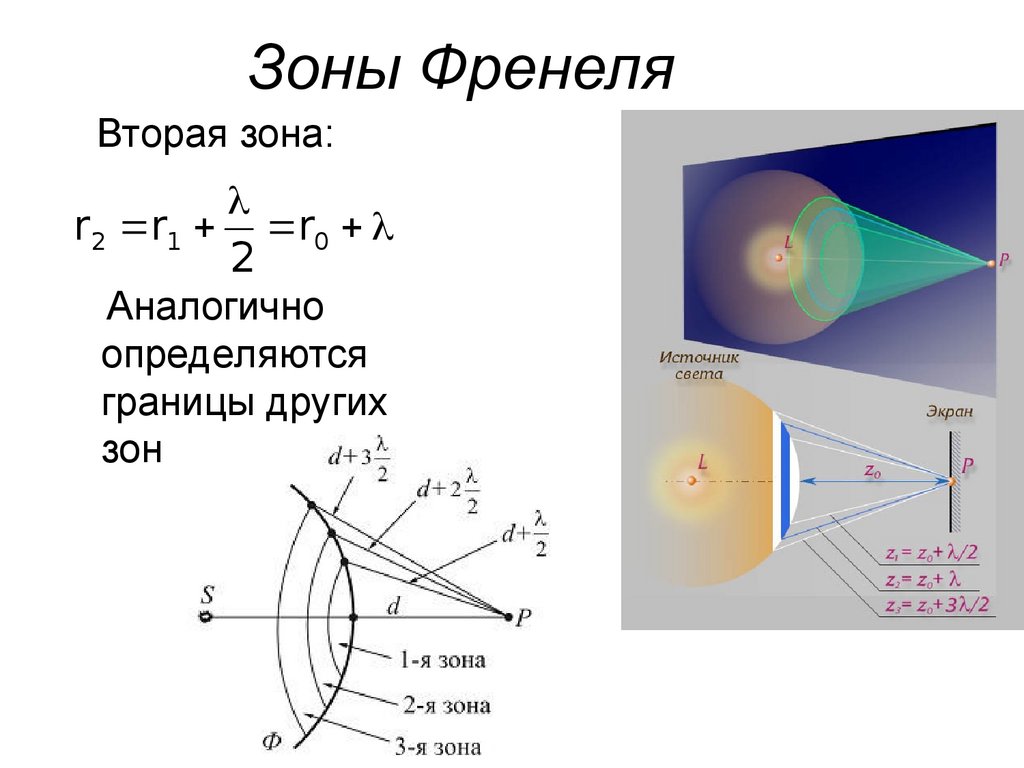
формулировка метода, радиус зоны, формула, расчет, принцип построения зон, принцип Гюйгенса-Френеля
Научиться настройке MikroTik можно на онлайн курсе по оборудованию этого производителя. Автор курса является сертифицированным тренером MikroTik. Подробней Вы можете прочитать в конце статьи.
Зоны Френеля используются теорией распространения для расчета отражений и дифракционных потерь между передатчиком и приемником. Зоны Френеля нумеруются и называются «F1», «F2», «F3» и т. д.
Существует бесконечное количество зон Френеля, однако только первые 3 имеют реальное влияние на распространение радиоволн.
Содержание
- Что такое зона Френеля и почему это важно?
- Определяем размер зоны
- Метод зон Френеля
- Зона Френеля 1 (F1)
- Зона Френеля 2 (F2)
- Зона Френеля 3 (F3)
- Эффект зоны Френеля
- Радиотерминалы «точка-точка»
- Радиус зоны Френеля и расстояние до Земли
- Дифракция Френеля на круглом отверстии
- Дифракция Френеля на маленьком круглом экране
- Каковы условия для дифракции Френеля?
- Почему дифракция Френеля отличается от других видов дифракции?
- Как дифракция Френеля решается математически?
- Принцип Гюйгенса — Френеля
- Принцип Гюйгенса
- Пятно Пуассона
Что такое зона Френеля и почему это важно?
Рис 1.
Первая и вторая зоны Френеля.Зона Френеля — это цилиндрический эллипс, проведенный между передатчиком и приемником. Размер эллипса определяется частотой работы и расстоянием между двумя участками.
Определяем размер зоны
Когда радиосигнал проходит между передатчиком и приемником, он может распространяться несколькими путями. Он может идти напрямую между передатчиком и приемником (основной сигнал). Сигнал может отражаться от земли и затем переноситься на удаленный приемник (отраженный сигнал). Он может идти влево или вправо и отражаться от «холма» (еще один отраженный сигнал).
Радиус зоны Френеля описывает это отражение относительно общей длины радиотрассы. Рисунок выше показывает основные и отраженные сигналы и F1 (первая зона Френеля) и F2 (вторая зона Френеля). Отражение может происходить в любом месте между передатчиком и приемником. На рисунке показано отражение, происходящее в случайном месте, а не в центре пути.
Когда сигнал отражается, происходят две вещи:
- фаза сигнала меняется на противоположную, а сигнал изменяется по фазе на 180º;
- Поскольку сигнал отражается и не идет по прямой линии, он проходит немного дальше к точке рефактинга, а затем к приемнику.
Следовательно, сигнал сдвигается дальше по фазе из-за разницы в длине пути.
Следовательно, сигнал сдвигается дальше по фазе из-за разницы в длине пути.ВАЖНО! На длинном пути сдвиг может составить 180º или больше.
Почему это важно? Приемная антенна не может различить основной и отраженный сигналы. Они оба на одной частоте. Он принимает как основной, так и отраженный сигналы. Он также получает любые другие сигналы в пределах своего заданного диапазона частот.
Когда антенна получает основной сигнал и отраженный сигнал, эти два сигнала будут объединяться и суммироваться на антенне. Если они сдвинуты на 360º (по фазе), это не проблема. Однако, если сигналы разнесены на 180º (противоположная фаза), они будут взаимно поглощаться, и приемник ничего не получит.
Метод зон Френеля
Для нахождения результата интерференции вторичных волн Френель предложил метод разбиения волнового фронта на зоны, называемые зонами Френеля.
Зона Френеля 1 (F1)
Радиус первой зоны Френеля рассчитывается так, чтобы разница в длине пути между основным сигналом и отраженным сигналом от расстояния радиуса F1 составляла 180º.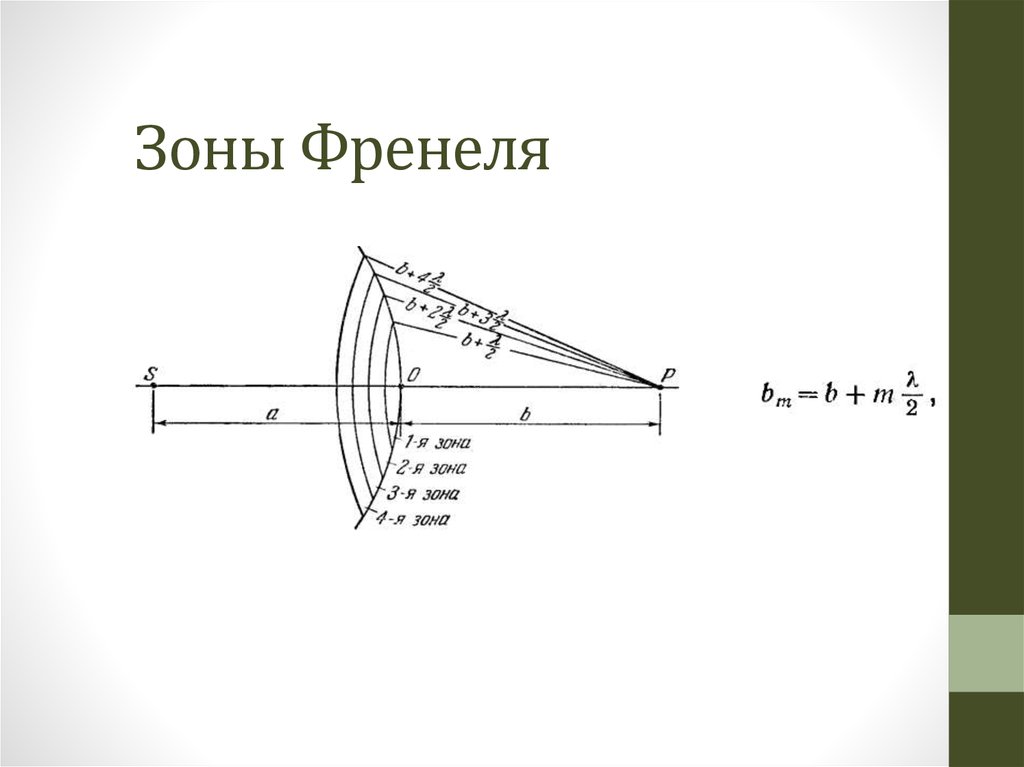
Отраженный сигнал, смещенный на 180º расстояния пути плюс 180º от фактической точки отражения, составляет 360º фазового сдвига. Два сигнала, основной и отраженный, поступают на антенну на 360º друг от друга или в фазе. Они будут складываться и не влияют на производительность приемника.
Этот сдвиг фазы отражения может происходить в любом месте от вычисленной «трубки» зоны Френеля, известной как эллипс.
Зона Френеля 2 (F2)
Радиус второй зоны Френеля рассчитывается так, чтобы разница в длине пути между основным и отраженным сигналами от второй трубки зоны Френеля составляла 360º.
Это очень важно, так как отраженный сигнал имеет автоматический фазовый сдвиг на 180º плюс разница в длине пути 360º равна сдвигу фазы 540º. 540º и 180º имеют одинаковый фазовый сдвиг в математической модели, и два сигнала будут отменены, не оставляя сигнала на приемнике.
Вторая зона Френеля, F2, является зоной отражения, которая не учитывается при проектировании радиотрассы.
Зона Френеля 3 (F3)
Третья зона Френеля имеет разницу в длине пути 540º.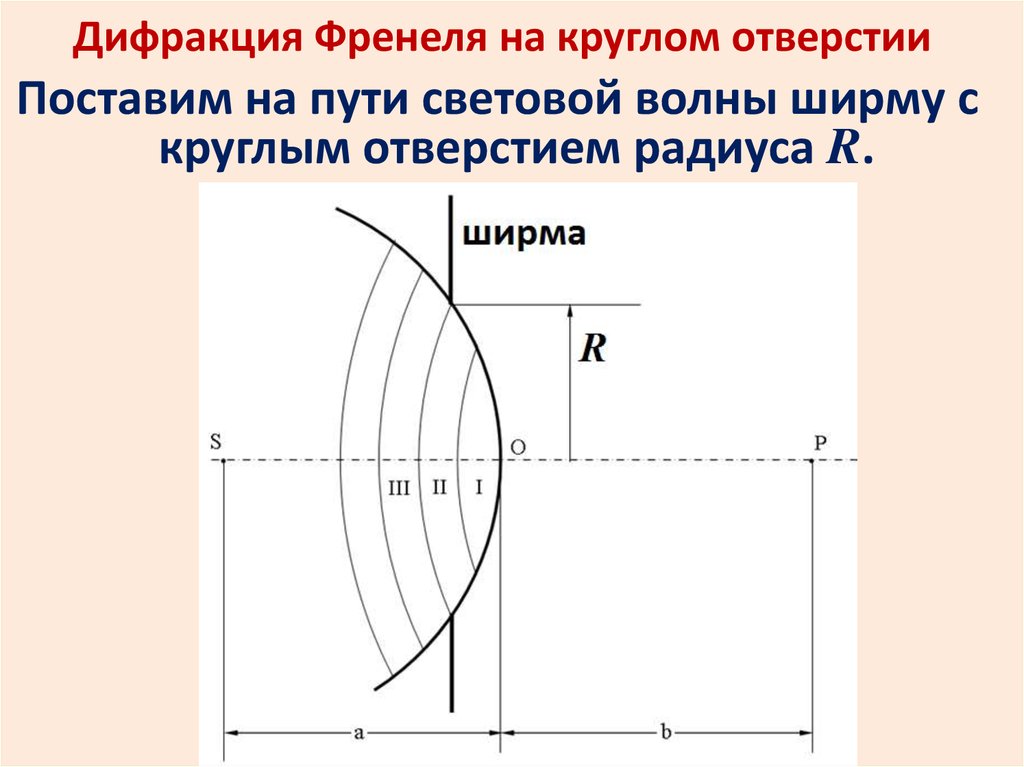
Добавьте это к сдвигу отражения 180º; общее количество составляет 720º, и 2 сигнала находятся в фазе.
Эффект зоны Френеля
Конечным результатом является то, что четные зоны Френеля отражают сигнал 180 градусов. Это вредно для распространения по радио. Зоны Френеля с нечетным номером имеют фазовый сдвиг на 360º и не имеют никакого эффекта. Нечетные зоны Френеля — это «хорошие парни».
Эффект этих отражений в мобильной работе может ощущаться, например, вблизи крайнего конца ретранслятора.
В приемнике слышно быстрое увеличение / уменьшение сигнала, которое часто называют «пикетным ограждением».Быстрое увеличение и уменьшение сигнала от движущегося радио или транспортного средства называется замиранием Рэлея. Это является прямым результатом появления и исчезновения отражений в зоне Френеля, когда транспортное средство движется по шоссе.
Радиотерминалы «точка-точка»
Радиосвязи точка-точка обсуждаются далее в этой статье, однако стоит отметить одну хитрость при проектировании линий связи точка-точка.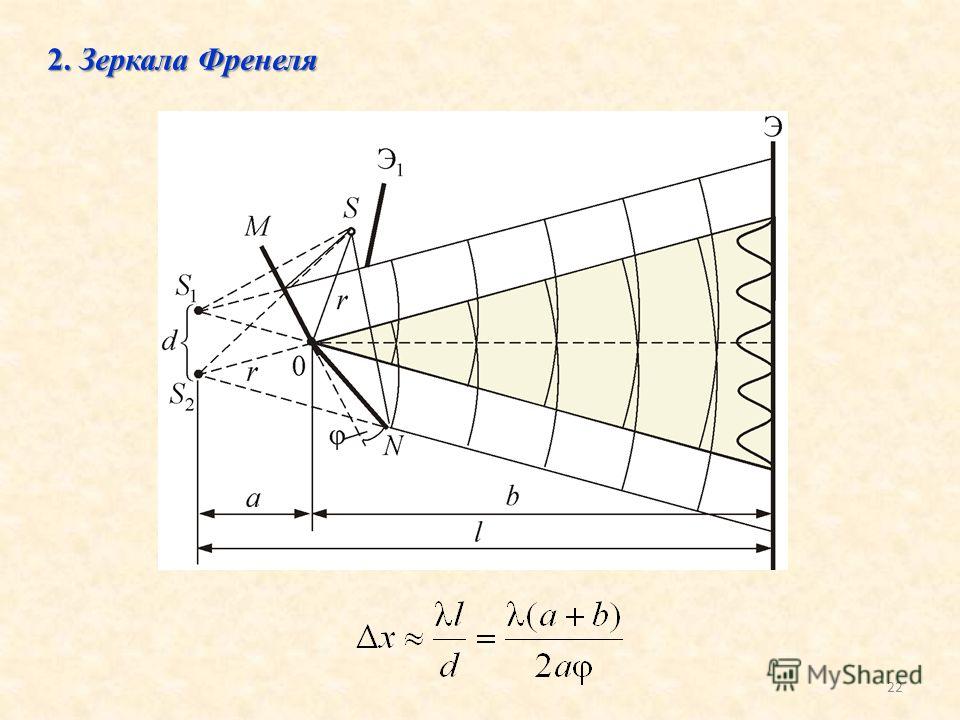
Поскольку зона F2 вредна для уровня принимаемого сигнала, высоту антенны часто выбирают таким образом, чтобы F1 была беспрепятственной траекторией, а F2 препятствовала возвышению или утолщению земли вдоль трассы.
Любые 180º отраженные сигналы вдоль зоны F2 ослабляются холмом или землей и не достигают приемной антенны, чтобы создавать помехи и подавлять основной приемный сигнал.
Радиус зоны Френеля и расстояние до Земли
Рис 2. Радиус зоны Френеля и расстояние до ЗемлиДиаметр зоны Френеля (половина диаметра — это радиус) эллиптического цилиндра можно рассчитать. Важным компонентом радиуса зоны Френеля является зазор между цилиндром зоны Френеля и поверхностью земли. Как показано на рисунке 2, показаны радиус зоны Френеля и расстояние от нижней части зоны Френеля до Земли.
При превышении 60% радиоканал считается «чистым, прямой видимости» и не несет дифракционных потерь.
Это понимание зон Френеля и их влияния помогает понять, как и почему радиопокрытие может быть предсказано с использованием математики, а теперь и компьютеров.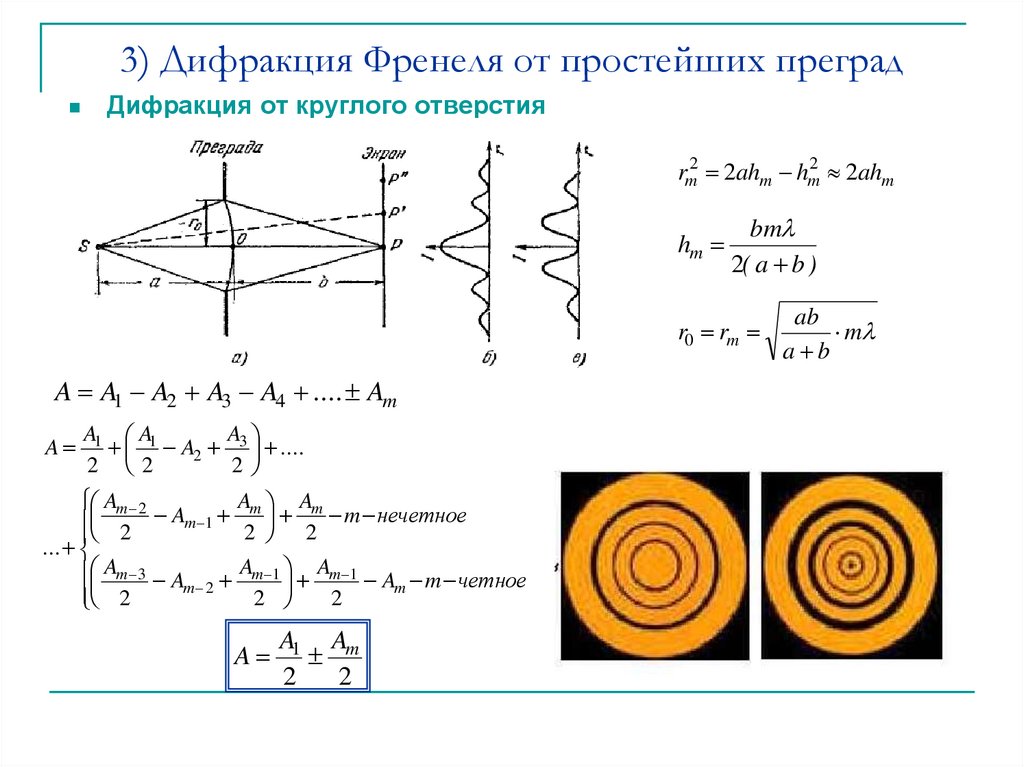
Дифракция Френеля на круглом отверстии
Предположим, что монохроматический луч света падает на экран с круглым отверстием в нем. На определенном расстоянии от отверстия на втором экране можно наблюдать дифракционную картину. Структура рисунка зависит от длины волны, и распределение фаз входящего волнового фронта, а также по диаметру, отверстия и расстояния, от дыры до экрана.
В этом так называемом дифракционном режиме ближнего поля или Френеля монохроматическая плоская или сферическая волна, которая освещает отверстие, будет создавать дифракционную картину в виде набора концентрических колец. Излучение на оптической оси будет минимальным или максимальным, когда при постоянной длине волны и диаметре отверстия расстояние от отверстия до экрана наблюдения уменьшается от бесконечности до нуля.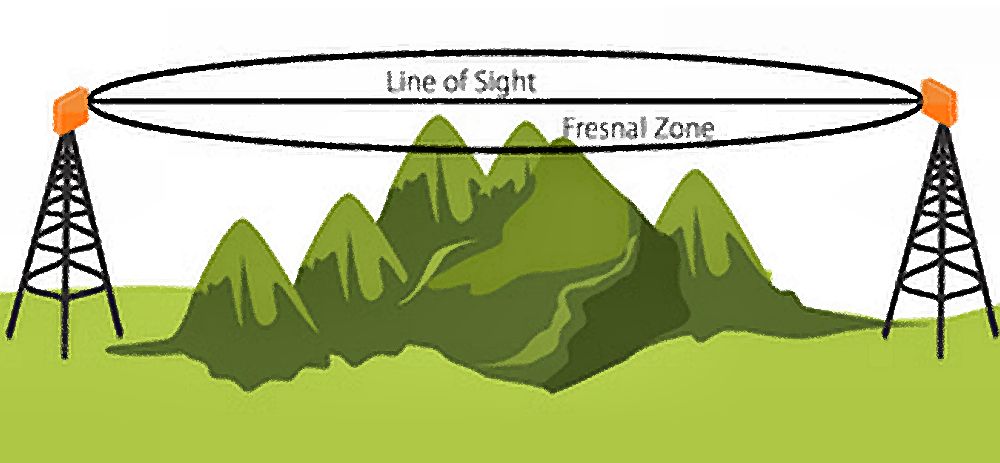
Кольца появляются после прохождения критического расстояния (также называемого длиной Рэлея):
\( z_p = A \lambda Z_p = A \lambda \)
Если \( r > 3pZ>Z_p \)— колец нет, но наблюдается плавное распределение освещенности в виде квадрата функции Бесселя, форма которого (но не диаметр пучка) остается постоянной при увеличении z. Это дальнее поле также называется дифракцией Фраунгофера.
То, появляется ли максимум или минимум на оптической оси, можно понять с помощью теории зон Френеля. Если число полу-лямбда-зон, «видимых» наблюдателем, нечетно, наблюдается максимум, четное количество зон создает минимальное излучение. Количество зон Френеля указывается номером Френеля:
\( NF=Z_pZNF=Z_pZ \)
В этих экспериментах измеряются расстояния, на которых появляются максимальная или минимальная интенсивность на оптической оси. Из этих измерений можно определить длину волны света, если известен диаметр отверстия.
Экспериментальная установка в лаборатории проста: она состоит из (HeNe) -лазера, расширителя луча или сильной линзы для создания плоской или сферической волны, экрана с отверстием и ПЗС-камеры.
Все компоненты смонтированы на оптической шине, чтобы легко регулировать и измерять расстояния.
В этом упражнении рассматриваются два входящих волновых фронта: плоская волна и сферическая волна.
Дифракция Френеля на маленьком круглом экране
Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути экран с круглым отверстием
Каковы условия для дифракции Френеля?
Дифракция Френеля возникает, когда либо расстояние от источника до препятствия, либо расстояние от препятствия до экрана сравнимо с размером препятствия. Эти сопоставимые расстояния и размеры приводят к уникальному дифракционному поведению.
Почему дифракция Френеля отличается от других видов дифракции?
Аппроксимации, которые относятся к дифракции Фраунгофера , больше не действительны. Источник света больше нельзя считать плоским волновым фронтом в апертуре, поскольку его можно больше аппроксимировать, чтобы он возник на бесконечности.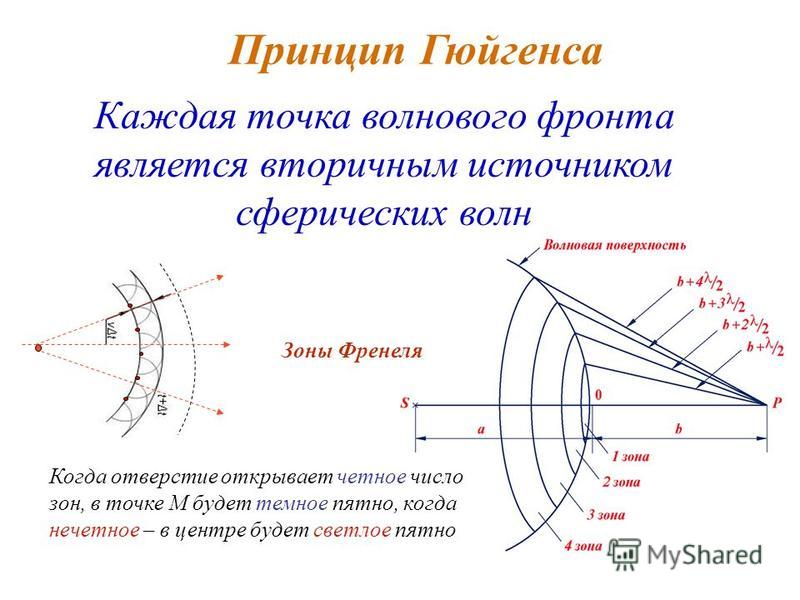
Это следует считать сферическим волновым фронтом .
- Относительная разность фаз для изогнутого волнового фронта не является постоянной
- Амплитуды отдельных световых волн (вторичных волновых фронтов) в точке наблюдения не равны, поскольку расстояния, пройденные каждым элементом или волновым фронтом, больше нельзя считать приблизительно равными. Поэтому интенсивность света на экране варьируется от точки к точке.
Как дифракция Френеля решается математически?
- Все параметры (длины, расстояния, ширины и т. д.) Должны учитываться в математической интерпретации дифракции Френеля из-за их сопоставимых размеров.
- Один можно определить дифракционную картину, вызванную дифракцией Френеля, путем определения интенсивности света в каждой точке на экране просмотра.
Принцип Гюйгенса — Френеля
Принцип Гюйгенса-Френеля гласит, что каждая точка на волновом фронте является источником вейвлетов. Эти вейвлеты распространяются в прямом направлении с той же скоростью, что и исходная волна.
Новый волновой фронт — это линия, касающаяся всех вейвлетов.
Кристиан Гюйгенс был голландским ученым, который разработал полезную технику для определения того, как и где распространяются волны. В 1678 году он предположил, что каждая точка, к которой относится световое возмущение, сама становится источником сферической волны. Сумма вторичных волн (волн, являющихся результатом возмущения) определяет форму новой волны, показывает вторичные волны, идущие вперед от их источника. Он смог придумать объяснение линейного и сферического распространения волн и вывести законы отражения и преломления (описанные в предыдущих атомах), используя этот принцип. Однако он не мог объяснить то, что обычно называют дифракционными эффектами. Эффекты дифракции — это отклонения от прямолинейного распространения, которое возникает, когда свет сталкивается с краями, экранами и отверстиями.
Прямой волновой фронт: принцип Гюйгенса, применяемый к прямому волновому фронту.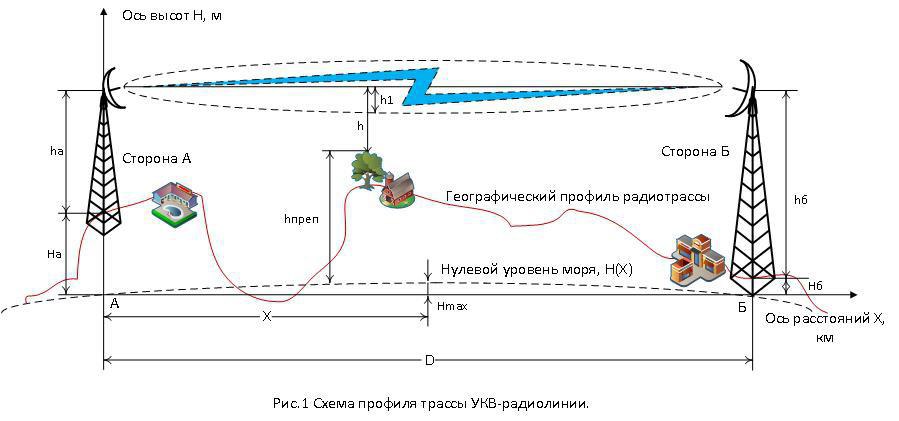
Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние:
\[ S = V*t \]
Новый волновой фронт представляет собой линию, касательную к вейвлетам.
Принцип Гюйгенса
На рисунке показан простой пример дифракционного принципа Гюйгенса. Принцип может быть показан с помощью уравнения ниже:
\( s = Vts \)
где s — расстояние, V — скорость распространения, а t — время.
Каждая точка на волновом фронте испускает волну со скоростью V. Испускаемые волны полукруглые и появляются в момент времени t. Новый волновой фронт касается вейвлетов. Этот принцип работает для всех типов волн, а не только для световых волн. Принцип полезен при описании отражения, преломления и интерференции. наглядно показывает, как принцип Гюйгенса может быть использован для объяснения отражения, и показывает, как его можно применять к преломлению.
Рис 4. Рефракционная составляющаяРефракция Гюйгенса: принцип Гюйгенса применяется к прямому волновому фронту, перемещающемуся из одной среды в другую, где его скорость меньше.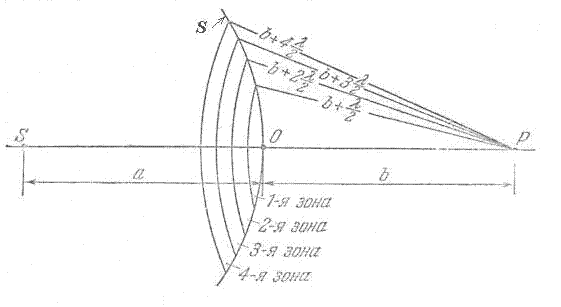
Луч изгибается в направлении перпендикуляра, поскольку вейвлеты имеют меньшую скорость во второй среде.
Отражение : принцип Гюйгенса применяется к прямому волновому фронту, ударяющемуся о зеркало. Показанные вейвлеты испускались, когда каждая точка на фронте волны ударялась о зеркало. Касательная к этим вейвлетам показывает, что новый волновой фронт был отражен под углом, равным углу падения. Направление распространения перпендикулярно фронту волны, как показано стрелками, направленными вниз.
Пятно Пуассона
Пятно Пуассона является доказательством того, что даже если вы правы, вы можете быть не правы. Узнайте, почему эта концепция физики привела к тому, что имя Симеона Пуассона прожило в позоре почти 200 лет.
В начале восемнадцатого столетия Французская академия решила провести товарищеский конкурс. Члены Академии, как и ученые всего мира, заметили, что когда свет перемещался из одной среды в другую, он изгибался.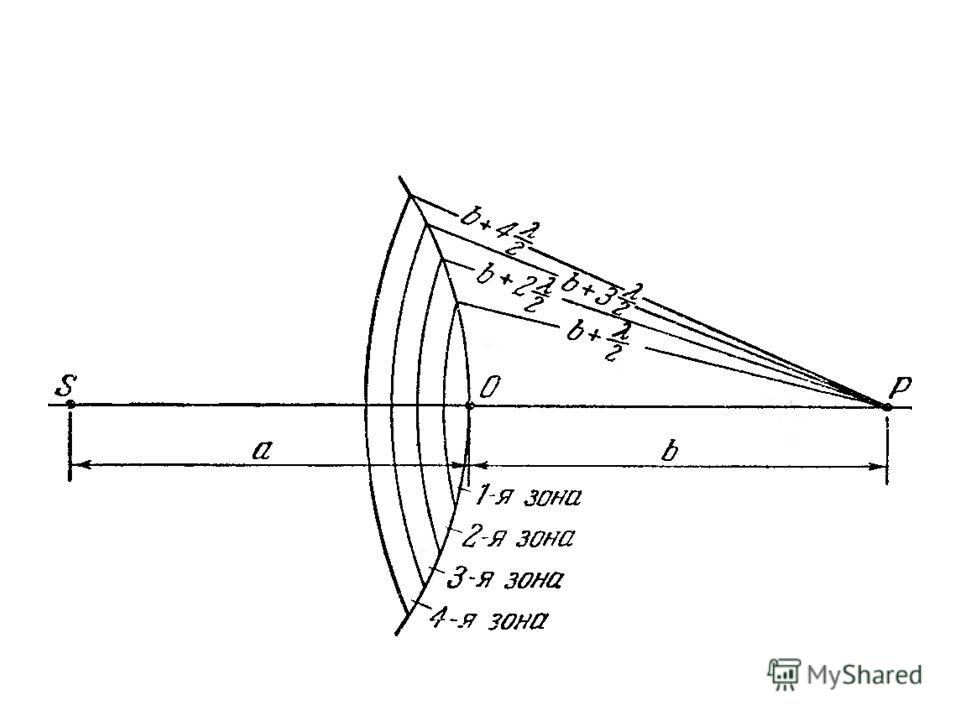
Стекло, вода, гель, все, что позволяет свету проходить через него, даст ему проход, только если он изменит свой ход. Люди могли измерить изгиб света, но были озадачены тем, что заставило это произойти. Французская академия пыталась решить эту проблему, противопоставляя умы разных ученых.
Помните Августина Френеля? Он был инженером и изучал эффекты света. Работая оттуда, он придумал новую идею; свет излучался волнами, перпендикулярными направлению, в котором он проходил. Его идея вызвала волнение, особенно у пуассоновских пэров. Они полагали, что свет путешествовал как ряд частиц, все из которых имели сложные взаимодействия друг с другом. Пуассон, Френель и другие ученые собрались вместе и провели волнующую серию дискуссий о природе света и наблюдаемых эффектах его путешествия через различные среды.
К концу дебатов Пуассон выдвинул аргумент, который, казалось, сжег теорию Френеля до основания и «засолил землю под ней». Если кого-то забрасывают предметами, его лучший шанс избежать травмы — спрятаться за более крупным предметом (по крайней мере, пока ракеты, ищущие тепло, не разрушат его для всех). Спрячьтесь за скалой, и поток гальки отскочит от скалы и пролетит мимо, не задев вас. Если, с другой стороны, человек по пояс в воде и хочет спрятаться от волны, он не будет в безопасности, приседая за скалой. Волны огибают твердые предметы.
Пуассон рассуждал, что если свет действительно был волной, то когда свет включался на совершенно сферическом объекте, световые волны могли бы огибать этот объект. Идеальная симметрия сферы означала, что все световые волны встретятся в точном центре тени позади нее, ведь там люди смогут увидеть яркое пятно света.
Это было нелепо. После выступления, как все закончили смеяться, успешные французские ученые пошли развлечься или выпить что-нибудь в близлежащем заведении. По крайней мере, один человек не присоединился к ним. Доминик Араго, один из судей, понял, что Пуассон описал идеальный эксперимент. Он нашел круглый предмет, он нашел свет, и довольно скоро он нашел это пятно. Что явилось подтверждением словам Пуассона.
Ничего не оставалось, кроме как вручить приз Френелю. Пуассон выдвинул следствие света как волны, которая была настолько нелепой, настолько маловероятной, что это не могло быть объяснено ничем другим. Френель был достаточно умен, чтобы выдвинуть теорию. Пуассон был достаточно умен, чтобы доказать, что Френель прав, и доказать, что он не прав. Несмотря на то, что Доминик Араго действительно прошел тест, крошечная точка света в центре тени сферического объекта всегда называлась Пятном Пуассона. В физике нет вечного движения, но есть постоянные насмешки.
MikroTik: куда нажать, чтобы заработало?
При всех своих достоинствах, есть у продукции компании MikroTik один минус – много разобщенной и далеко не всегда достоверной информации о ее настройке. Рекомендуем проверенный источник на русском языке, где все собрано, логично и структурировано – видеокурс «Настройка оборудования MikroTik».
Что такое зона Френеля?
Что такое зона Френеля?
Что такое зона Френеля?
19 июня 2020 г. Кай Фролик
Wireless Links
Системы беспроводной связи широко распространены в Великобритании и многих других странах. Типичные области применения включают сети мобильной связи, в которых отдельные мачты подключаются к более широкой сети через каналы связи «точка-точка».
Рис. 1: Антенны СВЧ-связи – Испания
Помехи
Связь между двумя антеннами лучше всего работает при наличии свободного, беспрепятственного [1] пути между каждым концом. Структуры, расположенные между передатчиками и приемниками, могут исказить или заблокировать передаваемый сигнал.
Потенциальные помехи от местности, растительности, зданий, ветряных электростанций и множества других препятствий необходимо учитывать при проектировании и обслуживании систем беспроводной связи.
В этой статье основное внимание уделяется эффекту блокировки сигнала, который в данном контексте официально известен как «дифракция». Другие механизмы помех включают отражение передаваемого сигнала и проблемы с излучением от электронного оборудования. Эти вопросы здесь не обсуждаются.
Обеспечение безопасности
Прямая линия между передатчиком и приемником известна как линия прицеливания. Если конструкция размещена таким образом, что нарушает линию визирования, могут возникнуть высокие дифракционные потери. Препятствие, которое находится близко к линии визирования, но не нарушает ее, может вызвать меньшие потери. Вопрос в том, насколько близко слишком близко?
Ответ зависит от:
- Типа канала (длина, частота, функция и т. д.).
- Препятствие (местность и ветряные турбины могут трактоваться по-разному).
Однако в большинстве случаев защита достигается за счет учета зон Френеля.
Зоны Френеля
Зона Френеля представляет собой сигарообразную область в трех измерениях с центром на линии прицеливания. Рисунок ниже иллюстрирует это.
Рисунок 2: Иллюстрация зоны Френеля.
Видно, что зона Френеля самая широкая в середине и самая узкая на концах. Радиус зоны Френеля вместе с формулой его расчета показан на рисунке ниже.
Рисунок 3: Радиус зоны Френеля.
Радиус зависит от:
- Длина ссылки.
- Расстояние по пути ссылки.
- Частота ссылки.
- Номер зоны Френеля «n» — это число больше нуля.
Номер зоны Френеля ‘n’
Обычно используемые на практике значения n включают 0,6, 1, 2 и 8. Последняя может также называться первой, второй или восьмой зоной Френеля. Зона Френеля 0,6 часто применяется при проектировании двухточечных телекоммуникационных линий над землей и растительностью, а вторая зона Френеля обычно используется для защиты телекоммуникационных линий от возможных помех от ветряных турбин.
В любой точке пути связи радиус зоны Френеля пропорционален квадратному корню из n. Это означает, что если вы не знаете радиус одной зоны Френеля, вы можете относительно легко вычислить радиус другой. Радиус восьмой зоны Френеля в два раза больше радиуса второй зоны Френеля, потому что квадратный корень из восьми, разделенный на два (четыре), равен двум.
Почему это важно?
Структуры, нарушающие зоны Френеля, могут негативно повлиять на производительность канала. Это может привести к возражениям на этапе предварительного планирования разработки и требований по смягчению последствий.
Понимание размеров зон Френеля дает разработчикам хорошее представление о том, вероятны ли проблемы с помехами. На приведенном ниже рисунке показана эта концепция с использованием двух ветряных турбин с одинаковыми размерами под линией связи, показанной на рисунке 1. Этот принцип применим и к другим конструкциям, таким как здания.
Рисунок 4: Важность зоны Френеля.
Сноска
[1] Существуют случаи, когда система может приспособиться к пути с препятствиями. Обычно это в большей степени относится к системам УВЧ, чем к высокочастотным каналам связи.
Ссылки
- Bacon (2002): Предлагаемый метод для установления зоны отчуждения вокруг наземной фиксированной радиолинии, за пределами которой ветряная турбина вызовет незначительное ухудшение характеристик радиолинии.
- Объединенная радиокомпания (2009 г.): Расчет безопасных зон ветряных турбин для систем телеметрии JRC UHF (460 МГц), когда размеры и расположение турбин точно известны.
- Manning (1999): Руководство по проектированию микроволновой радиопередачи, Artech House.
ЗОНА ФРЕНЕЛЯ И ПОТЕРИ | антенны и аксессуары
Информация и советы
Зона Френеля Помехи –
Зона Френеля представляет собой круглую область, перпендикулярную линии прямой видимости и центрированную на ней. В теории радиоволн, если 80% первой зоны Френеля свободны от препятствий, потери при распространении волны эквивалентны потерям в свободном пространстве.
Уравнение для расчета первой зоны Френеля использует расстояния до точки на линии прямой видимости с возможным препятствием на пути:
где FZ = 72,1 x квадратный корень (D1 x D2) / (f x Rm )
f = частота в ГГц
Rm = расстояние между антеннами в милях
D1 = первое расстояние до препятствия в милях
D2 = второе расстояние до препятствия в милях = Rm – D1 FZ = радиус зоны Френеля в футах от прямой линия прямой видимости
Мы рассчитаем радиус зоны Френеля позже в этом обсуждении. В домашней и офисной сети в здании расчет зоны Френеля обычно не требуется из-за всех соображений прохождения через стену/потолок/пол для любого пути РЧ-сигнала. Но на внешних путях радиочастотного сигнала (линках) расчеты зоны Френеля могут быть очень важными на расстоянии в четверть мили и больше.
Мой опыт работы с высокими лоблоловыми соснами является хорошим тому примером. Беспроводная связь была спроектирована и установлена для двух медицинских учреждений (двухэтажных зданий) в Уилмингтоне, Северная Каролина, которые находились в 0,5 и 0,75 мили от одиннадцатиэтажной больницы. Прямая видимость между двумя медучреждениями отсутствовала, но была из обоих корпусов на крышу больницы. После получения надлежащих разрешений была установлена линия радиочастотного сигнала от каждой антенны здания к антеннам, установленным на крыше больницы. Несмотря на то, что от одного здания до крыши больницы был хороший визуальный путь, некоторые очень высокие, очень тощие сосны нарушали радиус зоны Френеля, который был рассчитан для этой связи. Это было всего лишь несколько ветвей с широко расставленными дольчатыми иголками, но нам пришлось залезть на вершину деревьев, чтобы получить удовлетворительное соотношение сигнал/шум для надежной связи. Удивительно, сколько микроволновой энергии (2,4 ГГц) эти длинные иглы поглощают, отражают, отклоняют и/или рассеивают.
В более раннем примере анализа беспроводной связи с использованием расстояния между антеннами в 3 км и сужением посередине пути (D1 = D2) зона Френеля рассчитывается следующим образом с использованием общих коэффициентов преобразования для стандартных измерений США.
Преобразование 3 км в мили путем деления на коэффициент преобразования 1,6 километра на милю, что дает при частоте f = 2,4 ГГц:
Rm = 3 км / 1,6 км/миля = 1,88 мили FZ = 31,9 фута
Радиус зоны Френеля 80% для эквивалента потерь в свободном пространстве будет получен путем умножения FZ на 0,8, что дает радиус 25,5 футов. Таким образом, концентрический цилиндр свободного пути вокруг линии прямой видимости вашей системы для проанализированных расстояний и частоты будет иметь диаметр 51 фут в середине радиоканала.
Системный рабочий запас (SOM)
SOM (Системный рабочий запас), также известный как запас на затухание, представляет собой разницу уровня сигнала приемника в дБм минус чувствительность приемника в дБм. Это мера запаса безопасности в радиолинии. Более высокий SOM означает более надежное воздушное соединение. Мы рекомендуем минимум 10 дБ, но лучше всего 20 дБ или больше.
SOM – это разница между сигналом, который фактически принимает радиостанция, и тем, что необходимо для хорошего восстановления данных (т. е. чувствительностью приемника). Используя мощность передаваемого и принимаемого радиочастотного сигнала, потери в кабеле, усиление антенны и потери в свободном пространстве, рассмотренные в этом уроке, мы можем рассчитать SOM. Таким образом, у нас есть метод проектирования и анализа линий радиочастотных сигналов, используемых в беспроводных сетях.
Уровень сигнала Rx = мощность Tx — потери в кабеле Tx + усиление антенны Tx — потери в свободном пространстве + усиление антенны Rx — потери в кабеле Rx
SOM = Уровень сигнала Rx — Чувствительность Rx
Мы можем изменить выражение SOM, чтобы учесть потери затухания из-за передачи через стены и т. д. в реальном здании, в котором будет установлена домашняя или офисная сеть. Это просто добавление дополнительных членов потерь в уравнение SOM. Но сначала нам придется рассмотреть уровень потерь через различные материалы. Потери затухания сигнала для передачи на частоте 2,4 ГГц через следующие структуры могут быть включены в уравнение уровня сигнала Rx для каждого прохода на прямолинейном пути прохождения сигнала (на линии прямой видимости). Значения потерь в дБ будут вычтены из мощности передаваемого сигнала, чтобы отразить потери при прохождении через материальные структуры.
Вам интересно, почему у вашего дома плохой Wi-Fi или даже часть дома? Это может быть связано с материалом, использованным для стены, или другими физическими барьерами, которые блокируют или ослабляют сигналы Wi-Fi.
Structure Loss dB in 2. 4 GHz
