Скорость распространения волны – формулы для различных сред
4.6
Средняя оценка: 4.6
Всего получено оценок: 94.
4.6
Средняя оценка: 4.6
Всего получено оценок: 94.
Волны любой природы распространяются в пространстве не мгновенно, следовательно, это распространение имеет конечную скорость. Поговорим об этой скорости более подробно.
Распространение колебаний
Далеко не любые колебательные процессы приводят к распространению волн. Колебательная система представляет собой лишь источник колебаний. Для того, чтобы эти колебания могли распространяться, необходимо также существование упругой среды без разрывов, связанной с этим источником. Природа упругих сил может быть различна в различных средах, однако, их наличие обязательно, без этого второго условия, распространение волн в среде невозможно.
Рис. 1. Распространение волн на поверхности воды.Каждая точка среды, через которую проходит волна, в простейшем случае начинает колебаться по гармоническому закону (в более сложных случаях колебания точек можно представить в виде суммы таких функций с различными параметрами):
$$x=Asin(\omega t+\varphi)$$
Однако, уравнение колебания соседних точек будет немного различаться. Во-первых, чем дальше точка расположена от источника колебаний, тем больше потерь происходит по пути, и тем меньше амплитуда колебаний (параметр $A$ в представленной формуле). Однако, когда потери невелики, заметное изменение амплитуды происходит лишь на больших расстояниях.
Во-первых, чем дальше точка расположена от источника колебаний, тем больше потерь происходит по пути, и тем меньше амплитуда колебаний (параметр $A$ в представленной формуле). Однако, когда потери невелики, заметное изменение амплитуды происходит лишь на больших расстояниях.
Гораздо важнее другое отличие – отличие фазы колебаний (параметр $\varphi$ ) для различных точек. По мере удаления от источника колебаний, фаза плавно изменяется, постоянно увеличиваясь. Поскольку синус – круговая функция, то рано или поздно разность фаз между двумя точками становится равной ${2\pi}$, а значит, эти две точки колеблются одинаково – синфазно. Для более далеких точек фаза увеличивается дальше, и для точек, разность фаз которых составит ${4\pi}$ колебания опять будут синфазны.
Таким образом, по мере удаления от источника колебаний в среде будет ряд точек, колеблющихся в одной фазе. Минимальное расстояние между двумя такими точками называется длиной волны. Она обозначается греческой буквой $\lambda$ (лямбда).
Скорость распространение волн
Плавное изменение фазы колебаний по мере удаления от источника колебаний можно представить в виде распространения этих колебаний, и определить скорость этого распространения. Разность фаз между ближайшими точками, колеблющимися синфазно, составляет $2\pi$, это один период колебаний. А значит, волна проходит расстояние между этими точками за время одного периода $T$. Зная длину волны – можно вычислить скорость ее распространения:
$$v = {\lambda \over T}$$
Иногда известен не период, а частота колебаний $\nu$. В этом случае формула скорости распространения волны примет вид:
$$v = {\lambda \nu}$$
Если среда первоначально была спокойна, то начало возмущений (иногда его называют «фронт волны») будет удаляться от источника колебаний как раз с указанной скоростью.
Что мы узнали?
Колебания среды распространяются не мгновенно, а с конечной скоростью. Каждая точка среды колеблется с некоторой фазой, которая изменяется, по мере удаления от источника колебаний. Минимальная длина между точками, колеблющимися синфазно, называется длиной волны, а отношение длины волны к периоду колебаний – скорости распространения волн.
Минимальная длина между точками, колеблющимися синфазно, называется длиной волны, а отношение длины волны к периоду колебаний – скорости распространения волн.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 94.
А какая ваша оценка?
Формула скорости волны в физике
Формула скорости волны в физикеОпределение
Фронт волны (волновая поверхность) — это геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
\[Ф_s=\omega t-kx+\varphi \ \left(1\right),\]
где${\ Ф}_s$ — фаза волны; $k=\frac{2\pi }{\lambda }$ — волновое число; $\lambda $ — длина волны; $\omega $ — циклическая частота; $\varphi $ — начальная фаза.
\[x=\frac{\omega t+\varphi -Ф_s}{k}\left(2\right).\]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
\[\frac{dx}{dt}=\frac{\omega }{k}=\frac{\lambda }{T}=v\ \left(3\right),\]
где $T$ — период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны — это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
\[v=\sqrt{\frac{K}{\rho }}\left(4\right),\]
где $K$ — модуль объемной упругости вещества; $\rho =const$ — плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
\[v=\sqrt{\frac{\gamma p}{\rho }}\left(5\right),\]
где $\gamma $ — показатель адиабаты; $p$ — давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
\[v=\sqrt{\frac{E}{\rho }}\left(6\right),\]
где $E$ — модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах.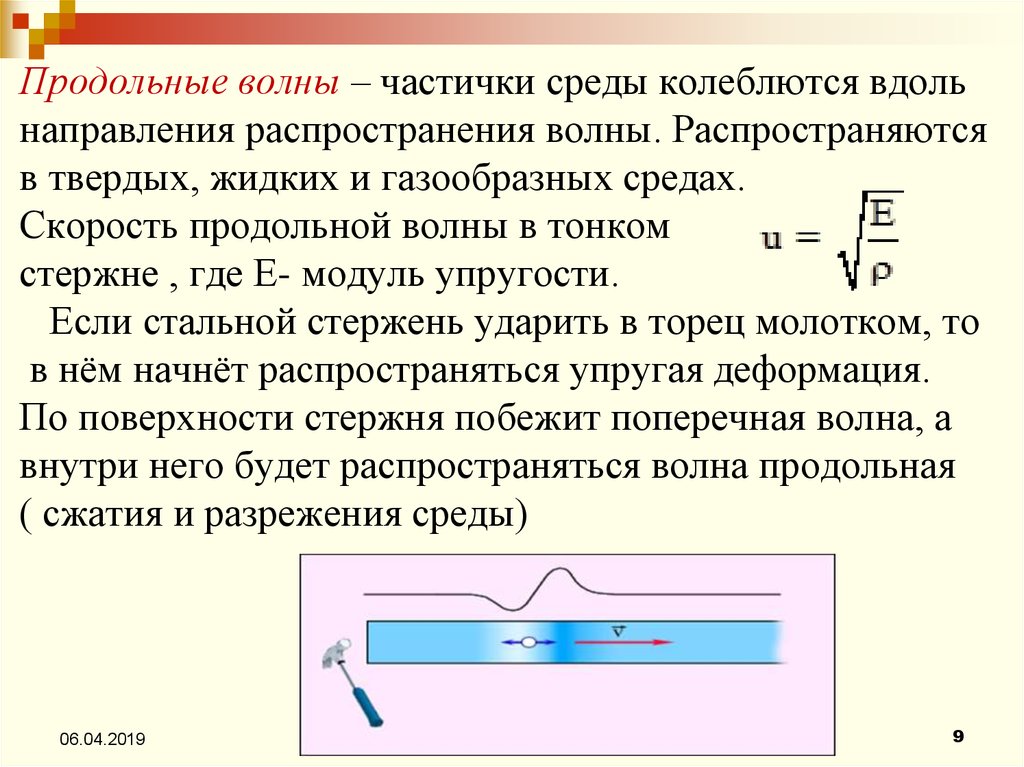 Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
\[v=\sqrt{\frac{G}{\rho }\left(7\right),}\]
где $G$ — модуль сдвига среды; $\rho $ — плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
\[u=v-\frac{dv}{d\lambda }\left(8\right).\]
Если дисперсия отсутствует, то $\frac{dv}{d\lambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
\[v=\frac{\lambda }{T}\ \left(1. 1\right).\]
1\right).\]
Найдем период колебаний как время одного полного колебания:
\[T=\frac{t}{N}\ \left(1.2\right).\]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
\[v=\frac{\lambda N}{t}.\]
Вычислим искомую скорость:
\[v=\frac{1\cdot 100}{20}=5\left(\frac{м}{с}\right).\]
Ответ. $v=5\frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $\xi \left(x,t\right)=2{\cos \left[\omega \left(t-\frac{x}{v}\right)\right]\ }\left(м\right).$ Частота колебаний $\nu =450$Гц, длина волны $\lambda =0,8\ $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
\[v=\frac{\lambda }{T}=\lambda \nu \ \left(2. 1\right),\]
1\right),\]
где период — величина обратная частоте колебаний:
\[T=\frac{1}{\nu }\left(2.2\right).\]
Вычислим фазовую скорость:
\[v=450\cdot 0,8=360\ \left(\frac{м}{с}\right).\]
Скорость колебания частиц равна:
\[\frac{d\xi }{dt}=\frac{d}{dt}\left(2{cos \left[\omega \left(t-\frac{x}{v}\right)\right]\ }\right)=-2\omega {\sin \left[\omega \left(t-\frac{x}{v}\right)\right]\left(2.3\right).\ }\]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
\[{\left(\frac{d\xi }{dt}\right)}_{max}=\left|2\omega \right|\left(2.4\right).\]
Циклическую частоту найдем как:
\[\omega =2\pi \nu ,\]
тогда:
\[{\left(\frac{d\xi }{dt}\right)}_{max}=\left|2\cdot 2\pi \nu \right|=4\pi \nu .\]
Вычислим максимальную скорость колебаний частиц:
\[{\left(\frac{d\xi }{dt}\right)}_{max}=4\pi \cdot 450=5,65\cdot {10}^3\left(\frac{м}{с}\right). 3\frac{м}{с}$
3\frac{м}{с}$
Читать дальше: формула скорости свободного падения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
13.2 Свойства волны: скорость, амплитуда, частота и период
Цели обучения Волновые переменные Связь между частотой волны, периодом, длиной волны и скоростьюРешение волновых задачПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее: период, длина волны и скорость волны
| длина волны | скорость волны |
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны. Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.
Советы по достижению успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , потому что возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0055 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны. Важно отметить, что это движение волны на самом деле является 9-м.0055 возмущение движение вправо, а не сама вода; в противном случае птица двигалась бы вправо. Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.
Рисунок 13.7 Волна имеет длину волны λ , что является расстоянием между соседними идентичными частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v в .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Это видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Щелкните для просмотра содержимого
Советы для достижения успеха
Гребень волны иногда также называют вершиной .
Проверка захвата
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1 м, какова высота волны с вашего местоположения?
- 1м
- 2 м
- 4 м
- 8м
Связь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по существу, количество секунд на волну, соотношение между частотой и периодом составляет
13. 1f=1Tf=1T
1f=1Tf=1T
или
13.2T=1f,T=1f,
так же, как и в случае гармонического движения объекта. Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
13.3vw=λTvw=λT
или
13.4vw=fλ.vw=fλ.
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок 13.8. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Лаборатория Snap
Волны в чаше
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Материалы
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из миски и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, опуская пробку с разной высоты и записывая полученные длины волн и периоды.

- Интерпретируйте свои результаты.
Проверка захвата
Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
- Нет, влияет только на амплитуду.
- Да, длина волны затронута.
Виртуальная физика
Волна на струне
Рисунок 13.10 Щелкните здесь для моделирования волны на струне.
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, демпфирование или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.

- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: чайка в океане
Рассчитайте скорость океанской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м и время, за которое чайка качается вверх и вниз составляет 5,00 с.
СТРАТЕГИЯ
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем используйте vw=λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
13,5vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с.
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны. Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Расчет периода и скорости волны игрушечной пружины
Женщина на рис. 13.3 каждую секунду создает две волны, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (б) Если каждая волна проходит 0,9метров после одного полного волнового цикла, какова скорость распространения волны?
СТРАТЕГИЯ ДЛЯ (A)
Чтобы найти период, мы решаем для T=1fT=1f, учитывая значение частоты (f=2s−1).(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
13,6T=12 с-1=0,5 с.T=12 с-1=0,5 с.
СТРАТЕГИЯ ДЛЯ (B)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, значения длины волны (λ = 0,9м)(λ=0,9 м), а также частота. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с−1)(0,9 м) = 1,8 м/с.vw=fλ=(2 с-1 )(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
Частота волны 10 Гц. Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Упражнение 7
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
Упражнение 8
Что понимают под длиной волны?
- Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.

- Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, перпендикулярное направлению распространения.
Упражнение 9
Как можно математически выразить частоту волны через период волны?
- f=1T
- ф=(1Т)2
- ф=Т
- ф=(Т)2
Упражнение 10
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
- Печать
- Поделиться
Скорость волны
Волна — это возмущение, которое движется вдоль среды от одного конца к другому. Если наблюдать за океанской волной, движущейся вдоль среды (воды океана), можно заметить, что гребень волны перемещается из одного места в другое за заданный интервал времени. Гребень наблюдается до покрытие расстояние. Скорость объекта относится к тому, насколько быстро объект движется, и обычно выражается как расстояние, пройденное за время движения. В случае волны скорость — это расстояние, пройденное данной точкой волны (например, гребнем) за заданный интервал времени. В виде уравнения
Если наблюдать за океанской волной, движущейся вдоль среды (воды океана), можно заметить, что гребень волны перемещается из одного места в другое за заданный интервал времени. Гребень наблюдается до покрытие расстояние. Скорость объекта относится к тому, насколько быстро объект движется, и обычно выражается как расстояние, пройденное за время движения. В случае волны скорость — это расстояние, пройденное данной точкой волны (например, гребнем) за заданный интервал времени. В виде уравнения
Если гребень океанской волны проходит расстояние 20 метров за 10 секунд, то скорость океанской волны равна 2,0 м/с. С другой стороны, если гребень океанской волны проходит расстояние 25 метров за 10 секунд (столько же времени), то скорость этой океанской волны равна 2,5 м/с. Более быстрая волна проходит большее расстояние за то же время.
Иногда волна сталкивается с концом среды и присутствием другой среды. Например, волна, введенная человеком в один конец обтекателя, будет проходить через обтекатель и в конечном итоге достигнет конца обтекателя и присутствия руки второго человека. Одно поведение, которому подвергаются волны в конце среды, — это отражение. Волна отразится или отскочит от руки человека. Когда волна претерпевает отражение, она остается в среде и просто меняет направление своего движения. В случае гибкой волны можно увидеть, как возмущение возвращается к исходному концу. Слинки-волна, доходящая до конца слинки и обратно, имеет удвоил расстояние . То есть, отражаясь обратно в исходное положение, волна прошла расстояние, равное удвоенной длине обтекателя.
Одно поведение, которому подвергаются волны в конце среды, — это отражение. Волна отразится или отскочит от руки человека. Когда волна претерпевает отражение, она остается в среде и просто меняет направление своего движения. В случае гибкой волны можно увидеть, как возмущение возвращается к исходному концу. Слинки-волна, доходящая до конца слинки и обратно, имеет удвоил расстояние . То есть, отражаясь обратно в исходное положение, волна прошла расстояние, равное удвоенной длине обтекателя.
Явления отражения обычно наблюдаются у звуковых волн. Когда вы издаете крик в каньоне, вы часто слышите эхо этого крика. Звуковая волна проходит через среду (в данном случае воздух), отражается от стены каньона и возвращается к своему источнику (вам). В результате вы слышите эхо (отраженную звуковую волну) вашего крика. Классическая задача по физике звучит так:
Ной стоит в 170 метрах от крутой стены каньона. Он кричит и через секунду слышит эхо своего голоса.Какова скорость волны?
В этом примере звуковая волна проходит 340 метров за 1 секунду, поэтому скорость волны составляет 340 м/с. Помните, что при отражении волна удваивает свое расстояние . Другими словами, расстояние, пройденное звуковой волной за 1 секунду, эквивалентно 170 метрам до стены каньона плюс 170 метрам назад от стены каньона.
Переменные, влияющие на скорость волны
Какие переменные влияют на скорость, с которой волна распространяется в среде? Влияет ли частота или длина волны на ее скорость? Влияет ли амплитуда волны на ее скорость? Или другие переменные, такие как массовая плотность среды или упругость среды, ответственны за влияние на скорость волны? Эти вопросы часто исследуются в форме лаборатории в классе физики.
Предположим, генератор волн используется для создания нескольких волн в веревке с измеримым натяжением. Определяются длина волны, частота и скорость. Затем частота вибрации генератора изменяется, чтобы исследовать влияние частоты на скорость волны. Наконец, натяжение веревки изменяется, чтобы исследовать влияние натяжения на скорость волны. Образцы данных для эксперимента показаны ниже.
Наконец, натяжение веревки изменяется, чтобы исследовать влияние натяжения на скорость волны. Образцы данных для эксперимента показаны ниже.
(Н) | (Гц) | (м) | (м/с) | |
 03 03 | ||||
В первых пяти испытаниях натяжение веревки поддерживалось постоянным, а частота систематически изменялась. Данные в строках 1-5 таблицы выше демонстрируют, что изменение частоты волны не влияет на скорость волны. Скорость оставалась почти постоянной и составляла примерно 16,2 м/с. Небольшие вариации значений скорости были результатом экспериментальной ошибки, а не демонстрации какого-то физического закона. Данные убедительно показывают, что частота волны не влияет на скорость волны. Увеличение частоты волны вызывало уменьшение длины волны, в то время как скорость волны оставалась постоянной.
Данные в строках 1-5 таблицы выше демонстрируют, что изменение частоты волны не влияет на скорость волны. Скорость оставалась почти постоянной и составляла примерно 16,2 м/с. Небольшие вариации значений скорости были результатом экспериментальной ошибки, а не демонстрации какого-то физического закона. Данные убедительно показывают, что частота волны не влияет на скорость волны. Увеличение частоты волны вызывало уменьшение длины волны, в то время как скорость волны оставалась постоянной.
Последние три испытания включали одну и ту же процедуру с разным натяжением веревки. Обратите внимание, что скорость волн в рядах 6-8 заметно отличается от скорости волны в рядах 1-5. Очевидной причиной этой разницы является изменение натяжения веревки. Скорость волн была значительно выше при более высоких напряжениях. Волны проходят через более натянутые канаты на более высоких скоростях. Таким образом, хотя частота не влияла на скорость волны, влияло натяжение среды (веревки). На самом деле скорость волны не зависит от свойств самой волны (причинно от них не зависит). Скорее скорость волны зависит от свойств среды, таких как натяжение веревки.
Скорее скорость волны зависит от свойств среды, таких как натяжение веревки.
Одной из тем этого раздела было то, что «волна — это возмущение, движущееся в среде». В этой фразе есть два различных объекта — «волна» и «среда». Среда может быть водой, воздухом или слинки. Эти среды различаются своими свойствами — материалом, из которого они сделаны, и физическими свойствами этого материала, такими как плотность, температура, упругость и т. д. Такие физические свойства описывают сам материал, а не волну. С другой стороны, волны отличаются друг от друга своими свойствами — амплитудой, длиной волны, частотой и т. д. Эти свойства описывают волну, а не материал, через который волна движется. Урок описанного выше лабораторного занятия состоит в том, что скорость волны зависит от среды, в которой движется волна. Только изменение свойств среды вызовет изменение скорости.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Slinky Lab Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Slinky Lab предоставляет учащимся простую среду для изучения движения волны в среде и факторов, влияющих на ее скорость.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Slinky Lab Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Slinky Lab предоставляет учащимся простую среду для изучения движения волны в среде и факторов, влияющих на ее скорость.
Посетите: Slinky Lab Interactive
1. Воспитатель прикрепляет слинки к стене и начинает подавать импульсы разной амплитуды. Какой из двух импульсов (A или B) ниже пройдет от руки до стены за наименьшее количество времени? Обосновать ответ.
2. Затем учитель начинает вводить импульсы с другой длиной волны. Какой из двух импульсов (C или D) пройдет от руки к стене за наименьшее время? Обосновать ответ.
3. Время, необходимое звуковым волнам (v = 340 м/с) для прохождения от камертона до точки A, равно ____ .
а. 0,020 секунды
б. 0,059 секунды
в. 0,59 секунды
д. 2,9второй
4. Две волны проходят через один и тот же сосуд с газообразным азотом. Волна А имеет длину волны 1,5 м. Волна B имеет длину волны 4,5 м. Скорость волны B должна быть ________ скорости волны A.
а. одна девятая
б. одна треть
в. то же, что
д. в три раза больше, чем
5. Камера с автоматической фокусировкой способна фокусироваться на объектах с помощью ультразвуковой звуковой волны. Камера посылает звуковые волны, которые отражаются от удаленных объектов и возвращаются в камеру. Датчик определяет время, необходимое для возвращения волн, а затем определяет расстояние, на котором объект находится от камеры. Затем объектив камеры фокусируется на этом расстоянии. Вот это умная камера! В следующей жизни вам, возможно, придется стать фотоаппаратом; так что попробуйте эту задачу для практики:
Датчик определяет время, необходимое для возвращения волн, а затем определяет расстояние, на котором объект находится от камеры. Затем объектив камеры фокусируется на этом расстоянии. Вот это умная камера! В следующей жизни вам, возможно, придется стать фотоаппаратом; так что попробуйте эту задачу для практики:
Если звуковая волна (скорость = 340 м/с) возвращается в камеру через 0,150 секунды после выхода из камеры, то на каком расстоянии находится объект?
6. ИСТИНА или ЛОЖЬ :
Удвоение частоты источника волн удваивает скорость волн.
7. Во время прогулки по каньону Формула Ноя издает крик. Эхо (отражение крика от ближайшей стены каньона) слышно через 0,82 секунды после крика. Скорость звуковой волны в воздухе 342 м/с. Вычислите расстояние от Ноя до ближайшей стены каньона.
8.





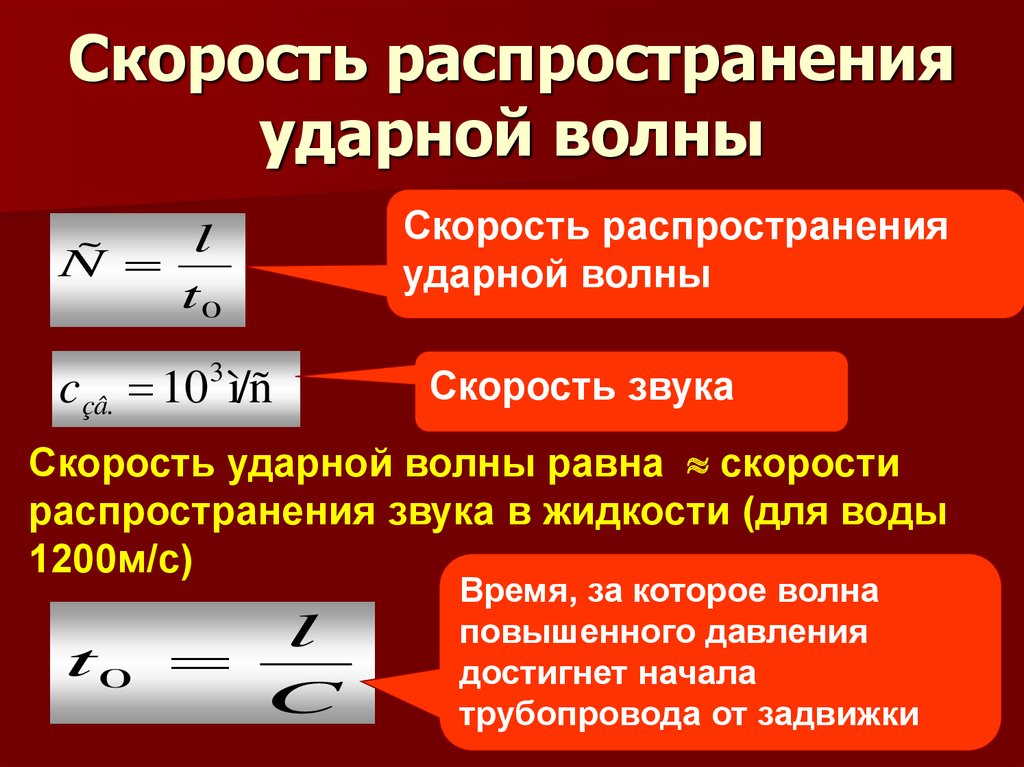 Какова скорость волны?
Какова скорость волны?