3. Принцип действия полевого транзистора. Вах полевого транзистора
В отличии от биполярных транзисторов, униполярные транзисторы относятся к классу полевых элементов, принцип действия которых основан на использовании носителей одного знака. Управление током производится за счет изменения проводимости канала, через который протекает ток, под действием электрического поля.
Общие свойства: 1) Высокая технологичность изготовления, 2) Хорошая воспроизводимость параметров, 3) Большая плотность упаковки 4) сравнительно невысокая стоимость.
Главная особенность высокое входное сопротивление.
У
 стройство
полевого транзистора.
стройство
полевого транзистора.
Полевой транзистор — это полупроводниковый прибор, усилительные свойства которого обусловлены потоком основных носителей, протекающим через проводящий канал и управляемый электрическим полем. В отличие от биполярных работа полевых транзисторов основана на использовании основных носителей заряда в полупроводнике.
По конструктивному исполнению и технологии изготовления полевые транзисторы можно разделить на две группы: полевые транзисторы с управляющим р- п — переходом и полевые транзисторы с изолированным затвором.
Полевой транзистор с управляющим р-п- переходом — это полевой транзистор, затвор которого отделен в электрическом отношении от канала р-п — переходом, смещенным в обратном направлении. Электрод , из которого в канал входят носители заряда, называют истоком; электрод, через который из канала уходят носители заряда, — стоком; электрод, служащий для регулирования поперечного сечения канала, — затвором. При подключении к истоку отрицательного (для п-канала), а к стоку положительного напряжения (рис. 1 ) в канале возникает электрический ток, создаваемый движением электронов от истока к стоку, т.е. основными носителями заряда. В этом заключается существенное отличие полевого транзистора от биполярного. Движение носителей заряда вдоль электронно-дырочного перехода (а не через переходы, как в биполярном транзисторе) является второй характерной особенностью полевого транзистора.
Электрическое поле, создаваемое между затвором и каналом, изменяет плотность носителей заряда в канале, т.е. величину протекающего тока. Так как управление происходит через обратно смещенный р-п-переход, сопротивление между управляющим электродом и каналом велико, а потребляемая мощность от источника сигнала в цепи затвора ничтожно мала. Поэтому полевой транзистор может обеспечить усиление электромагнитных колебаний как по мощности, так и по току и напряжению.
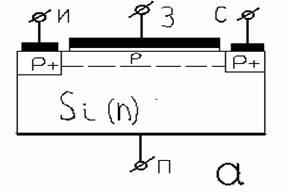
 Рис. 2. Структура полевого транзистора
с изолированным затвором: а — с
индуцированным каналом ; б — со встроенным
каналом.
Рис. 2. Структура полевого транзистора
с изолированным затвором: а — с
индуцированным каналом ; б — со встроенным
каналом.
Полевой транзистор с изолированным затвором — это полевой транзистор, затвор которого отделен в электрическом отношении от канала слоем диэлектрика. Полевой транзистор с изолированным затвором состоит из пластины полупроводника (подложки) с относительно высоким удельным сопротивлением, в которой созданы две области с противоположным типом электропроводности (рис. 2 ). На эти области нанесены металлические электроды — исток и сток. Поверхность полупроводника между истоком и стоком покрыта тонким слоем диэлектрика (обычно слоем оксида кремния). На слой диэлектрика нанесен металлический электрод — затвор. Получается структура, состоящая из металла, диэлектрика и полупроводника. Поэтому полевые транзисторы с изолированным затвором часто называют МДП- транзисторами или МОП- транзисторами (металл — оксид- полупроводник).
Существуют две разновидности МДП-транзисторов с индуцированным и со встроенным каналами.
В МДП-транзисторах с индуцированным каналом проводящий канал между сильнолегированными областями истока и стока и, следовательно, заметный ток стока появляются только при определенной полярности и при определенном значении напряжения на затворе относительно истока (отрицательного при р-канале и положительного при п-канале). Это напряжение называют пороговым (UЗИ.пор ). Так как появление и рост проводимости индуцированного канала связаны с обогащением его основными носителями заряда, то считают, что канал работает в режиме обогащения.
В МДП — транзисторах со встроенным каналом проводящий канал, изготавливается технологическим путем, образуется при напряжении на затворе равном нулю. Током стока можно управлять, изменяя значение и полярность напряжения между затвором и истоком. При некотором положительном напряжении затвор — исток транзистора с р — каналом или отрицательном напряжении транзистора с n -каналом ток в цепи стока прекращается. Это напряжение называют напряжением отсечки (UЗИ.отс ). МДП — транзистор со встроенным каналом может работать как в режиме обогащения, так и в режиме обеднения канала основными носителями заряда.
Схемы включения полевого транзистора.
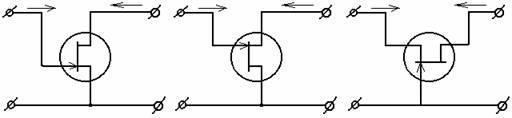
В зависимости от того, какой из электродов полевого транзистора подключен к общему выводу, различают схемы: с общим истоком и входом затвор; с общим стоком и входом на затвор; с общим затвором и входом на исток. Схемы включения полевого транзистора показаны на рис. 3.
Параметры полевого транзистора.
Входная проводимость определяется проводимостью участка затвор — исток уЗИ. = у11 + у12 ; выходная проводимость — проводимость участка сток — исток уСИ = у22 + у21 ; функции передачи — крутизной вольт-амперной характеристики S = у21 — у12 ; функция обратной передачи — проходной проводимостью уЗС = у12 . Эти параметры применяются за первичные параметры полевого транзистора, используемого в качестве четырехполюсника. Если первичные параметры четырехполюсника для схем с общим истоком определены, то можно рассчитать параметры для любой другой схемы включения полевого транзистора.
Начальный ток стока IС.нач — ток стока при напряжении между затвором и истоком, равном нулю и напряжении на стоке, равном или превышающим напряжение насыщения. Остаточный ток стока IС.ост — ток стока при напряжении между затвором и истоком, превышающем напряжение отсечки. Ток утечки затвора IЗ.ут — ток затвора при заданном напряжении между затвором и остальными выводами, замкнутыми между собой. Обратный ток перехода затвор — сток IЗСО — ток, протекающий в цепи затвор — сток при заданном обратном напряжении между затвором и стоком и разомкнутыми остальными выводами. Обратный ток перехода затвор — исток I ЗИО — ток, протекающий в цепи затвор — исток при заданном обратном напряжении между затвором и истоком и разомкнутыми остальными выводами.
Напряжение отсечки полевого транзистора UЗИ.отс — напряжение между затвором и истоком транзистора с р -п переходом или изолированным затвором, работающего в режиме обеднения, при котором ток стока достигает заданного низкого значения. Пороговое напряжение полевого транзистора UЗИ.пор — напряжение между затвором и истоком транзистора с изолированным затвором, работающего в режиме обогащения, при котором ток стока достигает заданного низкого значения.
Крутизна характеристик полевого транзистора S — отношение изменения тока стока к изменению напряжения на затворе при коротком замыкании по переменному току на выходе транзистора в схеме с общим истоком.
Коэффициент усиления по мощности Кур — отношение мощности на выходе полевого транзистора к мощности на входе при определенной частоте и схеме включения.
Частотные свойства.
Частотные свойства полевых транзисторов определяются постоянной времени RC — цепи затвора. Поскольку входная емкость С11и у транзисторов с р-п переходом велика (десятки пикофарад), их применение в усилительных каскадах с большим входным сопротивлением возможно в диапазоне частот, ре превышающих сотен килогерц — единиц мегагерц.
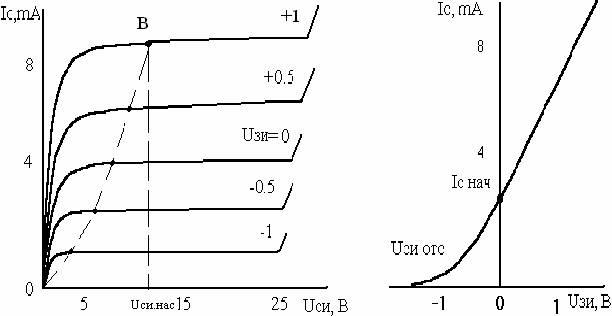
Рис. 7. Вольт – амперные характеристики полевого транзистора со встроеным
каналом n- типа: а – стоковые; б – стоко – затворные.
Вольт — амперные характеристики полевых транзисторов устанавливают зависимость тока стока I C от одного из напряжений UСИ или UЗИ при фиксированной величине второго.
В МДП — транзисторе с индуцированным каналом с подложкой р-типа при UЗИ = 0 канал п-типа может находиться в проводящем состоянии. При некотором пороговом напряжении UЗИ.ПОР < 0 за счет обеднения канала основными носителями проводимость его значительно уменьшается. Статические стоковые характеристики в этом случае будут иметь вид , изображенный на рис. 7 , а стоко — затворная характеристика пересекает ось ординат в точке со значением тока IC.НАЧ.
Особенностью МДП — транзистора с индуцированным каналом п — типа является возможность работы без постоянного напряжения смещения ( U ЗИ = 0) в режиме как обеднения, так и обогащения канала основными носителями заряда. МДП — транзистор с встроенным каналом имеет вольт-амперные характеристики , аналогичные изображенным на рис. 7 .
3. Принцип действия полевого транзистора. Вах полевого транзистора с указанием
Общие свойства: 1) Высокая технологичность изготовления, 2) Хорошая воспроизводимость параметров, 3) Большая плотность упаковки 4) сравнительно невысокая стоимость.
Главная особенность высокое входное сопротивление.
МОП – ТРАНЗИСТОРЫ
1. Устройство полевого транзистора.

Полевой транзистор — это полупроводниковый прибор, усилительные свойства которого обусловлены потоком основных носителей, протекающим через проводящий канал и управляемый электрическим полем. В отличие от биполярных работа полевых транзисторов основана на использовании основных носителей заряда в полупроводнике. По конструктивному исполнению и технологии изготовления полевые транзисторы можно разделить на две группы: полевые транзисторы с управляющим р- п — переходом и полевые транзисторы с изолированным затвором.
Рис.1. Структура полевого транзистора
Полевой транзистор с управляющим р-п- переходом — это полевой транзистор, затвор которого отделен в электрическом отношении от канала
р-п — переходом, смещенным в обратном направлении. Электрод , из которого в канал входят носители заряда, называют истоком; электрод, через который из канала уходят носители заряда, — стоком; электрод, служащий для регулирования поперечного сечения канала, — затвором. При подключении к истоку отрицательного (для п-канала), а к стоку положительного напряжения (рис. 1 ) в канале возникает электрический ток, создаваемый движением электронов от истока к стоку, т.е. основными носителями заряда.
В этом заключается существенное отличие полевого транзистора от биполярного. Движение носителей заряда вдоль электронно-дырочного перехода (а не через переходы, как в биполярном транзисторе) является второй характерной особенностью полевого транзистора.
Электрическое поле, создаваемое между затвором и каналом, изменяет плотность носителей заряда в канале, т.е. величину протекающего тока. Так как управление происходит через обратно смещенный р-п-переход, сопротивление между управляющим электродом и каналом велико, а потребляемая мощность от источника сигнала в цепи затвора ничтожно мала. Поэтому полевой транзистор может обеспечить усиление электромагнитных колебаний как по мощности, так и по току и напряжению.
Рис. 2. Структура полевого транзистора с изолированным затвором: а — с индуцированным каналом ; б — со встроенным каналом.
Полевой транзистор с изолированным затвором — это полевой транзистор, затвор которого отделен в электрическом отношении от канала слоем диэлектрика. Полевой транзистор с изолированным затвором состоит из пластины полупроводника (подложки) с относительно высоким удельным сопротивлением, в которой созданы две области с противоположным типом электропроводности (рис. 2 ). На эти области нанесены металлические электроды — исток и сток. Поверхность полупроводника между истоком и стоком покрыта тонким слоем диэлектрика (обычно слоем оксида кремния). На слой диэлектрика нанесен металлический электрод — затвор. Получается структура, состоящая из металла, диэлектрика и полупроводника. Поэтому полевые транзисторы с изолированным затвором часто называют МДП- транзисторами или МОП- транзисторами (металл — оксид- полупроводник).
Существуют две разновидности МДП-транзисторов с индуцированным и со встроенным каналами.
В МДП-транзисторах с индуцированным каналом проводящий канал между сильнолегированными областями истока и стока и, следовательно, заметный ток стока появляются только при определенной полярности и при определенном значении напряжения на затворе относительно истока (отрицательного при р-канале и положительного при п-канале). Это напряжение называют пороговым (UЗИ.пор ). Так как появление и рост проводимости индуцированного канала связаны с обогащением его основными носителями заряда, то считают, что канал работает в режиме обогащения.
В МДП — транзисторах со встроенным каналом проводящий канал, изготавливается технологическим путем, образуется при напряжении на затворе равном нулю. Током стока можно управлять, изменяя значение и полярность напряжения между затвором и истоком. При некотором положительном напряжении затвор — исток транзистора с р — каналом или отрицательном напряжении транзистора с n -каналом ток в цепи стока прекращается. Это напряжение называют напряжением отсечки (UЗИ.отс ). МДП — транзистор со встроенным каналом может работать как в режиме обогащения, так и в режиме обеднения канала основными носителями заряда.
2. Схемы включения полевого транзистора.
Рис. 3. Схемы включения полевого транзистора. Полевой транзистор в качестве элемента схемы представляет собой активный несимметричный четырехполюсник, у которого один из зажимов является общим для цепей входа и выхода. В зависимости от того, какой из электродов полевого транзистора подключен к общему выводу, различают схемы: с общим истоком и входом затвор; с общим стоком и входом на затвор; с общим затвором и входом на исток. Схемы включения полевого транзистора показаны на рис. 3. По аналогии с ламповой электроникой, где за типовую принята схема с общим катодом, для полевых транзисторов типовой является схема с общим истоком.
П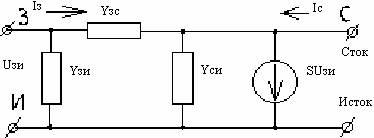 о
аналогии с ламповой электроникой, где
за типовую принята схема с общим катодом,
для полевых транзисторов типовой
является схема с общим истоком.
о
аналогии с ламповой электроникой, где
за типовую принята схема с общим катодом,
для полевых транзисторов типовой
является схема с общим истоком.
3. Эквивалентная схема полевого транзистора.
Рис. 4. Эквивалентная схема полевого транзистора. Эквивалентная схема полевого транзистора, элементы которой выражены через у-параметры, приведен на рис. 4. При таком подключении каждая из проводимости имеет физический смысл.
4. Параметры полевого транзистора. Входная проводимость определяется проводимостью участка затвор — исток уЗИ. = у11 + у12 ; выходная проводимость — проводимость участка сток — исток уСИ = у22 + у21 ; функции передачи — крутизной вольт-амперной характеристики S = у21 — у12 ; функция обратной передачи — проходной проводимостью уЗС = у12 . Эти параметры применяются за первичные параметры полевого транзистора, используемого в качестве четырехполюсника. Если первичные параметры четырехполюсника для схем с общим истоком определены, то можно рассчитать параметры для любой другой схемы включения полевого транзистора.
 Начальный
ток стока IС.нач — ток стока при напряжении
между затвором и истоком, равном нулю
и напряжении на стоке, равном или
превышающим напряжение насыщения.
Остаточный ток стока IС.ост — ток стока
при напряжении между затвором и истоком,
превышающем напряжение отсечки. Ток
утечки затвора IЗ.ут — ток затвора при
заданном напряжении между затвором и
остальными выводами, замкнутыми между
собой. Обратный ток перехода затвор —
сток IЗСО — ток, протекающий в цепи
затвор — сток при заданном обратном
напряжении между затвором и стоком и
разомкнутыми остальными выводами.
Обратный ток перехода затвор — исток
I ЗИО — ток, протекающий в цепи затвор —
исток при заданном обратном напряжении
между затвором и истоком и разомкнутыми
остальными выводами. Напряжение отсечки
полевого транзистора UЗИ.отс — напряжение
между затвором и истоком транзистора
с р -п переходом или изолированным
затвором, работающего в режиме обеднения,
при котором ток стока достигает заданного
низкого значения. Пороговое напряжение
полевого транзистора UЗИ.пор —
напряжение между затвором и истоком
транзистора с изолированным затвором,
работающего в режиме обогащения, при
котором ток стока достигает заданного
низкого значения. Крутизна характеристик
полевого транзистора S — отношение
изменения тока стока к изменению
напряжения на затворе при коротком
замыкании по переменному току на выходе
транзистора в схеме с общим истоком.
Входная емкость полевого транзистора
С11и — емкость между затвором и истоком
при коротком замыкании по переменному
току на выходе в схеме с общим истоком.
Выходная емкость полевого транзистора
С22и — емкость между стоком и истоком
при коротком замыкании по переменному
току на входе в схеме с общим истоком.
Проходная емкость полевого транзистора
C12и — емкость между затвором и стоком
при коротком замыкании по переменному
току на входе в схеме с общим истоком.
Емкость затвор -сток СЗСО — емкость
между затвором и стоком при разомкнутых
по переменному току остальных выводах.
Емкость затвор — исток СЗИО емкость
между затвором и истоком при разомкнутых
по переменному току остальных выводах.
Коэффициент усиления по мощности
Кур — отношение мощности на выходе
полевого транзистора к мощности на
входе при определенной частоте и схеме
включения.
Начальный
ток стока IС.нач — ток стока при напряжении
между затвором и истоком, равном нулю
и напряжении на стоке, равном или
превышающим напряжение насыщения.
Остаточный ток стока IС.ост — ток стока
при напряжении между затвором и истоком,
превышающем напряжение отсечки. Ток
утечки затвора IЗ.ут — ток затвора при
заданном напряжении между затвором и
остальными выводами, замкнутыми между
собой. Обратный ток перехода затвор —
сток IЗСО — ток, протекающий в цепи
затвор — сток при заданном обратном
напряжении между затвором и стоком и
разомкнутыми остальными выводами.
Обратный ток перехода затвор — исток
I ЗИО — ток, протекающий в цепи затвор —
исток при заданном обратном напряжении
между затвором и истоком и разомкнутыми
остальными выводами. Напряжение отсечки
полевого транзистора UЗИ.отс — напряжение
между затвором и истоком транзистора
с р -п переходом или изолированным
затвором, работающего в режиме обеднения,
при котором ток стока достигает заданного
низкого значения. Пороговое напряжение
полевого транзистора UЗИ.пор —
напряжение между затвором и истоком
транзистора с изолированным затвором,
работающего в режиме обогащения, при
котором ток стока достигает заданного
низкого значения. Крутизна характеристик
полевого транзистора S — отношение
изменения тока стока к изменению
напряжения на затворе при коротком
замыкании по переменному току на выходе
транзистора в схеме с общим истоком.
Входная емкость полевого транзистора
С11и — емкость между затвором и истоком
при коротком замыкании по переменному
току на выходе в схеме с общим истоком.
Выходная емкость полевого транзистора
С22и — емкость между стоком и истоком
при коротком замыкании по переменному
току на входе в схеме с общим истоком.
Проходная емкость полевого транзистора
C12и — емкость между затвором и стоком
при коротком замыкании по переменному
току на входе в схеме с общим истоком.
Емкость затвор -сток СЗСО — емкость
между затвором и стоком при разомкнутых
по переменному току остальных выводах.
Емкость затвор — исток СЗИО емкость
между затвором и истоком при разомкнутых
по переменному току остальных выводах.
Коэффициент усиления по мощности
Кур — отношение мощности на выходе
полевого транзистора к мощности на
входе при определенной частоте и схеме
включения.
4.1. Частотные свойства. Частотные свойства полевых транзисторов определяются постоянной времени RC — цепи затвора. Поскольку входная емкость С11и у транзисторов с р-п переходом велика (десятки пикофарад), их применение в усилительных каскадах с большим входным сопротивлением возможно в диапазоне частот, ре превышающих сотен килогерц — единиц мегагерц. При работе в переключающих схемах скорость переключения полностью определяется постоянной времени RC — цепи затвора. У полевых транзисторов с изолированным затвором входная емкость значительно меньше, поэтому их частотные свойства намного лучше, чем у полевых транзисторов с р-п — переходом. Граничная частота определяется по формуле fгр.=159/С11и , где fгр = частота, МГц; S — крутизна характеристики транзистора, мА/В; С11и — емкость между затвором и истоком при коротком замыкании по переменному току выходной цепи, пФ.
4.2. Шумовые свойства. Шумовые свойства полевых транзисторов оцениваются коэффициентом шума КШ , который мало зависит от напряжения сток — исток, тока стока и окружающей температуры (ниже 50 0 С) и монотонно возрастает с уменьшением частоты и внутреннего сопротивления источника сигнала. Коэффициент шума измеряют в заданном режиме по постоянному току UСИ, IC на определенной частоте.
 Вместо
коэффициента шума иногда указывают
шумовое напряжение полевого транзистора
Uш — эквивалентное шумовое напряжение,
приведенное ко входу, в полосе частот
при определенном полном сопротивлении
генератора в схеме с общим истоком;
шумовой ток Iш — эквивалентный шумовой
ток , приведенный ко входу, при разомкнутом
входе в полосе частот в схеме с общим
истоком.
Вместо
коэффициента шума иногда указывают
шумовое напряжение полевого транзистора
Uш — эквивалентное шумовое напряжение,
приведенное ко входу, в полосе частот
при определенном полном сопротивлении
генератора в схеме с общим истоком;
шумовой ток Iш — эквивалентный шумовой
ток , приведенный ко входу, при разомкнутом
входе в полосе частот в схеме с общим
истоком.
 4.3.
Тепловые параметры. Тепловые параметры
полевого транзистора характеризуют
его устойчивость при работе в диапазоне
температур. При изменении температуры
свойства полупроводниковых материалов
изменяются. Это приводит к изменению
параметров полевого транзистора, в
первую очередь , тока стока, крутизны и
тока утечки затвора. Зависимость
изменения тока стока от температуры
определяется двумя факторами: контактной
разностью потенциалов р-п перехода и
изменением подвижности основных
носителей заряда в канале. При повышении
температуры контактная разность
потенциалов уменьшается, сопротивление
канала падает, а ток увеличивается. Но
повышение температуры приводит к
уменьшению подвижности носителей заряда
в канале и тока стока. При определенных
условиях действие этих факторов
взаимнокомпенсируется и ток полевого
транзистора перестает зависеть от
температуры. На рис. 5. приведены
стокозатворные характеристики при
различных температурах окружающей
4.3.
Тепловые параметры. Тепловые параметры
полевого транзистора характеризуют
его устойчивость при работе в диапазоне
температур. При изменении температуры
свойства полупроводниковых материалов
изменяются. Это приводит к изменению
параметров полевого транзистора, в
первую очередь , тока стока, крутизны и
тока утечки затвора. Зависимость
изменения тока стока от температуры
определяется двумя факторами: контактной
разностью потенциалов р-п перехода и
изменением подвижности основных
носителей заряда в канале. При повышении
температуры контактная разность
потенциалов уменьшается, сопротивление
канала падает, а ток увеличивается. Но
повышение температуры приводит к
уменьшению подвижности носителей заряда
в канале и тока стока. При определенных
условиях действие этих факторов
взаимнокомпенсируется и ток полевого
транзистора перестает зависеть от
температуры. На рис. 5. приведены
стокозатворные характеристики при
различных температурах окружающей
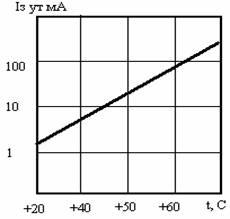
Рис. 5. Сток — затворные характеристики полевого транзистора при разных температурах. среды и указано положение термостабильной точки. Зависимость крутизны характеристики от температуры у полевых транзисторов такая же как и у тока стока. С ростом температуры ток утечки затвора увеличивается. Хотя абсолютное изменение тока незначительно , его надо учитывать при больших сопротивлениях в цепи затвора. В этом случае изменение тока утечки затвора может вызвать существенное изменение напряжения на затворе полевого транзистора и режима его работы. Температурная зависимость тока утечки затвора полевого транзистора с р-п переходом приведена на рис. 6 .
рис. 6. Зависимость тока утечки затвора полевого транзистора от температуры.
В полевом транзисторе с изолированным затвором ток затвора практически не зависит от температуры.
4.4. Максимально допустимые параметры. М а к с и м а л ь н о д о п у с т и м ы е п а р а м е т р ы определяют значения конкретных режимов полевых транзисторов, которые не должны превышаться при любых условиях эксплуатации и при которых обеспечивается заданная надежность. К максимально допустимым параметрам относятся: максимально допустимое напряжение затвор — исток UЗИmax , затвор — сток UЗСmax , сток — исток UСИmax , максимально допустимое напряжение сток — подложка UСПmax , исток — подложка UИПmax , затвор — подложка U ЗПmax . Максимально допустимый постоянный ток стока I Сmax максимально допустимый прямой ток затвора IЗ(пр)max , максимально допустимая постоянная рассеиваемая мощность Рmax .
4.5. Вольт – амперные характеристики полевых транзисторов.
а б
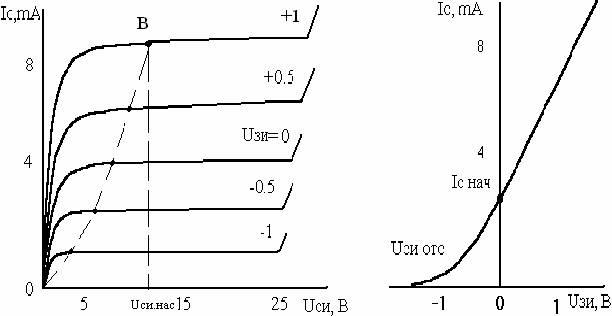
Рис. 7. Вольт – амперные характеристики полевого транзистора со встроеным каналом n- типа: а – стоковые; б – стоко – затворные. Вольт — амперные характеристики полевых транзисторов устанавливают зависимость тока стока I C от одного из напряжений UСИ или UЗИ при фиксированной величине второго. В МДП — транзисторе с индуцированным каналом с подложкой р-типа при UЗИ = 0 канал п-типа может находиться в проводящем состоянии. При некотором пороговом напряжении UЗИ.ПОР < 0 за счет обеднения канала основными носителями проводимость его значительно уменьшается. Статические стоковые характеристики в этом случае будут иметь вид , изображенный на рис. 7 , а стоко — затворная характеристика пересекает ось ординат в точке со значением тока IC.НАЧ. Особенностью МДП — транзистора с индуцированным каналом п — типа является возможность работы без постоянного напряжения смещения ( U ЗИ = 0) в режиме как обеднения, так и обогащения канала основными носителями заряда. МДП — транзистор с встроенным каналом имеет вольт-амперные характеристики , аналогичные изображенным на рис. 7 . У МДП — транзисторов всех типов потенциал подложки относительно истока оказывает заметное влияние на вольт -амперные характеристики и соответственно параметры транзистора. Благодаря воздействию на проводимость канала подложка может выполнять функцию затвора. Напряжение на подложке относительно истока должно иметь такую полярность, чтобы р-п переход исток — подложка включался в обратном направлении. При этом р-п переход канал — подложка действует как затвор полевого транзистора с управляющим р-п переходом.
5. Рекомендации по применению полевых транзисторов. Рекомендации по применению полевых транзисторов. Полевые транзисторы имеют вольт-амперные характеристики, подобные ламповым, и обладают всеми принципиальными преимуществами транзисторов. Это позволяет применять их в схемах, в большинстве случаев использовались электронные лампы, например, в усилителях постоянного тока с высокоомным входом , в истоковых повторителях с особо высокоомным входом , в электрометрических усилителях, различных реле времени, RS — генераторах синусоидальных колебаний низких и инфранизких частот, в генераторах пилообразных колебаний , усилителях низкой частоты , работающих от источников с большим внутренним сопротивлением, в активных RC — фильтрах низких частот. Полевые транзисторы с изолированным затвором используют в высокочастотных усилителях, смесителях , ключевых устройствах. В рекомендации по использованию транзисторов для случая полевых транзисторов следует внести дополнения:
1. На затвор полевых транзисторов с р-п ( отрицательное для транзисторов с р — каналом и положительным для транзистора с п — каналом).
2. Полевые транзисторы с изолированным затвором следует хранить с закороченными выводами. При включении транзисторов в схему должны быть приняты все меры для снятия зарядов статического электричества. Необходимую пайку производить на заземленном металлическом листе, заземлить жало паяльника, а так же руки монтажника при помощи специального металлического браслета. Не следует применять одежду из синтетических тканей. Целесообразно подсоединять полевой транзистор к схеме, предварительно закоротив его выводы.
3. Принцип действия полевого транзистора. Вах полевого транзистора с указанием
В отличии от биполярных транзисторов, униполярные транзисторы относятся к классу полевых элементов, принцип действия которых основан на использовании носителей одного знака. Управление током производится за счет изменения проводимости канала, через который протекает ток, под действием электрического поля.
Общие свойства: 1) Высокая технологичность изготовления, 2) Хорошая воспроизводимость параметров, 3) Большая плотность упаковки 4) сравнительно невысокая стоимость.
Главная особенность высокое входное сопротивление.
МОП – ТРАНЗИСТОРЫ
1. Устройство полевого транзистора.
Полевой транзистор — это полупроводниковый прибор, усилительные свойства которого обусловлены потоком основных носителей, протекающим через проводящий канал и управляемый электрическим полем. В отличие от биполярных работа полевых транзисторов основана на использовании основных носителей заряда в полупроводнике. По конструктивному исполнению и технологии изготовления полевые транзисторы можно разделить на две группы: полевые транзисторы с управляющим р- п — переходом и полевые транзисторы с изолированным затвором.
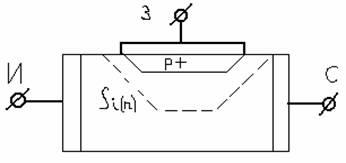
Рис.1. Структура полевого транзистора
Полевой транзистор с управляющим р-п- переходом — это полевой транзистор, затвор которого отделен в электрическом отношении от канала
р-п — переходом, смещенным в обратном направлении. Электрод , из которого в канал входят носители заряда, называют истоком; электрод, через который из канала уходят носители заряда, — стоком; электрод, служащий для регулирования поперечного сечения канала, — затвором. При подключении к истоку отрицательного (для п-канала), а к стоку положительного напряжения (рис. 1 ) в канале возникает электрический ток, создаваемый движением электронов от истока к стоку, т.е. основными носителями заряда. В этом заключается существенное отличие полевого транзистора от биполярного. Движение носителей заряда вдоль электронно-дырочного перехода (а не через переходы, как в биполярном транзисторе) является второй характерной особенностью полевого транзистора.
Электрическое поле, создаваемое между затвором и каналом, изменяет плотность носителей заряда в канале, т.е. величину протекающего тока. Так как управление происходит через обратно смещенный р-п-переход, сопротивление между управляющим электродом и каналом велико, а потребляемая мощность от источника сигнала в цепи затвора ничтожно мала. Поэтому полевой транзистор может обеспечить усиление электромагнитных колебаний как по мощности, так и по току и напряжению.
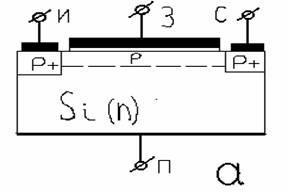

Рис. 2. Структура полевого транзистора с изолированным затвором: а — с индуцированным каналом ; б — со встроенным каналом.
Полевой транзистор с изолированным затвором — это полевой транзистор, затвор которого отделен в электрическом отношении от канала слоем диэлектрика. Полевой транзистор с изолированным затвором состоит из пластины полупроводника (подложки) с относительно высоким удельным сопротивлением, в которой созданы две области с противоположным типом электропроводности (рис. 2 ). На эти области нанесены металлические электроды — исток и сток. Поверхность полупроводника между истоком и стоком покрыта тонким слоем диэлектрика (обычно слоем оксида кремния). На слой диэлектрика нанесен металлический электрод — затвор. Получается структура, состоящая из металла, диэлектрика и полупроводника. Поэтому полевые транзисторы с изолированным затвором часто называют МДП- транзисторами или МОП- транзисторами (металл — оксид- полупроводник).
Существуют две разновидности МДП-транзисторов с индуцированным и со встроенным каналами.
В МДП-транзисторах с индуцированным каналом проводящий канал между сильнолегированными областями истока и стока и, следовательно, заметный ток стока появляются только при определенной полярности и при определенном значении напряжения на затворе относительно истока (отрицательного при р-канале и положительного при п-канале). Это напряжение называют пороговым (UЗИ.пор ). Так как появление и рост проводимости индуцированного канала связаны с обогащением его основными носителями заряда, то считают, что канал работает в режиме обогащения.
В МДП — транзисторах со встроенным каналом проводящий канал, изготавливается технологическим путем, образуется при напряжении на затворе равном нулю. Током стока можно управлять, изменяя значение и полярность напряжения между затвором и истоком. При некотором положительном напряжении затвор — исток транзистора с р — каналом или отрицательном напряжении транзистора с n -каналом ток в цепи стока прекращается. Это напряжение называют напряжением отсечки (UЗИ.отс ). МДП — транзистор со встроенным каналом может работать как в режиме обогащения, так и в режиме обеднения канала основными носителями заряда.
2. Схемы включения полевого транзистора.
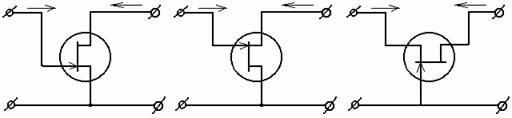
Рис. 3. Схемы включения полевого транзистора.
Полевой транзистор в качестве элемента схемы представляет собой активный несимметричный четырехполюсник, у которого один из зажимов является общим для цепей входа и выхода. В зависимости от того, какой из электродов полевого транзистора подключен к общему выводу, различают схемы: с общим истоком и входом затвор; с общим стоком и входом на затвор; с общим затвором и входом на исток. Схемы включения полевого транзистора показаны на рис. 3.
По аналогии с ламповой электроникой, где за типовую принята схема с общим катодом, для полевых транзисторов типовой является схема с общим истоком.
3. Эквивалентная схема полевого транзистора.
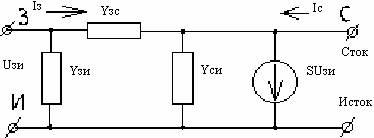
Рис. 4. Эквивалентная схема полевого транзистора.
Эквивалентная схема полевого транзистора, элементы которой выражены через у-параметры, приведен на рис. 4. При таком подключении каждая из проводимости имеет физический смысл.
4. Параметры полевого транзистора.
Входная проводимость определяется проводимостью участка затвор — исток уЗИ. = у11 + у12 ; выходная проводимость — проводимость участка сток — исток уСИ = у22 + у21 ; функции передачи — крутизной вольт-амперной характеристики S = у21 — у12 ; функция обратной передачи — проходной проводимостью уЗС = у12 . Эти параметры применяются за первичные параметры полевого транзистора, используемого в качестве четырехполюсника. Если первичные параметры четырехполюсника для схем с общим истоком определены, то можно рассчитать параметры для любой другой схемы включения полевого транзистора.
Начальный ток стока IС.нач — ток стока при напряжении между затвором и истоком, равном нулю и напряжении на стоке, равном или превышающим напряжение насыщения. Остаточный ток стока IС.ост — ток стока при напряжении между затвором и истоком, превышающем напряжение отсечки. Ток утечки затвора IЗ.ут — ток затвора при заданном напряжении между затвором и остальными выводами, замкнутыми между собой. Обратный ток перехода затвор — сток IЗСО — ток, протекающий в цепи затвор — сток при заданном обратном напряжении между затвором и стоком и разомкнутыми остальными выводами. Обратный ток перехода затвор — исток I ЗИО — ток, протекающий в цепи затвор — исток при заданном обратном напряжении между затвором и истоком и разомкнутыми остальными выводами.
Напряжение отсечки полевого транзистора UЗИ.отс — напряжение между затвором и истоком транзистора с р -п переходом или изолированным затвором, работающего в режиме обеднения, при котором ток стока достигает заданного низкого значения. Пороговое напряжение полевого транзистора UЗИ.пор — напряжение между затвором и истоком транзистора с изолированным затвором, работающего в режиме обогащения, при котором ток стока достигает заданного низкого значения.
Крутизна характеристик полевого транзистора S — отношение изменения тока стока к изменению напряжения на затворе при коротком замыкании по переменному току на выходе транзистора в схеме с общим истоком.
Входная емкость полевого транзистора С11и — емкость между затвором и истоком при коротком замыкании по переменному току на выходе в схеме с общим истоком. Выходная емкость полевого транзистора С22и — емкость между стоком и истоком при коротком замыкании по переменному току на входе в схеме с общим истоком. Проходная емкость полевого транзистора C12и — емкость между затвором и стоком при коротком замыкании по переменному току на входе в схеме с общим истоком. Емкость затвор -сток СЗСО — емкость между затвором и стоком при разомкнутых по переменному току остальных выводах. Емкость затвор — исток СЗИО емкость между затвором и истоком при разомкнутых по переменному току остальных выводах.
Коэффициент усиления по мощности Кур — отношение мощности на выходе полевого транзистора к мощности на входе при определенной частоте и схеме включения.
4.1. Частотные свойства.
Частотные свойства полевых транзисторов определяются постоянной времени RC — цепи затвора. Поскольку входная емкость С11и у транзисторов с р-п переходом велика (десятки пикофарад), их применение в усилительных каскадах с большим входным сопротивлением возможно в диапазоне частот, ре превышающих сотен килогерц — единиц мегагерц.
При работе в переключающих схемах скорость переключения полностью определяется постоянной времени RC — цепи затвора. У полевых транзисторов с изолированным затвором входная емкость значительно меньше, поэтому их частотные свойства намного лучше, чем у полевых транзисторов с р-п — переходом.
Граничная частота определяется по формуле fгр.=159/С11и , где fгр = частота, МГц; S — крутизна характеристики транзистора, мА/В; С11и — емкость между затвором и истоком при коротком замыкании по переменному току выходной цепи, пФ.
4.2. Шумовые свойства.
Шумовые свойства полевых транзисторов оцениваются коэффициентом шума КШ , который мало зависит от напряжения сток — исток, тока стока и окружающей температуры (ниже 50 0 С) и монотонно возрастает с уменьшением частоты и внутреннего сопротивления источника сигнала. Коэффициент шума измеряют в заданном режиме по постоянному току UСИ, IC на определенной частоте.
Вместо коэффициента шума иногда указывают шумовое напряжение полевого транзистора Uш — эквивалентное шумовое напряжение, приведенное ко входу, в полосе частот при определенном полном сопротивлении генератора в схеме с общим истоком; шумовой ток Iш — эквивалентный шумовой ток , приведенный ко входу, при разомкнутом входе в полосе частот в схеме с общим истоком.
4.3. Тепловые параметры.
Тепловые параметры полевого транзистора характеризуют его устойчивость при работе в диапазоне температур. При изменении температуры свойства полупроводниковых материалов изменяются. Это приводит к изменению параметров полевого транзистора, в первую очередь , тока стока, крутизны и тока утечки затвора.
Зависимость изменения тока стока от температуры определяется двумя факторами: контактной разностью потенциалов р-п перехода и изменением подвижности основных носителей заряда в канале. При повышении температуры контактная разность потенциалов уменьшается, сопротивление канала падает, а ток увеличивается. Но повышение температуры приводит к уменьшению подвижности носителей заряда в канале и тока стока. При определенных условиях действие этих факторов взаимнокомпенсируется и ток полевого транзистора перестает зависеть от температуры. На рис. 5. приведены стокозатворные характеристики при различных температурах окружающей
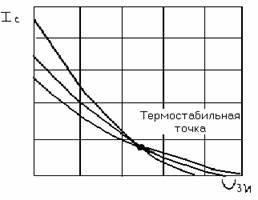
Рис. 5. Сток — затворные характеристики полевого транзистора при разных температурах.
среды и указано положение термостабильной точки. Зависимость крутизны характеристики от температуры у полевых транзисторов такая же как и у тока стока. С ростом температуры ток утечки затвора увеличивается. Хотя абсолютное изменение тока незначительно , его надо учитывать при больших сопротивлениях в цепи затвора. В этом случае изменение тока утечки затвора может вызвать существенное изменение напряжения на затворе полевого транзистора и режима его работы. Температурная зависимость тока утечки затвора полевого транзистора с р-п переходом приведена на рис. 6 . В
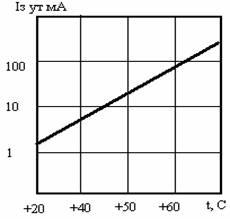
рис. 6. Зависимость тока утечки затвора полевого транзистора
от температуры.
полевом транзисторе с изолированным затвором ток затвора практически не зависит от температуры.
4.4. Максимально допустимые параметры.
М а к с и м а л ь н о д о п у с т и м ы е п а р а м е т р ы определяют значения конкретных режимов полевых транзисторов, которые не должны превышаться при любых условиях эксплуатации и при которых обеспечивается заданная надежность. К максимально допустимым параметрам относятся: максимально допустимое напряжение затвор — исток UЗИmax , затвор — сток UЗСmax , сток — исток UСИmax , максимально допустимое напряжение сток — подложка UСПmax , исток — подложка UИПmax , затвор — подложка U ЗПmax . Максимально допустимый постоянный ток стока I Сmax максимально допустимый прямой ток затвора IЗ(пр)max , максимально допустимая постоянная рассеиваемая мощность Рmax .

4.5. Вольт – амперные характеристики полевых транзисторов.
а б
Рис. 7. Вольт – амперные характеристики полевого транзистора со встроеным
каналом n- типа: а – стоковые; б – стоко – затворные.
Вольт — амперные характеристики полевых транзисторов устанавливают зависимость тока стока I C от одного из напряжений UСИ или UЗИ при фиксированной величине второго.
В МДП — транзисторе с индуцированным каналом с подложкой р-типа при UЗИ = 0 канал п-типа может находиться в проводящем состоянии. При некотором пороговом напряжении UЗИ.ПОР < 0 за счет обеднения канала основными носителями проводимость его значительно уменьшается. Статические стоковые характеристики в этом случае будут иметь вид , изображенный на рис. 7 , а стоко — затворная характеристика пересекает ось ординат в точке со значением тока IC.НАЧ.
Особенностью МДП — транзистора с индуцированным каналом п — типа является возможность работы без постоянного напряжения смещения ( U ЗИ = 0) в режиме как обеднения, так и обогащения канала основными носителями заряда. МДП — транзистор с встроенным каналом имеет вольт-амперные характеристики , аналогичные изображенным на рис. 7 .
У МДП — транзисторов всех типов потенциал подложки относительно истока оказывает заметное влияние на вольт -амперные характеристики и соответственно параметры транзистора. Благодаря воздействию на проводимость канала подложка может выполнять функцию затвора. Напряжение на подложке относительно истока должно иметь такую полярность, чтобы р-п переход исток — подложка включался в обратном направлении. При этом р-п переход канал — подложка действует как затвор полевого транзистора с управляющим р-п переходом.
5. Рекомендации по применению полевых транзисторов.
Рекомендации по применению полевых транзисторов. Полевые транзисторы имеют вольт-амперные характеристики, подобные ламповым, и обладают всеми принципиальными преимуществами транзисторов. Это позволяет применять их в схемах, в большинстве случаев использовались электронные лампы, например, в усилителях постоянного тока с высокоомным входом , в истоковых повторителях с особо высокоомным входом , в электрометрических усилителях, различных реле времени, RS — генераторах синусоидальных колебаний низких и инфранизких частот, в генераторах пилообразных колебаний , усилителях низкой частоты , работающих от источников с большим внутренним сопротивлением, в активных RC — фильтрах низких частот. Полевые транзисторы с изолированным затвором используют в высокочастотных усилителях, смесителях , ключевых устройствах.
В рекомендации по использованию транзисторов для случая полевых транзисторов следует внести дополнения:
1. На затвор полевых транзисторов с р-п ( отрицательное для транзисторов с р — каналом и положительным для транзистора с п — каналом).
2. Полевые транзисторы с изолированным затвором следует хранить с закороченными выводами. При включении транзисторов в схему должны быть приняты все меры для снятия зарядов статического электричества. Необходимую пайку производить на заземленном металлическом листе, заземлить жало паяльника, а так же руки монтажника при помощи специального металлического браслета. Не следует применять одежду из синтетических тканей. Целесообразно подсоединять полевой транзистор к схеме, предварительно закоротив его выводы.
ВОЛЬТ-АМПЕРНЫЕ ХАРАКТЕРИСТИКИ ПОЛЕВЫХ ТРАНЗИСТОРОВ
Ток стока ПТ зависит как от значения, так и от полярности напряжений сток — исток и затвор — исток. При постоянном смещении на затворе увеличение напряжения на стоке от нуля вызывает резкое возрастание тока стока, которое продолжается до наступления насыщения тока стока. Затем ток устанавливается и остаётся относительно постоянным. Эта зависимость показана на рис. 3, а для типичного полевого прибора с p-n-переходом. Для сравнения на рис. 3, б приведены коллекторные характеристики биполярного транзистора.
Характеристики транзисторов обоих видов похожи друг на друга, за исключением того, что у биполярного транзистора перегиб характеристик происходит при значительно более низких напряжениях на коллекторе.
На выходной характеристике ПТ можно выделить две характерные области (рис. 4). При малых напряжениях сток — исток (область АВ) сопротивление канала имеет омический характер, и ток может протекать в обоих направлениях. В этом состоит отличие полевых транзисторов от электронных ламп, в которых поток электронов всегда имеет одно направление — от катода к аноду. Рабочая область АВ выходной характеристики ПТ используется в том случае, когда полевой транзистор применяется в схеме в качестве переменного сопротивления, управляемого напряжением (аттенюаторы, регуляторы АРУ).
Рис. 3. Выходные характеристики транзисторов, а — ПТ с p-n-переходом; б — биполярного транзистора.
В области насыщения тока (область ВС на рис. 4) часть канала обеднена носителями заряда из-за влияния электрического поля между затвором и каналом, благодаря чему сопротивление канала становится значительным. Дальнейшее увеличение напряжения между стоком и истоком в этой области вызывает относительно небольшое изменение тока стока, который практически будет зависеть только от напряжения на затворе [1].
Рис. 4. Выходная характеристика ПТ при Uз.и=0
Характерной особенностью полевых транзисторов является то, что напряжение, соответствующее точке B характеристики (точка перегиба характеристики на рис. 4, после которой идёт область насыщения), при напряжении на затворе, равном нулю, численно равно напряжению отсечки и называется напряжением насыщения.
Входные характеристики полевого транзистора существенно отличаются от характеристик биполярного транзистора. Входные характеристики последнего подобны характеристикам открытого полупроводникового диода, в то время как у полевого транзистора они подобны характеристикам запертого диода (смещённого в обратном направлении). Поэтому ток затвора очень мал. Он равен нескольким наноамперам (для ПТ с управляющим p-n-переходом) при температуре 25°С и экспоненциально зависит от температуры.
Рис. 5. Проходные характеристики ПТ при различной температуре.
Проходная характеристика, показывающая зависимость тока стока от напряжения на затворе, изображена на рис. 5. С достаточной для практических расчётов точностью проходная характеристика полевого транзистора определяется выражением (1), т. е. носит квадратичный характер. Эта особенность проходной характеристики используется в преобразователях частоты для уменьшения перекрёстной модуляции и помех от гармоник гетеродина.
PREV CONTEXT NEXT
Вах полевого транзистора
u, В | 0 | –0,5 | –1,0 | –1,5 | –2,0 | –2,5 | –3,0 | –3,5 | –4,0 | –4,5 | –5,0 | –6,0 |
i, мА | 7,5 | 6,5 | 5,5 | 4,5 | 3,6 | 2,7 | 2,0 | 1,4 | 0,75 | 0,4 | 0,25 | 0,1 |
Г рафикВАХ,
построенный по таблице, приведен на
рисунке 18.6. Если выбрать интервал
аппроксимации
рафикВАХ,
построенный по таблице, приведен на
рисунке 18.6. Если выбрать интервал
аппроксимации
0 u – 5,0 В
и сделать привязку полинома к ВАХ в трех следующих точках:
1) u1 = 0 В, i1 = 7,5 мА;
2) u2 = – 2,5 В, i2 = 2,7 мА;
3) u3 = – 5,0 В, i3 = 0,25 мА,
то, решая систему из трех получившихся уравнений:
1) i = 7,5 = а0 ,
2) i =2,7=а0 – 2,5 а1+ 6,25 а2 ,
3) i =0,25 =а0 – 5 а1+25 а2 ,
находим коэффициенты аппроксимирующего полинома
а0 = 7,5 мА, а1 = 2,39 мА/В, а2 = 0,188 мА/В2
и, собственно, полином второй степени:
i = 7,5 + 2,39 u + 0,188 u2, мА. (18.5)
При дальнейшем использовании этого аналитического представления ВАХ необходимо помнить, что оно справедливо только для выбранного интервала аппроксимации, в нашем случае от u = 0 до u = – 5 В.
Рабочий участок ВАХ, определяемый величиной воздействия, всегда должен находиться внутри интервала аппроксимации. Иными словами, это значит, что любое мгновенное значение воздействия не имеет права выходить за рамки интервала аппроксимации.
В нижней части рис. 18.6 сделана иллюстрация выполнения этого условия: относительно рабочей точки U0 = – 2 В действуют два гармонических колебания – низкочастотное с амплитудой 0,5 В и высокочастотное с амплитудой 1,5 В, при этом в любой момент времени величина воздействия не выходит за рамки интервала аппроксимации (на рисунке заштрихованы).
Относительные ошибки приближения при использовании выражения (18.5) на интервале аппроксимации сведены для иллюстрации в таблицу 18.3.
Таблица 18.3
Относительные ошибки приближения
Точки ВАХ | u, B | 0 | –1,0 | –2,0 | –2,5 | –3,0 | –3,5 | –4,0 | –4,5 | –5,0 |
Относит. ошибка | % | 0 | +3,6 | +3,5 | 0 | –1,1 | –2,7 | –24 | –38 | 0 |
Как видно из таблицы 18.3, точность аппроксимации имеет приемлемое для практики значение с одной стороны ВАХ и резко ухудшается с другой, что объясняется малыми абсолютными значениями тока в этой области ВАХ.
При желании или необходимости можно повысить точность приближения, увеличивая количество точек привязки на интервале аппроксимации, однако это влечет за собой повышение степени полинома и ведет к прогрессивному усложнению процедуры дальнейшего математического анализа.
Продолжая рассматриваемый пример, приведем полином пятой степени при прежнем интервале аппроксимации для той же ВАХ полевого транзистора, коэффициенты которого рассчитаны из условия привязки в шести точках u = 0, –1, –2, –3, –4, –5, В ;
i = 7,5 + 1,8458 u – 0,327 u2 – 0,2167 u3 – 0,0479 u4 – 0,0042 u5 , мА . (18.6)
Читателю предоставляется возможность сравнить относительную точность представления ВАХ полиномом пятой степени по отношению к полиному второй степени.
Д ругим
способом степенной аппроксимации
является представлениеВАХ
рядом Тейлора
относительно выбранной рабочей точки U0. При этом
рабочий участок ВАХ предполагается
симметричным относительно рабочей
точки U0,
поскольку в практике анализа
нелинейных устройств преимущественным
видом воздействия является
гармоническое (рис. 18.7).
ругим
способом степенной аппроксимации
является представлениеВАХ
рядом Тейлора
относительно выбранной рабочей точки U0. При этом
рабочий участок ВАХ предполагается
симметричным относительно рабочей
точки U0,
поскольку в практике анализа
нелинейных устройств преимущественным
видом воздействия является
гармоническое (рис. 18.7).
Разложение ВАХ в ряд Тейлора в окрестности рабочей точки Uо имеет вид
i = a0 + a1 ( u – U0) + a2 ( u – U0) 2 + … + an ( u – U0) n, (18.7)
где коэффициенты an являются производными порядка «n» в данной точке ВАХ:
an = 
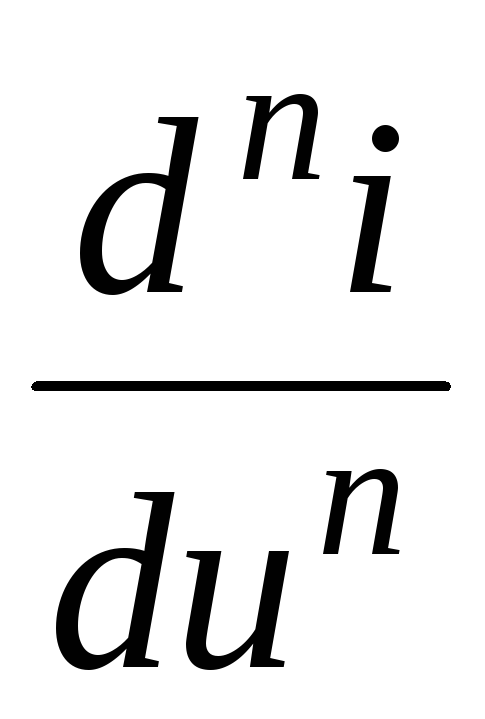 РТ (18.8)
РТ (18.8)
и могут быть определены графическим путем или аналитически, если в наличии имеется любое другое аппроксимирующее выражение, например, (18.5) или (18.6).
В качестве примера ниже приведен ряд Тейлора для ВАХ, заданной таблицей 18.2, записанный для окрестностей рабочей точки U0 = – 2,5 В. Коэффициенты ряда определены по формуле (18.8). За аппроксимирующий полином принято выражение (18.5), полученное ранее для той же ВАХ путем интерполяционного приближения. В выражении ряда Тейлора
i = 2,7 + 1,45 ( u + U0 ) + 0,188 ( u + U0 ) 2 , (мA) (18.9)
переменная «u» заключена в пределах – 5 В … 0 В и является абсциссой графика ВАХ (рисунок 18.7). При замене переменных в выражении (18.9)
us = u + U0 (18.10)
ряд Тейлора приобретает вид
i = 2,7 + 1,45 us + 0,188 us2, (мA), (18.11)
где переменная «us» может изменяться в пределах ± 2,5 В, причем начало ее отсчета привязано теперь к рабочей точке U0 = – 2,5 В, как показано на рисунке 18.7.
Для полноты сопоставлений приведем ряд Тейлора пятой степени для той же ВАХ. Коэффициенты ряда определены в прежней рабочей точке U0 = – 2,5 В на основе степенного ряда (18.6):
i = 2,7 + 1,5986 us + 0,1531 us2 + 0,0019 us3 +
+ 0,0042 us4 – 0,0042 us5 , ( мА ) . (18.12)
В
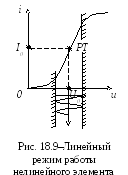 практике обычно удается уйти от
необходимости использовать аппроксимирующие
полиномы высоких степеней. Это
уменьшает трудоемкость расчетов при
сохранении требуемой точности. В
зависимости от видаВАХ,
расположения на ней рабочей точки и
величины сигнала можно выделить
несколько частных случаев использования
« усеченного» аппроксимирующего
полинома.
практике обычно удается уйти от
необходимости использовать аппроксимирующие
полиномы высоких степеней. Это
уменьшает трудоемкость расчетов при
сохранении требуемой точности. В
зависимости от видаВАХ,
расположения на ней рабочей точки и
величины сигнала можно выделить
несколько частных случаев использования
« усеченного» аппроксимирующего
полинома.
На рисунках 18.8-18.11 на условных ВАХ отмечены положения рабочих точек и сделана графическая иллюстрация особенностей режимов работы нелинейного элемента (статического и динамического). При этом вертикальными штриховыми линиями обозначены рабочие интервалы ВАХ. Ниже приведены соответствующие этим частным случаям усеченные аппроксимирующие полиномы.
1. Статический режим работы (рис. 18.8). Рабочая точка РТ на ВАХ однозначно определяется приложенным напряжением U0 .
Ток через нелинейный элемент равен I0 и, следовательно,
i = a0 = I0 . (18.13)
2. Линейный режим работы нелинейного элемента (рис. 18.9).
В этом случае в пределах рабочего участка ВАХ аппроксимирующий полином содержит только линейное слагаемое
i = a0 + a1 u = I0 + S u. (18.14)
Крутизна характеристики S определяется как первая производная ВАХ в рабочей точке U0(18.8). Линейный режим имеет место не только в случае, когда рабочая точка выбрана в центре линейного участка ВАХ (кстати, в этом случае можно допустить наибольшую величину сигнала), но и в любой другой точке ВАХ при условии «малой» величины сигнала, когда его размах не выходит за пределы линейного участка.
3. Довольно часто в практике встречается случай, когда нелинейный элемент работает в режиме малого сигнала и при этом рабочая точка U0 расположена в начале ВАХ, у нижнего ее сгиба. Рабочий интервал ВАХ симметричен относительно рабочей точки (рисунок 18.10).
П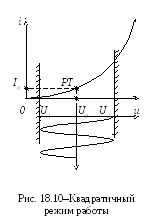 римерами
могут служить«
малосигнальные»
режимы работы модулятора, преобразователя
частоты, амплитудного детектора и
другие. Принято говорить, что такие
устройства работают в «квадратичном» режиме. Удовлетворительную аппроксимацию
в этом случае дает полином второй степени
римерами
могут служить«
малосигнальные»
режимы работы модулятора, преобразователя
частоты, амплитудного детектора и
другие. Принято говорить, что такие
устройства работают в «квадратичном» режиме. Удовлетворительную аппроксимацию
в этом случае дает полином второй степени
i = a0 + a1 u + a2 u 2. (18.15)
Коэффициенты а0 , а1, а2 полинома можно определить с помощью уже описанного выше способа интерполяционного приближения, привязавшись к ВАХ в трех точках интервала аппроксимации, например:
u = U1, u = U0 , u = U2 .
Те же коэффициенты для аппроксимирующего ряда Тейлора несложно найти, либо определяя их по формуле (18.8) в выбранной рабочей точке на основе, например, полинома (18.15), либо путем решения простых алгебраических уравнений, составляемых на основе канонического ряда Тейлора (18.7) для ряда выбранных точек на ВАХ. Придерживаясь принятых на рисунке 18.10 обозначений, имеем в точке u = U0 , ( учитывая, что us = u – U0 = 0 ):
i = a0 = I0, a1 = S,
где S – крутизна ВАХ в рабочей точке Uо определяется графически;
в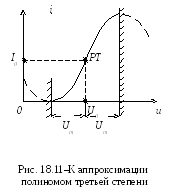 точке u = U1 , ( us = U1 – U0 ):
точке u = U1 , ( us = U1 – U0 ):
i = 0 = I0 + S (U1 – U0) + а2 (U1 – U0) 2 , а2 = – [ I0 + S (U1 – U0)] / (U1 – U0).
4. Рабочая точка расположена в центре симметричной ВАХ, воздействие выходит за пределы линейного участка (рис. 18.11).
Математически в данном случае рабочая точка U0 является точкой перегиба ВАХ. В точке перегиба кривой все производные четного порядка равны нулю. Поэтому коэффициенты при четных степенях в выражении (18.7) обращаются в нуль и его можно записать, сделав замену переменных (18.10) us = u – U0 , в форме
i = a0 + a1 us + a3 us3 + a5 us5 + … (18.16)
Для упрощения последующего анализа можно ограничиться полиномом третьей степени (усеченным полиномом третьей степени):
i = a0 + a1 us + a3 us3 . (18.17)
Соответствующая этой аппроксимации кривая показана на рис. 18.11 штриховой линией. Напряжение Um, соответствующее экстремумам аппроксимирующей функции и отсчитываемое от рабочей точки U0, иногда называют напряжением насыщения. Задание этого напряжения, а также коэффициента a1 ( крутизны S в рабочей точке U0) однозначно определяют коэффициент a3 в выражении (18.17). Действительно, в точке
u = U0 + Um ,
т.е. при амплитуде сигнала, равной Um, производная от ВАХ обращается в нуль, поэтому, в соответствии с (18.17),
a1 + 3 a3 Um2 = 0 ,
откуда
a3 = – S / 3 Um2 . (18.18)
Аппроксимирующей функцией (18.17) допустимо пользоваться, пока амплитуда воздействия не превышает величины Um .
1.3. Вах полевого транзистора (математическая модель).
Транзистор с управляющим n-p-переходом. Поведение выходных характеристик в начальной области можно описать выражением:
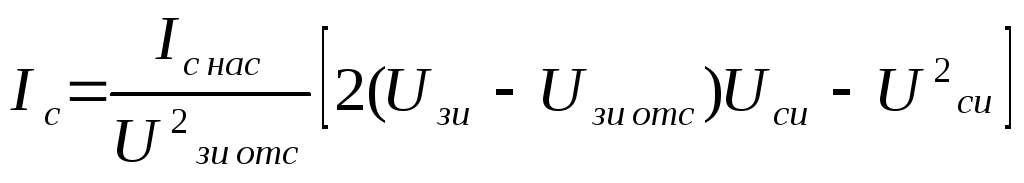 1.2.
1.2.
Здесь Ic нас – начальный ток стока при Uзи=0; Uзи отс – напряжение отсечки; Uзи – текущее напряжение на затворе, которое является параметром для данного семейства; Ucи– текущее напряжение на стоке.
В области насыщения выходные характеристики описываются приближенным выражением:

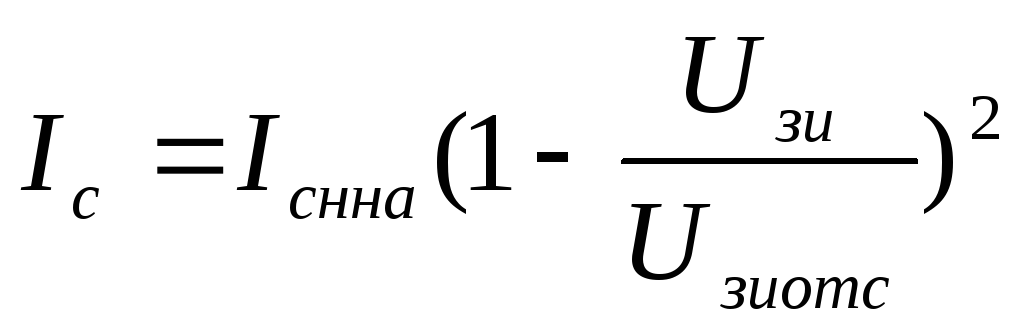 1.3.
1.3.
Транзистор с изолированным затвором. Для транзистора с индуцированным каналом зависимость тока стока от напряжения на начальном участке выходных ВАХ может быть описана как
 1.4.
1.4.
где Sуд – удельная крутизна, зависящая от конструкции транзистора, материала и размеров проводящего канала:

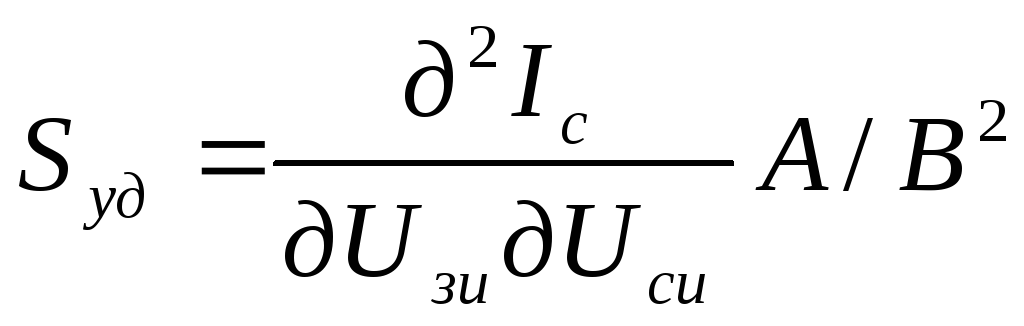 .
.
Продифференцировав (5.4.) по переменной Uси и приравняв производную нулю, получим
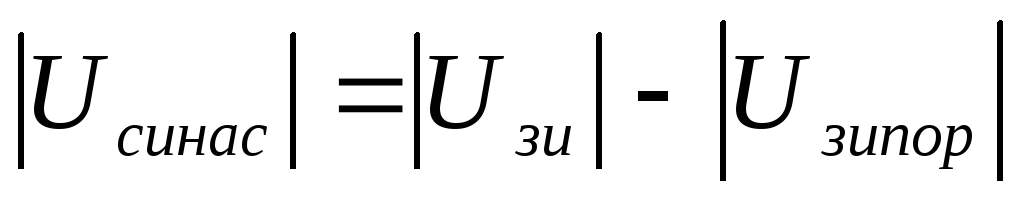 1.5.
1.5.
Подставив Uси нас в (5.4.), получим выражение для тока в области насыщения:
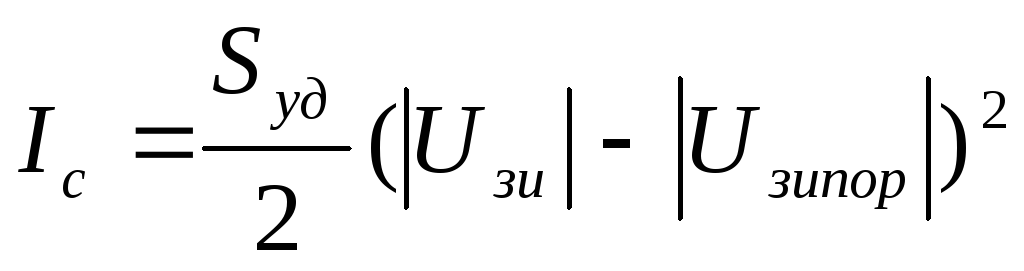 5.6.
5.6.
Характеристики транзистора со встроенным каналом аналитически с достаточной точностью описываются выражениями (5.2) и (5.3), если в этих формулах под напряжением отсечки Uзи отс понимать напряжение, при котором встроенный канал перекрывается.
1.5. Формальная схема замещения полевого транзистора и ее дифференциальные параметры
Полевой транзистор, как и биполярный, можно представить в виде активного четырехполюсника и при работе с сигналами малых амплитуд характеризовать формальной схемой замещения и ее дифференциальными параметрами. На практике в качестве дифференциальных параметров используют у-параметры, в общем случае это комплексные функции частоты, а в частности на низкой частоте, это вещественные величины. К ним относятся:
1) крутизна стокозатворной ВАХ полевого транзистора
 ;
1.7.
;
1.7.
2) входная проводимость полевого транзистора
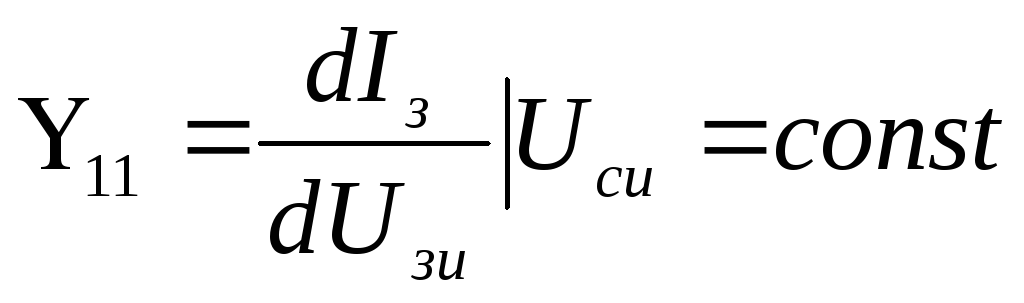 ,
,
на низких частотах близка к нулю;
3) выходная проводимость
 1.8.
1.8.
Часто при расчетах схем на полевых транзисторах используют выходное сопротивление Ri = 1/Y22, которое для области насыщения у маломощных транзисторов равно 10 — 100 кОм. Кроме того, полевой транзистор можно характеризовать статическим коэффициентом усиления
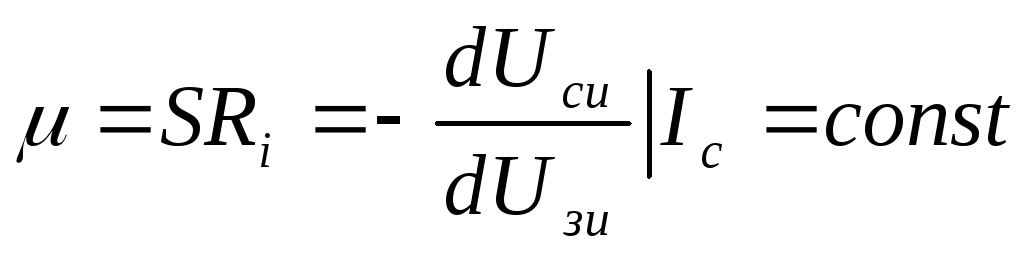 1.9.
1.9.
Здесь знак минус
означает, что для сохранения неизменной
величины тока стока при определении  знаки
приращений напряженийUcи и Uзи должны
быть разными.
знаки
приращений напряженийUcи и Uзи должны
быть разными.
1.6. Физическая эквивалентная схема полевого транзистора
Для описания частотных свойств полевого транзистора в широком диапазоне частот применяется физическая эквивалентная схема (рис. 1.10).
У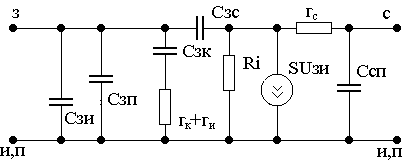 силительные
свойства транзистора, имеющего крутизну
S, отражаются
идеальным
генератором тока SUmзи.
Ri = 1/Y22 — выходное
сопротивление полевого транзистора.
rс rк,
rи – это
обьемные сопротивления области стока,
канала и истока. В эквивалентной схеме
учтены также емкости. В транзисторе с
управляющим р-n-переходом
емкость Сси в основном определяется емкостью между
электродами стока и истока, а в МДП-
транзисторе емкость Сси определяется еще и емкостью р-n- перехода
между подложкой и областями истока и
стока. Поэтому в МДП- транзисторах
силительные
свойства транзистора, имеющего крутизну
S, отражаются
идеальным
генератором тока SUmзи.
Ri = 1/Y22 — выходное
сопротивление полевого транзистора.
rс rк,
rи – это
обьемные сопротивления области стока,
канала и истока. В эквивалентной схеме
учтены также емкости. В транзисторе с
управляющим р-n-переходом
емкость Сси в основном определяется емкостью между
электродами стока и истока, а в МДП-
транзисторе емкость Сси определяется еще и емкостью р-n- перехода
между подложкой и областями истока и
стока. Поэтому в МДП- транзисторах
Рис. 1.10
емкость Сси существенно выше, чем в транзисторах с р-n- переходом. Поскольку полевой транзистор работает с обратно смещенным р-n- переходом, то емкости Сзи и Сзс являются барьерными. Для МДП- транзистора — это емкости затвора относительно областей истока и стока. Ориентировочно, для маломощных транзисторов различного типа Сзи=2-15 пФ, Сзс=0,3-10 пФ; для МДП – транзисторов Сси=315 пФ; для транзисторов с управляющим р-n
– переходом емкость Сси, как правило, не превышает 1 пФ.
Рассмотренная схема справедлива до частоты, равной примерно 0,7fг. Частота fг на которой коэффициент усиления по мощности в режиме согласования по входу и выходу равен единице, называется предельной частотой генерации транзистора. Предельная частота генерации полевого транзистора определяется как:
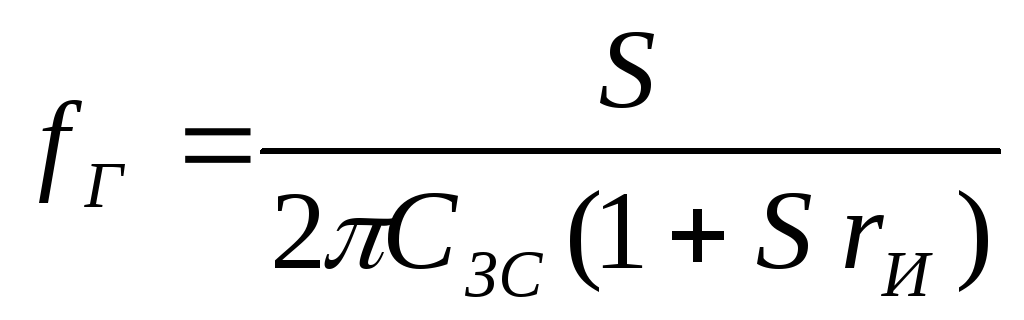
здесь rИ — сопротивление неуправляемого участка канала вблизи области истока, зависящее от тока насыщения и, как правило, не превышающее нескольких десятков ом.
Используя схему рис. 5.10, можно найти у — параметры полевого транзистора:
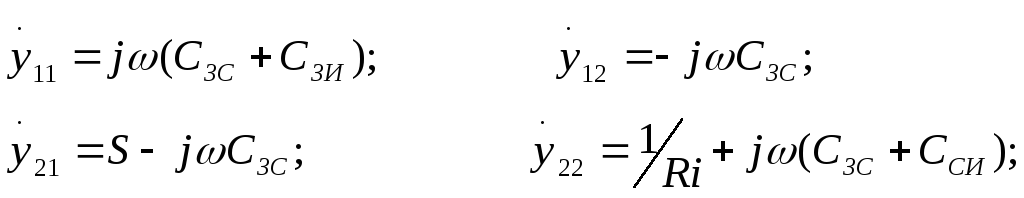 5.10
5.10
3нак
минус в формуле для 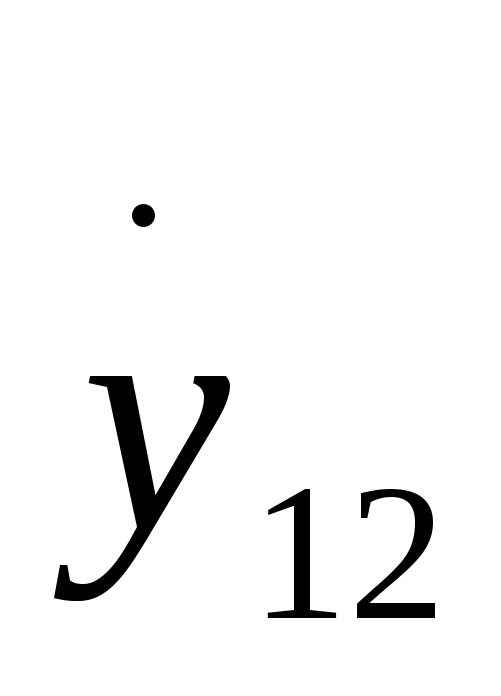 означает, что ток во входной цепи,
вызванный напряжением Uси,
вследствие обратной связи в транзисторе,
имеет направление, противоположное
тому, которое принято положительным
для тока затвора. Из (5.10) следует, что с
ростом рабочей частоты транзистора
величины всех проводимостей растут.
Поскольку емкость Сзс невелика, ее влиянием даже на достаточно
высоких частотах можно пренебречь и
считать, что
означает, что ток во входной цепи,
вызванный напряжением Uси,
вследствие обратной связи в транзисторе,
имеет направление, противоположное
тому, которое принято положительным
для тока затвора. Из (5.10) следует, что с
ростом рабочей частоты транзистора
величины всех проводимостей растут.
Поскольку емкость Сзс невелика, ее влиянием даже на достаточно
высоких частотах можно пренебречь и
считать, что 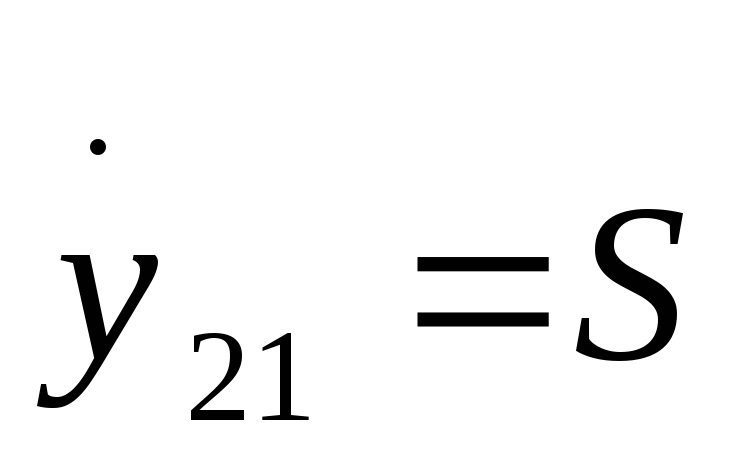 .
.
10. Полевые транзисторы. Изменение сечения канала проводимости от напряжения между затвором и истоком. Вах:
Полевой транзистор—полупроводниковыйприбор, в которомтокизменяется в результате действия «перпендикулярного» токуэлектрического поля, создаваемого напряжением на затворе.
Протекание в полевом транзисторе рабочего тока обусловлено носителями заряда только одного знака (электронами или дырками), поэтому такие приборы часто включают в более широкий класс униполярных электронных приборов (в отличие от биполярных).
По способу создания канала различают полевые транзисторы с затвором в виде управляющего р-n- перехода и с изолированным затвором (МДП — или МОП — транзисторы): встроенным каналом и индуцированным каналом.
В зависимости от проводимости канала полевые транзисторы делятся на: полевые транзисторы с каналом р- типа и n- типа. Канал р- типа обладает дырочной проводимостью, а n- типа — электронной.
Изменение сечения канала проводимости от напряжения между затвором и истоком:
Управляющее напряжение прикладывается между затвором и ис-
током. От напряжения между затвором и истоком зависит проводимость кана-
ла, следовательно, и величина тока. Таким образом, полевой транзистор можно
рассматривать как источник тока, управляемый напряжением затвор-исток. Ес-
ли амплитуда изменения управляющего сигнала достаточно велика, сопротив-
ление канала может изменяться в очень больших пределах. В этом случае поле-
вой транзистор можно использовать в качестве электронного ключа.
Полевой транзистор с управляющим p-n переходом описывается тремя статическими характеристиками:
выходными (стоковые)характеристикамиIс=f(Uси) приUзи=const;
сток-затворнымихарактеристиками (характеристики передачи)Iс=f(Uзи) приUси=const;
входными (затворные)характеристикамиIз=f(Uзи) приUси=const;
При подаче на затвор обратного напряжения и при увеличении этого напряжения по абсолютному значению уменьшается начальное поперечное сечение канала. Это приводит к изменению наклона начальных участков стоковых характеристик, что соответствует большим начальным статическим сопротивлениям канала.
Геометрическое место точек, соответствующих условному перекрытию канала и наступлению режима насыщения.
В крутой области стоковых характеристик транзистор можно использовать как электрически управляемое сопротивление. Пологий участок характеристик является рабочим при применении транзистора в усилительных устройствах.
При увеличении обратного напряжения на p-n переходе уменьшается сечение канала, что приводит к уменьшению тока стока. При = через канал протекает обратный ток стока малой величины, и это может быть использовано для ориентировочного определения напряжения отсечки.
Характеристика передачи может быть получена экспериментально или с помощью перестройки стоковых характеристик.
Входная (затворная) характеристика полевого транзистора с управляющим p-n переходом представляет собой обратную ветвь вольтамперной характеристики p-n перехода. Изменение напряжения влияет на распределение поля в канале, что вызывает изменения тока затвора. Наибольшего своего значения, которое называется током утечки, ток затвора достигает при условии короткого замыкания выводов истока и стока, однако оно очень мало и им часто пренебрегают.
ВАХ:
Ток стока ПТ зависит как от значения, так и от полярности напряжений сток — исток и затвор — исток. При постоянном смещении на затворе увеличение напряжения на стоке от нуля вызывает резкое возрастание тока стока, которое продолжается до наступления насыщения тока стока. Затем ток устанавливается и остаётся относительно постоянным. Эта зависимость показана на рис. 3, а для типичного полевого прибора с p-n-переходом. Для сравнения на рис. 3, б приведены коллекторные характеристики биполярного транзистора.
Характеристики транзисторов обоих видов похожи друг на друга, за исключением того, что у биполярного транзистора перегиб характеристик происходит при значительно более низких напряжениях на коллекторе.
На выходной характеристике ПТ можно выделить две характерные области (рис. 4). При малых напряжениях сток — исток (область АВ) сопротивление канала имеет омический характер, и ток может протекать в обоих направлениях. В этом состоит отличие полевых транзисторов от электронных ламп, в которых поток электронов всегда имеет одно направление — от катода к аноду. Рабочая область АВ выходной характеристики ПТ используется в том случае, когда полевой транзистор применяется в схеме в качестве переменного сопротивления, управляемого напряжением (аттенюаторы, регуляторы АРУ).
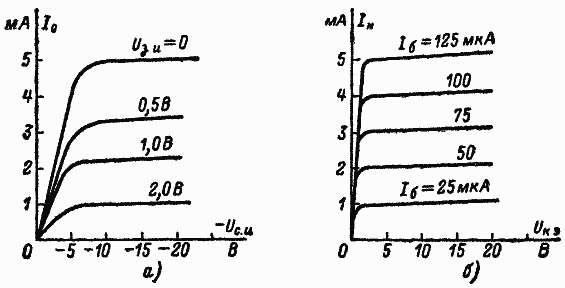
Рис. 3. Выходные характеристики транзисторов, а — ПТ с p-n-переходом; б — биполярного транзистора.
В области насыщения тока (область ВС на рис. 4) часть канала обеднена носителями заряда из-за влияния электрического поля между затвором и каналом, благодаря чему сопротивление канала становится значительным. Дальнейшее увеличение напряжения между стоком и истоком в этой области вызывает относительно небольшое изменение тока стока, который практически будет зависеть только от напряжения на затворе [1].
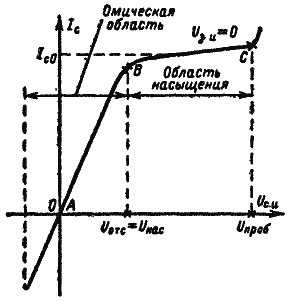
Рис. 4. Выходная характеристика ПТ при Uз.и=0
Характерной особенностью полевых транзисторов является то, что напряжение, соответствующее точке B характеристики (точка перегиба характеристики на рис. 4, после которой идёт область насыщения), при напряжении на затворе, равном нулю, численно равно напряжению отсечки и называется напряжением насыщения.
Входные характеристики полевого транзистора существенно отличаются от характеристик биполярного транзистора. Входные характеристики последнего подобны характеристикам открытого полупроводникового диода, в то время как у полевого транзистора они подобны характеристикам запертого диода (смещённого в обратном направлении). Поэтому ток затвора очень мал. Он равен нескольким наноамперам (для ПТ с управляющим p-n-переходом) при температуре 25°С и экспоненциально зависит от температуры.
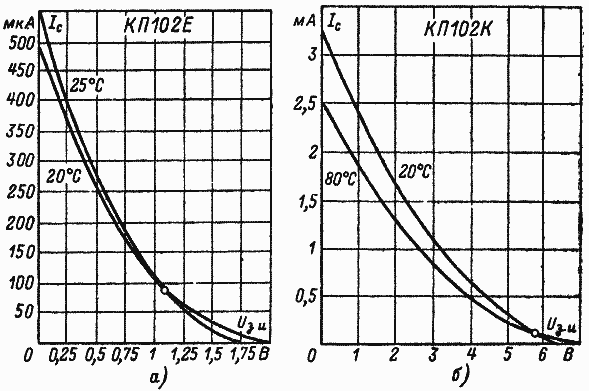
Рис. 5. Проходные характеристики ПТ при различной температуре.
Проходная характеристика, показывающая зависимость тока стока от напряжения на затворе, изображена на рис. 5. С достаточной для практических расчётов точностью проходная характеристика полевого транзистора определяется выражением (1), т. е. носит квадратичный характер. Эта особенность проходной характеристики используется в преобразователях частоты для уменьшения перекрёстной модуляции и помех от гармоник гетеродина.


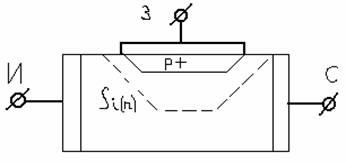 стройство
полевого транзистора.
стройство
полевого транзистора.