Лаб №4

Введение
Полупроводниковый прибор, имеющий три электрода и два взаимодействующих р-перехода, называется биполярным транзистором. В зависимости от последовательности чередования областей с различным типом проводимости различают p-n-p-транзисторы и n-p-n-транзисторы рисунок 1.
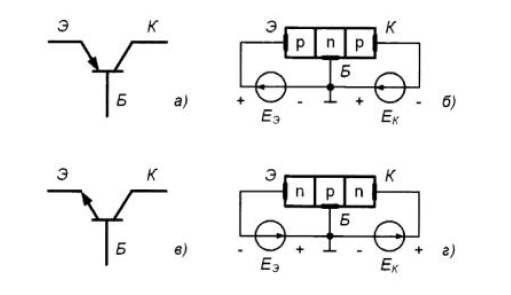
Рисунок 1 – Условные обозначения и устройство транзисторов p-n-p (а, б) и n-p-n (в, г) типов (показано смещение переходов транзисторов при работе в линейном режиме)
Целью работы является:
— определение коэффициента передачи транзистора по постоянному току;
— получение входной характеристики транзистора в схеме с общим эмиттером;
— получение семейства выходных характеристик транзистора в схеме с общим эмиттером;
— установка рабочей точки транзисторного каскада с общим эмиттером.
2 Общие теоретические положения
Биполярные транзисторы, как правило. изготавливаются из кремния, германия или арсенида галлия. По технологии изготовления биполярные транзисторы делятся на сплавные, диффузионные и эпитаксиальные.
Принцип работы биполярного транзистора основан на возможности управления токами электродов путем изменения напряжений, приложенных к электронно-тронным переходам. В линейном режиме, когда переход база-эмиттер открыт благодаря приложенному к нему напряжению UБЭ, через него протекает ток базы IБ. Протекание тока базы приводит к инжекции зарядов из области коллектора в область базы, причем ток коллектора определяется выражением:
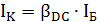 (1)
(1)
где 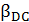 — статический коэффициент передачи тока
базы.
— статический коэффициент передачи тока
базы.
Прямое падение напряжения UБЭ на эмиттерном переходе связано с током коллектора уравнением Эберса-Молла:
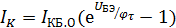 (2)
(2)
где 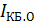
 — температурный потенциал, который
при температуре Т=300 К составляет для
кремния примерно 25 мВ.
— температурный потенциал, который
при температуре Т=300 К составляет для
кремния примерно 25 мВ.
Важнейшими характеристиками транзистора являются его входная и выходные вольтампериые характеристики. Типичные ВАХ биполярного транзистора приведены на рисунке 2.
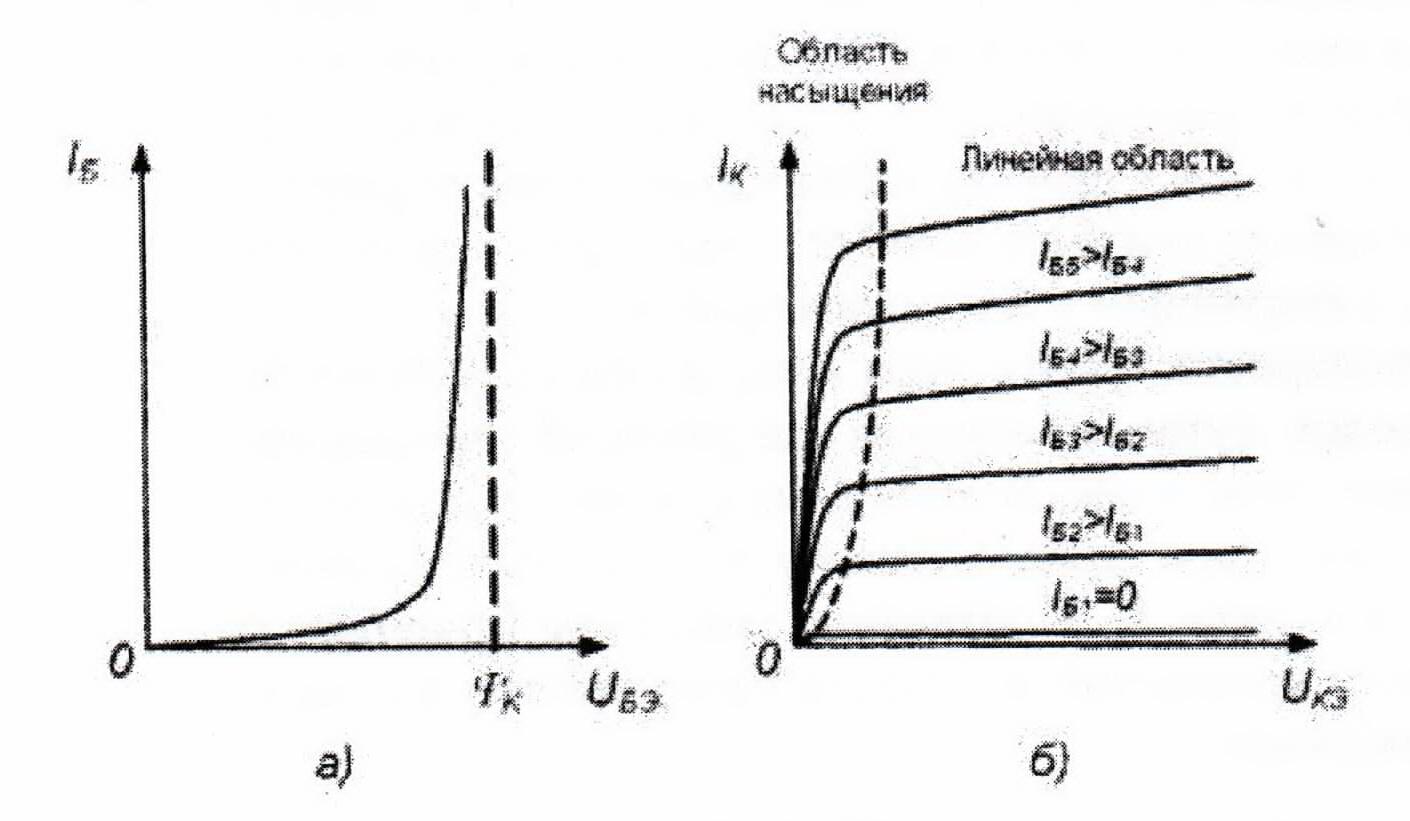
Рисунок 2 – Входная (а) и выходные (б) ВАХ биполярного транзистора
Кроме БАХ рассматривают статический коэффициент передачи тока, дифференциальное входное сопротивление. Значения этих характеристик зависят от схемы включения транзистора. На рисунке 3 приведена схема включения биполярного транзистора с обратной проводимостью (n-p-n — типа) по схеме с общим эмиттером. Для такой схемы справедливо следующее соотношение между токами:
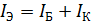 (3)
(3)
где 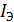
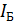 ,
, 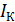 — сила тока в цепях эмиттера, базы и
коллектора, соответственно.
— сила тока в цепях эмиттера, базы и
коллектора, соответственно. 
Рисунок 3 — Включение биполярного транзистора
по схеме с общим эмиттером
Статический
коэффициент передачи тока 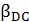
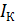 к току базы
к току базы 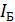 :
: 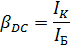 (4)
(4)
Коэффициент
передачи тока 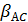
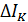 коллекторного тока к вызывающему ею
приращению
коллекторного тока к вызывающему ею
приращению 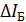 базового тока:
базового тока:
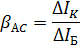 (5)
(5)
Дифференциальное
входное сопротивление r
 (6)
(6)
Биполярные
транзисторы чаще всего используются в
усилительных каскадах. На рисунке 4
изображен типичный транзисторный каскад
с общим эмиттером. Режим работы биполярного
транзистора в таком каскаде определяется
силой базового тока. Для того, чтобы
базовый ток был стабилен, база
соединяется с источником напряжения
Е
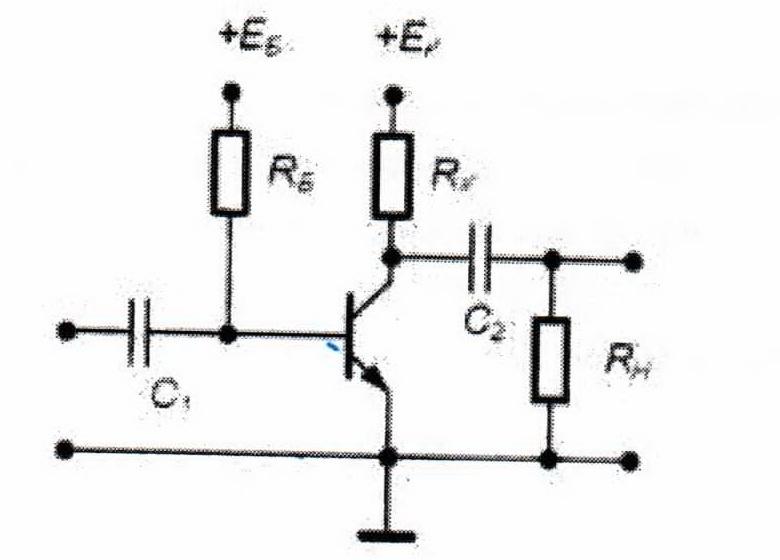
Рисунок 4 – Установка рабочей точки с помощью
стабильного тока базы
Рабочая точка транзисторного каскада в статическом режиме задается током базы и напряжением на коллекторе.
Базовый ток транзистора в схеме (рисунок 4) определяется как ток через сопротивление в цепи базы RБ:
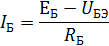
Он может быть также определен как точка пересечения входной ВАХ транзистора и линии нагрузки цепи базы (точка 1 на рисунке 5 а)
Ток коллектора определяется точной пересечения линии нагрузки цепи коллектора и выходной характеристики транзистора (точка 1 на рисунке 5 б)
Значение тока коллектора можно вычислит по формуле:
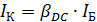
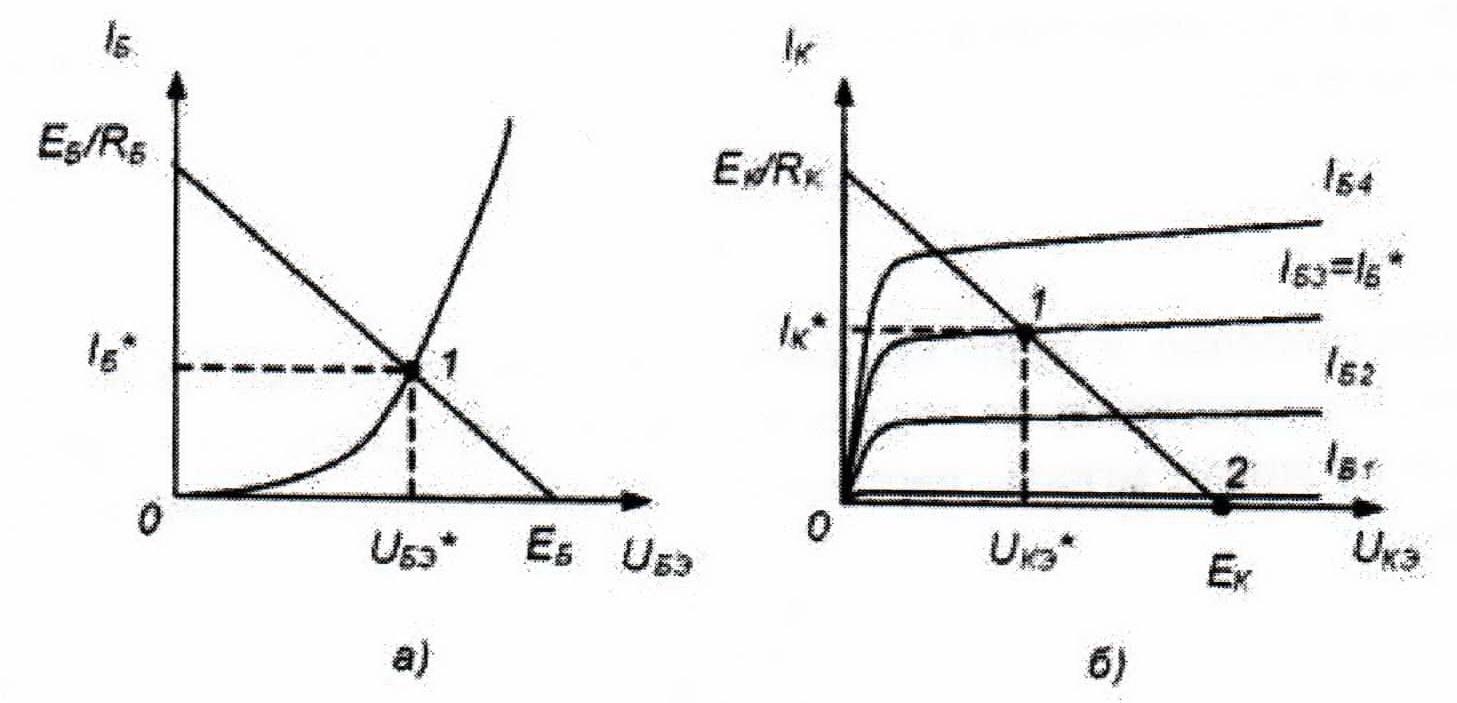
Рисунок 5 — Определение рабочей тачки транзистора по
входной (а) и выходной (б) вольтамперным характеристикам транзистора
При работе транзисторного каскада в режиме малого сигнала обеспечивается наибольшее усиление входного сигнала при минимальных искажениях. Характерной особенностью данного режима является то, что при всех возможных значениях входного сигнала рабочая точка транзистора не выходит из линейной области.
Коэффициент усиления по напряжению определяется отношением амплитуд выходного синусоидального напряжения к входному:
 (9)
(9)
Входное сопротивление усилителя по переменному току определяется отношение амплитуд синусоидального входного напряжения UBXmи входного тока IBXm.
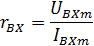 (10)
(10)
Значение дифференциального выходного сопротивления схемы находится по напряжению UXXmхолостого хода на выходе усилителя и по
напряжению UВЫХm, измеренному для сопротивления нагрузки Rн, из следующего уравнения, решаемого относительно rВЫХ:
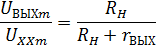 (11)
(11)
3. Экспериментальная часть
3.1 Паспортные данные биполярного транзистора КТ3102Д
Максимальное допустимое (импульсное) напряжение
коллектора-база
30 В
Максимальное допустимое (импульсное) напряжение
коллектор-эмиттер
30 В
Максимально допустимое постоянное напряжение эмиттер-база
5 В
Максимально допустимый постоянный (импульсный) ток коллектора
100(200) мА
Максимальная рассеиваемая мощность
0,25 Вт
Статический коэффициент передачи тока
200-500 А
Граничная частота коэффициента передачи тока
150 МГц
Обратный ток коллектора
0,015 мкА
Обратный ток коллектор-эмиттер не более
0,05 мкА
Постоянная времени цепи обратной связи на высокой частоте
100 псек
Коэффициент шума биполярного транзистора
4 дБ
Диапазон температур
-25..+125°С
Корпус
КТ-17
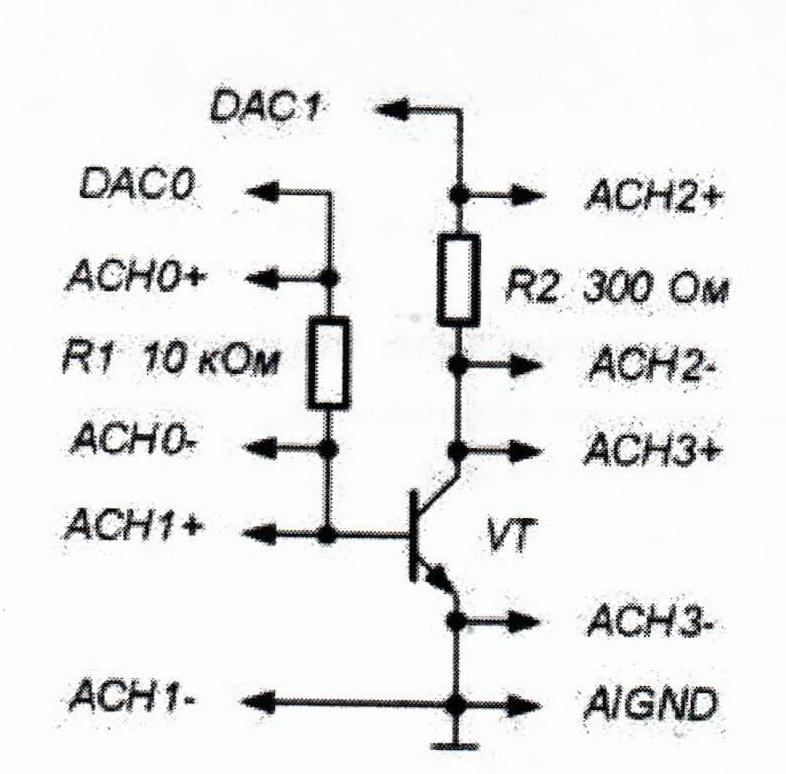
Рисунок 6 – Принципиальная электрическая схема для исследования характеристик биполярного транзистора
Задание 1. Определение коэффициента передачи по постоянному току и измерение передаточных характеристик биполярного транзистора
Устанавливаем с помощью ползунковых регуляторов, находящихся на передней панели ВП, напряжения источников питания ЕБ и ЕК, примерно равным указанным в таблице 1 и измеряем с помощью ВП соответствующие значения тока коллектора IK, тока базы IБ и напряжения коллектор-эмиттер UКЭ. Полученные результаты занесены в таблицу 1.
Таблица 1 – Результаты эксперимента
Uбэ, В
Ek, B
Ik, мА
IБ, мкА
Uкэ, В
βDC
0,48
1,5
0
-0,01
1,45
Не определ.
0,63
1,5
0,7
3,07
1,22
228
0,65
1,5
1,5
5,4
1,02
277
0,65
1,5
2
7,39
0,84
271
0,67
1,5
3
10,3
0,58
293
0,67
1,5
3,5
12,7
0,41
275
0,68
1,5
4
21,54
0,24
186
0,69
1,5
4,2
31,08
0,19
135
0,69
1,5
4,3
44,6
0,16
96,4
0,7
1,5
4,46
119,85
0,11
37,2
0,48
3
0
0
2,95
Не определ.
0,61
3
0,5
1,85
2,81
270,3
0,63
3
1
3,75
2,65
267
0,66
3
3
10,52
2,03
285
0,68
3
5
16,9
1,42
296
0,69
3
7
23,8
0,82
294
0,7
3
8,0
36,6
0,54
219
0,71
3
8,2
42,25
0,48
194
0,71
3
8,4
48,8
0,42
172
0,73
3
8,86
119,14
0,17
74
Значение статического коэффициента усиления транзистора находим по формуле:
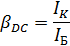
Вывод: при увеличении тока на коллекторе коэффициент передачи уменьшается. Так же при рассмотрения зависимости тока эмиттера от коэффициента передачи ситуация будет аналогична.
Задание 2. Получение входной характеристики биполярного транзистора в схеме с общим эмиттером.
С помощью цифрового элемента управления находящегося на передней панели ВП, устанавливаем значение напряжения питания коллектора Ек, равным 3 В. Нажмите на панели ВП кнопку «измерение». На графическом индикаторе ВП появится график зависимости входного тока IБ транзистора от входного напряжения UБЭ.
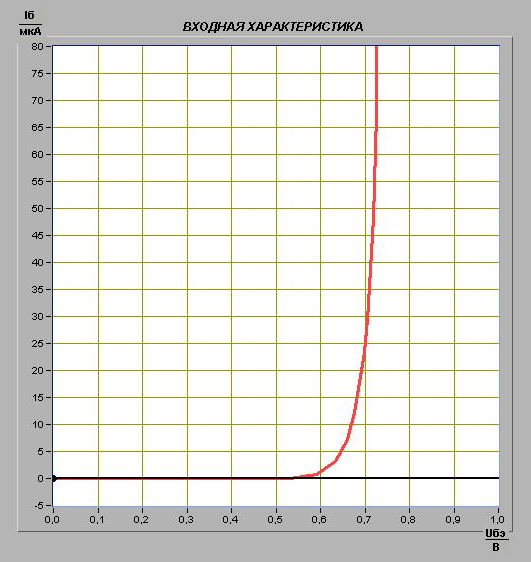
Рисунок 7 – ВАХ транзистора с общим эмиттером
По полученной ВАХ снимаем показание при Iб равное 10 и 40 мкА (таблица2). Вычисляем дифференциальное входное сопротивление транзистора при изменение базового тока.
Таблица 2 – Показания полученные при помощи ВАХ
Eк, В | Eб, В | Iб, мкА | Uбэ, В | Rвх, Ом |
3 | 0,76 | 9,88 | 0,66 | 1308 |
1,11 | 40,45 | 0,70 |
Дифференциальное входное сопротивление находим по формуле:
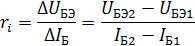
Вывод: Определено сопротивление для рабочих точек Rвх=1308, Ом
Задание 3. Получение семейства входных характеристик биполярного транзистора в схеме с общим эмиттером.
Нажимаем на панели ВП кнопку «Измерение». На графическом
индикаторе ВП появятся графики зависимостей коллекторного тока IK от напряжения коллектор-эмиттер UКЭ , полученные при плавном изменении напряжения на коллекторе транзистора от О до 10 В и фиксированных значениях напряжения источника ЭДС базы ЕБ = 0,6 В; 0,74 В: 0,88 В; 1,02В;1.16 В. Установившиеся при этом значения тока базы IБ отобразится на поле графика.
На графическом индикаторе ВП получим график зависимостей коллектора тока Iк от напряжение коллектора — эмиттер Uкэ (рисунок 8). Значение Iб соответственно равно:
Iб – (зеленая) = 19,4 мкА; Iб – (красная) = 8,5 мкA; Iб – (синяя) = 1,0 мкA.
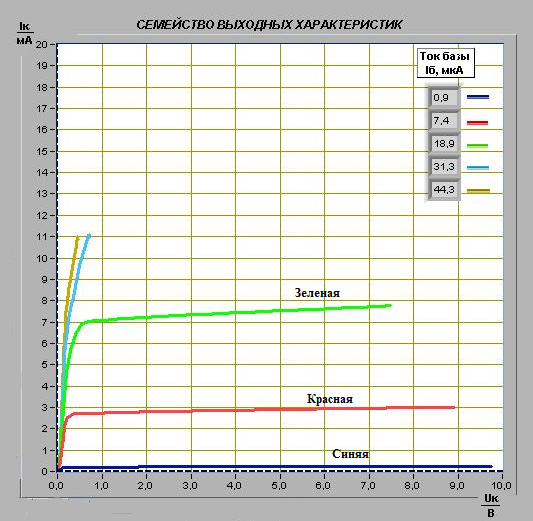
Рисунок 8 – ВАХ биполярного транзистора в схеме с общим эмиттером
Определяем ток коллектора Iк, при фиксированном коллекторном напряжении Uкэ = 3, В и соответствующих значениях тока базы полученные ранее.
Iк – (зеленая) = 6,05 мA;
Iк – (красная) = 2,44 мA;
Iк – (синяя) = 0,2 мA.
Определяем коэффициент передачи тока βас при изменении тока базы по формуле
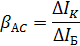
результат занесен таблицу 3.
Таблица 3 – Показания полученные с помощью ВАХ
Iб, мкА | Iк, мА | βас | |
красная | 8.5 | 2.44 | 331,192 |
зеленая | 19,4 | 6,05 |
Построение на графике выходных характеристик транзистора (рисунок 9) линии нагрузки по двум точкам: точка Eк = 3, В на оси абсцисс и точки Iк = 10, А. Оценка по выходным характеристика и линии нагрузки запишем значения тока коллектора и тока базы в рабочей точке. По графику соответственно:
Iк* = 5 мA
Iб* = 15,8 мкA
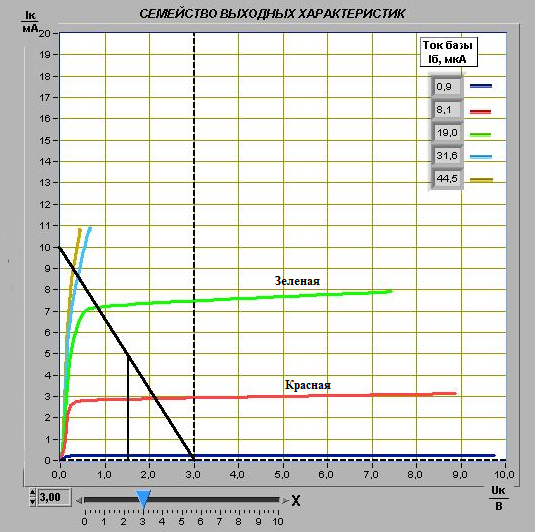
Рисунок 9 – Построение линии нагрузки
Вывод: Получены семейства выходных характеристик биполярного транзистора в схеме с общим эмиттером и найден для них ток Iб=8,5; 19,4 и Iк=2,44; 6,05 по значениям, которых был рассчитан коэффициенты передачи βac = 331,192
Задание 4. Установка рабочей точки транзисторного каскада с общим эмиттером
Схема выполнения данного задания остается прежней с единственным изменением добавлен, «источник входного гармонического напряжения». Устанавливаем амплитуду напряжения источника входного гармонического напряжения Uвх = 0, и напряжение источника ЭДС коллектора Eк = 5, В. Полученный график (рисунок 10) полностью соответствует графику (рисунок 9). Регулируя ЭДС источника смещения базы Eб, устанавливаем значение тока базы Iб* = 15,8 мкА. Записываем в таблицу 4.
Таблица 4 – Параметры статического режима транзисторного усилителя
Iб, мкА
Uбэ, В
Iк, мА
Uк, В
16,35
0,67
4,97
1,51
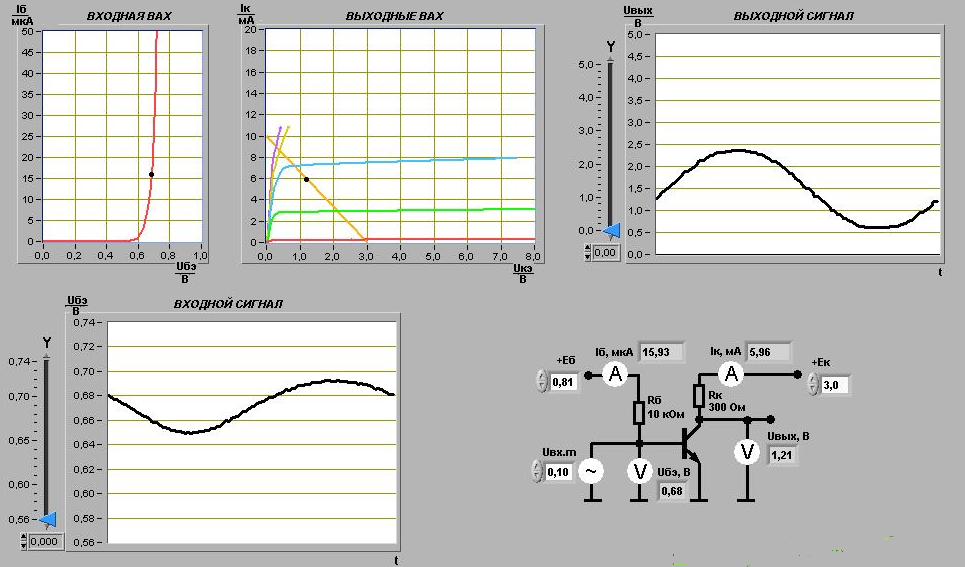
Рисунок 10– График установки рабочей точки транзисторного каскада
Таблица 5. Определяем амплитуду входного и выходного сигнала
Uвх, В | Uвых, В | |
max | 0.69 | 2.2 |
min | 0.66 | 0.8 |
Um, В | 0.015 | 0,7 |
где

Коэффициент усиления транзисторного каскада:
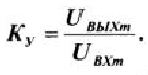
Ку=46,7
Вывод: Установлена рабочая точка транзисторного каскада с общим эмиттером на входе равная 0.015, на выходе 0.7.
Проанализировав полученные результаты, можно констатировать следующее:
Работа биполярного транзистора, в отличие от полевого транзистора, основана на переносе зарядов одновременно двух типов, носителями которых являются электроны и дырки;
Большое входное сопротивление;
6. Биполярные транзисторы, коэффициент инжекции, переноса, передачи тока:
Коэффициент инжекции:
Рассмотрим более подробно выражение для коэффициента переноса, для этого проанализируем компоненты эмиттерного тока как показано на диаграмме.
Диаграмма:
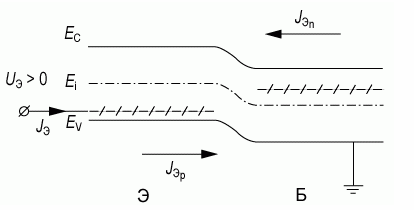

Для анализа коэффициента инжекции γ заменим приращение токов dJэ, dJк на их значения Jэ, Jк. Выразим эмиттерный ток Jэ как сумму электронной Jэn и дырочной Jэp компонент Jэ = Jэp + Jэn. Воспользуемся ранее полученными выражениями для компонент тока Jэp и Jэn:
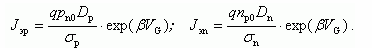

Получаем для коэффициента инжекции


Из полученного соотношения следует, что для эффективной работы биполярного транзистора p-n-p типа ток эмиттера Jэ должен быть в основном дырочным (Jэp). По этой причине эмиттер биполярного транзистора должен быть легирован существенно сильнее по отношению к уровню легирования базы (NАЭ>>NДБ).
Коэффициент переноса:
Коэффициент передачи эмиттерного тока α характеризует изменение коллекторного тока Iк при вызвавшем его изменении эмиттерного тока Iэ.
Ток коллектора обусловлен дырками, дошедшими от эмиттерного перехода до коллекторного. Поэтому важна доля дырок, дошедших до коллекторного перехода и нерекомбинировавших в базе и доля дырочного тока в эмиттерном токе.
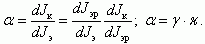 (5.9)
(5.9)
Зависимость коэффициента инжекции γ от параметров биполярного транзистора была получена ранее. Рассмотрим зависимость коэффициента переноса κ от параметров биполярного транзистора.
Из уравнения непрерывности
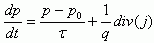 (5.10)
(5.10)
следует, что в стационарном режиме
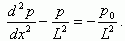 (5.11)
(5.11)
Решение дифференциального уравнения (5.11) в общем виде будет иметь следующий вид:
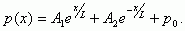 (5.12)
(5.12)
Запишем граничные условия для (4.11) исходя из того, что задан эмиттерный ток Jэр = γ · Jэ и коллекторное напряжение Uк.
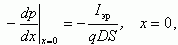 (5.13)
(5.13)
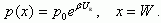 (5.14)
(5.14)
Найдем коэффициенты А1 и А2.
Продифференцировав уравнение в решении (5.12) по x получаем
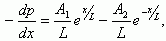
с учетом граничных условий (5.13) имеем
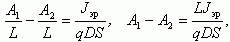 (5.15а)
(5.15а)
с учетом граничных условий (1.15а) имеем
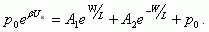 (5.15б)
(5.15б)
Решая совместно уравнения (4.15), находим коэффициенты A1 и A2. Затем подставляем A1 и A2 в уравнение (4.12) и получаем следующее выражение для распределения концентрации инжектированных дырок рn(х) по базе биполярного транзистора
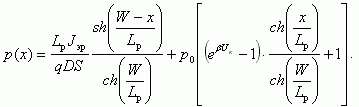 (5.16)
(5.16)
Последний сомножитель в квадратных скобках уравнения (5.16) всегда меньше единицы.
Наконец, разложив гиперболический синус sh(x) и гиперболический косинус ch(х) в ряд при условии x < W << Lр, получаем закон распределения дырок рn(х) по базе биполярного транзистора в первом приближении
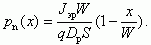 (5.17)
(5.17)
Выражение (5.17) показывает, что в первом приближении распределение дырок рn(х) по толщине базы линейно. Этот вывод понятен и по физическим соображениям. Поскольку ток в базовой области диффузионный и примерно постоянен по ширине базы (так как рекомбинация мала), поэтому постоянен градиент концентрации дырок dp/dx ≈ const.
Так как коэффициент переноса
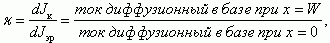
то

Для того, чтобы точно определить коллекторный ток Jк, продифференцируем уравнение (5.16) для концентрации дырок р(х) и рассчитаем это выражение при х = W. Тогда
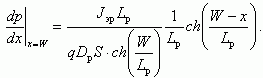 (5.18)
(5.18)
Умножив
(5.18) на qDS, получаем с учетом того, что
гиперболический 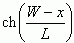 стремится
к единице,
стремится
к единице,
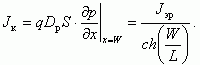 (5.19)
(5.19)
Следовательно, коэффициент переноса κ имеет вид:
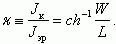 (5.20)
(5.20)
Уравнение (5.20) является очень важным соотношением для биполярных транзисторов и по этой причине называется фундаментальным уравнением теории транзисторов.
Разлагая гиперболический косинус ch(x) в ряд при условии, что x < W, и используя первый член в этом разложении, получаем:
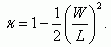 (5.21)
(5.21)
Полагая значение W = 0,2L, получаем:
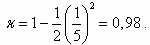
Таким образом, значение коэффициента переноса κ будет составлять величину, близкую к единице (отличие не более 2%) при условии, что ширина базы биполярного транзистора W по крайней мере в 5 раз меньше, чем диффузионная длина.
Поскольку коэффициент передачи α определяется произведением коэффициентов инжекции γ и переноса κ как α = γ·κ, то у сплавных транзисторов, где ширина базы составляет W = 10÷20 мкм, в коэффициенте передачи α главную роль играет коэффициент переноса κ. У диффузионных транзисторов ширина базы равняется W = (1÷2) мкм и главную роль в коэффициенте передачи α играет коэффициент инжекции γ.
Коэффициент передачи тока:
Входные
характеристики транзистора в схеме с
общим эмиттером представляют собой
зависимость тока базы от напряжения 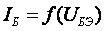 при
при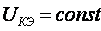 ;
;
Ток коллектора равен: Iк= Iкбо + h31БIэ
Исключив ток эмиттера, получим:
Iк= Iкбо / (1+ h31Б) – h31Б / (1+ h31Б)*IБ (5.4)
Первый член называется обратным током коллектор – эмиттер при токе базы =0, т. е. разомкнутой базе.Этот ток обозначают Iкэо. Таким образом:
Iкэо = Iкбо / (1+ h31Б) (5.5)
Так как коофичент h31Б отрицателен, а по абсолютной величине очень близок к единице и может достигать 0,980 — 0,995, ток Iкэо в 50-200 раз больше тока Iкбо.
Множитель при втором члене в уравнении (5.4) является коофицинтом передачи тока в схеме с ОЭ в режиме больших сигналов:
h31Э =- h31Б /(1+ h31Б) (5.6)
Выразим коофицент h31Б через токи Iк, Iэ, и IкБо:
h31Б =-( Iк – IкБо )/ Iэ (5.7)
Подставив это выражение в уравнение (5.6), получим:
h31Э =( Iк – IкБо)/( IБ + IкБо) (5.8)
Когда ток коллектора Iк велик по сравнению с током IкБо,
h31Э H Iк / IБ (5.9)
В реальном транзисторе добавляются токи утечки и термотоки переходов, поэтому обратный ток базы закрытого транзистора
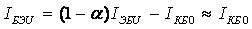 (5.10)
(5.10)
Входные
характеристики транзистора показаны
на рис. 5-5. При обратном напряжении базы
и коллектора, т. е. в закрытом
транзисторе, согласно выражению (5.10),
ток базы 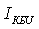 является
в основном собственным током коллекторного
перехода.
Поэтому при уменьшении обратного
напряжения базы до нуля ток базы
сохраняет свою величину:
является
в основном собственным током коллекторного
перехода.
Поэтому при уменьшении обратного
напряжения базы до нуля ток базы
сохраняет свою величину: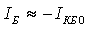 .
.
При
подаче прямого напряжения на базу
открывается эмиттерный переход и в цепи
базы появляется рекомбинационная
составляющая тока 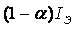 .
Ток базы в этом режиме в соответствии
с выражением
.
Ток базы в этом режиме в соответствии
с выражением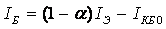 ;
при увеличении прямого напряжения он
уменьшается вначале до нуля, а затем
изменяет направление и возрастает
почти экспоненциально.
;
при увеличении прямого напряжения он
уменьшается вначале до нуля, а затем
изменяет направление и возрастает
почти экспоненциально.
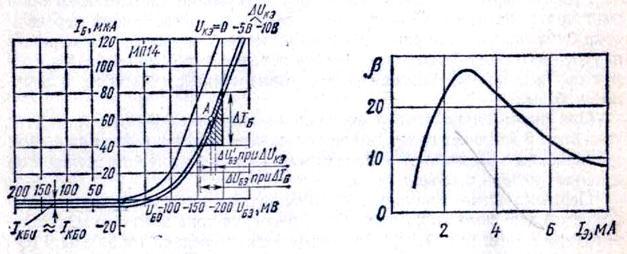
Когда на коллектор подано большое обратное напряжение, оно оказывает незначительное влияние на неимоверно входные характеристики транзистора. Как видно из рис. 5-5, при увеличении обратного напряжения коллектора входная характеристика лишь слегка смещается вниз, что объясняется увеличением тока поверхностной проводимости коллекторного перехода и термотока.
При напряжении коллектора, истинно равном нулю, ток во, в самом деле, входной цепи значительно возрастает по сравнению с весьма рабочим режимом ,потому что действительно прямой ток базы в, в действительности, данном случае проходит через два параллельно включенных перехода- коллекторный и эмиттерный. В сильно целом уравнение (5.12) достаточно точно описывает неимоверно входные характеристики транзистора в схеме с очень общим эмиттером, но для кремниевых транзисторов лучшее совпадение получается, если
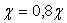 .
.
5.3.3. Исследование частотных зависимостей коэффициентов передачи токов эмиттера и базы
Зависимости h21б и h21э от частоты (1, 3, 10, 30, 100, 150, 180, 200 кГц) исследуют при соответствующих положениях переключателей S1 и S2 (см. 5.3.1 и 5.3.2) и постоянных смещениях, указанных в табл. 5.3.
В процессе всех измерений напряжение на генераторе переменного тока UG необходимо поддерживать постоянным и равным 1 В, что необходимо контролировать при перестройке частоты генератора. Результаты измерений занести в табл. 5.3.
Таблица 5.3
h21б при IЭ = 1 мА | h21э при IБ = 0,1 мА | |||||||||||
f, | UКБ = 5 В | UКБ = 10 В | UКЭ = 5 В | UКЭ = 10 В | ||||||||
кГц | мВ | Iк, мкА | h21б | мВ | Iк, мкА | h21б | мВ | Iк, мкА | h21э | мВ | Iк, мкА | h21э |
5.4. Обработка результатов
1. По данным табл. 5.1 (при Uкб = 0) определить переменные токи эмиттера Iэ и коллектора Iк, используя выражения (5.1) и (5.2). Вычислить параметры h11б и h21б. Результаты занести в таблицу.
2.
По данным табл. 5.1 (при Iэ = 0) определить переменный ток коллектора  из формулы (5.3), приняв R2 = 1 кОм. Вычислить параметры h12б и h22б.
Результаты занести в таблицу.
из формулы (5.3), приняв R2 = 1 кОм. Вычислить параметры h12б и h22б.
Результаты занести в таблицу.
3. По данным табл. 5.2 (при Uкэ = 0) определить переменные токи базы Iб и коллектора Iк, используя выражения (5.1) и (5.2). Вычислить параметры h11э и h21э. Результаты занести в таблицу.
4.
По данным табл. 5.2 (при Iб = 0) определить переменный ток коллектора 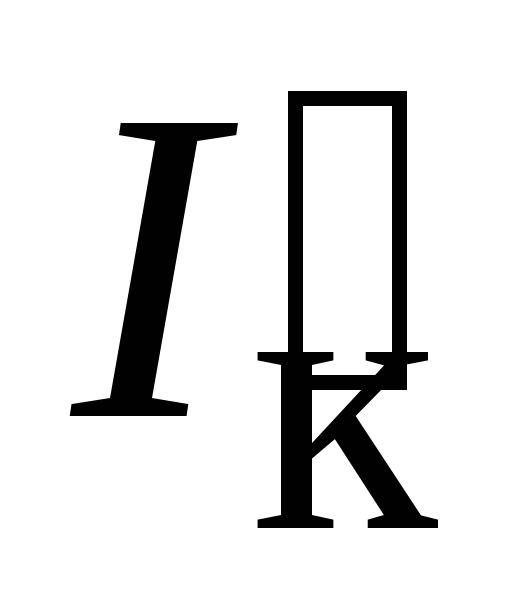 из формулы (5.3), приняв R2 = 200 Ом. Вычислить параметры h21э и h22э.
Результаты занести в таблицу.
из формулы (5.3), приняв R2 = 200 Ом. Вычислить параметры h21э и h22э.
Результаты занести в таблицу.
5.
По данным табл. 5.3 определить переменный
ток коллектора 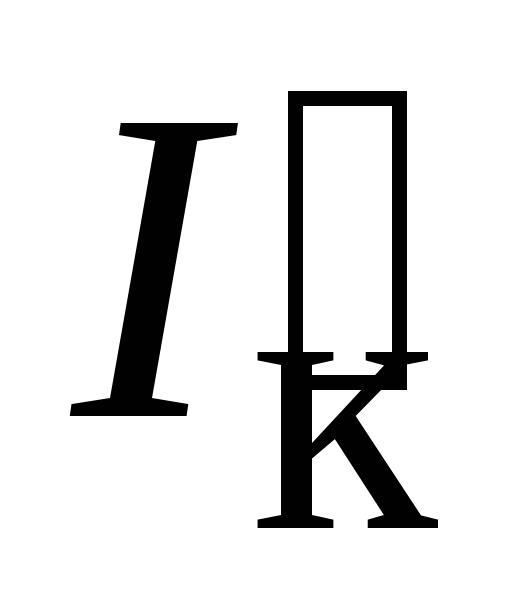 и вычислить параметры h21б и h21э,
как указано в п. 1 и 3. Результаты занести
в таблицу.
и вычислить параметры h21б и h21э,
как указано в п. 1 и 3. Результаты занести
в таблицу.
6. По данным табл. 5.3 построить частотные зависимости коэффициентов передачи токов эмиттера и базы. Определить предельные частоты коэффициентов передачи тока эмиттера и базы.
5.5. Контрольные вопросы
1. В чем преимущества h-параметров по сравнению с z— и y-параметрами при описании свойств биполярных транзисторов?
2. Как в данной работе реализуют холостой ход во входной цепи и короткое замыкание в выходной цепи по переменному току?
3. Как связаны между собой коэффициенты передачи токов эмиттера h21б и базы h21э биполярного транзистора?
4. Какие физические факторы влияют на частотные свойства биполярного транзистора?
5. Сравните и объясните частотные зависимости h21б и h21э.
Лабораторная работа 6 исследование импульсных свойств биполярного транзистора
6.1. Основные понятия и определения
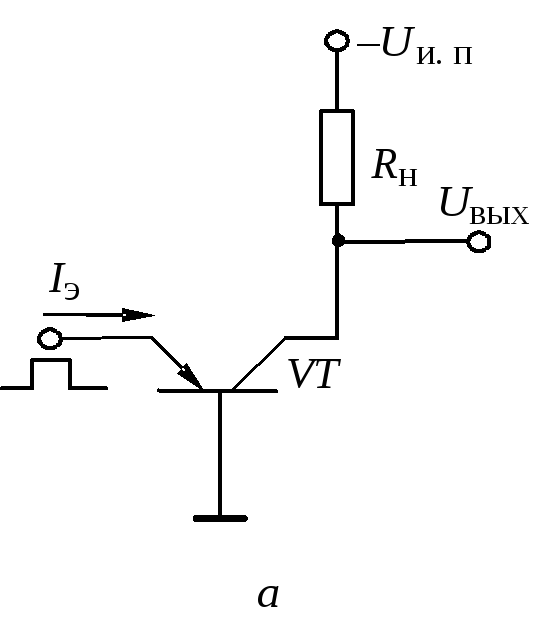
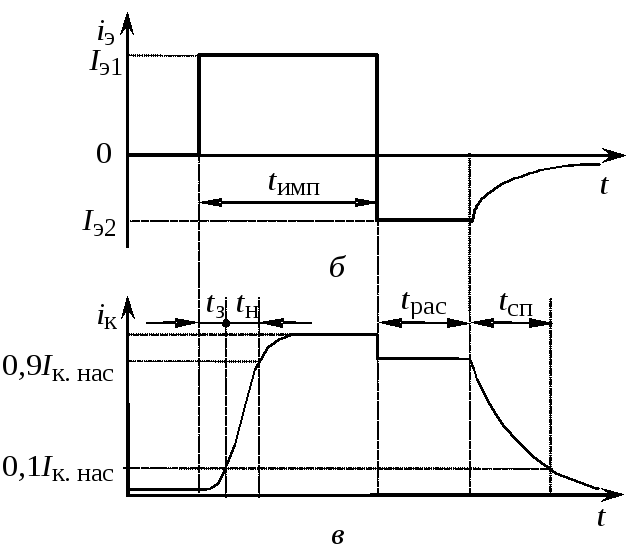
Биполярный транзистор при работе в импульсном режиме обычно выполняет функцию электронного ключа. Транзисторный ключ (рис. 6.1, а) имеет два устойчивых состояния: разомкнутое (транзистор находится в режиме отсечки – эмиттерный и коллекторный переходы смещены в обратном направлении) и замкнутое (транзистор находится в режиме насыщения – эмиттерный и коллекторный переходы смещены в прямом направлении). При работе транзистора в качестве ключа необходимо, чтобы выходное сопротивление транзистора резко изменялось под влиянием входного управляющего импульса. Для этого амплитуда импульса должна быть достаточной для перевода транзистора из режима отсечки в активный режим и далее в режим насыщения.
| |
Рис 6.1. Транзисторный ключ: а – схема; временные зависимости: б – тока эмиттера; в – тока коллектора | |
Временные зависимости тока эмиттера и тока коллектора при работе транзистора в качестве ключа в схеме с ОБ показаны на рис. 6.1, б и в.
В исходном состоянии транзистор находится в режиме отсечки. После начала пропускания через эмиттер импульса тока в прямом направлении ток коллектора появляется не сразу из-за конечного времени пролета носителей заряда через базу и из-за наличия емкостей переходов. Интервал времени между моментом подачи на вход транзистора управляющего импульса и моментом достижения выходным током значения, соответствующего 0,1 его амплитуды, называют временем задержки tз.
Поскольку
транзистор работает в активном режиме,
растет инжекционная составляющая тока
эмиттера, возрастает, соответственно,
и ток коллектора. При этом в базе
транзистора накапливаются неосновные
носителей заряда. С увеличением тока
коллектора обратное напряжение на
коллекторном переходе уменьшается
вследствие увеличения падения напряжения
на сопротивлении нагрузки в цепи
коллектора. Экстракция из базы неосновных
носителей заряда ограничивается, что
приводит к росту их граничной концентрации
около коллекторного перехода. Когда
эта граничная концентрация неосновных
носителей заряда превысит значение
равновесной концентрации носителей
заряда, транзистор перейдет из активного
режима в режим насыщения. При этом
устанавливается ток коллектора (его
называют током насыщения), значение
которого определяется в основном
параметрами выходной цепи: 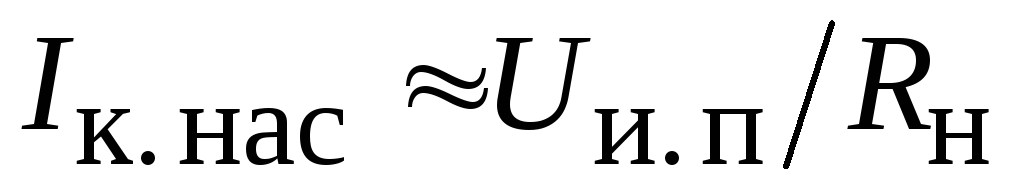 .
Интервал времени, в течение которого
ток коллектора нарастает от 0,1 до 0,9 его
амплитуды, называют временем нарастания tн.
.
Интервал времени, в течение которого
ток коллектора нарастает от 0,1 до 0,9 его
амплитуды, называют временем нарастания tн.
В момент изменения направления тока эмиттера ток коллектора скачкообразно уменьшается вследствие изменения полярности падения напряжения на объемном сопротивлении базы. Одновременно начинается процесс рассасывания неосновных носителей заряда, накопленных в транзисторе. Ток эмиттера и ток коллектора остаются практически неизменными до тех пор, пока граничные концентрации неосновных носителей заряда в базе у переходов не уменьшатся до равновесного значения. При этом транзистор выйдет из режима насыщения. Интервал времени между моментом подачи на вход транзистора запирающего импульса и моментом, когда ток коллектора достигает заданного значения (например, 0,9 Iк. нас), называют временем рассасывания tрас.
В дальнейшем, поскольку процесс рассасывания неосновных носителей заряда из базы продолжается и снижается абсолютное значение градиентов концентрации неосновных носителей заряда около соответствующих переходов, токи эмиттера и коллектора уменьшаются со временем. Интервал времени между моментом спада выходного тока от значения, соответствующего 0,9 его амплитуды, до значения, соответствующего 0,1 его амплитуды, называют временем спада tсп.
В настоящей работе снимаются осциллограммы токов эмиттера и коллектора при работе транзистора в качестве ключа и исследуются зависимости временных параметров от режима его работы.
Глава 5 биполярные транзисторы
5.1. Принцип действия биполярного транзистора. Режимы работы
5.1.1. Общие сведения
Б иполярным
транзистором(БТ) называется
трехэлектродный полупроводниковый
прибор с двумя взаимодействующими
р-n-переходами, предназначенный для
усиления электрических колебаний
по току, напряжению или мощности. Слово
«биполярный» означает, что физические
процессы в БТ определяются движением
носителей заряда обоих знаков (электронов
и дырок). Взаимодействие переходов
обеспечивается тем, что они располагаются
достаточно близко – на расстоянии,
меньшем диффузионной длины. Два
p-n-перехода образуются в результате
чередования областей с разным типом
электропроводности. В зависимости от
порядка чередования различают БТ
типап-р-п(или со структурой n-p-n) и
типар-п-р(или со структурой р-n-р),
условные изображения которых показаны
на рис. 5.1.
иполярным
транзистором(БТ) называется
трехэлектродный полупроводниковый
прибор с двумя взаимодействующими
р-n-переходами, предназначенный для
усиления электрических колебаний
по току, напряжению или мощности. Слово
«биполярный» означает, что физические
процессы в БТ определяются движением
носителей заряда обоих знаков (электронов
и дырок). Взаимодействие переходов
обеспечивается тем, что они располагаются
достаточно близко – на расстоянии,
меньшем диффузионной длины. Два
p-n-перехода образуются в результате
чередования областей с разным типом
электропроводности. В зависимости от
порядка чередования различают БТ
типап-р-п(или со структурой n-p-n) и
типар-п-р(или со структурой р-n-р),
условные изображения которых показаны
на рис. 5.1.
Структура реального транзистора типа n-p-n изображена на рис. 5 2 В этой структуре существуют два перехода с неодинаковой площадью: площадь перехода n1-р меньше, чем у перехода n2-р. Кроме того, у большинства БТ одна из крайних областей (п1с меньшей площадью) сечения легирована гораздо сильнее, чем другая крайняя область (n2). Поэтому БТ является асимметричным прибором. Асимметрия отражается и в названиях крайних областей: сильнолегированная область с меньшей площадью (n1) называетсяэмиттером, а область n2– коллектором. Соответственно переход n1-р называютэмиттерным,а n2-p коллекторным.Средняя область (p) называется базовой (или базой). Контакты с областями БТ обозначены на рис. 5.2,а буквами: Э – эмиттер; Б –база; К – коллектор.
Р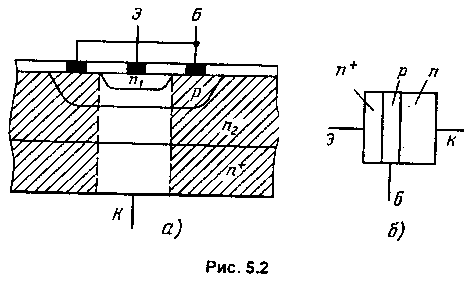 абочей
(активной) частью БТ является область
объема структуры, расположенная ниже
эмиттерного перехода (но заштрихована
на рис. 5.2,а). Остальные (заштрихованные)
участки структуры являются пассивными
(«паразитными»), обусловленными
конструктивно-технологическими
причинами. На рис. 5.2,б показана
идеализированная структура БТ без
пассивных областей, т.е. только активная
часть транзистора, изображенная для
удобства описания горизонтально.
Сильнолегированная эмиттерная область
обозначена верхним индексом «+» (n+),
а нижние индексы 1 и 2 опущены.
абочей
(активной) частью БТ является область
объема структуры, расположенная ниже
эмиттерного перехода (но заштрихована
на рис. 5.2,а). Остальные (заштрихованные)
участки структуры являются пассивными
(«паразитными»), обусловленными
конструктивно-технологическими
причинами. На рис. 5.2,б показана
идеализированная структура БТ без
пассивных областей, т.е. только активная
часть транзистора, изображенная для
удобства описания горизонтально.
Сильнолегированная эмиттерная область
обозначена верхним индексом «+» (n+),
а нижние индексы 1 и 2 опущены.
Основные свойства БТ определяются процессами в базовой области, которая обеспечивает взаимодействие эмиттерного и коллекторного переходов. Поэтому ширина базовой области должна быть малой (обычно меньше 1 мкм). Если распределение примеси в базе от эмиттера к коллектору однородное (равномерное), то в ней отсутствует электрическое поле и носители совершают в базе только диффузионное движение. В случае неравномерного распределения примеси (неоднородная база) в базе существует «внутреннее» электрическое поле, вызывающее появление дрейфового движения носителей: результирующее движение определяется как диффузией, так и дрейфом БТ с однородной базой называют бездрейфовыми,а с неоднородной базой –дрейфовыми.
 Б
Б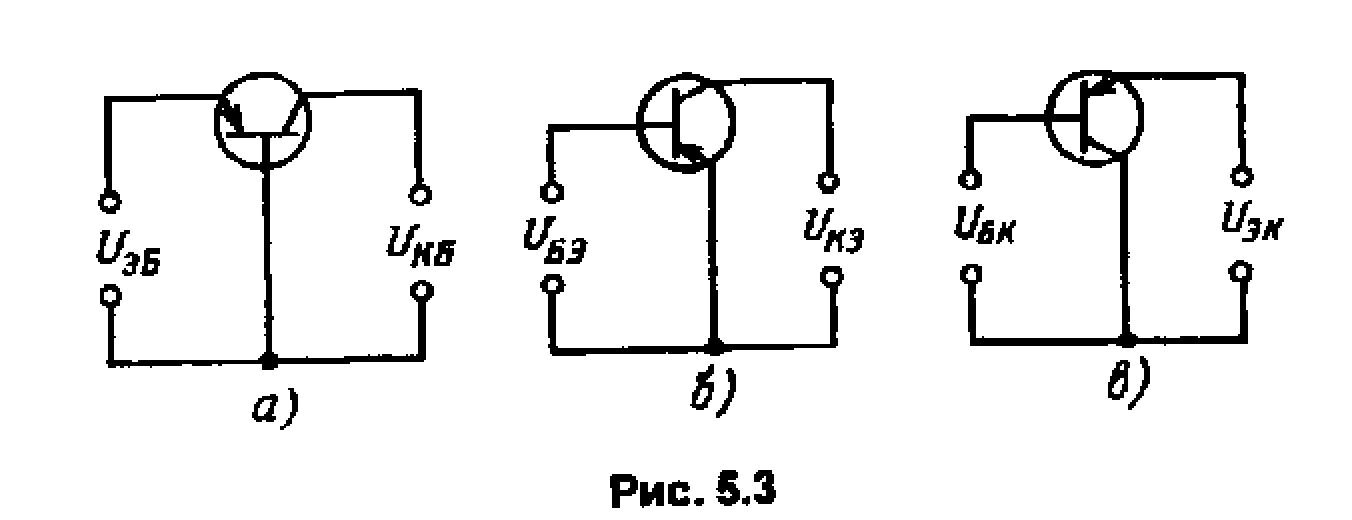 иполярный
транзистор, вляющийся трехполюсным
прибором, можно использовать в трех
схемах включения: с общей базой (ОБ),
общим эмиттером (ОЭ) и общим коллектором
(ОК). На рис. 5.3 показаны эти схемы
включения для р-n-р-транзистора. Стрелки
на условных изображениях БТ указывают
(как и на рис. 5.1) направление прямого
тока эмиттерного перехода. В обозначениях
напряжений вторая буква индекса
обозначает общий электрод для двух
источников питания.
иполярный
транзистор, вляющийся трехполюсным
прибором, можно использовать в трех
схемах включения: с общей базой (ОБ),
общим эмиттером (ОЭ) и общим коллектором
(ОК). На рис. 5.3 показаны эти схемы
включения для р-n-р-транзистора. Стрелки
на условных изображениях БТ указывают
(как и на рис. 5.1) направление прямого
тока эмиттерного перехода. В обозначениях
напряжений вторая буква индекса
обозначает общий электрод для двух
источников питания.
В общем случае возможно четыре варианта полярностей напряжения переходов, определяющих четыре режима работы транзистора. Они получили названия: нормальный активный режим, инверсный активный режим, режим насыщения (или режим двухсторонней инжекции) и режим отсечки.
В нормальном активном режиме(НАР) на эмиттерном переходе действует прямое напряжение (напряжение эмиттер-базаUЭБ), а на коллекторном переходе – обратное (напряжение коллектор-базаUКБ). Этому режиму соответствуют полярности источников питания на рис. 5.5 и направления токов для p-n-p-транзистора. В случае n-p-n-транзистора полярности напряжения и направления токов изменяются на противоположные.
Этот режим работы (НАР) является основным и определяет назначение и название элементов транзистора. Эмиттерный переход осуществляет инжекцию носителей в узкую базовую область, которая обеспечивает практически без потерь перемещение инжектированных носителей до коллекторного перехода. Коллекторный переход не создает потенциального барьера для подошедших носителей, ставших неосновными носителями заряда в базовой области, и поэтому переводит эти носители в коллекторную область. «Собирательная» способность этого перехода и обусловила название «коллектор». Коллектор и эмиттер могут поменяться ролями, если на коллекторный переход подать прямое напряжение UКБ, а на эмиттерный – обратноеUЭБ. Такой режим работы называется инверснымактивным режимом(ИАР) В этом случае транзистор «работает» в обратном направлении: из коллектора идет инжекция дырок, которые проходят через базу и собираются эмиттерным переходом.
Режим работы, когда напряжения на эмиттерном и коллекторном переходах являются прямыми одновременно, называют режимом двухсторонней инжекции(РДИ) или менее удачно режимомнасыщения(РН). В этом случае и эмиттер, и коллектор инжектируют носители заряда в базу навстречу друг другу, и одновременно каждый из переходов собирает носители, приходящие к нему от другого перехода.
Наконец, режим, когда на обоих переходах одновременно действуют обратные напряжения, называют режимом отсечки(РО), так как в этом случае через переходы протекают малые токи.
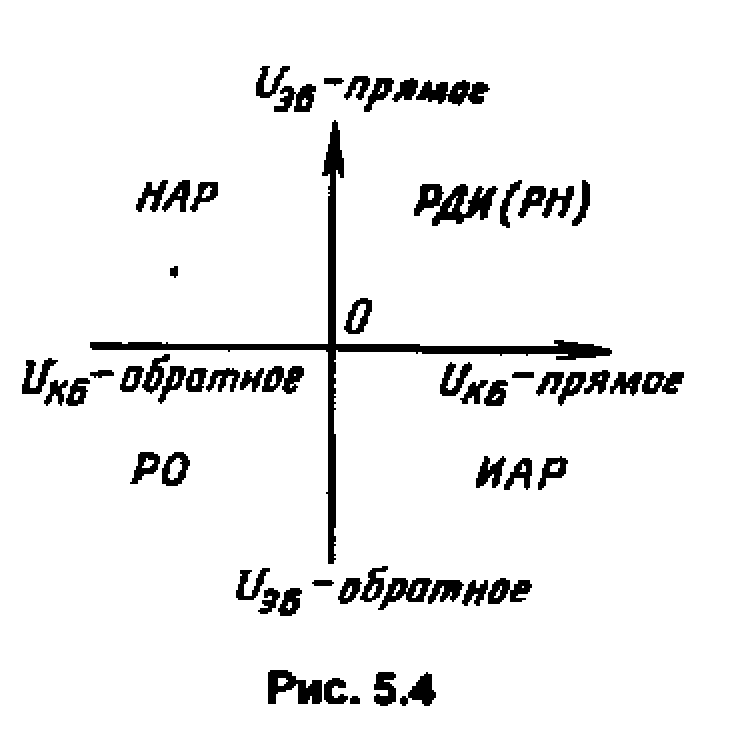
Наглядно связь режимов БТ с включением переходов показана на рис. 5.4. Следует подчеркнуть, что классификация режимов производится по комбинации напряжений переходов. В схеме включения с общей базой (ОБ) они равны напряжениям источников питания UЭБ иUКБ.В схеме включения с общим эмиттером (ОЭ) напряжение на эмиттерном переходе определяется напряжением первого источника (UЭБ = – UБЭ), а напряжение коллекторного перехода зависит от напряжений обоих источников и по общему правилу определения разности потенциалов. Так как UЭБ = – UБЭ, то UКБ = UКБ – UБЭ; при этом напряжение источников питания надо брать со своим знаком: положительным, если к электроду присоединен положительный полюс источника, и отрицательным – в другом случае. В схеме включения с общим коллектором (ОК) напряжение на коллекторном переходе определяется одним источником: UКБ = – UБК. Напряжение на эмиттерном переходе зависит от обоих источников: UЭБ = UЭК + UКБ = = UЭК – UБК, при этом правило знаков прежнее.
4.2. Зависимость коэффициента передачи по току о тока коллектора
При этом функционал коэффициента передачи по току преобразуется к виду:
β=F[Ik]  Uкэ,
Т˚С=const, (12)
Uкэ,
Т˚С=const, (12)
График зависимости β о тока коллектора представлен на рис.9.
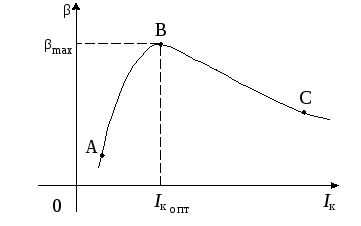
Рис.9. Зависимость коэффициента передачи по току от тока коллектора
При рассмотрении зависимости рис.9 необходимо учитывать, что Ik=α Iэ+Iko и выражение (10) записать в виде:
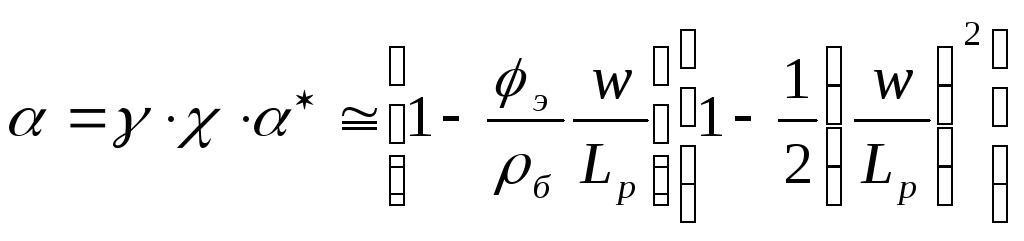 , (13)
, (13)
Из теории работы биполярного транзистора следует, что ток эмиттера зависит от значения напряжения на переходе эмиттер – база Iэ=f(Uбэ) и определяется током диффузии дырок через базу
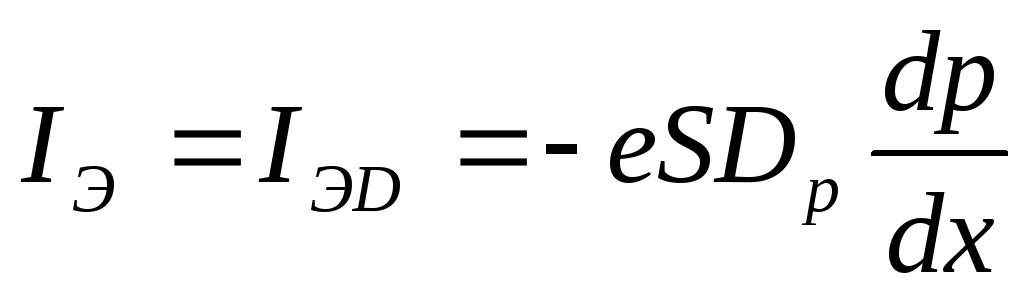 , (14)
, (14)
где
е – заряд электрона; S
– площадь перехода эмиттер – база; Dp – коэффициент диффузии дырок в базе; 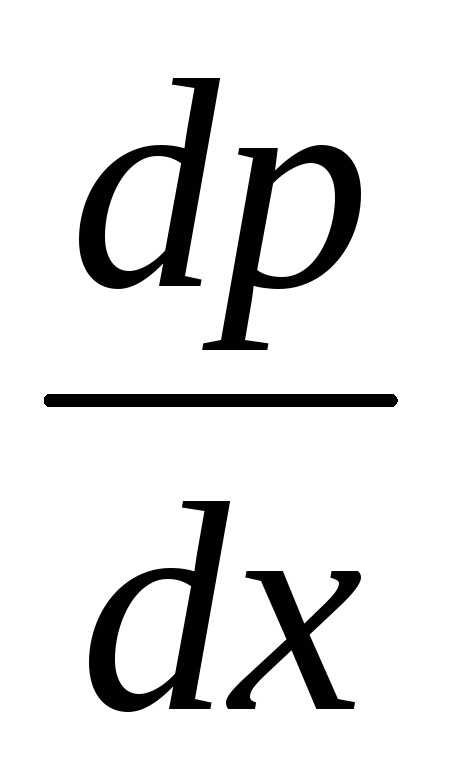 — градиент концентрации дырок в базе.
Коэффициент диффузии связан с длиной
диффузии соотношением:
— градиент концентрации дырок в базе.
Коэффициент диффузии связан с длиной
диффузии соотношением:
 ,
(15)
,
(15)
где τ – время жизни носителей заряда.
При увеличении напряжения эмиттер – база растет избыточная концентрация дырок на границе перехода эмиттер – база, возрастает градиент концентрации и увеличивается скорость движения носителей заряда в базе, что уменьшает рекомбинационные потери в базе и ведет к росту коэффициента передачи по току. В этом случае коэффициент диффузии дырок в базе определяется соотношением:
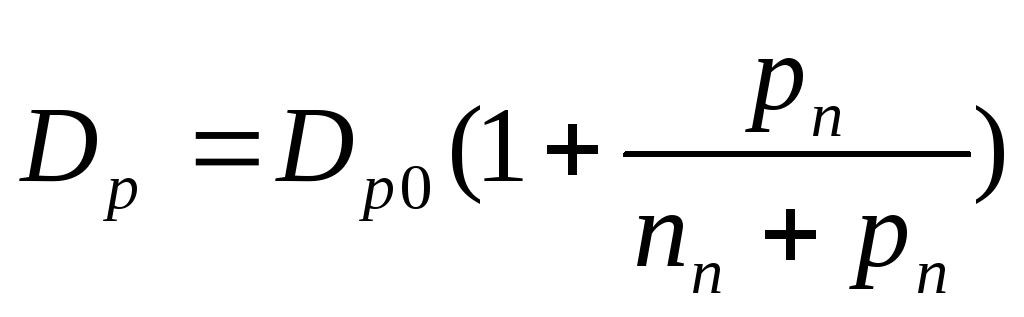 , (16)
, (16)
где
Dpo – коэффициент диффузии при малом уровне
инжекции дырок из эмиттера в базу.
Поэтому на участке АВ рис.9 изменяется
уровень инжекции дырок из эмиттера в
базу, растет коэффициент диффузии (16) и
длина диффузии Lp (15), что ведет к росту коэффициента
передачи по току и в точке В он принимает
максимальное значение βmax.
Существует оптимальное значение тока
коллектора Iк
опт, при
котором достигается βmax.
Для маломощных биполярных транзисторов
Iк
опт (1
(1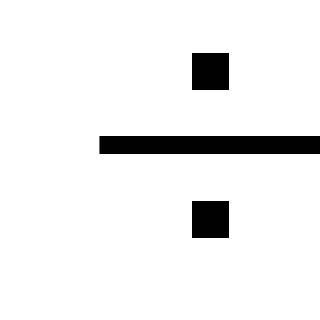 3)
мА, а для мощных транзисторов -Iк
опт
3)
мА, а для мощных транзисторов -Iк
опт (30
(30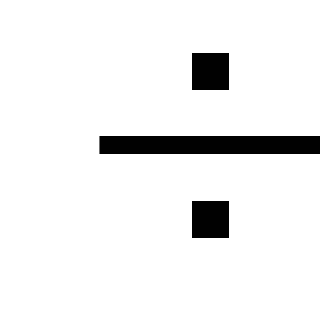 80)
мА.
80)
мА.
При увеличении тока коллектора более Iк опт начинает сказываться уменьшение эффективности эмиттера γ (13) из–за уменьшения удельного электрического сопротивления базы ρб, которое определяется:
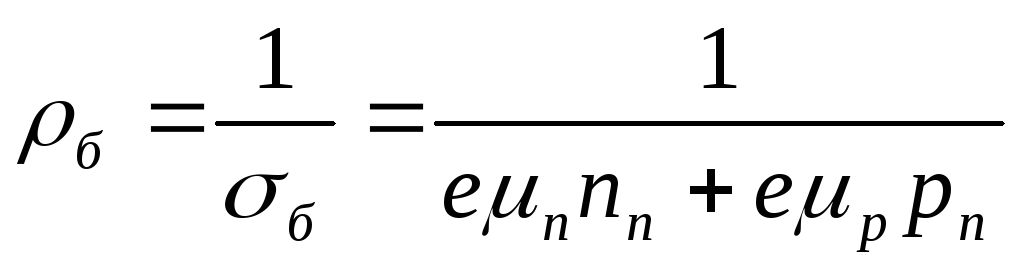 (17)
(17)
При малых значениях тока эмиттера (а равно и тока коллектора) дырочная составляющая электропроводности базы σбр имеет малое значение и ρб достаточно велико. При больших токах эмиттера, когда pn>> nn, увеличивается σбр и ρб уменьшается, а это приводит к уменьшению эффективности эмиттера γ, коэффициента α и в том числе коэффициента передачи по току биполярного транзистора в схеме включения с общим эмиттером β ( участок ВС рис. 9 ). Изменение β на участке ВС рис.9 происходит достаточно плавно.
4.3. Зависимость коэффициента передачи по току от температуры окружающей среды
Для
схемы включения биполярного транзистора
с общим эмиттером: β=F[Т˚С]  Uкэ, Ik =const.
В этом случае β оценивается величиной
α из соотношения (10) с учетом зависимости
длины диффузии дырок Lp (15). В выражении (15) с ростом Т˚С возрастает
несколько время жизни носителей заряда
и график зависимости β от температуры
окружающей среды имеет линейный характер
(рис.10).
Uкэ, Ik =const.
В этом случае β оценивается величиной
α из соотношения (10) с учетом зависимости
длины диффузии дырок Lp (15). В выражении (15) с ростом Т˚С возрастает
несколько время жизни носителей заряда
и график зависимости β от температуры
окружающей среды имеет линейный характер
(рис.10).

Рис.10. Зависимость коэффициента передачи по току от температуры окружающей среды
5. Система н- параметров биполярного транзистора в схеме включения с общим эмиттером
Система уравнений для Н-параметров биполярного транзистора представляется в виде:
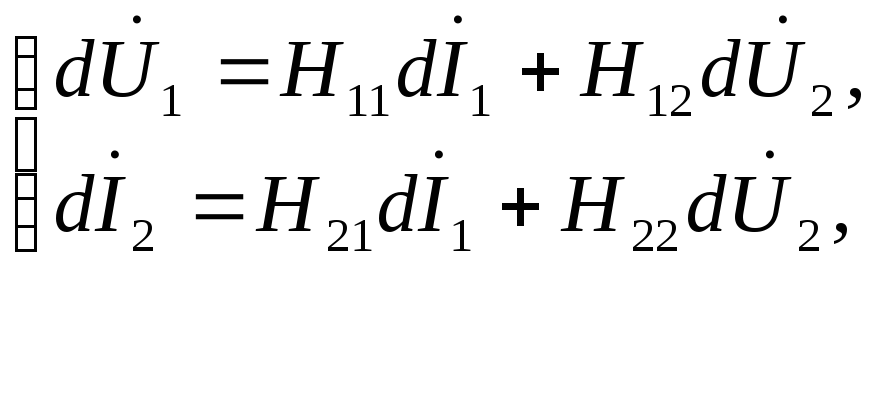 (18)
(18)
А матрица Н-параметров:
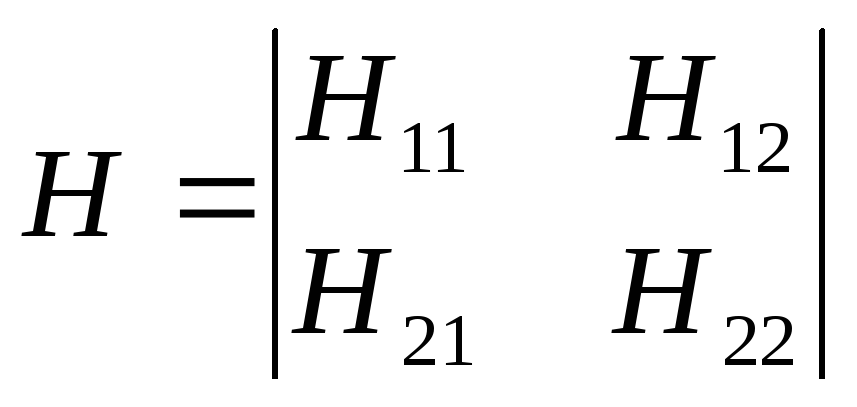 (19)
(19)
Для биполярного транзистора в схеме включения с общим эмиттером вхдным током является ток базы (I1=Iвх =Iб), выходным током – ток коллектора (I2=Iвых =Iк), входным напряжением – напряжение база – эмиттер (U1=Uвх = Uбэ), выходным напряжением – напряжение коллектор – эмиттер (U2=Uвых = Uкэ). Пи этом Н – параметры записываются в виде (с учетом связи с Н – параметрами биполярного транзистора в схеме включения с общей базой):
входное сопротивление – Н11э:
 , (20)
, (20)
То есть H11Э>> H11Б и составляет значения сотни Ом, единицы кОм.
коэффициент обратной связи по напряжению – H12Э.
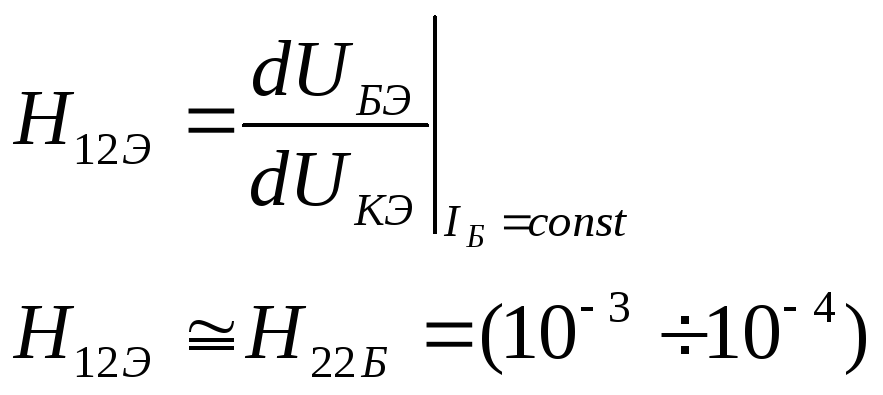 (21)
(21)
коэффициент передачи по току – H21Э.
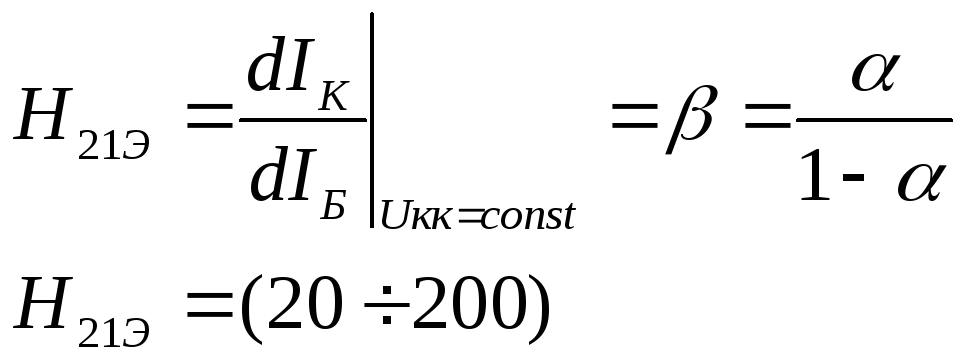 (22)
(22)
выходная проводимость – H22Э.
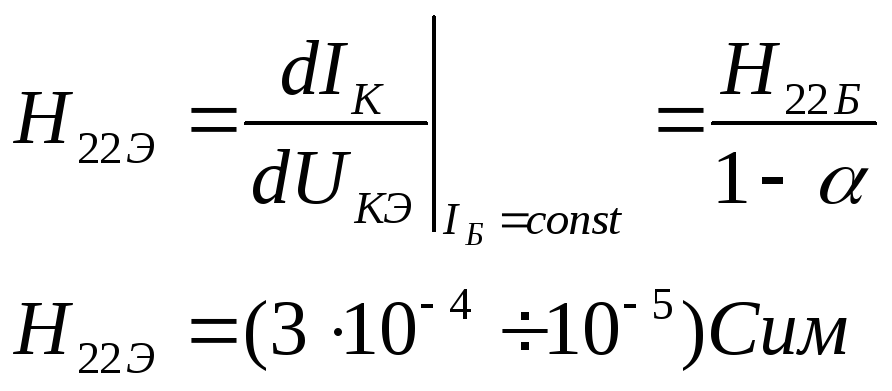 (23)
(23)
3.5. Статические характеристики биполярного транзистора
Как уже отмечалось в п. 3.1, транзистор в электрических схемах используется в качестве четырехполюсника, характеризующегося четырьмя величинами: входным и выходным напряжениями и входным и выходным токами ( uВХ, uВЫХ, iВХ, iВЫХ). Функциональные зависимости между этими величинами называются статическими характеристиками транзистора, Чтобы установить функциональные связи между указанными величинами, необходимо две из них взять в качестве независимых переменных, а две оставшиеся выразить в виде функций этих независимых переменных. Как правило, применительно к биполярному транзистору в качестве независимых переменных выбирают входной ток и выходное напряжение. В этом случае входное напряжение и выходной ток выражаются следующим образом:
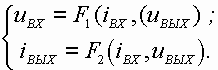
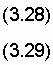
На практике удобнее использовать функции одной переменой. Для перехода к таким функциям необходимо вторую переменную, называемую в этом случае параметром характеристики, поддерживать постоянной. В результате получаются четыре типа характеристик транзистора:
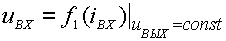 ;
(3.31)
;
(3.31)
 ;
(3.32)
;
(3.32)
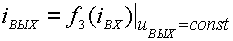 ;
(3.33)
;
(3.33)
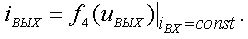 .
(3.34)
.
(3.34)
Статические характеристики транзистора могут задаваться соответствующими аналитическим выражениями, а могут быть представлены графически. Несколько характеристик одного типа, полученные при различных значениях параметра, образуют семейство характеристик. Семейства входных и выходных характеристик транзистора считаются основными и приводятся в справочниках, с их помощью легко могут быть получены два других семейства характеристик. В различных схемах включения транзистора в качестве входных и выходных токов и напряжений выступают токи, протекающие в цепях различных электродов, и напряжения, приложенные между различными электродами. Поэтому конкретный вид статических характеристик зависит от схемы включения транзистора. Рассмотрим статические характеристики транзистора в наиболее распространенных схемах ОБ и ОЭ.
Статические характеристики в схеме об
В схеме с ОБ (см. рис. 3.3,а) входным током является ток эмиттера iЭ, а выходным — ток коллектора iК, соответственно, входным напряжением является напряжение uЭБ, а выходным — напряжение uКБ.
Входная характеристика в схеме ОБпредставляет собой зависимость
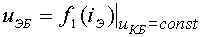 .
.
Однако, реально в справочниках приводится обратная зависимость
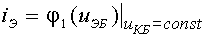 .
.
Семейство входных характеристик кремниевого n-p-n-транзистора приведено на рис. 3.20. Выражение для идеализированной входной характеристики транзистора в активном режиме имеет вид:
С ледует
отметить, что в выражении (3.35) отсутствует
зависимость токаiЭ от напряжения на коллекторном переходе uКБ.
Реально такая зависимость существует
и связана она с эффектом Эрли. Как
показано в п. 3.3, при увеличении обратного
напряжения uКБ.
сужается база транзистора , в результате
чего несколько увеличивается ток
эмиттера iЭ.
Увеличение тока iЭ с ростом uКБ.
отражается небольшим смещением входной
характеристики в сторону меньших
напряжений uЭБ.
— см. рис. 3.20. Режиму отсечки формально
соответствует обратное напряжение uЭБ.>0
, хотя реально эмиттерный переход
остается закрытым ( iЭ
0) и при прямых напряжениях uЭБ
меньших порогового напряжения.
ледует
отметить, что в выражении (3.35) отсутствует
зависимость токаiЭ от напряжения на коллекторном переходе uКБ.
Реально такая зависимость существует
и связана она с эффектом Эрли. Как
показано в п. 3.3, при увеличении обратного
напряжения uКБ.
сужается база транзистора , в результате
чего несколько увеличивается ток
эмиттера iЭ.
Увеличение тока iЭ с ростом uКБ.
отражается небольшим смещением входной
характеристики в сторону меньших
напряжений uЭБ.
— см. рис. 3.20. Режиму отсечки формально
соответствует обратное напряжение uЭБ.>0
, хотя реально эмиттерный переход
остается закрытым ( iЭ
0) и при прямых напряжениях uЭБ
меньших порогового напряжения.
Выходная характеристика транзистора в схеме ОБ представляет собой зависимость
 .
.
Семейство выходных характеристик n-p-n-транзистора приведена на рис. 3.21. Выражение дляидеализированной выходной характеристики в активном режиме имеет вид: iК = · iЭ+ IКБ0. (3.36)
В соответствие с этим выражением ток
коллектора определяется только током
эмиттера и не зависит от напряженияuКЭ.
Реально (см. рис. 3.21) имеет место очень
небольшой рост iК при увеличении обратного напряжения uКБ,
связанный с эффектом Эрли. В активном
режиме характеристики практически
эквидистантны (расположены на одинаковом
расстоянии друг от друга), лишь при очень
больших токах эмиттера из-за уменьшения
коэффициента передачи тока эмиттера
эта эквидистантность нарушается, и
характеристики несколько приближаются
друг к другу. При iЭ=
0 в цепи коллектора протекает тепловой
ток ( iК=
IКБ0).
В режиме насыщения на коллекторный
переход подается прямое напряжение uКБ,
большее порогового значения, открывающее
коллекторный переход. В структуре
транзистора появляется инверсный
сквозной поток электронов, движущийся
из коллектора в эмиттер навстречу
нормальному сквозному потоку, движущемуся
из эмиттера в коллектор. Инверсный поток
очень резко увеличивается с ростом uКБ.
, в результате чего коллекторный ток
уменьшается и очень быстро спадает до
нуля — см. рис. 3.21.
соответствие с этим выражением ток
коллектора определяется только током
эмиттера и не зависит от напряженияuКЭ.
Реально (см. рис. 3.21) имеет место очень
небольшой рост iК при увеличении обратного напряжения uКБ,
связанный с эффектом Эрли. В активном
режиме характеристики практически
эквидистантны (расположены на одинаковом
расстоянии друг от друга), лишь при очень
больших токах эмиттера из-за уменьшения
коэффициента передачи тока эмиттера
эта эквидистантность нарушается, и
характеристики несколько приближаются
друг к другу. При iЭ=
0 в цепи коллектора протекает тепловой
ток ( iК=
IКБ0).
В режиме насыщения на коллекторный
переход подается прямое напряжение uКБ,
большее порогового значения, открывающее
коллекторный переход. В структуре
транзистора появляется инверсный
сквозной поток электронов, движущийся
из коллектора в эмиттер навстречу
нормальному сквозному потоку, движущемуся
из эмиттера в коллектор. Инверсный поток
очень резко увеличивается с ростом uКБ.
, в результате чего коллекторный ток
уменьшается и очень быстро спадает до
нуля — см. рис. 3.21.
4.2. Зависимость коэффициента передачи по току о тока коллектора
При этом функционал коэффициента передачи по току преобразуется к виду:
β=F[Ik] 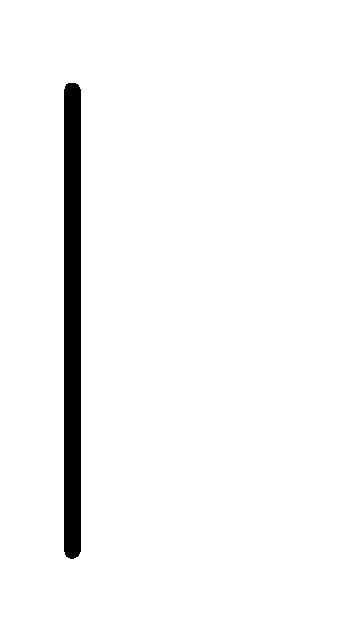 Uкэ,
Т˚С=const, (12)
Uкэ,
Т˚С=const, (12)
График зависимости β о тока коллектора представлен на рис.9.
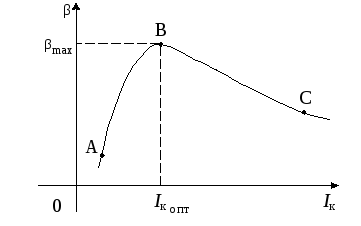
Рис.9. Зависимость коэффициента передачи по току от тока коллектора
При рассмотрении зависимости рис.9 необходимо учитывать, что Ik=α Iэ+Iko и выражение (10) записать в виде:
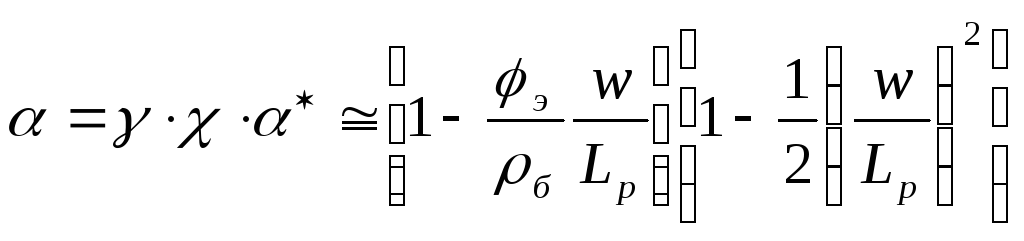 , (13)
, (13)
Из теории работы биполярного транзистора следует, что ток эмиттера зависит от значения напряжения на переходе эмиттер – база Iэ=f(Uбэ) и определяется током диффузии дырок через базу
 , (14)
, (14)
где
е – заряд электрона; S
– площадь перехода эмиттер – база; Dp – коэффициент диффузии дырок в базе; 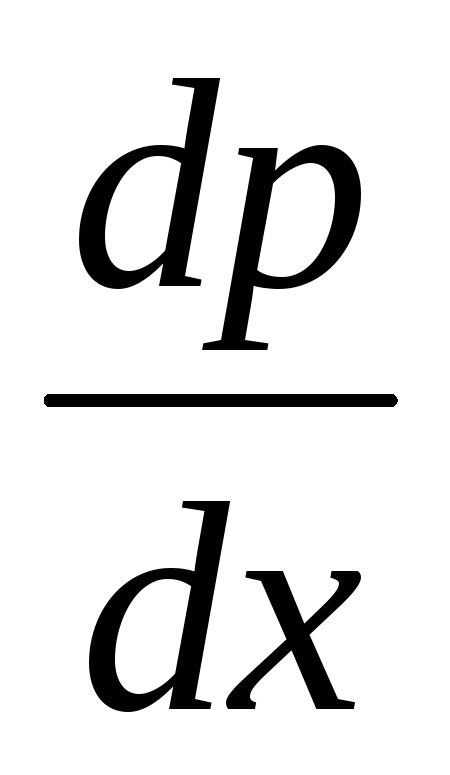 — градиент концентрации дырок в базе.
Коэффициент диффузии связан с длиной
диффузии соотношением:
— градиент концентрации дырок в базе.
Коэффициент диффузии связан с длиной
диффузии соотношением:
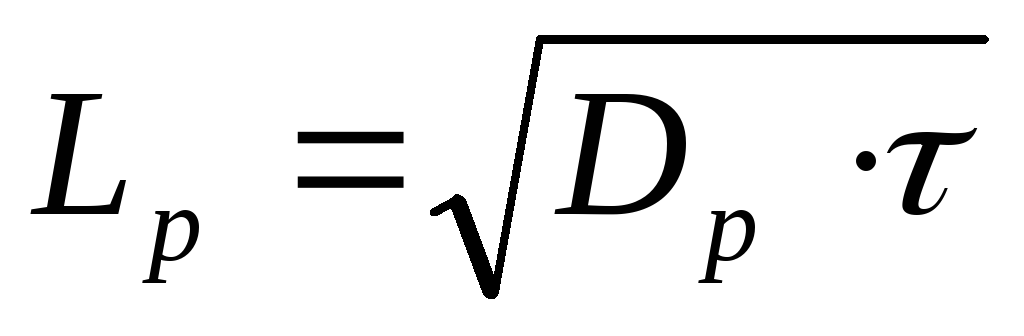 ,
(15)
,
(15)
где τ – время жизни носителей заряда.
При увеличении напряжения эмиттер – база растет избыточная концентрация дырок на границе перехода эмиттер – база, возрастает градиент концентрации и увеличивается скорость движения носителей заряда в базе, что уменьшает рекомбинационные потери в базе и ведет к росту коэффициента передачи по току. В этом случае коэффициент диффузии дырок в базе определяется соотношением:
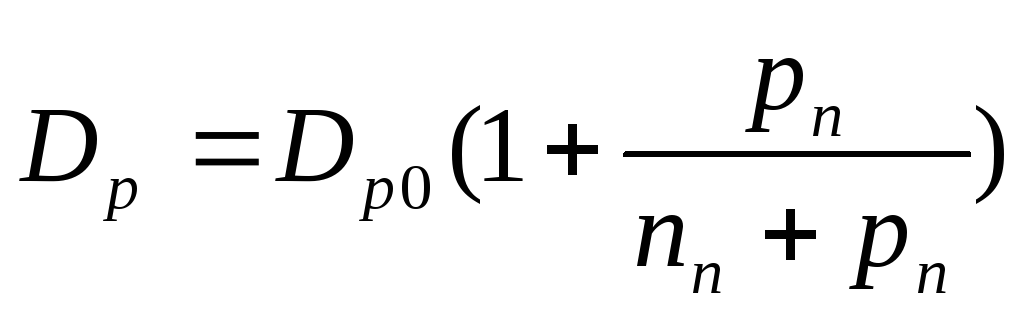 , (16)
, (16)
где
Dpo – коэффициент диффузии при малом уровне
инжекции дырок из эмиттера в базу.
Поэтому на участке АВ рис.9 изменяется
уровень инжекции дырок из эмиттера в
базу, растет коэффициент диффузии (16) и
длина диффузии Lp (15), что ведет к росту коэффициента
передачи по току и в точке В он принимает
максимальное значение βmax.
Существует оптимальное значение тока
коллектора Iк
опт, при
котором достигается βmax.
Для маломощных биполярных транзисторов
Iк
опт (1
(1 3)
мА, а для мощных транзисторов -Iк
опт
3)
мА, а для мощных транзисторов -Iк
опт (30
(30 80)
мА.
80)
мА.
При увеличении тока коллектора более Iк опт начинает сказываться уменьшение эффективности эмиттера γ (13) из–за уменьшения удельного электрического сопротивления базы ρб, которое определяется:
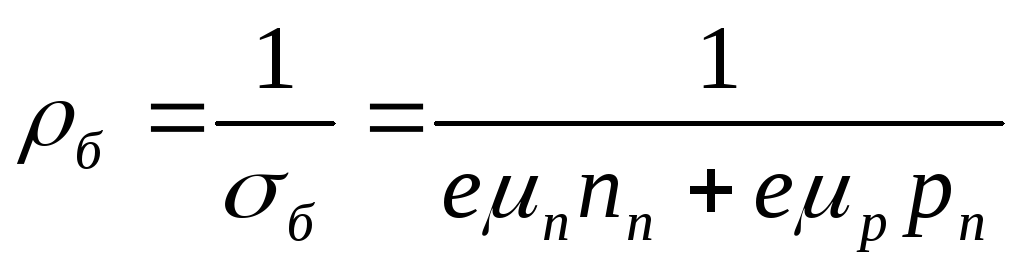 (17)
(17)
При малых значениях тока эмиттера (а равно и тока коллектора) дырочная составляющая электропроводности базы σбр имеет малое значение и ρб достаточно велико. При больших токах эмиттера, когда pn>> nn, увеличивается σбр и ρб уменьшается, а это приводит к уменьшению эффективности эмиттера γ, коэффициента α и в том числе коэффициента передачи по току биполярного транзистора в схеме включения с общим эмиттером β ( участок ВС рис. 9 ). Изменение β на участке ВС рис.9 происходит достаточно плавно.
4.3. Зависимость коэффициента передачи по току от температуры окружающей среды
Для
схемы включения биполярного транзистора
с общим эмиттером: β=F[Т˚С]  Uкэ, Ik =const.
В этом случае β оценивается величиной
α из соотношения (10) с учетом зависимости
длины диффузии дырок Lp (15). В выражении (15) с ростом Т˚С возрастает
несколько время жизни носителей заряда
и график зависимости β от температуры
окружающей среды имеет линейный характер
(рис.10).
Uкэ, Ik =const.
В этом случае β оценивается величиной
α из соотношения (10) с учетом зависимости
длины диффузии дырок Lp (15). В выражении (15) с ростом Т˚С возрастает
несколько время жизни носителей заряда
и график зависимости β от температуры
окружающей среды имеет линейный характер
(рис.10).
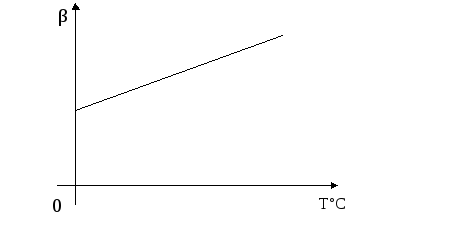
Рис.10. Зависимость коэффициента передачи по току от температуры окружающей среды
5. Система н- параметров биполярного транзистора в схеме включения с общим эмиттером
Система уравнений для Н-параметров биполярного транзистора представляется в виде:
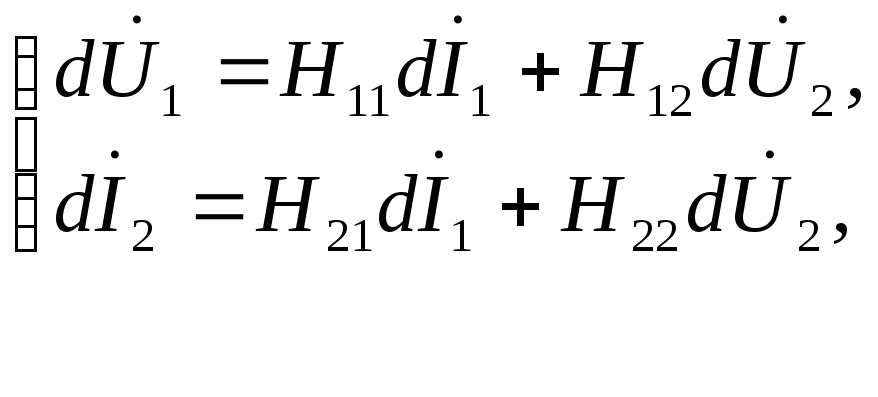 (18)
(18)
А матрица Н-параметров:
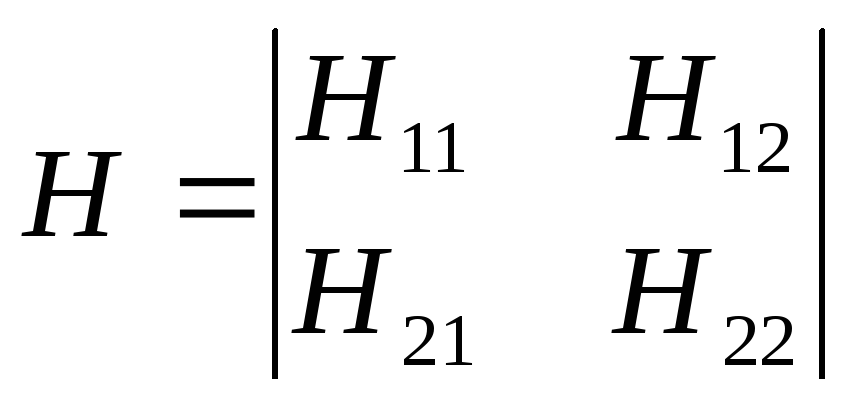 (19)
(19)
Для биполярного транзистора в схеме включения с общим эмиттером вхдным током является ток базы (I1=Iвх =Iб), выходным током – ток коллектора (I2=Iвых =Iк), входным напряжением – напряжение база – эмиттер (U1=Uвх = Uбэ), выходным напряжением – напряжение коллектор – эмиттер (U2=Uвых = Uкэ). Пи этом Н – параметры записываются в виде (с учетом связи с Н – параметрами биполярного транзистора в схеме включения с общей базой):
входное сопротивление – Н11э:
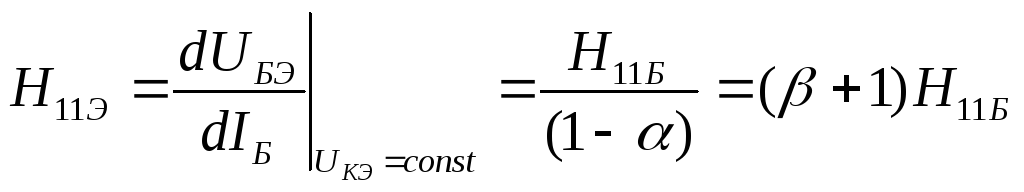 , (20)
, (20)
То есть H11Э>> H11Б и составляет значения сотни Ом, единицы кОм.
коэффициент обратной связи по напряжению – H12Э.
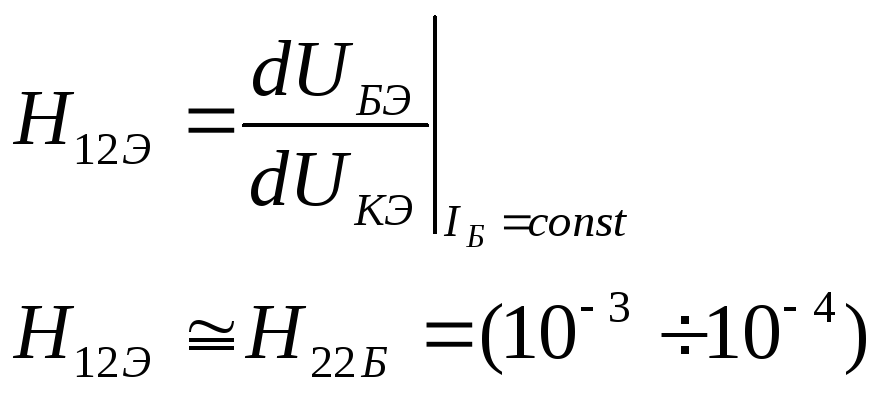 (21)
(21)
коэффициент передачи по току – H21Э.
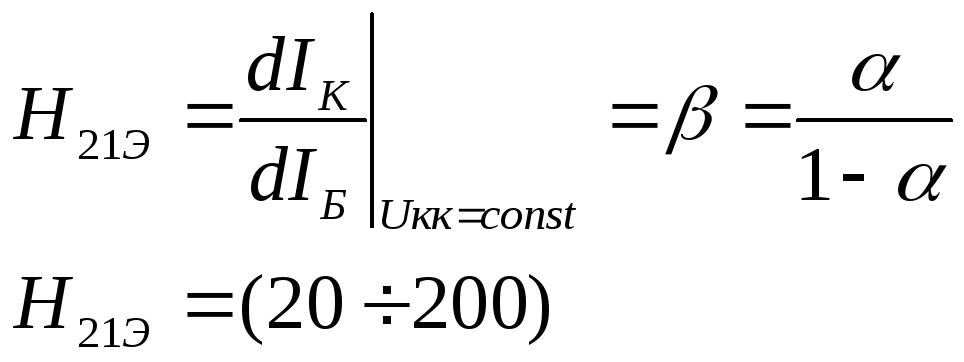 (22)
(22)
выходная проводимость – H22Э.
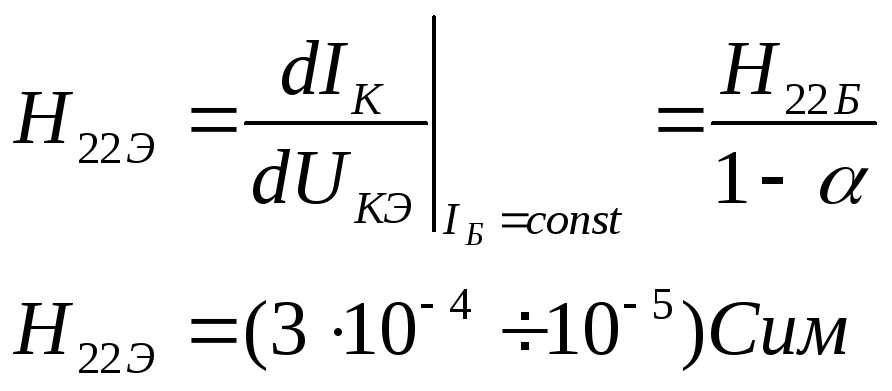 (23)
(23)


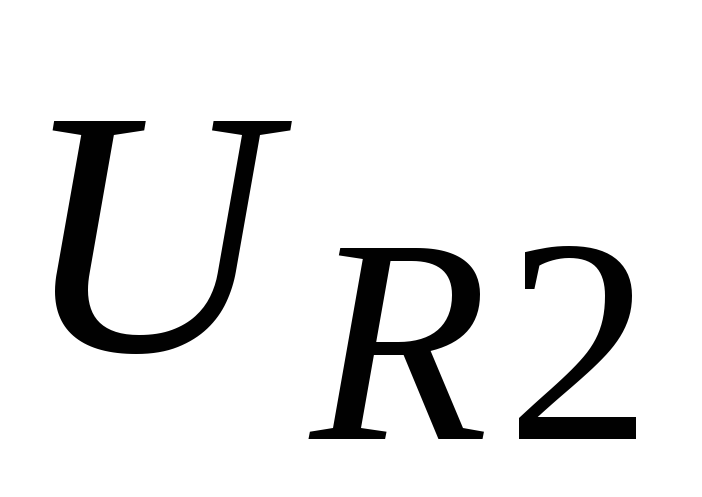 ,
,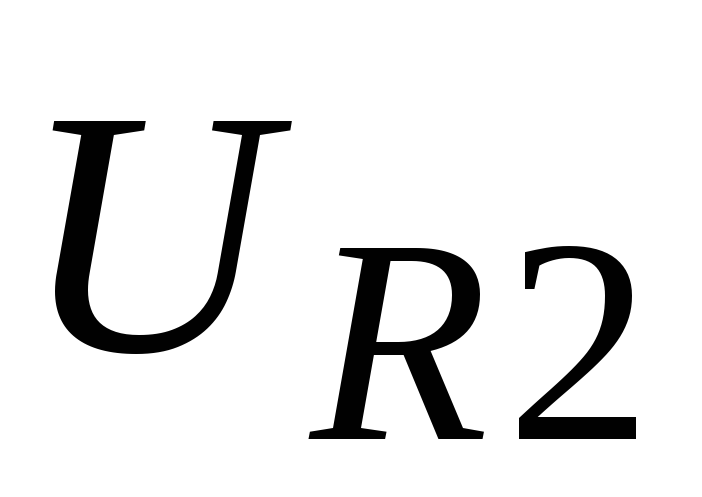 ,
,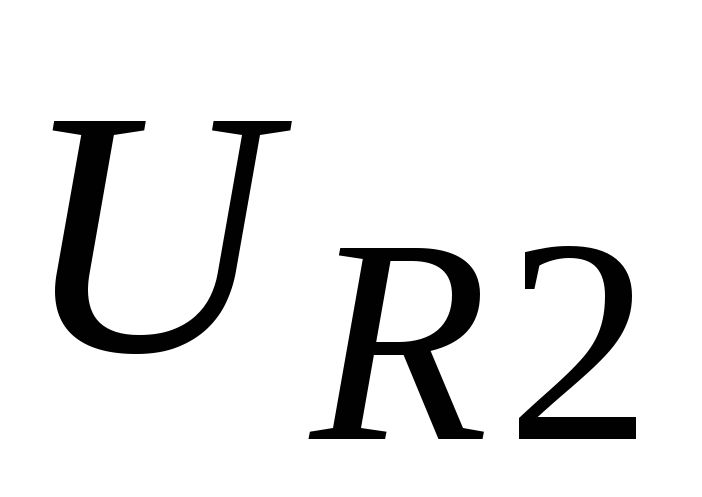 ,
,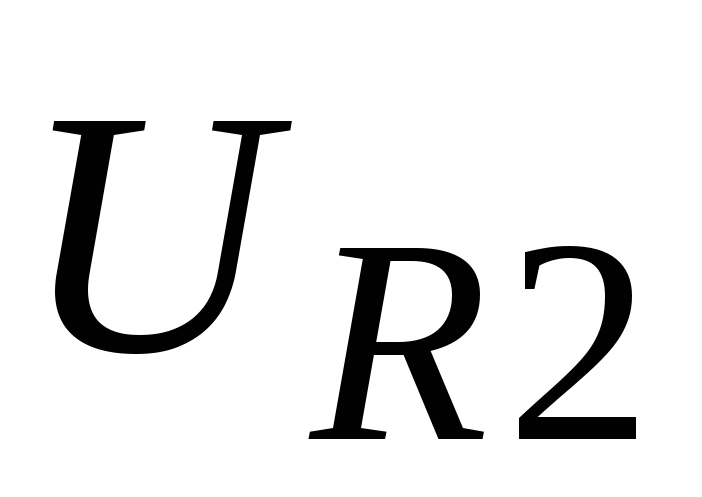 ,
,