Активные фильтры на ОУ

Активные фильтры реализуются на основе усилителей (обычно ОУ) и пассивных RC- фильтров. Среди преимуществ активных фильтров по сравнению с пассивными следует выделить:

· отсутствие катушек индуктивности;

· лучшая избирательность;

· компенсация затухания полезных сигналов или даже их усиление;

· пригодность к реализации в виде ИМС.

Активные фильтры имеют и недостатки:

¨ потребление энергии от источника питания;

¨ ограниченный динамический диапазон;

¨ дополнительные нелинейные искажения сигнала.

Отметим так же, что использование активных фильтров с ОУ на частотах свыше десятков мегагерц затруднено из-за малой частоты единичного усиления 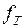большинства ОУ широкого применения. Особенно преимущество активных фильтров на ОУ проявляется на самых низких частотах, вплоть до долей герц.

В общем случае можно считать, что ОУ в активном фильтре корректирует АЧХ пассивного фильтра за счет обеспечения разных условий для прохождения различных частот спектра сигнала, компенсирует потери на заданных частотах, что приводит к получению крутых спадов выходного напряжения на склонах АЧХ. Для этих целей используются разнообразные частотно-избирательные ОС в ОУ. В активных фильтрах обеспечивается получение АЧХ всех разновидностей фильтров: нижних частот (ФНЧ), верхних частот (ФВЧ) и полосовых (ПФ).

Первым этапом синтеза всякого фильтра является задание передаточной функции (в операторной или комплексной форме), которая отвечает условиям практической реализуемости и одновременно обеспечивает получение необходимой АЧХ или ФЧХ (но не обеих) фильтра. Этот этап называют аппроксимацией характеристик фильтра.

Операторная функция представляет собой отношение полиномов:

K(p)=A(p)/B(p),

и однозначно определяется нулями и полюсами. Простейший полином числителя — константа. Число полюсов функции (а в активных фильтрах на ОУ число полюсов обычно равно числу конденсаторов в цепях, формирующих АЧХ) определяет порядок фильтра. Порядок фильтра указывает на скорость спада его АЧХ, которая для первого порядка составляет 20дБ/дек, для второго — 40дБ/дек, для третьего — 60дБ/дек и д.д.

Задачу аппроксимации решают для ФНЧ, затем с помощью метода инверсии частоты полученную зависимость используют для других типов фильтров. В большинстве случаев задают АЧХ, принимая нормированный коэффициент передачи:

,

где f(х) — функция фильтрации; 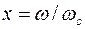— нормированная частота; 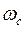— частота среза фильтра; e — допустимое отклонение в полосе пропускания.

В зависимости от того, какая функция принимается в качестве f(х) различают фильтры (начиная со второго порядка) Баттерворта, Чебышева, Бесселя и др. На рисунке 7.15 приведены их сравнительные характеристики.

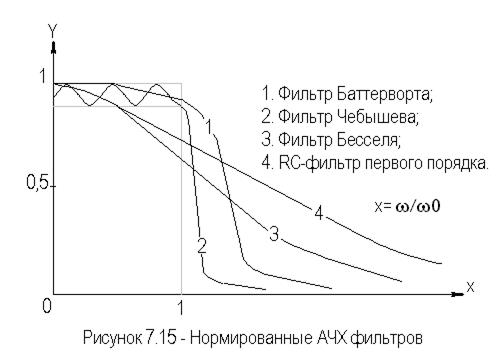
Фильтр Баттерворта (функция Батерворта) описывает АЧХ с максимально плоской частью в полосе пропускания и относительно небольшой скоростью спада. АЧХ такого ФНЧ может быть представлена в следующем виде:

,

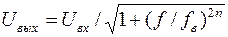где n — порядок фильтра.

Фильтр Чебышева (функция Чебышева) описывает АЧХ с определенной неравномерностью в полосе пропускания, но не большей скоростью спада.

Фильтр Бесселя характеризуется линейной ФЧХ, в результате чего сигналы, частоты которых лежат в полосе пропускания, проходят через фильтр без искажений. В частности, фильтры Бесселя не дают выбросов при обработке колебаний прямоугольной формы.

Помимо перечисленных аппроксимаций АЧХ активных фильтров известны и другие, например, обратного фильтра Чебышева, фильтра Золотарева и т.д. Заметим, что схемы активных фильтров не изменяются в зависимости от типа аппроксимации АЧХ, а изменяются соотношения между номиналами их элементов.

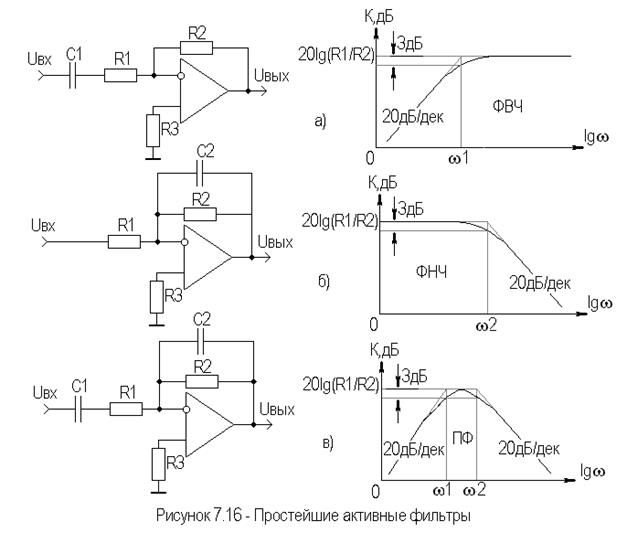
Простейшие (первого порядка) ФВЧ, ФНЧ, ПФ и их ЛАЧХ приведены на рисунке 7.16.

В этих фильтрах конденсатор, определяющий частотную характеристику, включен в цепь ООС.

Для ФВЧ (рисунок 7.16а) коэффициент передачи равен:

,

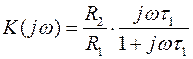где .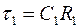

Частоту сопряжения асимптот 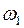находят из условия 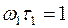, откуда

.

Для ФНЧ (рисунок 7.16б) имеем:

,

.

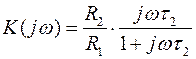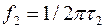где .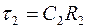

В ПФ (рисунок 7.16в) присутствуют элементы ФВЧ и ФНЧ.

 

 

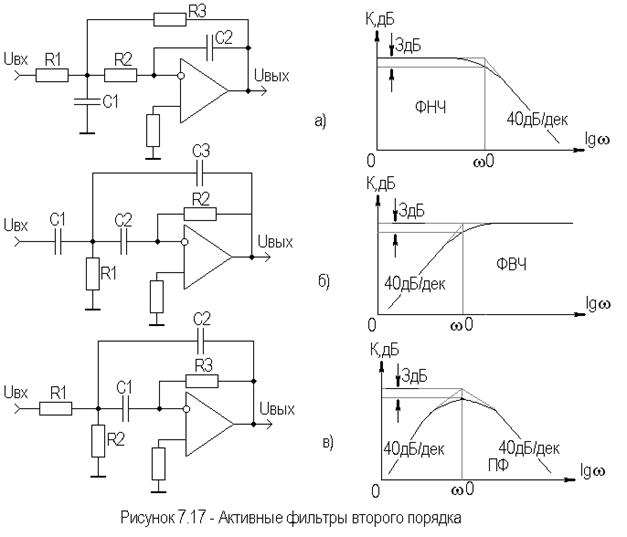
Можно увеличить крутизну спада ЛАЧХ, если увеличить порядок фильтров. Активные ФНЧ, ФВЧ и ПФ второго порядка приведены на рисунке 7.17.

Наклон асимптот у них может достигать 40дБ/дек, а переход от ФНЧ к ФВЧ, как видно из рисунков 7.17а,б, осуществляется заменой резисторов на конденсаторы, и наоборот. В ПФ (рисунок 7.17в) имеются элементы ФВЧ и ФНЧ. Передаточные функции равны [13]:

¨ для ФНЧ:

;

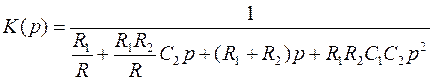¨ для ФВЧ:

;

 

¨ для ПФ:

.

 

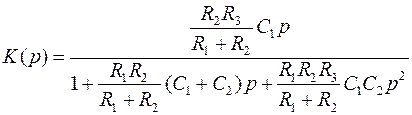Для ПФ резонансная частота равна:

.

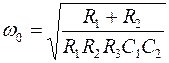
Для ФНЧ и ФВЧ частоты среза соответственно равны:

;

.

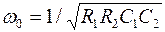Довольно часто ПФ второго порядка реализуют с помощью мостовых цепей. Наиболее распространены двойные Т-образные мосты, которые «не пропускают» сигнал на частоте резонанса (рисунок 7.18а) и мосты Вина, имеющие максимальный коэффициент передачи на резонансной частоте (рисунок 7.18б).

 

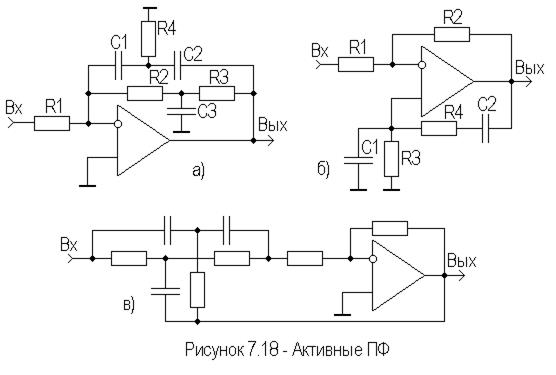
Мостовые схемы включены в цепи ПОС и ООС. В случае двойного Т-образного моста глубина ООС минимальна на частоте резонанса, и усиление на этой частоте максимально. При использовании моста Вина, усиление на частоте резонанса максимально, т.к. максимальна глубина ПОС. При этом для сохранения устойчивости глубина ООС, введенной с помощью резисторов 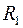и 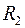, должна быть больше глубины ПОС. Если глубины ПОС и ООС близки, то такой фильтр может иметь эквивалентную добротность Q»2000.

Резонансная частота двойного Т-образного моста при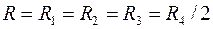

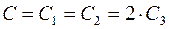и , и моста Вина при 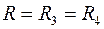и , равна 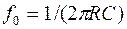, и ее выбирают исходя из условия устойчивости 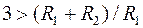, т.к. коэффициент передачи моста Вина на частоте равен 1/3.

Для получения режекторного фильтра двойной Т-образный мост можно включить так, как показано на рисунке 7.18в, или мост Вина включить в цепь ООС.

Для построения активного перестраемого фильтра обычно используют мост Вина, у которого резисторы и 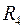выполняют в виде сдвоенного переменного резистора.

Возможно построение активного универсального фильтра (ФНЧ, ФВЧ и ПФ), вариант схемы которого приведен на рисунке 7.19.

 

 

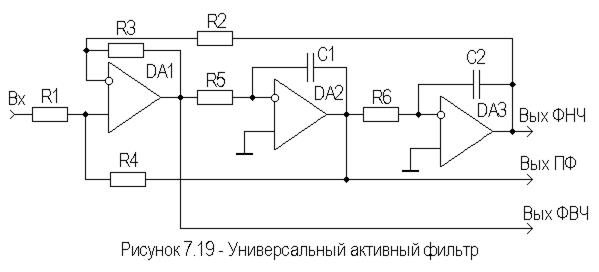
В его состав входят сумматор на ОУ 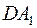и два ФНЧ первого порядка на ОУ и 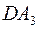, которые включены последовательно. Если 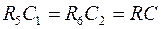, то частота сопряжения 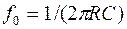. ЛАЧХ имеет наклон асимптот порядка 40дБ/дек. Универсальный активный фильтр имеет хорошую стабильность параметров и высокую добротность (до 100). В серийных ИМС довольно часто используется подобный принцип построения фильтров.

 

Гираторы

 

Гиратором называется электронное устройство, преобразующее полное сопротивление реактивных элементов. Обычно это преобразователь емкости в индуктивность, т.е. эквивалент индуктивности. Иногда гираторы называют синтезаторами индуктивностей. Широкое распространение гираторов в ИМС объясняется большими трудностями изготовления катушек индуктивностей с помощью твердотельной технологии. Использование гираторов позволяет получить относительно большую индуктивность с хорошими массогабаритными показателями.

На рисунке 7.20 приведена электрическая схема одного из вариантов гиратора, представляющего собой повторитель на ОУ, охваченный частотно-избирательной ПОС ( 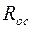и ).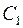

 

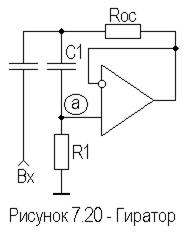
Поскольку с увеличением частоты сигнала емкостное сопротивление конденсатора 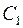уменьшается, то напряжение в точке а будет возрастать. Вместе с ним будет возрастать напряжение на выходе ОУ. Увеличенное напряжение с выхода по цепи ПОС поступает на неинвертирующий вход, что приводит к дальнейшему росту напряжения в точке а, причем тем интенсивнее, чем выше частота. Таким образом, напряжение в точке а ведет себя подобно напряжению на катушке индуктивности. Синтезированная индуктивность определяется по формуле [12]:

.

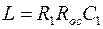Добротность гиратора определяется как [12]:

.

Одной из основных проблем при создании гираторов является трудность в получении эквивалента индуктивности, у которой оба вывода не соединены с общей шиной. Такой гиратор выполняется, как минимум, на четырех ОУ. Другой проблемой является относительно узкий диапазон рабочих частот гиратора (до нескольких килогерц на ОУ широкого применения).

 

---

Дата добавления: 2016-06-18; просмотров: 13262;

---

Похожие статьи:

Активные и пассивные электрические фильтры

Библиографическое описание:

Магеррамов Р. В. Активные и пассивные электрические фильтры // Молодой ученый. — 2017. — №2. — С. 148-152. — URL https://moluch.ru/archive/136/38046/ (дата обращения: 06.02.2020).



Фильтр — устройство, которое передает сигналы в определенной области частот и препятствует прохождению сигналов вне этой области. Идеальный фильтр имеет постоянную и отличную от нуля передаточную характеристику в необходимом диапазоне частот (полоса пропускания или прозрачности) и нулевую в остальном диапазоне (полоса подавления или затухания).

Применение фильтров имеет очень большую потребность в радио и телеаппаратуре, в которой осуществляется настройка каналов на определённой частоте с помощью фильтрования принимаемых сигналов. Помимо радиотехники, фильтры применяются в аналого-цифровом и цифро-аналоговом преобразовании сигналов, а также в различных электронных системах, с целью фильтрации помех.

Одна из классификаций электрических фильтров — классификация по типам элементов, используемых для схемотехнической реализации: активные, пассивные фильтры, LC, RC-фильтры, фильтры на переключаемых конденсаторах и т. д. Пассивные фильтры (Рисунок 1) имеют в своем составе только пассивные элементы такие, как резисторы, индуктивности, конденсаторы. Данный тип фильтров не требует источника питания для функционирования и не усиливает мощность выходного сигнала (в отличие от активного фильтра). В активном фильтре (Рисунок 2) используется один или несколько активных компонентов: транзистор или операционный усилитель.

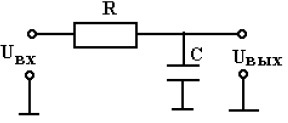
Рис. 1. Схема пассивного фильтра нижних частот

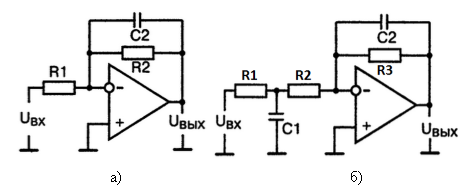
Рис. 2. Схемы активного фильтра нижних частот на операционном усилителе: а) первого б) второгопорядка

Порядок фильтра определяет максимальное количество нулей и полюсов передаточной функции фильтра. Что бы увеличить крутизну амплитудно-частотной характеристики необходимо увеличить порядок фильтра, но стоит отметить, что при увеличении порядка увеличивается и количество реактивных элементов (конденсаторов, резисторов) что в свою очередь усложняет сам фильтр и увеличивает его чувствительность к разбросу параметров его компонентов.

В идеальном случае разработчику хотелось бы получить амплитудно-частотную характеристику (АЧХ) имеющую резкий переход между полосой пропускания и подавления (Рисунок 3). Применяя пассивные элементы фильтрации, увеличение крутизны перехода характеристики АЧХ добиваются применением фильтров более высокого порядка, данных подход требует больших расчетов и более точной настройки. Однако применение активных фильтров основным элементом, которых является операционный усилитель с обратной связью, позволяет получить крутой спад характеристики АЧХ, затрачивая значительно меньше усилий и средств во время разработки и при изготовлении.

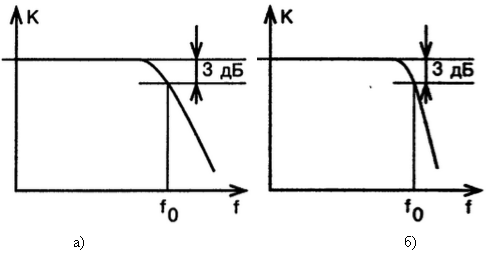
Рис. 3. АЧХ фильтра нижних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду

Помимо классификации фильтров по типам элементов, на которых они построены, фильтры классифицируются и по виду амплитудно-частотной характеристики:

– Фильтр высоких частот (ФВЧ) — подавляет амплитуды гармонического сигнала ниже частоты среза (Рисунок 4).

– Фильтр низких частот (ФНЧ) — подавляет амплитуды гармонического сигнала выше частоты среза (Рисунок 2).

– Полосовой фильтр — подавляет амплитуды гармонического сигнала выше и ниже определенной полосы (Рисунок 6).

– Полосно-заграждающий фильтр — подавляет амплитуды гармонического сигнала в определенном диапазоне частот, т. е. фильтр, подавляющий колебания определенной полосы и пропускающий колебания, выходящие за границы этой полосы.

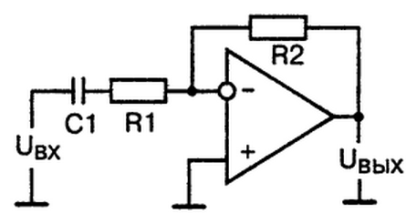
Рис. 4. Схема активного фильтра верхних частот первого порядка

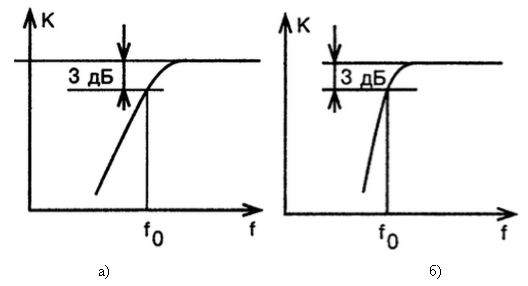
Рис. 5. АЧХ фильтра верхних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду

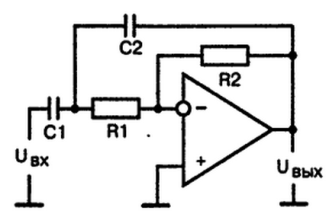
Рис. 6. Схема активного полосового фильтра

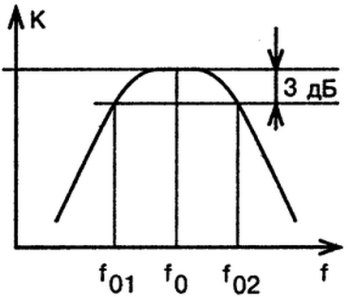
Рис. 7. АЧХ активного полосового фильтра

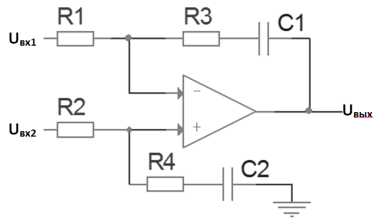
Рис. 8. Пропорционально-интегрирующий фильтр низких частот

Пропорционально-Интегриующий фильтра на ОУ (ПИ-фильтр), также является активным фильтром. ПИ-фильтр сравнивает средние значения двух входных сигналов за период частоты, резисторы R1 и R2 определяют масштабный коэффициент сравнения. Произведение C1*R1 (постоянная времени интегратора Ти) определяет интегрирующий эффект фильтра, резистор R3 обеспечивает устойчивость схемы ФАПЧ, а отношение R3 к R1 определяет пропорциональный коэффициент фильтра Кп.

Заключение

Фильтрация сигналов является важной функцией в аналоговых и аналого-цифровых устройствах, в зависимости от поставленных задач используется тот или иной тип схемотехнической реализации фильтра. В данной статье были рассмотрены несколько разновидностей электрических фильтров и их амплитудно-частотная характеристика. Широкое применение фильтров встречается в электротехнике, радиотехнике и электронике.

Активные фильтры часто применяются в геофизических, медицинских устройствах, а также в различных устройствах связи. Обычно фильтр такого типа представляет собой соединение цепей второго-первого порядка. Благодаря этому упрощается расчет и настройка данного фильтра.

Литература:

1. Изюмов Н. М. — Радиорелейная связь, Рипол Классик, 2013
2. Кеоун Д. — OrCAD Pspice. Анализ электрических цепей, Litres, 2014
3. Мелешин В. — Транзисторная преобразовательная техника, Litres, 2016
4. Тимошенков В. П., А. А. Миндеева — Элементная база систем связи, учебное пособие, 2015
5. Миндеева А. А. — Элементная база аналоговых схем, учебное пособие, 2012
6. У.Титце, К.Шенк — Полупроводниковая схемотехника, 2010 г.
7. M. Williamsen, «Notch-Filter Design», Audio Electronics, Jan. 2000
8. W. Jung, «Bootstrapped IC Substrate Lowers Distortion in JFET Op Amps», Analog Devices AN232
9. H. Zumbahlen, «Passive and Active Filtering», Analog Devices AN281
10. P. Toomey & W. Hunt, «AD7528 Dual 8-Bit CMOS DAC», Analog Devices AN318
11. http://www.dsplib.ru/content/filters/ch3/ch3.html
12. http://radio-hobby.org/modules/news/article.php?storyid=1162

Основные термины (генерируются автоматически): фильтр, активный фильтр, амплитудно-частотная характеристика, гармонический сигнал, частота, операционный усилитель, активный полосовой фильтр, полоса пропускания, порядок фильтра, тип элементов.

59 Частотно зависимые схемы усиления на оу » СтудИзба

Фильтры электрических сигналов. Исходные положения.

Фильтры – электронные устройства, предназначенные для выделения или подавления сигналов в определенной полосе частот из сигнала широкого спектрального состава.

Типы фильтров:

                       1.            ФНЧ – фильтр нижних частот

К(w) = К₀ = const, пока 0 £ w £ w_в

К(w) = 0, если w > w_в

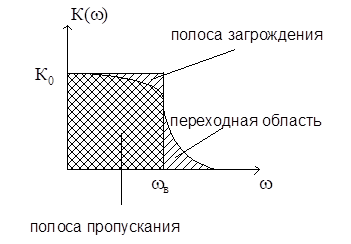
Идеальный фильтр имеет характеристику прямоугольную, реальный – плавный переход.

В реальных фильтрах переход от полосы пропускания к полосе задержания занимает определенную область частот, где К(w) = var.

0 £ К(w) £ К₀

Чем уже переходная полоса, тем ближе характеристика фильтра (частотная) к идеальной.

В реальных фильтрах переходная область характеризуется скоростью спада (подъема) переходной характеристики и выражается в [дб/дек] или [дб/октаву].

Фильтры строятся на основе RLC элементов.

Скорость спада (подъема) определяет порядок фильтра:

1-го порядка скорость 20

2-го порядка скорость 40 и т. д.

Порядок фильтра определяет число элементов (реактивных, используемых в схеме).

2.      ФВЧ

К(w) = К₀ = const, когда ¥ > w ³ w_н

К(w) = 0, если w_н > w > w_в

                       2.            ЗФ – заграждающий фильтр

К(w) = 0, если w_н £ w £ w_в

К(w) = К₀, если w_н ³w ³ w_в

1)    Фильтры, не содержащие усилительных или активных элементов – пассивные фильтры

К(w) £ 1

Пассивные фильтры строят на R, L, C элементах. Пассивные фильтры обладают более стабильными характеристиками, менее шумят, меньшими нелинейными искажениями, но, особенно на НЧ, габариты фильтров значительны (большие емкости, большие индуктивности).

2)    Активные фильтры, – в которых используются усилительные элементы: ПТ, БТ.

Использование ОУ позволяет унифицировать фильтры, сделать их малогабаритными, особенно на НЧ приблизить характеристику к прямоугольной. Появляется «-» — обладают большей нестабильностью, чем пассивные, шумовые характеристик хуже, требуют источник питания.

«+» — повторяемость характеристик, хорошие совпадения расчетов с опытами, относительная простота управления, перестройка.

Фильтры 1-го порядка

ФНЧ пассивным является интегрирующая цепочка.

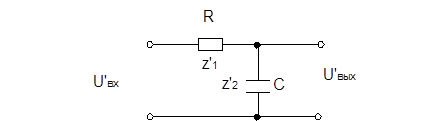
R_г = 0, z = ¥

;

z’₁ = R

z’₂ = -j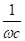

t = RC – постоянная времени интегрирования

w₀ = 1/t

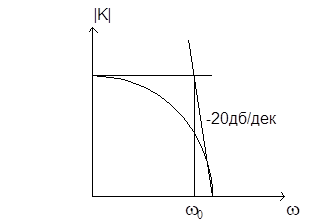
Простейшее дифференциальное звено – ФВЧ

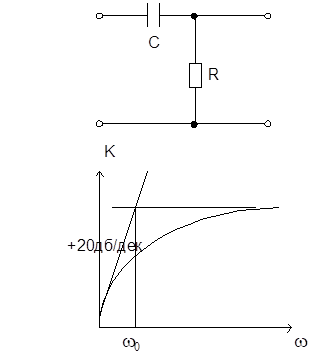
w₀ = 1/RC

С аналогичными характеристиками могут быть построены фильтры на L-R элементах.

Простейшим фильтром 1-го порядка на ОУ является интегратор (ФНЧ), а дифференциатор – это ФВЧ 1-го порядка.

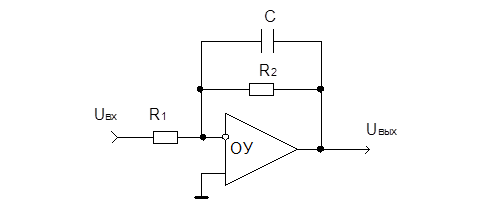
K’(w) = -z’₂/z’₁

z’₁ = R₁

z’₂ = R₂||x’_c =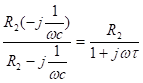

t = R₂*C

K’(w) = —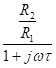

w₀ = 1/t

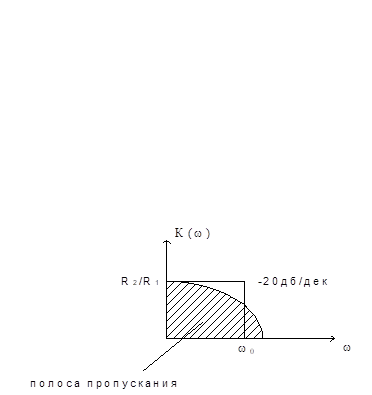
Если R₂/R₁ > 1, то имеет место усиление входного сигнала.

Если R₂ Þ ¥, то характеристика начинается от нулевой частоты (спад с К₀).

ФВЧ:

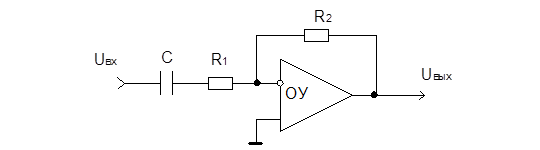
K’(w) = -z’₂/z’₁

z’₂ = R₂

z’₁ = R₁ — j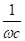

K’(w) = —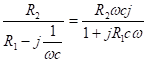

t₁ = CR₁; t₂ = CR₂ = t_д Þ

K’(w) =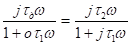

Если

w₀ = 1/t₁

Если R₁ Þ 0, то характеристика идет до K_max

Дифференциатор на ОУ – фильтр 1-го порядка.

При дифференцировании входного сигнала ФВЧ подчеркивает шумы и высокочастотные сигналы, поэтому в дифференциаторе для исключения насыщения ОУ ВЧ сигналом его усиление на ВЧ ограничивают с помощью дополнительного резистора на входе R₁, что ограничивает диапазон дифференцирования.

Полосовой фильтр (усилитель переменного тока)

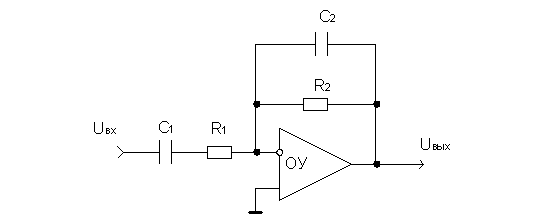
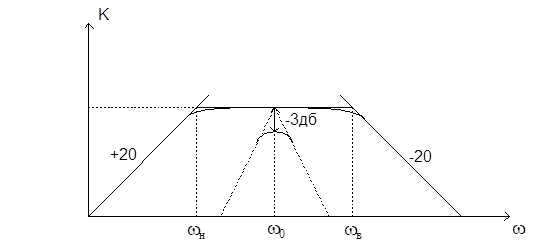
t₂ < t₁

К^дб = 20lg(R₂/R₁)

w_н = 1/t₁ = 1/R₁C₁

w_в = 1/t₂ = 1/R₂C₂

Когда t₂ =t₁, то пунктир.

Достоинства фильтров на ОУ:

Ø Усиление входного сигнала в выбранном диапазоне частот

Ø Фильтры более высоких порядков (2 и выше) в принципе могут быть построены при каскадном соединении фильтров 1го порядка, но при этом на каждый порядок необходим ОУ. Таким образом, например, в фильтрах 2-го порядка, требуются 2 ОУ. Известны схемы и структуры, которые позволяют реализовать фильтр 2-го порядка на одном ОУ.

Фильтры 2-го порядка на ОУ

В основе построения фильтра 2-го порядка широко используются свойства ОУ, которые позволяют рассматривать его как:

q  ИНУН – источник напряжения управляемый напряжением. В простейшем случае – не инвертирующий усилитель, у которого

R_вх Þ ¥

R_вых Þ 0

U_вых = kU_вх

q  ИТУН – источник тока, управляемый напряжением. Это источник тока на ОУ.

q  ИНУТ – источник напряжения, управляемый током. Это инвертирующий усилитель.

q  ИТУТ – источник тока, управляемый током. Это источник тока на ОУ в не инвертирующем включении.

Наиболее простая – ИНУН.

Фильтры на этих усилителях называют фильтрами Саллена и КИ или фильтры на основе ИНУН.

ФНЧ

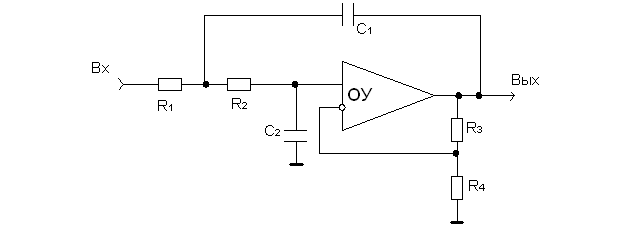ФВЧ

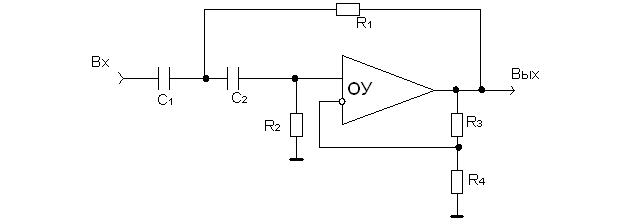
Используется не инвертирующее включение ОУ, в результате ОУ не нагружает фильтр. Включение С₁ и R₁ (для ФВЧ) в ОС обеспечивает необходимую крутизну передаточной функции фильтров. Т. к. это связь положительная, то необходимо, чтобы кb < 1 (для ПОС), в противном случае такая схема возбуждается и становится просто генератором. Поэтому существуют ограничения на выбор R₃ и R₄, т. к.

K_u = 1 + R₃/R₄, то

R₃/R₄ = 2 — a, где a — коэффициент затухания фильтра и определяет тип фильтра.

Фильтры 2-го порядка в зависимости от вида передаточной функции делятся на следующие типы:

                               I.      Фильтры Баттерворта

v a = 1,414

v наклон характеристики = 40 дб/дек

v в пределах полосы пропускания характеристика гладкая

v фазовая характеристика нелинейная

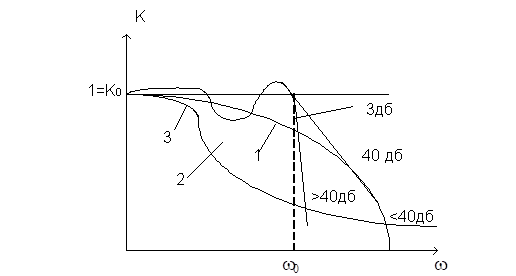Т. к. имеет место в схеме ПОС, то крутизна переходной характеристики может быть как больше, так и меньше 40 дб/дек.

                            II.      Фильтр Чебышева

v a = 1,578¸0,766

Фильтр Чебышева имеет колебания в пределах полосы пропускания, но более крутую характеристику в переходной полосе. Чем круче переходная полоса, тем больше выбросы. Имеет более нелинейную ФЧХ, чем фильтр Баттерворта. Нелинейность ФЧХ для этих фильтров приводит к тому, что при прохождении импульсных сигналов появляются выбросы на них.

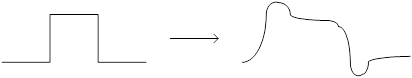
                         III.      Фильтр Бесселя

v a = 1,732

Гладкая спадающая характеристика в пределах полосы пропускания и плавная в пределах переходной области, но скорость спада < 40 дб.

«+» линейная ФЧХ, т. е. Dj = 1/кw (кw)

Это эквивалентно тому, что все сигналы задерживаются линейно в полосе пропускания. Эти фильтры не искажают импульсные сигналы.

Фильтры используются для выравнивания и компенсации задержек, возникающих в линиях связи.

Также используются эллиптические фильтры, которые имеют неравномерную характеристику, как в полосе пропускания, так и в полосе заграждения, и более крутую характеристику в переходной области, чем фильтр Чебышева.

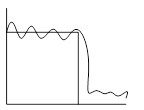
Фильтры высоких порядков (n > 2)

Строят на основе фильтров 1 и 2 порядков.

Если n = 6, то достаточно 3-х фильтров Саллена и Ки.

Если n = 5, то 2-х фильтров Саллена и Ки и 1-го фильтра 1 порядка и т. д.

При построении полосовых фильтров используют ФНЧ и ФВЧ соответствующего порядка, причем

На входе фильтра ставятся ФНЧ, которые ослабляют ВЧ шумы, что позволяет повысить отношение сигнал/шум в рабочей полосе.

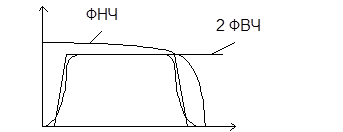
Фильтры на гираторах

При построении фильтров 2-го порядка и выше минимальное число элементов получается, если использовать L-C элементы (последовательное и параллельный колебательный контур).

Однако на НЧ габариты таких фильтров значительны, т. к. необходимы большие L и С.

w₀ = 1/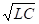

С помощью ОУ можно синтезировать как эквивалент индуктивности и эквивалент емкости. Такие схемы принято называть конверторами сопротивлений. Они позволяют преобразовать R в – R и наоборот, x_L ® x_c. Т. е. используют емкость, а на выходе схемы – как индуктивность.

Гираторы – схемы, преобразующие реактивность сопротивление одного вида в реактивное сопротивление другого вида. В основе таких схем лежит также использование ИНУН, ИТУН и т. д.

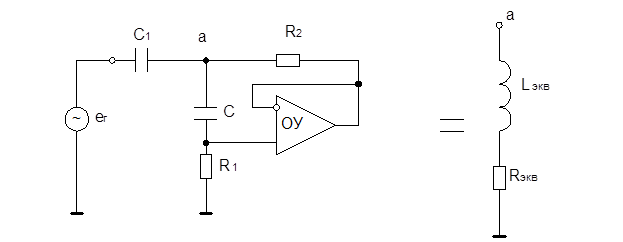L_экв = R₁*R₂*C, если R₁ >> R₂

R_экв = 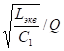, где

Q – добротность синтезированной индуктивности

Q = 1/2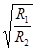

Добротность реальная: Q < 10

x_L = wL Þ при w­ ® x_L­

С w­ ® x_c¯ Þ U_R1­ ® U_R2­ Þ

В т. а поступает через R₂ возрастающее напряжение.

Таким образом, с т. зр. частотных свойств схема ведет себя как эквивалентная индуктивность.

При соединении её с емкостью С₁ образуется последовательный колебательный контур L_эквС₁, его резонансная частота:

w₀ = 1/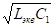

Таким образом, особенно на НЧ можно строить эквивалентные индуктивности с малыми размерами, т. к. при большой величине R₁ емкости С может быть достаточно маленькой.

Синтезирование реактивности позволяет создавать фильтры высоких порядков эквивалентные LC фильтры на пассивных элементов с малыми габаритами. Однако такие фильтры имеют «-»:

Ø требуется источник питания;

Ø имеет меньшую добротность, чем пассивный;

Ø имеет большую нестабильность, особенно температурную;

Ø обладает худшими шумовыми характеристиками.

Универсальные фильтры на ОУ

Для построения ФНЧ, ФВЧ, ПФ требуются различные схемы, однако существуют структуры на ОУ, позволяющие на одной схеме получать все 3 характеристики. При построении таких фильтров используют как интеграторы, так и дифференциаторы на ОУ.

Структура универсального фильтра 2-го порядка на 3-х ОУ

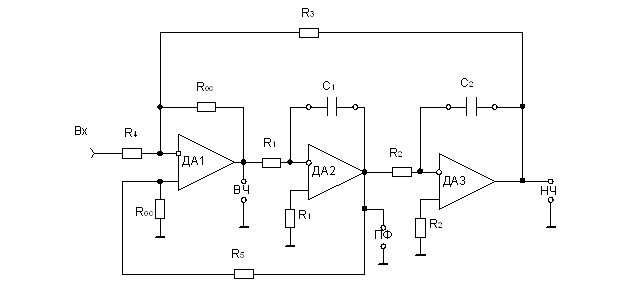
R₁ = R₂ = R

C₁ = C₂ = C

f_ф = 1/(2pRC)

R₃ = R₅

|K| = R_oc/R₄ < 3

В основе структуры фильтра лежат 2 интегратора на ДА2 и ДА3, которые обеспечивают частотную характеристику схемы и порядок фильтра. Для построения универсального фильтра используются многопетлевые ОС через R₃, R₅ и R_oc, которые обеспечивают суммирование внешних и внутренних сигналов на ОУ ДА1. Обычно используют одинаковые элементы, тогда f_ср = 1/2pRC.

Внешними элементами являются конденсаторы С₁ и С₂. На выходе схемы ДА3 имеет место дважды проинтегрированный сигнал, т. е. выход фильтра ФНЧ. После ДА1 имеет место выход фильтра ФВЧ, т. к. на выход ДА1 имеет место сигнал, у которого из полного входного сигнала вычтены нижние частоты, следовательно, остаются только ВЧ. НА выходе ДА2 ослабляется ВЧ, следовательно, если R₁C₁ < R₂C₂ на выходе ДА2 остается полосовой сигнал или ПФ. Таким образом, в зависимости от использования выхода, эта схема выполняет функции ФНЧ, ФВЧ и ПФ, что позволяет на ее основе создавать различные фильтры.

По похожей структуре может быть построен универсальный фильтр и на дифференциаторах. Однако фильтр на интеграторах более устойчив.

Общее свойство фильтров на ОУ:

Потенциально устойчивые фильтры требуют использования полного числа ОУ. Фильтры с минимальным числом ОУ потенциально неустойчивы и при неблагоприятном сочетании параметров могут возбуждаться.

Фазовые фильтры на ОУ

Это фильтры, которые имеют характеристику пропускания в рабочей полосе = 1.

К(w) = 1

j(w) – меняется.

Такие фильтры строят на основе фазовращателей.

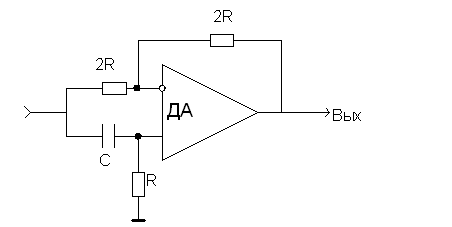
W(p) = (RCp — 1)/(RCp + 1), где p = jw

w₀ = 1/RC

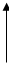W(p) = (1 — RCp)/(1 + RCp)

Фазовое звено первого порядка

Для получения фазового звена более высоких порядков обеспечивается последовательное включение.

Фазовые фильтры используются для выравнивания фазовых характеристик цепей, например, совместно с ФНЧ, ФВЧ, а также для создания схем, обеспечивающих заданный сдвиг фаз (чаще всего p/2 – квадратурный сдвиг фаз) в заданной полосе частот (достаточно широкой). При кодировании, декодировании и передачи звуковых сигналов – квадратурная модуляция, демодуляция звуковых сигналов. Используются в модемах, сотовой связи и т. д.

Активный фильтр — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 мая 2016; проверки требуют 4 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 мая 2016; проверки требуют 4 правки.

Активный фильтр — один из видов аналоговых электронных фильтров, в котором присутствует один или несколько активных компонентов, к примеру, транзистор или операционный усилитель.

В активных фильтрах используется принцип отделения элементов фильтра от остальных электронных компонентов схемы. Часто бывает необходимо, чтобы они не оказывали влияния на работу фильтра. Применение усилителей в активных фильтрах позволяет увеличить наклон частотной характеристики в полосе подавления, что недостижимо при каскадном соединении пассивных RC-цепочек.

Существует несколько различных типов активных фильтров, некоторые из которых также имеют и пассивную форму:

• Фильтр высоких частот — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала выше частоты среза.
• Фильтр низких частот — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала ниже частоты среза.
• Полосовой фильтр — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала выше и ниже некоторой полосы.
• Режекторный фильтр — ослабляет (обычно значительно) амплитуды гармонических составляющих сигнала в определённой ограниченной полосе частот.

Пассивные и активные режекторные фильтры. Онлайн расчёт.

Режекторный фильтр — не частый гость в наших краях. Зверь редкий, нелюдимый, но для радиолюбительского хозяйства — весьма полезный. Внешне напоминает полосовых собратьев, но охотится исключительно за сигналами вокруг центральной частоты и мало активен на частотах, выходящих за пределы отведённого ему диапазона.

Для начала определимся с терминологией.

Полосно-заграждающий фильтр (он же — режекторный фильтр, он же — фильтр-пробка) — электронный или любой другой фильтр, не пропускающий сигналы со входа на выход в определённой полосе частот, но имеющий близкий к единице коэффициент передачи при более низких и более высоких частотах.
Эта полоса подавления характеризуется шириной полосы заграждения и расположена вокруг центральной частоты подавления fо.
Заграждающий фильтр, предназначенный для подавления одной определённой частоты, называется узкополосным заграждающим фильтром или фильтром-пробкой.

Для описания режекторных фильтров используют следующие параметры:
центральная частота подавления fо;
две граничных частоты – нижняя fн и верхняя fв, при которых Кu = 0,7mах;
диапазон частот Δf = fв − fн, называемый полосой задержания;
параметр Q = (fв + fн)/(2Δf), называемый добротностью.

Простейшие Т-образные фильтры и их амплитудно-частотная характеристика приведены на Рис.1.

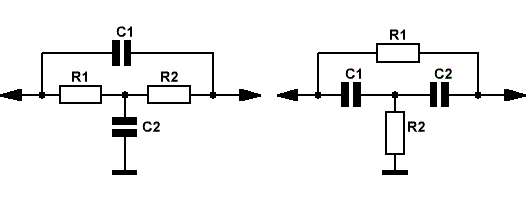
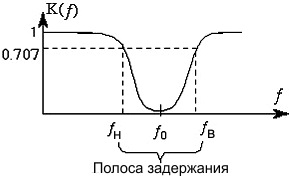
Рис.1

Центральная частота подавления этих фильтров рассчитывается по формуле: fо = 1/(2π*R*C) при R1=R2=R, C1=C2=C. Глубина режекции — всего 10 дБ, а полоса задержания составляет значение, в 5-6 раз превышающее fо.

Именно в силу указанных выше хилых характеристик — подобные простейшие цепи уступили позиции двойным Т-образным RC-фильтрам (Рис.2), часто называемым 2ТФ.

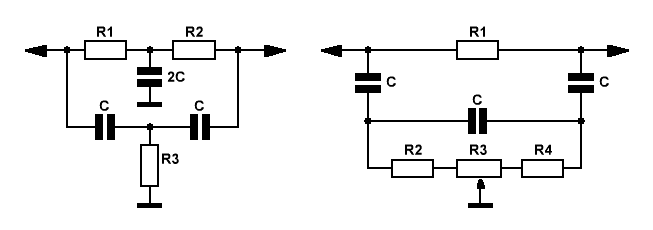
Рис.2 Рис.3

Двойной Т-образный RC-фильтр при определённых условиях (симметрия моста, точный подбор элементов, согласование входа и выхода) почти полностью подавляет центральную частоту fo. Глубина режекции (подавления частоты fo) при работе на высокоомную нагрузку достигает 50 дБ. Добротность Q — около 0,3.

На Рис.2 приведена классическая схема двойного Т-образного режекторного фильтра, на Рис.3 — с возможностью плавной регулировки центральной частоты подавления.

Начнём с нерегулируемой схемы.
Обычно выбираются следующие соотношения элементов R2=R1, R3=R1/2.
Номиналы этих резисторов должны быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления последующего.
Ничего не изменилось, центральная частота вычисляется по формуле fо = 1/(2π*R*C).

РИСУЕМ ТАБЛИЦУ ДЛЯ ДВОЙНЫХ Т-ОБРАЗНЫХ RC-ФИЛЬТРОВ

При желании ввести регулировку центральной частоты подавления fо с диапазоном перекрытия по частоте более чем в 2 раза, при сохранении параметров, присущих двойным Т-образным режекторным фильтрам, имеет смысл воспользоваться схемой, приведённой на Рис.3.

Значение резистора R1 должно в 6 раз превышать суммарную величину R2, R3 и R4, поэтому его следует выбирать номиналом — не менее 100 кОм.
Формула для расчёта частоты подавления fо = 1/(2πС√3×R_{3_1}×R_{3_2}), где R_{3_1} — сумма сопротивлений слева от регулирующего вывода R3, а R_{3_2} — справа.

Рисуем таблицу и для таких фильтров.

ТАБЛИЦА ДЛЯ ПЕРЕСТРАИВАЕМЫХ РЕЖЕКТОРНЫХ RC-ФИЛЬТРОВ

Дальнейшего улучшения параметров режекторных фильтров можно добиться введением в схему на Рис.2 положительной обратной связи, подаваемой в точки, идущие к земляной шине.
В результате подобных действий фильтры становятся активными и приобретают следующий вид.

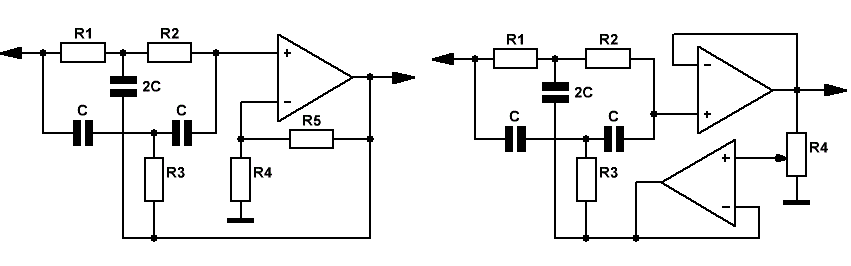
Рис.4 Рис.5

На Рис.4 приведена схема активного режекторного фильтра на основе простого двойного Т-моста.

Значение добротности определяется отношением значений резисторов K=R5/R4. При изменении этого отношения в диапазоне К=0.01-0.2 добротность Q меняется практически линейно и принимает значения от 30 до 2. Дальнейшее увеличение параметра К не приветствуется, в связи с ухудшением неравномерности АЧХ в полосе пропускания.

Для желающих же регулировать значение добротности в более широких пределах на Рис.5 приведена схема активного режекторного фильтра на двух операционных усилителях. Здесь переменный резистор R4 позволяет изменять добротность в пределах 50 — 0.3.

А при необходимости получить перестраиваемый по частоте активный режекторный фильтр, регулирующий вывод переменного резистора R3 на Рис.3, точно таким же образом подключается к выходу операционного усилителя. Результатом является схема, изображённая на Рис.6 .

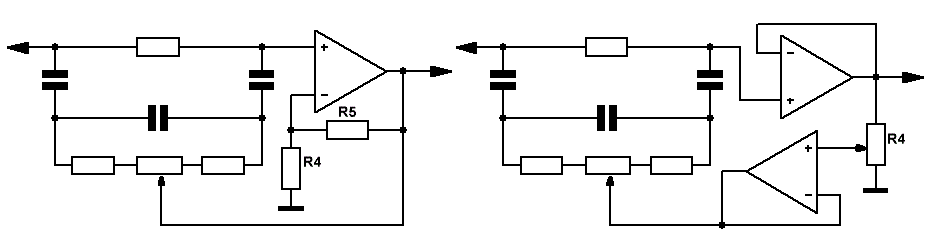
Рис.6 Рис.7

На Рис.7 приведена схема режекторного фильтра, позволяющая регулировать как частоту подавления, так и добротность в широких пределах.

Обе таблицы для расчёта частотозадающих элементов остаются в силе!

Ну, да и хватит, на следующей странице будем мурыжить режекторные LC фильтры.

 

Фильтры на ОУ — начало

Идеальный ОУ — Примитивный метод анализа фильтров на ОУ

09.11.2013 | Рубрика: Операционный усилитель

Фильтры на операционных усилителях строятся при помощи частотно-зависимых элементов – конденсаторов и катушек индуктивности. Такие фильтры часто называют активными фильтрами на ОУ. Сейчас поговорим о фильтрах на ОУ с применением конденсаторов, ибо, так чаще всего и бывает…

Конденсаторы являются важным инструментом разработчика схем. По этой причине необходимо обсудить их роль и влияние на характеристики схем, в которых они применяются. Импеданс конденсаторов описывается выражением

Отметим, что на постоянном токе импеданс конденсатора бесконечен, а на бесконечно высокой частоте он равен нулю. АЧХ (АЧХ  — это амплитудно- частотная характеристика) конденсатора показана на рис. 1.

Рис. 1. АЧХ конденсатора

При последовательном соединении конденсатора и резистора АЧХ имеет точку излома. Не вдаваясь в математические расчёты, отметим, что частота, соответствующая точке излома, равна

а коэффициент передачи на этой частоте изменяется на 3 дБ.

На рис. 2 приведена схема фильтра нижних частот (ФНЧ), в которой конден­сатор включён параллельно с резистором цепи ОС (ОС – обратная связь). Коэффициент передачи этой схемы описывается выражением

Рис. 2. Фильтр НЧ на ОУ

Заметьте — на рис. 2 ОУ включен как инвертирующий усилитель.

На очень низких частотах X_C стремится к бесконечности, конденсатор не оказывает влияния на схему и сопротивление ОС определяется резистором R_F. Коэффициент усиления на низких частотах равен

На очень высоких частотах импеданс конденсатора стремится к нулю, резистор в цепи ОС оказывается замкнут через конденсатор накоротко, что уменьшает коэффициент усиления до нуля. На частоте, при которой X_C = R_F, коэффициент усиления уменьшается в √2 раз по сравнению с его максимальным значением. Это происходит из-за векторного сложения равных по модулю импедансов конденсатора и резистора в цепи ОС.

АЧХ схемы на рис. 2. показана на двух графиках ниже, в логарифмическом и линейном представлении:

АЧХ ФНЧ на ОУ (логарифмический масштаб)

АЧХ ФНЧ на ОУ (линейный масштаб)

Соединение конденсатора параллельно с резистором R_G создаёт противоположный эффект, и схема превращается в фильтр верхних частот (ФВЧ) рис. 3, где ОУ включен как неинвертирующий усилитель. АЧХ этого фильтра описывается выражением

Рис. 3. Фильтр верхних частот на ОУ

На очень низких частотах импеданс конденсатора стремится к бесконечности, так что его влияние в параллельной цепи с R_G пренебрежимо мало. Коэффициент усиления на низких частотах равен

На высоких частотах импеданс конденсатора уменьшается, а коэффициент усиления увеличивается.

АЧХ схемы на рис. 3 показана ниже:

АЧХ ФВЧ на ОУ

(какой чудный всплеск на АЧХ)

В этой статье был использован примитивный метод качественного анализа поведения фильтров на ОУ. Более точный метод анализа работы фильтров будет представлен в следующих статьях.

Метки:: Операционный усилитель

Изучение работы активных фильтров с применением операционных усилителей

Цель работы

1 Изучить принципы работы активных фильтров на базе операционных усилителей (ОУ).

2 Ознакомиться с работой пакетa MicroCap.

 

7.1 Теоретические сведения

Интегральная технология не позволяет создавать конденсаторы большой емкости и катушки большой индуктивности для получения на их основе соответствующих фильтров в ИМС. В связи с этим в интегральной схемотехнике находят широкое применение активные фильтры на базе ОУ, представляющие собой определенные комбинации ОУ с внешними по отношению к ним избирательными RC-цепями, входящими в цепи общих ООС ОУ.

На рис. 7.1,а приведена простая схема активного фильтра нижних частот (ФНЧ), полученного на основе инвертирующего ОУ путем охвата его частотнозависимой ООС на верхних частотах. Здесь в цепь ООС в дополнение к R2 включен конденсатор C2. На рис. 7.1,б показана его АЧХ.

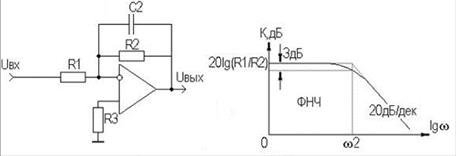
а) б)

Рис. 7.1 Схема (а) и АЧХ (б) активного фильтра нижних частот на ОУ

На нижних и средних частотах сопротивление конденсатора C2 велико (его как бы нет), ООС будет частотнонезависимой и сквозной коэффициент усиления схемы будет определяться ранее полученными для инвертирующего ОУ выражением K_U = -R2/R1.

В области же верхних частот сопротивление конденсатора X_C2 уменьшается и становится меньше R2 (X_C2 <R2), ООС оказывается частотнозависимой, её глубина возрастает пропорционально увеличению частоты сигнала, начиная с верхней граничной частоты w_2., на которой сквозной коэффициент усиления K_U уменьшается до уровня 0,707К_U (на 3 дБ):

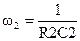
АЧХ схемы (рис.7.1,б) имеет вид, типичный для ФНЧ. Выбором параметров цепи ООС (C2 и R2) можно получить требуемую полосу пропускания ФНЧ.

Схема активного ФНЧ на ОУ (рис.7.1) может быть интегратором входного напряжения при соответствующих параметрах цепи общей ООС. Аналогично могут быть построены ФНЧ и интегратор на основе неинвертирующего ОУ.

На рис.7.2,а приведена простая схема активного фильтра верхних частот (ФВЧ) на инвертирующем ОУ с частотнозависимой общей ООС на нижних частотах, полученная путем включения в петлю ООС конденсатора C1 последовательно с резистором R1. На рис.7.2, б показана его АЧХ.

Выбором параметров цепи ООС (C1, R1) получают требуемое значение нижней граничной частоты w₁:

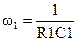
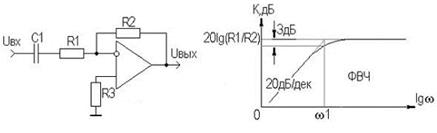
а) б)

Рис. 7.2 Схема (а) и АЧХ (б) активного фильтра верхних частот на ОУ

 

Коэффициент усиления с понижением частоты будет падать пропорционально частоте сигнала, начиная с частоты w₁.

Схема активного ФВЧ на ОУ (рис. 7.2,а) может быть дифференциатором входного напряжения при соответствующих параметрах цепи общей ООС. Аналогично могут быть построены ФВЧ и дифференциатор на неинвертирующем ОУ.

На рис.7.3,а представлена схема активного полосового фильтра на инвертирующем ОУ с частотнозависимой общей ООС как в области верхних частот, так и в области нижних частот, объединяющая в себе схемы рис.7.1 и 7.2. На рис. 7.3,б показана его АЧХ.

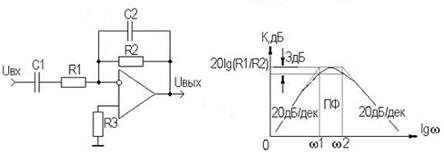
а) б)

Рис. 7.3 Схема (а) и АЧХ (б) активного полосового фильтра на ОУ

 

Вид АЧХ схемы (рис.7.3,б) определяется характером общей ООС. В полосе пропускания влияние емкостей C1 и С2 пренебрежимо мало, ООС частотнонезависима и коэффициент усиления определяется выражением K_U = — R₂/R₁ (как и в ранее рассмотренном инвертирующем ОУ). В областях же верхних и нижних частот ООС становятся частотнозависимой, ее глубина возрастает, что уменьшает коэффициент усиления схемы.

 

7.2 Проведение компьютерного эксперимента

7.2.1 Запустить программу MicroCap.

7.2.2 Составить схему для исследования АЧХ инвертирующего каскада на ОУ, согласно показанной на рис. 7.4.

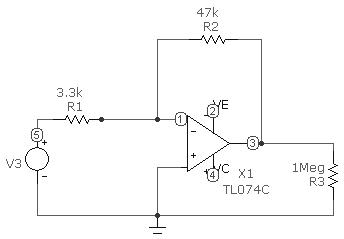
Рис. 7.4 Схема для снятия АЧХ инвертирующего каскада на ОУ

 

7.2.3 Определить вид АЧХ каскада по схеме рис. 7.4. Запустить анализ по переменному току (AC Analysis), выбрав пункт меню «Анализ ® Частотный анализ (АС)». Задать установки анализа аналогично представленным на рис. 7.5: диапазон частот: от 1Гц до 10⁸Гц; выражение по оси Х – частота (F), выражение по оси Y – коэффициент передачи по напряжению, K_U=u_вых/u_вх (по схеме на рис. 7.4. v(3)/v(5)), автомасштабирование включено.

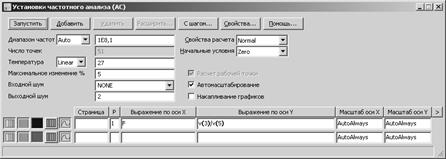
Рис. 7.5 Окно установок анализа по переменному току

 

7.2.3 Определить частоту среза активного фильтра нижних частот, сравнить полученное значение с результатом моделирования.

7.2.3.1 Составить схему для исследования АЧХ активного фильтра нижних частот на ОУ, согласно показанной на рис. 7.6.

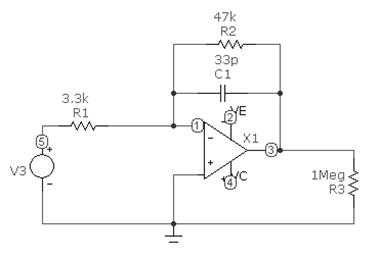
Рис. 7.6 Схема для снятия АЧХ активного ФНЧ на ОУ

7.2.3.2 По формуле раздела 7.1 определить частоту среза для указанного фильтра.

7.2.3.3 Исследовать АЧХ каскада по схеме рис. 7.6. Запустить анализ по переменному току (AC Analysis), выбрав пункт меню «Анализ ® Частотный анализ (АС)». Задать установки анализа аналогично представленным на рис. 7.5: диапазон частот: от 1Гц до 10⁸Гц; выражение по оси Х – частота (F), выражение по оси Y – коэффициент передачи по напряжению, K_U=u_вых/u_вх (по схеме на рис. 7.6. v(3)/v(5)), автомасштабирование включено.

7.2.3.4 Сделать вывод о соответствии расчетного и полученного в результате моделирования значений частоты среза фильтра.

7.2.3.5 Составить схему для исследования АЧХ активного фильтра верхних частот на ОУ, согласно показанной на рис. 7.7.

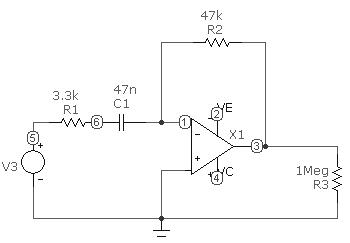
Рис. 7.7 Схема для снятия АЧХ активного ФВЧ на ОУ

 

7.2.3.6 По формуле раздела 7.1 определить частоту среза для указанного фильтра.

7.2.3.7 Исследовать АЧХ каскада по схеме рис. 7.7. Запустить анализ по переменному току (AC Analysis), выбрав пункт меню «Анализ ® Частотный анализ (АС)». Задать установки анализа аналогично представленным на рис. 7.5: диапазон частот: от 1Гц до 10⁸Гц; выражение по оси Х – частота (F), выражение по оси Y – коэффициент передачи по напряжению, K_U=u_вых/u_вх, по схеме на рис. 7.7. v(3)/v(5), автомасштабирование включено.

7.2.3.8 Сделать вывод о соответствии расчетного и полученного в результате моделирования значений частоты среза фильтра.

7.2.3.9 Составить схему для исследования АЧХ активного полосового фильтра на ОУ, согласно показанной на рис. 7.8.

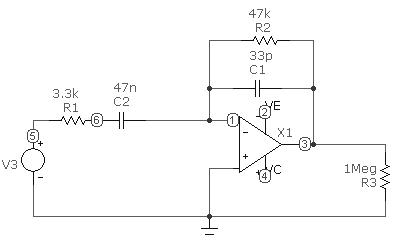
Рис. 7.8 Схема для снятия АЧХ активного полосового фильтра на ОУ

 

7.2.3.10 Исследовать АЧХ каскада по схеме рис. 7.8. Запустить анализ по переменному току (AC Analysis), выбрав пункт меню «Анализ ® Частотный анализ (АС)». Задать установки анализа аналогично представленным на рис. 7.5: диапазон частот: от 1Гц до 10⁸Гц; выражение по оси Х – частота (F), выражение по оси Y – коэффициент передачи по напряжению, K_U=u_вых/u_вх (по схеме на рис. 7.8. v(3)/v(5)), автомасштабирование включено.

7.2.3.11 Определить полосу пропускания фильтра.

 

7.3 Содержание отчета

— название и цель лабораторной работы;

-схема для снятия АЧХ инвертирующего усилительного каскада на ОУ;

— АЧХ усилительного каскада;

— схема для снятия АЧХ активного ФНЧ на ОУ;

-рассчитанное значение частоты среза фильтра;

— АЧХ активного ФНЧ на ОУ;

— схема для снятия АЧХ активного ФВЧ на ОУ;

-рассчитанное значение частоты среза фильтра;

— АЧХ активного ФВЧ на ОУ;

— схема для снятия АЧХ полосового фильтра на ОУ;

— АЧХ полосового фильтра на ОУ;

— определенная по АЧХ полоса пропускания фильтра;

— краткие выводы по результатам работы.

 

7.4 Контрольные вопросы

1 Поясните принципы, лежащие в основе фильтрующих свойств рассмотренных схем.

2 В чем заключаются особенности использования активных фильтров?

3 Качественно изобразите АЧХ ФНЧ, ФВЧ, полосового и режекторного фильтров.

4 Перечислите важнейшие характеристики активных фильтров.

5 Как влияют на параметры фильтров величины номиналов резисторов R1 и R2?

 

Лабораторная работа 8