Основные логические элементы и схемы их построения
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
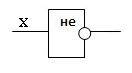
 Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
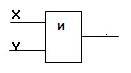
 Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
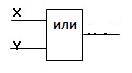
 Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.
Составьте логическую схему для логического выражения: F=A \/ B /\ A.
1. Две переменные – А и В.
2. Две логические операции: 1-/\, 2-\/.
3. Строим схему:
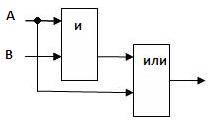

Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
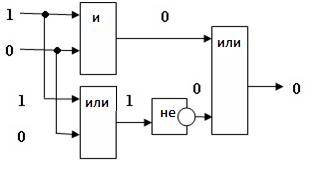

4. Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0
правила соединения модулей между собой и анализ простых логических схем / Habr
Приветствую всех.Продолжаю написание статей про простейшие логические цепи.
В этом посте – правила соединения логических элементов и цепей между собой, а также два простых метода анализа логических схем.
По многочисленным просьбам хабралюдей, а также для упрощения восприятия написанного, буду кроме западного названия определённого элемента приводить и русское.
Правила соединения цепей и их компонентов
В прошлой статье мы познакомились с такими логическими модулями, как Not-1 (логическое отрицание, !A), Or-2 (логическая сумма, AvB) и And-2 (логическое умножение, A^B), но ни слова не было сказано о том, как соединять между собой эти простейшие комбинационные логические цепи (КЛЦ, они же – комбинационные схемы).
Вот несколько правил, которые помогут избежать ошибок при соединении проводников и логических модулей:
1. Не соединяйте два выхода напрямую. Это может привести к конфликту сигналов.
2. Если у логического модудя два входа, они оба должны иметь значение. Если неизвестен сигнал на одном из входов, то скорее всего не получится узнать значение исходящего сигнала.
3. Не должно быть циклов. Эффект может быть любым – от нестабильности работы цепи до её неспособности функционировать.
Анализ логических схем
Для упрощения анализа цепей мы будем использовать некоторые условные обозначения. Например:
Как видите, определённый набор элементов изображается с помощью одного-единственного модуля.
Анализ цепи из 6-8 элементов
Возьмём любую сделанную по правилам комбинационную схему. Например вот эту:
Если вам по каким-то причинам не нравится моя схема, нарисуйте свою 🙂
Суть анализа цепи заключается в выявлении исходящих сигналов в зависимости от значений входов.
Существует два метода этого самого анализа – горизонтальный (по строкам) и вертикальный (по столбцам).
Анализ по строкам
Этот тип исследования цепей заключается в следующем: мы поочерёдно выставляем разные значения на входах цепи, и смотрим, как изменяется сигнал во время его прохождения дальше по цепи. Вот наглядный пример:
Таким способом удобно анализировать небольшие схемы с одним-двумя входами, потому что не обязательно строить таблицу истинности.
Для таких цепей, как выбранная нами ранее, лучше всё-таки нарисовать эту самую таблицу и вписывать туда найденные значения. Вот так, например:
Анализ по столбцам
Суть этого метода – поочерёдно, с помощью логических выражений, найти значения для всех частей цепи, и только потом вычислить результат для выходов цепи.
Как видно на картинке, мы вычисляем значения сигнала для каждого элемента цепи, постепенно приближаясь к выходу. Для нашей цепи это будет выглядеть так:
Теперь можно сравнить результаты, полученные с помощью двух методов. Если они совпадают, то это значит, что либо всё сделано правильно, либо мы допустили больше одной ошибки ( 😀 ).
На данный момент всё.
В следующей статье мы начнём создавать свои логические схемы по заданным параметрам.
Спасибо за внимание, и хороших всем выходных!
Логические элементы
 В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
В данной статье расскажем что такое логические элементы, рассмотрим самые простые логические элементы.
Любое цифровое устройство — персональный компьютер, или современная система автоматики состоит из цифровых интегральных микросхем (ИМС), которые выполняют определённые сложные функции. Но для выполнения одной сложной функции необходимо выполнить несколько простейших функций. Например, сложение двух двоичных чисел размером в один байт происходит внутри цифровой микросхемы называемой «процессор» и выполняется в несколько этапов большим количеством логических элементов находящихся внутри процессора. Двоичные числа сначала запоминаются в буферной памяти процессора, потом переписываются в специальные «главные» регистры процессора, после выполняется их сложение, запоминание результата в другом регистре, и лишь после результат сложения выводится через буферную память из процессора на другие устройства компьютера.
Процессор состоит из функциональных узлов: интерфейсов ввода-вывода, ячеек памяти – буферных регистров и «аккумуляторов», сумматоров, регистров сдвига и т.д. Эти функциональные узлы состоят из простейших логических элементов, которые, в свою очередь состоят из полупроводниковых транзисторов, диодов и резисторов. При конструировании простых триггерных и других электронных импульсных схем, сложные процессоры не применить, а использовать транзисторные каскады – «прошлый век». Тут и приходят на помощь – логические элементы.
Логические элементы, это простейшие «кубики», составные части цифровой микросхемы, выполняющие определённые логические функции. При этом, цифровая микросхема может содержать в себе от одного, до нескольких единиц, десятков, …и до нескольких сотен тысяч логических элементов в зависимости от степени интеграции. Для того, чтобы разобраться, что такое логические элементы, мы будем рассматривать самые простейшие из них. А потом, наращивая знания, разберёмся и с более сложными цифровыми элементами.
Начнём с того, что единица цифровой информации это «один бит». Он может принимать два логических состояния – логический ноль «0», когда напряжение равно нулю (низкий уровень), и состояние логической единицы «1», когда напряжение равно напряжению питания микросхемы (высокий уровень).
Поскольку простейший логический элемент это электронное устройство, то это означает, что у него есть входы (входные выводы) и выходы (выходные выводы). И входов и выходов может быть один, а может быть и больше.
Для того, чтобы понять принципы работы простейших логических элементов используется «таблица истинности». Кроме того, для понимания принципов работы логических элементов, входы, в зависимости от их количества обозначают: Х1, Х2, … ХN, а выходы: Y1, Y2, … YN.
Функции, выполняемые простейшими логическими элементами, имеют названия. Как правило, впереди функции ставится цифра, обозначающая количество входов. Простейшие логические элементы всегда имеют лишь один выход.
Рассмотрим простейшие логические элементы

 — «НЕ» (NOT) – функция отрицания (инверсии сигнала). Потому его чаще называют — «инвертор». Графически, инверсия обозначается пустым кружочком вокруг вывода элемента (микросхемы). Обычно кружок инверсии ставится у выхода, но в более сложных логических элементах, он может стоять и на входе. Графическое обозначение элемента «НЕ» и его таблица истинности представлены на рисунке слева.
— «НЕ» (NOT) – функция отрицания (инверсии сигнала). Потому его чаще называют — «инвертор». Графически, инверсия обозначается пустым кружочком вокруг вывода элемента (микросхемы). Обычно кружок инверсии ставится у выхода, но в более сложных логических элементах, он может стоять и на входе. Графическое обозначение элемента «НЕ» и его таблица истинности представлены на рисунке слева.
У элемента «НЕ» всегда один вход и один выход. По таблице истинности следует, что при наличии на входе элемента логического нуля, на выходе будет логическая единица. И наоборот, при наличии на входе логической единицы, на выходе будет логический ноль. Цифра «1» внутри прямоугольника обозначает функцию «ИЛИ», её принято рисовать и внутри прямоугольника элемента «НЕ», но это ровным счётом ничего абсолютно не значит.
 Обозначение D1.1 означает, что D — цифровой логический элемент, 1 (первая) — номер микросхемы в общей схеме, 1 (вторая) — номер элемента в микросхеме. Точно также расшифровываются и другие логические элементы.
Обозначение D1.1 означает, что D — цифровой логический элемент, 1 (первая) — номер микросхемы в общей схеме, 1 (вторая) — номер элемента в микросхеме. Точно также расшифровываются и другие логические элементы.
Часто, чтобы отличить цифровые микросхемы от аналоговых микросхем, применяют обозначения из двух букв: DD – цифровая микросхема, DA – аналоговая микросхема. В последующем, мы не будем заострять внимание на это обозначение, а вернёмся лишь тогда, когда это будет необходимым.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «НЕ», является интегральная микросхема (ИМС) К155ЛН1, внутри которой имеется шесть элементов «НЕ». Нумерация выводов этой микросхемы показана справа.

 — «И» (AND) – функция сложения (если на всех входах единица, то на выходе будет единица, в противном случае, если хотя бы на одном входе ноль, то и на выходе всегда будет ноль). В алгебре-логике элемент «И» называют «конъюнктор». Графическое обозначение элемента «2И» и его таблица истинности представлены слева.
— «И» (AND) – функция сложения (если на всех входах единица, то на выходе будет единица, в противном случае, если хотя бы на одном входе ноль, то и на выходе всегда будет ноль). В алгебре-логике элемент «И» называют «конъюнктор». Графическое обозначение элемента «2И» и его таблица истинности представлены слева.
Название элемента «2И» обозначает, что у него два входа, и он выполняет функцию «И». На схеме внутри прямоугольника микросхемы рисуется значок «&», что на английском языке означает «AND» (в переводе на русский — И).
По таблице истинности следует, что на выходе элемента «И» будет логическая единица только в одном случае — когда на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то и на выходе будет ноль.
 Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «2И», является интегральная микросхема (ИМС) К155ЛИ1, внутри которой имеется четыре элемента «2И». Нумерация выводов этой микросхемы показана справа.
Самой распространённой микросхемой «транзисторно-транзисторной логики» (ТТЛ), выполняющей функцию «2И», является интегральная микросхема (ИМС) К155ЛИ1, внутри которой имеется четыре элемента «2И». Нумерация выводов этой микросхемы показана справа.
 Для того, чтобы вам было понятнее что такое «2И», «3И», «4И», и т.д., приведу графическое обозначение и таблицу истинности элемента «3И».
Для того, чтобы вам было понятнее что такое «2И», «3И», «4И», и т.д., приведу графическое обозначение и таблицу истинности элемента «3И».
По таблице истинности следует, что на выходе элемента «3И» будет логическая единица только в том случае — когда на всех трёх входах будет логическая единица. Если хотя бы на одном входе будет логический ноль, то и на выходе элемента также будет логический ноль. Самой распространённой микросхемой ТТЛ, выполняющей функцию «3И», является микросхема К555ЛИ3, внутри которой имеется три элемента «3И».

 — «И-НЕ» (NAND) – функция сложения с отрицанием (если на всех входах единица, то на выходе будет ноль, в противном случае на выходе всегда будет единица). Графическое обозначение элемента «2И-НЕ» и его таблица истинности приведены слева.
— «И-НЕ» (NAND) – функция сложения с отрицанием (если на всех входах единица, то на выходе будет ноль, в противном случае на выходе всегда будет единица). Графическое обозначение элемента «2И-НЕ» и его таблица истинности приведены слева.
По таблице истинности следует, что на выходе элемента «2И-НЕ» будет логический ноль только в том случае, если на обоих входах будет логическая единица. Если хотя бы на одном входе ноль, то на выходе будет единица.
 Самой распространённой микросхемой ТТЛ, выполняющей функцию «2И-НЕ», является ИМС К155ЛА3, а микросхемами КМОП (комплементарный металлооксидный полупроводник) – ИМС К561ЛА7 и К176ЛА7, внутри которых имеется четыре элемента «2И-НЕ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2И-НЕ», является ИМС К155ЛА3, а микросхемами КМОП (комплементарный металлооксидный полупроводник) – ИМС К561ЛА7 и К176ЛА7, внутри которых имеется четыре элемента «2И-НЕ». Нумерация выводов этих микросхем показана справа.
Сравнив таблицы истинности элемента «2И-НЕ» и элемента «2И» можно догадаться об эквивалентности схем:

Добавив к элементу «2И» элемент «НЕ» мы получили элемент «2И-НЕ». Так можно собрать схему, если нам необходим элемент «2И-НЕ», а у нас в распоряжении имеются только элементы «2И» и «НЕ».
И наоборот:

Добавив к элементу «2И-НЕ» элемент «НЕ» мы получили элемент «2И». Так можно собрать схему, если нам необходим элемент «2И», а у нас в распоряжении имеются только элементы «2И-НЕ» и «НЕ».
Аналогичным образом, путём соединения входов элемента «2И-НЕ» мы можем получить элемент «НЕ»:

Обратите внимание, что было введено новое в обозначении элементов – дефис, разделяющий правую и левую часть в названии «2И-НЕ». Этот дефис непременный атрибут при инверсии на выходе (функции «НЕ»).

 — «ИЛИ» (OR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – единица, в противном случае на выходе всегда будет ноль). В алгебре-логике, элемент «ИЛИ» называют «дизъюнктор». Графическое обозначение элемента «2ИЛИ» и его таблица истинности приведены слева.
— «ИЛИ» (OR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – единица, в противном случае на выходе всегда будет ноль). В алгебре-логике, элемент «ИЛИ» называют «дизъюнктор». Графическое обозначение элемента «2ИЛИ» и его таблица истинности приведены слева.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ», является ИМС К155ЛЛ1, внутри которой имеется четыре элемента «2ИЛИ». Нумерация выводов этой микросхемы показана справа.
 Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать схему, которая будет выполнять функцию «2ИЛИ»:
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать схему, которая будет выполнять функцию «2ИЛИ»:


 — «ИЛИ-НЕ» (NOR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – ноль, в противном случае на выходе всегда будет единица). Как вы поняли, элемент «ИЛИ-НЕ» выполняет функцию «ИЛИ», а потом инвертирует его функцией «НЕ».
— «ИЛИ-НЕ» (NOR) – функция выбора (если хотя бы на одном из входов – единица, то на выходе – ноль, в противном случае на выходе всегда будет единица). Как вы поняли, элемент «ИЛИ-НЕ» выполняет функцию «ИЛИ», а потом инвертирует его функцией «НЕ».
Графическое обозначение элемента «2ИЛИ-НЕ» и его таблица истинности приведена слева.
 Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ-НЕ», является ИМС К155ЛЕ1, а микросхемами КМОП – К561ЛЕ5 и К176ЛЕ5, внутри которых имеется четыре элемента «2ИЛИ-НЕ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «2ИЛИ-НЕ», является ИМС К155ЛЕ1, а микросхемами КМОП – К561ЛЕ5 и К176ЛЕ5, внутри которых имеется четыре элемента «2ИЛИ-НЕ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «2ИЛИ-НЕ», но у нас есть в распоряжении только элементы «НЕ» и «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «2ИЛИ-НЕ»:

По аналогии с элементом «2И-НЕ», путём соединения входов элемента «2ИЛИ-НЕ» мы можем получить элемент «НЕ»:


 — «Исключающее ИЛИ» (XOR) — функция неравенства двух входов (если на обоих входах элемента одинаковые сигналы, то на выходе – ноль, в противном случае на выходе всегда будет единица). Операция, которую он выполняет, часто называют «сложение по модулю 2».
— «Исключающее ИЛИ» (XOR) — функция неравенства двух входов (если на обоих входах элемента одинаковые сигналы, то на выходе – ноль, в противном случае на выходе всегда будет единица). Операция, которую он выполняет, часто называют «сложение по модулю 2».
Графическое обозначение элемента «Исключающее ИЛИ» и его таблица истинности приведены слева.
 Самой распространённой микросхемой ТТЛ, выполняющей функцию «Исключающее ИЛИ», является ИМС К155ЛП5, а микросхемами КМОП – К561ЛП2 и К176ЛП2, внутри которых имеется четыре элемента «Исключающее ИЛИ». Нумерация выводов этих микросхем показана справа.
Самой распространённой микросхемой ТТЛ, выполняющей функцию «Исключающее ИЛИ», является ИМС К155ЛП5, а микросхемами КМОП – К561ЛП2 и К176ЛП2, внутри которых имеется четыре элемента «Исключающее ИЛИ». Нумерация выводов этих микросхем показана справа.
Предположим, что нам в схеме необходим элемент, выполняющий функцию «Исключающее ИЛИ», но у нас есть в распоряжении только элементы «2И-НЕ», тогда можно собрать следующую схему, которая будет выполнять функцию «Исключающее ИЛИ»:

 В цифровой схемотехнике процессоров главная функция — «Суммирование двоичных чисел», поэтому сложный логический элемент – «Сумматор» является неотъемлемой частью арифметико-логического устройства любого, без исключения процессора. Составной частью сумматора является набор логических элементов, выполняющих функцию «Исключающее ИЛИ с переносом остатка». Что это такое? В соответствии с наукой «Информатика», результатом сложения двух двоичных чисел, две единицы одного разряда дают ноль, при этом формируется «единица переноса» в следующий старший разряд, который участвует в операции суммирования в старшем разряде. Для этого в схему добавляется ещё один вывод «переноса» — «Р».
В цифровой схемотехнике процессоров главная функция — «Суммирование двоичных чисел», поэтому сложный логический элемент – «Сумматор» является неотъемлемой частью арифметико-логического устройства любого, без исключения процессора. Составной частью сумматора является набор логических элементов, выполняющих функцию «Исключающее ИЛИ с переносом остатка». Что это такое? В соответствии с наукой «Информатика», результатом сложения двух двоичных чисел, две единицы одного разряда дают ноль, при этом формируется «единица переноса» в следующий старший разряд, который участвует в операции суммирования в старшем разряде. Для этого в схему добавляется ещё один вывод «переноса» — «Р».
Графическое обозначение элемента «Исключающее ИЛИ с переносом» и его таблица истинности представлена слева.
Такая функция сложения одноразрядных чисел в простых устройствах обычно не используется, и как правило, интегрирована в состав одной микросхемы – сумматора, с минимальным количеством разрядов – четыре, для сложения четырехбитных чисел. По причине слабого спроса, промышленность таких логических элементов не выпускает. Поэтому, в случае необходимости, функцию «Исключающее ИЛИ с переносом» можно собрать по следующей схеме из элементов «2И-НЕ» и «2ИЛИ-НЕ», которая активно применяется как внутри простых сумматоров, так и во всех сложных процессорах (в том числе Pentium, Intel-Core, AMD и других, которые появятся в будущем):

Вышеперечисленные логические элементы выполняют статические функции, а на основе них строятся более сложные статические и динамические элементы (устройства): триггеры, регистры, счётчики, шифраторы, дешифраторы, сумматоры, мультиплексоры.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Функция «НЕ» — инвертор (‾)
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
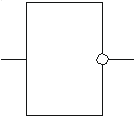
Таблица истинности инвертора
Обозначается 
Функция «2И» — логическое умножение (&)
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
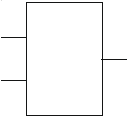
Таблица истинности логической функции 2И
X1 | X2 | F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Обозначается 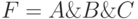
Функция «ИЛИ» — логическое сложение (V)
Правило логического сложения
Таблица истинности логической функции 2ИЛИ
X1 | X2 | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Обозначается 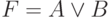
Логическая функция и элемент И-НЕ
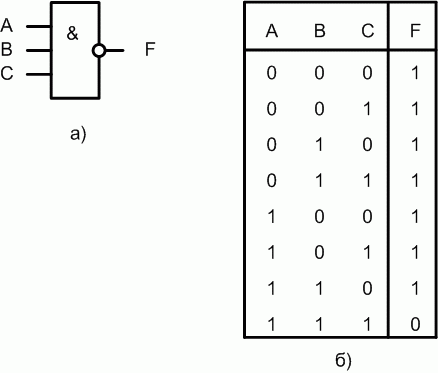
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.

Логическая функция и элемент ИЛИ-НЕ
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.
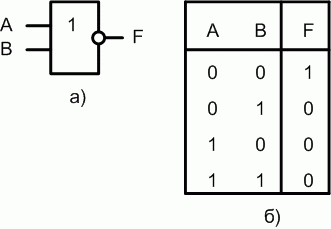
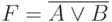
Комбинированные цифровые схемы. Построение цифровой схемы по произвольной таблице истинности (сднф)
СДНФ — Совершенная дизъюктивная нормальная форма
Для реализации таблицы истинности при помощи логических элементов «И» (СДНФ) достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении цифровой схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического элемента «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этого логического элемента непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этого же логического элемента «И» через инверторы. Объединение сигналов с выходов логических элементов «И», реализующих отдельные строки таблицы истинности, производится при помощи логического элемента «ИЛИ». Количество входов в логическом элементе «ИЛИ» определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 1:
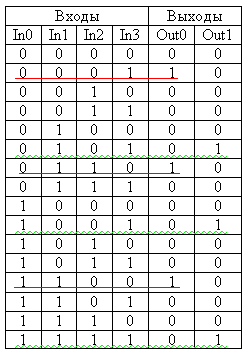
Рисунок 1. Произвольная таблица истинности.
Для синтеза цифровой схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные красным цветом. В таблице истинности три строки, содержащие единицу в выходном сигнале Out0, поэтому в формуле СДНФ будет содержаться три произведения входных сигналов —
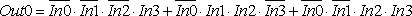
Так как количество переменных в каждом терме (ранг терма) данного логического выражения равно, то такое логическое выражение называется совершенным. (Совершенная Дизъюнктивная Нормальная Форма — СДНФ)
Полученное логическое выражение реализуются микросхемой D2 в схеме, приведенной на рисунке 2. Как и в формуле, каждая строка (терм) реализуется своим логическим элементом «И», затем выходы этих логических элементов объединяются при помощи логического элемента «ИЛИ». Количество входов логического элемента «И» (дизъюнкция) в СДНФ однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе «ИЛИ» определяется количеством строк с единичным сигналом на реализуемом выходе цифровой схемы.
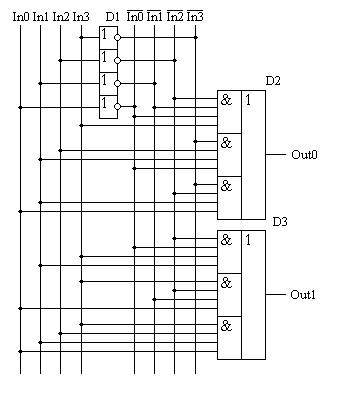 Рисунок 2.
Принципиальная схема, реализующая
таблицу истинности, приведенную на
рисунке 1
Рисунок 2.
Принципиальная схема, реализующая
таблицу истинности, приведенную на
рисунке 1
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего три строки, содержащие единицу в выходном сигнале Out1, поэтому в формуле СДНФ выхода Out1 будет содержаться три произведения входных сигналов:
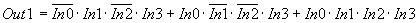
Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но для упрощения понимания материала сейчас минимизация производиться не будет. Это оправдано еще и с той точки зрения, что неминимизированные схемы обычно обладают максимальным быстродействием. При реализации схемы на ТТЛ микросхемах быстродействие всего узла будет равно быстродействию одиночного инвертора (см. описание ТТЛ микросхем).
По СДНФ форме логического выражения обычно строятся современные микросхемы большой интеграции — программируемые логические интегральные схемы (ПЛИС), такие какпрограммируемые логические матрицы (ПЛМ), программируемые матрицы логики ПМЛ или CPLD.
Основы логики: построение логических схем
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №22 г. Владикавказа
Конспект урока по информатике
на тему:
«Основы логики:
построение логических схем»
учитель информатики
Гресева Т.В.
2015 г.
Конспект урока на тему: «Основы логики: построение логических схем».
Данный урок четвёртый в рамках темы «Основы логики». Предполагается, что обучающиеся уже знакомы с основными определениями и логическими операциями, умеют строить таблицы истинности для простых и сложных логических выражений.
Цели урока:
Задачи:
изучить принципы построения логических схем для сложных выражений;
способствовать развитию логического мышления;
сформировать у учащихся представления об устройствах элементной базы компьютера.
Тип урока:
урок совершенствования знаний, умений и навыков;
целевого применения усвоенного.
Вид урока: комбинированный.
Используемое оборудование:
компьютер;
приложение Microsoft Office PowerPoint 2003 и выше;
мультимедиа проектор;
интерактивная доска (по возможности).
План урока:
Организационный момент (1 мин)
Опрос по материалу прошлого урока (4 мин)
Представление нового материала (20 мин)
Выполнение практического задания (12 мин)
Подведение итогов урока. Задание на дом (3 мин)
Ход урока:
Организационный момент.
Приветствие учащихся. Проверка присутствующих. Настрой на урок.
Опрос по материалу прошлого урока.
На прошлом уроке мы с вами познакомились с основными логическими операциями. Обучающимся предлагается ответить на следующие вопросы:
Что такое сложное высказывание?
Сколько Вы знаете базовых логических операций? (5)
Перечислите названия базовых логических операций. (Коньюнкция, Дизъюнкция, Инверсия, Импликация, Эквивалентность)
Какими знаками обозначается логическое умножение? (& и
 )
)Как называется логическое отрицание и что оно выполняет?
Представление нового материала.
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933) говорил «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе – система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М. А. Гавриловым (1903 – 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему.

На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой.

Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
Виды логических элементов (вентилей):
1. Конъюнктор (И):

2. Дизъюнктор (ИЛИ):

3. Инвертор НЕ:

Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение к качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы.
Логический элемент (вентиль) — это электронное устройство, реализующее одну из логических функций.
Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Логическая схема — это электронное устройство, которое реализует любую логическую функцию, описывающую работу устройств компьютера.
Физически каждый логический элемент представляет собой электронную схему, в которой на вход подаются некоторые сигналы, кодирующие 0 либо 1, а с выхода снимается также сигнал, соответствующий 0 или 1 в зависимости от типа логического элемента.
Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико-логическое устройство. Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах.
Важнейшими из таких устройств являются регистры и сумматоры.
Регистр представляет собой электронный узел, предназначенный для хранения многоразрядного двоичного числового кода. Упрощенно можно представить регистр как совокупность ячеек, в каждой из которых может быть записано одно из двух значений: 0 или 1, то есть один разряд двоичного числа. Такая ячейка, называемая триггером, представляет собой некоторую логическую схему, составленную из рассмотренных выше логических элементов.
Под воздействием сигналов, поступающих на вход триггера, он переходит в одно из двух возможных устойчивых состояний, при которых на выходе будет выдаваться сигнал, кодирующий значение 0 или 1. Для хранения в регистре одного байта информации необходимо 8 триггеров.
Сумматор — это электронная схема, предназначенная для выполнения операции суммирования двоичных числовых кодов.
Правила построения логических схем:
1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей логический элемент.
4) Соединить логические элементы в порядке выполнения логических операций.
Построим логическую схему для логического выражения:

Для этого нам потребуется 3 логических элемента:
Логический элемент И
Логический элемент ИЛИ
Л
 огический элемент НЕ
огический элемент НЕ
Выполнение практического задания.
Задание №1
Построить логическую схему для логического выражения и выяснить, при каких входных сигналах на выходе схемы не будет напряжения?

Задание №2
По построенной логической схеме составить логическое выражение


Подведение итогов урока. Задание на дом.
Ответы на вопросы учащихся. Подведение итога урока. Выставление оценок.
Домашнее задание (слайд 18).
Логические схемы
Логические элементы, включая вентили, счетчики и запоминающие устройства, изготавливаются в виде интегральных модулей, или интегральных схем (ИС). Эти ИС разбивают на классы, называемые семействами, по числу полупроводниковых приборов, содержащихся в одной ИС. В настоящее время существуют следующие семейства.
|
1. |
ИС низкой степени интеграции |
до 10 приборов. |
|
2. |
ИС средней степени интеграции |
10-100 приборов. |
|
3. |
ИС большой степени интеграции, или большие ИС (БИС) |
100-1000 приборов. |
|
4. |
ИС сверхбольшой степени интеграции, или сверхбольшие ИС (СБИС) |
1000-10000 приборов. |
|
5. |
Ультрабольшие ИС (УБИС) |
10000-100000 приборов. |
Степень интеграции определяет сложность интегральной схемы. Каждое следующее по сложности семейство характеризуется десятикратным увеличением числа элементов по сравнению с предыдущим. К ИС низкой и средней степени интеграции относятся дискретные логические элементы, такие, как вентили, счетчики и регистры. БИС иСБИС используются в качестве запоминающих устройств, микропроцессоров и законченных систем, таких, как микрокомпьютеры.
Логические состояния
Логический элемент имеет два различных состояния: состояние логического 0, представляемое низким уровнем напряжения, обычно 0 В; и состояние логической 1. представляемое высоким уровнем напряжения (положительной полярности в случае положительной логики и отрицательной полярности в случае отрицательной логики). Уровень напряжения, который представляет логическую 1. зависит от используемого типа ИС. Для ИС, изготавливаемых по биполярной технологии, например для ПС ТТ, I (ИС на основе транзисторно-транзисторной логики), логической 1 соответствует напряжение 5 В, в то время как для ИС КМОП (ИС на комплементарных, или дополняющих, МОП-транзисторах) логическая 1 может быть представлена напряжением в диапазоне от 3 до 15 В и выше. ИС ТТЛ имеют преимущество в быстродействии, а ИС КМОП позволяют реализовать более высокую степень интеграции компонентов
(т. е. позволяют разместить большее число логических элементов в одном интегральном модуле) и не требуют использования стабилизированных источников питания.
Транзисторно-транзисторные логические элементы (ТТЛ)
ТТЛ-элементы применяются в интегральных схемах и обеспечивают высокую скорость переключения. На рис. 34.1 показана упрощенная схема логического элемента И-НЕ с многоэмиттерным транзистором T1 на входе. Когда на обоих входах присутствует логический 0, транзистор T1 насыщен и напряжение на его коллекторе близко к 0 В. Следовательно, транзистор T2 находится в состоянии отсечки, и на выходе мыимеем логическую 1. Когда на оба входа подается логическая 1, транзистор T1 закрывается и переключает транзистор T2 в состояние насыщения. В этом случае на выходе элемента мы имеем логический 0.

Рис. 34.1. Логический элемент И-НЕ (ТТЛ-типа).
Логические элементы на полевых транзисторах
Логические схемы в настоящее время изготавливаются только в виде интегральных схем. Огромное количество логических элементов можно разместить на мельчайшем кристалле (чипе) кремния размером 1х2 мм. В силу своей простоты полевые транзисторы применяются чаще, чем биполярные транзисторы. Наиболее широко распространены логические элементы на основе так называемых КМОП-ячеек (здесь они не рассматриваются). На рис. 34.2 приведена схема логического элемента ИЛИ-НЕ на МОП-транзисторах, который работает на основе отрицательной логики. В этой схеме T1 и T2 — полевые МОП-транзисторы с каналом p-типа (работающие в режиме обогащения). Когда на обоих входах присутствует Уровень логического 0, транзисторы T1 и T2 находятся в состоянии отсечки и на выходе мы имеем логическую 1 (-VDD= -20 В). Когда на один или на оба входа подается логическая 1 (например, -20 В), открываются один или оба транзистора и на выходе мы получаем логический 0.

Рис. 34.2. Логический элемент Рис. 34.3. Логический элемент на И-НЕ
ИЛИ-НЕ на МОП-транзисторах. МОП-транзисторах.
На рис. 34.3 показана схема логического элемента И-НЕ на основе полевых МОП-транзисторов с каналом п-типа. Поскольку используется источник питания положительной полярности, данный логический элемент работает на основе положительной логики. Транзистор T3 постоянно смещен в активную рабочую область напряжением VDD, подаваемым на затвор, и выполняет функцию активной нагрузки логического элемента. Когда на одном или на обоих входах присутствует логический 0, один или оба транзистора находятся в состоянии отсечки, выдавая логическую 1 на выходе. Ток через транзисторы будет протекать только в том случае, когда на оба входа будет подана логическая 1, и только в этом случае мы получим на выходе логический 0.
Булевы выражения
Функции, реализуемые отдельным логическим элементом или комбинацией логических элементов, могут быть выражены логическими формулами, называемыми булевыми выражениями. В булевой алгебре используются следующие обозначения логических функций (см. табл. 34.1):
• Функция И обозначается символом точки (·). Двухвходовый (входы А и В) логический элемент И вырабатывает на выходе сигнал, представляемый булевым выражением А · В.
• Функция ИЛИ обозначается символом (+). Двухвходовый логический элемент ИЛИ вырабатывает на выходе сигнал, представляемый булевым выражением А + В.
Таблица 34.1. Булевы выражения
|
Функция |
Обозначение в булевой алгебре |
|
И |
А·В |
|
или |
А+В
|
|
НЕ |
|
|
И-НЕ |
|
|
ИЛИ-НЕ |
|
|
Исключающее ИЛИ |
|
|
Исключающее ИЛИ-НЕ |
• Логическая функция НЕ обозначается символом черты над обозначением входного сигнала. Логическая схема НЕ с одним входом А вырабатывает на выходе сигнал, представляемый булевым выражением (читается «НЕ А»).
Через эти простые функции можно выразить более сложные:
• Функция Н-НЕ записывается как .
• Функция ИЛИ-НЕ записывается как .
• Функция Исключающее ИЛИ записывается как . Ее можно также записать, используя специальное обозначение, .
• Функция Исключающее ИЛИ-НЕ записывается как . Ее можно также записать, используя специальное обозначение, .
Комбинаторная логика
Рассмотрим логическую схему на рис. 34.4. Логическую функцию, выполняемую этой схемой, можно описать с помощью следующих булевых выражений.
Выходной сигнал логического элемента ИЛИ (i): A + В
Выходной сигнал логического элемента И-ИЕ (ii):
Выходной сигнал логического элемента ИЛИ (iii): (А + В) +

Пример 1
Обратимся к рис. 34.5.
а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.
б) Составьте таблицу истинности, показывающую логические состояния во всех точках схемы, и докажите, что эту схему можно свести к одному логическому элементу.
Решение
а) Булево выражение для точки С = .
Булево выражение для точки D= .
Булево выражение для точки F = ·.
б) Таблица истинности
|
Входы |
Точки |
Выход |
||
|
А
|
В
|
С
|
D
|
F
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу ИЛИ-НЕ.
Пример 2
Обратимся к рис. 34.6.
а) Найдите булево выражение для логической функции изображенной комбинации логических элементов.
б) Составьте таблицу истинности, показывающую логические состояния во всех точках схемы, и докажите, что эту схему можно свести к одному логическому элементу.


Решение
а) Булево выражение для точки С = .
Булево выражение для точки D = .
Булево выражение для точки F = +.
6) Таблица истинности
|
Входы |
Точки |
Выход |
||
|
А
|
В
|
С
|
D
|
F
|
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
Как видно из таблицы истинности, приведенная комбинация логических элементов эквивалентна логическому элементу И-НЕ.
Счетчики
Функцию счета в двоичном счетчике выполняет бистабильный мультивибратор, или делитель на 2, чаще называемый триггером. Цепочка из нескольких таких триггеров образует счетчик. На рис. 34.7 показан двоичный счетчик, состоящий из трех триггеров. Каждый триггер делит частоту поступающих импульсов на 2. Таким образом, два последовательных триггера обеспечивают деление на 4 (2 · 2), а три триггера – на 8 (2 · 2 · 2). Другими словами, на каждые восемь входных импульсов на выходе А появятся четыре импульса, на выходе В — два импульса и на выходе С — один импульс (рис. 34.7).
Как уже говорилось в гл. 32, бистабильный мультивибратор изменяет свое состояние только во время действия одного из фронтов входного импульса. Уровень входного импульса изменяется от 0 к 1 и обратно к 0, и так для каждого приходящего импульса. Обычно предполагается, что состояние триггера изменяется при приходе отрицательного фронта импульса (т. е. при переходе от 1 к 0).
Сигнал на выходе QА триггера А соответствует 20, или столбцу «единиц» в табл. 34.2, сигнал на выходе QB— 21, или столбцу «двоек», и наконец, сигнал на выходе QC — 22, или столбцу «четверок». После поступления 6 импульсов на вход счетчика он оказывается в следующем состоянии: А (число единиц) = 0, В (число двоек) = 1. С (число четверок) = 1; это состояние соответствует десятичному числу 6 (0 + 2 + 4).

5. Логические элементы цифровых устройств
Логические элементы — это электронные устройства, предназначенные для обработки информации представленной в виде двоичных кодов, отобpажаемыx напpяжeниeм (сигналом) выcoкого и низкого уpовня. Логические элементы реализyют логические функции И, ИЛИ, НЕ и их комбинации. Указанные логические операции выполняются с помощью электронных схем, входящих в состав микросхем. Из логических элементов И, ИЛИ, НЕ, можно сконстpуировать цифровое электронное устройство любой сложности.
Логические элементы могут выполнять логические функции в режимах положительной и отрицательной логики. В режиме положительной логики логической единице соответствует высокий уровень напряжения, а логическому нулю — низкий уровень напряжения. В режиме отрицательной логики наоборот логической единице соответствует низкий уровень напряжения, а логическому нулю — высокий.
Если в режиме положительной логики логический элемент, реализует операцию И, то в режиме отрицательной логики выполняет операцию ИЛИ, и наоборот. И если в режиме положительной логики — И-НЕ, то в режиме отрицательной логики — ИЛИ-НЕ.
Условное графическое обозначение логического элемента представляет собой прямоугольник, внутри которого ставится изображение указателя функции. Входы изображают линиями с левой стороны прямоугольника, выходы элемента — с правой стороны. При необходимости разрешается располагать входы сверху, а выходы снизу. У логических элементов И, ИЛИ может быть любое начиная с двух количество входов и один выход. У элемента НЕ один вход и один выход. Если вход обозначен окружностью, то это значит, что функция выполняется для сигнала низкого уровня (отрицательная логика). Если окружностью обозначен выход, то элемент производит логическое отрицание (инверсию) результата операции, указанной внутри прямоугольника.
Все цифровые устройства делятся на комбинационные и на последовательностные. В комбинационных устройствах выходные сигналы в данный момент времени однозначно определяются входными сигналами в тот же момент. Выходные сигналы последовательностного устройства (цифрового автомата) в данный момент времени определяются не только логическими переменными на его входах, но еще зависят и от предыдущего состояния этого устройства. Логические элементы И, ИЛИ, НЕ и их комбинации являются комбинационными устройствами. К последовательностным устройствам относятся триггеры, регистры, счетчики.
Логический элемент И (рис. 1) выполняет операцию логического умножения (конъюнкцию). Такую операцию обозначают символом /\ или значком умножения (·). Если все входные переменные равны 1, то и функция Y=X1·X2 принимает значение логической 1. Если хотя бы одна переменная равна 0, то и выходная функция будет равна 0.
| Таблица 1 | |||
Y=X1·X2 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 0 | ||
1 | 0 | 0 | ||
Рис. 1 | 1 | 1 | 1 |
Наиболее наглядно логическая функция характеризуется таблицей, называемой таблицей истинности (Табл. 1). Талица истинности содержит всевозможные комбинации входных переменных Х и соответствующие им значения функции Y. Количество комбинаций составляет 2n, где n – число аргументов.
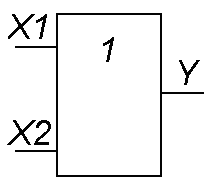
Логичеcкий элeмент ИЛИ (рис. 2) выполняет операцию логического сложения (дизъюнкцию). Обозначают эту операцию символом \/ или знаком сложения (+). Функция Y=X1\/X2 принимает значение логической 1, если хотя бы одна переменная равна 1. (Табл. 2).
| Таблица 2 | |||
Y=X1\/X2 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 2 | 1 | 1 | 1 |
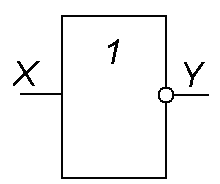
Логический
элемент НЕ
(инвертор) выполняет
операцию логического отрицания
(инверсию). При
логическом отрицании функция Y
принимает значение противоположное
входной переменной Х (Табл. 3). Эту операцию
обозначают 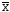 .
.
| Таблица 3 | ||
Y= | X1 | Y | |
0 | 1 | ||
Рис. 3 | 1 | 0 |
Кроме указанных выше логических элементов, на практике широко используются элементы И-НЕ, ИЛИ-НЕ, Исключающее ИЛИ.
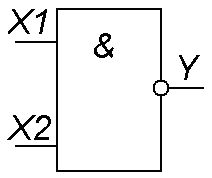
Логичеcкий элемeнт И-НЕ (рис. 4) выполняет операцию логического умнoжения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
| Таблица 4 | |||
| X1 | X2 | Y | |
0 | 0 | 1 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 4 | 1 | 1 | 0 |
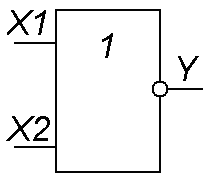
Логический элемент ИЛИ-НЕ (рис. 5) выполняет операцию логического сложения над входными переменными, а затем инвертирует полученный результат и выдаёт его на выход.
| Таблица 5 | |||
| X1 | X2 | Y | |
0 | 0 | 1 | ||
0 | 1 | 0 | ||
1 | 0 | 0 | ||
Рис. 5 | 1 | 1 | 0 |
Логический
элемент Исключающее ИЛИ представлен
на рис. 6. Логическая функция Исключающее
ИЛИ (функция
«неравнозначность» или сумма по модулю
два) записывается в виде 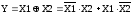 и принимает значение 1 при X1≠X2,
и значение 0 при X1=X2=0
или X1=X2=1
(Табл. 6).
и принимает значение 1 при X1≠X2,
и значение 0 при X1=X2=0
или X1=X2=1
(Табл. 6).
| Таблица 6 | |||
Y=X1 | X1 | X2 | Y | |
0 | 0 | 0 | ||
0 | 1 | 1 | ||
1 | 0 | 1 | ||
Рис. 6 | 1 | 1 | 0 |
Любой из выше
перечисленных элементов можно заменить
устройством, собранным только из базовых
двухвходовых элементов ИЛИ-НЕ или И-НЕ.
Например: операция НЕ
(рис. 7, а) 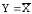
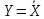 приX1
= X2
= X;
операция И
(рис. 7, б)
приX1
= X2
= X;
операция И
(рис. 7, б) 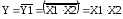 .
.
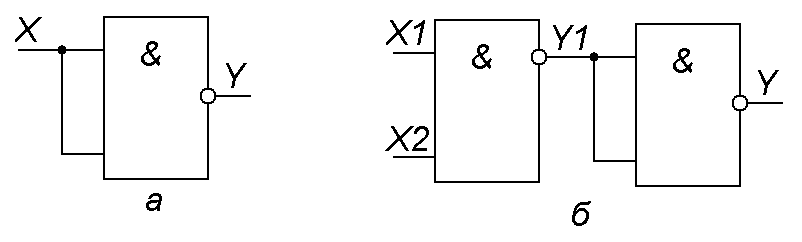
Рис. 7
Интегральные логические элементы выпускаются в стандартных корпусах с 14 или 16 выводами. Один вывод используется для подключения источника питания, еще один является общим для источников сигналов и питания. Оставшиеся 12 (14) выводов используют как входы и выходы логических элементов. В одном корпусе может находится несколько самостоятельных логических элементов. На рисунке 8 показаны условные графические обозначения и цоколевка (нумерация выводов) некоторых микросхем.
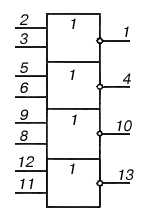
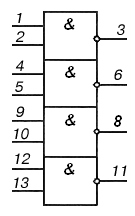
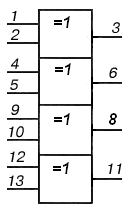
К155ЛЕ1 К155ЛА3 К155ЛП5
Рис. 8
Базовый элемент транзисторно-транзисторной логики (ТТЛ). На рисунке 9 показана схема логического элемента И-НЕ ТТЛ с простым однотранзисторным ключом.
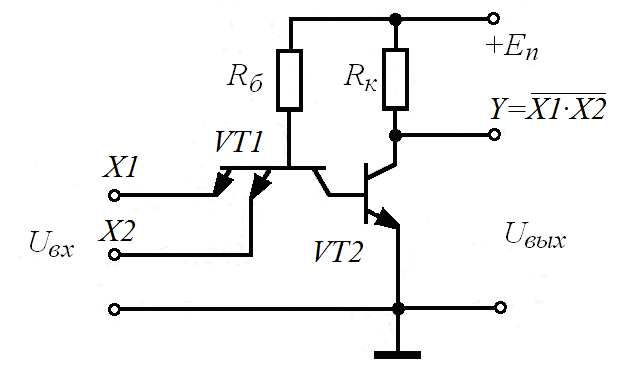 Рис.
9
Рис.
9
Простейший логический элемент ТTЛ строится на базе многоэмиттерного транзистор VT1. Пpинцип дейcтвия такого транзистора тот же, что и у обычного биполяpного транзистора. Oтличие заключается в том, что инжекция носителей заряда в базу осуществляется через несколько самостoятельных эмиттерных р—n-переходов. При поступлении на входы логической единицы U1вх, запираются все эмиттерные переxоды VT1. Ток, текущий через резистор Rб, замкнется через открытые р-n—переходы: коллектoрный VT1 и эмиттерный VT2. Этoт ток откpоет транзиcтор VT2, и напряжение на его выходе станет близким к нулю, т. е. Y=U0вых. Если хотя бы на один вход (или на все входы) VT1 будет подан сигнал логического нуля U0вх, то ток, текyщий по Rб, замкнeтся через откpытый эмиттерный переход VT1. Пpи этoм входной ток VT2 будет близoк к нулю, и выходной транзистоp окажется запеpтым, т. е. Y=U1вых. Таким образом, рассмотренная схема осуществляет логическую операцию И-НЕ.
Контрольные вопросы.
Что называется логическим элементом?
Чем различаются положительная и отрицательная логики?
Что называется таблицей истинности?
Каким символом обозначают логическое умножение?
Как на схемах изображают логический элемент И?
При каких входных переменных на выходе логического элемента И формируется логическая 1?
Каким символом обозначают логическое сложение?
Как на схемах изображают логический элемент ИЛИ?
При каких входных переменных на выходе логического элемента ИЛИ формируется логическая 1?
Как на схемах изображают логический элемент НЕ?
Как на схемах изображают логический элемент И-НЕ?
При каких входных переменных на выходе логического элемента И-НЕ формируется логическая 1?
Как на схемах изображают логический элемент ИЛИ-НЕ?
При каких входных переменных на выходе логического элемента ИЛИ-НЕ формируется логическая 1?
Как на схемах изображают логический элемент Исключающее ИЛИ?
При каких входных переменных на выходе логического элемента Исключающее ИЛИ формируется логическая 1?
Как из элемента ИЛИ-НЕ получить элемент НЕ?
Как из элемента И-НЕ получить элемент НЕ?
Опишите принцип действия базового элемента ТТЛ.


 )
) огический элемент НЕ
огический элемент НЕ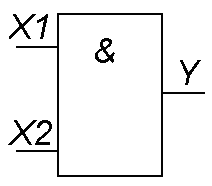
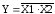
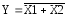
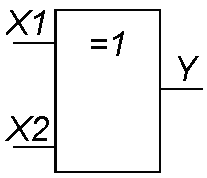
 X2
X2