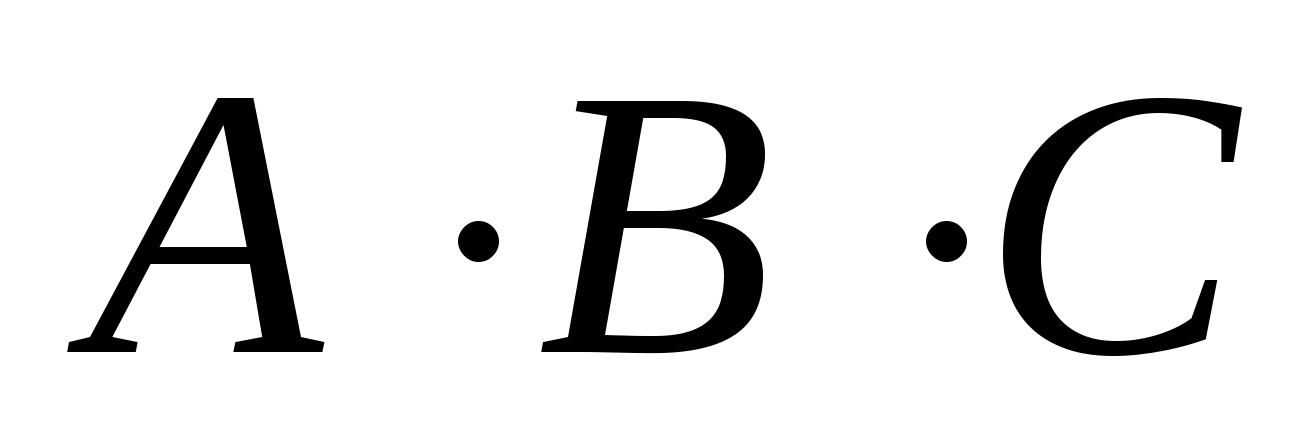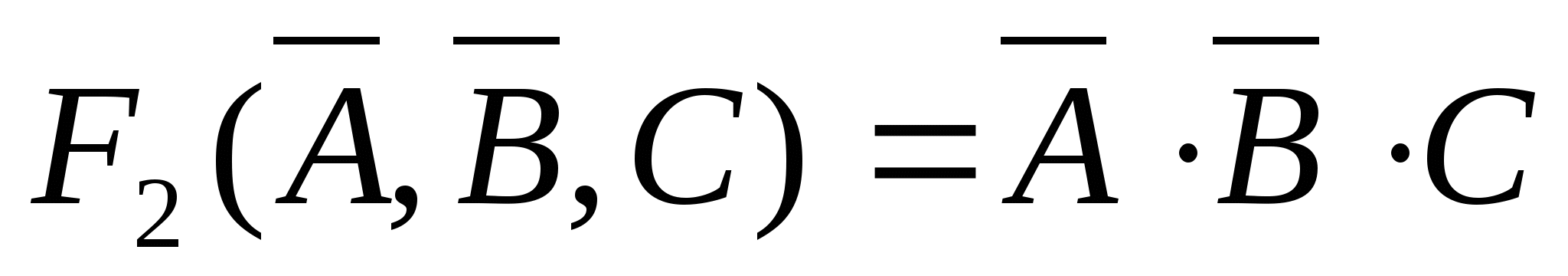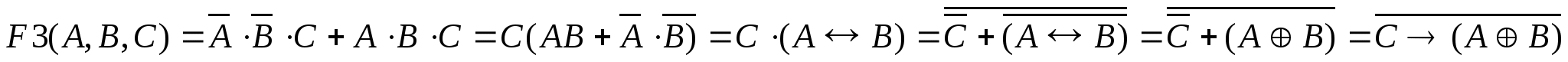Построение логических схем по аналитическим выражениям функций
Логической схемой (ЛС) называется схема, составленная из ЛЭ путем соединения выходов одних ЛЭ со входами других.
Построение логических схем по аналитическим выражениям функций другими словами называется реализацией логических функций.
Существует ряд базисов, из числа которых были рассмотрены И, ИЛИ, НЕ; И—НЕ и ИЛИ—НЕ. В каждом базисе могут быть реализованы любые логические функции.
Схема, которая получается на основании логического выражения, носит название комбинационной схемой.
При переходе от логического выражения к логической схеме элементы, выполняющие в выражении те или иные операции, располагаются в схеме, начиная от входов.
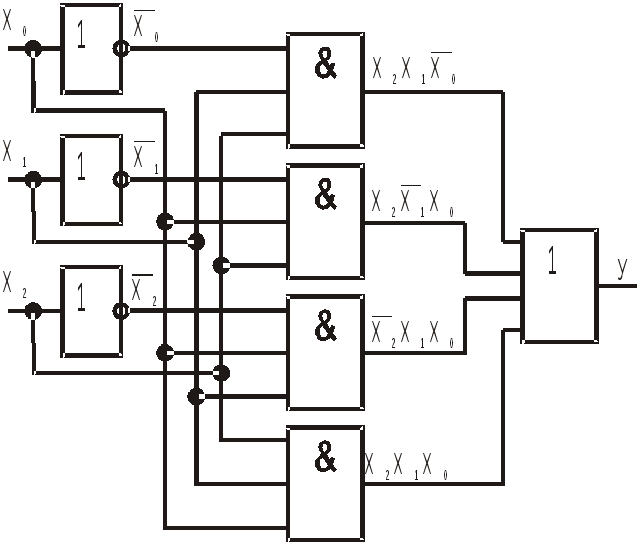
Рассмотрим принцип построения логических схем на примере выражения (1.1) для мажоритарной функции в СДНФ, полученной ранее:
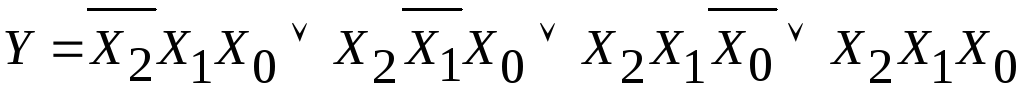 .
.  Н
Н
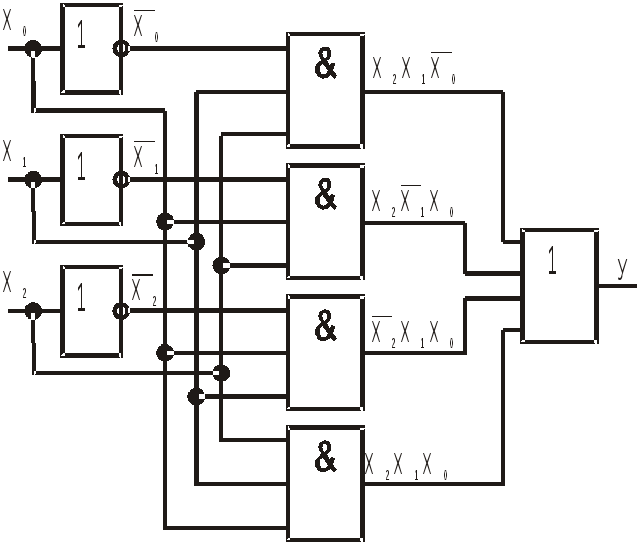 а
логической схеме сначала изображаются
3 инвертора, для отрицания входных
переменных, затем 3 элемента И на три
входа каждый и наконец 1 элемент ИЛИ на
четыре входа. После размещения элементов
изоб
а
логической схеме сначала изображаются
3 инвертора, для отрицания входных
переменных, затем 3 элемента И на три
входа каждый и наконец 1 элемент ИЛИ на
четыре входа. После размещения элементов
изоб ражаются
электрические связи (проводники),
соединяющие входные переменных и
выходные сигналы одних элементов со
входами других согласно логическому
выражению.
ражаются
электрические связи (проводники),
соединяющие входные переменных и
выходные сигналы одних элементов со
входами других согласно логическому
выражению.
Построение ЛС основано на следующих правилах:
Выход ЛЭ можно подсоединять ко входам нескольких ЛЭ;
На входы ЛЭ можно подавать сигналы, представляющие собой константы 0 и 1.
Выходы ЛЭ нельзя соединять вместе;
Выходы ЛЭ нельзя подключать к собственным входам.
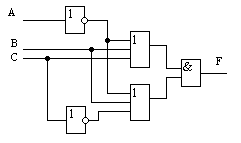
Логическая схема для рассматриваемой функции в СДНФ реализована в базисе И, ИЛИ, НЕ и изображена на рис. 1.13.
Аналогично строится логическая схема для этой же функции после её минимизации по аналитической записи в МДНФ (1.4):
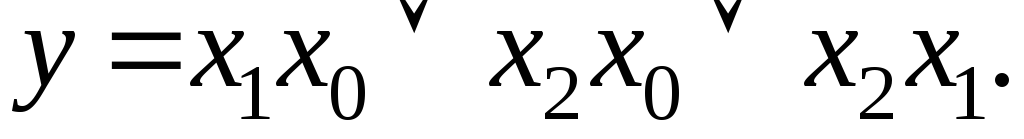
Такая логическая схема в булевом базисе приведена на рис.1.14. Сравнив две построенные схемы можно видеть что последняя схема содержит в два раза меньшее количество ЛЭ, которые имеют меньшее число входов.
Можно построить логическую схему в булевом базисе для этой же функции после её минимизации по аналитической записи в МКНФ (1.5),
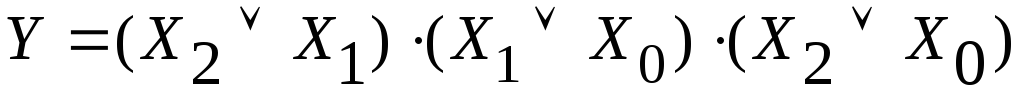 ,
,
к
Часто необходимо построить схему из однотипных ЛЭ. Для этого требуется реализовать схему в базисе И–НЕ или в базисе ИЛИ–НЕ. Переход к другому базису осуществляется путем выполнения тождественных преобразований исходных выражений в формах СДНФ, МДНФ или СКНФ, МКНФ.
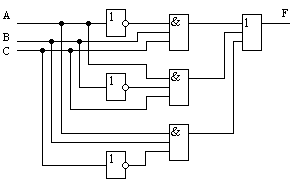
Для построения схемы в базисе И–НЕ можно преобразовать аналитическую запись функции в МДНФ (1.4) путем её двойного инвертирования и применения закона Де Моргана:
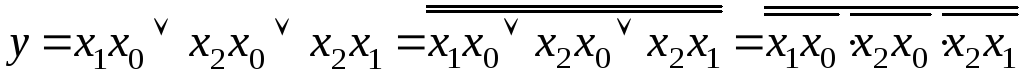 .
.
Логическая схема в базисе И–НЕ приведена на рис.1.16.
Для построения схемы в базисе ИЛИ–НЕ можно преобразовать аналитическую запись функции в МКНФ (1.5) также путем её двойного инвертирования и применения закона Де Моргана:
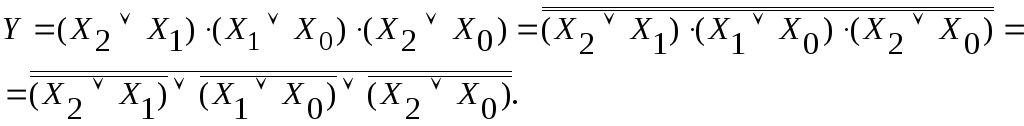
Логическая схема в базисе ИЛИ–НЕ приведена на рис.1.17.
Далее рассматривается несколько простых логических функций, реализуемых элементами рассмотренных базисов.
Элемент «Сравнение». На выходе такого элемента должна быть логическая 1, если на входах одновременно присутствуют одинаковые логические переменные (единицы или нули).
Легко установить, что при равнозначности переменных х1 и х0 конъюнкции их прямых или инверсных значений равны единице, т. е. функция рассматриваемого элемента выразится в базисе как
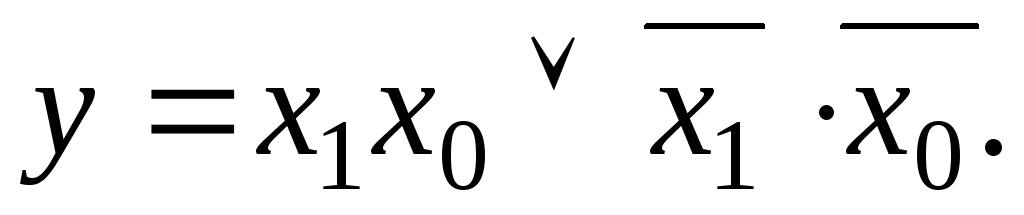
Используя теорему де Моргана, представим эту функцию в базисе И—НЕ:
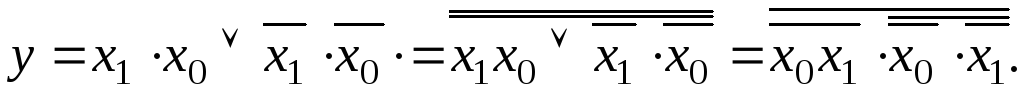
Н а
рис. 1.17, а, б приведены логические схемы
элемента «Сравнение» на ЛЭ базисов И,
ИЛИ, НЕ и И—НЕ соответственно. Условное
графическое изображение элемента дано
на рис. 1.18, в.
а
рис. 1.17, а, б приведены логические схемы
элемента «Сравнение» на ЛЭ базисов И,
ИЛИ, НЕ и И—НЕ соответственно. Условное
графическое изображение элемента дано
на рис. 1.18, в.
Элемент «Исключающее ИЛИ». На выходе такого элемента должна быть логическая 1, если на входах присутствуют неравнозначные логические переменные:
у=1, если х1=1, x0=0 или ;х1=0, x0= 1.
Исходя из самого определения, легко записать логическую функцию: конъюнкции неравнозначных переменных должны быть равны единице, т. е.
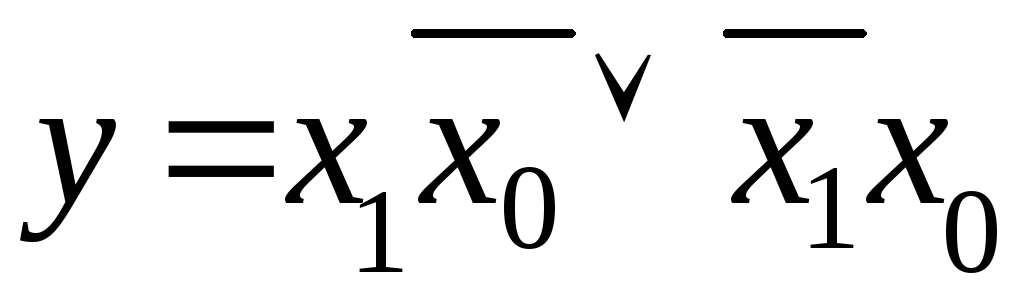 .
.
Применяя теорему де Моргана, запишем эту функцию в базисе И—НЕ:
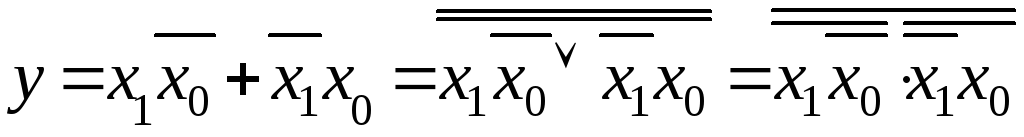 ,
,
где правая часть выражения дополнительно дважды инвертирована.
Ф ункциональные
схемы рассматриваемого элемента в
соответствии с выражениями приведены
на рис. 1.18, а, б. Условное обозначение
элемента «Неравнозначность» дано на
рис. 1.18,в.
ункциональные
схемы рассматриваемого элемента в
соответствии с выражениями приведены
на рис. 1.18, а, б. Условное обозначение
элемента «Неравнозначность» дано на
рис. 1.18,в.
Элемент «исключающее ИЛИ» иначе называют сумматором по модулю два: сумма двоичных цифр дает в результате 1; если одна из них 1, а другая — 0; эта сумма равна 0, если обе цифры одинаковы – 0 или 1.
Практическая работа на тему «Логические функции и логические схемы»
Цели работы:
освоить алгоритм построения таблиц истинности для логических функций;
научиться определять и анализировать функции проводимости переключательных схем.
Задачи:
- обучающие: закрепление знаний о логических операциях, освоение алгоритма построения таблиц истинности, умение определять и анализировать функции проводимости переключательных схем;
- развивающие: развитие умений и навыков построения таблиц истинности, внимания;
- воспитательные: воспитание аккуратности, терпения, усидчивости.
Тип урока: практическая работа.
Порядок выполнения работы.
Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Буль первым показал, что существует аналогия между алгебраическими и логическими действиями, так как и те, и другие предполагают лишь два варианта ответов – истина или ложь, нуль или единица.
На основе анализа логической связи
между высказываниями делается логический вывод.
Для получения логического вывода
составляется
Работа ЭВМ как автоматических устройств
основана исключительно на математически
строгих правилах выполнения команд, программ и
интерпретации данных. Тем самым работа
компьютеров допускает строгую однозначную
проверку правильности своей работы в плане
заложенных в них процедур и алгоритмов обработки
информации. Это позволяет использовать
математический аппарат для анализа и разработки
логических устройств вычислительной техники.
Функцией логических переменных называют
взаимосвязь логических переменных по законам
логики. Значения входных переменных и выходных
функций связаны некоторым преобразованием,
которое реализует логическую функцию.
Логические операции
Инверсия (логическое отрицание)
Операция, выражаемая словом «не», называется логическим отрицанием (инверсией) делает истинное выражение ложным и, наоборот, ложное – истинным. Обозначается «».
Обозначение: НЕ, OА, , NOT A
Таблица истинности для логического выражения А имеет вид
А |
|
0 |
1 |
1 |
0 |
Конъюнкция (логическое умножение)
Операция, выражаемая связкой «и», называется логическим умножением (конъюнкцией) и обозначается » U» (может также обозначаться знаками «?» (точка) или &). Высказывание АUВ истинно тогда и только тогда, когда оба высказывания А и В истинны.
Обозначение: А и В, AUB, A?B, A AND B
Таблица истинности для логических переменных A и B
А |
В |
А/\B |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Дизъюнкция (логическое сложение)
Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется логическим сложением (дизъюнкцией) и обозначается знаком U (или +). Высказывание А U В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Обозначение: А ИЛИ В, AUB, A+B, A OR B
Таблица истинности для логических переменных A и B
А |
В |
А U B |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
В алгебре логики любую логическую
функцию можно выразить через основные
логические операции, записать ее в виде
логического выражения и упростить ее, применяя
законы логики и свойства логических операций. По
формуле логической функции легко рассчитать ее
таблицу истинности. Необходимо только учитывать
порядок выполнения логических операций
(приоритет) и скобки. Операции в логическом
выражении выполняются слева направо с учетом
скобок.
Приоритет выполнения логических операций:
- инверсия,
- конъюнкция,
- дизъюнкция.
Задание 1.
Построить таблицу истинности для логической функции
1. Определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение: количество строк = 2n, где n – количество переменных
Количество логических переменных – 3 (A, B, C) поэтому количество строк – 2n = 8.
А |
С |
||||||
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
2. Определить количество столбцов:
количество столбцов=количество переменных+количество операций.
Количество логических операций -5 (умножение – 2, сложение – 1, отрицание – 2), поэтому количество столбцов 3+5=8
3. Построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных.
А |
С |
||||||
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
4.Заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности
Задание 2.
Построить таблицы истинности для логических функций
1)
2)
3)
Часть 2. Построение логических выражений для переключательных схем.
Переключательная схема — это схематическое
изображение некоторого устройства, состоящего
из переключателей и соединяющих их проводников,
а также из входов и выходов, на которые подаётся и
с которых снимается электрический сигнал.
В компьютерах и других автоматических
устройствах широко применяются электрические
схемы, содержащие сотни и тысячи
переключательных элементов: реле, выключателей и
т.п. При разработке схем используется аппарат
алгебры логики.
Каждый переключатель имеет только два состояния:
замкнутое и разомкнутое. Переключателю Х
поставим в соответствие логическую переменную х,
которая принимает значение 1 в том и только в том
случае, когда переключатель Х замкнут и
схема проводит ток; если же переключатель
разомкнут, то х равен нулю.
Будем считать, что два переключателя Х и
связаны таким образом,
что когда Х замкнут, то разомкнут, и наоборот. Следовательно,
если переключателю Х поставлена в соответствие
логическая переменная х, то
переключателю должна
соответствовать переменная .
Всей переключательной схеме также можно
поставить в соответствие логическую переменную,
равную единице, если схема проводит ток, и равную
нулю — если не проводит. Эта переменная является
функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией
проводимости.
Функции проводимости F некоторых переключательных схем:
1) |
Схема не содержит переключателей и проводит ток всегда, следовательно F=1; |
|
2) |
Схема содержит один постоянно разомкнутый контакт, следовательно F=0; |
|
3) |
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x; | |
4) |
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, (x) = ; |
|
5) |
Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x,y) = x Uy; | |
6) |
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x,y)=x U y; |
Любая сложная схема может быть преобразована в отдельные группы и представлена в виде логических функций нескольких переменных.
Задание 3.
Определить и проанализировать функцию проводимости переключательной схемы
рис.1
Функция проводимости имеет вид: F(a,b,c) = aU(bUc)
Построим таблицу истинности
a |
b |
c |
bUc |
aU(bUc) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Основы логики. Построение логических схем (4-й урок)
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
План урока информатики 11 класс «Построение логический схем по заданной логической функции»
ПЛАН УРОКА
Тема: Построение логических схем по заданной логической функции.
Цель урока: Рассмотреть понятие СДНФ и СКНФ, научиться строить схемы, используя СДНФ и СКНФ, закрепить полученные знания на примере решения задач.
В задачах по логике часто встречаются следующие задания: записать функцию, реализующую логическую схему, упростить её и построить таблицу истинности для этой функции. А как решить обратную задачу? Дана произвольная таблица истинности, нужно построить функциональную или релейно-контактную схему. Этот вопрос мы сейчас и рассмотрим.
Любую функцию алгебры логики можно представить комбинацией трёх операций: конъюнкции, дизъюнкции и инверсии. Как это делается?
Минтерм – это функция, образованная конъюнкцией некоторого числа переменных или их отрицаний. Минтерм принимает значение 1 при единственном из всех возможных наборов аргументов, и значение 0 при всех остальных.
Например: 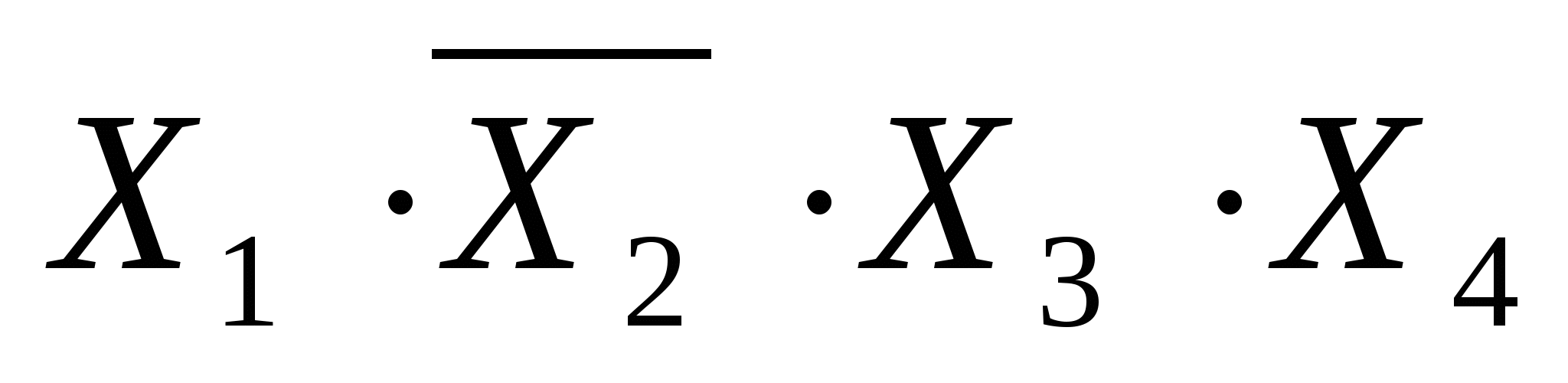
Макстерм – это функция, образованная дизъюнкцией некоторого числа переменных или их отрицаний. Макстерм принимает значение 0 в одном из возможных наборов аргументов, и значение 1 при всех других.
Например: 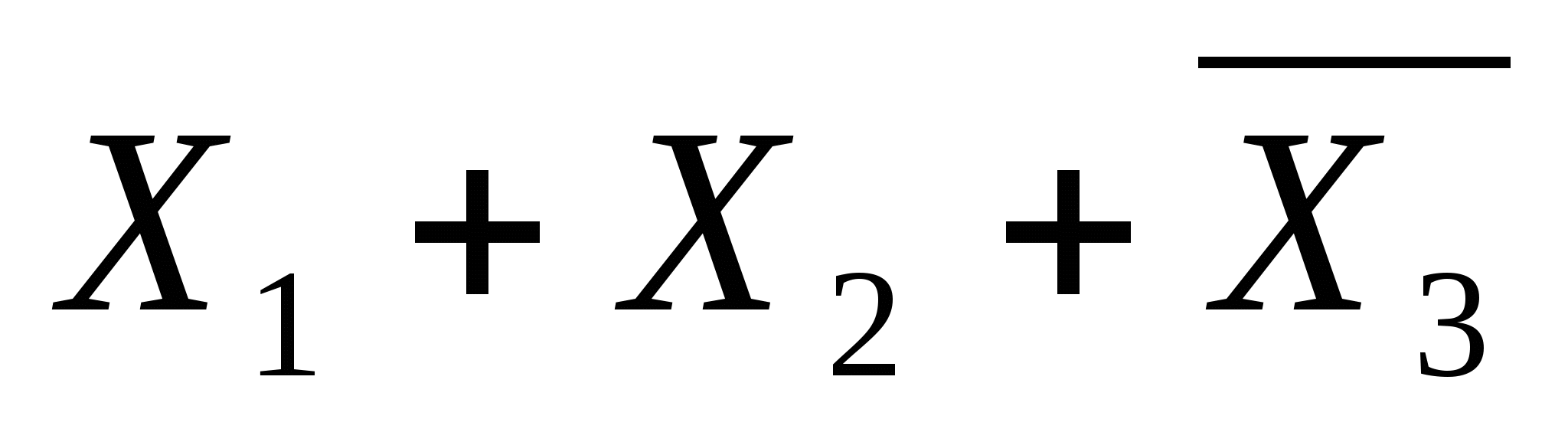
Функция в дизъюнктивной нормальной форме (ДНФ) является суммой Минтермов.
Например: 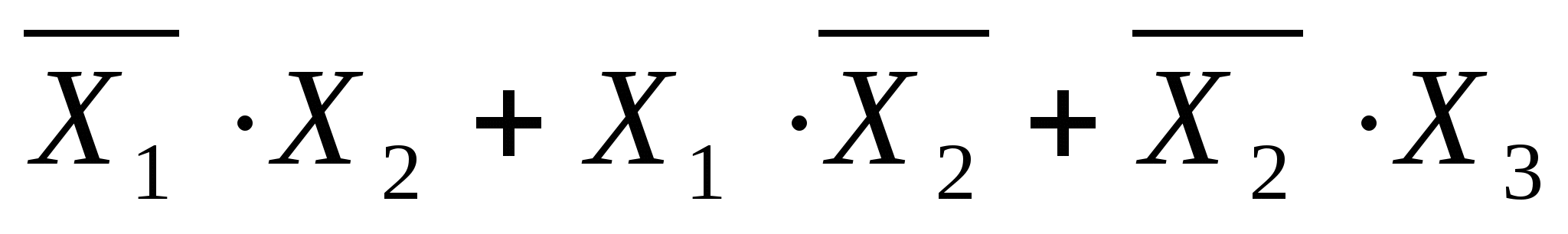
Конъюнктивная нормальная форма (КНФ) является логическим произведением элементарных дизъюнкций (макстермов)
Например: 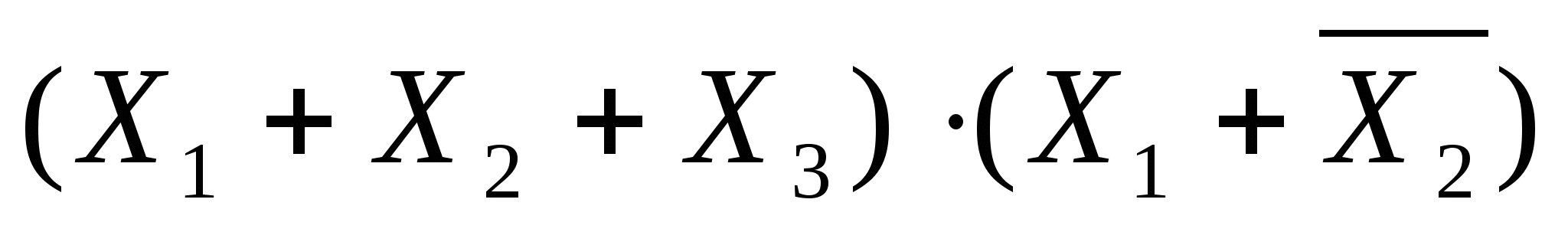
Совершенной дизъюнктивно-нормальной формой (СДНФ) называется ДНФ, в каждом минтерме которой присутствуют все переменные или их отрицания.
Например: 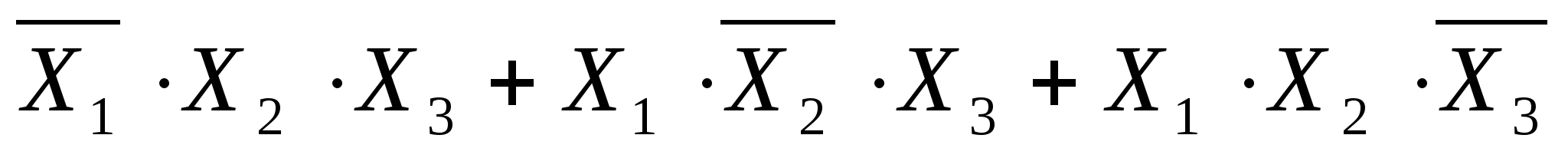
Совершенной конъюнктивно-нормальной формой (СКНФ) называется КНФ, в каждом минтерме которой присутствуют все переменные или их отрицания.
Например: 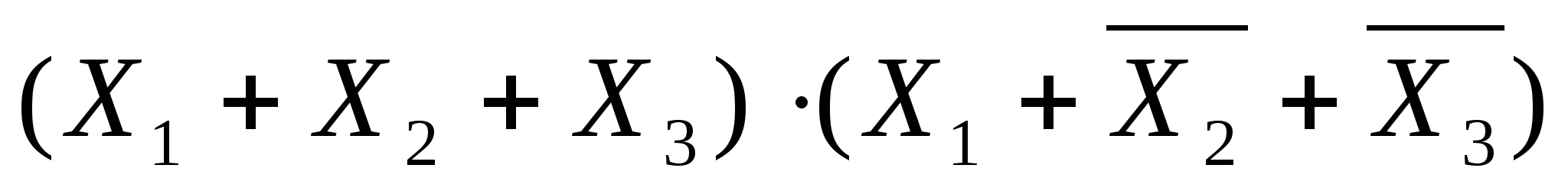
Запись логической функции по таблице.
Любая логическая функция может быть выражена в виде СДНФ или СКНФ.
В качестве примера рассмотрим функцию F , представленную в таблице.
Функции G0, G1, G4, G5, G7 – это минтермы. Каждая из этих функций является произведением трёх переменных или их инверсией и принимает значение 1 только в одной ситуации.
Видно, что для того, чтобы получить 1 в значении функции f, нужен один минтерм, следовательно количество минтермов, составляющих СДНФ этой функции, равно количеству единиц в значении функции:

Таким образом СДНФ имеет вид:

Аналогично можно построить СКНФ. Количество сомножителей равно количеству нулей в значении функции.

Таким образом, можно записать в виде формулы любую логическую функцию, заданную в виде таблицы.
Алгоритм построения СДНФ по таблице истинности.
Дана таблица истинности некоторой логической функции.
Для построения СДНФ нужно выполнить следующее:
Выбрать все строки таблицы, в которых функция принимает значение 1.
Каждой такой строке поставить в соответствие конъюнкцию всех аргументов или их инверсий (минтерм). При этом аргумент, принимающий значение 0, входит в минтерм с отрицанием, а значение 1 – без отрицания.
Наконец, образуем дизъюнкцию всех полученных минтермов. Количество минтермов должно совпадать с количеством единиц логической функции.
Алгоритм построения СКНФ по таблице истинности.
Дана таблица истинности некоторой логической функции.
Для построения СКНФ нужно выполнить следующее:
Выбрать все строки таблицы, в которых функция принимает значение 0.
Каждой такой строке поставить в соответствие дизъюнкцию всех аргументов или их инверсий (макстерм). При этом аргумент, принимающий значение 1, входит в макстерм с отрицанием, а значение 0 – без отрицания.
Наконец, образуем конъюнкцию всех полученных макстермов. Количество макстермов должно совпадать с количеством нулей логической функции.
Если условиться из двух форм (СДНФ или СКНФ) отдавать предпочтение той, которая содержит меньше букв, то СДНФ предпочтительней, если среди значений функции таблицы истинности меньше единиц, СКНФ – если меньше нулей.
Пример: Дана таблица истинности логической функции от трёх переменных. Построить логическую схему, реализующую эту функцию.
Выберем те строки в таблице истинности, в которых значение функции равно нулю

Проверим выведенную функцию, составив таблицу истинности .
Сравнив начальную и итоговую таблицы истинности, можно сделать вывод, что логическая функция построена верно.

Решение задач.
Три преподавателя отбирают задачи для олимпиады. На выбор предлагается несколько задач. По каждой задаче каждый преподаватель высказывает своё мнение: легкая (0) или трудная (1) задача. Задача включается в олимпиадное задание, если не менее двух преподавателей отметили её как трудную, но если все три преподавателя считают её трудной, то такая задача не включается в олимпиадное задание как слишком сложная.
Составьте логическую схему устройства, которое будет выдавать на выходе 1, если задача включается в олимпиадное задание и 0, если не включается.
Анализируя условия задачи, получаем следующую таблицу истинности:
Строим СДНФ:

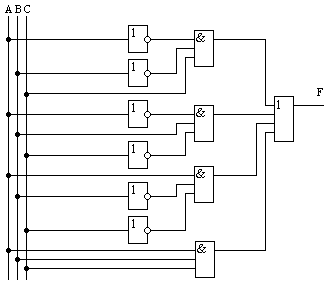
Теперь строим логическую схему этой функции

Постройте логическую схему для подъезда трёхэтажного дома такую, чтобы выключателем на любом этаже можно было бы включить или выключить свет во всём доме.
Итак, у нас есть три выключателя, которыми мы должны включать и выключать свет. У каждого выключателя есть два состояния: верхнее (0) и нижнее (1). Предположим, что если все три выключателя в положении 0, свет в подъезде выключен. Тогда при переводе одного из выключателей в положение 1, свет в подъезде должен загореться. Очевидно, что при переводе любого другого переключателя в положение 1, свет в подъезде выключится. Если третий выключатель перевести в положение 1, свет в подъезде загорится. Строим таблицу истинности:
Строим СДНФ:


Условие изменения значения логической функции

при одновременном изменении аргументов B и С равно:
1)
 2)
2)  3)
3) 
4)
 5)
5) 
Для успешного решения данной задачи вспомним следующие формулы:



Решение
Нам дана логическая функция от трёх переменных


Изменим одновременно переменные B и С :

Построим таблицы истинности этих двух функций:
Анализируем полученную таблицу. Из восьми строк только в двух (2-й и 3-й) функция не изменяет своего значения. Обратите внимание что в этих строках переменная А не изменяет своего значения, а переменные В и С – изменяют своё значение на противоположное.
Строим СКНФ функции по этим строкам:


Искомый ответ – 4.
Условие изменения значения логической функции

при одновременном изменении аргументов А и В равно:
1)
 2)
2)  3)
3) 
4)
 5)
5) 
Решение:


Строим таблицу истинности:
Анализируем полученную таблицу. Из восьми строк только в двух (1-й и 7-й) функция меняет своё значение. Обратите внимание, что в этих строках переменная С не меняет своё значение, а переменные А и В меняют своё значение. Строим СДНФ этой функции:

Искомый ответ – 2.
5) Условие изменения значения логической функции
 при одновременном изменении аргументов А и В равно :
при одновременном изменении аргументов А и В равно :1)
 2)
2)  3)
3) 
4)
 5)
5) 
Р
 ешение:
ешение:  =
= 
 =
= 

B
C
F1
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
0
1
1
1
1
0
1
0
1
0
0
0
1
1
1
0
0
1
0
0
0
1
0
1
0
1
0
1
0
1
1
0
0
0
0
1
1
1
0
0
0

Функция изменяет своё значение только в строках 2 и 8. Причём, в этих строках переменные А и В не изменяются, а переменная с – изменила своё значение.
Построим СДНФ функции F3.

Искомый ответ 2.


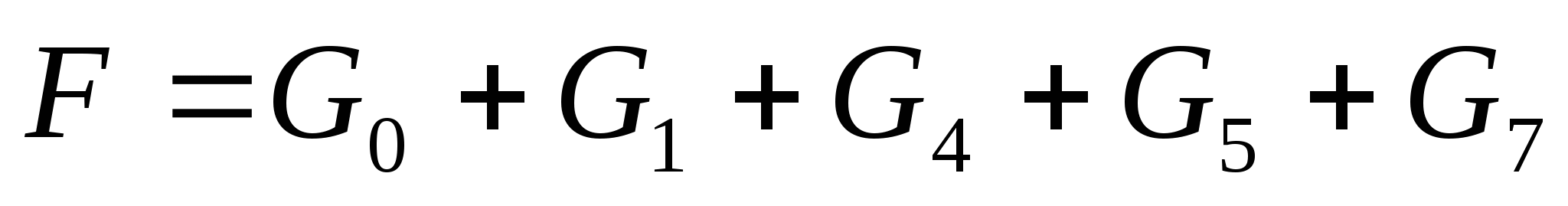
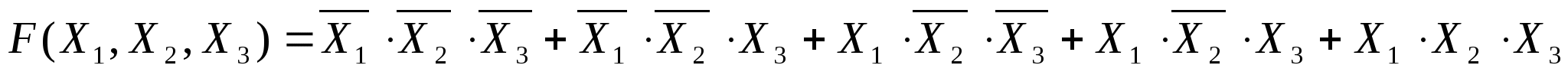
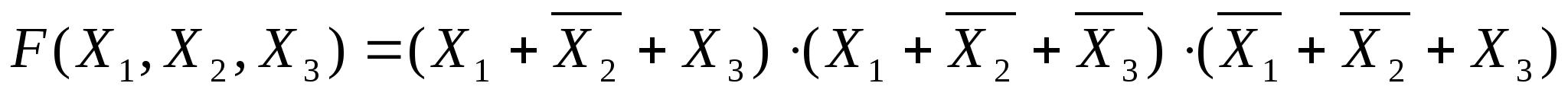
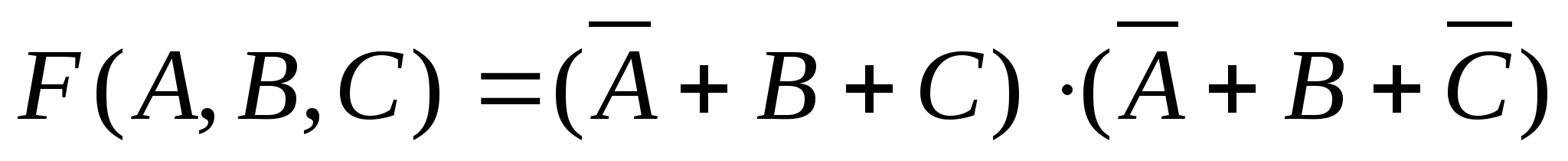
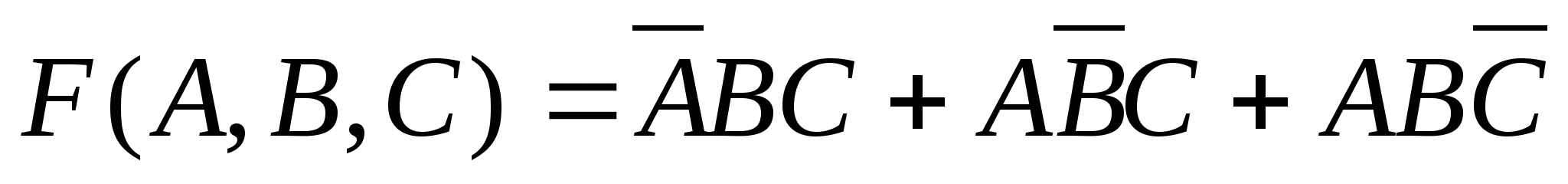
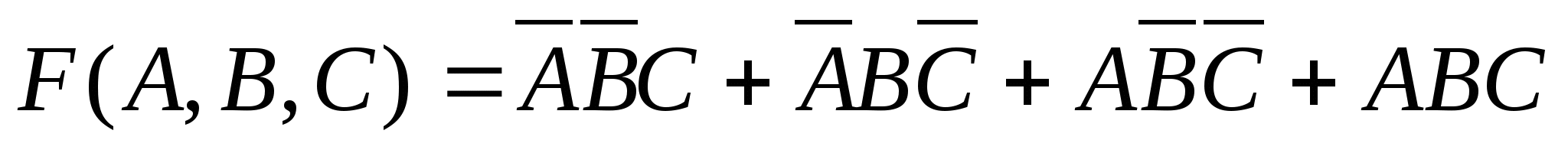
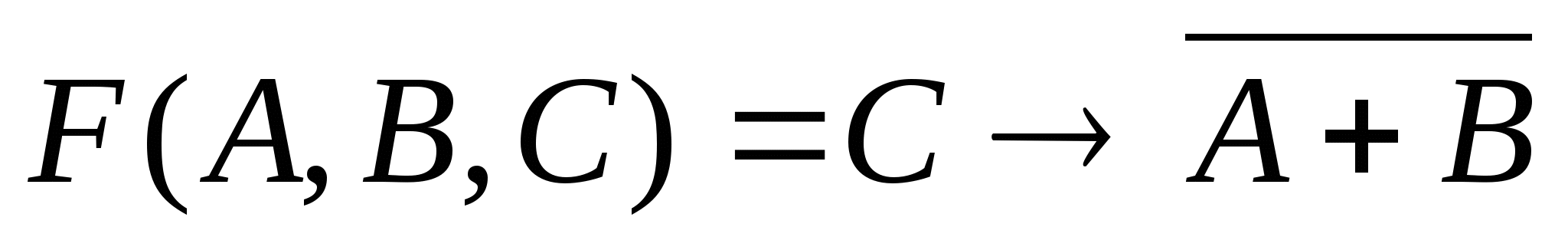
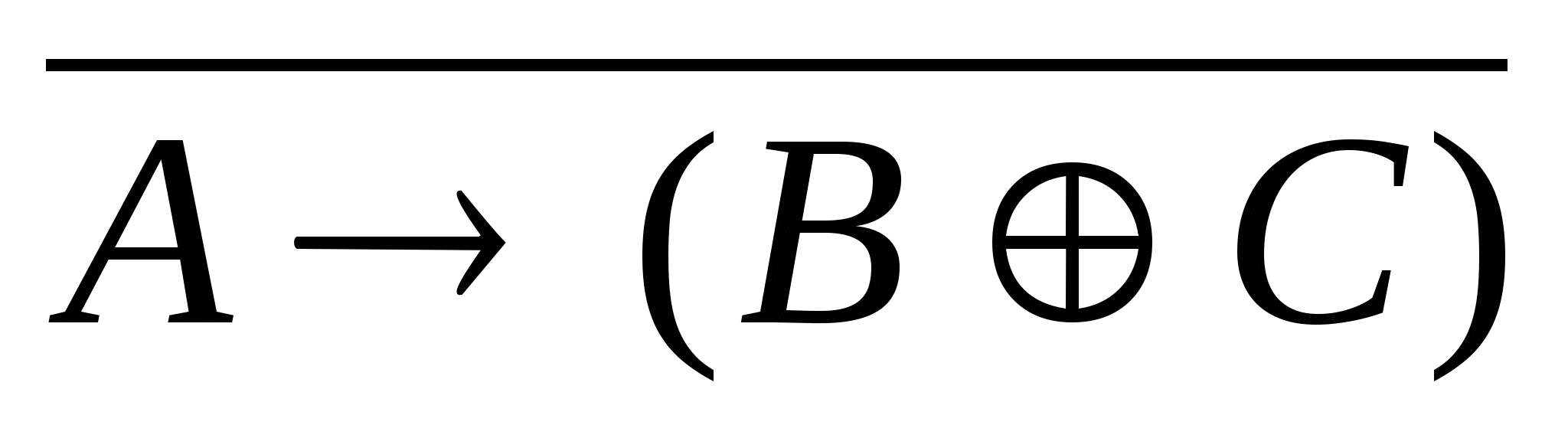 2)
2) 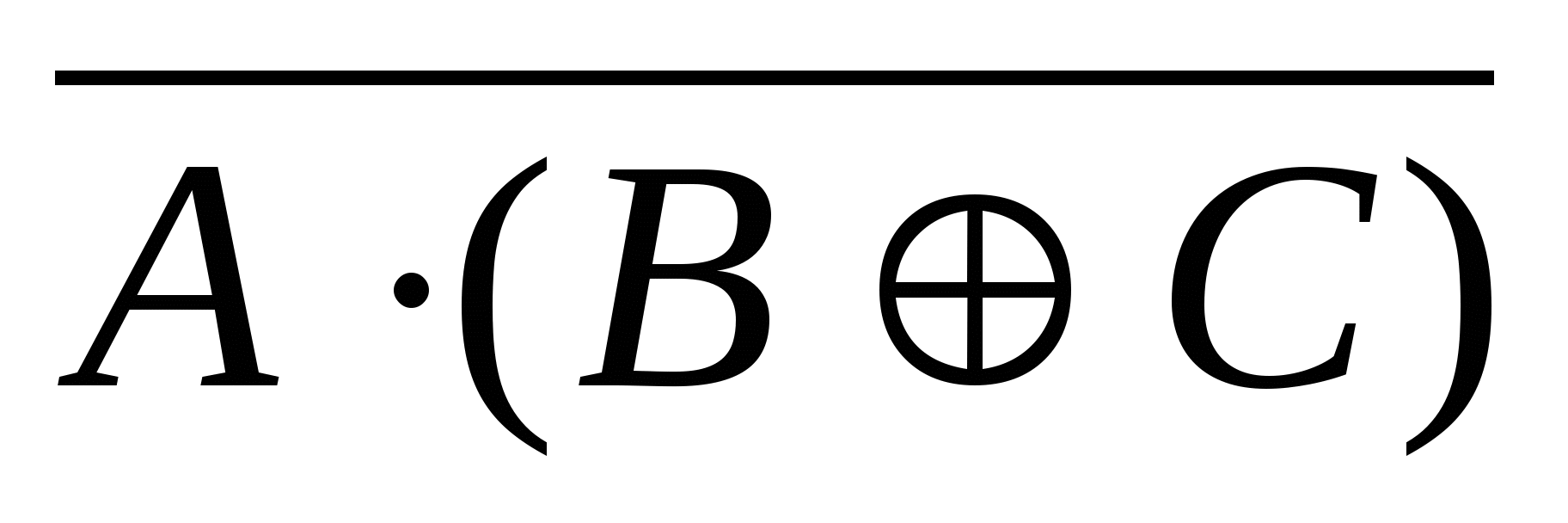 3)
3) 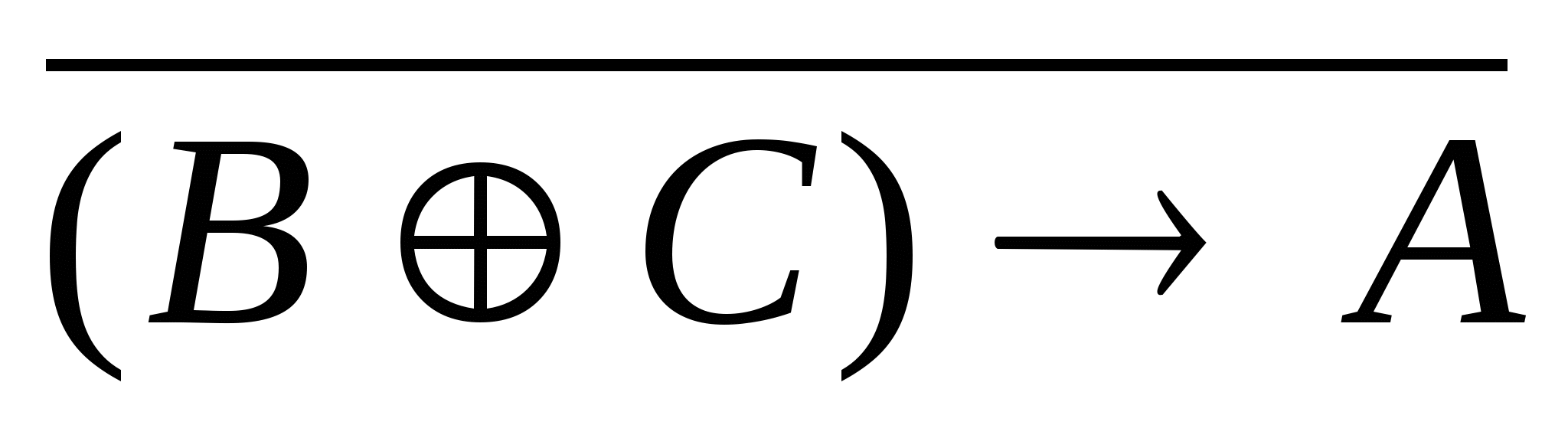
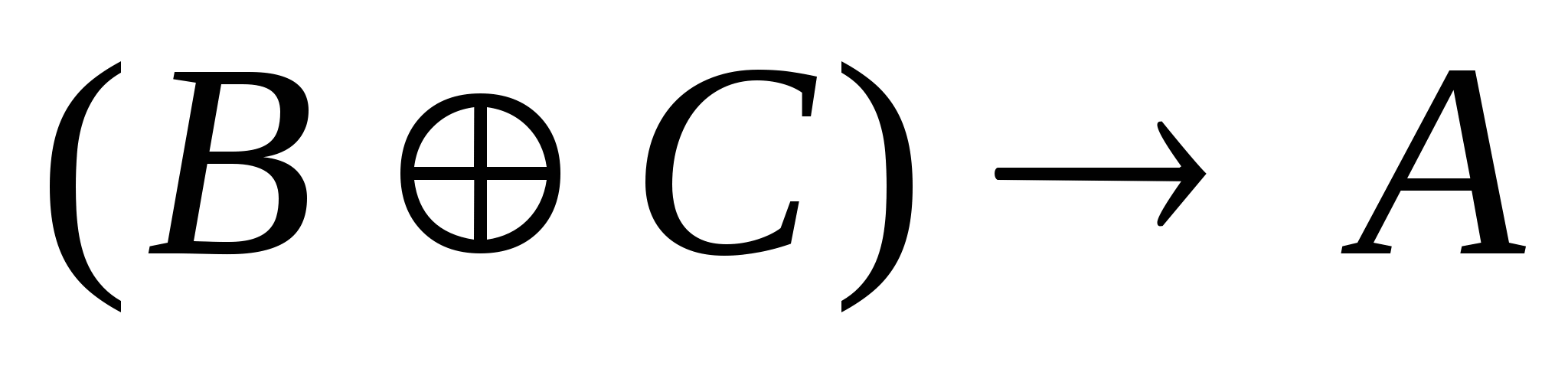 5)
5) 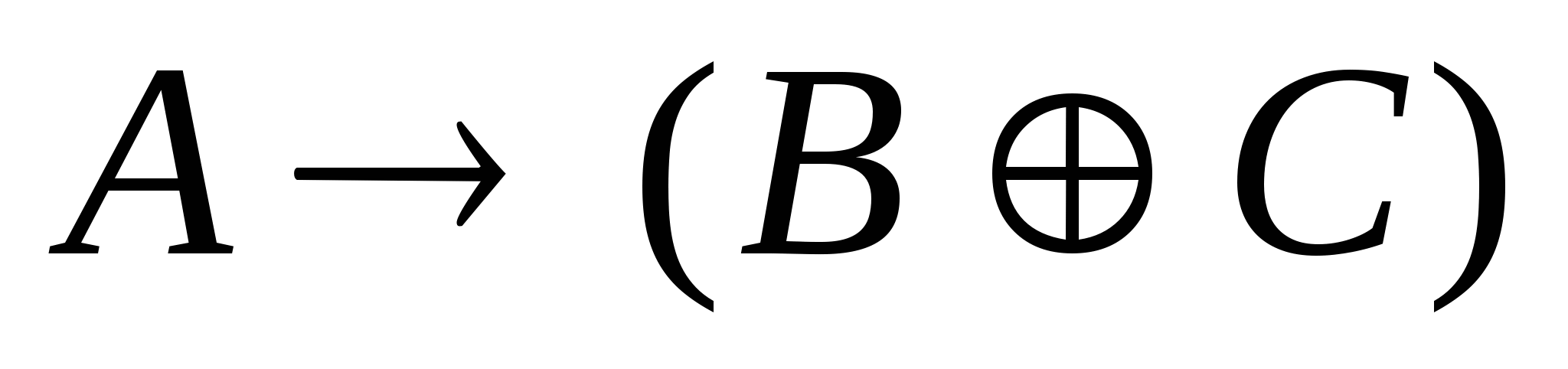
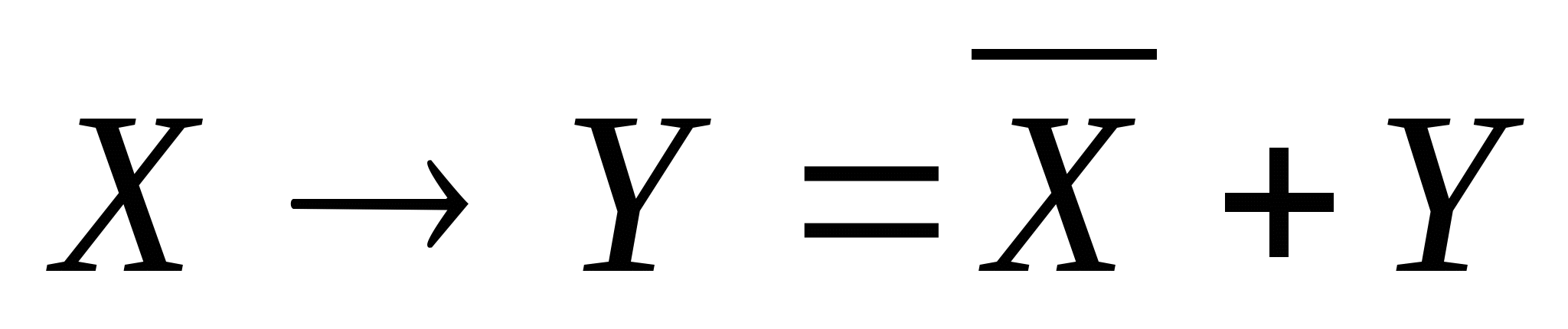
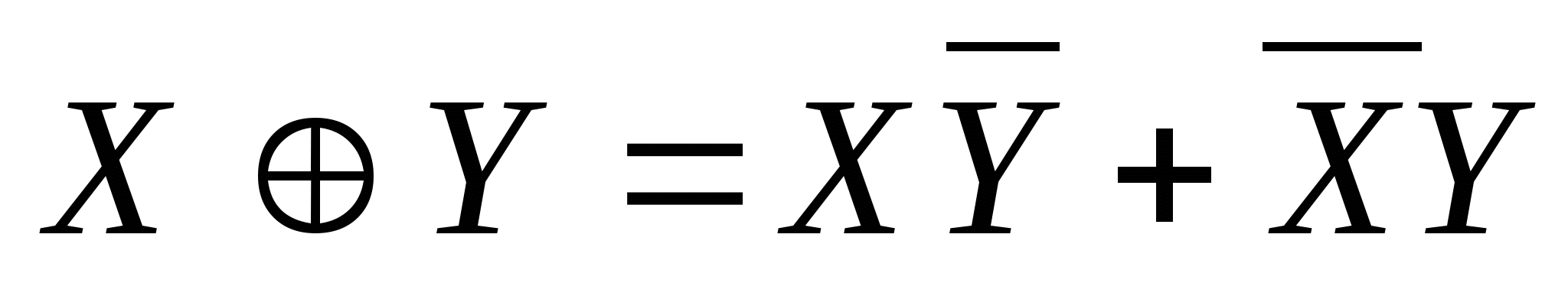
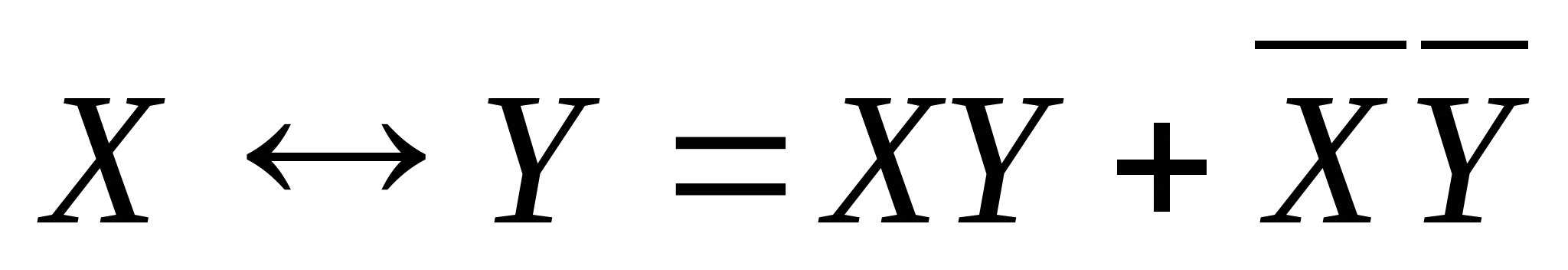
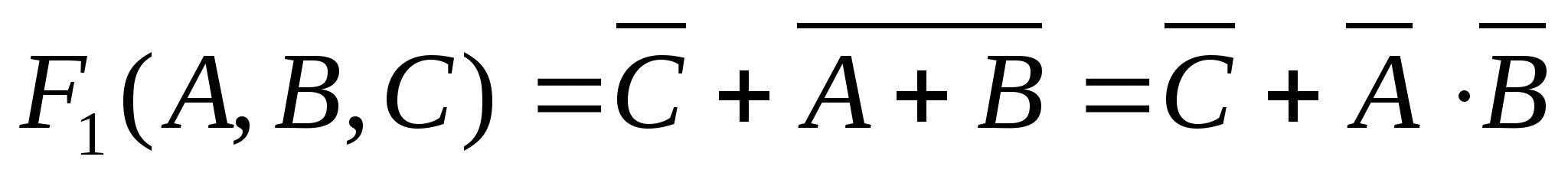
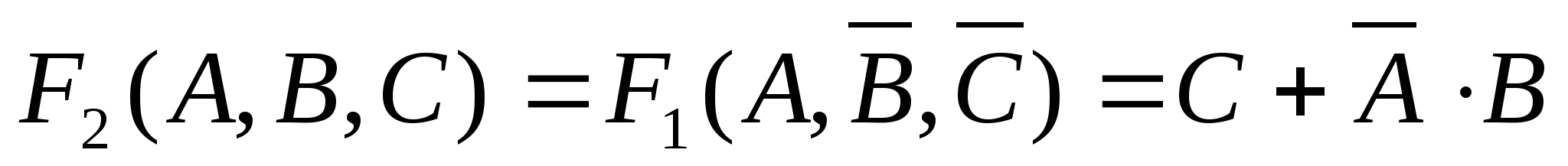
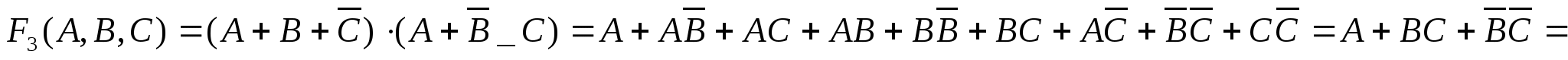
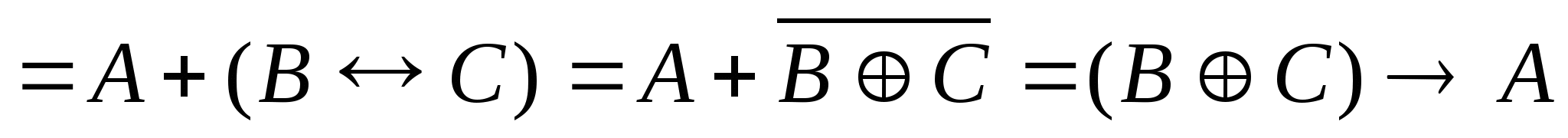
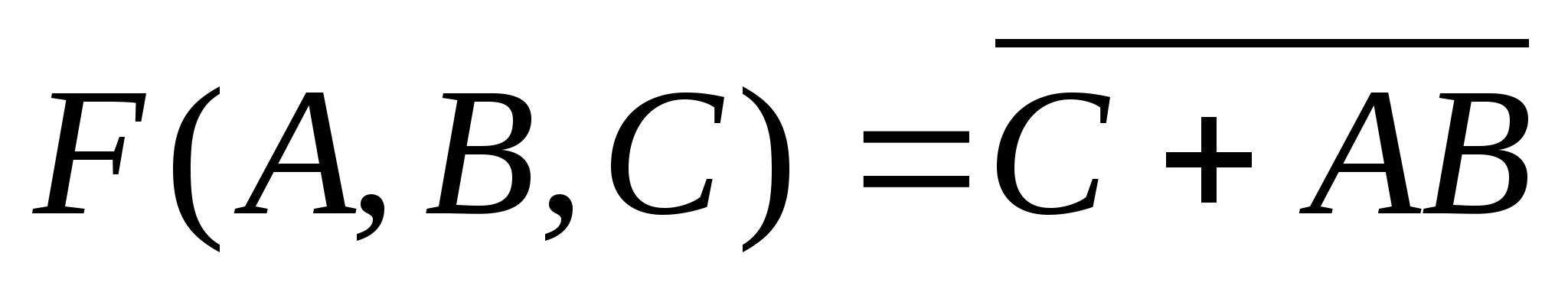
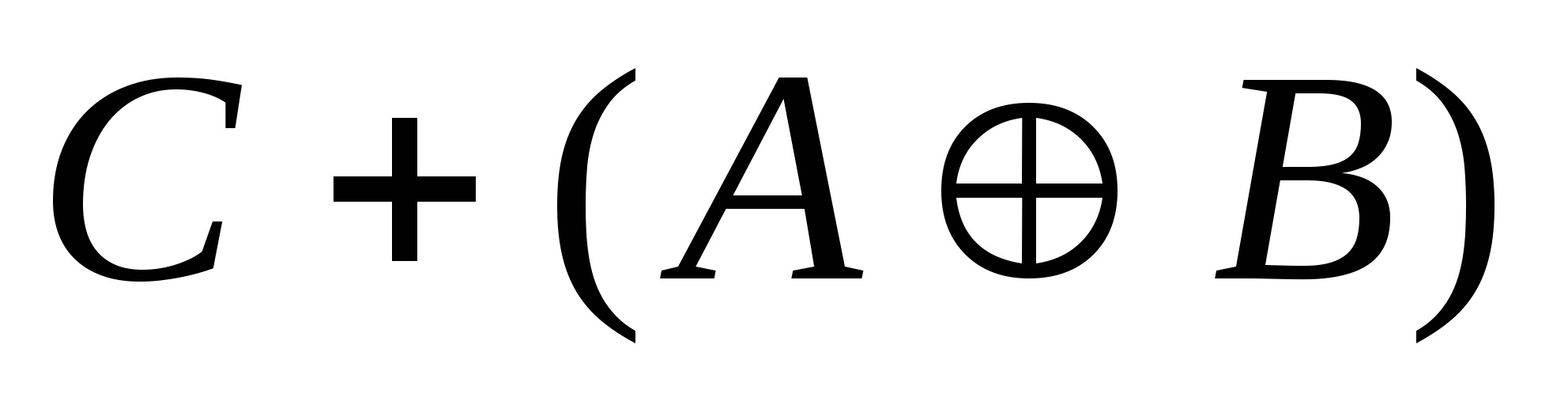 2)
2) 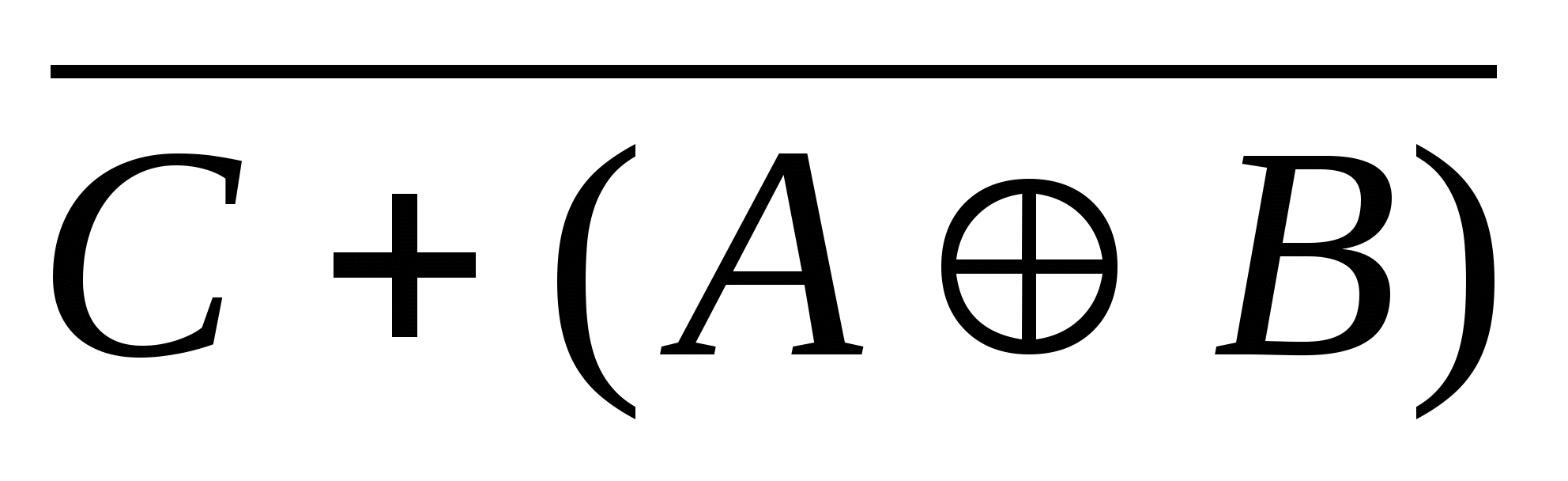 3)
3) 
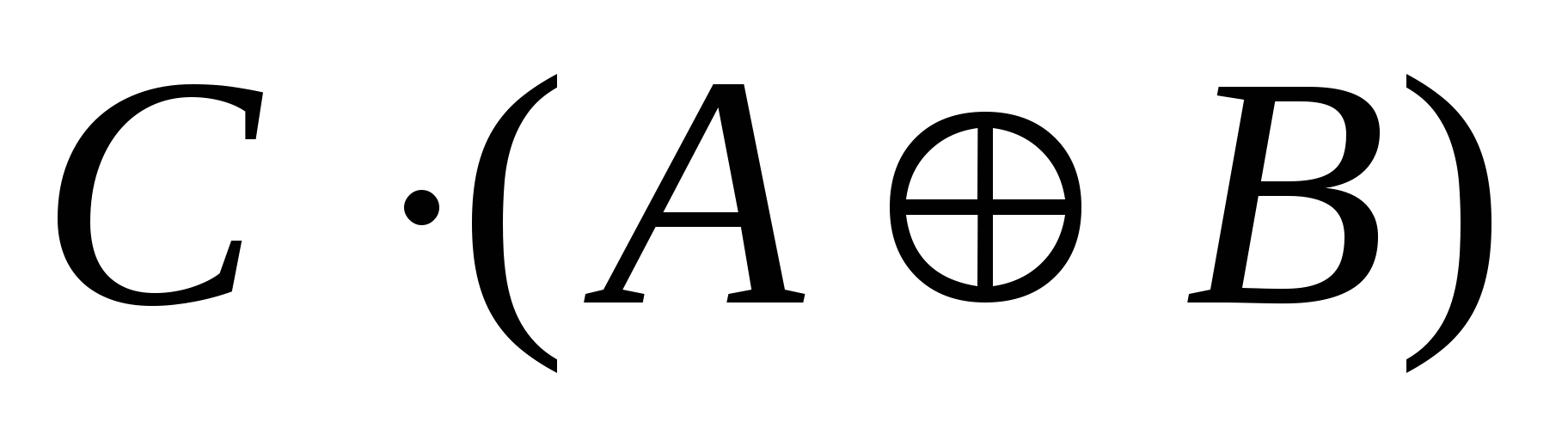 5)
5) 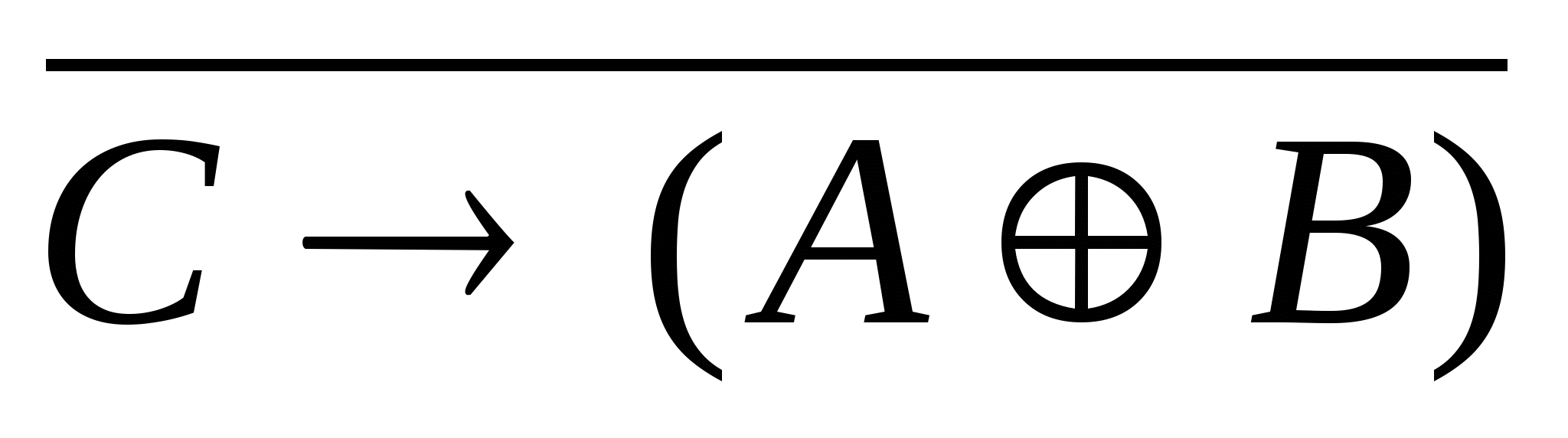
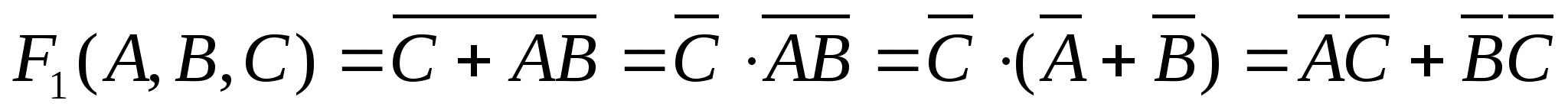
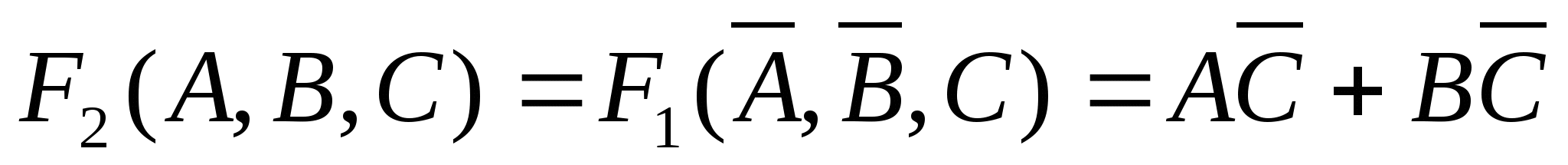
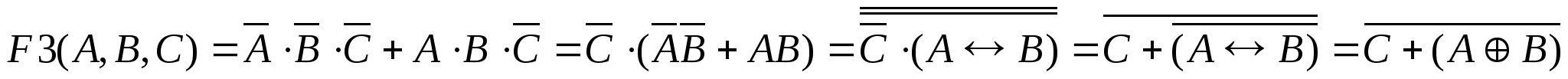
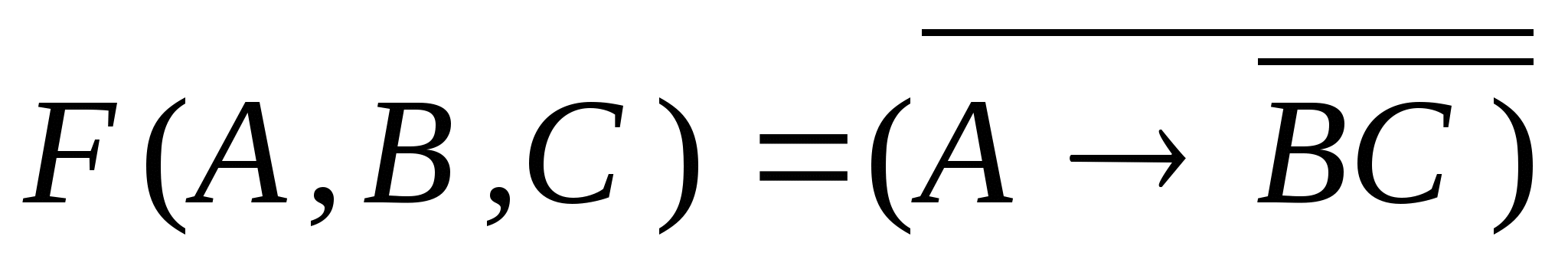 при одновременном изменении аргументов А и В равно :
при одновременном изменении аргументов А и В равно :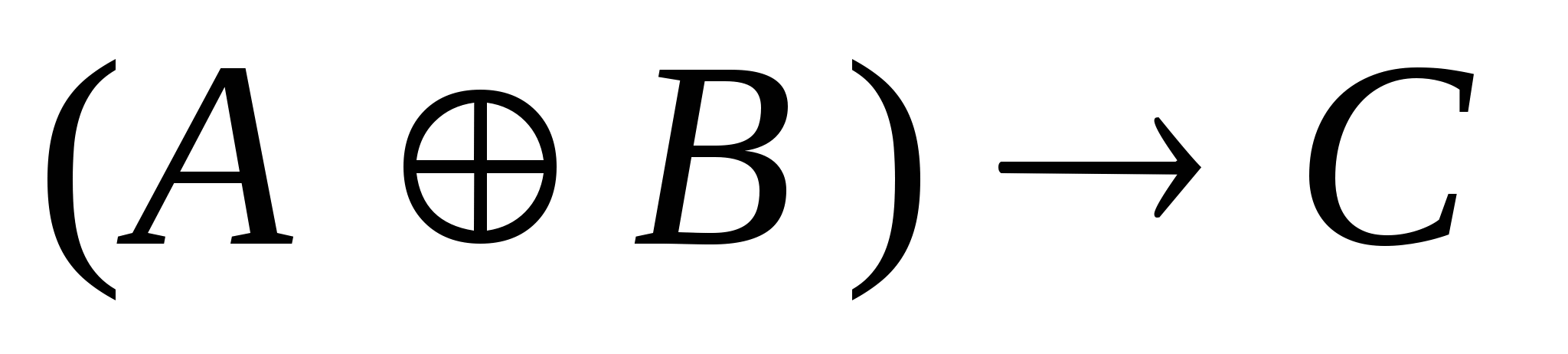 2)
2)  3)
3) 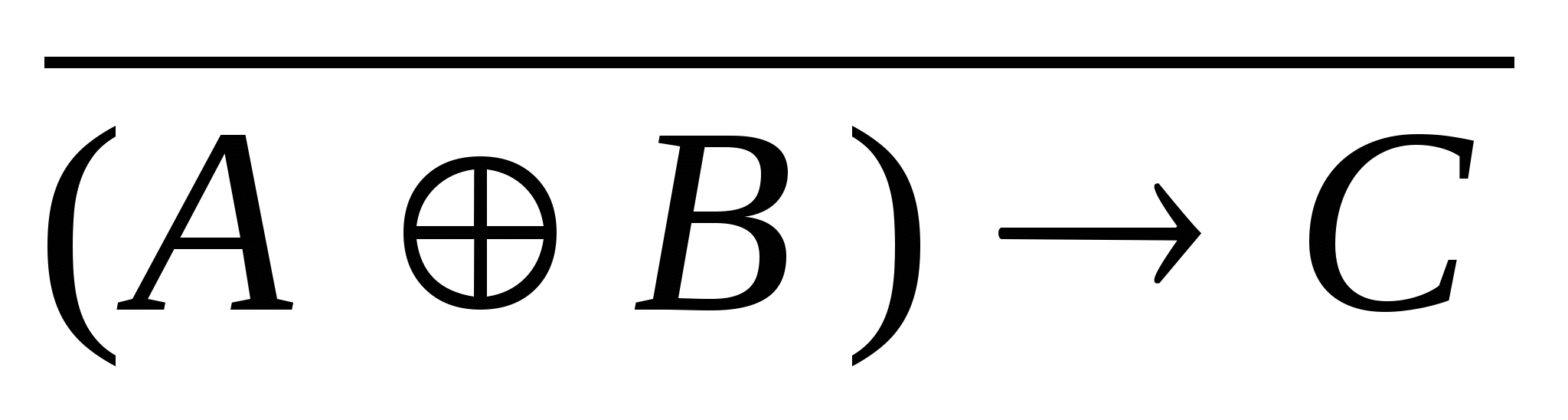
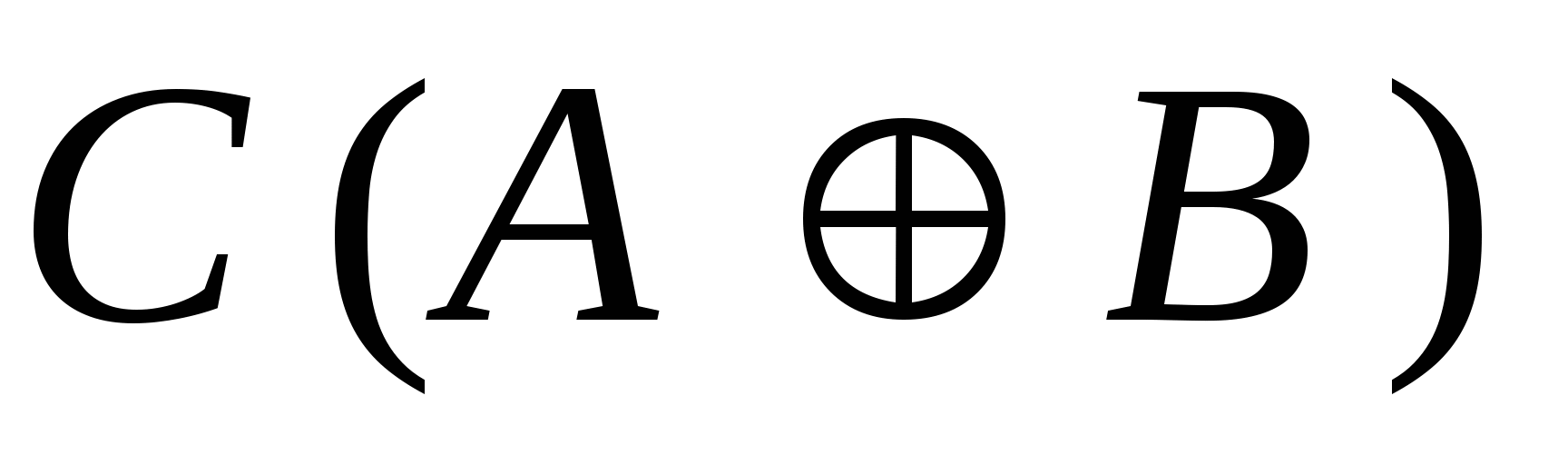 5)
5) 
 ешение:
ешение:  =
= 
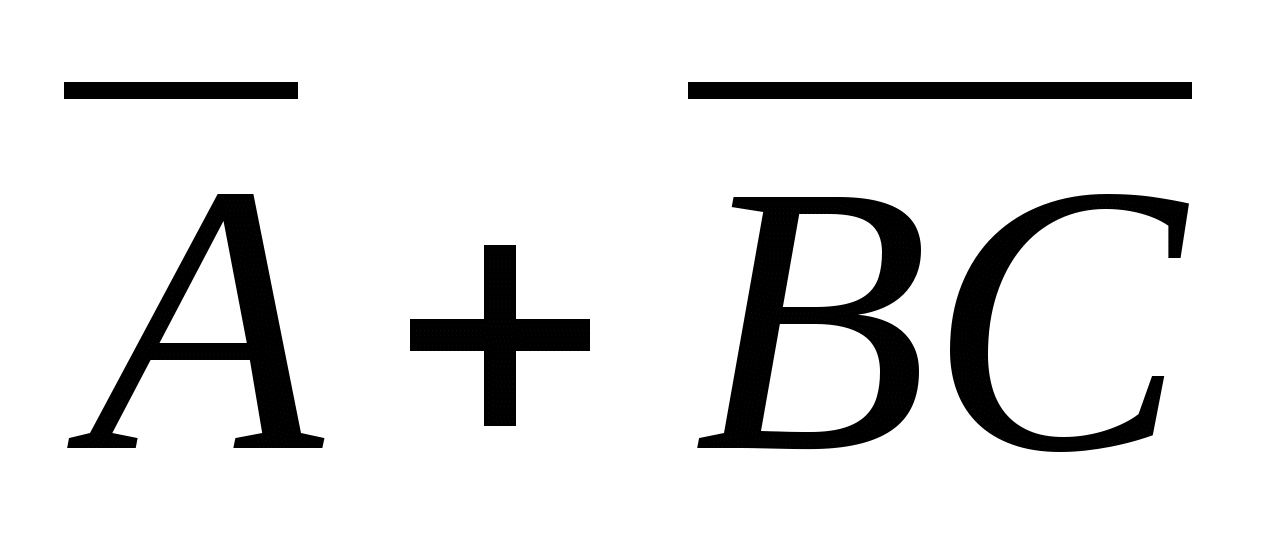 =
=