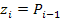Полный одноразрядный сумматор
Связь между двоичной арифметикой и алгеброй логики позволяет реализовать логические схемы основных элементов процессора и памяти компьютера.
Сумматор — это устройство, предназначенное для сложения двоичных чисел.
Рассмотрим сначала более простое устройство – полусумматор.
Построим таблицу истинности для устройства реализующего арифметическую операцию сложения. Операция «+» бинарная, поэтому полусумматор должен иметь два входа (A и B). В результате сложения двух одноразрядных двоичных чисел может получиться двухразрядное число (с переносом в следующий разряд). Значит, устройство должно иметь два выхода (P — перенос в следующий разряд, S — результат, остающийся в текущем разряде).
По данной таблице истинности построим СДНФ (см. алгоритм построения СДНФ):
- Для переноса в старший разряд: P = A ∧ B
- Для текущего разряда: S = ¬ A ∧ B ∨ A ∧ ¬ B
Преобразуем логическую формулу для S:
(¬ A • B) + (A • ¬ B) = (¬ A • A) + ( ¬ A • B) + (A • ¬ B) + (¬ B • B) =
С учетом формулы для переноса имеем:
S = (A + B) • ¬ (A • B) = (A + B) • ¬ P
Таким образом, полусумматор можно построить, используя четыре простейших логических элемента: два конъюнктора, дизъюнктор и инвертор (см. рис.1, слева показано условное обозначение полусумматора):
Итак, получено устройство, реализующее суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Для реализации полного одноразрядного сумматора необходимо учесть перенос из младшего разряда (P0). Поэтому сумматор должен иметь три входа. Построим таблицу истинности для устройства с учетом третьего входа:
| A | B | P0 | P | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Построим СДНФ для выхода P (перенос в старший разряд):
Преобразуем:
1) (A ∧ B ∧ ¬ P0) ∨ (A ∧ B ∧ P0) = (A ∧ B) ∧ (¬ P0 ∨ P0) = A ∧ B
Имеем, P = (¬ A ∧ B ∧ P0) ∨ (A ∧ ¬ B ∧ P0) ∨ (A ∧ B)
2) (¬ A ∧ B ∧ P0) ∨ (A ∧ B) = B ∧(¬ A ∧ P0 ∨ A) = B ∧ (¬ A ∨ A ) ∧ (P0 ∨ A) =
= B ∧ (P0 ∨ A) = (B ∧ P0) ∨ (A ∧ B)
Имеем, P = (A ∧ ¬ B ∧ P0) ∨ (B ∧ P0) ∨ (A ∧ B)
3) (A ∧ B) ∨ (A ∧ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B ∧ P0) = A ∧ (B ∨ ¬ B)(B ∨ P0
= A ∧ (B ∨ P0) = (A ∧ B) ∨ (A ∧ P0)
Таким образом, для переноса в старший разряд получили:
P = A ∧ B ∨ A ∧ P0 ∨ B ∧ P0
Проанализируем таблицу истинности для выхода S. Значение S отлично от нуля в том случае, если единица поступает ровно на один вход (при этом на двух других входах фиксируется ноль), или на все три входа сразу, т. е.:
S = ¬ (A ∧ B ∨ A ∧ P0 ∨ B ∧ P0) ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
С учетом формулы для переноса в старший разряд, имеем:
S = ¬ P ∧ (A ∨ B ∨ P0) ∨ (A ∧ B ∧ P0)
Таким образом, одноразрядный двоичный сумматор можно реализовать с помощью следующей схемы (см. рис. 2, слева показано условное обозначение сумматора), которая соответствует полученным логическим формулам (1) и (2).
Заметим, что логические функции P и S можно выразить с помощью других формул. В таком случае для одноразрядного двоичного сумматора потребуется другая логическая схема.
Полусумматор — Википедия
 Обобщённое изображение полусумматора.
Обобщённое изображение полусумматора.Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где
Существуют сумматоры и полусумматоры работающие не в двоичной логике.
Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда. Для построения полного сумматора необходимо иметь дополнительный вход переноса из предыдущего разряда, таким образом, полный сумматор имеет 3 входа.
Двоичный полный сумматор строится из двух полусумматоров и логического элемента 2ИЛИ, именно поэтому рассматриваемая схема называется полусумматором.
Полусумматоры используется для построения полных сумматоров.
 Стандартное изображение двоичного полусумматора по DIN 40900.
Стандартное изображение двоичного полусумматора по DIN 40900.  Полусумматор, реализованный на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ и И.
Полусумматор, реализованный на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ и И. 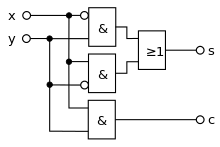 Полусумматор, реализованный на элементах ИЛИ с инверсными входами и И.
Полусумматор, реализованный на элементах ИЛИ с инверсными входами и И.Двоичный полусумматор может быть определён тремя способами:
- табличным, в виде таблиц истинности,
- аналитическим, в виде формул (СДНФ),
- графическим, в виде логических схем.
Так как формулы и схемы могут преобразовываться в соответствии с алгеброй логики, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.
Двоичный полусумматор формирует две бинарные (двухоперандные) двоичные логические функции: это сумма по модулю два, иначе эта функция называется ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) — формирует бит суммы S и функция
- S
- C
или в другом виде:
| x0=A | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | Название действия (функции) | Номер функции |
| S | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F2,6 |
| C | 1 | 0 | 0 | 0 | Бит переноса | F2,8 |
- Ненулевой перенос образуется в 1-м случае из 4-х.
СДНФ суммы по модулю 2:
- S=f(x1,x0)=(x1¯⋅x0)∨(x1⋅x0¯){\displaystyle S=\mathbf {f} (x_{1},x_{0})=({\overline {x_{1}}}\cdot {x_{0}})\vee ({x_{1}}\cdot {\overline {x_{0}}})}
СДНФ бита переноса:
- C=f(x1,x0)=x1⋅x0{\displaystyle C=\mathbf {f} (x_{1},x_{0})={x_{1}}\cdot {x_{0}}}
Полусумматор Штибица «Model K Аdder»[править | править код]
Демонстрационный полусумматор Штибица «Model K Аdder» используется в учебных целях и состоит: из двух последовательно соединённых гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (
Так как существуют две троичных системы счисления — несимметричная, в которой в разряде переноса не бывает значения больше «1» и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем — трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.
Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «сложение по модулю 3» и «разряд переноса при троичном сложении».
- S
| 2 | 2 | 0 | 1 |
|---|---|---|---|
| 1 | 1 | 2 | 0 |
| 0 | 0 | 1 | 2 |
| 0 | 1 | 2 |
- C
| 2 | 0 | 1 | 1 |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 2 |
или в другом виде:
| x1=x | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | Название действия (функции) | Номер функции |
| S | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Трит суммы по модулю 3 | |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Трит переноса |
Троичный полусумматор в симметричной троичной системе счисления является также и полувычитателем и представляет собой объединение двух бинарных троичных логических функций — «младший разряд (трит) суммы-разности» и «старший разряд (трит) суммы-разности (разряд переноса при сложении-вычитании в троичной симметричной системе счисления)».
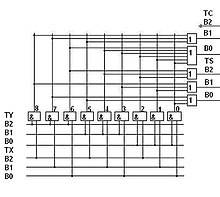 Троичный полусумматор.
Троичный полусумматор.- S
| +1 | 0 | +1 | -1 |
|---|---|---|---|
| 0 | -1 | 0 | +1 |
| -1 | +1 | -1 | 0 |
| -1 | 0 | +1 |
- C
| +1 | 0 | 0 | +1 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| -1 | -1 | 0 | 0 |
| -1 | 0 | +1 |
или в другом виде:
| x1=x | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | Название действия (функции) | Номер функции |
| S | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | Младший трит суммы | F710107071=F-4160 |
| C | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | Старший трит суммы (трит переноса) | F100000007=F6560 |
Цифра «7» здесь обозначает «-1»
Ненулевой перенос образуется в 2-х случаях из 9-ти.
Троичный трёхуровневый полусумматор описан в[3].
Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный (BCT) полусумматор, работающий в несимметричной троичной системе счисления приведён в[4], в разделе BCT Addition, в подразделе (f) Circuit diagram и, с ошибочным названием «двухразрядный BCT сумматор», в[5] на рисунке.
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов, описанного в[6].
Троичный зеркально-симметричный одноразрядный полусумматор описан в[7].
Состоит из двух таблиц размером 10х10. Первая таблица — суммы по модулю 10, вторая таблица — единицы переноса при бинарном (двухоперандном) десятичном сложении[8].
- S
| 9 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
- C
| 9 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Состоит из двух таблиц размером 16х16. Первая таблица — суммы по модулю 16, вторая таблица — единицы переноса при бинарном (двухоперандном) шестнадцатиричном сложении.
- S
| F | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D |
| D | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C |
| C | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B |
| B | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A |
| A | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 9 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 8 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 | 1 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 0 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
- C
| F | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| C | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| B | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| A | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
- ↑ 1 2 http://www.computerhistory.org/collections/accession/XD127.80 Computer History Museum
- ↑ http://www.computer-museum.ru/histussr/setun2.htm Малая автоматическая цифровая машина «Сетунь». Н. П. Брусенцов, Е. А. Жоголев, В. В. Веригин, С. П. Маслов, А. М. Тишулина
- ↑ http://spanderashvili.narod.ru/PA.pdf Астраханский Государственный Технический Университет, Кафедра «Автоматизированные системы обработки информации и управления», Курсовая работа по дисциплине «Объектно-ориентированное программирование» по специальности 220200 «Автоматизированные системы обработки информации и управления», Выполнили Морозов А. В., Спандерашвили Д. В., Алтуфьев М. Ю., Проверил к.т. н., доц. Лаптев В. В., Гл. XXIV Троичный полусумматор. Астрахань-2001 г.
- ↑ http://www.dcs.gla.ac.uk/~simon/teaching/CS1Q-students/systems/tutorials/tut3sol.pdf CS1Q Computer Systems
- ↑ http://314159.ru/kushnerov/kushnerov1.pdf Троичная цифровая техника. Ретроспектива и современность
- ↑ Троичный трёхбитный (3B BCT) полусумматор в троичной несимметричной системе счисления
- ↑ Компьютеры Фибоначчи. Троичное зеркально-симметричное сложение и вычитание (неопр.) (недоступная ссылка). Дата обращения 28 сентября 2010. Архивировано 30 октября 2010 года.
- ↑ М. А. Карцев. Арифметика цифровых машин. Главная редакция физико-математической литературы издательства «Наука», 1969, 576 стр. 2. Сумматоры и другие схемы для выполнения элементарных операций. 2.3. Одноразрядные комбинационные сумматоры для десятичной и других систем счисления. Стр.71
Двоичный сумматор на логических микросхемах
Заметим сразу, что схема этого устройства в том виде, в котором мы ее сейчас будем конструировать, сама по себе довольно бесполезна — если вы, конечно, не хотите повторить подвиг советского конструктора Михаила Александровича Карцева. Он создал в 1970-х годах на микросхемах малой степени интеграции (то есть фактически на отдельных логических элементах) очень удачную ЭВМ под названием М-10, отличившуюся тем, что отдельные ее экземпляры в нашем оборонном комплексе, по слухам, продержались аж до начала нового тысячелетия. При желании повторить такой подвиг, учтите, что основная проблема, которую вам придется решать, состоит вовсе не в том, чтобы такую машину сконструировать схемотехнически — это не самая трудная часть работы. Самое трудное для подобных суперконструкций — решить проблему отвода тепла, выделяемого сотнями тысяч быстродействующих логических микросхем. Суперкомпьютеры Cray на дискретных элементах, выпускаемые в 1980-х годах, даже имели водяное охлаждение.
Наконец, если очень хочется, то готовый двоичный сумматор есть в интегральном исполнении (561ИМ1; есть сумматоры и помощнее). Зачем же мы тогда будем его конструировать? А затем, что его устройство очень хорошо иллюстрирует две вещи: во-первых, само применение логических микросхем, во-вторых— разве не любопытно знать, как устроен самый главный узел компьютера, арифметико-логическое устройство, АЛУ? Знание этого вам очень пригодится для лучшего понимания работы микроконтроллеров и принципов их пррграммирования. Кроме того, мы на этом примере познакомимся еще с одним важным типом логических элементов.
Итак, вспомним, что нам, собственно, нужно делать — а именно воспроизвести таблицу сложения двоичных чисел, которая была показана для одноразрядных чисел в предыдущей главе. Так как при сложении единиц получается двухразрядное число, то перепишем эту таблицу в двухразрядном представлении:
Вх1 | 8×2 | Вых |
0 | 0 | 00 |
0 | 1 | 01 |
1 | 0 | 01 |
1 | 1 | 10 |
Теперь разобьем таблицу на две: одну для разряда собственно суммы, другую для значения переноса в следующий разряд:
Сумма | Перенос | |||||
Вх1 | Вх2 | Вых | Вх1 | Вх2 | Вых | |
0 | 0 | 0 | 0 | 0 | 0 | |
0 | 1 | 1 | 0 | 1 | 0 | |
1 | 0 | 1 | 1 | 0 | 0 | |
1 | 1 | 0 | 1 | 1 | 1 |
Сравним вторую таблицу с таблицей состояний для базовых логических функций (я их повторю, чтобы не приходилось листать книгу):
«или» | «и» | |||||
Вх1 | Вх2 | Вых | Вх1 | Вх2 | Вых | |
0 | 0 | 0 | 0 | 0 | 0 | |
0 | 1 | 1 | 0 | 1 | 0 | |
1 | 0 | 1 | 1 | 0 | 0 | |
1 | 1 | 1 | 1 | 1 | 1 |
Для переноса имеем полное совпадение с функцией «И». То есть для того чтобы обеспечить перенос, нам нужен всего лишь один логический элемент «И», который получается комбинированием стандартного «И-НЕ» с инверто-ром^ Хуже с разрядом суммы: первые три значения обеспечивает элемент «ИЛИ», однако при сложении единиц возникает несоответствие (логическое и арифметическое сложения, как мы говорили, не адекватны друг другу). Нужен специальный элемент, который мог бы получить название «элемент несовпадения»: в самом деле, у него логическая единица на выходе тогда, когда входы имеют разное состояние, а если они одинаковы — на выходе ноль. Для того чтобы его сконструировать, взглянем на таблицу истинности элемента «И-НЕ» (для наглядности я повторю и ее):
«И-НЕ» | ||
Вх1 | 8×2 | Вых |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Сравним таблицы «ИЛИ», «И-НЕ» и необходимой нам суммы: в первом случае мы получаем то, что надо, в верхних трех строках, во втором — в нижних. Как бы их объединить? Да очень просто — через функцию «И»:
Сумма | ||||
8×1 | 8×2 | Вых | Вых | «или» ж «И-НЕ» |
«ИЛИ» | «И-НЕ» | («Исключающее ИЛИ») | ||
0 | 0 | 0 | 1 | 0 |
0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 |
Логический элемент с такой функцией «несовпадения» носит специальное название — «Исключающее ИЛИ». Существует и обратный элемент «совпадения», который представляет собой инверсию выхода «Исключающего ИЛИ» и носит название «Включающего ИЛИ».
Исключающее или | ||
Вх1 | Вх2 | Вых |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Рис. 15.5. Варианты реализации элемента «Исключающее ИЛИ» и его таблица истинности
Обозначение элемента «Исключающее ИЛИ» уже было показано на рис. 15.3. Как можно его составить из элементов «И-НЕ» и «ИЛИ-НЕ», показано на рис. 15.5. Верхний вариант полностью соответствует нашим рассуждениям и потребует двух корпусов микросхем, а нижний вариант — пример того, как можно построить «Исключающее ИЛИ» с использованием только одного типа элементов, в данном случае — «И-НЕ». Он более экономичен, так как потребует всего одного корпуса типа 561ЛА7. Попробуйте построить таблицу истинности для второго варианта, и вы убедитесь, что он работает «как заказывали» (есть и много других способов). Отметьте, что в первом варианте специальных элементов-инверторов мы не используем, а с целью экономии корпусов микросхем образуем их из элементов «И-НЕ» или «ИЛИ-НЕ» путем объединения входов — обычно так и поступают.
В любой логической серии есть, разумеется, и специальные микросхемы «Исключающее ИЛИ» (561ЛП2). Элемент «Исключающее ИЛИ», помимо способности выдавать сумму одноразрядных чисел, обладает многими интересными свойствами, к которым мы обратимся далее, а пока вернемся к сумматору.
Рис. 15.6. Схема одноразрядного полусумматора
На самом деле одноразрядный сумматор мы уже построили. Его схема приведена на рис. 15.6 вверху. Внизу на рис. 15.6 мы обозначили все устройство одним квадратиком. Однако почему там написано «полусумматор»? Такой. одноразрядный сумматор носит название полусумматора, потому что он не «умеет» одной важной вещи, а именно: разряд переноса-то он выдает, а вот учесть перенос от предыдущего разряда он не может. Поэтому, чтобы складывать многоразрядные числа по-настоящему, нужно в каждом разряде поставить по два таких полусумматора, причем объединить их выходы переносов через «ИЛИ» (рис. 15.7).
Рис. 15.7. Схема многоразрядного сумматора
Так мы получили одноразрядный полный сумматор. Объединением таких сумматоров несложно соорудить устройство для сложения чисел любой разрядности. Если вы попробуете разрисовать схему сумматора для, скажем, восьми разрядов полностью, с использованием принципиальных схем логических элементов по рис. 15.1, то ужаснетесь — это же сколько транзисторов надо, чтобы построить такое устройство? Много — в восьмибитном КМОП-сумматоре их получается 480 штук (а современные микросхемы, бывает, содержат и больше транзисторов). И это без учета того, что в систему должны входить еще, как минимум, два регистра для хранения исходных чисел и результата (в целях экономии результат помещают в регистр одного из слагаемых, тем самым слагаемое это уничтожая), а также другие логические схемы (для сдвига, для инверсии битов при манипуляции с отрицательными числами). То есть общее количество транзисторов составляет порядка тысячи.
Теперь понятно, почему микросхемы высокой степени интеграции содержат миллионы транзисторов и почему проблема отвода тепла стоит так остро! Один логический элемент КМОП из четырех транзисторов, согласно рис. 15.2, выделяет при частоте в единицы мегагерц всего-навсего пол милливатта тепла, но что будет, если таких элементов приходится ставить в количестве миллион штук? И еще при этом как можно сильнее повышать рабочую частоту?
Сумматоры, построенные по описанной схеме, выпускают, естественно, в интегральном исполнении (в «классической» КМОП это микросхема четырехразрядного сумматора 561ИМ1, есть и схема более универсального АЛУ— 561ИПЗ). В связи с многоразрядным сумматором возникает только один вопрос: а что делать с входом переноса самого первого, младшего разряда? Если просто складываем двоичные числа разрядности, соответствующей возможностям нашего сумматора (например, восьмиразрядные, то есть длиной в один байт), то вход переноса младшего разряда присоединяется к логическому нулю. Соответственно, выход переноса старшего разряда остается «висеть в воздухе». Легко сообразить, что при этом, если мы складываем числа, в сумме составляющие более величины диапазона, старший разряд суммы «потеряется». Это явление при всей своей очевидности стоит того, чтобы разобрать его подробнее.
Предположим, мы имеем такой байтовый сумматор и под числами имеем в виду обычные беззнаковые положительные числа, диапазон которых составит 0—255. Если мы сложим 128 (1000 0000) и 128 (1000 0000), то получим число 256 (1 0000 0000), которое имеет единицу в 9-м, отсутствующем у нас разряде (заодно отметим этот результат как хорошую иллюстрацию к положению, гласящему, что умножение на 2 есть просто сдвиг всех разрядов влево). Таким образом, в разрядах сумматора мы получаем просто О, что, конечно, есть результат некорректный, для корректного сложения, к примеру, восьмибитовых чисел нам надо иметь 9 разрядов результата.
А как наращивать разряды, если, например, в микроконтроллере все регистры восьмиразрядные? Да очень просто — надо взять два таких регистра и соединить выход переноса одного со входом переноса другого. Тогда мы получим двубайтовое число (или «слово», как его чаще называют). В микропроцессорах, в том числе и в микроконтроллерах, мы, конечно, физически такое объединение сделать не можем — схема уже сделана заранее, но в них зато есть специальный бит переноса (сапу bit), в который автоматически помещается перенос в результате операций сложения, умножения и, кстати, вычитания и деления тоже.
4.8 Сумматоры двоичных кодов чисел.
С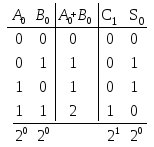 умматором
называется устройство для арифметического
сложения чисел. В цифровых вычислительных
машинах они представляются в двоичном
коде и таблица истинности простейшего
сумматора одноразрядных двоичных чиселвыглядиттак. Из нее
следует, что разрядность суммы совпадает
с разрядностью слагаемых если они оба
не равны единице. Когда
умматором
называется устройство для арифметического
сложения чисел. В цифровых вычислительных
машинах они представляются в двоичном
коде и таблица истинности простейшего
сумматора одноразрядных двоичных чиселвыглядиттак. Из нее
следует, что разрядность суммы совпадает
с разрядностью слагаемых если они оба
не равны единице. Когда результат сложения получается равным
2 и разрядность суммы становится на
единицу больше чем у слагаемых. Это
явление называется переполнением
разрядной сетки, а появляющаяся в старшем
разряде единица – сигналом переноса.
Обычно он обозначается буквойС(от
английского словаcarry), а
нижний индекс характеризует его вес.
результат сложения получается равным
2 и разрядность суммы становится на
единицу больше чем у слагаемых. Это
явление называется переполнением
разрядной сетки, а появляющаяся в старшем
разряде единица – сигналом переноса.
Обычно он обозначается буквойС(от
английского словаcarry), а
нижний индекс характеризует его вес.
И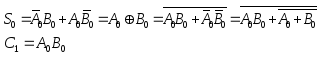 з
таблицы следует, что алгебраические
представления выходных функций сумматора
имеют вид, причем значения сигнала суммы
совпадают с функцией логической
неравнозначности от операндов. Чтобы
избавиться от инверсий входных переменных
з
таблицы следует, что алгебраические
представления выходных функций сумматора
имеют вид, причем значения сигнала суммы
совпадают с функцией логической
неравнозначности от операндов. Чтобы
избавиться от инверсий входных переменных  удобно представить в несколько иной
форме.
удобно представить в несколько иной
форме.
И
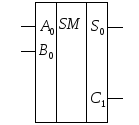 з
полученных соотношений вытекает, что
структура сумматора будет иметь вид.
На принципиальных схемах сумматор, как
функциональный узел, обозначается
следующим образом.
з
полученных соотношений вытекает, что
структура сумматора будет иметь вид.
На принципиальных схемах сумматор, как
функциональный узел, обозначается
следующим образом.
Однако, правильное название данного устройства – полусумматор. У полного одноразрядного сумматора должен быть дополнительный вход для обработки сигнала переноса С0, имеющего тот же вес, что и разряды операндов. Это необходимо при построении многоразрядных сумматоров, так как появляющиеся переносы требуется учитывать при суммировании более старших разрядов.
П ри
возникновении переноса
ри
возникновении переноса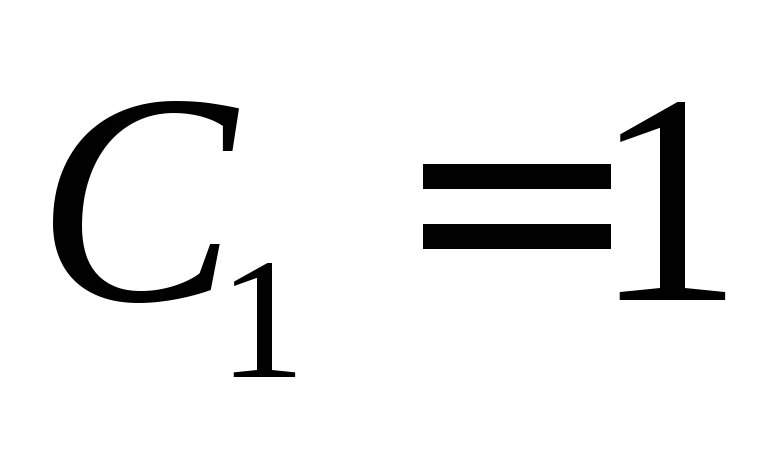 ,
а при его отсутствии
,
а при его отсутствии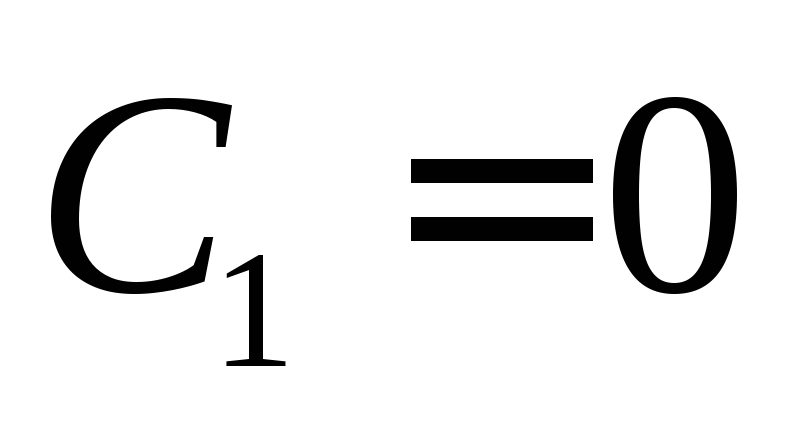 .
Однако для удобства считают, что сигнал
переноса присутствует всегда, но в
зависимости от ситуации имеет либо
нулевое, либо единичное значение. В
качестве примера можно привести процедуру
сложения чисел в десятичной системе
счисления.
.
Однако для удобства считают, что сигнал
переноса присутствует всегда, но в
зависимости от ситуации имеет либо
нулевое, либо единичное значение. В
качестве примера можно привести процедуру
сложения чисел в десятичной системе
счисления.
Т
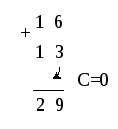 ак
как все суммируемые разряды имеют
одинаковые веса, то таблица истинности
полного одноразрядного сумматора имеет
следующий вид.
ак
как все суммируемые разряды имеют
одинаковые веса, то таблица истинности
полного одноразрядного сумматора имеет
следующий вид.
Д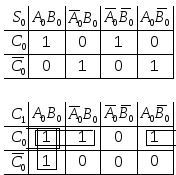 ля
получения алгебраического представления
выходных функций
ля
получения алгебраического представления
выходных функций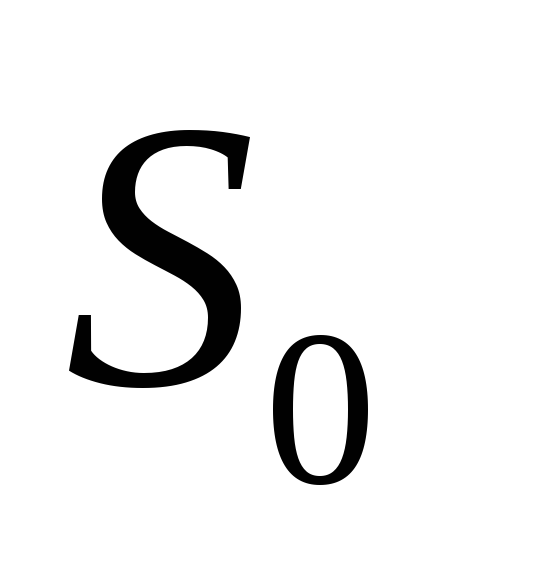 и
и удобно воспользоваться картами Карно.
удобно воспользоваться картами Карно. Из
них можно установить, что функция
Из
них можно установить, что функция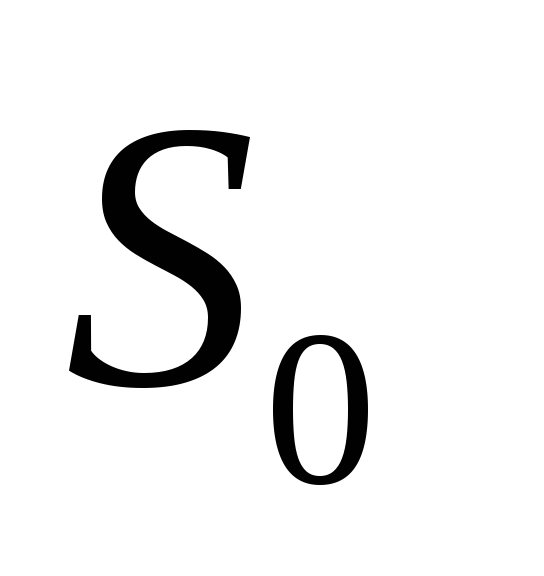 неминимизируема.
неминимизируема.
О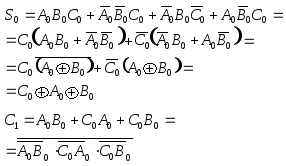 днако,
выражение для нее можно преобразовать
таким образом, чтобы при представлении
днако,
выражение для нее можно преобразовать
таким образом, чтобы при представлении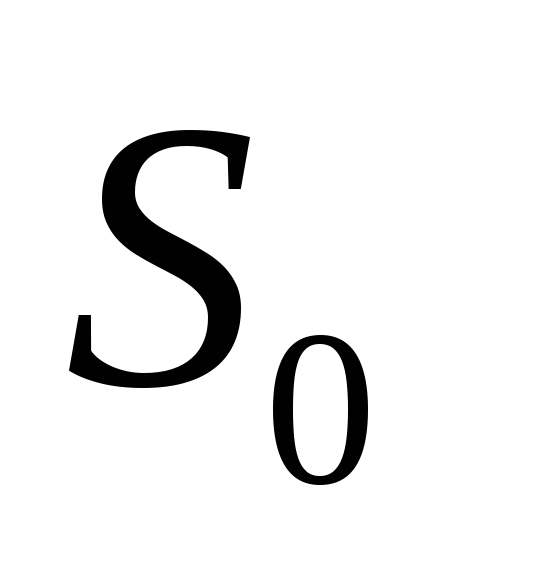 использовать операцию суммирования по
модулю два (функцию логической
неравнозначности). В этом случае запись
получается достаточно компактной и
схема сумматора будет иметь вид.
использовать операцию суммирования по
модулю два (функцию логической
неравнозначности). В этом случае запись
получается достаточно компактной и
схема сумматора будет иметь вид.
С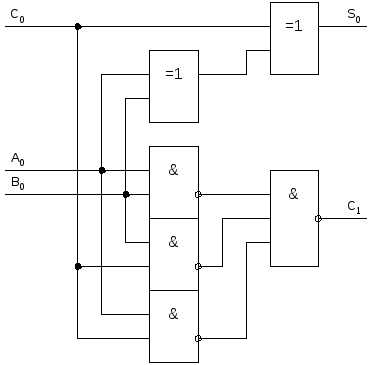 труктура
ее верхней части представляет собой
схему контроля четности. Если
проанализировать по таблице свойства
функции
труктура
ее верхней части представляет собой
схему контроля четности. Если
проанализировать по таблице свойства
функции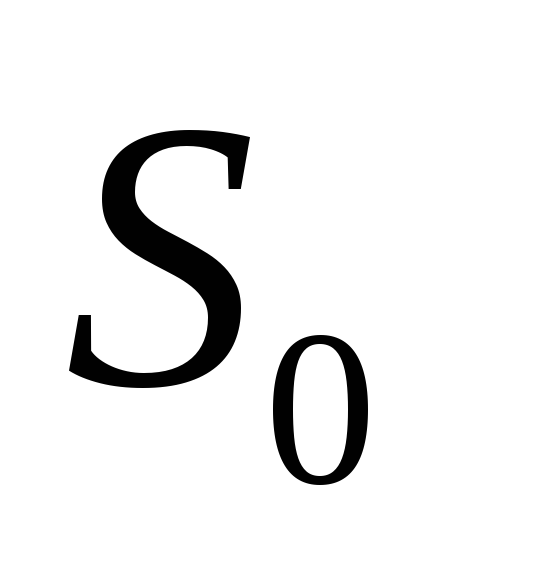 ,
то можно увидеть, что она действительно
принимает единичное значение, когда
количество единиц в трехразрядной
комбинации
,
то можно увидеть, что она действительно
принимает единичное значение, когда
количество единиц в трехразрядной
комбинации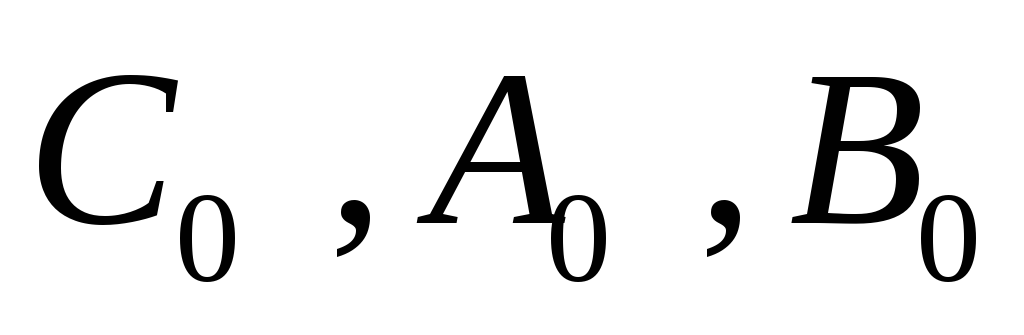 нечетное.
нечетное.
Промышленностью в составе серий цифровых микросхем выпускаются одноразрядные сумматоры – К155ИМ1, К555ИМ5 (два в одном корпусе) и ряд других.
В цифровых системах
обработки информации требуется
осуществлять процедуру сложения
многоразрядных чисел. Ее можно реализовать
либо последовательным образом, либо
параллельно. Разряды операндов не
зависят друг от друга, поэтому процесс
их суммирования сводится к сложению
разрядов, имеющих одинаковые веса. Если
при этом возникает перенос, он должен
быть добавлен к сумме следующих по
старшинству разрядов, как это показано
на примере с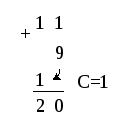
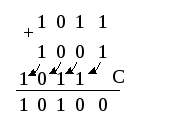 уммированиячисел в десятичной и двоичной системах
счисления.
уммированиячисел в десятичной и двоичной системах
счисления.
Отсюда следует, что для сложения чисел произвольной разрядности можно использовать одноразрядный сумматор, подавая разряды на обработку последовательно друг за другом и учитывая сигналы переносов.
В этом случае, процедура сложения чисел 11 и 9, представленных двоичными кодами 1011 и 1001 должна происходить так, как показано на рисунке, где представлен один и тот же сумматор, в разные моменты времени. На первом этапе на него поступают младшие разряды операндов и нулевой сигнал переноса. Младший разряд суммы, равный нулю, может быть считан с соответствующего выхода S0, а единичный сигнал переноса должен быть прибавлен на следующем шаге к значениям соответствующих разрядов операндов. При этом сформируется разряд суммыS1 и так далее.
Т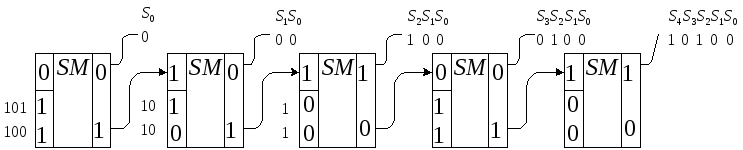 ак
как разрядность суммы на единицу больше
разрядности слагаемых, то для считывания
с выходаS0последнего разряда суммыS4потребуется дополнительный этап, на
котором сигнал переноса необходимо
передать на выходS0. Для этого его надо просуммировать с
двумя нулями.
ак
как разрядность суммы на единицу больше
разрядности слагаемых, то для считывания
с выходаS0последнего разряда суммыS4потребуется дополнительный этап, на
котором сигнал переноса необходимо
передать на выходS0. Для этого его надо просуммировать с
двумя нулями.
П роцесс
сложенияn-разрядных чисел
в таком сумматоре займетN+1
шаг. Если среднюю задержку формирования
выходных сигналов сумматора
роцесс
сложенияn-разрядных чисел
в таком сумматоре займетN+1
шаг. Если среднюю задержку формирования
выходных сигналов сумматора  принять заτ, то время, потребуемое
для выполнения процедуры сложения может
быть оценено как
принять заτ, то время, потребуемое
для выполнения процедуры сложения может
быть оценено как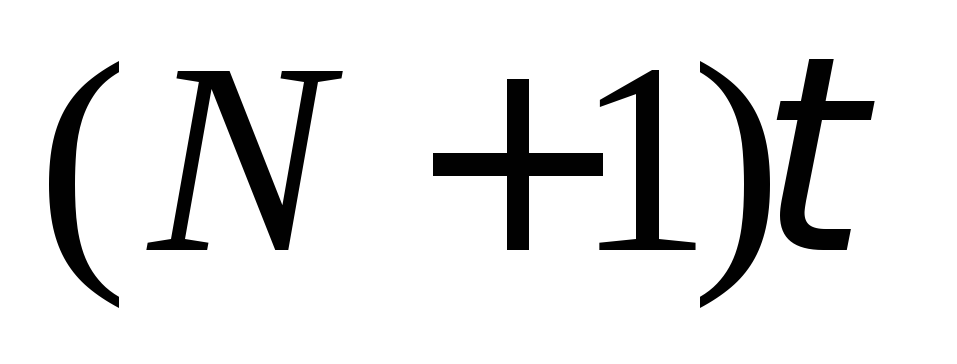 .
.
Такой сумматор должен содержать узел для последовательного ввода разрядов слагаемых (УПВ), а также устройство для запоминания на один такт разряда переноса (УП). Сам сумматор является комбинационным устройством, то есть при поступлении новых данных сразу же изменится и результат обработки, а так как сигнал переноса требуется в следующем такте, то его необходимо запомнить.
Несмотря на относительную простоту, существенным недостатком такого сумматора является его низкое быстродействие, поэтому подобные узлы находят применение там, где скорость вычислений не играет существенной роли, например в калькуляторах.
При работе с большими массивами цифровых данных, скорость вычислений становится очень важной, и в этом случае используются параллельные методы обработки.
Т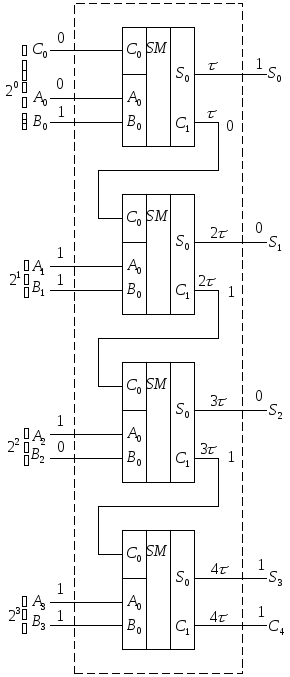 ак
какв ходе суммирования разряды
связаны только через сигналы переносов,
то структура параллельного двоичного
сумматора на примере четырехразрядного
устройства может быть представлена
следующим образом.
ак
какв ходе суммирования разряды
связаны только через сигналы переносов,
то структура параллельного двоичного
сумматора на примере четырехразрядного
устройства может быть представлена
следующим образом.
Здесь разряды операндов поступают одновременно (параллельно) и сигналы переносов с предшествующих разрядов подаются на соответствующие входы сумматоров, обрабатывающих последующие. Такая структура называется параллельным сумматором с последовательным распространением переносов.
Проверить правильность работы данного устройства можно на примере сложения двоичных кодов чисел 14 и 11.
Н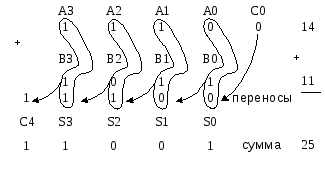 есмотря
на идентичность одноразрядных сумматоров,
их функции несколько отличаются. Это
связано с тем, что здесь осуществляется
обработка арифметических данных и
поэтому значение разряда определяется
не только его состоянием (0,1), но и
местоположением, то есть весом. Отсюда
следует, что для получения правильного
результата разряды данных на такой
сумматор требуется подавать в строго
определенном порядке.
есмотря
на идентичность одноразрядных сумматоров,
их функции несколько отличаются. Это
связано с тем, что здесь осуществляется
обработка арифметических данных и
поэтому значение разряда определяется
не только его состоянием (0,1), но и
местоположением, то есть весом. Отсюда
следует, что для получения правильного
результата разряды данных на такой
сумматор требуется подавать в строго
определенном порядке.
Б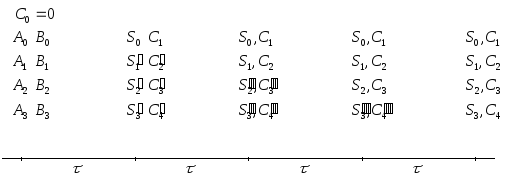 ыстродействие
этой схемы можно оценить, зная время
задержки появления сигнала суммы
ыстродействие
этой схемы можно оценить, зная время
задержки появления сигнала суммы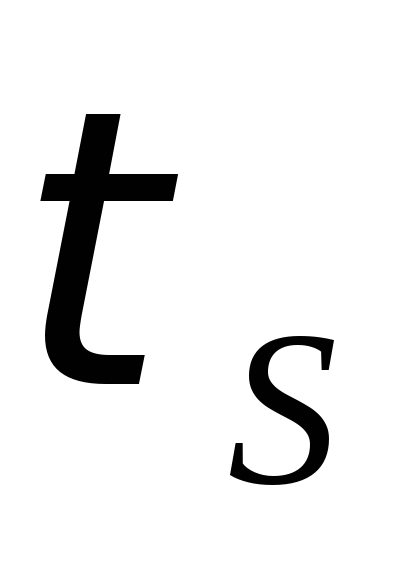 и переноса —
и переноса — .
В первом приближении их можно считать
равными
.
В первом приближении их можно считать
равными .
Тогда условная диаграмма процедуры
сложения будет выглядеть следующим
образом.
.
Тогда условная диаграмма процедуры
сложения будет выглядеть следующим
образом.
Через время  после
прихода операндов сформируется правильное
значение нулевого разряда суммы
после
прихода операндов сформируется правильное
значение нулевого разряда суммы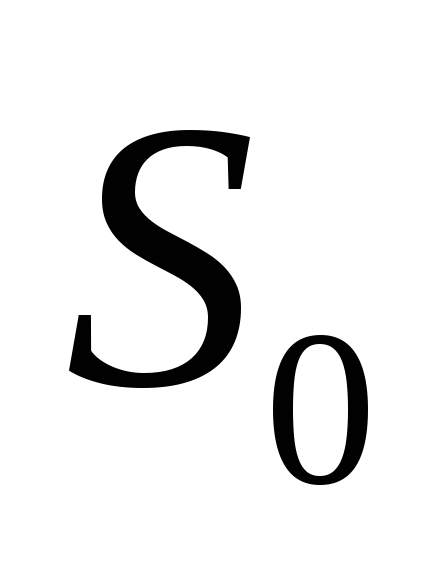 и
переноса в первый разряд
и
переноса в первый разряд .
Остальные разряды суммы и переносов,
отмеченные штрихами, могут иметь неверные
значения, так как к этому моменту
правильное значение
.
Остальные разряды суммы и переносов,
отмеченные штрихами, могут иметь неверные
значения, так как к этому моменту
правильное значение только поступит на соответствующий
вход второго сумматора и на его обработку
совместно с разрядами
только поступит на соответствующий
вход второго сумматора и на его обработку
совместно с разрядами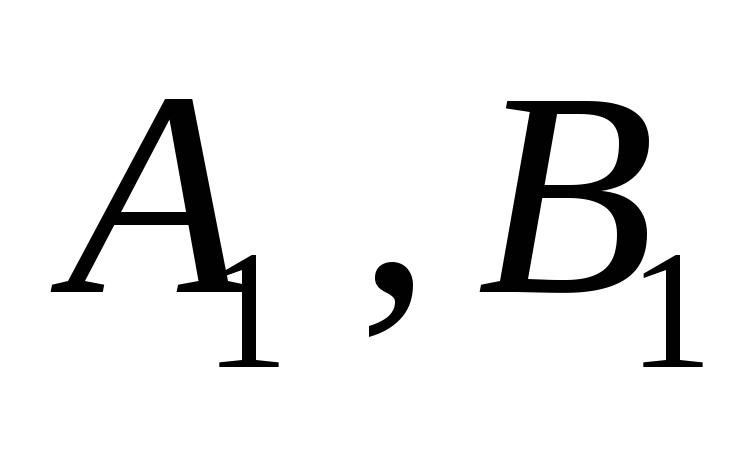
 также
понадобится интервал времени
также
понадобится интервал времени .
.
Таким образом
через  истинными будут значения разрядов суммы
истинными будут значения разрядов суммы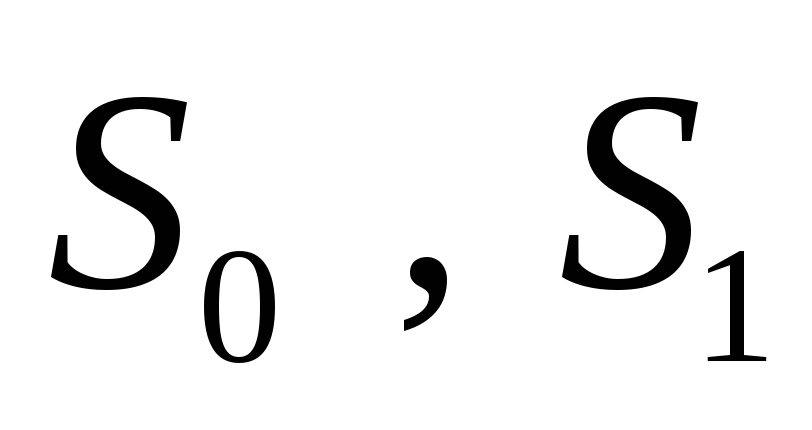 ,
через
,
через —
—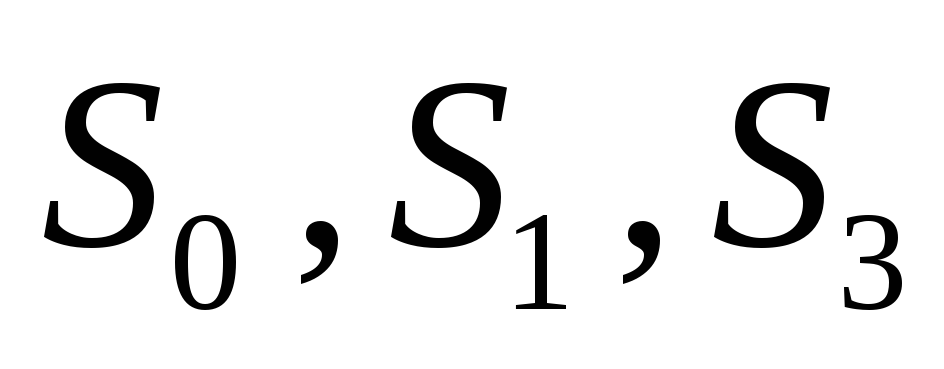 и т. д. Отсюда следует, что несмотря на
параллельное (одновременное) поступление
всех разрядов операндов, правильное
значение суммы может быть считано лишь
через
и т. д. Отсюда следует, что несмотря на
параллельное (одновременное) поступление
всех разрядов операндов, правильное
значение суммы может быть считано лишь
через .
В общем случае этот интервал зависит
от разрядности суммируемых чисел и
среднее время задержки такого устройства
равно
.
В общем случае этот интервал зависит
от разрядности суммируемых чисел и
среднее время задержки такого устройства
равно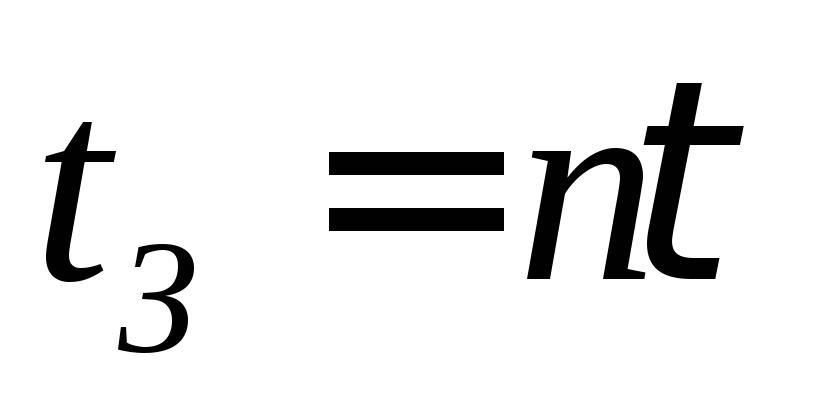 ,
где
,
где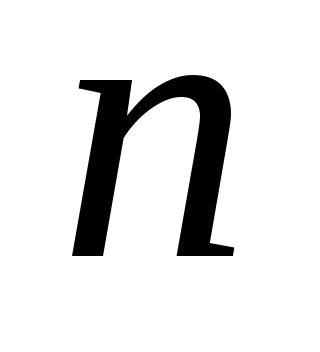 — количество разрядов слагаемых. Наличие
множителя
— количество разрядов слагаемых. Наличие
множителя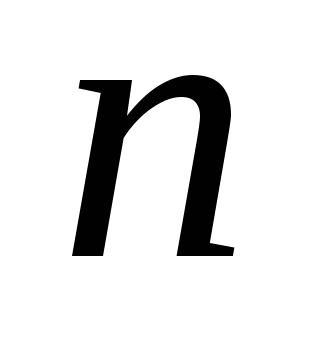 объясняется тем, что перенос на сумматор,
обрабатывающий последний разряд,
поступает пройдя
объясняется тем, что перенос на сумматор,
обрабатывающий последний разряд,
поступает пройдя последовательно соединенных аналогичных
узлов.
последовательно соединенных аналогичных
узлов.
Н
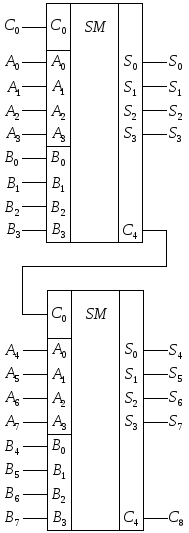 а
принципиальных схемах четырехразрядный
сумматор изображается следующим образом.
Такие устройства можно использовать
для построения сумматоров большей
разрядности, соединяя их соответствующими
выходами и входами переносов, как это
показано для восьмиразрядного варианта.
а
принципиальных схемах четырехразрядный
сумматор изображается следующим образом.
Такие устройства можно использовать
для построения сумматоров большей
разрядности, соединяя их соответствующими
выходами и входами переносов, как это
показано для восьмиразрядного варианта.
Для суммирующих
блоков с внутренним последовательным
переносом такой способ соединения
является единственно возможным. При
этом задержка формирования результата
будет возрастать пропорционально их
количеству. В общем случае, если
использовать 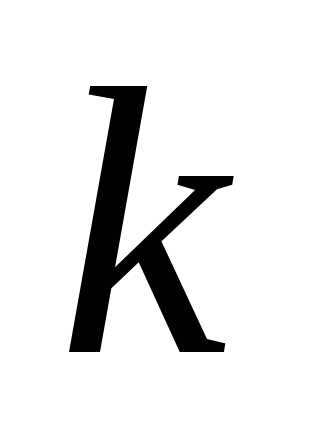 штук
штук — разрядных блоков, то время задержки
сложения
— разрядных блоков, то время задержки
сложения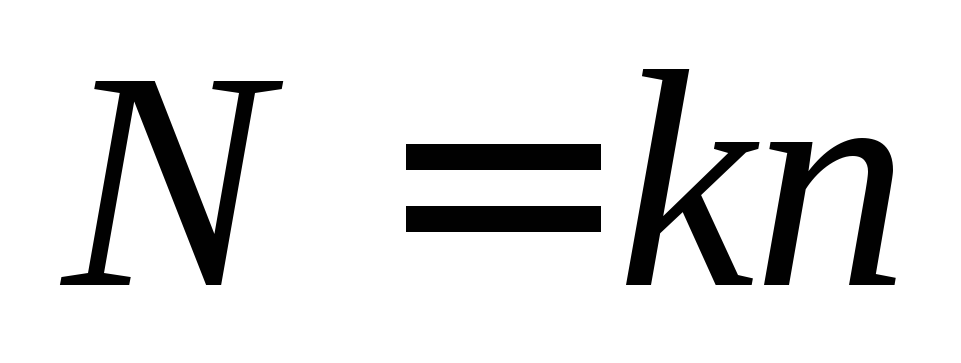 разрядных чисел будет определяться
соотношением
разрядных чисел будет определяться
соотношением .
.
Повысить быстродействие многоразрядного сумматора можно, ускорив процесс формирования и передачи сигналов переноса по разрядам.
П усть
имеется устройство – схема формирования
переноса (СФП), которое по результатам
анализа разрядов операндов, способно
сформировать сигнал выходного переноса
с задержкой τ. Структура четырехразрядного
сумматора будет в этом случае будет
выглядеть следующим образом.
усть
имеется устройство – схема формирования
переноса (СФП), которое по результатам
анализа разрядов операндов, способно
сформировать сигнал выходного переноса
с задержкой τ. Структура четырехразрядного
сумматора будет в этом случае будет
выглядеть следующим образом.
Однако к повышению
быстродействия суммирующего блока
данное решение не приведет, так как
несмотря на то, что перенос  появится с задержкой τ, результат
сложения сформируется не ранее, чем
через
появится с задержкой τ, результат
сложения сформируется не ранее, чем
через ,
(
,
( в суммирующем блоке соответствующей
разрядности).
в суммирующем блоке соответствующей
разрядности).
В то же время при
последовательном соединении 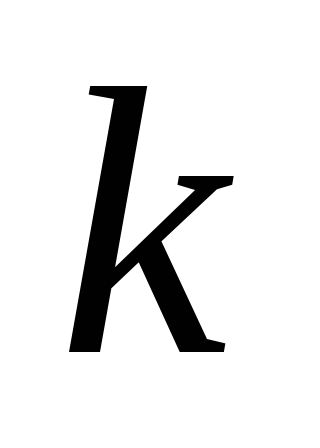 таких блоков время сложения будет
определяться соотношением
таких блоков время сложения будет
определяться соотношением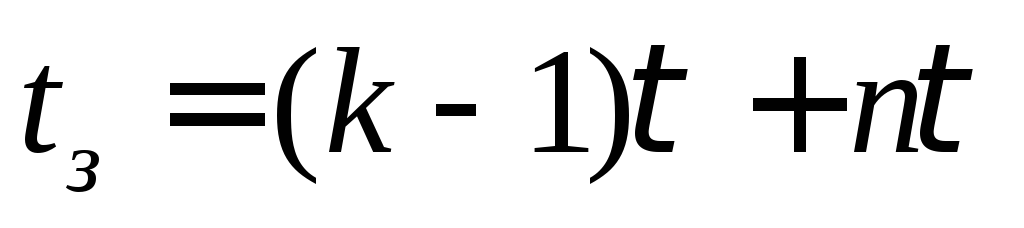 .
За
.
За перенос достигнет последнего блока и
перенос достигнет последнего блока и понадобится для завершения процедуры
сложения старших разрядов операндов.
понадобится для завершения процедуры
сложения старших разрядов операндов.
Если аналогичные
схемы формирования переносов подключить
ко входам переносов всех одноразрядных
сумматоров внутри блока, то задержка
формирования суммы станет равной  при любой его разрядности.
при любой его разрядности.
Д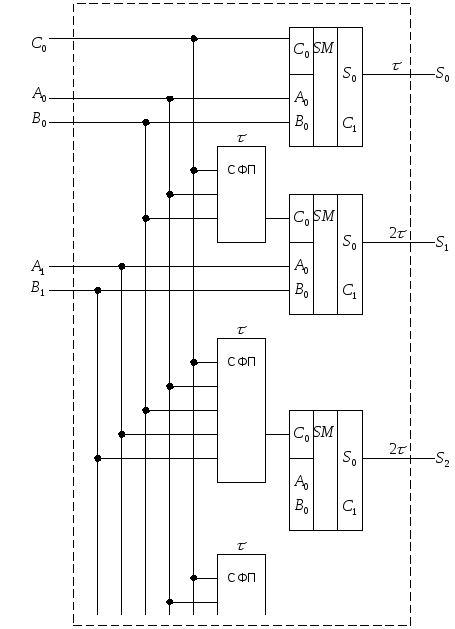 ля
структуры из
ля
структуры из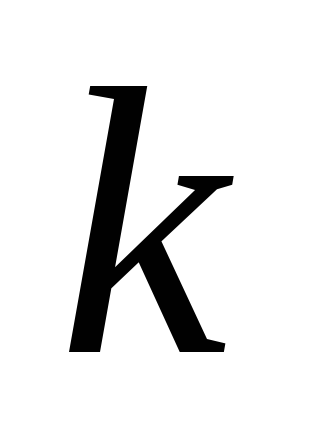 штук
штук — разрядных блоков она составит
— разрядных блоков она составит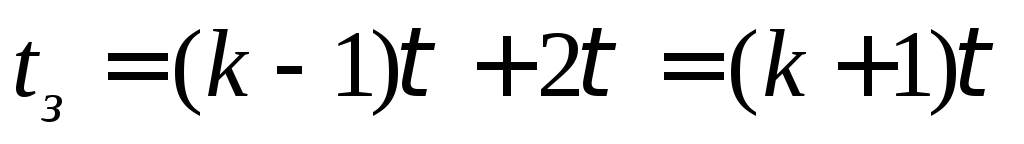 то есть быстродействие такого
многоразрядного сумматора окажется
существенно выше, чем у предыдущих
вариантов.
то есть быстродействие такого
многоразрядного сумматора окажется
существенно выше, чем у предыдущих
вариантов.
Можно ли создать
устройства, формирующие переносы в
старшие разряды, не дожидаясь промежуточных
результатов сложения? Сигнал переноса,
одноразрядного сумматора описывается
соотношением 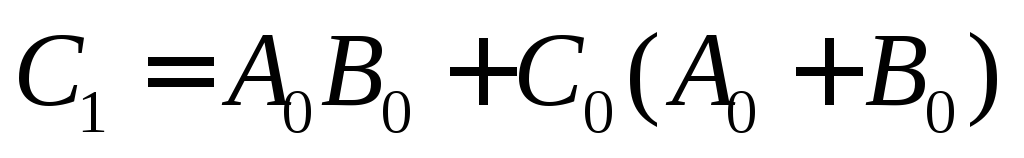 Если
аналогичное устройство применяется
для сложения следующих по старшинству
разрядов, то в данной формуле изменятся
индексы, то есть
Если
аналогичное устройство применяется
для сложения следующих по старшинству
разрядов, то в данной формуле изменятся
индексы, то есть .
.
Э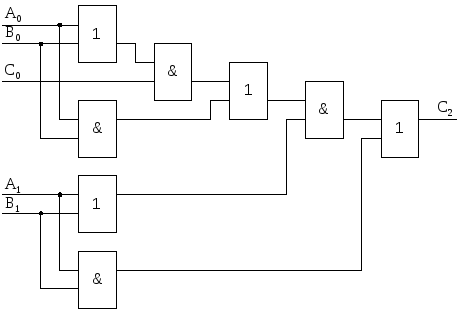 то
выражение можно преобразовать следующим
образом
то
выражение можно преобразовать следующим
образом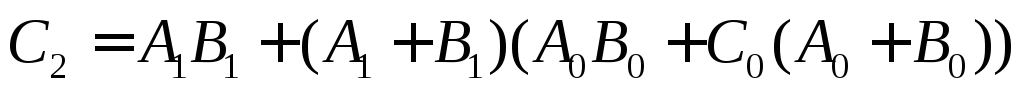 ,
то есть перенос
,
то есть перенос можно получить не дожидаясь сигнала
можно получить не дожидаясь сигнала ,
а обработав все разряды операндов и
сигнал входного переноса
,
а обработав все разряды операндов и
сигнал входного переноса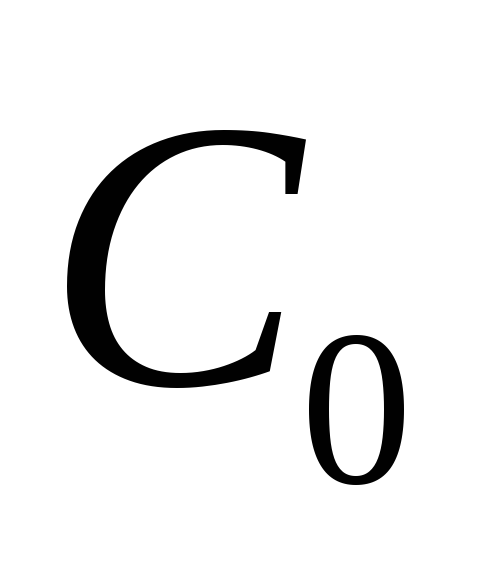 .
.
При такой форме
представления функции переноса выигрыша
в скорости формирования  не будет, так как из-за последовательной
процедуры обработки задержка появления
выходного сигнала составит
не будет, так как из-за последовательной
процедуры обработки задержка появления
выходного сигнала составит или примерно
или примерно ,
если под
,
если под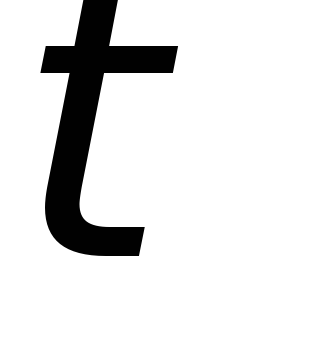 понимать задержку в сумматоре.
понимать задержку в сумматоре.
Однако если это выражение преобразовать, в частности раскрыть скобки, то оно трансформируется к виду
 .
Реализация функции
.
Реализация функции  в новом представлении позволит осуществить
параллельную обработку компонент, что
существенно уменьшит время формирования
сигнала переноса (до
в новом представлении позволит осуществить
параллельную обработку компонент, что
существенно уменьшит время формирования
сигнала переноса (до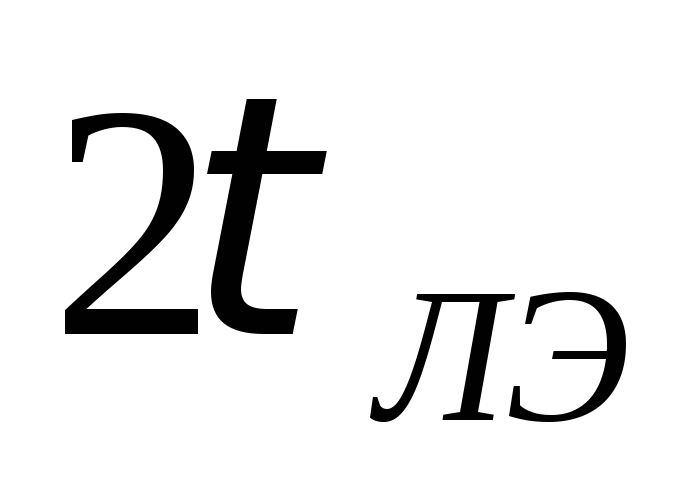 .
Аналогичным образом решалась задача
повышения быстродействия приоритетного
шифратора.
.
Аналогичным образом решалась задача
повышения быстродействия приоритетного
шифратора.
Сумматоры с такой
внутренней структурой называются
сумматорами с параллельным переносом.
Однако их каскадирование возможно
только путем соединения выхода переноса
предыдущего блока с соответствующим
входом последующего, то есть минимальная
задержка формирования результата будет
равна 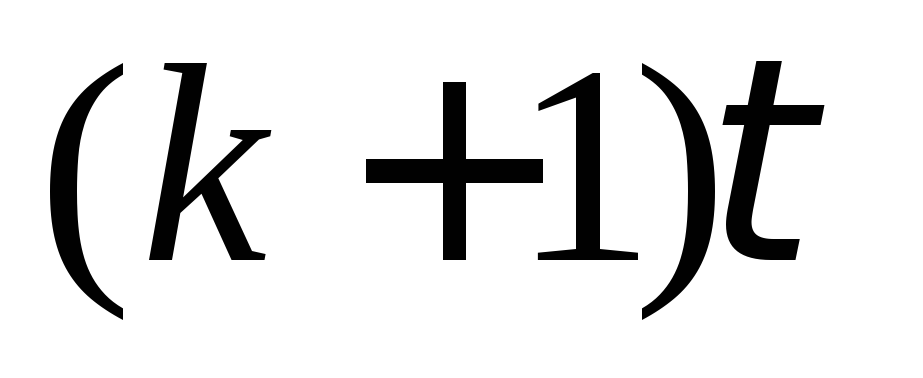 .
.
Е сли
подобные формирователи переносов
устанавливать между суммирующими
блоками, то при теоретической задержке
в
сли
подобные формирователи переносов
устанавливать между суммирующими
блоками, то при теоретической задержке
в структура сумматора из
структура сумматора из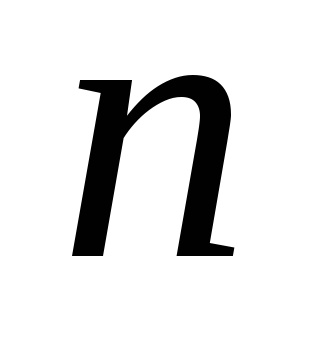 блоков будет нерегулярной, так как
каждой последующей схеме придется
обрабатывать весь предшествующий набор
операндов. То есть они должны иметь
разную конфигурацию и, кроме того, резко
возрастет количество связей между
элементами такого многоразрядного
сумматора.
блоков будет нерегулярной, так как
каждой последующей схеме придется
обрабатывать весь предшествующий набор
операндов. То есть они должны иметь
разную конфигурацию и, кроме того, резко
возрастет количество связей между
элементами такого многоразрядного
сумматора.
Повысить быстродействие при сохранении регулярности структуры оказалось возможным после разработки сумматоров с ускоренным переносом. В них схемы формирования переносов выносятся за суммирующие блоки, а с целью уменьшения числа связей на сумматоры возлагается частичная обработка сигналов переносов.
Для этого функция 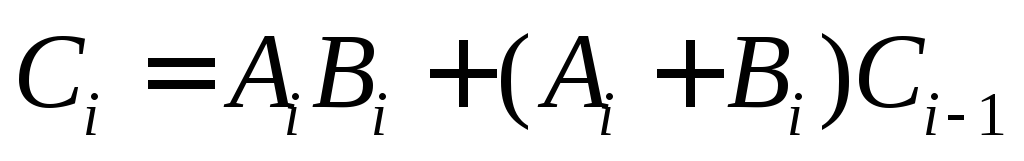 ,
описывающая сигнал переноса в
,
описывающая сигнал переноса в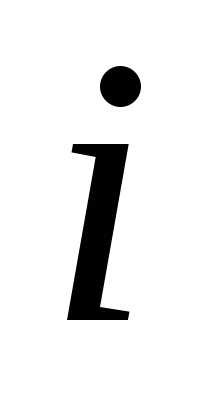 —
том разряде представляется в виде
—
том разряде представляется в виде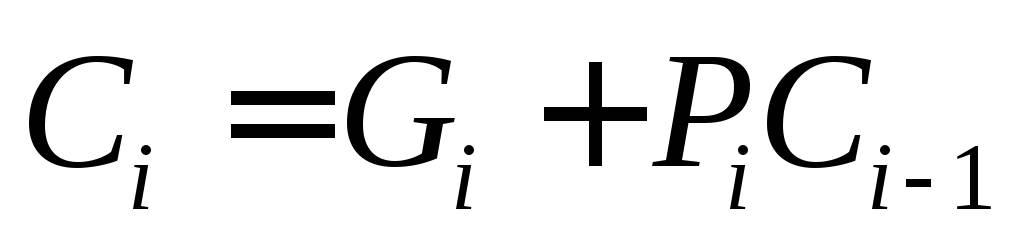 .
Компонента
.
Компонента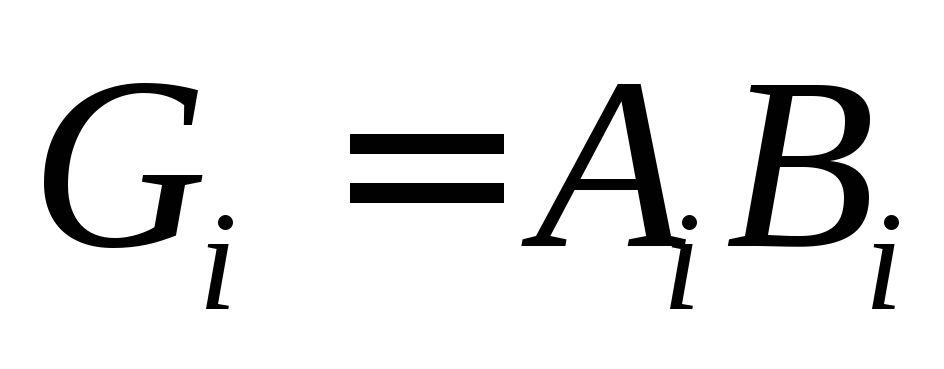 называется функцией генерации, а
называется функцией генерации, а — распространения переноса и задача их
формирования в
— распространения переноса и задача их
формирования в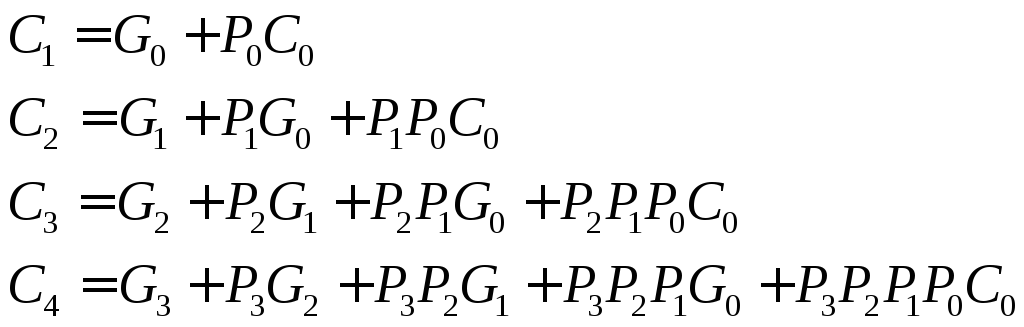 озлагается
на одноразрядные сумматоры. Система
уравнений, описывающая работу схемы
ускоренного формирования переносов
для четырех разрядов сумматора, выглядит
следующим образом, а структура сумматора
имеет вид.
озлагается
на одноразрядные сумматоры. Система
уравнений, описывающая работу схемы
ускоренного формирования переносов
для четырех разрядов сумматора, выглядит
следующим образом, а структура сумматора
имеет вид.
П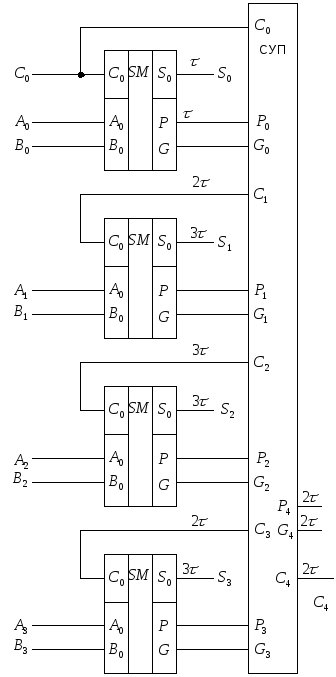 оследнее
выражение представляет сигнал переноса
в следующий суммирующий блок и может
быть записано как
оследнее
выражение представляет сигнал переноса
в следующий суммирующий блок и может
быть записано как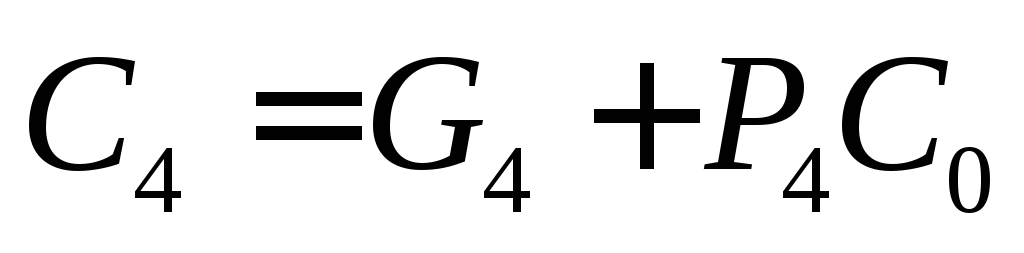 ,
где
,
где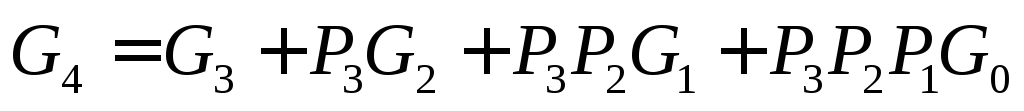 ,
а
,
а .
Это позволяет рассматривать каждый
такой блок как эквивалент некоторого
сумматора со стандартными значениями
функций распространения и генерации
переноса, что дает возможность объединять
их в многоразрядную структуру посредством
аналогичных схем ускоренного переноса
(СУП).
.
Это позволяет рассматривать каждый
такой блок как эквивалент некоторого
сумматора со стандартными значениями
функций распространения и генерации
переноса, что дает возможность объединять
их в многоразрядную структуру посредством
аналогичных схем ускоренного переноса
(СУП).
Задержка формирования
сигнала в представленном четырехразрядном
сумматоре составит  (по
(по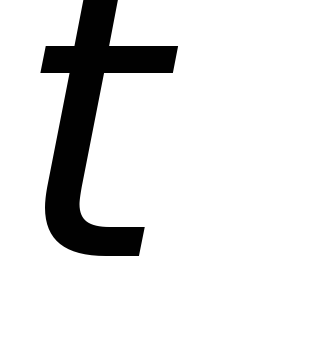 на формирование функций
на формирование функций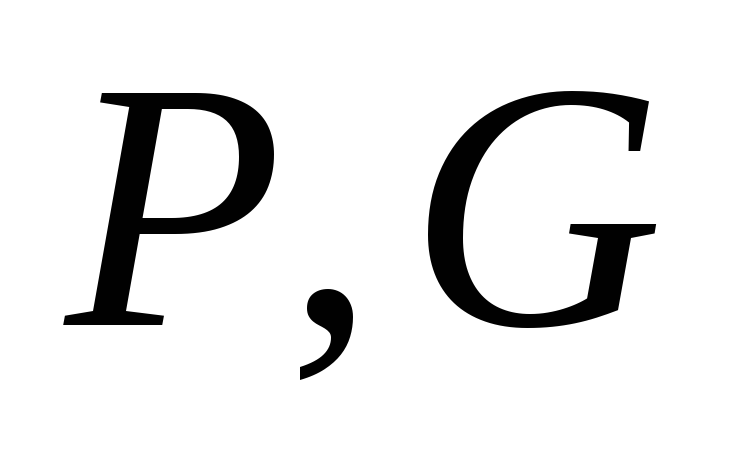 ,
переносов во все разряды и самого
результата).
,
переносов во все разряды и самого
результата).
В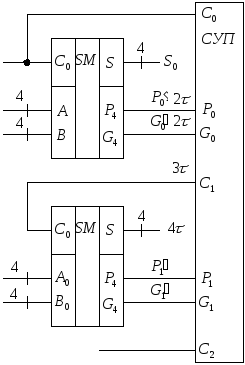 ремя
задержки в шестнадцатиразрядном
сумматоре, четырехразрядные блоки
объединяются через схемы ускоренного
переноса, составит
ремя
задержки в шестнадцатиразрядном
сумматоре, четырехразрядные блоки
объединяются через схемы ускоренного
переноса, составит ,
а в шестидесятичетырехразрядной
структуре
,
а в шестидесятичетырехразрядной
структуре .
.
Промышленностью выпускается большой ассортимент микросхем сумматоров в интегральном исполнении: К155ИМ3 – четырехразрядный параллельный сумматор с последовательными переносами, К555ИМ6 – аналогичный сумматор, с параллельными переносами между разрядами, К155ИП3 – многофункциональное устройство, включающее четырехразрядный сумматор с ускоренным переносом, К155ИП4 – четырехразрядная схема ускоренного переноса.
В приведенной таблице представлены результаты сравнения быстродействия 16 разрядных параллельных сумматоров, построенных на основе четырехразрядных блоков.
N=16, n=4, k=4 Структура | Время задержки теоретическое | Время задержки реальное | Тип микросхем |
С последовательным переносом | 16τ | 180 нС | К155ИМ3 |
С паралл. переносом в сумматоре и последоват. между блоками | 5τ | 75 нс | К555ИМ6, К155ИП3 |
С ускоренным переносом | 4τ | 50 нС | К155ИП3 К155ИП4 |
Сумматор и полусумматор
Раздел:
Логические основы компьютера
Номер темы:
4
Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа.
Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100.
Полусумматор
Теперь не будем обращать внимание на перенос из предыдущего разряда и рассмотрим только, как формируется сумма текущего разряда. Если были даны две единицы или два нуля, то сумма текущего разряда равна 0. Если одно из двух слагаемых равно единице, то сумма равна единицы. Получить такие результаты можно при использовании вентиля ИСКЛЮЧАЮЩЕГО ИЛИ.
Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И.
Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И.

Сумматор
В отличие от полусумматора сумматоручитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа.
Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров.
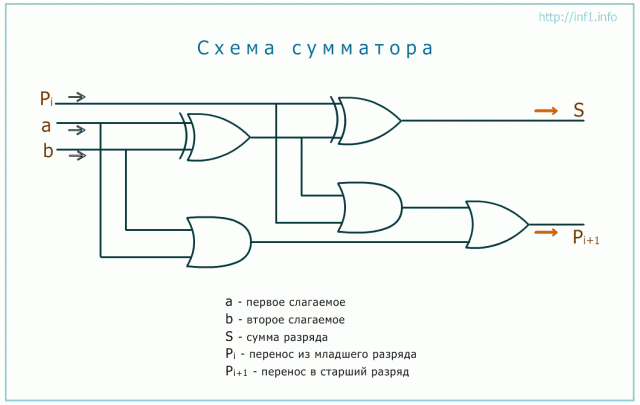
Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определяем сумму текущего разряда. Судя по левой схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0.
Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
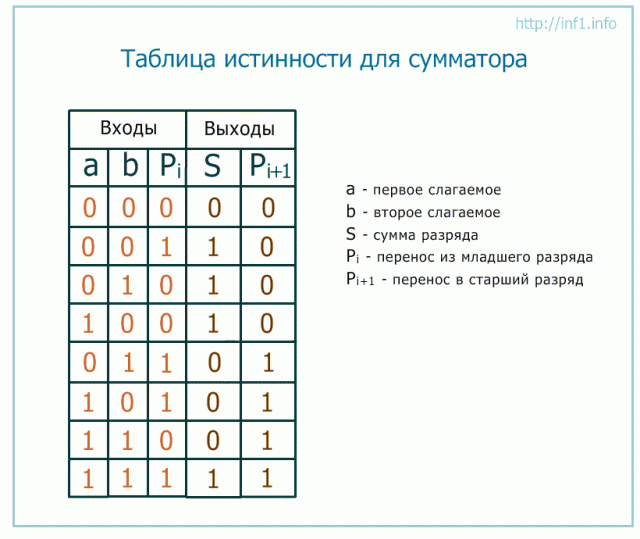
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности.
Изображения, использованные в статье
Сумматор
Схема полусумматора
Таблица истинности для сумматора
Триггер как элемент памяти. Схема rs-триггера
Раздел:
Логические основы компьютера
Номер темы:
5
Память (устройство, предназначенное для хранения данных и команд) является важной частью компьютера. Можно сказать, что она его и определяет: если вычислительное устройство не имеет памяти, то оно уже не компьютер.
Элементарной единицей компьютерной памяти является бит. Поэтому требуется устройство, способное находиться в двух состояниях, т.е. хранить единицу или ноль. Также это устройство должно уметь быстро переключаться из одного состояния в другое под внешним воздействием, что дает возможность изменять информацию. Ну и наконец, устройство должно позволять определять его состояние, т.е. предоставлять во вне информацию о своем состоянии.
Устройством, способным запоминать, хранить и позволяющим считывать информацию, является триггер. Он был изобретен в начале XX века Бонч-Бруевичем.
Разнообразие триггеров весьма велико. Наиболее простой из них так называемый RS-триггер, который собирается из двух вентилей. Обычно используют вентили ИЛИ-НЕ или И-НЕ.
48. Сумматор. Синтез одноразрядного двоичного сумматора. Многоразрядный сумматор.
Одноразрядный двоичный сумматоробеспечивает сложение одноименных разрядов операндов с учетом переноса, поступающего от ближайшего младшего разряда. Сумматор вырабатывает значение соответствующегоразряда суммы (S) и перенос (P), который должен быть учтен в соседнем старшем разряде. Синтез схемы, реализующей функции одноразрядного сумматора, можно выполнить на основании таблицы истинности.

Исходя из реализуемой функции сумматор представляет собой логический узел с двумя выходами (выход суммы S и выход переноса Р) и тремя входами: а — разряд первого операнда; b — разряд второго операнда; р — перенос из младшего разряда. На основании таблицы истинности можно записать логические выражения для формируемых суммы и переноса, которые будут иметь следующий вид:

Полученные функции удобно минимизировать с помощью карты Карно, так как количество переменных невелико. Карты Карно с представленными в них функциями S и P приведены на рис. 1.7.
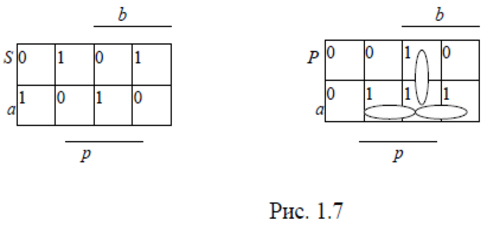
На основании представления функции S на карте можно заключить, что логическое выражение для этой функции не минимизируется.
Минимизированная функция переноса с учетов введенных контуров имеет вид:

Ввиду того что функции P и S формируются в одном и том же узле, при формировании S целесообразно использовать средства, примененные для реализации функции Р. С этой целью рассмотрим функцию Р как переменную для функции S. Тогда модифицированная функция S, зависящая теперь от четырех переменных a, b, p, P, будет записываться в карту Карно как функция четырех переменных.
Многоразрядный двоичный сумматорстроится на основе одноразрядных сумматоров с введением соответствующих связей между разрядами. На рис. 1.11 приведена простейшая схема такого сумматора. На схеме показана только часть сумматора, относящаяся к некоторому i-му разряду и его соседям: (i + 1)-й соседний младший разряд и (i — 1)-й соседний старший разряд.
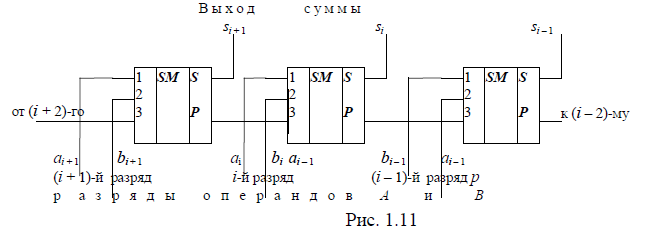
Приведенная схема многоразрядного сумматора называется схемой сумматора с последовательным переносом. Схема очень простая.Сумматор обладает малым быстродействиемиз-за последовательного учета переноса, возникшего в младшем разряде, в непрерывной цепочке старших разрядов, имеющих значение поразрядной суммы, равное единице. Такие разряды называются разрядами, пропускающими перенос. В худшем случае перенос, возникший в младшем разряде, распространяется до самого старшего разряда формируемой суммы.
49.Программируемые логические матрицы.
Программируемая логическая матрица (ПЛМ) — комбинационный зел, обеспечивающий формирование нескольких функциональных зависимостей на основе заданных переменных.
В состав ПЛМ входят дизъюктивная (ДМ) и конъюктивная (КМ) матрицы.
КМ — формирует множество неповторяющихся конъюкций, используемых во всех формируемых логических функциях.
ДМ — для каждой выходной функции формирующие логическое сложение.

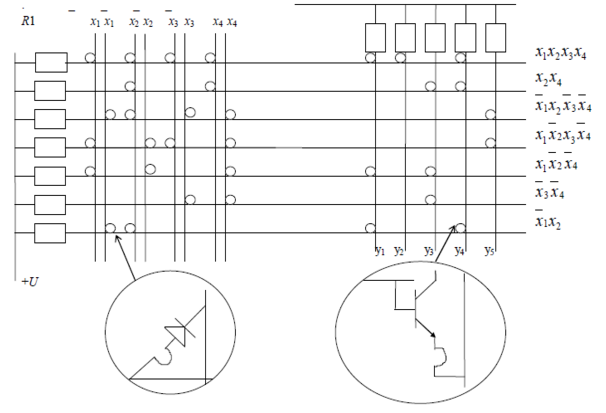
Программирование ПЛМ выполняется следующим образом. При производстве одним из методов интегральной технологии создается заготовка ПЛМ, в которой на пересечениях горизонтальных и вертикальных шин дизъюнктивной матрицы имеет место диодная цепочка, а на пересечениях горизонтальных и вертикальных шин конъюнктивной матрицы располагается транзисторная цепочка. Пользователь в зависимости от логики, которую он собирается реализовать, удаляет перемычки в «ненужных» цепочках. Удаление перемычки осуществляется посредством пропускания по соответствующей горизонтальной и вертикальной шинам мощного тока, который разогревает и испаряет соответствующую легкоплавкую перемычку.
Сумматоры. Одноразрядный полный комбинационный сумматор. Построение полного сумматора из полусумматоров.
Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов.
Построение полного сумматора из полусумматора
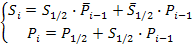
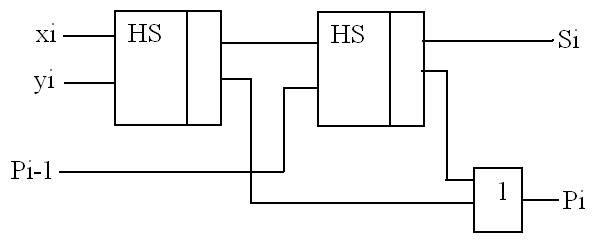
Комбинационный сумматор — это некоторое логическое устройство, обеспечивающее получение сигналов суммы и переноса при одновременной подаче кодов исходных слов.
Если говорить о сумматоре комбинационного типа: у нас имеется некоторая схема КС.
На её входы одновременно приходят данные: первый операнд X и второй операнд Y.
Отличительная особенность комбинационной схемы сумматора — одновременная подача первого и второго слагаемых.
Полный комбинационный сумматор
УГО:
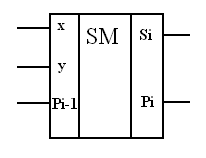
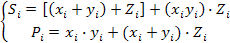
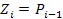
S = 1 слагаемое + 2 слагаемое + перенос из предыдущего разряда
Таблица истинности:
xi | yi |
| si | Pi | |
0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 | 0 |
2 | 0 | 1 | 0 | 1 | 0 |
3 | 0 | 1 | 1 | 0 | 1 |
4 | 1 | 0 | 0 | 1 | 0 |
5 | 1 | 0 | 1 | 0 | 1 |
6 | 1 | 1 | 0 | 0 | 1 |
7 | 1 | 1 | 1 | 1 | 1 |
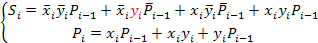
Полный комбинационный сумматор:
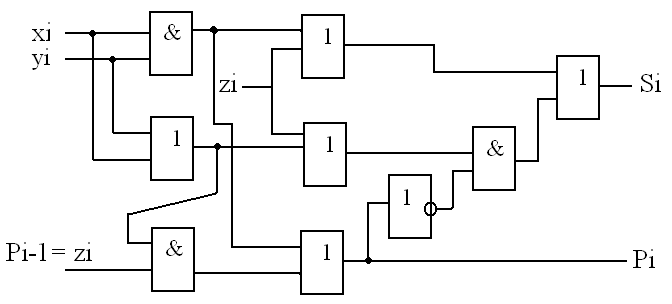
Сумматоры. Одноразрядный последовательностный сумматор.
Последовательностные схемы – логические схемы с запоминанием переменных (элементы с памятью) — схемы, выходные сигналы к-рых зависят не только от значения входных сигналов в данный момент времени, но и от последовательности значений входных сигналов в предшествующие моменты времени. Последовательностные схемы собираются из комбинационных путём введения в них обратных связей.
Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов.
Сумма двух двоичных чисел с числом разрядов N может иметь число разрядов (N + 1). Этот дополнительный (старший) разряд называется выходом переноса.
Сумматоры
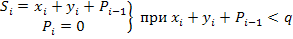
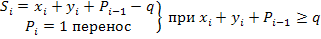
xi– первое слагаемое yi – второе слагаемое Pi-1 – перенос и предыдущего разряда
Si – разряд сумм q – основание системы счисления Pi – перенос в следующий разряд
Сложение и сдвиг – 2 операции, которыми можно заменить все остальные.
Сумматор на схеме с памятью:
Одноразрядный сумматор накапливающего типа (последовательностный сумматор):
Это сумматор с аккумулированием результата
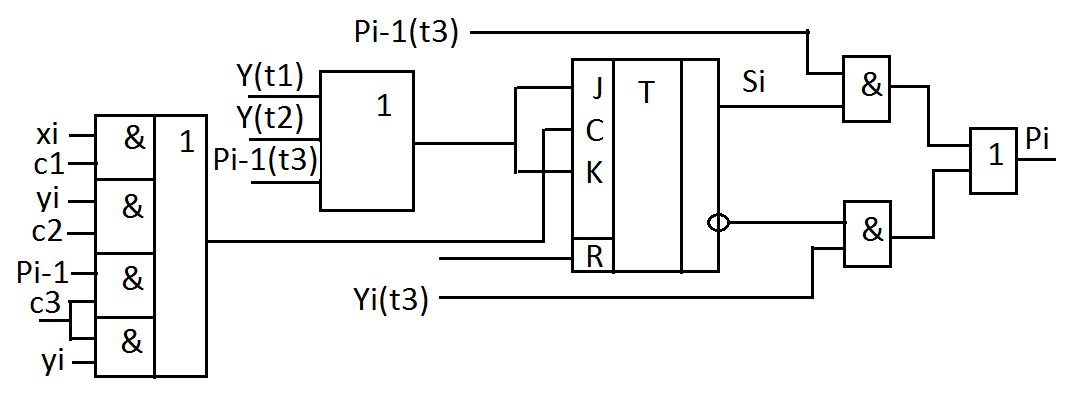
Временная диаграмма:
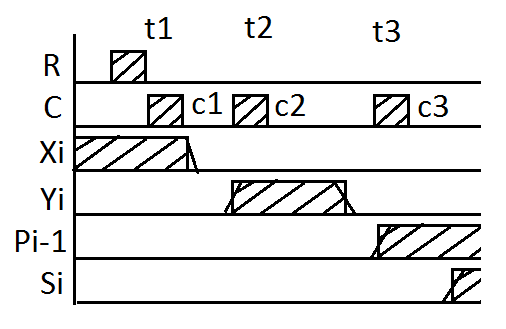
Многоразрядные сумматоры. Накапливающий сумматор.
Если говорить о сумматоре накапливающего типа, передача слагаемых на вход происходит последовательно (а не одновременно).
Сумматор накапливающего типа — это схема с памятью. Сначала задаётся в какой-то момент времени t1 первое слагаемое X; оно запоминается в памяти сумматора. Затем, в момент времени t2 подаётся второе слагаемое Y. Через некоторое время t-задержки на выходе сумматора возникает S и сигнал переноса P.
В обычном сумматоре накапливающего типа используются триггерные схемы.
Кстати говоря, из сумматора комбинационного очень легко получается сумматор накапливающего типа: если выход сумматора комбинационного типа нагрузить на какой-нибудь регистр.
Вначале происходит обнуление этого регистра. Тогда вы можете в первый момент времени подать первое слагаемое и запомнить результат в регистре хранения. А затем, в момент времени t2 за счёт обратной связи, на второй вход комбинационного сумматора подаётся предыдущее слагаемое.
Такая комбинация — регистра хранения и комбинационного сумматора – позволяет реализовать сумматор накапливающего типа.
Схема многоразрядного последовательного сумматора:
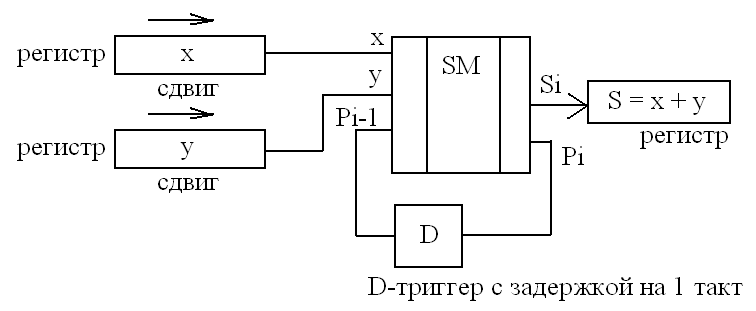
Последовательные сумматоры преобразуют последовательные коды слагаемых в последовательный код суммы этих слагаемых. Сложение начинается с младшего разряда и выполняется поразрядно последовательно за столько тактов, сколько разрядов содержится в числе. В состав многоразрядного сумматора последовательного действия, кроме комбинационного одноразрядного сумматора, применяют три сдвигающих регистра для двух слагаемых x и y и для результата S, триггер переноса D и схемы управления вводов и выводов чисел.
Два
суммируемых числа загружаются в регистры
x
и y
по последовательным и параллельным
входам. Триггер переноса первоначально
установлен в 0, следовательно C=0.
сигнал суммы записывается в регистр
сдвига S.
Каждый сигнал переноса, вырабатываемый
сумматором, появляется на выходе P и запоминается триггером переноса.
Тактовый импульс вводит бит суммы в
регистр S и одновременно сдвигает на один разряд
регистры x
и y.
Кроме того, он вносит значение переноса P и D,
в результате чего на входе С всегда действует значение разряда
переноса, имевшее место при сложении
двух предыдущих разрядов. Так суммируются
все разряды двоичных чисел и результат
записывается в регистр S.
Этот результат можно считать по
параллельным или последовательным
выходам. Основное достоинство такого
сумматора – малое количество оборудования;
к недостаткам относится малое
быстродействие, т.к. время суммирования
двух n-разрядных
чисел 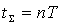 ,
где T
– период следования тактовых импульсов.
,
где T
– период следования тактовых импульсов.
Накапливающий сумматор:
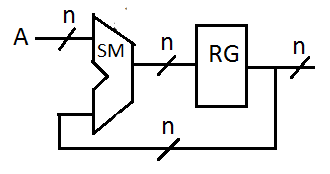
Требования:
Хранение
Парал. прием
CLR-вход