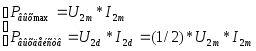16.Однокаскадный усилитель на биполярном транзисторе с общим эмиттером: принцип действия

Типичная схема усилительного каскада на транзисторе с ОЭ показана на рис.3.4,а.

Входное усиливаемое переменное напряжение Uвх подводится ко входу усилителя через разделительный конденсатор С1. Конденсатор С1 препятствует передаче постоянной составляющей напряжения входного сигнала на вход усилителя, которая может вызвать нарушение режима работы по постоянному току транзистора VT. Усиленное переменное напряжение, выделяемое на коллекторе транзистора VT, подводится к внешней нагрузке с сопротивлением Rн через разделительный конденсатор С2. Этот конденсатор служит для разделения выходной коллекторной цепи от внешней нагрузки по постоянной составляющей коллекторного тока Iкр

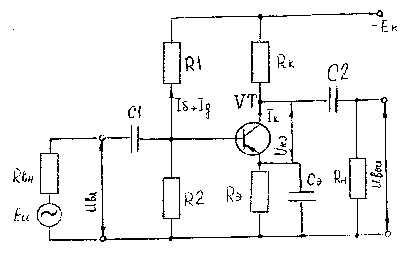
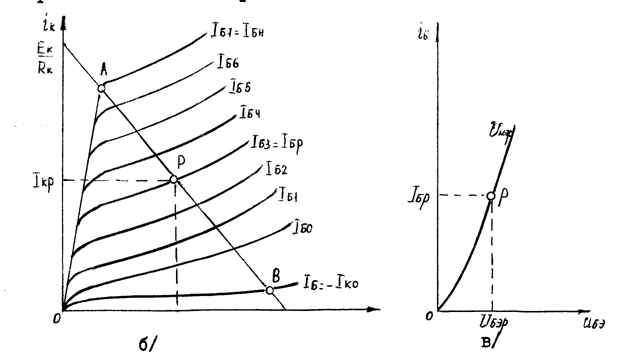
Рис. 3.4

Значения Iкр и других постоянных составляющих тока и напряжения в цепях транзистора зависят от режима его работы ( начального положения рабочей точки ).

Рабочей точкой транзистора называют точку пересечения динамической характеристики (нагрузочной прямой) с одной из статических вольт-амперных характеристик. Режим работы транзистора определяется начальным положением рабочей точки (при отсутствии входного переменного сигнала). Это положение определяется на характеристиках совокупностью постоянных составляющих токов и напряжений в выходной IКр, UКЭр и входной IБр, UБЭр цепях (рис. 3.4, б, в).

При работе транзистора в активном (усилительном) режиме (класса А) рабочая точка должна находиться примерно посередине отрезка АВ нагрузочной прямой. Предельные изменения входного тока базы должны быть такими, чтобы рабочая точка не выходила за пределы отрезка АВ.

Начальное положение рабочей точки обеспечивается делителем напряжения, состоящим из резисторов R1 и R2, значения сопротивлений которых определяются из соотношений:

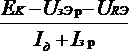
R1 = ;

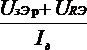
R2 = .

где Iд = (2…5)IБр — ток в цепи делителя.

При обеспечении режима работы транзистора необходимо осуществить температурную стабилизацию положения рабочей точки (уменьшить влияние температуры на начальное положение рабочей точки). C этой целью в эмиттерную цепь введен резистор Rэ, на котором создается напряжение ООС по постоянному току URэ.

Для устранения ООС по переменному току (при наличии входного переменного сигнала) резистор Rэ шунтируют конденсатором Сэ, сопротивление которого на частоте усиливаемого сигнала должно быть незначительным.

17.Многокаскадный усилитель

В большинстве случаев одиночные каскады не обеспечивают необходимое усиление и заданные параметры усилителей. Поэтому усилители, которые применяют в аппаратуре связи и измерительной технике, многокаскадные. При анализе и расчете многокаскадного усилителя необходимо определить общий коэффициент усиления усилителя, искажения, вносимые им, распределять их по каскадам, определить требование к источникам, решить вопросы введения обратных связей и т.д.

2. КОЭФФИЦИЕНТ УСИЛЕНИЯ МНОГОКАСКАДНОГО УСИЛИТЕЛЯ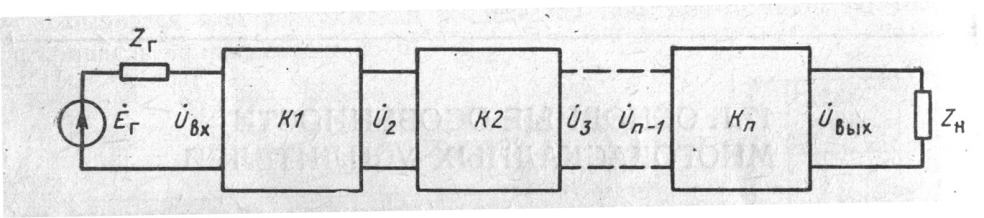

рис.1

Коэффициент усиления усилителя можно определить, исходя из структурной схемы (рис.1):

Кобщ = Uвых/Uвх = (Uвых/Un-1) … (U₃/U₂)(U₂/Uвх)=KnKn-1…K₂K₁ или

Kобщ = K₁K₂…Kn e^{f(1+2+…+n)}

где K₁,…, Kn – коэффициенты усиления каскадов, 1,…, n – фазовые сдвиги, вносимые каждым усилительным каскадом.

Таким образом, для многокаскадного усилителя общий коэффициент усиления равен произведению коэффициентов усиления каждого каскада. Суммарный фазовый сдвиг, вносимый усилителем, равен сумме фазовых сдвигов каждого каскада. Сквозной коэффициент усиления

Kобщ = k_вхKобщ

где k_вх=Zвх/(Zг + Zвх) – коэффициент передачи входной цепи. Если коэффициент усиления отдельных каскадов выразить в логарифмических единицах, то общий коэффициент усиления многокаскадного усилителя будет равен сумме коэффициентов

K_общ[дб] = K_1[дб] + … + K_n[дб]

В аппаратуре связи для компенсации потери мощности на отдельных участках (затухания) необходимо, чтобы усилитель работал на согласованную нагрузку, т.е. его входное сопротивление должно быть равно сопротивлению источника (выходного сопротивления предыдущего тракта аппаратуры или линии), а выходное сопротивление должно равняться сопротивлению нагрузки. Для согласования усилителей по входу и выходу используют уси­лители с обратной связью и согласующие трансформаторы. Отклонение от согласования в рабочей полосе частот оценивается коэф­фициентом отражения

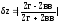
При использовании согласующих трансформаторов пересчитанное сопротивление нагрузки в первичную обмотку R’₁=R_нn², где п— коэффициент трансформатора, т. е. отношение витков первичной обмотки к вторичной (рис. 2,а).

На рис.2,а имеем: U₂=U₁/n; I₂=I₁n₂, тогда Rн=U₂/I₂ = (U₁/I₁)n²

или R’₁ = U₁/I₁=R_нn²=Rг. Отсюда с учетом потерь в трансформаторе коэффициент трансформации: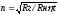

где n_t – КПД трансформатора.

Применение входного и выходного трансформаторов позволяет достаточно просто осуществить переход с симметричной схемы на несимметричную (рис.2, б).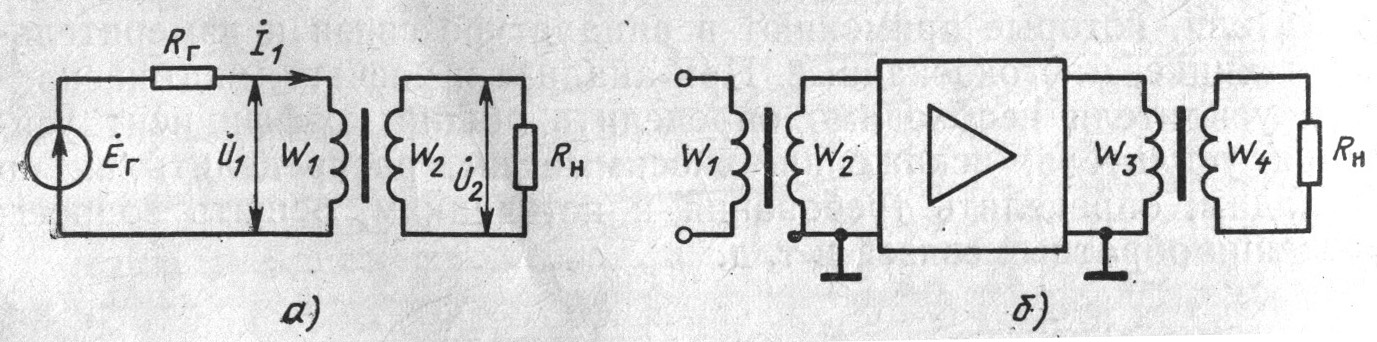

Классы усилительных каскадов

Рабочая точка покоя определяет режим работы каскада или класс усиления. В зависимости от положения рабочей точки различают три класса усиления:

1. класс А – рабочая точка лежит в середине линейного участка передаточной характеристики. Для него характерны минимальные нелинейные и непрерывные проникновения тока через транзистор, вследствие чего КПД класса «А» составляет 20 – 30%. Он применяется в предв. каскадах усиления, т.е там где высоки требования к нелинейным искажениям и мала мощность.

2. класс В – точка покоя лежит в начале линейного участка. Он обладает высоким КПД 60 – 70%, вследствие отсутствия постоянной составляющей, т.е при отсутствии входного сигнала каскад не потребляет энергии. Этот класс каскада применяется оконч. выходных каскадах усилителей мощности.

3. класс С – точка покоя лежит ниже линейного участка, КПД ещё выше – 80%

Применяется в оконеч. каскадах большой мощности на избирательную нагрузку.

Усилители мощности.

Это обычно выходные каскады много каскадных усилителей. Они предназначены для увеличения нагрузочной способности и создания нагрузки сигнала заданной мощности. Такие усилители работают в режиме большого сигнала. Их основными параметрами являются:

1. Величины выходной мощности Р_вых=

2. КПД= (Р_{вых действ}/Р

   0)*100%

3. КНИ

Классификация усилителей мощности.

1. В зависимости от РТ класса А, АВ, В, С, Д.

2. В зависимости от связи между каскадами.

а) с трансформаторной связью

б) с без трансформаторной связью

3. В зависимости от схемы технического решения

а) однотактные

б)двухтактные

2.7 Усилитель на биполярном транзисторе с емкостной связью

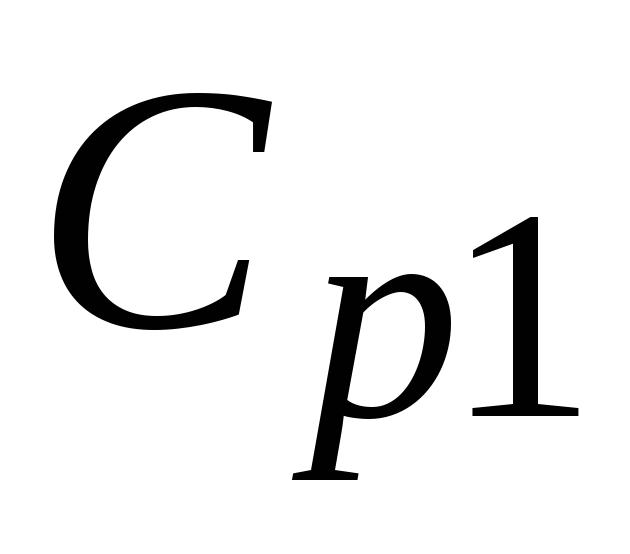Широкое применение нашли усилители с емкостной связью (рисунок 2.16) в которых на входе и выходе устанавливаются разделительные конденсаторы и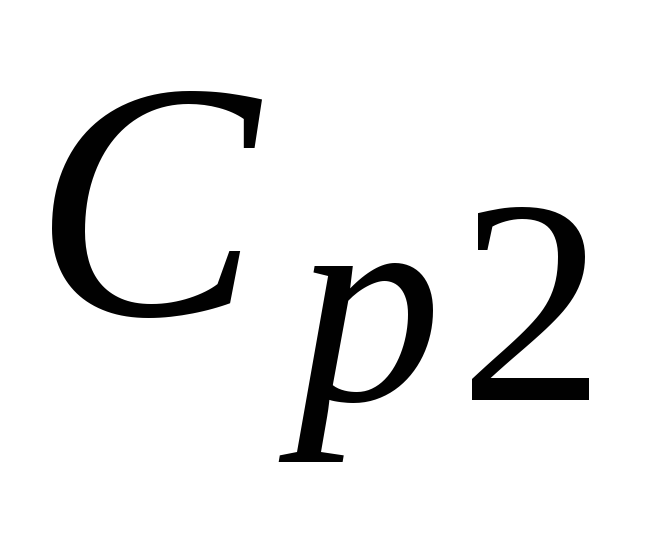. За счет них исключается влияние источника входного сигнала и нагрузки на режим работы по постоянному току. Конденсаторы выбираются настолько большой емкости, чтобы они не оказывали влияние на переменные составляющие токов.

Рисунок 2.16 — Усилитель с емкостной связью на биполярном транзисторе

Рассмотрим назначение других элементов.

Резисторы и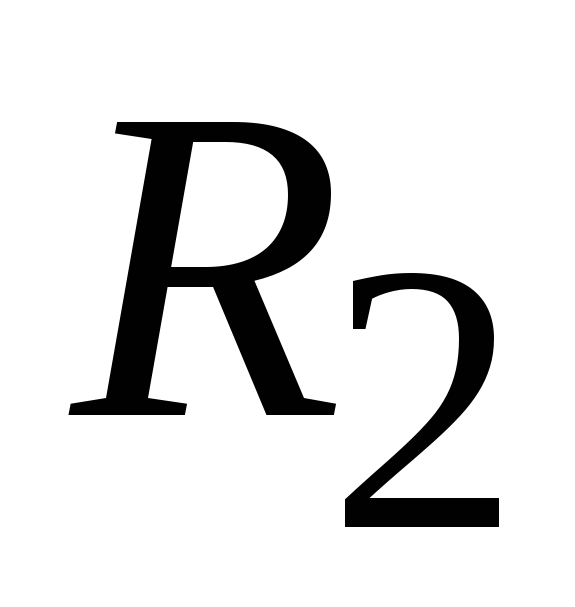образуют делитель напряжения и служат для задания режима покоя, т.е. создают напряжение смещения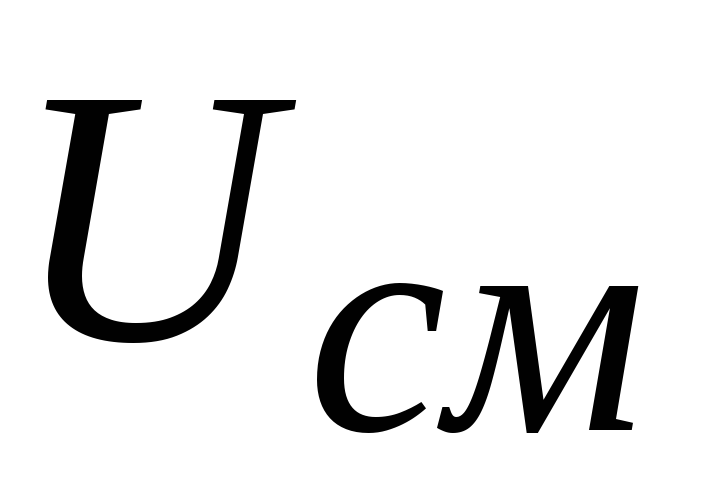, которое и определяет ток базы покоя.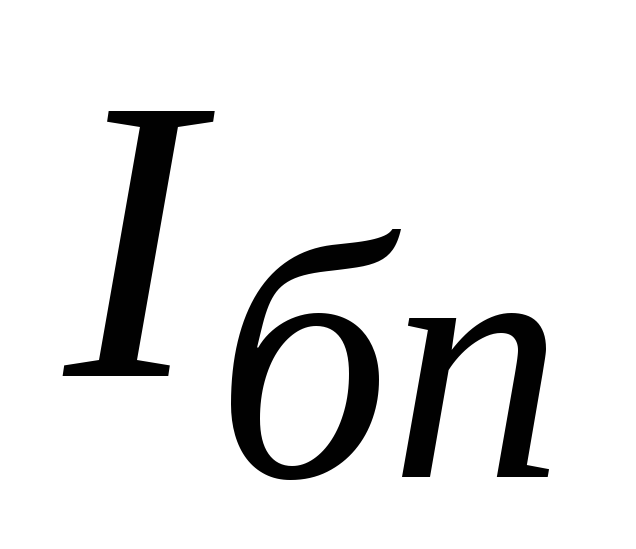

Резистор 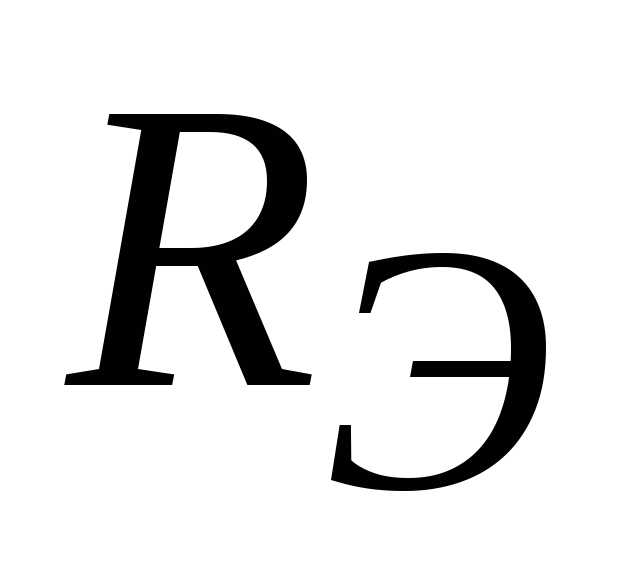служит для стабилизации положения точки покоя за счет отрицательной обратной связи по постоянному току. Параметры режима покоя сильно зависят от температуры, это в основном проявляется в прямой зависимости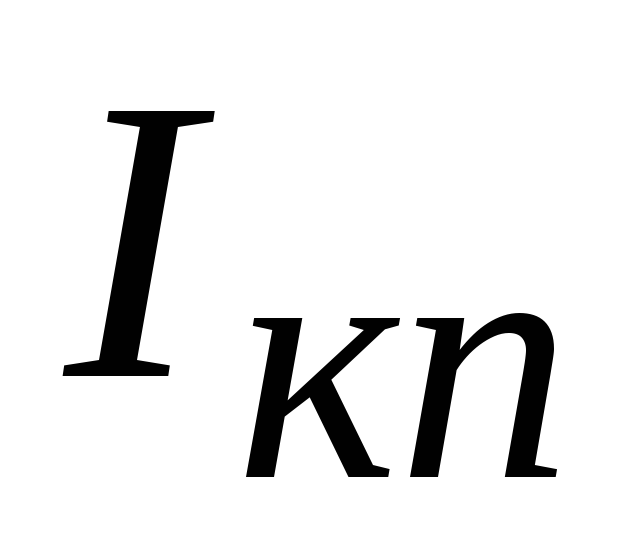от температуры. Основными причинами такой зависимости являются изменения от температуры сквозного начального тока коллектора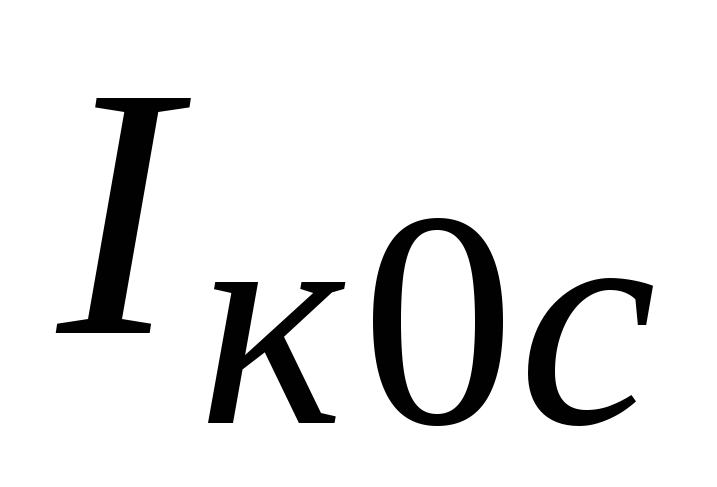, напряжения на эмиттерном переходе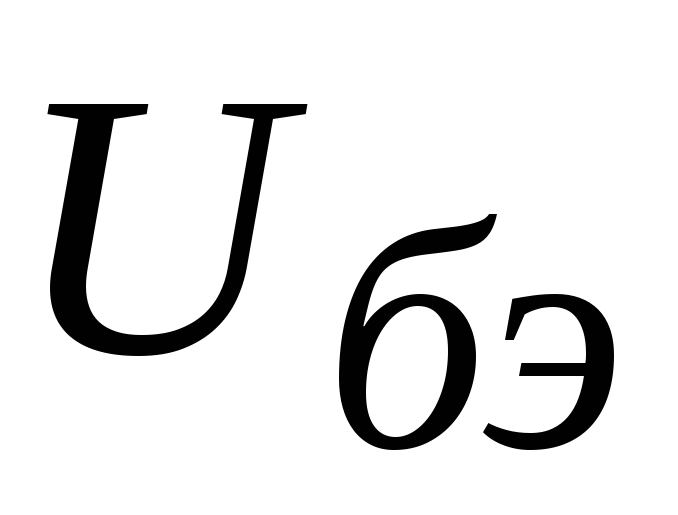и коэффициента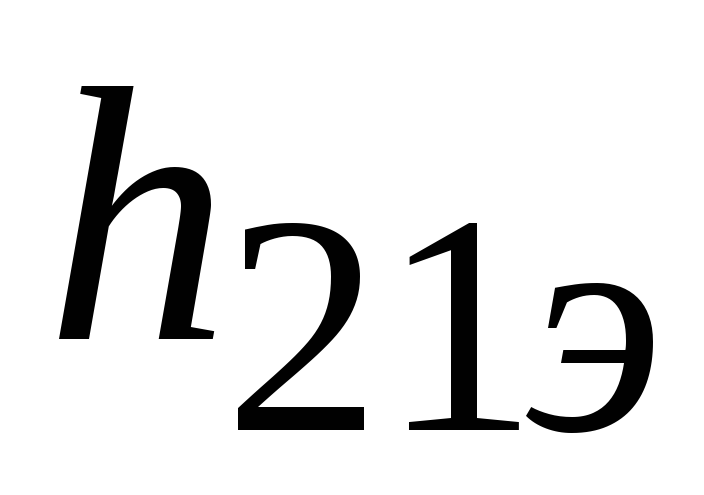. При отсутствии мер по стабилизации тока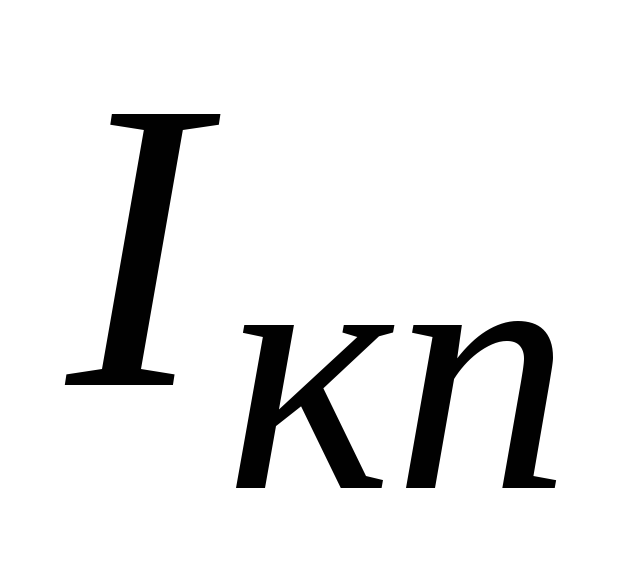, его температурные изменения могут привести к перемещению точки покоя настолько, что при заданной амплитуде входного сигнала колебания рабочей точки может выходить за приделы рабочего участка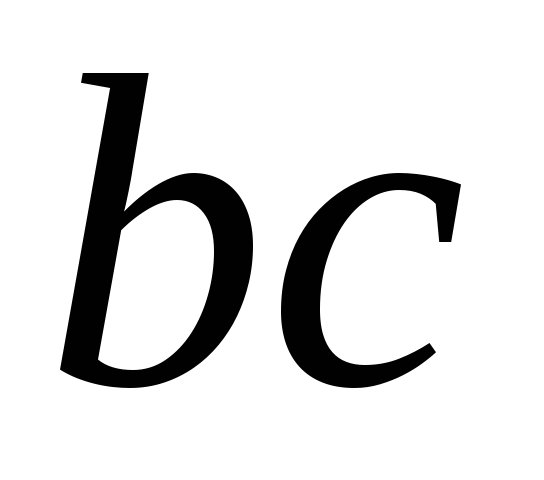(рис.17). Это может привести к искажению формы кривой выходного сигнала. Стабилизирующее влияние обратной связи можно показать, рассмотрев ее влияние на ток покоя базы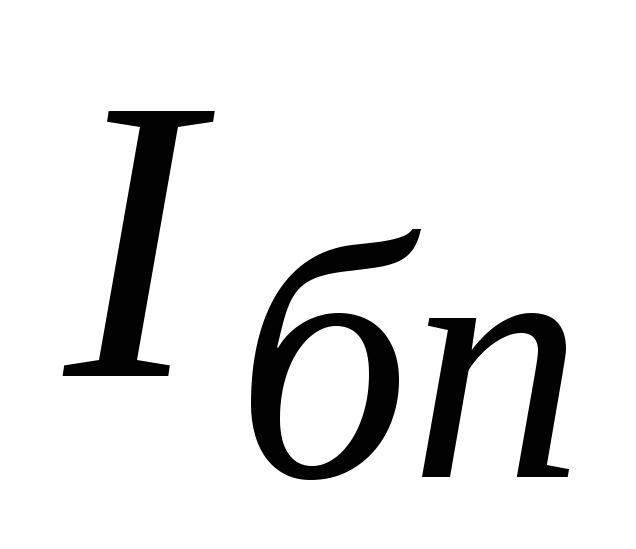, который определяется из схемы (рисунок 2.17,а).

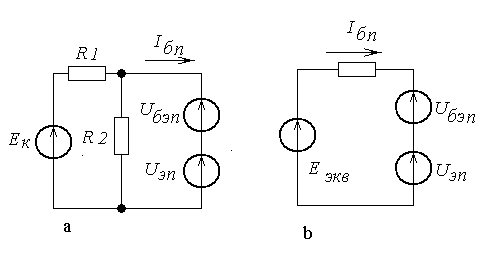
Рисунок 2.17 -. К расчету тока базы покоя

В этой схеме 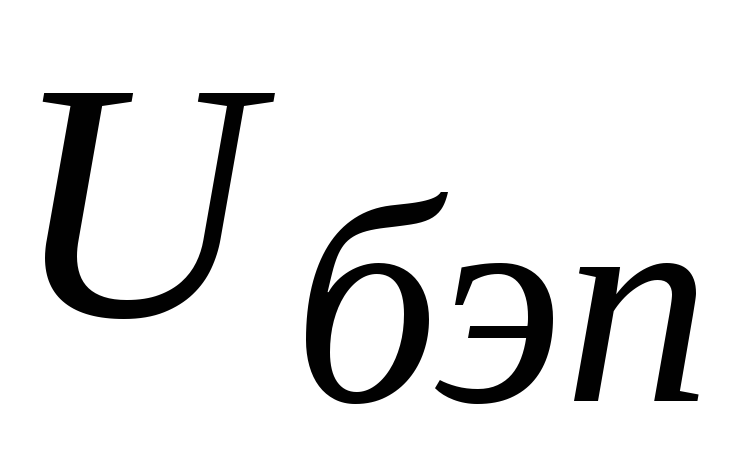— напряжение покоя на эмиттерном переходе,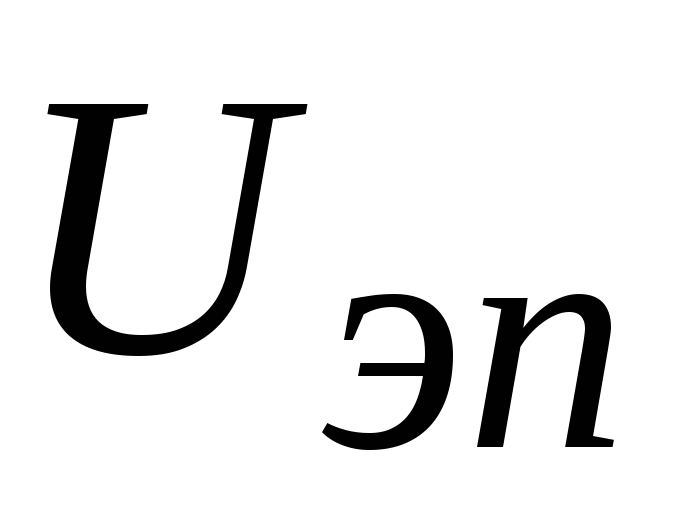— напряжение покоя на резисторе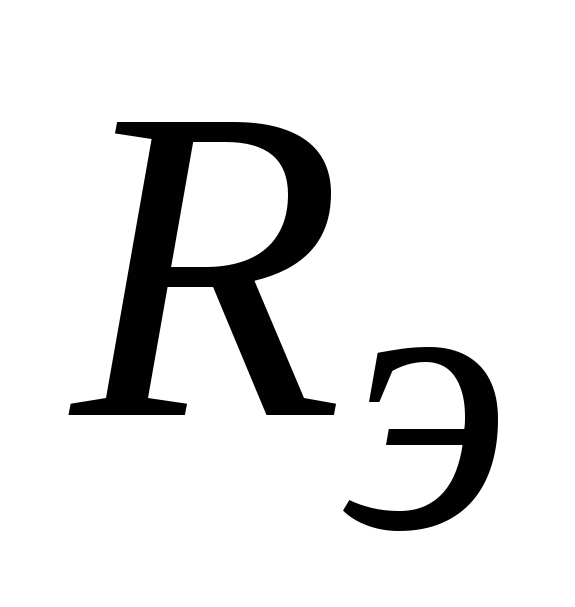

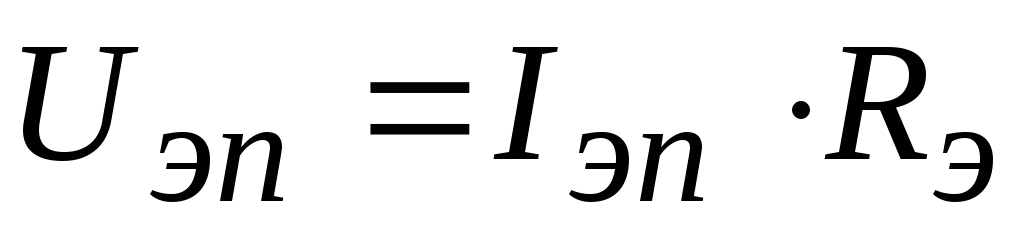. (2.30)

Для удобства определения 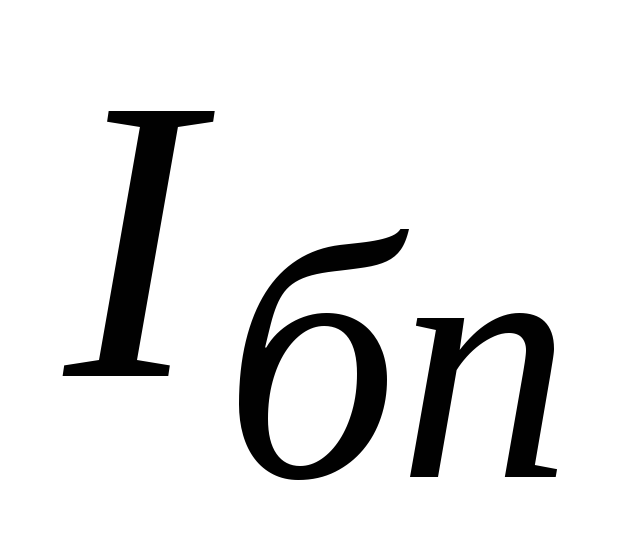, используя понятия об эквивалентном генераторе, заменим исходную схему (рисунок 2.17,а) эквивалентной (рисунок 2.17,b), из которой найдем

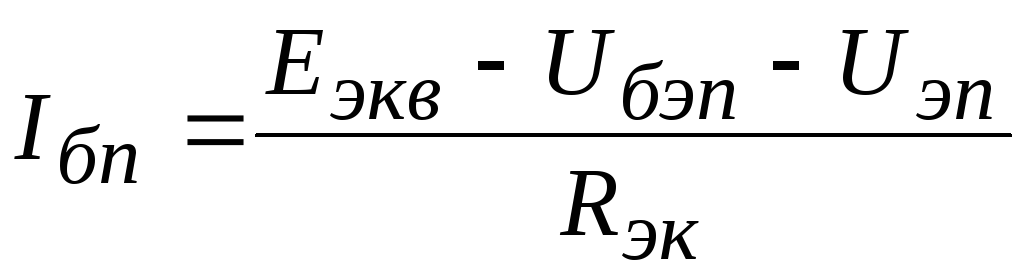, (231)

где ;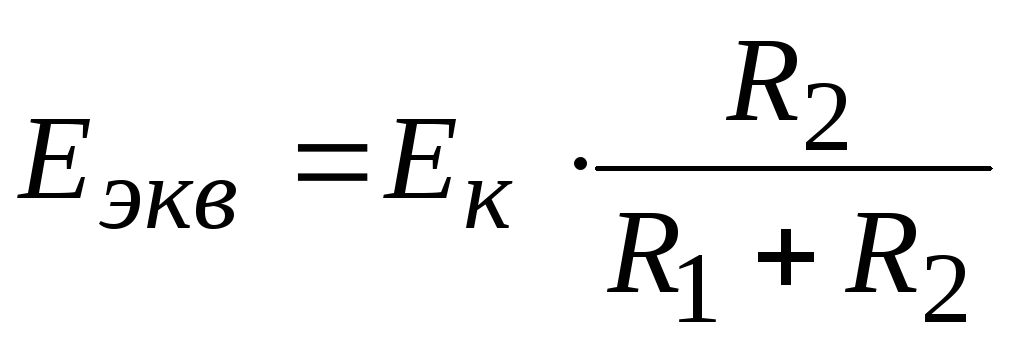

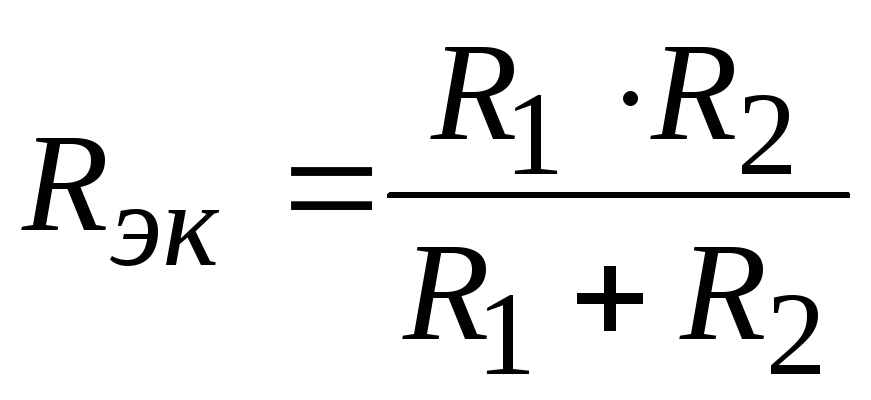. (2.32)

Предположим, что под влиянием температуры ток 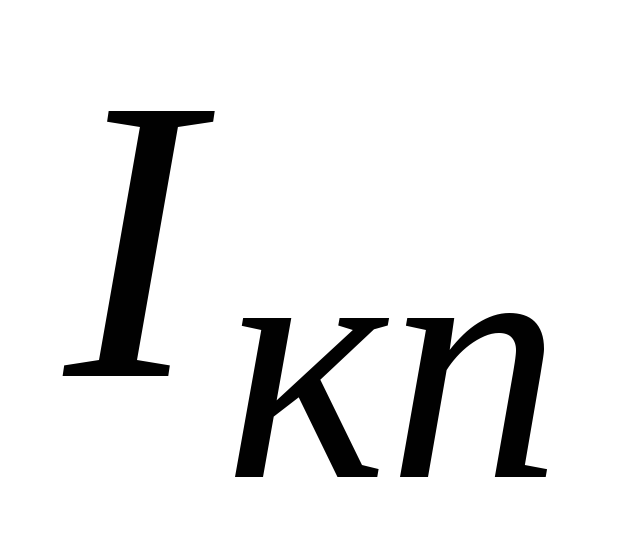увеличится, точка покоя переместится вверх по нагрузочной прямой. Это приводит к увеличению тока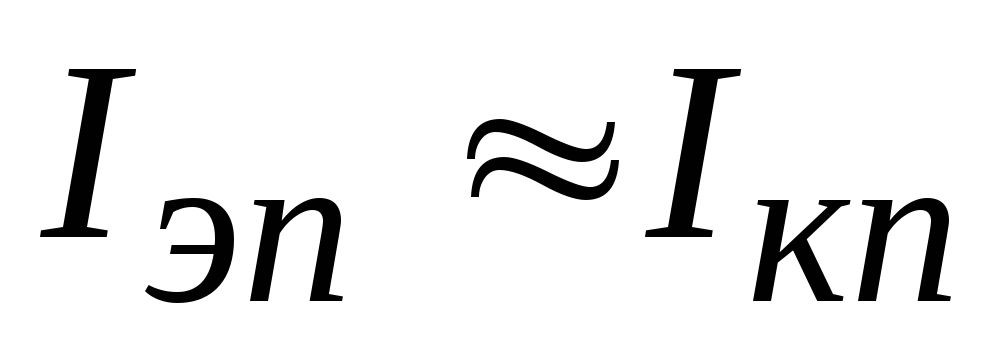и ,соответственно, к уменьшению базового тока, и точка покоя переместится вниз в состояние, близкое к исходному. Отрицательная обратная связь по постоянному току стремится поддержать ток покоя коллектора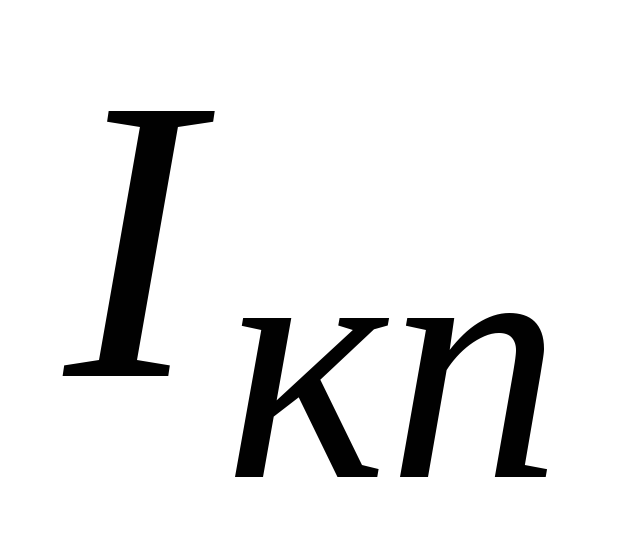на неизменном уровне, а, следовательно, стабилизирует положение рабочей точки.

Конденсатор шунтирует (уменьшает сопротивление) по переменному току, уменьшая тем самым проявление отрицательной обратной связи по переменной составляющей. Отсутствие конденсатора привело бы к уменьшению коэффициента усиления схемы.

Эквивалентная схема усилителя с учетом всех элементов имеет вид показанный на рисунке 2.18.

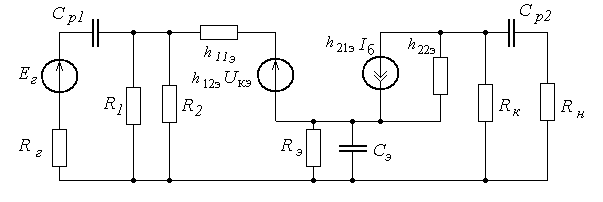
Рисунок 2.18 -. Эквивалентная схема усилителя с емкостной связью

Эту схему легко упростить, если принять во внимание следующие соотношения:

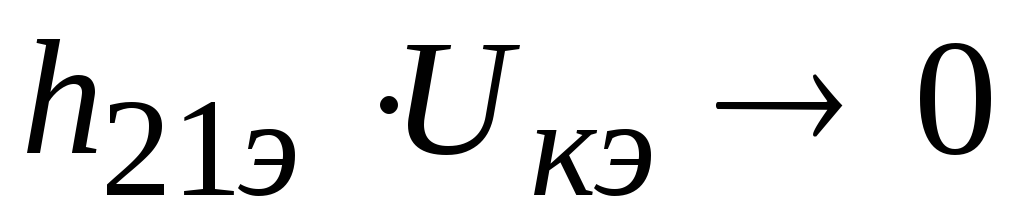, (2.33)

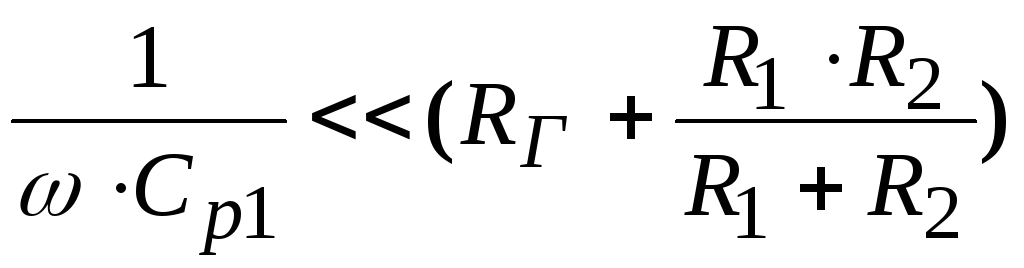, (2.34)

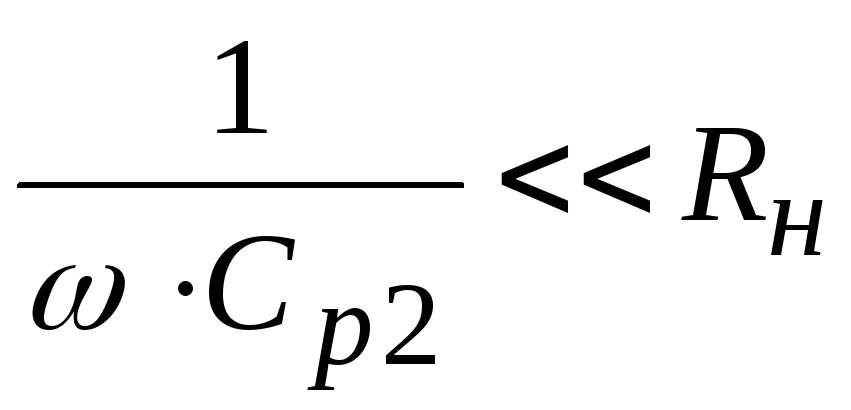, (2.35)

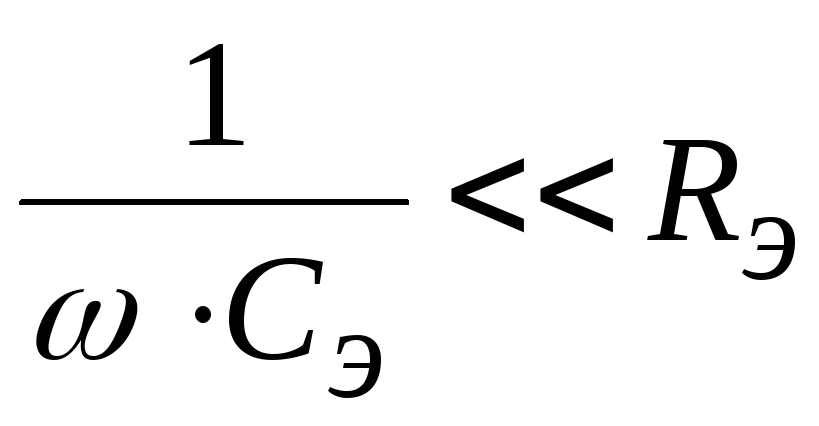, (2.36)

т.е. все конденсаторы выбираются настолько большими, что их сопротивлениями на самой низкой рабочей частоте можно пренебречь по сравнению с сопротивлениями резисторов подключенных к ним.

Упрощенная эквивалентная схема будет иметь вид показанный на рисунке 2.19.

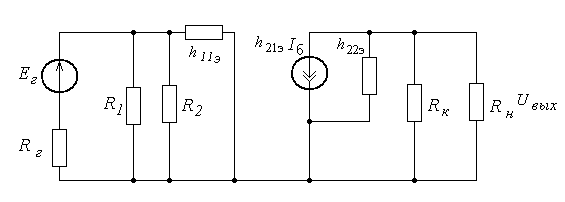
Рисунок 2.19 -. Упрощенная эквивалентная схема усилителя с емкостной связью

Анализируя эту эквивалентную схему, можно определить основные параметры усилителя:

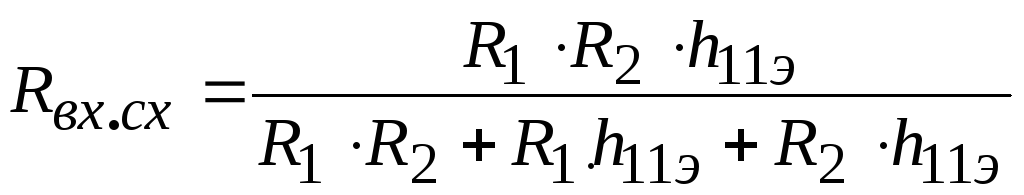, (2.37)_

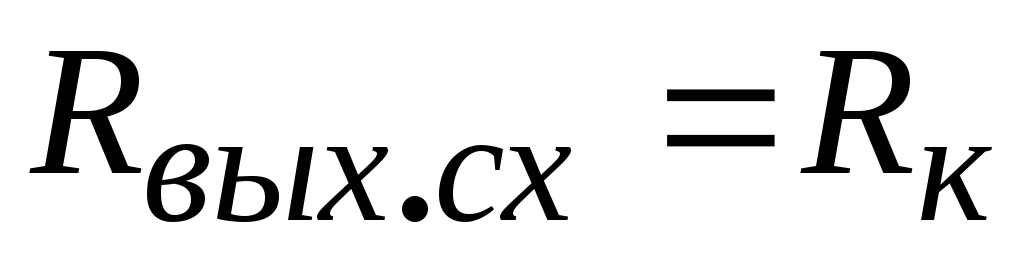, (2.38)

, (2.39)

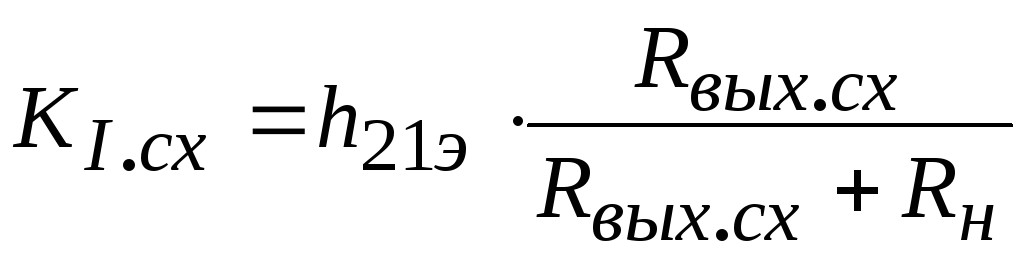. (2.40)

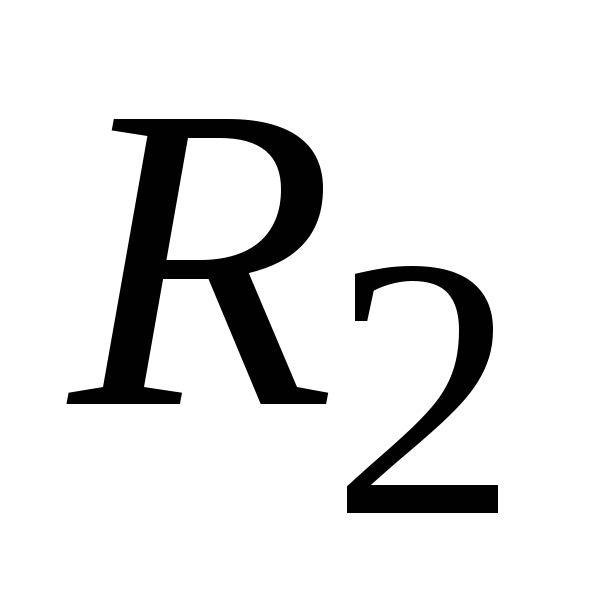с учетом сопротивлений делителя и, сопротивления источника усиливаемого сигнала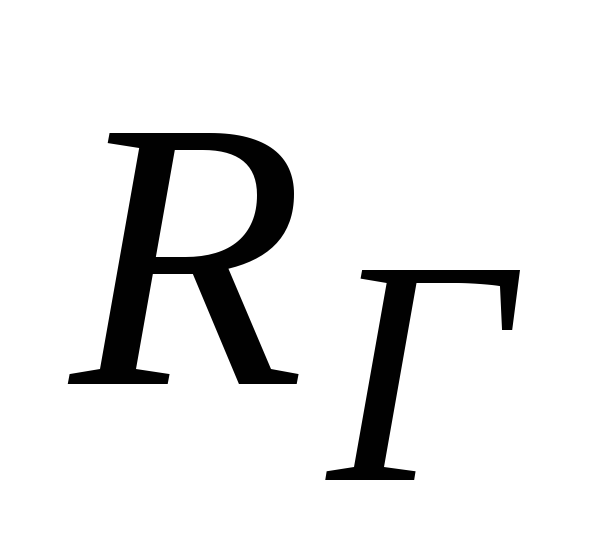и сопротивления нагрузки.

Лабораторная работа №4 Исследование резистивного усилительного каскада с общим эмиттером на биполярном транзисторе

Цель работы: Ознакомление с методом получения воль-амперных характеристик, изучение характеристик и параметров усилительного каскада низкой частоты на биполярном транзисторе включенного по схеме с общим эмиттером:

Продолжительность работы – 2 часа.

Теоретическая часть

Прежде чем приступить к лабораторным исследованиям проработайте лекционный материал, а затем прочитайте в учебнике [1] (В.И.Лачин, Н.С.Савёлов Электроника раздел 2.1. Классификации, основные параметры и характеристики усилителя) или в учебнике [2] (О.В. Миловзоров, И.Г. Панков Электроника §2.1. Усилители). Непонятные места, а также вопросы, вызывающие сомнения, запишите в лабораторную тетрадь, обсудите с товарищами и преподавателем.

Усилителем электрических сигналов называется устройство, у которого мощность электрических сигналов на выходе больше чем на входе.

На структурных схемах усилитель изображают в виде прямоугольника, как показано на рисунке 1.

Рисунок 1 — Условное графическое обозначение усилителя на структурных схемах

Основными параметрами, определяющими работу усилителя, являются три коэффициента:

• коэффициент усиления по напряжению – Кu,

• коэффициент усиления по току – КI

• коэффициент усиления по мощности – КP:

, ,,

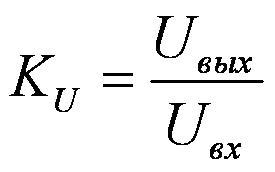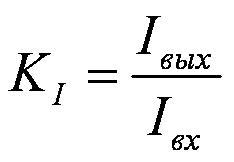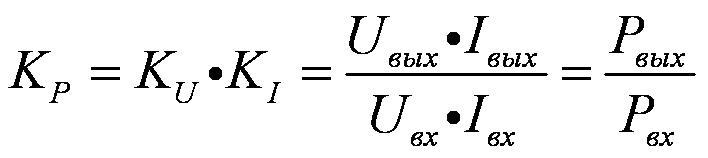а также входное R_ВХ­ и выходное R_ВЫХ сопротивления.

При использовании биполярных транзисторов различают:

• усилитель с общим эмиттером (ОЭ),

• усилитель с общей базой (ОБ),

• усилитель с общим коллектором (ОК).

На рисунке 2 представлена структурная схема усилителя в виде схемы замещения, на которой внутренний источник напряжения Е_вых = К·U_вх получает энергию от источника питания. R_вх — входное сопротивление усилителя, а R_вых — выходное сопротивление усилителя.

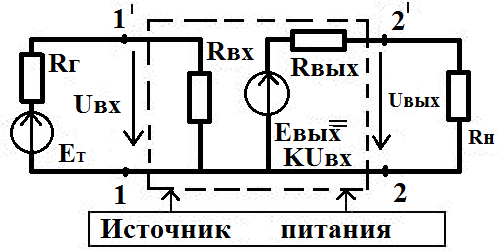
Рисунок 2 — Эквивалентная схема каскада с общим эмиттером

К входу усилителя (зажимы 1¹-1) подключен источник сигнала с действующим значением ЭДС Er и внутренним сопротивлением Rr. Он создает на выходе усилителя напряжение Uвых. К выходу усилителя (зажимы 2¹-2) подключена нагрузка с сопротивлением Rн.

Обычно усилитель представляет собой многокаскадное устройство, состоящее из ряда последовательно соединенных простейших каскадов. Схема с общим эмиттером, представляющая каскад с RC связями приведена на рисунке 3.

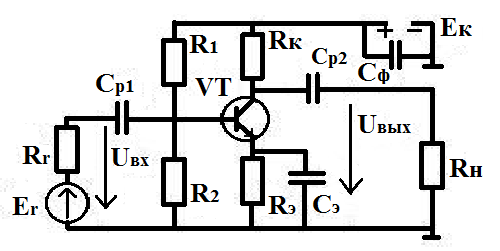
Рисунок 3 — Схема каскада с общим эмиттером

Эмиттер транзистора соединен с общей точкой усилителя. Источник питания E_Кчерез делительR1-R2 подает на базу биполярного транзистора VT n-p-n типа напряжение смещения 0,5…0,8В. Входным является ток базы I_б, который управляет током коллектора по формуле I_к=h_Э21·I_б. Параметрh_Э21называется коэффициентом передачи по току в схеме с общим эмиттером. При этом на коллекторе транзистора создается усиленное переменное напряжение U_кэ = E_К— I_к·R_к, которое, далее, через разделительный конденсатор C_р2 передается на нагрузочное сопротивление R_н. РезисторRк ограничивает ток коллектора.

Резисторы R1, R2 обеспечивают необходимый режим транзистора по постоянному току (начальное положение рабочей точки). Правильный выбор этой точки влияет на коэффициент нелинейных искажений и на коэффициент полезного действия. Это поясняют графики входной характеристики биполярного транзистора и семейства выходных характеристик, показанные на рисунке 4.

Входная характеристика транзистора (на рисунке 4 слева) показывает зависимость тока базы I_Бот входного напряженияU_БЭмежду базой и эмиттером. Базовыйp-nпереход у кремниевого транзистора начинает открываться при напряжении примерно 0,6 вольта, поэтому при меньшем напряжении транзистор закрыт и находится в состоянии отсечки. При напряжении большем 0,6 вольта входная характеристика нелинейная. Это означает, что равномерное увеличение напряжения между базой и эмиттеромU_БЭприводит к неравномерному увеличению тока базы, поскольку ток коллектора пропорционален току базы, то и ток коллектора увеличивается неравномерно. Это явление и объясняет появление нелинейных искажений усилителя на биполярном транзисторе.

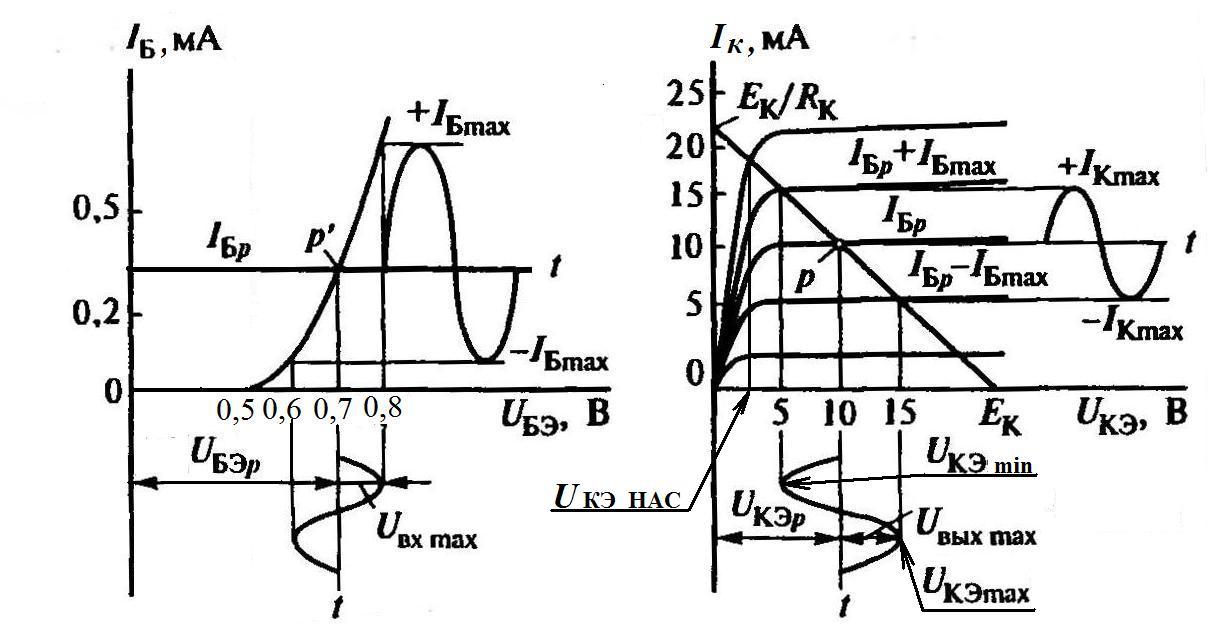
Рисунок 4 — Вольт-амперные характеристики усилительного каскада

Нелинейные искажения приводят к появлению в усиленном сигнале гармоник высшего порядка, которые оцениваются коэффициентом нелинейных искажений. Наибольшая нелинейность входной характеристики имеет место в районе 0,6 вольта, поэтому работа транзистора в этой области крайне нежелательна. Работа при напряжениях U_БЭ> 0,8 уменьшает нелинейные искажения, но приводит к увеличению тока коллектора, что ведет к увеличению нагрева транзистора и ухудшает коэффициент полезного действия.

Начальное положение рабочей точки на выходной характеристике обозначено буквой р, на входной характеристике буквой —р’. Для этого подбирают такое значение резистораR2, чтобы напряжение на коллекторе при отсутствии входного сигнала удовлетворяло формуле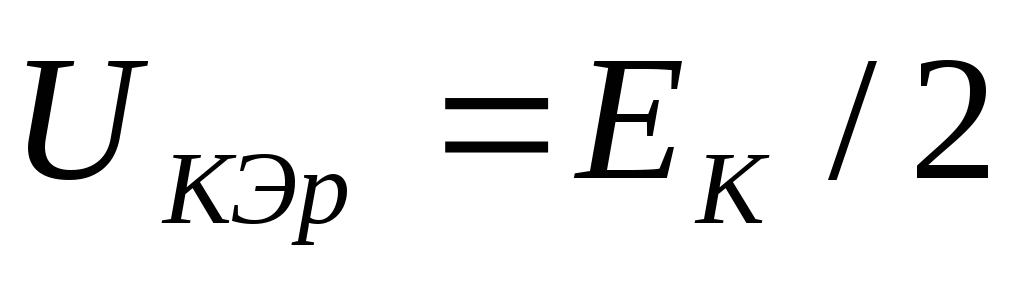

Конденсаторы Cp1 и Cp2 называются разделительными. Они обеспечивают изоляцию (разделение) источника сигнала и нагрузки от каскада по постоянному току и соединение (связь) их по переменной составляющей между собой. Для устранения отрицательной обратной связи по переменной составляющей, которая возникает из-за эмиттерного резистора Rэ его шунтируют конденсатором Cэ, сопротивление Xcэ которого на низшей частоте усиливаемого сигнала должно быть на порядок меньше Rэ (Rэ>>Xcэ). Это ослабляет отрицательную обратную связь в каскаде по переменному току и устраняет влияние Rэ на коэффициент усиления по переменной составляющей.

Кроме нелинейных искажений появляются линейные искажения. Линейные искажения обусловлены наличием в усилителе реактивных элементов, сопротивление которых зависит от частоты f. Из-за этого отдельные гармонические составляющие входного сигнала усиливаются неодинаково, нарушается их взаимный фазовый сдвиг относительно друг друга, форма сигнала искажается.

Линейные искажения усилителей оцениваются с помощью амплитудно-частотной (АЧХ), фазочастотной (ФЧХ) и переходной характеристик. Под АЧХ усилителя понимается зависимость К_U = f(f). Пример АЧХ представлен на рисунке 5.

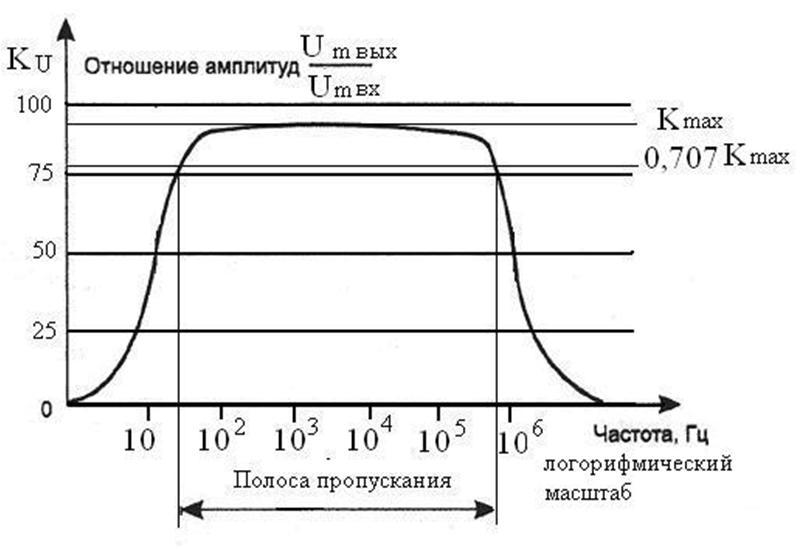
Рисунок 5 — Амплитудно-частотная характеристика усилителя

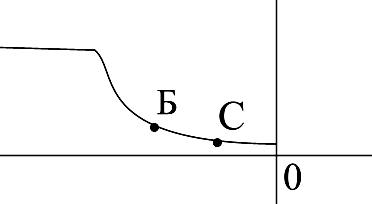
Амплитудная характеристика (АХ) усилителя представлена на рисунке 6 и снимается при подаче на вход усилителя гармонического колебания частотой f, лежащей в полосе пропускания. Для усилителей низкой частоты обычно f = 1000Гц

Начальный нелинейный участок обусловлен собственными шумами усилителя и наводками, которые приводят к появлению напряжения на входе усилителя при отсутствии входного сигнала.

При больших напряжениях Uвх сказывается нелинейность ВАХ активных элементов, из-за чего падает средняя крутизна и уменьшается усиление.

Количественно мера нелинейности γ оценивается как отношение отклонения АХ от линейной характеристики

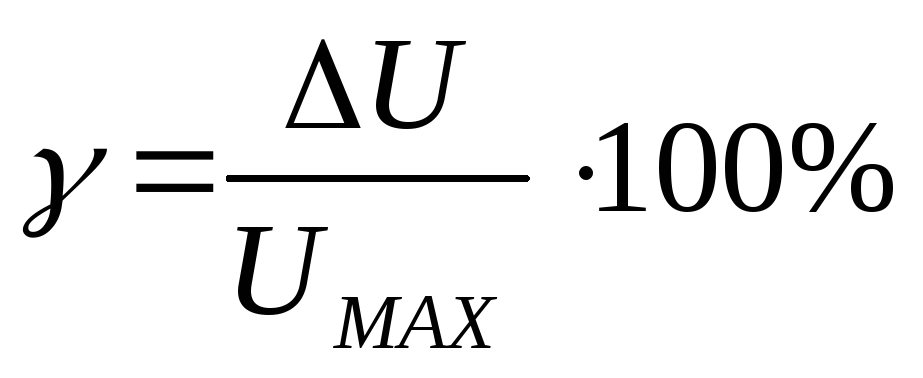
АХ считается линейной на участках, где усиление происходит с допустимым уровнем нелинейных искажений (в пределах 1 децибелла). В этом случае коэффициент усиления К не зависит от амплитуды и может быть определен, как тангенс угла наклона АХ к оси абсцисс.

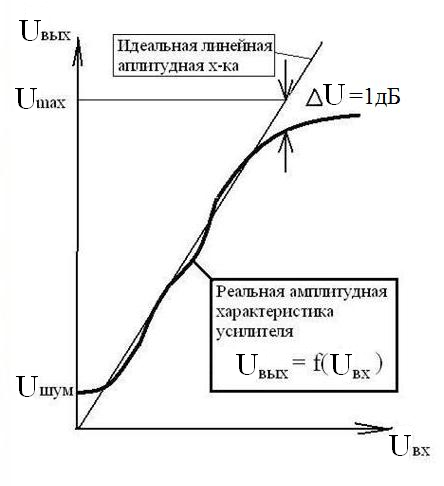
Рисунок 6 — Амплитудная характеристика усилителя

Динамический диапазон усилителя оценивается как отношение максимального и минимального напряжения выходных сигналов, выраженное в децибелах. Минимальный сигнал определяется уровнем собственных шумов усилителя, а максимальный — нелинейными искажениями. В этом случае динамический диапазон определяют по формуле

,

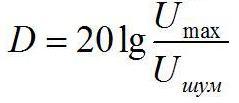где U_мах– максимальное напряжение на выходе усилителя в линейной области амплитудной характеристики,

U_шум– напряжение сигнала на выходе усилителя при отсутствии полезного сигнала на входе.

Рабочее задание

1. Включить компьютер и настроить прибор АКИП  4107. Включить установку «ЛОЭ-АиПУ» и установить начальное положение рабочей точки усилителя.

2. Снять амплитудную характеристику усилителя: Uвых = F(Uвх) при f = 1000 Гц для двух различных нагрузок (резисторов) и режима холостого хода.

3. Построить графики амплитудных характеристик усилителя для двух различных нагрузок и режима холостого хода, и определить динамический диапазон усилителя для каждого случая.

4. Снять амплитудно-частотную характеристику усилителя: Uвых = F(f ) для одной нагрузки (по указанию преподавателя).

5. Построить график амплитудно-частотной характеристики и определить полосу пропускания.

Методические указания

1. Включить компьютер и настроить прибор АКИП  4107. Включить установку «ЛОЭ-АиПУ» и установить начальное положение рабочей точки усилителя .

Подготовить к работе универсальный цифровой прибор АКИП 4107, подключив три измерительных кабеля: один к входу канала А (СНА), другой к входу канала В (СНВ) и третий к выходу генератора (Signal OUT). Убедиться, что прибор АКИП4107 подключен к компьютеру. Запустить на компьютере программу PicoScope6.

Измерительный кабель канала А подключить к стенду следующим образом: черный штекер к гнезду XS5, а красный штекер к гнезду XS9.Установить на пиктограмме значение ±10.

Установить напряжение питания усилителя, поставив тумблеры SA2 в верхнее положение; SA6 в нижнее положение; CA9, CA10 в верхнее положение ; SA7, SA8 в нижнее положение; и один из тумблеров сигнальной лампы в верхнее положение, например SA3, а остальные SA4, SA5 в нижнее положение. После этого включить питание от сети поставив тумблер SA1 в верхнее положение. Убедиться что лампа горит в полнакала, что соответствует напряжению питания 6В (либо 5В на одном из учебных стендов).

Определить напряжение питания по экрану осцилографа АКИП 4107 (прямая линия на уровне 5 или 6B, может иметь небольшие помехи не превышающие 0,1B).

Для установки рабочей точки усилителя в правильное начальное положение необходимо вынуть красный штекер провода канала А из гнезда XS9 и переставить в гнездо XS4.Вращая ручку переменного резистора R4 установить напряжение на коллекторе транзистора равным половине напряжения питания.

2. Снять амплитудную характеристику усилителя: Uвых = F(Uвх) при f = 1000 Гц для двух различных нагрузок (резисторов) и режима холостого хода.

Включить генератор сигналов, щелкнув по пиктограмме . Впоявившемся окне установить :

Сигнал Вкл сигнал: Синусоидальный

Начальная частота : 1кГц

Амплитуда: 250 мB (щёлкая мышкой по стрелке вниз)

Смещение: 0B

Подключить чёрный штекер кабеля от генератора «SIGNAL OUT» к гнезду XS2, а красный к гнезду XS1.

Для измерения сигнала на выходе усилителя U_ВЫХ подключить черный штекер кабеля канала В к гнезду XS12 а красный к гнезду XS11.

Для измерения сигнала на входе усилителя U_ВХ переключить красный штекер канала А из гнезда XS4 в гнездо XS3. Включить автоматический режим выбора диапазона измерений щелкнув по галочке «Диапазон входного сигнала» и в выпадающем меню выбрать режим «Авто.»

Установить коэффициент развертки 200µs/div, щелкнув по галочке на пиктограмме . Для синхронизации изображения щелкнуть по галочке на пиктограмме и выбрать режим «Авто».

К выходу усилителя подключить нагрузку резистор R6, для этого повернуть преключатель SA11 по часовой стрелке до упора ( при этом подключается резистор R6).

Для измерения среднеквадратических величин сигнала на входе U_вх необходимо щелкнуть один раз по кнопке «+» на пиктограмме в нижней части экрана. В появившемся окне необходимо щелкнуть мышкой по галочке в окне «Выберите тип измерения».

В появившемся окне типов измерения выбрать тип измерения «Перем. СКЗ».

Для измерения среднеквадратических величин сигнала на выходе U_ВЫХ необходимо сначала включить в работу канал В щелкнув по галочке и выбрать в выпадающем меню режим Авто. Затем щелкнуть один раз по кнопке «+» на пиктограммев нижней части экрана. В появившемся окне необходимо выбрать «Перем. СКЗ» для канала В.

Для заполнения таблицы 1 необходимо вращать ручку переменного резистора R1. Для значения U_ВХ = 0 небходимо повернуть ручку резистора R1 до упора против часовой стрелки.

Для определения собственных шумов на выходе усилителя прочитать среднеквадратическое значение переменной составляющей сигнала канала В в столбце «Среднее».Результат измерения записать в первый столбец таблицы 1.

Для установки значения U_ВХ = 2 мВ плавно поворачивать ручку резистора R1 по часовой стрелки до тех пор пока в графе «среднее» канала А не появится значение 2 (сотые доли милливольта не учитывать). Результат из графы «среднее» канала В записать в таблицу.

Аналогично заполняется таблица для других значений U_ВХ.

Если R1 окажется в крайнем правом положении и входное напряжение больше не поднимается, то необходимо щёлкнуть по пиктограмме и в графе «Амплитуда» установить значение 2 В.

Таблица 1 — Нагрузка R6

UВХ, мВ f=1000	0	2	5	10	20	30	40	50	60	70	80	90	100	120	150	200	300
UВЫХ, мВ
KU

Аналогично заполняется таблица 2 для другой величины нагрузки (по указанию преподавателя).

Таблица 2 — Нагрузка R__

UВХ, мВ f=1000	0	2	5	10	20	30	40	50	60	70	80	90	100	120	150	200	300
UВЫХ, мВ
KU

Аналогично заполняется таблица 3 для режима холостого хода (без нагрузки).

Таблица 3 — Без нагрузки

UВХ, мВ f=1000	0	2	5	10	20	30	40	50	60	70	80	90	100	120	150	200	300
UВЫХ, мВ
KU

Заполнить нижнюю строчку таблиц 1,2 и 3, рассчитав коэффициент усиления K_U.

3. Построить графики амплитудных характеристик усилителя для четырех различных нагрузок и режима холостого хода, и определить динамический диапазон усилителя для каждого случая.

Построить график амплитудной характеристики усилителя (по горизонтальной оси – U_ВХ,по вертикальной – U_ВЫХ)на миллиметровой бумаге или с использованием программы MathCad или Exсel.

Определите по графику напряжение собственных шумов U_Ш (при U_ВХ = 0), максимальное напряжение на выходе, соответствующее линейной области, динамический диапазон усилителя в дБ для каждой нагрузки и режима холостого хода.

Определить значение входного напряжения, соответствующее середине линейной области амплитудной характеристики для каждой нагрузки и выделить его цветным карандашом в таблицах 1, 2 и 3. Это значение использовать в следующем опыте при снятии амплитудно-частотной характеристики.

4. Снять амплитудно-частотную характеристику усилителя: Uвых = F(f ) для одной нагрузки (по указанию преподавателя).

Щёлкнуть по пиктограмме и в графе «Амплитуда» установить значение 250 мВ.

Вращая ручку R1 установить амплитуду сигнала на входе усилителя , соответствующей середине линейной области амплитудной характеристики для данной нагрузки, выделенное цветным карандашом в предыдущем опыте.

В режиме генератора задавать различные частоты, указанные в таблице 2, щёлкнув по пиктограмме . При изменении частоты изменяется входное сопротивление усилителя, поэтому вращая ручку R1 корректировать значение «перем. СКЗ» канала А для каждого значения частоты. Занести значения выходного напряжения в таблицу 2.

При изменении частоты также необходимо изменять время развертки так, чтобы на экране было видно несколько периодов сигнала (от 3-х до 15-ти).

Таблица 2

f, Гц	20	50	100	300	1000	5000	10000	20000	100000
UВЫХ, mВ
KU

5. Построить график амплитудно-частотной характеристики и определить полосу пропускания.

Построить график амплитудно-частотной характеристики усилителя (по горизонтальной оси отложить частоту – f Гц (в логарифмическом масштабе),по вертикальной коэффициент усиления — K_U)на миллиметровой бумаге или с использованием программы MathCad или Exel.

Определите по графику нижнюю границу полосы пропускания f_Н . Для этого максимальное значение коэффициента усиления K_U, умножить на 0,707 и провести горизонтальную линию. Точки пересечения графика с проведенной горизонтальной линией определяют границы полосы пропускания. Поскольку генератор, встроенный в АКИП 4107, не работает на частотах более 100 кГц, мы не можем определить верхнюю границу полосы пропускания.

Схемы электронных устройств на биполярных и полевых транзисторах Усилитель, собранный по схеме с общим эмиттером, на биполярном p-n-p-транзисторе

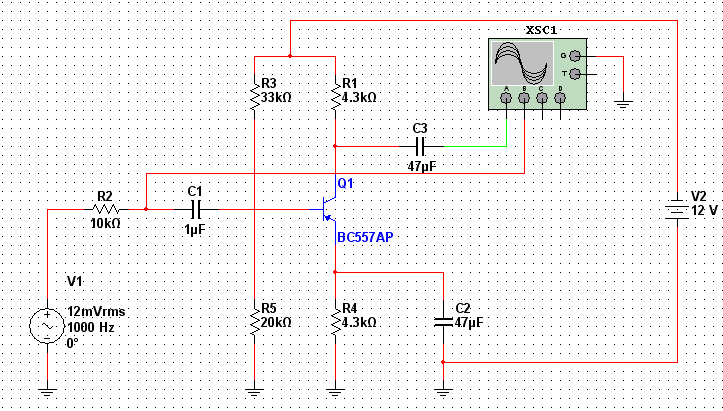
Рис. 5. Усилитель, собранный по схеме с общим эмиттером

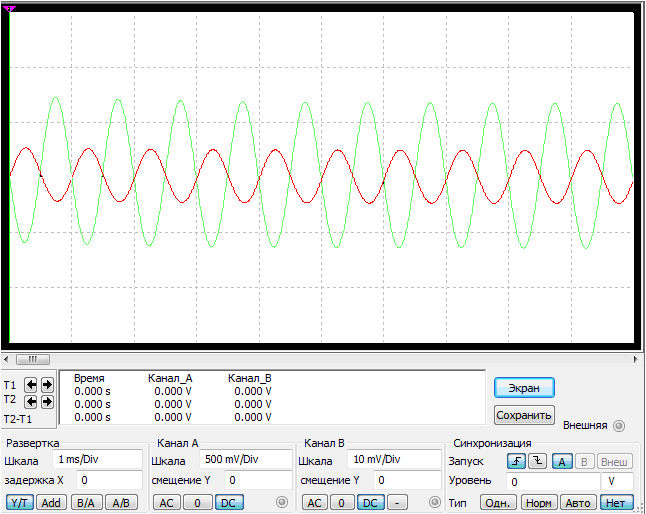
Рис. 6. Осциллограмма напряжений

Каскад усилителя, собранный по схеме с общим эмиттером (ОЭ), дает усиление по мощности, напряжению и току. Это одна из самых часто применяемых схем во многих базовых элементах электроники. Усилитель собран на биполярном транзисторе обратной проводимости.

Для получения параметров схемы, близких к оптимальным, необходимо задать транзистору режим работы по постоянному току, выбрать рабочую точку.

Нормальный активный режим может быть задан выбором рабочей точки на середине линейного участка ВАХ. Этот режим также называется усилительным.

В нашем случае это реализуется подачей напряжения смещения на транзистор (задается режим работы по постоянному току) с делителя напряжения R2-R3 и источника питания постоянного тока V1.

Снимается выходное напряжение с нагрузки, которой в данном случае является резистор R4 , включенный в цепь коллектора.

Для стабилизации режима работы транзистора к эмиттеру подключена цепочка отрицательной обратной связи (резистор R1 и конденсатор C2), её ещё часто называют цепью эмиттерной термостабилизации.

Конденсатор C2 включен для устранения отрицательной обратной связи по переменному току (препятствует снижению коэффициента усиления).

Особенностью работы каскада является то, что переменные входной и выходной импульсы напряжения сдвинуты по фазе на 180 градусов, находятся в противофазе.

Эту картину можно наблюдать на осциллограмме, снятой при работе усилителя в электронной лаборатории на IBM PC в автоматизированной среде N1.Multisim 10.1.1.

Осциллограмма напряжений представлена на рис. 6.

Усилитель с общим коллектором (ок) или эмиттерный повторитель

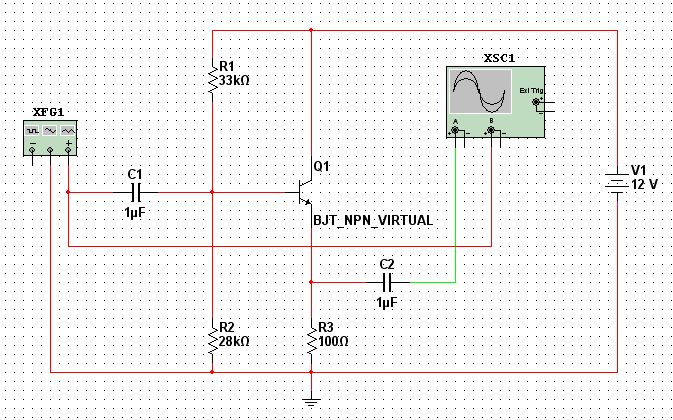
Рис. 7. Усилитель с общим коллектором

Схема с общим коллектором (ОК) или, как ее еще называют, эмиттерный повторитель имеет высокий коэффициент усиления по току и не дает усиления по напряжению. Это связано с действием 100%-й отрицательной обратной связи через резистор R3. В усилителе с ОК фазы входного и выходного сигналов совпадают. Здесь C1 и C2 – входной и выходной разделительные конденсаторы, резисторы R1 и R2 образуют цепь смещения по постоянному току. Коллекторный резистор отсутствует, так как выходной сигнал снимается с резистора R3.

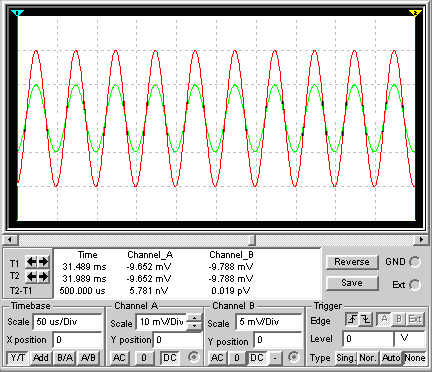
Рис. 8. Осциллограмма напряжений

Достоинством схемы является высокое входное сопротивление (десятки кОм) и низкое выходное сопротивление (единицы кОм – сотни Ом), поэтому эту схему используют для согласования различных устройств по входному сопротивлению, а недостатком — схема не усиливает напряжение.

Усилитель с общей базой

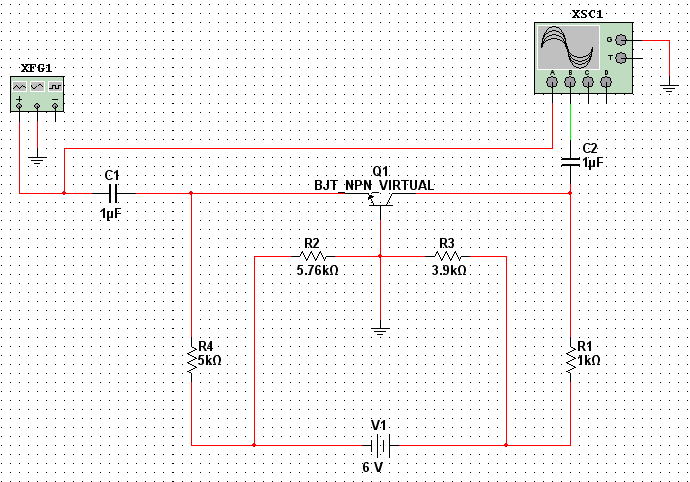
Рис. 9. Усилитель с общей базой

Усилитель с общей базой (ОБ) имеет низкое входное сопротивление (50 –100 Ом) и более низкий коэффициент усиления по мощности по сравнению с усилителем, собранным по схеме с ОЭ, так как дает усиление по напряжению и не дает усиления по току. Преимущество этого усилителя – хорошие частотные характеристики (широкая полоса пропускания). Поэтому усилители с ОБ используются при очень высоких частотах. Разделительный конденсатор C1 обеспечивает передачу переменного входного сигнала на эмиттер транзистора (входное напряжение прикладывается между эмиттером и базой). Резистор R3 включен в цепь эмиттера для обеспечения обратной связи. Делителем напряжения R1-R2 задается режим работы усилителя. Выходной сигнал снимается с нагрузочного резистора R4.

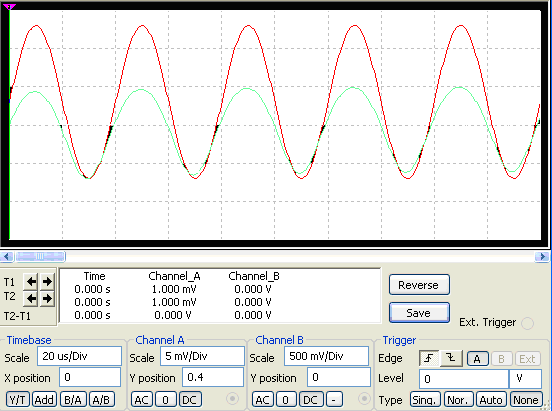
Рис. 10. Осциллограмма напряжений