Одноразрядные двоичные сумматоры. Карты Карно для переноса и суммы. Схема одноразрядного сумматора, реализующая уравнения, страница 3

Математика \ Дискретная математика

Используя метод разбиения разрядов сумматора на группы, можно построить схемы параллельного переноса внутри групп, а затем, применив аналогичный подход, можно создать схему параллельного переноса между группами. Такой способ позволяет получить значительный выигрыш по быстродействию за счет дополнительных аппаратурных затрат.

Некоторое снижение объема оборудования получается при разбиении сумматора на группы разной длины. Однако при этом получается нерегулярная структура сумматора. Поэтому чаще всего рекомендуется разбиение сумматоров на группы с одинаковым числом разрядов (до 8).

ЗАДАНИЕ 3. Разработайте четырехразрядную группу сумматора с параллельным переносом.

4.4. Двоичный сумматор–вычитатель

Суммирование здесь выполняется как в обычном двоичном сумматоре, а вычитание заменяется сложением в дополнительном коде.

Напомним, дополнительный код положительного двоичного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется из обратного кода добавлением 1 в младший разряд.

При кодировании двоичных чисел самый старший разряд отводится под знак числа: 0 – число положительное, 1 – число отрицательное.

Пример.

Положительное число + 6 в двоичной системе счисления с учетом знака числа имеет код (как прямой, так и дополнительный) 0 110 (знаковый разряд отделен пробелом).

Отрицательное число – 6 имеет прямой код 1 110, обратный код 1 001 и дополнительный код 1 010.

Поскольку суммирование положительных чисел это просто сложение прямых кодов, а вычитание – сложение дополнительных кодов, то для реализации двоичного сумматора–вычитателя нужен двоичный сумматор и преобразователи отрицательных чисел в дополнительный код. Получить обратный код отрицательного числа можно с помощью элементов М2, работающих в режиме управляемого инвертора (см.

рис. 4.7), а добавить к обратному коду 1 можно с помощью сумматора, необходимого для выполнения основной операции – суммирования.

	U	X	Y
0	0	0	0	U = 0 Y = X
1	0	1	1
2	1	0	1	U = 1 Y =
3	1	1	0

Рис.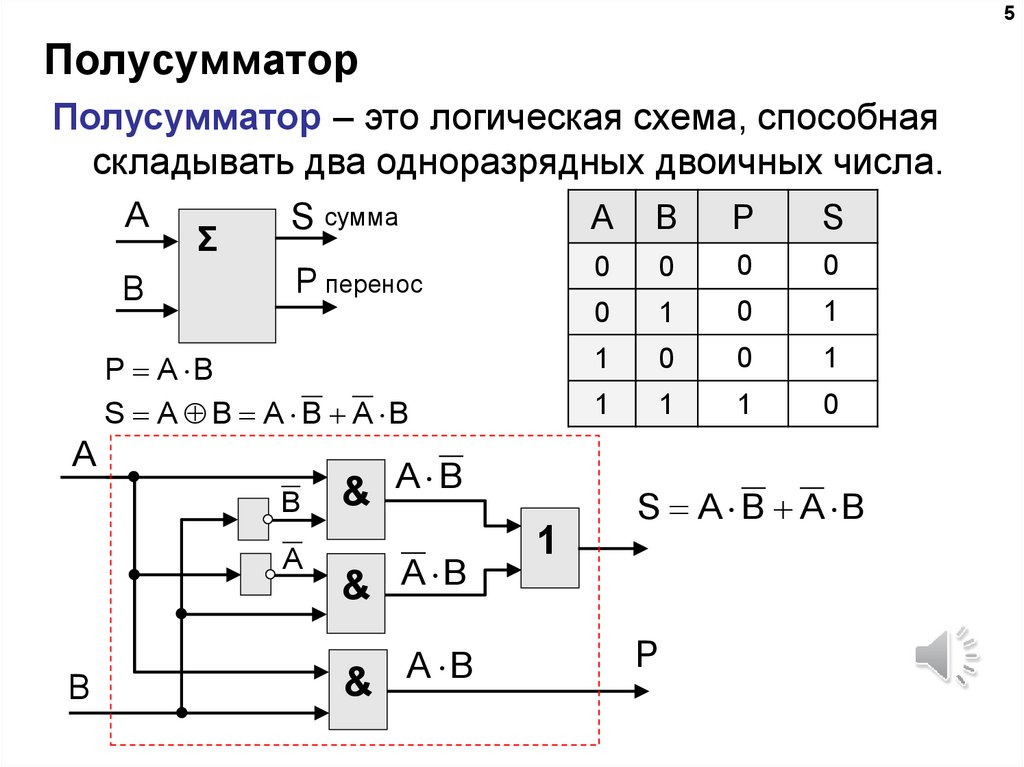

4.7. Управляемый инвертор

Схема четырехразрядного сумматора–вычитателя показана на рис. 4.8, где слагаемое А подается с генератора двоичных слов, слагаемое В фиксировано и равно 3. Результат С получается таким .

Переключение сложение – вычитание осуществляется переключателем Space.

Рис. 4.8. Трехразрядный двоичный сумматор–вычитатель

4.5. Четырехразрядное АЛУ

В базе данных Electronics Workbench имеется микросхема 74181 четырехразрядного арифметико-логического устройства (АЛУ) (отечественный аналог К155ИП3). Данное АЛУ может работать в 32 режимах в зависимости от управляющих сигналов на входах M, S3, S2, S

1, S0. В библиотеке программы Electronics Workbench приведена схема включения этого АЛУ в режиме сумматора с переносом из младшей тетрады (рис. 4.9). В рассмотренном случае вычисления выполняются по формуле

F = A + B +1.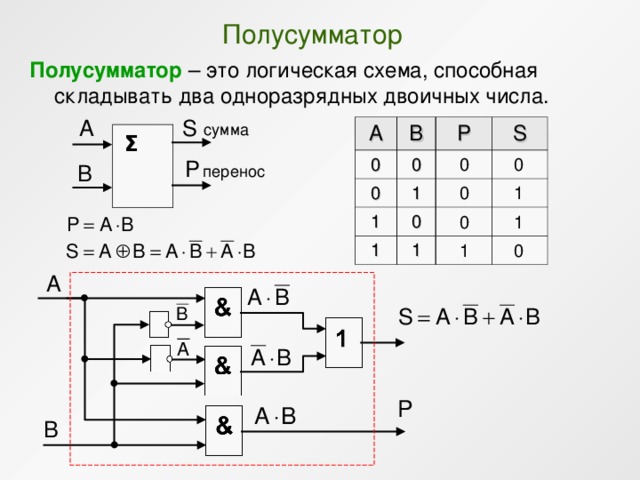

Все возможные режимы работы микросхемы К155ИП3 подробно изложены в [1], а ее функциональная схема дана, например, в [2].

Рис. 4.9. Схема включения четырехразрядного АЛУ (микросхема 74181)

4.6. Одноразрядный двоично‑десятичный сумматор

Сумма двух одноразрядных десятичных чисел с учетом переноса из младшей декады может принимать значения 0…19 (19, т.к. 9+9= 18+ 1 переноса).

Все возможные варианты суммы двух одноразрядных десятичных чисел показаны в табл. 4.3.

В таблице символом * обозначен перенос, которого нет, но он должен быть, так как сумма  10.

Вычитание 10 можно заменить сложением с дополнительным кодом 10.

10 в двоичной системе – это  1010.

Обратный код  10 – это 0101.

Дополнительный код 10 получается таким 0101 + 0001 = 0110 (в десятичной системе это 6).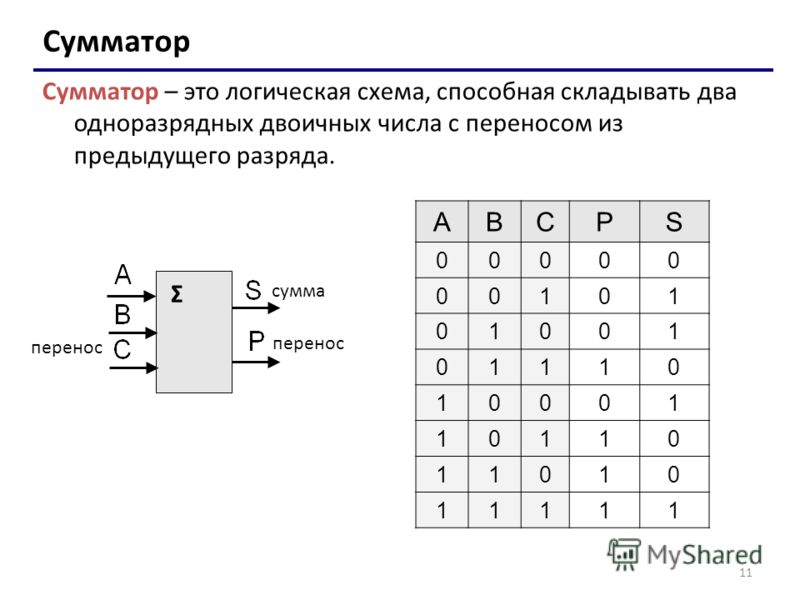

Таким образом, коррекция суммы от 10 до 19 сводится к добавлению 6. Признаком необходимости такой коррекции является наличие переноса. Правда, перенос получается автоматически только для сумм 16…19, а для сумм 10…15 его необходимо создать.

Скачать файл

Цифровая электроника | Страница 15 из 32

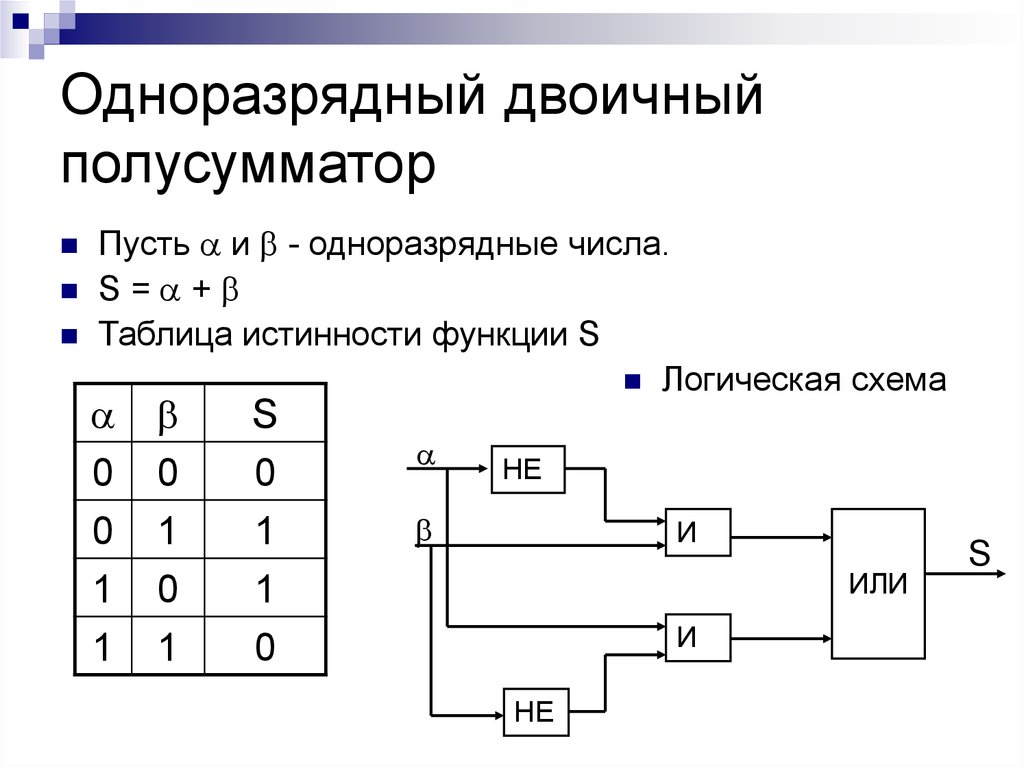
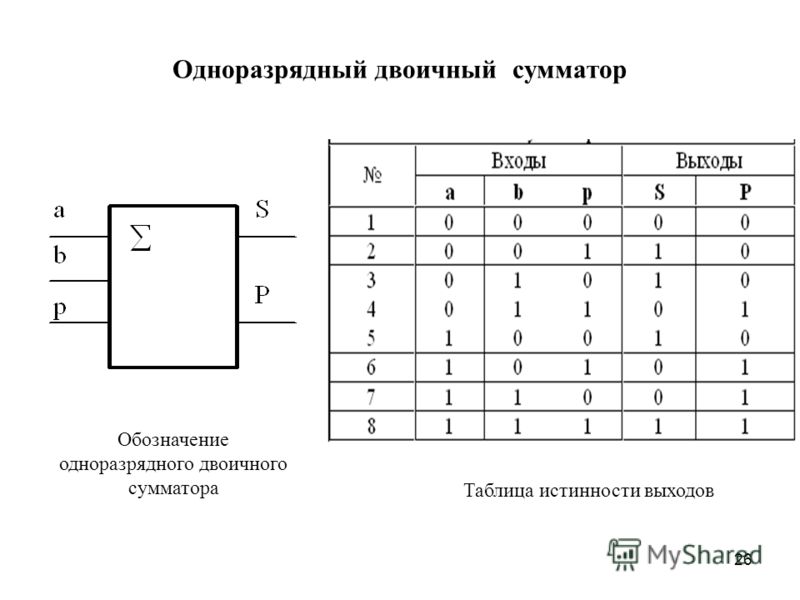
Сумматоры – это класс КЦУ, выполняющих операцию арифметического сложения двух двоичных n-разрядных чисел. Сумматоры бывают полными и неполными. Неполный сумматор или полусумматор — это комбинационное устройство с двумя входами и двумя выходами, выполняющее операцию сложения двух одноразрядных чисел в соответствии с таблицей истинности, где

А и В – входные одноразрядные числа, S_п/см. – выход суммы, а P_п/см. – выход переноса в старший разряд:

Входы		Выходы
А	В	Sп/см.	Pп/см.
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Записанные по таблице истинности ФАЛ для переменных S_п/см. и P_п/см. имеют вид

,

.

Первое уравнение для S_п/см. обозначает операцию Исключающее ИЛИ (Сложение по модулю два), а второе — для P_п/см. – операцию логической конъюнкции. Поскольку во всех сериях микросхем имеются элементы Исключающее ИЛИ, то структурную схему полусумматора удобно синтезировать на основе именно этого элемента и элемента И (рис. 4.6,

а). Условное графическое обозначение полусумматора приведено на рис. 4.6,б.

 

а)  б)

Рис. 4.6.Структурная схема и УГО полусумматора.

Полный одноразрядный сумматор выполняет операцию арифметического сложения двух одноразрядных чисел A и B с учетом переноса из младшего разряда Р_-1. Он имеет три входа и два выхода. Работа полного одноразрядного сумматора задается таблицей истинности:

Входы			Выходы
A	B	Р-1	S	P
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

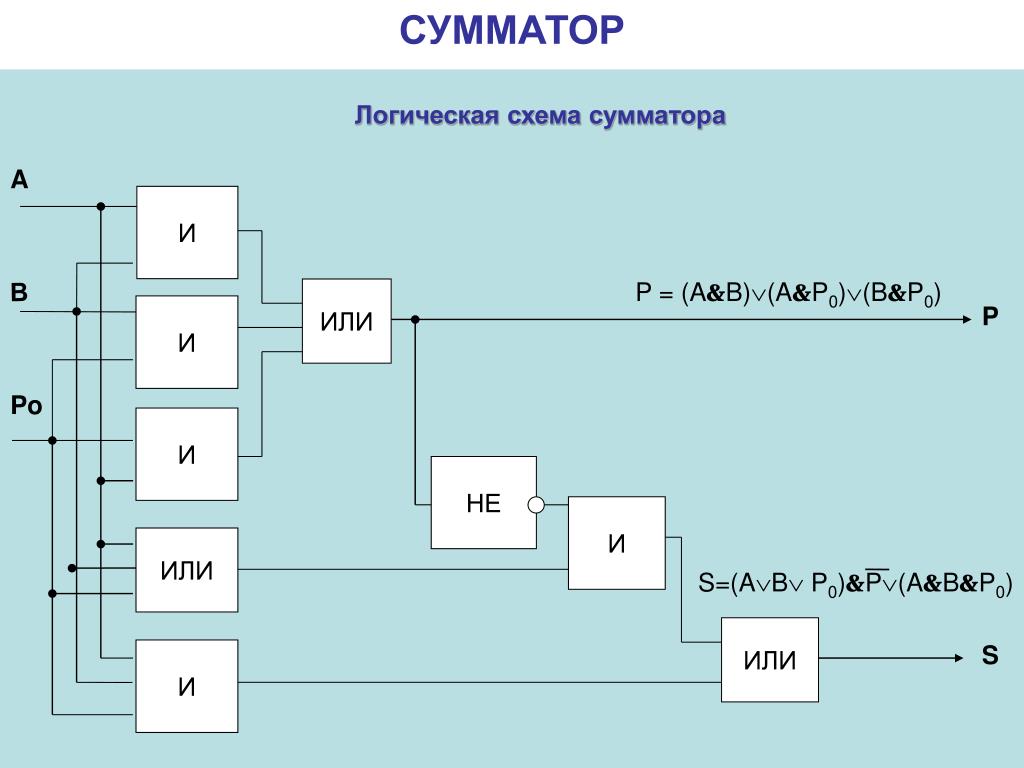
Записав СДНФ для переменных S и P и выполнив ряд тождественных преобразований можно получить следующие ФАЛ для полного сумматора:

,

.

Выражение  есть ни что иное, как значение выхода переноса полусумматора над величинами S_п/см. и Р_-1. Учитывая этот факт и анализируя полученные логические уравнения, можно сделать заключение о возможности реализации полного сумматора на основе двух полусумматоров и одного элемента ИЛИ. Структура полного одноразрядного сумматора представлена на рис. 4.7,а, а его УГО – на рис. 4.7,б.

 

а) б)

Рис. 4.7. Схема и УГО полного одноразрядного сумматора.

Из таблицы истинности полного одноразрядного сумматора очевидно, что на выходе суммы S формируется единица, а на выходе переноса Р – нуль при наличии единицы на одном из входах A, B или Р_-1. При наличии единиц на любых двух из трех входов полного сумматора, на выходе S будет нуль, а на выходе P – единица. При наличии на всех трех входах логических единиц, на обоих выходах сумматора присутствуют единицы. При нулях на всех трех входах выходы также принимают нулевые состояния. Структура, реализующая описанное правило и положенная в основу микросхем сумматоров 155 и 555 серий, приведена на рис. 4.8.

Рис. 4.8.Структурная схема одноразрядного полного сумматора, положенная в основу микросхем ТТЛ-типа.

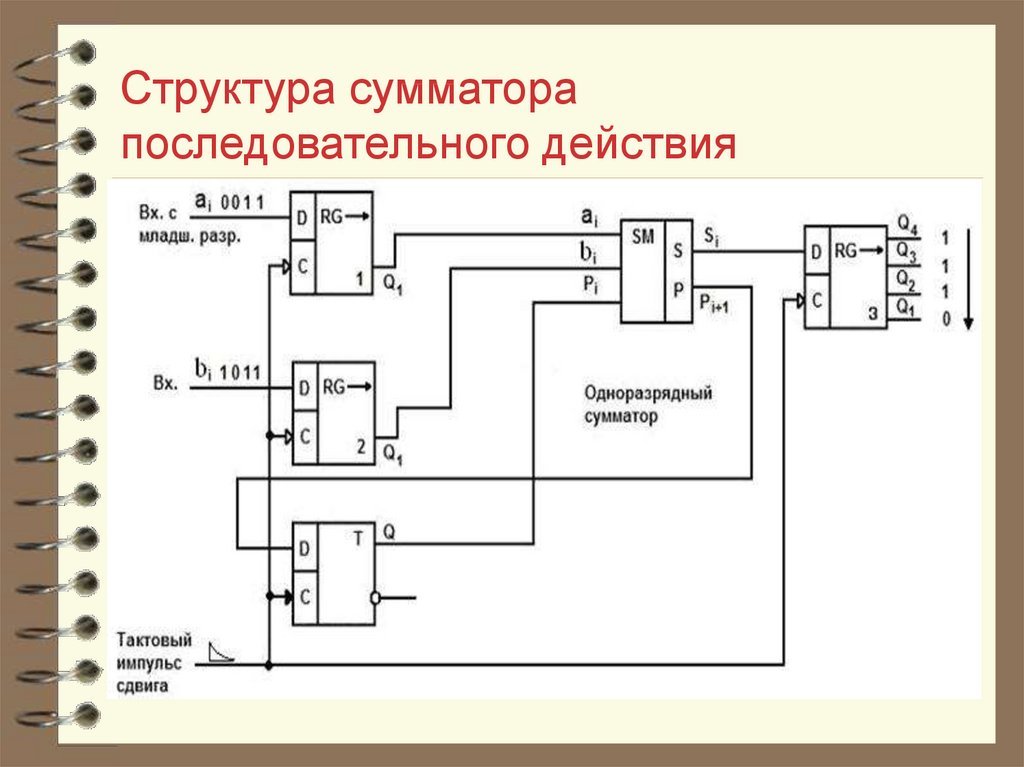
При суммировании многоразрядных двоичных чисел с помощью одноразрядных сумматоров их необходимо соединить в последовательные структуры. Выходы переноса Р микросхем младших разрядов подключаются к входам переноса Р_-1 микросхем старших разрядов. Отдельные разряды слагаемых подаются на входы А и В микросхем соответствующих разрядов, а с их выходов S снимаются разряды результата суммирования. Выход переноса P микросхемы самого старшего разряда является выходом переноса результата суммирования всего n-разрядного числа.

Такой способ наращивания разрядности сумматоров путем последовательного объединения нескольких полных сумматоров меньшей разрядности достаточно прост в схемной реализации, но при этом имеет существенный недостаток – низкое быстродействие.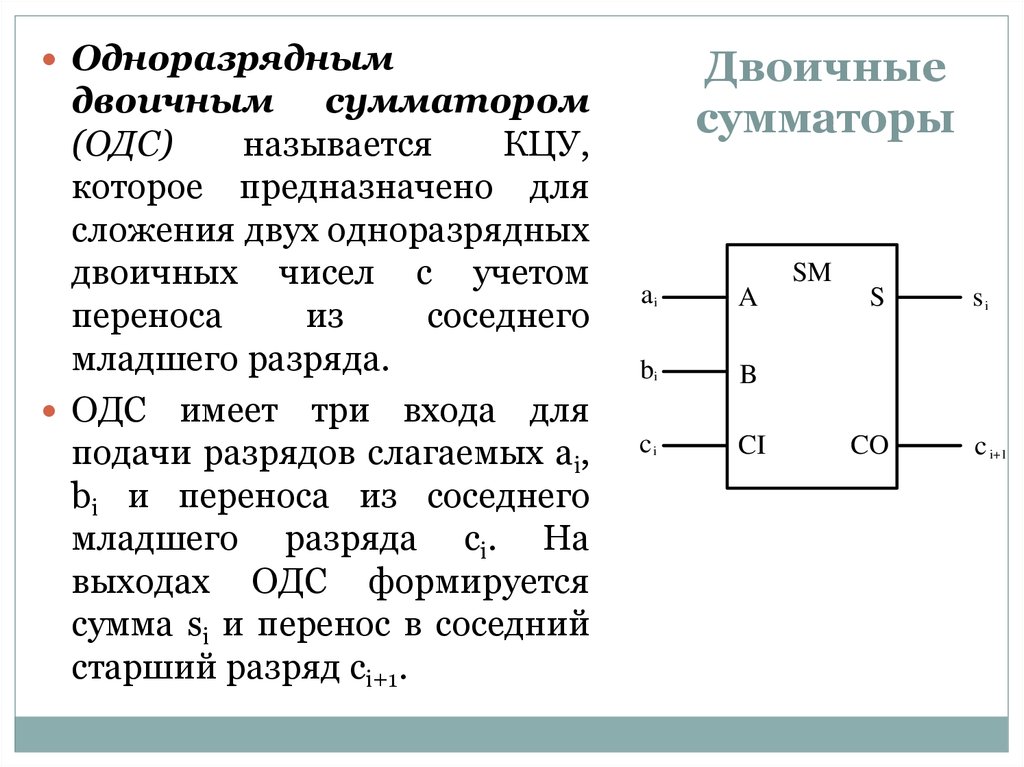 Распространение переноса в таких структурах осуществляется последовательно от микросхемы к микросхеме. Этого недостатка лишены сумматоры с параллельным переносом. Выражение для переноса в старший разряд одноразрядного полного сумматора можно преобразовать к следующему виду

Введем обозначения  и , где g_i – функция переноса, h_i – функция передачи переноса. Тогда

.

В общем случае можно записать

,

где  — перенос в самый младший разряд из предыдущего сумматора, если таковой предусмотрен в структуре цифрового устройства. В противном случае =0. Таким образом, сигнал p_i можно получить одновременно с появлением всех разрядов а_i и в_i на входах сумматора, не дожидаясь формирования переноса в отдельных разрядах полных одноразрядных сумматоров. В случае четырехразрядных чисел А и В можно записать

,

,

.

Для построения четырехразрядного сумматора с параллельным переносом необходимо полученные ФАЛ для p_i каждого разряда реализовать в каком-либо базисе, например И-НЕ. Далее выходные сигналы p_i с каждой части такой комбинационной схемы должны быть поданы на соответствующие входы Р_-1 полных одноразрядных сумматоров. Пример такой структуры приведен на рис. 4.9.

Из рисунка видно, что даже для четырехразрядного сумматора требуется достаточно сложная комбинационная схема формирования переноса. Поэтому схемы сумматоров с параллельным переносом реализуют обычно для сложения чисел с разрядностью не более четырех бит.

При необходимости реализации быстродействующих сумматоров для сложения двоичных чисел большей разрядности используют два подхода. Первый заключается в использовании полных сумматоров с параллельным переносом в качестве базовых элементов и объединении их в общую последовательную структуру. Сумматоры, реализованные по такой структуре, называются сумматорами с цепным переносом. Подобная структура не может обладать максимальным быстродействием, но при этом является простой в схемотехнической реализации.

Рис. 4.9. Схема четырехразрядного сумматора с параллельным переносом.

Второй подход также основан на использовании набора сумматоров с параллельным переносом. Но их объединение в общую структуру основано на принципе параллельной передачи переноса. В этом случае требуется дополнительная комбинационная схема, реализующая параллельный перенос между параллельными сумматорами. Сумматоры с такой структурой называются параллельно-параллельными. Они имеют максимальное быстродействие, но их реализация требует дополнительных аппаратных затрат.

Схема полного сумматора

— принцип работы

27 октября 2022 г. Автор Omar Muñoz Urias 1 комментарий

Полный сумматор — это цифровая схема, выполняющая сложение трех двоичных входов. В этом руководстве вы узнаете, как работает эта схема, ее таблицу истинности и как реализовать ее с помощью логических вентилей.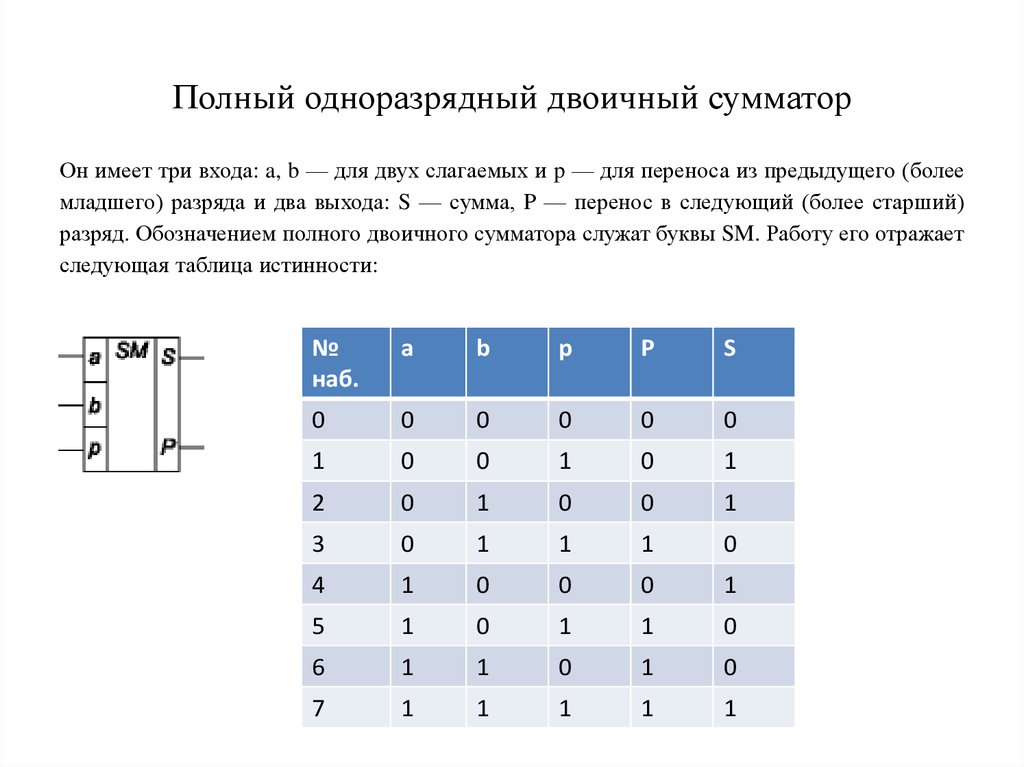

Полный сумматор

Что такое полный сумматор?

Сумматоры могут быть полусумматорами или полными сумматорами. Разница в том, что Полусумматор используется для сложения только двух 1-битных двоичных чисел, поэтому его сумма может принимать значения только от 0 до 2. Чтобы улучшить эту производительность, был разработан Полный сумматор. Он может складывать три однобитных двоичных числа, получая диапазон суммы от 0 до 3, который может быть выражен двумя выходными битами («11»).

A	B	C в	S	C out
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Полная таблица истинности сумматора

Если вы будете следовать приведенной выше таблице истинности, A и B представляют входные переменные, которые вы хотите добавить, а C _в — это ввод переноса. S — выходная сумма, а C _out — выходной сигнал, указывающий, произошел ли перенос. Но в бинарной логике что означает перенос? Хорошо, давайте посмотрим на следующий пример:

Обратите внимание, что когда вы добавляете «0» и «0» или «1» и «0», результат может быть выражен всего одним битом, но когда вы добавляете «1» и «1», вам нужно два бита и один из них нести.

Но зачем нужен вход переноса в полных сумматорах? Что ж, если вы хотите суммировать входные данные с более чем 1-битными числами, например, сложив два 4-битных двоичных числа, вам нужно будет объединить несколько сумматоров и обеспечить ввод переноса между ними, чтобы показать, что предыдущая менее значимая операция произвела нести.

Схема полного сумматора

Полный сумматор может быть построен с использованием двух схем полусумматора и вентиля ИЛИ. Первый полусумматор имеет два 1-битных бинарных входа: A и B. Он производит два выхода; Сумма и Перенос .

Результат Sum первого полусумматора будет первым входом второго полусумматора. А выход Carry первого полусумматора будет вторым входом дополнительного вентиля ИЛИ.

Второй вход второго полусумматора становится Перенести ввод (C _в ) полного сумматора.

Второй половинный сумматор также обеспечивает выходы Sum и Carry . Его выход Sum представляет собой Sum выход (S) полного сумматора, а его выход Carry является первым входом дополнительного вентиля ИЛИ. Наконец, логический элемент ИЛИ будет генерировать вывод переноса (C _из ) полного сумматора.

Заменим блоки реальными схемами:

Применение полного сумматора: 4-битный двоичный сумматор

Предположим, вы хотите сложить следующие два 4-битных двоичных числа A и B:

A = 1111 B = 1111

Результат будет 5-битным номер:

11110

Где старший бит указывает на перенос.

Таким образом, чтобы сложить два 4-битных двоичных числа, как указано выше, вам потребуется объединить четыре полных сумматора следующим образом:

Как видите, входы A и B каждого сумматора содержат элементы двух 4-битных битовые двоичные числа, распределенные от их младших разрядов справа налево. Кроме того, обратите внимание, как выход переноса одного полного сумматора является вводом переноса следующего. Просто помните, что это нужно учитывать, если предыдущая менее важная операция произвела перенос.

Обратите внимание на микросхему CMOS CD4008, которая может складывать два 4-битных двоичных числа.

Вопросы?

У вас есть вопросы о Full Adder? Позвольте мне знать в комментариях ниже.

Другие учебные пособия по цифровой электронике

Рубрики: Цифровая электроника

Взаимодействие с читателем

Бинарные арифметические схемы

• Изучив этот раздел, вы должны уметь:
• Понимание работы цепей двоичного сумматора.
• • Полусумматор.
• • Полный сумматор.
• • 4-битные параллельные сумматоры.
• • 8-битный сумматор/вычитатель.
• • Переполнение дополнения до двух.
• • Переносить сумматоры с опережением.
• Используйте бесплатное программное обеспечение для имитации работы логической схемы.

 

Полусумматор

Рис. 4.1.1 Полусумматор

Рис. 4.1.1 Полусумматор

Двоичная арифметика осуществляется комбинационными логическими схемами, простейшей из которых является полусумматор, показанный на рис. 4.1.1. Эта схема состоит в своей самой простой форме из двух вентилей, вентиля XOR, который выдает логическую 1 на выходе всякий раз, когда A равен 1, а B равен 0, или когда B равен 1, а A равен 0. Логический вентиль AND выдает логическую 1 на выходе. нести вывод, когда и A, и B равны 1. Таблица истинности полусумматора показана в таблице 4.1.1 и описывает результат двоичного сложения.

Рис. 4.1.2 Схема полного сумматора.

1 плюс 0 = 1 ₂ (1 ₁₀ )

и

1 плюс 1 = 10 ₂ (2 ₁₀ )

3 9 , но для двоичных чисел, содержащих несколько битов, в какой-то момент может возникнуть перенос (в результате добавления 1 и 1), который необходимо добавить в следующий столбец.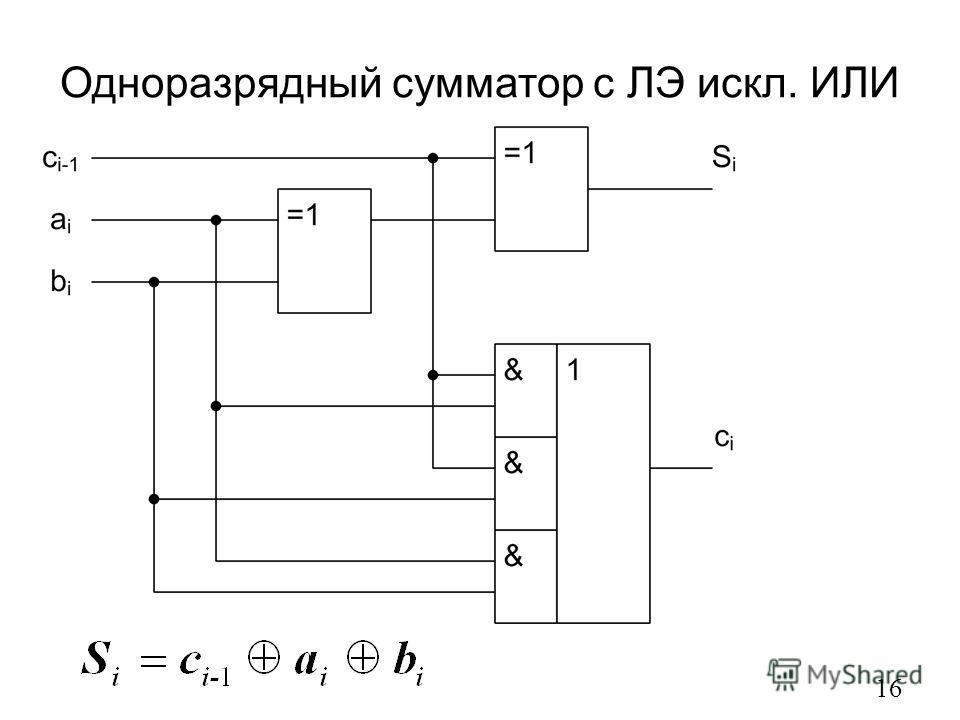 Поскольку полусумматор имеет только два входа, он не может добавить бит переноса из предыдущего столбца, поэтому он нецелесообразен для чего-либо, кроме 1-битных дополнений.

Полный сумматор

Когда необходимо добавить 2 или более битов, используется схема полного сумматора, показанная на рис. 4.1.2 (синий фон) вместе с символом упрощенной блок-схемы. Эта схема просто состоит из двух полусумматоров, сумма A и B из первого полусумматора используется в качестве входа A для второго полусумматора, который теперь производит сумму первого полусумматора (S ₁ ) плюс любой ‘ перенос с терминала C _IN . Любые переносы, произведенные двумя полусумматорами, затем объединяются по ИЛИ для получения одного C _ВЫХОД . вывод. Таблица истинности схемы приведена в таблице 4.1.2.

Рис. 4.1.3 4-битный параллельный сумматор.

Параллельные сумматоры

Даже полный сумматор складывает только два однобитовых двоичных числа, но полные сумматоры могут быть объединены для формирования параллельных сумматоров, которые будут складывать два многобитных числа.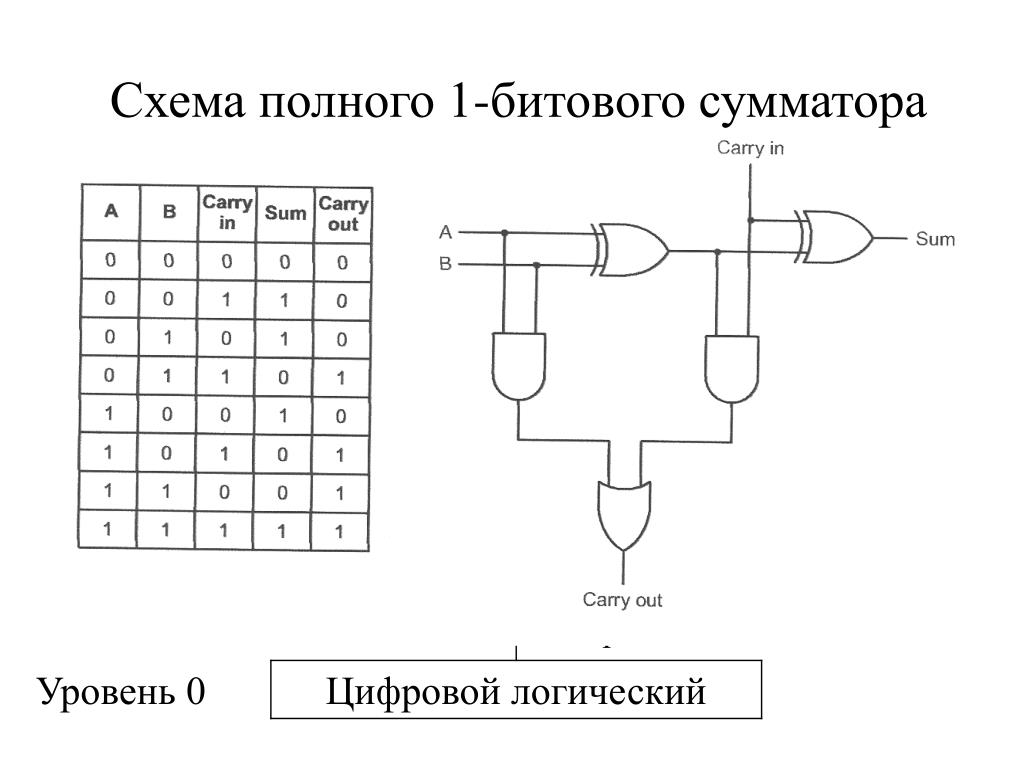 Параллельные сумматоры могут быть построены в нескольких формах для сложения многобитных двоичных чисел, при этом каждый бит параллельного сумматора использует одну полную схему сумматора. Поскольку параллельные схемы сумматора выглядели бы довольно сложными, если бы на них были показаны все отдельные вентили, обычно полную принципиальную схему сумматора заменяют упрощенной версией блок-схемы.

4-битный параллельный сумматор

На рис. 4.1.3 показано, как несколько полных сумматоров могут быть объединены для создания параллельного сумматора, также называемого «сумматор пульсирующего переноса» из-за того, что любой перенос появляется на входе переноса ( C _IN ) или производится при добавлении любого из 4-битных входов, «рябь» вдоль каскадов сумматора до тех пор, пока на выходе переноса (C _OUT ) окончательного полного сумматора для бита A _{не появится окончательный перенос. 3} +B ₃ .

Рис. 4.1.4 8-битный сумматор/вычитатель с дополнением до двух.

8-битный сумматор/вычитатель с дополнением до двух

Однако для выполнения арифметических операций также необходимо уметь вычитать. Дальнейшее развитие параллельного сумматора показано на рис.4.1.4. Это 8-битный параллельный сумматор/вычитатель. Эта схема складывает так же, как сумматор на рис. 4.1.3, но вычитает с использованием метода дополнения до двух, описанного в модуле 1.5 цифровой электроники (дополнение до единиц и до двух).

Когда требуется вычитание, управляющий вход устанавливается в логическую 1, что приводит к тому, что бит на любом конкретном входе B дополняется логическим элементом XOR перед подачей на вход B полной схемы сумматора.

Вычитание с дополнением до двух в 8-разрядном сумматоре/вычитателе требует, чтобы 8-разрядное число на входе B было дополнено (инвертировано) и к нему была добавлена ​​1, прежде чем оно будет добавлено к 8-разрядному числу на входе A. Результат из них будет 8-битное число в формате дополнения до двух, т. е. его значение представлено младшими 7 битами (от 0 до 6 бит), а знак представлен старшим значащим битом (бит 7). Таким образом, логическая единица на входе управления также подается на первый вход переноса сумматора для включения в сложение, которое, таким образом, для вычитания:

Вход A + Вход B + 1

(Здесь + означает сложение, а не ИЛИ)

В качестве альтернативы, если требуется сложение A и B, то управляющий вход находится в состоянии логического 0, а число B подается на сумматор без дополняющий.

Управление сумматором/вычитателем

Рис. 4.1.5 Шлюз XOR, используемый в качестве селектора данных.

Как здесь используется вентиль XOR для преобразования сумматора в вычитатель путем инвертирования входов B, видно из таблицы истинности вентиля XOR, показанной в таблице 4.1.3 (на рис. 4.1.5). Обратите внимание, что если вход A (используемый как вход CONTROL) вентиля XOR находится в состоянии логического 0, то вентиль XOR выбирает вход B, но если вход A равен логической 1, то он выбирает инверсию входа B (т. е. B).

Переполнение с дополнением до двух

8-битный сумматор/вычитатель, показанный на рис. 4.1.4, предназначен для сложения или вычитания 8-битных двоичных чисел с использованием записи с дополнением до двух. В этой системе старший бит (бит 7) не используется как часть значения числа, он используется для указания знака числа (0 = положительный и 1 = отрицательный).

Независимо от размера слова цифровой системы (8 битов, 16 битов, 32 бита и т. д.), заданное количество битов может обрабатывать числа только до максимального значения, которое может содержаться в расчетной длине слова.

Во время арифметических операций возможно, что сложение двух чисел (с положительными или отрицательными значениями), которые оба находятся в пределах системного предела, может привести к результату, слишком большому для длины слова системы.

Например, в сумматоре с дополнением до двух, таком как показанный на рис. 4.1.4, при сложении как положительных, так и отрицательных 7-битных значений результат может быть больше, чем могут вместить 7 бит.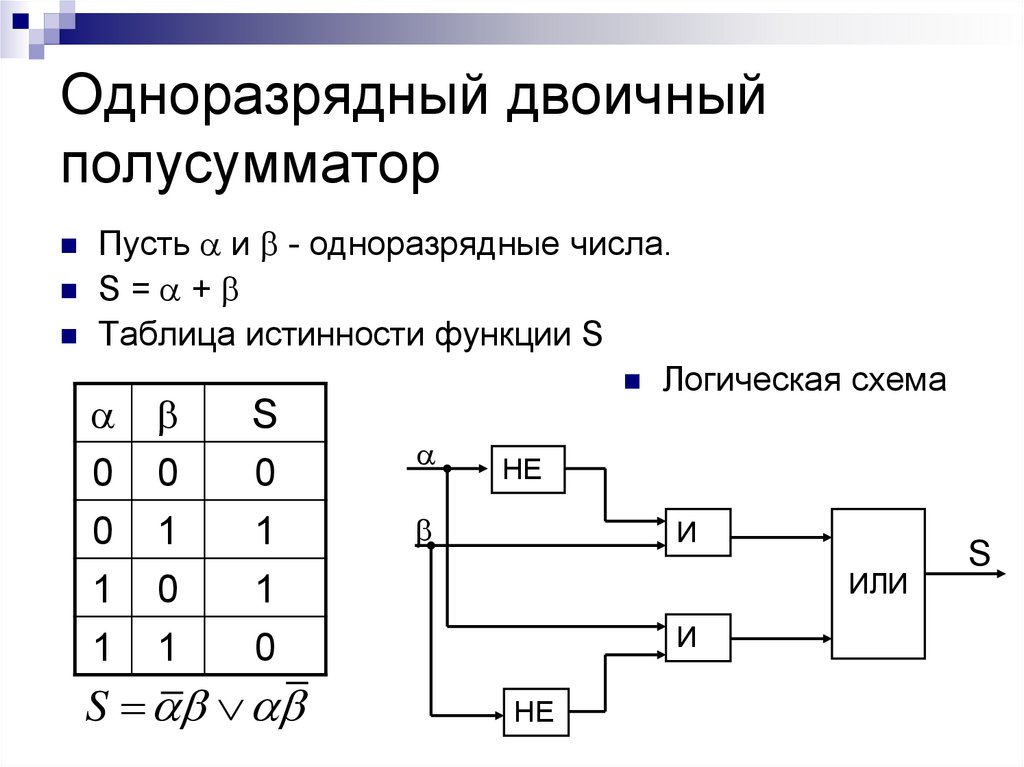 Следовательно, результат должен будет занимать один дополнительный бит, а это означает, что вычисленное значение «переполнит» восьмой бит, потеряв большую часть (128 ₁₀ ) значения и изменение знака результата.

Чтобы преодолеть эту проблему, необходимо сначала обнаружить, что возникла проблема переполнения, а затем решить ее либо с помощью дополнительных схем, либо, в вычислительной технике, с помощью корректирующей процедуры в программном обеспечении.

К счастью, есть довольно простой способ обнаружения переполнения. Как показано на рис. 4.1.5, система обнаружения переполнения состоит из одного вентиля исключающего ИЛИ (исключающее ИЛИ), который получает входные данные от соединений переноса и выполнения сумматора битов 7 (знаковый бит).

Когда проверяются биты переноса (C _IN ) и переноса (C _OUT ) этого сумматора, можно увидеть, что если произошло переполнение, C _IN и C _OUT будут разными , но если переполнения не произошло, они будут идентичными.

Сложение двух положительных (в пределах диапазона) чисел

В таблице 4.1.4 показан результат сложения двух положительных значений, сумма которых находится в пределах диапазона, который может храниться в 7 битах (≤127 ₁₀ ). Результат сложения двух положительных чисел дал правильный положительный результат без переноса и переполнения.

Вычитание с дополнением до двух

В таблице 4.1.5 показано вычитание с дополнением до двух, выполняемое путем прибавления отрицательного числа к положительному числу. Результат равен 3110 (в диапазоне от 0 до +127 ₁₀ ), знаковый бит равен 0, что указывает на положительный результат, C _IN и C _OUT равны 1, поэтому переполнение не обнаружено, и бит переноса будет отброшен.

Сложение отрицательных чисел с дополнением до двух

В таблице 4.1.6 показан эффект добавления двух отрицательных значений, когда сумма меньше +127 ₁₀ , следовательно, был получен правильный отрицательный результат −73 ₁₀ (в записи с дополнением до двух). Оба C _IN и C _OUT имеют логическую 1, и сигнал о переполнении не подается. Поскольку рассматриваются только 8-битные вычисления, перенос будет отброшен.

Вне диапазона Результат вызывает переполнение

При сложении двух положительных чисел, показанных в табл. 4.1.7 приводит к сумме, превышающей +127 ₁₀ , бит знака меняется с 0 на 1, что неверно означает отрицательный результат. Поскольку «перенос» из бита 6 в бит 7 равен 1, а «перенос» из бита 7 в бит переноса равен 0, обнаруживается переполнение, указывающее на неправильный ответ.

Обратите внимание, что если бы результат 10011101 ₂ рассматривался как двоичное значение без знака, добавление в Таблице 4.1.7 было бы правильным (157 ₁₀ ). Однако, поскольку в расчетах используется запись с дополнением до двух, ответ −99 ₁₀ следует считать неправильным.

Вне диапазона Сложение отрицательных значений

Таблица 4.1.8 показывает, что добавление двух отрицательных значений может также привести к изменению знака и неправильному результату дополнения до двух, если оно больше -128 ₁₀ . В этом случае сложение -63 ₁₀ и -73 ₁₀ должно было дать отрицательный результат -136 ₁₀ , а не +120 ₁₀ . Чтобы проверить это, можно было получить правильный ответ (хотя и с неправильным знаком), если, отметив, что произошло переполнение, ответ был дополнен и добавлен 1, что дало беззнаковый двоичный результат 10001000 ₂ , который преобразуется в 128 + 8 = 136 ₁₀ . Ошибки переполнения можно исправить, но для этого потребуется либо дополнительная электроника, либо программное действие в ответ на сигнал переполнения.

Сумматоры переноса с опережением

Сумматоры, описываемые в этом модуле, обычно называются сумматорами с последовательным переносом из-за того, как бит переноса передается от одного каскада сумматора к другому, проходя по цепочке полных сумматоров до тех пор, пока не будет выполнен перенос. выход производится на выводном штифте заключительного этапа.

Этот процесс занимает некоторое время, пропорциональное количеству добавленных битов. Хотя это может быть незначительной проблемой в небольших сумматорах, с увеличением числа битов в двоичных словах, которые должны быть добавлены, временная задержка перед выполнением окончательного выполнения становится неприемлемой.

Чтобы решить эту проблему, производители интегральных схем предлагают ряд «сумматоров переноса с опережением», в которых сложение и выполнение выполняются одновременно. Система использует сложную комбинационную логику для оценки того, будет ли производиться перенос в каждом отдельном сумматоре, на основе состояния входов A и B на этом этапе и логического состояния бита переноса на первый этап.

Рис. 4.1.7 Первый каскад сумматора с опережением переноса

На рис. 4.1.7 показано устройство для выполнения переноса путем разделения полного сумматора на частичный полный сумматор (серый блок), который имеет два дополнительных выхода. , выход распространения (P), который принимает логическую 1, когда входы A и B равны 1,0 или 0,1, и генерирует (G) выход, который будет логической 1, когда входы A и B равны 1,1. Используя эту информацию, можно принять решение о логическом состоянии выполнения в зависимости от комбинации C _{Состояние IN} и состояния A и B.

В генераторе переноса (синий блок) вход P объединяется по И с C _IN и по ИЛИ с входом G для получения переноса. Вынос подается на последовательные сумматоры обычным образом, но сигналы C _IN P и G подаются параллельно другим каскадам сумматора, где состояние переноса для каждого каскада сумматора может быть установлено из общий сигнал C _IN и состояния A и B для последовательных этапов, в зависимости от входных состояний на каждом этапе, вместо того, чтобы ждать завершения вычислений на всех этапах.

Рис. 4.1.8 Упреждающий сумматор переноса, блок-схема

Обобщенная компоновка в форме блок-схемы (рис. 4.1.8) показывает перенос (C _OUT ), производимый генератором параллельного переноса из A и входные сигналы B и сигнал C _IN , а не от выполнения конечного каскада сумматора, как в сумматорах пульсаций.