Схемы соединения резисторов: Схемы соединения резисторов — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Исследование схем соединений резисторов. Проверка законов Ома и Киркхгофа. Изучение магнитных цепей. Неразветвлённая цепь переменного тока с активным сопротивлением

Содержание

1. Исследование схем соединений резисторов. Проверка законов Ома и Киркхгофа.

2. Изучение магнитных цепей.

3. Неразветвлённая цепь переменного тока с активным сопротивлением.

4. Исследование цепи с параллельным соединением катушки, содержащей активное сопротивление и индуктивность, конденсатор.

5. Исследование трёхфазной цепи при соединении потребителей энергии по схеме «звезда».

6. Исследование трёхфазной цепи при соединении потребителей по схеме «треугольник».

7. Исследование конструкций электромеханических измерительных приборов.

8. Измерение сопротивлений методом амперметра и вольтметра, омметром.

9. Исследование однофазного трансформатора.

10. Снятие характеристик трёхфазного асинхронного двигателя с короткозамкнутым ротором.

11. Исследование двигателя постоянного тока с параллельным возбуждением.

12. Исследование генератора постоянного тока с параллельным возбуждением.

13. Определение потерь напряжения и мощности в проводах линии электропередачи.

14. Сборка и проверка работы схем релейно-контактного управления трёхфазным асинхронным двигателем с короткозамкнутым ротором.

15. Снятие входных и выходных характеристик транзистора.

16. Исследования схем однофазного выпрямителя со сглаживающими фильтрами.

17. Исследование электронного усилителя.

Проверка законов Ома и Кирхгофа.

ЦЕЛЬ РАБОТЫ: проверка опытным путём формул, на основании которых выполняются расчёты электрических цепей.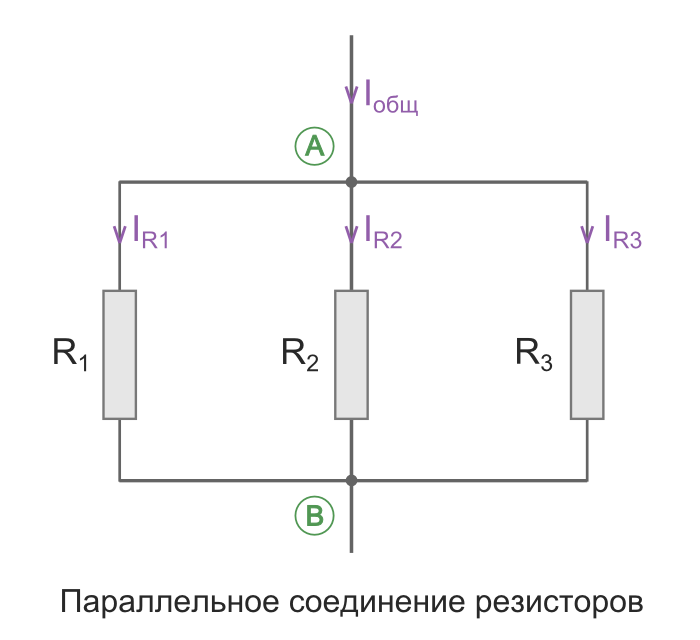

ОБЩИЕ СВЕДЕНИЯ.

Резистор – это структурный элемент электрической цепи, основное назначение которого оказывать известное (номинальное) сопротивление электрическому току, например, для регулирования значений тока и напряжения. В электроустановках резисторы применяются в качестве нагрузочных и пускорегулирующих реостатов, добавочных сопротивлений к некоторым электроприёмникам, электроизмерительным приборам и др. Электрические цепи могут состоять из соединённых между собой электроприёмников или резисторов: последовательно, параллельно и смешанно. При расчётах таких цепей руководствуются формулами, вытекающими из законов Ома и Кирхгофа.

ОБОРУДОВАНИЕ.

Источник напряжения 250В.

Резисторы.

Амперметры с пределом измерения 1А – 4шт.

Вольтметры с пределами измерения 50В, 150В, 250В – 3шт.

Соединительные провода.

ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА.

Электрические схемы соединений резисторов.

Последовательное соединение.

Рис. 1.

Параллельное соединение.

Рис.2.

Смешанное соединение.

Рис. 3.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Собрать электрическую схему, изображённую на рис. 1.

2. Данные приборов, включенных в электрическую схему, занести в таблицу 1.

Таблица 1.

Прибор	Система	Условное обозначение системы прибора	Предел измерения	Цена деления	Класс точности

3. Включить стенд в сеть.

4. Включить источник 250В.

5. Показания приборов записать в таблицу 1.

6. Выполнить расчёты, данные расчётов занести в таблицу 2.

Таблица 2.

Данные наблюдений					Данные расчётов
I	U₁	U₂	U₃	U	R₁	R₂	R₃	R_ЭКВ	R¹_ЭКВ	U_{ОБ. РАСЧ}

7. Собрать электрическую схему, изображённую на рис. 2.

8. Данные приборов занести в таблицу 1.

9. Включить стенд в сеть.

10. Показания приборов записать в таблицу 3.

11. Выполнить расчёты, данные расчётов занести в таблицу 3.

Таблица 3.

Данные наблюдений

Данные расчётов

I₁

I₂

I_ОБ

I_ОБ_.

R₁

R₂

R₃

R_ЭКВ

R¹_ЭКВ

12. Собрать электрическую схему, изображенную на рис.3.

13. Включить стенд в сеть.

14. Показания приборов записать в таблицу 4.

15. Выполнить расчеты, данные расчётов занести в таблицу 4.

Таблица 4.

Данные наблюдений

Данные расчетов

I₁

I₂

I₃

U₁

U₂

U₃

I_об

U_об

R₁

R₂

R₃

R_экв

R¹_экв

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ РАБОТЫ

И ВЫПОЛНЕНИЮ РАСЧЁТНО-ГРАФИЧЕСКОЙ ЧАСТИ.

Сопротивление каждого участка цепи определяется по закону Ома:

R=U/I

Сопротивление всей цепи: Rэкв = Uоб/I.

Последовательное соединение.

Эквивалентное сопротивление цепи определяется по формуле:

R¹экв=R₁+R₂+R₃

Общее напряжение определяется по формуле: Uоб=U₁+U₂+U₃

Полученные расчетом значения: Rэкв и R¹экв. должны совпадать.

Uоб. должно быть равно измеренному U.

Небольшое различие может быть вследствие погрешностей приборов при измерениях.

Параллельное соединение.

В этой схеме проверяется справедливость первого закона Кирхгофа:

Iоб = I₁ + I₂ + I₃

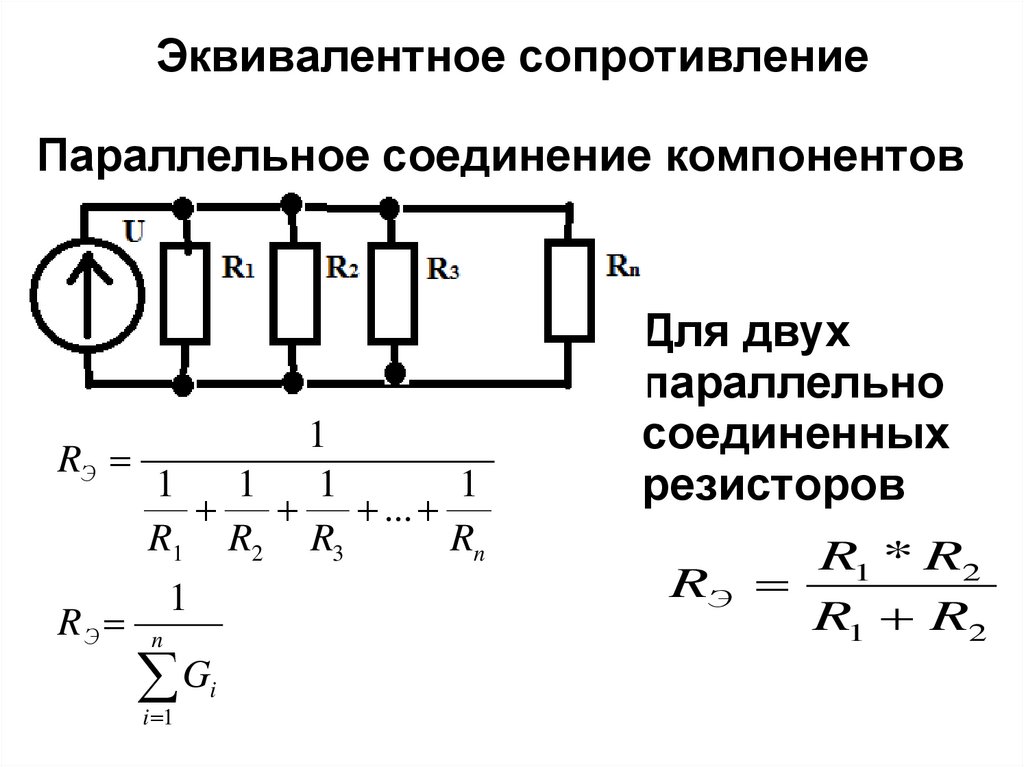
Эквивалентное сопротивление определяется по формуле:

Rэкв=R₁R₂R₃/(R₁R₂+R₂R₃R₃R₁),

вытекающей из формулы для определения общей проводимости как суммы проводимостей участков цепи:

1/Rэкв = 1/R₁+1/R₂+1/R₃.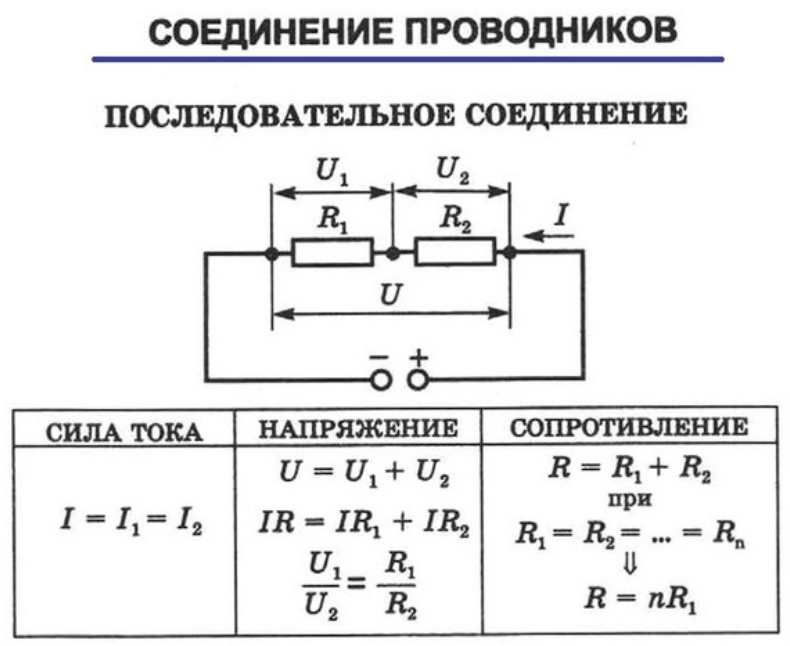

Эквивалентное сопротивление можно также определить по закону Ома:

R¹экв = U/ Iоб.

Оба значения должны совпадать.

По данным таблицы 3 можно проверить привило, согласно которому токи в ветвях обратно пропорциональны их сопротивлениям:

I₁ / I₂=R₂/R₁, I₃ / I₂=R₂/R₃.

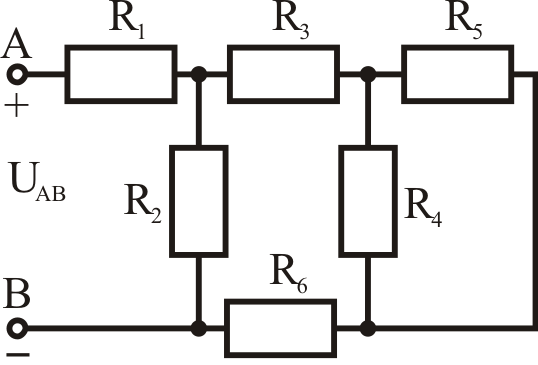
Смешанное соединение.

.Эквивалентное сопротивление Rэкв вычисляется по формуле: Rэкв=(R₂*R₃/R₂+R₃)+R_1.

Эквивалентное сопротивление можно определить по закону Ома:

R¹=U/Iоб

Сила тока в неразветвлённой части схемы:

Iоб=I₁=I₂+I₃

Общее напряжение:

Uоб= U₁+U₂_; (U₂=U₃)

СОДЕРЖАНИЕ ОТЧЁТА.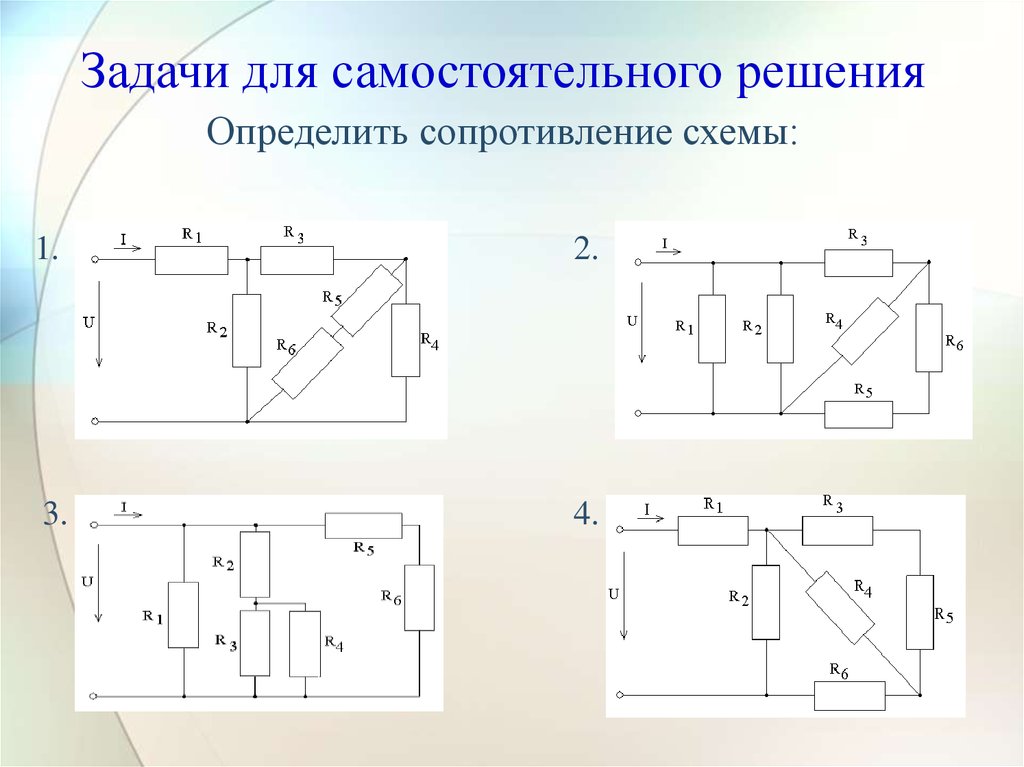

1. Название работы.

2. Цель работы.

3. Принципиальные электрические схемы соединений резисторов.

4. Таблица с данными приборов.

5. Таблицы с экспериментальными и расчётными данными.

6. Расчётные формулы, расчёты.

7. Выводы: укажите, подтверждаются ли практически законы Ома и Кирхгофа.

Контрольные вопросы:

Рис. 4.

1. Как изменится накал лампы (рис. 4 а), если увеличить сопротивление резистора?

2. Как изменится падение напряжения на резисторе, если уменьшить

Резистор. Основы. Соединения. Переменные резисторы.- Elektrolife

Резистор

Резисторы поистине вездесущи. Типы резисторов почти столь же многочисленны, как и схемы, в которых они применяются. Резисторы используются в усилителях, в качестве нагрузки для активных устройств, в схемах смещения и в качестве элементов обратной связи. Вместе с конденсаторами они используются для задания постоянной времени и работают как фильтры.

Они служат для установки величин рабочих токов и уровней сигналов. В схемах питания резисторы используются для уменьшения напряжения за счет рассеяния мощности, для измерения токов и для разряда конденсаторов после снятия питания. В прецизионных схемах они помогают устанавливать нужные токи, обеспечивать точные коэффициенты пропорциональности для напряжения, устанавливать точные коэффициенты усиления. В логических схемах резисторы выступают в качестве конечных элементов линий и шин, «повышающих» и «понижающих» элементов. В высоковольтных схемах резисторы служат для измерения напряжений, для выравнивания токов утечки через диоды или конденсаторы, соединенные последовательно. На радиочастотах они используются даже в качестве индуктивностей.

Промышленность выпускает резисторы с сопротивлением от 0,01 Ом до 10

¹² Ом и мощностью от 1/8 до 250 Вт с допуском от 0,005 до 20 %. Резисторы изготавливают из графитовых смесей, металлических пленок, проводов, накрученных на каркас, или на основе полупроводниковых элементов, подобных полевым транзисторам.

Наиболее распространены углеродистые композиционные резисторы, имеющие мощность 1/4 или 1/2 Вт. Существует стандартный диапазон значений сопротивлений ‑ от 1 Ом до 100 МОм, причем для резисторов с допуском на сопротивление, равным 5 %, выпускается в два раза больше значений сопротивлений, чем для резисторов с допуском 10 %

Резисторы настолько просты в обращении, что очень часто их принимают как нечто само собой разумеющееся. Между тем они не идеальны, и стоит обратить внимание на некоторые их недостатки.

Основной недостаток состоит в изменении сопротивления во времени под действием температуры, напряжения, влажности. Другие недостатки связаны с индуктивными свойствами (они существенно сказываются на высоких частотах), с наличием термальных точек в мощных схемах или шумов в усилителях с низким уровнем шума.

В схемах, где требуется высокая точность или стабильность, следует использовать резисторы из металлической пленки с допуском 1 %.

Они обеспечивают стабильность не хуже 0,1 % в нормальных условиях и не хуже 1 % в самых жестких условиях.

Прецизионные проволочные резисторы способны удовлетворить наиболее высоким требованиям.

Если ожидается, что мощность, рассеиваемая в схеме, будет составлять более 0,1 Вт, то следует выбрать резистор с большим значением рассеиваемой мощности. Композиционные углеродистые резисторы характеризуются мощностью до 2 Вт, а мощные проволочные резисторы ‑ более высокими значениями. Для мощных схем наилучшие характеристики обеспечивает резистор с отводом тепла. Резисторы этого типа выпускаются с допуском 1 % и могут надежно работать при собственной температуре до 250 °C в течение длительного периода времени. Допустимая рассеиваемая мощность зависит от воздушного потока, температурных условий на выводах и плотности схемы; следовательно, мощность на резисторе следует рассматривать как грубую ориентировочную величину.

Резистор характеризуется величиной сопротивления.

R = U /I;

Резисторы наиболее распространенного типа – углеродистые композиционные – имеют сопротивление от 1 ома (1 Ом) до 22 мегаом (22 МОм).

Резисторы характеризуются еще и мощностью, которую они рассеивают в пространство (наиболее распространены резисторы с мощностью рассеяния 1/4 Вт) и такими параметрами, как допуск (точность), температурный коэффициент, уровень шума, коэффициент напряжения (показывающий, в какой степени сопротивление зависит от приложенного напряжения), стабильность во времени, индуктивность и пр.

Нельзя называть резистор сопротивлением.

На практике, когда речь идет о резисторах с сопротивлением более 1000 Ом (1 кОм), иногда оставляют только приставку, опуская в обозначении «Ом», т. е. резистор с сопротивлением 10 кОм иногда обозначают как 10 К, а резистор с сопротивлением 1 МОм – как 1 М. На схемах иногда опускают и обозначение «Ом», оставляя только число.

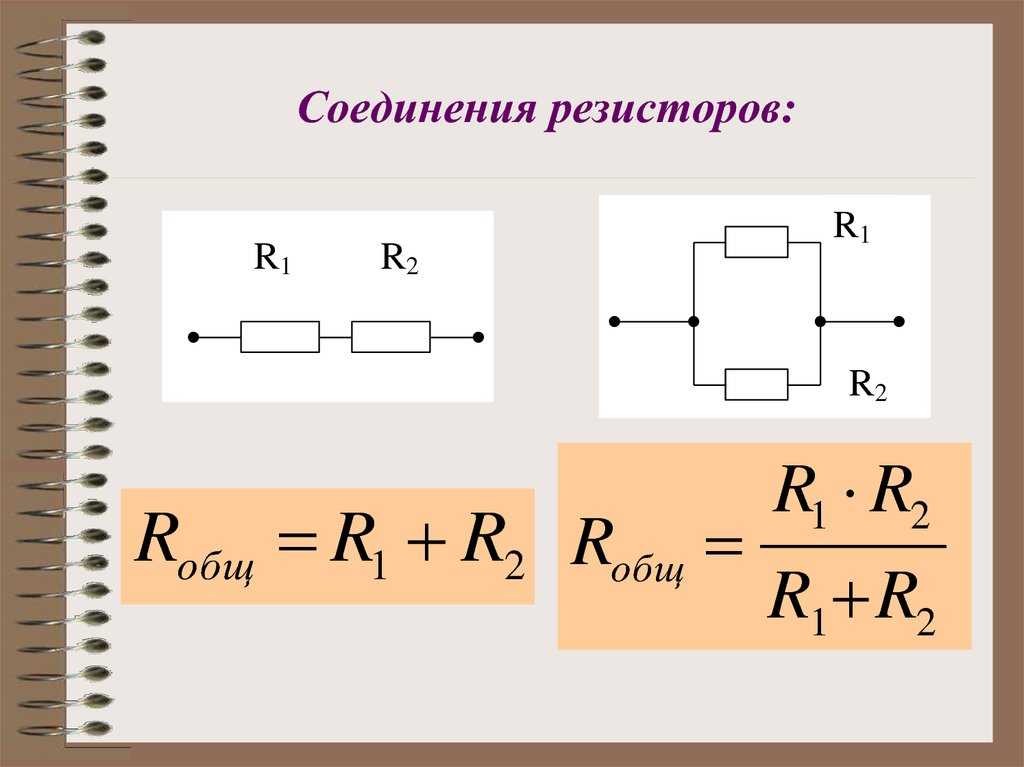
Сопротивление двух последовательно соединенных резисторов равно:

R = R₁ + R₂ .

При последовательном соединении резисторов всегда получаем большее сопротивление, чем сопротивление отдельного резистора.

Сопротивление двух параллельно соединенных резисторов равно

R = R₁R₂ /(R₁ + R₂ ) или R = 1/(1/R₁ + 1/R₂ ).

При параллельном соединении резисторов всегда получаем меньшее сопротивление, чем соединение отдельных резисторов.

Интуитивные правила вычисления сопротивления

Правило 1. Сопротивление двух резисторов, один из которых обладает большим сопротивлением, а другой малым, соединенных между собой последовательно (параллельно), приблизительно равно большему (меньшему) из двух сопротивлений.

Правило 2. Допустим, вы хотите узнать, чему равно сопротивление двух параллельно соединенных резисторов, обладающих сопротивлением 5 и 10 кОм. Если вообразить, что резистор сопротивлением 5 кОм представляет собой параллельное соединение двух резисторов сопротивлением 10 кОм, то схема будет представлена параллельным соединением трех резисторов с сопротивлением 10 кОм.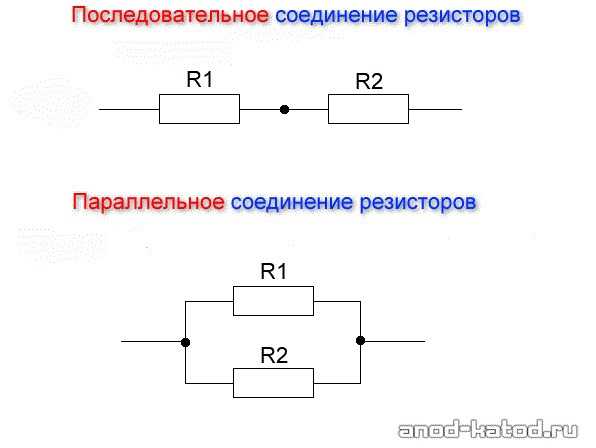 Так как сопротивление одинаковых параллельно соединенных резисторов равно 1/n ‑й части сопротивления одного из них, то ответ в нашей задаче будет 10 кОм/3, или 3,33 кОм.

Переменные резисторы

Переменные резисторы или потенциометры используют для регулирования в схемах, их ручки часто выводят на панели приборов. Наиболее распространенным является потенциометр типа АВ, рассчитанный на мощность до 2 Вт; этот потенциометр изготовлен из того же материала, что и постоянный композитный резистор, и имеет скользящий контакт. Потенциометры других типов изготовляют из керамических материалов и пластиков; они обладают улучшенными характеристиками. Более высоким разрешением и более высокой линейностью обладают многооборотные потенциометры (3,5 или 10 оборотов). В ограниченном количестве промышленность выпускает также сблокированные потенциометры (несколько независимых секций, собранных на одной оси) для тех областей применения, где нужны именно такие потенциометры.

Потенциометры, о которых шла речь, устанавливают чаще всего на лицевых панелях приборов, внутри же приборов устанавливают

подстроенные потенциометры, которые также бывают одно‑ и многооборотными и могут быть установлены на платах с печатным монтажом.

Они используются, например, при калибровке прибора, которая выполняется «раз и навсегда». Полезный совет: не поддавайтесь соблазну установить в схеме побольше потенциометров. Лучше потратить больше сил на разработку, чем на регулировку.

На показано условное обозначение потенциометра. Обозначения «по часовой стрелке» и «против часовой стрелки» указывают направление вращения.

Потенциометр (переменный резистор с тремя выводами)

Совет по работе с переменными резисторами: не стремитесь к тому, чтобы заменить потенциометром резистор с определенным сопротивлением. Соблазн, конечно, велик ‑ ведь с помощью потенциометра можно установить такое значение сопротивления, какое хочется. Вся беда в том, что стабильность потенциометра ниже, чем стабильность хорошего (1 %) резистора и, кроме того, потенциометры не дают хорошего разрешения (т. е. с их помощью нельзя точно установить значение сопротивления). Если на каком‑либо участке схемы нужно установить точное значение сопротивления, воспользуйтесь сочетанием прецизионного резистора (1 % и выше) и потенциометра, причем большая часть сопротивления должна определяться постоянным резистором.

Например, если нужно получить сопротивление 23,4 кОм, воспользуйтесь последовательным соединением постоянного резистора с сопротивлением 22,6 кОм (точность 1 %) и подстроечного потенциометра с сопротивлением 2 кОм. Можно также использовать последовательное соединение нескольких прецизионных резисторов, в котором самый маленький по величине резистор дополняет полное сопротивление до нужного точного значения.

В некоторых случаях в качестве переменных резисторов, управляемых напряжением, можно использовать полевые транзисторы. Транзисторы можно использовать в качестве усилителей с переменным коэффициентом усиления, управляемым напряжением.

Схемы резисторов

: понимание соединений и функций

О схемах резисторов，Резисторы являются одним из наиболее важных электронных компонентов электронного устройства. Они являются пассивными компонентами, ограничивающими протекание тока, обеспечивающими определенное падение напряжения и действующими в качестве электрических нагрузок для цепей.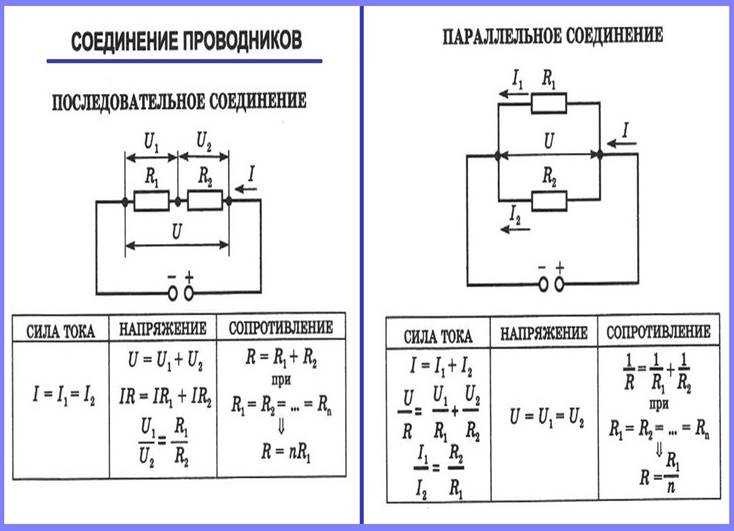

Вы можете сделать конфигурацию резисторов различными способами для достижения этих целей. Есть три первичных резистора в последовательном соединении, резисторы в параллельном соединении и комбинации резисторов в последовательном и параллельном соединении.

В этой статье будут рассмотрены все три типа со схемами, показывающими, как они работают! Давайте начнем!

Резисторы в последовательном соединении

Резисторы в последовательном соединении имеют два или более резистора, соединенных встык с одинаковым напряжением на всех них.

Как последовательно соединить резисторы

Подсоедините концы каждого резистора к источнику выходной мощности, предполагая, что провода имеют незначительное сопротивление. Резисторы соединены последовательно, поэтому, если один резистор имеет сопротивление R1, другой резистор также имеет сопротивление R2. Общее сопротивление равно сумме номинал отдельного резистора; в этом случае мы используем закон Ома для расчета.

Закон Ома в цепях с последовательным сопротивлением

Закон Ома гласит, что ток прямо пропорционален напряжению в двух точках любого проводника. В нашем случае резисторы.

На приведенной ниже схеме показана простая схема с последовательностью соединений резисторов. Первый резистор имеет значение сопротивления R1, а второй резистор имеет значение сопротивления R2.

По закону Ома; В=ИК

В = I * R_t

Где R_t — эффективное сопротивление резисторов, включенных в цепь. Напряжение источника (В) в цепи резистора такое же, как и напряжение. Причем резисторы включены последовательно, поэтому падение потенциала на них одинаковое. Мы также можем использовать закон Ома, чтобы найти это значение.

Ток и мощность в последовательных цепях

(цепь с последовательным резистором)

В цепи с последовательным резистором общий ток (I) одинаков для всех резисторов. То есть ток, протекающий через резистор_1, является тем же током, который будет протекать через резистор_2.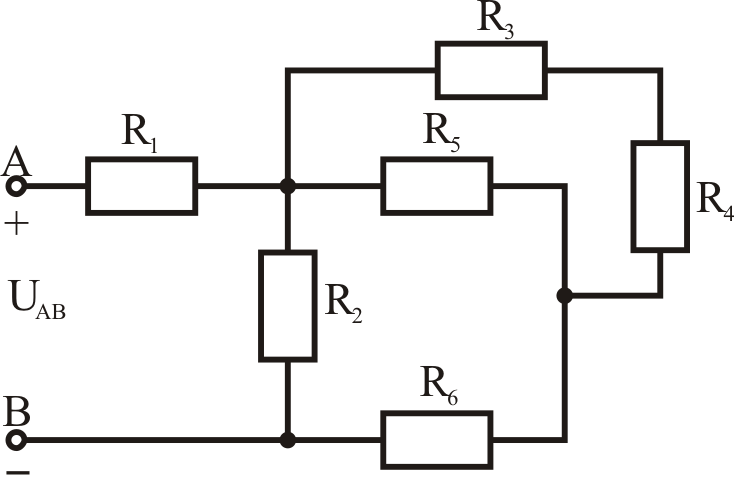 Кроме того, выходной ток равен тому, который обеспечивает батарея. Примечательно, что если вы добавите в цепь больше резисторов, текущее значение со временем уменьшится. Это связано с тем, что резисторы одинаково распределяют ток, несмотря на разницу в сопротивлении.

Итак, текущий; I_t = I_1=I_2.

Аналогично, Ток, я тоже =V/Rt

Другими словами, приложенное напряжение батареи (В), деленное на эффективное сопротивление (Rt).

Мощность определяется по формуле; P=V*I

В последовательной цепи приложенная разность потенциалов представляет собой общую сумму отдельных напряжений на каждом резисторе.

Следовательно, при расчете электроэнергии; P=V_total*I_total

Эффективное сопротивление в последовательной цепи

Эквивалентное сопротивление — это величина сопротивления, которая необходима одному резистору, чтобы сравняться с общим эффектом набора резисторов, присутствующих в трассе.

В простой последовательной цепи общее сопротивление равно сумме номиналов отдельных резисторов.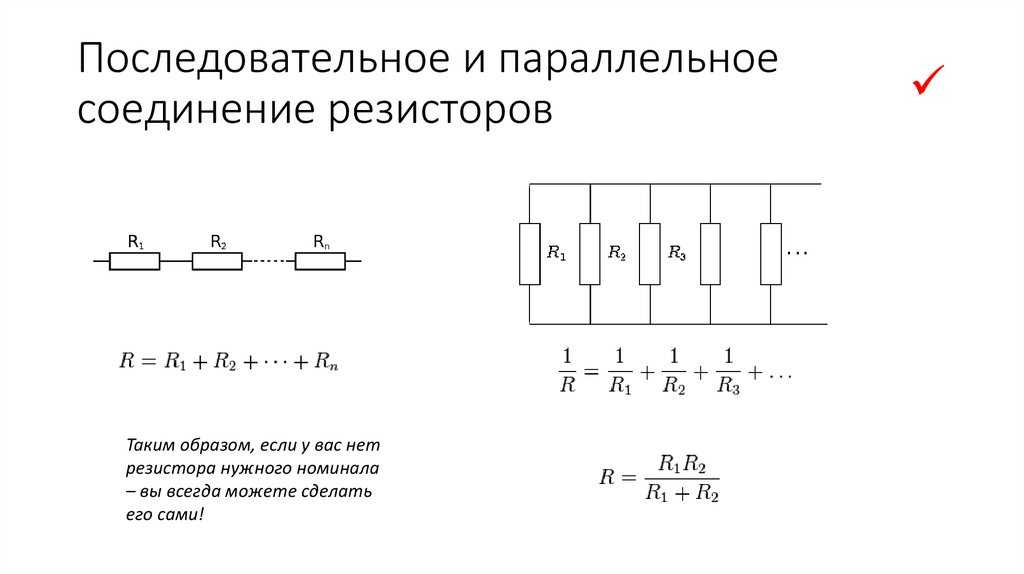 Чтобы уточнить, сложите номиналы резисторов. Но резисторы также имеют такое же падение потенциала. Например, в приведенной выше схеме уравнение эффективного сопротивления имеет вид;

Rtotal = R1 + R2 + R3

R_t = 5 Ом + 10 Ом + 5 Ом = 20 Ом следовательно, каждому нужен ток, равный или меньший, чем его номинал. В противном случае они будут повреждены или разрушены, если через цепь будет протекать слишком большой ток. Это опасно и может привести к повреждению компонентов или, что еще хуже, к пожару! Поэтому лучше всего использовать последовательное соединение резисторов для защиты ваших электрических цепей. Последовательный резистор ограничивает максимальное падение напряжения на светодиоде, что позволяет ему работать в безопасных условиях!

Резисторы в параллельном соединении

Для резисторов в параллельном соединении один конец всех резисторов подключается через стандартный провод. Аналогично все остальные концы соединяются через стандартный провод.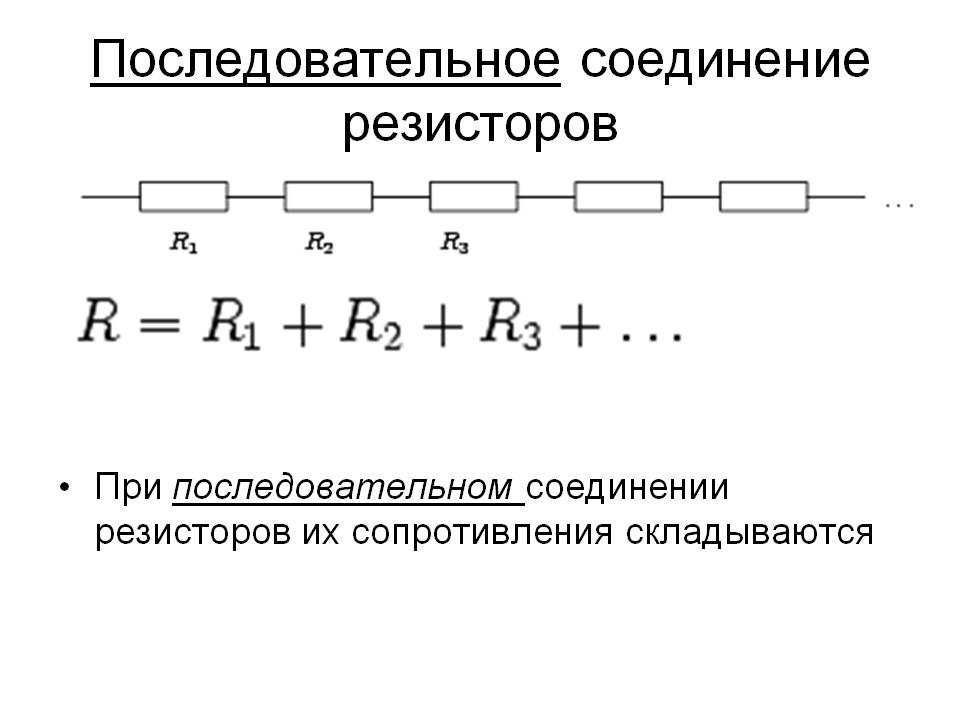

Как соединить резисторы параллельно

(Схема параллельного соединения резисторов)

В приведенном выше примере у нас есть простая схема с параллельным соединением резисторов. Параллельное соединение резисторов отличается тем, что концы каждого резистора не подключены к источнику питания, а вместо этого они имеют одну общую точку в качестве общего соединения. Кроме того, предположим, что провода имеют незначительное сопротивление.

Схемы резисторов – Закон Ома в цепи параллельного сопротивления

Мы используем закон Ома, чтобы найти индивидуальный ток, который протекает через каждый резистор параллельно. Это связано с тем, что падение потенциала одинаково на каждом резисторе. В случае, когда выходное напряжение постоянно на каждом резисторе, ток I=V/R

Схемы цепей резисторов– Ток и мощность в параллельных цепях

Для резисторов в цепи с параллельной конфигурацией падение напряжения на параллельной ветки одинаковые.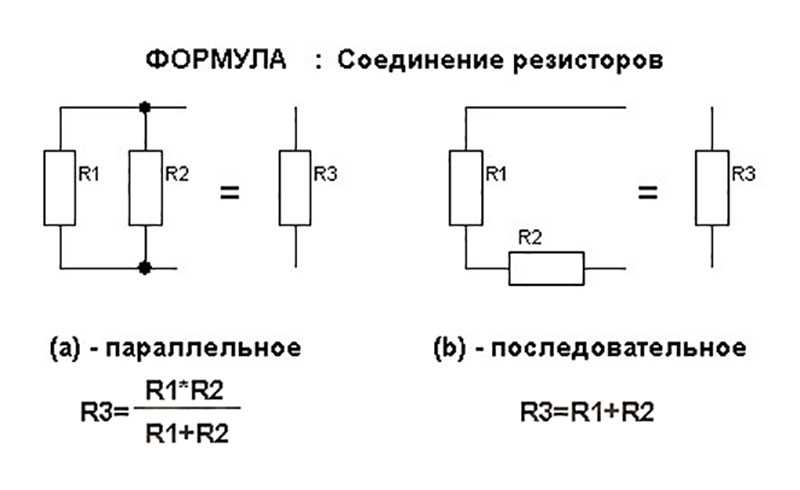 Кроме того, ток, протекающий по всей цепи, равен сумме индивидуальных токов, протекающих через каждый резистор. Однако, если вы добавите в цепь больше резисторов, общее сопротивление цепи уменьшится.

(Разделение тока при параллельном соединении)

Поскольку общий общий ток делится на каждый резистор.

Итак, применим уравнение для тока I_t=I_1+I_2

То есть общий ток, протекающий в цепи, равен добавленным разделенным токам, протекающим через резисторы.

Суммарная мощность, рассеиваемая резисторами, определяется с помощью P=VI. Где I — общий ток в амперах, а V — напряжение на каждом параллельном резисторе. Резисторы с самым значительным сопротивлением получают самый низкий ток, в то время как резисторы с самым маленьким индивидуальным сопротивлением получают самый превосходный ток.

Поэтому; P=VI

P = (I_1 + I_2) * V

Итак, для каждого резистора, резистор R_1 I1= V1/R1. Резистор R_2 I2= V2/R2

Эффективное сопротивление в параллельной цепи

На приведенной ниже диаграмме показано, как найти эффективное сопротивление в параллельной цепи.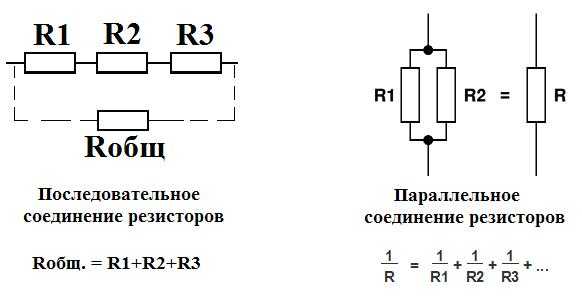

(схематическая диаграмма, объясняющая эффективное сопротивление)

Чтобы рассчитать эквивалентное сопротивление, нам нужно понять правило соединения в соответствии с петлевым законом Кирхгофа . Общее сопротивление в цепи с параллельной конфигурацией является обратной величиной суммы всех обратных сопротивлений. То есть; если у вас есть два резистора в параллельном соединении, практический расчет сопротивления становится;

Уравнения цепи следующие;

Так как ток разделяется в месте соединения, согласно правилу контура, то I=I1+I2

И, так как V=I1R1 и I1R1=I2R2

Тогда Ток, I =I_1+ I_2

Р2

, но V то же самое = V/R1+ V/R2

= V [1/R1+ 1/R2] = V/REQ

1/REQ = 1/R1+ 1/R2

Также, уравнение резистентности = [1/R1+ 1/R2]⁻¹

Комбинация резисторов в последовательном и параллельном соединении

В комбинации резисторов некоторые резисторы расположены последовательно, а другие — параллельно.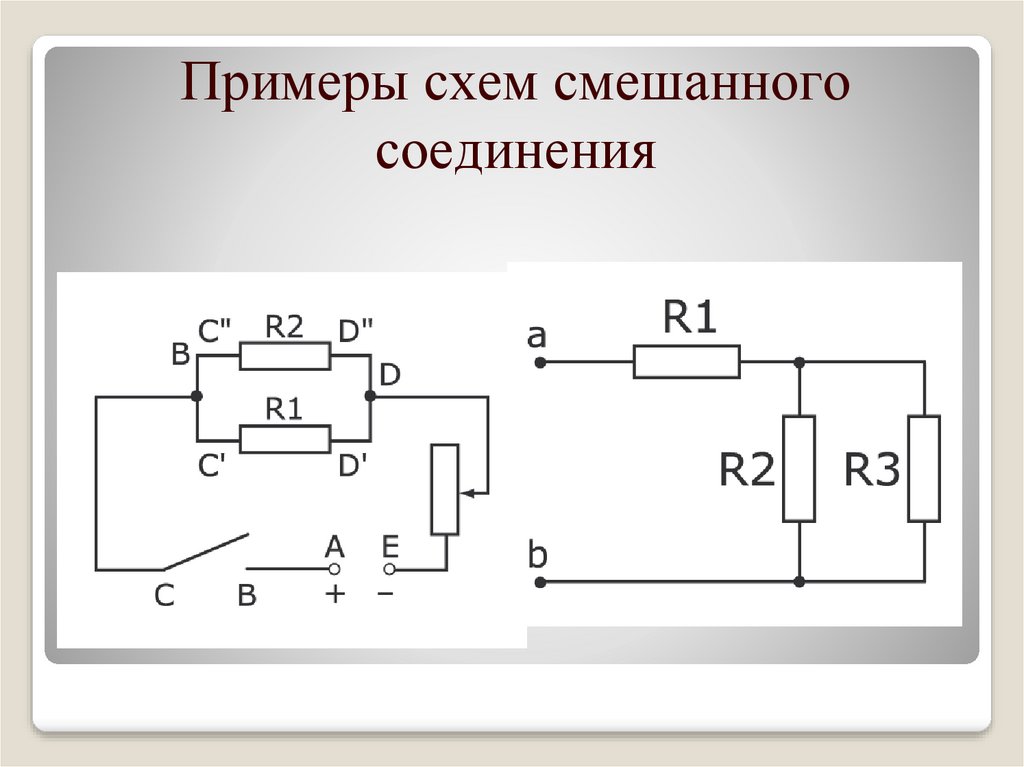

Самое главное, это больше сложных схем для понимания. Центральная концепция определения сопротивления в комбинированных цепях заключается в преобразовании всего курса в схему последовательного соединения. Это быстро делается путем применения понимания эквивалентного сопротивления в параллельной цепи ко всей комбинированной цепи.

Схемы резисторов – Как соединить резисторы последовательно и параллельно

(Схема комбинирования резисторов)

Соединение резисторов последовательно и параллельно довольно просто. Во-первых, все, что вам нужно сделать, это подключить R2 и R3 параллельно. Затем щелкните концы каждого резистора, чтобы создать узел. Теперь добавьте еще один резистор R1 к соединительному узлу, как показано на схеме выше. Наконец, подключите концы проводов к источнику питания. Общее сопротивление представляет собой сумму номиналов каждого резистора; в этом случае используйте для расчетов закон Ома.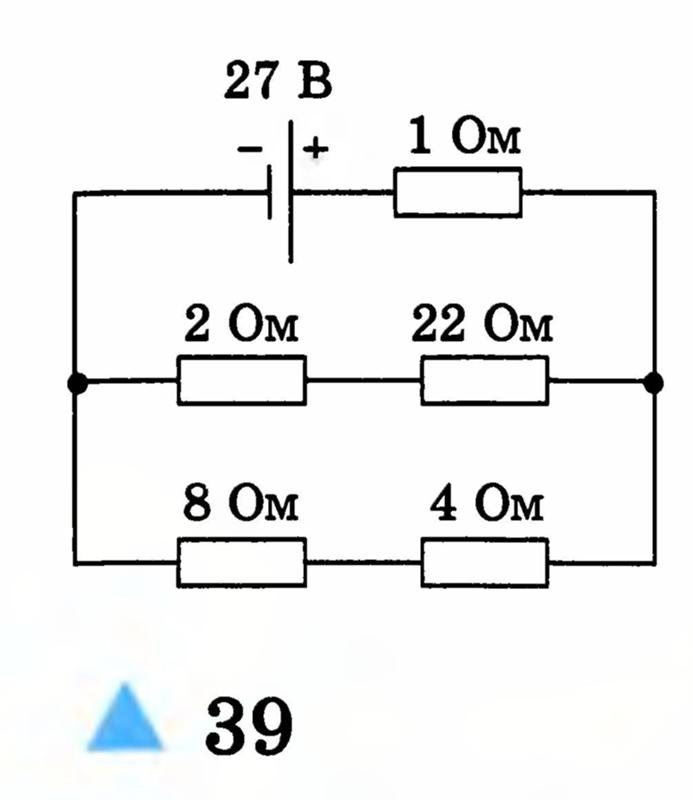

Схемы резисторных цепей – Ток и мощность в комбинации последовательных и параллельных цепей резисторов

Общий ток представляет собой сумму всех отдельных токов, как и мощность. Если несколько резисторов включены параллельно, то они будут иметь общий источник выходного напряжения. Важно отметить, что это при условии, что внутреннее сопротивление пренебрежимо мало. Это также означает, что напряжение на каждом резисторе будет меньше, чем если бы оно было последовательно.

(резисторы, подключенные последовательно и параллельно)

Если у вас есть комбинации резисторов, подключенных как последовательно, так и параллельно, вам придется использовать различные деления напряжения и тока. Помните, что это сложные связи для понимания.

Используйте комбинированную форму закона Ома, чтобы найти общий выходной ток, где I=V/R_total.

Это означает, что подключенные резисторы распределяют ток между собой.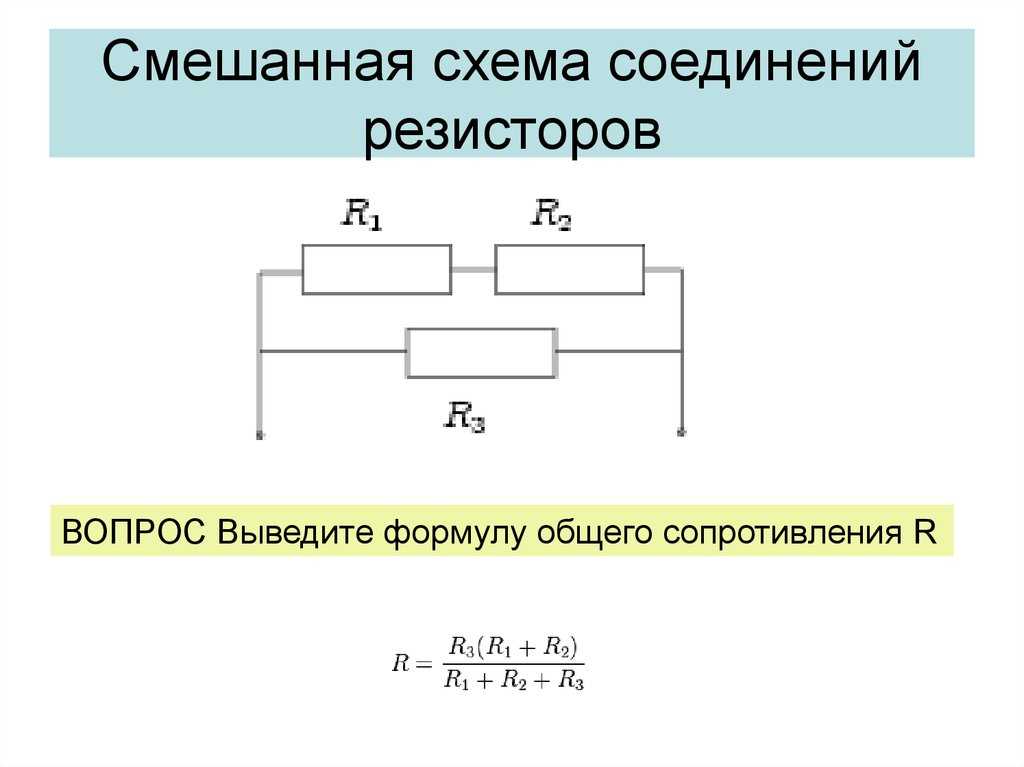

Общая мощность такая же, как и при последовательном соединении, но каждый резистор рассеивает меньший ток и напряжение.

P=VI = (Vsource/R_total) * I

Схемы резисторов – Эффективное сопротивление в последовательных и параллельных цепях

(Сочетание последовательных и параллельных цепей резисторов) резисторов зависит от их номиналов и способа соединения. Следовательно, общее сопротивление в различных цепях последовательных и параллельных резисторов находится с использованием закона Ома.

Во-первых, R_total = Req(Series) + Req(Parallel)

Тогда Req parallel= Req₂₃=(1/R2+ 1/R3)⁻¹

= (1/10 Ом + 1/10 Ом)⁻¹ = 5 Ом, параллельные резисторы

теперь последовательно с R1.

Таким образом, R-total=Req(серия) +Req(Parallel)

Rt= 5 Ом + 5 Ом = 10 Ом.

Объединение резисторов последовательно и параллельно помогает контролировать токи, ограничивая падение потенциала на электрической нагрузке.

Схемы резисторов – пример применения

(Схема холодильника)

В цепях холодильника присутствует комбинация цепей резисторов. На приведенной выше диаграмме, когда дверца холодильника открывается, лампочка тускнеет. Это связано с тем, что двигатель холодильника потребляет большой ток. В результате лампочка получает низкую мощность и затемняется, так как R1 в цепи испытывает большие перепады напряжения. Комбинации резисторов помогают ограничить максимальную величину тока, проходящего через цепь. В то же время они обеспечивают определенное снижение потенциала электрических нагрузок.

Резюме

В заключение мы рассмотрели три наиболее распространенных типа схем резисторов. Мы надеемся, что теперь вы лучше понимаете различные типы подключения и то, как они работают.

Теперь вы можете создавать схемы резисторов! Если у вас есть дополнительные вопросы о том, как это сделать, пожалуйста, свяжитесь с нами.

Резисторы в цепях — Задачи — Гиперучебник по физике

[закрыть]

практика

Определите следующие величины для каждой из двух цепей, показанных ниже…
1. эквивалент сопротивления
2. ток от блока питания
3. ток через каждый резистор
4. падение напряжения на каждом резисторе
5. мощность, рассеиваемая на каждом резисторе
На кухне в Северной Америке есть три прибора, подключенных к сети 120 В с автоматическим выключателем на 15 А: кофеварка на 850 Вт, микроволновая печь на 1200 Вт и 900 Вт тостер.
1. Нарисуйте принципиальную схему этой цепи.
2. Какие из этих приборов могут работать одновременно без срабатывания автоматического выключателя?
На приведенной ниже схеме показана схема с одной батареей и 10 резисторами; 5 слева и 5 справа. Определять…
1. ток через
2. падение напряжения на
3. мощность, рассеиваемая каждым резистором
Учитывая схему ниже…
1. Рассчитайте эквивалентное сопротивление цепи.
2. Рассчитайте ток через батарею.
3. Нарисуйте график зависимости напряжения от положения в цепи, предполагая, что В _a = 0 В на отрицательной клемме аккумулятора.
4. График тока в зависимости от положения в цепи.

концептуальный

Что происходит с полным током, когда резисторы добавляются в цепь…
1. последовательно?
2. параллельно?
Укажите две причины, по которым бытовые розетки не соединены последовательно.
Что означает термин «короткое замыкание»? Чем опасно короткое замыкание?

Источник питания и четыре одинаковые пронумерованные лампочки соединены вместе, как показано на схеме справа.

Расположите лампочки в порядке яркости.
Одним словом опишите влияние удаления любой из лампочек на яркость трех других.
1. Снять лампу 1
2. Снять лампу 2
3. Снять лампу 3
4. Удалить лампу 4

Соберите свои ответы на этот вопрос в таблицу, подобную приведенной ниже.

	Р ₁	Р ₂	Р ₃	Р ₄
а.
б. я.	×
б. II.		×
б. III.			×
б. IV.				×

Источник питания и четыре одинаковые пронумерованные лампочки соединены вместе, как показано на схеме справа.
1. Расположите лампочки в порядке яркости.
2. Одним словом опишите влияние удаления любой из лампочек на яркость трех других.
  1. Снять лампу 1
  2. Снять лампу 2
  3. Снять лампу 3
  4. Удалить лампу 4
Соберите свои ответы на этот вопрос в таблицу, подобную приведенной ниже.
Р ₁ Р ₂ Р ₃ Р ₄
а.
б. я. ×
б. II. ×
б. III. ×
б. IV. ×

цифровой

Учитывая схему справа, найдите …
1. падение напряжения на резисторе 4 Ом
2. падение напряжения на резисторе 5 Ом
3. ток через резистор 2 Ом
4. ток через резистор 7 Ом
Учитывая приведенную ниже схему, определите…
1. эквивалентное сопротивление всей цепи
2. ток от блока питания
3. ток через каждый резистор
4. падение напряжения на каждом резисторе
Четыре одинаковых резистора объединены четырьмя различными способами, как показано на схеме ниже. Для удобства пусть каждый имеет сопротивление 1 Ом. Знаки + и — показывают клеммы каждой комбинации.
1. Какая комбинация строго параллельна? Определить его полное сопротивление.
2. Какая комбинация строго серия? Определить его полное сопротивление.
3. Какую из двух комбинаций вы проанализировали в частях а. и б. имеет меньшее сопротивление? Почему сопротивление меньше?
4. Определите эквивалентное сопротивление двух оставшихся комбинаций.
5. Какие из двух комбинаций вы проанализировали в части d. имеет меньшее сопротивление? Почему сопротивление меньше?
Приведенная ниже схема состоит из одиннадцати одинаковых резисторов сопротивлением 1 Ом, подключенных к источнику питания 15 В. Определять…
1. общее сопротивление всей цепи
2. ток от блока питания
3. ток через резистор R ₁
4. ток через резистор R ₂
5. ток через резистор R ₃
Двенадцать одинаковых резисторов сопротивлением 1 Ом соединены в цепь, состоящую из двух квадратных контуров, как показано на схеме справа.