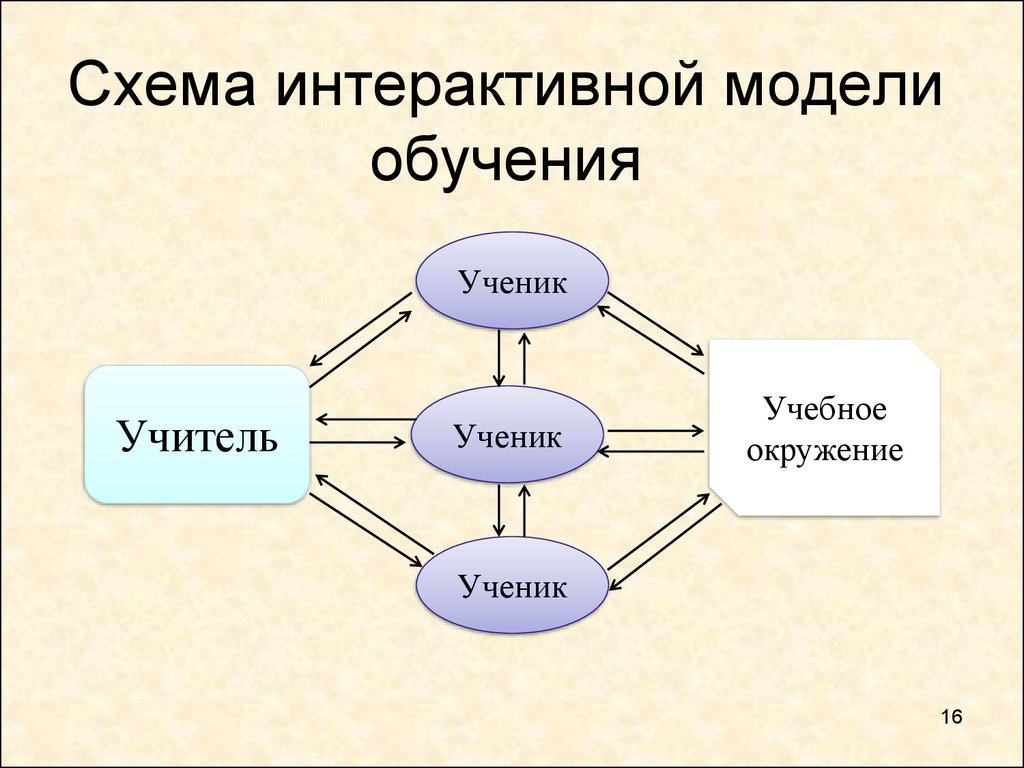
Математические схемы моделирования систем.

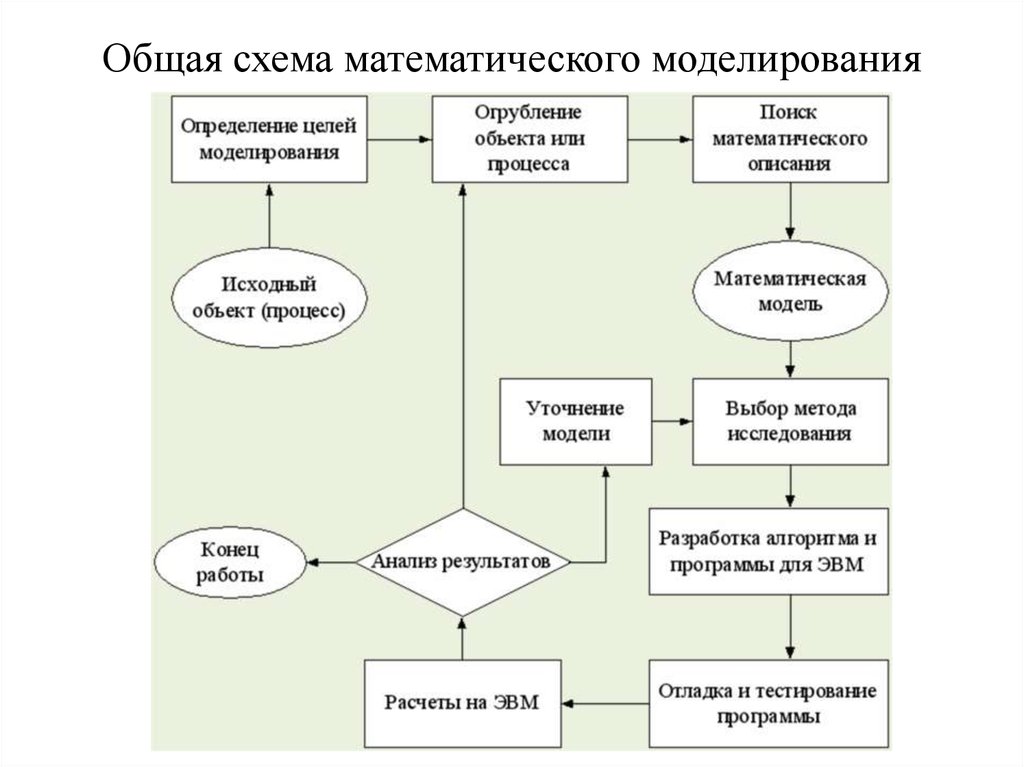
Исходной информацией при построении математических моделей процессов функционирования системы служат данные о назначении системы, условиях функционирования системы. Эта информация определяет цель моделирования и позволяет сформулировать требования, предъявляемые к моделям. На первом этапе моделирования составляется содержательное описание процессов, являющееся первой попыткой описать закономерности, характерные для исследуемого объекта. На основе словесного описания составляется формальная или математическая схема процесса.

Математическая схема – это звено при переходе от описательного к строго функциональной записи объекта, т.е. к математической модели.

Математическая схема представляет собой набор графов, таблиц или логических условий, формализация которых (запись с помощью полиномов, дифференциальных, интегральных уравнений) дает математическую модель. Математическая схема является необязательным звеном.

При составлении математической модели необходимо решить вопрос о ее полноте. Полнота определяется выбором границы «система S – внешняя среда Е». Также на этом этапе необходимо решить задачу упрощения модели, т.е. выделить основные свойства и отбросить второстепенные.

Описывать процессы в объекте можно с помощью различных математических схем. Среди них выделяют типовые математические схемы. Они отличаются наглядностью и простотой, но при этом существенным снижением возможности их применения.

При построении математических моделей процесса функционирования систем можно выделить следующие подходы:

1. Непрерывно — детерминированный подход

2. Дискретно — детерминированный подход

3. Дискретно — стохастический подход

4. Непрерывно — стохастический подход

5. Обобщенный подход (универсальный)

При непрерывно-детерминированном подходе в качестве модели используются обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и интегральные уравнения.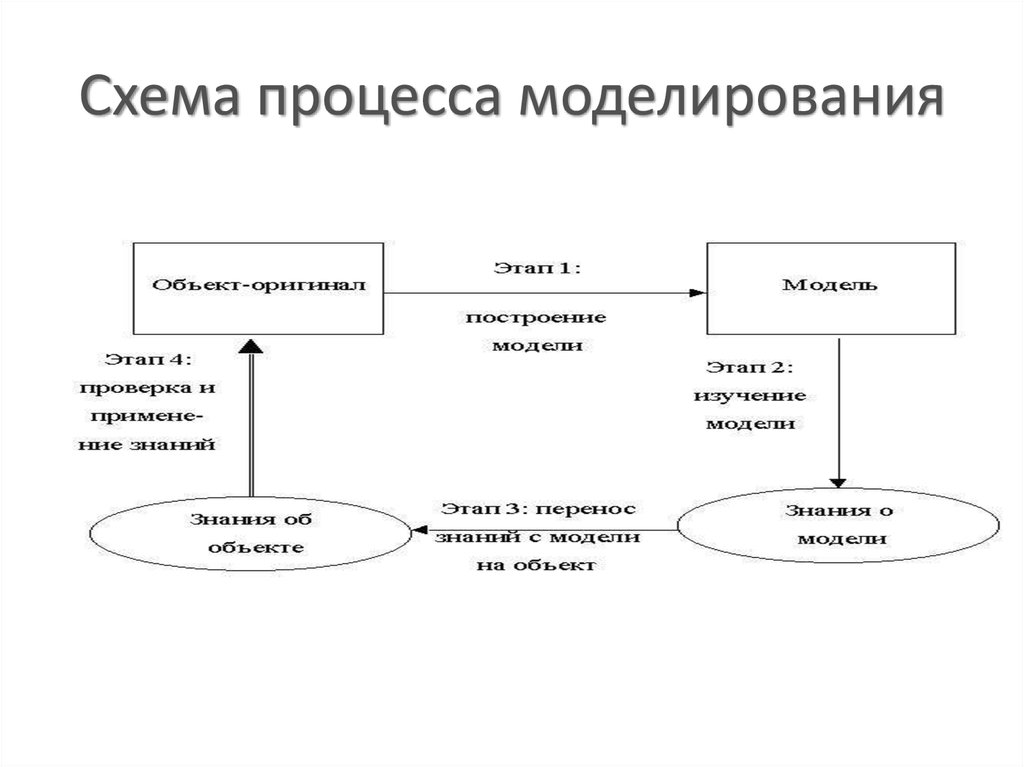 В этих моделях в качестве независимой переменной, от которой зависит искомая функция, рассматривают время.

Построение математических схем при дискретно-детерминированном подходе основано на использовании автоматов. Автомат – устройство, на которое подаются входные сигналы и снимаются выходные сигналы, которое может иметь некоторые внутренние состояния.

Построение математических схем при дискретно-стохастическом подходе основано на использовании вероятностных автоматов (Р-автоматов). Вероятностным автоматом называется дискретный потактовый преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти и описывается статистически.

Построение математических схем при непрерывно – стохастическом подходе основано на использовании систем массового обслуживания. Система массового обслуживания – класс математических схем для формализации процесса функционирования систем, которые по сути являются процессами обслуживания.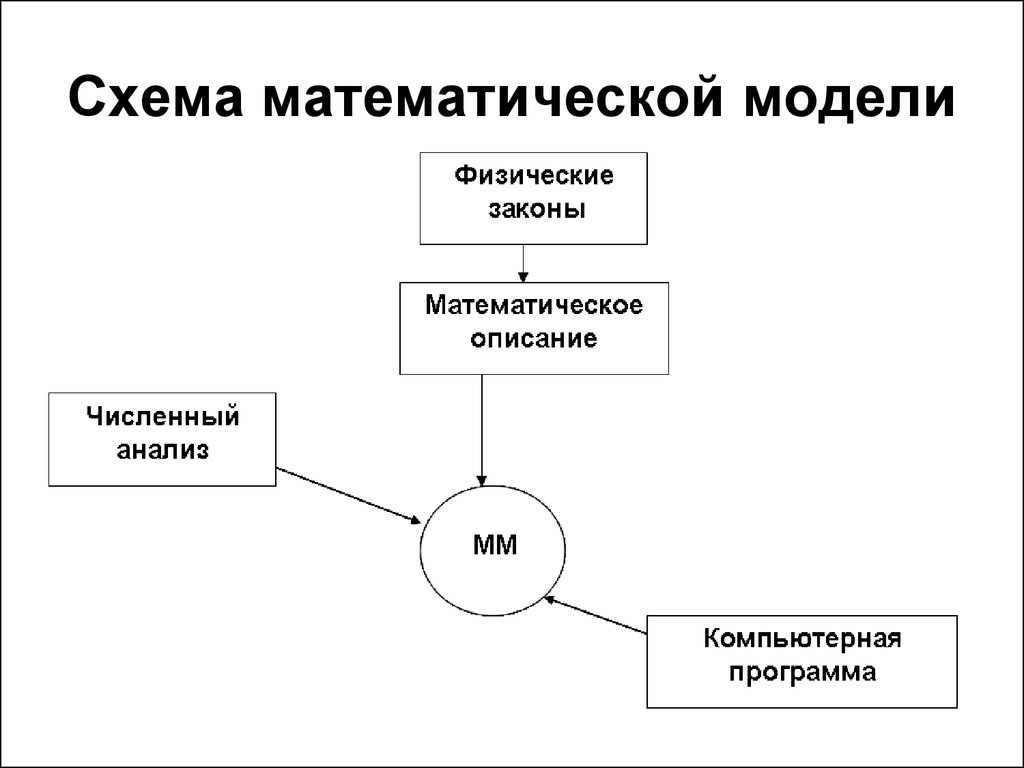

Обобщенный подход описывает поведение непрерывных и дискретных, детерминированных и стохастических систем, то есть является обобщенным (универсальным) и основан на понятии агрегативной системы (англ. Aggregate system), представляющей собой формальную схему общего вида, которая называется А-схемой.

Страница не найдена — 404 ошибка

Инновационный подход к разработке электроники

авторизация

• О компании
  • Дистрибьюторы
  • Партнеры
  • Логотипы
• Продукты

  • Система автоматизированного проектирования электронных устройств

    Узнать больше

    модули

    • LiBerty
      Менеджер библиотек
    • FlexyS
      Схемотехнический редактор
    • SimOne
      Система аналогового моделирования
    • Simtera
      Система цифрового моделирования
    • DRM
      Система управления правилами
    • RightPCB
      Редактор плат
    • TopoR
      Автоматический трассировщик
    • ЕСКД
      Модуль подготовки комплекта конструкторской документации
    • IPR
      Система хранения данных
    • DeltaCAM
      Проверка и редактирование производственных файлов

  • ОСРВ для встраиваемых систем

    Узнать больше

    модули
  • Истории успеха
  • Учебный центр
  • Скачать/Купить
    • Delta Design
    • Delta ЭКБ
    • FX-RTOS
  • База знаний
  • Сообщество
    • Блог
    • Новости
    • Мероприятия
    • Форум
  • Карьера
  • Контакты

  Будьте в курсе новостей и спецпредложений

  Симулятор схемы Spice и разработка аналоговой схемы

  Бесплатная пробная версия Как купить Свяжитесь с нами

  Вы находитесь здесь

  Главная » ПРОДУКТЫ » OrCAD PSpice Designer

  Особенности продукта

  Мощное моделирование

  Анализ и оптимизация важных аналоговых схем и компонентов с помощью родных технологий OrCAD PSpice , смешанные сигналы и механизмы анализа

  Оптимизация схемы

  Повышение производительности схемы, выхода и надежности с помощью анализа температуры и нагрузки, анализа наихудшего случая, анализа методом Монте-Карло и анализа оптимизации производительности

  Непревзойденный просмотр и анализ сигналов

  Глубокое погружение в результаты моделирования благодаря мощной поддержке просмотра, анализа и постобработки сигналов без повторного запуска моделирования

  Расширенные возможности

  Широкая поддержка моделей

  Более 33 000 готовых к моделированию аналоговых и смешанных устройств, математических функций и поведенческого моделирования

  Платформа с открытой архитектурой

  Пользовательская адаптация среды PSpice для улучшения и расширения ее возможности создания пользовательских функций, решений и потоков

  Предыдущая Пауза Next

  PSpice AA New Feature

  Добавление допусков к моделям

  Enhanced PSpice AA Flow

  Обзорная демонстрация

  Новое в PSpice AA

  Назначение глобальных допусков3

  9 PSpice0003

  История клиента

  Tata Motors and Pspice

  Виртуальное прототипирование

  Автоматизация кода генерация

  Pspice

  Частичное моделирование дизайна

  Matlab Simulink

  Electromechanical

  Smovemulate Smoade Smoade

  Smovemulate

  Smovemulate

  Smovemulate

  Domit

  Анализ напряжений в компонентах

  Подгонка кривой

  Соответствие заранее определенной цели

  Свяжитесь с местным торговым партнером OrCAD

  Глобальные торговые партнеры OrCAD предлагают технические знания и услуги мирового уровня, необходимые для достижения успеха. По вопросам продаж, технической поддержки или обучения OrCAD обращайтесь к местному торговому партнеру.

   

  Как купить

  Запустите бесплатную пробную версию OrCAD

  Получите бесплатный доступ к полной версии последней версии программного обеспечения для электронного проектирования OrCAD, включая OrCAD Capture CIS, OrCAD PSpice Designer, OrCAD PCB Designer Professional, OrCAD Sigrity ERC и многое другое.

   

  Бесплатная пробная версия

  Сообщество пользователей PSpice

  Сообщество пользователей PSpice предоставляет единый источник всех ресурсов по PSpice: заметок по применению, примеров проектирования, видеоруководств и имитационных моделей от основных поставщиков ИС. Кроме того, для пользователей PSpice создано новое онлайн-сообщество,  вы можете делиться идеями о дизайне, задавать технические вопросы, получать рекомендации по продуктам и услугам и строить сеть со своими коллегами.

   

  Посетите PSpice.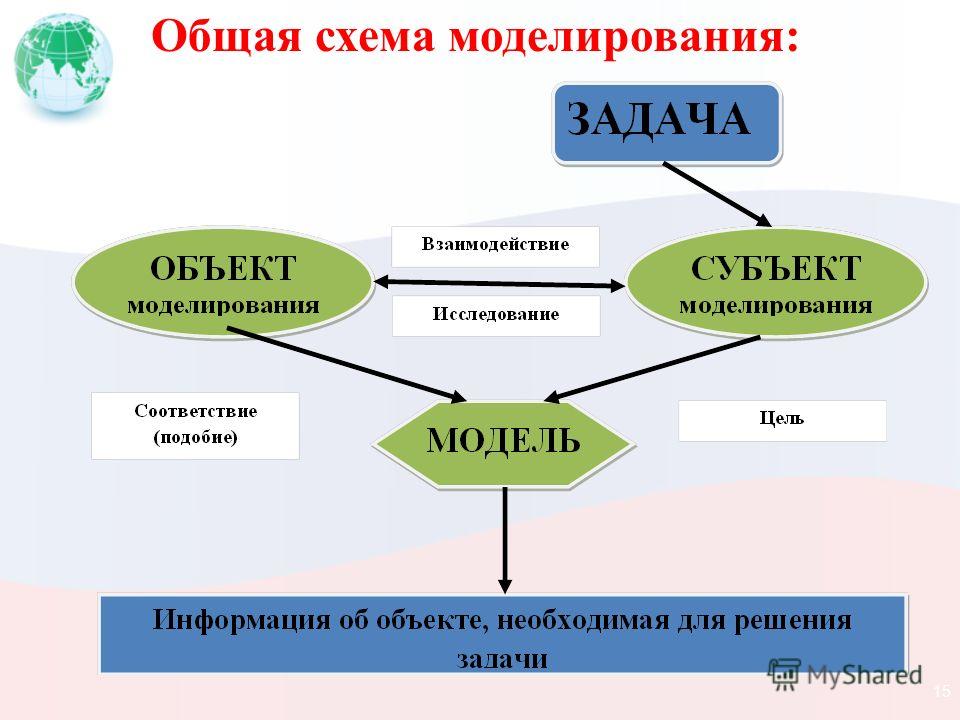 com

  Моделирование схем | Wiley

  Выбранный тип: Электронная книга

  130,00 $

  Фарид Н. Наджм

  ISBN: 978-0-470-56120-1 апрель 2010 г. Wiley-IEEE Press 352 страницы

  • Электронная книга

    Всего от 130 долларов США

  • Распечатать

    Всего от 161,95 долл. США

  • О-бук

     

  Электронная книга

  com, you will access either Wiley Reader or the VitalSource Bookshelf Software.</li> <li>E-books have DRM protection on them, which means only the person who purchases and downloads the e-book can access it.</li> <li>E-books are non-returnable and non-refundable.</li> <li>To learn more about our e-books, please refer to our&nbsp;<a href="https://www.wiley.com/wiley-ebooks" target="_blank">FAQ</a>.</li> </ul> » data-original-title=»» title=»»/>

  130,00 $

  Твердый переплет

  161,95 $

  O-Book </p>» data-original-title=»» title=»»/>

  Загрузить флаер продукта

  Загрузить рекламный проспект

  Загрузить флаер продукта для загрузки PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.

  Описание

  ОПИСАНИЕ ПО РАЗРАБОТКЕ СИМУЛЯТОРОВ СХЕМ

  Circuit Simulation дает четкое описание численных методов и алгоритмов, которые являются частью современных симуляторов цепей, с акцентом на наиболее часто используемые режимы моделирования: анализ постоянного тока и анализ переходных процессов. Этот уникальный текст, протестированный в рамках курса по моделированию схем в Университете Торонто, дает читателю достаточную детализацию и математическую точность для написания собственного базового симулятора схем.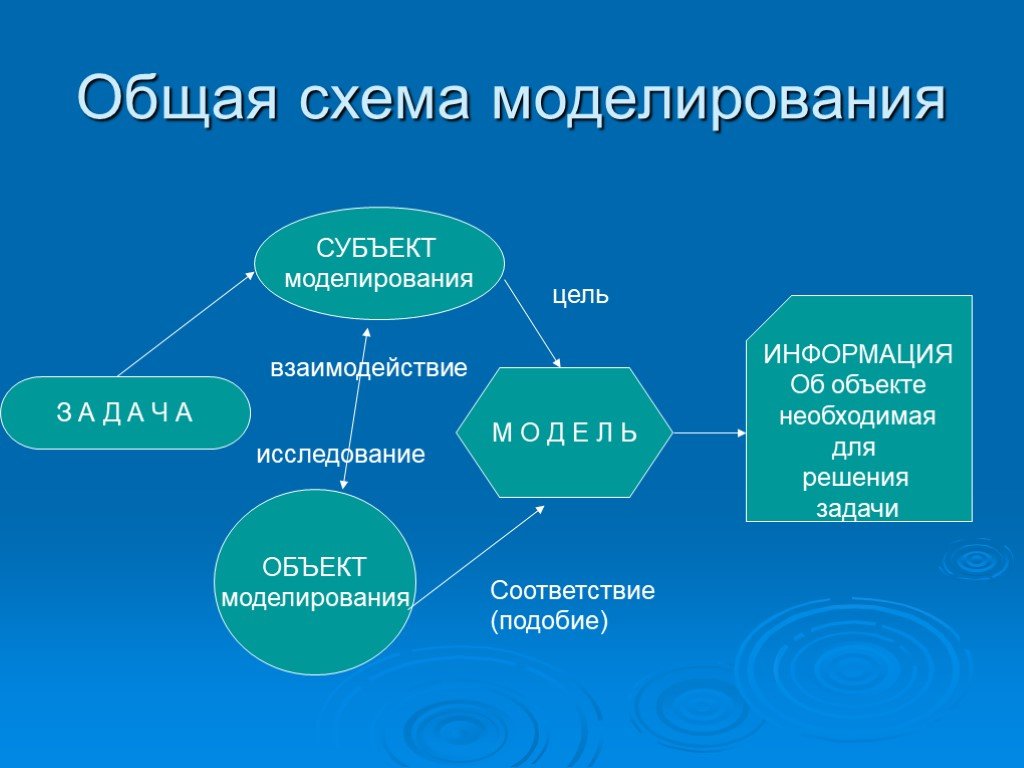 Везде подробно описаны математические и численные методы, лежащие в основе различных тем моделирования, что способствует полному пониманию практических методов моделирования. Кроме того, имитация цепей:

  • Исследует ряд современных методов численного анализа, которые нигде больше не синтезированы
  • Подробно описывает формулировку сетевого уравнения с акцентом на модифицированный узловой анализ
  • Дает всестороннее рассмотрение наиболее важных аспектов линейной и нелинейной системы методы решения
  • Формулирует все теоремы без доказательства, чтобы сосредоточить внимание на конечной цели обеспечения охвата практических методов моделирования
  • Содержит множество справочных материалов для дальнейшего изучения
  • Позволяет новичкам в моделировании цепей понять материал конкретным и целостным образом

  С наборами задач и компьютерными проектами в конце каждой главы «Моделирование цепей» идеально подходит для курса для выпускников на эту тему. Это также практический справочник для инженеров-конструкторов и специалистов по автоматизированному проектированию, а также для исследователей и разработчиков как в промышленности, так и в научных кругах.

  Об авторе

  ФАРИД Н. НАДЖМ — профессор кафедры электротехники и вычислительной техники (ECE) Университета Торонто. Он получил степень бакалавра в области электротехники в Американском университете Бейрута (AUB) в 1983 году и степень доктора философии ECE в Университете Иллинойса в Урбана-Шампейн (UIUC) в 1989 году. Затем он работал в Texas Instruments, прежде чем присоединиться к ECE. кафедрой в UIUC в должности доцента, позже доцента. Д-р Наджм присоединилась к кафедре ДО в Университете Торонто в 1999, где он в настоящее время является профессором и заведующим кафедрой. Его опыт находится в области автоматизированного проектирования интегральных схем с упором на проблемы на уровне схемы, связанные с мощностью, синхронизацией, изменчивостью и надежностью. Доктор Наджм является членом IEEE.

  Разрешения

  Запросить разрешение на повторное использование контента с этого сайта

  Содержание

  Список рисунков xiii

  Список таблиц XIX

  Предисловие XXI

  1 ВВЕДЕНИЕ 1

  1.1 Уравнения устройства 2

  1,2 Уравнение состав 3

  1.3. 8

  1.4 Процесс моделирования схемы 8

  1.4.1 Режимы анализа 9

  Примечания 10

  Проблемы 10

  2 Сетевые уравнения 13 Сеть 13

  .

  Элементы0003

  2.1.1 Пассивные элементы 13

  2.1.2 Активные элементы 15

  2.1.3 Эквивалентная схема модели 17

  2.1.4 Классификация сети 18

  2.2 Топологические ограничения 19

  2.2.1 Сетевые графики 19

  2.3 Пространство циклов и пространство связей 23

  2. 3.1 Назначение тока 23

  2.3.2 Назначение напряжения 24

  2.3.3 Ортогональные пространства 24

  2.3.4 Топологические ограничения 25

  2 20003

  2.3.6 Разница в фундаментальной потенциалах 27

  2.4 Составление линейных алгебраических уравнений 27

  2.4.1 Анализ Sparse Tableau 28

  2.4.2. Анализ 33

  2,5 Составление линейных динамических уравнений 42

  2.5.1 Глопов динамических элементов 43

  2.5.2 Уникальная уникальность 44

  Примечания 45

  Проблемы 45

  3 Решение линейной аллежной схемы 49 4

  3.1 Прямые методы 50

  3.1.1. 73

  3.2 Точность и стабильность GE 74

  3.2.1 Ошибка 75

  3.2.2 Номера плавающей запятой 78

  3.2.3 Нормы 80

  3.2.4 Стабильность GE и факторизации LU 83

  3.2.5 Поворот для точности 86

  3.2.6 Кондиционирование AX = B 89

  3.2.7 Итеративная уточнение 96

  3.3 Косвенные/итерационные методы 97

  3. 3.1 Гаусс-Якоби 98

  3.3.2 Гаусс-Сидель 99

  3.3.3 Конвергенция 100

  3.4 Методы разделения 104

  3.4.1 Разрыв узела 104

  3.4.2 Прямые методы 106

  3.4.3 Коскреционные методы 107

  3,5 ТЕХНОСТИЦА SPARSE MATRIX 109

  3.5.1 SPARSE MATRIX MATRIX MATRIX 110

  3.5.1 SPARSE MATRIX MATRIX 110 0003

  3.5.1. 3.5.2 Разреженная GE и LU факторизация 112

  3.5.3 Переупорядочение и редкость 113

  3.5.4 Поворота для редкости 115

  3.5.5 Марковиц. Переворажение 116

  3.5.6 Диагональный поворот 119

  3.5.7 Симметричный (SPD). Случай 120

  3.5. 8 Расширение на случай не-SPD.0002 4.1.2 Нелинейная формулировка MNA 129

  4.1.3 Подготовка к анализу постоянного тока 133

  4.2 Методы решения 133

  4.2.1 Итерационные методы и сходимость 134

  4.2.2 Введение в метод Ньютона 136

  4.2.3 Одномерный случай 139

  4.2.4 Многомерный случай 148

  4. 2.5 Квазиньютоновские методы 152

  4.3 Применение к моделированию цепей 154

  4.3.1 Линеаризация и сопутствующие модели 153

  0002 4.3.2 Некоторые тестовые случаи 156

  4.3.3 Обобщение 162

  4.3.4 Воспитания для многомерных элементов 166

  4.3.5 Многомерная дифференциация 167

  4.3.6 Линеаризация многомерных элементов 171

  4.3.7 Элементы с Внутренние узлы 176

  4.4 Квазиньютоновские методы моделирования 181

  4.4.1 Методы демпфирования 182

  4.4.2 Обзор более общих методов 186

  4.4.5 Псевдо-транзистое 189

  4.4.6 Обоснование для псевдо-транспортного средства 193

  Примечания 196

  Проблемы 197

  5 Решение уравнений дифференциальной схемы 201

  5.1 Дифференциальные сетевые уравнения 201

  5.1. 1 Динамические элементы 201

  5.1.2 Динамические уравнения MNA 203

  5.1.3 ДАУ и ОДУ 204

  5.2 Методы решения ОДУ 206

  5.2.1 Системы ОДУ и основные теоремы 206

  0002 5. 2.2 Обзор методов решения 209

  5.2.3 Три основных метода: FE, BE и TR 211

  5.2.4 Метрики качества 215

  5.2.5 Линейные многошаговые методы 220

  Точность 2 методов LMS 5.3

  5.3.1 Заказ 221

  5.3.2. Согласованность 223

  5.3.3. Формулы обратной дифференциации 224

  5.3.4 Ошибка локального усечения 225

  5.3.5. Получение методов LMS 228

  5.3.6 Implyce Методы 229

  5.3.7 Интерполяция полиномиал 231

  5.3.8 Оценка LTE 237

  5.4 Стабильность методов LMS 241

  5.4.1 Теория линейной стабильности 242

  5.4.2 Тестовое уравнение 243

  5.4.3 Абсолютная стабильность 246

  5.4.4 Жесткие системы 252

  5.4.5 Стабильность жесткой стабильности 253

  5.4.6 ЗАМЕЧАНИЯ 256

  5.5 ТРЕЗОВОДНОЕ ЗВЕЛОВОЕ Пошаговые методы 261

  5.6.1 Реализация изменения шага по времени 262

  5.6.2 Методы интерполяции 262

  5.6.3 Методы с переменным коэффициентом 264

  5.