12 Полусумматор, сумматор, алу. Схемы. Основные понятия. Сложить два числа и показать результат сложения на пк.
Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа.
Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100.
Полусумматор
Теперь
не будем обращать внимание на перенос
из предыдущего разряда и рассмотрим
только, как формируется сумма текущего
разряда. Если были даны две единицы или
два нуля, то сумма текущего разряда
равна 0. Если одно из двух слагаемых
равно единице, то сумма равна единицы. Получить такие результаты можно при
использовании вентиля ИСКЛЮЧАЮЩЕГО
ИЛИ.
Получить такие результаты можно при
использовании вентиля ИСКЛЮЧАЮЩЕГО
ИЛИ.
Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И.
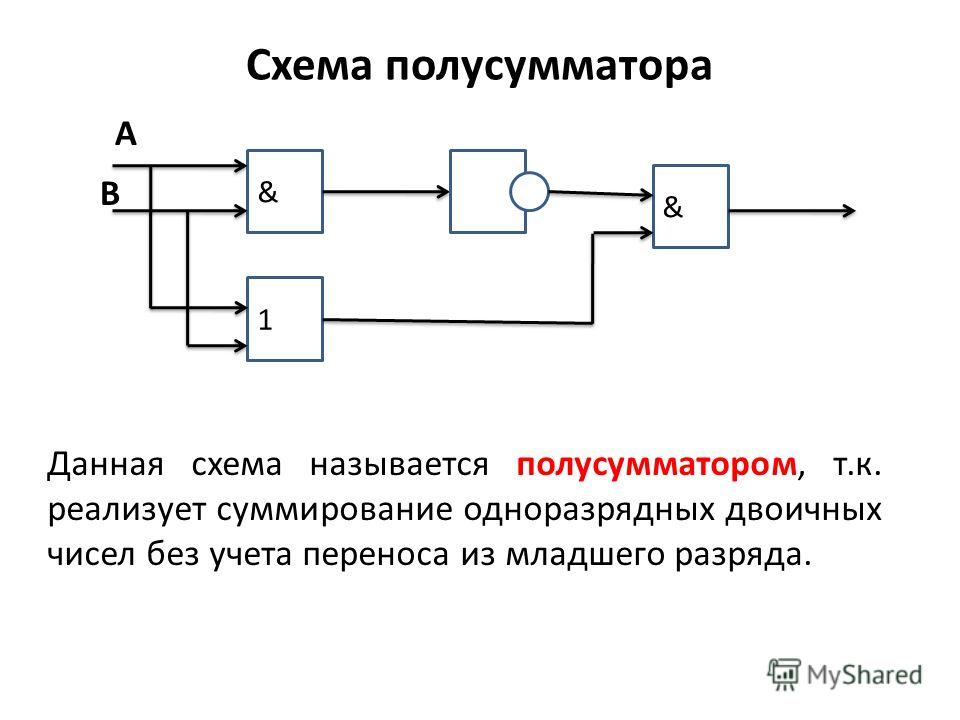
Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И.
Сумматор
В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа.
Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров.
Рассмотрим
один из случаев. Требуется сложить 0 и
1, а также 1 из переноса. Сначала определяем
сумму текущего разряда. Судя по левой
схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и
b, на выходе получаем единицу.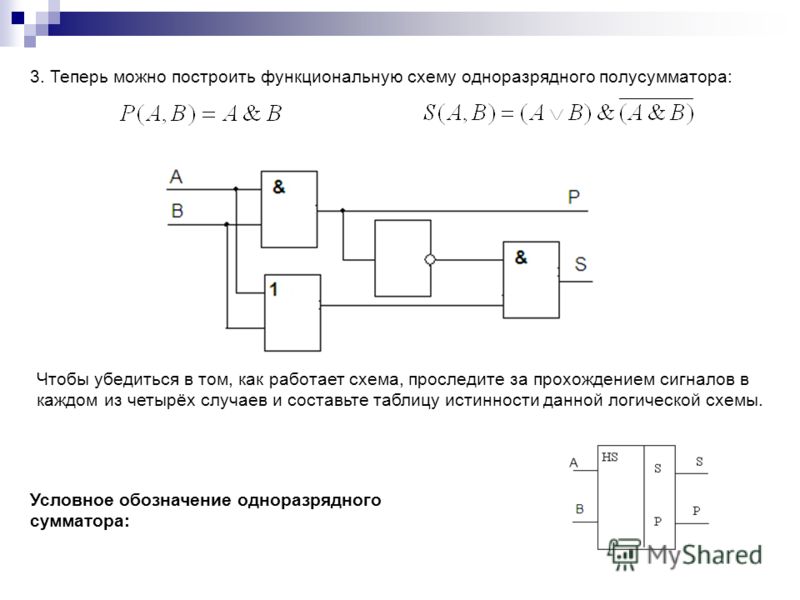 В следующее
ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы.
Следовательно, сумма будет равна 0.
В следующее
ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы.
Следовательно, сумма будет равна 0.
Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности.
13.Синхронные суммирующие счётчики
14.Синхронные вычитающие счётчики
На
рис. 3.34 приведена схема асинхронного
трехразрядного двоичного вычитающего
счетчика, построенного на базе D-триггеров.
Отметим, что условия для изменения
состояний триггеров вычитающих счетчиков
аналогичны условиям для суммирующих
счетчиков с той лишь разницей, что они
должны “опираться” на значения
инверсных, а не прямых выходов триггеров.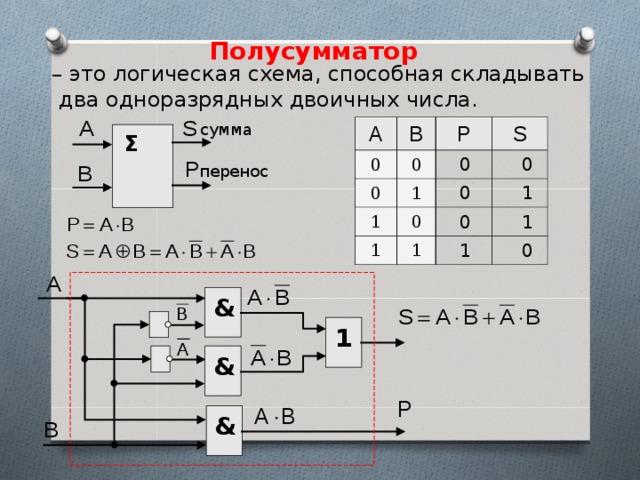
Работа вычитающего счетчика на D-триггерах наглядно иллюстрирована на рис. 3.34, (б). Из рис. 3.34 следует, что после нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние “1”. Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, снова, все триггеры обнуляются и цикл счета повторяется, что соответствует модулю М=8.
В
некоторых случаях необходимо, чтобы
счетчик мог работать как в прямом, так
и в обратном направлении счета.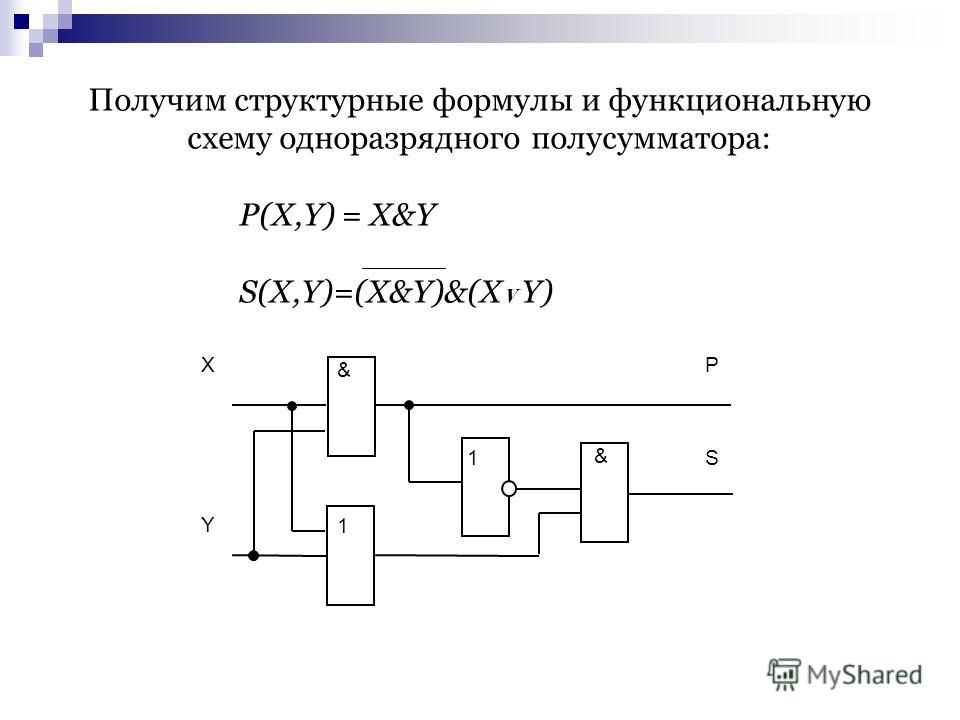 Такие счетчики называются реверсивными.
Реверсивные счетчики могут быть как
асинхронного, так и синхронного типа.
Они строятся путем применения логических
коммутаторов (мультиплексоров) в цепях
связи между триггерами. Так, например,
асинхронный реверсивный двоичный
счетчик можно построить, если обеспечить
подачу сигналов с прямого (при суммировании)
или с инверсного (при вычитании) выхода
пре-дыдущего JK- или Т-триггера на счетный
вход последующего. В случае, когда
реверсивный счетчик строится на базе
D-триггеров, управляемых передним
фронтом, для получения режима прямого
счета следует соединить инверсный выход
предыдущего с счетным входом последующего
триггера.
Такие счетчики называются реверсивными.
Реверсивные счетчики могут быть как
асинхронного, так и синхронного типа.
Они строятся путем применения логических
коммутаторов (мультиплексоров) в цепях
связи между триггерами. Так, например,
асинхронный реверсивный двоичный
счетчик можно построить, если обеспечить
подачу сигналов с прямого (при суммировании)
или с инверсного (при вычитании) выхода
пре-дыдущего JK- или Т-триггера на счетный
вход последующего. В случае, когда
реверсивный счетчик строится на базе
D-триггеров, управляемых передним
фронтом, для получения режима прямого
счета следует соединить инверсный выход
предыдущего с счетным входом последующего
триггера.
Все
рассмотренные типы счетчиков могут
быть использованы в цифровых устройствах
“умеренного” быстродействия, когда
частота следования синхроимпульсов не
превышает критического значения, при
котором время задержки установки
триггеров последних (старших) разрядов
счетчика становится соизмеримым с
длительностью периода входных тактовых
импульсов.
15.Синхронный счётчик с изменённым коэффициентом пересчёта. Собрать счётчик по М=10.Последовательное включение двоично-десятичных счётчиков.
16.Дешифраторы. Условные понятия. Пример дешифратор 3×8. Таблица истинности.
Дешифратор
(декодер) — это узел, преобразующий код,
поступающий на его входы, а сигнал только
на одном из его выходов. Дешифраторы
широко применяются в устройствах
управления, в системах цифровой индикации
с газоразрядными индикаторами, для
построения распределителей импульсов
по различным цепям и т.д. Схема используется
я перевода двоичных цифр в десятичные.
Дешифратор двоичного n-разрядного кода
имеет 2n выходов, т.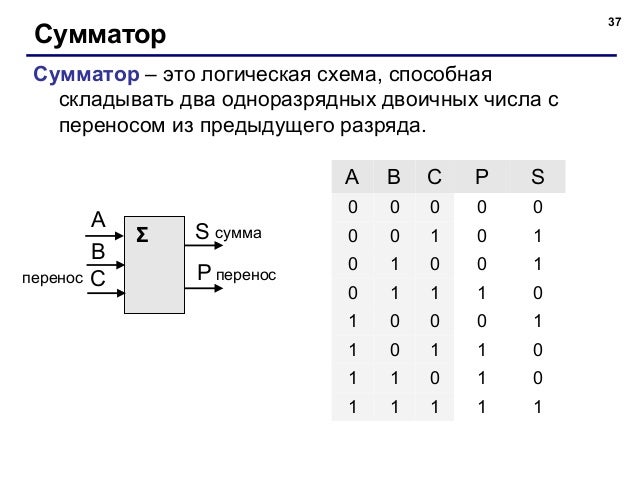 к. каждому из 2
к. каждому из 2
Таблица С.
Входы | Выходы (Y) | |||
Х2 | Х1 | Х0 |
| |
0 | 0 | 0 | 0 | |
0 | 0 | 1 | 1 | |
0 | 1 | 0 | 2 | |
0 | 1 | 1 | 3 | |
1 | 0 | 0 | 4 | |
1 | 0 | 1 | 5 | |
1 | 1 | 0 | 6 | |
1 | 1 | 1 | 7 | |
Логические
функции, описывающие работу такого
дешифратора:
Y0=
Y1=
X0 .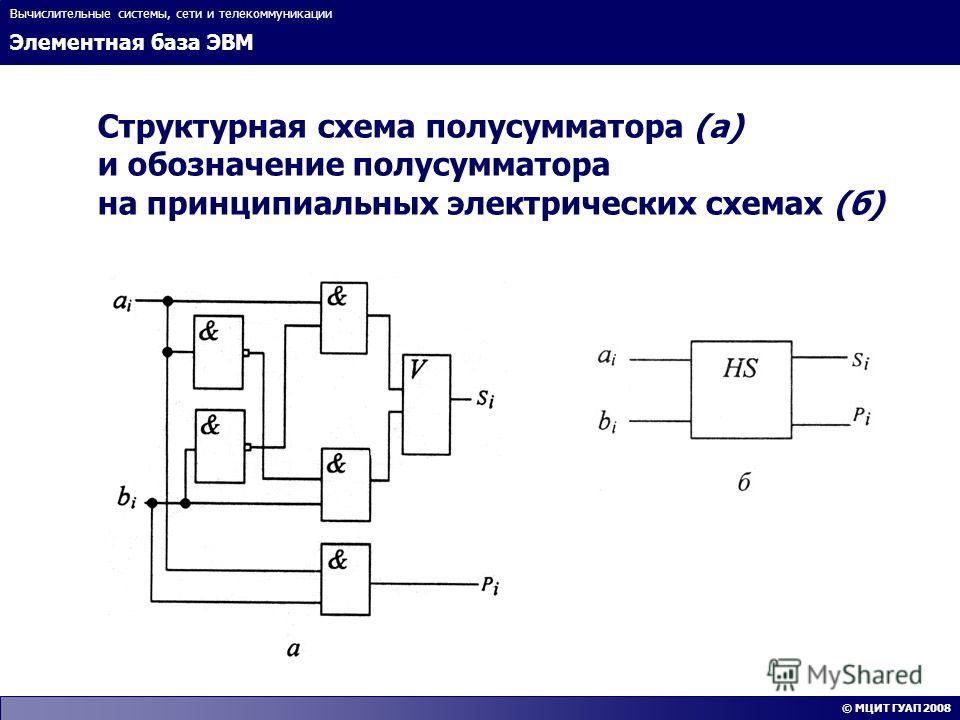 .
.
Y7=X2X1X0 На
рисунке 13.2. показаны функциональная
схема и условное обозначение
одноступенчатого дешифратора на 3 входа.
.
.
Y7=X2X1X0 На
рисунке 13.2. показаны функциональная
схема и условное обозначение
одноступенчатого дешифратора на 3 входа.
Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Полусумматор подходит для сложения битов нижних разрядов двух многобитовых слов. Но он не годится для сложения битов в середине слова, потому что не может осуществлять перенос в эту позицию. Из схемы должно быть ясно, что полный сумматор состоит из двух полусумматоров. Два полусумматора порождают и биты суммы, и биты переноса. [1]
| Логическая схема полусумматора. [2] |
Полусумматор ( или одноразрядный сумматор на два входа) представляет собой схему, обеспечивающую сложение цифр одного разряда двух слагаемых, не учитывающую возможности переноса из соседнего младшего разряда.
Полусумматор — это такая реализация сумматора, в которой предусмотрены только входы для битов, первого и второго слагаемых, а на выходе генерируются сумма и бит переноса. [4]
Полусумматор производит сложение двух одноразрядных двоичных чисел. Суммирование производится элементом Исключающее ИЛИ, а перенос — элементом И. [5]
| Полный сумматор. [6] |
Полусумматоры и полные сумматоры обычно используются вместе. [7]
Полусумматоры и полные сумматоры — сравнительно простые схемы, однако при необходимости сложения многоразрядных двоичных чисел таких схем требуется довольно много. [8]
Двоичный полусумматор, рассмотренный в гл. [9]
Порядок двоичного суммирования.| Логическая структура полусумматора. а — общий вид.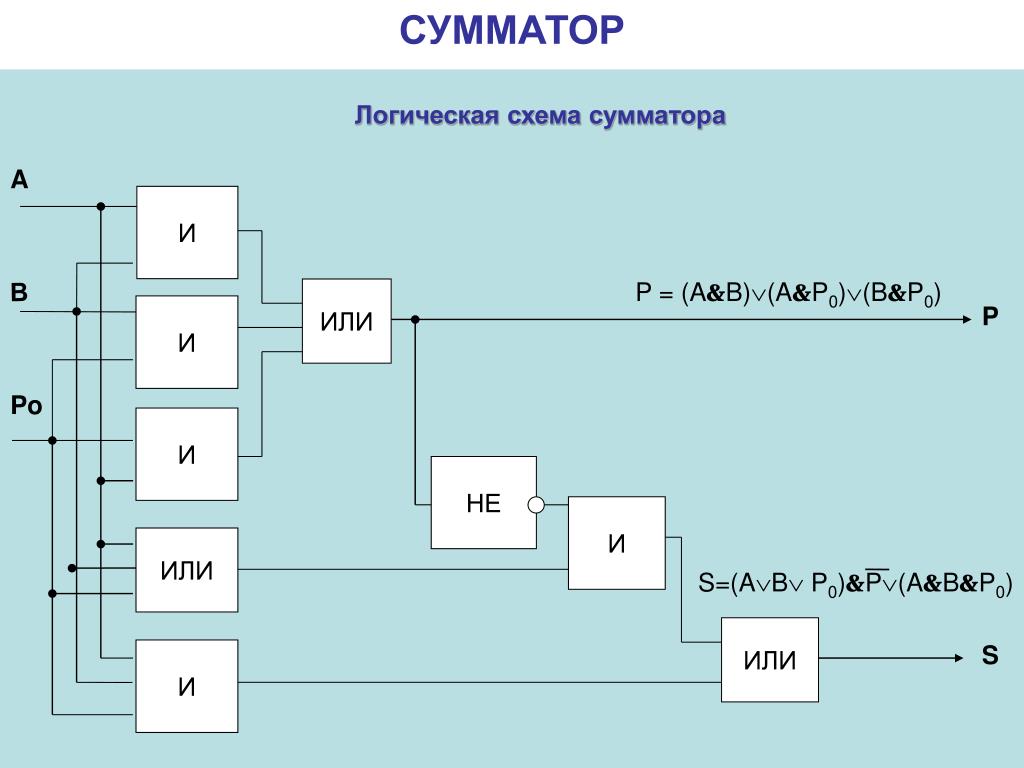 б-развернутая форма.| Сложение двух л-разрядных чисел.
[10] б-развернутая форма.| Сложение двух л-разрядных чисел.
[10] |
Полусумматор имет два входа и пригоден поэтому для использования только в младшем разряде. Устройство для суммирования двух многоразрядных чисел должно иметь, начиная со второго разряда, три входа: два для слагаемых Л и В; и один для сигнала переноса Pi-i с предыдущего разряда. [11]
Рассмотренный полусумматор представляет собой типичный пример комбинационной схемы потенциального типа, так как изменение сигналов на входах сразу приводит к изменению выходных потенциалов. [12]
Комбинационный полусумматор HS ( рис. 3.64, а) предназначен для суммирования двух одноразрядных двоичных чисел. Выход pl i является выходом переноса, а выход Si — выходом суммы. [13]
Полусумматором называется устройство, обеспечивающее выполнение операции сложения двух одноразрядных двоичных чисел А и В. В результате сложения в общем случае наряду с суммой может получиться перенос. Поэтому полусумматор имеет два выхода.
[14]
Поэтому полусумматор имеет два выхода.
[14]
Каждый полусумматор, как показано на рис. 4.1, а, имеет два входных и два выходных канала. В каждом из этих последних выражений вторая цифра есть цифра суммы, а первая — цифра переноса. [15]
Страницы: 1 2 3 4 5
Схема полусумматора— принцип работы
You are here: Home / Digital Electronics / Схема полусумматора — принцип работы
Автор Omar Muñoz Urias Оставить комментарий
Полусумматор — это цифровая схема, которая складывает двоичные числа. В этом руководстве вы узнаете, как это работает, его таблицу истинности и как реализовать ее с помощью логических вентилей.
Схема полусумматораЧто такое полусумматор?
Полусумматор — это цифровая схема, выполняющая сложение двоичных чисел. Это простейший из цифровых сумматоров, и вы можете построить его, используя всего два логических элемента; вентиль XOR и вентиль AND.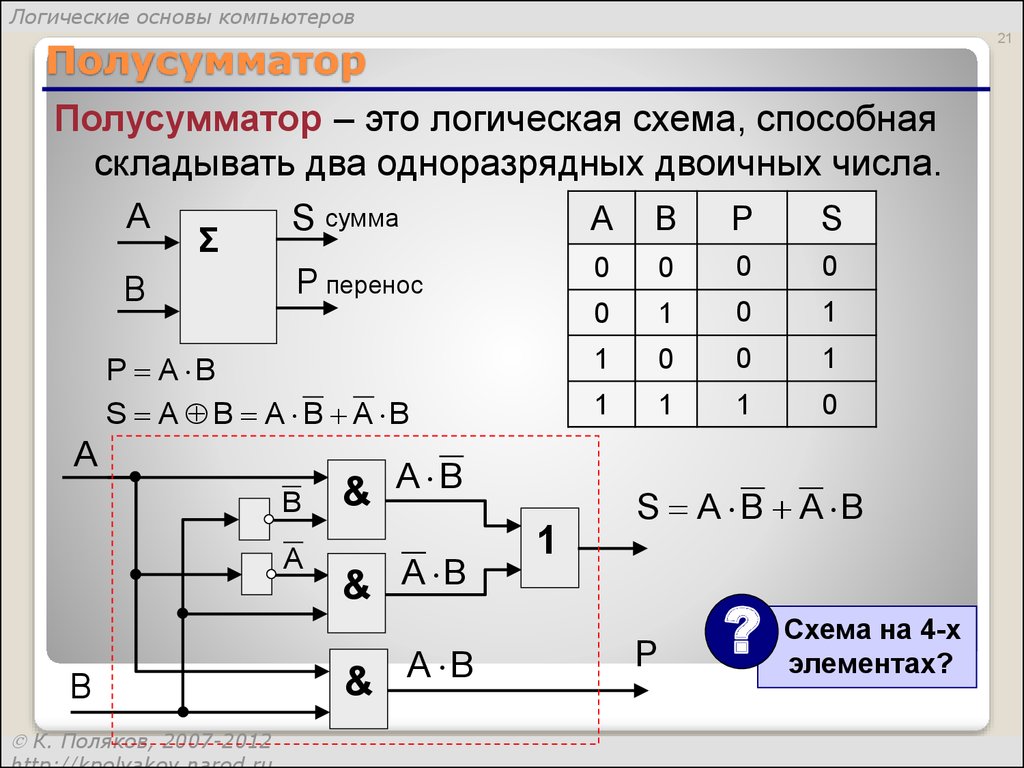
Полусумматор может складывать только два однобитных числа. Разница между Half Adder и Full Adder заключается в том, что первый не имеет входа Carry .
Все возможные комбинации 1-битных двоичных сложений показаны ниже:
Вам нужно два бита для представления результата, поскольку наибольший возможный результат сложения двух 1-битных чисел равен 2 («10» в двоичном формате).
Вы можете добавить это в таблицу истинности, используя четыре возможные комбинации 1-битных двоичных сложений, приведенные выше. Сумматор принимает два входа, А и B и генерирует два выхода: один для суммы (S), а другой для переноса (C). So the truth table becomes:
| Input A | Input B | Output S | Output C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Как работает полусумматор?
Чтобы понять, как создать схему Half Adder, вы можете использовать ее таблицу истинности.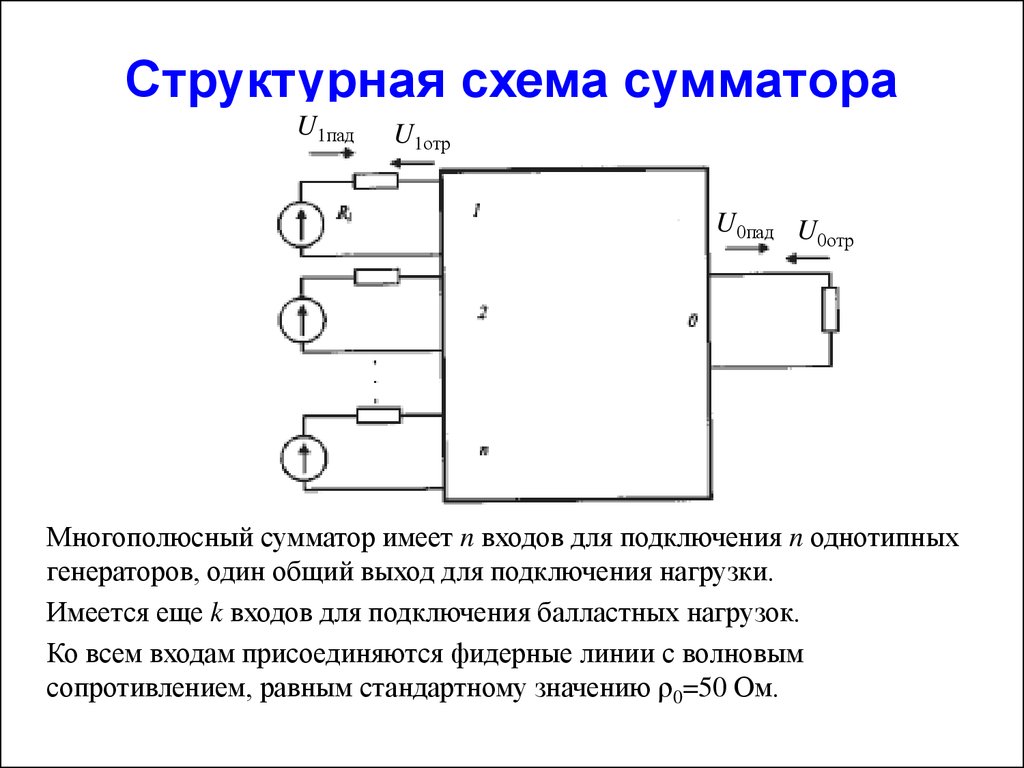 Первое, что вам нужно сделать, это отделить вывод S и построить собственную таблицу истинности.
Первое, что вам нужно сделать, это отделить вывод S и построить собственную таблицу истинности.
| Вход A | Вход B | Выход S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| Input A | Input B | Output C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
 Это означает, что для создания выхода C вы можете использовать логический элемент И:
Это означает, что для создания выхода C вы можете использовать логический элемент И:Наконец, вы можете объединить схемы для создания выходов S и C, чтобы построить полную принципиальную схему полусумматора. Простые переключатели представляют входы A и B. Выходы S и C представлены светодиодами, где горящий светодиод означает «1», а негорящий светодиод означает «0».
Вопросы?
У вас есть вопросы о том, как работает эта сумматорная схема? Позвольте мне знать в комментариях ниже.
Рубрики: Digital Electronics
Взаимодействие с читателями
Теория, таблица истинности и построение
Компьютер использует двоичные числа 0 и 1 . Схема сумматора использует эти двоичные числа и вычисляет сложение. Схема двоичного сумматора может быть создана с использованием логических элементов EX-OR и AND . Результат суммирования содержит два элемента: первый — SUM , а второй — Carry Out 9. 0033 .
0033 .
Когда мы используем процесс арифметического суммирования в нашей математике с основанием 10, например сложение двух чисел
, мы складываем каждый столбец справа налево, и если сложение больше или равно 10, мы используем перенос. В первом сложении 6+4 равно 10. Мы написали 0 и перенесли 1 в следующий столбец. Таким образом, каждое значение имеет взвешенное значение, основанное на позиции его столбца.
В случае сложения двоичных чисел процесс такой же. Вместо двух десятичных чисел здесь 9Используются двоичные числа 0032 . В двоичном формате мы получаем только два числа: 1 или 0 . Эти два числа могут представлять SUM или CARRY или оба . Как и в двоичной системе счисления, 1 является самой большой цифрой , мы производим перенос только тогда, когда сложение равно или больше, чем 1 + 1 , и из-за этого бит переноса будет передан в следующий столбец для добавления .
В основном существует два типа сумматоров: Полусумматор и полный сумматор . В половинном сумматоре мы можем сложить 2-битные двоичные числа, но мы не можем добавить бит переноса в половинный сумматор вместе с двумя двоичными числами. Но в полной схеме сумматора мы можем добавить переноса в бит вместе с двумя двоичными числами. Мы также можем складывать многобитные двоичные числа путем каскадирования полных цепей сумматора. В этом уроке мы сосредоточимся на схеме полусумматора, а в следующем уроке мы рассмотрим схему полного сумматора. Мы также используем некоторые микросхемы для практической демонстрации схемы полусумматора .0033 .
Схема полусумматора:
Ниже представлена блок-схема полусумматора, который требует только два входа и обеспечивает два выхода.
Посмотрим возможное двоичное сложение двух битов,
| 1 ст Бит или цифра | 2 nd Бит или цифра | Сумма всего < | Переноска |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Первую цифру мы можем обозначить как A , а вторую цифру мы можем обозначить как B, складываются вместе, и мы видим результат суммирования и бит переноса.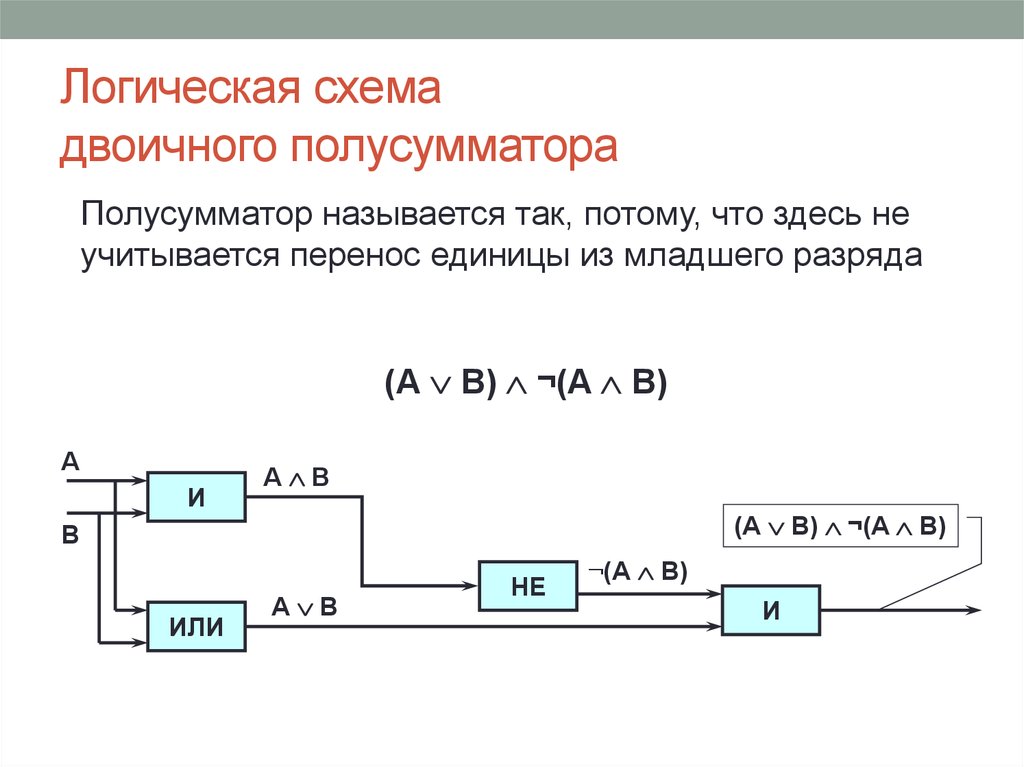 В первых трех строках 0 + 0, 0 + 1 или 1+ 0 добавлено 0 или 1 , но нет бита переноса. Но в последней строке мы добавили 1 + 1 , и это дает перенесите бит 1 вместе с результатом 0 .
В первых трех строках 0 + 0, 0 + 1 или 1+ 0 добавлено 0 или 1 , но нет бита переноса. Но в последней строке мы добавили 1 + 1 , и это дает перенесите бит 1 вместе с результатом 0 .
Итак, если мы видим работу схемы сумматора, нам нужны только два входа, и она даст два выхода, один из которых является результатом сложения, обозначенным как SUM и другой CARRY OUT бит.
Построение схемы полусумматора:
Выше мы видели блок-схему схемы полусумматора с двумя входами A, B и двумя выходами — Sum, Carry Out. Мы можем создать эту схему, используя два основных вентиля
- 2-входовой вентиль Исключающее ИЛИ или вентиль Исключающее ИЛИ
- 2-входовой И вентиль .
Строб исключающее ИЛИ с 2 входами или Строб исключающее ИЛИ
Логический элемент Ex-OR используется для получения бита SUM , а логический элемент AND создает бит переноса одного и того же входа A и B.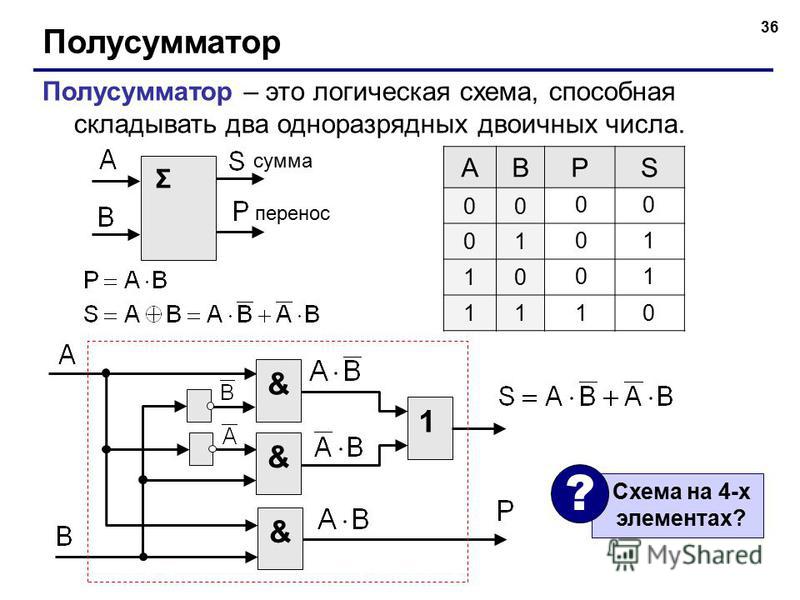
Это символ двух входов EX-OR ворота. A, и B — два двоичных входа, а SUMOUT — конечный результат после сложения двух чисел.
Таблица истинности вентиля EX-OR: –
| Вход A | Вход B | СУММ |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
В приведенной выше таблице мы видим общую сумму выходных данных логического элемента EX-OR. Когда любой из битов A и B равно 1 выход вентиля становится 1 . В двух других случаях, когда оба входа равны 0 или 1 , логический элемент Ex-OR выдает 0 выходных данных.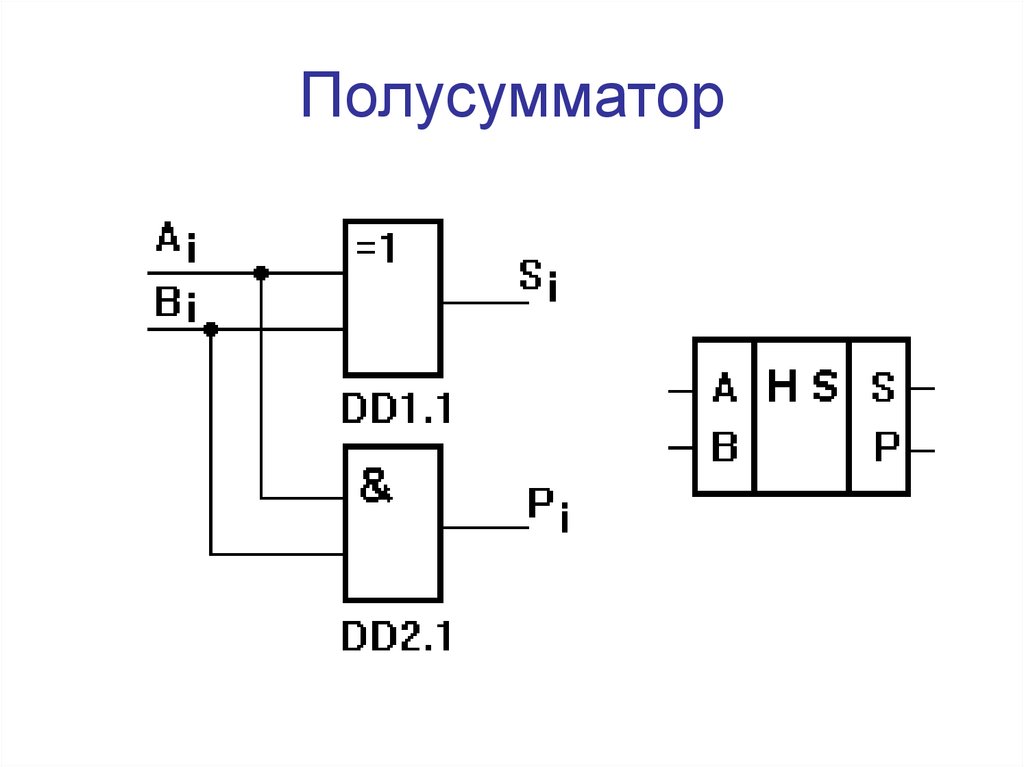 Узнайте больше о воротах EX-OR здесь.
Узнайте больше о воротах EX-OR здесь.
2-входовой вентиль И:
Вентиль X-OR предоставляет только сумму и не может обеспечить бит переноса на 1 + 1, нам нужен еще один вентиль для переноса. Ворота и идеально подходят для этого применения.
Это базовая схема двухвходового вентиля И . Так же, как и вентиль EX-OR , он имеет два входа . Если мы предоставим A и B бит на входе, это приведет к выходу.
Выход зависит от таблицы истинности вентиля И —
Вход А | Вход Б | Вывод переноса |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
В приведенном выше примере показана таблица истинности логического элемента И, где он будет производить выходные данные только тогда, когда оба входа равны 1 .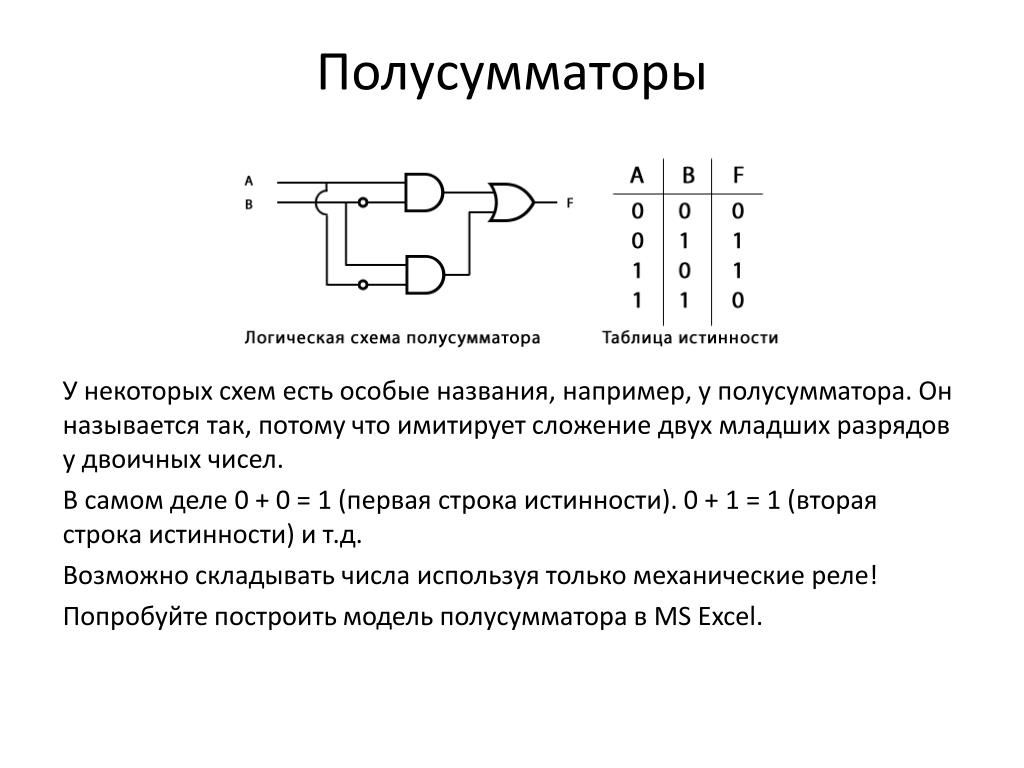 входы 1 . Узнайте больше о воротах AND здесь.
входы 1 . Узнайте больше о воротах AND здесь.
Логическая схема полусумматора:
Таким образом, логическая схема полусумматора может быть создана путем объединения этих двух вентилей и предоставления одного и того же входа в обоих вентилях.
Это построение схемы полусумматора, так как мы можем видеть, что два вентиля объединены, и одни и те же входы A и B предоставляются в обоих вентилях, и мы получаем SUM на выходе через вентиль EX-OR. и бит выполнения через вентиль И .
Логическое выражение схемы полусумматора равно
. СУММ = А исключающее ИЛИ В (А+В) CARRY = A AND B (A.B)
Таблица истинности схемы полусумматора выглядит следующим образом:
Вход А | Вход Б | СУММ (исключающее ИЛИ) | ПЕРЕНОС (И выход) |
0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 |
Практическая демонстрация схемы полусумматора:
Мы можем сделать схему в реальном виде на макетной плате, чтобы ясно понять ее.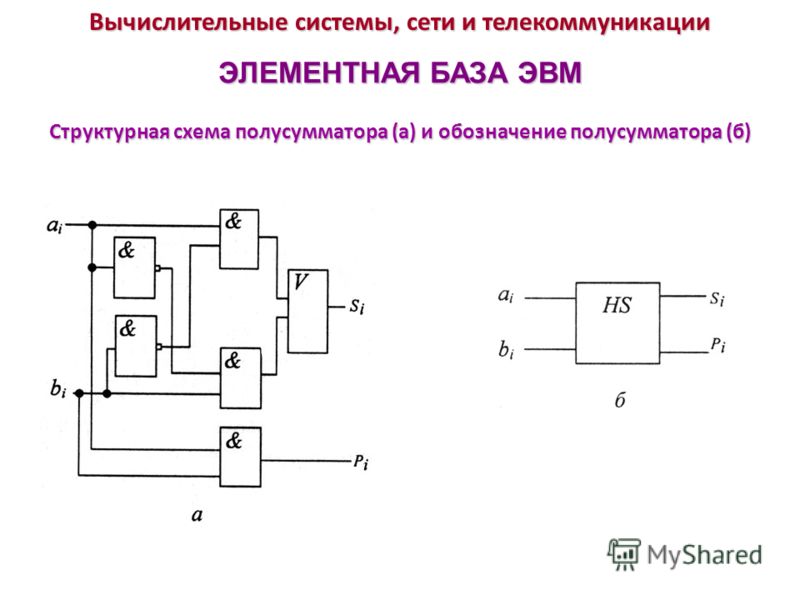 Для этого мы использовали два широко используемых чипа XOR и AND из серии 74 74LS86 и 74LS08.
Для этого мы использовали два широко используемых чипа XOR и AND из серии 74 74LS86 и 74LS08.
Обе микросхемы затвора. 74LS86 имеет внутри микросхемы четыре вентиля XOR, а 74LS08 — четыре вентиля AND. Эти две микросхемы широко доступны, и мы создадим схему полусумматора , используя эти две.
Ниже приведена схема выводов обеих микросхем:
Принципиальная схема для использования этих двух ИС в качестве схемы полусумматора-
Мы построили схему на макетной плате и наблюдали за выходом.
В приведенной выше принципиальной схеме используется один из вентилей XOR из 74LS86 , а также один из вентилей И из 74LS08 используется . Контакты 1 и 2 74LS86 являются входом затвора, а контакт 3 — выходом затвора, с другой стороны, контакты 1 и 2 74LS08 — входом затвора И, а контакт 3 — выходом затвора.

