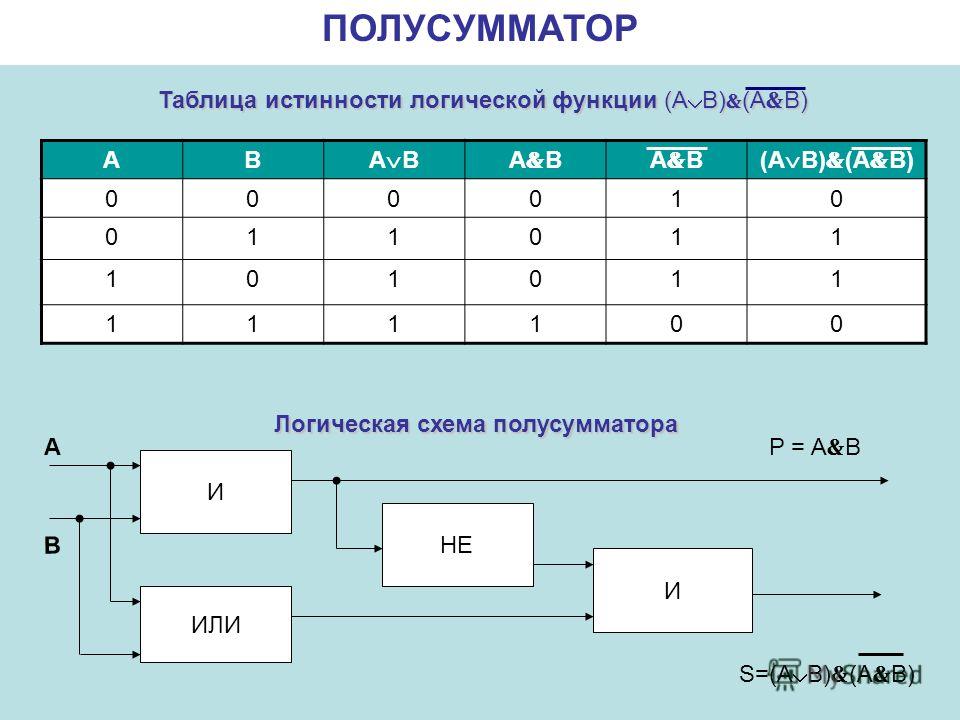
Как компьютер складывает числа?
- Информация о материале
13 сен 2013
Все компьютерные вычисления производятся в двоичной системе с использованием базовых электронных элементов — разнообразных видов переключателей. Некоторые из этих переключателей — AND(и), OR(или), XOR(исключающее или) — называются логическими элементами, потому что каждый из них дает логический предустановленный результат при использовании двоичного кода.
Поскольку они работают и на проведении и на сопротивлении электрического тока: нет напряжения — означает 0, есть напряжение — означает 1, логические элементы иначе называются воротами.
Все эти «ворота» похожи между собой тем, что каждый из них имеет больше одного ввода, но всего один вывод. Логический элемент AND(и) дает 1 на выводе, только если все его вводы соответствуют единице. Точно так же «ворота» OR(или) дают ноль на выводе, если все его вводы равны 0.
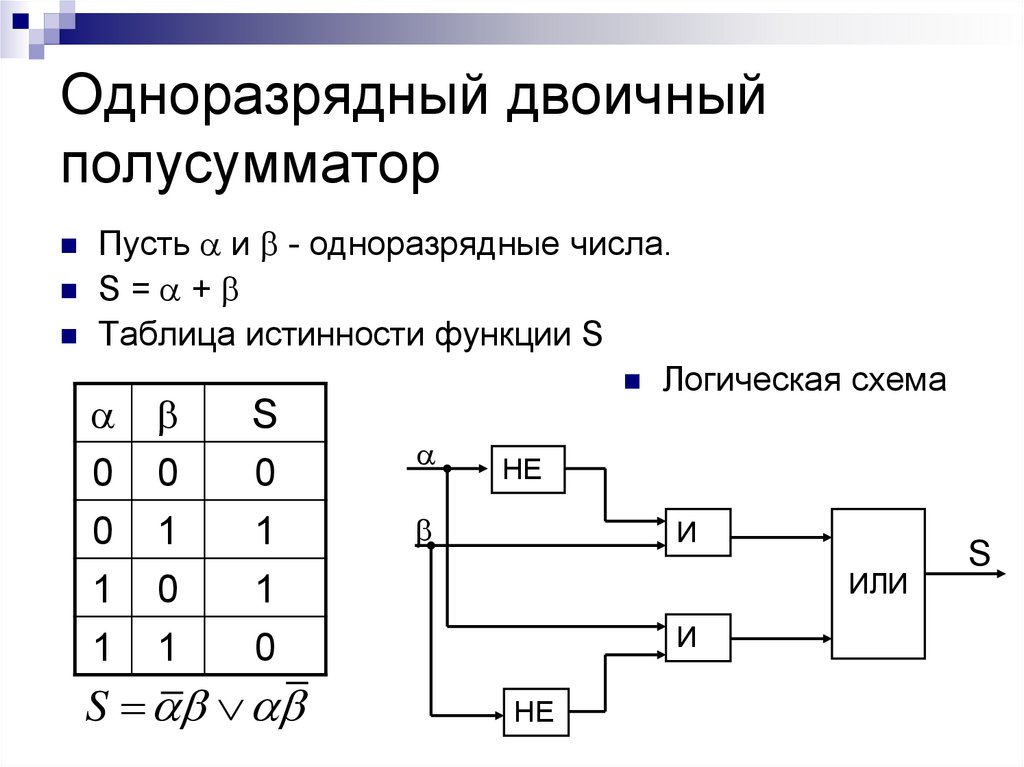
Полусумматор назван так потому, что он может складывать только две цифры в двоичной системе и производить результат, состоящий из одной цифры и одного переноса. Поскольку они не могут оперировать со следующими один за другим переносами, полусумматоры часто используются в качестве первой строки логической схемы. Каждый полный сумматор может оперировать с двумя цифрами и переносом и принимать перенос из предыдущей суммы в цепи.
Сумматоры справляются с любыми арифметическими задачами, поскольку сложение является основным арифметическим действием: умножение — это повторное сложение, вычитание — это прибавление отрицательного числа, деление — это повторное вычитание.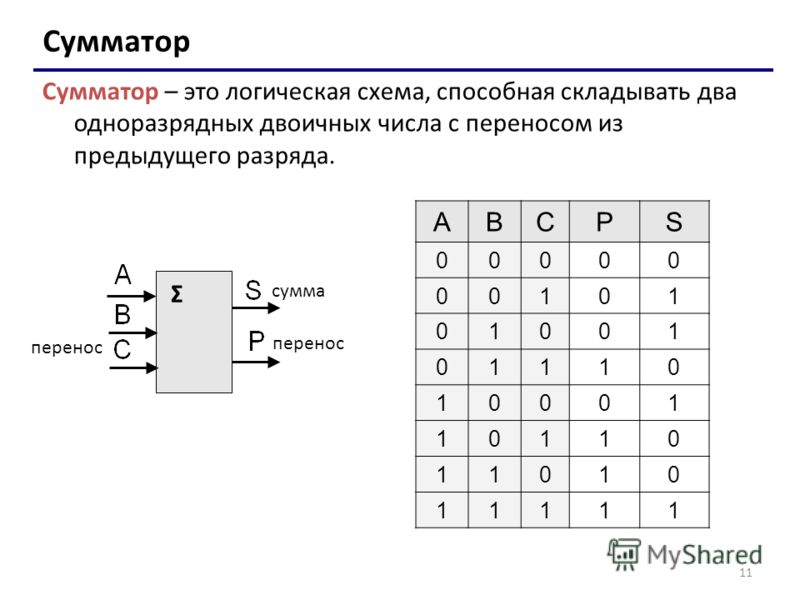
«Ворота» AND(и) выпустят 1, если на обоих вводах окажется 1. Любая другая комбинация на вводе произведет 0 на выводе.
«Ворота» OR(или) выпустят ноль, если на обоих вводах окажется ноль. Если хотя бы на одном из вводов появится единица, то следует ожидать единицу и на выводе.
«Ворота» XOR(исключающее или) выпустят 0, если оба ввода впустят по нулю или по единице. Если на вводе 1 и 0, на выводе будет 1.
Как работает полусумматорНаверху представлена схема сложения двух одноцифровых двоичных чисел, состоящая из схемы XOR(сверху) и схемы AND(внизу). При слбжении двух единиц напряжение верхнего сумматорного канала проходит через ворота XORи дает 0 на выходе. Ворота ANDпреобразовывают две единицы на вводе в одну 1 на выводе. Результат 10 (читается как один-ноль) двоичной системы соответствует числу 2 десятичной системы.
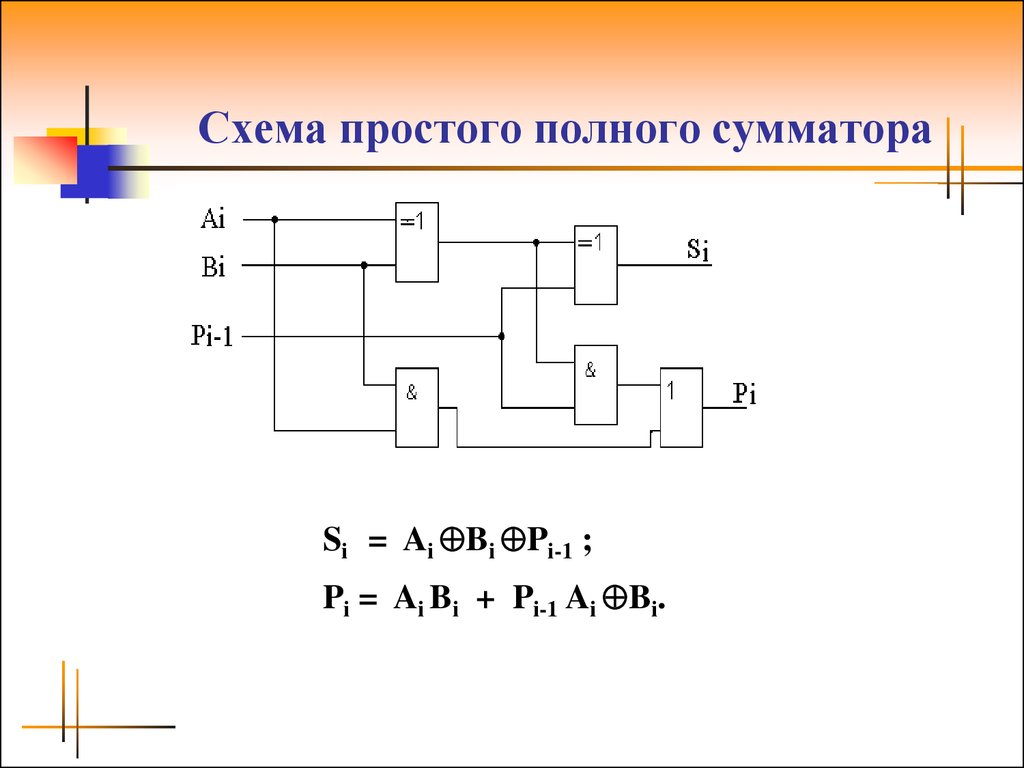
Полный сумматор
В комбинации полусумматор (сверху) и полный сумматор (снизу) могут выполнять операции с большими числами, требующими переноса.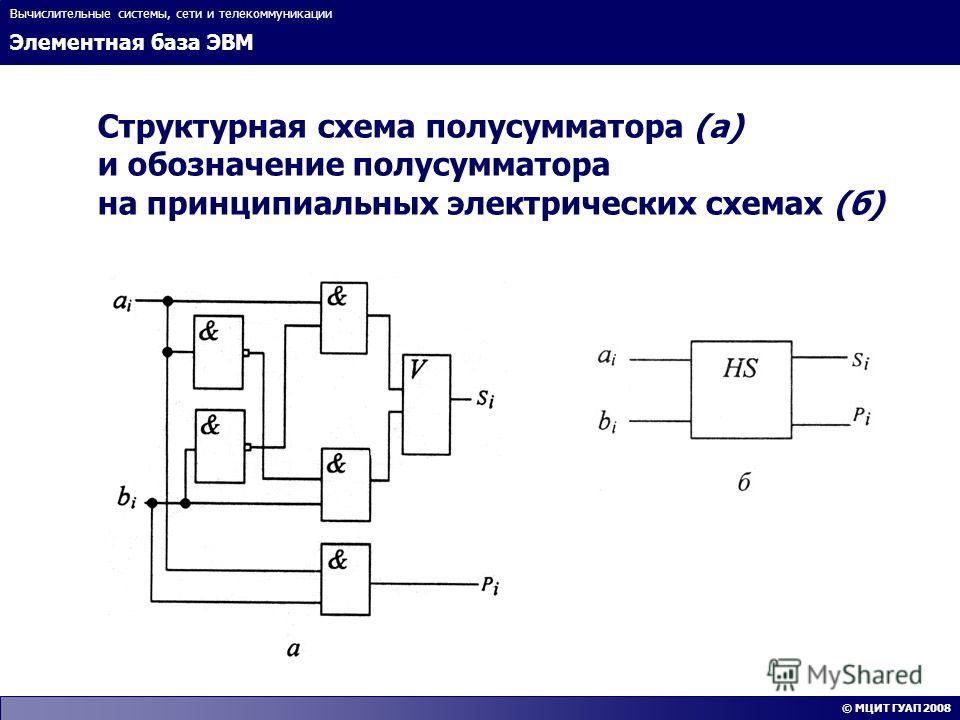
Чтобы сложить 2 и 3 или 10 и 11 в двоичном исчислении, полусумматор начинает работу с ворот XORи производит 1. Ворота ANDгенерируют 0, который переносится в полный сумматор. В свою очередь, полный сумматор проводит напряжение числа 11 через пять ворот, подбирает перенос из полусумматора и выводит 1 и 0. Когда эти цифры комбинируются с 1 из полусумматора, получается результат 101, или 5 в десятичном исчислении. Для сложения больших чисел используется больше полусумматоров, один для каждой цифры двоичного кода.
Исследование арифметического сумматора (Лабораторная работа) | EWB
EWB
Цель работы: исследовать арифметический сумматор, полусумматор и полный сумматор.
Теория
Арифметические сумматоры – составная часть
арифметико-логических устройств (АЛУ) микропроцессоров (МП). Арифметический
сумматор состоит из двух устройств: полусумматора и n полных сумматоров.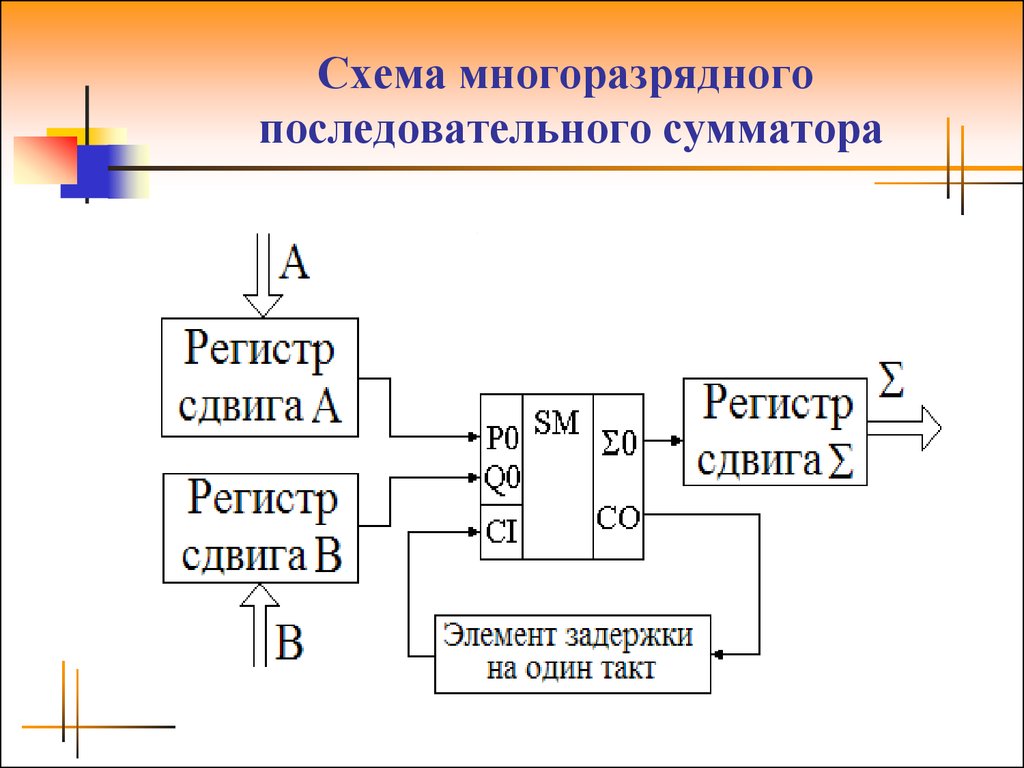
Полный сумматор имеет три входа: A, B – входы суммируемых операндов, Ci– вход переноса из предыдущего разряда сумматора и два выхода: S – выход полного сумматора и C0 – выход переноса. Полусумматор отличается от полного тем, что у него нет входа переноса из предыдущего разряда. Полусумматор используется в качестве первого разряда арифметического сумматора, а в качестве остальных разрядов – полные сумматоры. Полусумматор – одна из простейших комбинационных логических схем.
Рис. Четырехразрядный арифметический сумматор
Рассматривая таблицу истинности полусумматора можно заметить, что выход S полусумматора выполняет функции элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», а выход переноса С полусумматора – элемента «И». Таким образом, логические выражения для функций S и C равны:
S=AB′+A′B, C=AB.
Таблица
Входы |
Выходы |
||
А |
В |
S |
C |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
|
Схема полусумматора
представлена на рисунке далее.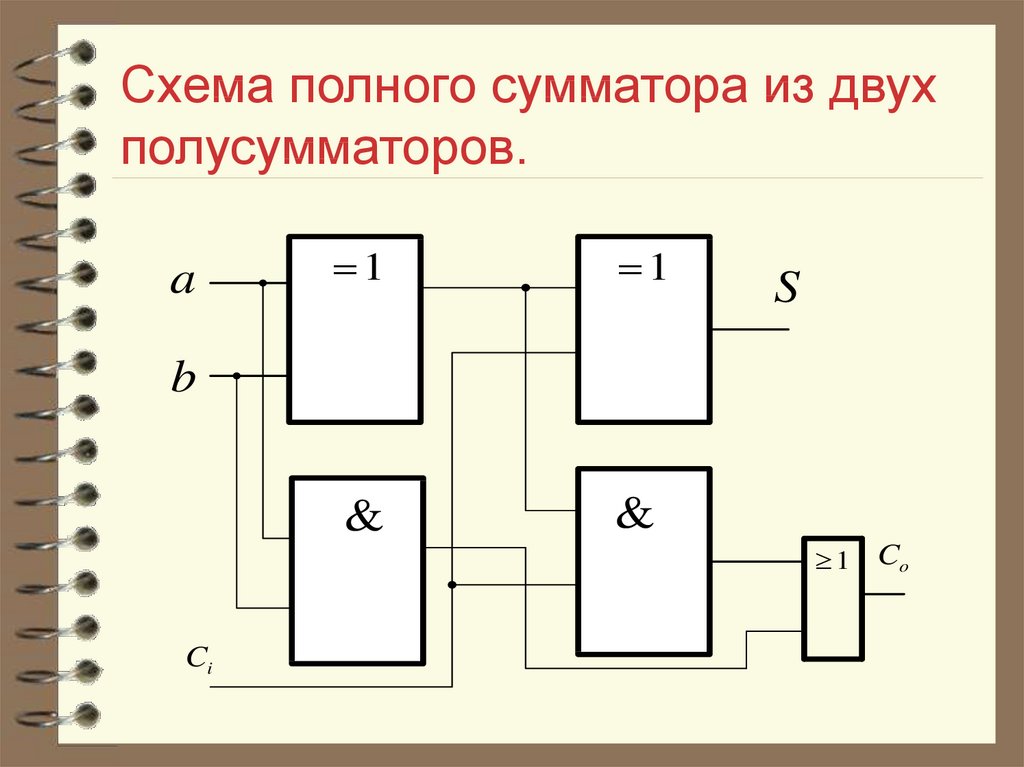
Рис. Структура полусумматора
Из таблицы истинности полного сумматора можно получить логические выражения для S (суммы) и C (переноса в следующий разряд). Логическое выражение для S будет иметь четыре слагаемых, соответствующих строкам таблицы, в которых выход S равен единице (стоки 4, 5, 7, 10),
S= A′B′Ci-1+A′BCi-1′+AB′Ci-1
Таблица. Входы и выходы
Входы |
Выходы |
|||
А |
В |
Ci-1 |
S |
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Логическое выражение для C также будет иметь четыре слагаемых (строки 6, 8, 9, 10):
Ci=A′BCi-1+A′BCi-1′+ABCi-1′+ABCi-1.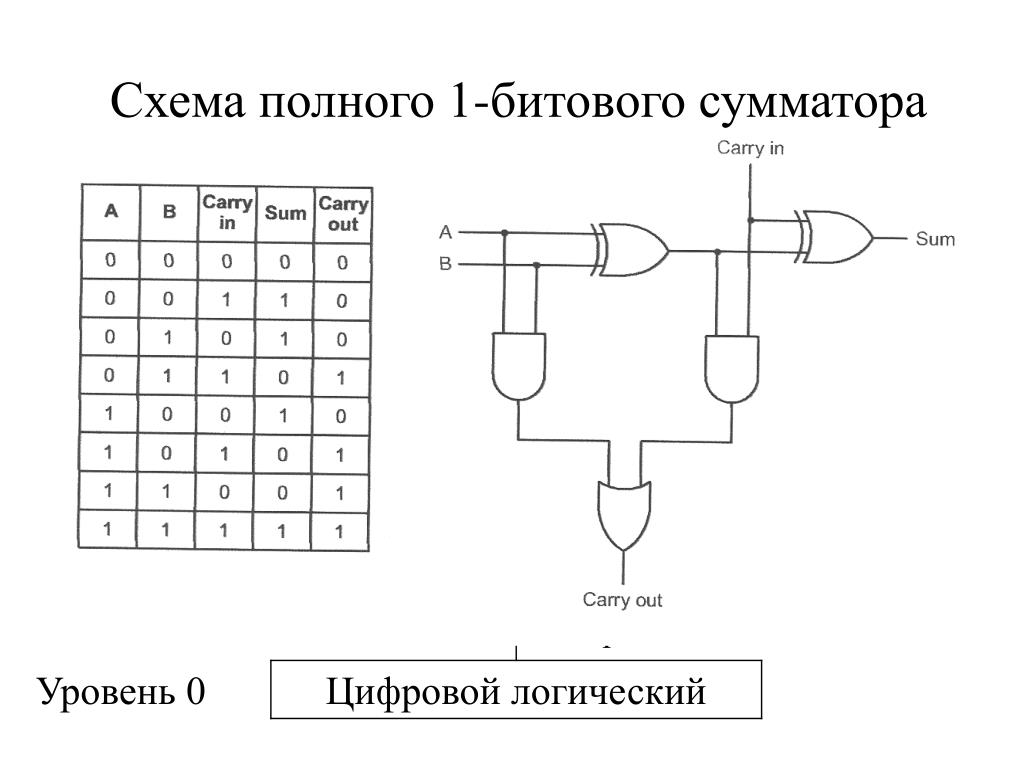
С помощью законов булевой алгебры это выражение можно упростить, тогда оно будет иметь вид:
Сi=ACi-1+BCi-1+AB.
Схема полного сумматора изображена далее.
Рис. Структура полного сумматора
Последовательность выполнение работы
1. Собрать (нарисовать) схему четырехразрядного арифметического сумматора. Поместить на схему три 16-ричных индикатора и генератор слова.
2. Открыть генератор слова и задать суммируемые числа. Четыре младших разряда каждого генерируемого слова составляют первое слагаемое (операнд). Следующие четыре разряда составляют второе слагаемое (операнд).
3. Запустить процесс моделирования и следить за
показаниями индикаторов. Записать суммируемые числа и результат суммирования.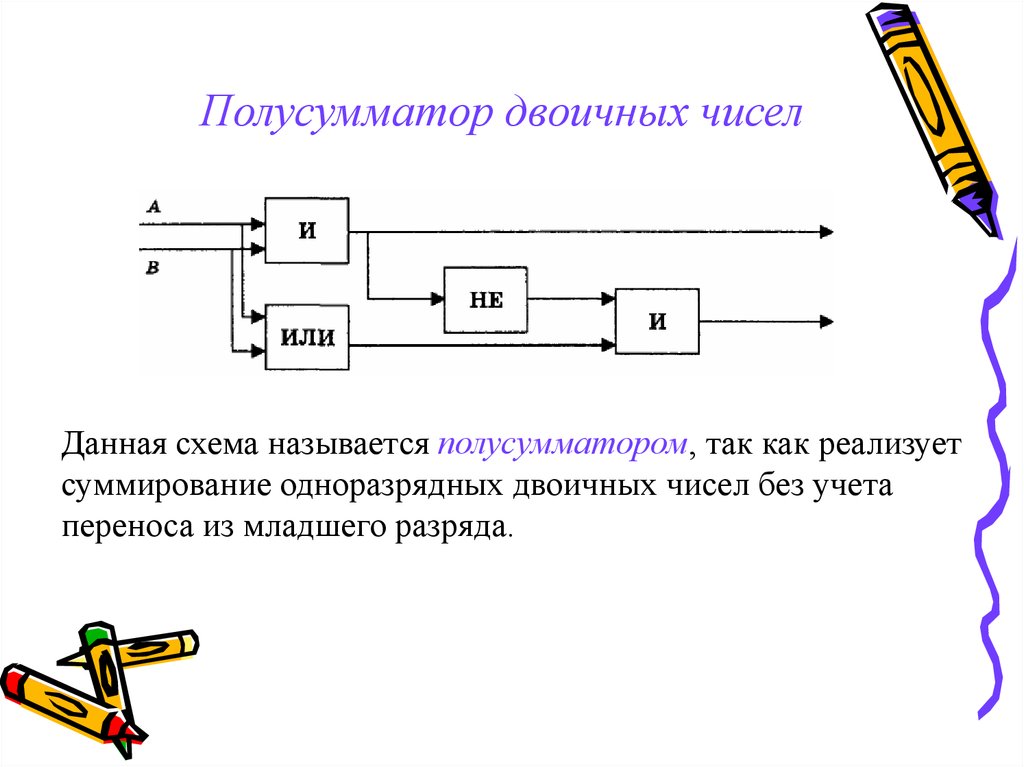
Рис. Схема исследования четырехразрядного сумматора
4. Собрать схему и с помощью логического анализатора, последовательно нажимая кнопки Circuit to Truth Table (таблица истинности цепи) , Truth Table to Boolean Expression (булево выражение по таблице истинности) , Boolean Expression to Circuit (создание схемы по булеву выражению) , получить:
· таблицу истинности полусумматора,
· логические выражения для выходов S и C,
· схемную реализацию логических выражений для выходов S и C.
Рис. Схема исследования полусумматора:
a – выход S, б – выход C
5. Собрать схему и с помощью логического
анализатора получить таблицу истинности полного сумматора, логические выражения
для выходов S и C и схемную реализацию логических выражений.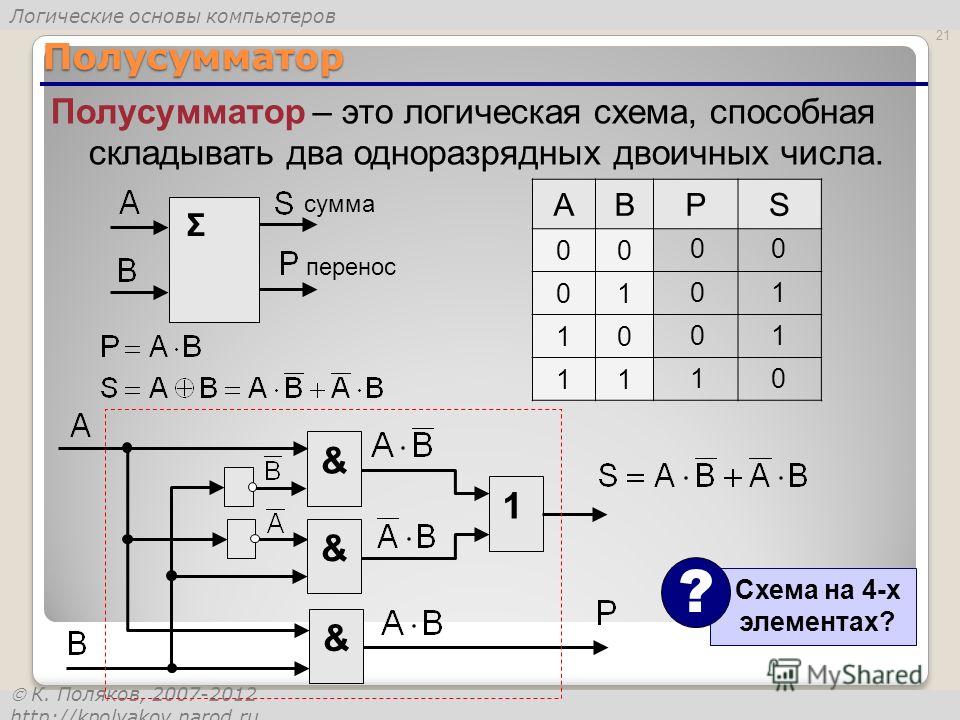
Рис. Схема исследования полного сумматора:
a – выход S; б – выход C
Описание используемых контрольно-измерительных приборов
Генератор слова (или кодовый генератор) предназначен для генерации 32-разрядных двоичных слов, которые набираются пользователем в 16-ричном коде в строке Hex или в двоичном коде в строке Binary на панели Edit .
Рис. Лицевая панель генератора слова
На панели Address расположены четыре окна. Каждое кодовое слово из списка имеет адрес, выраженный 4-разрядным 16-ричным числом.
В окне Edit отображается адрес выбранного в таблице слова, в окне Current – адрес выдаваемого кодового слова.
В окне Initial устанавливается адрес
первого кодового слова множества слов, поступающих на выход генератора, в окне Final –
адрес последнего кодового слова множества слов, поступающих на выход генератора.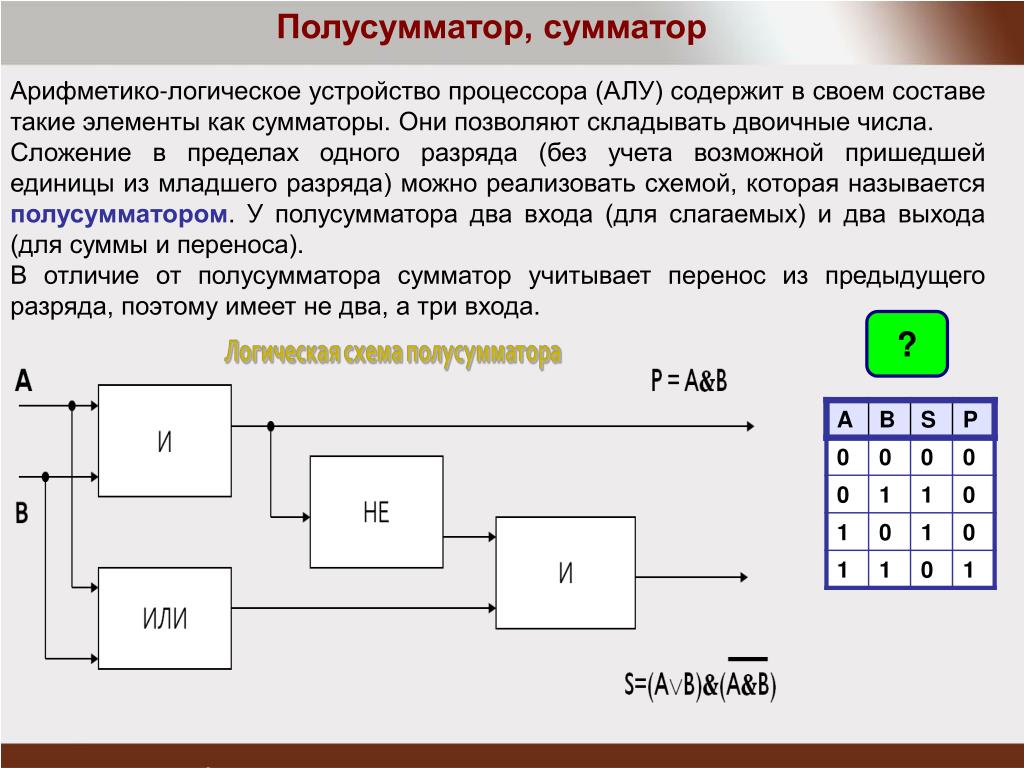
Для того чтобы создать множество кодовых слов, выдаваемых генератором слова, нужно ввести адрес первого и последнего слова в окно Initial и Final соответственно.
На панели Controls устанавливается режим выдачи кодовых слов.
Чтобы выдать 32-разрядное слово на выход прибора, надо щелкнуть по одной из кнопок Step, Burst or Cycle. Номер этого слова отобразится в окне Current на панели Address.
Если необходимо выдать только одно слово, следует щелкнуть по кнопке Step, если все кодовые слова множества, то щелкнуть по кнопке Burst.
Если щелкнуть по кнопке Cycle, то будут выдаваться все кодовые слова множества непрерывно циклически. Остановить выдачу слов можно, повторно щелкнув по кнопке Cycle.
Если нужно остановить и возобновить выдачу слов с определенного слова, нужно щелкнуть по кнопке Breakpoint.
Чтобы установить контрольную точку (Breakpoint), нужно выбрать в списке
кодовое слово, на котором следует остановить вывод слов, и затем щелкнуть по
кнопке Breakpoint.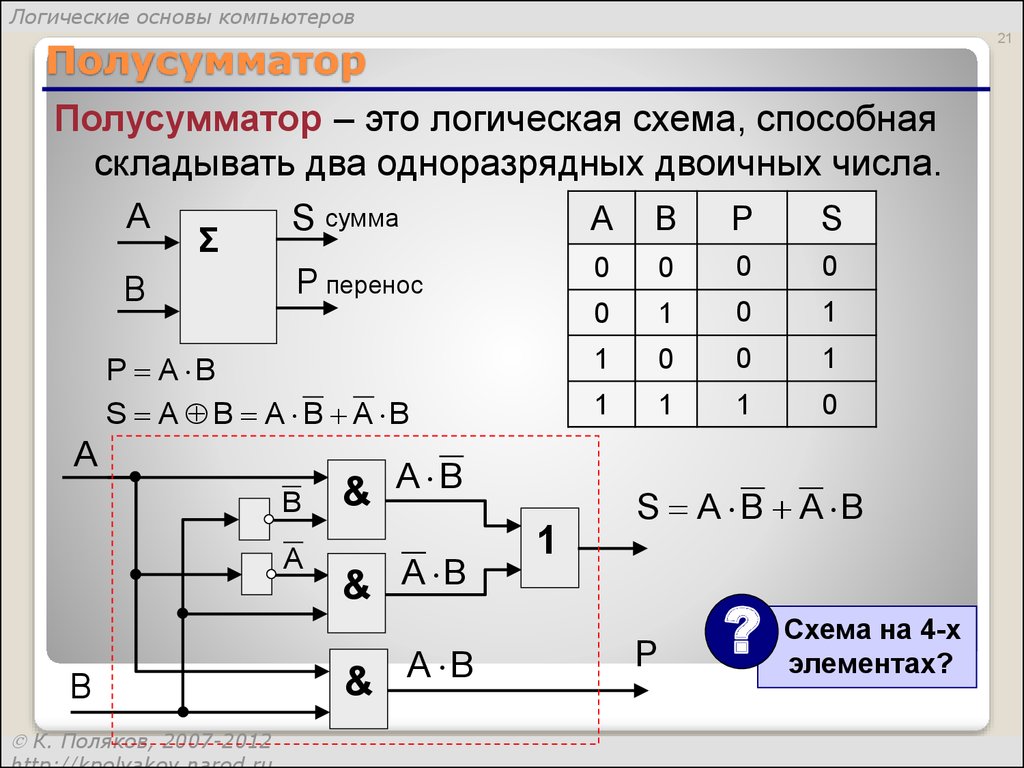
У
этого слова появится метка в виде звездочки.
Чтобы удалить контрольную точку, нужно выбрать существующую контрольную точку, затем щелкнуть по кнопке Breakpoint.
Можно установить несколько контрольных точек. Контрольные точки могут использоваться как при непрерывной (Cycle), так и при однократной (Burst) выдаче множества слов.
С помощью кнопки Pattern можно создавать новые или использовать ранее записанные множества кодовых слов.
На панели Triggering расположены четыре кнопки, с помощью которых можно установить источник запускающего сигнала (внутренний (Internal) или внешний (External)) и фазу запускающего сигнала (по переднему или заднему фронту).
На панели Frequency устанавливается
тактовая частота генератора слова в герцах, кило- или мегагерцах. Кодовые слова
поступают на выход генератора с каждым тактом генератора. Рядом расположена
клемма, на которую выдается сигнал готовности выдавать данные.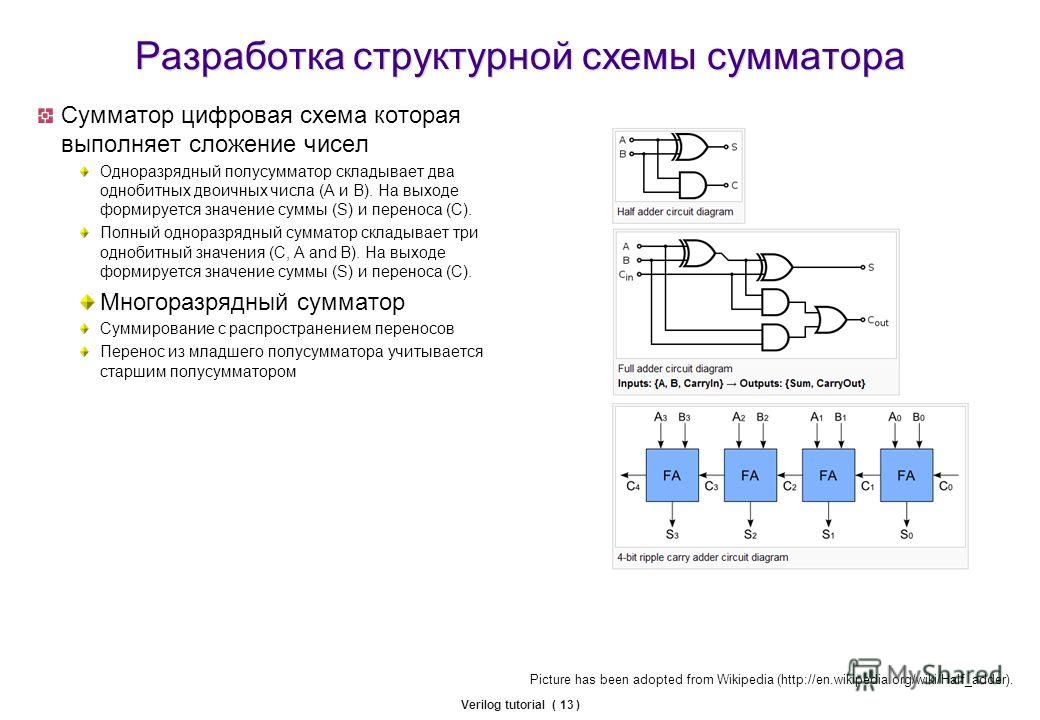
Логический преобразователь (Logic Converter)
На лицевой панели преобразователя расположены клеммы-индикаторы входов A, B, C, …, H и клемма выхода Out, окно для отображения таблицы истинности исследуемой схемы, строка для отображения ее булева выражения и панель Conversions.
На панели Conversions расположены шесть кнопок, используемых для получения:
· – таблицы истинности исследуемого устройства,
· – булева выражения, реализуемого исследуемым устройством,
· – минимизированного булева выражения;
· – таблицы истинности по булевому выражению;
· – схемы устройства по логическому выражению на логических элементах без ограничения их типа,
· – создания схемы устройства только на логических элементах «И-НЕ».
Рис. Лицевая панель логического преобразователя
Содержание отчета
Отчет должен включать:
1) название пункта работы,
2) исследуемую схему,
3) результат моделирования.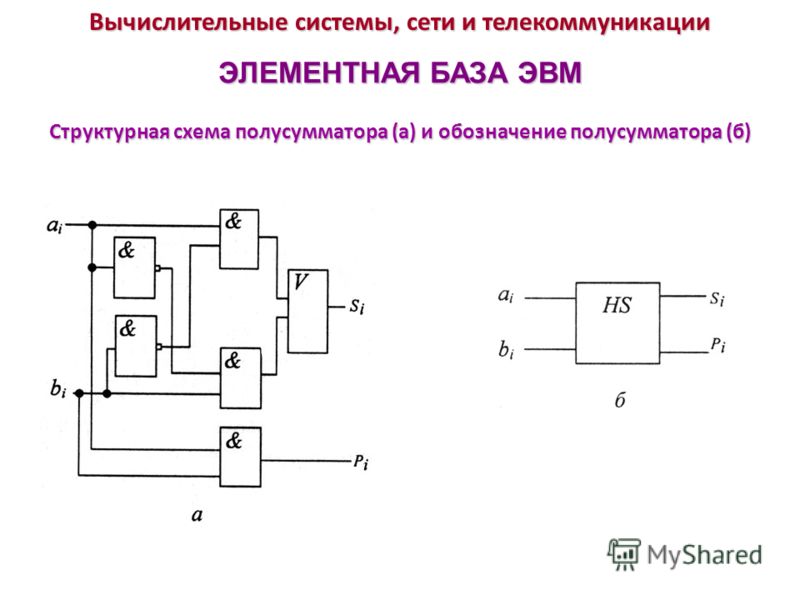
Virtual Labs
Введение
Сумматоры — это цифровые схемы, выполняющие сложение чисел. Сумматоры являются ключевым компонентом арифметико-логического устройства. Сумматоры могут быть созданы для большинства числовых представлений, таких как двоично-десятичный код (BCD), превышение — 3, код Грея, двоичный код и т. Д. Из них двоичное сложение является наиболее часто выполняемой задачей наиболее распространенных сумматоров. Кроме того, сумматоры также используются в некоторых цифровых приложениях, таких как вычисление индекса таблицы, декодирование адреса и т. д.
Двоичное сложение аналогично десятичному сложению. Некоторые основные бинарные дополнения показаны ниже.
Рис. 1. Схематическое изображение полусумматора
### 1)Полусумматор
Полусумматор — это комбинационная схема, выполняющая простое сложение двух двоичных чисел.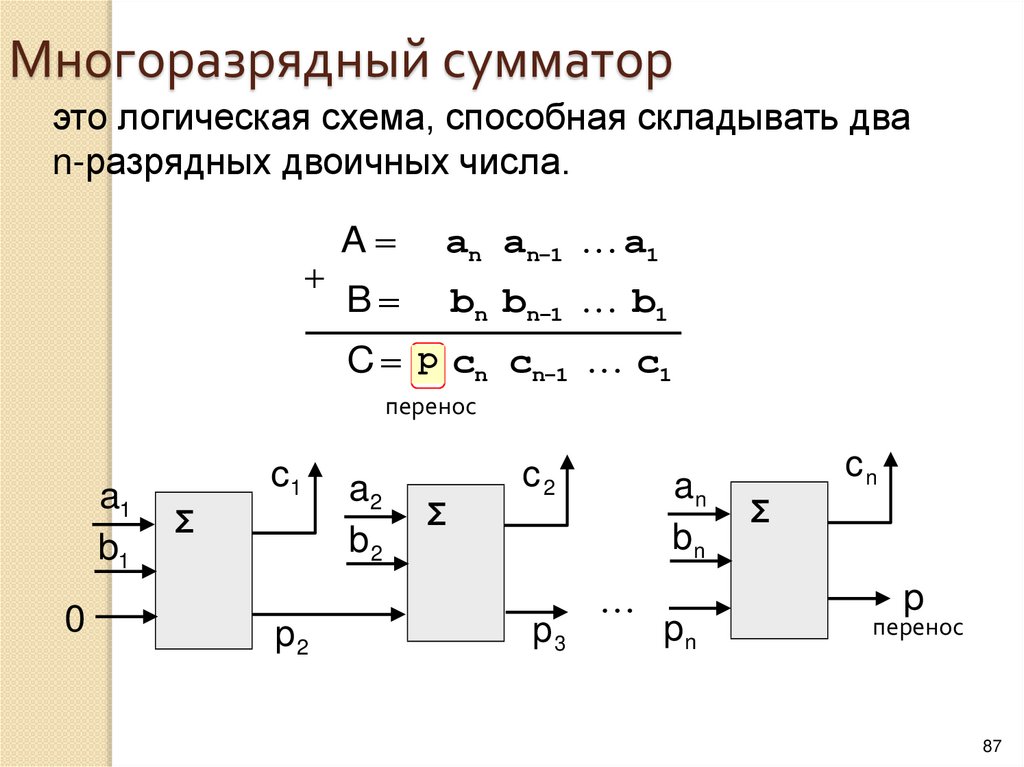
Если мы предположим, что A и B являются двумя битами, сложение которых должно быть выполнено, блок-схема и таблица истинности для полусумматора с A, B в качестве входов и Sum, Carry в качестве выходов могут быть сведены в таблицу следующим образом.
Рис. 2. Блок-схема и таблица истинности полусумматора
Выходная сумма двоичного сложения, выполненного выше, аналогична операции Ex-OR, в то время как вывод переноса аналогичен результату операции AND. То же самое можно проверить с помощью карты Карно.
Таблица истинности и упрощенная K-карта, а также логическая схема для вывода суммы показаны ниже.
Рисунок 3. Таблица истинности, упрощение K-карты и логическая диаграмма для вывода суммы полусумматора
Таблица истинности и упрощение K Map и логическая диаграмма для переноса показаны ниже.
Рисунок 4. Таблица истинности, упрощение K-карты и логическая диаграмма для вывода суммы полусумматора
Carry = AB
Если A и B являются двоичными входами полусумматора, то логическая функция для вычисления суммы S представляет собой Ex – OR для A и B, а логическая функция для вычисления переноса C представляет собой AND для A и B. Комбинируя эти два, логическая схема для реализация комбинационной схемы полусумматора показана ниже.
Рисунок 5. Логическая схема полусумматора
Поскольку мы знаем, что И-НЕ и НЕ-ИЛИ называются универсальными вентилями, так как с их помощью может быть реализована любая логическая система, с их помощью может быть реализована и схема полусумматора. Мы знаем, что схема полусумматора имеет один вентиль Ex-OR и один вентиль AND.
### 1.1) Полусумматор с использованием вентилей И-НЕ
Для создания полусумматора требуется пять вентилей И-НЕ.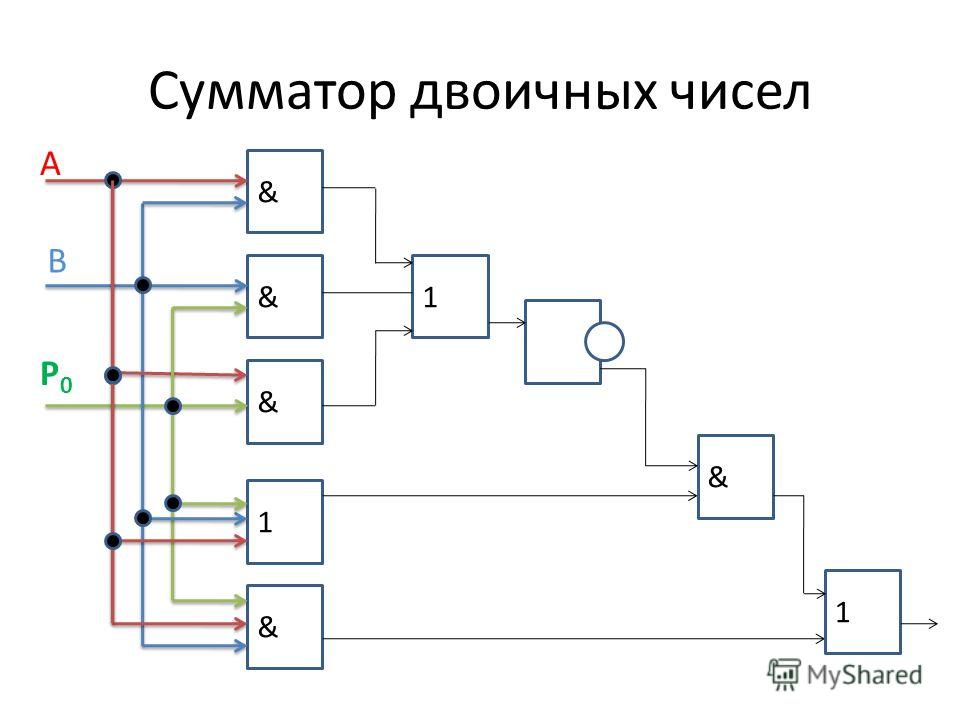
Схема для реализации полусумматора с использованием вентилей И-НЕ показана ниже.
Рис. 6. Реализация полусумматора с использованием вентилей И-НЕ
### 1.2) Полусумматор с использованием вентилей ИЛИ-НЕ
Для создания полусумматора требуется пять вентилей НЕ-ИЛИ. Схема для реализации полусумматора с использованием вентилей ИЛИ-НЕ показана ниже.
Рисунок 7. Реализация полусумматора с использованием NOR Gates
2)Полный сумматор
Полный сумматор — это цифровая схема, используемая для вычисления суммы трех двоичных битов. Полные сумматоры сложны и трудны в реализации по сравнению с половинными сумматорами. Два из трех битов такие же, как и раньше: A, бит augend и B, бит addend. Дополнительный третий бит является битом переноса из предыдущего этапа и называется «переносом» — обычно обозначается CIN.
Он вычисляет сумму трех битов вместе с переносом. Выходной перенос называется Carry-out и обозначается как Carry OUT.
Блок-схема полного сумматора с A, B и CIN в качестве входов и S, Carry OUT в качестве выходов показана ниже.
Рисунок 8. Полная блок-схема сумматора и таблица истинности
Рисунок 9. Полная логическая схема сумматора
быть получено с помощью K – Map.
### 2.1)Полный сумматор с использованием вентилей И-НЕ
Как упоминалось ранее, вентиль И-НЕ является одним из универсальных вентилей и может использоваться для реализации любой логической схемы.
Схема полного сумматора, использующая только вентили И-НЕ, показана ниже.
Рисунок 12. Полный сумматор с использованием вентилей НЕ-И
2.2) Полный сумматор с использованием вентилей НЕ-ИЛИ
Как упоминалось ранее, вентиль ИЛИ-НЕ является одним из универсальных вентилей и может использоваться для реализации любой логической схемы. Ниже показана схема полного сумматора, использующего только вентили ИЛИ-НЕ.
Рисунок 13. Полный сумматор с использованием вентилей НЕ-ИЛИ
Полусумматор с использованием базовых вентилей
<НазадЦель
Изучить и проверить полусумматор с использованием базовых вентилей.Цели обучения
- Понять поведение и продемонстрировать Half Adder с использованием основных вентилей.
- Чтобы применить знания об основных вратах для создания таблиц истинности.
- Развитие навыков построения цифровых схем и устранения неполадок.
- Чтобы понять ключевые элементы спецификации логики TTL или таблиц данных.
IC Используется
Для Half Adder с использованием базовых вентилей :| Номер IC | Название IC |
|---|---|
| 74LS08 | Quad 2-input AND Gates |
| 74LS86 | Quad 2-input Exclusive-OR Gates |
Circuit Tutorials:
- Half Adder Using Basic Gates
Procedure
- Поместите ИС в комплект для обучения ИС.
- Подсоедините VCC и заземление к соответствующим контактам комплекта IC Trainer Kit.
- Реализуйте схему, как показано на принципиальной схеме.
- Подключите входы к входным переключателям, входящим в комплект IC Trainer Kit.
- Подключите выходы к переключателям O/P светодиодов
- Применяйте различные комбинации входов в соответствии с таблицей истинности и наблюдайте за состоянием светодиодов.
- Запишите соответствующие выходные показания для различных комбинаций входов.
- Комплект для обучения отключению питания, отсоедините все проводные соединения и извлеките ИС из базы ИС.
Теория
ПОЛОВИНА СУММИТЕЛЯ — Сумматор представляет собой цифровую логическую схему в электронике, реализующую сложение чисел. Во многих компьютерах и других типах процессоров сумматоры используются для вычисления адресов, подобных операций и табличных индексов в АЛУ, а также в других частях процессоров. Они могут быть построены для многих числовых представлений, таких как избыток-3 или двоично-десятичный код. Сумматоры делятся на два типа: полусумматоры и полные сумматоры. Схема полусумматора имеет два входа: A и B, которые добавляют две входные цифры и генерируют перенос и сумму.
Сумматор — это цифровая схема, выполняющая сложение чисел. Полусумматор складывает две двоичные цифры, называемые augend и addend, и выдает два результата: сумму и перенос; XOR применяется к обоим входам для получения суммы, а вентиль AND применяется к обоим входам для получения переноса.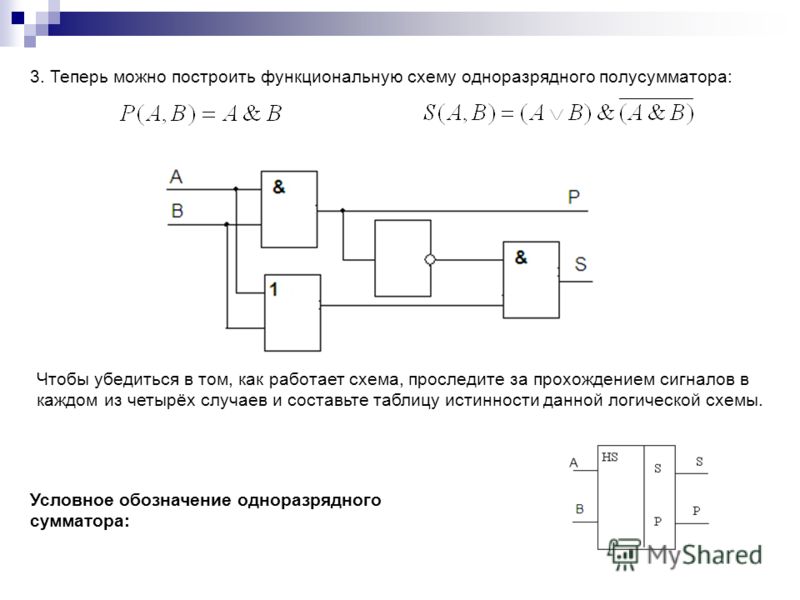
Используя полусумматор, вы можете разработать простое сложение с помощью логических вентилей. Полусумматор используется для сложения двух одноразрядных двоичных чисел и приводит к двузначному выводу. Он назван так потому, что объединение двух полусумматоров вместе с использованием вентиля ИЛИ приводит к полному сумматору. Другими словами, он выполняет только половину работы полного сумматора.
И ВОРОТ — Это цифровая схема, которая имеет два или более входа и производит выход, который представляет собой логическое И всех этих входов. Необязательно представлять логическое И символом ‘.’
Логические элементы И доступны с использованием цифровых схем для выполнения желаемой логической функции и имеют символ, форма которого представляет логическую операцию элемента И. Поскольку логическое выражение для логической функции И определяется как (.), что является бинарной операцией, логические элементы И могут быть объединены каскадом для формирования любого количества отдельных входов.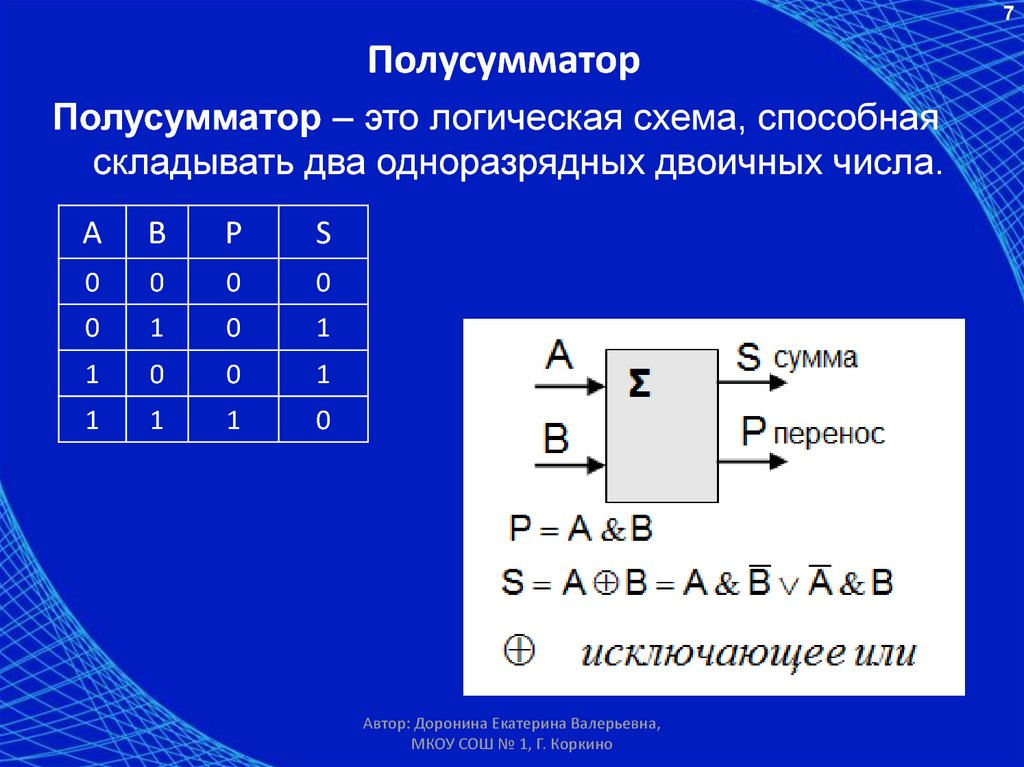
Однако имеющиеся в продаже микросхемы вентилей И доступны только в стандартных корпусах с 2, 3 или 4 входами. Если требуются дополнительные входы, то стандартные логические элементы И должны быть каскадированы вместе, чтобы получить требуемое выходное значение.
Логическое выражение Y = A.B
«Если A и B истинны, то Y истинно»
Этот логический элемент И производит выход Y, который является логическим И двух входов A, B.
ВОРОТА «ИСКЛЮЧАЮЩЕЕ ИЛИ» — Полная форма ворот «Исключающее ИЛИ» — ворота «Исключающее ИЛИ». Его функция такая же, как у вентиля ИЛИ, за исключением некоторых случаев, когда на входах имеется четное количество единиц.
Другими словами, выход вентиля исключающее ИЛИ становится «ВЫСКИМ» ТОЛЬКО, когда две его входные клеммы находятся на «РАЗНЫХ» логических уровнях по отношению друг к другу. Функция вентиля исключающее ИЛИ, или сокращенно Исключающее ИЛИ, достигается путем объединения стандартных логических вентилей вместе для формирования более сложных вентильных функций, которые широко используются при построении арифметико-логических схем, компараторов вычислительной логики и схем обнаружения ошибок.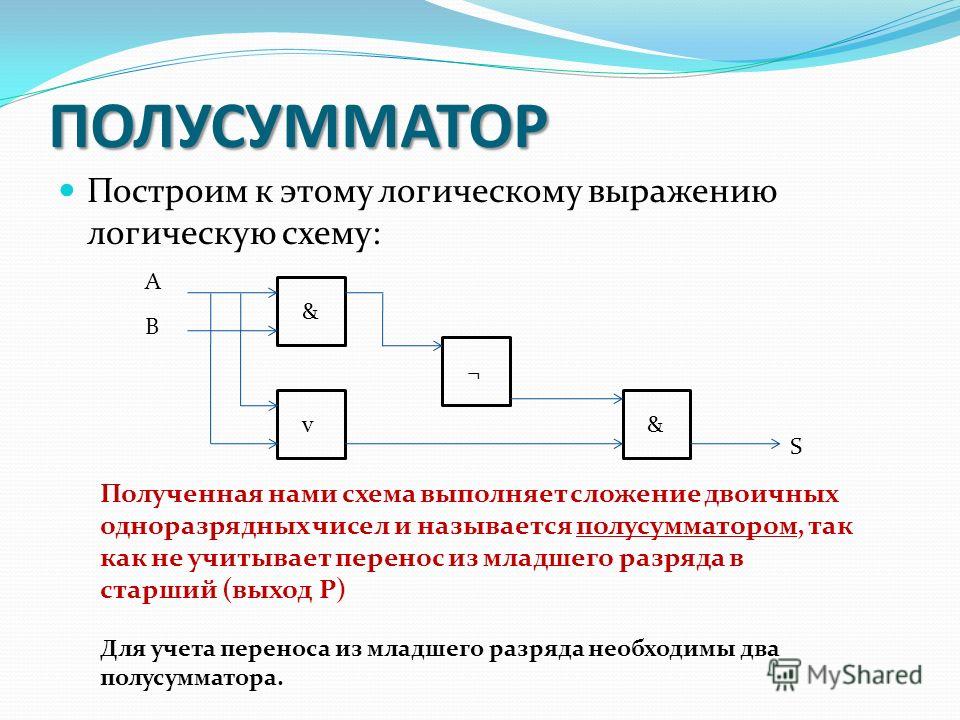
Логический элемент «исключающее ИЛИ» с двумя входами в основном представляет собой сумматор по модулю два, поскольку он дает сумму двух двоичных чисел.
Логическое выражение Y = A.B’ + ‘A.B = (A ⊕ B)
«Если на входах нечетное количество единиц, то Y истинно» Ворота ИЛИ, за исключением нескольких комбинаций входов. Выход вентиля Ex-OR равен «1», когда на входах присутствует нечетное количество единиц. Следовательно, выход вентиля Ex-OR также называется нечетной функцией.
Блок-схема
Меры предосторожности
- Выполните соединения в соответствии со схемой контактов ИС.
- Соединения тренажерного комплекта должны быть тугими.
- Напряжение питания и заземление следует применять осторожно только к указанному контакту.
Заключение
Мы изучили полусумматор, используя базовые вентили.Рекомендации
Функция полного сумматора с использованием декодера 3:8
Цель: изучить и проверить функцию полного сумматора с использованием декодера 3:8.
