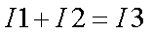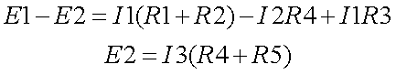Расчет простых электрических цепей
Тема. Расчет простых электрических цепей
Решение любой задачи по расчету электрической цепи следует начинать с выбора метода, которым будут произведены вычисления. Как правило, одна и таже задача может быть решена несколькими методами. Результат в любом случае будет одинаковым, а сложность вычислений может существенно отличаться. Для корректного выбора метода расчета следует сначала определиться к какому классу относится данная электрическая цепь: к простым электрическим цепям или к сложным.
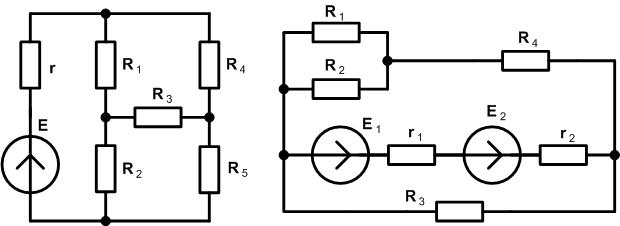
К простым относят электрические цепи, которые содержат либо один источник электрической энергии, либо несколько находящихся в одной ветви электрической цепи. Ниже изображены две схемы простых электрических цепей. Первая схема содержит один источник напряжения, в таком случае электрическая цепь однозначно относится к простым цепям. Вторая содержит уже два источника, но они находятся в одной ветви, следовательно это также простая электрическая цепь.
Расчет простых электрических цепей обычно производят в такой последовательности:
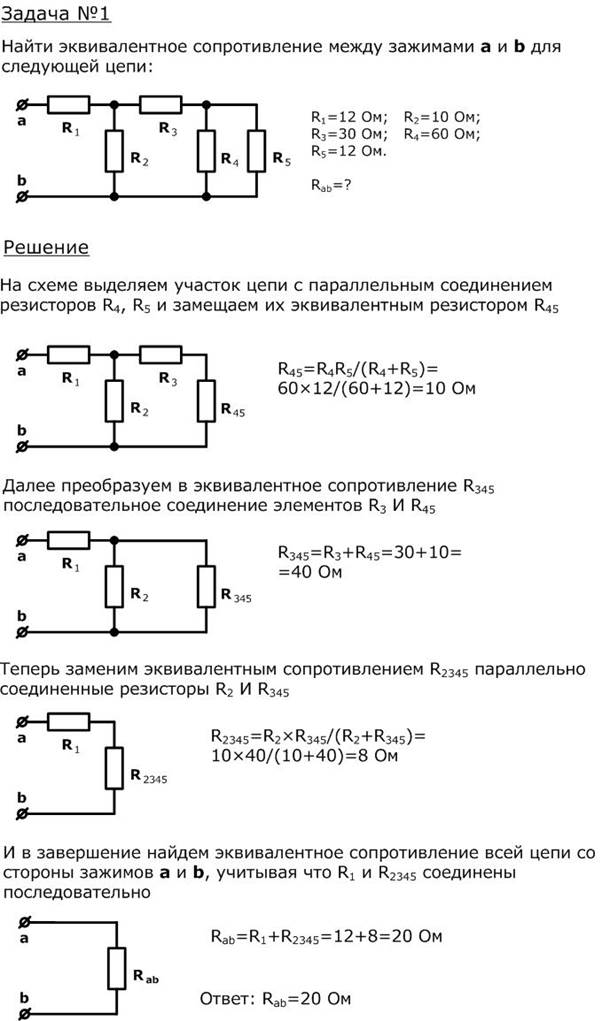
1. Сначала упрощают схему последовательно преобразовав все пассивные элементы схемы в один эквивалентный резистор. Для этого необходимо выделять участки схемы, на которых резисторы соединены последовательно или параллельно, и по известным формулам заменять их эквивалентными резисторами (сопротивлениями). Цепь постепенно упрощают и приводят к наличию в цепи одного эквивалентного резистора.
2. Далее подобную процедуру проводят с активными элементами электрической цепи (если их количество более одного источника). По аналогии с предыдущим пунктом упрощаем схему до тех пор, пока не получим в схеме один эквивалентный источник напряжения.
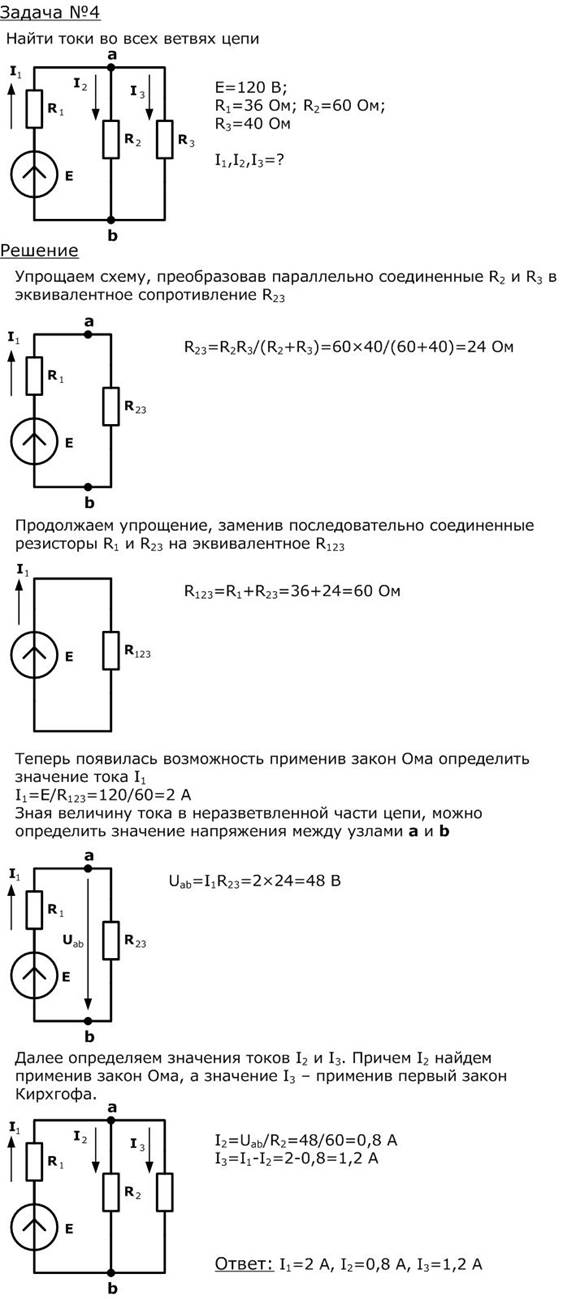
3. В итоге мы приводим любую простую электрическую схему к следующему виду:  Теперь есть возможность применить закон Ома — соотношение и фактически определить значение тока протекающего через источник электрической энергии.
Теперь есть возможность применить закон Ома — соотношение и фактически определить значение тока протекающего через источник электрической энергии.
соотношение (1.22) и фактически определить значение тока протекающего через источник электрической энергии.

правила расчета для определения силы тока
На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Пример сложных электрических цепей
Пути вычисления электрических схем
Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.
Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.
Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.
Все элементы и устройства подразделяются на три категории:
- Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
- Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
- Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.
Также к основным понятиям электрической схемы относятся:
- Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
- Узел электрической схемы – точка соединения трех и более ветвей схемы;
- Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.
Обозначение ветвей, узлов и контуров на схеме
Метод расчета по законам Ома и Кирхгофа
Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.
Закон Ома для участка цепи
По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:
UR=RI.
Исходя из этой формулы, найти силу тока можно по выражению:
I=UR/R, где:
- UR – напряжение или падение напряжения на резисторе;
- I – ток в резисторе.
Закон Ома для полной цепи
В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:
I=E/Rэ = E/r0+R, где:
- E – ЭДС источника питания;
- rо – внутреннее сопротивление источника питания.
Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.
Первый закон Кирхгофа
Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:
∑mIk=0, где m – число ветвей, подведенных к узлу.
Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».
Второй закон Кирхгофа
Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:
∑nEk=∑mRkIk=∑mUk, где:
- n – число источников ЭДС в контуре;
- m – число элементов с сопротивлением Rk в контуре;
- Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.
Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:
- Указать относительно положительные направления ЭДС, токов и напряжений;
- Указать направление обхода контура, описываемого уравнением;
- Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.
Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:
∑EI=∑RI2.
Метод преобразования электрической цепи
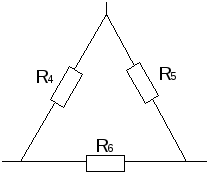
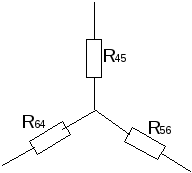
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.
Последовательное и параллельное соединение элементов
Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
- R1=R12R31/R12+R31+R23,
- R2=R12R23/R12+R31+R23,
- R3=R31R23/R12+R31+R23.
Треугольник и звезда соединений
Дополнительные методы расчета цепей
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Видео
Оцените статью:Методы расчета электрических цепей
Постановка задачи: в известной схеме цепи с заданными параметрами необходимо рассчитать токи, напряжения, мощности на отдельных участках. Для этого можно использовать следующие методы:
преобразования цепи;
непосредственного применения законов Кирхгофа;
контурных токов;
узловых потенциалов;
наложения;
эквивалентного генератора.
Будем рассматривать первых два метода.
Метод преобразования цепи. Суть метода: если несколько последовательно или (и) параллельно включенных сопротивлений заменить одним, то распределение токов в электрической цепи не изменится.
а) Последовательное соединение резисторов. Сопротивления включены таким образом, что начало следующего сопротивления подключается к концу предыдущего (рис. 6).
Ток во всех последовательно соединенных элементах одинаков.
З
 аменим
все последовательно соединенные
резисторы одним эквивалентным
аменим
все последовательно соединенные
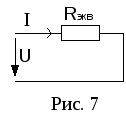
резисторы одним эквивалентным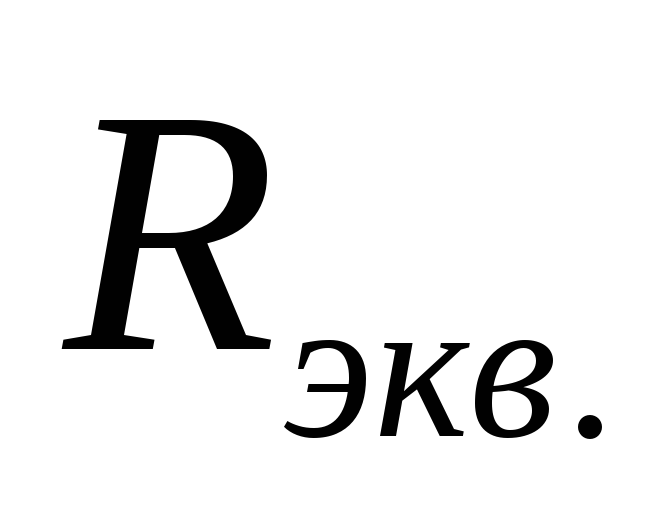 (рис. 7.).
(рис. 7.).
По IIзакону Кирхгофа:
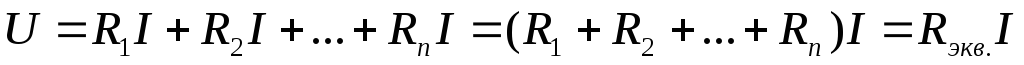 ;
;
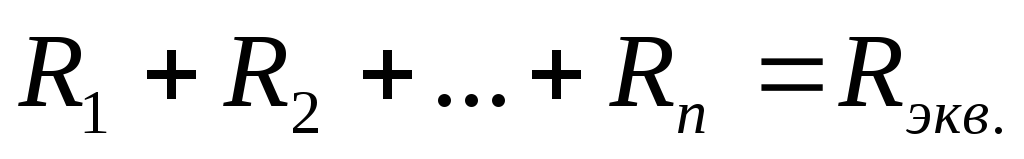 ;
;
т.е. при последовательном соединении резисторов эквивалентное сопротивление участка цепи равно сумме всех последовательно включенных сопротивлений.
б) Параллельное соединение резисторов. При этом соединении соединяются вместе одноименные зажимы резисторов (рис. 8).
В се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.
се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.
По Iзакону Кирхгофа: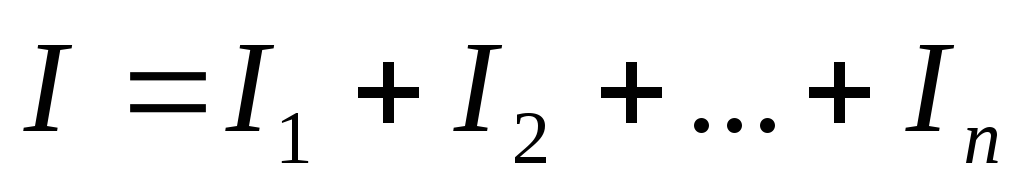 .
.
По
закону Ома 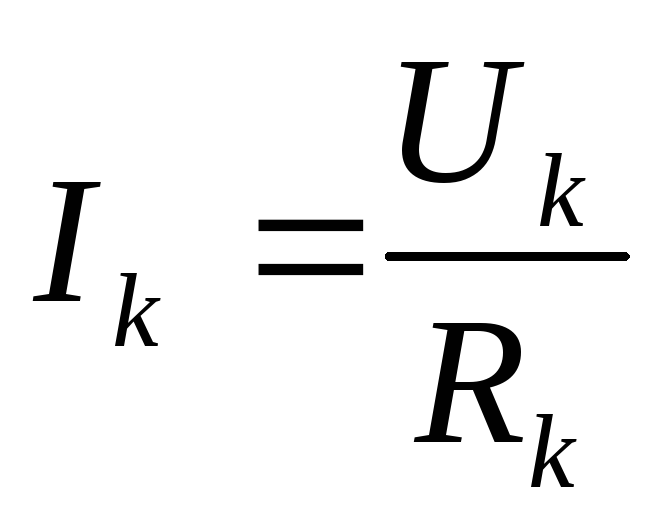 .
Тогда
.
Тогда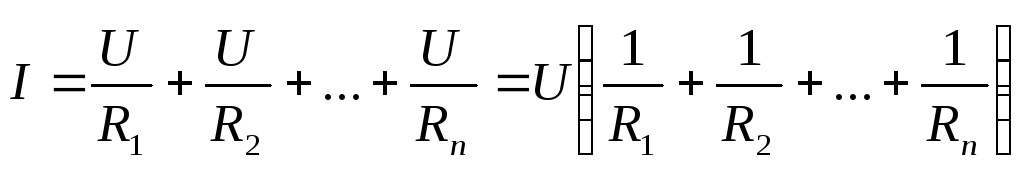
Для
эквивалентной схемы (см рис. 7): 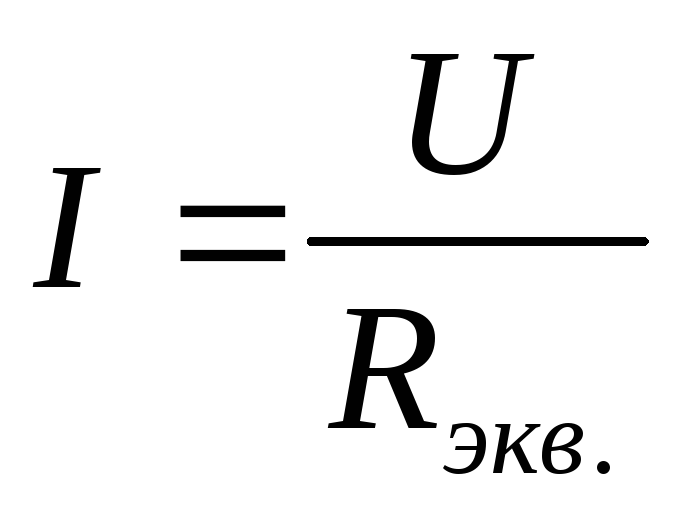 ;
; 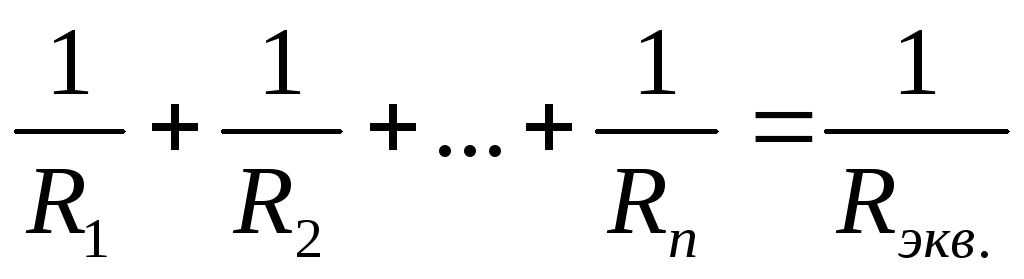 .
.
Величина 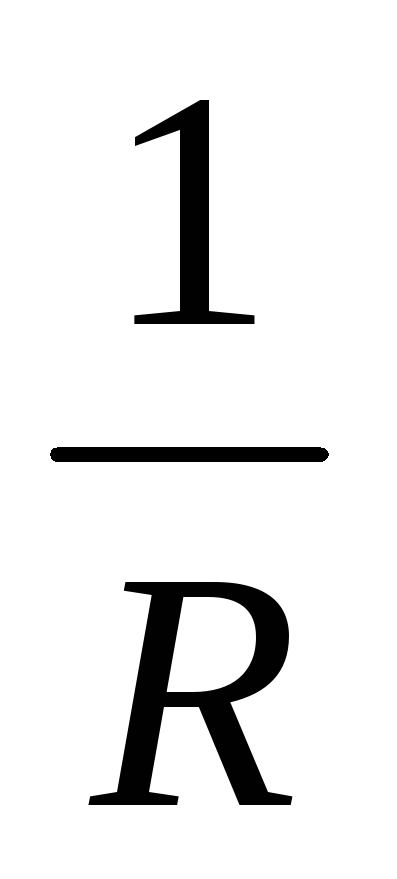 ,
обратная сопротивлению, называется
проводимостьюG.
,
обратная сопротивлению, называется
проводимостьюG.
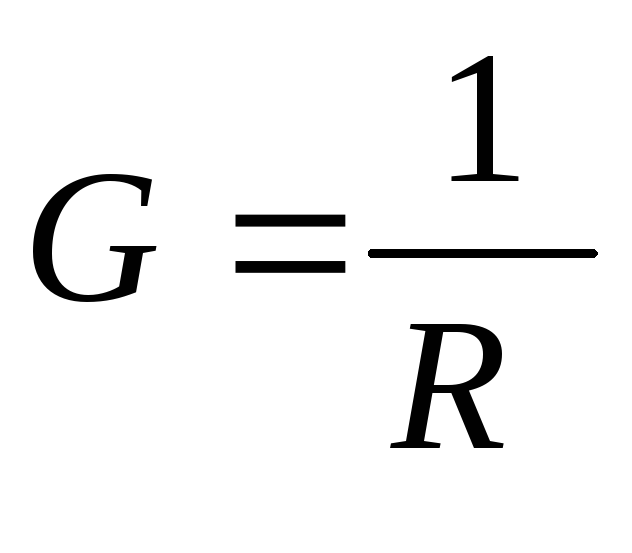 ;
;
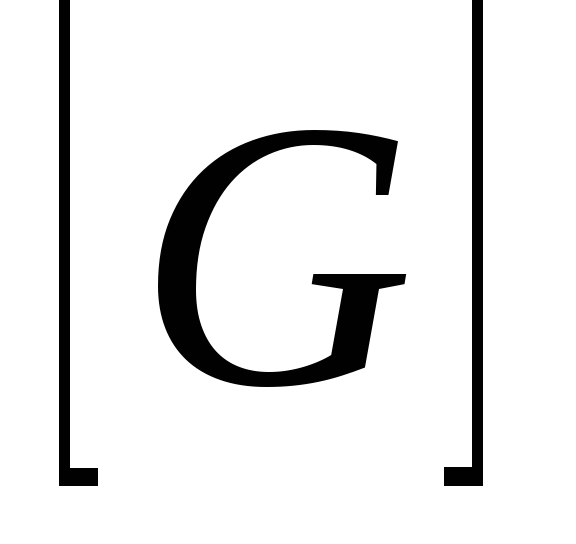
Ч астный
случай: параллельно соединены два
резистора (рис. 9).
астный
случай: параллельно соединены два
резистора (рис. 9).
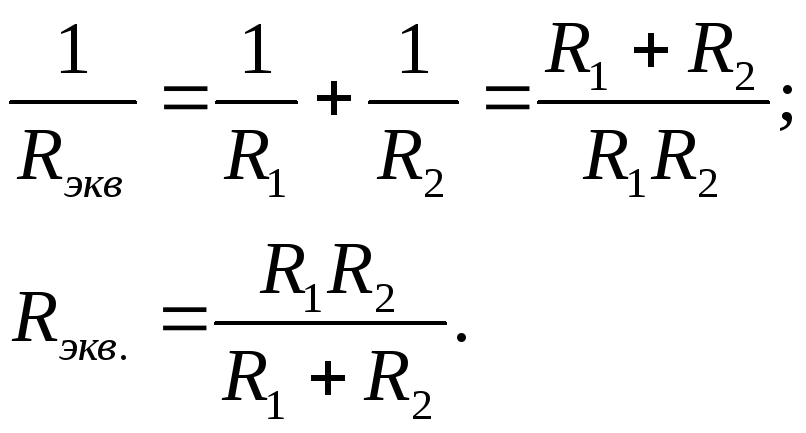


в) Взаимное преобразование звезды (рис.10а) и треугольник сопротивлений (рис. 10б).
— преобразование звезды сопротивлений в треугольник:

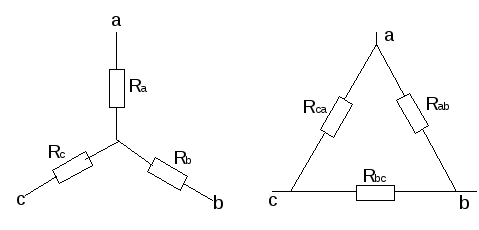
— преобразование «треугольника» сопротивлений в «звезду»:
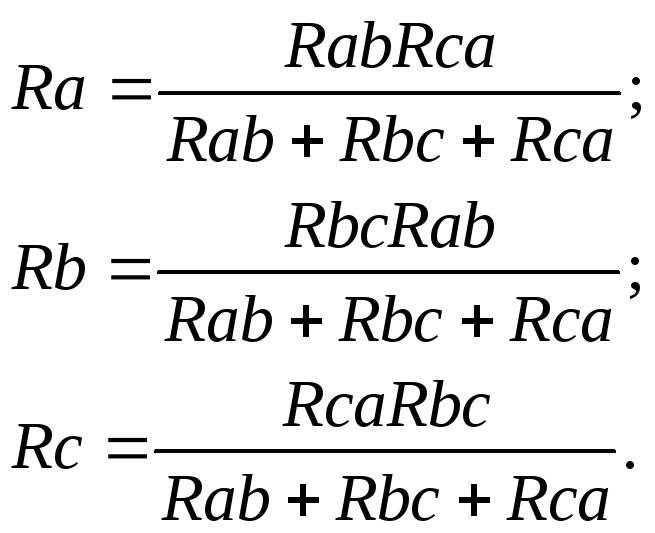
Метод непосредственного применения законов Кирхгофа. Порядок расчета:
Определить число ветвей (т.е. токов) и узлов в схеме.
Произвольно выбрать условно-положительные направления токов. Общее число уравнений должно быть равно числу неизвестных токов.
Определить, сколько уравнений должно быть составлено по Iзакону Кирхгофа, а сколько — поIIзакону Кирхгофа.
Составить уравнения для
 узлов
поIзакону Кирхгофа и
для
узлов
поIзакону Кирхгофа и
для независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.Решить система уравнений относительно токов. Если в результате ток получился отрицательным, то его действительное направление противоположно выбранному.
Проверить правильность решения задачи, составив уравнение баланса мощности и смоделировав электрическую цепь средствами моделирующего пакета ElectronicsWorkbench.
Примечание: если есть возможность, то перед составлением системы уравнений по законам Кирхгофа, следует преобразовать «треугольник» сопротивлений в соответствующую «звезду».
Пример расчет электрических цепей постоянного тока
Расчет будем выполнять с применением законов Кирхгофа, предварительно преобразовав треугольник сопротивлений в звезду.
П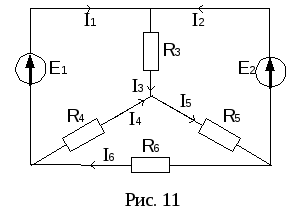 ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
Преобразуем треугольник сопротивлений R4
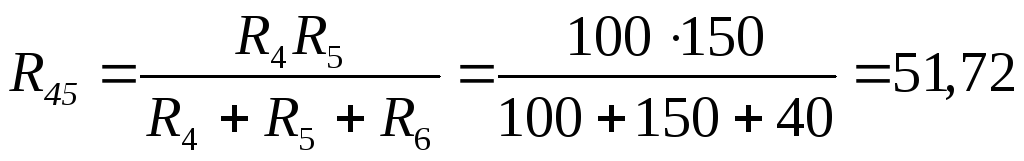 Ом;
Ом;
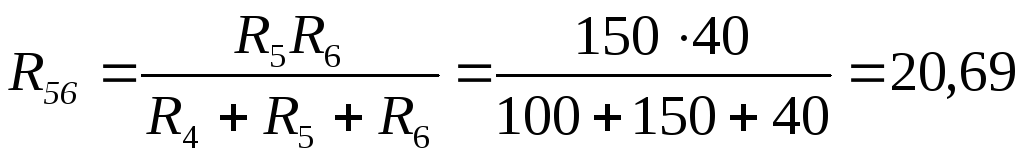 Ом;
Ом;
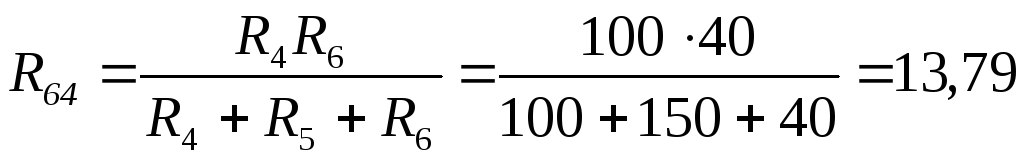 Ом.
Ом.
| |
а) | б) |
Рис. 12 | |
После преобразования электрическая цепь примет вид рис. 13 (в непреобразованной части электрической цепи направления токов не изменятся).
В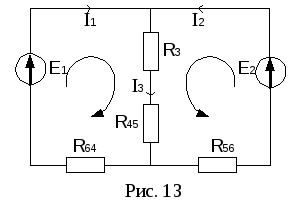 полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
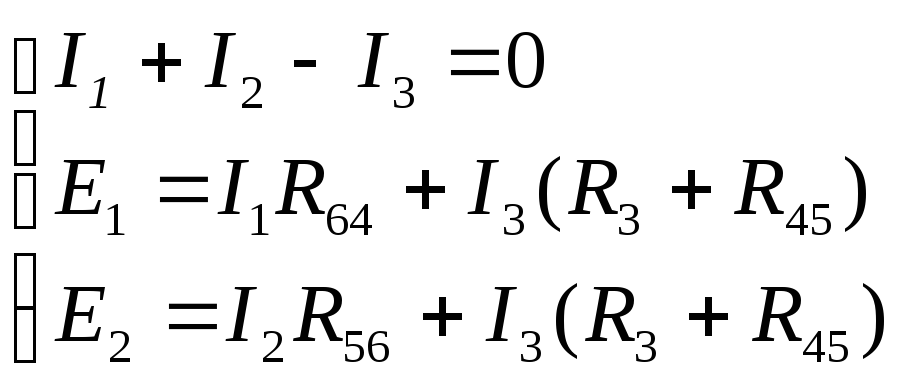
Подставим в полученную систему уравнений известные значения ЭДС и сопротивлений:
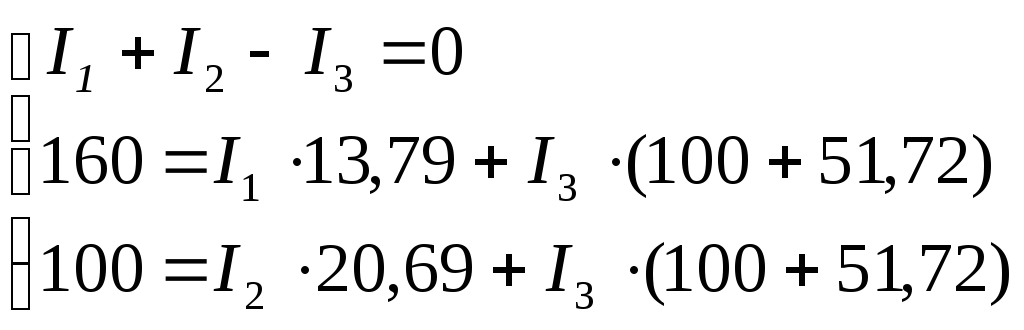
Решая систему уравнений любым способом, определяем токи схемы электрической цепи рис. 13:
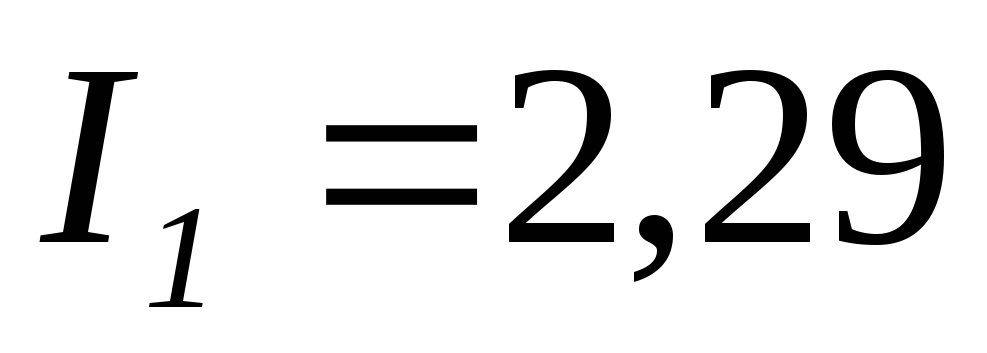 А;
А;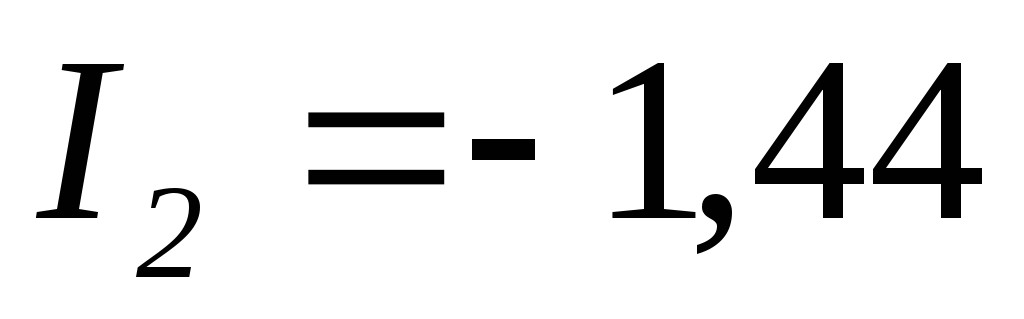 А;
А;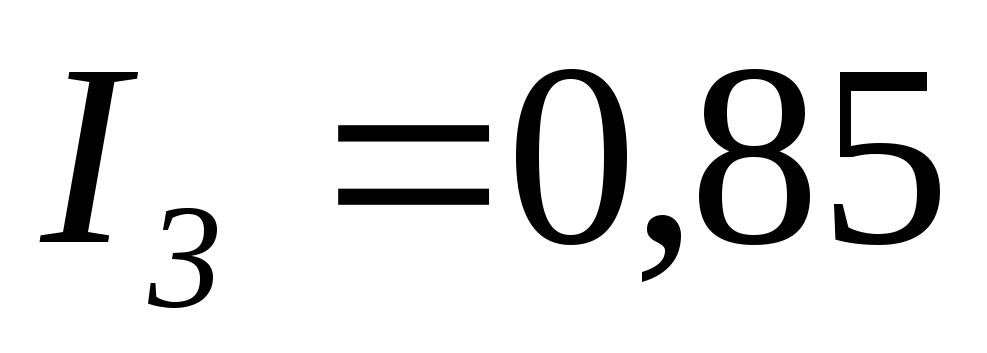 А.
А.
Переходим к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:
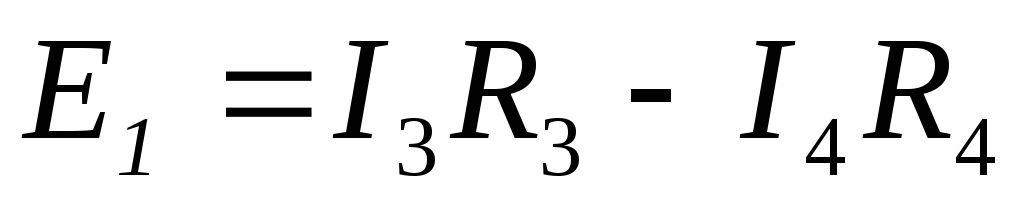 ;
;
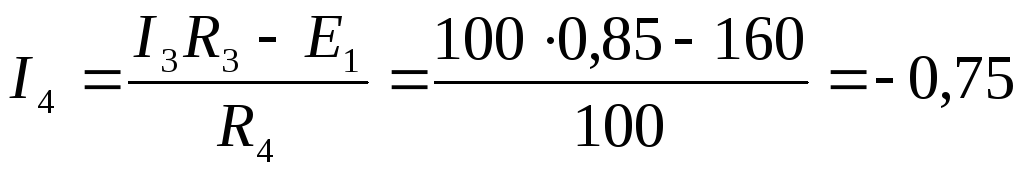 А.
А.
По Iзакону Кирхгофа:
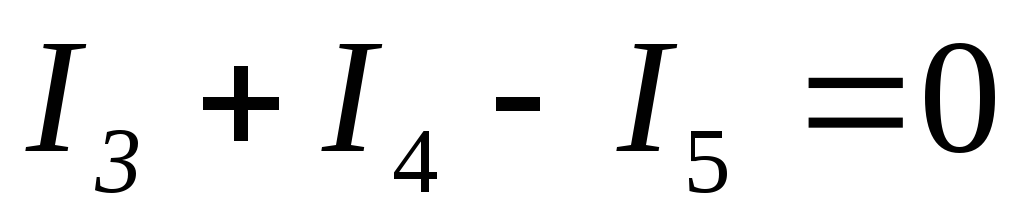 ;
;
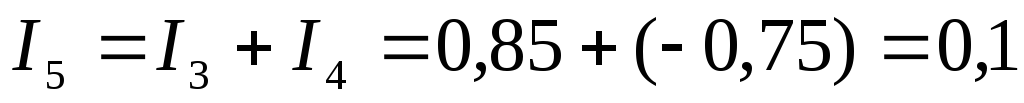 А;
А;
;
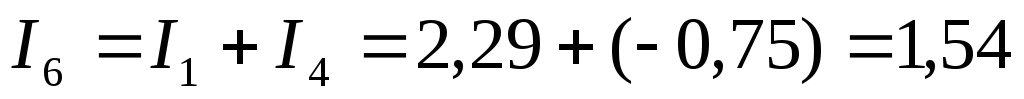 А.
А.
Т оки
оки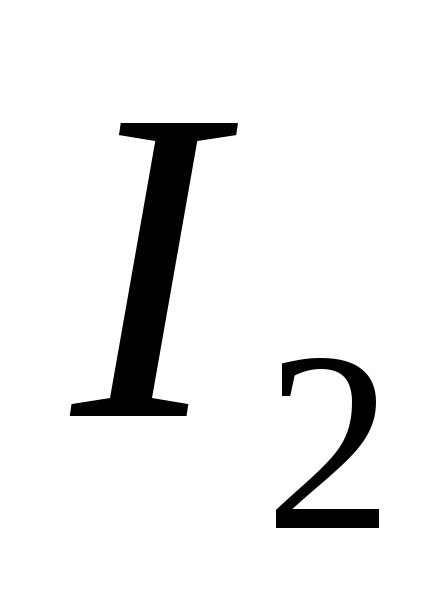 и
и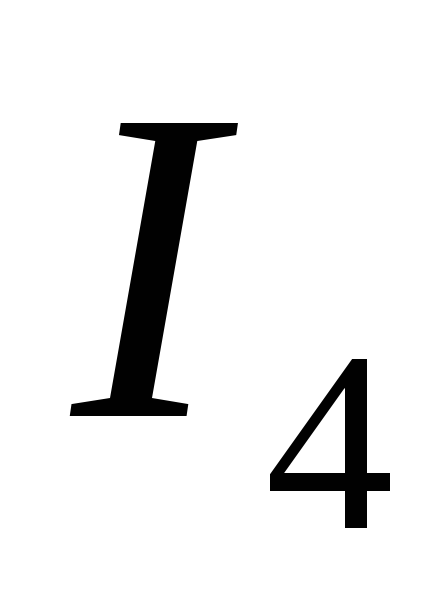 получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
Правильность решения проверяем, составив уравнение баланса мощности. Мощность источников (учтем, что ЭДС источника E2направленно встречно токуI2, протекающему через него):
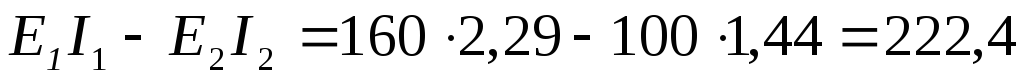 Вт.
Вт.
Мощность потребителей:

Погрешность вычислений в пределах допустимого (меньше 5%).
Смоделируем электрическую цепь рис. 11 средствами моделирующего пакета ElectronicsWorkbench(рис. 15):
Р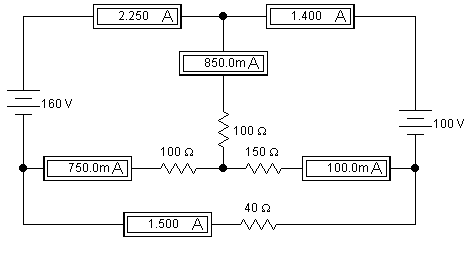 ис.
15
ис.
15
При сравнении расчетных результатов и результатов моделирования, можно увидеть, что они отличаются (различия не превышают 5%), т.к. измерительные приборы имеют внутренние сопротивления, которые моделирующая система учитывает
Электротехника Часть 5 Методы расчёта электрических цепей
Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Расчёт электрических цепей с помощью законов Кирхгофа
Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.
Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением
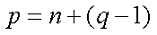
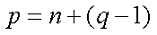
В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже
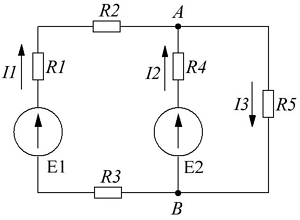

Пример электрической цепи для расчёта по законам Ома и Кирхгофа.
В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.
- Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид


- Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3 и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид


Таким образом, получившаяся система уравнений будет иметь следующий вид
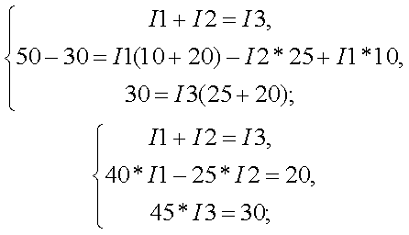
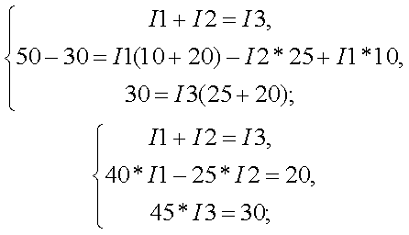
Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.
В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.
Метод контурных токов
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже
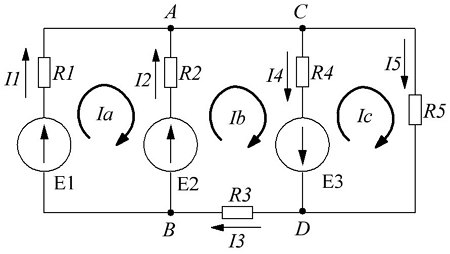

Расчет цепи методом контурных токов.
Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях
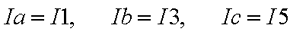
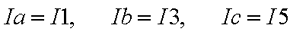
Остальные же токи можно найти как разность двух контурных токов
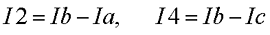
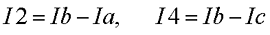
В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа
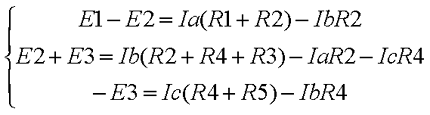
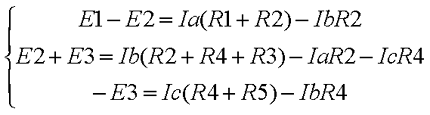
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
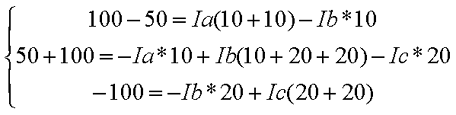
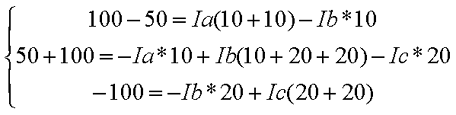
В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.
Метод узловых напряжений
Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает
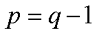
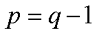
где q – количество узлов в электрической цепи.
Принцип расчёта электрической цепи заключается в следующем:
- Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
- Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
- После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.
В качестве примера возьмём предыдущую цепь и составим систему уравнений
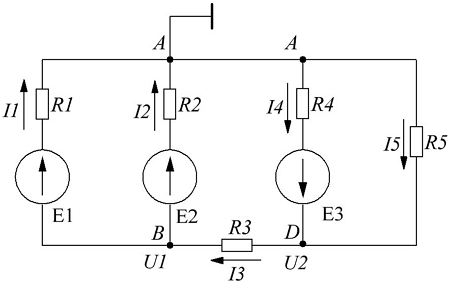

Схема для решения уравнений методом узловых потенциалов.
В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа
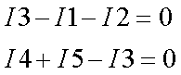
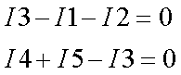
Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома
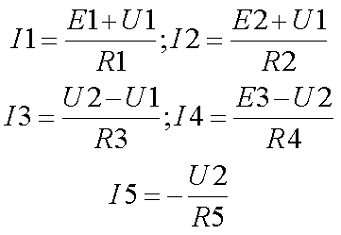
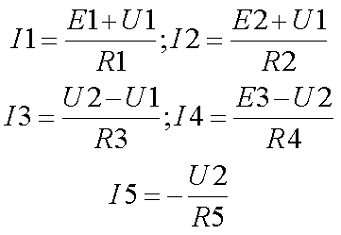
В результате получившаяся система будет иметь следующий вид
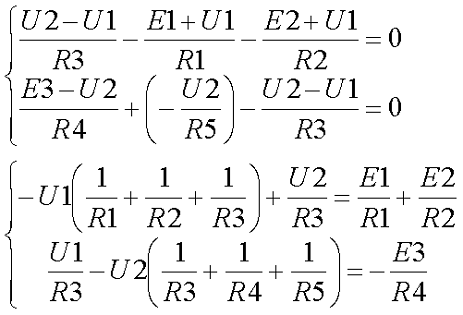
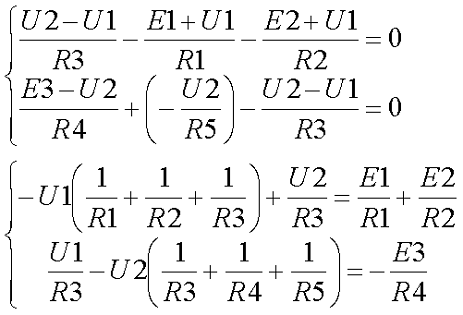
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
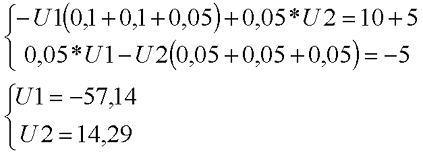
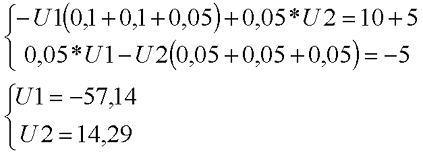
В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны
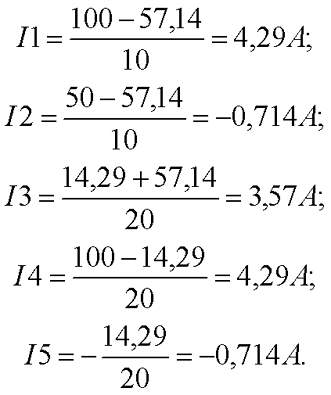
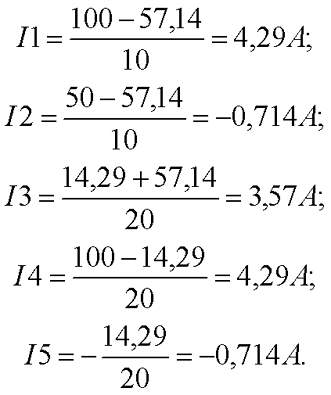
Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Виды электрических схем: как сделать электропроект квартиры
Вступление
Все работы по ремонту квартиры имеют важное значение. Нельзя сказать, что какие-то работы важнее, чем другие. Но среди всех работ я бы выделил работы по устройству новой электропроводки. Как правило, новая электропроводка выполняется в скрытом виде и поэтому переделать некачественно или неправильно сделанную электропроводку после завершения ремонтных работ будет затруднительно.
Виды электрических схем
Рассмотрим виды электрических схем и сделаем упрощенный электропроект квартиры своими руками.
Разобьем работы по организации новой электропроводки 3-х комнатной квартиры на несколько этапов.
- Самостоятельно сделаем упрощенный электропроект 3-х комнат, коридора и кухни с учетом потребностей в розетках и светильниках;
- Реализуем, согласно проекту, скрытую электропроводку во всей квартире;
- Установим встроенный квартирный щиток;
- После окончания чистовых ремонтных работ установим розетки и выключатели по местам.
Перед началом любых работ по электропроводке необходимо сделать, хотя бы упрощенный электропроект квартиры. В этой статье рассмотрим виды электрических схем используемых в электромонтаже и применим эти знания для 3 х-комнатной квартиры электропроекта этой серии из 4-х статей.
Электрическая схема и виды электрических схем
Электрическая схема квартиры включает в себя все электротехнические устройства в квартире, подключаемые к электрической сети, изображенные на плане в виде условных графических обозначений. Также на электрической схеме обозначены все взаимосвязи между электротехническими устройствами. (ГОСТ 2.702-75)
По степени наполнения и раскрытия информации электрические схемы подразделяются следующим образом.
Структурная электрическая схема
Структурная электрическая схема это самая простая схема первого этапа проектирования. На ней в виде прямоугольников показываются основные элементы электропроводки квартиры: электрощиты, распределительные коробки, электропроводка комнат, электропроводка ванной, электропроводка кухни. Структурная схема дает самые общие представления об электропроводке квартиры.
В нашем варианте это выглядит так.
Функциональная электрическая схема
Функциональная электрическая схема это достаточно абстрактная схема, которая показывает все функциональные связи между отдельными элементами квартирной электросети. То есть, на функциональной схеме мы в общих чертах раскрываем электропроводку каждой комнаты квартиры.
В нашем варианте это выглядит так.
Условные обозначения на электрических схемах ниже:
Расчетная электрическая схема
Расчетная электрическая схема делается на основе функциональной схемы. С помощью несложных расчетов определяем какое разбиение электропроводки по группам нужно сделать, а также, какой электрический кабель и какие установочные устройства (автоматы защиты, УЗО) нужно приобретать для электромонтажных работ в квартире.
Расчетная электрическая схема квартиры может быть выполнена в варианте однолинейной схемы или в варианте полнолинейной электрической схемы.
Полнолинейная расчетная электрическая схема
- На полнолинейной схеме показывают электрооборудование всех фаз электросети, при условии, что электропитание квартиры трехфазное.
Однолинейная расчетная электрическая схема
- На однолинейной электрической схеме показывается оборудование только одной фазы.
- Электрическая однолинейная схема главных электрических цепей квартиры с краткими характеристиками электрооборудования принято называть главной схемой.
- Та как мы делаем упрощенный электропроект, выполнять однолинейную расчетную схему мы не будем, да и технически это не просто. Но пример однолинейной расчетной схемы я приведу.
Как видите, однолинейная расчетная схема достаточно сложный документ и сделать его в таком виде самостоятельно, без профессиональных навыков вряд ли удастся. Однако вам под силам сделать упрощенный расчет сечения проводов в электрическом кабеле для электропроводки квартиры.
Расчет сечения проводов электропроводки
Расчет сечения проводов производится следующим образом.
- Разделите всю электропроводку в квартире на отдельные группы. Лучше розетки каждой комнаты выделить в отдельную группу. К группам розеток добавить группу освещения и отдельные линии электропитания для мощных бытовых приборов: стиральной машины, электроплиты, посудомоечной машины, бойлера и т.п.;
- Определитесь, какие бытовые приборы будут включены в линию каждой розеточной группы;
- Сложите потребляемую мощность бытовых приборов каждой группы, согласно их технического паспорта. Получится общая потребляемая мощность группы, в Киловаттах;
- Один Киловатт потребляемой мощности соответствует 5 Амперам величины рабочего тока при 220 вольтовом электропитании;
- Далее по таблице ниже можно рассчитать сечение проводов, которые нужно прокладывать для электропитания данной Группы.
Например:
- Варочная панель максимальной мощности 4 Киловатта.
- Рабочий ток 4 × 5 ампер=20 Ампер.
- Из таблице видим, что нужен медный электрический кабель сечением: 2,5 кв. мм.
| Проложенные открыто | ||||||
| S | Медные жилы | Алюминиевые жилы | ||||
| мм2 | Ток | Мощн.кВт | Ток | Мощн.кВт | ||
| А | 220 В | 380 В | А | 220 В | 380 В | |
| 0,5 | 11 | 2,4 | ||||
| 0,75 | 15 | 3,3 | ||||
| 1 | 17 | 3,7 | 6,4 | |||
| 1,5 | 23 | 5 | 8,7 | |||
| 2 | 26 | 5,7 | 9,8 | 21 | 4,6 | 7,9 |
| 2,5 | 30 | 6,6 | 11 | 24 | 5,2 | 9,1 |
| 4 | 41 | 9 | 15 | 32 | 7 | 12 |
| 5 | 50 | 11 | 19 | 39 | 8,5 | 14 |
| 10 | 80 | 17 | 30 | 60 | 13 | 22 |
| 16 | 100 | 22 | 38 | 75 | 16 | 28 |
| 25 | 140 | 30 | 53 | 105 | 23 | 39 |
| 35 | 170 | 37 | 64 | 130 | 28 | 49 |
| Проложенные в трубе | ||||||
| S | Медные жилы | Алюминиевые жилы | ||||
| мм2 | Ток | Мощн.кВт | Ток | Мощн.кВт | ||
| А | 220 В | 380 В | А | 220 В | 380 В | |
| 0,5 | ||||||
| 0,75 | ||||||
| 1 | 14 | 3 | 5,3 | |||
| 1,5 | 15 | 3,3 | 5,7 | |||
| 2 | 19 | 4,1 | 7,2 | 14 | 3 | 5,3 |
| 2,5 | 21 | 4,6 | 7,9 | 16 | 3,5 | 6 |
| 4 | 27 | 5,9 | 10 | 21 | 4,6 | 7,9 |
| 5 | 34 | 7,4 | 12 | 26 | 5,7 | 9,8 |
| 10 | 50 | 11 | 19 | 38 | 8,3 | 14 |
| 16 | 80 | 17 | 30 | 55 | 12 | 20 |
| 25 | 100 | 22 | 38 | 65 | 14 | 24 |
| 35 | 135 | 29 | 51 | 75 | 16 | 28 |
Такой расчет нужно провести для каждой группы электропроводки.
Этот расчет не является абсолютно правильным, но для средней квартиры при отсутствии асинхронных двигателей, то есть для любой нормальной квартиры такой расчет достаточно точный и он позволит не только рассчитать сечения проводов для электропроводки, но и даст номинальные значения токов отсечки автоматов защиты для каждой группы или проще, с какими номиналами нужно покупать автоматы защиты.
Принципиальная электрическая схема
Принципиальная электрическая схема это чертеж, сделанный согласно разнообразным стандартам. На принципиальной схеме подробно показаны полные электрические, магнитные и электромагнитные связи всех элементов квартиры. На принципиальной схеме указываются все параметры компонентов сети: напряжение, сила тока, потребляемая мощность. На принципиальной схеме обозначаются рассчитанные нагрузки, выбранные автоматы защиты и сечения проводов (кабелей) отдельных линий электропроводки .
Принципиальные электрические схемы делаются отдельно для освещения квартиры и электрооборудования квартиры.
Пример
Приведу пример принципиальной электрической схемы электрооборудования квартиры сделанной в проектной мастерской.
Как видите из схемы можно понять где будут находиться розетки, какая планируется мощность бытовых приборов. Из пояснения становиться ясно какой кабель для электропроводки нужен, какая высота розеток от пола. каким способом выполняется электропроводка. В общем вполне достаточная схема для проведения электромонтажных работ.
Для себя вы должны сделать похожую, но более простую схему электропроводки. Для освещения нужно сделать аналогичную схему, изобразив на ней расположение светильников и выключателей квартиры.
Монтажная схема
Монтажная схема электропроводки квартиры наиболее полная из всех электрических схем. На ней показывается реальное расположение всех элементов сети: розеток, выключателей, распаячных коробок в квартире, так и за ее пределами: этажный щиток, вводное устройство.
На монтажной схеме обозначается расстояния и привязки установок элементов сети по отношению к геометрии комнаты. Иначе говоря, на монтажной схеме точно показаны места расположения всех розеток, выключателей, коробок с указанием всех координат расположения: расстояния от пола, от углов комнат, от потолка.
Монтажные схемы выполняются отдельно для освещения и для электрооборудования. Для упрощения монтажная и принципиальная схемы могут объединяться, как на примере выше.
Другие электрические схемы
Также для электропроводки квартиры могут составляться кабельные планы, на которых показываются расположение и марки всех электрических проводов и кабелей, запланированных в квартире. К другим схемам квартиры можно отнести электросхемы слаботочных сетей (телефония и компьютер).
Выводы
Для дальнейших работ по электропроводке трехкомнатной квартиры этой серии статей, посмотрим схему электропроводки ниже.
виды электрических схем
Электропроводку разбиваем на 9 Групп:
- 6 Групп для розеток;
- 1 Группу для освещения;
- 2 Группы для мощных бытовых приборов(плиты и стиральной машины)
Электропроводку розеточных групп будем выполнять медным кабелем ВВГ 3×2,5 мм(три однопроволочных жилы, сечением 2,5 мм, в виниловой изоляции).
Электропроводку плиты будем выполнять кабелем ВВГнг (кабель с негорючей изоляцией ) 3×4 мм.кв.
Электроосвещение будем выполнять кабелем ВВГ 3×1,5 мм.кв. можно заменить на кабель ПВС (провод виниловый соединительный) 3 × 1,5 мм. На следующем этапе работ соберем и установим в квартире встроенный распределительный щиток в квартире, установим все автоматы защиты, введем в квартиру новый питающий кабель.
©www.otdelochnik24.ru
Другие статьи сайта близкие по теме
55.61953237.741349
Поделись ссылкой:
РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ИСПОЛЬЗОВАНИЕМ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
РАСЧЁТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ИСПОЛЬЗОВАНИЕМ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Ли Геннадий Инокентиевич
студент 1 курса, кафедра Электроэнергетики и электротехники Дальневосточного федерального университета, РФ, г. Владивосток
E —mail: li—gena-1996@mail.ru
Дмух Галина Юрьевна
научный руководитель, канд. пед. наук, доц. кафедры алгебры, геометрии и анализа ШЕН Дальневосточного Федерального Университета, РФ, г. Владивосток
Статья посвящена методу расчёта электрических цепей с использованием систем линейных алгебраических уравнений. В ней рассмотрены основные методы и понятия. Приведён пример, показывающий рациональность и практичность использования систем линейных алгебраических уравнений в электротехнике. Так же рассматриваются вопросы взаимодействия и связи математики и инженерии.
Инженерное дело тесно связано с математикой. Математические методы нашли широкое применение в различных инженерных специальностях. Можно сказать, что инженерия стимулирует развитие математики, ведь многие математические методы появлялись из потребностей инженерной практики. Например, метод наименьших квадратов, который используется для обработки результатов наблюдений, возник из потребностей геодезической практики. Цель инженерной математики, помочь инженеру в познании практически важных моделей и методов, которые ориентированы на решение различных инженерных задач. Следовательно, инженерное дело не может развиваться и реализоваться без математического аппарата.
Например, инженер-электротехник, при решении различных задач использует системы линейных алгебраических уравнений (СЛАУ).
Системой линейных алгебраических уравнений содержащей m уравнений и n неизвестных, называется система вида:
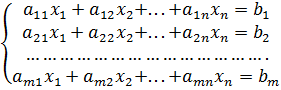
где: числа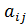 ,
, 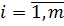 ,
, 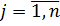 называются коэффициентами системы, числа
называются коэффициентами системы, числа 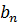 – свободными членами.
– свободными членами.
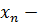 подлежат нахождению [1, с. 29].
подлежат нахождению [1, с. 29].
Первые СЛАУ встречаются ещё в вавилонских и египетских рукописях II века до н. э., а также в трудах древнегреческих, индийских и китайских мудрецов. В китайском трактате «Математика в девяти книгах» словесно изложены правила решения систем уравнений, были замечены некоторые закономерности при решении. На протяжении многих лет выдающиеся математики своего времени разрабатывали методы решения СЛАУ. На данный момент существует множество различных методов решения систем. В своей работе я разберу один из основных методов решения СЛАУ, метод Гаусса.
Суть метода заключается в том, что систему линейных алгебраических уравнений приводят к ступенчатому виду, используя элементарные преобразования.
Приведённая система имеет ступенчатый вид

где  . Коэффициенты
. Коэффициенты 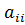 называются главными элементами системы [1, c. 34].
называются главными элементами системы [1, c. 34].
Составив ступенчатую систему, решаем её. Если система оказывается треугольной, то есть 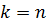 , то система имеет единственное решение. Если же
, то система имеет единственное решение. Если же 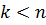 , то исходная система имеет множество решений.
, то исходная система имеет множество решений.
В электротехнике часто встречаются задачи, в которых необходим расчёт электрической цепи, то есть необходим расчёт напряжения и силы тока во всех ветвях цепи. Например, известны сопротивления и ЭДС, но нет значений силы тока. Для решения таких задач используют правила Кирхгофа.
Разберём этот метод на конкретной задаче. При решении будем использовать метод Гаусса. Этот метод является наиболее простым, и подходит практически к любой системе.
Пример:
Дана схема (рисунок 1), и известны сопротивления резисторов и ЭДС источников( 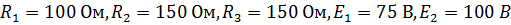 ). Требуется найти токи в ветвях
). Требуется найти токи в ветвях
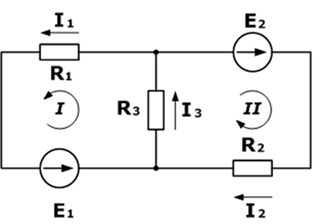
Рисунок 1. (Схема электрической цепи)
Решение:
Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равно 0. Значит: 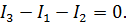
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. С помощью этого закона составим уравнения для первого и второго контура цепи: 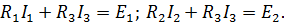
Теперь из трёх уравнений составляем систему уравнений:
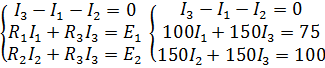
Из коэффициентов перед неизвестными составляем матрицу:
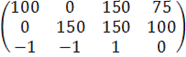
Решение можно разбить на два этапа. Сначала с помощью элементарных преобразований приведём систему к ступенчатому виду:
1-ую строку делим на 100: 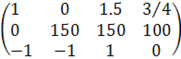
к 3 строке добавляем 1 строку, умноженную на 1: 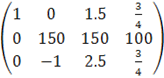
2-ую строку делим на 150: 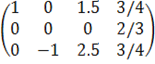
к 3 строке добавляем 2 строку: 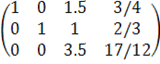
Теперь решаем ступенчатую систему:
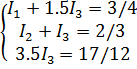
Так как 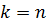 , система имеет единственное решение.
, система имеет единственное решение.
Находим значения токов:
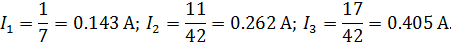
Вычислительная техника выполняет такие операции за доли секунд. Таким образом, СЛАУ играет большую роль в электротехнике. С помощью СЛАУ можно быстро и точно рассчитать эклектическую цепь.
Список литературы:
1.Письменный Д. «Конспект лекций по высшей математике», Айрис-пресс, 2006, 4-е изд., — 608 с.
2.Сигорский В.П. Математический аппарат инженера. Изд. 2-е, стереотип. «Texнiкa», 1977, — 768 с.
3.Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич. спец. вузов. 4-е изд., перераб. и доп. М.: Высш. шк., 1990. — 544 с.
Выбор и расчет элементов электрической схемы
1 Расчет мостового выпрямителя
Для правильного выбора элементов схемы необходимо знать величины токов, текущих по цепям. Рассмотрим выбор диодов выпрямителя и расчет сопротивления нагрузки.
Рассчитаем сопротивление нагрузки. Максимально допустимое напряжение:
Umax
доп = Uвх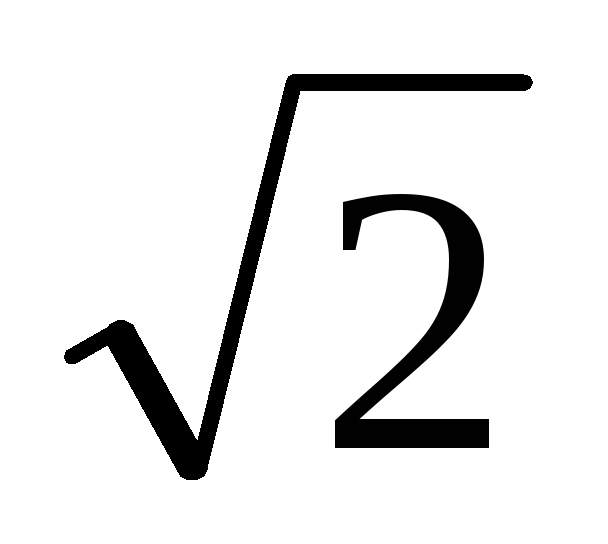 ,
(1)
,
(1)
где Uвх – напряжение источника питания.
Согласно требованиям технического задания Uвх = 24 В. Следовательно, Umax доп = 34 В. Исходя из этих данных можно выбрать диоды. Диоды выбирают так, чтобы значения выпрямленного тока и допустимого обратного напряжения были равны расчетным значениям или превышали их. В данной схеме целесообразно использовать диоды типа КД103Б, у которых Uобр max = 50 В, Iпр max = 100 мА и Uпр max = 1,2 В [].
Предположим, что ток нагрузки Iн = 0,1 А. Напряжение на нагрузке можно вычислить по формуле:
Uн = Uвх – Uпр max 2, (2)
где Uн – напряжение на нагрузке;
Uвх – напряжение источника питания;
Uпр max 2 – напряжение для последовательного соединения диодов мостовой схемы.
Известно, что у каждого из четырех диодов Uпр max = 1,2 В. В мостовой схеме два диода всегда соединены последовательно, а значит Uпр max2 = 2,4 В. Подставив данные значения в формулу (2), получим значение напряжения на нагрузке Uн = 21,6 В.
Зная ток нагрузки Iн и напряжение нагрузки Uн, по закону Ома можно найти сопротивление нагрузки Rн =216 Ом.
2 Расчет сглаживающего фильтра
Поскольку в схеме частота сети 50 Гц (после удвоения на выпрямителе – 100 Гц), то типичная емкость конденсатора находится в диапазоне от 100 мкФ до 30000 мкФ.
Конденсатор подбирают так, чтобы выполнялось условие []:
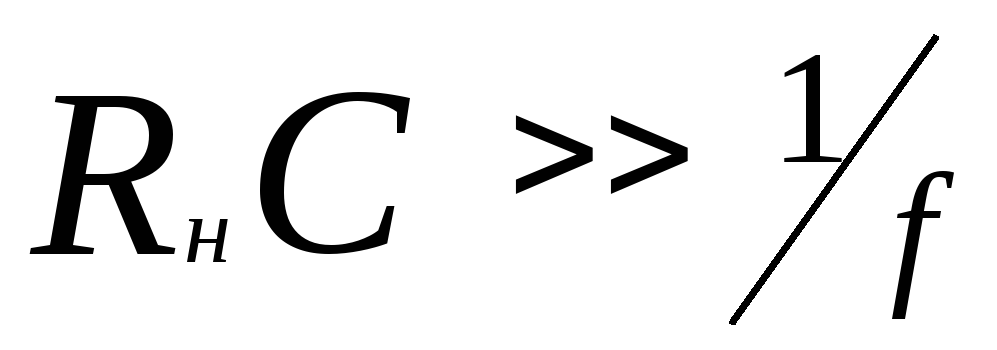 ,
(3)
,
(3)
где f – частота пульсаций;
Rн – сопротивление нагрузки;
C – емкость конденсатора.
При этом происходит ослабление пульсаций за счет того, что постоянная времени для разрядки конденсатора существенно превышает время между перезарядками [].
Выразив из (3) величину С:
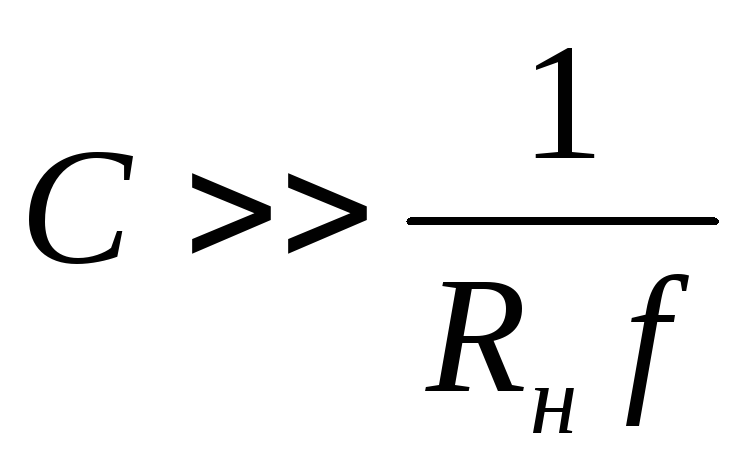 (4)
(4)
и
подставив численные значения, получим
емкость конденсатора 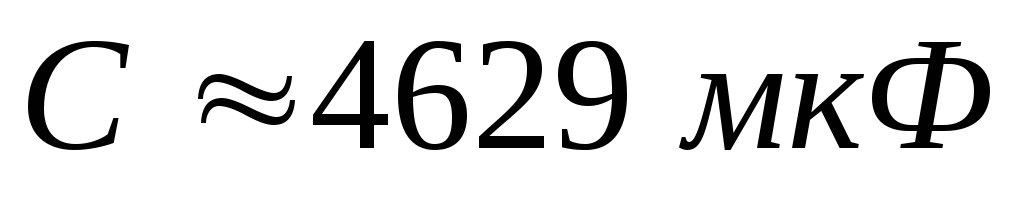 .
.
Для определения коэффициента пульсации выходного напряжения воспользуемся формулой 5:
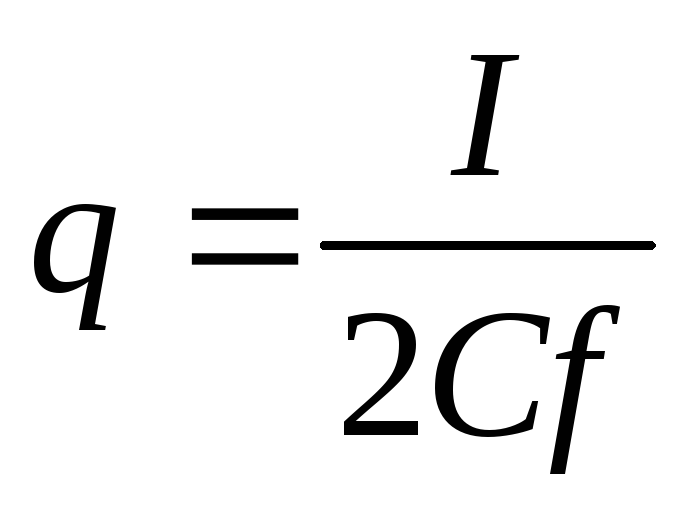 (5)
(5)
где I – средний ток нагрузки
C – емкость конденсатора
f – частота переменного напряжения в герцах
Подставив численные значения, получим q ≈ 0,2.
3 Стабилизатор напряжения
В данном проекте используются стабилизаторы серий 142ЕН. Основными критериями выборов данных стабилизаторов, послужили их номинальные значения, приведенные в таблице 1 и коэффициент нестабильности по напряжению стабилизатора, влияющий на нестабильность напряжения всего ИОН, которая должна соответствовать заданию.
Емкость входного конденсатора С1 должна быть не менее 0,33 мкФ, а емкость выходного конденсатора С2 не менее 1 мкФ [].
4 Делителя напряжения
П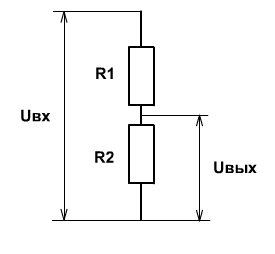 ростейший
делитель напряжения – схема, которая
для данного напряжения на входе создает
на выходе напряжение, являющееся частью
входного, приведена на рисунке 5.
ростейший
делитель напряжения – схема, которая
для данного напряжения на входе создает
на выходе напряжение, являющееся частью
входного, приведена на рисунке 5.
Рисунок 5 – Делитель напряжения
5 Расчет источников опорного напряжения
Для получения выходных напряжений минус 8,14 В используется схема, на основе стабилизатора 142ЕН11 изображенная на рисунке 6.
Рисунок 6 – Схема включения 142ЕН11
Требуемый
уровень выходного напряжения, указанного
в задании, устанавливается резисторами
R1
и R2
[]. Для первого источника выходное
напряжение должно быть минус 8,14 В.
Следовательно Uвых варьируется между минус 8,123 и минус
8,156. Для стабилизатора серии 142ЕН11 Uвых рассчитывается по формуле 3.6 []. 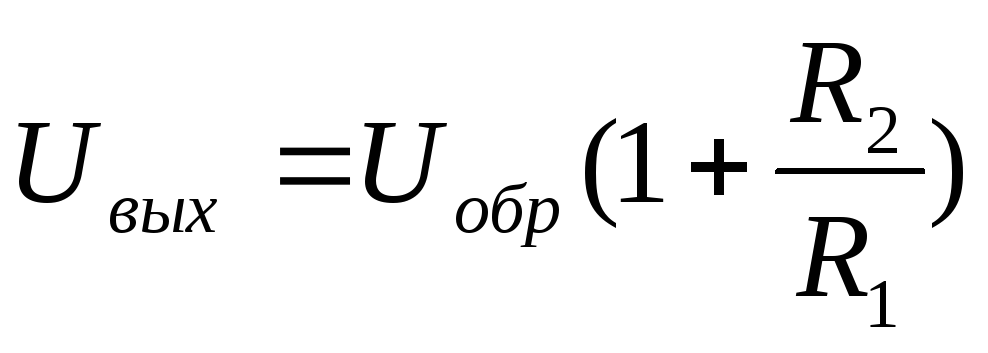 (6)
(6)
Следовательно:
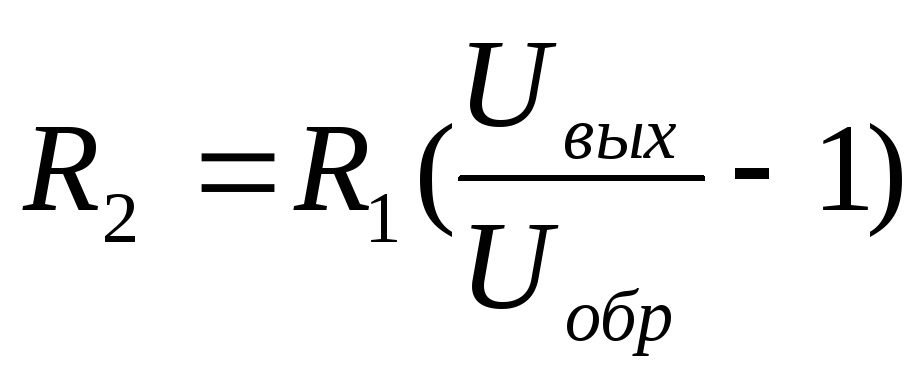 (7)
(7)
Uобр – образцовое напряжение, формируемое внутренним источником микросхемы, для данного стабилизатора Uобр = -1,25 В, а резистор R1 = 120 Ом []. Подставив значения получим, что при выходном напряжении минус 8.123 R2 = 659 Ом, а при минус 8.156 R2 = 663 Ом.
Для получения выходных напряжений 15,4 В и 4,5 В (второй и третий источник) используется схема, на основе стабилизаторов 142ЕН8А – во втором источнике и 142ЕН5А – в третьем источнике, изображенная на рисунке 7.
Рисунок 7 – Схема включения стабилизаторов 142ЕН8А и 142ЕН5А
Требуемый уровень выходного напряжения, указанного в задании, устанавливается резисторами R1 и R2 []. При данном включении таких стабилизаторов, сопротивление резистора R2 вычисляется по формуле 8 [].
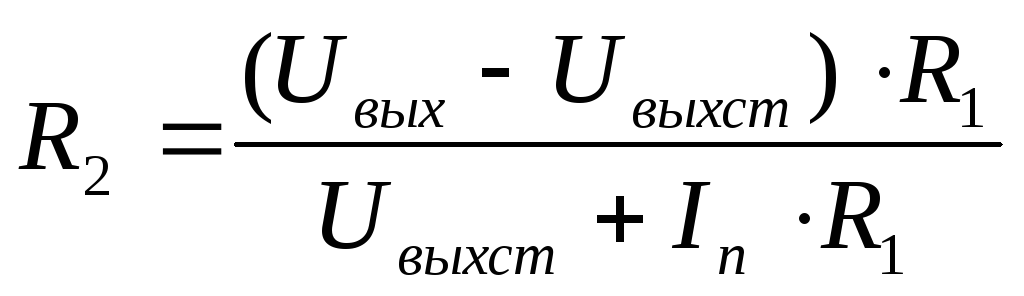 (8)
(8)
Uвых – выходное напряжение источника;
Uвыхст – выходное напряжение стабилизатора, для стабилизатора 142ЕН8А оно равно 9 В, а для 142ЕН5А равняется 5В;
Iп – ток потерь микросхемы, для обоих стабилизаторов он равен 10 мА;
R1 = 300 Ом [].
Подставив в формулу 8 численные значения, получим, что в третьем источнике опорного напряжения при выходном напряжении 15,37 В сопротивление резистора R2= 210 Ом, при выходном напряжении 15,43 В сопротивление резистора R2 = 212 Ом; в четвертом источнике опорного напряжения при выходном напряжении 4,49 В сопротивление резистора R2 = 22,5 Ом, при выходном напряжении 4,51 В сопротивление резистора R2 = 45 Ом.
Так же в четвертом источнике опорного напряжения, так стабилизатор выдавал напряжение выше указанного в задании, я его понизил его двумя диодами по 0,7 В.
Во всех источниках регулировка выходного напряжения осуществлялась за счет регулируемого резистора R2 соответственно.
Нестабильность напряжения источников, рассчитывается по формуле 9
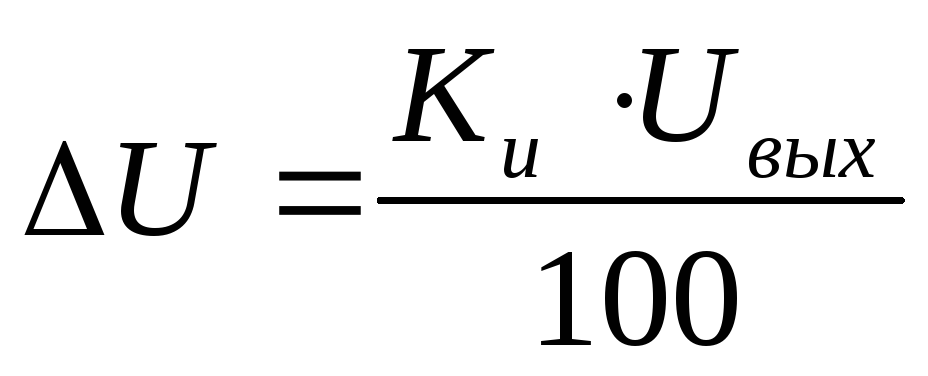 (9)
(9)
Кu – коэффициент нестабильности по напряжению стабилизатора;
У стабилизатора 142ЕН11 Кu = 0,02 , у стабилизаторов 142ЕН8А и 142ЕН5А Кu = 0,05. Подставив значения выходных напряжений, указанных в задании и коэффициенты соответствующих стабилизаторов, получим значения нестабильности, указанные в таблице 2.
Выходное сопротивление источников рассчитывалось по формуле (3.10)
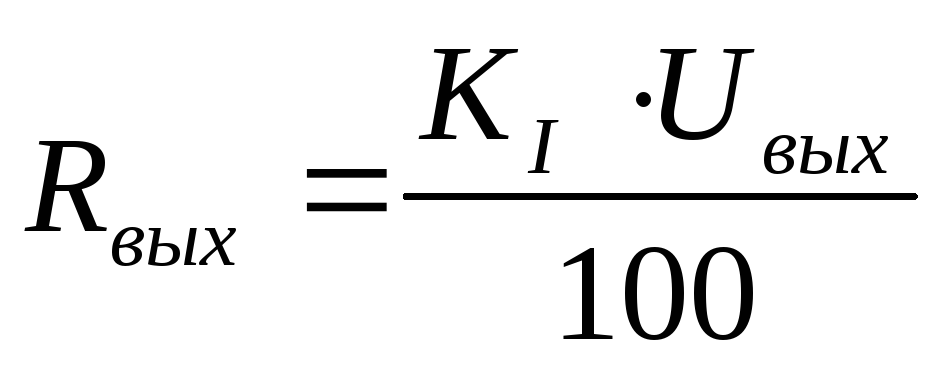 (10)
(10)
КI – коэффициент нестабильности по току стабилизатора
Таблица 1 –
142ЕН11 | 142ЕН8А | 142ЕН5А | |
Uвх, В | 5…45 | 11,5…35 | 7,5…15 |
Uвых, В | 1,2…37 | 8,73…9,27 | 4,9…5,1 |
2


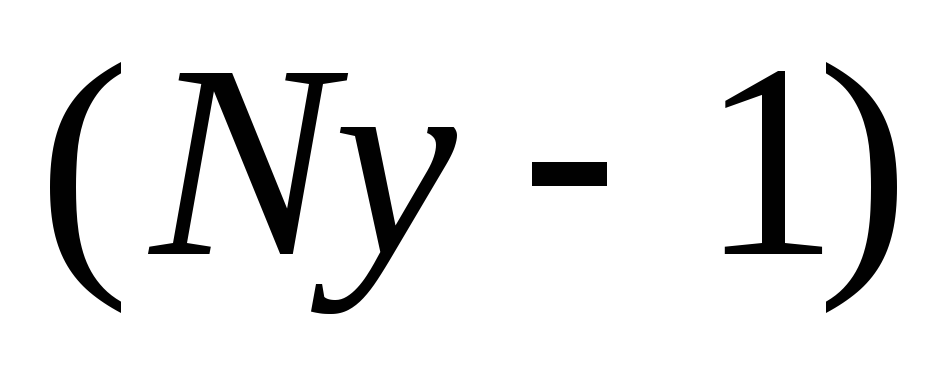 узлов
поIзакону Кирхгофа и
для
узлов
поIзакону Кирхгофа и
для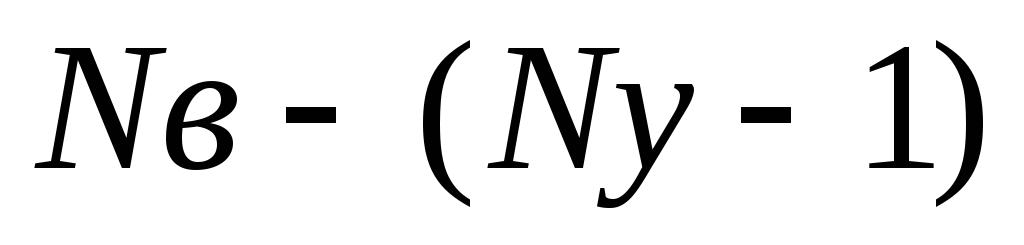 независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.