правила расчета для определения силы тока
Содержание
- 1 Пути вычисления электрических схем
- 2 Метод расчета по законам Ома и Кирхгофа
- 2.1 Закон Ома для участка цепи
- 2.2 Закон Ома для полной цепи
- 2.3 Первый закон Кирхгофа
- 2.4 Второй закон Кирхгофа
- 3 Метод преобразования электрической цепи
- 4 Дополнительные методы расчета цепей
- 5 Видео
На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.
Пример сложных электрических цепей
Пути вычисления электрических схем
Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.
Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.
Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.
Все элементы и устройства подразделяются на три категории:
- Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
- Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
- Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.

Также к основным понятиям электрической схемы относятся:
- Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
- Узел электрической схемы – точка соединения трех и более ветвей схемы;
- Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.
Обозначение ветвей, узлов и контуров на схеме
Метод расчета по законам Ома и Кирхгофа
Расчет емкости конденсатора
Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.
Закон Ома для участка цепи
По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:
UR=RI.
Исходя из этой формулы, найти силу тока можно по выражению:
I=UR/R, где:
- UR – напряжение или падение напряжения на резисторе;
- I – ток в резисторе.

Закон Ома для полной цепи
В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:
I=E/Rэ = E/r0+R, где:
- E – ЭДС источника питания;
- rо – внутреннее сопротивление источника питания.
Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.
Первый закон Кирхгофа
Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:
∑mIk=0, где m – число ветвей, подведенных к узлу.
Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».
Второй закон Кирхгофа
Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:
∑nEk=∑mRkIk=∑mUk, где:
- n – число источников ЭДС в контуре;
- m – число элементов с сопротивлением Rk в контуре;
- Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.

Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:
- Указать относительно положительные направления ЭДС, токов и напряжений;
- Указать направление обхода контура, описываемого уравнением;
- Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.
Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:
∑EI=∑RI2.
Метод преобразования электрической цепи
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.
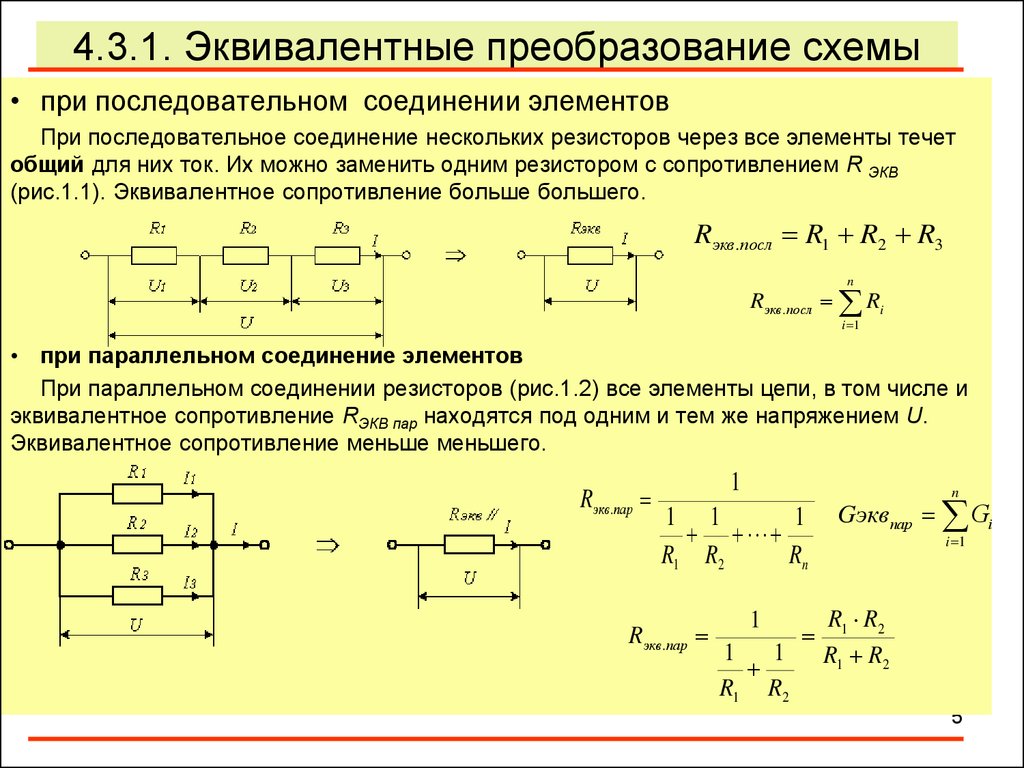
Последовательное и параллельное соединение элементов
Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:
- R1=R12R31/R12+R31+R23,
- R2=R12R23/R12+R31+R23,
- R3=R31R23/R12+R31+R23.
Треугольник и звезда соединений
Дополнительные методы расчета цепей
Закон Кирхгофа
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях.
 Метод базируется на первом законе Кирхгофа;
Метод базируется на первом законе Кирхгофа; - Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Видео
Расчет падения напряжения в кабеле
Оцените статью:
Расчет электрических цепей | Физика
1.
 Смешанное соединение проводников
Смешанное соединение проводниковРассмотрим электрическую схему на рисунке 61.1. Некоторые проводники в ней соединены последовательно друг с другом, а некоторые – параллельно.
? 1. Какие проводники в этой схеме соединены последовательно друг с другом? Какие – параллельно?
Соединение проводников, при котором часть проводников соединена последовательно друг с другом, а часть – параллельно, называют смешанным.
При расчете сопротивления смешанного соединения проводников часто используют метод эквивалентного преобразования схем. При этом данную схему последовательно преобразуют в более простую, но имеющую такое же сопротивление.
Например, схему, изображенную на рисунке 61.1, можно преобразовать по следующему плану:
1. Заменить участок цепи с резисторами 1 и 2 одним резистором с сопротивлением, которое мы обозначим R12.
2. Заменить участок цепи, содержащий резисторы с сопротивлениями R12 и R3, одним резистором с сопротивлением, которое мы обозначим R123.
3. Заменить участок цепи с резисторами 4 и 5 одним резистором с сопротивлением, которое мы обозначим R45.
4. Заменить участок цепи с резисторами сопротивлением R123 и R45 одним резистором. Его сопротивление и будет равно сопротивлению всего участка цепи.
? 2. В цепи, схема которой изображена на рисунке 61.1, сопротивление каждого резистора, выраженное в омах, примите равным номеру этого резистора. Начертите схемы, соответствующие каждому пункту намеченного выше плана; найдите R12, R123, R45 и сопротивление всего участка.
Не всегда с первого взгляда на электрическую схему можно распознать вид соединения проводников.
В таком случае полезно найти точки с одинаковым потенциалом (например, соединенные проводами, сопротивление которых в таких задачах считают обычно пренебрежимо малым). Затем надо перечертить схему, объединив точки с одинаковым потенциалом.
Рассмотрим, например, схему участка цепи, изображенную на рисунке 61. 2.
2.
Точки А и С соединены проводом с пренебрежимо малым сопротивлением, поэтому потенциалы этих точек равны. То же можно сказать и о точках В и D.
Следовательно, схему можно перечертить, объединив точки А и С в одну точку (обозначим ее АС), а точки В и D объединив в точку ВD. При этом, согласно исходной схеме, один конец каждого из трех резистов соединен с точкой АС, а другой – с точкой BD (рис. 61.3).
Теперь мы видим, что резисторы соединены параллельно.
? 3. Перенесите в тетрадь рисунок 61.2 и отметьте на нем направление тока в каждом резисторе, считая, что потенциал точки А выше потенциала точки D.
? 4. На рисунке 61.4 изображена схема участка электрической цепи. Сопротивление каждого резистора, выраженное в омах, равно номеру резистора. Обратите внимание: потенциалы точек А и С различны.
а) Перечертите схему, изображенную на рисунке 61.4, так, чтобы легко было распознать вид соединения резисторов.
б) Найдите сопротивление всего участка цепи.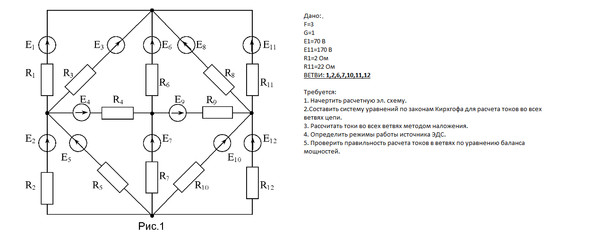
К сожалению, не всякую электрическую схему можно поэтапно упрощать, используя только формулы для последовательного и параллельного соединений. На рисунке 61.5 приведен пример схемы участка цепи, которую нельзя упростить таим образом.
Но для некоторых частных случав можно найти сопротивление и такого участка цепи уже известными нам способами. Чтобы догадаться, каковы эти случаи, заменим резистор 5 идеальным вольтметром (рис. 61.6). (Напомним, что идеальным считают вольтметр, сопротивление которого можно принять бесконечно большим.)
? 5. Разность потенциалов между точками А и В равна 21 В. Сопротивления резисторов, выраженные в омах, равны их номерам.
а) Чему равна разность потенциалов между точками А и С?
б) Чему равна разность потенциалов между точками А и D?
в) Каковы показания вольтметра?
г) Резистором с каким сопротивлением надо заменить резистор 4, чтобы показания вольтметра были равны нулю?
? 6. Объясните, почему показания вольтметра будут равны нулю независимо от напряжения между точками А и В, если сопротивления резисторов на схеме, изображенной на рисунке 61.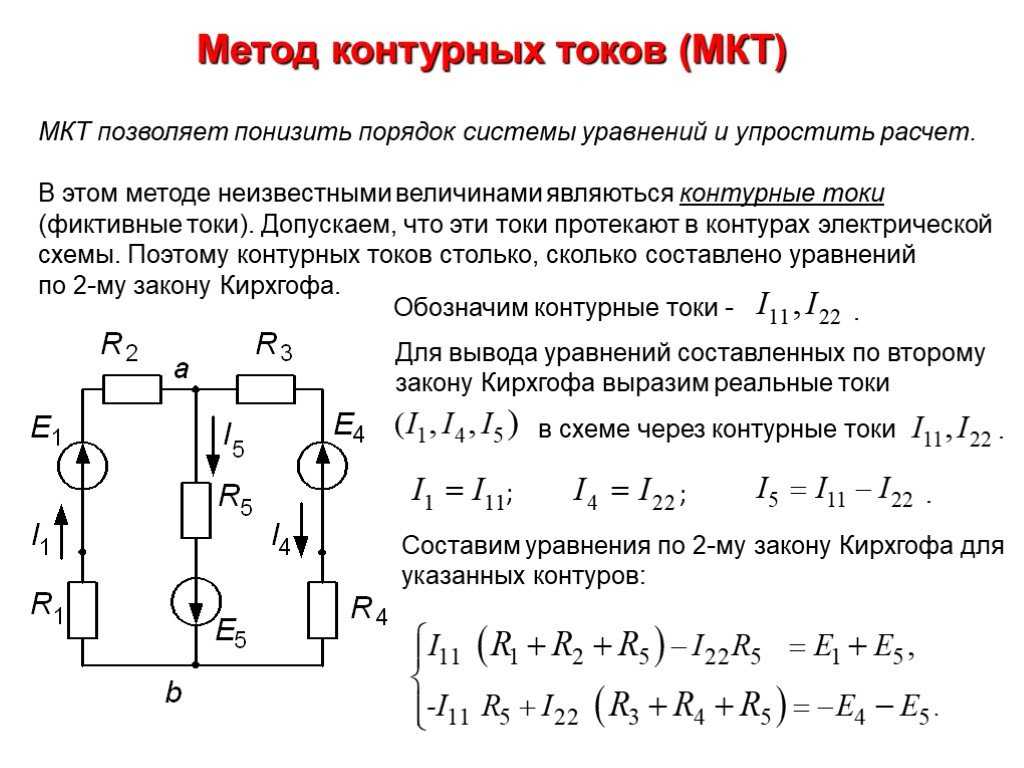 6, удовлетворяют соотношению
6, удовлетворяют соотношению
R1/R2 = R3/R4. (1)
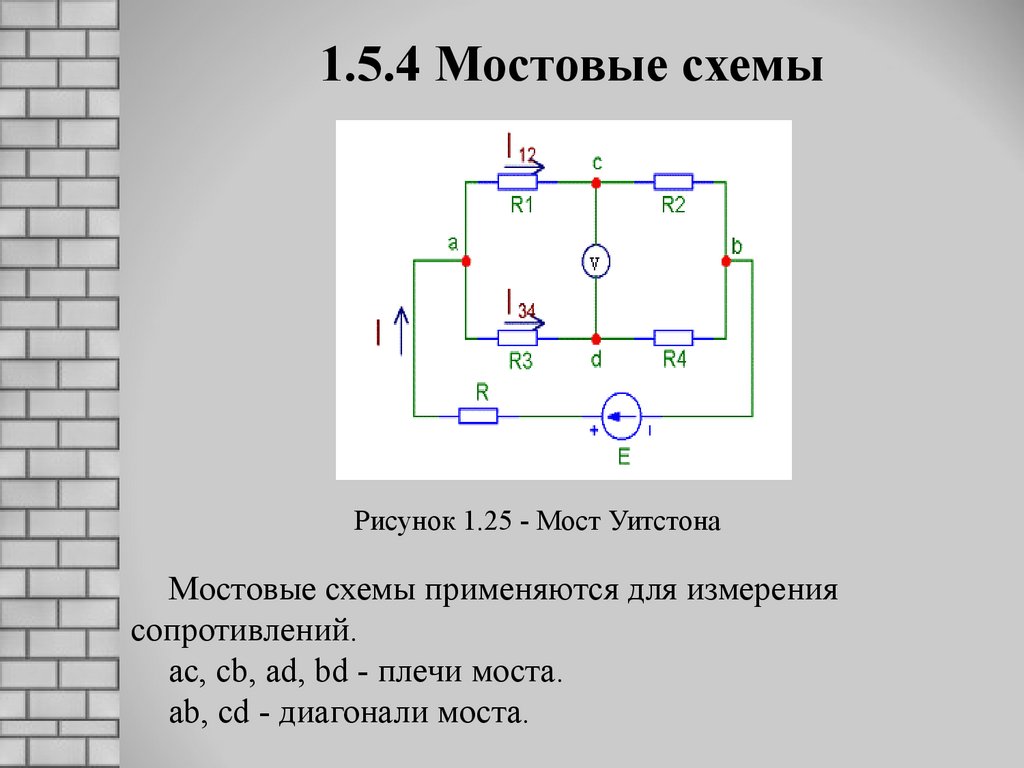
Схему, изображенную на рисунке 61.6, называют мостиком Уитстона. С ее помощью можно измерить сопротивление одного из четырех резисторов, подбирая сопротивления остальных трех так, чтобы выполнялось соотношение (1).
? 7. Для сопротивлений резисторов 1 – 4 в цепи, изображенной на рисунке 61.5, выполняется соотношение (1).
а) Объясните, почему сопротивление данного участка цепи не зависит от сопротивления резистора 5.
б) Сопротивления резисторов 1 и 3 равны соответственно 10 Ом и 15 Ом. Подберите такие значения сопротивлений резисторов 2 и 4, чтобы сопротивление всего участка было равно 24 Ом независимо от сопротивления резистора 5.
2. Максимальная мощность во внешней цепи
? 8. К источнику с ЭДС ξ и внутренним сопротивлением r подключено внешнее сопротивление R (рис. 61.7).
а) Выразите мощность тока во внешней цепи через ξ, r и R.
б) Используя производную, найдите, при каком R мощность тока во внешней цепи будет максимальной.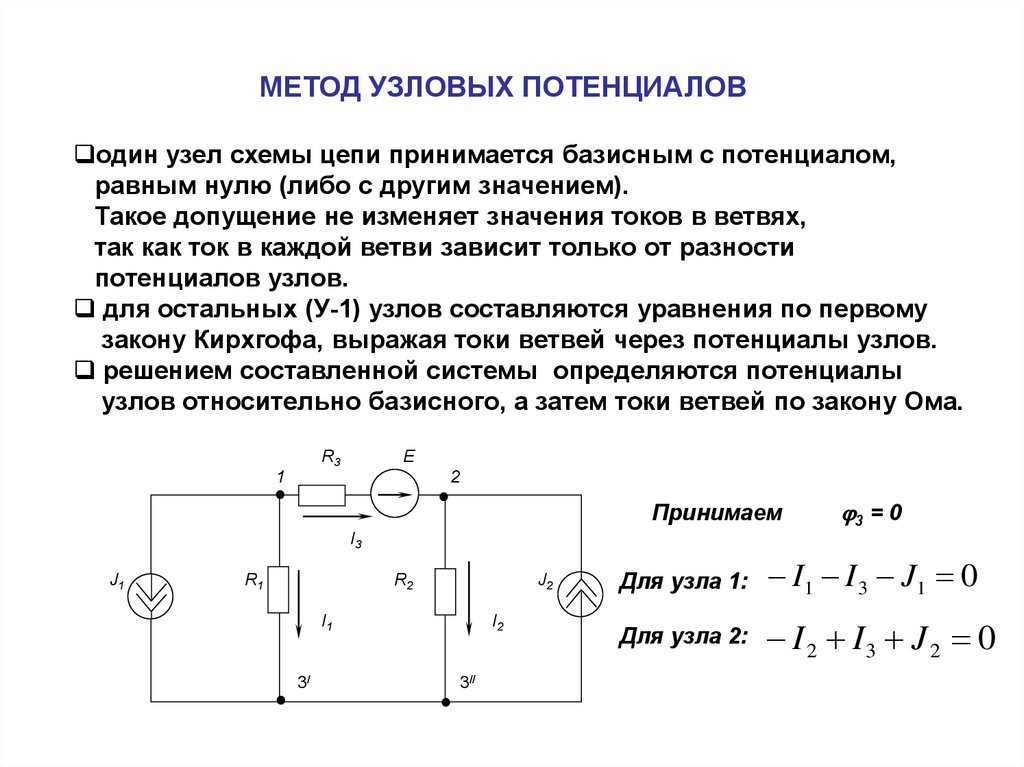
Эту задачу можно решить и без помощи производной. Для этого надо воспользоваться формулой для мощности тока во внешней цепи
P = UI,
где U – напряжение на внешнем сопротивлении (напомним, что оно равно напряжению на полюсах источника тока), I – сила тока в цепи.
? 9. Объясните, почему мощность тока во внешней цепи выражается формулой
P = (ξ – Ir)I. (2)
Подсказка. Выразите напряжение на полюсах источника через ξ, I, r, используя закон Ома для всей цепи.
Правая часть равенства (2) представляет собой квадратичную функцию от силы тока I. Графиком ее является парабола.
? 10. Начертите график зависимости P(I) при изменении силы тока I от нуля до максимального значения (равного силе тока при коротком замыкании).
а) При каком значении I достигается максимум функции P(I)?
б) Какому сопротивлению внешней цепи соответствует это значение I?
Подсказка. Воспользуйтесь законом Ома для всей цепи.
Итак, максимальная мощность тока во внешней цепи достигается, когда сопротивление внешней цепи равно внутреннему сопротивлению источника тока.
? 11. Чему при этом равен КПД источника тока?
3. Конденсаторы в цепи постоянного тока
Постоянный ток не может идти через конденсатор, потому что между его обкладками находится диэлектрик. Однако между обкладками конденсатора, включенного в цепь постоянного тока, может существовать разность потенциалов, и тога конденсатор будет заряженным. Начнем с самых простых случаев, когда в цепи, помимо конденсатора, есть только один резистор.
? 12. На рисунке 61.8 изображена схема электрической цепи. ЭДС источника тока ξ = 12 В, его внутреннее сопротивление r = 2 Ом, сопротивление резистора R = 10 Ом, электроемкость конденсатора С = 2 мкФ.
61.8
а) Чему равна разность потенциалов между точками А и В?
б) Чему равна разность потенциалов между точками А и D?
в) Чему равен заряд конденсатора?
г) Каков знак заряда обкладки конденсатора, соединенной с резистором?
? 13. На рисунке 61.9 изображена схема электрической цепи. ЭДС источника тока ξ, его внутреннее сопротивление r, сопротивление резистора R, электроемкость конденсатора C.
а) Чему равна разность потенциалов между точками А и В?
б) Чему равен заряд конденсатора?
Рассмотрим теперь более сложный случай, когда в цепи есть несколько резисторов, причем они по-разному подключены к конденсатору.
? 14. В цепи (рис. 61.10) ЭДС источника ξ = 6 В, его внутреннее сопротивление r = 1 Ом, сопротивления резисторов R1 = 3 Ом, R2 = 5 Ом, R3 = 12 Ом, электроемкость конденсатора C = 8 мкФ.
а) Перенесите схему в тетрадь и обозначьте, через какие элементы цепи идет ток.
б) Какова сила тока в резисторе 3?
в) Чему равна разность потенциалов между точками А и D?
г) Чему равна разность потенциалов между точками А и В?
д) Чему равно напряжение на конденсаторе?
е) Чему равен заряд конденсатора?
ж) Каков знак заряда обкладки конденсатора, соединенной с резистором 2?
Дополнительные вопросы и задания
15. На рисунке 61.11 изображена схема участка электрической цепи. Сопротивление каждого резистора 1 Ом. Используя метод эквивалентного преобразования схем:
Используя метод эквивалентного преобразования схем:
а) начертите схемы последовательного упрощения данной схемы, содержащие меньше резисторов;
б) для каждой схемы рассчитайте ее сопротивление и найдите общее сопротивление всего участка.
16. На схеме участка цепи, изображенной на рисунке 61.5, сопротивления резисторов R1 = 20 Ом, R2 = 100 Ом, R3 = 10 Ом, R4 = 50 Ом, R5 = 80 Ом. Каково общее сопротивление участка цепи?
17. Сопротивление внешней цепи в 4 раза больше того значения, при котором мощность тока во внешней цепи максимальна.
а) Чему равен КПД источника тока?
б) Во сколько раз при этом мощность тока во внешней цепи меньше максимально возможной?
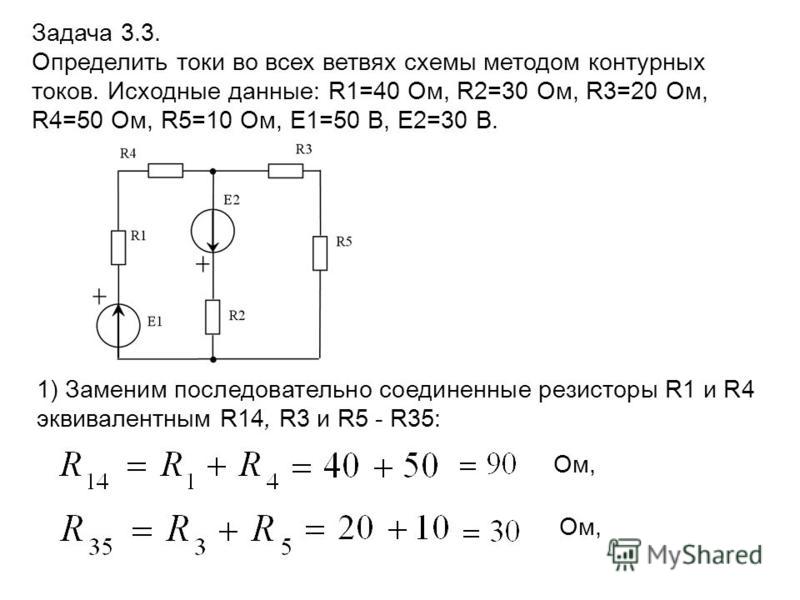
1.2. Методы расчета электрических схем
20
Федеральное агентство по образованию
Рыбинская государственная авиационная технологическая академия им. П. А. Соловьева
Кафедра «Вычислительные системы»
В. М. Комаров
М. Комаров
Расчет линейных электрических цепей
постоянного тока
Лабораторная работа по дисциплине
«Основы электротехники и электроники»
Рыбинск 2008
Введение
Линейные электрические цепи постоянного тока составляют значительную часть многих электротехнических и радиоэлектронных устройств, проектирование которых тесно связано с анализом этих цепей, опирающимся на их свойства и различные методы расчета.
Цель работы
Целью настоящей работы является изучение свойств и основных методов расчета электрических цепей постоянного тока:
– метода расчета на основании законов Кирхгофа;
– метода узловых потенциалов;
– метода контурных токов;
– линейных соотношений в электрических цепях.
1. Краткие теоретические сведения
1.1. Электрическая цепь, ее схема и граф
Электрическая цепь характеризуется
совокупностью элементов, которые она
содержит, и способом их соединения.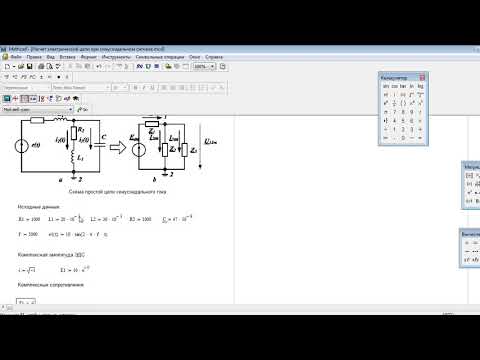 Линейная электрическая цепь состоит
из линейных элементов, свойства которых
не зависят от величины и направления
воздействующих на них токов и напряжений,
температуры и т. п. Напряжение и ток в
любом линейном элементе связаны линейным
алгебраическим или дифференциальным
уравнением первого порядка. Основными
линейными элементами электрических
цепей являются источник э.д.с., источник
тока, сопротивление, индуктивность и
емкость.
Линейная электрическая цепь состоит
из линейных элементов, свойства которых
не зависят от величины и направления
воздействующих на них токов и напряжений,
температуры и т. п. Напряжение и ток в
любом линейном элементе связаны линейным
алгебраическим или дифференциальным
уравнением первого порядка. Основными
линейными элементами электрических
цепей являются источник э.д.с., источник
тока, сопротивление, индуктивность и
емкость.
Для упрощения расчетов реальные элементы электрических цепей заменяются их идеализированными моделями, которым приписываются свойства, позволяющие с достаточной степенью точности представлять процесс, происходящий в реальном элементе. Каждому идеализированному элементу электрической цепи соответствует условное графическое обозначение (рис. 1).
Графическое изображение электрической
цепи с помощью условных графических
обозначений ее элементов называется
электрической схемой этой цепи.
Электрические цепи постоянного тока,
как правило, состоят из идеальных
источников э.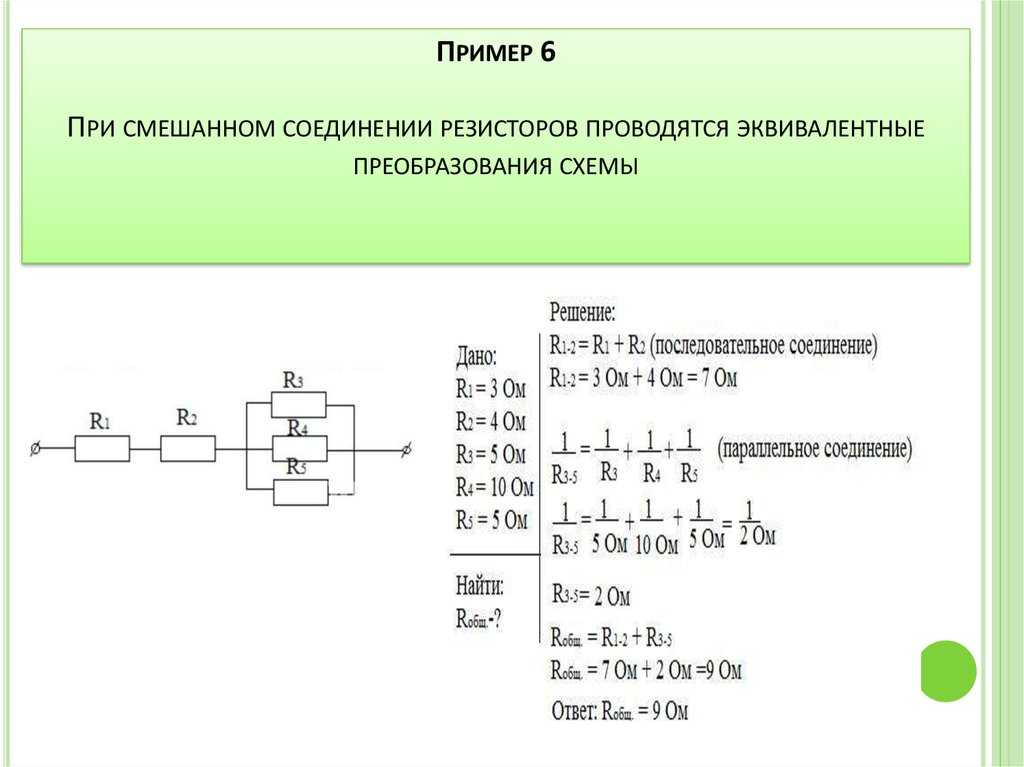
а) б) в) г) д)
Р ис. 1. Основные элементы линейных электрических цепей а) идеальный источник э.д.с.; б) идеальный источник тока; в) сопротивление; г) индуктивность; д) емкость
Рис. 2. Электрические схемы цепей постоянного тока
Участок схемы, характеризующийся одним и тем же током в его начале и конце в любой момент времени, называется ветвью электрической схемы. Следовательно, любая ветвь содержит только последовательное соединение элементов. Например, ветвями являются участки цепей, состоящие из элементов
Место соединения трех или большего числа ветвей называется узлом. На электрических схемах, приведенных на рис. 2, узлы обозначены цифрами 1, 2, 3, 4.
Любой замкнутый путь, проходящий по нескольким ветвям электрической схемы, называется контуром. При расчете схемы необходимо выбирать независимые контура. Независимые контура удобно выбирать, используя понятия графа электрической схемы и его дерева.
Графом электрической схемы называется ее условное изображение, в котором каждая ветвь заменяется отрезком линии, называемой ветвью графа. На рис. 3 приведены графы вышерассмотренных электрических схем.
Совокупность ветвей графа, соединяющая все узлы, но не образующая ни одного контура, называется деревом графа. Каждый граф может иметь несколько деревьев. На рис. 4 в каждом из вышерассмотренных графов толстыми линиями выделено по одному (из нескольких возможных) дереву. Если граф содержит

Рис. 3. Графы электрических схем
Рис. 4. Дерево, ветви, связи и главные контура графов
Ветви графа, дополняющие его дерево до полного графа, называются ветвями связи. На рис. 4 ветви связи изображены тонкими линиями. Если граф схемы содержит
В качестве независимых контуров при расчете электрической схемы выбираются ее главные контура, состоящие из ветвей дерева и только одной ветви связи. Следовательно, число главных контуров равно числу ветвей связи. На рис. 4 главные контура выделены цифрами I, II, III, IV.
Суть расчета электрической схемы сводится к определению токов во всех ее ветвях. Все методы расчета рассмотрим на примере схемы, приведенной на рис. 5,а. Эта схема имеет 3 узла и 5 ветвей.
e3
а) б)
в) г)
Рис. 5. Расчет
электрических схем
а) на основании
законов Кирхгофа; б) выбор независимых
контуров;
в) метод узловых потенциалов;
г) метод контурных токов
5. Расчет
электрических схем
а) на основании
законов Кирхгофа; б) выбор независимых
контуров;
в) метод узловых потенциалов;
г) метод контурных токов
1.2.1. Расчет схемы на основании законов Кирхгофа
Законы Кирхгофа устанавливают соотношение между токами и напряжениями в электрической цепи.
Первый закон Кирхгофа:
Алгебраическая сумма токов в любом узле равна нулю
где m – общее количество ветвей, подключенных к данному узлу.
Общее количество уравнений, которое может быть составлено по первому закону Кирхгофа, равно числу узлов
Для составления этих уравнений необходимо
произвольным образом выбрать положительные
направления токов в ветвях и обозначить
их на чертеже. При этом токи, направленные
к рассматриваемому узлу считаются
положительными, а от узла – отрицательными.
При этом токи, направленные
к рассматриваемому узлу считаются
положительными, а от узла – отрицательными.
Отсюда, для рассматриваемой схемы (см. рис. 5,а) количество уравнений, составляемое по первому закону Кирхгофа, равно N1 = 3 – 1 = 2 и они имеют вид:
(узел 1)
(узел 2)
Этих уравнений недостаточно для расчета схемы. Недостающие уравнения составляются на основании второго закона Кирхгофа.
Второй закон Кирхгофа:
Алгебраическая сумма э.д.с. в любом контуре электрической цепи равна алгебраической сумме падений напряжений на элементах этого контура
где l – общее количество источников э.д.с. в контуре;
t – общее количество сопротивлений в контуре.
Для составления уравнений по второму
закону Кирхгофа необходимо с помощью
дерева графа схемы выбрать главные
контура и направление их обхода (рис.
5,б). При этом соблюдается следующее
правило знаков для э.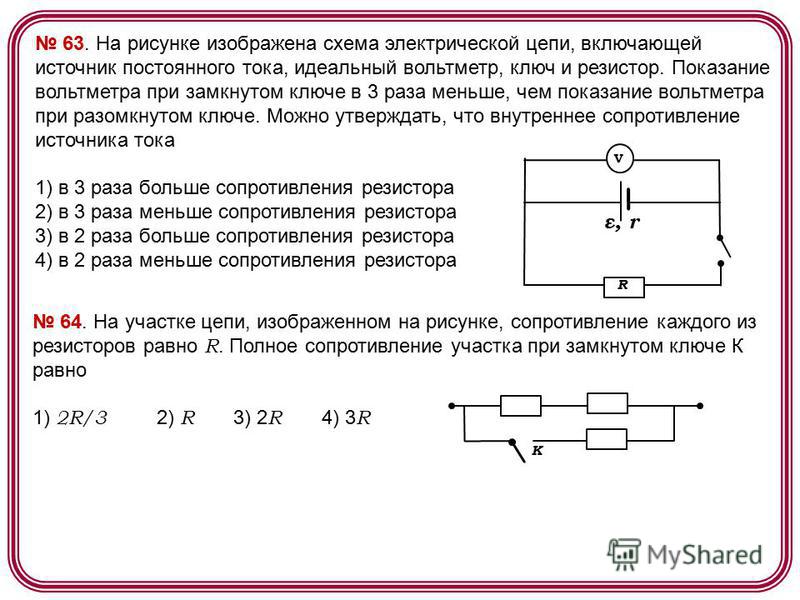 д.с. и падений
напряжений, входящих в ( ): э.д.с. и падения
напряжения, совпадающие по направлению
с направлением обхода, считаются
положительными, а противоположно
направленные – отрицательными. Общее
количество независимых уравнений,
записываемое по второму закону Кирхгофа,
равно количеству главных контуров и
составляет N2 = Nв – (Ny – 1).
д.с. и падений
напряжений, входящих в ( ): э.д.с. и падения
напряжения, совпадающие по направлению
с направлением обхода, считаются
положительными, а противоположно
направленные – отрицательными. Общее
количество независимых уравнений,
записываемое по второму закону Кирхгофа,
равно количеству главных контуров и
составляет N2 = Nв – (Ny – 1).
Отсюда, для рассматриваемой схемы (см. рис. 5,а,б) количество уравнений, составляемое по второму закону Кирхгофа, равно
(контур I)
(контур II)
(контур III).
Таким образом, по законам Кирхгофа
составлены пять уравнений, полностью
описывающих состояние электрической
цепи. После этого расчет схемы сводится
к решению системы этих уравнений и
нахождению искомых токов.
Решение системы линейных уравнений можно искать методом Крамера. В этом случае
где Δ – общий определитель системы, составленной из коэффициентов при неизвестных;
Δk – частный определитель системы, полученный из общего определителя Δ путем замены столбца, содержащего коэффициенты при ik, свободными членами.
Для рассматриваемой системы уравнений
Для определенности положим R1 = 100 Ом, R2 = 500 Ом, R3 = 1 К, R4 = 50 ОМ, R5 = 300 Ом, e1 = 2 В, e2 =10 В, e3 = 20 В и, пользуясь свойствами определителей, найдем, в качестве примера, значение Δ
Аналогичным образом можно найти значения
остальных определителей Δ1 =
–2,05·106, Δ2 = –6,1·106, Δ3 = –5,2·106, Δ4 = 0,9·106, Δ5 = 1,15·106.
Таким образом, искомые токи имеют следующие значения
Положительные значения токов i1, i2, i3, полученные при расчете, означают, что их фактическое направление совпадает с направлением этих токов, принятом и расчете; отрицательные значения токов i4 и i5 означают, что их фактическое направление противоположно принятому при расчете направлению этих токов.
После определения токов в ветвях расчет электрической схемы можно считать практически законченным, т.к. определение потенциалов узлов, падений напряжений на сопротивлениях и рассеиваемой в них мощности в этом случае не составляет труда. Узловые потенциалы и падения напряжений на сопротивлениях могут быть определены в соответствии с законом Ома, а мощность, рассеиваемая в сопротивлениях, – по формуле .
Недостатком метода расчета электрических
схем на основании законов Кирхгофа
является необходимость совместного
решения большого количества уравнений,
т.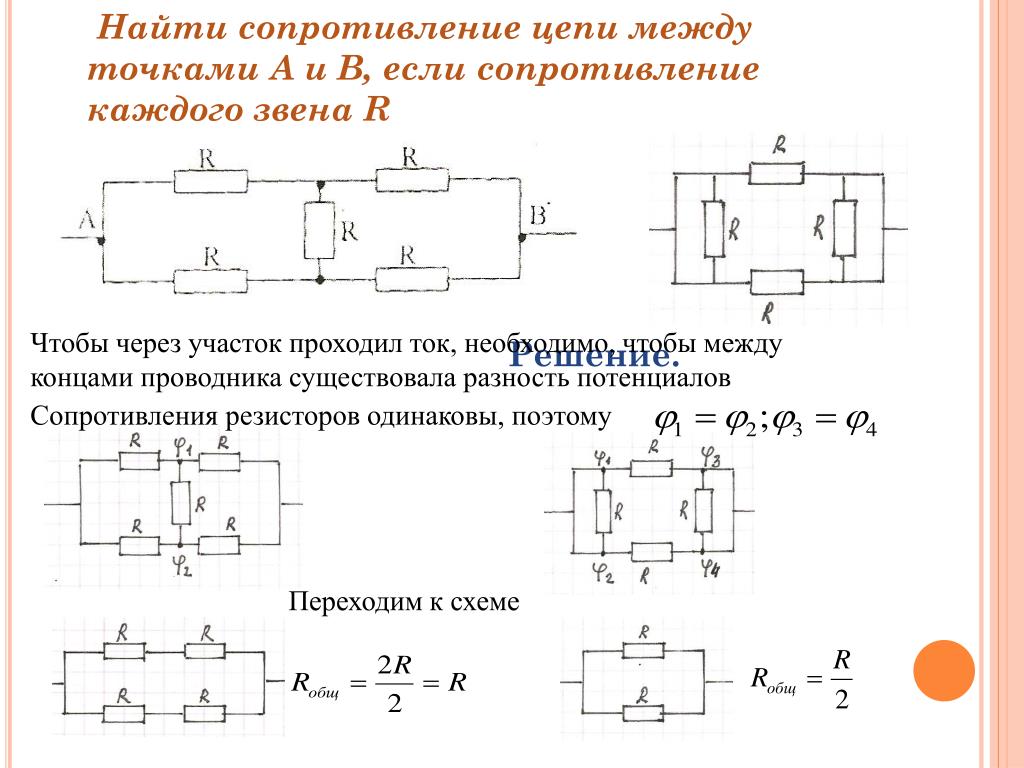 е. громоздкость математических
расчетов.
е. громоздкость математических
расчетов.
Расчёт электрических цепей методом структурных чисел для детей и взрослых / Хабр
В нулевые годы, когда, скорее в качестве отдушины, я подрабатывал в Альма-матер, ведя лабораторные работы по радиотехнике, мне попалась на глаза эта книжечка:
С.Беллерт, Г. Возняцки
«Анализ и синтез электрических цепей методом структурных чисел».
Перевод с польского
Под редакцией проф. П.А. Ионкина
ИЗДАТЕЛЬСТВО «МИР»
Москва 1972
После беглого просмотра я испытал странное ощущение, которое, наверное, правильно было бы назвать когнитивным диссонансом. В этой книге предлагался эффективный и очень простой в применении (но не с точки зрения теории) метод расчета электрических цепей, но при этом я никогда даже не слышал об этом подходе. Не могу назвать себя профессионалом, радиотехника была скорее хобби, но я неплохо знал всё, что преподавалось у нас в институте и всё же.
Чем больше я вникал в теорию, тем больше очаровывался.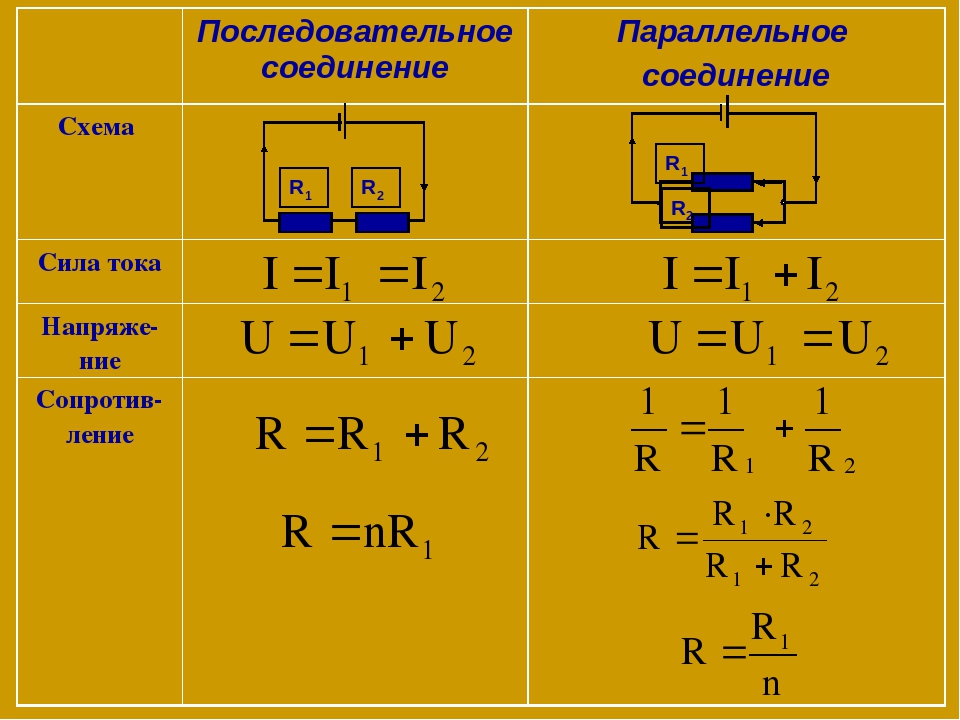 Получив эстетическое удовлетворение, я благополучно забыл об этом небольшом открытии, к тому же через некоторое время я переехал в Европу, и моя преподавательская деятельность, да и вообще любая деятельность, связанная с радиотехникой, закончилась.
Получив эстетическое удовлетворение, я благополучно забыл об этом небольшом открытии, к тому же через некоторое время я переехал в Европу, и моя преподавательская деятельность, да и вообще любая деятельность, связанная с радиотехникой, закончилась.
Но вот, недавно, приехав погостить в Россию, разбирая старые книжки, я опять наткнулся на этот забытый мною (и возможно миром) труд. Покопавшись в интернете, я обнаружил некоторые статьи на эту тему, но, по-прежнему, всё выглядит так, что этот метод мало кому знаком.
И я подумал, что может быть это будет интересно читателям Хабра.
О простоте
Кажется, что этому алгоритму можно научить даже ребенка, что я и попытался проверить.
Думаю, эксперимент удался. За 10 минут я сумел научить рассчитывать электрические цепи моего сына. На картинке вы видите его расчет передаточной функции по напряжению для двухкаскадного делителя. Поверьте моему опыту преподавателя радиотехники — не каждый студент с этим справится.
Ах, да. Сыну 7 лет!
Сыну 7 лет!
Черными чернилами я составил «карту», которая должна помочь сыну в расчетах.
Синие чернила — это его расчёт.
Внизу вы видите правильный ответ — коэффициент усиления по напряжению.
Умея получать правильный результат, он, конечно же, абсолютно ничего не понимает — для него это просто картинка. Но, если я нарисую ему другую схему того же уровня сложности, он найдет правильный ответ.
Пояснения к записям:
Я нарисовал граф, соответствующий данной цепи. Ребра графа пронумерованы так же, как и импедансы.
Далее, мне пришлось немного рассказать сыну о графах — я показал, что такое вершины и что такое ребра графа. Потом объяснил ему, что такое элементарные контуры (пустые «кружочки») и обратил внимание на грани, из которых они состоят.
Предварительная стадия на этом была закончена, и мы перешли к расчетам.
Комментарий Далее в статье мы будем называть это структурным числом графа, и это будет главным объектом, вокруг которого всё и крутится. Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
Но нет смысла пытаться объяснить это ребенку — для того, чтобы найти ответ, знание элементов теории структурных чисел не является обязательным.
В общем случае нужно удалять не только столбцы, в которых есть одинаковые элементы, но и попарно убирать столбцы с одинаковым набором элементов (порядок следование элементов в столбцах и порядок следования самих столбцов неважны).
Затем (это написано мною на листке) я попросил найти все столбцы с единичкой («входное» ребро) и удалить единичку из этих столбцов. Понятно, что столбцы с единичкой это
Отбросив единичку, получаем , что и написано в виде
То же самое нужно сделать для двойки («выходное» ребро):
В теории структурных чисел эта функция называется алгебраической производной по элементу.
КомментарийЭта функция от двух структурных чисел и называется конъюнкцией. Мы будем обозначать её как . В данном случае имеем
В принципе на этом все вычисления закончены.
 Осталось только написать ответ.
Осталось только написать ответ.Я провел черту (деление), и попросил сына над чертой написать (независимо от наших расчетов, выходное сопротивление присутствует всегда в формуле передаточной функции по напряжению) и с индексом, который он получил в предыдущем пункте (конъюнкция) — вы видите мою чёрную стрелочку на картинке, указывающую на этот индекс.
Под чертой интересней. Для каждого столбца структурного числа нужно взять числа в этом столбце и использовать их как индексы для в произведении и сложить все полученные таким образом «столбцевые» произведения. Это тот случай, когда легче показать, чем объяснить. Так, в нашем случае для столбцов, которые мы получили
это будет .
Это отношение и есть искомый коэффициент передачи.
Функция в знаменателе — это детерминант структурного числа по и записывается как . Точное определение будет дано ниже в статье.
Комментарий 2В общем виде для данного вида графов (входное и выходное ребра имеют общую вершину и сонаправлены) коэффициент передачи напряжения может быть выражен следующей формулой
Более общая формула, которая подходит для всех пассивных четырёхполюсников
Функция совпадения будет объяснена позже в этой статье
Теперь давайте по-взрослому.
Основные понятия теории структурных чисел
Мы ограничимся достаточно узкой прикладной областью данной математики — для нашей статьи нам будет интересен только расчет пассивных электрических цепей с одним источником (пассивный четырёхполюсник).
Нас будет интересовать лишь прикладной аспект. Мы не будем ничего доказывать. Также некоторые понятия будут представлены упрощенно, главная цель — научиться получать результат. Нас будет интересовать только вопрос «как», и мы даже не будем пытаться ответить на вопрос «почему». Тем, кому станет интересен математический аспект — обращайтесь к первоисточнику.
Структурное число
Структурное число это неупорядоченный набор столбцов элементов со следующими свойствами:
в общем случае, столбцы могут содержать разное количество элементов, но в рамках нашей задачи структурное число всегда будет иметь вид прямоугольной матрицы, то есть все столбцы в структурном числе будут иметь равную длину
каждый столбец представляет собой неупорядоченный (порядок не важен) набор натуральных чисел
в столбце нет повторяющихся элементов.
 Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.в структурном числе нет повторяющихся столбцов. Если в процессе алгебраических операций появляются такие столбцы, то они попарно удаляются. Это значит, что четное количество одинаковых столбцов аннигилируют, а при нечетном количестве один столбец остаётся.
Дополнительное структурное число
Найдем множество всех элементов в структурном числе. Возьмем произвольный столбец этого числа и составим столбец из элементов, которых не хватает в этом столбце до множества всех элементов. Структурное число, составленное из таких столбцов называется дополнительным.
ПримерРассмотрим структурное число
Множество всех элементов:
Тогда дополнительное число:
Сумма структурных чисел
Комментарий:
Мы нигде не будем использовать сумму структурных чисел в данной статье.
Суммой двух структурных чисел A и B называется структурное число, содержащее все столбцы чисел A и B, за исключением идентичных столбцов.
Произведение структурных чисел
Комментарий:
В данной статье мы будем иметь дело только с произведением структурных чисел состоящих из строк (все столбцы имеют лишь один элемент), например,
Произведением двух структурных чисел A и B называется структурное число, столбцы которого представляют собой суммы (согласно понятиям теории множеств) всех возможных комбинаций столбцов A и B, за исключением наибольшего четного числа идентичных столбцов и таких столбцов, в которых какой-либо элемент повторяется.
ПримерСтолбцы 2,3,4,6,7,9 удаляются потому что содержат повторяющиеся элементы.
Столбцы 1 и 5 удаляются в паре потому, что содержат идентичный набор элементов (важно помнить, что если бы одинаковых столбцов было бы нечетное количество, то один столбец остался бы).
Поэтому остается только столбец 8.
Алгебраическая производная
Алгебраическая производная структурного числа по элементу называется структурное число , состоящее только из столбцов , содержащих элементы с исключением этих элементов.
Возьмём структурное число
Алгебраическая обратная производная
Обратная производная структурного числа по элементу называется структурное число состоящее только из столбцов , не содержащих элементы .
ПримерКонъюнкция
Конъюнкцией двух структурных чисел и называется структурное число , состоящее из совпадающих столбцов и . Мы будет обозначать ее как .
ПримерДетерминантная фунция
Давайте возьмем -й столбец структурного числа . Возьмем все индексы в этом столбце и найдем произведение импедансов с этими индексами. Далее, если сложить такие произведения для всех столбцов, то это и будет детерминант. Детерминант от пустого (нет столбцов) структурного числа равен 1.
ПримерСтруктурные числа и электрические схемы
Мы подбираемся к сути, которая заключается в том, что каждому пассивному четырёхполюснику может быть поставлено в соответствие структурное число, и с помощью нововведенной алгебры может быть произведен ее расчет.
Сначала построим граф, соответствующий электрической цепи.
Построение графа
Проще всего это понять на примерах. Начнем с элементарных схем.
Схемы делителя:
Первая схема — элементарный делитель. При этом мы считаем источник напряжения идеальным (сопротивление = 0), и вольтметр (или следующий каскад) имеет входное сопротивление равное бесконечности.
Вторая схема относится к случаю, когда вы подаете напряжение E, на сопротивление , но источник напряжения не идеальный (сопротивление Z1), и вольтметр (или следующий каскад) имеет входное сопротивление Z2.
Третья схема — уже знакомая нам схема двухкаскадного делителя.
То есть, чтобы получить граф, мы просто перерисовываем схему с импедансами со следующими изменениями:
мы «опускаем» идеальный источник напряжения, что выглядит разумно, т.к. его выходное сопротивления равно 0 (его сопротивление мы вынесли в )
мы заменяем импедансы на их индексы
у нас только 2 направленных ребра: входное (мы всегда будем обозначать его индексом 1) и выходное (индекс 2).
 Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное)
Попробуем применить этот подход для более сложного случая.
Мост Уитстона:
Нахождение структурного числа графа
Теперь давайте построим структурные числа для каждого случая.
Есть два подхода: через произведение структурных чисел, соответствующих вершинам графа, и через произведение структурных чисел, соответствующих элементарным контурам.
Рассмотрим первый метод — через произведение «вершинных» структурных чисел
Метод перемножения «вершинных» структурных чисел
Предположим, что в нашем графе вершин. «Отбрасываем» любую вершину и берем оставшиеся вершины.
Для каждой вершины найдем «вершинное» структурное число. Для этого выписываем все ребра графа, опирающиеся на эту вершину. Предположим, что для i-ой вершины мы имеем ребер. Тогда такое «вершинное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра.
 То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).Перемножаем эти вершинных структурных числа. Получаем некое структурное число .
Находим дополнительное к структурное число . Это и будет наше искомое структурное число.
Для первой схемы (простой делитель) получим:
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .
У нас всего одно число, поэтому произведением является то же самое число.
У нас всего два элемента: , поэтому дополнительным элементом опять-таки является тоже самое число.
Итак, для первой схемы нашим структурным числом будет .
В графе две вершины, значит, для нашего расчета мы будем использовать одну.
«Вершинное» структурное число (для любой из двух вершин): .

У нас всего одно число, поэтому произведением является то же самое число.
У нас есть три элемента: , поэтому дополнительным структурным числом будет
В графе три вершины, значит, для нашего расчета мы будем использовать две.
Возьмем верхнюю и нижнюю вершины. Структурные числа для них: и .
Произведение этих двух структурных чисел даёт:
У нас есть 4 элемента: , поэтому дополнительным структурным числом будет
Это совпадает с результатом, который получил мой сын. Там мы использовали метод перемножения «контурных» структурных чисел, который рассматривается ниже.
Пример 4. Мост УитстонаМы видим 4 вершины. Отбросим нижнюю вершину.
Тогда для оставшихся трех вершин мы получим следующие «вершинные» структурные числа:
Перемножим эти 3 числа
Всевозможная комбинация столбцов будет выглядеть следующим образом:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы.
 Получаем
Получаем
Теперь мы можем выписать структурное число, соответствующее данной схеме — это будет число , являющееся дополнением к
Метод перемножения «контурных» структурных чисел
Найдем наименьшее количество замкнутых контуров, покрывающее все ребра графа.
Для каждого такого контура составим «контурное» структурное число. Предположим, что для -го контура мы имеем рёбер. Тогда такое «контурное» структурное число будет состоять из столбцов, состоящих из одного элемента, равного индексу ребра. То есть, не строго говоря, это строка, состоящая из ребер (для данного контура).
Выполним произведение всех таких контурных чисел — получим искомое структурное число.
Опять-таки проще это понять на примерах.
Очевидно, что у нас только один контур.
Контурное структурное число для него: .

Т.к. это единственное структурное число, то оно и будет ответом, что, как и ожидалось, совпадает с результатом первого метода.
Таких контуров 2.
У нас есть возможность разных комбинаций, но возьмем следующие: , .
Найдем произведение этих двух чисел, что и будет искомым структурным числом:
И опять, конечно же, структурные числа полученные двумя разными методами совпадают.
Пример 3. Двухкаскадный делитель.Структурное число, соответсвующее двухкаскадному делителю, мы нашли в самом начале статьи. Оно равно
Пример 4. Мост УитстонаТаких контуров 3.
Возьмем, например, следующие:
.
Найдем искомое структурное число A через произведение этих трех чисел.
Берем все возможные комбинации столбцов:
Убираем все столбцы, содержащие одинаковые элементы и попарно равные столбцы. Получаем искомое структурное число:
Получаем искомое структурное число:
С учетом того, что порядки следования столбцов и элементов в самих столбцах неважны, легко видеть, что в обоих методах мы получили одинаковые результаты.
Расчет пассивной трёхточки (трёхполюсника)
Комментарий:
Не уверен, что термины «трёхточка» или «трёхполюсник» является общепринятыми, но дальнейшее поясняет, что я имею ввиду.
У нас всё готово для расчета пассивной трёхточки, которую можно представить в виде пассивного четырёхполюсника с общей землей на входе и выходе.
Например, схемы делителей, которые мы рассматривали выше — это трёхточки (в том смысле, в котором мы определили трёхточку).
Передаточные функции напряжения и тока в этой схеме это
а первичный, входной и выходной импедансы:
А теперь самое главное — все эти величины мы легко можем найти, если знаем структурное число A, соответствующее схеме.
Расчет схем трёхточек
Давайте начнем с простейших схем. Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Хотя, в этом случае данный метод не дает ощутимых преимуществ, но простейшие схемы, как предельный вариант, интересны для оценки адекватности метода.
Схема 1. Простой делитель
Вспомним наше структурное число:
Тогда, помня, что детерминант от пустого (нет столбцов) структурного числа равен 1, легко получить:
Схема 2. Напряжение на сопротивлении.
Что соответствует действительности (расчетам другими известными методами).
Схема 3. Двукаскадный делитель (который мы рассчитывали с сыном)
Рассматриваемые нами трёхточки покрывают довольно большой процент случаев, поэтому уже здесь можно было бы поставить точку.
Но всё же не всегда вход и выход схемы имеют общий контакт (например, мост Уитстона). Метод структурных чисел позволяет найти решение и для общего случая пассивного четырёхполюсника.
Расчет четырехполюсника
Трехполюсник рассмотренный выше является частным случаем четырехполюсника.
Разница лишь в том, что вход и выход в данном случае необязательно имеют общий контакт.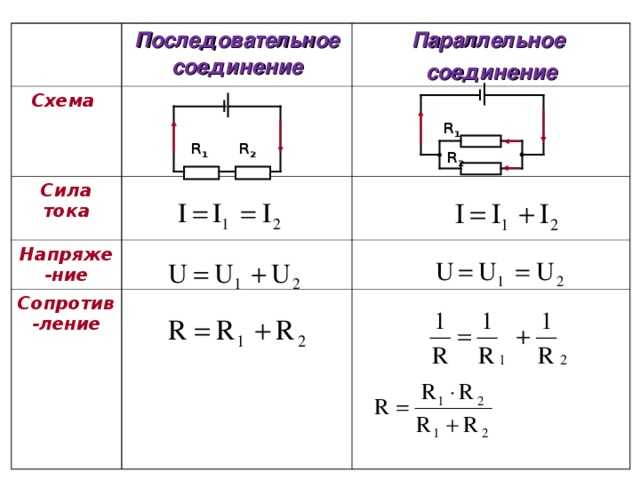
Формулы расчета для четырехполюсника
Как можно видеть, формулы для четырехполюсника такие же, как и для трехполюсника, за исключением коэффициентов передачи по напряжению и току. Здесь в числителе вместо
мы имеем
Это новая функция, которую проще объяснить на примере, и это будет рассмотрено ниже на примере моста Уитстона.
Понятно, что в случае трёхточки, которую мы рассматривали (с правильным выбором направления выходного ребра) мы имеем
Мост Уитстона
Структурное число
Давайте найдем некоторые важные для нашего анализа функции этого структурного числа.
Это рассмотрение позволит нам также ввести последнюю важную функцию — функция совпадения.
Детерминант
Легко видеть что детерминант этого числа это
Алгебраическая производная
Для обратных алгебраических производных соответственно имеем
Конъюнкция
Функция совпадения
Комментарий:
Это и есть та дополнительная функция, которой нам не хватало для расчет четырехполюсника.
Найдем функцию совпадения чисел и . Эта функция вычисляется через конъюнкцию, найденную выше:
где , равны или .
То есть эта функция похожа на детерминант конъюнкции, но со знаками «+» или «-» у каждого слагаемого (в детерминанте все слагаемые имеют знак «+»). Как найти эти коэффициенты? Чтобы найти знак у каждого слагаемого мы должны исключить из графа рёбра, определенные в этом слагаемом. При этом получится цикл, в котором «входное» и «выходное» ребра ориентированы согласно или встречно. В первом случае (согласно) — это даст нам «+», а во втором — «-«. Так, например, в нашем случае для мы должны исключить ребра 5 и 6 из нашего графа, а в случае — ребра 3 и 4. Таким образом получим
В первом случае направления ребер 1 и 2 согласованы, а во втором случае противоположны. Таким образом имеем
Расчет моста Уитстона
Для моста Уитстона, логика и уровень простоты в точности тот же. Но расчет требует внимательности и аккуратности.
В принципе у нас уже все готово.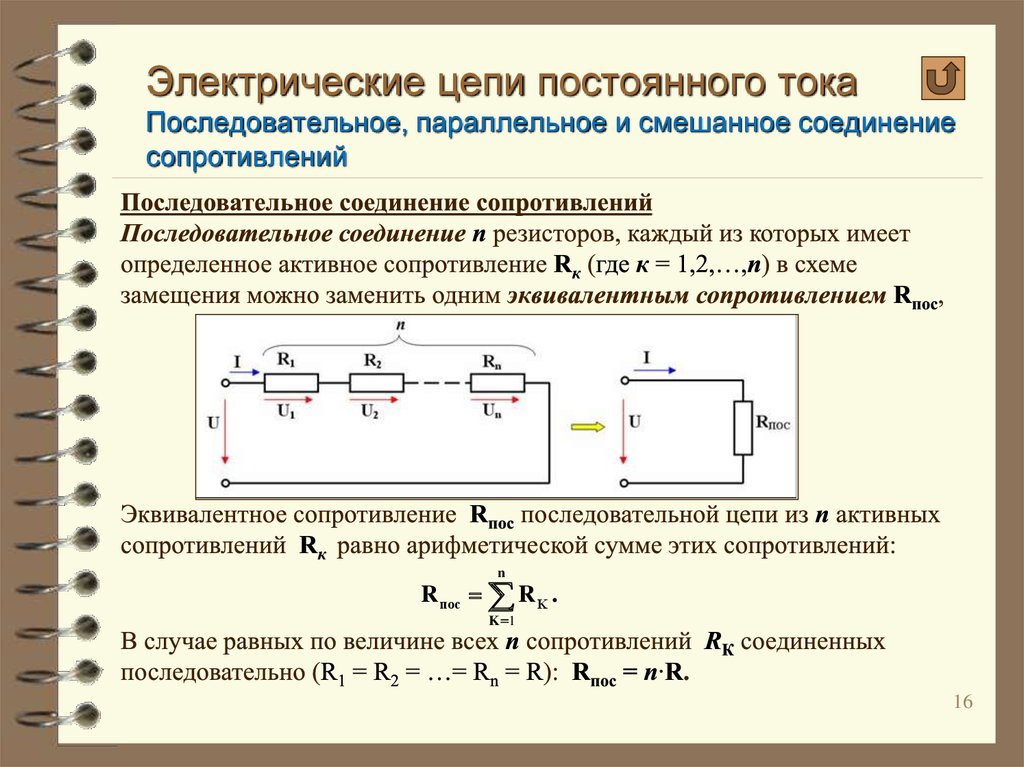
О блеске и нищете
Этот метод создавался в эпоху зарождения компьютеров и предназначался для компьютерного расчёта и синтеза электрических цепей. Поэтому наряду с эффективностью и, не побоюсь этого слова, поразительной простотой в применении этот подход обладает еще и органичной программируемостью. Вы легко можете автоматизировать процесс, описанный выше, и больше не переживать по поводу внимательности и большого количества бумаги.
И, несмотря на все явные достоинства, я не сумел найти этот метод в списке методов расчета электрических цепей в википедии, также я не встречал ни одного учебника или институтского курса, где бы давался этот метод. Думаю профессионалы (коим я никогда не был) знают об этом подходе, но ему не обучают в ВУЗах и, похоже, мало кто им пользуется.
Причина, думаю, понятна. Несмотря на весь блеск, эта тема просто не вписывается в учебную программу. То, что мы можем позволить себе в рамках статьи недопустимо в рамках учебного процесса — невозможно обойтись без теории, представив только манипулятивный подход. А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
А если преподавать с теорией, то это минимум один семестр — и это только для того, чтобы уметь рассчитывать электрические схемы? Скорее этот курс подходит для математиков, но, опять-таки, применение слишком узкое. Поэтому все следуют давно проторенному подходу: стандартные методы линейной алгебры, правила Кирхгофа, различные преобразования схем… И готов согласиться, что с точки зрения образования это позволяет лучше понять суть, а также вписывается в общий курс математики и физики.
И получается, что оригинальность, во многом определяющая изящество и красоту данного подхода, обернулась для него своего рода проклятием.
Рекомендации по решению нетрадиционных задач на расчет электрических цепей постоянного тока
Введение
Решение задач — неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и успешно реализованы следующие дидактические цели:
- Выдвижение проблемы и создание проблемной ситуации;
- Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.
§1. Задачи по расчету электрических цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:
1) содержат большое число элементов – резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений элементов.
В общем случае всякую цепь можно рассчитать, используя законы Кирхгофа. Однако эти законы не входят в школьную программу. К тому же, правильно решить систему из большого числа уравнений со многими неизвестными под силу не многим учащимся и этот путь не является лучшим способом тратить время. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при подаче одинаковых напряжений на исходную и преобразованную схемы, ток в обеих цепях будет одинаков на соответствующих участках. В этом случае все расчеты производятся с преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи со сложным смешанным соединением резисторов можно воспользоваться несколькими приемами. Мы ограничимся рассмотрением в подробностях лишь одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.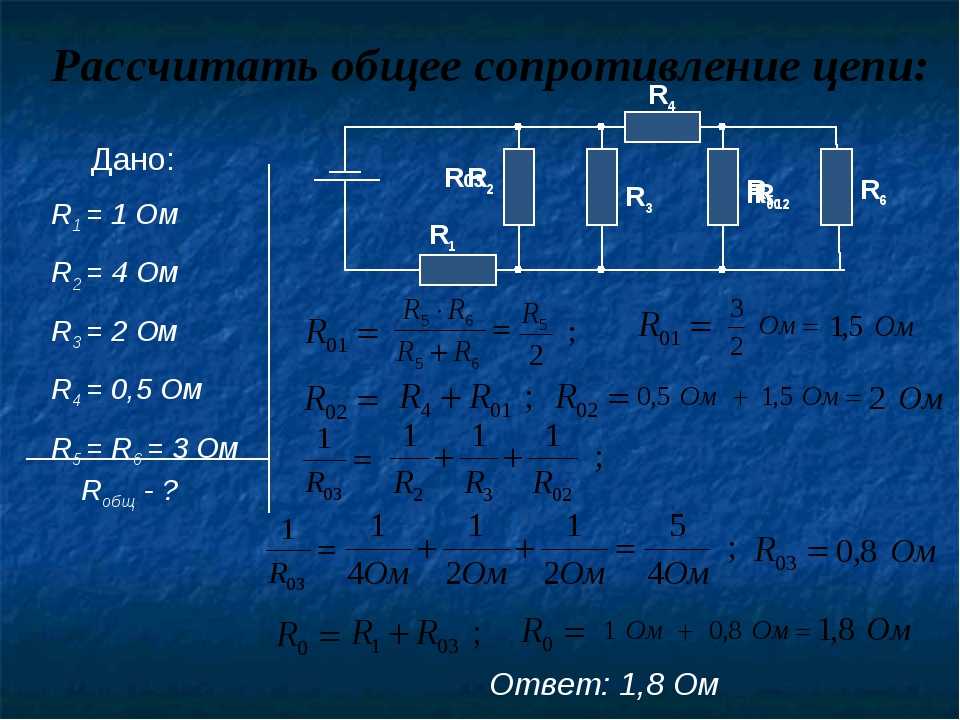
Таким образом, замена нескольких узлов равных потенциалов приводит к более простой эквивалентной схеме. Но иногда бывает целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части.
Рассмотрим примеры решения задач эти методом.
З а д а ч а №1
Рассчитать сопротивление между точками А и В данного участка цепи. Все резисторы одинаковы и их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и Д соединяем в один узел. Получаем очень простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить. Эквивалентная схема выглядит так:
Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная схема:
Ее сопротивление и сопротивление исходной цепи RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы. Исключением сопротивление между ними. Получаем эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.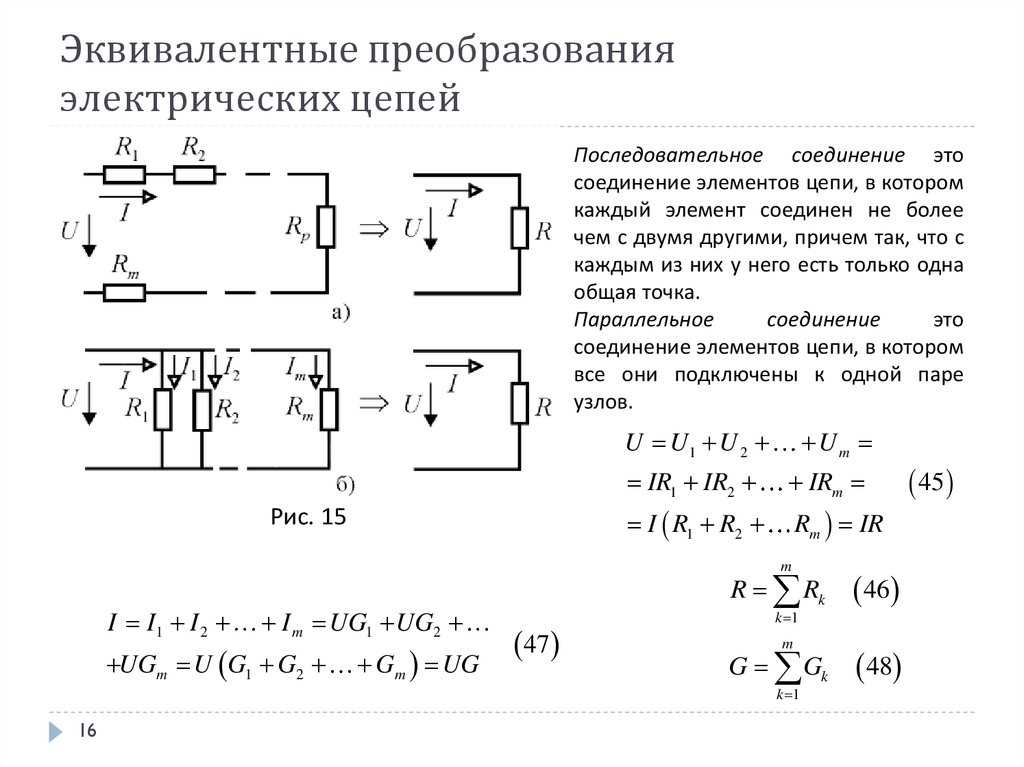 Получим такую эквивалентную схему:
Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один узел. Тогда эквивалентная схема будет иметь следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
Получим
эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB равно:
RAB= (8/10)*r.
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных угла О1 и О2. Теперь схему можно представить, как параллельные соединение двух одинаковых цепей. Поэтому достаточно подробно рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Сопротивление на участке A- I равно сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
З а д а ч а №9
В ветви ОС заменим сопротивление на два параллельно соединенных сопротивления по 2r. Теперь узел С можно разделить на 2 эквипотенциальных узла С1 и С2. Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r.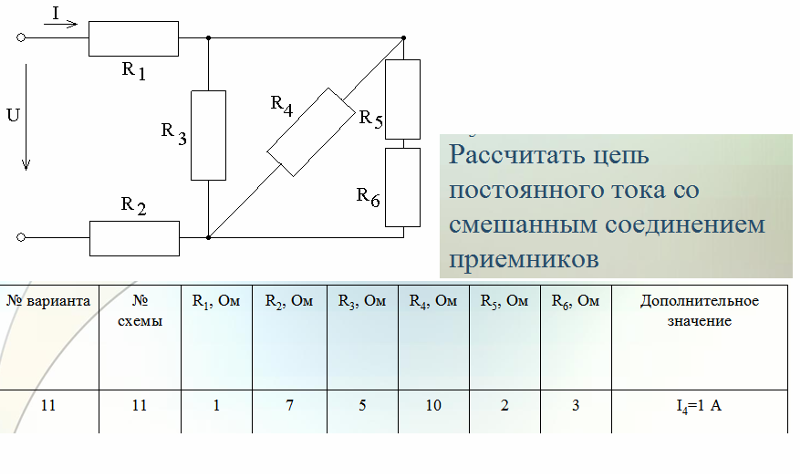 Опять
чертим соответствующую эквивалентную схему:
Опять
чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно сопротивлению на участке ADB и равно (7/4)*r. Таким образом получаем окончательную эквивалентную схему из трех параллельно соединенных сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их в один узел ОI .Эквивалентная схема изображена на рисунке :
Сопротивление на участке А ОI равно . На участке ОIВ сопротивление равно .Получаем совсем простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся звено, оно состоит в данном случае из трех первых сопротивлений. Если мы отбросим это звено, то полное сопротивление бесконечной цепи R не измениться от этого , так как получится точно такая же бесконечная цепь. Так же ничего не измениться, если мы выделенное звено подключим обратно к бесконечному сопротивлению R, но при этом следует обратить внимание , что часть звена и бесконечная цепь сопротивлением R соединены параллельно. Таким образом получаем эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету электрических цепей способом эквипотенциальных узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно считать усвоенными только тогда, когда они удачно применяются на практике. Задачи по физике описывают часто встречающиеся в жизни и на производстве проблемы, которые могут быть решены с помощью законов физики и, если ученик успешно решает задачи, то можно сказать, что он хорошо знает физику.
Для того, чтобы ученики успешно решали задачи, недостаточно иметь набор методов и способов решения задач, необходимо еще специально учить школьников применению этих способов.
Рассмотрим план решения задач по расчету электрических цепей постоянного тока методом эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов;
- начертить эквивалентную схему;
- найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом участке по законам последовательного и параллельного соединения;
- начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями;
- пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи.

- Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.
Примеры:
1)
Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.
2)
Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.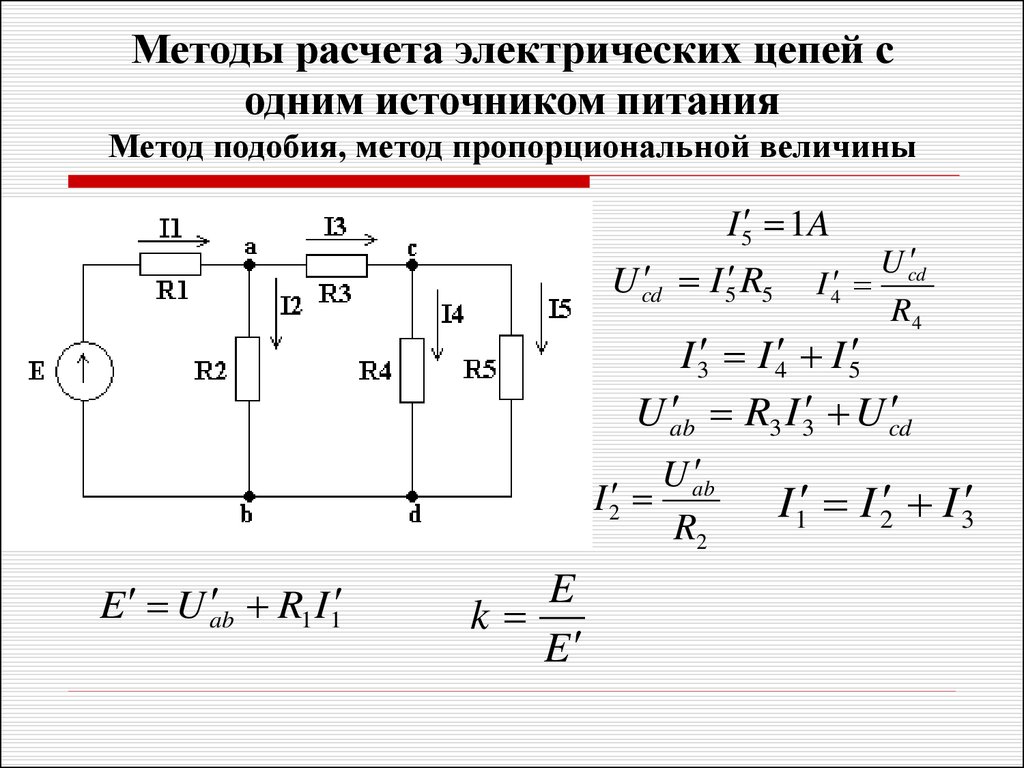
Пример:
Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.
в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.
Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.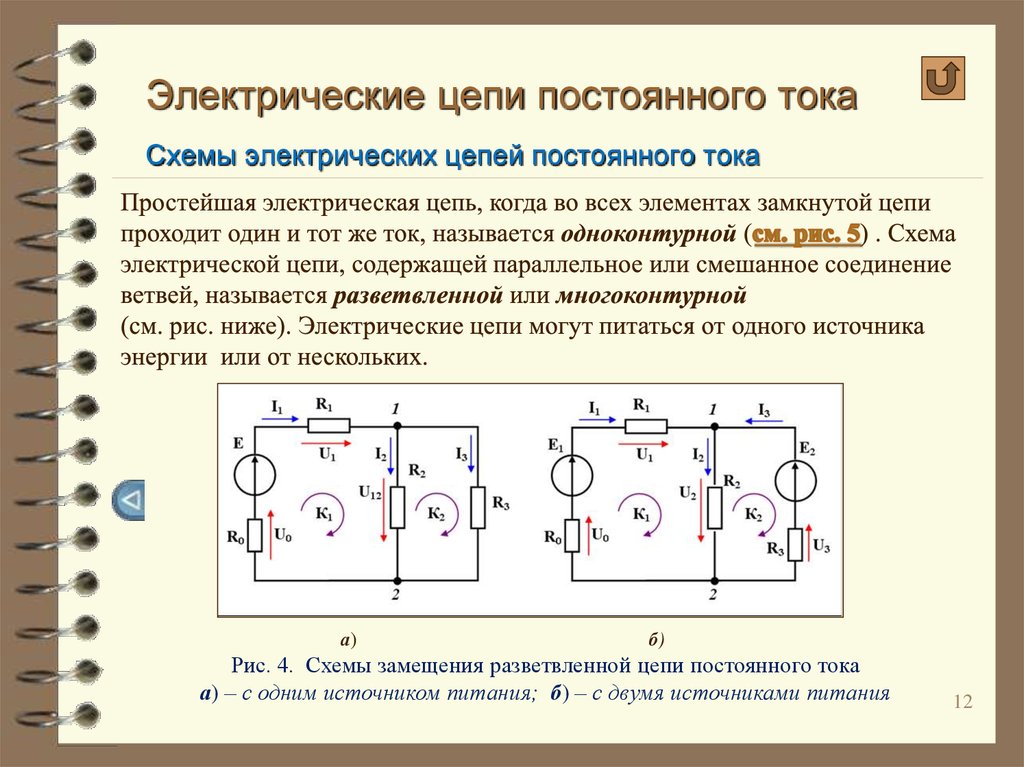
Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.
Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.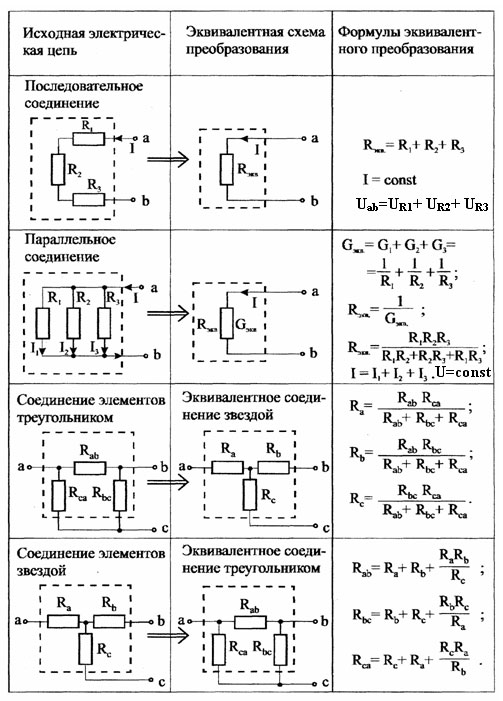
Повторяем пункт е): чертим эквивалентную схему:
Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала можно учащимся предложить задания для самостоятельной работы, взятые из дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. - М: Просвещение,1983.
- Лукашик В.И. Физическая олимпиада.- М: Просвещение, 2007
- Усова А.В., Бобров А.А. Формирование учебных умений и навыков учащихся на уроках физики.- М: Просвещение,1988
- Хацет А. Методы расчета эквивалентных схем //Квант.
- Чертов А. Г. Задачник по физике. – М.: Высшая школа,1983
- Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г.
 Бирск,1994г
Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические материалы. Москва, “Дрофа”, 2004г
Расчет гармонических колебаний в электрических цепях
Федеральное государственное казенное военное
образовательное учреждение высшего профессионального образования
«Военная академия связи имени Маршала Советского Союза С.М. Буденного»
Министерства обороны Российской Федерации
2 кафедра
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
по учебной дисциплине«Электроника, электротехника и схемотехника»
(Д-0201-2)
Раздел № 1
Электротехника
Тема № 2
Режим гармонических колебаний
в линейных электрических цепях
Занятие №8
Расчет гармонических колебаний
в электрических цепях
Санкт-Петербург
УЧЕБНЫЕ ВОПРОСЫ:
1. Анализ гармонических колебаний в простейших
электрических цепях
2. Анализ гармонических колебаний в сложных
электрических цепях
3. Контроль усвоения изученного материала
ЛИТЕРАТУРА:
1) Улахович Д. А.Основы теории линейных электрических цепей:
А.Основы теории линейных электрических цепей:
Учебное пособие. — СПб.: БХВ-Петербург, 2009.
2) Бабкова Л.А., Киселев О.Н. Методические рекомендации к
практическим занятиям и руководство к лабораторным
работам по дисциплине «Основы теории цепей»: Учеб.
пособие.– СПб.: ВАС, 2011, стр.19-27.
Вопрос №1. Анализ гармонических колебаний в простейших
электрических цепях
Задача 1
Определить амплитуду и начальную фазу гармонического колебания,
представляющего собой сумму двух гармонических колебаний одинаковой
частоты:
u(t) = u1(t)+u2(t) = 1,5 cos(ωt + 30°) + 2,4 cos(ωt + 120°)
Решение
1) Переведем гармонические колебания u1(t) и u2(t) в комплексные значения
амплитуды напряжения:
u1(t)= 1,5 cos(ωt + 30°)
U m1 1,5cos 30 j1,5sin 30 В
U m1 1, 29 j 0, 75 В
u2(t)= 2,4 cos(ωt +120°)
U m 2 2, 4 cos120 j 2, 4sin120 В
U m1 1, 2 j 2, 06 В
2) Произведем сложение комплексных значений амплитуд напряжения:
Um 1,2 1, 29 j 0,75 ( 1, 2) j 2,06 0,09 j 2,81
2,83e j 88 В
u (t)
u(t)
t
.
Задача 2
В цепи определить гармоническое напряжение
на резистивном элементе и элементе емкости,
если:
е(t) = 10 cos(2000t + 30°) В;
R = 100 Ом;
С = 1,5∙10-6 Ф.
Решение
1) Определим комплексную амплитуду воздействия:
е(t) = 10 cos(2000t +
30°)
U m 10e
j 30o
В
2) Рассчитаем комплексные сопротивления элементов:
Z R R 100 Ом
ZC
1
j 333,3 333,3e-j90 Ом
j C
3. Схема замещения цепи будет выглядеть следующим образом:
4) Произведем расчет комплексных амплитуд
реакции.
3.1) Определим эквивалентное комплексное
сопротивление:
Z RC
1
Z R ZC R
100 j 333,3 Ом
j C
Переведем в показательную форму:
Z RC 100 j 333,3 348е j 73,3 Ом
3.2) Определим комплексное амплитудное значение тока (первую реакцию).
Применим закон Ома в комплексной форме:
Um
10e j 30
j103,3
Im
0,
02873
е
А
j 73,3
Z RC 348е
3.3) Определим комплексное амплитудное значение напряжения на элементе
сопротивления (вторую реакцию).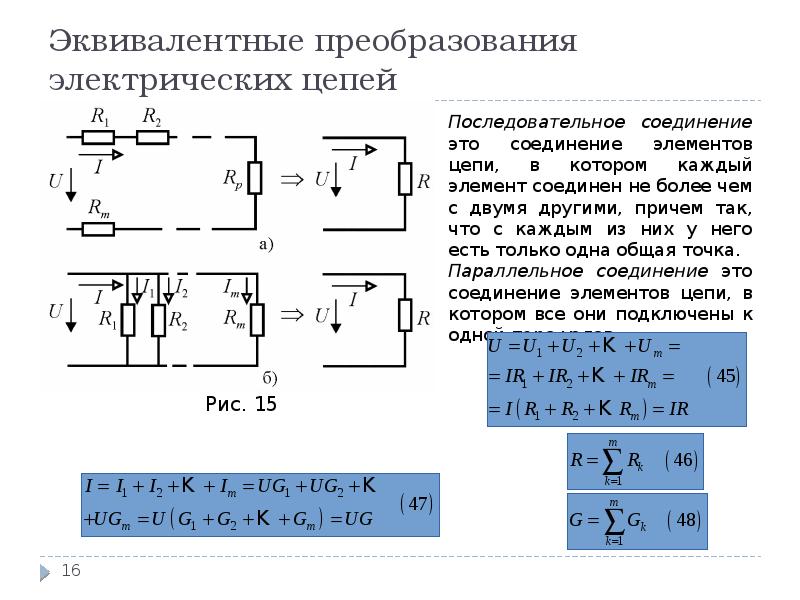
U mR I m Z R 0, 02873е j103,3 100 2,873е j103,3 В
3.4) Определим комплексное амплитудное значение напряжения на элементе
емкости (третью реакцию).
U mC I m Z C 0, 02873е j103,3 333,3e-j90 9,578e j13,3 В
Проведем проверку полученных результатов по второму закону Кирхгофа в
комплексной форме:
U m U mR U mС 0 U m U mR U mС
10e j 30 2,873е j103,3 9,578e j13,3
o
10 cos 30 j10sin 30 2,873cos(103,3) j 2,873sin(103,3) 9,578cos13,3 j 9,578sin13,3
4) Запишем мгновенные значения полученных реакций:
i(t) = 0,02873 cos(2000t +103,3°) А
uR(t) = 2,873 cos(2000t + 103,3°) В
u(t)
i (t)
t
uС(t) = 9,578 cos(2000t + 13,3°) В
5) Вывод: а) анализируя мгновенное значение напряжения на элементе
сопротивления можно видеть, что данный элемент частотно
независимый, и начальная фаза совпадает с начальной фазой тока;
б) анализируя мгновенное значение напряжения на элементе емкости
можно видеть, что начальная фаза отстает от начальной фазы тока
на 90°.
Вопрос №2. Анализ гармонических колебаний в сложных
электрических цепях
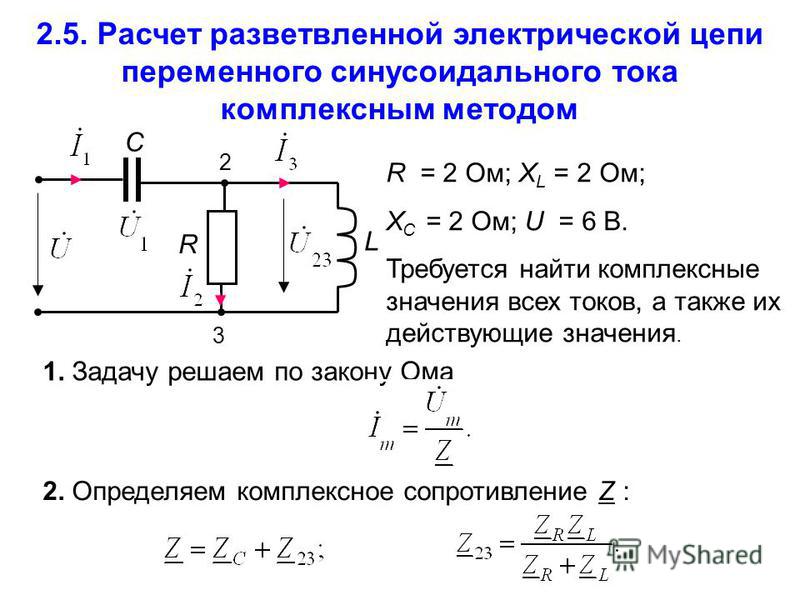
Задача 3
Для электрической цепи определить мгновенное
значение iL(t), если известно:
u(t) = 4 cos(106t — 40°) В;
R = 1 Ом;
С = 0,5∙10-6 Ф;
L= 10-6 Г.
Решение
1) Определим комплексную амплитуду воздействия:
u(t) = 4
cos(106t
—
40°)
U m 4e
j 40o
2) Рассчитаем комплексные сопротивления элементов:
Z R R 1 Ом
1
ZC
j2 2e-j90 Ом
j C
Z L j L j e
j90
Ом
B
Схема замещения цепи будет выглядеть следующим образом:
3) Произведем расчет комплексных амплитуд
реакции.
3.1) Определим эквивалентное комплексное
сопротивление:
Z RL
ZRZL
1j
j (1 j )
1 j
1 j Ом
Z R Z L 1 j (1 j ) (1 j )
1
ZCRL ZC Z RL 1 j j 2 1 j Ом
Переведем в показательную форму:
ZCRL 1 j 1, 41e j 45
3.2) Определим комплексное амплитудное значение тока.
Применим закон Ома в комплексной форме:
j 40o
Um
4e
j 5o
Im
2,83е А
j 45
Z RCL 1, 41е
3. 3) Определим комплексное амплитудное значение напряжения на элементе
3) Определим комплексное амплитудное значение напряжения на элементе
емкости.
U mC I m Z C 2,83е
j 5o
2e
j 90
5, 66е
j 85o
B
Применим второй закон Кирхгофа в комплексной форме:
U m U mRL U mС 0 U mRL U m U mС
U mRL 4е
j 40o
5, 66e
j 85o
(3, 06 j 2,57) (0,5 j5, 64) 2,56 j3, 07 4e j 50 B
Т.к. элемент сопротивления и элемент емкости соединены параллельно, то
U mRL U mR U mL
3.4) Определим комплексное амплитудное значение тока на элементе
индуктивности.
o
I mL
U mRL 4е j 50
j 40o
j 90o 4e
А
ZL
e
4) Запишем мгновенное значение полученной реакции:
iL(t) = 4 cos(106t -40°) A
5) Вывод: анализируя мгновенное значение тока на элементе индуктивности
можно видеть, что колебания тока и напряжения одинаковы, а
начальная фаза тока отстает от начальной фазы напряжения на
90°.
Расчеты и концепции схем — физика для старших классов
Все ресурсы по физике для старших классов
6 диагностических тестов 233 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Справка по физике для старших классов » Электричество и магнетизм » Электрические схемы » Расчеты и концепции цепей
Какое напряжение в цепи с током и сопротивлением?
Возможные ответы:
Правильный ответ:
Пояснение:
Для этой задачи используйте закон Ома: . В этом уравнении напряжение, ток и сопротивление.
В этом уравнении напряжение, ток и сопротивление.
Подставьте данные значения и определите напряжение.
Сообщить об ошибке
Какова сила тока в цепи с напряжением и общим сопротивлением ?
Возможные ответы:
Правильный ответ:
Пояснение:
Для этой задачи используйте закон Ома: . В этом уравнении напряжение, ток и сопротивление.
Мы можем изменить уравнение, чтобы решить его специально для .
Подставьте данные значения напряжения и сопротивления, чтобы найти ток.
Сообщить об ошибке
Какое сопротивление в цепи при напряжении и токе ?
Возможные ответы:
Правильный ответ:
Пояснение:
Для этой задачи используйте закон Ома: . В этом уравнении напряжение, ток и сопротивление.
В этом уравнении напряжение, ток и сопротивление.
Мы можем изменить уравнение, чтобы решить его специально для .
Подставьте данные значения напряжения и тока и определите сопротивление.
Сообщить об ошибке
Аккумулятор подключен к цепи. Измеренный ток. Чему равно сопротивление?
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче используйте закон Ома: .
Нам известны напряжение и ток, что позволяет нам найти сопротивление.
Сообщить об ошибке
Замкнутая электрическая цепь устроена так, что есть ток и напряжение . Какое сопротивление в цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче используйте закон Ома: .
Нам даны ток и напряжение. Используя эти термины, мы можем найти сопротивление.
Сообщить об ошибке
Ток в цепи равен . Если напряжение, то каково общее сопротивление?
Возможные ответы:
Правильный ответ:
Объяснение:
Для этой задачи используйте закон Ома:
Нам известны ток и напряжение, что позволяет нам найти сопротивление.
Сообщить об ошибке
Суммарное сопротивление электрической цепи составляет . Какой ток?
Возможные ответы:
Правильный ответ:
Объяснение:
Для этой задачи используйте закон Ома:
Нам известны сопротивление и напряжение, что позволяет нам найти ток.
Сообщить об ошибке
Электрическая цепь имеет ток и сопротивление. Какое напряжение?
Возможные ответы:
Правильный ответ:
Объяснение:
Для этой задачи используйте закон Ома:
Нам известны сопротивление и ток, что позволяет нам найти напряжение.
Сообщить об ошибке
Электрическая цепь имеет ток и сопротивление. Какое напряжение?
Возможные ответы:
Правильный ответ:
Пояснение:
Для этой задачи используйте закон Ома:
Нам известны сопротивление и ток, что позволяет нам найти напряжение.
Сообщить об ошибке
Цепь имеет ток, , напряжение, и сопротивление, . Если напряжение остается постоянным, а ток удваивается (), каким должно быть новое сопротивление?
Если напряжение остается постоянным, а ток удваивается (), каким должно быть новое сопротивление?
Возможные ответы:
Недостаточно информации для решения
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, используйте закон Ома:
Поскольку мы удваиваем ток, но напряжение остается прежним, мы можем приравнять наши старое и новое уравнения друг к другу.
Мы знаем, что второй ток в два раза больше первого.
Используйте это уравнение, чтобы подставить ток в первое уравнение.
Теперь начальный ток компенсируется с обеих сторон.
Разделите обе части на два, чтобы выделить окончательную переменную сопротивления.
Сообщить об ошибке
← Назад 1 2 3 4 5 Далее →
Уведомление об авторских правах 233 практических теста Вопрос дня Карточки Учитесь по концепции
Анализ схемы для хит-шпаргалки
: Джон Сантьяго и
Обновлен: 01-26-2022
Из книги: Анализ схемы для Dummies
.
 Купить на Amazon При анализе цепей вам необходимо знать некоторые основные законы, электрические величины, взаимосвязи и теоремы.
Купить на Amazon При анализе цепей вам необходимо знать некоторые основные законы, электрические величины, взаимосвязи и теоремы.Закон Ома является ключевым уравнением устройства, которое связывает ток, напряжение и сопротивление. Используя законы Кирхгофа, вы можете упростить сеть резисторов, используя один эквивалентный резистор. Вы также можете выполнить такой же расчет, чтобы получить эквивалентную емкость и индуктивность для сети конденсаторов или катушек индуктивности.
Для более сложных схем пригодятся методы анализа узловых напряжений и токов сетки. А если вы хотите попробовать разные нагрузки для конкретной схемы источника, вы можете использовать эквивалент Тевенина или Нортона.
Три основных закона работы со схемами
На самом базовом уровне анализ схем включает в себя расчет тока и напряжения для конкретного устройства. Вот тут-то и появляются уравнения устройства и соединения. Уравнения устройства описывают взаимосвязь между напряжением и током для конкретного устройства.
Одним из наиболее важных уравнений устройства является закон Ома, который связывает ток (I) и напряжение (В) с использованием сопротивления (R) , , где R равно a константа V = IR или I = V/R или R = V/I .
Вам необходимо знать два уравнения связи: закон Кирхгофа для тока (KCL) и закон Кирхгофа для напряжения (KVL):
Электрические величины и единицы измерения
Определенные электрические величины, отношения и электрические единицы необходимо знать при анализе и характеристике поведения схемы. Следующая таблица поможет вам сохранить эту информацию в чистоте.
Эквивалентное сопротивление, емкость и индуктивность
При анализе цепей можно упростить сети, состоящие только из резисторов, конденсаторов или катушек индуктивности, заменив их одним эквивалентным устройством. Следующие уравнения показывают эквивалентные последовательные и параллельные соединения для комбинаций только резистора, только конденсатора и только катушки индуктивности.
Следующие уравнения показывают эквивалентные последовательные и параллельные соединения для комбинаций только резистора, только конденсатора и только катушки индуктивности.
Методы анализа сложных цепей
При работе со сложными цепями, такими как схемы с большим количеством петель и узлов, можно использовать несколько приемов для упрощения анализа. Следующие методы анализа цепей пригодятся, когда вы хотите найти напряжение или ток для определенного устройства. Они также полезны, когда у вас есть много устройств, подключенных параллельно или последовательно, устройства, образующие петли, или несколько устройств, подключенных к определенному узлу.
Анализ напряжения узла: Узлы — это определенные точки в цепи. Когда к определенной точке подключено много устройств, вы можете сделать этот узел опорным узлом и думать о нем как о имеющем напряжение 0 В. Затем вы используете его в качестве опорной точки для измерения напряжения для определенного узла.

С помощью анализа узловых напряжений вы находите неизвестные узловые напряжения в цепи, используя закон тока Кирхгофа. После нахождения узловых напряжений вы используете ток-напряжение ( i-v ) взаимосвязей, таких как закон Ома, для определения токов устройств и использование узловых напряжений для определения напряжений устройств.
Текущий анализ сетки: Сетка представляет собой петлю без устройств, заключенных в петлю, где границы сетки — это те устройства, которые образуют петлю. Анализ токов сетки позволяет находить неизвестные токи сетки в цепи с помощью закона напряжения Кирхгофа (KVL). Уравнения сетки представляют собой уравнения КВЛ с неизвестными токами сетки в качестве переменных. После нахождения токов сетки вы используете i – v связи для определения напряжения устройства.
Суперпозиция: Для линейных цепей с независимыми источниками вы можете использовать суперпозицию, чтобы найти выходное напряжение и ток для конкретного устройства.
 Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника.
Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника.Эквиваленты Thévenin/Norton: Анализ цепи может стать утомительным, если вы пробуете разные нагрузки с одной и той же цепью источника. Чтобы избавить себя от работы, замените схему источника эквивалентами Тевенина и Нортона. Теорема Тевенина говорит, что вы можете заменить линейную сеть источников и резисторов между двумя терминалами одним независимым источником напряжения (V T ) последовательно с одним резистором (R T ) , and Norton’s theorem says you can replace the linear network of sources and resistors with one independent current source (I N ) in parallel с одним резистором (R N ) — см.
 следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткозамкнутыми), если они имеют одинаковые отношения напряжения и тока на клеммах.
следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткозамкнутыми), если они имеют одинаковые отношения напряжения и тока на клеммах.Finding the Thévenin or Norton equivalent requires calculating the following variables: V T = V OC , I N = I SC , и R T = R N = N = = 5 = = = 5 .0347 /I SC (где T означает Thévenin, OC означает нагрузку холостого хода, N означает нагрузку Norton и 8 SC означает нагрузку короткого замыкания). Если вы хотите проанализировать различные нагрузки, подключенные последовательно к цепи источника, полезен эквивалент Тевенина; когда нагрузки подключены параллельно цепи источника, лучшим выбором будет аналог Norton.
 Два эквивалента связаны друг с другом преобразованием источника.
Два эквивалента связаны друг с другом преобразованием источника.
Об этой статье
Эта статья из книги:
- Анализ цепей для чайников,
Об авторе книги:
Джон М. Сантьяго-младший, доктор наук, служил в ВВС США (USAF). ) в течение 26 лет. В течение этого времени он занимал различные руководящие должности в области управления техническими программами, разработки приобретений и поддержки исследований в области эксплуатации. Находясь в Европе, он руководил более чем 40 международными научными и инженерными конференциями/семинарами.
Эту статью можно найти в категории:
- Схемы,
11.3 Энергия | Электрические цепи
Предыдущий 11. | Следующий 11.4 Краткое содержание главы |
11.3 Мощность и энергия (ESBQD)
Электроэнергия (ESBQF)
temp textДля подачи тока по полной цепи требуется источник энергии. Это обеспечивается аккумуляторами. в схемах, которые вы рассматривали. Батареи преобразуют химическую потенциальную энергию в электроэнергия. Энергия используется для совершения работы с электронами в цепи.
Мощность — это мера того, насколько быстро работа выполнена. Мощность — это скорость , при которой
работа совершается, работа совершается в единицу времени. Работа измеряется в джоулях (Дж), а время в секундах (с), поэтому мощность
будет \(\frac{\text{J}}{\text{s}}\), который мы называем ваттом (Вт).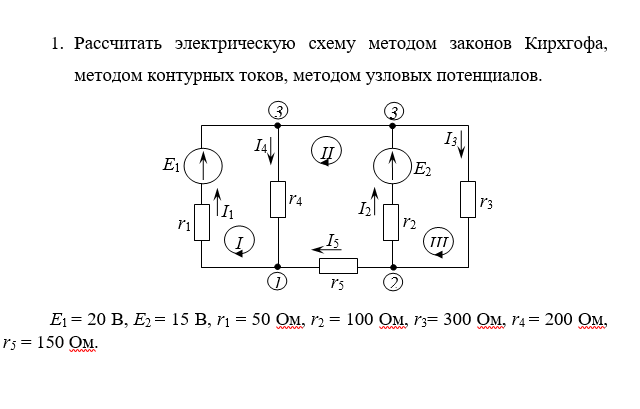
В электрических цепях мощность зависит как от напряжения, так и от тока, и мы говорим о мощности рассеянный в элементе цепи:
- Электроэнергия
Электрическая мощность — это скорость, с которой электрическая энергия преобразуется в электрической цепи. Это рассчитывается как:
\[P = I·V\]Мощность (P) точно равна току (I), умноженному на напряжение (V) дополнительной константы пропорциональности нет. Единица единицей измерения мощности является ватт (сокращенно W).
92}{Р} \конец{выравнивание*}Рабочий пример 8: Электроэнергия
Дан компонент цепи с напряжением \(\text{5}\) \(\text{V}\) и сопротивлением \(\text{2}\) \(\text{Ω}\) какая рассеиваемая мощность?
Запишите, что вам дали и что вам нужно найти
\begin{align*} В & = \текст{5}\текст{В} \\ R & = \text{2}\text{ Ом} \\ Р & = ? \end{выравнивание*} 9{2}}{(\текст{2})} \\ & = \text{12,5}\text{W} \конец{выравнивание*} Мощность равна \(\text{12,5}\) \(\text{W}\).

Рабочий пример 9: Электроэнергия
Изучите электрическую схему ниже:
Сопротивление резистора равно \(\text{15}\) \(\text{Ом}\) и ток, протекающий через резистор \(\text{4}\) \(\text{A}\). Какова мощность резистора? 92 \раз \текст{15} \\ &= \текст{240}\текст{W} \конец{выравнивание*}
Напишите окончательный ответ
Мощность резистора равна \(\text{240}\) \(\text{Вт}\).
Рабочий пример 10: питание в последовательной цепи
Два омических резистора (\(R_{1}\) и \(R_{2}\)) соединены последовательно с ячейкой. Найди сопротивление и мощность \(R_{2}\), учитывая, что ток, протекающий через \(R_{1}\) и \(R_{2}\) равно \(\text{0,25}\) \(\text{A}\) и что напряжение на ячейке равно \(\text{6}\) \(\текст{V}\). \(R_{1}\) = \(\text{1}\) \(\text{Ω}\).

Нарисуйте схему и заполните все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:
\[R = R_{1} + R_{2}\]
, потому что он находится в последовательной цепи.
Найти общее сопротивление
\begin{align*} V &=R\cdot I \\ R &= \frac{V}{I} \\ & =\frac{\text{6}}{\text{0,25}} \\ & = \text{24}\text{ Ом} \end{выравнивание*}
Найти неизвестное сопротивление
Мы знаем, что:
\[R = \text{24}\text{Ом}\]
и тот
\[R_{1} = \text{1}\text{Ом}\]
Начиная с
\[R = R_{1} + R_{2}\] \[R_{2} = R — R_{1}\]
Следовательно,
\[R = \text{23}\text{Ом}\] 92(\текст{23}) \\ &=\текст{1,44}\текст{W} \конец{выравнивание*}
Напишите окончательный ответ
Мощность резистора \(R_2\) равна \(\text{1,44}\) \(\text{Вт}\).
temp text
Обратите внимание , что мы используем те же схемы в примерах, поскольку мы расширяем наши знания о электрические цепи. Это делается для того, чтобы подчеркнуть, что вы всегда можете комбинировать все имеющиеся у вас принципы. изучены при работе с любой схемой.
Рабочий пример 11: Мощность в последовательной и параллельной сети резисторов
Для следующей цепи:
Ток, выходящий из батареи, равен \(\text{1,07}\) \(\text{A}\), общая мощность, рассеиваемая в схема \(\text{6,42}\) \(\text{W}\), отношение полных сопротивлений двух параллельных сетей \(R_{P1} : R_{P2}\) равно 1:2, соотношение \(R_1 : R_2\) равно 3:5 и \(R_3=\text{7}\text{Ω}\).
Определить:
- напряжение аккумулятора,
- мощность, рассеиваемая в \(R_{P1}\) и \(R_{P2}\), а
- номинал каждого резистора и мощность, рассеиваемая на каждом из них.

Что требуется
В этом вопросе вам дается различная информация и предлагается определить мощность рассеивается на каждом резисторе и каждой комбинации резисторов. Обратите внимание, что информация, предоставленная в основном для общей схемы. Это ключ к тому, что вы должны начать с общей схемы и работайте вниз к более конкретным элементам схемы.
Расчет напряжения батареи
В первую очередь мы сосредоточимся на батарее. Нам дана мощность для всей цепи, а также ток, выходящий из батареи. Мы знаем, что напряжение на клеммах аккумулятора равно напряжение по цепи в целом.
Мы можем использовать соотношение \(P=VI\) для всей цепи, потому что напряжение такое же, как напряжение на клеммах аккумулятора: \начать{выравнивать*} Р &=VI \\ V &= \frac{P}{I} \\ &=\frac{\text{6,42}}{\text{1,07}} \\ &= \текст{6,00}\текст{В} \end{выравнивание*}
Напряжение на аккумуляторе равно \(\text{6,00}\) \(\text{В}\).

Мощность, рассеиваемая в \(R_{P1}\) и \(R_{P2}\)
Помните, что мы работаем от общей схемы к деталям для отдельных элементов, это противоположно тому, как вы относились к этой схеме ранее.
Мы можем рассматривать параллельные сети как эквивалентные резисторы, так что схема, которую мы в настоящее время работа с выглядит так:
Мы знаем, что ток через два элемента цепи будет одинаковым, потому что это серия цепи и что сопротивление всей цепи должно быть: \(R_T=R_{P1}+R_{P2}\). Мы можем определить полное сопротивление из закона Ома для цепи в целом: \начать{выравнивать*} V_{батарея}&=IR_T \\ R_T &=\frac{V_{батарея}}{I} \\ &=\frac{\text{6,00}}{\text{1,07}}\\ &=\текст{5,61}\текст{Ом} \end{выравнивание*}
Мы знаем, что соотношение между \(R_{P1} : R_{P2}\) равно 1:2, что означает, что мы знаем: \начать{выравнивать*} R_{P1} &= \frac{1}{2}R_{P2} \\\text{and} \\ R_T &= R_{P1} + R_{P2} \\ & = \frac{1}{2}R_{P2} + R_{P2} \\ &=\frac{3}{2}R_{P2} \\ (\text{5,61}) &=\frac{3}{2}R_{P2} \\ R_{P2} &= \frac{2}{3}(\text{5,61}) \\ R_{P2} &= \text{3,74}\text{ Ом} \конец{выравнивание*} и поэтому: \начать{выравнивать*} R_{P1} &= \frac{1}{2}R_{P2} \\ &=\frac{1}{2}(\text{3,74}) \\ &= \text{1,87}\text{ Ом} \end{выравнивание*} 92(\текст{3,74}) \\ &= \текст{4,28}\текст{W} \конец{выравнивание*}
Расчеты для параллельной сети 1
Теперь мы можем приступить к детальным расчетам для первого набора параллельных резисторов.

Мы знаем, что отношение между \(R_{1} : R_{2}\) равно 3:5, что означает, что мы знаем \(R_{1}= \frac{3}{5}R_{2}\). Мы также знаем общее сопротивление двух параллельных резисторов в этой схеме. сеть \(\text{1,87}\) \(\text{Ω}\). Мы можем использовать соотношение между значениями два резистора, а также формула для полного сопротивления (\(\frac{1}{R_PT}=\frac{1}{R_1}+\frac{1}{R_2}\)) чтобы найти номиналы резисторов: \начать{выравнивать*} \frac{1}{R_{P1}}&=\frac{1}{R_1}+\frac{1}{R_2} \\ \frac{1}{R_{P1}}&=\frac{5}{3R_2}+\frac{1}{R_2} \\ \frac{1}{R_{P1}}&=\frac{1}{R_2}(\frac{5}{3}+1) \\ \frac{1}{R_{P1}}&=\frac{1}{R_2}(\frac{5}{3}+\frac{3}{3}) \\ \frac{1}{R_{P1}}&=\frac{1}{R_2}\frac{8}{3} \\ R_2&=R_{P1}\frac{8}{3} \\ &=(\text{1,87})\frac{8}{3} \\ &=\текст{4,99}\text{ Ом} \конец{выравнивание*} Мы также можем вычислить \(R_{1}\): \начать{выравнивать*} R_{1}&= \frac{3}{5}R_{2} \\ &= \frac{3}{5}(\text{4,99}) \\ &= \text{2,99}\text{ Ом} \end{align*}
Для определения мощности нам понадобится сопротивление, которое мы рассчитали, и либо напряжение, либо Текущий.
 Два резистора включены параллельно, поэтому напряжение на них одинаковое.
такое же, как напряжение в параллельной сети. Мы можем использовать закон Ома, чтобы определить напряжение
через сеть параллельных резисторов, поскольку мы знаем общее сопротивление, и мы знаем
Текущий:
\начать{выравнивать*}
V &= I R \\
&=(\текст{1,07})(\текст{1,87}) \\
&=\текст{2,00}\текст{В}
\end{выравнивание*} 92}{\текст{4,99}} \\
&=\текст{0,80}\текст{W}
\конец{выравнивание*}
Два резистора включены параллельно, поэтому напряжение на них одинаковое.
такое же, как напряжение в параллельной сети. Мы можем использовать закон Ома, чтобы определить напряжение
через сеть параллельных резисторов, поскольку мы знаем общее сопротивление, и мы знаем
Текущий:
\начать{выравнивать*}
V &= I R \\
&=(\текст{1,07})(\текст{1,87}) \\
&=\текст{2,00}\текст{В}
\end{выравнивание*} 92}{\текст{4,99}} \\
&=\текст{0,80}\текст{W}
\конец{выравнивание*}Расчет параллельной сети 2
Теперь мы можем приступить к детальному расчету второго набора параллельных резисторов.
Нам дано \(R_3=\text{7,00}\text{ Ω}\), и мы знаем \(R_{P2}\), поэтому мы можем вычислить \(R_4\) из: \начать{выравнивать*} \frac{1}{R_{P2}} &= \frac{1}{R_3}+\frac{1}{R_4} \\ \frac{1}{\text{3,74}} &= \frac{1}{\text{7,00}}+\frac{1}{R_4} \\ R_4&=\text{8,03}\text{ Ом} \end{выравнивание*} 9{\ текст {2}} \) \ (\ текст {С} \) пройти через него в \(\text{0,50}\) \(\text{h}\) использовать, если его напряжение \(\text{3,00}\) \(\текст{V}\)?
Сначала нужно найти ток.
 {\text{2}}}{\text{1 800}}\\
& = \текст{0,333}\текст{А}
\конец{выравнивание*}
\начать{выравнивать*}
Р &=VI \\
&=(\текст{3,00})(\текст{0,333}) \\
&= \текст{0,9{2}(\текст{0,30}) \\
&= \текст{7,5}\текст{W}
\end{align*}
{\text{2}}}{\text{1 800}}\\
& = \текст{0,333}\текст{А}
\конец{выравнивание*}
\начать{выравнивать*}
Р &=VI \\
&=(\текст{3,00})(\текст{0,333}) \\
&= \текст{0,9{2}(\текст{0,30}) \\
&= \текст{7,5}\текст{W}
\end{align*}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{4} + \frac{1}{2} \\ & = \фракция{3}{4}\\ R_{p} & = \text{1,33}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть цепь с двумя последовательно соединенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{3} + R_{p} \\ & = \текст{2} + \текст{1,33} \\ & = \text{3,33}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать общий ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{6}{\text{3,33}} \\ & = \текст{1,8}\текст{А} \конец{выравнивание*}
Это ток в резисторе \(\text{2}\) \(\text{Ом}\) и через весь параллельное подключение.
 Используя это, мы можем найти мощность, рассеиваемую в \(\text{2}\)
\(\text{Ом}\) резистор: 9{2}(\текст{2}) \\
& = \text{6,48}\text{W}
\конец{выравнивание*}
Используя это, мы можем найти мощность, рассеиваемую в \(\text{2}\)
\(\text{Ом}\) резистор: 9{2}(\текст{2}) \\
& = \text{6,48}\text{W}
\конец{выравнивание*}Затем мы находим напряжение на этом резисторе и используем его, чтобы найти напряжение на параллельная комбинация:
\начать{выравнивать*} V & = ИК \\ & = (\текст{1,8})(\текст{2}) \\ & = \текст{3,6}\текст{В} \конец{выравнивание*} \начать{выравнивать*} V_{T} & = V_{1} + V_{2} \\ V_{2} & = V_{T} — V_{1} \\ & = \текст{6} — \текст{3,6} \\ & = \текст{2,4}\текст{В} \конец{выравнивание*} 9{2}}{\текст{2}} \\ & = \текст{2,88}\текст{W} \конец{выравнивание*}
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{1} + \frac{1}{2} \\ & = \ гидроразрыва {3} {2} \\ \поэтому R_{p} & = \text{0,6666}\ldots\text{ Ω} \конец{выравнивание*}
Теперь у нас есть схема с тремя последовательными резисторами, поэтому мы можем рассчитать эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{3} + R_{4} + R_{p} \\ & = \text{4} + \text{6} + \text{0,6666}\ldots \\ & = \text{10,6666}\ldots\text{Ом} \конец{выравнивание*}
Теперь мы можем рассчитать общий ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{6}{\text{10,6666}\ldots} \\ & = \текст{0,5625}\текст{А} \конец{выравнивание*}
Это ток в двух последовательных резисторах и через весь параллельный связь.
 Используя это, мы можем найти мощность, рассеиваемую в двух последовательных резисторах: 9{2}(\текст{4}) \\
& = \text{1,2656}\ldots\text{W}
\конец{выравнивание*}
Используя это, мы можем найти мощность, рассеиваемую в двух последовательных резисторах: 9{2}(\текст{4}) \\
& = \text{1,2656}\ldots\text{W}
\конец{выравнивание*}Затем мы находим напряжение на каждом из этих резисторов и используем это, чтобы найти напряжение через параллельную комбинацию:
\начать{выравнивать*} V & = ИК \\ & = (\текст{0,5625})(\текст{6}) \\ & = \текст{3,375}\текст{В} \конец{выравнивание*} \начать{выравнивать*} V & = ИК \\ & = (\текст{0,5625})(\текст{4}) \\ & = \текст{2,25}\текст{В} \конец{выравнивание*} \начать{выравнивать*} V_{T} & = V_{1} + V_{2} + V_{p} \\ V_{p} & = V_{T} — V_{1} — V_{2} \\ & = \текст{6} — \текст{3,375} — \текст{2,25} \\ & = \текст{0,375}\текст{В} \конец{выравнивание*} 9{2}}{\текст{2}} \\ & = \text{0,0703}\ldots\text{W} \\ & \приблизительно \text{0,07} \text{W} \конец{выравнивание*}
Также определите номинал неизвестного резистора, если общая рассеиваемая мощность \(\text{9,8}\) \(\text{W}\)
Начнем с расчета эквивалентного сопротивления резисторов.
 Мы знаем общее
мощность и общее напряжение, поэтому мы используем это, чтобы найти общее сопротивление. 9{2}}{\текст{9,8}} \\
& = \text{3,67}\text{ Ом}
\конец{выравнивание*}
Мы знаем общее
мощность и общее напряжение, поэтому мы используем это, чтобы найти общее сопротивление. 9{2}}{\текст{9,8}} \\
& = \text{3,67}\text{ Ом}
\конец{выравнивание*}Теперь мы можем найти неизвестное сопротивление, сначала рассчитав эквивалентную параллель сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{1} + \frac{1}{5} + \frac{1}{3} \\ & = \ гидроразрыва {23} {15} \\ R_{p} & = \text{0,65}\text{ Ом} \конец{выравнивание*} \начать{выравнивать*} R_{s} & = R_{4} + R_{p} \\ R_{4} & = R_{s} — R_{p} \\ & = \текст{3,67} — \текст{0,65} \\ & = \text{3,02}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать общий ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{6}{\text{3,67}} \\ & = \текст{1,63}\текст{А} \конец{выравнивание*}
Это ток в последовательном резисторе и через все параллельное соединение.
 Используя это, мы можем найти мощность, рассеиваемую в последовательном резисторе: 9{2}(\текст{3,02}) \\
& = \текст{0,89}\текст{W}
\конец{выравнивание*}
Используя это, мы можем найти мощность, рассеиваемую в последовательном резисторе: 9{2}(\текст{3,02}) \\
& = \текст{0,89}\текст{W}
\конец{выравнивание*}Затем мы находим напряжение на этих резисторах и используем это, чтобы найти напряжение на этих резисторах. параллельная комбинация:
\начать{выравнивать*} V & = ИК \\ & = (\текст{1,63})(\текст{3,02}) \\ & = \текст{4,92}\текст{В} \конец{выравнивание*} \начать{выравнивать*} V_{T} & = V_{1} + V_{p} \\ V_{p} & = V_{T} — V_{1} \\ & = \текст{6} — \текст{4,92} \\ & = \текст{1,08}\текст{В} \конец{выравнивание*}
Это напряжение на каждом из параллельных резисторов.
 Таким образом, мы можем найти силу
рассеивается каждым из этих резисторов: 9{2}}{\текст{3}} \\
& = \текст{3,5}\текст{W}
\конец{выравнивание*}
Таким образом, мы можем найти силу
рассеивается каждым из этих резисторов: 9{2}}{\текст{3}} \\
& = \текст{3,5}\текст{W}
\конец{выравнивание*}ток \(I\) через ячейку.
Мы можем найти эквивалентное параллельное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{1} + \frac{1}{5} + \frac{1}{3} \\ & = \ гидроразрыва {23} {15} \\ R_{p} & = \text{0,65217}\ldots\text{ Ом} \конец{выравнивание*}
Теперь мы можем найти эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{4} + R_{p} \\ & = \text{2} + \text{0,65217}\ldots \\ & = \text{2,65217}\ldots\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать общий ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{7}{\text{2,65217}\ldots} \\ & = \текст{263934}\ldots\text{ А} \\ & \ приблизительно \ текст {2,64 А} \конец{выравнивание*}
ток через резистор \(\text{5}\) \(\Omega\)
Для последовательной цепи общий ток равен току в каждом из резисторов.
 Поскольку мы можем рассматривать полную параллельную комбинацию как одно последовательное соединение,
ток через соединение равен \(\text{2,64}\) \(\text{A}\).
Поскольку мы можем рассматривать полную параллельную комбинацию как одно последовательное соединение,
ток через соединение равен \(\text{2,64}\) \(\text{A}\).Используя это и общее параллельное сопротивление, мы можем рассчитать напряжение на каждом резистор:
\начать{выравнивать*} V & = ИК \\ & = (\text{2,63934}\ldots)(\text{0,65217}\ldots) \\ & = \text{1,72131}\ldots\text{V} \конец{выравнивание*}
Теперь мы можем рассчитать ток через резистор \(\text{5}\) \(\Omega\):
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{\text{1,72131}\ldots}{\text{5}} \\ & = \text{0,34426}\ldots\text{A} \\ & \ приблизительно \ текст {0,34 А} \конец{выравнивание*}
мощность, рассеиваемая на резисторе \(\text{5}\) \(\Omega\)
Мы знаем сопротивление, напряжение и ток этого резистора, поэтому можем использовать любой два из них, чтобы найти силу.
 Мы будем использовать сопротивление и ток: 9{2}(\текст{5}) \\
& = \text{0,59258}\ldots\text{W} \\
& \ приблизительно \ текст {0,59 Вт}
\конец{выравнивание*}
Мы будем использовать сопротивление и ток: 9{2}(\текст{5}) \\
& = \text{0,59258}\ldots\text{W} \\
& \ приблизительно \ текст {0,59 Вт}
\конец{выравнивание*}Если ток, протекающий через ячейку, равен \(\text{2}\) \(\text{A}\) и все резисторы омический, рассчитайте мощность, рассеиваемую на каждом из резисторов, \(R_1\), \(R_2\) и \(R_3\) соответственно.
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{4} + \frac{1}{2} \\ & = \фракция{3}{4}\\ R_{p} & = \text{1,33}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть цепь с двумя последовательно соединенными резисторами, поэтому мы можем рассчитать эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{p} \\ & = \текст{4,66} + \текст{1,33} \\ & = \text{5,99}\text{Ом} \конец{выравнивание*}
Нам дан общий ток и это ток в последовательном резисторе и через полное параллельное соединение.
 Используя это, мы можем найти мощность, рассеиваемую в серии
резистор: 9{2}(\текст{4,66}) \\
& = \text{18,64}\text{W}
\конец{выравнивание*}
Используя это, мы можем найти мощность, рассеиваемую в серии
резистор: 9{2}(\текст{4,66}) \\
& = \text{18,64}\text{W}
\конец{выравнивание*}Далее находим напряжение на этом резисторе:
\начать{выравнивать*} V & = ИК \\ & = (\текст{2})(\текст{4,66}) \\ & = \текст{9,32}\текст{В} \конец{выравнивание*}
И мы используем общее сопротивление и общий ток, чтобы найти общее напряжение:
\начать{выравнивать*} V & = ИК \\ & = (\текст{2})(\текст{5,99}) \\ & = \текст{12}\текст{В} \конец{выравнивание*}
Теперь мы можем найти напряжение на параллельной комбинации резисторов:
\начать{выравнивать*} V_{T} & = V_{1} + V_{p} \\ V_{p} & = V_{T} — V_{1} \\ & = \текст{12} — \текст{9{2}}{\текст{2}} \\ & = \текст{5,36}\текст{W} \конец{выравнивание*}
Электроэнергия (ESBQG)
temp textКогда мощность рассеивается в устройстве, происходит передача энергии от одного вида к другому.
 Например,
резистор может сильно нагреваться, что указывает на то, что энергия рассеивается в виде тепла. Власть была
скорость, с которой была совершена работа, скорость, с которой передается энергия. Если мы хотим вычислить общую
количество энергии, которое нам нужно, чтобы умножить скорость передачи энергии на время, в течение которого эта энергия
передача состоялась.
Например,
резистор может сильно нагреваться, что указывает на то, что энергия рассеивается в виде тепла. Власть была
скорость, с которой была совершена работа, скорость, с которой передается энергия. Если мы хотим вычислить общую
количество энергии, которое нам нужно, чтобы умножить скорость передачи энергии на время, в течение которого эта энергия
передача состоялась.Электрическая энергия — это просто мощность, умноженная на время. Математически пишем: \[E = P \times t\] Энергия измеряется в джоулях (Дж) и время в секундах (с).
Рабочий пример 12: Электрическая энергия
\(\text{30}\) \(\text{W}\) лампочка остается включенной на \(\text{8}\) часов на ночь, сколько энергия была потрачена впустую?
Что требуется
Нам нужно определить общее количество электрической энергии, рассеиваемой лампочкой.
 Мы знаем
отношения между силой и энергией, и нам дано время. Время не указано в
правильные единицы, поэтому нам сначала нужно преобразовать в единицы СИ:
\начать{выравнивать*}
\text{8}\text{ ч}&= 8 \times \text{3 600}\text{ с} \\
&=\текст{28 800}\текст{с}
\end{выравнивание*}
Мы знаем
отношения между силой и энергией, и нам дано время. Время не указано в
правильные единицы, поэтому нам сначала нужно преобразовать в единицы СИ:
\начать{выравнивать*}
\text{8}\text{ ч}&= 8 \times \text{3 600}\text{ с} \\
&=\текст{28 800}\текст{с}
\end{выравнивание*}Рассчитайте энергию
Мы знаем, что: \начать{выравнивать*} Е&=Пт \\ &=(\текст{30})(\текст{28 800})\\ &=\текст{864 000}\текст{J} \конец{выравнивание*}
Рабочий пример 13: Электрическая энергия
Изучите электрическую схему ниже:
Сопротивление резистора равно \(\text{27}\) \(\text{Ом}\) и ток, протекающий через резистор \(\text{3,3}\) \(\text{A}\).
 Какая мощность резистора и сколько
энергия рассеивается в \(\text{35}\) \(\text{s}\)? 92 \раз \текст{27} \\
&= \текст{294,03}\текст{W}
\end{align*}
Какая мощность резистора и сколько
энергия рассеивается в \(\text{35}\) \(\text{s}\)? 92 \раз \текст{27} \\
&= \текст{294,03}\текст{W}
\end{align*}Теперь, когда мы определили мощность, мы можем вычислить энергию:
\начать{выравнивать*} Е &= Пт \\ &= (\текст{294,03})(\текст{35}) \\ &= \text{10 291,05 Дж} \конец{выравнивание*}
Напишите окончательный ответ
Мощность резистора \(\text{294,03}\) \(\text{W}\) и \(\text{10 291,05}\) \(\text{J}\) рассеиваются.
Электричество продается в единицах, равных одному киловатт-часу (\(\text{кВтч}\)). Киловатт-час — это просто использование \(\text{1}\) \(\text{кВт}\) для \(\text{1}\) \(\text{hr}\). Используя это, вы можете точно определить сколько электроэнергии будут потреблять различные приборы и сколько это будет стоить вам.

Рабочий пример 14: Стоимость электроэнергии
Сколько стоит запустить \(\text{900}\) \(\text{W}\) микроволновую печь для \(\text{2,5}\) \(\text{минут}\), если стоимость электроэнергии составляет \(\text{61,6}\) \(\text{c}\) за \(\текст{кВтч}\)?
Что требуется
Нам сообщают детали устройства, использующего электрическую энергию, и цену электроэнергии. Учитывая определенное количество времени использования, нам нужно определить, сколько энергии было использовано и какая. стоимость этого будет.
Различные количества указаны в разных единицах измерения. Нам нужно использовать последовательные единицы, чтобы получить ответ, который имеет смысл.
Микроволновая печь указана в \(\text{Вт}\), но мы можем преобразовать в \(\text{кВт}\):\(\text{900}\text{ Вт}=\текст{0,9}\текст{кВт}\).
временный текст {-\text{2}}\text{h}\). 9{-\text{2}}\text{кВтч} \\
&=\текст{2,31}\текст{с}
\конец{выравнивание*}
{-\text{2}}\text{h}\). 9{-\text{2}}\text{кВтч} \\
&=\текст{2,31}\текст{с}
\конец{выравнивание*}Использование электричества
В следующей таблице указана стоимость электроэнергии для пользователей, потребляющих менее \(\text{450}\) \(\text{кВтч}\) в среднем в месяц.
Единицы (\(\text{кВтч}\)) Стоимость за единицу (\(\text{c}\)) \(\text{0}\)–\(\text{150}\) \(\текст{61,60}\) \(\text{150}\)–\(\text{350}\) \(\текст{81,04}\) \(\text{350}\)–\(\text{600}\) \(\текст{107,43}\) \(>\) \(\text{600}\) \(\текст{118,06}\) Вам предоставлены следующие электроприборы с их номинальной мощностью.

Прибор Номинальная мощность Плита \(\text{3 600}\) \(\text{W}\) Микроволновая печь \(\text{1 200}\) \(\text{W}\) Стиральная машина \(\text{2 200}\) \(\text{W}\) Чайник \(\text{2 200}\) \(\text{W}\) Холодильник \(\текст{230}\) \(\текст{W}\) Тостер \(\текст{750}\) \(\текст{W}\) Глобус энергосбережения \(\текст{40}\) \(\текст{W}\) Лампочка \(\текст{120}\) \(\текст{W}\) Пылесос \(\text{1 600}\) \(\text{W}\) У вас есть \(\text{R}\,\text{150,00}\) ежемесячные расходы на электроэнергию.

К какому классу использования вы относитесь?
Заполните следующую таблицу.
Прибор Стоимость работы за 1 час Плита Микроволновая печь Стиральная машина Чайник Холодильник Тостер Глобус энергосбережения Пылесос Как долго вы можете использовать каждое устройство, чтобы гарантировать, что вы тратите меньше \(\text{R}\,\text{150,00}\) в месяц? Предположим, вы используете не более 20 энергосберегающих глобусы вокруг вашего дома.

Предыдущий
11.2 Закон Ома
Оглавление Следующий
11.4 Краткое содержание главы
схема, схема, расчет, разветвленные и линейные схемы
При обустройстве новой квартиры или дома, ремонте или ремонте жилья приходится иметь дело с элементами, рассчитанными на прохождение электрического тока. Важно знать, что такое электрическая цепь, из чего она состоит, зачем нужна схема и какие расчеты необходимо произвести.
Содержание
- Что такое электрические цепи
- Основные компоненты
- Классификация цепей
- Разветвленные и неразветвленные
- Линейные и нелинейные
- Обозначения элементов на схеме
- Трехфазные электрические цепи
- Законы, действующие в электрических цепях
- Как рассчитываются электрические цепи 7 90 Что такое электрические цепи Электрической цепью называется совокупность устройств, необходимых для прохождения через них электрического тока.
- Первичные источники электрической энергии и сигналов могут преобразовывать неэлектромагнитную энергию в электрическую. Например, гальванический элемент, аккумулятор, электромеханический генератор.
- Вторичный тип как на входе, так и на выходе имеет электрическую энергию. Меняются только его параметры — напряжение и ток, их форма, величина и частота. Примером могут служить выпрямители, инверторы, трансформаторы.
- Потребители активной энергии преобразуют электрический ток в освещение или тепло. Это электротермические приборы, лампы, резисторы, электродвигатели.

- Вспомогательные компоненты включают коммутационные устройства, измерительные устройства, соединительные элементы и провод.
- Функционал имеет минимальную детализацию. Основные функции узлов представлены прямоугольником с буквенными обозначениями.
- На принципиальной схеме подробно показана конструкция используемых элементов, а также их соединения и контакты. Необходимые параметры могут быть отображены непосредственно на схеме или в отдельном документе. Если указана только часть установки, это однолинейная схема, когда указаны все элементы — полная.

- На электрической схеме используются условные обозначения элементов, их расположение, способ установки и последовательность.
- экономичность производства и транспортировки электроэнергии по сравнению с однофазной системой;
- простая генерация магнитного поля, необходимая для работы трехфазного асинхронного электродвигателя;
- одна и та же генераторная установка выдает два рабочих напряжения — линейное и фазное.

- Закон Ома для прямого участка цепи, определяющий связь между электродвижущей силой, напряжением источника при токе, протекающем в проводнике, и сопротивлением самого проводника.

- Для нахождения всех токов и напряжений используются правила Кирхгофа, действующие между токами и напряжениями любой части электрической цепи.
- Закон Джоуля-Ленца количественно определяет тепловой эффект электрического тока.
- метод, основанный на законе Ома и правилах Кирхгофа;
- метод определения контурных токов;
- прием эквивалентных преобразований;
- Метод измерения сопротивления защитных проводников;
- расчет узловых потенциалов;
- метод идентичного генератора и другие.

- Электрический заряд измеряется в кулонах; символ для кулон C.
- Электрический ток измеряется в амперах; символ для ампер A.
- Один ампер равен одному кулону прохождения точки на проводе за одну секунду.
- Мы можем рассчитать ток, 𝐼, используя формулу 𝐼=𝑄𝑡, где 𝑄 представляет собой количество заряда, проходящего через точку за время, 𝑡.

Электрическая цепь представляет собой комплекс различных элементов, связанных между собой. Он предназначен для протекания электрического тока, где возникают переходные процессы. Движение электронов обеспечивается наличием разности потенциалов и может быть описано с помощью таких терминов, как напряжение и ток.
Внутренняя цепь обеспечивается подключением напряжения в качестве источника питания. Остальные элементы образуют внешнюю сеть. Для движения зарядов в источнике питания поля потребуется внешняя сила. Это может быть обмотка генератора, трансформатора или гальванического источника.
Для правильной работы такой системы ее цепь должна быть замкнута, иначе ток не пойдет. Это обязательное условие согласованной работы всех устройств. Не всякая цепь может быть электрической цепью. Например, линии заземления или защиты не являются таковыми, потому что по ним нормально не протекает ток. Их можно назвать электрическими по принципу действия. В аварийной ситуации через них проходит ток, и цепь замыкается, уходя в землю.

В зависимости от источника питания напряжение в цепи может быть постоянным или переменным. Батарея ячеек обеспечивает постоянное напряжение, а обмотки генераторов или трансформаторов — переменное.
Основные компоненты
Изобретатель электрического токаВсе компоненты цепи участвуют в одном электромагнитном процессе. Их условно делят на три группы.
Основой электрической сети является схема. Это графический рисунок, который содержит условные изображения и обозначения элементов и их соединения. Выполняются по ГОСТ 2.721-74 — 2.758-81
Простейшая линейная схема включает гальванический элемент. С помощью проводов к нему через выключатель подключается лампа накаливания. Для измерения тока и напряжения в него включены вольтметр и амперметр.
Классификация цепей
Электрические цепи классифицируют по виду сложности: простые (неразветвленные) и сложные (разветвленные). Различают цепи постоянного и переменного тока, а также синусоидальные и несинусоидальные. По характеру элементов они бывают линейными и нелинейными. Линии переменного тока могут быть однофазными и трехфазными.
Разветвленная и неразветвленная
Во всех элементах неразветвленной цепи протекает одинаковый ток.
 Простейшая разветвленная линия включает три ответвления и два узла. Каждая ветка имеет свой ток. Ветвь определяется как участок цепи, образованный последовательно соединенными элементами, заключенными между двумя узлами. Узел — это точка, в которой сходятся три ветви.
Простейшая разветвленная линия включает три ответвления и два узла. Каждая ветка имеет свой ток. Ветвь определяется как участок цепи, образованный последовательно соединенными элементами, заключенными между двумя узлами. Узел — это точка, в которой сходятся три ветви.Если на схеме поставить точку на пересечении двух прямых, то в этом месте имеется электрическое соединение двух линий. Если узел не отмечен, цепочка не разветвлена.
Линейная и нелинейная
Электрическая цепь, в которой потребители не зависят от величины напряжения и направления токов, а все составляющие линейны, называется линейной. К элементам такой схемы относятся зависимые и независимые источники токов и напряжений. В линейном сопротивление элемента не зависит от силы тока, например, электропечи.
В нелинейных пассивные элементы зависят от значений направления токов и напряжений, имеют хотя бы один нелинейный элемент. Например, на сопротивление лампы накаливания влияют скачки напряжения и скачки тока.

Обозначения элементов на схеме
Прежде чем приступить к монтажу оборудования, необходимо изучить нормативные сопроводительные документы. Схема позволяет донести до пользователя полные характеристики изделия с помощью буквенных и графических обозначений, внесенных в единый реестр конструкторской документации.
К чертежу прилагаются дополнительные документы. Их список может быть указан в алфавитном порядке с цифровой сортировкой на самом чертеже, либо на отдельном листе. Классифицируются десять типов цепей; в электротехнике обычно используют три основные схемы.
Для чтения электрических схем необходимо знать условные графические символы. Провода, соединяющие элементы, показаны линиями. Сплошная линия – это общее обозначение проводки. Над ним могут быть указаны данные о способе прокладки, материале, напряжении, силе тока. На однолинейной схеме группа проводников показана пунктирной линией. В начале и в конце укажите маркировку провода и место его присоединения.Вертикальные насечки на проводной линии указывают количество проводов. Если их больше трех, выполняется цифровое обозначение. Штриховой линией обозначены цепи управления, сеть охраны, эвакуации, аварийного освещения.
Переключатель на схеме выглядит как круг с линией, наклоненной вправо. По типу и количеству черточек определяются параметры устройства.
Кроме основных чертежей есть схемы замещения.

Трехфазные электрические цепи
Трехфазные цепи в работеСреди электрических цепей распространены как однофазные, так и многофазные системы. Каждая часть многофазной цепи характеризуется одним и тем же значением тока и называется фазой. В электротехнике различают два понятия этого термина. Первый является непосредственным компонентом трехфазной системы. Второе значение изменяется синусоидально.
Трехфазная цепь — одна из многофазных систем переменного тока, где действуют синусоидальные ЭДС (электродвижущая сила) одной частоты, сдвинутые во времени относительно друг друга на определенный фазовый угол. Он образован обмотками трехфазного генератора, тремя энергоприемниками и соединительными проводами.
Такие схемы служат для обеспечения производства электрической энергии, для ее передачи, распределения и имеют следующие преимущества:
Трехфазная система выгодна при передаче электроэнергии на большие расстояния. Кроме того, расход материалов значительно ниже, чем у однофазных. Основными потребителями являются трансформаторы, асинхронные электродвигатели, преобразователи, индукционные печи, мощные тепловые и электрические установки. Среди однофазных маломощных устройств можно отметить электроинструмент, лампы накаливания, бытовую технику, блоки питания.Трехфазная схема отличается значительной сбалансированностью системы. Способы соединения фаз получили структуру «звезда» и «треугольник». Обычно фазы генерирующих электрических машин соединяют «звездой», а фазы потребителей — «звездой» и «треугольником».
Законы, действующие в электрических цепях
На схемах направление токов указано стрелками. Для расчета нужно взять направления по напряжениям, токам, ЭДС. При расчетах в электротехнике используются следующие основные законы:
В цепях постоянного тока направление действия электродвижущей силы указывается от отрицательного потенциала к положительному. Направление принимается за движение положительных зарядов. В этом случае стрелка направлена от более высокого потенциала к более низкому. Напряжение всегда направлено в том же направлении, что и ток.
В синусоидальных цепях ЭДС напряжение и ток указывают с помощью полупериода тока, при этом он не меняет своего направления. Чтобы подчеркнуть разницу потенциалов, их обозначают знаками «+» и «-».
Как рассчитывают электрические цепи
Путь расчета делится на множество способов, которые используются на практике:
Основой расчета простой электрической цепи по закону Ома является определение силы тока на отдельном участке при известном сопротивлении проводников и заданном напряжении.
По условию задачи известны сопротивления резисторов R1, R2, R3, R4, R5, R6, включенных в цепь (без учета сопротивления амперметра). Необходимо рассчитать силу токов J1, J2… J6.
На схеме есть три последовательных участка. Более того, второй и третий имеют разветвления. Сопротивления этих участков будем обозначать как R1, R’, R». Тогда общее сопротивление равно сумме сопротивлений:
R = R1 + R’+ R» , где
R’ — суммарное сопротивление параллельно соединенных резисторов R2, R3, R4.
R» — суммарное сопротивление резисторов R5 и R6 .
Используя закон параллельного соединения, вычисляем сопротивление R’ и R». /R5+1/R6
Для определения силы тока в неразветвленной цепи, зная полное сопротивление при заданном напряжении, можно воспользоваться следующей формулой:
I = U / R, затем I = I1
Для расчета силы тока в отдельных ветвях необходимо определить напряжения на участках последовательных цепей по закону Ома:
U1 = IR1; U2 = ИК’; U3 = IR»;
Зная напряжение конкретных участков, можно рассчитать силу тока на отдельных ответвлениях:
I2 = U2/R2; I3 = U2/R3; I4 = U2/R4; I5 = U3/ R5;I6 = U3/R6
Иногда необходимо узнать сопротивление участков по известным параметрам напряжения, силы тока, сопротивления других участков или произвести расчет напряжения по имеющимся данным сопротивления и силы тока
Основная часть методик направлена на упрощение расчетов.
 Это достигается адаптацией системы уравнений или самой схемы. Расчет электрических цепей производят различными способами в зависимости от класса их сложности.
Это достигается адаптацией системы уравнений или самой схемы. Расчет электрических цепей производят различными способами в зависимости от класса их сложности.Объяснение урока: Расчет силы тока в проводе
В этом объяснении мы научимся рассчитывать силу тока в простой цепи.
Цепь — это путь, по которому может протекать электрический заряд.
Электрический заряд измеряется в кулонах. Символ единицы для кулона С; например, заряд электрона выражается как −1,6×10 C.
Поток электрического заряда представляет собой электрический ток. Электрический ток измеряется в единицах «ампер». Символ единицы для ампер A.
Кулоны и ампер обычно используются, когда изучая электричество, и важно помнить, что они измеряют разные вещи.
 кулон измеряет заряд, а
ампер измеряет поток бесплатно.
кулон измеряет заряд, а
ампер измеряет поток бесплатно.Один ампер тока равен один кулон заряда, проходящего через точку провода в одна секунда. Мы можем измерить, сколько заряда проходит в течение любого промежутка времени — это не должно быть только одна секунда. Мы просто находим ток, разделив сумма заряда по времени, за которое был измерен заряд.
Ток можно рассчитать по формуле 𝐼=𝑄𝑡, где 𝐼 представляет ток, 𝑄 представляет заряд, а 𝑡 представляет время.
Определение: электрический ток в проводе
Электрический ток 𝐼 в проводе можно найти по формуле 𝐼=𝑄𝑡, где 𝑄 представляет собой количество заряда, которое проходит через точку провода в течение некоторого времени, 𝑡.
Мы можем попрактиковаться в использовании этого уравнения на нескольких примерах.
Пример 1: расчет потока заряда при заданном токе
На схеме показана электрическая цепь, состоящая из элемента и лампочки.
 Ток в цепи равен
2 ампера. Сколько зарядов проходит мимо точки
P в цепи за 1 секунду?
Ток в цепи равен
2 ампера. Сколько зарядов проходит мимо точки
P в цепи за 1 секунду?Ответ
Напомним, что один ампер тока определяется как один кулон заряда, проходящего через точку за одну секунду.
Нам говорят, что сила тока в цепи равна 2 А.
Следовательно, мы знаем, что через точку проходит 2 кулона заряда П за 1 секунду.
Пример 2: Сравнение токов в нескольких цепях
Fares устанавливает три цепи. Он измеряет, сколько заряда проходит через каждую цепь за то же время. Его результаты представлены в следующей таблице.
Charge Time Circuit 1 20 coulombs 5 seconds Circuit 2 25 coulombs 5 seconds Circuit 3 12 coulombs 5 секунд Какая цепь имеет наибольший ток?
Ответ
Напомним, что ток можно найти по формуле 𝐼=𝑄𝑡, где 𝐼 — ток, 𝑄 — заряд, а 𝑡 — время.

Мы подставим значения из таблицы в приведенное выше уравнение для расчета текущих значений 𝐼, 𝐼 и 𝐼. Нижние индексы 1, 2 и 3 указывают, для какой цепи измеряется ток.
Подставляя в схему 1 измерения заряда и времени, имеем 𝐼=205=4.CsA
Следовательно, сила тока в цепи 1 составляет 4 ампера.
Переходя к схеме 2, мы имеем 𝐼=255=5.CsA
Ток в цепи 2 составляет 5 ампер.
Для контура 3, 𝐼=125=2,4.CsA
Значит, сила тока в цепи 3 составляет 2,4 ампера.
Следовательно, цепь 2 имеет наибольший ток.
Пример 3: Сравнение токов в нескольких цепях
На схеме показаны две цепи, цепь 1 и цепь 2. В цепи 1, Через лампочку протекает заряд 28 Кл. 14 секунд. В цепи 2, Через зуммер проходит заряд 9 кул. 3 секунды. В какой цепи сила тока больше?
Ответ
Мы хотим сравнить ток в двух разных цепях. Напомним формулу расчета тока, 𝐼=𝑄𝑡, где 𝐼 — ток, 𝑄 — заряд, а 𝑡 — время.
 Мы можем найти ток в цепях, подставив данные количества заряда и времени для каждой цепи в
это уравнение.
Мы можем найти ток в цепях, подставив данные количества заряда и времени для каждой цепи в
это уравнение.Для контура 1 имеем 𝐼=2814=2.CsA
Итак, мы нашли, что сила тока в цепи 1 составляет 2 ампера.
Для контура 2 имеем 𝐼=93=3.CsA
Ток в цепи 2 составляет 3 ампера.
Следовательно, ток больше в цепи 2 .
Пример 4: Зависимость между током и количеством заряда, движущегося в цепи
На схеме показана электрическая цепь, содержащая элемент и лампочку. Количество заряда, протекающего мимо точки P в одну секунду 12 кулонов. Если количество заряда, протекающего мимо точки P за одну секунду должны были удвоиться, на во сколько раз изменится сила тока в цепи?
Ответ
Мы хотим понять, как удвоение количества заряда, протекающего через точку, влияет на ток в цепи. мы можем начать вспомнив формулу тока, 𝐼=𝑄𝑡, где 𝐼 — ток, 𝑄 — заряд, а 𝑡 — время.
 Мы будем
используйте эту формулу, чтобы найти два текущих значения, которые мы будем называть 𝐼o и 𝐼d.
нижние индексы o и d указывают на схему с исходным или удвоил сумму заряда.
Мы будем
используйте эту формулу, чтобы найти два текущих значения, которые мы будем называть 𝐼o и 𝐼d.
нижние индексы o и d указывают на схему с исходным или удвоил сумму заряда.Чтобы рассчитать первоначальную величину тока, мы имеем 𝐼=121=12,oCsA поэтому ток изначально 12 ампер.
После удвоения количества заряда получается 24 кулона прохождение точки P за одну секунду. Подставляя это в уравнение, мы имеем 𝐼=241=24.dCsA
После удвоения заряда ток 24 ампера.
Таким образом, увеличение точки прохождения заряда P в одна секунда в 2 раза увеличивает ток до увеличить на а коэффициент 2 .
Пример 5: Понимание электрического тока в цепи
Объясните, что подразумевается под фразой электрический ток в цепи .
Ответ
Нас попросили написать краткое описание электрического тока в цепи. Для начала вспомним, что электрический ток это движение электрического заряда.
 Ток измеряет, насколько быстро заряд проходит через что-либо.
Ток измеряет, насколько быстро заряд проходит через что-либо.В цепи мы видим отрицательно заряженные электроны, движущиеся по проводу. Мы смотрим на одну точку провода, чтобы измерить его ток.
Давайте закончим резюмированием некоторых важных понятий.
Ключевые положения
| Формула электроэнергии в цепях постоянного и переменного тока
Мы используем электроэнергию, предоставляемую нашей коммунальной компанией, для обеспечения нас светом, теплом, работающими приборами и т.
 д. Поскольку электрический потенциал (напряжение) и ток являются двумя величинами, доступными нам, когда коммунальная служба поставляет электрическую энергию, эти два параметра являются основными параметрами, определяющими электрическую мощность. В этом руководстве давайте подробно рассмотрим электрическую мощность, формулу электрической мощности в цепях переменного и постоянного тока.
д. Поскольку электрический потенциал (напряжение) и ток являются двумя величинами, доступными нам, когда коммунальная служба поставляет электрическую энергию, эти два параметра являются основными параметрами, определяющими электрическую мощность. В этом руководстве давайте подробно рассмотрим электрическую мощность, формулу электрической мощности в цепях переменного и постоянного тока.Краткое описание
Что такое электроэнергия?
Электрическая энергия является одной из широко используемых форм энергии в нашей повседневной жизни, будь то питание от сети переменного тока или батареи. Наша коммунальная компания поставляет эту электрическую энергию в виде электрического потенциала и тока, а скорость, с которой электрическая энергия передается в электрической цепи, называется электрической мощностью.
С точки зрения физики, Энергия — это способность выполнять Работу, а скорость выполнения этой Работы известна как Сила.
Итак, если P — мощность, W — работа, а t — время, то
Power P = работа, выполненная в единицу времени = W/t
Единицами мощности являются ватты.

Мы знаем, что электрический потенциал — это количество работы, совершаемой при перемещении единичного заряда, а ток — это скорость движения заряда.
Используя приведенное выше утверждение, мы можем переписать предыдущее уравнение мощности как:
P = Вт/т = (Вт/Q) × (Q/т) Вт
Первый член (Вт/Q) представляет электрический потенциал (V), а второй член (Q/t) представляет ток (I).
Итак, электрическая мощность P = V × I.
Формула электрической мощности в цепях переменного и постоянного тока
В зависимости от типа тока в цепи, т. е. переменного тока или постоянного тока, электрическая мощность может быть дополнительно классифицирована на переменный ток Мощность и мощность постоянного тока.
Давайте теперь посмотрим на различные формулы электроэнергии в цепях постоянного и переменного тока.
Формулы мощности в цепях постоянного тока
В простых цепях постоянного тока, т. е. электрических цепях с источником питания постоянного тока, формула мощности приведена ниже:
P = V × I
Мощность в резистивных цепях постоянного тока — это просто произведение напряжения и тока.

Дальнейшие формулы мощности можно вывести, применяя закон Ома. Согласно закону Ома, напряжение в цепи (или компоненте) является произведением сопротивления и тока.
V = I × R
Итак, если мы используем это уравнение в приведенной выше формуле мощности, мы получим
P = V × (V/R) = V 2 /R
P = (I×R ) × I = I 2 R
В зависимости от имеющихся величин можно использовать одну из трех формул мощности для расчета мощности постоянного тока.
Формулы мощности в цепях переменного тока
Измерить мощность в цепях постоянного тока очень просто, так как все, что вам нужно сделать, это умножить напряжение и силу тока. Но то же самое невозможно в цепях переменного тока, поскольку значения напряжения и тока постоянно меняются как по величине, так и по направлению (знаку).
Значения переменного напряжения и тока обычно записываются как
В Переменный ток = В P × sin(ωt) и I Переменный ток = I P × sin(ωt)
Чтобы рассчитать мощность переменного тока, мы должны каким-то образом рассчитать средние значения напряжения и тока.
 Математически мы используем среднеквадратичное значение или среднеквадратичное значение для определения средних значений синусоидальных функций.
Математически мы используем среднеквадратичное значение или среднеквадратичное значение для определения средних значений синусоидальных функций.Если V RMS — это среднеквадратичное значение напряжения переменного тока, а I RMS — это среднеквадратичное значение переменного тока, тогда средняя мощность переменного тока равна
P AC (среднее значение) = V RMS × I RMS
Если f(t) является функцией времени t, то ее среднеквадратичное значение равно
Applying the above formula to our alternating voltage and current sinusoidal values, we get:
V RMS = V P /√2 and I RMS = I P /√ 2
Мощность, которую мы рассчитали ранее (P AC (Average)) на самом деле известна как полная мощность. Это не что иное, как произведение среднего (или эффективного) напряжения и тока, т. Е. Это максимальная средняя мощность, подаваемая на чисто резистивную нагрузку.

Но катушки индуктивности и конденсаторы имеют фазовые сдвиги и реактивное сопротивление. Итак, с катушками индуктивности и конденсаторами есть еще два способа определить мощность в цепях переменного тока. Это реальная мощность (активная мощность) и реактивная мощность.
Реальная мощность, также известная как активная мощность, представляет собой мощность, рассеиваемую в цепи из-за ее резистивных элементов.
Активная мощность = В СКЗ × I СКЗ × cos(θ), где θ — фазовый угол, на который напряжение опережает ток.
Реактивная мощность — это мощность, рассеиваемая в цепи за счет индуктивности и емкости (или реактивного сопротивления).
Задается как реактивная мощность = V RMS × I RMS × sin(θ)
Таким образом, мы можем сказать, что (полная мощность) 2 = (активная мощность) 2 + (реактивная мощность ) 2
Формулы мощности постоянного и переменного тока
В следующей таблице перечислены все формулы мощности для цепей переменного и постоянного тока.

Цепь Мощность DC Р = В × I Р = В 2 /Р P = I 2 × R Фактическая мощность однофазного переменного тока ½ В P × I P × cos(θ) = V СКЗ × I СКЗ × cos(θ) Однофазная реактивная мощность переменного тока ½ В P × I P × sin(θ) = V СКЗ × I СКЗ × sin(θ) Реальная мощность трехфазного переменного тока 3 × V L-N × I L-N × cos(θ) = √3 × V L-L × I L-L × cos(θ) Реактивная мощность трехфазного переменного тока 3 × V L-N × I L-N × sin(θ) = √3 × V L-L × I L-L × sin(θ) Заключение
Простое руководство по изучению электроэнергии.





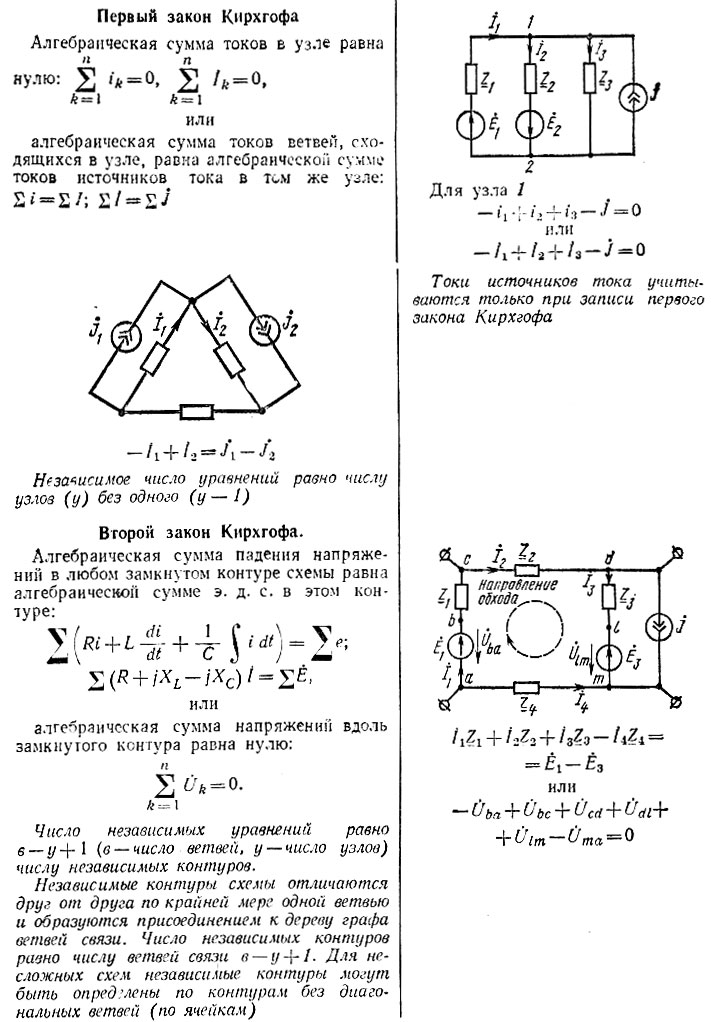 Метод базируется на первом законе Кирхгофа;
Метод базируется на первом законе Кирхгофа; Осталось только написать ответ.
Осталось только написать ответ.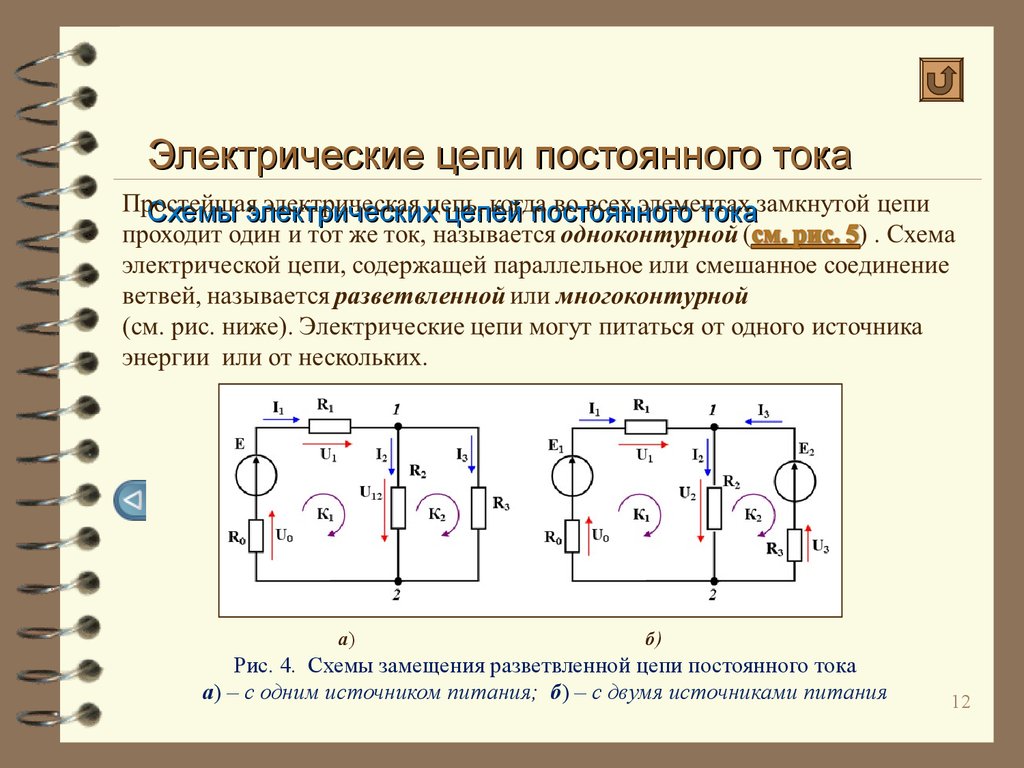 Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.
Если в процессе алгебраических операций появляются столбцы с одинаковыми элементами, то эти столбцы удаляются.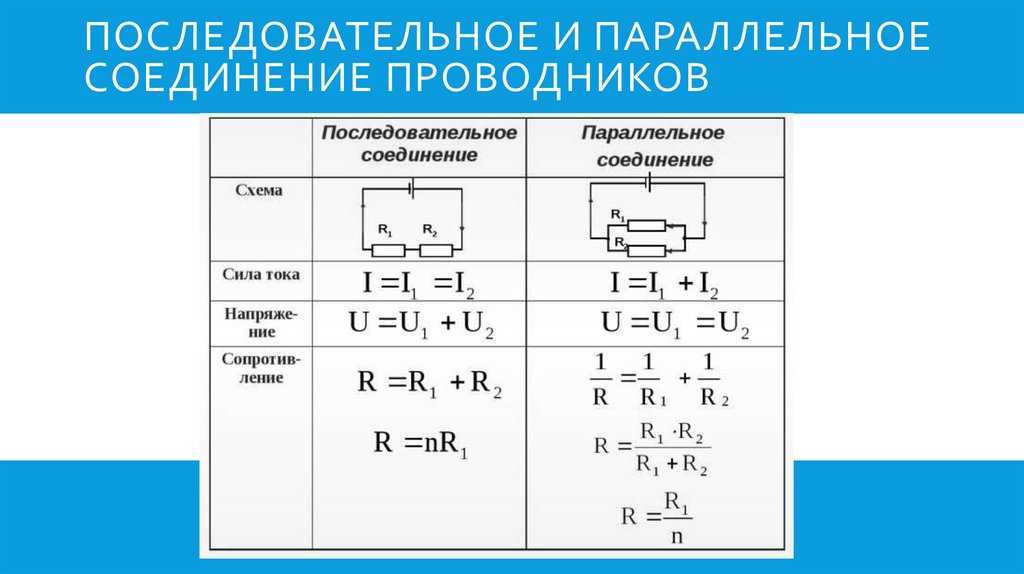 Стрелками обозначено направление тока (которое мы приняли за положительное)
Стрелками обозначено направление тока (которое мы приняли за положительное)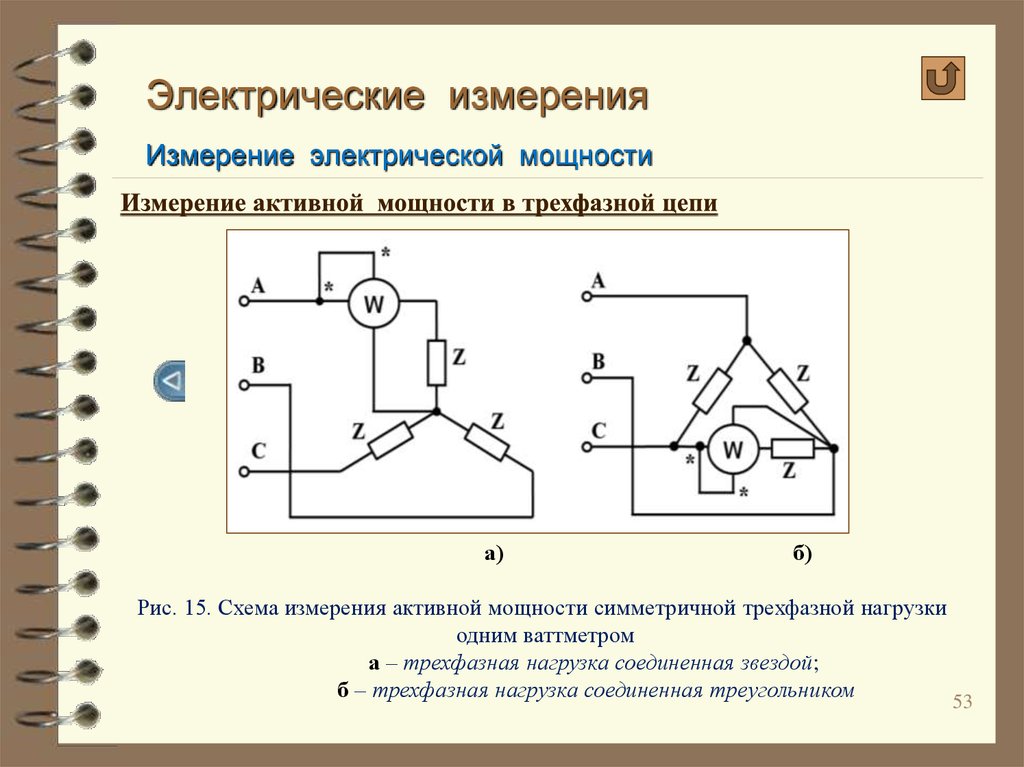 То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).
То есть, не строго говоря, это строка, состоящая из индексов ребер (для данной вершины).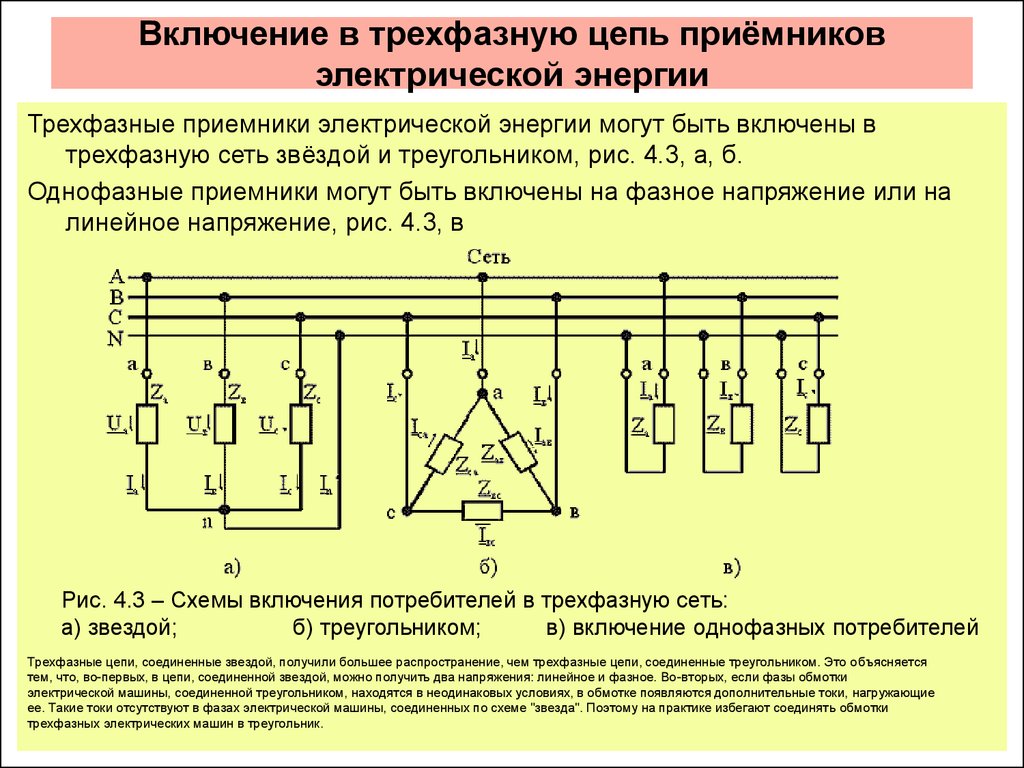
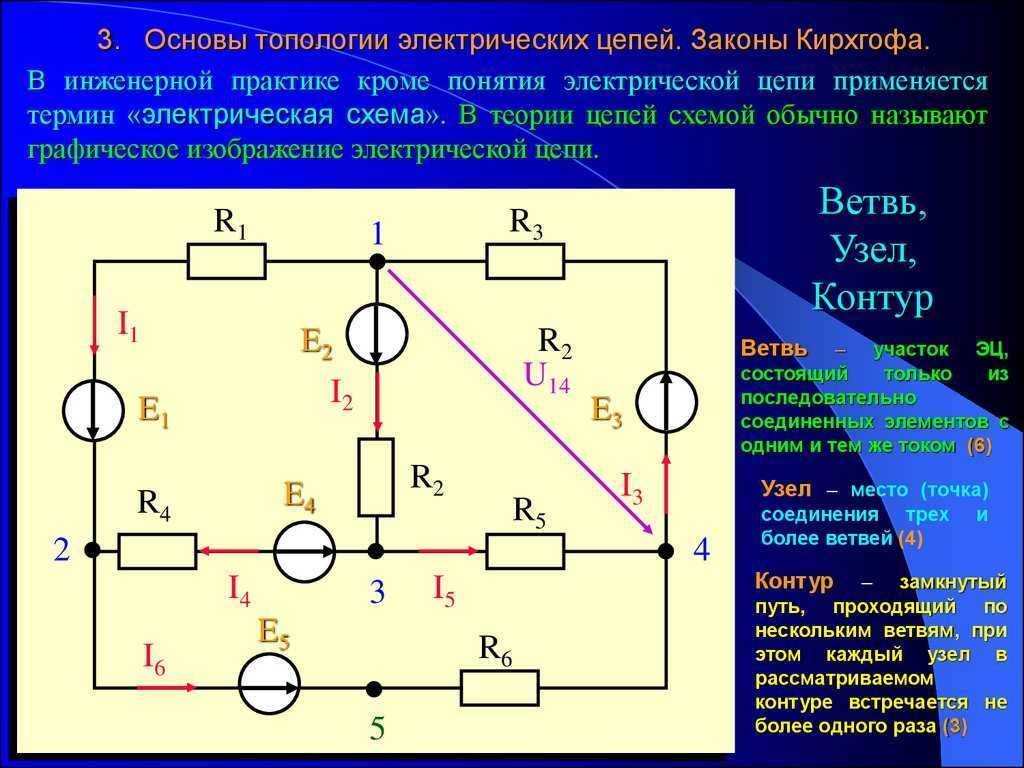 Получаем
Получаем

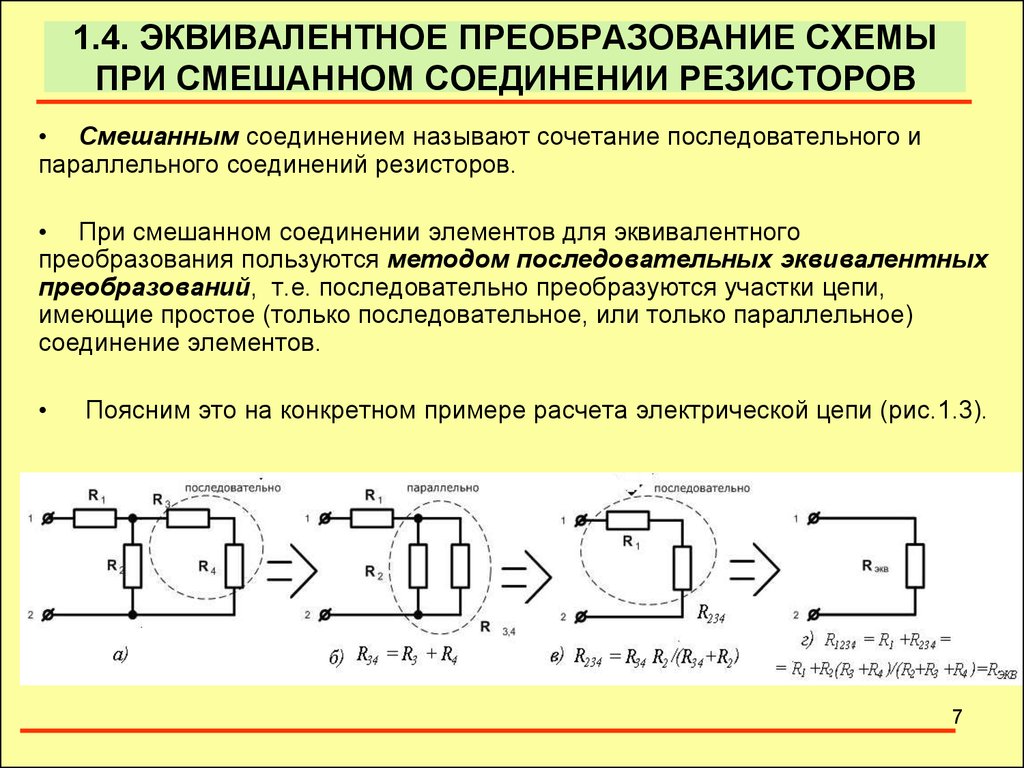 Бирск,1994г
Бирск,1994г
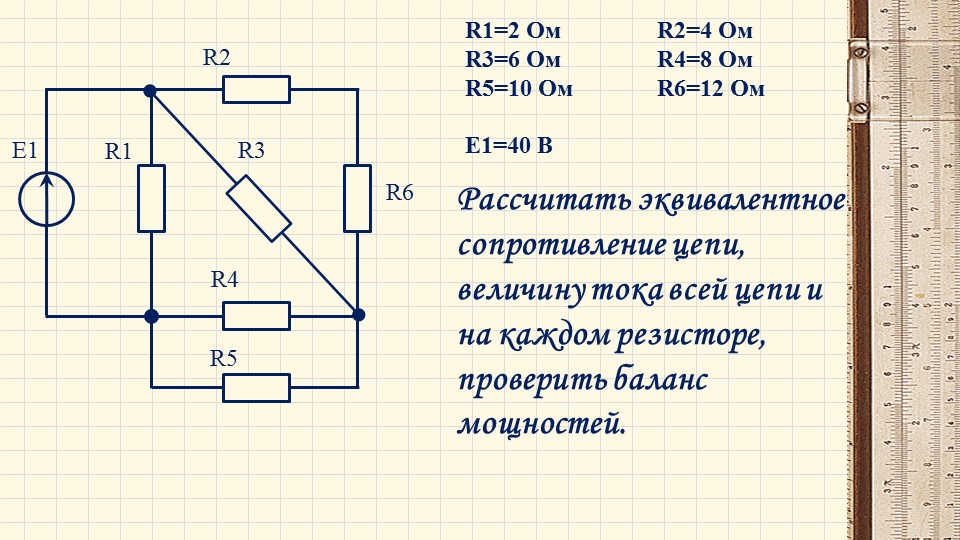 Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника.
Суперпозиция включает в себя включение источников по одному при выключении других источников. Вы отключаете источник тока, заменяя его разомкнутой цепью, и вы отключаете источник напряжения, заменяя его коротким замыканием. Чтобы получить общий результат, вы вычисляете алгебраическую сумму индивидуальных вкладов каждого источника. следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткозамкнутыми), если они имеют одинаковые отношения напряжения и тока на клеммах.
следующий рисунок . Эквивалентные схемы будут работать для всех нагрузок (включая нагрузки с разомкнутой цепью и короткозамкнутыми), если они имеют одинаковые отношения напряжения и тока на клеммах. Два эквивалента связаны друг с другом преобразованием источника.
Два эквивалента связаны друг с другом преобразованием источника.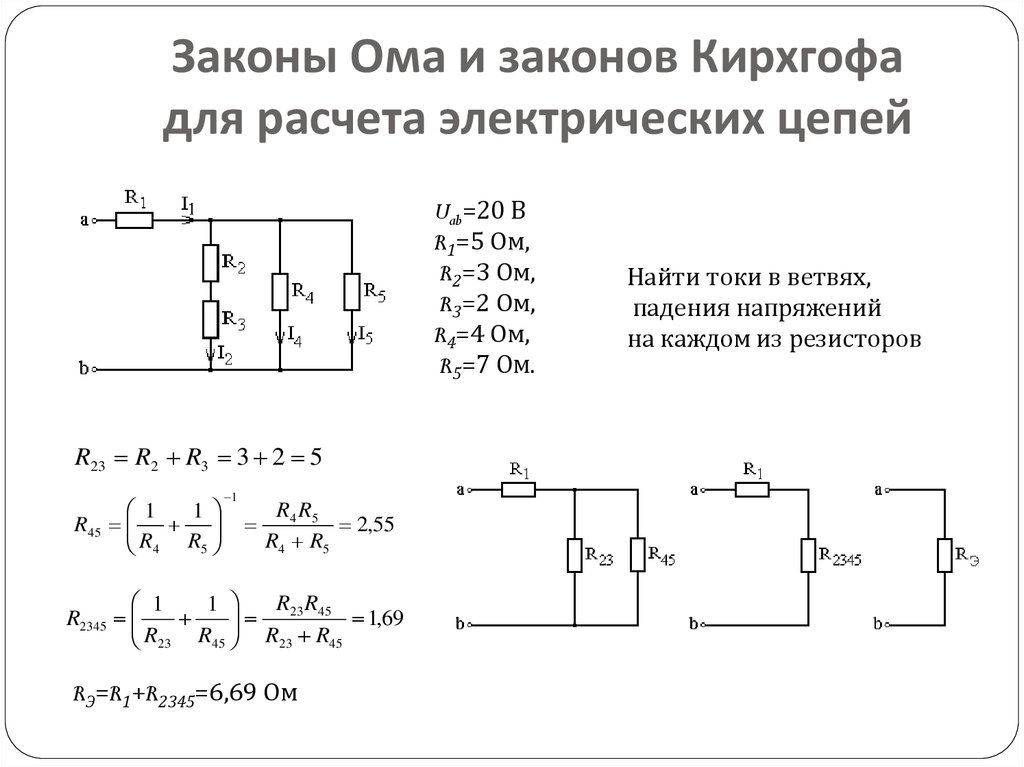 2 Закон Ома
2 Закон Ома