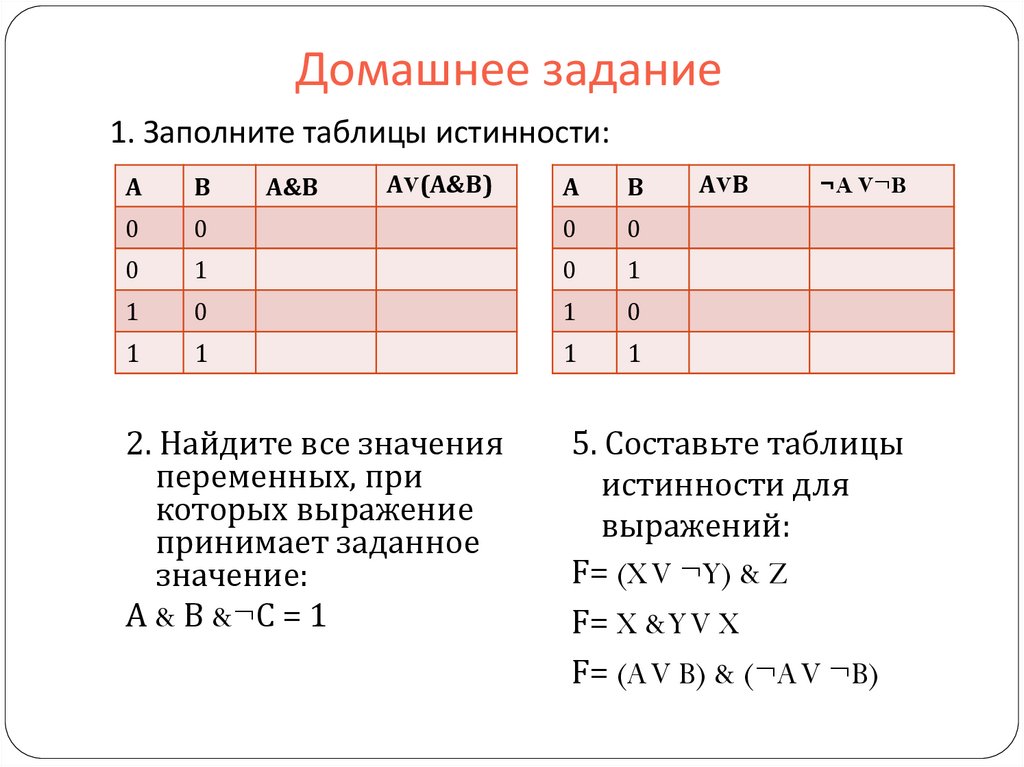
Математика и информатика в Плесской школ
Математика и информатика в Плесской школ — Построение логических схем и таблиц истинности в Excel| Приветствую Вас Гость | RSS |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Copyright MyCorp © 2023 |
Логические схемы — презентация онлайн
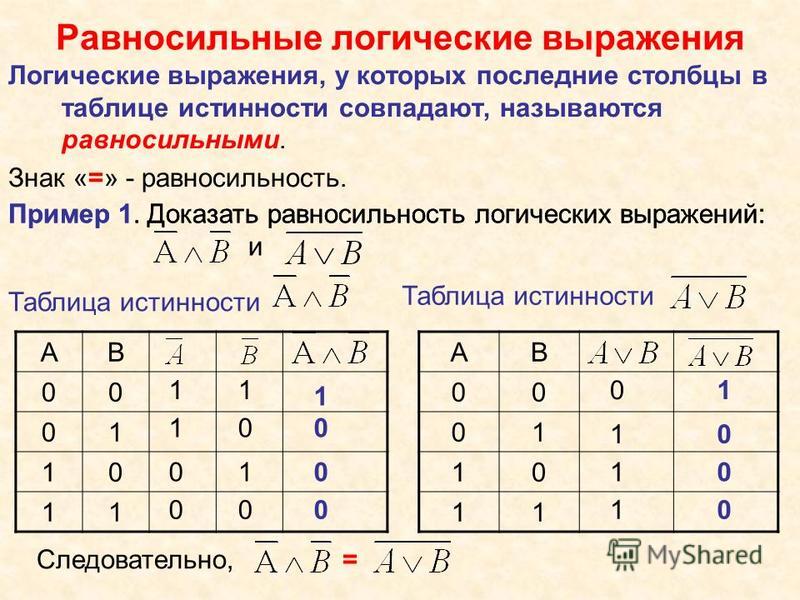
1.
 Логические схемыЛогические схемы нужны для того чтобы в наглядной графической форме
Логические схемыЛогические схемы нужны для того чтобы в наглядной графической формеотобразить последовательность выполнения операций при вычислении логических
формул.
Входящие слева линии и цифры около них обозначают значения операндов, линия
справа и соответствующая цифра — результат операции (значение на выходе
логических элементов). 1 — это логическая единица (истина), 0 — логический ноль
(ложь).
Таблицы истинности в форме логических схем будут выглядеть т.о.
3. Логический элемент НЕ (инвертор)
Логический элемент НЕ (инвертор)Простейшим логическим элементом является инвертор,
выполняющий функцию отрицания (инверсию). У этого элемента один
вход и один выход. На функциональных схемах он обозначается:
Если на вход поступает сигнал, соответствующий 1, то на выходе
будет 0. И наоборот.
вход
выход
1
0
0
1
4. Логический элемент ИЛИ (дизъюнктор)
Логический элемент, выполняющий логическое сложение, называетсядизъюнктор.
 Он имеет, как минимум, два входа. На функциональных схемах
Он имеет, как минимум, два входа. На функциональных схемахон обозначается:
Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1.
вход 1
вход 2
выход
0
0
0
0
1
1
1
0
1
1
1
1
5. Логический элемент И (конъюнктор)
Логический элемент, выполняющий логическое умножение, называетсяконъюнктор. Он имеет, как минимум, два входа. На функциональных
схемах он обозначается:
На выходе этого элемента будет сигнал 1 только в том случае,
когда на все входы поступает сигнал 1. Когда хотя бы на одном входе
будет ноль, на выходе также будет ноль.
вход 1
вход 2
выход
0
0
0
0
1
0
1
0
0
1
1
1
Другие логические элементы построены из трех простейших базовых
элементов и выполняют более сложные логические преобразования
информации.
Рассмотрим еще два логических элемента, которые играют роль
базовых при создании более сложных элементов и схем.
Логический элемент И-НЕ
Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он
обозначается:
вход 1
вход 2
выход
0
0
1
0
1
1
1
0
1
1
1
0
Логический элемент ИЛИ-НЕ
Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (ИНЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается:
вход. 1
вход 2
выход
0
0
1
0
1
0
1
0
0
1
1
0
Логические основы компьютеров
7
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
ИЛИ
A
1
B
И-НЕ
К. Поляков, 2007-2012
A B
1
ИЛИ-НЕ
A B
A B
Логические основы компьютеров
8
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
ИЛИ:
A
A
B
A
&
& A B
A
A B A B
&
B
&
B
К.
 Поляков, 2007-2012
Поляков, 2007-2012&
A B
A B
9. Составление схем
Логические основы компьютеров9
Составление схем
последняя операция — ИЛИ
X A B A B C
И
A
B
C
К. Поляков, 2007-2012
A
B
&
A
B
& A B
A B
A B C
C
&
1
X
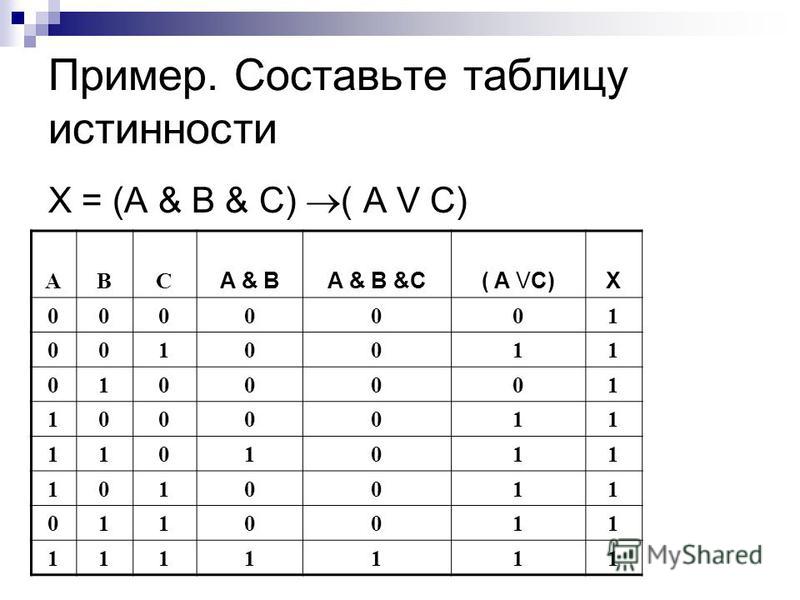
Пример 1. Нарисовать схему для логического выражения: 1 ИЛИ 0 и 1.
Читать эту схему надо слева направо. Первой выполняется операция И (что
наглядно видно на схеме), затем ИЛИ.
Теперь в порядке слева направо припишем к выходящим линиям
результаты операций:
В результате получилась 1, т.е. «истина».
Пример 2. Представить в виде логической схемы логическую формулу:
НЕ (А И (В ИЛИ С) И D)
Логическая схема будет выглядеть так:
Теперь с помощью схемы рассчитаем значение формулы при А=С=D=1,
B=0
В результате получится логический ноль, т.е. «ложно».
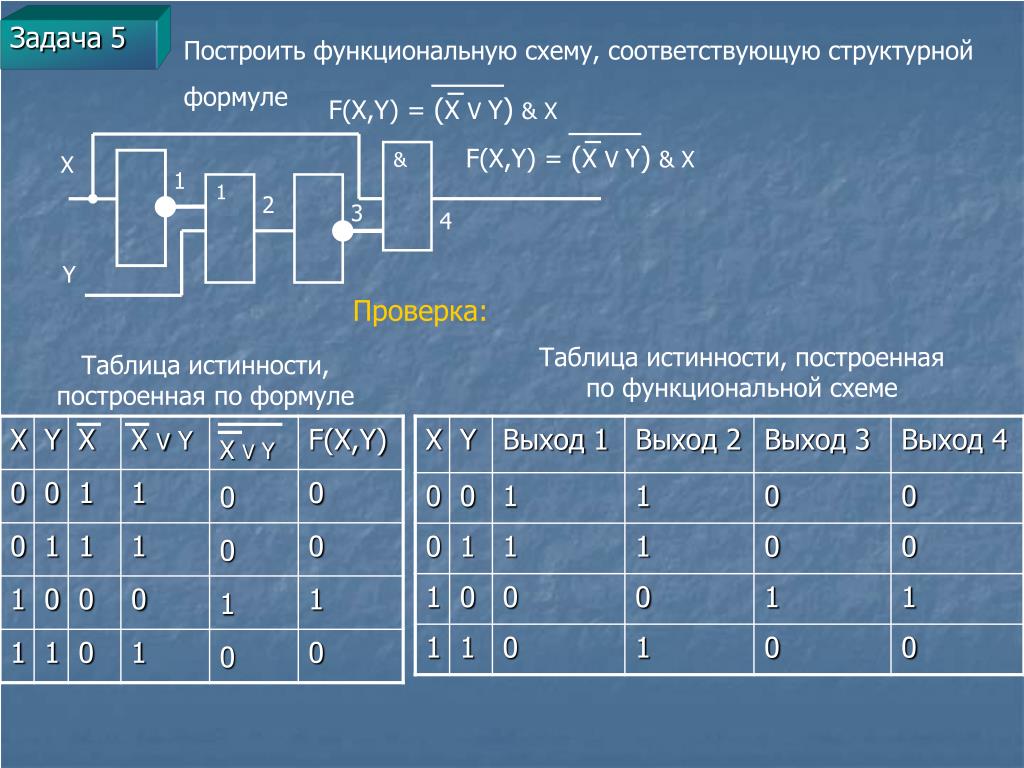
12. Функциональные схемы
Сигнал, выработанный одним логическим элементом, можноподавать на вход другого элемента, это дает возможность образовывать
цепочки из отдельных логических элементов — функциональные схемы.
Функциональная (логическая) схема – это схема, состоящая из
логических элементов, которая выполняет определённую функцию.
Анализируя функциональную схему, можно понять, как работает логическое
устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Важной формой описания функциональных схем является структурная
формула. Покажем на примере, как выписывают формулу по заданной
функциональной схеме.
Ясно, что элемент “И” осуществляет логическое умножение значений ¬А и В.
Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е.
вычисляется значение выражения:
A&B
Таким образом структурной формулой данной функциональной
схемы является формула:
C A&B
13. Таблица истинности функциональной схемы
Для функциональной схемы можно составить таблицу истинности, то естьтаблицу значений сигналов на входах и выходах схемы, по которой можно
понять какую функцию выполняет данная схема. Таблица истинности это табличное представление логической (функциональной) схемы в
котором перечислены все возможные сочетания значений входных
сигналов вместе со значением выходного сигнала для каждого из этих
сочетаний.
 Составим таблицу истинности для данной логической схемы:
Составим таблицу истинности для данной логической схемы:Начертим таблицу: количество столбцов = количество входов + количество
выходов, количество строк = 2 количество входов. В данной таблице 3 столбца и 4
строки. Заполним первые столбцы всеми возможными вариантами входных
А
В
С
сигналов
(вход 1)
(вход 2)
0
0
0
1
1
0
1
1
(выход)
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=0), запишем в таблицу.
Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и
преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим четвёртый вариант входных сигналов: А=1, В=1.
 Проследим по схеме, как проходят
Проследим по схеме, как проходяти преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
В результате получаем таблицу истинности данной логической схемы:
А
(вход 1)
В
(вход 2)
С
(выход)
0
0
1
0
1
0
1
0
1
1
1
1
Задание. Построить таблицу истинности для данной логической схемы и записать формулу
для данной схемы:
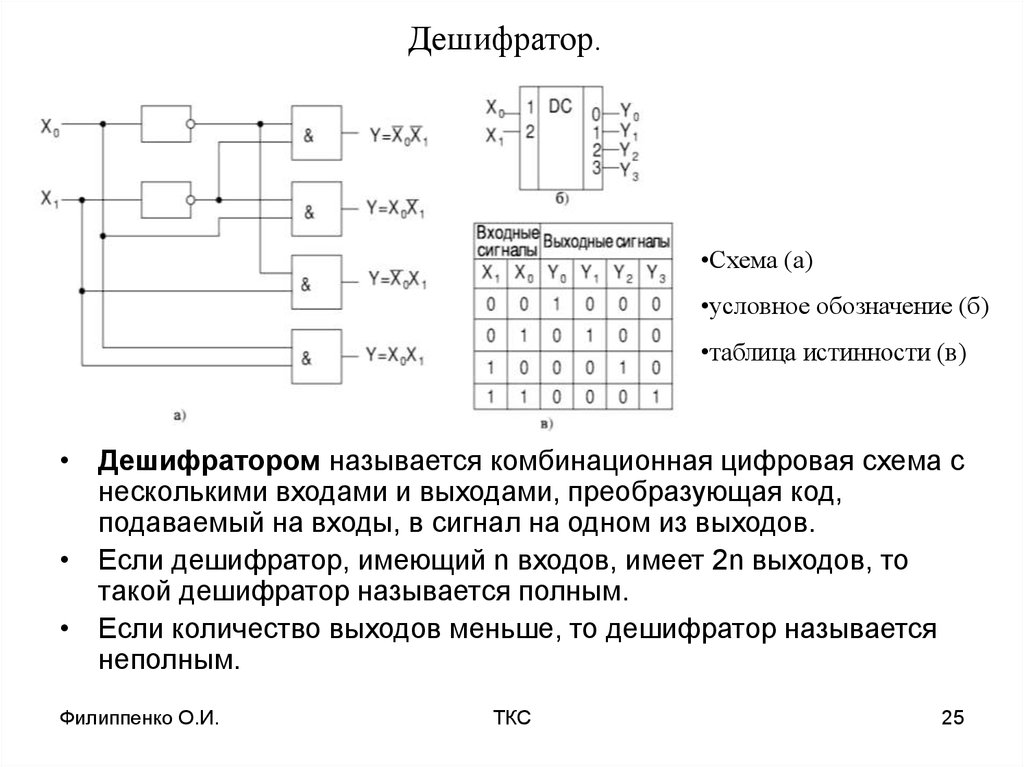
16. Логическая реализация типовых устройств компьютера
Обработка любой информации на компьютересводится к выполнению процессором различных
арифметических и логических операций. Для этого в
состав процессора входит так называемое арифметикологическое устройство (АЛУ). Оно состоит из ряда
устройств, построенных на рассмотренных выше
логических элементах. Важнейшими из таких устройств
являются триггеры, полусумматоры, сумматоры,
шифраторы, дешифраторы, счетчики, регистры.
Выясним , как из логических элементов
разрабатываются логические устройства.
Логическая реализация типовых
устройств компьютера
17. Этапы конструирования логического устройства.
Конструирование логического устройства состоит изследующих этапов:
1. Построение таблицы истинности по заданным
условиям работы проектируемого узла (т.е. по
соответствию его входных и выходных сигналов).
2. Конструирование логической функции данного узла
по таблице истинности, ее преобразование (упрощение),
если это возможно и необходимо.
3. Составление функциональной схемы проектируемого
узла по формуле логической функции.
После этого остается только реализовать полученную
схему.
Задание. Построить логическую схему для заданной таблицы истинности:
Запишем логическую функцию по данной таблице
истинности:
F A & B &C A& B &C
Упростим полученное логическое выражение:
F С & ( A & B A & B ) С & (( A B ) A & B )
Построим логическую схему для данного выражения:
А
В
С
F
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
Попробуем, действуя по этому плану, сконструировать устройство для
сложения двух двоичных чисел (одноразрядный полусумматор).

Пусть нам необходимо сложить двоичные числа А и В. Через P и S
обозначим первую и вторую цифру суммы: A + B = PS. Вспомните таблицу
сложения двоичных чисел.
1. Таблица истинности, определяющая результат сложения, имеет вид:
Слагаемые
Перенос
Сумма
А
В
Р
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
2. Сконструируем функции P(A,B) и S(A,B) по этой таблице:
Р( A, B) A & B
S ( A, B) A & B A & B
Преобразуем вторую формулу, пользуясь законами логики:
S ( A, B) A & B A & B A & B A & B A & A B & B ( A & A A & B) ( A & B B & B )
A & ( A B) B & ( A B) ( A B) & ( A & B ) ( A B) & ( A & B)
3. Теперь можно построить функциональную схему одноразрядного
полусумматора:
Р( A, B) A & B
S ( A, B) ( A B) & ( A & B)
Чтобы убедиться в том, как работает схема, проследите за прохождением
сигналов в каждом из четырёх случаев и составьте таблицу истинности
данной логической схемы.
Условное обозначение одноразрядного
сумматора:
21. Полусумматор
Логические основы компьютеров21
Полусумматор
Полусумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа.
A
S сумма
A B
P
S
Σ
B
P перенос
P A B
S A B A B A B
A
B
A
B
К. Поляков, 2007-2012
& A B
& A B
& A B
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S A B A B
P
?
Схема на 4-х
элементах?
22. Полный одноразрядный сумматор.
Одноразрядный двоичный сумматор на три входа и два выхода называетсяполным одноразрядным сумматором.
Логика работы одноразрядного сумматора на три входа или полного
сумматора приведена в таблице, где А, В — суммируемые двоичные цифры
, Pо — перенос из младшего разряда, S — образующаяся сумма данного
разряда и осуществляет перенос P в следующий старший разряд.

Слагаемые
Перенос из
младшего
разряда
Сумма
Перенос
А
B
P0
S
P
0
0
0
0
0
.0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
Формула переноса:P A & B & P0 A & B & P0 A & B & P0 A & B & P0
Формула для вычисления суммы: S A & B & P0 A & B & P0 A & B & P0 A & B & P0
После преобразования формулы переноса и суммы принимают вид:
P A & B A & P0 B & P0
S ( A B P0 ) & P0 ( A & B & P0 )
Теперь можно построить схему полного одноразрядного сумматора с
учётом переноса из младшего разряда.
Сумматор — это электронная логическая схема,
выполняющая суммирование двоичных чисел поразрядным
сложением. Сумматор является центральным узлом
арифметико-логического устройства процессора.
 Находит он
Находит онприменение и в других устройствах компьютера. В реальных
электронных схемах сумматор изображается так:
Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой
последовательное соединение одноразрядных двоичных сумматоров, каждый из которых
осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то
перенос суммируется с содержимым старшего соседнего разряда.
На рисунке показано, как из N сумматоров можно составить устройство для сложения двух Nразрядных двоичных кодов, это схема многоразрядного сумматора.
25. Сумматор
Логические основы компьютеров25
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа с
переносом из предыдущего разряда.
перенос
A
B
C
Σ
К. Поляков, 2007-2012
A
B
C
P
S
0
0
0
0
0
S сумма
0
0
1
0
1
P перенос
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
26.
 Многоразрядный сумматорЛогические основы компьютеров
Многоразрядный сумматорЛогические основы компьютеров26
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
A
an an-1 a1
B
bn bn-1 b1
C p cn cn-1 c1
перенос
a1
b1
c1
Σ
0
К. Поляков, 2007-2012
p2
a2
b2
Σ
c2
p3
an
bn
pn
cn
Σ
p
перенос
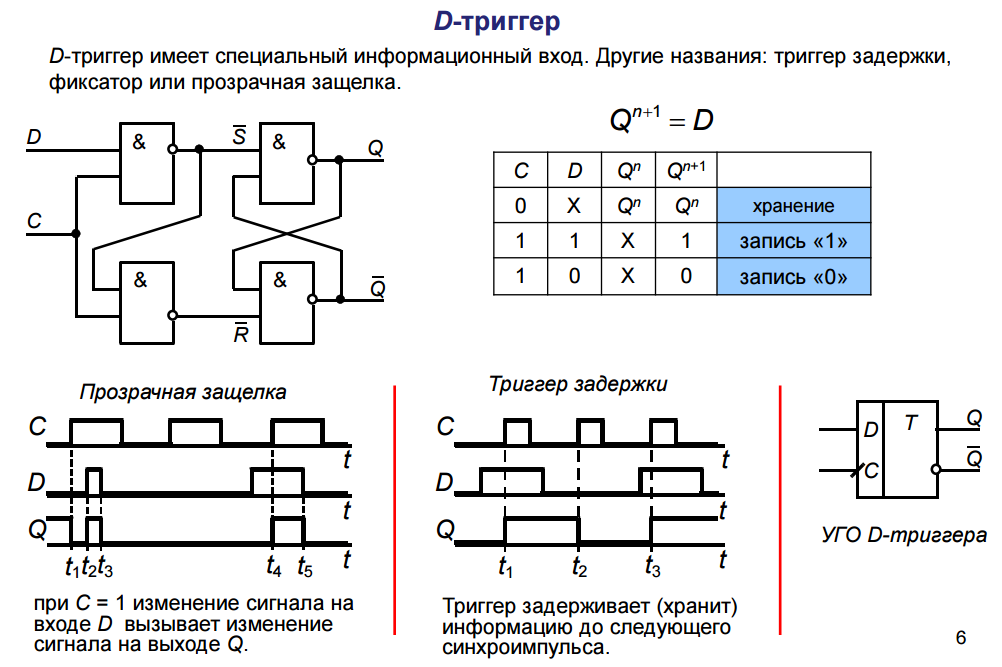
27. ТРИГГЕР
Триггер — электронная схема, применяемая для хранения значенияодноразрядного двоичного кода.
Воздействуя на входы триггера, его переводят в одно из двух возможных
состояний (0 или 1). С поступлением сигналов на входы триггера в
зависимости от его состояния либо происходит переключение, либо
исходное состояние сохраняется. При отсутствии входных сигналов триггер
сохраняет свое состояние сколь угодно долго.
Термин триггер происходит от английского слова trigger — защёлка,
спусковой крючок. Для обозначения этой схемы в английском языке чаще
употребляется термин flip-flop, что в переводе означает «хлопанье».
 Это
Этозвукоподражательное название электронной схемы указывает на её
способность почти мгновенно переходить («перебрасываться») из одного
электрического состояния в другое.
Существуют разные варианты исполнения триггеров в зависимости от
элементной базы (И-НЕ, ИЛИ-НЕ) и функциональных связей между
сигналами на входах и выходах (RS, JK, T, D и другие).
Самый распространённый тип триггера — это RS-триггер (S и R
соответственно от английских set — установка, и reset — сброс). Условное
обозначение RS-триггера:
28. RS-триггер
RS-триггер построен на 2-х логических элементах: ИЛИ — НЕ либо И – НЕ.Как, правило, триггер имеет 2 выхода: прямой и инверсный Q и
Как он работает?
Пусть на вход элемента №1 подан сигнал 1, а на вход элемента № 3 — 0. На выходе элемента №1
независимо от того, какой второй сигнал поступит на вход, будет 1, т.к. это элемент ИЛИ (по
свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение 0 (Q=0).

Следовательно, и на втором входе элемента № 3 установится сигнал 0. На выходе элемента №3
— 0. Пройдя через элемент № 4 сигнал изменится на 1. Следовательно,
= 1.
Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0,
=1.
В момент прекращения входных сигналов (S=0, R=0) на выходе =1. Это напряжение подается на
вход элемента № 1. На выходе элемента №1 сохраняется 1, и на Q — сигнал 0. На входах
элемента №3 — 0, следовательно
=1. Таким образом, при отсутствии на внешних входах
сигналов 1 триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить
напряжение на выходах триггера, надо подать сигнал 1 на вход элемента № 3. Тогда Q=1, =0.
29. Триггер (англ. trigger – защёлка)
Логические основы компьютеров29
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.

set, установка
S
1
1
R
reset, сброс
К. Поляков, 2007-2012
вспомогательный
выход
Q
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1
0
1
сброс
Q
1 0
1 1
1
0
0
0
установка 1
основной
выход
запрещен
3: Логические схемы, булева алгебра и таблицы истинности
Загрузить примечания
ТЕМА 1: Логическое представление
Существует три распространенных способа представления логики.
1. Таблицы истинности
2. Логическая схема
3. Логическое выражение
Здесь мы обсудим каждую и продемонстрируем способы преобразования между ними.
ТЕМА 2: Таблицы истинности
Таблица истинности представляет собой диаграмму единиц и нулей, организованную для отображения результатов (или выходов) всех возможных входных данных. Список всех возможных входов расположен в столбцах слева, а результирующие выходы перечислены в столбцах справа.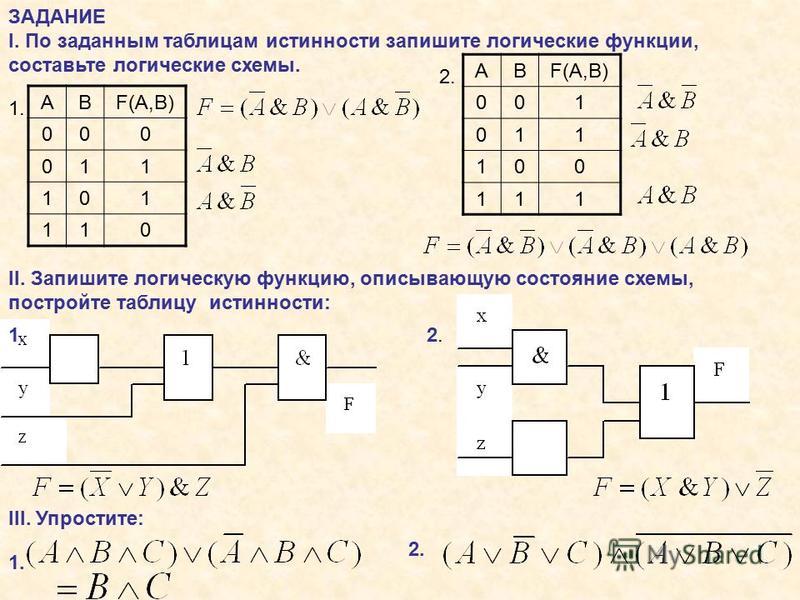 3=8 комбинаций входов. (Аудио)
3=8 комбинаций входов. (Аудио)
ТЕМА 3: Логическая диаграмма
Логическая диаграмма использует графическое описание логических вентилей в комбинации для представления логического выражения. В приведенном ниже примере показана логическая схема с тремя входами (A, B и C) и одним выходом (Y). Интерпретация этого станет ясной в следующих разделах.
ТЕМА 4: Логическое выражение
Булева алгебра может использоваться для записи логического выражения в форме уравнения. Есть несколько символов, которые вы узнаете, но вам нужно переопределить.
Примечание. Иногда, когда ! используется для обозначения НЕ, оно используется перед буквой, а иногда и после буквы. Следует соблюдать осторожность, чтобы вы понимали, какой метод используется!
Ниже приведен пример логического выражения. Фактически, он представляет ту же логику, что и приведенная выше примерная логическая схема. Эта концепция также станет более ясной, когда мы рассмотрим преобразование из логического выражения и в него ниже.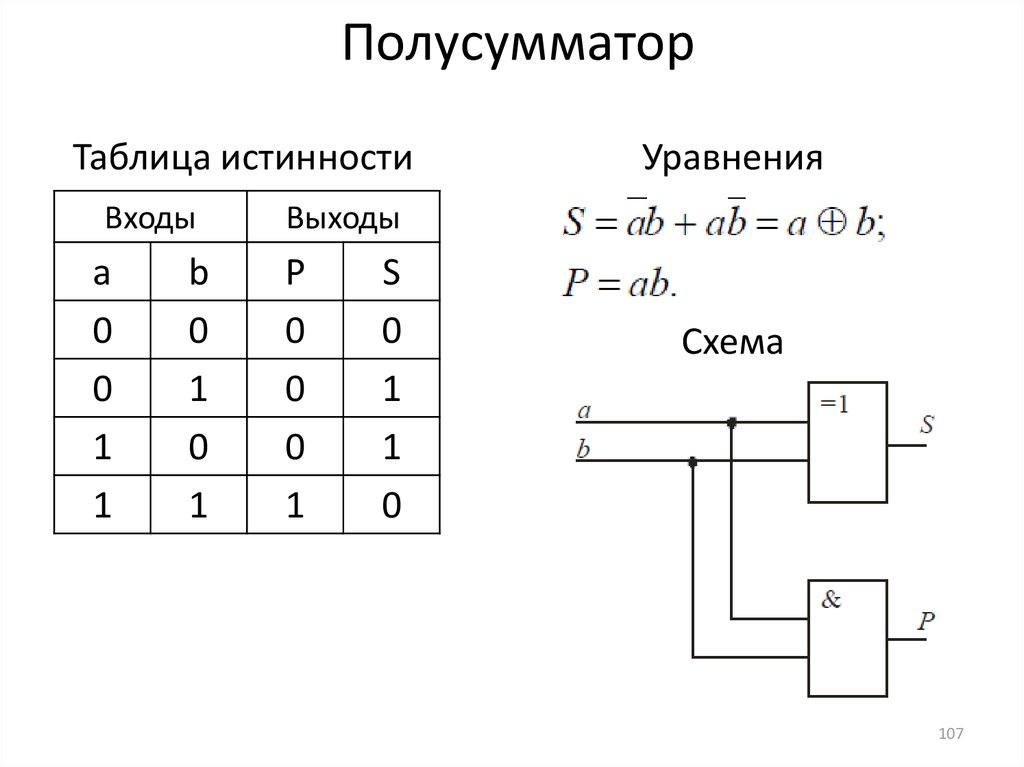
ТЕМА 5: Преобразование логической схемы в истинную таблицу
Это преобразование выполняется путем выбора каждого состояния (или комбинации входов) по одному, замены входов их соответствующими значениями и расчета значения каждой точки схемы до тех пор, пока не будет достигнут выход. Окончательное выходное значение для каждого состояния затем указывается в таблице истинности рядом со значением каждого входа. Ниже представлена логическая схема с входными значениями. Внимательно изучите его в течение длительного периода времени, это анимированное изображение, и входные и выходные данные будут меняться каждые несколько секунд. (Щелкните изображение, если оно не меняется) Ниже приведены результаты преобразования в форме таблицы истинности.
ТЕМА 6: Преобразование логических схем в логические выражения
Чтобы преобразовать логические схемы в логические выражения, мы начинаем с перечисления наших входных данных в правильном месте и обрабатываем входные данные через логические элементы, по одному вентилю за раз.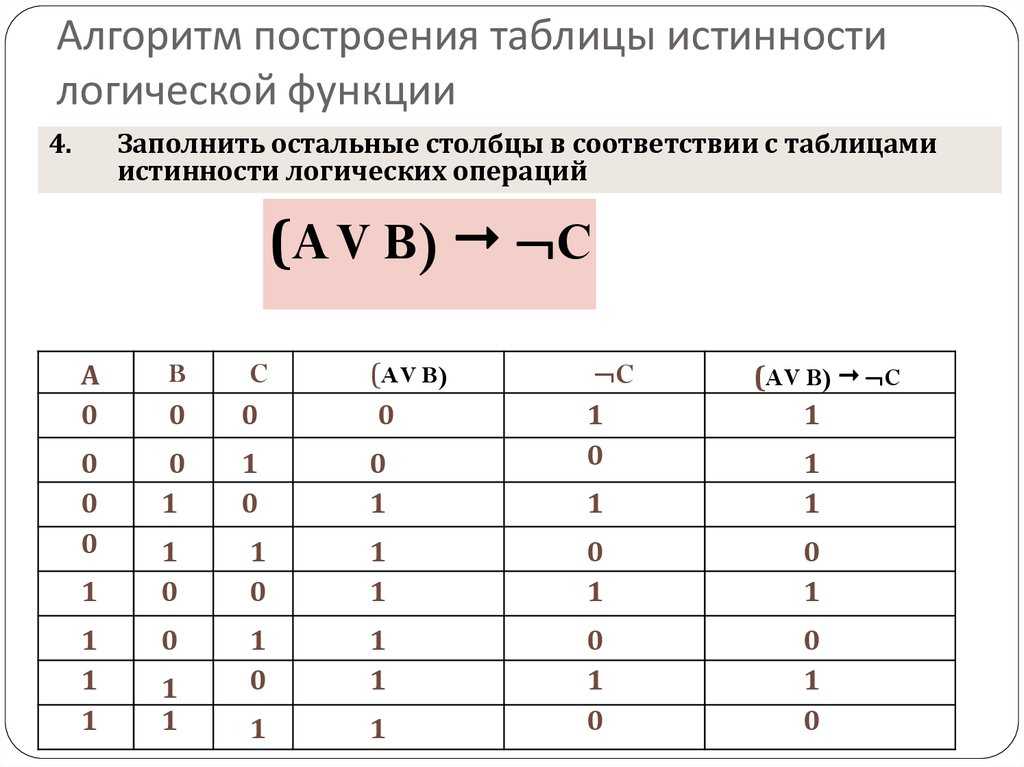 , записывая результат на выходе каждого вентиля. Ниже приводится результирующее логическое выражение каждого из вентилей.
, записывая результат на выходе каждого вентиля. Ниже приводится результирующее логическое выражение каждого из вентилей.
А вот пример выполняемого процесса. Тот факт, что результат упрощается до XOR, просто совпадение. (Аудио)
РАЗДЕЛ 7: Преобразование таблиц истинности в логические выражения
Существует два метода преобразования таблиц истинности в логические выражения.
Сумма произведений (аудио)
Произведение сумм (аудио)
ТЕМА 8. Преобразование логических выражений в логические диаграммы
странице, потому что это требует очень хорошего понимания порядка операций. Ниже приведен порядок операций, используемых в этом преобразовании. (Аудио)
Для того, чтобы завершить это преобразование, мы выполним порядок операций. Сначала мы будем искать количества в квадратных скобках или что-то в скобках. Внутри любых скобок мы будем искать дополнительные скобки, а затем НЕ, затем И, затем ИЛИ. Лучше всего начать с примера.
Лучше всего начать с примера.
Аудио
АудиоАудиоАудио ТЕМА 9. Преобразование таблицы истинности в логическую диаграмму
Самый простой способ добиться этого — сначала преобразовать таблицу истинности в логическое выражение, а затем в логическую диаграмму.
Теперь вы должны быть готовы ответить на следующие вопросы. Щелкните здесь для Webct.
1. Логическая система имеет 5 входов. Сколько возможных состояний существует в этой системе?
2. Какой символ используется для обозначения элемента НЕ, когда черта над буквой неудобна для использования?
3. Логическая система имеет 3 входа и, следовательно, 8 возможных состояний. Представление логической схемы показано ниже. Заполните таблицу истинности и преобразуйте выходной столбец в шестнадцатеричный, если состояние 0 является младшим значащим битом, а состояние 7 — старшим значащим битом.
4. Введите логическое выражение из приведенной выше принципиальной схемы.
5. Таблица истинности имеет те же состояния, что и в пункте 3 выше. Однако выходной столбец сверху вниз показывает 00110101. Приведите результат метода суммы произведений.
6. Приведите результат метода произведения сумм в пункте 5 выше.
7. Задано логическое выражение Y = (A+B)C+!BA+!C(A+B)+!(AC). Как и в 3 выше, создайте таблицу истинности и преобразуйте выходной столбец в шестнадцатеричный формат.
Нравится:
Нравится Загрузка…
Символы логических элементов и таблицы истинности
1. Что такое символы логических вентилей
Logic Gate — это идеализированная модель физического электронного устройства, реализующего логическую функцию. Логические ворота также называют строительными блоками цифровой электронной схемы, которые очень полезны в наши дни. Логические схемы включают в себя такие устройства, как компьютерная память, мультиплексоры и арифметико-логические устройства.
Символы логических элементов можно использовать в настоящее время, поскольку они называются строительными блоками цифровой электронной схемы, поэтому они используются в каждой цифровой схеме.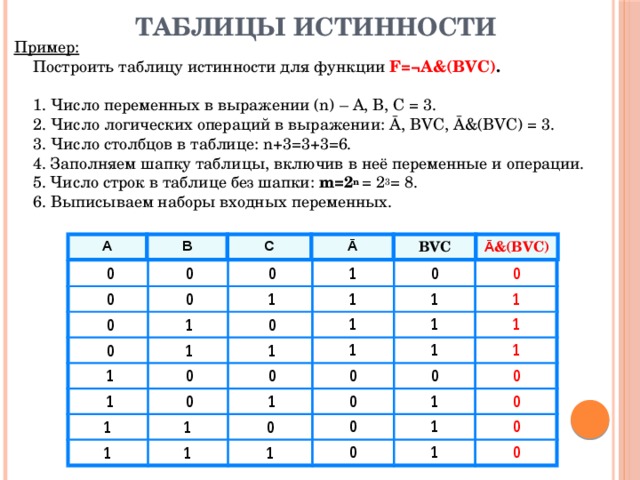
Символы логических элементов являются графическим представлением логических элементов, которые обычно используются для создания цифровых схем. Некоторые символы логических вентилей приведены ниже:
2. Объяснение символов логических элементов
2.1 Стандартные символы логических вентилей
Символы логических элементов обычно используются для графического обозначения логических элементов. Благодаря им мы можем легко распознать Врата. Как и в школах, мы узнаем только об одном типе символа Врат, то есть о традиционных символах. Но есть два типа символов, которые перечислены ниже;
Существует два типа символов логических ворот.
Традиционные символы
Это обычно используемые символы с характерными диаграммами, которые помогают нам легко их распознавать. Обычно мы очень часто используем этот тип символов.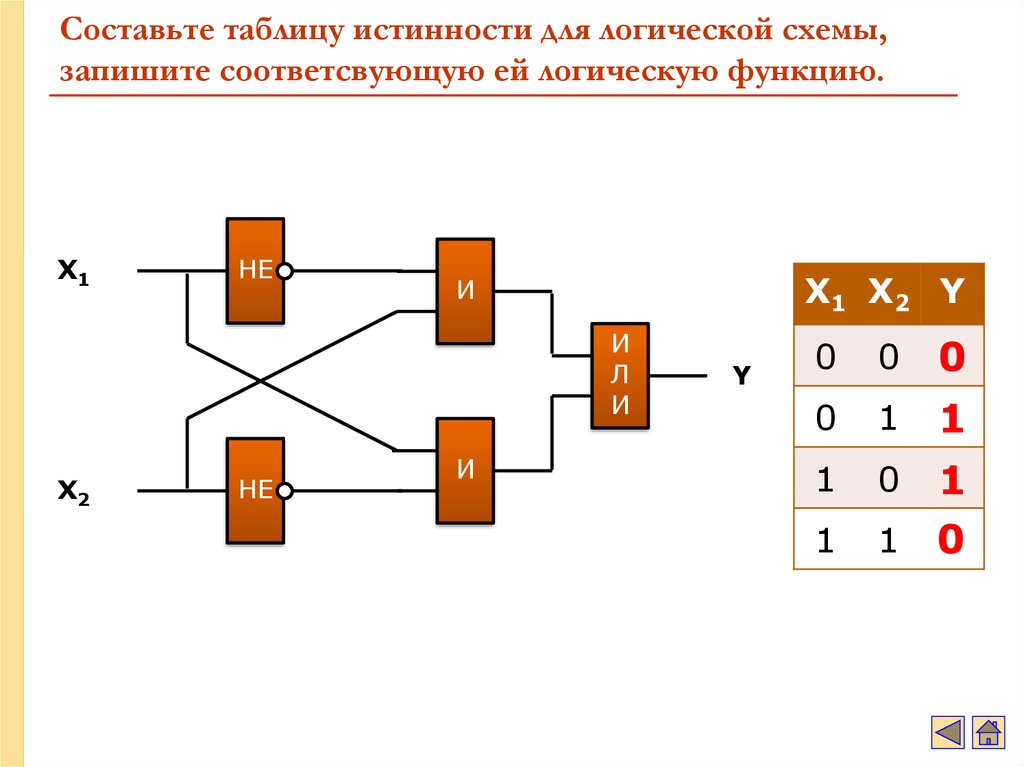 Как и в школах, мы изучаем только эти традиционные символы.
Как и в школах, мы изучаем только эти традиционные символы.
Символы МЭКС
2.2 Ниже приведены все 5 чисел символов логических вентилей и таблицы истинности.
НЕ Ворота
Это тип ворот, который имеет только один вход и один выход. Этот гейт также называют инвертором. Когда на входе 1, на выходе 0, а когда на входе 0, то на выходе 1, поэтому он называется инвертором. ВЫВОД=НЕ А
И Ворота
Это тип ворот, который имеет два или более двух входов, а также один выход. Его выход включен, когда оба входа истинны. ВЫХОД= А и В
ИЛИ Ворота
Это тип, который может иметь два или более двух входов, но иметь один выход. Его выход включен, когда хотя бы один вход включен. ВЫХОД= А ИЛИ В
ВЫХОД= А ИЛИ В
Ворота И-НЕ
Эти ворота состоят из комбинации двух других ворот, которые являются воротами НЕ и И. Здесь все настроено как вентиль И, но выход инвертируется вентилем НЕ. Здесь выход выключен, когда оба входа включены. ВЫХОД=НЕ (А и В)
Ворота НО
Эти ворота также состоят из комбинации двух других ворот, которые являются воротами НЕ и ИЛИ. Здесь, в этом шлюзе, ВЫХОД включен, когда оба входа выключены. ВЫХОД= НЕ (А ИЛИ В)
Сводная таблица истинности цифровых логических вентилей
Таблица истинности используется для демонстрации функций логических вентилей. Каждая возможная комбинация входного состояния показывает свое выходное состояние. Вход и выход имеют форму 1 и 0, что означает состояние ВКЛ и ВЫКЛ.
В следующей таблице показана сводка входов и выходов всех логических вентилей, описанных выше:
Источник: Сообщество EdrawMax
Эквиваленты вентилей NAND
Ворота И-НЕ состоят из комбинации двух других вентилей, НЕ и И-Гейтов. Здесь все настроено как вентиль И, но выход инвертируется вентилем НЕ. Здесь выход выключен, когда оба входа включены.
Здесь все настроено как вентиль И, но выход инвертируется вентилем НЕ. Здесь выход выключен, когда оба входа включены.
Этот вентиль эквивалентен инвертированному входному вентилю ИЛИ. Из этих ворот мы можем сделать любые другие ворота типа НЕ Ворота, И Ворота, ИЛИ Ворота и все остальные ворота. На следующих диаграммах показано сочетание вентилей NAND, которые образуют другие вентили:
Ворота НЕ сделаны из одного ворот И-НЕ
Мы можем легко создать NOT Gate, используя NAND Gate, только нам нужно объединить вход NAND Gate вместе, тогда он будет вести себя как NOT Gate. Таким образом, мы можем сказать, что NOT Gate легко сделан из одного NAND Gate.
AND Gate, сделанный из комбинации двух NAND Gate
Мы также можем создать вентиль И, используя этот вентиль И-НЕ, но здесь мы должны использовать два из них, как показано на схеме. Таким образом, мы можем сказать, что AND Gate легко сделан из соединения двух NAND Gate.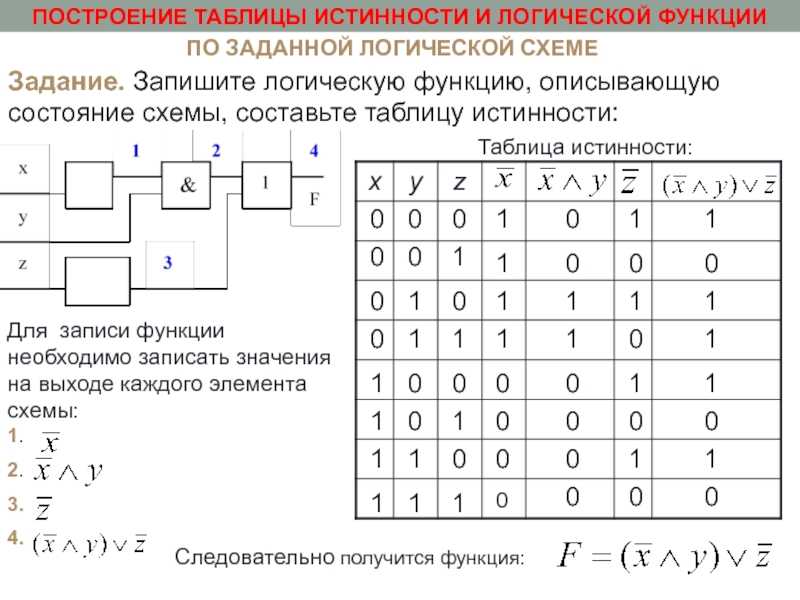
Ворота ИЛИ, сделанные из комбинации трех вентилей И-НЕ
Мы также можем сделать вентиль ИЛИ, используя этот вентиль И-НЕ, но здесь мы должны использовать три из них, как показано на схеме. Таким образом, мы можем сказать, что OR Gate легко состоит из трех NAND Gate.
NOR Gate состоит из комбинации четырех NAND Gate.
Мы также можем сделать NOR Gate, используя этот NAND Gate, но здесь мы должны использовать четыре из них, как показано на схеме. Таким образом, мы можем сказать, что ворота ИЛИ-НЕ легко состоят из четырех ворот И-НЕ.
3. Советы по использованию символов логических вентилей
Если вы хотите нарисовать схему и вам нужны символы для этого, вам нужно использовать EdrawMax Online, чтобы найти символы логических элементов и других электронных компонентов.
3.1 Используйте профессиональный инструмент для построения схем
Вы можете быстро найти символы логических вентилей в EdrawMax Online, просто нажав на библиотеку символов и выбрав там нужный символ. Вы можете получить почти все символы, которые нам нужны для рисования принципиальной схемы, такие как сопротивление, конденсатор, индуктор, логический вентиль и т. Д. Вы также можете следовать следующему изображению, чтобы получить больше информации об этом:
Вы можете получить почти все символы, которые нам нужны для рисования принципиальной схемы, такие как сопротивление, конденсатор, индуктор, логический вентиль и т. Д. Вы также можете следовать следующему изображению, чтобы получить больше информации об этом:
3.2 Создание символов самостоятельно
Если вы не нашли нужный символ в этой онлайн-библиотеке символов EdrawMax, вы также можете импортировать символ в библиотеку.
Предположим, вам нужно нарисовать принципиальную схему и вам нужен символ, которого нет, тогда вы также можете импортировать файл этого символа. Вы также можете легко создавать символы в EdrawMax Online. Из следующего изображения вы можете лучше понять.
Вы также можете узнать больше из этого видео. YouTube.
4. Дополнительные вопросы о символах логических вентилей
Мы предоставили всю информацию о Logic Gate и ее символах. Но я знаю, что у вас есть много вопросов по этому поводу, мы перечислили несколько вопросов, которые могут вам помочь.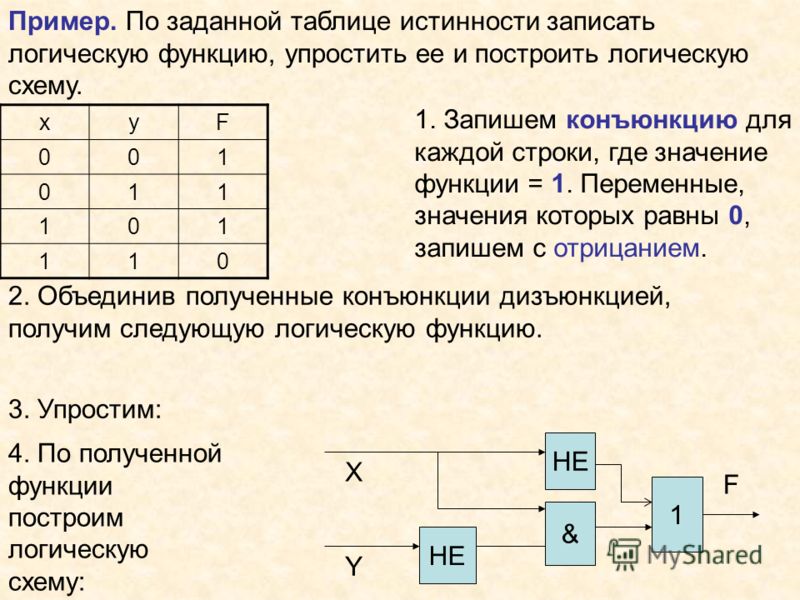
Почему мы называем их воротами?
Это устройство, которое реализует логическую функцию, что означает, что оно выполняет логические операции с единицей или нулем на входах и выдает бит на выходе. Их также называют строительными блоками цифровой схемы.
Где мы используем логические ворота?
Как мы уже обсуждали, логические элементы являются строительными блоками цифровой системы и цепей. Поэтому мы используем Logic Gates при создании цифровых схем, таких как микроконтроллеры, микропроцессоры, электрические и электронные проекты, а также встроенные приложения.
Сколько входных сигналов может иметь гейт?
Как вы знаете, существует шесть типов вентилей NOT, OR, AND, NAND, OR Gate. Ворота НЕ имеют только один вход с двумя вариантами, т. е. 1 и 0, но в других вентилях, таких как И, ИЛИ, ИЛИ, И-НЕ, у нас есть два входа с четырьмя парами возможных вариантов 1 и 0.
5. Вывод
Итак, из приведенной выше информации вы получили всю информацию о логических воротах и их символах.


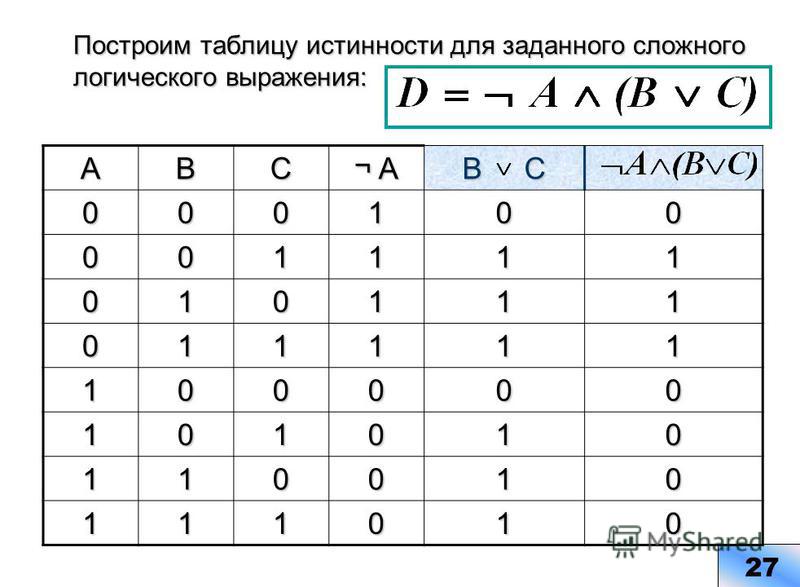
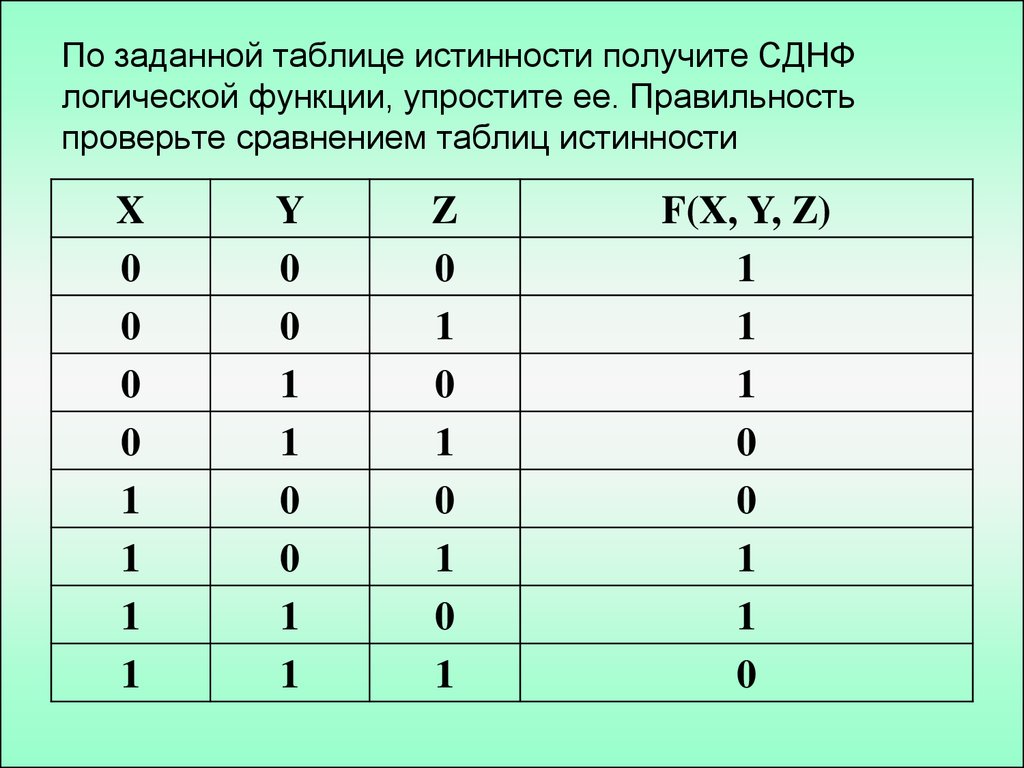
 По формуле построить таблицу истинности. Сложное выражение разбить на действия. Над таблицей написать эти действия, введя для каждого новую переменную. Столбцы в таблице лучше назвать именами вспомогательных переменных. В данном примере: в ячейку D5 вводится формула =И(A5;B5). В ячейку E5 вводится формула =НЕ(A5). В ячейку F5 вводится формула =И(E5;C5). В ячейку G5 — формула =ИЛИ(D5;F5). Дальше эти формулы размножаются по столбцам. Строится рамка и таблица готова
По формуле построить таблицу истинности. Сложное выражение разбить на действия. Над таблицей написать эти действия, введя для каждого новую переменную. Столбцы в таблице лучше назвать именами вспомогательных переменных. В данном примере: в ячейку D5 вводится формула =И(A5;B5). В ячейку E5 вводится формула =НЕ(A5). В ячейку F5 вводится формула =И(E5;C5). В ячейку G5 — формула =ИЛИ(D5;F5). Дальше эти формулы размножаются по столбцам. Строится рамка и таблица готова