Моделирование логических схем с помощью электронных таблиц – УчМет
Автор:
Павел Ефимович Финкель
Учитель информатики
МБОУ СОШ №1 им. А. И. Герцена г. Тимашевска
Краснодарский край
352700, г. Тимашевск, ул. Ленина, 152
Домашний адрес:
352708 г. Тимашевск
Ул. 50 лет Октября. д. 166 кв. 29
т. сот. +79183176673
E-mail: [email protected]
Разработка урока по информатике
Класс 11
Тема:
«Моделирование логических схем и построение таблиц истинности в электронных таблицах»
Ключевые слова:
Информатика, модели, моделирование, электронная таблица, логика, проект, функция
Аннотация
Данный материал – разработка урока по информатике.
Тема «Моделирование» изучается в 11 профильном «Информационно-технологическом» классе
Тема урока: Моделирование логических схем и построение таблиц истинности с помощью Электронных таблиц»
На
данном уроке используется Электронная
таблица MS
Excel
2010.
Учащиеся должны научиться строить логические формулы по логическим схемам, использовать встроенные функции ЭТ MS Excel 2010.
Данный урок позволяет закрепить знания учащихся по теме «Логика», научить их использовать ЭТ для создания таблиц истинности используя встроенные логические функции.
Моделирование логических схем с помощью электронных таблиц
Цели:
Образовательные: определить роль математической логики в создании ЭВМ; сформировать у учащихся представление об устройствах элементной базы компьютера; сформировать навыки построения логических схем, построение таблиц истинности в ЭТ с помощью встроенных логических функций.
Развивающие: развивать умения анализировать, систематизировать, обобщать, структурировать полученные знания; развивать познавательные и творческие способности учащихся, развивать наглядно-образное мышление.
Воспитательные: воспитание усидчивости, аккуратности, внимательности при выполнении практических работ.

Требования к знаниям и умениям:
Учащиеся должны знать:
роль математической логики в создании ЭВМ;
основные базовые элементы логических схем;
правила составления логических схем.
Учащиеся должны уметь:
составлять электрические и логические схемы.
Составлять логические выражения по функциональным схемам.
Использовать встроенные логические функции ЭТ MS Excel
План:
Организационный момент. (1 минута)
Актуализация знаний. (3 минуты)
Объяснение нового материала. (15 минут)
Закрепление материала, выполнение индивидуальных практических заданий (15 мин)
Итог урока. (4 минуты)
Домашнее задание. (1 минута)
ХОД УРОКА
Организационный момент.

Сообщение темы и цели урока.
Актуализация знаний
На предыдущих уроках мы с вами познакомились с основными элементами математической логики и узнали, что именно математическая логика лежит в основе работы схем и узлов компьютера. Давайте вспомним, основные элементы логики:
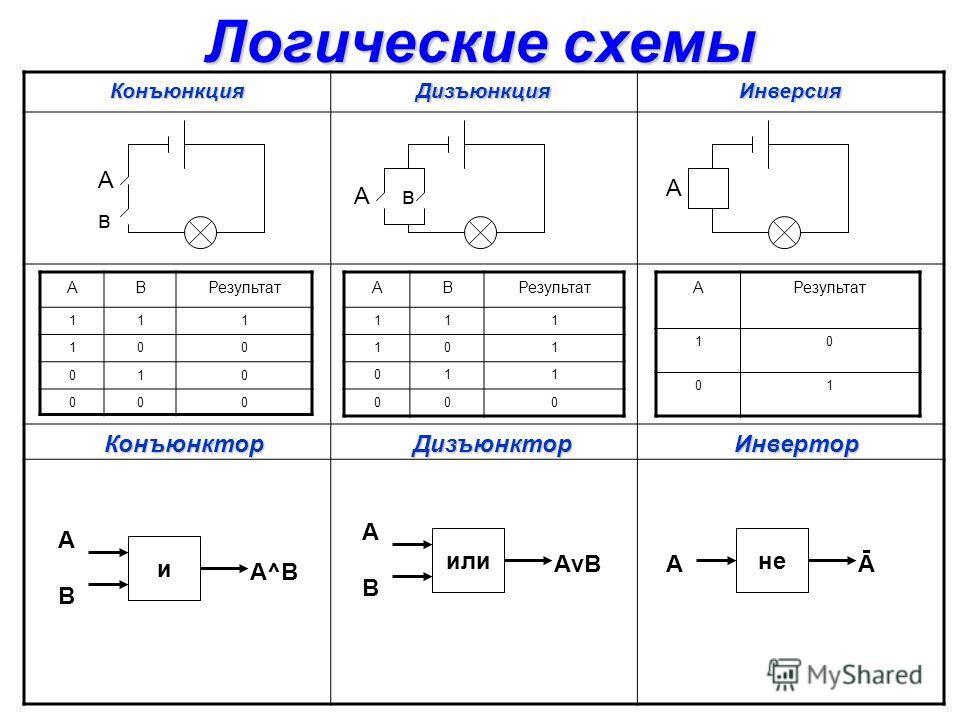
Вспомним таблицы истинности логических функций и их схемы:
Конъюнкция | ||
A | B | A&B |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
Дизъюнкция | ||
A | B | AVB |
1 | 1 | 1 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 0 |
Инверсия | |
A | ¬A |
1 | 0 |
0 | 1 |
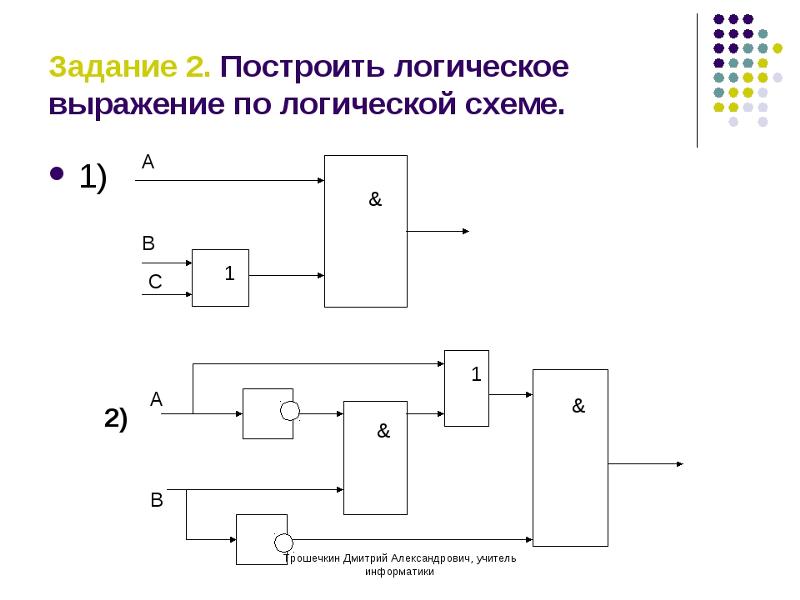
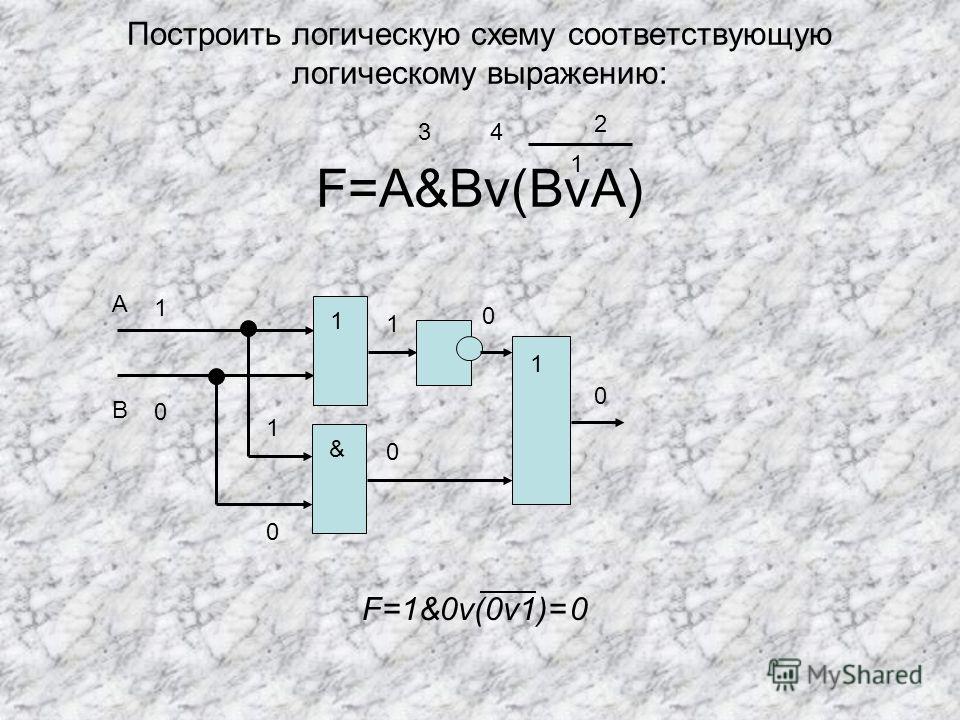
Задание:
По
логической схеме построить логическую
функцию и таблицу истинности.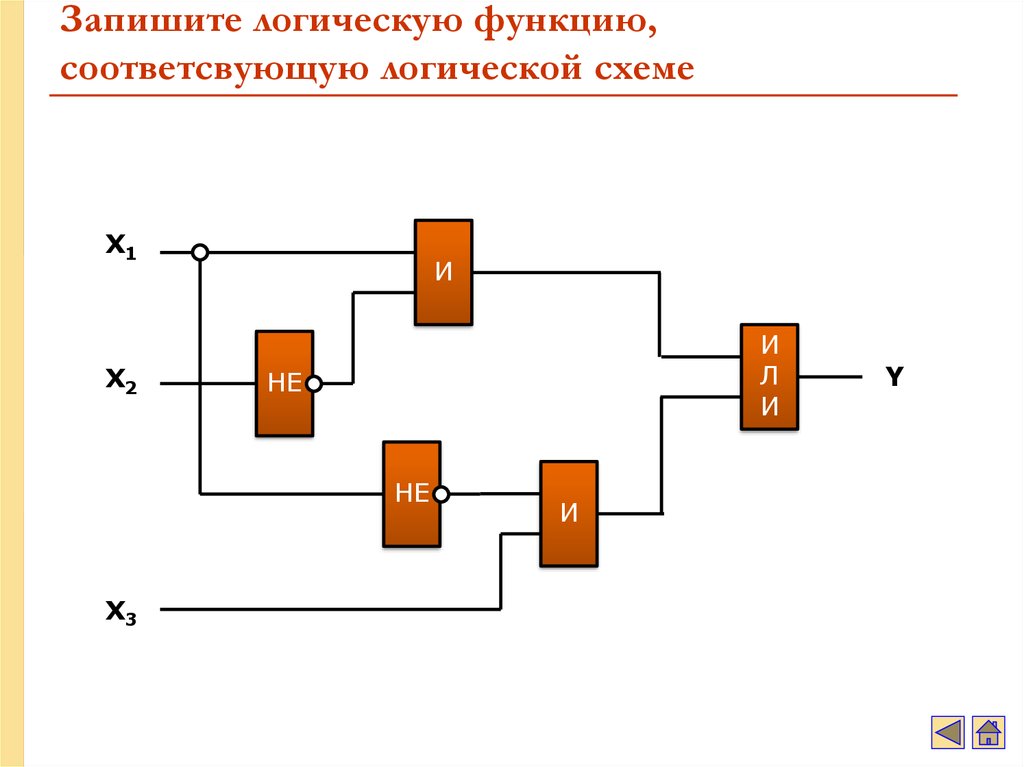
&
B
A
C
1
F
Логическая формула выглядит следующим образом:
F=A & B \/
Построим таблицу истинности для функции F:
A | B | C | A & B | F | |
0 | 0 | 0 | 1 | 0 | 1 |
0 | 1 | 0 | 0 | 0 | |
0 | 1 | 0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 | 0 | |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 | 1 | |
1 | 1 | 1 | 0 | 1 | 1 |
Объяснение нового материала
А
сейчас давайте эту схему и таблицу
истинности представим с помощью
электронной таблицы MS
Excel.
Электронная таблица MS Excel содержит встроенные логические функции:
Функция И соответствует логической конъюнкции:
И (арг1; арг2; арг3….)
Функция ИЛИ соответствует логической дизъюнкции:
ИЛИ (арг1; арг2; арг3….)
ЛОЖЬ() соответствует значению 0
ИСТИНА() соответствует значению 1
Функция НЕ соответствует логическому отрицанию или инверсии:
Изменяет значение ЛОЖЬ на ИСТИНА и значение ИСТИНА на ЛОЖЬ
Аргументами этих функций могут быть логические величины или адреса ячеек, содержащих логические величины.
Учитель выполняет работу вместе с учащимися, через проектор всё отображается на доске.
На рисунке показаны, какие формулы и функции MS Excel использованы.
Сравним полученные результаты с нашей первоначальной таблицей.
Физминутка.
Закрепление полученных знаний
Выполнение
учащимися практических заданий на
компьютере: по логической схеме записать
логическую формулу и построить таблицу
истинности в ЭТ MS
Excel. Учащиеся получают индивидуальные
карточки с заданиями.
Учащиеся получают индивидуальные
карточки с заданиями.
ВАРИАНТ №1
ВАРИАНТ №2
ВАРИАНТ №3
Подведение итогов урока, выставление оценок
Домашнее задание.
Список литературы:
Н. Д. Угринович «Информатика и информационные технологии 10-11» Бином 2005
Н. Д. Угринович «Информатика и ИКТ 10» Бином 2010
Н. Д. Угринович «практикум по информатике и информационным технологиям» Бином 2004
iMath Wiki — Минимизация булевых функций. Минимизирующие карты Карно. Метод Куайна-МакКласки
Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).
В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.
- Минимальная ДНФ
- Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.

- Минимальная КНФ
- Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.
Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя членами, содержащими одинаковые переменные, вхождения которых (с отрицанием и без) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
\[
\;\overline{x_1}\;x_2x_3x_4
\vee
\;\overline{x_1}\;x_2\;\overline{x_3}\;x_4 =
\;\overline{x_1}\;x_2x_4 (x_3 \vee\;\overline{x_3}\;) =
\;\overline{x_1}\;x_2x_4 \mathbin{\&}1 =
\;\overline{x_1}\;x_2x_4.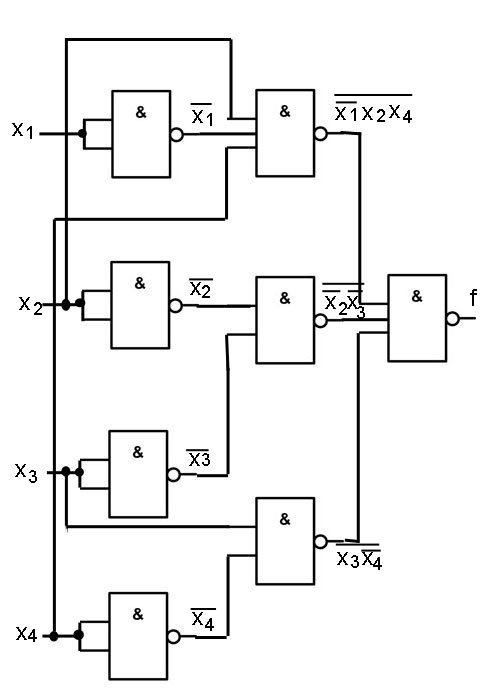 \]
\]
Аналогично для КНФ:
\[ (\;\overline{x_1}\;\vee x_2\vee x_3\vee x_4) (\;\overline{x_1}\;\vee x_2\vee\;\overline{x_3}\;\vee x_4) = \;\overline{x_1}\;\vee x_2\vee x_4\vee x_3\;\overline{x_3}\; = \;\overline{x_1}\;\vee x_2\vee x_4\vee 0 = \;\overline{x_1}\;\vee x_2\vee x_4. \]
Возможность поглощения следует из очевидных равенств
\[ A \vee\;\overline{A}\; = 1 \]\[ A\;\overline{A}\; = 0. \]
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
- Карта Карно
Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции.
Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В.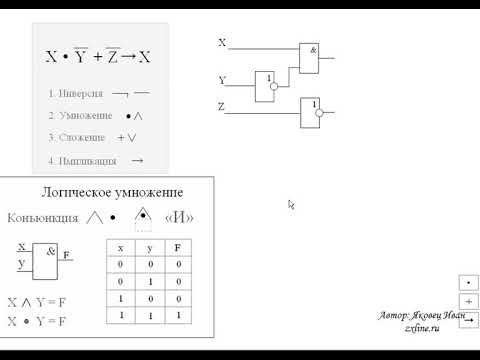 N\) различных элементарных членов.
N\) различных элементарных членов.
Элементарные члены СДНФ или СКНФ образуют структуру, топологически эквивалентную \(N\)-мерному кубу. Действительно, если рассматривать набор значений функции \(x_1,\,\ldots,\,x_N\) как \(N\)-мерный вектор \(\{x_1,\,\ldots,\,x_N\}\), мы получим набор точек, лежащих на ортах \(N\)-мерной системы координат, и удаленных друг от друга на \(1\). Другими словами, мы получим \(N\)-мерный гиперкуб с ребром \(1\).
Например, для функции двух переменных, заданной таблицей истинности:
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
можно построить эквивалентный ей квадрат:
001111000110Или, если обозначить вершины соответствующими элементарными конъюнкциями и выделить вершины, конъюнкции которых входят в СДНФ:
0x̅₁x₂1x₁x₂0x̅₁x̅₂1x₁x̅₂Или СКНФ:
0x₁∨x̅₂1x̅₁∨x̅₂0x₁∨x₂1x̅₁∨x₂Можно заметить, что члены, находящиеся на одной стороне квадрата, могут быть склеены.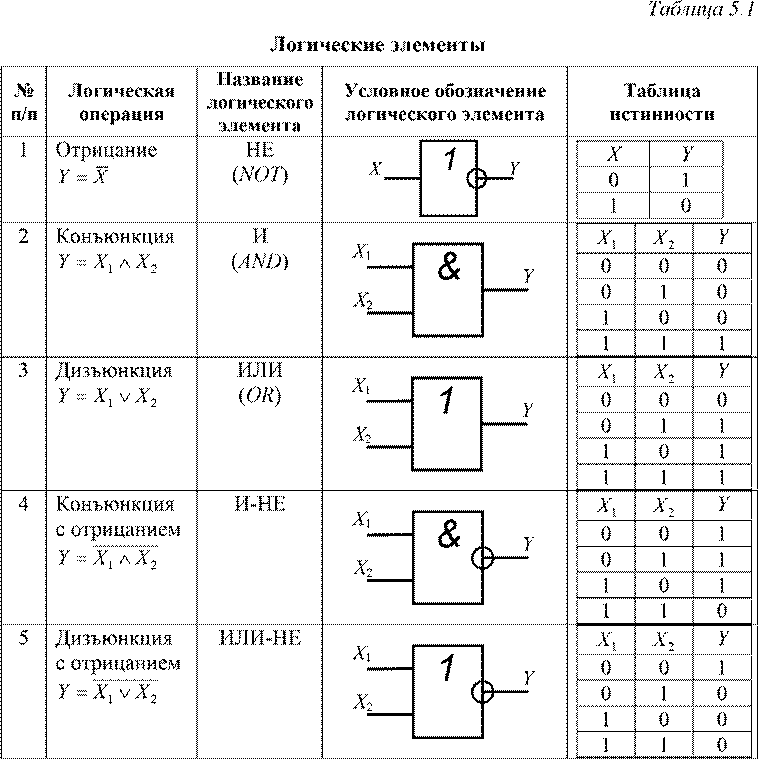 Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение \(1\) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение \(0\) (по правилам построения СКНФ).
Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение \(1\) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение \(0\) (по правилам построения СКНФ).
При этом, сохраняются переменные, значение которых на стороне постоянно.
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации. Например, четыре члена, принадлежащие одной грани куба, объединяются в один с поглощением двух переменных:
\[ \;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\; \vee x_1\;\overline{x_2}\;\;\overline{x_3}\; \vee \;\overline{x_1}\;\;\overline{x_2}\;x_3 \vee x_1\;\overline{x_2}\;x_3 =\]
\[ = \;\overline{x_2}\; (\;\overline{x_1}\;\;\overline{x_3}\; \vee\;\overline{x_1}\;x_3 \vee x_1\;\overline{x_3}\; \vee x_1x_3) = \;\overline{x_2}\; (\;\overline{x_1}\; \vee x_1)(\;\overline{x_3}\; \vee x_3) = \;\overline{x_2}\; \]
В общем случае можно сказать, что \(2^K\) членов, принадлежащие одной \(K\)–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются \(K\) переменных.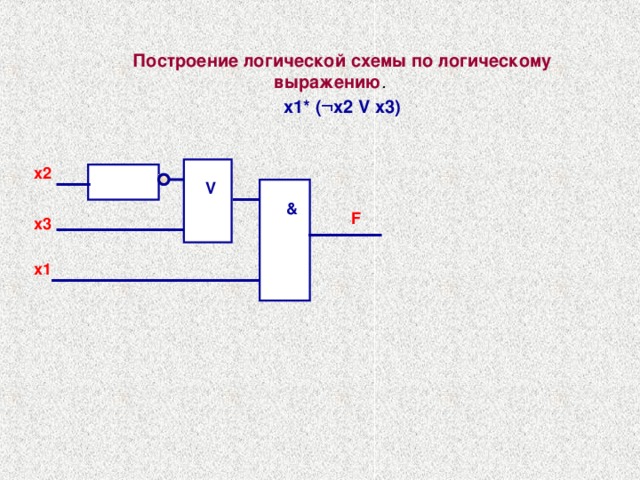 K\) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
K\) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
Для функций четырех переменных, требуется развертка 4-мерного гиперкуба. Карта Карно в таком случае имеет вид:
| \(00\) | \(f(0,0,0,0)\) | \(f(0,1,0,0)\) | \(f(1,1,0,0)\) | \(f(1,0,0,0)\) |
| \(01\) | \(f(0,0,0,1)\) | \(f(0,1,0,1)\) | \(f(1,1,0,1)\) | \(f(1,0,0,1)\) |
| \(11\) | \(f(0,0,1,1)\) | \(f(0,1,1,1)\) | \(f(1,1,1,1)\) | \(f(1,0,1,1)\) |
| \(10\) | \(f(0,0,1,0)\) | \(f(0,1,1,0)\) | \(f(1,1,1,0)\) | \(f(1,0,1,0)\) |
В данном случае, все крайние ячейки смежны друг другу.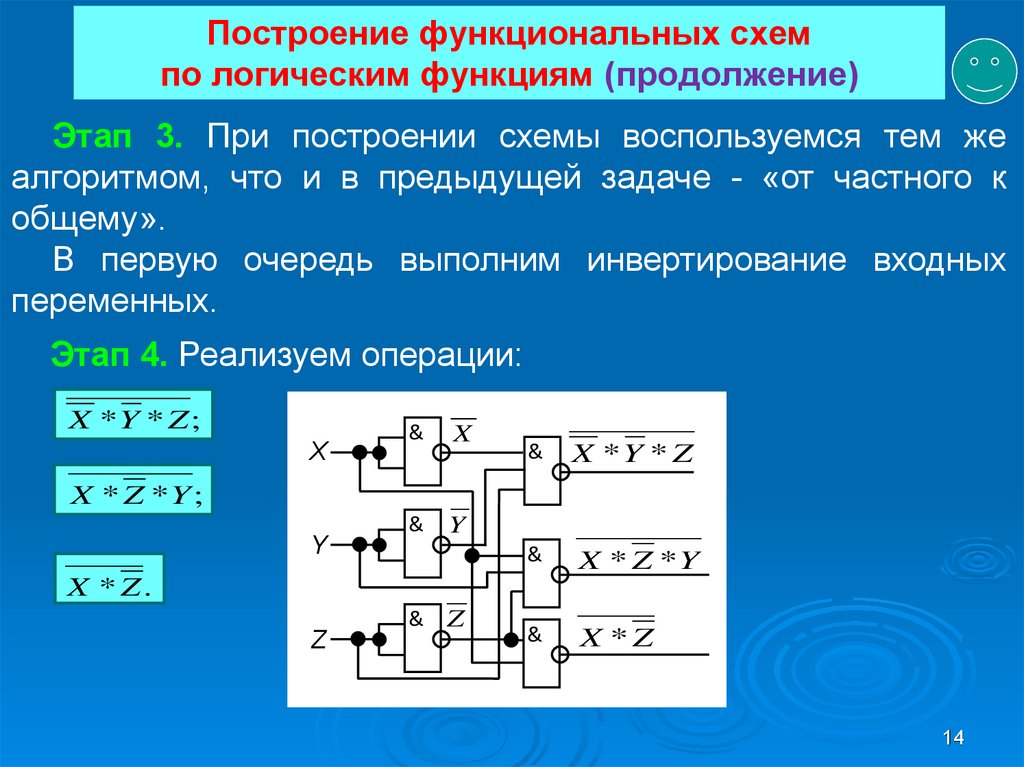 Это можно себе представить, натянув эту развертку на тор (“бублик”):
Это можно себе представить, натянув эту развертку на тор (“бублик”):
Возможно так же построение карт Карно для функций 5 и 6 переменных, однако работа с ними значительно затрудена. Для числа переменных, большего 6, использование карт Карно попросту непрактично.
Пример
Рассмотрим функцию, имеющую следующую таблицу истинности:
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Перепишем эту таблицу в виде карты Карно:
| 00 | 1 | 1 | 0 | 0 |
| 01 | 1 | 0 | 0 | 0 |
| 11 | 0 | 1 | 1 | 0 |
| 10 | 1 | 1 | 1 | 0 |
Легко выделяются три группы.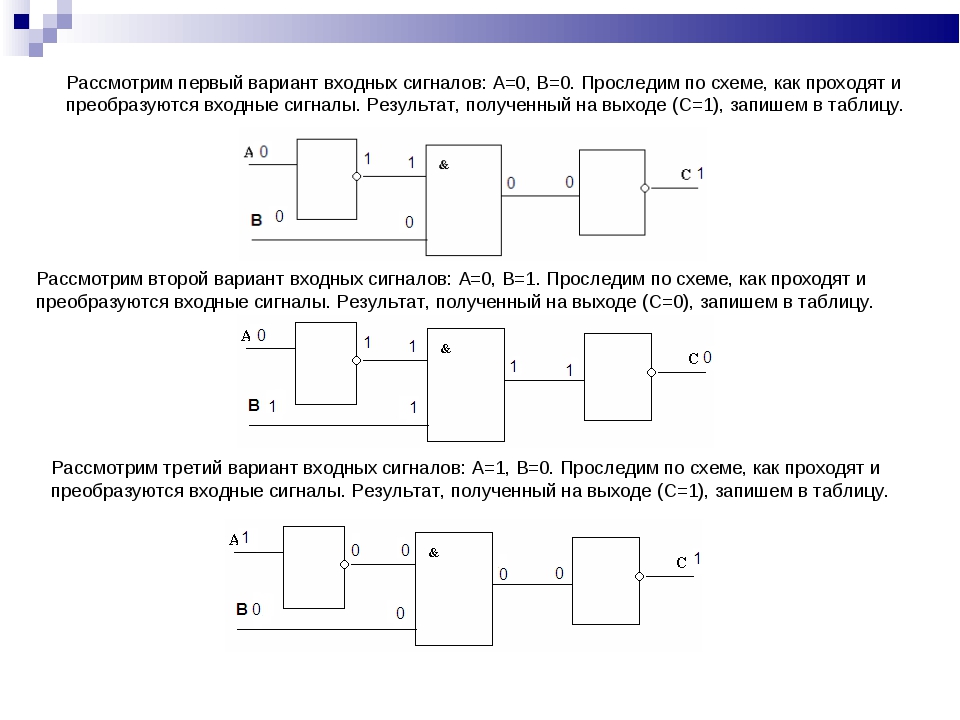 Исходя из этого, записывается ДНФ:
Исходя из этого, записывается ДНФ:
\(\;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\;\)\(\vee\)\(\;\overline{x_1}\;\;\overline{x_4}\;\)\(\vee\)\({x_2}{x_3}\)
Метод Куайна-МакКласси строится на основе того же аппарата, что и карты Карно, однако оказывается более практичным для большего количества переменных.
Алгоритм заключается последовательной склейке, и затем редукции результата.
Склейка
Сначала элементарные члены совершенной формы записываются в двоичной форме в таблицу, где группируются по количеству единиц.
Затем, члены, которые отличаются одной переменной (одним битом), могут быть склеены. В таком случае единица заменяется на “-”. Очевидно, что склеены могут быть только члены из соседних групп
Члены, которые нельзя склеить, обозначаются звездочкой «*».
Полученные склеенные члены могут, в свою очередь, так же быть склеены. При этом “-” трактуется как “третье” значение.
Когда никакие члены больше не могут быть склеены, из членов, отмеченных “*”, составляется сокращенная форма, которая не обязательно минимальна. После этого производится редукция.
После этого производится редукция.
Редукция
Для редукции, составляется таблица, в строки которой включаются члены сокращенной формы, а в столбцы – члены совершенной.
В ячейках ставится отметка (например, крестик “×”), если соответствующий член сокращенной формы поглощает соответствующий член совершенной формы (т.е. если заголовок строки является частью заголовка столбца).
Выбираются столбцы, содержащие только один “×”. Соответсвтующие им члены сокращенной формы составляют ядро, и должны войти в минимальную форму.
Если ядро не перекрывает все столбцы, то в минимальную форму так же включаются несколько членов сокращенной формы, не входящих в ядро, таким образом, чтобы члены минимальной формы перекрывали все столбцы таблицы.
Пример
Найдем минимальную форму функции
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 1 |
Члены СДНФ в двоичной нотации:
- 0000 = 0
- 0001 = 1
- 0010 = 2
- 0011 = 3
- 0101 = 5
- 0111 = 7
- 1000 = 8
- 1010 = 10
- 1100 = 12
- 1101 = 13
- 1111 = 15
Группировка:
0
- 0000 = 0
1
- 0001 = 1
- 0010 = 2
- 1000 = 8
2
- 0011 = 3
- 0101 = 5
- 1010 = 10
- 1100 = 12
3
- 0111 = 7
- 1101 = 13
4
- 1111 = 15
Склейка 1:
- 0, 1 = 000-
- 0, 2 = 00-0
- 0, 8 = -000
- 1, 3 = 00-1
- 1, 5 = 0-01
- 2, 3 = 001-
- 2,10 = -010
- 8,10 = 10-0
- 8,12 = 1-00
- 3,7 = 0-11
- 5,7 = 01-1
- 5,13 = -101
- 12,13 = 110-
- 7,15 = -111
- 13,15 = 11-1
Группировка 2:
- 0, 1 = 000-
- 2, 3 = 001-
- *12,13 = 110-
- 0, 2 = 00-0
- 1, 3 = 00-1
- 8,10 = 10-0
- 5,7 = 01-1
- 13,15 = 11-1
- 1, 5 = 0-01
- *8,12 = 1-00
- 3,7 = 0-11
- 0, 8 = -000
- 2,10 = -010
- 5,13 = -101
- 7,15 = -111
Склейка 2:
- *0,1,2,3 = 00–
- *0,2,8,10 = -0-0
- *5,7,13,15 = -1-1
- *1,3,5,7 = 0–1
Итого, члены сокращенной формы:
- 12,13 = 110-
- 8,12 = 1-00
- 0,1,2,3 = 00–
- 0,2,8,10 = -0-0
- 5,7,13,15 = -1-1
- 1,3,5,7 = 0–1
Редукция:
| 12,13 | × | × | |||||||||
| 8,12 | × | × | |||||||||
| 0,1,2,3 | × | × | × | × | |||||||
| 0,2,8,10 | × | × | × | ⊗ | |||||||
| 5,7,13,15 | × | × | × | ⊗ | |||||||
| 1,3,5,7 | × | × | × | × |
Кружком обведены члены ядра.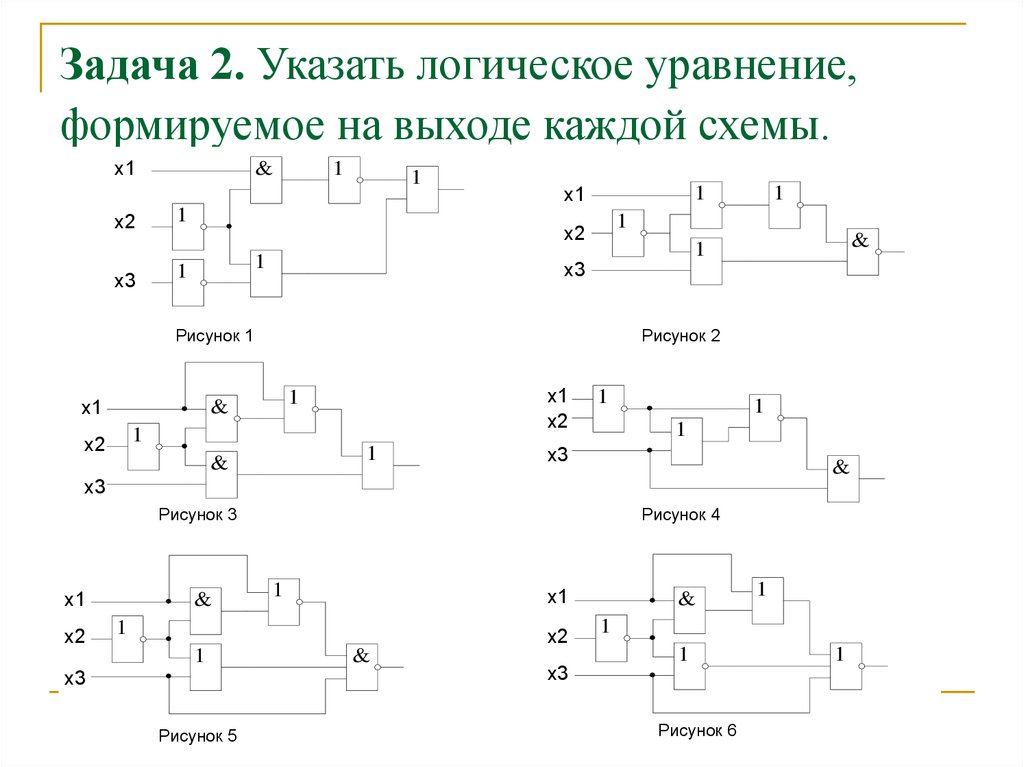
Ядро, таким образом, включает члены -0-0 и -1-1. Для получения минимальной формы, нам нужно перекрыть дополнительно столбцы 1, 3, 12. Для этого можно взять, например, 0,1,2,3 = 00– и 12,13 = 110-:
\[ f = \;\overline{x_2}\;\;\overline{x_4}\; \vee {x_2}{x_4} \vee \;\overline{x_1}\;\;\overline{x_2}\; \vee {x_1}{x_2}\;\overline{x_3}\; \]
Карта Карно:
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 |
ЕГЭ по информатике — академия разработки MediaSoft
О курсе
Для кого?
Школьники 10 и 11 классов, которые выбрали информатику для сдачи ЕГЭ.
Что дает курс?
- Изучим работу с информацией в базах данных, кодирование и декодирование информации и методы измерения количества информации.
- Разберем построение таблиц истинности и логических схем, работа в разных системах счисления, основы математической логики и работа с выражениями.

- Познакомим с принципами создания и анализа алгоритмов, построения дерева игры по заданному алгоритму и поиска выигрышной стратегии.
- Дадим представление об основах программирования.
О курсе
75 – средний балл посещавших занятие школьников с 2019 года.
Подготовка идет в течение всего учебного года. Занятия проходят онлайн на нашем YouTube-канале. В конце каждой недели даются домашние задания.
Программа курса
/01 тема
Представление и считывание данных в разных типах информационных моделей
Схемы;
Карты;
Таблицы;
Графики;
Формулы.
/02 тема
Построение таблиц истинности и логических схем
/03 тема
Технология хранения, поиска и сортировки информации в реляционных базах данных
/04 тема
Кодирование и декодирование информации
/05 тема
Формальное исполнение алгоритма, записанного на естественном языке
Умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд
/06 тема
Основные конструкции языка программирования
Понятие переменной;
Операторы присваивания.

/07 тема
Определение объема памяти, необходимого для хранения графической и звуковой информации
/08 тема
Методы измерения количества информации
/09 тема
Обработка числовой информации в электронных таблицах
/10 тема
Информационный поиск
С помощью операционной системы;
С помощью текстового процессора.

/11 тема
Подсчет информационного объема сообщения
/12 тема
Анализ результата исполнения алгоритма
/13 тема
Позиционные системы счисления
/14 тема
Основные понятия и законы математической логики
/15 тема
Вычисление рекуррентных выражений
/16 тема
Создание собственных программ для обработки целочисленной информации
Программа, состоящая из 20-40 строк
/17 тема
Обработка вещественных выражений в электронных таблицах
/18 тема
Анализ алгоритма логической игры
/19 тема
Поиск выигрышной стратегии игры
/20 тема
Построение дерева игры по заданному алгоритму и поиск выигрышной стратегии
/21 тема
Анализ алгоритма, содержащего ветвление и цикл
/22 тема
Анализ результата исполнения алгоритма
Регистрация на курс «Подготовка к ЕГЭ 2023 по информатике»
Регистрация на курс «Подготовка к ЕГЭ 2023 по информатике» прошла успешно.
Вступайте в telegram-канал курса.
Ссылка: https://t.me/+eoG9gVlmLKM4MGNi
Лучшие бесплатные онлайн-инструменты для моделирования логических элементов
Если вы изучаете электронику, вы, вероятно, знаете о важности логических элементов в цифровых схемах. Логические элементы являются одним из строительных блоков цифровых схем. Они выполняют все логические операции в цепи. Существует 7 типов логических элементов, а именно И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, XOR и XNOR. В этой статье мы перечислим некоторые лучшие бесплатные онлайн-инструменты для моделирования логических ворот, которые вы можете использовать для оттачивания своих навыков.
Здесь мы опишем функции трех бесплатных онлайн-инструментов моделирования логических ворот. Давайте начнем.
Симулятор логических ворот
Симулятор логических ворот имеет очень простой интерфейс, что делает его удобным инструментом для начинающих. Когда вы откроете его домашнюю страницу, вы обнаружите, что все логические элементы и другие входы и выходы расположены в нижней части интерфейса. Помимо логических элементов, он также содержит некоторые другие компоненты схемы, такие как защелка SR, триггер D-типа, триггер JK-типа, кнопка, переключатель, светодиодный выход и т. д.
Помимо логических элементов, он также содержит некоторые другие компоненты схемы, такие как защелка SR, триггер D-типа, триггер JK-типа, кнопка, переключатель, светодиодный выход и т. д.
Как использовать Logic Gate Simulator
Вы должны нарисовать свою схему в графическом пространстве, представленном на веб-сайте. Чтобы вставить логический элемент или другой компонент схемы, просто выберите его, а затем щелкните в любом месте графического пространства. После вставки компонентов вы можете использовать инструмент Move для перемещения компонентов в пространстве. Если вы хотите удалить компонент, сначала выберите инструмент Удалить на панели инструментов под графическим пространством, а затем щелкните элементы в пространстве, чтобы удалить их.
Когда вы закончите, нажмите кнопку Play , чтобы начать симуляцию.
Инструмент Logic Gate Simulator также поставляется с некоторыми предварительно разработанными моделями схем, в том числе:
- Flip Flop (два вентиля NOR)
- Счетчик пульсаций (триггеры JK)
- Сдвиговый регистр
- 4-битная дополнительная схема
Все эти схемы доступны в раскрывающемся меню Presets . Вы можете сохранить свой проект в формате файла JSON или экспортировать его в формате SVG.
Вы можете сохранить свой проект в формате файла JSON или экспортировать его в формате SVG.
CircuitVerse
CircuitVerse — еще один бесплатный онлайн-инструмент для моделирования логических элементов. Вы можете использовать этот инструмент без создания учетной записи на их веб-сайте, но если вы хотите сохранить свой проект в Интернете, вам необходимо создать учетную запись. При сохранении проекта вы можете сделать его общедоступным, частным и ограниченным. Кроме того, вы также можете написать описание вашего проекта. Если вы сохраните свой сохраненный проект в открытом доступе, он будет виден в поиске, и другие пользователи оценят его.
В CircuitVerse вы можете работать над несколькими проектами на разных вкладках. Чтобы открыть новую вкладку, нажмите на значок 9Значок 0015 Плюс .
Как пользоваться CircuitVerse
CircuitVerse прост в использовании. Все цифровые компоненты доступны в левой части интерфейса. К ним относятся вводы-выводы, логические элементы, декодеры и мультиплексоры, элементы последовательной схемы и т. д. Чтобы разместить логический элемент в рабочей области, разверните раздел Gates и выберите логический элемент по вашему выбору. Вы можете увеличивать и уменьшать масштаб рабочей области с помощью колеса прокрутки мыши или ползунка. Вы можете изменить свойства любого элемента, такие как пропускная способность, задержка и т. д., выбрав его в рабочей области.
д. Чтобы разместить логический элемент в рабочей области, разверните раздел Gates и выберите логический элемент по вашему выбору. Вы можете увеличивать и уменьшать масштаб рабочей области с помощью колеса прокрутки мыши или ползунка. Вы можете изменить свойства любого элемента, такие как пропускная способность, задержка и т. д., выбрав его в рабочей области.
CircuitVerse всегда остается в режиме симулятора. Это означает, что нет кнопки для запуска симуляции. Когда вы закончите проектирование схемы, просто нажмите на входы, чтобы изменить их состояние, и CircuitVerse покажет вам результат.
Он также имеет функцию Сохранить в автономном режиме , с помощью которой веб-сайт сохраняет ваш проект в локальном хранилище вашего веб-браузера. На мой взгляд, сохранение в автономном режиме не является правильным вариантом, потому что вы потеряете сохраненный проект, как только очистите файлы cookie и данные кеша в своем браузере. Поэтому лучше создать свою учетную запись на сайте, чтобы вы могли сохранить свой проект на сервере CircuitVerse.
Вы также можете скачать свой проект в виде изображения в различных форматах, включая PNG, JPEG, SVG, BMP, GIF и т.д. в этом списке. Он поставляется с удобным интерфейсом, который облегчает понимание для новичков. Компоненты цифровой схемы доступны на левой панели. Некоторые из компонентов цифровой схемы, которые содержит Logic.ly, включают тумблер, кнопку, лампочку, все логические элементы, триггеры и т. д.
Как использовать Logic.ly
Чтобы создать принципиальную схему, просто выберите компонент на левой панели и перетащите его в рабочее пространство. Когда вы размещаете компонент в пространстве, инструмент покажет вам его свойства. Вы можете изменить количество входов логического элемента в его свойствах. Максимально допустимое количество входов для логического элемента в этом инструменте равно восьми.
Чтобы нарисовать провода, просто поместите курсор мыши на входные или выходные узлы компонентов. После этого перетащите мышь, нажав ее левую кнопку мыши.
По умолчанию схема находится в режиме имитации. Это означает, что после создания схемы вам просто нужно нажать на входы, чтобы изменить их состояние. Вы можете остановить, возобновить и сбросить моделирование, щелкнув меню Simulate .
Вы можете создать таблицу истинности для любой схемы, нажав соответствующую кнопку на панели инструментов. Кроме того, вы можете перейти к «Редактировать > Таблица истинности ». По умолчанию он показывает вам таблицу истинности всех цепей вместе. Но если вы хотите просмотреть таблицу истинности для конкретной цепи, сначала вам нужно выбрать всю эту цепь, а затем нажать кнопку «Таблица истинности». Вы также можете экспортировать таблицу истинности в формате CSV.
Хотя параметры «Сохранить», «Печать» и «Экспорт» доступны только в платной версии, вы можете использовать этот инструмент для решения проблем с цифровыми схемами.
Связанные :
- Лучшие бесплатные онлайн-инструменты или веб-сайты для создания таблиц истинности.

- Лучшие бесплатные онлайн-инструменты для моделирования ПЛК.
Топ-5 бесплатных онлайн-сайтов для моделирования логических ворот
Рейтинги редакторов:
Рейтинги пользователей:
[Всего: 1 Среднее: 4]
В этой статье рассматриваются Топ-5 бесплатных онлайн-сайтов симуляторов логических ворот . С помощью этих симуляторов логических элементов вы можете легко проектировать и тестировать свои логические схемы в режиме онлайн. Некоторые из них довольно просты и будут очень полезны для новичков. Вы можете проектировать, тестировать и загружать свои схемы с помощью этих симуляторов логических элементов. В некоторых из них вы также можете загрузить свою схему и перепроектировать или проанализировать ее. Итак, давайте обсудим их один за другим.
Схема проектирования, таблица истинности, логическое выражение с использованием Logic Friday, универсального автономного решения для проектирования логических элементов.
Вот 5 лучших веб-сайтов онлайн-симуляторов логических ворот:
Academo.org
Academo.org — это веб-сайт, который предлагает различные интерактивные образовательные демонстрации и инструменты. У него есть бесплатный онлайн-симулятор логических вентилей , где вы можете моделировать логические схемы. Этот симулятор прост и удобен в использовании. Первоначально он дает вам источник ввода и индикатор вывода. Вы можете добавлять узлы с панели узлов справа. Панель содержит:
- Источник ввода
- НЕ
- И
- НЕ-И
- ИЛИ
- НИ
- Исключающее ИЛИ
Вы можете добавлять узлы, пока вся область не будет заполнена. Изменить положение компонентов легко, просто перетащив их. Соединения можно легко сделать с помощью курсора мыши. Чтобы удалить узел, просто щелкните маленький крестик в правом верхнем углу.
Попробуйте здесь.
NeuroProductions.be
NeuroProductions. be — вторая запись в этом списке из Онлайн-моделирование логических вентилей веб-сайтов. На этом веб-сайте есть симулятор «Лаборатория логики» , где вы можете спроектировать и протестировать свою логическую схему. Этот симулятор имеет некоторые дополнительные компоненты по сравнению с предыдущим. Эти компоненты:
be — вторая запись в этом списке из Онлайн-моделирование логических вентилей веб-сайтов. На этом веб-сайте есть симулятор «Лаборатория логики» , где вы можете спроектировать и протестировать свою логическую схему. Этот симулятор имеет некоторые дополнительные компоненты по сравнению с предыдущим. Эти компоненты:
- Ввод
- Логические элементы (И, НЕ-И, ИЛИ, ИЛИ, исключающее ИЛИ, исключающее ИЛИ, НЕ)
- Вьетнамки
- Дополнительно
- Выход
Чтобы добавить новый компонент, вам просто нужно перетащить его на доску. Соединения можно легко установить, просто перетащив курсор. Но вы не можете сделать два соединения в одной и той же точке. Для этого нужно использовать делитель.
В этом симуляторе логических элементов , когда вы закончите логическую схему, вы можете создать ссылку для обмена. И вы можете легко поделиться своей логической схемой с другими, просто поделившись этой ссылкой.
Попробуйте здесь.
DoCircuits.com
DoCircuits.com — веб-сайт для моделирования различных типов электронных схем. Он имеет «Моделирование логических элементов» , где вы можете моделировать логические элементы . Этот тренажер имеет большое разнообразие компонентов. Краткий список всех типов компонентов, которые есть в этом симуляторе логических вентилей, приведен ниже.
- Логические элементы
- Цифровые источники
- Измерительные устройства
- Комбинационная логика
- Последовательная логика (защелки и триггеры)
- Интегральные схемы (базовые ИС и усовершенствованные ИС)
Этот симулятор имеет функцию «Запуск и анализ» , которая отличает его от других. Здесь вы можете запускать и анализировать свою логическую схему в течение определенного интервала времени. Он показывает подробный анализ схемы для разных временных интервалов в виде графика. И вы можете сохранить этот аналитический график как изображение.
Логическую схему можно сохранить в вашей учетной записи DoCircuits.com. Также вы можете скачать свою схему в виде файла ‘.ckt’ .
Попробуйте здесь.
ScienceDemos.org
Следующей записью в этом списке бесплатных онлайн-симуляторов логических вентилей является ScienceDemos.org. Этот веб-сайт предлагает различные типы демонстраций Science; один из них — Симулятор логических ворот . Вместо списка компонентов по категориям все доступные компоненты расположены под рабочей областью платы. Чтобы добавить компонент на плату, сначала нажмите и выберите нужный компонент, а затем щелкните на плате, где вы хотите разместить этот компонент. Чтобы удалить компонент с платы, сначала активируйте режим удаления, щелкнув опцию удаления. Затем дважды щелкните компоненты, которые вы хотите удалить с платы.
Вы можете загрузить локальный файл схемы в симулятор для тестирования или перепроектирования. Чтобы проверить свою схему, нажмите кнопку воспроизведения в правом верхнем углу. По завершении вы можете загрузить свою схему, нажав кнопку Сохранить, , и схема будет загружена в вашу систему в формате файла .json .
По завершении вы можете загрузить свою схему, нажав кнопку Сохранить, , и схема будет загружена в вашу систему в формате файла .json .
Попробуйте здесь.
Doc.Gold.ac
Doc.Gold.ac — последний в этом списке онлайн-симуляторов логических вентилей. У этого нет функций, как у других. это простейший тренажер в этом списке. В разделе компонентов у вас есть логические вентили с некоторыми основными входными и выходными компонентами. В этом симуляторе также нет кнопки «Выполнить», поскольку он показывает результаты в режиме реального времени. Как только вы подносите компонент к плате, он начинает работать.
Чтобы добавить компонент, просто перетащите его на доску с боковой панели. И двойной щелчок по компоненту, присутствующему на плате, удалит его оттуда.
Чтобы переключить входное значение, вам нужно просто нажать на этот входной компонент. Этот симулятор логических ворот является базовым, что делает его хорошим вариантом для начинающих и детей.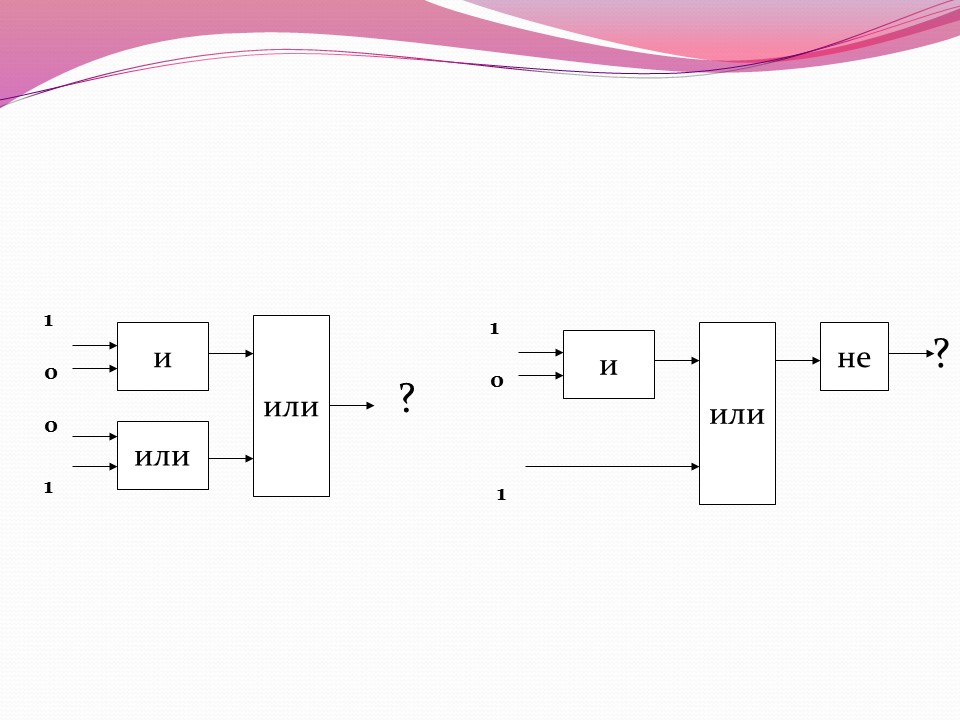
Проверьте это здесь.
Подведение итогов:
Все эти онлайн-симуляторы логических вентилей просто делают то, для чего они созданы. Они очень хороши для проверки логической схемы. Я предпочитаю DoCircuit.com из-за большой коллекции компонентов. Попробуйте их сами и расскажите нам, какой из них вам нравится и почему.
Схемы логических вентилей | 101 Компьютеры
Опубликовано администратором Опубликовано в Информатика, Вычислительные концепции, GCSE Concepts, GCSE Quiz, Physical Computing
Этот набор задач предназначен для выполнения с помощью логической платы, такой как доска логики и арифметики, разработанная Саутгемптонским университетом и Фондом электронных навыков Великобритании.
В качестве альтернативы, если у вас нет доступа к физическому комплекту, вы все равно можете выполнить эти задачи, используя онлайн-симулятор логических вентилей logic.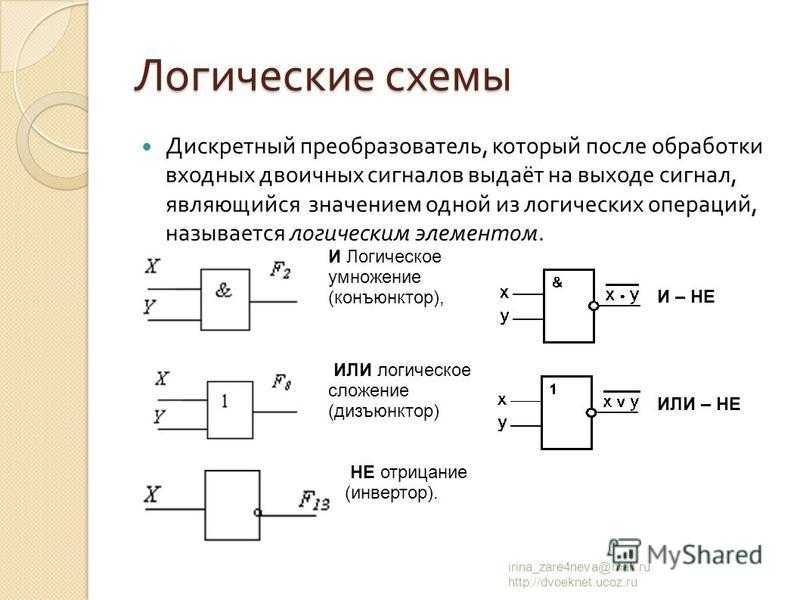 ly.
ly.
Шаг 1: Основные логические элементы
Для каждого из основных логических элементов воссоздайте схему, как показано на схеме. Затем используйте свою схему, чтобы составить таблицу истинности для логического элемента.
НЕ GateAND GateOR GateXOR GateNAND GateNOR Gate
| Вход J | Выход Х |
| 0 | 01 |
| 1 | 01 |
| Вход J | Вход К | Выход Х |
| 0 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 01 |
| Вход J | Вход К | Выход Х |
| 0 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 01 |
| Вход J | Вход К | Выход Х |
| 0 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 01 |
| Вход J | Вход К | Выход Х |
| 0 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 01 |
| Вход J | Вход К | Выход Х |
| 0 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 01 |
Шаг 2: Схемы логических элементов
Комбинируя несколько логических элементов вместе, вы можете создать схему, которая будет «вести себя» определенным образом.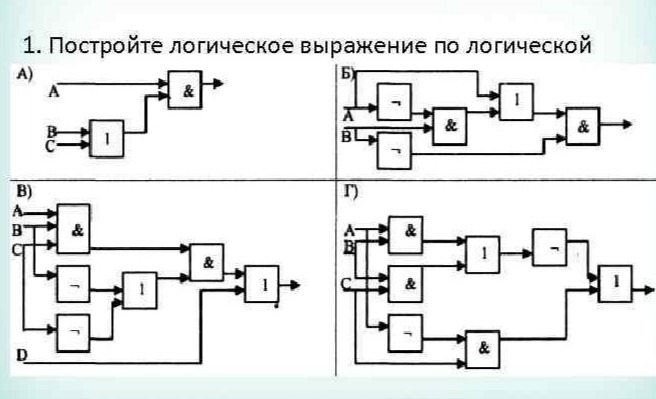 Чтобы записать, как схема «ведет себя» для любого заданного набора входных данных, мы используем таблицу истинности. Например, вы можете заполнить таблицу истинности для следующей схемы:
Чтобы записать, как схема «ведет себя» для любого заданного набора входных данных, мы используем таблицу истинности. Например, вы можете заполнить таблицу истинности для следующей схемы:
Схема логических элементов
| Вход J | Вход К | Вход L | Выход Х |
| 0 | 0 | 0 | 01 |
| 0 | 0 | 1 | 01 |
| 0 | 1 | 0 | 01 |
| 0 | 1 | 1 | 01 |
| 1 | 0 | 0 | 01 |
| 1 | 0 | 1 | 01 |
| 1 | 1 | 0 | 01 |
| 1 | 1 | 1 | 01 |
Шаг 3: Логические задачи
Ваша задача состоит в том, чтобы создать и протестировать схему логических элементов для каждой из данных задач:
Автомобильный светОхранная сигнализацияЗвук для смартфона
У маленького автомобиля 3 двери: 2 передние двери и хэтчбэк.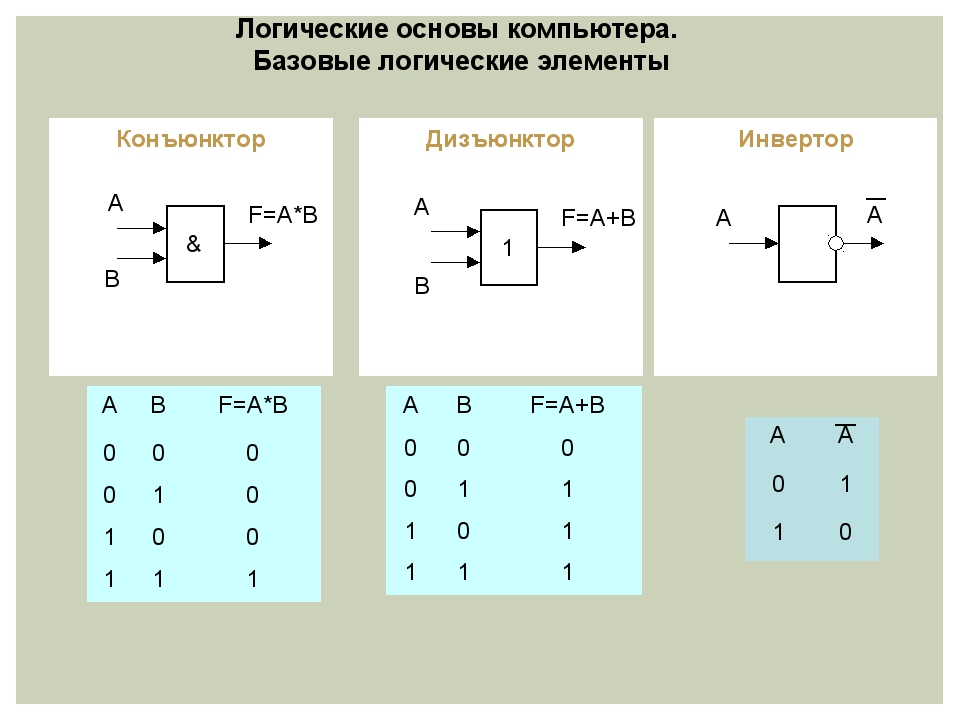 Внутренний свет автомобиля горит, когда любая из дверей автомобиля открыта.
Внутренний свет автомобиля горит, когда любая из дверей автомобиля открыта.
Создайте и протестируйте схему логических вентилей для управления внутренним освещением (X) автомобиля в зависимости от того, открыта ли дверь (J, K или L) (1) или закрыта (0).
| Вход J | Вход К | Вход L | Выход Х |
| 0 | 0 | 0 | 01 |
| 0 | 0 | 1 | 01 |
| 0 | 1 | 0 | 01 |
| 0 | 1 | 1 | 01 |
| 1 | 0 | 0 | 01 |
| 1 | 0 | 1 | 01 |
| 1 | 1 | 0 | 01 |
| 1 | 1 | 1 | 01 |
Охранная сигнализация имеет три входа:
- Вход J: Активирована ли охранная сигнализация (1) или нет (0).

- Вход K: датчик движения может обнаруживать движение (1) или нет (0).
- Вход L: датчик двери может определить, открыта ли передняя дверь (1) или закрыта (0).
Сирена сигнализации (X) должна быть включена, если сработала сигнализация и датчик движения обнаружил движение или датчик двери обнаружил, что дверь открыта.
Создайте и протестируйте схему логических элементов для управления сиреной этой охранной сигнализации на основе трех входов J, K и L.
| Вход J | Вход К | Вход L | Выход Х |
| 0 | 0 | 0 | 01 |
| 0 | 0 | 1 | 01 |
| 0 | 1 | 0 | 01 |
| 0 | 1 | 1 | 01 |
| 1 | 0 | 0 | 01 |
| 1 | 0 | 1 | 01 |
| 1 | 1 | 0 | 01 |
| 1 | 1 | 1 | 01 |
Рингтон на смартфоне воспроизводится, только если:
- На телефон поступает входящий вызов.
 (вход J = 1)
(вход J = 1) - Звук телефона включен. (вход К = 1)
- Телефон не находится в авиарежиме. (вход L = 0)
Создайте и протестируйте схему логических вентилей, чтобы контролировать, включена ли мелодия звонка смартфона (X=1) или нет (X=0) на основе трех входов J, K, L.
| Вход J | Вход К | Вход L | Выход Х |
| 0 | 0 | 0 | 01 |
| 0 | 0 | 1 | 01 |
| 0 | 1 | 0 | 01 |
| 0 | 1 | 1 | 01 |
| 1 | 0 | 0 | 01 |
| 1 | 0 | 1 | 01 |
| 1 | 1 | 0 | 01 |
| 1 | 1 | 1 | 01 |
Дополнительное задание: Таинственные врата!
Таинственные врата
Вышеупомянутая схема логических вентилей может быть заменена одним логическим вентилем! Воссоздайте эту схему на своей логической плате, чтобы протестировать ее и заполнить ее таблицу истинности.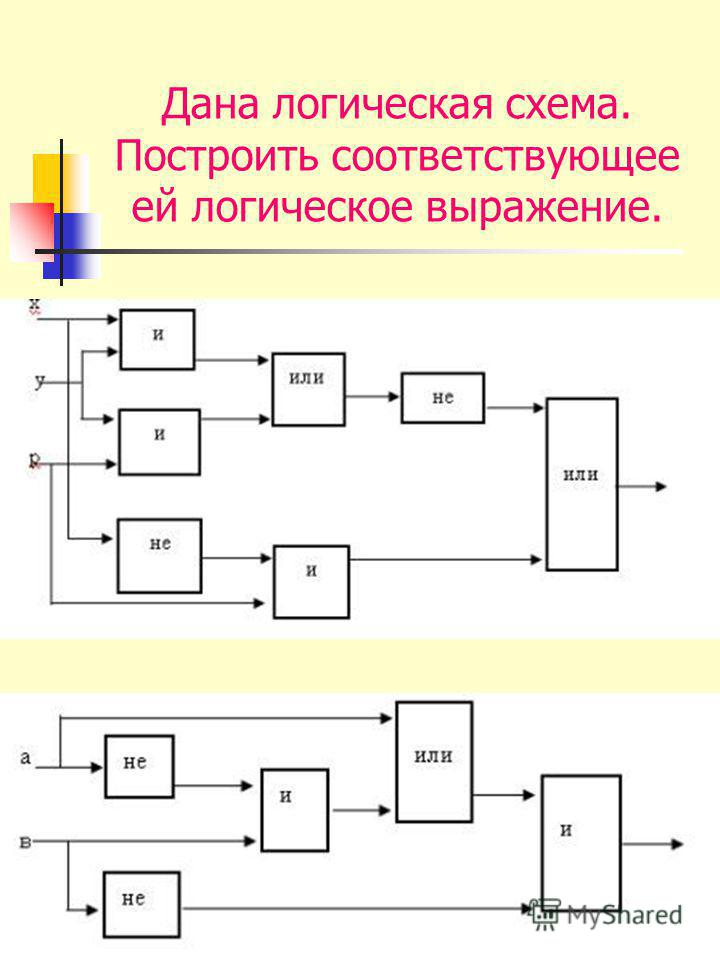



 (вход J = 1)
(вход J = 1)