§1.8.1. Логические схемы полусумматора и триггера
Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 11 классы | Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень) | §1.8. Модели логических устройств
Содержание урока
1.8.1. Логические схемы полусумматора и триггераПолусумматор
Триггер
Контрольные вопросы
1.8.2. Модели логических устройств компьютера на языке Visual Basic1.8.3. Модели логических устройств компьютера на языке Turbo Delphi1.8.4. Модели логических устройств компьютера в электронных таблицахПолусумматор
При изучении базовых логических устройств компьютера (сумматор, триггер) целесообразно использовать компьютерные модели. Такие модели позволяют визуализировать процесс преобразования логических значений входных сигналов в значения выходных сигналов.
Такие модели позволяют визуализировать процесс преобразования логических значений входных сигналов в значения выходных сигналов.
Полусумматор. Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в старший разряд. Обозначим слагаемые А, В, перенос Р и сумму S. Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом (табл. 1.3).
Таблица 1.3. Таблица сложения с учетом переноса
| Слагаемые | Перенос | Сумма | |
| A | B | S | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:
Р = А & В.
Получим теперь формулу для вычисления суммы. Значения суммы более всего совпадают с результатом операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
S = (A ∨ В) & (А & В).
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предположения (табл. 1.4).
Таблица 1.4. Таблица истинности логической функции S = (A ∨ В) & (А & В)
| A | B | A ∨ В | А & В | (А & В) | (A ∨ В) & (А & В) |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему полусумматора.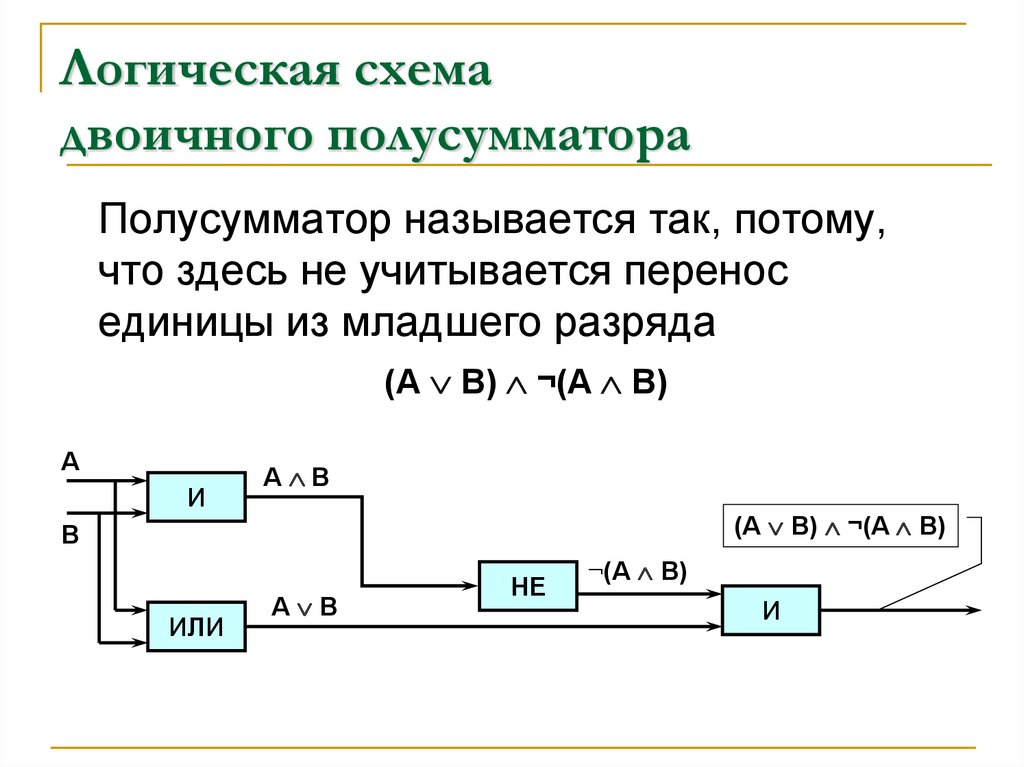 Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел А и В без учета переноса из младшего разряда.
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел А и В без учета переноса из младшего разряда.
По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент И.
Анализ логической формулы для суммы показывает, что на выходе должен стоять элемент логического умножения
На второй вход требуется подать результат инвертированного логического умножения исходных сигналов А & В, т. е. на второй вход подается сигнал с элемента НЕ, на вход которого, в свою очередь, поступает сигнал с элемента логического умножения И (рис.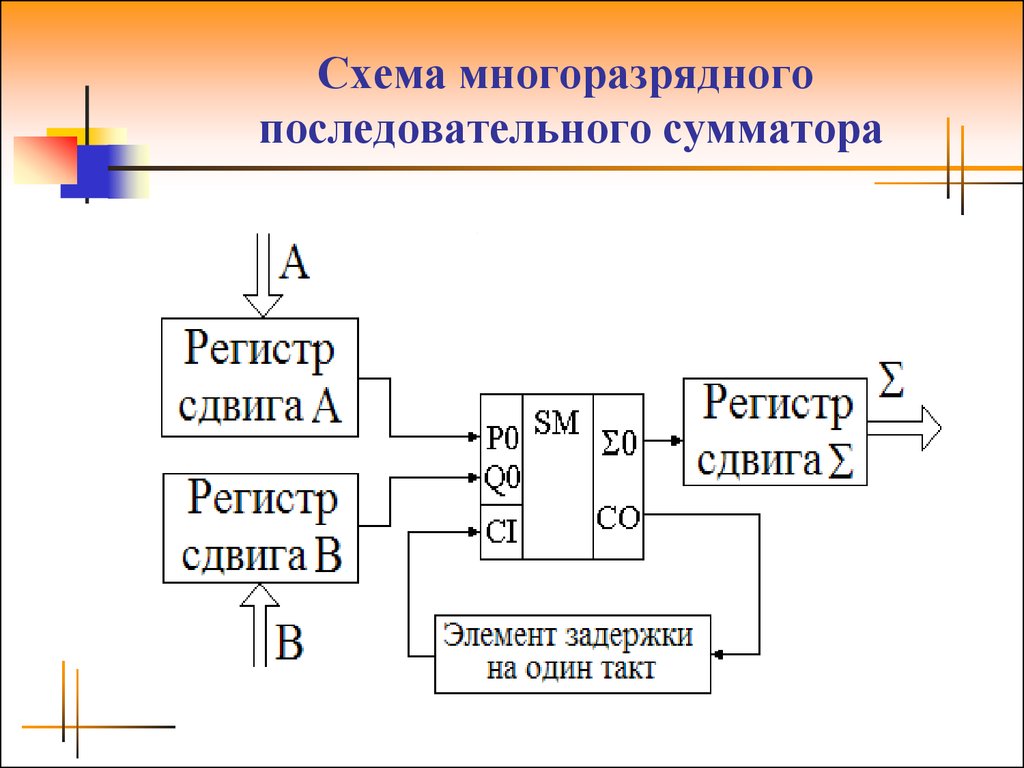
Рис. 1.39. Логическая схема полусумматора
Следующая страница Триггер
Cкачать материалы урока
Разработка сумматора для сложения в байтовом формате
Автор: Лобашевская Вероника Александровна
Рубрика: Информационные технологии
Опубликовано в Молодой учёный №3 (398) январь 2022 г.
Дата публикации: 25.01.2022 2022-01-25
Статья просмотрена: 117 раз
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание: Лобашевская, В.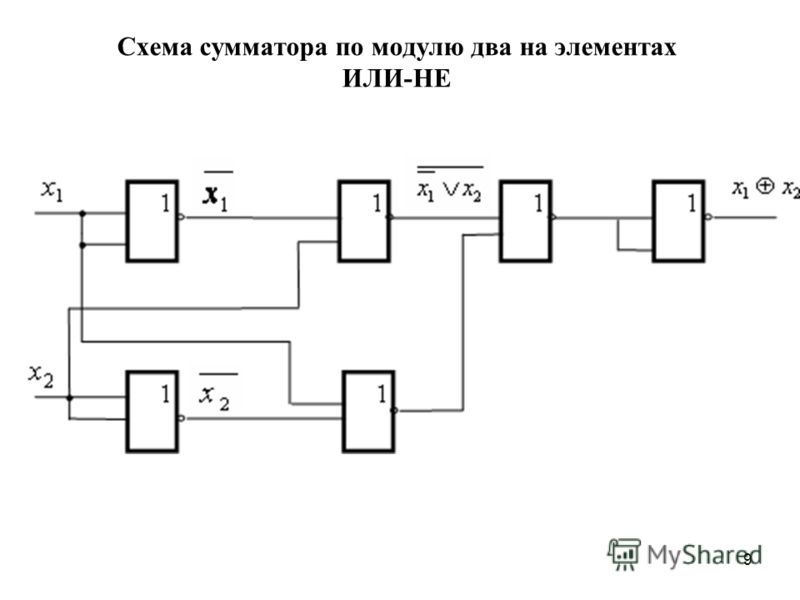 А. Разработка сумматора для сложения в байтовом формате / В. А. Лобашевская. — Текст : непосредственный // Молодой ученый. — 2022. — № 3 (398). — С. 5-10. — URL: https://moluch.ru/archive/398/88155/ (дата обращения: 31.12.2022).
А. Разработка сумматора для сложения в байтовом формате / В. А. Лобашевская. — Текст : непосредственный // Молодой ученый. — 2022. — № 3 (398). — С. 5-10. — URL: https://moluch.ru/archive/398/88155/ (дата обращения: 31.12.2022).
Статья посвящена описанию процесса проектирования и разработки сумматора для сложения в байтовом формате.
Ключевые слова: логический элемент, байтовый формат, полусумматор, сумматор, electronics workbench.
Введение
Одним из основных арифметических узлов ЭВМ является сумматор. Это так, потому что большинство математических операций (вычитание, умножение, деление, вычисление тригонометрических функций, извлечение корня и т. д.) можно свести к единственной операции сложения прямых, обратных или сдвинутых на определенное число разрядов кодов чисел.
Полусумматоры
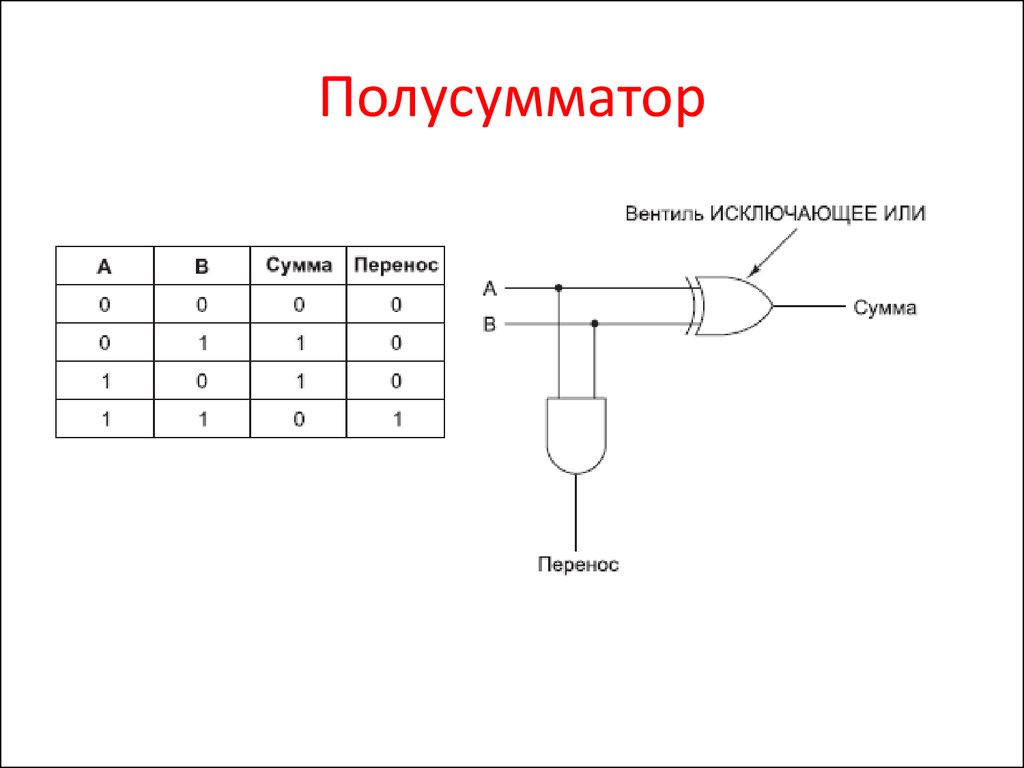
Полусумматор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор).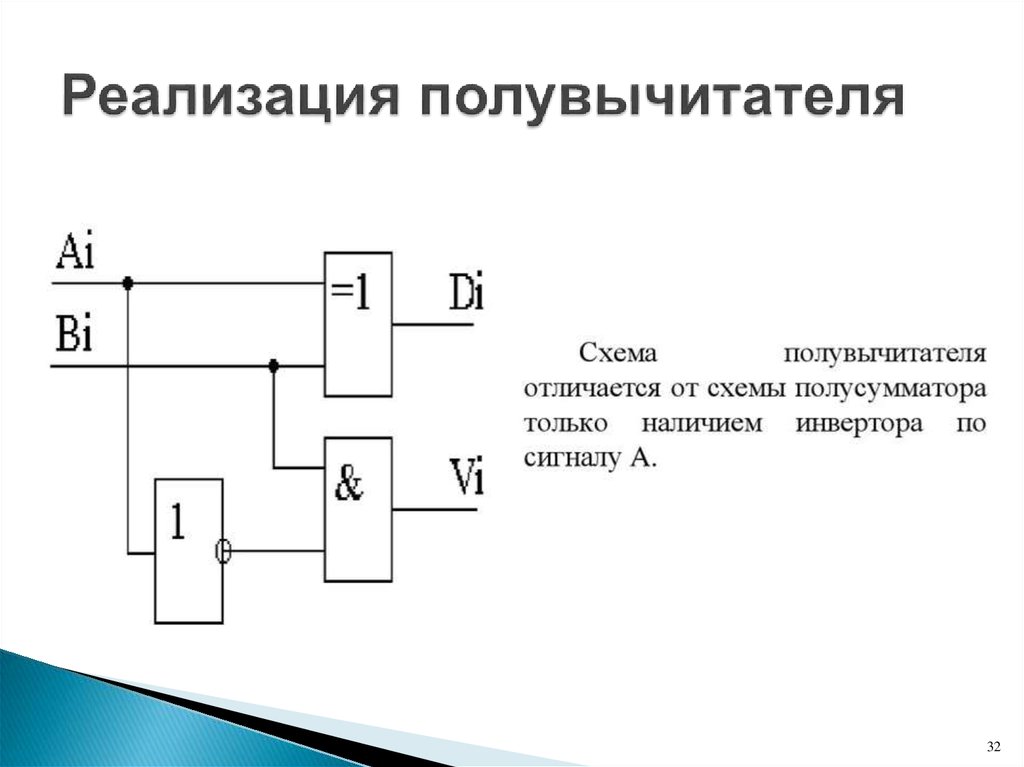 Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и P, где S — это бит суммы по модулю, а P — бит переноса. Схема полусумматора изображена на рисунке 1.
Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и P, где S — это бит суммы по модулю, а P — бит переноса. Схема полусумматора изображена на рисунке 1.
Рис. 1. Схема полусумматора
Простейшим вариантом сложения является сложение двух одноразрядных двоичных чисел, при котором возможны варианты:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10.
Операция суммирования двух одноразрядных чисел совпадает с логической функцией Исключающее ИЛИ, которая характеризуется таблицей истинности, представленной на рисунке 2. Логическим уравнением, полученным из этой таблицы, является , где — знак суммирования по модулю.
Рис. 2. Суммирования двух одноразрядных чисел
Полные сумматоры
Сумматор — это узел ЭВМ, в котором суммируются коды чисел. Сумматоры многоразрядных чисел, которыми оперирует машина, составляются из одноразрядных сумматоров.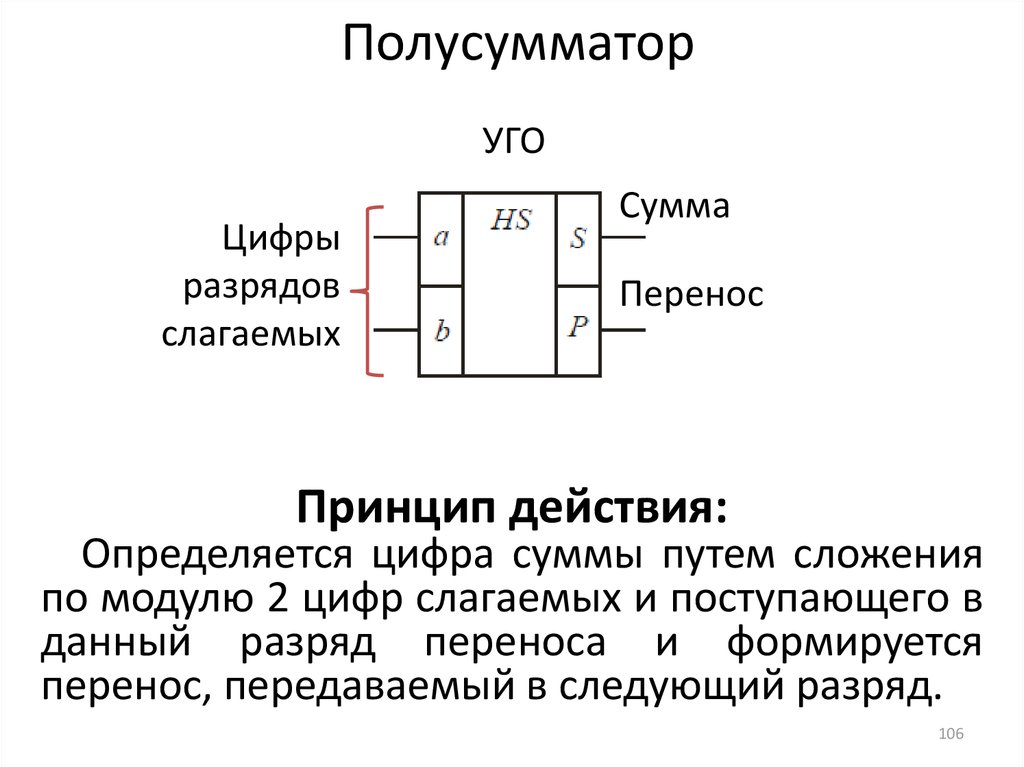
Сумматоры накапливающего типа строят на сложных JKRS-триггерах, дополняя их выходы достаточно сложными схемами формирования и распространения переносов. Процесс сложения при этом осуществляется поэтапно. Сначала на триггерах сумматора фиксируется код первого операнда, затем на счетные коды разрядов подается код второго операнда. По зависимостям на каждом триггере формируются одноразрядные суммы и значения переносов между разрядами. Учет возникающих переносов задерживает формирование окончательного результата суммы и может требовать дополнительных тактов сложения. Из-за этого многоразрядные схемы сумматора накапливающего типа используются достаточно редко.
Более часто для построения сумматоров используются сумматоры комбинационного типа. Обычно у такого сумматора на входе и выходе имеются регистры для хранения и преобразования кодов операндов и результата.
В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа. Чтобы учесть перенос получается схема из двух полусумматоров. Схема сумматора на рисунке 3.
Рис. 3. Схема сумматора
Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определим сумму текущего разряда. С помощью ИСКЛЮЧАЮЩЕГО ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее, ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0.
Теперь рассмотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль входят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т. е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности, представленной на рисунке 4.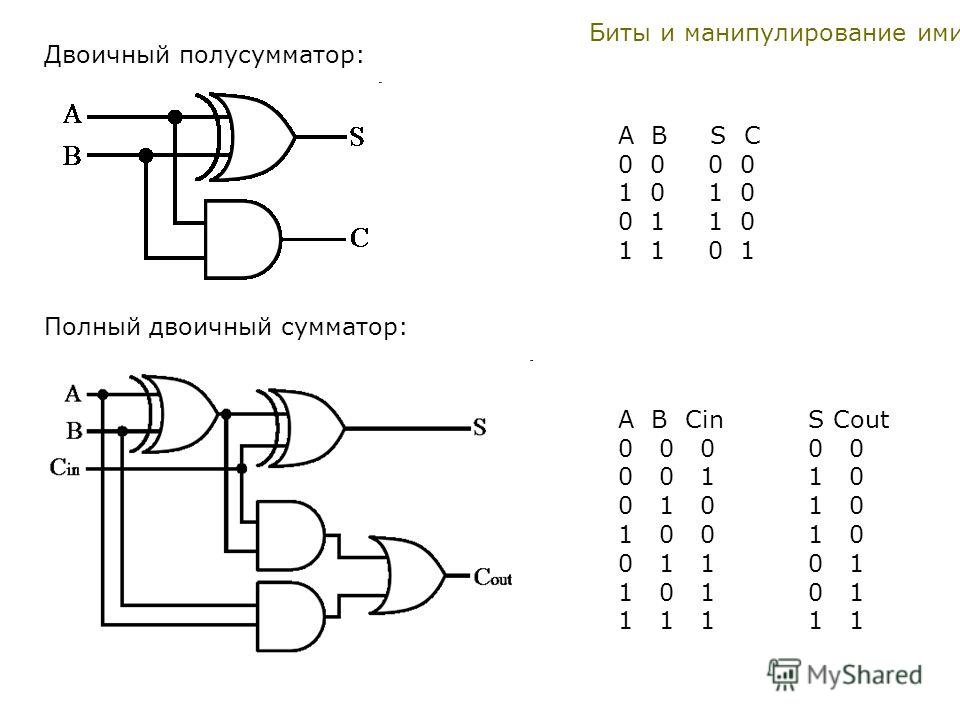
Рис. 4. Таблица истинности сумматора
Разработка схемы байтового сумматора
Необходимо собрать схему многоразрядного сумматора. Многоразрядный сумматор создается на базе одного полусумматора и полных сумматоров. В одном байте восемь бит, следовательно нам понадобится один полусумматор и семь полных сумматоров.
Числа для сложения будут заданы в генераторе слов. Первые 8 бит — первое число, вторые восемь бит — второе число.
Результат сложения покажут индикаторы. При условии, что сумматор был бы меньше чем на восемь бит, мы могли бы использовать индикатор дисплей на 4 или на 7 входов. Но так как 7 входов для байтового сумматора мало, используем индикатор красный зонд для каждой суммы. Получится ряд из восьми индикаторов, который покажет двоичную запись числа результата.
Схема байтового сумматора на рисунке 5. Числа в генераторе слов записываются справа налево. Восемь правых бит — это число B. Каждый бит начиная с самого правого подключается к блокам полусумматора и сумматоров начиная с полусумматора.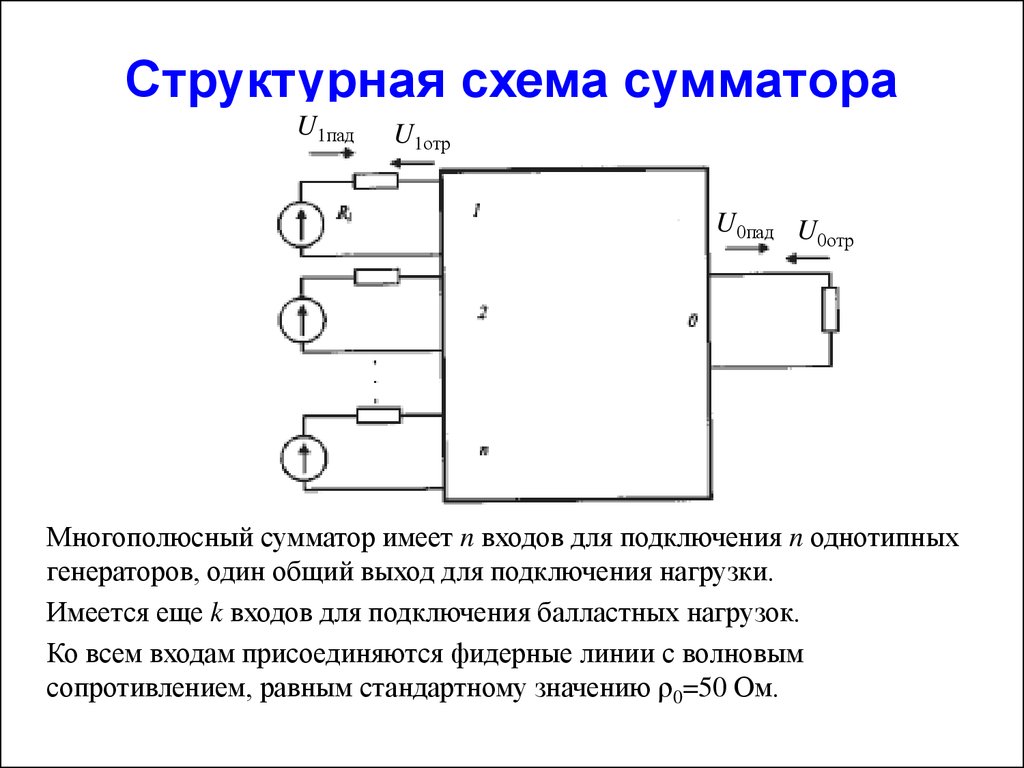 Восемь левых бит — это число A. Подключение происходит аналогично числу B, но на вход A.
Восемь левых бит — это число A. Подключение происходит аналогично числу B, но на вход A.
Рис. 5. Схема байтового сумматора
Результаты работы программы
Чтобы проверить работу программы, запустим ее несколько раз с различными входными данными.
1) 3 + 5 = 8, в двоичном представлении 1000. Результат на рисунке 6.
Рис. 6. 3 + 5 = 8, в двоичном представлении 1000
2) 7 + 6 = 13, в двоичном представлении 1101. Результат на рисунке 7.
Рис. 7. 7 + 6 = 13, в двоичном представлении 1101
3) 125 + 130 = 255, в двоичном представлении 11111111. Результат на рисунке 8.
Рис. 8. 125 + 130 = 255, в двоичном представлении 11111111
Расчет мощности и надежности
Значения потребляемой мощности на основе справочных данных для каждого элемента определяем по формуле
, где N — количество логических элементов в схеме;
— мощность, потребляемая одним элементом.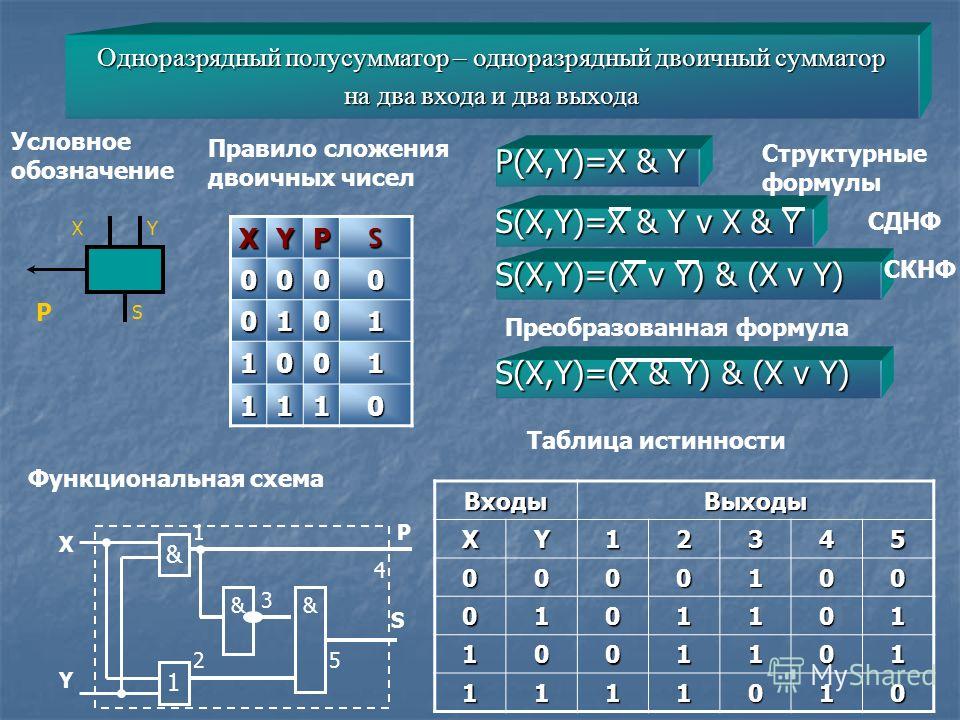
В схеме байтового сумматора 8 элементов. Один полусумматор и 7 сумматоров. Потребляемая мощность элементов указана в таблице 1.
Таблица 1
Потребляемая мощность элементов
Элемент | Мощность, Вт | Количество элементов |
Полусумматор | 1,05 | 1 |
Сумматор | 1,05 | 7 |
Следовательно мощность разрабатываемого устройства будет равна 1*1,05 + 7*1,05, то есть 8,4 Вт.
Среднее время наработки до отказа считаем по формуле:
, где
— суммарная интенсивность отказов всех элементов.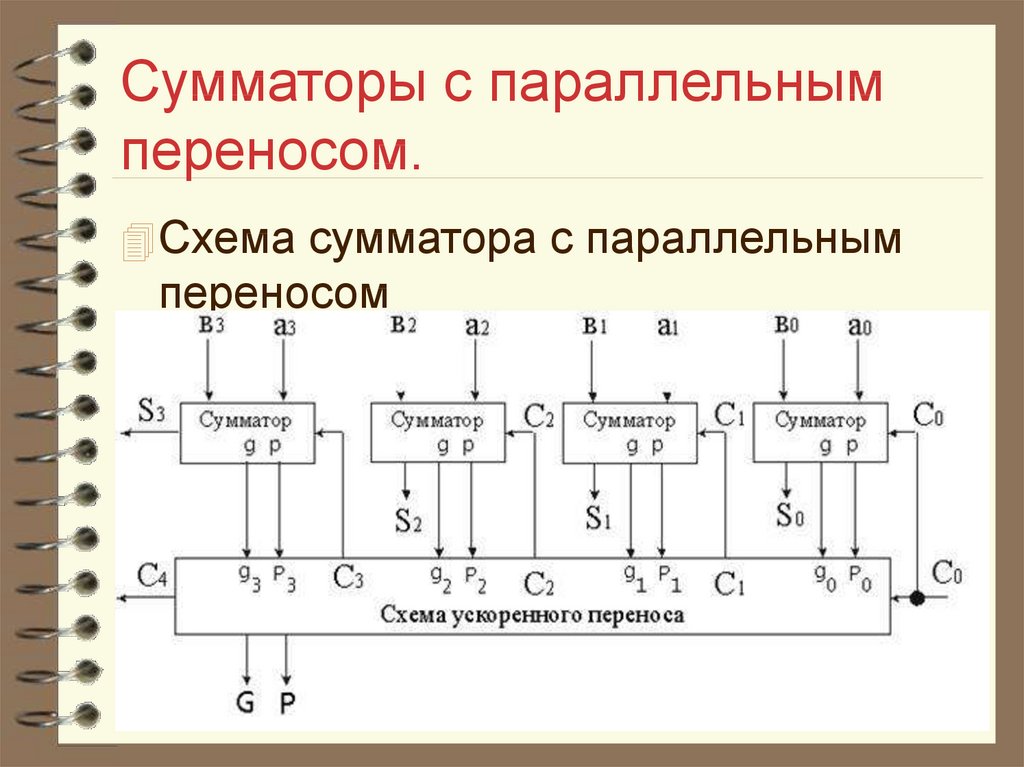
Таблица 2
Потребляемая мощность элементов
Элемент | Интенсивность отказа *10– 6 | Количество элементов |
Полусумматор | 0,023 | 1 |
Сумматор | 0,023 | 7 |
Следовательно среднее время наработки до отказа будет равно 1/(0,023*1*10– 6 + 0,023*7*10– 6 ), то есть 184000 часов. Из данных расчетов можно сделать вывод о высокой надежности.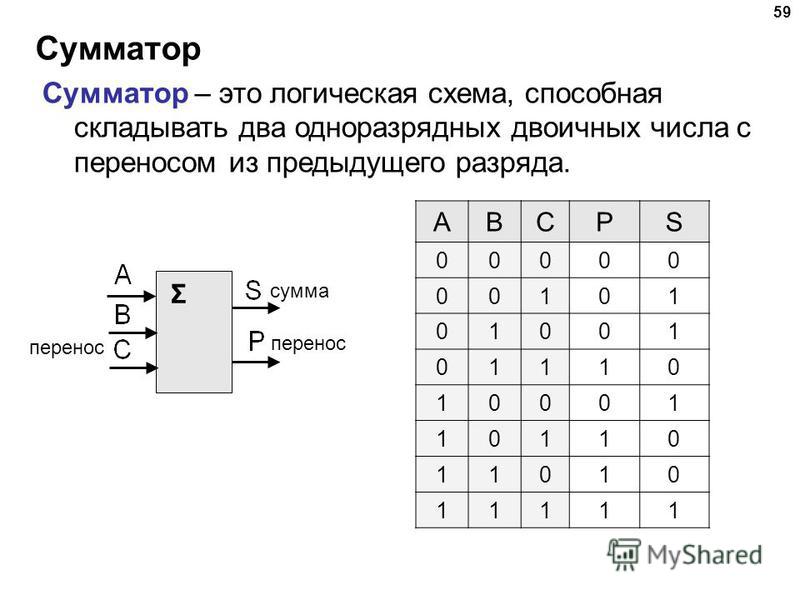
Заключение
В результате работы спроектирован и разработан сумматора для сложения в байтовом формате. Мощность устройства равна 8,4 Вт, среднее время наработки 184000 часов.
Литература:
- М. А. Карцев. Арифметика цифровых машин. Главная редакция физико-математической литературы издательства «Наука», 1969, 576 с.
- Лю, Цо-Кай; Хохулин, Кейт Р.; Шиау, Лих-Эр; Мурога, Сабуро (январь 1974 г.). «Оптимальные однобитовые полные сумматоры с разными типами вентилей», 1995, 243 с.
- Сведения о полусумматоре [Электронный ресурс]. — https://ru.wikipedia.org/wiki/Полусумматор
- Сведения о сумматоре [Электронный ресурс]. — https://inf1.info/adder
Основные термины (генерируются автоматически): сумматор, двоичное представление, байтовый сумматор, бит, полусумматор, число, байтовый формат, время наработки, накапливающий тип, потребляемая мощность элементов.
Ключевые слова
сумматор, логический элемент, байтовый формат, полусумматор, electronics workbenchлогический элемент, байтовый формат, полусумматор, сумматор, electronics workbench
Похожие статьи
Метод построения блока бесконтактных кнопок в системах.
 ..
..В статье проанализированы методы построения устройств с бесконтактными кнопками. Бесконтактные кнопки представляют собой датчики, с помощью которых возможен набор информации. Используются для нескольких целей, таких как: защита информации, борьба с…
Макроэконометрические модели в экономике | Статья в журнале…
Моделирование национальных экономик зародилось еще в далеком прошлом. Заполнив пробел между макроэкономической теорией и эмпирическими описаниями функционирования и роста национальных экономик, оно стало основным инструментом эмпирической проверки…
Структурная и параметрическая идентификация котельного…
В данной статье рассмотрен водогрейный котел как многомерный объект управления. В соответствии с технологическим процессом определены входные и выходные параметры объекта. Построена математическая модель многомерного, многосвязного объекта в виде.. .
.
QR-коды, их свойства и применение | Статья в журнале…
‒ Двоичный код — 2953 байта (следовательно, около 2953 букв кириллицы в кодировке windows-1251 или 1450 букв кириллицы в utf-8)
Сначала определяется количество байт в каждом из блоков, затем идет их последовательное заполнение.
Разработка четырехразрядного арифметико-логического…
Потребляемая мощность разрабатываемого устройства будет равна сумме мощностей, потребляемых его элементами.
Сумматор.
Среднее время наработки до отказа считаем по формуле
Big Data. Особенности и роль в современном бизнесе
Если говорить о типах данных, для которых применимы рассматриваемые методы обработки
‒ полное понимание о своей компании и бизнесе, в том числе с точки зрения статистической
А программное обеспечение, которое структурирует и анализирует накапливаемые данные.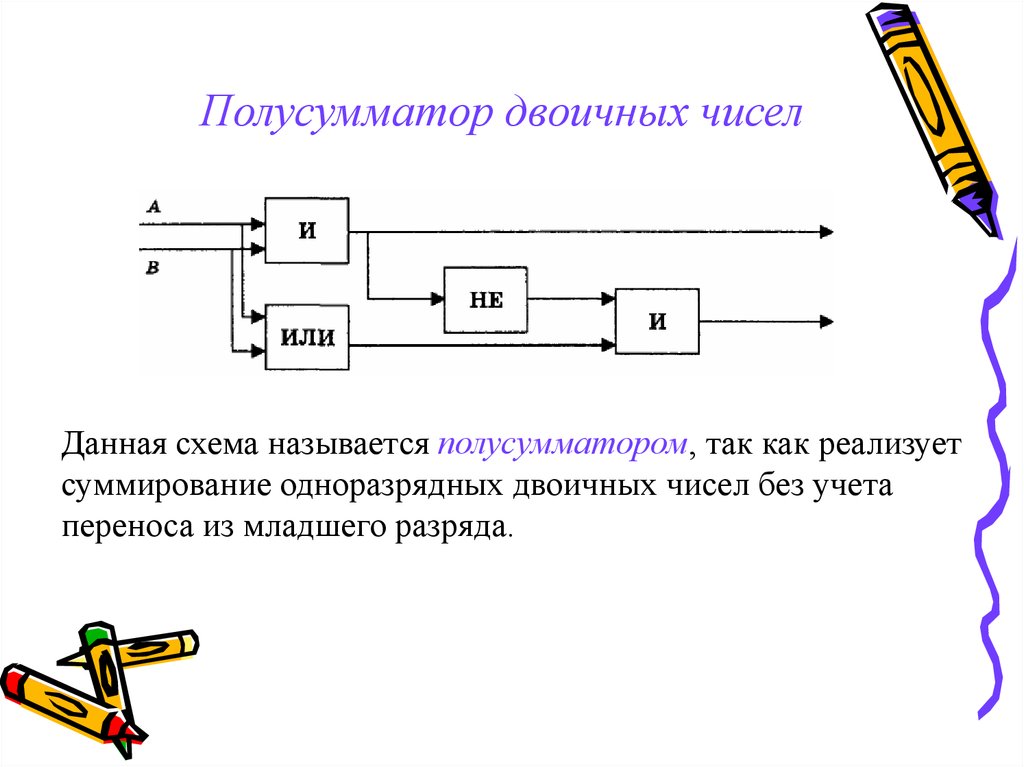 ..
..
О проверке кратности
чисел в двоичной системе счисления…Для определения кратности 5 число необходимо разбить на группы по 2 бита. Сложить между собой все группы на четных и на нечетных позициях отдельно.
Для проверки на кратность 9 10 (100110 2 ) разобьём 8 битов, формирующих двоичное число, на три группы по три бита…
Ключевые технологии цифровой экономики | Статья в журнале…
В данной статье рассматриваются некоторые из ключевых технологий цифровой экономики, такие, как BIM, PLM, IoT, SRM, BIG DATA. Определены преимущества и риски использования технологий цифровой экономики, а также их роль в её развитии.
Похожие статьи
Метод построения блока бесконтактных кнопок в системах…
В статье проанализированы методы построения устройств с бесконтактными кнопками. Бесконтактные кнопки представляют собой датчики, с помощью которых возможен набор информации. Используются для нескольких целей, таких как: защита информации, борьба с…
Бесконтактные кнопки представляют собой датчики, с помощью которых возможен набор информации. Используются для нескольких целей, таких как: защита информации, борьба с…
Макроэконометрические модели в экономике | Статья в журнале…
Моделирование национальных экономик зародилось еще в далеком прошлом. Заполнив пробел между макроэкономической теорией и эмпирическими описаниями функционирования и роста национальных экономик, оно стало основным инструментом эмпирической проверки…
Структурная и параметрическая идентификация котельного…
В данной статье рассмотрен водогрейный котел как многомерный объект управления. В соответствии с технологическим процессом определены входные и выходные параметры объекта. Построена математическая модель многомерного, многосвязного объекта в виде…
QR-коды, их свойства и применение | Статья в журнале…
‒ Двоичный код — 2953 байта (следовательно, около 2953 букв кириллицы в кодировке windows-1251 или 1450 букв кириллицы в utf-8)
Сначала определяется количество байт в каждом из блоков, затем идет их последовательное заполнение.
Разработка четырехразрядного арифметико-логического…
Потребляемая мощность разрабатываемого устройства будет равна сумме мощностей, потребляемых его элементами.
Сумматор.
Среднее время наработки до отказа считаем по формуле
Big Data. Особенности и роль в современном бизнесе
Если говорить о типах данных, для которых применимы рассматриваемые методы обработки
‒ полное понимание о своей компании и бизнесе, в том числе с точки зрения статистической
А программное обеспечение, которое структурирует и анализирует накапливаемые данные…
О проверке кратности
чисел в двоичной системе счисления…Для определения кратности 5 число необходимо разбить на группы по 2 бита.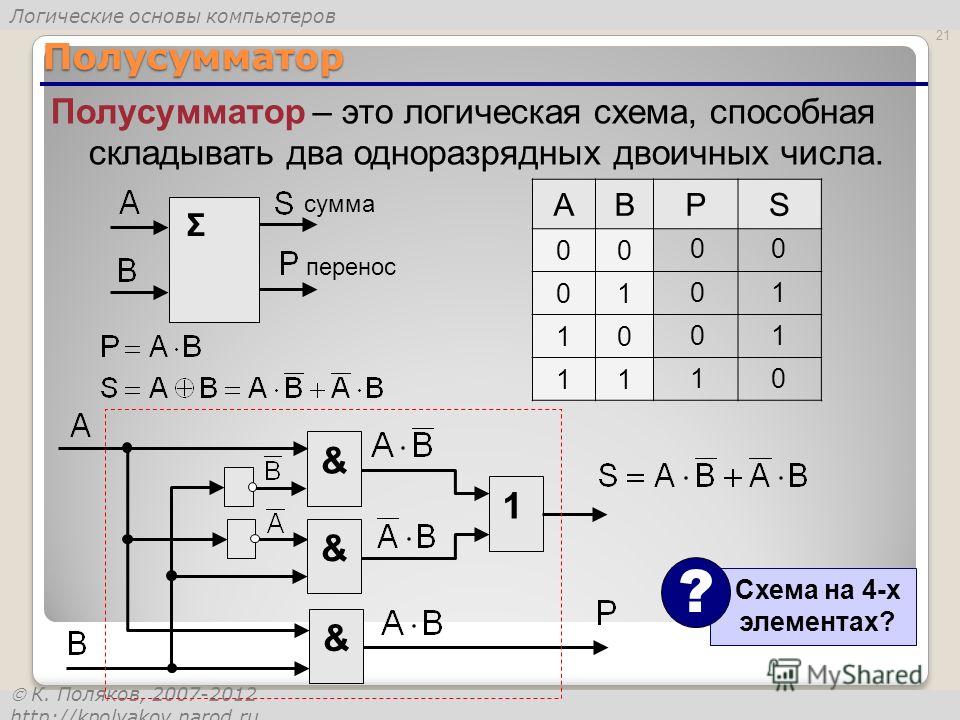 Сложить между собой все группы на четных и на нечетных позициях отдельно.
Сложить между собой все группы на четных и на нечетных позициях отдельно.
Для проверки на кратность 9 10 (100110 2 ) разобьём 8 битов, формирующих двоичное число, на три группы по три бита…
Ключевые технологии цифровой экономики | Статья в журнале…
В данной статье рассматриваются некоторые из ключевых технологий цифровой экономики, такие, как BIM, PLM, IoT, SRM, BIG DATA. Определены преимущества и риски использования технологий цифровой экономики, а также их роль в её развитии.
и схема полного сумматора с использованием вентилей NAND
В этом руководстве мы узнаем о двух важных схемах комбинационной логики, известных как схема полусумматора и схема полного сумматора. Они являются основными строительными блоками двоичных арифметических схем (схем, которые выполняют сложение, вычитание, умножение и деление).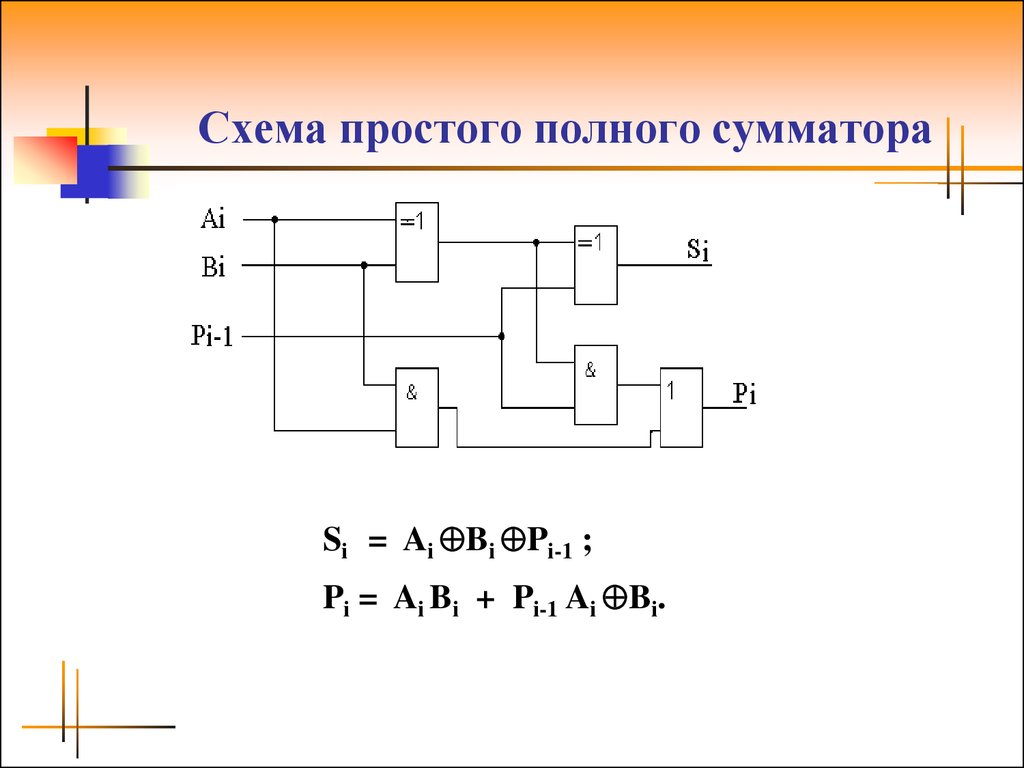 Давайте сосредоточимся на двоичном сложении с использованием схем полусумматора и полного сумматора, их логических выражений, а также на их аппаратной конструкции с использованием различных логических вентилей.
Давайте сосредоточимся на двоичном сложении с использованием схем полусумматора и полного сумматора, их логических выражений, а также на их аппаратной конструкции с использованием различных логических вентилей.
Краткое описание
Введение
Сумматоры представляют собой цифровые схемы, выполняющие сложение чисел. Сумматоры являются ключевым компонентом арифметико-логического устройства (АЛУ) внутри любого процессора. Сумматоры могут быть сконструированы для большинства числовых представлений, таких как двоично-десятичное числовое представление (BDC), превышение — 3, код Грея, двоичное число и т. д.
Из них двоичное сложение является наиболее часто выполняемой задачей наиболее распространенных сумматоров. Кроме того, сумматоры также используются в некоторых цифровых приложениях, таких как вычисление индекса таблицы, декодирование адреса и т. д.
Двоичное сложение аналогично десятичному сложению. Сложите первые цифры числа, и если счет превышает двоичную 2, то перенесите «1» в следующую строку.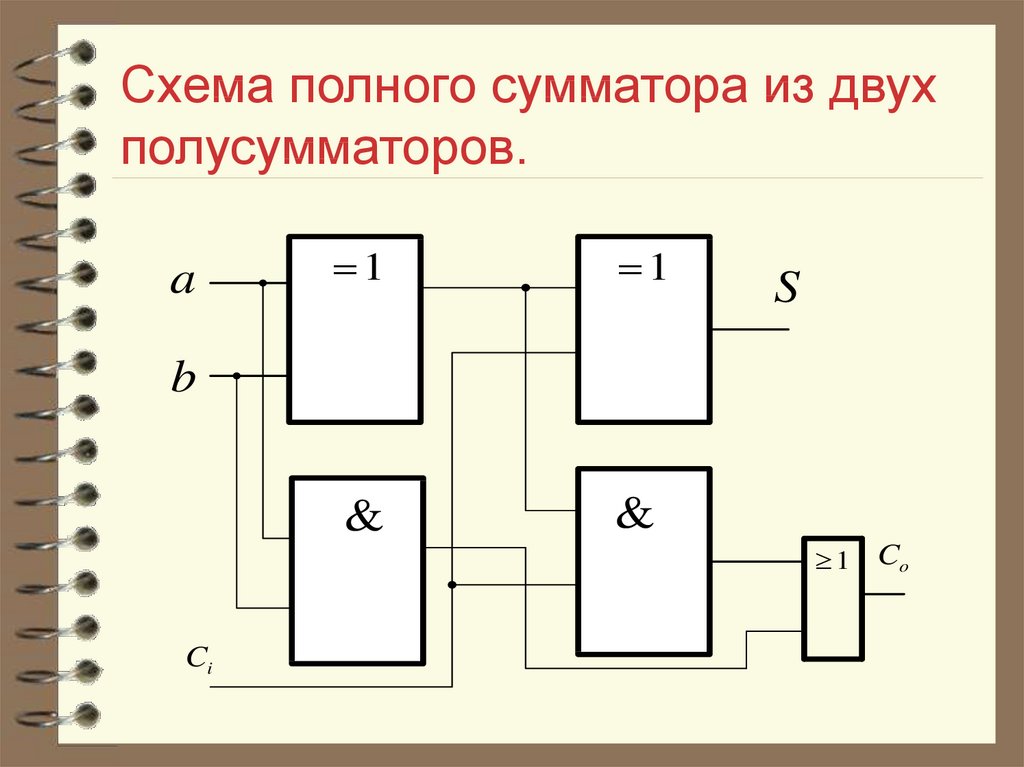 Некоторые основные бинарные дополнения показаны ниже.
Некоторые основные бинарные дополнения показаны ниже.
Сумматор, выполняющий простое двоичное сложение, должен иметь два входа (возврат и сложение) и два выхода (сумма и перенос). Устройство, выполняющее указанную выше задачу, называется полусуммером. Полный сумматор — это еще одна схема, которая может складывать три числа (два бита из чисел и один бит переноса из предыдущей суммы).
Схема полусумматора
Полусумматор представляет собой комбинационную схему, которая выполняет простое сложение двух однобитовых двоичных чисел и дает 2-битное число. Младший бит результата представляет собой сумму (обычно представленную как Sum или S 0 или ∑ 0 ), а старший бит представляет собой перенос (обычно представленный как C OUT ).
Блок-схема полусумматора показана ниже.
Здесь «A» и «B» представляют входные два бита, которые необходимо добавить, а выходы — «Sum» и «Carry».
Таблица истинности полусумматора
Если предположить, что A и B являются двумя битами, сложение которых должно быть выполнено, таблица истинности для полусумматора с A, B в качестве входов и Sum, Carry в качестве выходов может быть сведена в таблицу следующим образом.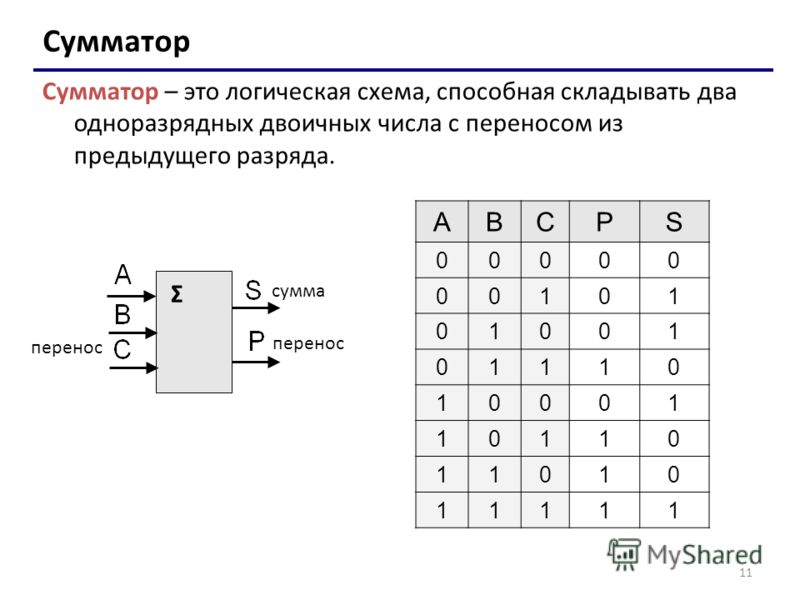
| ВХОД | ВЫХОД | ||
| А | Б | Сумма | Переноска |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Если вы наблюдаете таблицу истинности, вывод суммы двоичного сложения, выполненного выше, аналогичен выводу операции Ex-OR, а вывод переноса аналогичен выводу операции И. То же самое можно проверить с помощью карты Карно.
Таблица истинности и представление K-Map для вывода Sum показаны ниже.
| А | Б | Сумма |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мы можем вывести логическое выражение суммы следующим образом:
Сумма = A B + A B
Сумма = А ⊕ В
Таким образом, логическая схема для суммы показана ниже.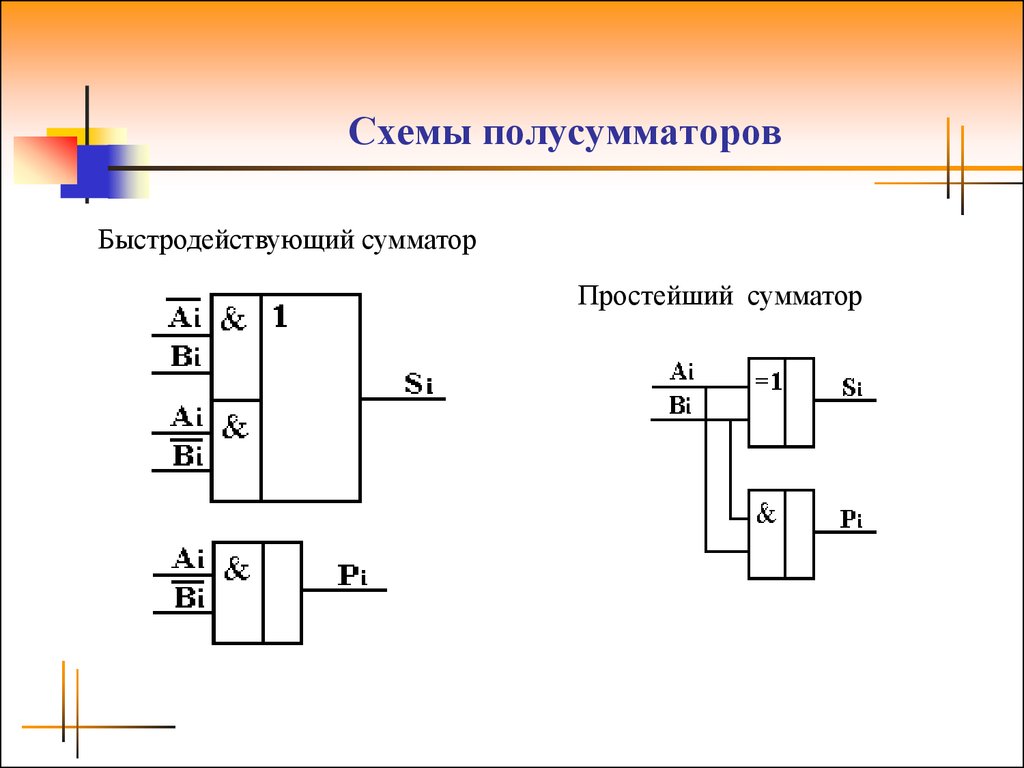
Таблица истинности и упрощение K Map для переноса показаны ниже.
| А | Б | Переноска |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мы можем вывести логическое выражение переноса следующим образом:
Перенос = A B
Логическая схема переноса показана ниже.
Если A и B являются двоичными входами полусумматора, то логическая функция для вычисления суммы S представляет собой Ex – OR для A и B, а логическая функция для вычисления переноса C представляет собой AND для A и B. Комбинируя эти два, логическая схема для реализации комбинационной схемы Half Adder показана ниже.
Как мы знаем, И-НЕ и ИЛИ-НЕ называются универсальными вентилями, поскольку с их помощью можно реализовать любую логическую систему.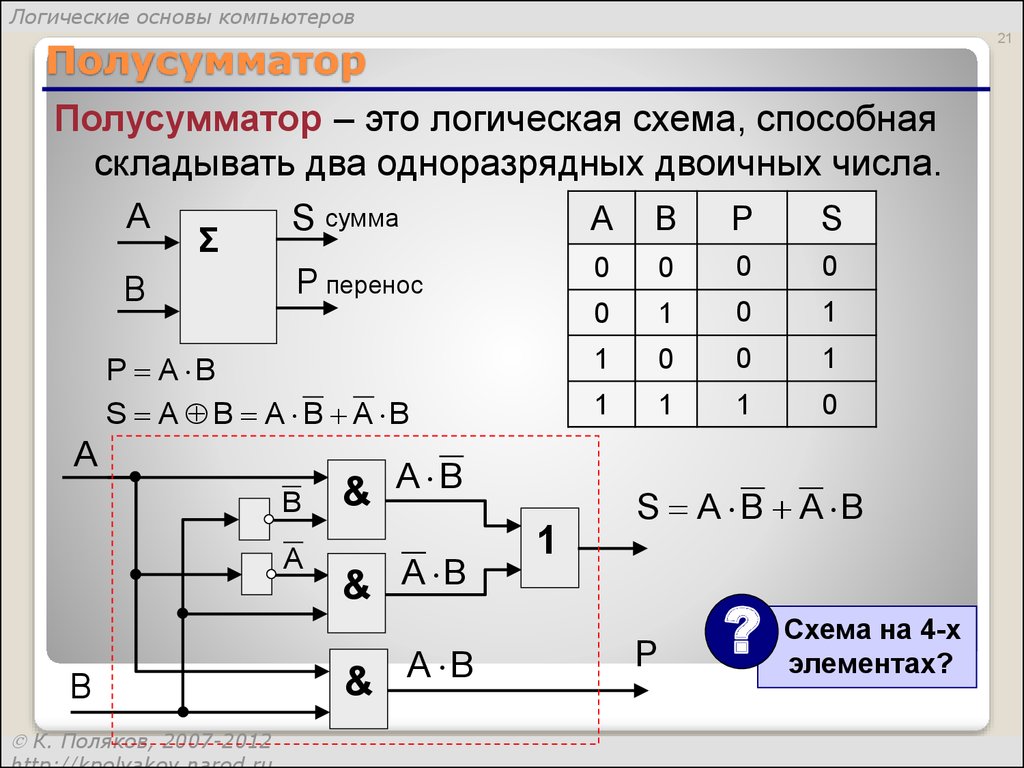 Схема полусумматора также может быть реализована с их использованием. Мы знаем, что схема полусумматора имеет один вентиль Ex-OR и один вентиль AND.
Схема полусумматора также может быть реализована с их использованием. Мы знаем, что схема полусумматора имеет один вентиль Ex-OR и один вентиль AND.
Полусумматор с использованием вентилей И-НЕ
Для создания полусумматора требуется пять вентилей И-НЕ. Схема для реализации полусумматора с использованием вентилей И-НЕ показана ниже.
Также получите представление о том, как построить вентили ИЛИ, И, НЕ, используя NAND Gate
Полусумматор с использованием вентилей НЕ-ИЛИ
Для создания полусумматора требуется пять вентилей НЕ-ИЛИ. Ниже показана схема реализации полусумматора с использованием вентилей ИЛИ-НЕ. Это основное ограничение половинных сумматоров при использовании в качестве двоичных сумматоров, особенно в сценариях реального времени, которые включают добавление нескольких битов. Для преодоления этого ограничения разработаны полные сумматоры.
Полный сумматор
Полный сумматор — это комбинационная логическая схема, выполняющая двоичное сложение двузначных чисел. Полные сумматоры сложны и трудны в реализации по сравнению с половинными сумматорами.
Полные сумматоры сложны и трудны в реализации по сравнению с половинными сумматорами.
Полный сумматор — это цифровая схема, используемая для вычисления суммы трех двоичных битов, что является основным отличием этого от полусумматора. Два из трех битов такие же, как и раньше: A, бит augend и B, бит addend. Дополнительный третий бит является битом переноса из предыдущего этапа и называется Carry-in, обычно обозначается C В . Он вычисляет сумму трех битов, включая перенос. Выходной перенос называется Carry-out и представлен C OUT .
Блок-схема полного сумматора с A, B и C IN в качестве входов и S, C OUT в качестве выходов показана ниже
Таблица истинности полного сумматора
ниже.| ВХОД | ВЫХОД | |||
| А | Б | С В | Сумма | С ВЫХОД |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
На основе таблицы истинности логические функции для суммы (S) и переноса (C OUT ) могут быть получены с использованием K-Map.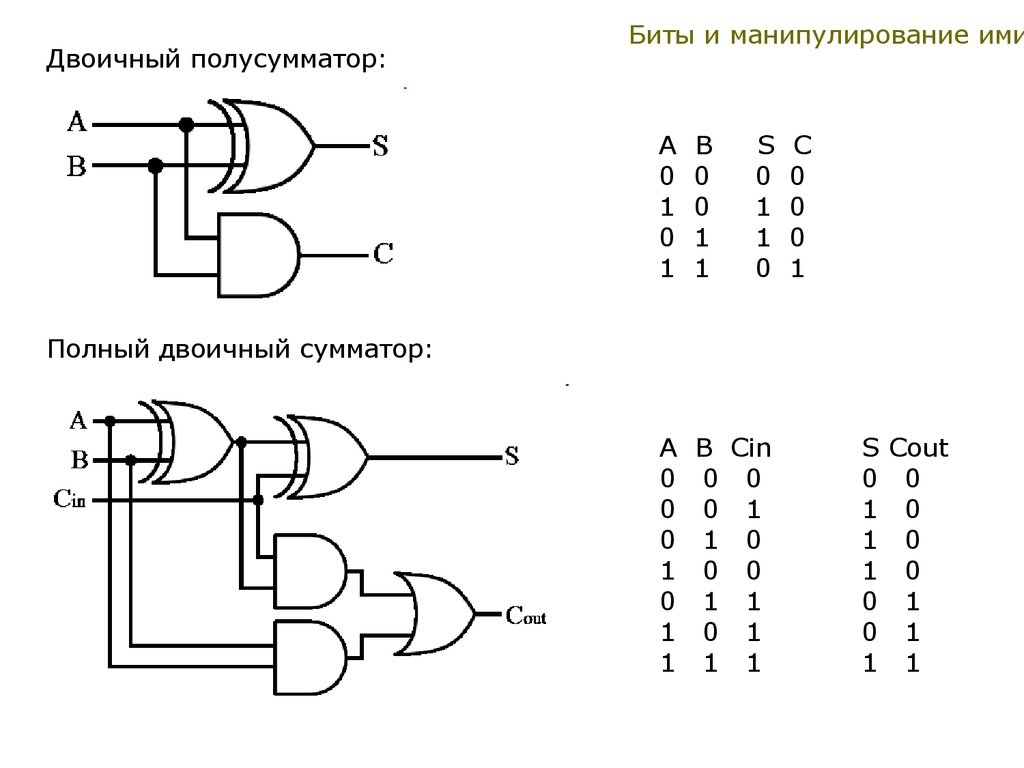
К-карта для вывода суммы (S) полного сумматора показана ниже:
Используя таблицу истинности и приведенную выше К-карту, можно получить логическое выражение суммы (S) вывода полного сумматора. как:
S = A B C IN + A B C IN + A B C В + А Б В В
Из приведенного выше логического выражения мы можем сказать, что выход суммы полного сумматора может быть реализован с использованием четырех логических элементов И с 3 входами, трех логических элементов НЕ и одного логического элемента ИЛИ с 4 входами. На следующем рисунке показана логическая схема выхода суммы (S) полного сумматора.
K-Map для вывода переноса (C OUT ) полного сумматора показана ниже:
Упрощенное логическое уравнение для C OUT :
C ВЫХОД = A B + A C ВХОД + B C ВХОД
Из приведенного выше логического выражения мы можем сказать, что перенос вывода полного сумматора может быть реализован с использованием трех логических элементов И с двумя входами и одного вентиля ИЛИ с тремя входами.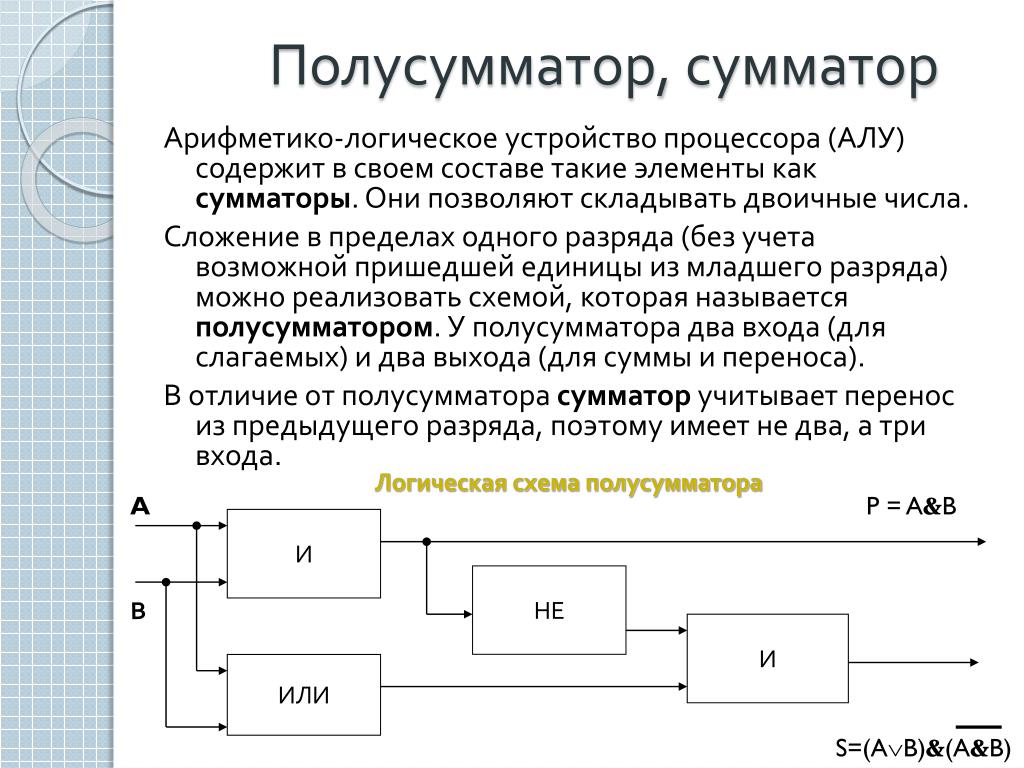 На следующем рисунке показана логическая схема выхода переноса (C OUT ) полного сумматора.
На следующем рисунке показана логическая схема выхода переноса (C OUT ) полного сумматора.
Реализация полного сумматора с использованием полусумматоров
Полный сумматор может быть образован путем логического соединения двух полусумматоров. Ниже приведена блок-схема, показывающая реализацию полного сумматора с использованием двух половинных сумматоров.
Мы знаем уравнения для S и C OUT полного сумматора из более ранних расчетов как:
C ВЫХОД = A B + A C ВХОД + B C ВХОД
Мы можем переписать уравнение для суммы следующим образом:
S = A B C IN + A B C IN + A B C IN + A B C IN
= С В (А В + А В) + С В (А В + А В)
=C IN (A Ex-NOR B) + C IN (A Ex-OR B)
= C IN (A ⊕ B) + C IN (A ⊕ B)
Следовательно, S = C IN ⊕ (A ⊕ B)
Аналогично, мы можем переписать C OUT следующим образом:
C OUT = A B + A C IN + B C IN
= A B + A C IN + B C IN (A + A)
= A B + A C IN + A B C IN + A B C IN
= A B (1 + C IN )+ A C IN + A B C IN
= A B + A C IN + A B C IN
= A B + A C IN (B + B) + A B C IN
= A B + A B C IN + A B C IN + A B C IN
= A B (1 + C IN )+ C IN (A B + A B)
= A B + C IN (A B + A B)
= A B + C IN (A Ex-OR B)
Следовательно, C OUT = A B + C IN (A ⊕ B)
На основе двух приведенных выше уравнений схема полного сумматора может быть реализована с использованием двух половинных сумматоров и вентиля ИЛИ. Реализация полного сумматора с использованием двух половинных сумматоров показана ниже.
Реализация полного сумматора с использованием двух половинных сумматоров показана ниже.
Полный сумматор с использованием вентилей И-НЕ
Как упоминалось ранее, вентиль И-НЕ является одним из универсальных вентилей и может использоваться для реализации любой логической схемы. Схема полного сумматора, использующая только вентили И-НЕ, показана ниже.
Полный сумматор — это простой 1-битный сумматор. Если мы хотим выполнить n-битное сложение, то нам нужно «n» число 1-битных полных сумматоров, которые должны использоваться в виде каскадного соединения.
Заключение
Полное руководство по полусумматору и полному сумматору. Вы узнали, как реализовать схему полусумматора, ее логические уравнения, логическую схему, а также разработать схему полусумматора с использованием вентилей НЕ-И и ИЛИ-НЕ, схему полного сумматора, ее логические выражения, логическую схему и реализацию полного сумматора с использованием полусумматора.
Таблица истинности половинного сумматора и полного сумматора, схема, рабочая и K-карта
— Реклама —
Двоичные сумматоры Двоичный сумматор — это цифровая схема, которая выполняет арифметическое двоичное сложение двух чисел в соответствии с логическими операциями и законами булевой алгебры.
Сумматоры используются в схемотехнике комбинационных и арифметико-логических устройств (АЛУ) микропроцессора для вычисления адресов.
Существует два типа цепей сумматора —
- Полугадеры
- Полные сумматоры
— Реклама —
Полусумматор — тип цифровой схемы для вычисления арифметического двоичного сложения двух однобитовых чисел. Это схема с двумя входами и двумя выходами.
Для двух одноразрядных двоичных чисел A и B полусумматор выдает два одноразрядных двоичных выхода S и C, где S — сумма, а C — перенос.
Рис.1 Полусумматор Вход ВыходСумма предназначена для младшего значащего бита (LSB), а перенос — для старшего значащего бита (MSB).
Таблица операций и истинности для полусумматора Операция:Случай 1: A= 0, B= 0;
В соответствии с двоичным сложением сумма этих чисел равна 0 без генерации битов переноса.
0
+ 0
. Случай 2: А=0, В=1;
В соответствии с двоичным сложением сумма этих чисел равна 1 без генерации битов переноса.
0
+ 1
一一一一一
1
一一一一一
Hence, S= 1, C= 0
Случай 3: А= 1, В= 0;
В соответствии с двоичным сложением сумма этих чисел равна 1 без генерации битов переноса.
1
+0
一一一 一一
1
一一一
. = 1, В = 1;
В соответствии с бинарным дополнением, сумма этих чисел составляет 1 с генерацией битов переноски 1.
1
1
+ 1
一一一
090一一一 903
一一一 9903
0一一一 + 1
. 0
0
一一一 一一
Следовательно, S = 0, C = 1
Правда Таблица:| A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A | 90||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A
|


 4 Карта Карно Half Adder для переноса
4 Карта Карно Half Adder для переноса Это цифровая схема с тремя входами и двумя выходами.
Это цифровая схема с тремя входами и двумя выходами.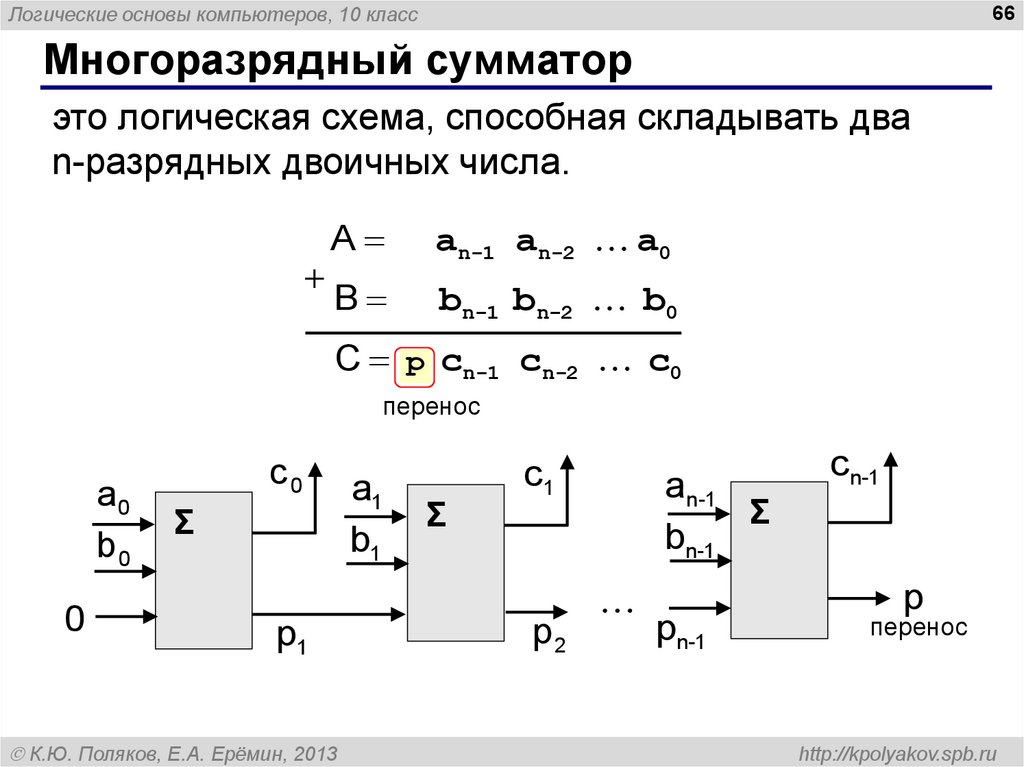 и D=1;
и D=1; 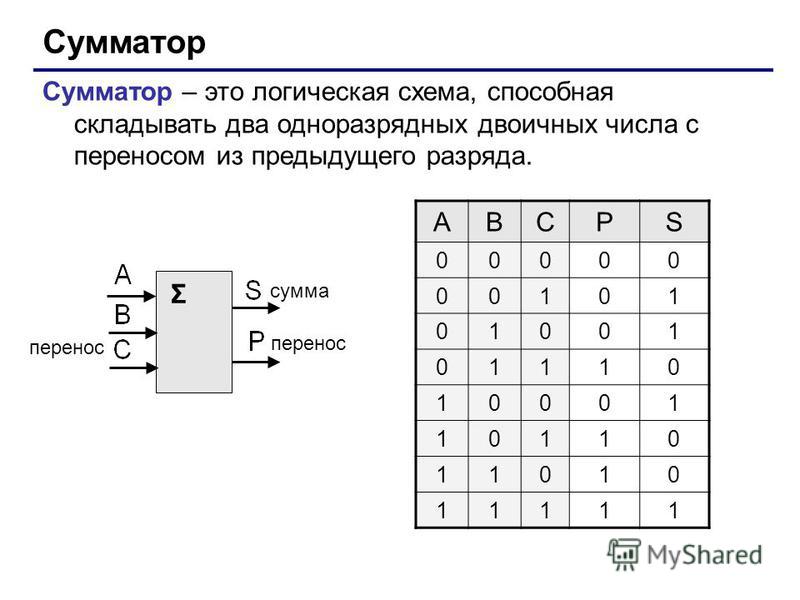 Д= 1;
Д= 1; 
 7 Схема полного сумматора Проектирование полного сумматора
7 Схема полного сумматора Проектирование полного сумматора 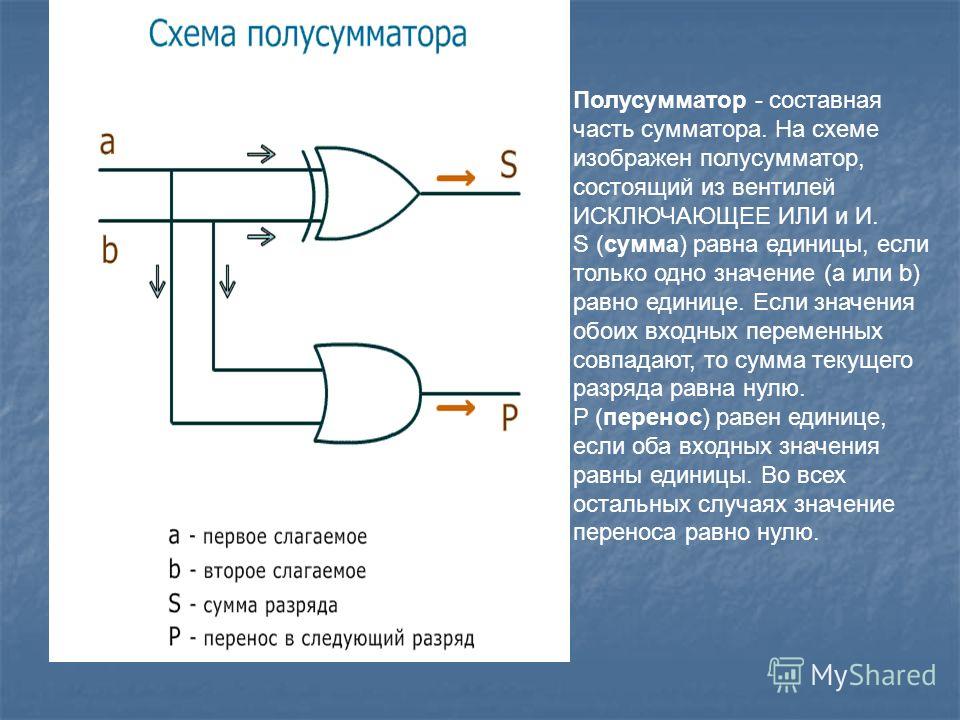 10 Проектирование полного сумматора с использованием двух половинных сумматоров Операция:
10 Проектирование полного сумматора с использованием двух половинных сумматоров Операция: