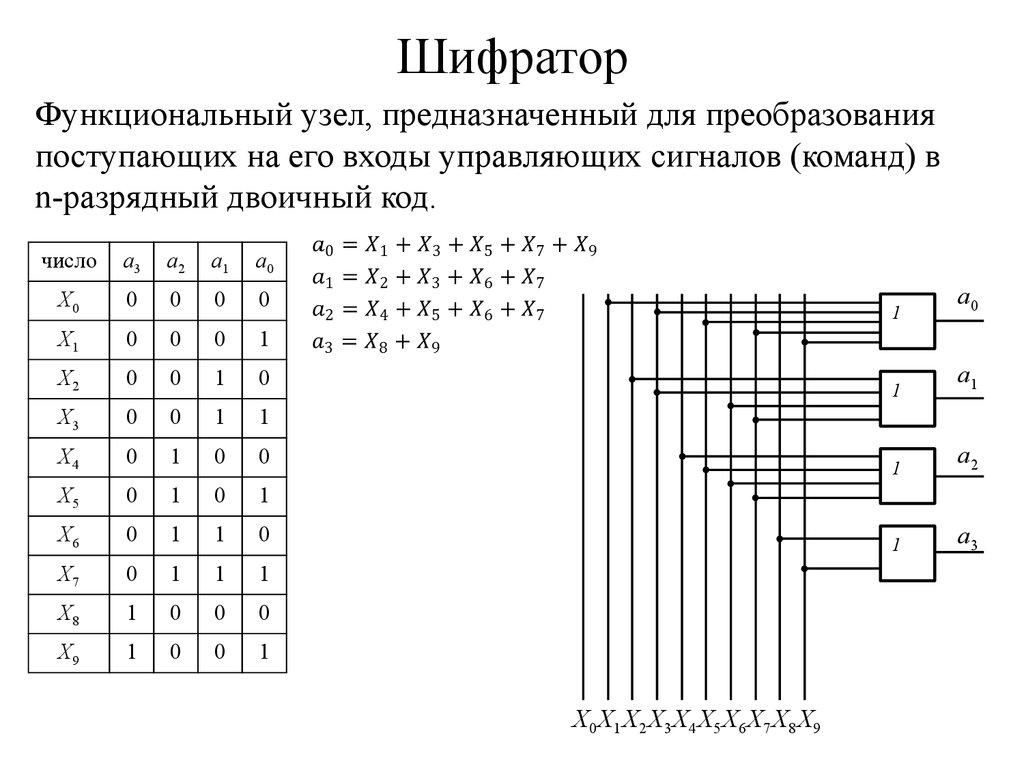
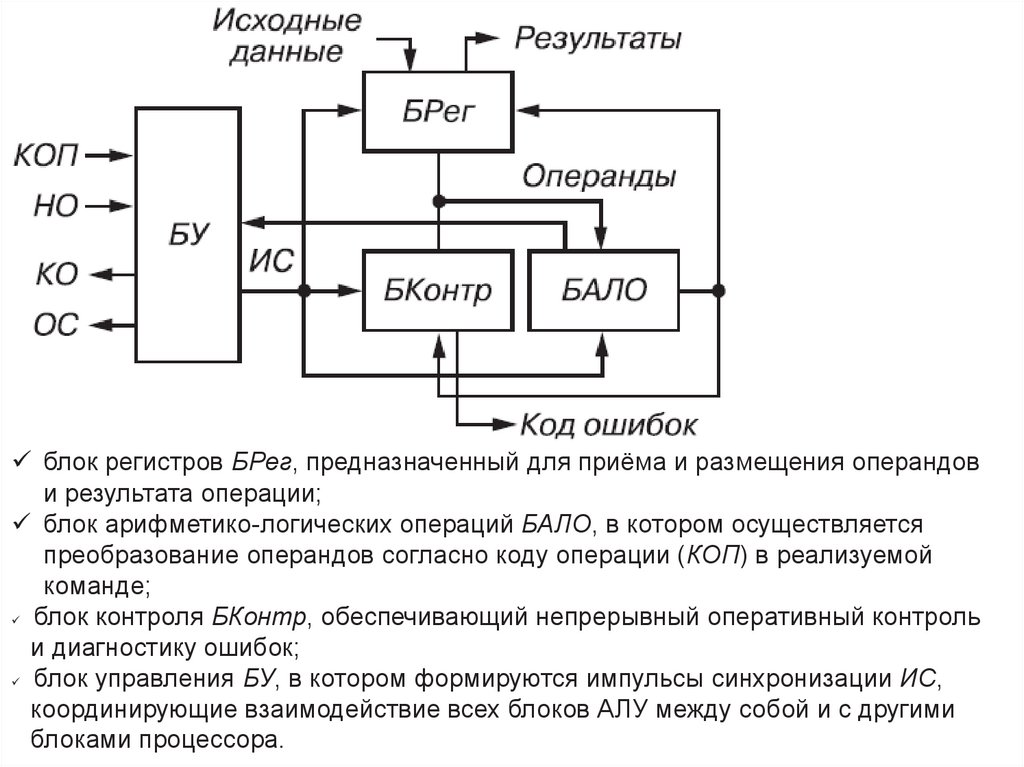
Построение комбинационных схем на логических элементах. Технологии минимизации комбинационных схем. Использование диаграмм Вейча для минимизации фал.
Схемы, выходное состояние которых однозначно определяется только комбинацией входных сигналов, называют комбинационными. Закон функционирования КС определяется системой переключательных (логических) функций:
Синтез (построение) комбинационной схемы состоит в построении схемы на основе заданного закона ее функционирования в виде системы переключательных функций (ПФ) или таблиц истинности. При синтезе комбинационной схемы чаще всего необходимо построить схему с использованием минимального числа элементов в заданном элементном базисе, например, на элементах И-НЕ.
Комбинационные
схемы строятся из элементарных логических
элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и других.
Соединяют эти элементы так, как это
следует из логической формулы, т.е. вход
одного элемента, в котором часть
аргументов обработана как указано в
формуле, подключается ко входу другого,
где выполняется дальнейшая обработка
логической функции.
Пример: Пусть дана логическая функция
Комбинационная схема представлена на рисунке.
Этапы синтеза:
Задание логической функции словесно, с помощью таблиц истинности или булевых выражений.
Минимизация логической функции с помощью алгебраического или графического метода (диаграммы Вейча, карты Карно).
Запись булевого выражения минимизированной переключательной функции.
Преобразование булевого выражения минимизированной ПФ для реализации её в заданном базисе И-НЕ или ИЛИ-НЕ.
Составление функциональной схемы, т.е. изображение нужных логических элементов и связей между ними.
Технологии
минимизации.
Минимизацией называют процедуру упрощения аналитического
выражения, представляющего переключательную
(логическую) функцию, направленную на
то, чтобы булево выражение ПФ содержало
минимальное количество членов с
минимальным числом переменных.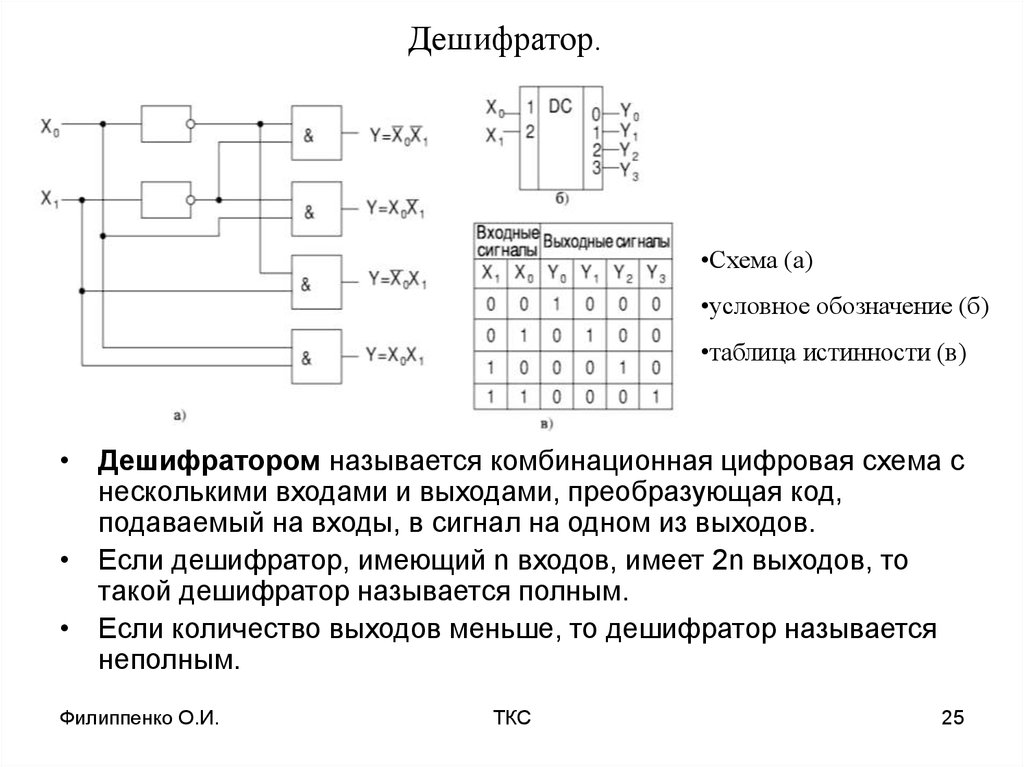 Способы
минимизации:
алгебраический; с помощью диаграмм
Вейча (карт Карно).
Способы
минимизации:
алгебраический; с помощью диаграмм
Вейча (карт Карно).
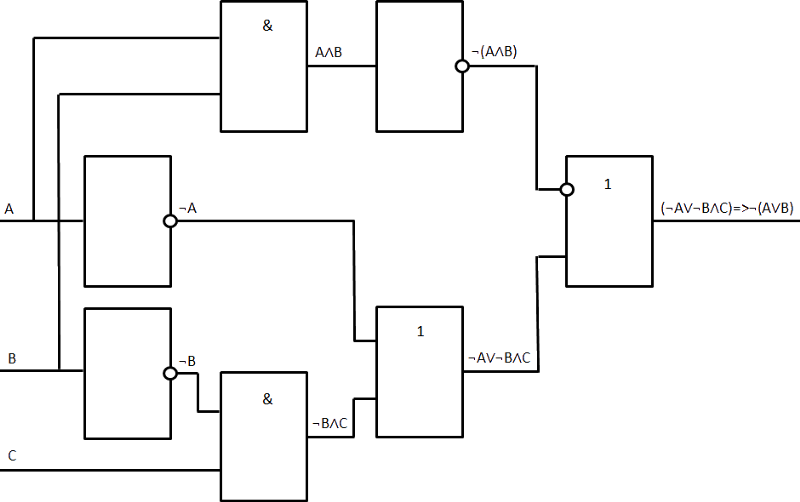
Алгебраический способ минимизации ПФ — используя тождества и теоремы булевой алгебры.
Пример 1. Исходное булево выражение:
Применяя теорему склеивания , получим булево выражение, которое равносильно (эквивалентно) исходному, но значительно проще его.
Диаграммы Вейча построены так, что их соседние клетки содержат члены исходной ПФ, отличающиеся значением одной переменной: один член содержит эту переменную в прямой форме, а другой – в инверсной. Благодаря этому возникает наглядное представление о различных вариантах склеивания смежных членов.
Исходным продуктом для применения диаграмм Вейча является представление ПФ таблицей истинности, в которой возможные наборы переменных упорядочены по возрастанию или по убыванию их десятичных эквивалентов.
Вид
диаграмм Вейча зависит от числа переменных
минимизируемой ПФ — n и от того, как упорядочены наборы
переменных в таблице. Если наборы
упорядочены по возрастанию их десятичных
эквивалентов, то диаграммы Вейча для n=2,3,4 имеют вид, приведенный на рисунке.
Если наборы
упорядочены по возрастанию их десятичных
эквивалентов, то диаграммы Вейча для n=2,3,4 имеют вид, приведенный на рисунке.
Число клеток диаграммы равно количеству наборов переменных: Nкл=Nнаб=2n.
Каждая клетка соответствует определенному набору переменных и имеет номер, одинаковый с номером набора.
Строки и столбцы диаграммы, помеченные чертой, определяют наборы, в которых переменные принимают единичные значения (входят в прямой форме). Строки и столбцы, не помеченные чертой, соответствуют наборам, в которых те же переменные принимают нулевые значения (входят в инверсной форме). В клетки записываются значения ПФ на соответствующем наборе (нулевое или единичное). Если на каком-то наборе функция не определена, то в клетке диаграммы ставится прочерк (или x).
ПФ считается неопределенной, если:
1) данный набор переменных в реальном логическом устройстве невозможен;
2)
значение функции на данном наборе
безразлично.
После заполнения диаграммы можно приступить непосредственно к минимизации, которую производят по единицам или нулям. В первом случае результатом минимизации будет булево выражение в ДНФ, а во втором – в КНФ.
Краткий алгоритм:
Функция, выраженная в СДНФ (СКНФ), записывается в диаграмму Вейча путём проставления единиц (нулей) в соответствующие координаты.
Производится объединение единиц (нулей), стоящих рядом, в так называемые m-кубы. Можно объединять единицы (нули), которые образуют правильный прямоугольник, содержащий 2, 4, 8, 16 единиц (нулей).
Замечание. Необходимо объединять максимально возможное количество смежных клеток, содержащих единицы (нули).
Замечание. Одна и та же единица (нуль) может охватываться несколько раз разными кубами.
Замечание. Верхняя и нижняя строки – смежные (можно
объединить). Левый и правый столбцы –
смежные. Угловые клетки – тоже смежные
(диаграмму можно мысленно свернуть в
тор).
Замечание. Перед выполнением минимизации в клетки, содержащие прочерки (где ПФ не определена), можно записать дополнительные единицы (нули), что способствует получению более простого конечного булевого выражения. При этом следует помнить, что хотя бы один раз необходимо объединить лишь основные единицы (нули). Дополнительные единицы (нули) могут увеличивать суммарное число единиц (нулей), входящих в куб, то есть уменьшать число переменных в результирующих конъюнкциях (дизъюнкциях).
Выписываются координаты получившихся m-кубов.
Объединённая дизъюнкция (конъюнкция) конъюнктивных (дизъюнктивных) координат всех m-кубов и есть минимальная форма.
Целью минимизации является получение минимальной ДНФ или КНФ, содержащей минимум членов с минимальным количеством входящих в них переменных.
Преобразование из базисов СДНФ и СКНФ в базис «Штрих Шеффера» и «Стрелка Пирса» (проверить, работает ли это как для Шеффера, так и для Пирса, сам алгоритм расписан вроде как только для Шеффера
Проставляются скобки;
Все знаки конъюнкции и дизъюнкции заменяются на Штрих Шеффера.

Исключение: если вся функция состоит из одной импликанты, то она берётся с отрицанием.
Исключение: В состав функции входит импликанта из одной буквы – эта импликанта берётся с отрицанием.
НОУ ИНТУИТ | Лекция | Структурное построение тестов для устройств с памятью
< Лекция 22 || Лекция 23: 123 || Лекция 24 >
Аннотация: В лекции рассматривается задача построения проверяющих тестов для цифровых устройств с памятью на структурном уровне, то есть для последовательностных логических схем. Рассматриваются основы структурного подхода к решению задачи на основе применения преобразования последовательностной логической схемы к модели итеративной комбинационной схемы.
Ключевые слова: комбинационная схема, обобщение, вектор, итерация, триггер, выход, очередь, значение, структурный метод, критический путь, алфавит, FAN, группа, мощность, пространство, тестовый набор, прямой, обратный, смешанная стратегия, переменные состояния, место, знание, вентиль, многозначная функция, пересечение, импликация, дерево решений, время выполнения, конфликт, псевдокод, оперативная память, список, множества
intuit.ru/2010/edi»>23.1 Итеративные комбинационные схемы
Рис. 23.1. Преобразование последовательностной логической схемы в комбинационный логический эквивалент
Согласно каноническому представлению последовательностное устройство можно представить в виде комбинационного блока и блока памяти, которые соединены линиями обратной связи (рис. 23.1- а,
«Модели цифровых устройств»
).
Если рассматривается поведение последовательностной схемы в течение тактов, то комбинационных эквивалентов соединяются последовательно в итеративную комбинационную схему, как показано на рис. 23.2. Здесь произвольная -я итерация итеративной комбинационной схемы соответствует состоянию исходной последовательностной схемы на -м такте времени. При этом компоненты векторов , соответствуют линиям первичных входов и выходов соответственно, , — псевдовходам и псевдовыходам соответственно на -м такте. Также очевидно, что , — это линии, определяющие состояние последовательностного ЦУ в начале и в конце -го такта соответственно.
Рис.
23.
Далее при генерации тестов можно применять один из методов, разработанных для комбинационных схем, с учётом специфики последовательностных. В качестве примера рассмотрим простейший триггер, представленный на рис. 23.3, и его комбинационный эквивалент на рис. 23.4.
Рис. 23.3. Триггер | Рис. 23.4. Комбинационный эквивалент триггера |
Рассмотрим построение теста, который проверяет константную неисправность const1 — на нижнем плече триггера на основе методов с использованием шестизначного алфавита , рассмотренных в
«Многомерная активизация путей в шестизначном алфавите»
, 19.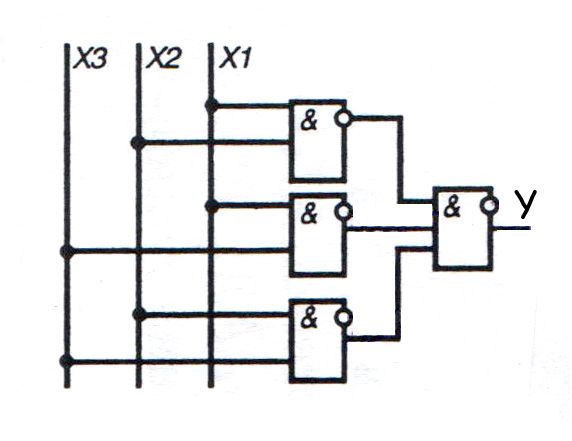 . Процесс построения теста начинается с внесения значения , соответствующего неисправности const 1, в итеративной схеме из одного комбинационного эквивалента, как это показано на рис. 23.5.
. Процесс построения теста начинается с внесения значения , соответствующего неисправности const 1, в итеративной схеме из одного комбинационного эквивалента, как это показано на рис. 23.5.
Рис. 23.5. Построение тестовой последовательности — 1 КЭ
Из примера видно, что в итеративной комбинационной схеме, как и ранее, надо выполнить распространение критического значения, в данном случае , от места неисправности до внешних выходов схемы при условии неопределенности начального состояния ЦУ, т.е. неопределённых значениях на псевдовходах первого комбинационного эквивалента итеративной комбинационной схемы. Поскольку в процессе доопределения мы получаем для псевдовхода вместо неопределенного значения , то это говорит о невозможности построения теста для итеративной схемы из одного эквивалента (единичной длины). Отметим, что мы строим тест, исходя из предположения, что начальное состояние ЦУ не известно.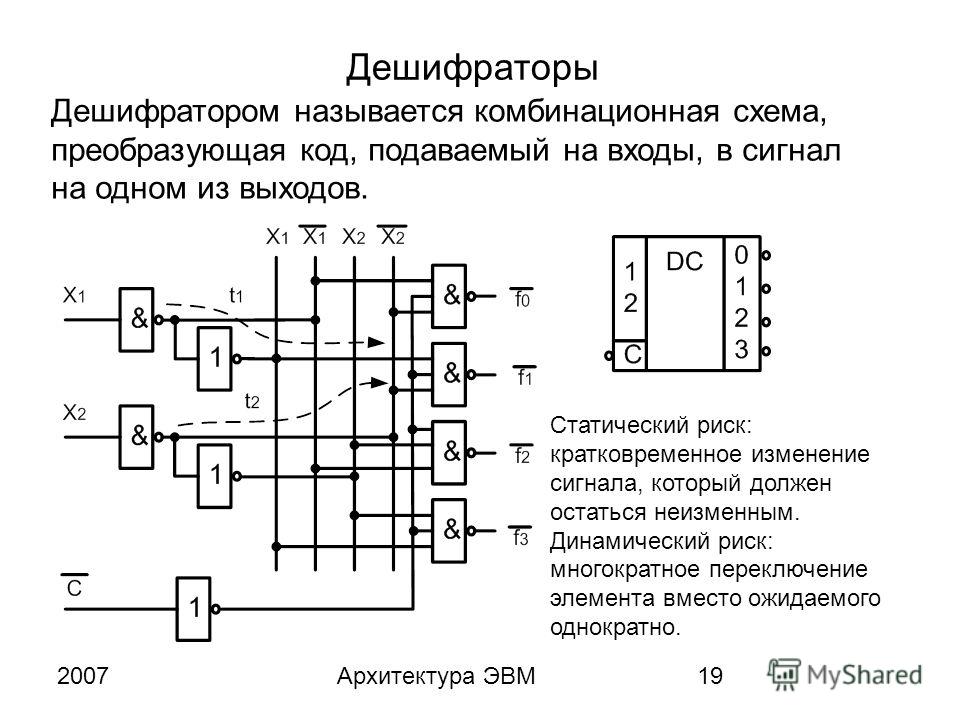
Рис. 23.6. Построение тестовой последовательности — 2 КЭ
Поэтому для нашего примера выполняем распространение критического значения на первичный выход для итеративной схемы, содержащей два комбинационных эквивалента (рис. 23.6). В результате этой процедуры и после доопределения значений прямого распространения получаем тестовую последовательность, состоящую из двух наборов:
Таким образом, для итеративной комбинационной схемы мы строим не один проверяющий набор, а последовательность входных наборов — тест.
Очевидно, что каждый комбинационный эквивалент в итеративной комбинационной схеме соответствует своему такту или моменту времени. При этом распространение критического значения может произойти как в рамках одного КЭ (т.е. за один такт), так и нескольких КЭ (т.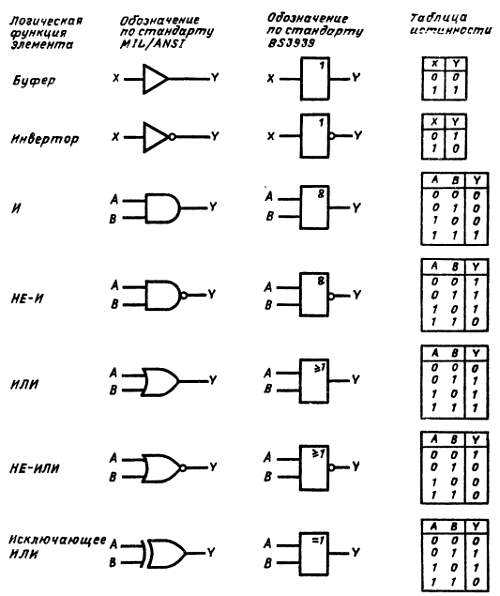 е. за несколько тактов).. Кроме этого, необходимо выполнить, также как и для комбинационных схем, подтверждение значений, полученных в процессе распространения критического значения на первичные выходы. При этом мы получаем значения внешних входов схемы, то есть тестовые наборы.
е. за несколько тактов).. Кроме этого, необходимо выполнить, также как и для комбинационных схем, подтверждение значений, полученных в процессе распространения критического значения на первичные выходы. При этом мы получаем значения внешних входов схемы, то есть тестовые наборы.
При внешней простоте и логичности такого подхода существуют принципиальные различия построения тестов для последовательностных и комбинационных ЦУ.
Отметим, что итеративная комбинационная схема в общем случае неадекватно отражает поведение асинхронных последовательностных схем. Строго говоря, эта модель соответствует синхронной последовательностной схеме с синхронизацией в точках обрыва обратных связей. Поэтому полученные при таком подходе результаты для асинхронных схем подлежат дальнейшей проверке, в первую очередь, на предмет отсутствия состязаний сигналов (например, методом Эйхельбергера, изложенным в
«Анализ состязаний »
).
Кроме того, при разворачивании последовательностной схемы в итеративную комбинационную неисправности «размножаются». Так, в приведенном примере одиночная константная неисправность на нижнем плече триггера в итеративной комбинационной схеме соответствует двум константным неисправностям и . Поэтому методы генерации тестов для последовательностных схем должны учитывать этот эффект.
При построении тестов производится активизация путей в многозначных алфавитах от неисправных линий до одного из выходов последней -й копии итеративной комбинационной схемы. При этом число копий КЭ определяется условием появления неопределённых значений на псевдовходах -й копии.
При невозможности установить неопределенное значение на псевдовходах возникает проблема установки схемы в заданное начальное состояние. В общем случае надо использовать установочную последовательность, переводящую схему с памятью из неизвестного начального состояния в некоторое известное.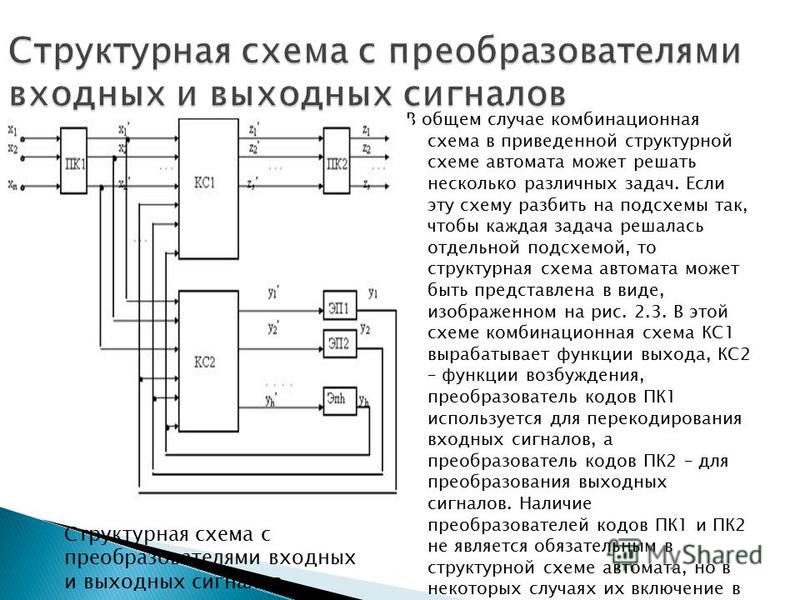 Причём эта последовательность должна устанавливать в определённое состояние исправную и неисправную схему.
Причём эта последовательность должна устанавливать в определённое состояние исправную и неисправную схему.
Дальше >>
< Лекция 22 || Лекция 23: 123 || Лекция 24 >
Проектирование комбинационных логических схем
Несмотря на то, что инструменты САПР используются на практике для создания комбинационных логических схем, важно, чтобы цифровая дизайнер должен научиться генерировать логическую схему из спецификации. Понимание этого процесса позволяет дизайнеру лучше использовать инструменты САПР и, при необходимости, вручную проектировать важные логические подсхемы.
Процедура проектирования
Процедура проектирования комбинационных логических схем начинается со спецификации задачи и включает следующие шаги:
- Определить необходимое количество входов и выходов из спецификаций.
- Получите таблицу истинности для каждого из выходных данных на основе их отношения к входным данным.
- Упростите логическое выражение для каждого выхода.
 Используйте Карты Карно или Булеву алгебру.
Используйте Карты Карно или Булеву алгебру. - Нарисуйте логическую схему, представляющую упрощенное логическое выражение. Проверьте конструкцию, проанализировав или имитация цепи.
Примеры
Ввод больше или равен 5?
Спецификация
Разработайте схему с 3-битным двоичным входом и одним выходом (Z), указанными ниже:
- Z = 0, если вход меньше 5 10
- Z = 1, иначе
Определить входы и выходы
- Обозначьте входы (3 бита) как A, B, C
- A — старший бит
- C — младший бит
- Выход (1 бит) Z
- Z = 1 -> 101 2 , 110 2 , 111 2
- Z = 0 -> другие входы
- Обозначьте входы (3 бита) как A, B, C
Получить таблицу истинности
Упростить логическое выражение
Из таблицы истинности мы используем один из следующих 2 методов для получения упрощенного логического выражение
- Используйте карту Карно, чтобы свести к минимуму логику или
- Из таблицы истинности найдите каноническую сумму
Логическое выражение продуктов.
 Z = А * ~ В * С + А * В * ~ С + А * В * С
Используйте булеву алгебру, чтобы упростить
логическое выражение для: Z = (В + С) * А
Z = А * ~ В * С + А * В * ~ С + А * В * С
Используйте булеву алгебру, чтобы упростить
логическое выражение для: Z = (В + С) * А
Нарисуйте логическую схему
Нарисуйте логическую схему, представляющую упрощенное логическое выражение. Проверьте дизайн по анализ или моделирование схемы.
BCD в 7-сегментный декодер
Спецификация
Разработка схемы декодера из двоично-десятичного кода в 7 сегментов для сегмента e который имеет 4-битный двоичный вход и один выход (7e), заданный таблицей истинности
Определить входы и выходы
- Обозначьте входы (4 бита) как A, B, C, D
- D — старший бит
- A — младший значащий бит
- Выход (1 бит) 7e — сегмент e 7-сегментного дисплея
- Обозначьте входы (4 бита) как A, B, C, D
Получить таблицу правды
Получено от BCD до 7-сегментного декодера истины стол.
 Обратите внимание, что 7e получено из столбца e.
Обратите внимание, что 7e получено из столбца e.Упростить логическое выражение
Из таблицы истинности мы используем один из следующих 2 методов для получения упрощенного логического выражение
- Использование логической алгебры для упрощения канонической суммы произведений boolean выражение, полученное из таблицы истинности или
- Используйте карту Карно, чтобы свести к минимуму логику. От карты Карно мы получили следующее логическое выражение: 7e = ~D*B*~A + ~C*~B*~A
Нарисуйте логическую схему
Нарисуйте логическую схему, представляющую упрощенное логическое выражение.
 Проверьте дизайн по
анализ или моделирование схемы.
Проверьте дизайн по
анализ или моделирование схемы.
Другие примеры
Сигнализация банка
Банк хочет установить систему сигнализации с 3 датчиками движения.
Для предотвращения ложных срабатываний при срабатывании одного датчика, тревога будет срабатывать только при наличии хотя бы двух датчики срабатывают одновременно.
Детектор простых чисел
Разработайте схему с 3-битным двоичным входом и одним выходом,
- выведите 1, если это простое число. например, 2 10 , 3 10 , 5 10 , 7 10
- , иначе выведите 0.
Сравните два однобитовых числа
Имея два входных бита A и B, выведите три выходных значения X, Y и Z так, чтобы
- X равно 1 только тогда, когда A > B,
- Y равен 1, только когда A Z равен 1, только когда A = B
Узнать больше примеров
Введение в комбинационные логические схемы
Цифровые сигналы обрабатываются цифровой системой, которая может быть построена с использованием различных логических элементов.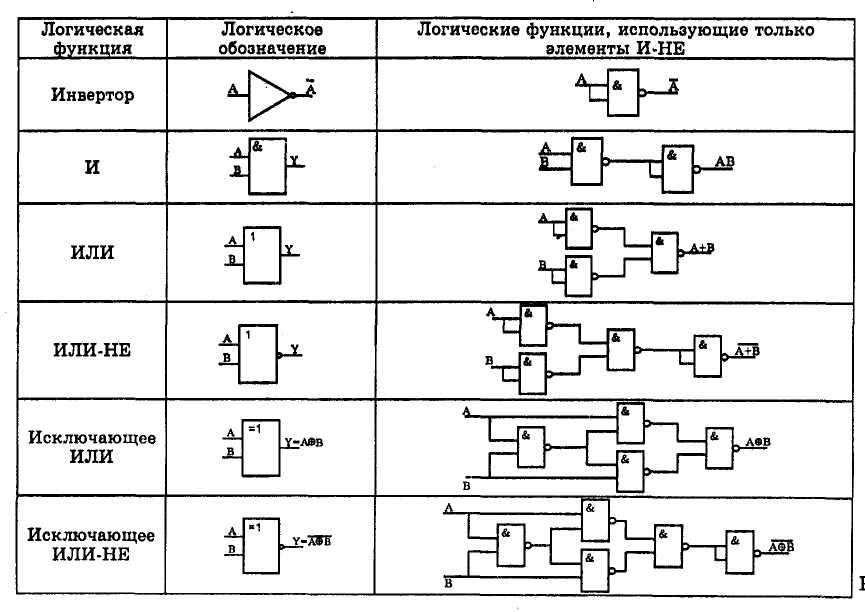 Эти логические схемы состоят из различных логических элементов, соединяя их в определенных комбинациях, чтобы получить требуемый результат. Цифровые логические схемы в основном подразделяются на два типа: последовательные логические схемы и комбинационные логические схемы. Эта статья дает краткое представление о комбинационных логических схемах.
Эти логические схемы состоят из различных логических элементов, соединяя их в определенных комбинациях, чтобы получить требуемый результат. Цифровые логические схемы в основном подразделяются на два типа: последовательные логические схемы и комбинационные логические схемы. Эта статья дает краткое представление о комбинационных логических схемах.
Краткое описание
Комбинационные логические схемы
Комбинационная логическая схема — это схема , в которой текущее состояние комбинации логических входов определяет выход . Термин «комбинированная логика» означает объединение двух или более логических элементов для формирования требуемой функции, где выход в данный момент времени зависит только от входа.
Логические элементы являются основными строительными блоками комбинационной схемы. Используя комбинацию логических вентилей, можно реализовать более сложные комбинационные схемы, такие как мультиплексоры и демультиплексоры, компараторы, сумматоры и вычитатели и т. д.
д.
Комбинированная схема состоит из входных переменных, логических вентилей и выходных переменных. Логические элементы принимают входы и в зависимости от типа функционирования логических элементов формируются выходные сигналы.
Требуемые выходные данные получаются из этого процесса путем преобразования двоичной информации, данной на входе. На рисунке ниже показано схематическое представление обобщенной комбинационной логической схемы, состоящей из n входных переменных и m выходных переменных.
На приведенном выше рисунке имеется n входных переменных и, следовательно, на входе будет 2n возможных комбинаций битов. Булевым выражением входных переменных выражается каждый выход. Таким образом, результат вышеприведенной обобщенной комбинационной логической схемы может быть выражен m булевыми выражениями.
На приведенном выше рисунке схема принимает двоичные переменные и в зависимости от логической комбинации вентилей генерирует выходные данные.
Наверх
Процедура проектирования комбинационных логических схем
Комбинационная схема может быть разработана с использованием следующих шагов.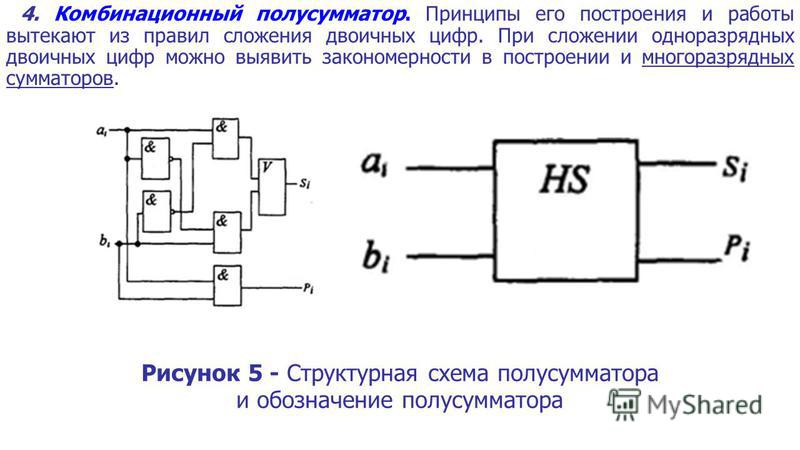
- Идентификация и определение количества доступных входных переменных и требуемых выходных переменных.
- Представление символов (алфавитов) для всех без исключения входных и выходных переменных.
- Выражение отношения входной и выходной переменных.
- Построение таблицы истинности, указывающей взаимосвязь между входными и выходными переменными.
- Получение логического выражения для каждой выходной переменной через входные переменные.
- Минимизация логических выражений различных выходных переменных.
- Получение логической схемы реализацией минимизированных логических выражений.
Для минимизации логических выражений доступны различные методы упрощения, позволяющие уменьшить количество логических элементов и, следовательно, снизить стоимость реализации. Эти методы включают теоремы и тождества булевой алгебры, карты Карно (K-карты), табулирование Куинна-МакКласки и т. д. Для аппаратной реализации комбинационной схемы в основном предпочтительны следующие рекомендации.
- Реализация схемы должна быть такой, чтобы она имела минимальное количество элементов, имеющих минимальное количество входов.
- Количество взаимосвязей между шлюзами должно быть минимальным, а время распространения должно быть минимальным.
- Всегда должно быть ограничение на проходимость ворот.
Это простой, эффективный и традиционный метод проектирования комбинационной схемы для малых цепей. Если схема более сложная, требуется больше вентилей, а также требуется большее количество проводов между ними. Следовательно, проектирование таких схем может быть менее надежным и трудоемким.
Чтобы преодолеть эти проблемы, большинство комбинационных схем доступны в виде интегральных схем (ИС), которые широко используются при разработке цифровых систем. В зависимости от интеграционных возможностей вентилей эти ИС подразделяются на малые, средние, большие и очень большие ИС.
Для выполнения определенных цифровых функций, таких как сложение, мультиплексирование, демультиплексирование, кодирование, декодирование, сравнение и т. д., в цифровых системах в основном используются интегральные схемы среднего масштаба (MSI).
д., в цифровых системах в основном используются интегральные схемы среднего масштаба (MSI).
Вернуться к началу
Пример комбинационной логической схемы
Утверждение. Разработайте комбинационную логическую схему с тремя входными переменными так, чтобы она выдавала на выходе логическую 1, когда одна или две входные переменные равны логической 1, но не все три.
Решение: Следуйте приведенным выше пунктам, чтобы разработать логическую схему в соответствии с данным утверждением. В данном операторе есть три входных переменных и одна выходная переменная. В качестве второго шага назначьте входным переменным буквенные символы как A, B, C и выходным как Y. Затем можно свести в таблицу взаимосвязь между входными и выходными переменными, построив таблицу истинности, как показано ниже.
Теперь упрощенное логическое выражение для приведенной выше таблицы истинности для получения выходных данных Y получается с использованием упрощения K-карты как
Применяя приведенное выше логическое уравнение, мы получаем логическую диаграмму как
Назад наверх
Классификация комбинационных логических схем
Комбинационные схемы используются в самых разных приложениях, включая калькуляторы, цифровые измерительные приборы, компьютеры, цифровую обработку, автоматическое управление машинами, промышленную обработку, цифровую связь и т.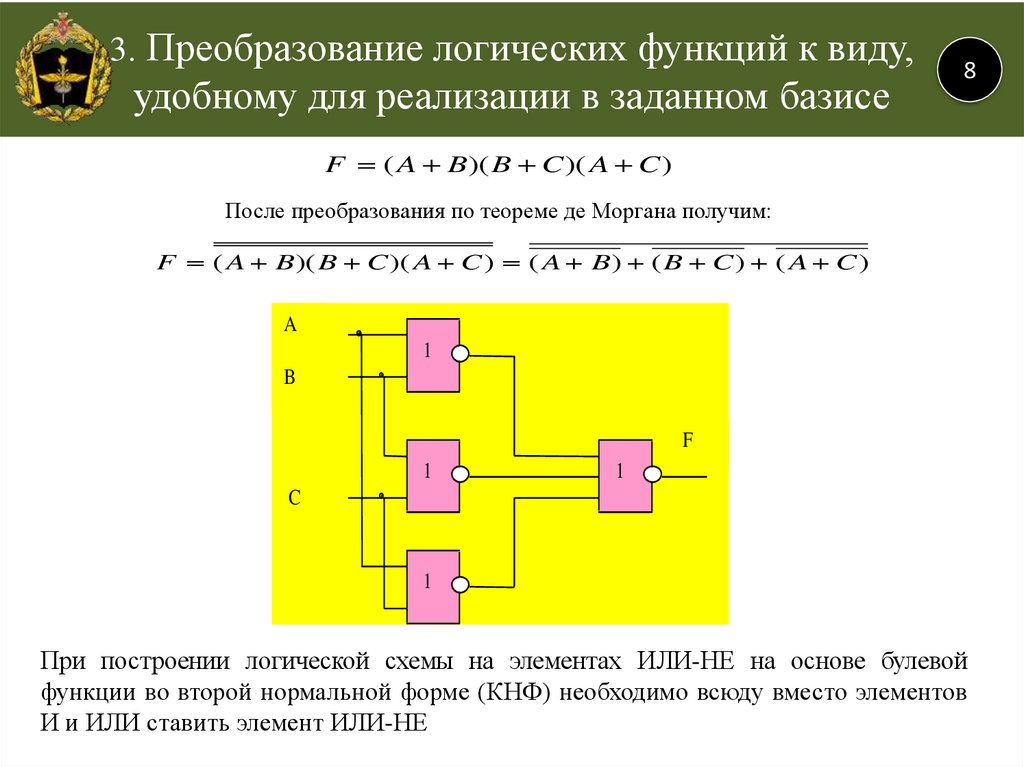 д.
д.
Различные типы комбинационных логических схем используются для различных приложений. В зависимости от функции используемой логической схемы, комбинационные логические схемы в основном подразделяются на три типа, а именно арифметические и логические схемы, схемы передачи данных и схемы преобразователя кода.
Арифметические и логические схемы
Арифметические операции являются одной из основных функций большинства компьютеров и калькуляторов. Эти операции выполняются логическими элементами или просто комбинационными схемами, которые объединяют несколько логических элементов для выполнения требуемой функции. Эти арифметические функции комбинационных схем включают сложение, вычитание, умножение и т. д.
Некоторые из комбинационных схем, используемых для этих операций: полусумматор, полный сумматор, полувычитатель, полный вычитатель, сумматор-вычитатель, компаратор, PLD (программируемое логическое устройство) и т. д.
Цепи передачи данных
наиболее часто используемыми комбинационными схемами являются мультиплексоры и демультиплексоры.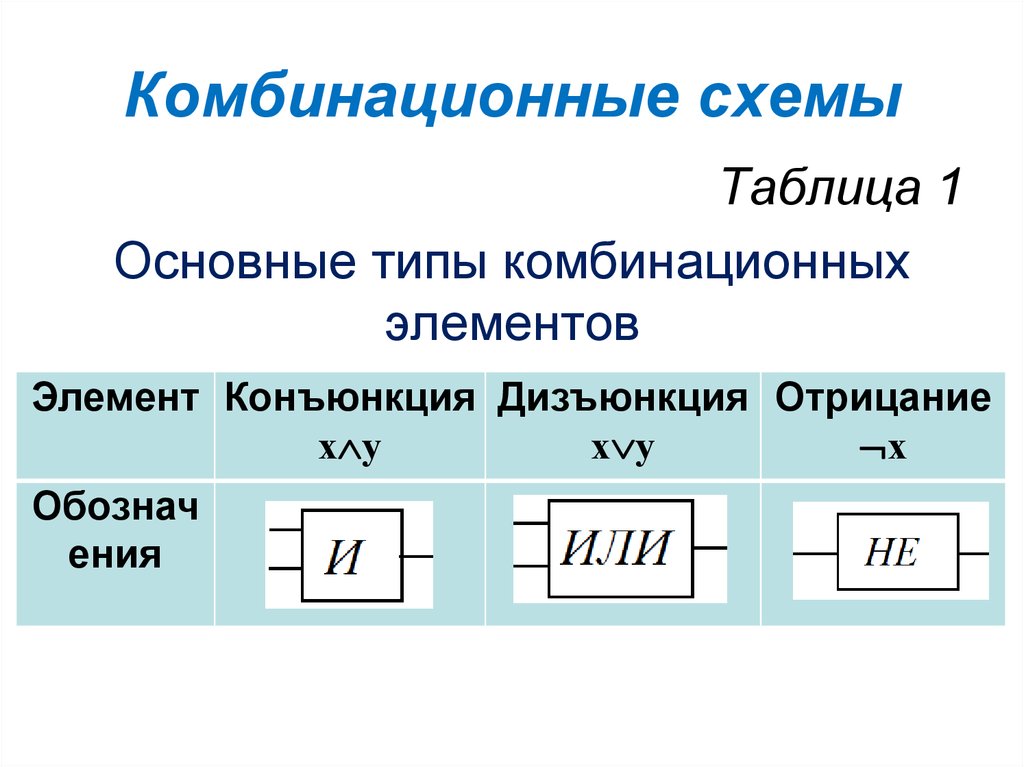 Логическая схема мультиплексора принимает несколько входных данных и пропускает один из них через выход за раз. Они используются для выбора данных, параллельного последовательного преобразования, приложений маршрутизации данных в цифровых системах.
Логическая схема мультиплексора принимает несколько входных данных и пропускает один из них через выход за раз. Они используются для выбора данных, параллельного последовательного преобразования, приложений маршрутизации данных в цифровых системах.
Схема демультиплексора выполняет операцию, обратную мультиплексору. Он принимает один вход и распределяет его на несколько выходов. Они используются в распределителях, а также в последовательно-параллельных преобразователях.
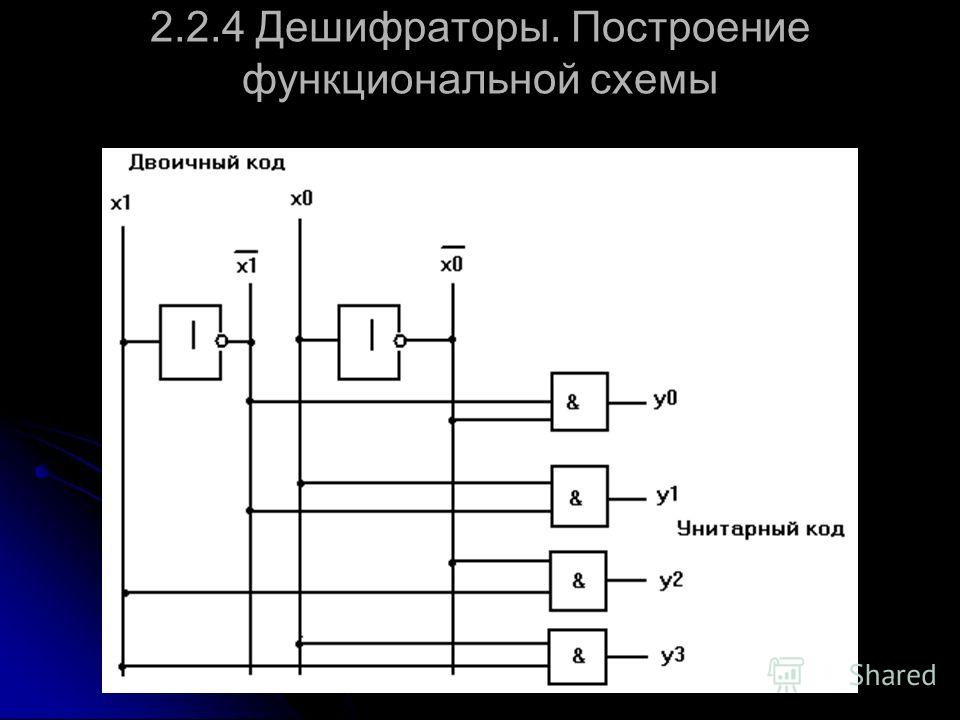
Другие важные схемы передачи данных включают кодеры и декодеры. Логическая схема декодера преобразует n-битный двоичный входной код в 2n выходных строк. Каждая выходная линия активируется только для одной из возможных комбинаций входов.
Они используются в демультиплексировании данных, цифро-аналоговых преобразователях и цифровых дисплеях. Цифровая схема энкодера преобразует активный входной сигнал в закодированный выходной сигнал как операцию, обратную декодеру. Они используются в приложениях для сжатия битов.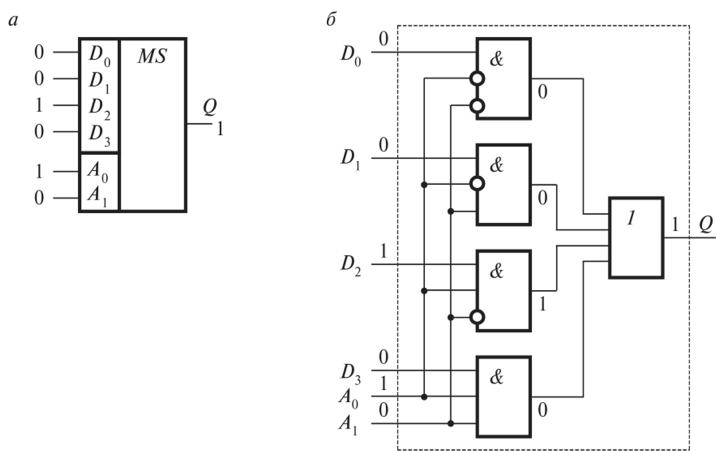



 Используйте Карты Карно или Булеву алгебру.
Используйте Карты Карно или Булеву алгебру. Z = А * ~ В * С + А * В * ~ С + А * В * С
Используйте булеву алгебру, чтобы упростить
логическое выражение для: Z = (В + С) * А
Z = А * ~ В * С + А * В * ~ С + А * В * С
Используйте булеву алгебру, чтобы упростить
логическое выражение для: Z = (В + С) * А  Обратите внимание, что 7e получено из столбца e.
Обратите внимание, что 7e получено из столбца e.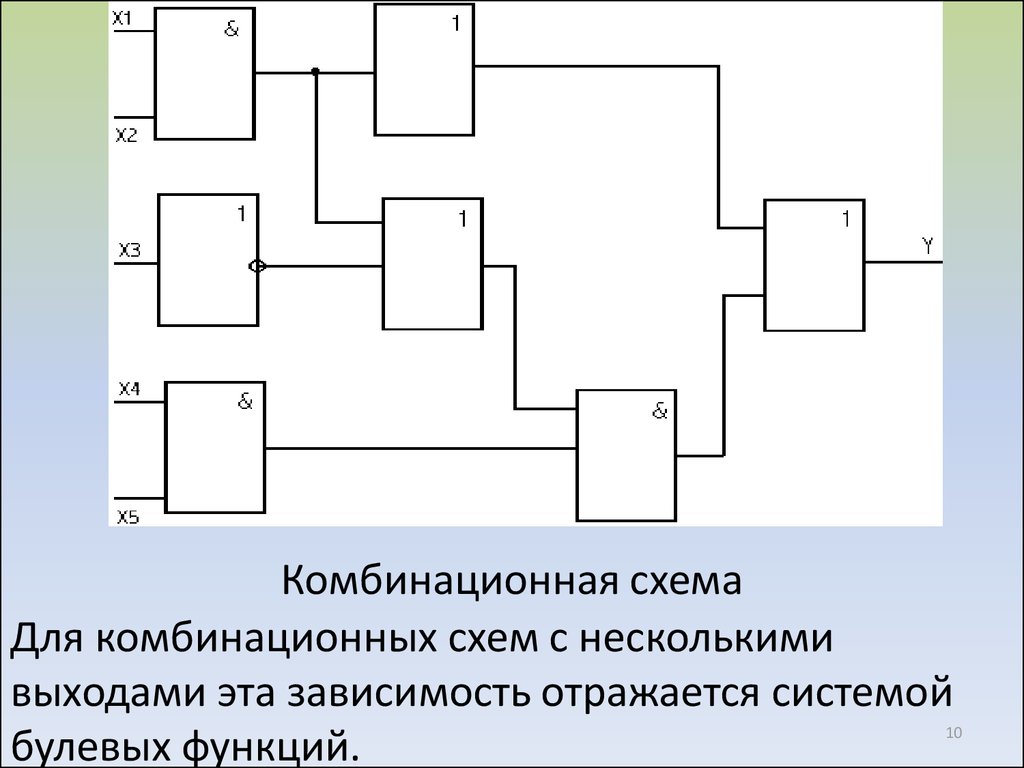 Проверьте дизайн по
анализ или моделирование схемы.
Проверьте дизайн по
анализ или моделирование схемы.