Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…ОбъявленияВидеоконференцияВопрос — ответOnline чатО науках «Электротехника» и «Электроника»Цель, задачи и результаты освоения дисциплиныСодержание дисциплиныМесто учебной дисциплины в структуре ОПОП ВОМетодика обучения студентов очной/заочной формы обученияАттестация по дисциплинеЧто нужно сделать чтобы получить оценку?Рекомендуемая литература по дисциплине «Общая электротехника и электроника»Лазута И.В. Реброва И.А. Основы электротехники и электроники. Учебное пособие. 2018Лазута И.В. Реброва И.А. Расчет и анализ электрических цепей и устройств. Учебно-методическое пособие. 2019Лазута И.В. Реброва И.А. Электротехника. Лабораторный практикум. 2022Литература для расширенного изучения дисциплиныПрограмма для чтения PDF и DJVUАнализ и расчёт цепей постоянного токаАнализ и расчёт линейных цепей однофазного синусоидального токаАнализ трёхфазных электрических цепейАнализ и расчёт магнитных цепейТрансформаторыЭлементная база современных электронных устройствИсточники вторичного электропитанияЛампочка в цепи постоянного токаЛампочка в цепи переменного токаКатушка в цепи постоянного токаКатушка в цепи переменного токаКонденсатор в цепи постоянного токаКонденсатор в цепи переменного токаДиод в цепи постоянного токаДиод в цепи переменного токаПараллельный колебательный контур в цепи переменного токаРезонанс токов в параллельном колебательном контуреТрансформаторДвухполупериодная мостовая выпрямительная схемаМостовая выпрямительная схема с фильтром и стабилизаторомПрезентации и заготовкиЗагрузка ЛР №1.
ГОСТ 19.
005-85 ЕСПД. Р-схемы алгоритмов и программ. Обозначения условные графические и правила выполненияЕдиная система программной документации Р-СХЕМЫ АЛГОРИТМОВ И ПРОГРАММ Обозначения условные графические и правила выполнения Unified system for program documentation. R-charts. Graphical chart symbols and conventions for charting | ГОСТ 19.005-85 |
Постановлением Государственного комитета СССР по стандартам от 27 марта 1985 г. № 893 дата введения установлена
01.07.86
Настоящий стандарт распространяется на алгоритмы, программы, данные и процессы для вычислительных машин, комплексов, автоматизированных систем и систем обработки информации независимо от их назначения и области применения.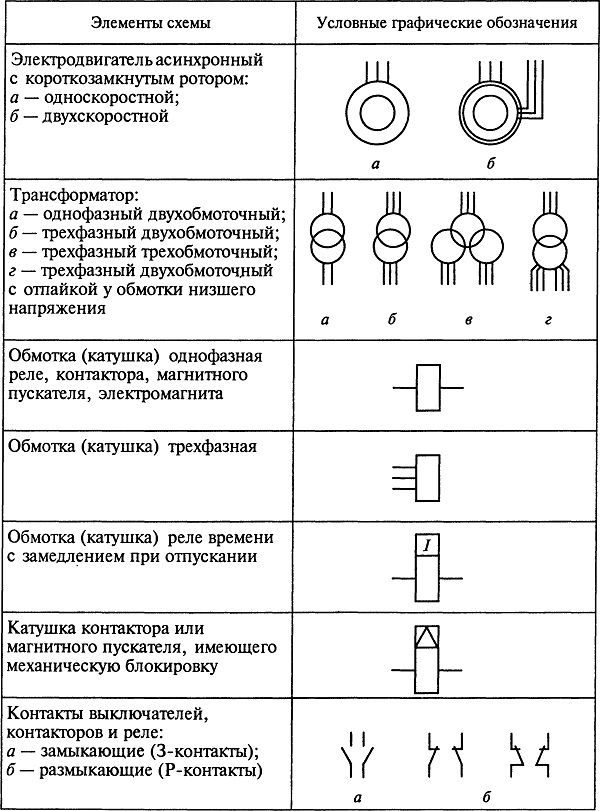
Стандарт устанавливает условные графические обозначения элементов и структур Р-схем, а также правила их выполнения автоматическим и (или) ручным способами.
Р-схема (R-chart) — нагруженный по дугам ориентированный граф, изображаемый с помощью вертикальных и горизонтальных линий и состоящий из структур (подграфов), каждая из которых имеет только один вход и один выход.
1. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЭЛЕМЕНТОВ Р-СХЕМ
1.1. Перечень, наименование, обозначение и функции элементов Р-схем должны соответствовать указанным в табл. 1.
1.2. В приложении 1 приведены примеры допустимых условных обозначений элементов Р-схем, выполненных на алфавитно-цифровых устройствах ввода-вывода.
1.3. В приложении 2 приведены примеры выполнения элементов Р-схем.
Таблица 1
Наименование | Обозначение и его содержание | Функция |
|---|---|---|
1. | Окружность диаметром не менее 2 мм | Вершина Р-схемы |
2. Вершина специальная | Левая и правая круглые скобки на расстоянии не менее 1 мм | Выделение вершины Р-схемы |
3. Дуга | Горизонтальная линия со стрелкой а) справа 6) слева | Направленное соединение двух вершин Р-схемы |
4. Дуга специальная | Две горизонтальные линии, отстоящие друг от друга на расстоянии 0,8-3 мм | Специальное соединение двух вершин Р-схемы |
5. | Вертикальная линия | Соединение по вертикали указанных выше элементов Р-схемы |
6. Комментарий | Пунктирная вертикальная (вверх или вниз) и горизонтальная (влево или вправо) линии, оканчивающиеся квадратной скобкой, за которой следует текст комментария | Связь между элементом Р-схемы и текстом комментария |
Линия соединительная2. СТРУКТУРЫ Р-СХЕМ
2.1. Структуры Р-схем должны соответствовать указанным в табл. 2 или полученным из них путем применения правил соединения структур (разд. 3).
Таблица 2
Наименование | Обозначение и его содержание | Функция |
1. | Две вершины, соединенные одной и более дугами любого направления и в любом сочетании | Последовательность переходов между вершинами в соответствии с направлением дуг |
2.Структура специальная | Две вершины, соединенные специальной дугой или специальной дугой и любым числом дуг любого направления и в любом сочетании | Последовательность переходов между вершинами, осуществляемых специальным образом |
Структура базоваяПримечания:
1. Вершина структуры, из которой исходит первая сверху дуга, называется начальной.
2. Вершина структуры, в которую входит первая сверху дуга, называется конечной.
3. Начальная и конечная вершины структуры, содержащей только специальную дугу, определяются ее конкретным использованием.
2.2. В приложении 3 и на черт. 1-4 приведены примеры записи структур Р-схем.
3. ПРАВИЛА СОЕДИНЕНИЯ СТРУКТУР Р-СХЕМ
3.1. Устанавливаются следующие соединения структур Р-схем:
последовательное;
параллельное;
вложенное.
В результате их применения получаются структуры Р-схем, к которым также применимы установленные правила их соединения.
3.1.1. Последовательное соединение структур Р-схем осуществляется путем слияния конечной вершины и соединительной линии одной структуры с начальной вершиной и соединительной линией
другой, располагаемой за ней структуры. Если конечная вершина первой и (или) начальная вершина второй структуры являются специальными, то в результате слияния образуется специальная вершина, при этом соединительные линии обеих структур не сливаются. Начальной и конечной вершинами результирующей структуры становятся соответственно начальная вершина первой и конечная вершина второй из соединяемых структур.
Пример последовательного соединения г структур а, б, в и а приведен на черт. 1.
Черт. 1
3.1.2. Параллельное соединение структур Р-схем осуществляется путем связи соединительными линиями начальной и конечной вершин одной структуры соответственно с начальной и конечной вершинами другой, расположенной под ней структуры. Начальной и конечной вершинами результирующей структуры становятся соответственно начальная и конечная вершины первой (верхней) из соединяемых структур.
На черт. 2 изображены примеры параллельного соединения структур: а— приведенных на черт. 1 а, 1 б и 1 а; б — приведенных на черт. 1 в и 1 б; в— приведенных на черт. 1 б и 1 б.
Черт. 2
3.1.3. Вложенное соединение структур Р-схем осуществляется путем замены дуги структуры, в которую производится вложение, на последовательное соединение дуги того же направления и вкладываемой структуры.
При этом соединительная линия из конечной вершины вкладываемой структуры и сама конечная вершина (если она не является конечной вершиной параллельного соединения структур) сливаются соответственно с соединительной линией и вершиной, в которые входила заменяемая дуга. Начальной и конечной вершинами результирующей структуры остаются соответственно начальная и конечная вершины структуры, в которую производится вложение.
Примеры вложенного соединения структур Р-схем приведены на черт. 3 и 4. На черт. 3 вложение осуществляется путем замены дуги со стрелкой справа, а на черт. 4 — слева.
На черт. 3 изображены примеры вложенного соединения: а — структуры 1 в в структуру 1 б; б — последовательного соединения структур 1 б и 1 а в структуру 1 в ; в — структуры 1 в в структуру 1 в; г — структуры 2 б в структуру 1 б.
Черт.3
На черт.
4 изображены примеры вложенного соединения: а — структуры 1 б в структуру 1 б; б — последовательного соединения структур 1 в, 1 б и 1 а в структуру 1 б; в — последовательного соединения структур 1 б и 2 б в структуру 1 б.
Черт. 4
4. НАДПИСИ НА ЭЛЕМЕНТАХ И СТРУКТУРАХ Р-СХЕМ
4.1. Надписи на элементах и структурах Р-схем должны соответствовать указанным в табл. 3.
4.2. В приложении 4 приведены примеры выполнения надписей на элементах и структурах Р-схем.
5. ПРАВИЛА ВЫПОЛНЕНИЯ Р-СХЕМ
5.1. Р-схемы в программных документах выполняются на листах формы 1 или формы 2 в соответствии с ГОСТ 19.106-78.
5.2. На одном листе может располагаться одна или несколько без переноса Р-схем, каждая из которых может сопровождаться текстом, записываемым до и (или) после нее. Правила оформления текстов Р-схем определяются при реализации.
Текст Р-схемы, текст ее комментария и ЗАПИСИ на элементах Р-схем для одного способа выполнения (ручного или автоматического) должны иметь одинаковый интервал между строками.
5.3.Р-схемы вместе с сопровождающими текстами Р-схем в программных документах могут оформляться в виде иллюстраций, приложений или располагаться в разрыве между строками текста документа без нумерации.
5.4. Расстояние между Р-схемой и сопровождающим ее текстом, а также между Р-схемами должно быть больше одного интервала между строками ЗАПИСЕЙ на элементах Р-схем.
Расстояние между Р-схемой и текстом документа должно быть больше одного интервала между строками текста документа.
5.5. Р-схемы и сопровождающие их тексты при ручном изготовлении должны быть выполнены черными чернилами, пастой или тушью, иметь одинаковую толщину линий и шрифт, соответствующий ГОСТ 2.304-81.
Специальные знаки (*, #, круглые скобки), используемые при изображении Р-схем, должны по высоте не превышать 1,5h, где h — максимальная высота строки ЗАПИСЕЙ на элементах Р-схемы.
5.6. Расстояние между ЗАПИСЯМИ, расположенными одна под другой на разных дугах одной Р-схемы, должно быть больше одного интервала между строками ЗАПИСЕЙ на элементах Р-схем.
5.7. Квадратная скобка в комментарии должна охватывать текст комментария.
5.8. Расстояние сверху и снизу от текста комментария должно быть больше одного интервала между строками текста комментария.
5.9. В приложении 5 приведен пример выполнения Р-схемы.
Таблица 3
Наименование | Обозначение и его содержание | Функция |
1.Надпись внутри специальной вершины | Тип структуры Р-схемы, определяющий ее особую реализацию | |
2. | Условие прохождения по дуге | |
3.Надпись под дугой | Действие, выполняемое при прохождении по дуге | |
4.Надпись над специальной дугой | Задает специальное (определенное при реализации) выполнение структуры Р-схемы | |
5.Надпись под специальной дугой | Действие, выполняемое специальным образом при прохождении по дуге | |
6.Надпись около начальной вершины структуры | Имя, записанное внутри структуры Р-схемы около начальной ее вершины без пробела | Имя структуры Р-схемы |
7. | Знаки «Звездочка» или «номер» с именем в конце дуги без пробелов. Имя может отсутствовать | Переход в начало (а) или в конец (б) структуры Р-схемы с указанным именем При отсутствии имени переход осуществляется в начало (а) или конец (б) данной Р-схемы |
Надпись над дугой
Надпись в конце дугиПримечания:
1. СТРОКА — последовательность любых знаков.
2. ЗАПИСЬ — любой текст, включая пустой, формульный, формальный (на языках программирования), содержащий любые специальные знаки, таблицы, рисунки и т. п. и записанный в одну или более строк таким образом, что длина любой строки не превышает длину дуги, соответствующей тексту.
3. ИМЯ — идентификатор по ГОСТ 19781-90.
Наименование | Обозначение |
|---|---|
1. | Знак «Плюс» или «Знак денежной единицы» по ГОСТ 19767-74 |
2. Вершина специальная | Левая и правая круглые скобки |
3. Дуга | Последовательность знаков «Минус», заканчивающаяся знаком «Больше» Последовательность из знака «Меньше» и следующих за ним знаков «Минус» |
4. Дуга специальная | Последовательность знаков «Равно» |
5. Линия соединительная | Последовательность расположенных друг под другом знаков «Восклицательный знак» |
6. | Вертикальная линия задается последовательностью расположенных друг под другом знаков «Двоеточие», горизонтальная линия задается последовательностью знаков «Минус», проведенных к первому или последнему знаку «Квадратная скобка», который ставится на каждой строке текста комментария |
Вершина
КомментарийНаименование | Выполнение от руки или автоматизированным способом на графических устройствах ввода-вывода | Выполнение автоматизированным способом на алфавитно-цифровых устройствах ввода-вывода |
|---|---|---|
1. Вершина | ||
2. | ||
3. Дуга | ||
4. Дуга специальная | ||
5. Линия соединительная | ||
6. |
Вершина специальная
КомментарийНаименование | Выполнение от руки или автоматизированным способом на графических устройствах ввода-вывода | Выполнение автоматизированным способом на алфавитно-цифровых устройствах ввода-вывода |
1. Структура базовая | ||
2. Структура специальная |
Наименование | Выполнение от руки или автоматизированным способом на графических устройствах ввода-вывода | Выполнение автоматизированным способом на алфавитно-цифровых устройствах ввода-вывода |
|---|---|---|
1. | ||
2. Надпись над дугой или специальной дугой | ||
3. Надпись под дугой или специальной дугой | ||
4.Надпись около начальной вершины структуры | ||
5.Надпись в конце дуги |
Надпись внутри вершины специальной Программа MINIMAX анализирует ряд чисел и выдает их количество, минимальное и максимальное числа.
Признаком конца ряда чисел является число нуль.
Традиционная линейная форма записи этой же программы имеет следующий вид:
В целом приложение 5 оформлено в соответствии с настоящим стандартом как сочетание ручного и автоматического способов. Р-схемы выполнены на двух листах формы 1 (в поле 3 — текст документа) по ГОСТ 19.106-78. На первом листе изображено две Р-схемы, которые друг от друга отделены более чем одним интервалом. Первая Р-схема сопровождается до, а вторая — после себя текстом.
Содержание
1. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЭЛЕМЕНТОВ Р-СХЕМ 2. СТРУКТУРЫ Р-СХЕМ 3. ПРАВИЛА СОЕДИНЕНИЯ СТРУКТУР Р-СХЕМ 4. НАДПИСИ НА ЭЛЕМЕНТАХ И СТРУКТУРАХ Р-СХЕМ 5. ПРАВИЛА ВЫПОЛНЕНИЯ Р-СХЕМ ПРИЛОЖЕНИЕ 1 ПРИМЕРЫ ДОПУСТИМЫХ УСЛОВНЫХ ОБОЗНАЧЕНИЙ ЭЛЕМЕНТОВ Р-СХЕМ, ВЫПОЛНЕННЫХ НА АЛФАВИТНО-ЦИФРОВЫХ УСТРОЙСТВАХ ВВОДА-ВЫВОДА ПРИЛОЖЕНИЕ 2 ПРИМЕРЫ ВЫПОЛНЕНИЯ ЭЛЕМЕНТОВ Р-СХЕМ ПРИЛОЖЕНИЕ 3 ПРИМЕРЫ ЗАПИСИ СТРУКТУР Р-СХЕМ ПРИЛОЖЕНИЕ 4 ПРИМЕРЫ ВЫПОЛНЕНИЯ НАДПИСЕЙ НА ЭЛЕМЕНТАХ И СТРУКТУРАХ Р-СХЕМ ПРИЛОЖЕНИЕ 5 ПРИМЕР ВЫПОЛНЕНИЯ Р-СХЕМЫ ПРОГРАММЫ НА ПАСКАЛЕ |
Условные выражения и диаграммы Эйлера — Криста Кинг Математика
Условный оператор — это оператор «если-то».
В этом уроке мы рассмотрим, как писать условные операторы и как рисовать и интерпретировать диаграммы Эйлера.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Условный оператор
Условный оператор – это оператор «если/то», в котором часть «если» является гипотезой и идет первой, а часть «тогда» является выводом и идет второй.
Вы всегда пишете такое условное выражение:
«Если ???A???, то ???B???».
Этот тип условного оператора говорит вам, что если ???A??? верно, то ???B??? тоже должно быть правдой.
Как строить диаграммы Эйлера из условных выражений
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Переписать операторы как условные операторы
Пример
Запишите оператор как условный оператор.
«У всех собак есть шерсть».
Нам нужно создать гипотезу и сделать вывод из утверждения «У всех собак есть мех» и записать его в виде утверждения «если/то». В этом утверждении гипотеза «это собака», а вывод «у нее есть мех». Это делает условное утверждение
«Если это собака, то у нее есть шерсть».
Поскольку нам сказали, что у всех собак есть мех, мы знаем, что если что-то является собакой, то у него должен быть мех.
Условный оператор – это оператор if/then, в котором часть «если» является гипотезой и идет первой, а часть «тогда» является выводом и идет второй.
Диаграммы Эйлера
Диаграмма Эйлера показывает точное отношение, описанное в условном выражении. Она отличается от диаграммы Венна тем, что диаграмма Венна показывает все возможности, включая те, которые не описаны в условном выражении.
Они часто имеют форму:
«Если ???A???, то ???B???».
«Если ???А???, то не ???В???».
Давайте рассмотрим пример.
Пример
Какое условное выражение представлено на диаграмме Эйлера?
Диаграмма имеет вид «Если ???A???, то ???B???».
Итак, мы заменяем ???A??? и ???Б??? со значениями из диаграммы, и пишем
«Если это кошка, то это млекопитающее».
Давайте свяжем обе идеи вместе.
Пример
Напишите следующий оператор как условный оператор и нарисуйте соответствующую диаграмму Эйлера.
«Я получаю пособие, когда делаю домашнее задание».
Давайте подумаем, что стоит на первом месте в утверждении. Сначала делается домашнее задание, потом пособие. Это делает условное утверждение
«Если я делаю домашнее задание, я получаю пособие».
???А??? домашнее задание, а ???B??? является допуском, который делает диаграмму Эйлера
Получить доступ к полному курсу геометрии
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, геометрия, логика, условные операторы, диаграммы Эйлера, условные операторы в диаграммах Эйлера, операторы if then, логические операторы if then
0 лайковсек. 3.6 – Математика колледжа для начального образования
Глава 3, Раздел 6
Математические темы – Диаграммы Эйлера и логические аргументы, «Если… то» (условные) утверждения
Тема обучения – Какие типы представлений подходят?
Логические аргументы
В предыдущем разделе у нас был пример
Все кошки — животные.
Флаффи — кот.
Если вы посмотрите на диаграмму (не используя собственные знания), то на диаграмме также видно, что Пушистик должен быть животным.
Мы можем записать это как заключение логического рассуждения:
Все кошки — животные. Помещение 1 Флаффи — кот. Помещение 2 Следовательно, Пушистик — животное. Заключение
Первые две строки аргумента — это предпосылки, то, что мы считаем истинным.
Последняя строка — заключение.
Чтобы быть действительным аргументом, заключение должно следовать из двух посылок. То есть, если мы за исключением того, что посылки истинны, вывод должен быть истинным на основе посылок . Приведенный выше аргумент действителен.
Что сделало бы аргумент не действительным? Попробуем немного изменить набор предпосылок и выводов:
Все кошки — животные.Помещение 1 Дэн - животное. Помещение 2 Следовательно, Дэн - кот. Заключение
Помещение 1
Дэн - животное. Помещение 2
Следовательно, Дэн - кот. Заключение Чтобы проверить, верный ли это аргумент, нарисуйте только помещения.
Даже не смотрите на вывод, когда рисуете!
Глядя на нашу картинку, мы видим, что вывод о том, что Дэн является котом , неверен. Дэн может быть котом, или Дэн может быть другим видом животных. На диаграмме показано, что D может находиться в двух возможных местах.
Это означает, что аргумент недействителен (недействителен).
Чтобы аргумент был действительным, мы должны быть на 100% уверены в том, что вывод верен на основе предпосылок.
Пример 1 Какой вывод верный?
Все квадраты четырехсторонние. Все квадраты четырехсторонние. М четырехгранный. Х - квадрат. Следовательно, М — квадрат. Следовательно, X четырехсторонний.
Чтобы решить, составьте диаграмму Эйлера, используя каждый набор предпосылок.
Помещения:
Все квадраты четырехгранные. Все квадраты четырехсторонние. М четырехгранный. Х - квадрат.
Помните, что для построения диаграммы используйте только предпосылки, , а не заключение.
Обратите внимание, что М может стоять в двух возможных местах. М должно быть в четырехстороннем круге вещей, потому что это первая предпосылка. M также может быть в круге квадратов, потому что это еще одно возможное место внутри четырехстороннего круга вещей.
Для X есть только одно возможное место внутри квадратного круга, так как это первая предпосылка этого аргумента. X не может быть вне этого круга, так как это означало бы, что X не был квадратом. Помните, мы принимаем каждую из предпосылок за абсолютно истинную.
Теперь посмотрим на выводы, чтобы увидеть, следуют ли они из посылок.
Верен ли вывод Следовательно, M является квадратом ?
№
Глядя на нашу диаграмму, мы видим, что M может быть квадратом, а может и не быть.
M может быть за пределами круга квадратов и иметь только 4 стороны. Например, M может выглядеть так:
M — 4-сторонний.
Верен ли вывод Следовательно, X является четырехсторонним ?
Да, потому что X находится внутри четырехстороннего круга вещей. Все квадрата четырехсторонние.
Но когда вы указываете причину, по которой аргумент действителен, используйте первую часть причины, приведенную выше: «Да, потому что X находится внутри четырехстороннего круга вещей». Вторая часть, « Все квадрата четырехсторонние», просто повторяет предпосылку. Переформулирование посылки (даже курсивом или подтекстом!) не является достаточным основанием для поддержки вашего аргумента. Вместо этого обратитесь к своей диаграмме и объясните, используя диаграмму.
Итог
НЕВЕРНЫЙ Аргумент и причина
Все квадраты четырехсторонние.
М четырехсторонний.
Следовательно, M — квадрат.
Недействительно, так как М может находиться в части круга вне квадратов
(см. схему).
ДЕЙСТВИТЕЛЬНО Аргумент и причина
Все квадраты четырехсторонние.
X — квадрат.
Следовательно, X четырехсторонний.
Действителен, потому что X должен быть в круге квадратных предметов,
внутри четырехсторонних предметов, так что это автоматически делает X
также четырехсторонним (см. схему).
Условное
Другой способ показать логический аргумент — использовать символы вместо диаграмм Эйлера или в дополнение к ним.
Все кошки — животные — это то же самое, что сказать: Если — это кошка, , то — это животное.
Оператор «if…then» известен как условное выражение .
Мы используем стрелку для обозначения условного выражения: с → а, где с — «это кошка, а а — это животное». Мы используем три точки, ∴, чтобы представить слово поэтому.
Допустимый аргумент
Использование «всех» Использование условных символов «В» Все кошки животные
| Использование «всех» | Использование условного обозначения | Символы |
| Если это кошка, то это животное. Это кошка. Следовательно, это животное. | c → a c ∴ a |
Обратите внимание, что когда мы используем условную стрелку, мы больше не называем кота Пушистиком.
Это делается для того, чтобы вторая посылка могла точно соответствовать первой части условного предложения.
В действительный ( не действительный) аргумент
| Использование «все» 900 12 | Использование условного обозначения | Символы |
| Все кошки — животные . Дэн — животное. Значит, Дэн — кот. | Если это кошка, то это животное. Это животное. Следовательно, это кошка. | с → а а ∴ с |
Посмотрите внимательно на порядок двух приведенных выше аргументов. Следуя этому шаблону, для оператора if-then типа A → B, какая вторая строка и вывод будут давать действительный аргумент?
| Допустимый аргумент (Modus Ponens) Порядок правильный | Неверный аргумент Порядок неправильный | А → В А ∴ В | А → В В ∴ А |
Официальное название действительной формы аргумента — латинская фраза modus ponens , но можно просто сказать «правильный порядок».
В правильном аргументе вторая посылка и вывод следуют в том же порядке, что и в условном выражении.
Ученик в моем классе указал, что порядок должен быть правильным, потому что условная стрелка не является коммутативной. То есть сказать A → B — это не то же самое, что сказать B → A. Или, вернувшись к нашему предыдущему примеру, если это кошка, то это животное это не то же самое, что сказать если это животное, то это кошка .
Мы можем использовать как диаграмму Эйлера , так и символическую логику , чтобы решить, является ли аргумент допустимым. Некоторым учащимся визуальное представление проще всего; для других студентов символическое представление является самым простым. Вот почему мы хотим всегда стараться дать нашим ученикам множество способов представления математики!
Пример 2 Верен или неверен следующий аргумент? Для принятия решения используйте диаграмму Эйлера и символическую логику с условным символом.
Все собаки дружелюбны.
Бонзо — собака.
Значит, Бонзо дружелюбен.
Чтобы принять решение, сначала перепишите аргумент в виде условного оператора («Если… то»). Посмотрите, к какому из приведенных выше шаблонов он подходит. Наконец, проверьте, нарисовав диаграмму Эйлера, чтобы визуально увидеть, действительна ли она.
| Использование «всех» | Использование условного обозначения | Символы |
| Если это собака, то она дружелюбная. Это собака. Значит, он дружелюбный. | d → f d ∴ f |
Этот аргумент действителен , потому что порядок аргумента верен. У вас есть d → f в качестве первой посылки, за которой следует первая буква d, а заключение — вторая буква f.
Итак, вторая посылка и заключение идут в том же порядке, что и условное в первой посылке.
Или, вместо букв d и f, вы можете думать о «собаках» как A, а о «дружелюбных» как B, и вы получите
A → B
A
∴ B
Это точное совпадение форму действительного аргумента, modus ponens, вверху этой страницы.
Диаграмма Эйлера подводит нас к тому же заключению. Аргумент действителен , потому что Бонзо находится внутри круга «Собаки», который, в свою очередь, находится внутри круга «дружеских вещей», что означает, что Бонзо находится внутри круга «дружественных вещей». » круг.
Пример 3 Верен или недействителен следующий аргумент?
Все собаки дружелюбны.
Рекс дружелюбный.
Значит, Рекс — собака.
Чтобы решить, мы перепишем аргумент как условное, чтобы увидеть шаблон. Затем мы рисуем диаграмму Эйлера, чтобы визуально увидеть, верна ли она.
| Использование «всех» | Использование условного | Символы |
Все собаки дружелюбны. Рекс дружелюбен. Следовательно, Рекс — собака. | Если это собака, то она дружелюбная. Это дружелюбно. Следовательно, это собака. | d → f f ∴ d |
Этот аргумент недействителен – вы можете видеть, что порядок d → f, сначала d, затем f, не соблюдается, так как вторая посылка есть f, за которой следует по заключению д. Если у нас есть d → f, правильный порядок будет иметь d в качестве первой посылки, за которой следует f. Но в этом аргументе сначала f, а затем d.
В качестве альтернативы вы можете думать о собаке как о A, а о дружелюбном как о B:
A → B
B
∴ A
Этот аргумент точно соответствует форме недопустимого аргумента в верхней части этой страницы.
Диаграмма Эйлера приводит нас к тому же выводу: аргумент неверен , потому что Рекс может быть в любом месте. Не факт, что Рекс находится внутри круга «Собаки». Чтобы быть действительным аргументом, вывод должен быть на 100% уверен.
Символ «не» в логических рассуждениях
В логических рассуждениях, если мы хотим сказать « не собака», мы будем использовать букву d, означающую «это собака», и мы поместим перед ним символ «не» ~: ~d означает «не собака». Этот символ подобен символу дополнения в наборах.
Пример 4 Верен или неверен следующий аргумент?
Если зеленый, то это не собака.
Зеленый.
Следовательно, это не собака.
Чтобы решить, пишем аргумент символами, чтобы увидеть закономерность. Мы также переписываем утверждение, чтобы мы могли нарисовать диаграмму Эйлера, чтобы визуально увидеть, верно ли оно.
| Условный | Символы | Слова |
| Если зеленый, то это не собака. Зеленый. Следовательно, это не собака. | г → ~d г ∴ ~d | Нет зеленых собак Генри зеленый Следовательно, Генри не собака.  |
Этот аргумент действителен: вторая посылка и вывод следуют в том же порядке, что и в условном (если… то). То есть в первой строке g → ~d, g стоит первой, а ~d — второй. Следующая посылка g и заключение ~d следуют в том же порядке.
С диаграммой Эйлера, Если зеленый, то это не собака разложится на два отдельных круга. Это то же самое, что нет собак зеленый .
Используя диаграмму Эйлера, мы видим, что аргумент действителен , так как Гарри находится в круге зеленых вещей, поэтому он не может быть в круге собак, так как они не пересекаются.
Логические аргументы с использованием «Некоторые» и «Нет»
Пример 5 Является ли следующий аргумент допустимым или недействительным?
Некоторые кошки являются домашними животными.
Пушистый кот.
Следовательно, Пушистик — домашнее животное.
Из предыдущего раздела мы знаем, что F можно поставить в двух местах: Пушистик может быть котом, который является домашним животным (в центре), или котом, который не является домашним животным (слева). Поскольку мы не знаем наверняка, что Пушистик находится в кошачьем круге, аргумент недействителен. Помните, чтобы аргумент был действительным, вывод должен следовать без сомнения из посылок.
В этом примере мы делаем , а не меняем аргумент на символы, потому что какой-то 9Оператор 0132 переводит , а не в условное выражение.
Некоторые кошки являются домашними животными не эквивалентны c → p, это будет все кошки являются домашними животными.
Важно уметь выбирать, какой тип представления — визуальный или символический — лучше всего использовать в данной ситуации.
Пример 6 Верен или неверен следующий аргумент? Используйте диаграмму Эйлера или символы, в зависимости от того, что лучше, чтобы решить.
Некоторые телешоу смешные.
Вебстер не смешной.
Следовательно, Вебстер — это не телешоу.
Для любого аргумента с «some» мы не можем использовать условное выражение , поэтому рисуем диаграмму Эйлера. Здесь у нас есть «Некоторые телешоу смешные».
Поскольку Вебстер не смешной, есть два возможных места, чтобы поместить Вебстера, кроме «Забавных вещей». Одно из этих возможных мест находится внутри телешоу, поэтому вывод «Вебстер — это не телешоу» будет 9.0011 неверный .
Все отношения и Транзитивность
Какой вывод правильный, чтобы сообщить нам о том, как связаны квадраты и четырехугольники?
Все квадратов являются прямоугольниками.
Все прямоугольники являются четырехугольниками (имеют четыре стороны).
Следовательно, все ____ являются _______.
Правильный вывод создаст действительный аргумент.
Используйте схему, чтобы увидеть, какой набор будет подмножеством другого.
действительный вывод равен Следовательно, все квадраты четырехугольники (имеют четыре стороны).
Мы знаем, что это так, потому что на нашей диаграмме набор квадратов равен внутри набора четырехугольников.
Мы также можем использовать условное выражение и символы, чтобы понять, почему.
Условный Символы
Если это квадрат, то это прямоугольник. с → р
Если это прямоугольник, то это четырехугольник r → q
Следовательно, если это квадрат, то это четырехугольник. ∴ s → q
Символы по порядку: s → r, r → q.
То есть s → r → q
Это образует непрерывную цепочку от s, хотя и r, до q. Таким образом, вывод s → q верен.
Этот тип аргумента,
A → B
B → C
∴ A → C
, называется действительным аргументом на транзитивность .
Он показывает цепочку, идущую от А к В, затем от В к С, следовательно, А идет к С. Если одно число на меньше другого на , мы пишем a < b . Например, 3 < 4.
Теперь предположим, что мы знаем, что a < b и мы знаем, что b < c. Мы можем записать это как одно неравенство: a < b < c ( a меньше b меньше c ).
Мы можем заключить, что a должно быть на меньше, чем c , то есть a < c.
Написанное числами, это все равно, что сказать, что если 3 < 4 и 4 < 5, мы знаем, что 3 < 5. .
А → В
С → В
∴ А → С
— это , а не , допустимый аргумент по транзитивности.
Это не , а не показывает цепочку, идущую от A к B, затем от B к C. Вместо этого и A, и C идут к B, так что ничего не связывает A с C.
Пример 7 Используйте ваше знание наборов чисел для создания действительного аргумента по транзитивности.
Все натуральные числа являются целыми числами. N → W
Все целые числа являются целыми числами W → I
Следовательно, все натуральные числа ____? ∴ N → ____?
Можно было бы правильно заключить, что N → I. Это следует из построения цепочки из посылок: N → W, W → I, значит имеем N → W → I
Пример 8 аргумент в силе?
Все целые числа являются целыми числами. W → I
Все натуральные числа целые N → I
Следовательно, все целые числа являются натуральными числами ∴ W → N
Мы можем видеть, что этот аргумент недействителен , глядя на ту же диаграмму – множество целых чисел не входит в множество натуральных чисел,
Мы также можем видеть, что этот аргумент неверен , взглянув на символы:
W → I, N → I
Цепочки от W до N нет, каждая стрелка указывает на I, ничто не указывает от до N.
Пример 9 Какие из следующих аргументов, показанных только символами, верны транзитивностью? Что недействительно? Совет: посмотрите, сможете ли вы найти цепочку, ведущую от одной буквы в заключении к другой.
Аргумент 1 Аргумент 2 Аргумент 3 Аргумент 4
p → q a → b
a → b m → r ~y → q c → b
д → г a → t q → m ∴ a → c
∴ p → r ∴ m → t ∴ x → q
Первый аргумент можно вывести в одну длинную строку, чтобы увидеть, что с чем связано. Имеем p → q, a → b, q → r. Мы можем избавиться от a → b, так как эта посылка не имеет ничего общего с остальными. Теперь у нас есть p → q, q → r, что дает нам цепочку: p → q → r, что означает, что p действительно ведет к r , p → r.
Аргумент равен действительный .
Можно удалить аргумент в предпосылках, который не влияет на ваш вывод! Предположим, кто-то сказал вам: «Все свиньи быстрые» (p → q), все аллигаторы большие (a → b) и все быстрые существа быстрые (q → r). Вы определенно можете проигнорировать эту часть об аллигаторах и сделать вывод, что все свиньи быстрые (p → r).
Для аргумента 2 имеем m → z, m → r, a → t. Поскольку в заключении m → t, мы ищем в посылках цепочку, связывающую m с t, например: m → ___ → ___ …→ t. Цепь, идущая от m к t, отсутствует. Вместо этого у нас есть m, идущий к z и к r, но ни z, ни r не ведут ни к чему другому. Аргумент неверный .
Для аргумента 3 имеем x → ~ y, ~ y → q и q → m в посылках. Поскольку вывод x → q, мы ищем в посылках цепочку, которая связывает x с q. У нас есть эта цепочка: у нас есть x → ~ y, ~ y → q, что становится x → ~ y → q, так что мы имеем x → q. Аргумент допустим .
