Вопрос: что такое резистор? Выходит, что резистор и сопротивление — это одно и то же? Или всё же не одно и то же? В этом имеет смысл разобраться прежде, чем делать следующие шаги. Но для этого полезно коротко, буквально в двух словах коснуться истории этого вопроса и договориться о смысле терминов которые мы будем применять в дальнейшем. Начнём с того, что английскому слову резистор в русском языке при дословном переводе действительно соответствует русское слово «сопротивление». Сопротивление — это одна из основных физических величин классической электротехники наряду с другими понятиями — напряжением, током, мощностью, электрической ёмкостью, индуктивностью. Сопротивление, строго говоря, величина абстрактная в том смысле, что определяя по формуле закона Ома его значение, вы вовсе не обязательно имеете в виду какую либо деталь. Речь может идти просто о величине электрического сопротивления, а чего именно — в большинстве случаев вообще не имеет значения. В то же время в ряде случаев сопротивление — понятие вполне осязаемое: его можно не только вычислить по формуле, но и точно измерить прибором. Резистор — это конкретная осязаемая деталь, которая всегда, во всех без исключения случаях обладает некоторым сопротивлением. Обязательно активным и положительным. Резистор помимо сопротивления может характеризоваться рядом других физических характеристик: предельным значением рассеиваемой мощности, допустимым приложенным напряжением и т.п., тогда как понятие сопротивление характеризуется только его значением в Омах (или др. производных единицах). Итак, сопротивление — это физическая величина, характеризующая некоторые электрические свойства материи. А точнее — способность препятствовать свободному, без потерь, распространению электрической энергии. В реальном материальном мире понятие электрического сопротивления присутствует всегда — по крайней мере до тех пор. пока имеет место самопроизвольное движение электронов (броуново движение). Если допустить на минуту, что значение сопротивления может быть равно нулю, то тогда становится бессмысленной формула основного закона электротехники — закона Ома. Между тем в практической электро- и особенно радиотехнике вполне корректными считаются понятия «нулевое сопротивление» и даже «отрицательное сопротивление». И это лишний раз подтверждает нашу мысль, что прежде всего надо четко ориентироваться в существующей терминологии. Начнем с того, что физики различают сопротивления активные и реактивные. С активными сопротивлениями все очень просто: зто такие сопротивления, на которых при протекании любого тока (переменного или постоянного) часть электрической энергии обязательно необратимо преобразуется в тепловую. Иногда зто полезно (например, в нагревательных приборах), чаще — бесполезно и даже вредно (например, нагрев деталей внутри телевизора), но во всех случаях — неизбежно. У реактивных сопротивлений протекающий ток не приводит к бесполезной потери энергии (по крайней мере, теоретически, если отбросить крайне незначительные потери, вызванные побочными причинами). Иными словами, они не нагреваются протекающим током. Но у реактивных сопротивлений есть два существенных отличия от активных сопротивлений. Резисторы — неотъемлемая и наиболее часто используемая деталь любого современного радиотехнического или электронного устройства. Сегодня невозможно представить себе радиоприемник, телевизор, осциллограф или магнитофон без единого резистора. Однако так было не всегда. Например, в первых детекторных радиоприемниках не было ни одного резистора, что не мешало осуществлять на них уверенный прием нескольких станций. Резисторы появились тогда, когда в них возникла потребность. А чтобы понять, почему возникла потребность, надо уяснить, какие функции выполняют в схеме резисторы. На заре радиотехники таких функций было не более трех-четырех, поэтому и самих резисторов в схеме любого радиоаппарата было, как принято говорить, раз-два — и обчелся. В современной радиоаппаратуре любого назначения резисторы выполняют без преувеличения десятки различных функций, а потому, к примеру, схема телевизора насчитывает порой не одну сотню резисторов. Вот далеко не полный перечень функций, которые сегодня выполняют в радиоприемной, измерительной и другой аппаратуре постоянные и переменные резисторы:
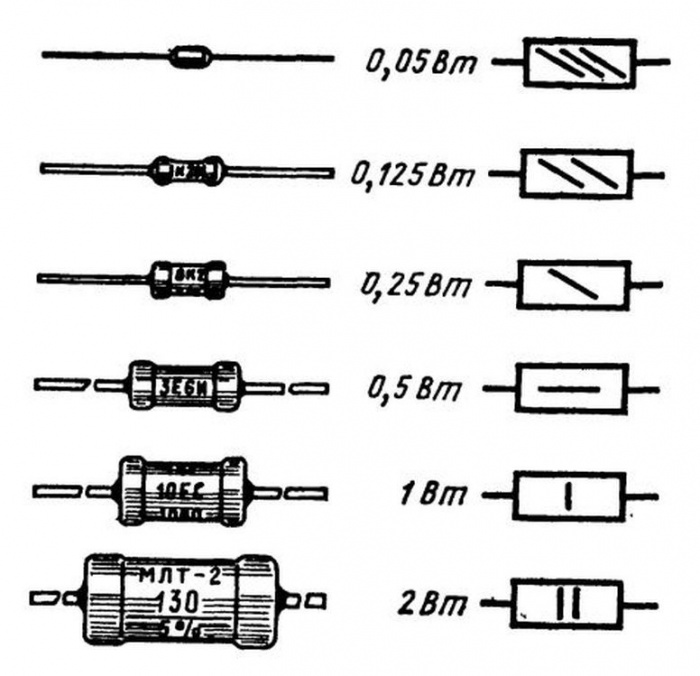
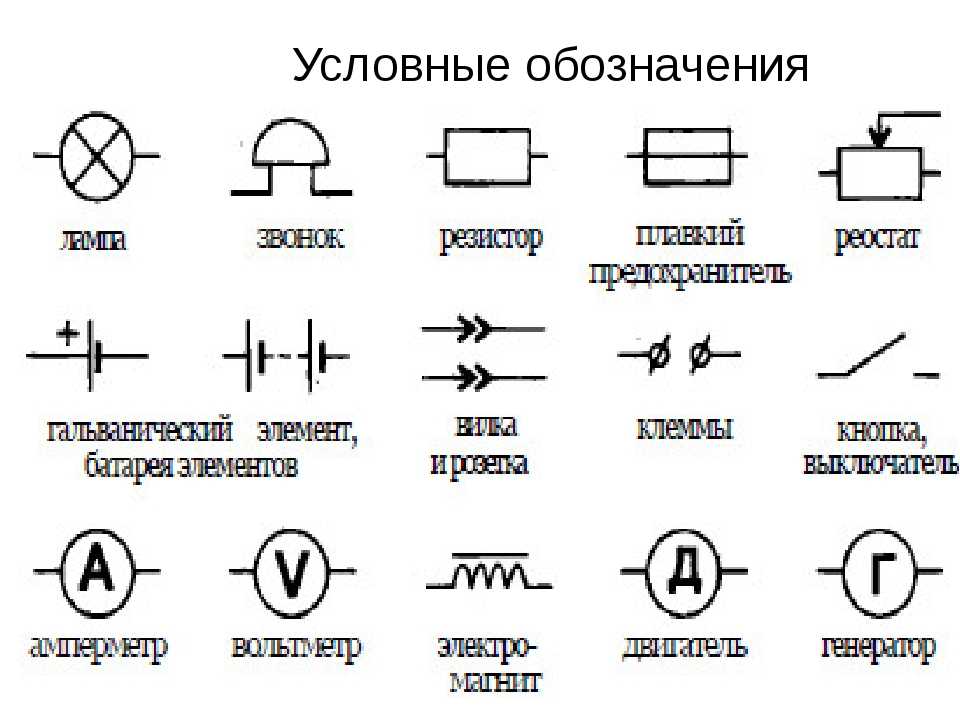
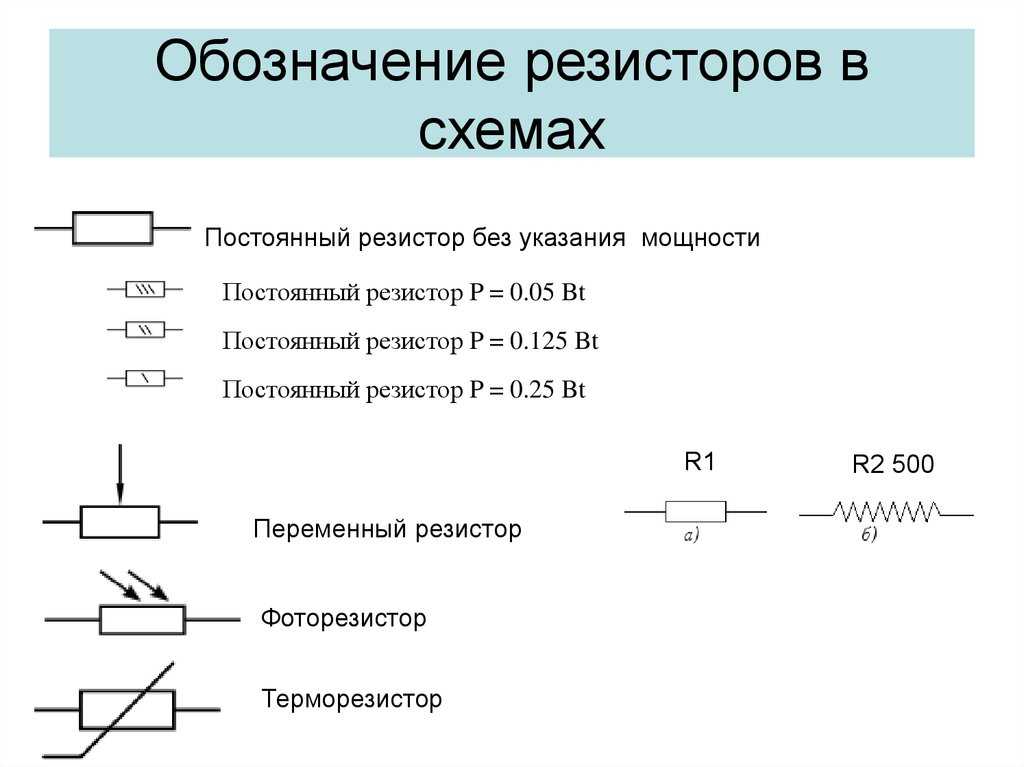
Даже этот, далеко не полный, перечень показывает, какое место занимают в современной схемотехнике резисторы и как велико должно быть их разнообразие, чтобы удовлетворить выбор конструктора. Как ни крути, но если Вы не знаете обозначения элементов на схемах и вообще не знаете, что такое радиосхема, то Вы — не электронщик! Но это дело поправимо, не переживайте ;-). Было бы желание — будут и знания! Я вам помогу. Каждый радиоэлемент на схеме имеет свое название и обозначение. Есть оно и у резистора. Резисторы бывают постоянными и переменными. В жизни постоянные резисторы могут выглядеть примерно вот так: Слева мы видим резистор, который рассеивает очень большую мощность, поэтому он такой большой. А вот так выглядит постоянный резистор на электрических схемах: Наше отечественное изображение резистора показывают прямоугольником (слева), а заморский вариант (справа), или как говорят — буржуйский, используется в иностранных радио схемах. А вот так выглядит маркировка мощности на них: Далее мощность маркируется с помощью римских цифр. Переменные резисторы выглядят как-то так: Переменный резистор, который управляет напряжением называется потенциометром, а тот, который управляет силой тока — реостатом. Здесь заложен принцип Делителя напряжения и Делителя тока соответственно. Вот так обозначаются переменные резисторы на схемах: Соответственно отечественный и зарубежный вариант. А вот и их цоколевка (расположение выводов): Переменники, у которых сопротивление можно менять только при помощи отвертки или шестигранного ключика, называются подстроечными переменными резисторами. А вот так обозначаются подстроечные резисторы: Чтобы включить его как реостат, нам нужно два вывода соединить вместе. Также существуют и другие виды резисторов. Это могут быть термисторы, варисторы, фоторезисторы. Термисторы — это резисторы на основе полупроводниковых материалов. Их сопротивление резко зависит от температуры окружающей среды. Есть такой важный параметр, как ТКС — тепловой коэффициент сопротивления. Грубо говоря, этот коэффициент показывает на сколько изменится сопротивление термистора при изменении температуры окружающей среды. Этот коэффициент может быть как отрицательный, так и положительный. Если ТКС отрицательный, то такой термистор называют термистором :-), а если ТКС положительный, то такой термистор называют позистором. Какой еще нафиг ТКС, что к чему? Не замарачивайтесь, все просто :-). У термисторов при увеличении температуры окружающей среды сопротивление падает. У позисторов с увеличением температуры окружающей среды растет и сопротивление. Так как термисторы обладают отрицательным коэффициентом (NTC — Negative Temperature Coefficient — отрицательный ТКС), а позисторы положительным коэффициентом (РТС — Positive Temperature Coefficient — положительный ТКС), то и на схемах они будут обозначаться соответствующим образом. Есть также особый класс резисторов, которые резко изменяют свое сопротивление при увеличении напряжения — это варисторы. Это свойство варисторов широко используют от защиты перенапряжений в цепи, а также от импульсных скачков напряжения. Допустим у нас скаканула напруга, при этом также сразу же резко увеличилось сопротивление варистора, тогда сила тока, протекающего в цепи будет ничтожно малой и не причинит вред цепи. На схемах варисторы обозначаются вот таким образом: Большой популярностью также пользуются фоторезисторы. Весь прикол заключается в том, что они изменяют свое сопротивление, если на них посветить. В этих целях можно применять как солнечный свет, так и искусственный, например от фонарика. На схемах они обозначаются вот таким образом: В настоящее время резисторы используются абсолютно во всей радиоаппаратуре. Переменные резисторы регулируют громкость ваших компьютерных колонок. Фоторезисторы и термисторы используются в охранно-пожарной сигнализации, как высокочувствительные датчики. Не знание схемотехники резисторов — это все равно, что не знание таблицы умножения. Материал взят отсюда Выпускаемые отечественной промышленностью резисторы классифицируются по различным признакам. В зависимости от характера изменения сопротивления резисторы разделяют на постоянные — значение сопротивления фиксировано и переменные — с изменяющимся значением сопротивления. В зависимости от назначения резисторы делятся на общего назначения и специальные (прецизионные, сверхпрецизионные, высокочастотные, высоковольтные, высокомегаомные). Резисторы общего назначения используются в качестве нагрузок активных элементов, поглотителей, делителей в цепях питания, элементов фильтров, шунтов, в RC — цепях формирования импульсных сигналов и т. Прецизионные и сверхпрецизионные резисторы отличаются высокой стабильностью параметров и высокой точностью изготовления (допуск ±0,0005…0,5 %). Данные резисторы применяются в основном в измерительных приборах, системах автоматики. Диапазон этих резисторов значительно шире, чем резисторов общего назначения. Примерами служат резисторы Р1-72, Р2-67, С2-10, С2-29, С2-36, Р1-16, Р1-8 и др. Высокочастотные резисторы отличаются малыми собственными индуктивностью и емкостью и предназначены для работы в высокочастотных цепях, кабелях и волноводах. Примерами служат резисторы Р1-69. Высоковольтные резисторы рассчитаны на работу при больших (от единиц до десятков киловольт) напряжениях. Примерами высоковольтных резисторов служат Р1-32, Р1-35, С2-33НВ и др. Высокомегаомные резисторы имеют диапазон номинальных сопротивлений от десятков мегаом до единиц тераом. Высокомегаомные резисторы применяются в цепях с рабочим напряжением до 400 В и обычно работают в режиме малых токов. Мощности рассеяния их невелики (до 0,5 Вт). Примером служит резистор Р1-33. В зависимости от способа защиты от внешних факторов резисторы делятся на неизолированные, изолированные, герметизированные и вакуумные. Неизолированные резисторы с покрытием или без него не допускают касания своим корпусом шасси аппаратуры. Пример: Р1-69. Изолированные резисторы имеют изоляционное покрытие (лак, компаунд, пластмасса) и допускают касание корпусом шасси и токоведущих частей радиоэлектронной аппаратуры (РЭА). Примеры: С5-35В, С5-36В, С5-37В, С5-43В, С5-47В и др. Герметизированные резисторы имеют герметичную конструкцию корпуса, которая исключает влияние окружающей среды на его внутреннее пространство. Герметизация осуществляется, с помощью опрессовки специальным компаундом. Вакуумные резисторы имеют резистивный элемент, помещенный в стеклянную вакуумную колбу. По способу монтажа резисторы подразделяются на резисторы для навесного и печатного монтажа, для микромодулей и интегральных микросхем. Проволочные — резисторы, в которых резистивным элементом является высокоомная проволока (изготавливается из высокоомных сплавов: константан, нихром, никелин). Непроволочные — резисторы, в которых резистивным элементом являются пленки или объемные композиции с высоким удельным сопротивлением. Металлофольговые — резисторы, в которых резистивным элементом является фольга определенной конфигурации. Непроволочные резисторы можно разделить на тонкопленочные (толщина слоя в нанометрах), толстопленочные (толщина в долях миллиметра), объемные (толщина в единицах миллиметра). Примеры: С2-23, С2-33, С2-14, Р1-32, Р1-35, Р1-12 и др. Тонкопленочные резисторы подразделяются на металлодиэлектрические, металлоокисные и металлизированные с резистивным элементом в виде микрокомпозиционного слоя из диэлектрика и металла, или тонкой пленки окиси металла, или сплава металла; углеродистые и бороуглеродистые, проводящий элемент которых представляет собой пленку пиролитического углерода или борорганических соединений. В объемных резисторах в качестве связующего компонента используют органические смолы или стеклоэмали. Проводящим компонентом является углерод. В резистивных керметных слоях основным проводящим компонентом являются металлические порошки и их смеси, представляющие собой керамическую основу с равномерно распределенными частицами металла.
Резисторы классифицируются на постоянные резисторы (сопротивление которых не регулируется), переменные регулируемые резисторы (потенциометры, реостаты, подстроечные резисторы) и различные специальные резисторы, например: нелинейные (которые, строго говоря, не являются обычными резисторами из-за нелинейности ВАХ), терморезисторы (с большой зависимостью сопротивления от температуры), фоторезисторы (сопротивление зависит от освещённости), тензорезисторы (сопротивление зависит от деформации резистора), магниторезисторы и пр. По используемому материалу резисторы классифицируются на:
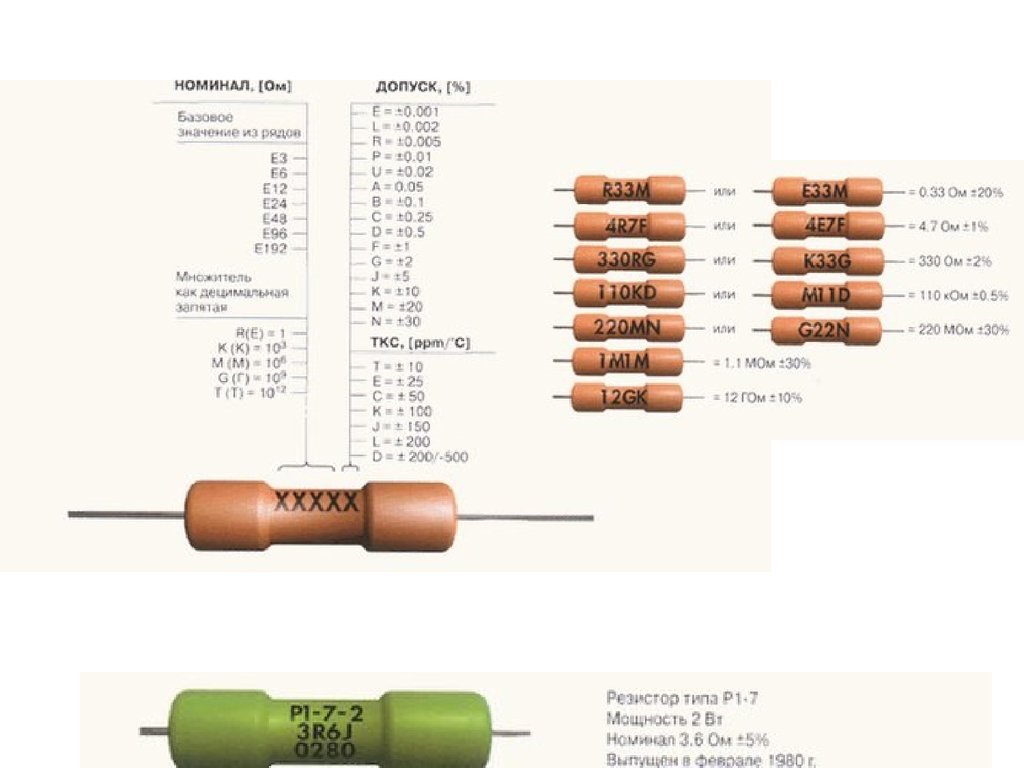
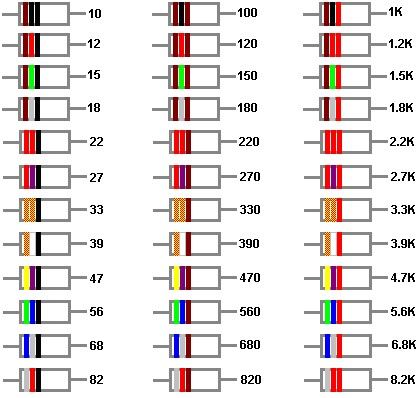
Резисторы, выпускаемые промышленностьюВыпускаемые промышленностью резисторы одного и того же номинала имеют разброс сопротивлений. Значение возможного разброса определяется точностью резистора. Выпускают резисторы с точностью 20 %, 10 %, 5 %, и т. д. вплоть до 0,01 %[1]. Номиналы резисторов не произвольны: их значения выбираются из специальных номинальных рядов, наиболее часто из номинальных рядов E12 или E24 (для резисторов с точностью до 5 %), для более точных резисторов используются более точные ряды (например E48). Резисторы, выпускаемые промышленностью характеризуются также определённым значением максимальной рассеиваемой мощности (выпускаются резисторы мощностью 0,125Вт 0,25Вт 0,5Вт 1Вт 2Вт 4Вт?) (Согласно ГОСТ 24013-80 и ГОСТ 10318-80 советской радиотехнической промышленностью выпускались резисторы следующих номиналов мощностей, в Ваттах, Вт. Маркировка резисторов с проволочными выводамиРезисторы, в особенности малой мощности — чрезвычайно мелкие детали, резистор мощностью 0,125Вт имеет длину несколько миллиметров и диаметр порядка миллиметра. Прочитать на такой детали номинал с десятичной запятой невозможно. Поэтому, при указании номинала вместо десятичной точки пишут букву, соответствующую единицам измерения (К — для килоомов, М — для мегаомов, E или R для единиц Ом). Например 4K7 обозначает резистор, сопротивлением 4,7 кОм, 1R0 — 1 Ом, 120К — 120 кОм и т. д. Однако и в таком виде читать номиналы трудно. Поэтому, для особо мелких резисторов применяют маркировку цветными полосками. По>Для резисторов с точностью 20% используют маркировку с тремя полосками, для резисторов с точностью 10% и 5% маркировку с четырьмя полосками, для более точных резисторов с пятью или шестью полосками. Следует отметить, что иногда встречаются резисторы с 5-ю полосами, но стандартной (5 или 10%) точностью. В этом случае первые две полосы задают первые знаки номинала, третья — множитель, четвёртая — точность, а пятая — температурный коэффициент. ПримерДопустим на резисторе видим 4 полоски коричневую, чёрную, красную, золотую. Первые две полоски дают 1 0, третья 100, четвёртая даёт точность 5 %, итого резистор сопротивлением 10•100 Ом = 1 кОм, с точностью ±5 %. Запомнить цветную кодировку резисторов нетрудно: после чёрной 0 и коричневой 1 идёт последовательность цветов радуги. Так как маркировка была придумана в англоязычных странах, голубой и синий цвета не различаются (вот она, иллюстрация гипотезы Сепира-Уорфа)! Поскольку резистор симметричная деталь, может возникнуть вопрос: «Начиная с какой стороны читать полоски?» Для четырёхполосной маркировки обычных резисторов с точностью 5 и 10 % вопрос решается просто: золотая или серебряная полоска всегда стоит в конце. Для трёхполосочного кода первая полоска стоит ближе к краю резистора, чем последняя. Для других вариантов важно, чтобы получалось значение сопротивления из номинального ряда, если не получается, нужно читать наоборот. По этой теме есть хорошая программа, которая позволяет определить номинал резистора по цветовым полосам. Скачать её можно здесь Маркировка SMD-резисторов«Резисторы» нулевого сопротивления (перемычки на плате) кодируются одной цифрой «0». Кодирование 3 или 4 цифрами
Кодирование буква-цифра-цифра По>Ряды E24 и E12, точность 2 %, 5 % и 10 %. (Ряд E48 не используется). Степень при 10 кодируется буквой (так же, как для 1 %-х сопротивлений, см список выше), мантисса m значения сопротивления и точность кодируется 2 цифрами (см таблицу). Примеры:• 2%, 1,00 Ом = S01 • 5%, 1,00 Ом = S25 • 5%, 510 Ом = A42 • 10%, 1,00 Ом = S49 • 10%, 820 кОм = D60 Даже идеальный резистор при температуре выше абсолютного нуля является источником шума. Это следует из фундаментальной флуктуационно-диссипационной теоремы ( в применении к электрическим цепям это утверждение известно также как теорема Найквиста). Далее >>> | Block title Меню сайта Календарь
Соц закладки Оцените мой сайт | ||||||||||||||||||||||||||||||||||||||||||||
Полное руководство по резисторам
Какие основные характеристики и характеристики влияют на выбор резистора? Факторы, которые следует принимать во внимание, включают исходный допуск и выбор значения. Однако на допуск или изменение значения резистора влияют несколько параметров, как описано ниже.
Однако на допуск или изменение значения резистора влияют несколько параметров, как описано ниже.
Это мера изменения номинального значения в результате изменений температуры. Обычно указывается как единое значение в частях на миллион на градус Цельсия (или по Кельвину), оно может быть положительным или отрицательным. Уравнение для расчета сопротивления при заданной температуре:
Rt=Ro[1+α(T-To)]
Где Ro – номинальное значение сопротивления комнатной температуре, – – температура, при которой указано номинальное сопротивление, T – рабочая температура, а α – TCR.
Проще говоря, сопротивление резистора 1 МОм с TCR 50 ppm/K будет изменяться на 50 Ом на каждый градус повышения или понижения температуры. Это может показаться не таким уж большим, но подумайте, использовали ли вы этот резистор в качестве резистора усиления в схеме неинвертирующего усилителя x10 с 0,3 В на + входе. В худшем случае изменение выходного сигнала может достигать 7,5 мВ, что эквивалентно примерно 5 младшим разрядам в 5-вольтовой 12-разрядной схеме АЦП. Такое изменение может быть весьма заметным в прецизионном проектировании. Помните также, что TCR указывается как ± x ppm / C, поэтому возможно, хотя и маловероятно, что второй резистор в цепи может измениться в противоположном направлении, что удвоит возможную ошибку. Наконец, стоит отметить, что некоторые прецизионные резисторы указывают переменные TCR для диапазона температур, в котором работает схема, и это может значительно усложнить процесс проектирования.
В худшем случае изменение выходного сигнала может достигать 7,5 мВ, что эквивалентно примерно 5 младшим разрядам в 5-вольтовой 12-разрядной схеме АЦП. Такое изменение может быть весьма заметным в прецизионном проектировании. Помните также, что TCR указывается как ± x ppm / C, поэтому возможно, хотя и маловероятно, что второй резистор в цепи может измениться в противоположном направлении, что удвоит возможную ошибку. Наконец, стоит отметить, что некоторые прецизионные резисторы указывают переменные TCR для диапазона температур, в котором работает схема, и это может значительно усложнить процесс проектирования.
Старение и стабильность представляют собой сложную смесь множественных изменений значения сопротивления с течением времени и являются результатом температурных циклов, работы при высоких температурах, проникновения влаги и т. д. Как правило, это значение приводит к увеличению сопротивления с течением времени, поскольку атомы проводимости мигрируют внутри устройства.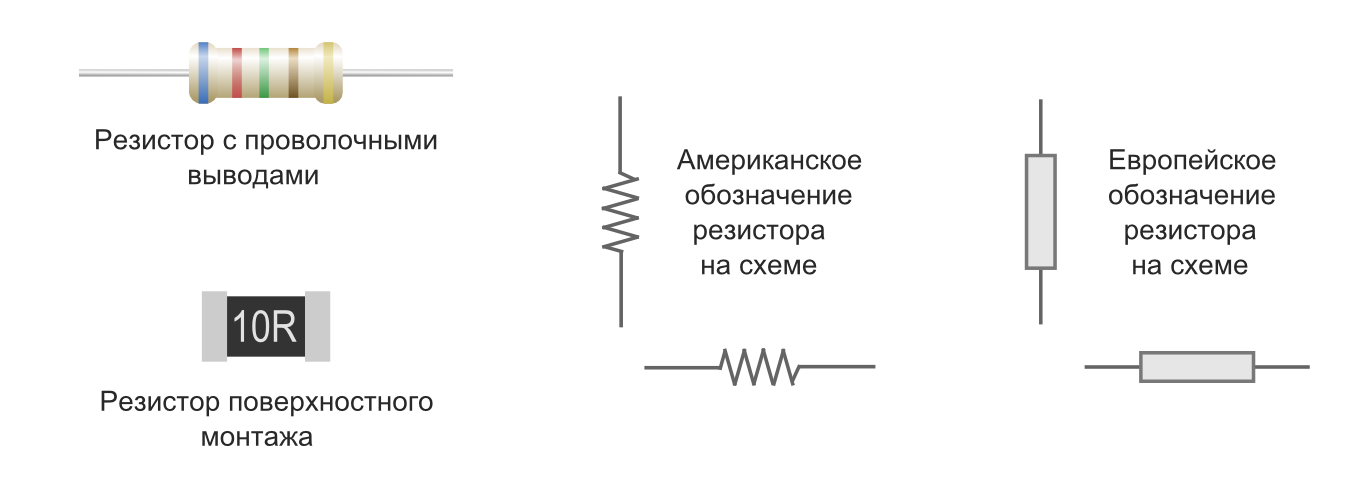
Тепловое сопротивление является мерой того, насколько хорошо резистор может рассеивать энергию в окружающую среду. На практике инженеры используют тепловое сопротивление для моделирования рассеивания тепла в системе — оно рассматривается как набор последовательных «тепловых резисторов», каждый из которых представляет один элемент рассеивания тепла в системе.
Это особенно важно, если конструкция предполагает, что резистор работает на максимальном или близком к нему значении и может существенно повлиять на долговременную надежность системы. Примером того, где этот параметр можно использовать, является расчет размера контактной площадки печатной платы или требования к заземляющему слою, которые будут использоваться для поддержания номинала резистора и рабочей температуры в допустимых пределах.
Номинальная тепловая мощность и мощность Все резисторы имеют максимальную номинальную мощность, указанную в ваттах. Это может быть что угодно, от 1/8 ватта до 10 ватт для мощных резисторов. При первом анализе инженер должен проверить, работает ли резистор в пределах своего номинального значения. Уравнение для расчета: P=I² R , где p — мощность, рассеиваемая на резисторе, i — протекающий ток, а R — сопротивление. К сожалению, все может быть сложнее; для точной работы инженер должен учитывать кривую теплового снижения номинальных характеристик резистора. Это определяет величину, на которую разработчику необходимо уменьшить максимальное рассеивание мощности при превышении заданной температуры.
Это может быть что угодно, от 1/8 ватта до 10 ватт для мощных резисторов. При первом анализе инженер должен проверить, работает ли резистор в пределах своего номинального значения. Уравнение для расчета: P=I² R , где p — мощность, рассеиваемая на резисторе, i — протекающий ток, а R — сопротивление. К сожалению, все может быть сложнее; для точной работы инженер должен учитывать кривую теплового снижения номинальных характеристик резистора. Это определяет величину, на которую разработчику необходимо уменьшить максимальное рассеивание мощности при превышении заданной температуры.
Это может показаться теоретическим, так как снижение номинальных характеристик часто происходит при довольно высоких температурах, но силовая цепь в закрытом корпусе в жарком регионе часто может превышать точку отключения, и максимальную рассеиваемую мощность необходимо будет уменьшить соответствующим образом. Также стоит отметить, что максимальное рабочее напряжение резистора снижается с рассеиваемой мощностью.
Любой электронный компонент с текущими электронами будет источником шума, и резисторы ничем не отличаются в этом отношении. Это необходимо учитывать в системах усилителей с высоким коэффициентом усиления или при работе с сигналами очень низкого напряжения.
Основным источником шума в резисторе является тепловой шум, вызванный случайными колебаниями электронов в резистивном материале. Обычно он моделируется как белый шум (т. е. постоянное среднеквадратичное напряжение в диапазоне частот) и задается уравнением E=√4RkT∆F , где E – среднеквадратичное напряжение шума, R – значение сопротивления, k – постоянная Больцмана, T – температура и 90 005 06 06 Δf системы.
Шум системы можно уменьшить, уменьшив сопротивление, рабочую температуру или полосу пропускания системы. Кроме того, существует еще один тип шума резистора, называемый токовым шумом, который является результатом потока электронов в устройствах. Это редко указывается, но его можно сравнить, если стандартные числа с использованием IEC60195 доступны от производителя.
Это редко указывается, но его можно сравнить, если стандартные числа с использованием IEC60195 доступны от производителя.
Последней проблемой, которую необходимо рассмотреть, являются характеристики конкретного резистора на высоких частотах. Проще говоря, вы можете смоделировать резистор как последовательную катушку индуктивности, питающую резистор, который имеет параллельно с ним паразитный конденсатор.
На таких низких частотах, как 100 МГц (даже для резисторов для поверхностного монтажа, которые имеют более низкие паразитные значения, чем резисторы для сквозного монтажа) параллельная емкость может начать доминировать, и импеданс упадет ниже номинального значения. Еще на более высокой частоте может преобладать индуктивность, а импеданс начнет увеличиваться от своих минимумов и вполне может оказаться выше номинального значения.
Сила | Ultimate Electronics Book
Ultimate Electronics: Практические схемы и анализ
≡ Оглавление
«
2. 6
6
»
2.8
Практические резисторы: производственные допуски, общие значения и цветовые кодыИсточники, нагрузки и поток энергии в цепи. КПД, мгновенная и средняя мощность, законы сохранения. 9min read
Мощность – это скорость потока энергии:
Мощность=ЭнергияВремя
Энергия обсуждалась ранее в разделе Термодинамика, Энергия и Равновесие.
Мощность измеряется в ваттах.
1 Ватт=1 Джоуль-секунда1 Вт=1 Джс
В модели с сосредоточенными элементами мощность может поступать либо в элемент, либо из элемента. Знак мощности указывает направление потока энергии.
Полезная мощность на схеме закрытой системы равна нулю. Это первый закон термодинамики в действии. Энергия сохраняется: она не создается и не уничтожается. (см. ниже некоторые потенциальные получил при применении этого правила к схеме!)
В общем, мы можем выбирать знаки произвольно, но мы определим, что источник имеет отрицательную мощность (т.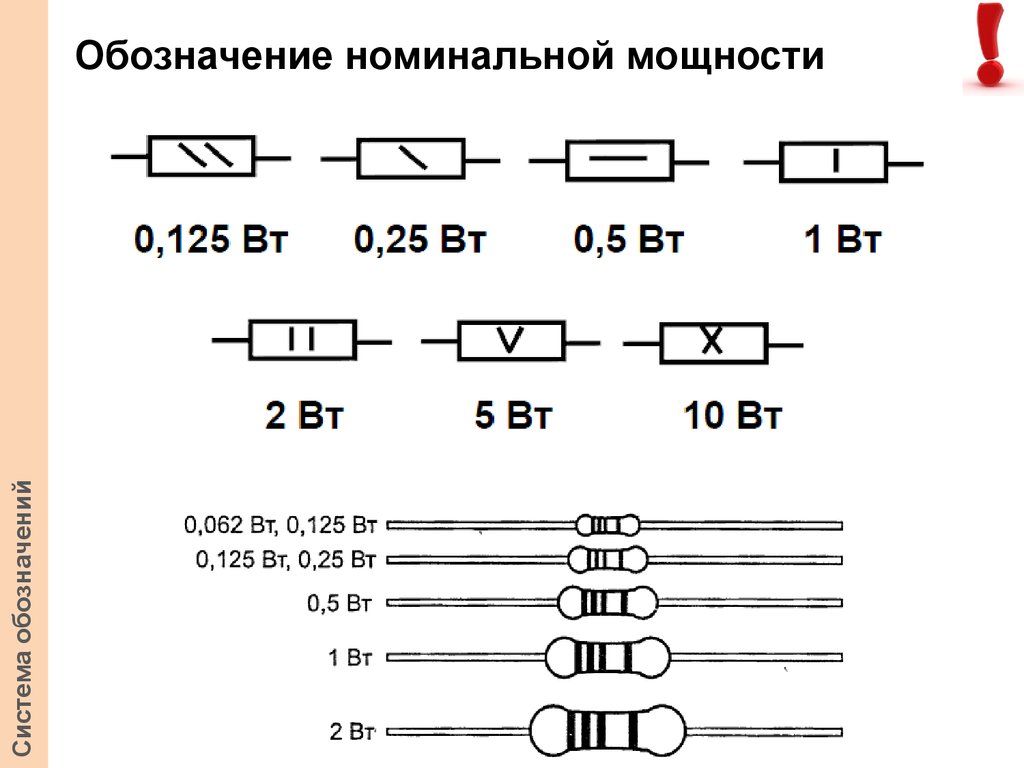 е. он питает схему), а Нагрузка имеет положительную мощность (т.е. она потребляет мощность от схемы). Мы определим его таким образом, тщательно определяя направления напряжения и тока.
е. он питает схему), а Нагрузка имеет положительную мощность (т.е. она потребляет мощность от схемы). Мы определим его таким образом, тщательно определяя направления напряжения и тока.
Правильная маркировка направления тока и напряжения на каждой клемме имеет решающее значение для решения схем. Мы поговорим об этом подробнее в следующем разделе «Маркировка напряжений, токов и узлов» после того, как изучим законы Кирхгофа.
Для элемента схемы только с двумя клеммами мы можем записать мощность P как:
P=vi
где v — разница напряжений между двумя клеммами, а i является текущим. (Одно и то же значение тока должно подаваться на одну из клемм и выходить из другой.)
Рассмотрим эти три элемента с двумя клеммами. Мы пометили положительный и отрицательный конец для каждой разности напряжений. По соглашению мы должны определить ток как переход в плюсовая клемма . (Иначе пришлось бы писать P=−vi .)
Линейные элементы с маркировкой тока и напряжения на клеммах
Circuitlab. com/cv5q6274rxjyv
com/cv5q6274rxjyv
Править — Simulate
Как указано, мощность, потребляемая каждым элементом, будет:
PV7=v7i7PI8=v8i8PR9=v9i9
Если этот элемент потребляет мощность, значение будет положительным .
Если элемент равен подает питание , значение будет отрицательным .
(На схеме, показанной выше, источник напряжения чаще всего сбивает с толку, потому что в большинстве случаев направление тока будет из положительным выводом источника напряжения. Однако это просто означает, что значение i7 будет отрицательным, как и мощность PV7 , поскольку он подает питание на остальную часть схемы. Это позволяет нам применять согласованное соглашение по маркировке для всех элементов с двумя клеммами, чтобы всегда определять мощность с точки зрения тока, протекающего на положительную клемму. Более подробную информацию см. в разделе Маркировка напряжений, токов и узлов.)
Если резистор потребляет мощность, эта мощность превращается в тепло. Это тепло может накапливаться внутри резистора (вызывая повышение его температуры) или рассеиваться в окружающую среду за счет теплопроводности, конвекции или излучения. (Дополнительную информацию см. в разделе «Практические резисторы: номинальная мощность (мощность)».)
Это тепло может накапливаться внутри резистора (вызывая повышение его температуры) или рассеиваться в окружающую среду за счет теплопроводности, конвекции или излучения. (Дополнительную информацию см. в разделе «Практические резисторы: номинальная мощность (мощность)».)
Если источник напряжения обеспечивает питание , эта мощность поступает откуда-то еще, например, из-за электрохимической реакции в батарее.
Конденсатор во время зарядки будет потреблять энергии из схемы. Эта энергия будет храниться в электрическом поле внутри диэлектрического материала конденсатора. Когда конденсатор разряжается, он будет , снабжая питанием другие элементы схемы.
В смысле двойной бухгалтерии, цепная сеть представляет только одну сторону транзакции энергии каждого компонента. Существует равная и противоположная сторона этого потока энергии, но какая она, зависит от конкретного элемента и не обязательно представлена на схеме.
В более общем случае для компонента с несколькими клеммами с двумя или более клеммами:
P=∑tvtit
На каждой клемме мы умножаем напряжение на клемме (относительно земли) на ток в этой клемме.
Выбор земли не имеет значения, потому что мы можем произвольно добавить любое число ко всем vt значения без изменения P . — это один из способов выразить Текущий Закон Кирхгофа. Все токи, втекающие в любое устройство, должны в сумме равняться нулю, потому что внутри устройства не может накапливаться суммарный заряд.
Вы можете использовать это правило суммирования для устройств с тремя выводами, таких как транзисторы, или устройств с любым количеством выводов. Однако имейте в виду, что некоторые компоненты, такие как операционные усилители и цифровые логические элементы, часто представлены на схеме с некоторыми скрытыми выводами.
В случае с двумя терминалами это правило для нескольких терминалов становится таким же, как приведенное выше упрощенное правило. Это потому, что v=v1−v2 (по определению разности напряжений на двух клеммах) и i=i1=-i2 (поскольку ток, втекающий в одну клемму, должен вытекать из другой), поэтому:
P=v1i1+v2i2P=v1i+v2(-i)P=(v1-v2)iP=vi
Для линейного резистора, подчиняющегося закону Ома:
P=vi=i2R=v2R
При решении задач , все три формы рассеивания мощности полезны.
Резистор превращает электрическую энергию в тепло посредством неупругих столкновений в резистивном материале.
Если ток известен, используйте P=i2R форма.
Если напряжение известно, используйте P=v2R форма.
Эффективность ранее обсуждалась в разделе «Термодинамика, энергия и равновесие».
Мы должны определить нашу эффективность в каждом конкретном приложении, но это всегда соотношение мощностей или соотношение энергий.
Для быстрого примера, хотя мы еще не говорили о светодиодах, давайте рассмотрим эффективность управления светодиодом от источника напряжения с последовательным резистором.
Представьте, что это фонарик с батарейным питанием, и нас интересует, сколько энергии уходит на светодиод по сравнению с тем, сколько тепла теряется в резисторе. В этом случае мы могли бы определить нашу эффективность как:
η=Мощность, потребляемая светодиодомМощность, поставляемая источником=PD1-PV1
Вот схема:
Энергоэффективность светодиода и резистора
Circuitlab. com/c43pbwr9e43c2
com/c43pbwr9e43c2
Править — Имитация
Упражнение Щелкните цепь, затем щелкните «Имитировать» и «Запустить развертку постоянным током». Вы увидите график выражения «P(D1)/-P(V1)», который представляет собой эффективность η мы определили выше, выраженные в нотации выражений CircuitLab.
Обратите внимание, что при различных входных напряжениях КПД меняется. И в целом КПД при питании от источника напряжения 5 В составляет всего около 43%. Мы теряем много энергии батареи только на то, чтобы нагреть резистор!
Это только электрическая эффективность ; есть еще квантовая эффективность светодиода, которую мы, возможно, пожелаем принять во внимание, потому что не вся мощность, подаваемая на светодиод, превращается в свет. Некоторая часть превращается в тепло внутри светодиода.
Если вы хотите поэкспериментировать с этой схемой, мы рекомендуем вам это сделать.
- Что произойдет, если изменить сопротивление?
- Сколько света будет излучаться, при условии, что количество света пропорционально току через светодиод?
- Что делать, если светодиод перегреется, если он должен рассеивать более 50 мВт?
Энергия измеряется в джоулях:
E=Pt
Мы платим электрической компании за поставленную энергию. Джоули можно преобразовать в киловатт-часы с помощью простого преобразования единиц измерения:
Джоули можно преобразовать в киловатт-часы с помощью простого преобразования единиц измерения:
1 кВтч=3,6 × 106 Дж
Батареи хранят энергию, хотя часто мы говорим о них в терминах ампер-часов (ток-время, а не мощность-время).
В действительности энергия является интегралом возможно изменяющейся во времени мощности:
E=∫t2t1P(t)dt
Во многих практических системах мощность не будет постоянной, а будет существенно меняться во времени. Этот интеграл заботится об этом, рассматривая полную энергию, а не мгновенную мощность.
Обратитесь к учебнику по схемам и моделированию, чтобы узнать, как вычислять интегралы в окне построения графиков имитационного моделирования во временной области CircuitLab.
Поскольку электроэнергия преобразуется в другие формы энергии и обратно, часто действуют другие постоянные времени.
Например, когда мы превращаем электрическую энергию в свет в светодиоде, мы можем включать и выключать свет очень быстро — быстрее, чем может различить человеческий глаз. Или, когда мы управляем двигателем с помощью ШИМ, мы можем очень быстро подавать и отключать питание двигателя, но механическая инерция того, что приводится в движение, скрывает этот факт.
Или, когда мы управляем двигателем с помощью ШИМ, мы можем очень быстро подавать и отключать питание двигателя, но механическая инерция того, что приводится в движение, скрывает этот факт.
Когда мы проектируем электрические или другие системы, очень важно заботиться о и мгновенная мощность и средняя мощность. Как обсуждалось в разделе «Установившееся состояние и переходный процесс», физические нагрузки на различные компоненты нашей системы могут быть значительно выше по сравнению с мгновенным или переходным поведением, и мы должны спроектировать все, чтобы приспособиться к этим силам.
Представьте себе, что у нас есть космический корабль, который сбрасывает термоядерную бомбу из задней части и взрывает ее, толкая корабль вперед каждые 60 секунд. В этом случае мы должны спроектировать космический корабль так, чтобы он мог выдержать мгновенную взрывную силу взрыва, и , общий суммарный импульс этих взрывов должен обеспечивать достаточную силу, чтобы космический корабль двигался так быстро, как это необходимо для нашей желаемой траектории! (Как бы дико это ни звучало, в 1950-х и 60-х годах серьезно изучали: 1 2 3. )
)
Как инженер, вы должны понимать, когда важна мгновенная или средняя точка зрения, и проектировать соответственно.
В соответствии с законом Кирхгофа о напряжении и током Кирхгофа, которые мы вскоре обсудим, мощность и энергия на схеме сохраняются.
Энергия может вытекать из чего-то вроде батареи, что означает, что (за пределами схемы) эта энергия исходит из химической потенциальной энергии.
Энергия может течь в что-то вроде резистора, что означает, что (вне схемы) эта энергия стала теплом.
Или может течь двунаправленно , например, сначала в конденсатор, а потом обратно.
Точно так же, как нетто-заряд не может храниться «на схеме», не может храниться и чистая энергия. Модель с сосредоточенными элементами предполагает, что это происходит мгновенно: если один элемент поставляет энергию, другие должны потреблять такое же количество энергии одновременно.
Иногда, однако, схемы рисуются для удобства таким образом, чтобы скрыть источник энергии.



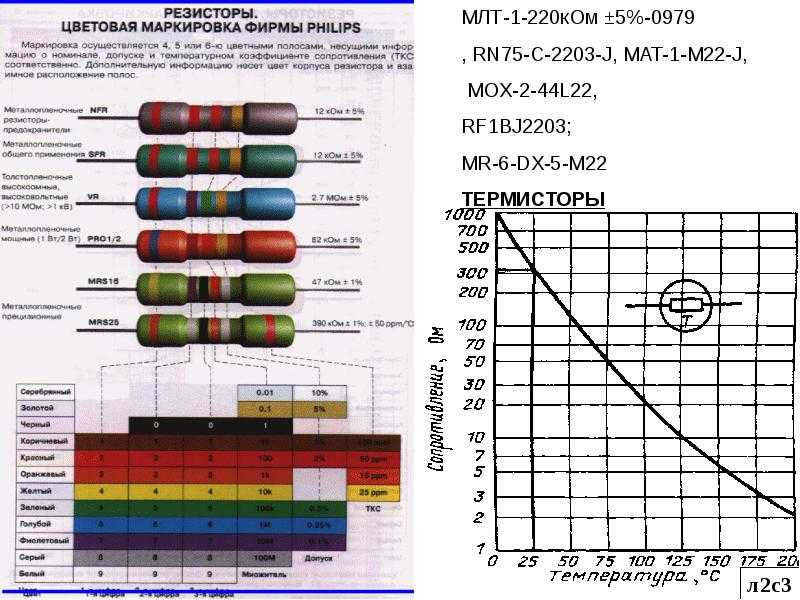

 Во-первых, реактивность может проявляться только на переменном токе, и при этом значение реактивного сопротивления напрямую зависит от частоты переменного тока. А во-вторых, сам термин «реактивное сопротивление» весьма условен и означает лишь, что в данной электрической цепи при данной частоте конденсатор или катушка индуктивности ведут себя не только как емкость или индуктивность, но и обладают некоторым последовательно включенным сопротивлением. Значение этого сопротивления эквивалентно значению такого же активного сопротивления, с той весьма существенной разницей, что на этом реактивном сопротивлении нет потери электрической энергии в виде тепла.
Во-первых, реактивность может проявляться только на переменном токе, и при этом значение реактивного сопротивления напрямую зависит от частоты переменного тока. А во-вторых, сам термин «реактивное сопротивление» весьма условен и означает лишь, что в данной электрической цепи при данной частоте конденсатор или катушка индуктивности ведут себя не только как емкость или индуктивность, но и обладают некоторым последовательно включенным сопротивлением. Значение этого сопротивления эквивалентно значению такого же активного сопротивления, с той весьма существенной разницей, что на этом реактивном сопротивлении нет потери электрической энергии в виде тепла.
 п.) при помощи переменных резисторов — потенциометров’, регулирование и подбор оптимальных (заданных) режимов питания и уровней полезных сигналов внутри схемы радиоаппарата в процессе его регулировки и настройки при помощи «установочных» переменных резисторов особой конструкции.
п.) при помощи переменных резисторов — потенциометров’, регулирование и подбор оптимальных (заданных) режимов питания и уровней полезных сигналов внутри схемы радиоаппарата в процессе его регулировки и настройки при помощи «установочных» переменных резисторов особой конструкции. Справа мы видим маленький крохотный SMD резистор, который рассеивает очень маленькую мощность, но при этом отлично выполняет свою функцию.
Справа мы видим маленький крохотный SMD резистор, который рассеивает очень маленькую мощность, но при этом отлично выполняет свою функцию.  У них есть специальные пазы, для регулировки сопротивления.
У них есть специальные пазы, для регулировки сопротивления.

 д. Диапазон номинальных сопротивлений этих резисторов 1 Ом…10 МОм, номинальные мощности рассеяния — 0,125… 100 Вт. Допускаемые отклонения сопротивления от номинального значения ±1; ±2; ±5; ±10; ±20 %. Примерами резисторов общего назначения служат С2-33, Р1-12 и др..
д. Диапазон номинальных сопротивлений этих резисторов 1 Ом…10 МОм, номинальные мощности рассеяния — 0,125… 100 Вт. Допускаемые отклонения сопротивления от номинального значения ±1; ±2; ±5; ±10; ±20 %. Примерами резисторов общего назначения служат С2-33, Р1-12 и др..
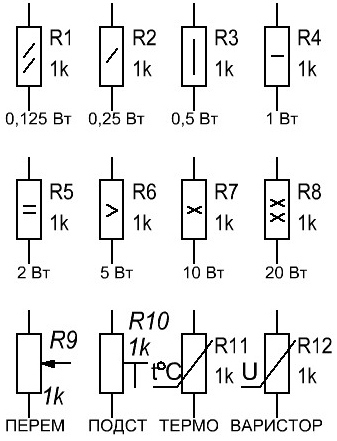 К толстопленочным относят лакосажевые, керметные и резисторы на основе проводящих пластмасс. Проводящие резистивные слои толстопленочных и объемных резисторов представляют собой гетерогенную систему (композицию) из нескольких фаз, получаемую механическим смешением проводящего компонента, например графита или сажи, металла или окисла металла, с органическими или неорганическими наполнителями, пластификаторами или отвердителем. После термообработки образуется монолитный слой с необходимым комплексом параметров. Примеры: С2-33, Р1-72, С2-10, С2-36, Р1-8 и др.
К толстопленочным относят лакосажевые, керметные и резисторы на основе проводящих пластмасс. Проводящие резистивные слои толстопленочных и объемных резисторов представляют собой гетерогенную систему (композицию) из нескольких фаз, получаемую механическим смешением проводящего компонента, например графита или сажи, металла или окисла металла, с органическими или неорганическими наполнителями, пластификаторами или отвердителем. После термообработки образуется монолитный слой с необходимым комплексом параметров. Примеры: С2-33, Р1-72, С2-10, С2-36, Р1-8 и др.
 Эти резисторы могут иметь большую нелинейность вольт-амперной характеристики. В основном используются в составе интегральных микросхем, где применить другие типы резисторов труднее.
Эти резисторы могут иметь большую нелинейность вольт-амперной характеристики. В основном используются в составе интегральных микросхем, где применить другие типы резисторов труднее. 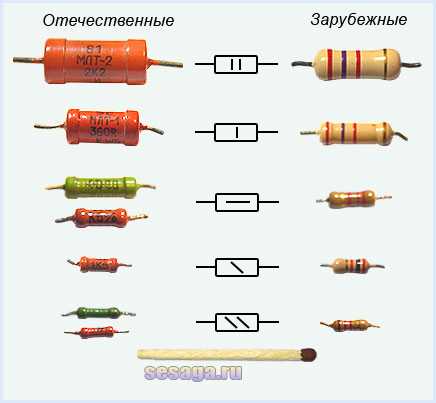 : 0.01, 0.025, 0.05, 0.062, 0.125, 0.5, 1, 2, 3, 4, 5, 8, 10, 16, 25, 40, 63, 100, 160, 250, 500)[А.А.Бокуняев, Н.М, Борисов, Р.Г. Варламов и др. Справочная книга радиолюбителя-конструктора.-М.Радио и связь 1990-624с.: ISBN 5-256-00658-4]
: 0.01, 0.025, 0.05, 0.062, 0.125, 0.5, 1, 2, 3, 4, 5, 8, 10, 16, 25, 40, 63, 100, 160, 250, 500)[А.А.Бокуняев, Н.М, Борисов, Р.Г. Варламов и др. Справочная книга радиолюбителя-конструктора.-М.Радио и связь 1990-624с.: ISBN 5-256-00658-4] Первые две полоски всегда означают первые два знака номинала. Если полосок 3 или 4, третья полоска означает десятичный множитель, то есть степень десятки, которая умножается на двузначное число, указанное первыми двумя полосками. Если полосок 4, последняя указывает точность резистора. Если полосок 5, третья означает третий знак сопротивления, четвёртая — десятичный множитель, пятая — точность. Шестая полоска, если она есть, указывает температурный коэффициент сопротивления (ТКС). Если эта полоска в 1,5 раза шире остальных, то она указывает надёжность резистора (% отказов на 1000 часов работы)[1]
Первые две полоски всегда означают первые два знака номинала. Если полосок 3 или 4, третья полоска означает десятичный множитель, то есть степень десятки, которая умножается на двузначное число, указанное первыми двумя полосками. Если полосок 4, последняя указывает точность резистора. Если полосок 5, третья означает третий знак сопротивления, четвёртая — десятичный множитель, пятая — точность. Шестая полоска, если она есть, указывает температурный коэффициент сопротивления (ТКС). Если эта полоска в 1,5 раза шире остальных, то она указывает надёжность резистора (% отказов на 1000 часов работы)[1]
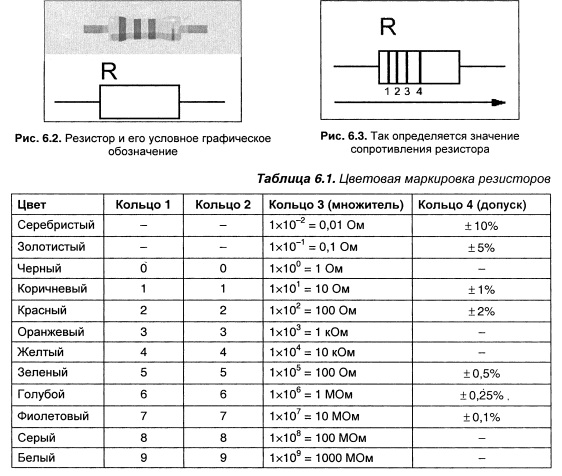 Большее количество знаков обозначает:
Большее количество знаков обозначает: При частоте, существенно меньшей чем (где — постоянная Больцмана, — абсолютная температура резистора в градусах Кельвина, — постоянная Планка) спектр теплового шума равномерный («белый шум»), спектральная плотность шума (преобразование Фурье от коррелятора напряжений шума) , где . Видно, что чем больше сопротивление, тем больше эффективное напряжение шума, также, эффективное напряжение шума пропорционально корню из температуры.
При частоте, существенно меньшей чем (где — постоянная Больцмана, — абсолютная температура резистора в градусах Кельвина, — постоянная Планка) спектр теплового шума равномерный («белый шум»), спектральная плотность шума (преобразование Фурье от коррелятора напряжений шума) , где . Видно, что чем больше сопротивление, тем больше эффективное напряжение шума, также, эффективное напряжение шума пропорционально корню из температуры.